Game⚓︎

在前面讨论的搜索问题中，我们并没有考虑到那些可能阻挡我们到达目标的敌方 (adversaries)（这类搜索问题称为对抗性搜索问题 (adverserial search problem) 或博弈 (game)）。在这种更复杂的情况下，之前介绍过的搜索算法就无效了，因为这些算法都是提前规划好路径的，并没有考虑到敌方会如何回应并阻挡我们的行动，因此需要引入新的算法来解决。在此之前，我们先简要介绍一下博弈的概念。

博弈中的行动可以带来确定性 (deterministic) 或随机性 (stochastic) 的结果，可以有单个或多个玩家，也可以零和 (zero-sum)（博弈双方势均力敌）或不零和。下面我们主要介绍的是确定性零和博弈 (determinisic zero-sum game)——有确定的行动；并且我们的收获 = 对方的损失（反之亦然），这个可以用一个单变量值来描述：比如我们希望让这个变量值尽可能大，而对手希望让这个值尽可能小，由此带来了直接的竞争。

不同于一般搜索算法返回完整的规划，对抗性搜索算法返回的是一个策略 (strategy/policy)，即一个根据代理体和敌方的布局而推荐的最佳可能移动方案。

下面给出一个对于标准博弈的定义：

• 初始状态 \(s_0\)
• 玩家 \(\text{Players}(s)\)
• 行动 \(\text{Actions}(s)\)
• 转变模型 (transition model)\(\text{Result}(s, a)\)
• 终止条件测试 (terminal test)\(\text{Terminal-test}(s)\)
• 终值 (terminal values)\(\text{Utility}(s, player)\)

Minimax⚓︎

第一个要介绍的零和博弈算法是极小化极大 (minimax) 算法：

• 它的实现基于一个前提：对手希望表现最优化，并且总是执行对于我们而言最不利的移动
• 状态值 (state value)/ 效用 (utility)：代理体控制某个状态时能够得到的最优分数
• 终止效用 (terminal utility)：终止状态值，该值总是确定的，并能反映博弈的固有性质
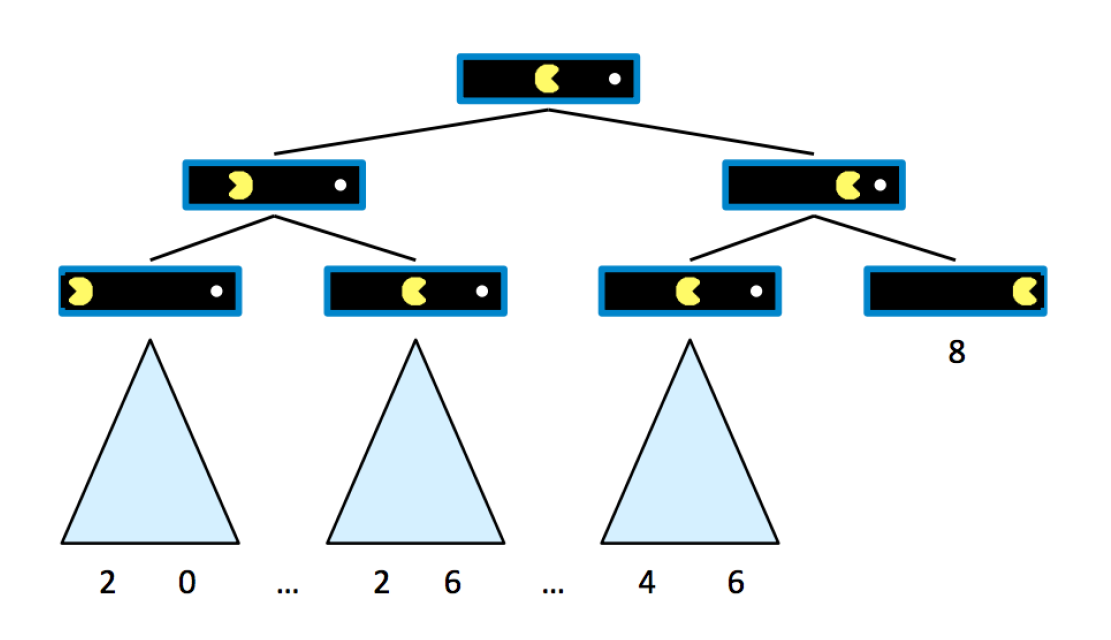
• 博弈树 (game tree)：用于分析博弈问题中各种状态的树状结构，可类比一般搜索问题中的搜索树

例子

这里给一个很简单的吃豆人游戏的例子：

假设吃豆人初始分数为 10，且每走 1 步就要扣 1 分，直到吃到豆子为止（此时游戏就进入了终止状态并结束）。下面给出对应的博弈树：

Alpha-Beta Pruning⚓︎

Evaluation Functions⚓︎

Expectimax⚓︎

Mixed Layer Types⚓︎

Monte Carlo Tree Search⚓︎

评论区