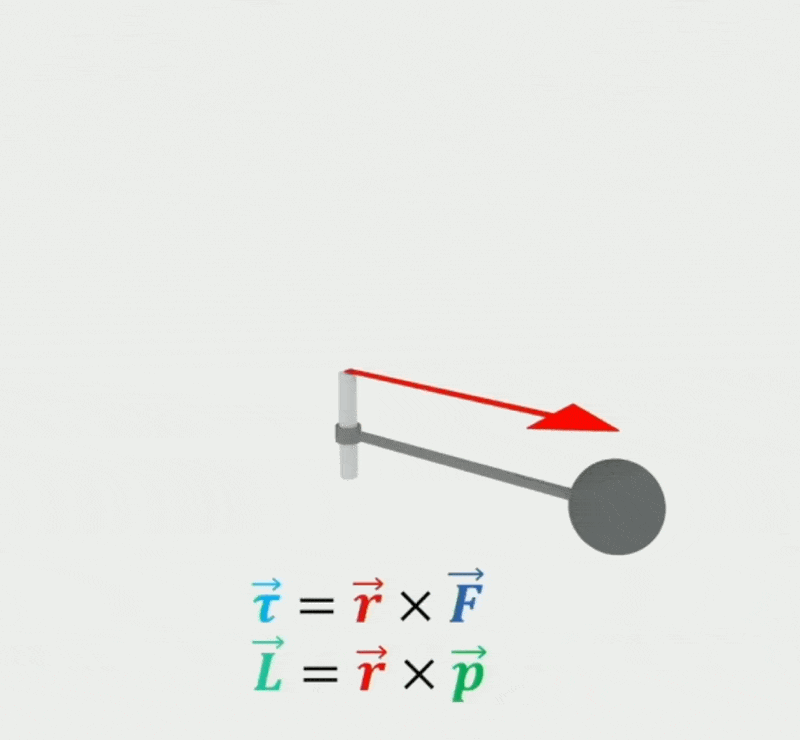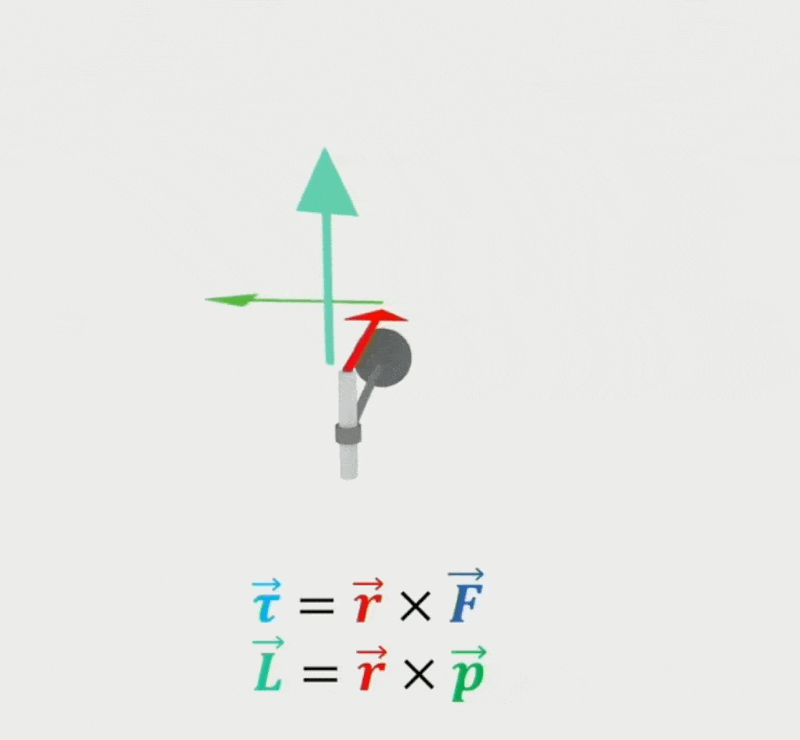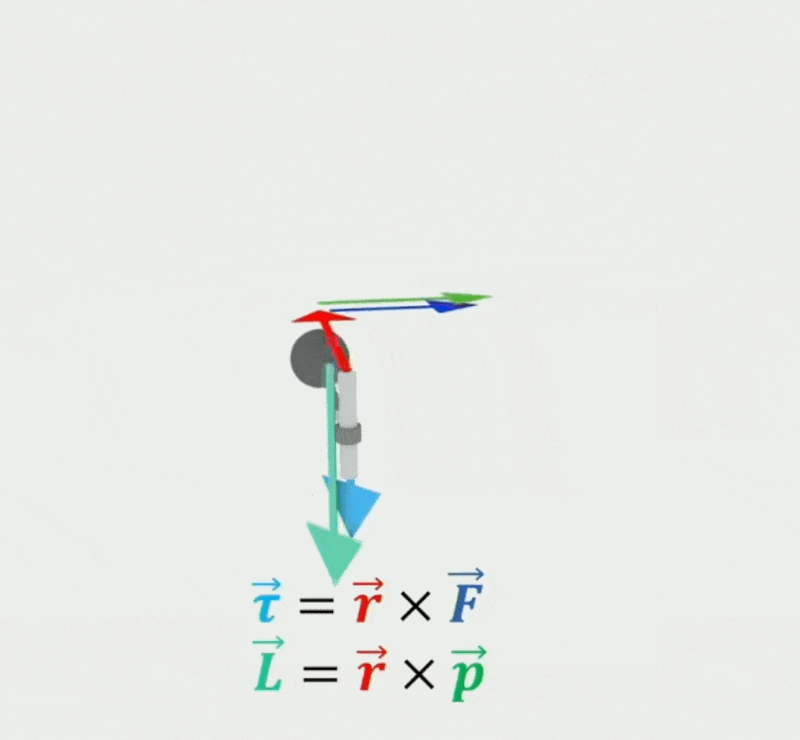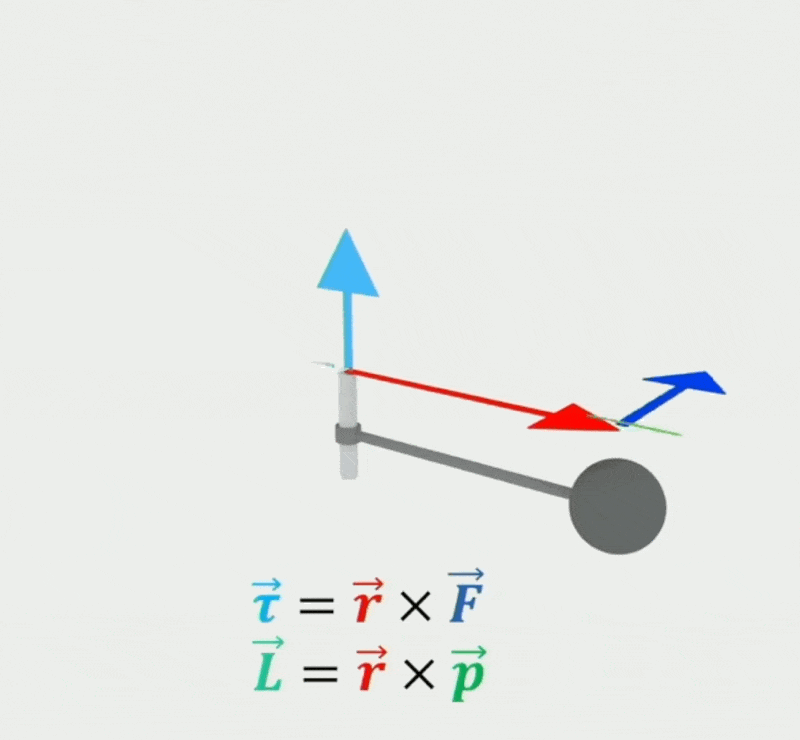Physical System Basics⚓︎
约 4730 个字 预计阅读时间 24 分钟
注意
这里介绍的物理系统和先前在渲染部分中介绍的 PBR 中的「物理」是两个概念。后者特指物理中的光学特征。
Physics Actors and Shapes⚓︎
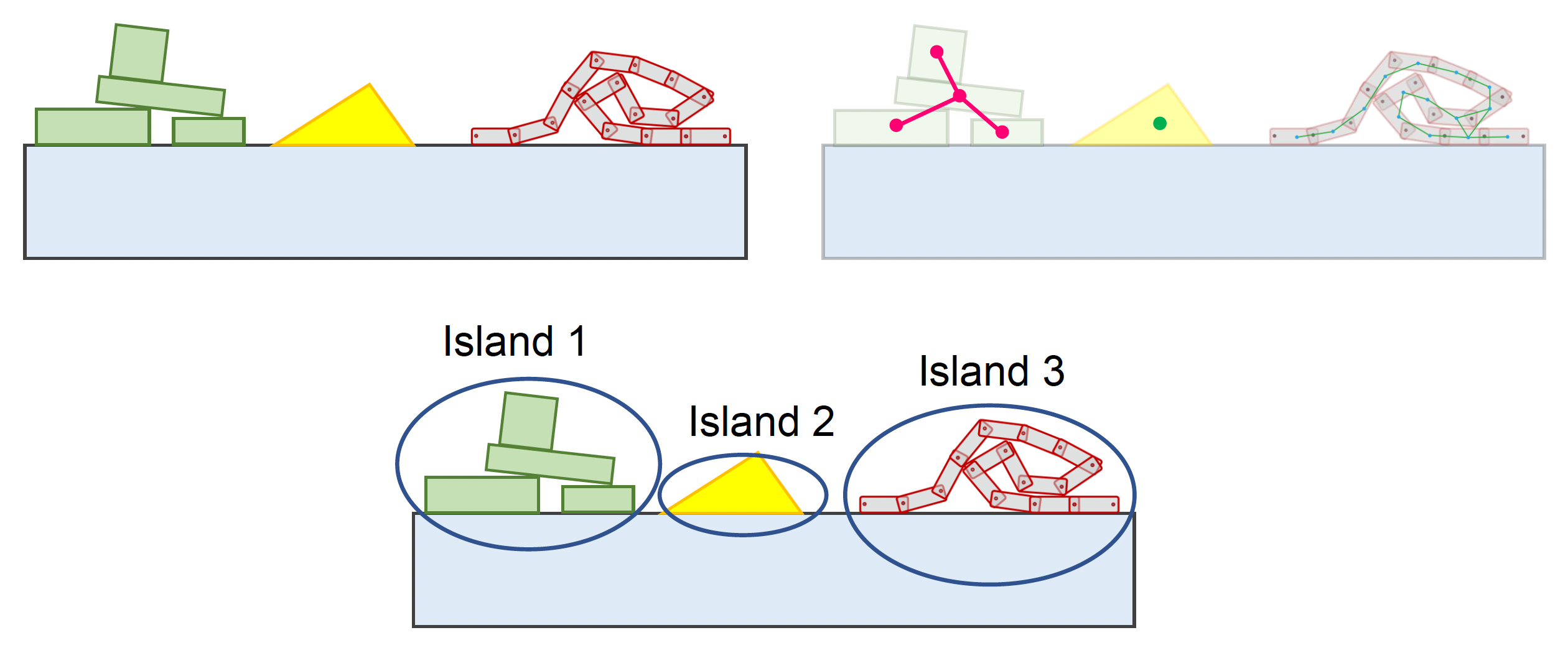
如下图所示,左图是渲染后的虚拟世界;而右图是物理世界,游戏的逻辑和模拟往往在这之上运行的。
Actors⚓︎
物理世界中的对象通常称为参与者(actor)。参与者可分为:
-
静态(static) 参与者:静止不动的物体,比如挡板等,在游戏中的占比是最大的
-
动态(dynamic) 参与者:符合物理原理的物体,比如下图的箱子会因重力和摩擦力的作用在斜面上运动
-
触发器(trigger):
- 像静态参与者那样不会移动,但不会阻塞
- 和游戏逻辑高度相关,会触发消息(或事件
) ,用于通知参与者进入 / 退出
-
运动学(kinematic) 参与者:根据游戏玩法逻辑直接控制物体运动,可以无视物理定律
-
但违背物理定律会给游戏引来很多麻烦
-
Shapes⚓︎
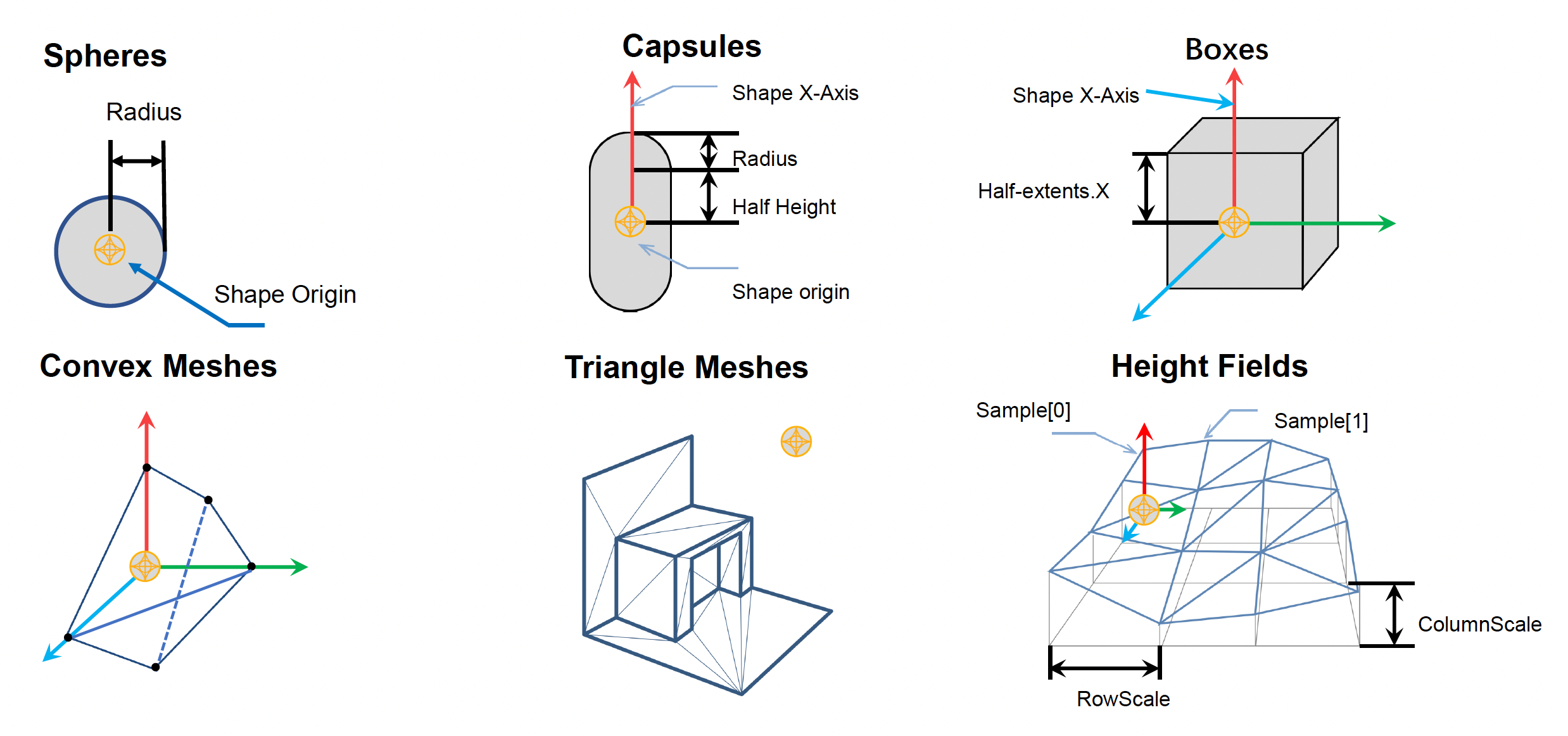
参与者的形状各异,需要根据实际情况选择合适的形状,否则会影响到游戏性能,甚至产生各种奇怪的 bug。常见的形状有:
-
球形(spheres)
- 像球类运动天然适合用球形表示
-
胶囊状(capsules)
- 很多游戏用胶囊表示一个角色,角色恰好能被一个胶囊包裹起来
- 但这种包裹往往是近似的
-
盒形(boxes)(正方体 / 长方体)
- 适合精度要求不高的情形
-
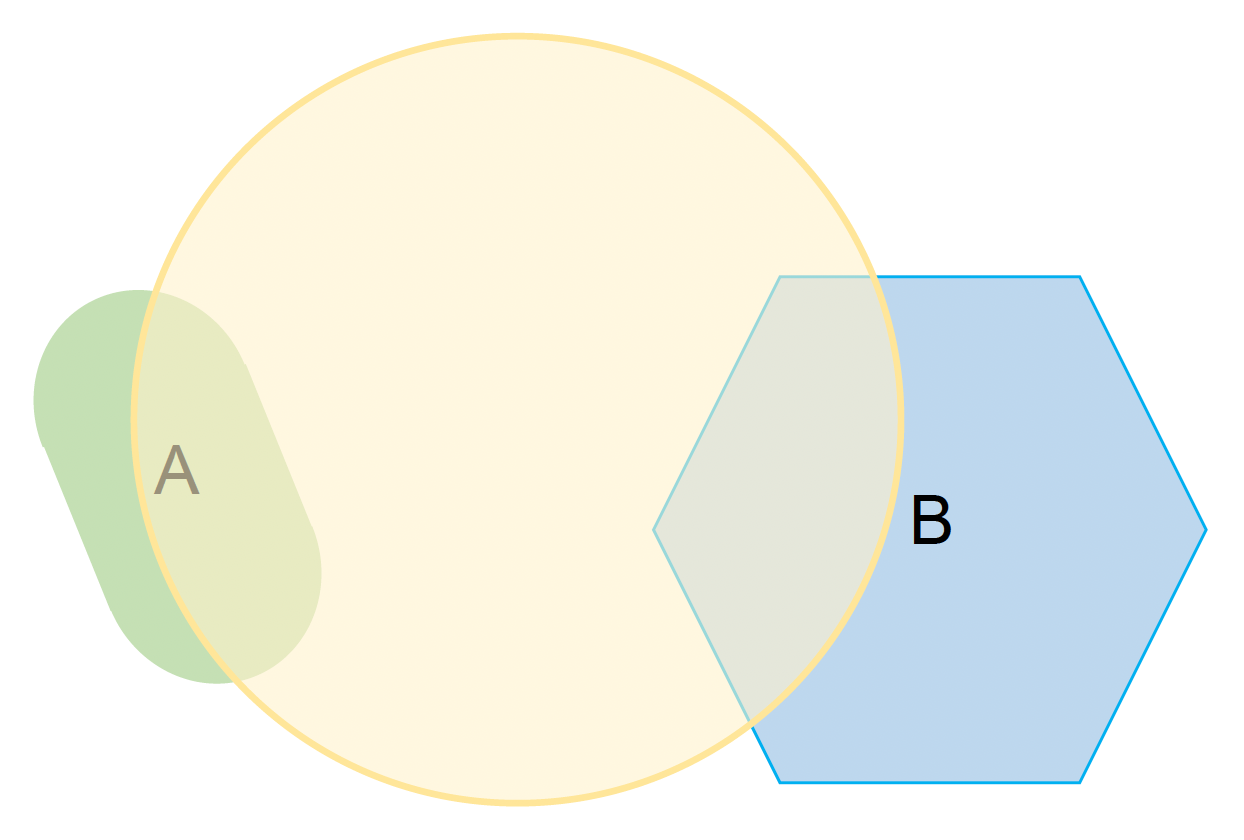
凸网格(convex meshes):
- 封闭,不能有洞
- 凸包:任意一个面做无限延伸都不会其他任何面相交
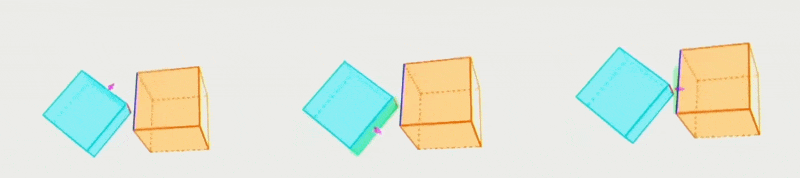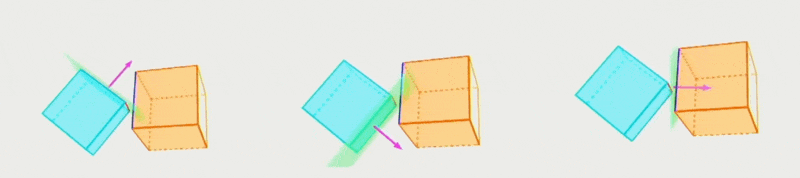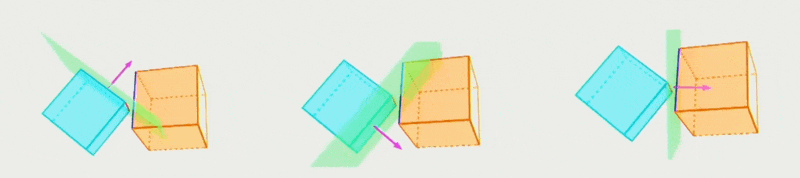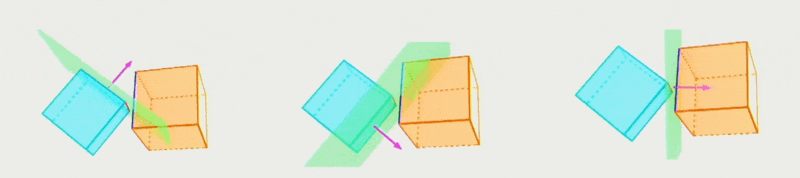
- 能表达更多样更复杂的形状(比如图中的可破坏队形)
-
三角形网格(triangle meshes)
- 要求物体是密闭的,且是静态的(因为动态物体势必涉及碰撞和求交运算,事情会变得很复杂)
-
高度场(height fields)
- 更适合表达地形(用盒形或凸包表示的成本很大)
使用物理形状包裹物体的原则
- 近似:不需要包裹得很精细
- 简单:偏好简单形状(如有可能请避免使用三角形网格
) 、最少的形状
形状有很多属性,包括(实际上有些引擎还会给出更多属性
-
质量(mass) 和密度(density):
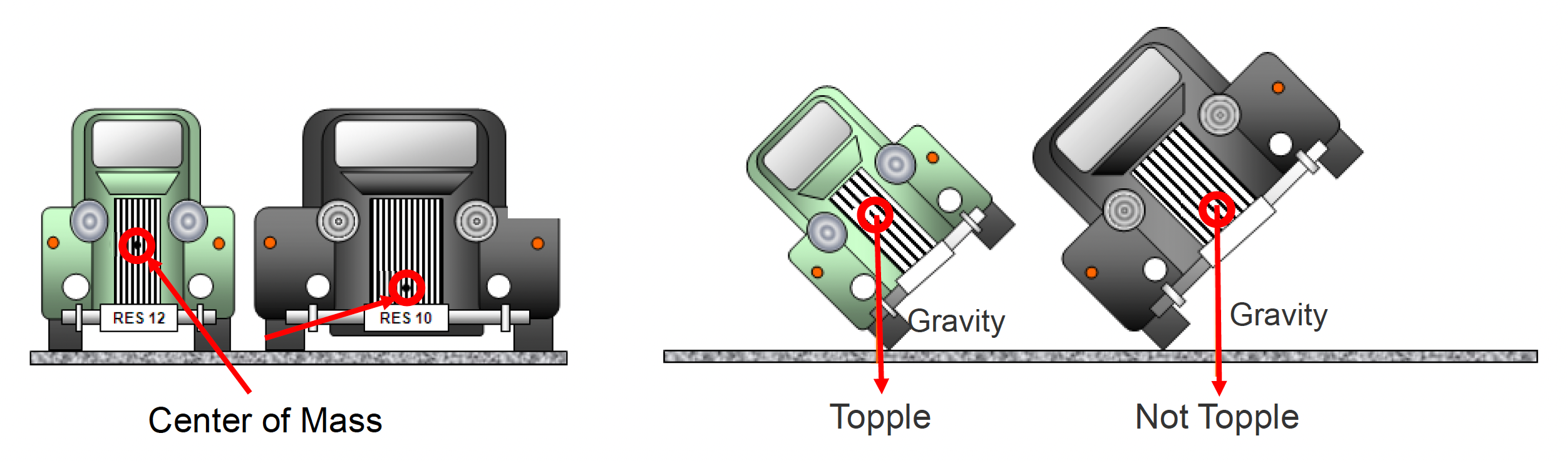
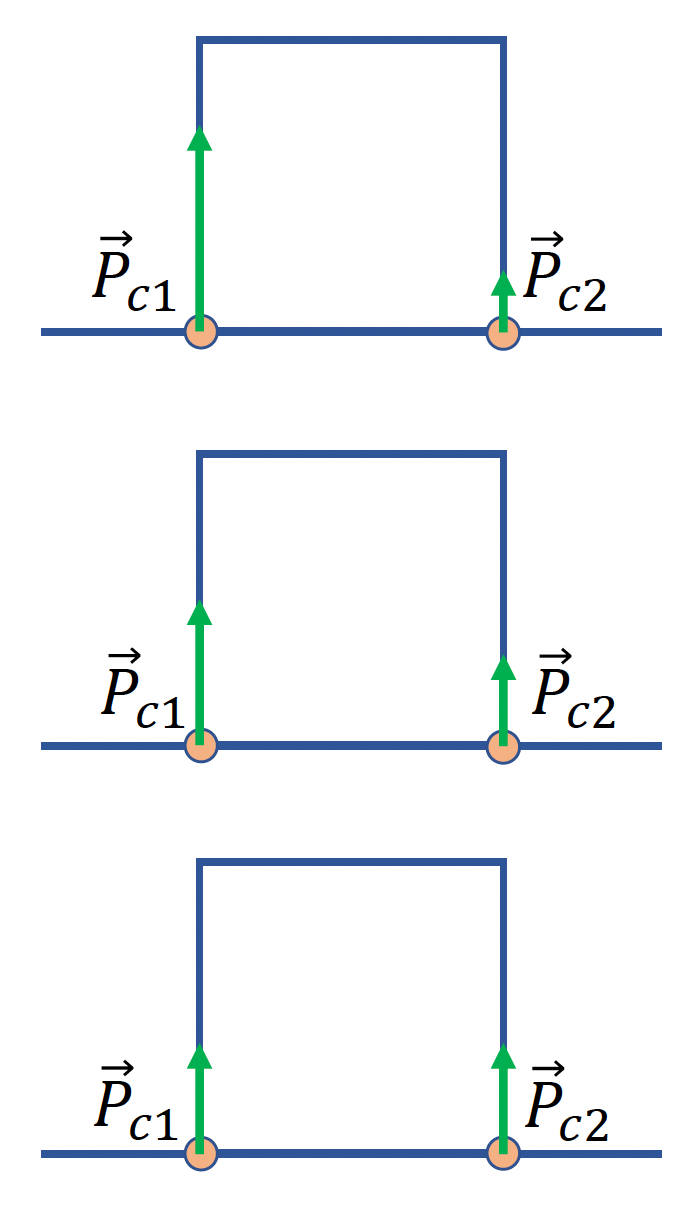
- 在物理系统中通常假设每个参与者是质量均匀的,这样的物体会有好几个平衡点;而质量不均匀的物体只有一个平衡点(比如不倒翁)
-
质心(center of mass):
- 决定了物体的稳定性
-
摩擦力(friction) 和弹性(restitution):
- 这两个属性由物理材质(physical materials) 定义
Forces⚓︎
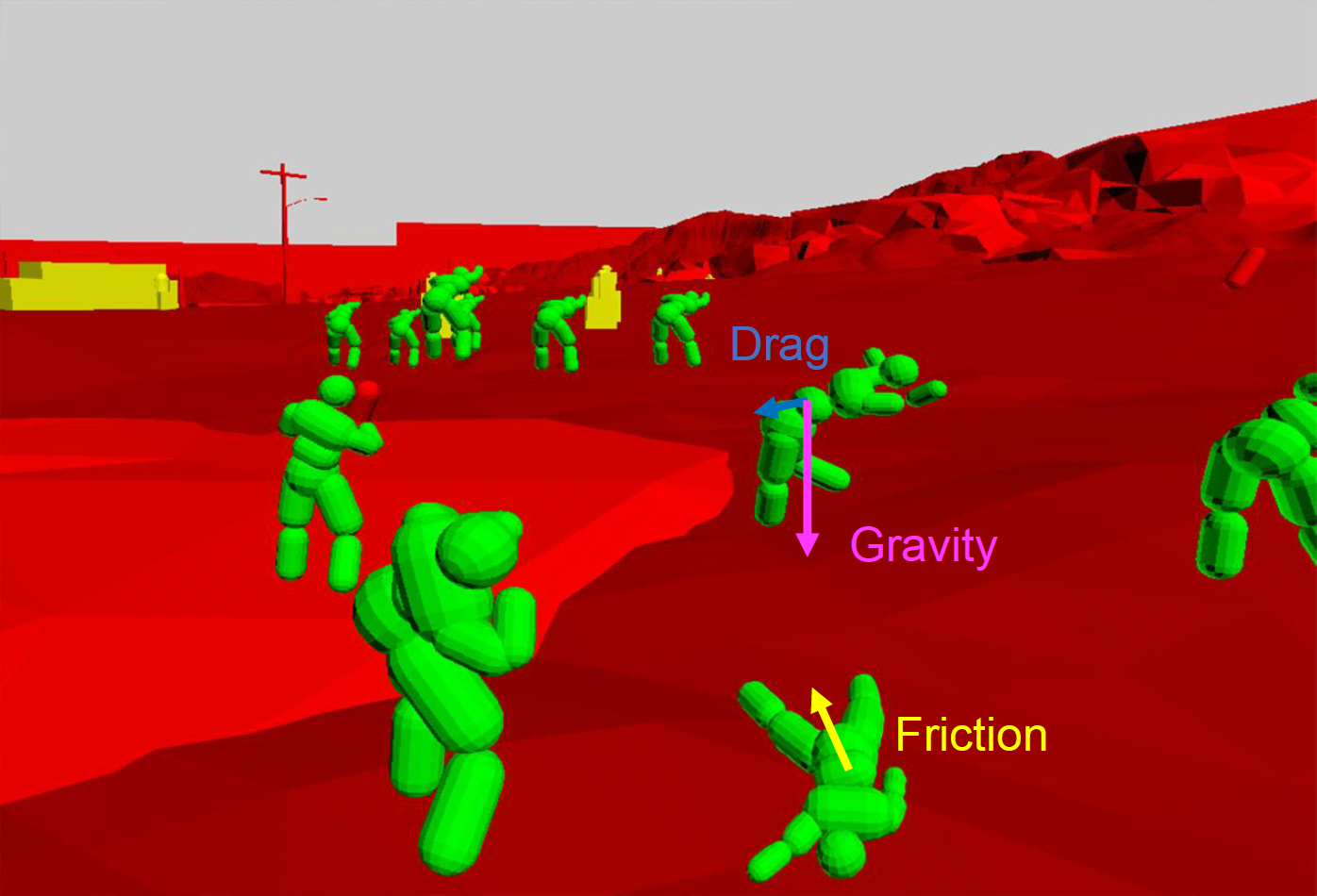
- 只有当力(force) 作用在(动态)物体上改变加速度时,才能影响到它们的移动
-
常见的力有重力 (gravity)、拉力 (drag)、摩擦力 (friction) 等
-
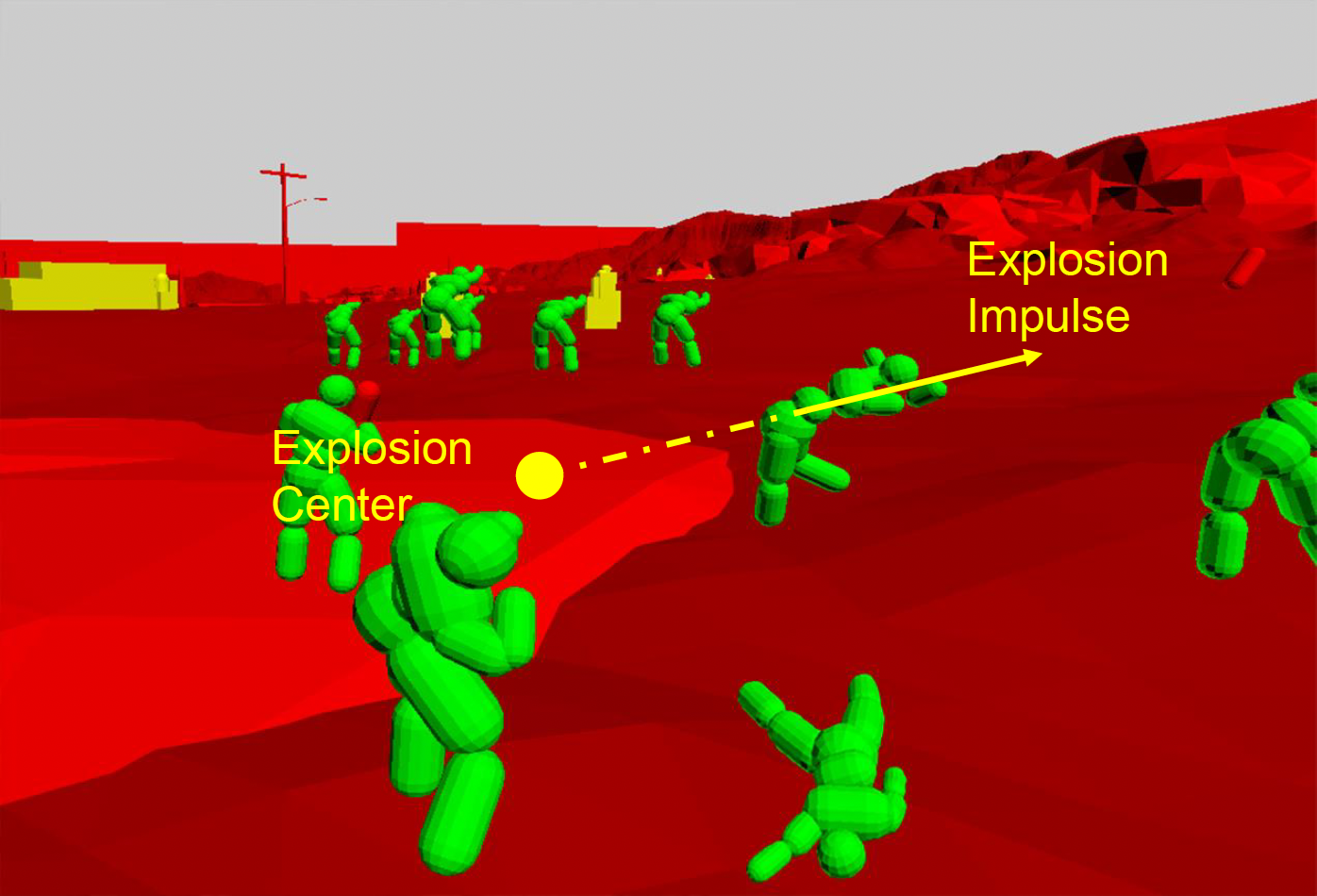
还可以通过施加冲量(impulse) 改变参与者的加速度,比如车辆冲撞、爆炸等
Movements⚓︎
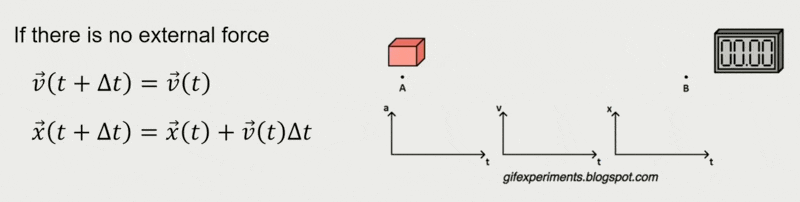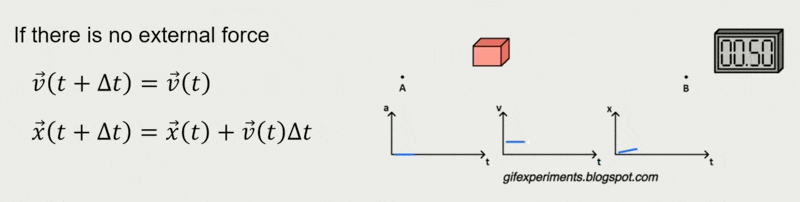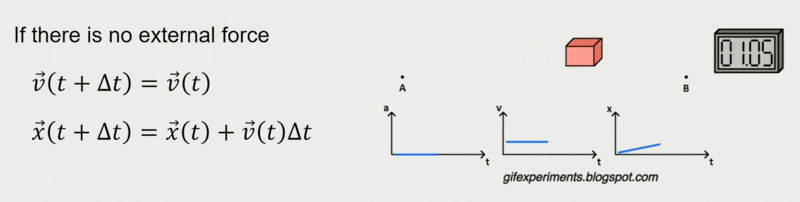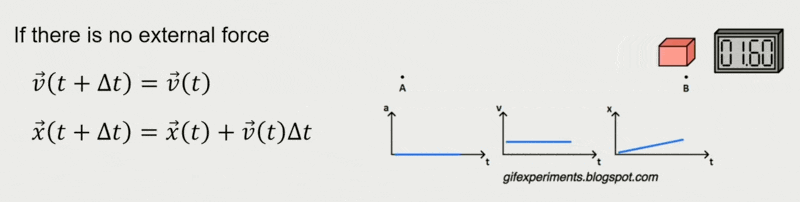
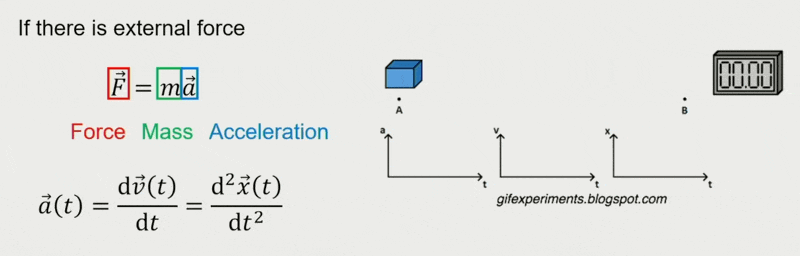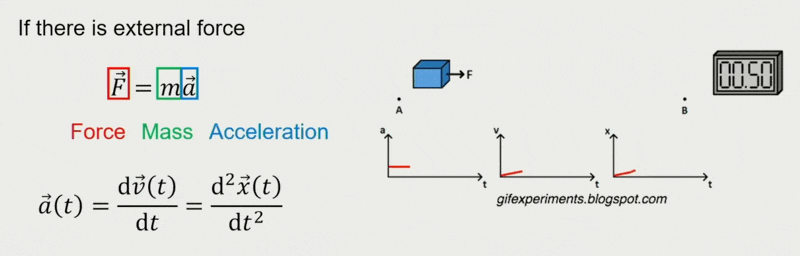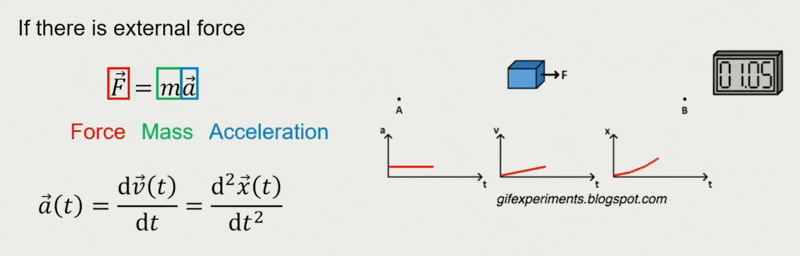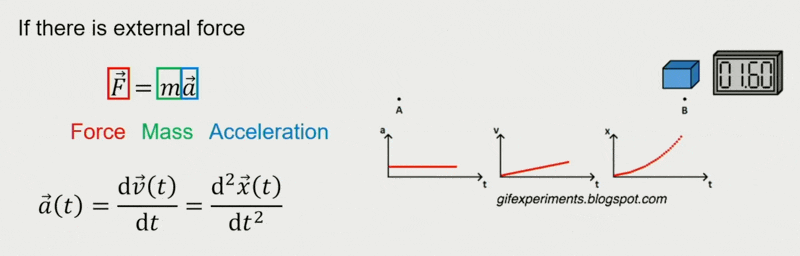
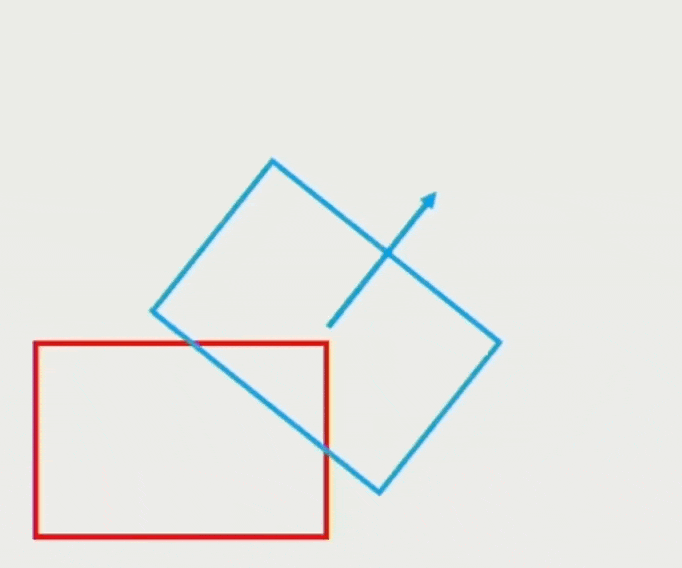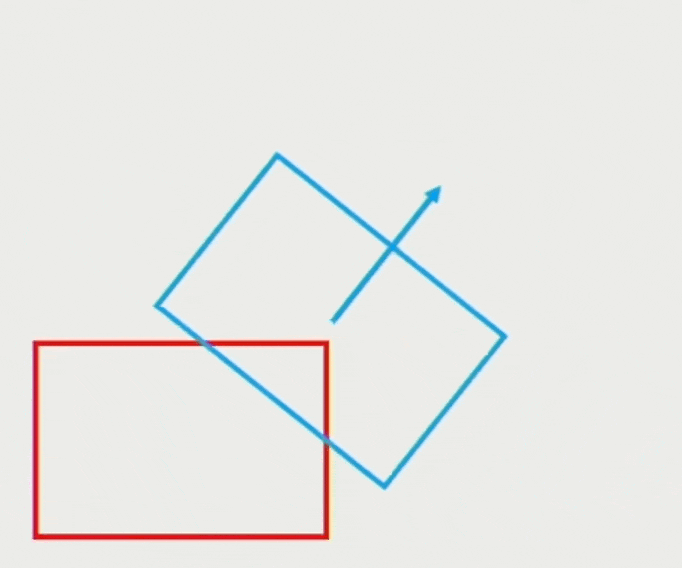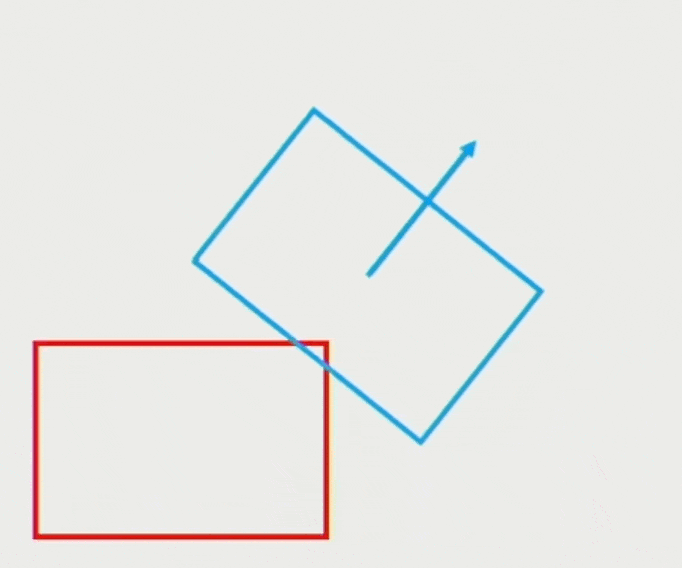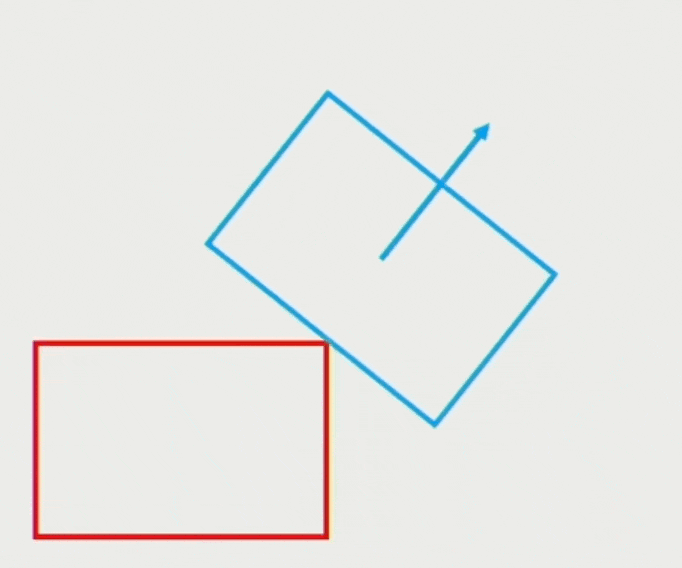
恒力(constant force) 作用下的移动:
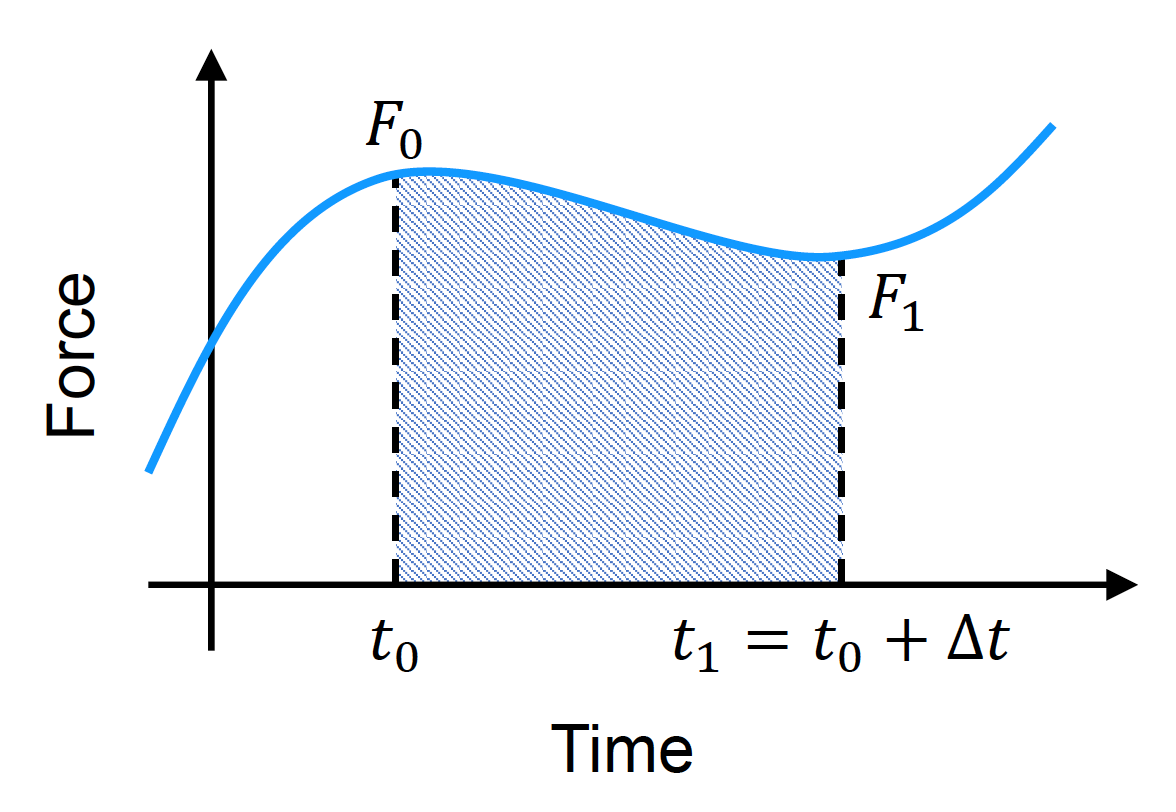
变力(varying force) 作用下的移动:
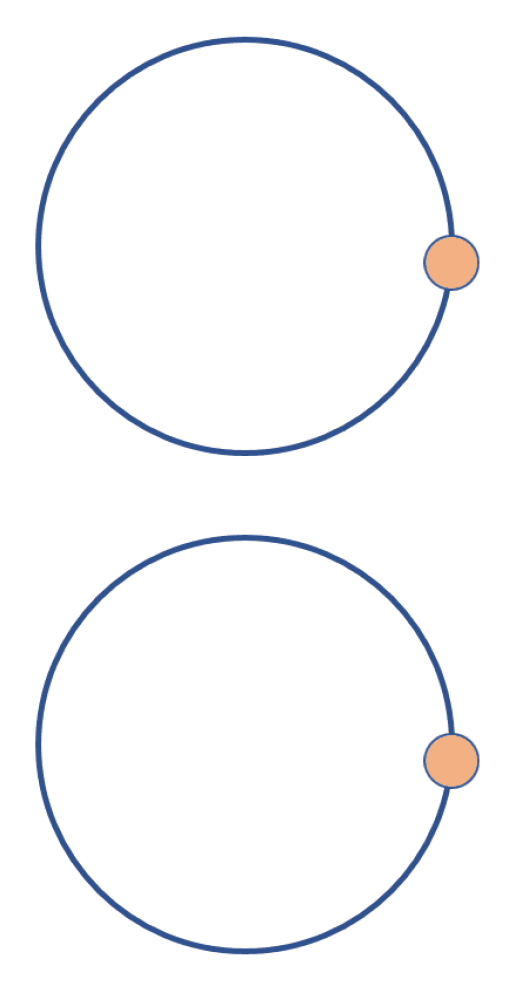
现在考虑地球绕太阳公转这样一个相对简单的运动的例子(假设是圆形轨道
而要在游戏中模拟这样一个圆周运动,可以这样做:
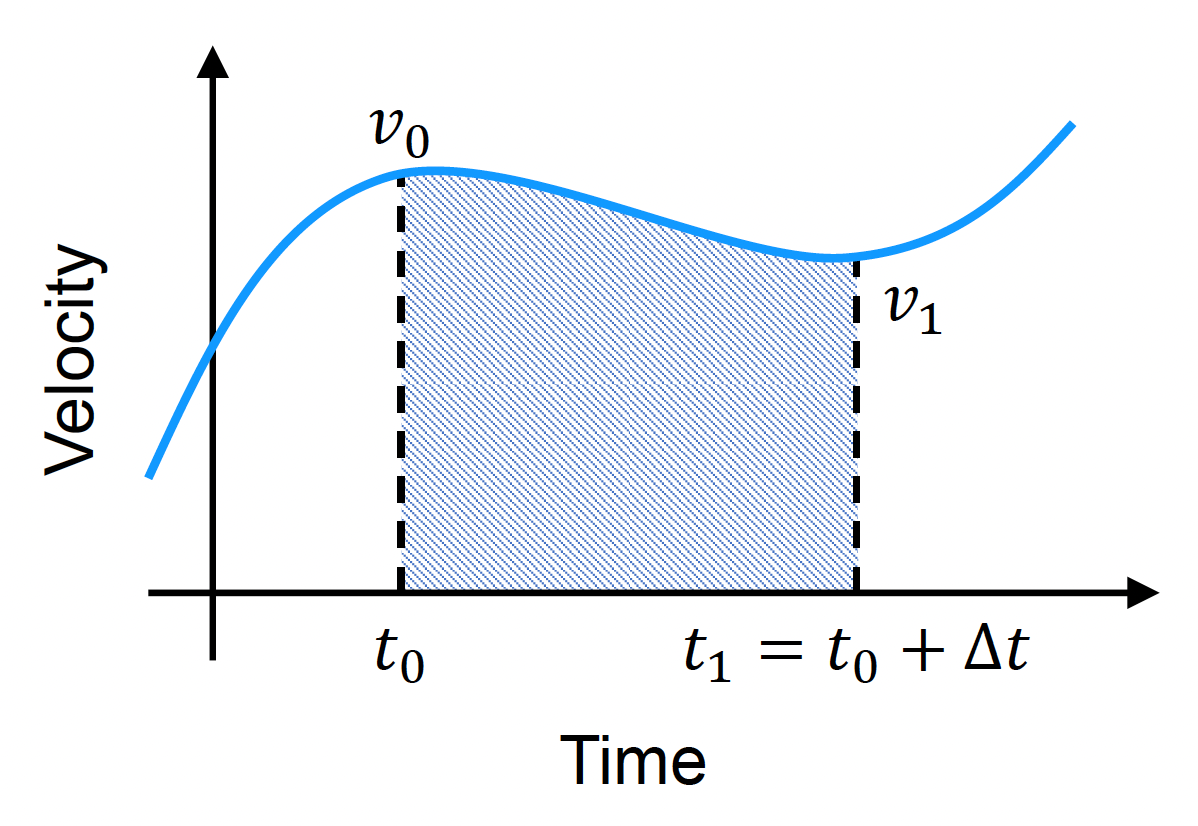
- 已知 \(t\) 时刻下位置为 \(\vec{x}(t)\),线速度为 \(\vec{v}(t) = \dfrac{d\vec{x}(t)}{dt}\)
- 在模拟步中,令时间步大小为 \(\Delta t\),我们要计算 \(\vec{x}(t + \Delta t), \vec{v}(t + \Delta t)\)
-
需要沿时间做积分:\(\vec{x}(t_1) = \vec{x}(t_0) + \int_{t_0}^{t_1} \vec{v}(t) dt\)
这个积分的求解需要用到欧拉法(Euler's method):
-
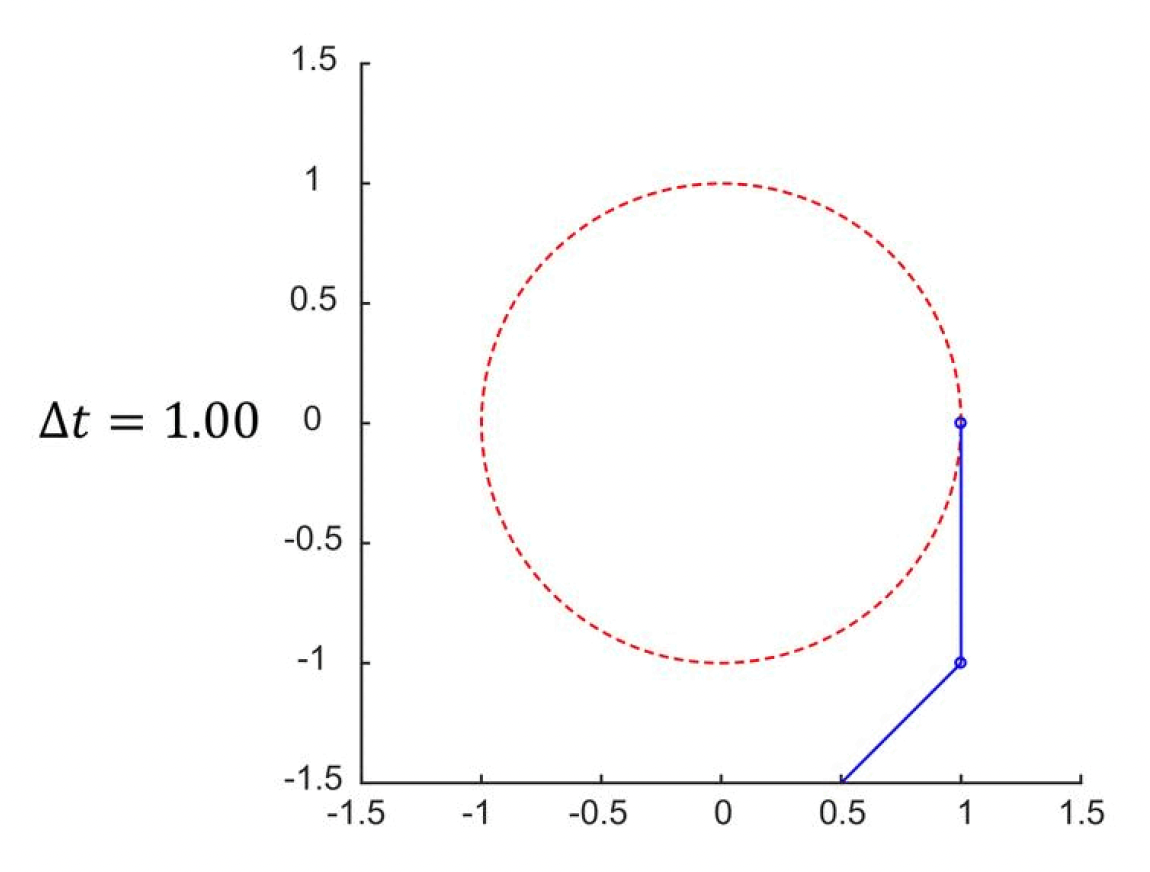
显式(正向)欧拉法:最简单的估计,假设力在时间步内是恒定的
\[ \begin{cases} \vec{v}(t_{1}) = \vec{v}(t_{0}) + M^{-1}\textcolor{cornflowerblue}{\vec{F}(t_{0})}\Delta t \\ \vec{x}(t_{1}) = \vec{x}(t_{0}) + \textcolor{cornflowerblue}{\vec{v}(t_{0})}\Delta t \end{cases} \]其中标蓝的量表示当前状态,它们都是已知的。
- 优点:计算简单高效
- 缺点:
- 不稳定
- 能量随时间增长
-
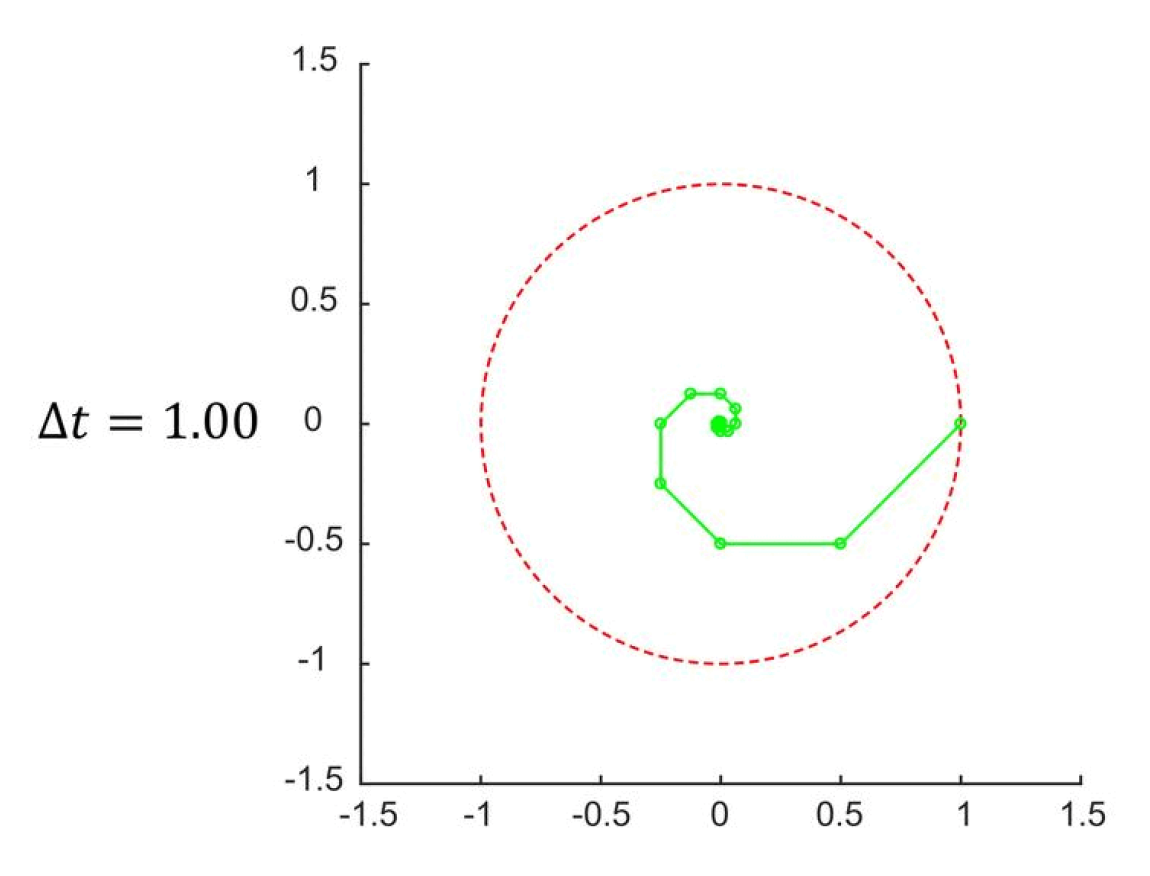
隐式(反向)欧拉法
\[ \begin{cases} \vec{v}(t_{1}) = \vec{v}(t_{0}) + M^{-1}\textcolor{red}{\vec{F}(t_{1})}\Delta t \\ \vec{x}(t_{1}) = \vec{x}(t_{0}) + \textcolor{red}{\vec{v}(t_{1})}\Delta t \end{cases} \]其中标红的量是未来状态,它们是未知的。
-
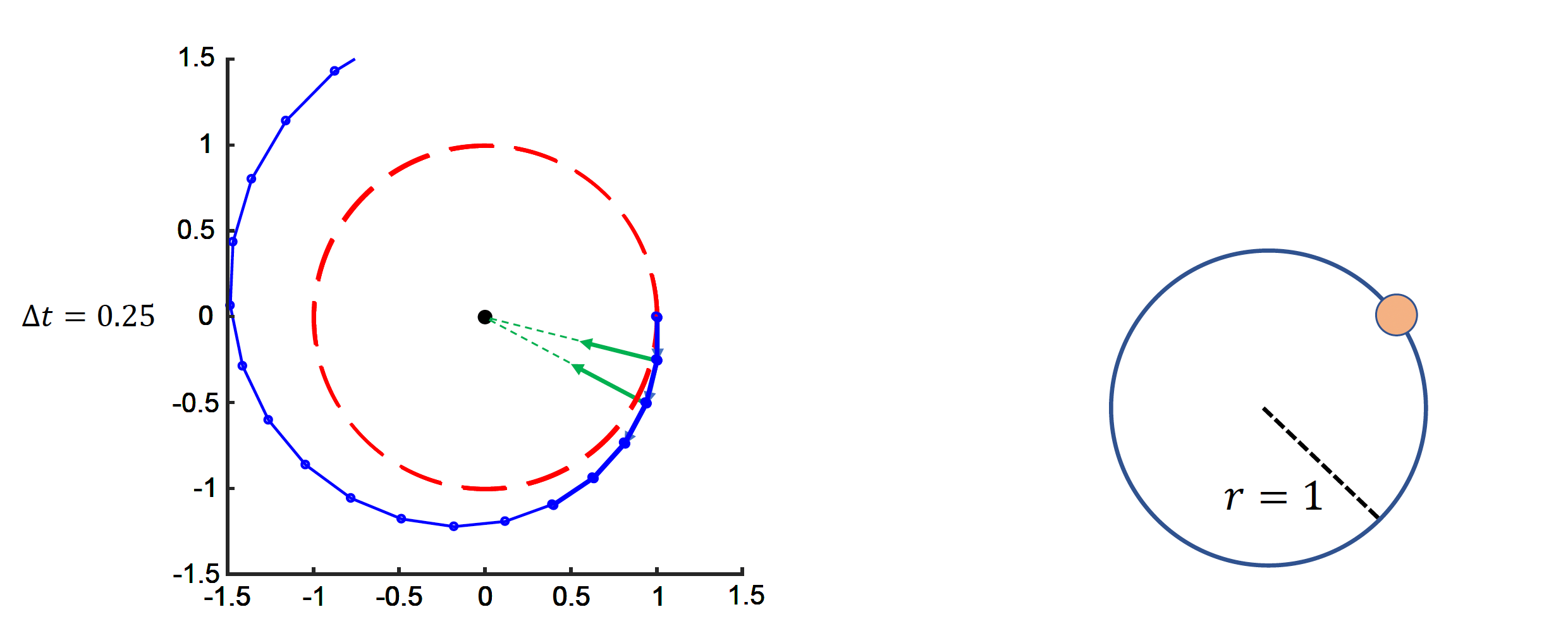
隐式欧拉法的结果是螺旋状的
-
优点:无条件稳定
- 缺点:
- 求解成本高
- 难以应对非线性问题
- 能量随时间衰减
-
-
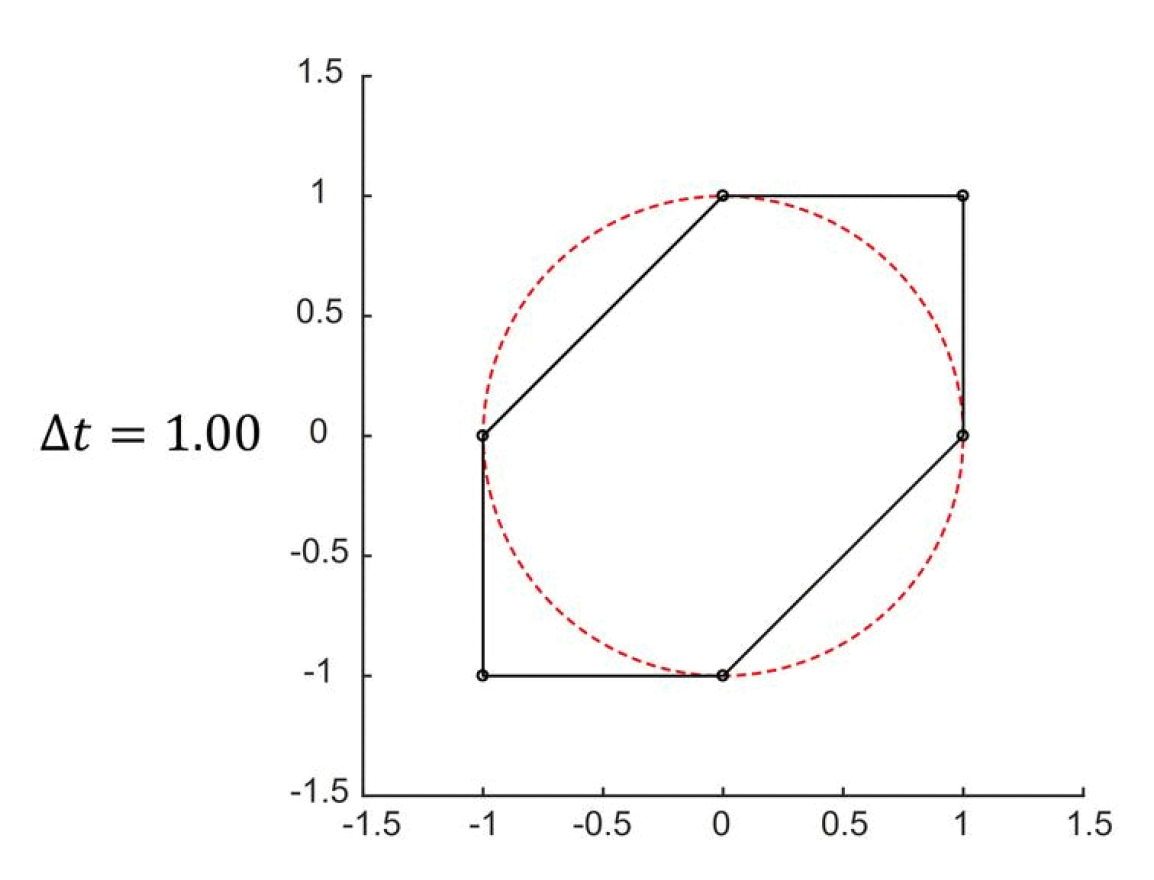
半隐式(semi-implicit)欧拉法
\[ \begin{cases} \vec{v}(t_{1}) = \vec{v}(t_{0}) + M^{-1}\textcolor{cornflowerblue}{\vec{F}(t_{0})}\Delta t \\ \vec{x}(t_{1}) = \vec{x}(t_{0}) + \textcolor{red}{\vec{v}(t_{1})}\Delta t \end{cases} \]同样地,标蓝量为当前状态,标红量为未来状态。
-
若时间步较小,结果近似为一个圆
-
不仅兼具前两种方法的优点,还确保能量不会随时间变化而增长或衰减,因此更适合用于游戏开发中
- 但它还是有一点小问题的:在简谐运动、圆周运动等涉及到三角函数的运动中,通过该方法积分得到的周期会比实际周期略长一些,因而产生一个小的相位差
-
Rigid Body Dynamics⚓︎
在之前介绍的内容中,我们假设任何物体都可用一个质点表示,涉及的物理量包括了:
- 位置 \(\vec{x}\)
- 线速度 (linear velocity) \(\vec{v} = \dfrac{d\vec{x}}{dt}\)
- 加速度 (acceleration) \(\vec{a} = \dfrac{d\vec{v}}{dt} = \dfrac{d^2\vec{x}}{dt^2}\)
- 质量 \(M\)
- 动量 (momentum) \(\vec{p} = M\vec{v}\)
- 力 \(\vec{F} = \dfrac{d\vec{p}}{dt} = M \vec{a}\)
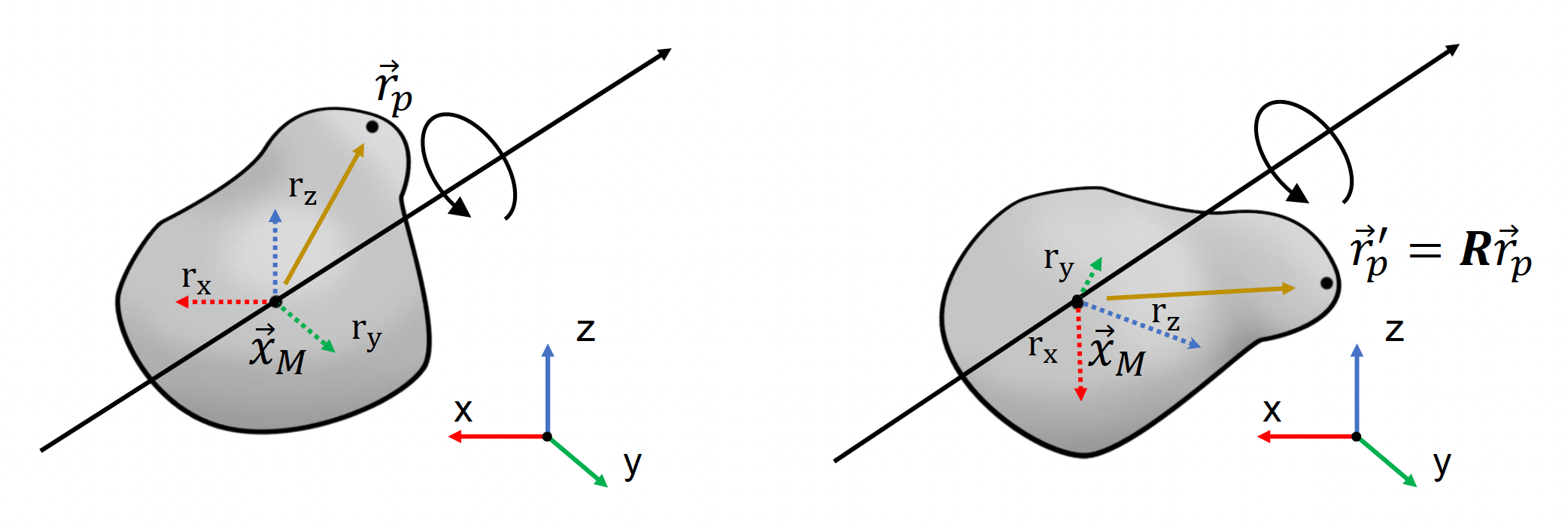
但大多数物体都有自己的形状,除了上述量(线性值)外,还得考虑自身的旋转(角值 (angular value)
-
朝向(orientation) \(\bm{R}\):形式可以是
- 矩阵 \(\bm{R}(t) = \begin{bmatrix}\textcolor{red}{r_{xx}} & \textcolor{green}{r_{yx}} & \textcolor{cornflowerblue}{r_{zx}} \\ \textcolor{red}{r_{xy}} & \textcolor{green}{r_{yy}} & \textcolor{cornflowerblue}{r_{zy}} \\ \textcolor{red}{r_{xz}} & \textcolor{green}{r_{yz}} & \textcolor{cornflowerblue}{r_{zz}}\end{bmatrix}\)
- 四元数 \(q = \begin{bmatrix}s & \vec{v}\end{bmatrix}\)
-
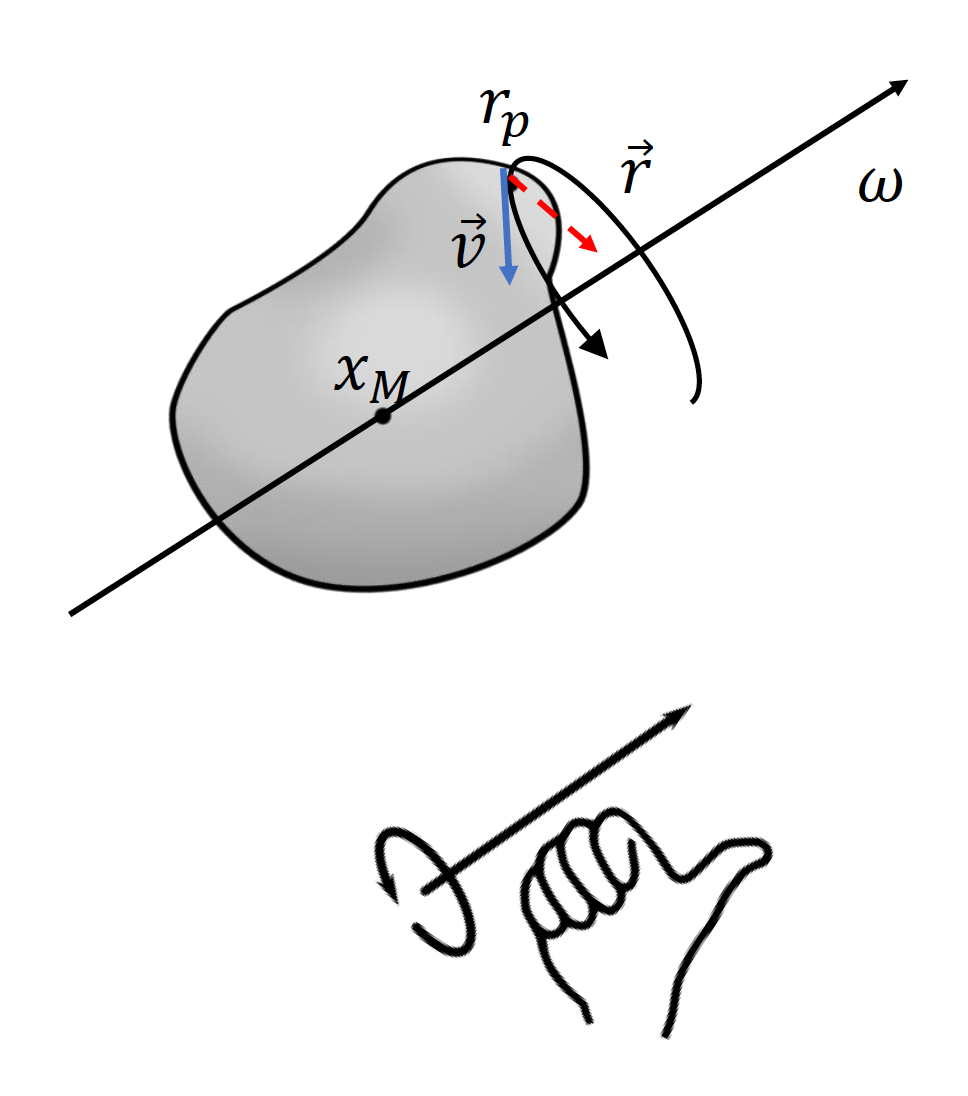
角速度(angular velocity) \(\vec{\omega}\):方向为旋转轴的方向
\[ \begin{aligned} \|\vec{\omega}\| &= \frac{d\theta}{dt} \\ \vec{\omega} &= \frac{\vec{v} \times \vec{r}}{\|\vec{r}\|^{2}} \end{aligned} \]其中 \(\theta\) 为用弧度表示的旋转角
-
角加速度(angular acceleration) \(\vec{\alpha}\)
\[ \vec{\alpha} = \frac{d\vec{\omega}}{dt} = \frac{\vec{a} \times \vec{r}}{\|\vec{r}\|^{2}} \] -
惯性张量(inertia tensor)/转动惯量(rotational inertia) \(\bm{I}\):描述了刚体的质量分布
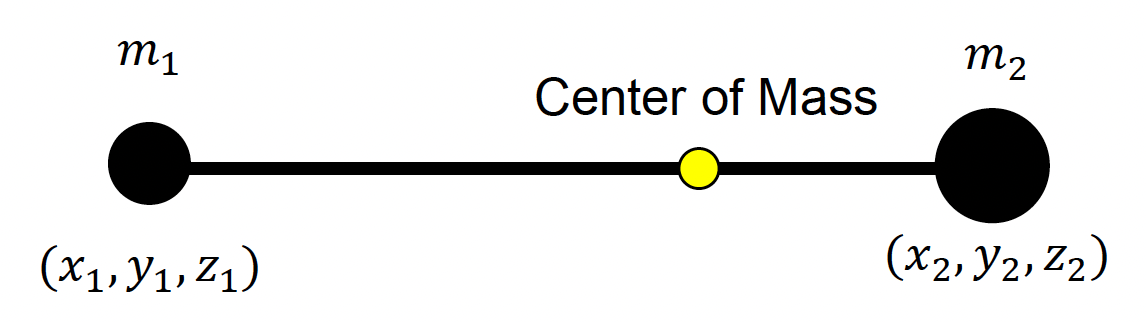
\[ \bm{I} = \bm{R} \cdot \bm{I}_0 \cdot \bm{R}^\top \]- 总质量:\(M = m_1 + m_2\)
- 质心:\(CoM = \dfrac{m_1}{M}(x_1, y_1, z_1) + \dfrac{m_2}{M}(x_2, y_2, z_2)\)
-
初始惯性张量:
\[ I_{0} = \begin{bmatrix} m_{1}(y_{1}^{2} + z_{1}^{2}) + m_{2}(y_{2}^{2} + z_{2}^{2}) & -m_{1}x_{1}y_{1} - m_{2}x_{2}y_{2} & -m_{1}x_{1}z_{1} - m_{2}x_{2}z_{2} \\ -m_{1}y_{1}x_{1} - m_{2}y_{2}x_{2} & m_{1}(x_{1}^{2} + z_{1}^{2}) + m_{2}(x_{2}^{2} + z_{2}^{2}) & -m_{1}y_{1}z_{1} - m_{2}y_{2}z_{2} \\ -m_{1}z_{1}x_{1} - m_{2}z_{2}x_{2} & -m_{1}z_{1}y_{1} - m_{2}z_{2}y_{2} & m_{1}(x_{1}^{2} + y_{1}^{2}) + m_{2}(x_{2}^{2} + y_{2}^{2}) \end{bmatrix} \]
-
角动量(angular momentum) \(\vec{L} = \bm{I} \vec{\omega}\)
- 角动量守恒是一个能被证明的定理
-
扭矩(torque) \(\vec{\tau}\)
\[ \vec{\tau} = \vec{r} \times \vec{F} = \frac{d\vec{L}}{dt} \]其中 \(\vec{F}\) 表示施加在刚体位置 \(\vec{r}\) 上的外力
以上便是刚体动力学(rigid body dynamics) 的内容了!
应用:台球 (billiard) 动力学
尽管我们已经了解了刚体动力学的基本概念,但台球游戏中的物理仍然很复杂。
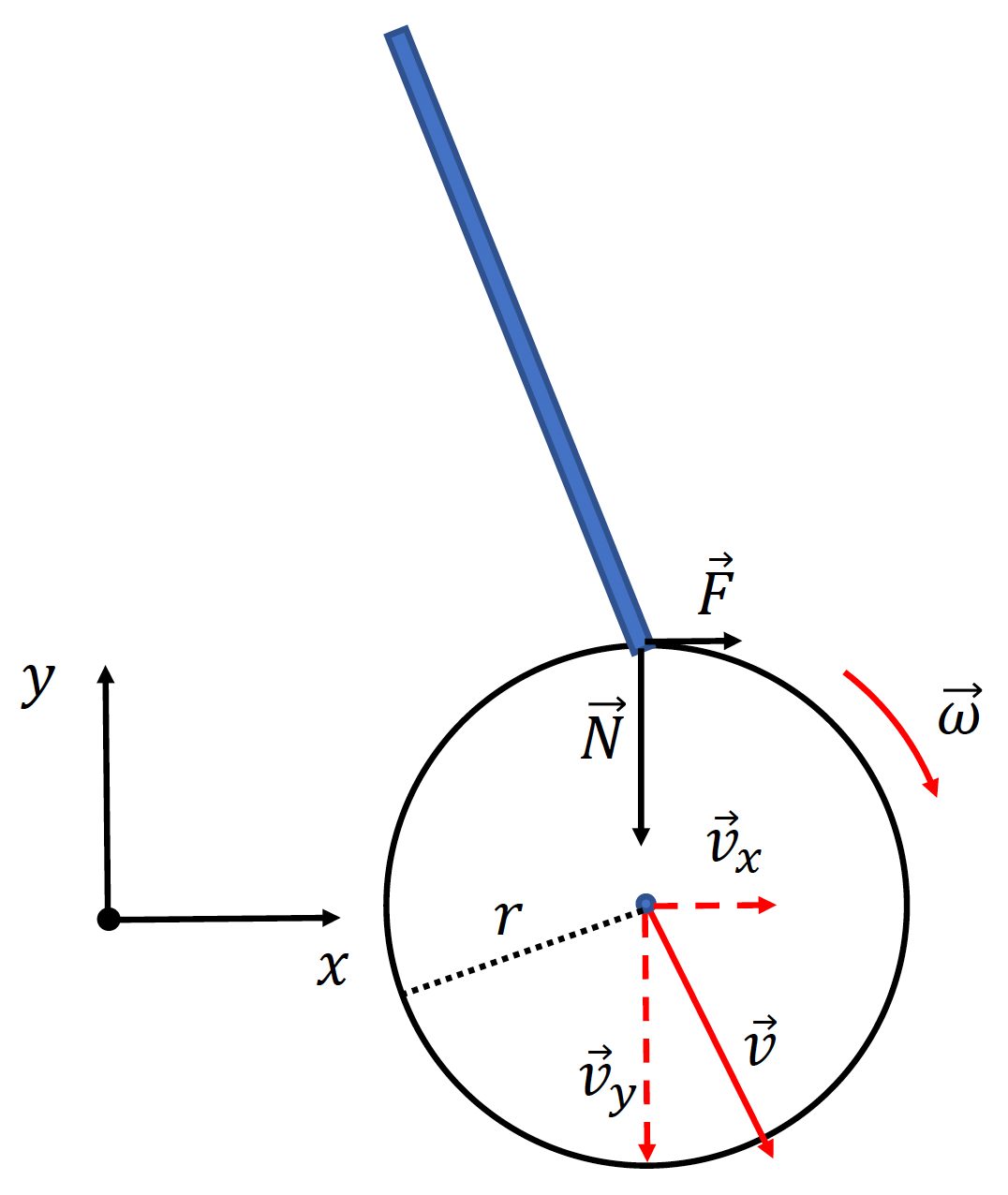
这里举一个简单的例子:用球杆侧面打击球
- 摩擦力冲量:\(\vec{p}_F = \int \vec{F} dt = m \vec{v}_x\)
- 压力冲量:\(\vec{p}_N = \int \vec{N} dt = m \vec{v}_y\)
- 球角动量:\(\vec{L}_b = \bm{I}_b \vec{\omega} = \vec{p}_F \times \vec{r}_F\)
- 球线速度:\(\vec{v} = \vec{v}_x + \vec{v}_y\)
Collision Detection⚓︎
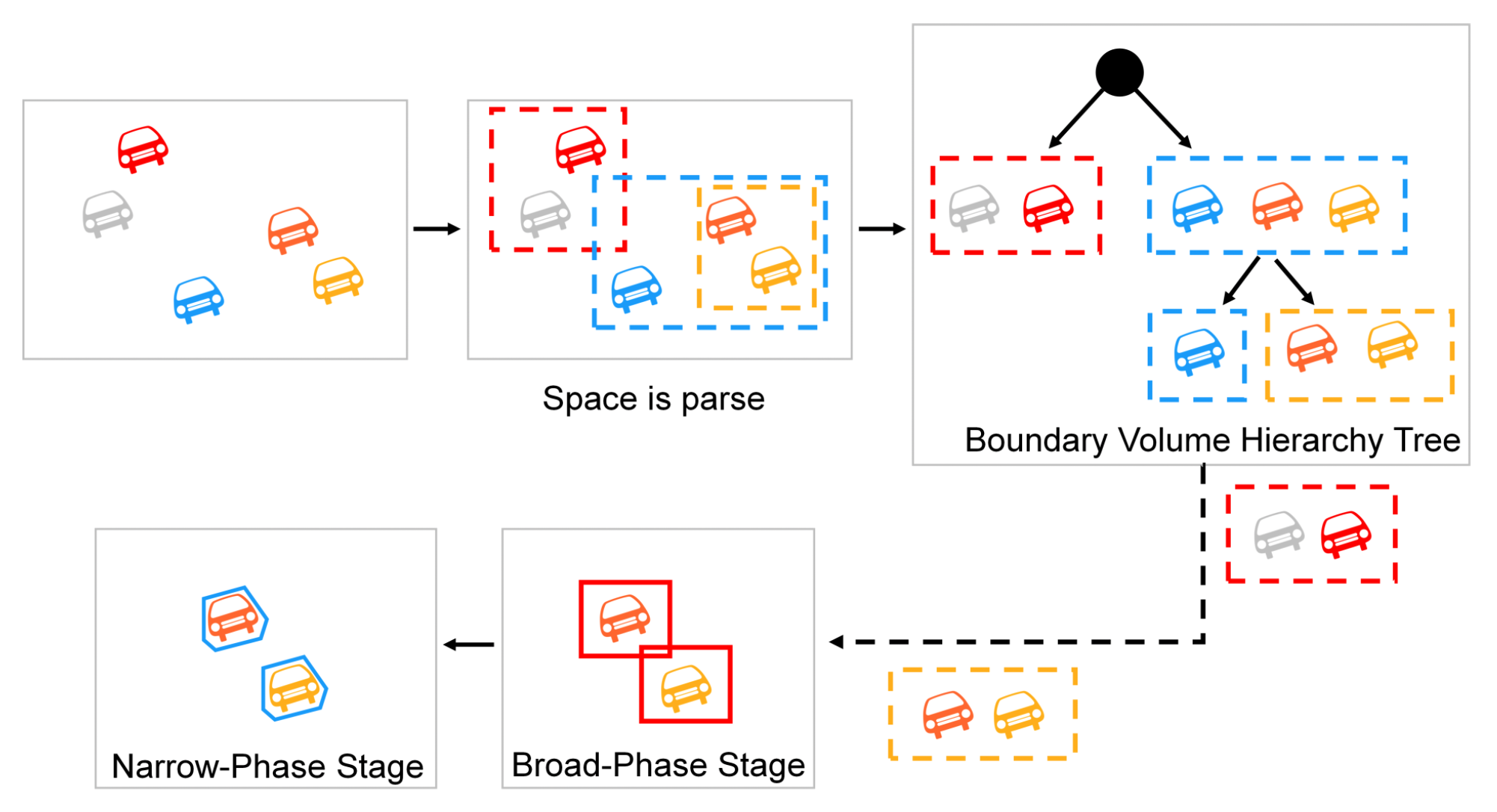
要想在物理世界中表达物体之间的相互作用,碰撞检测(collision detection) 是必不可少的一项技术。它一般分为以下两个阶段:
- 广阶段(broad phase)
- 窄阶段(narrow phase)
Broad Phase⚓︎
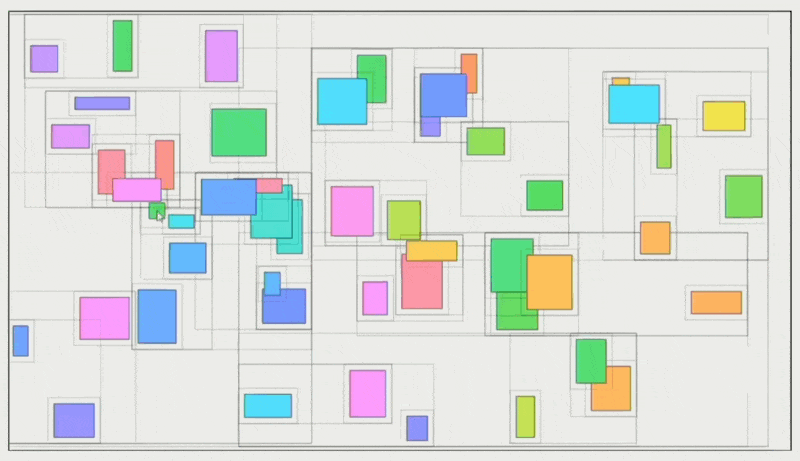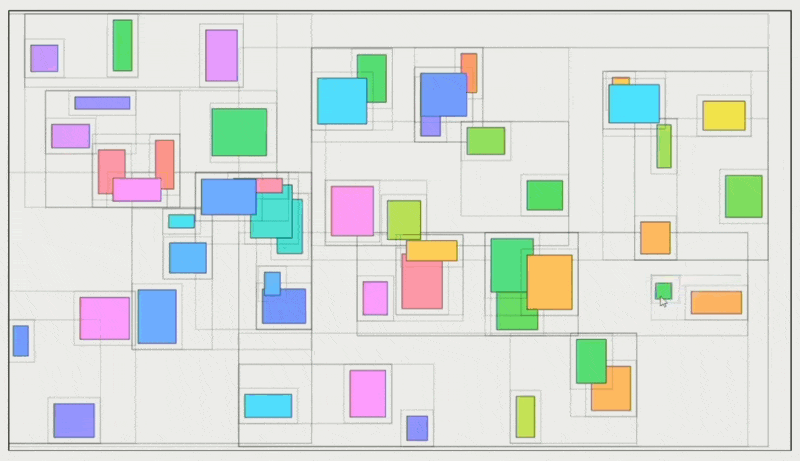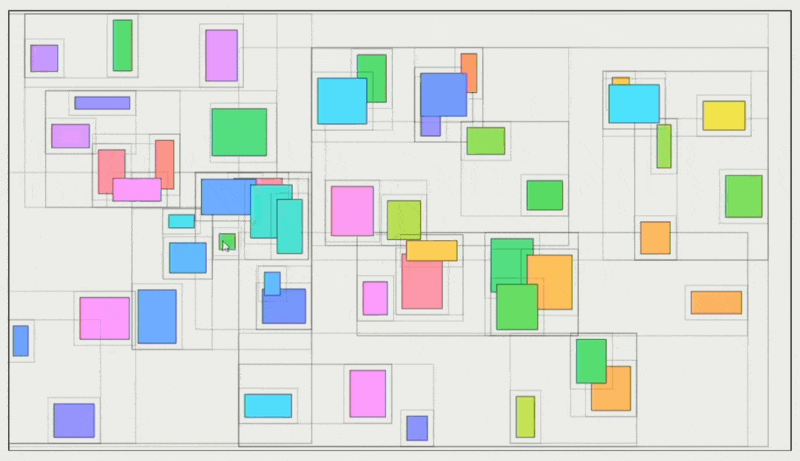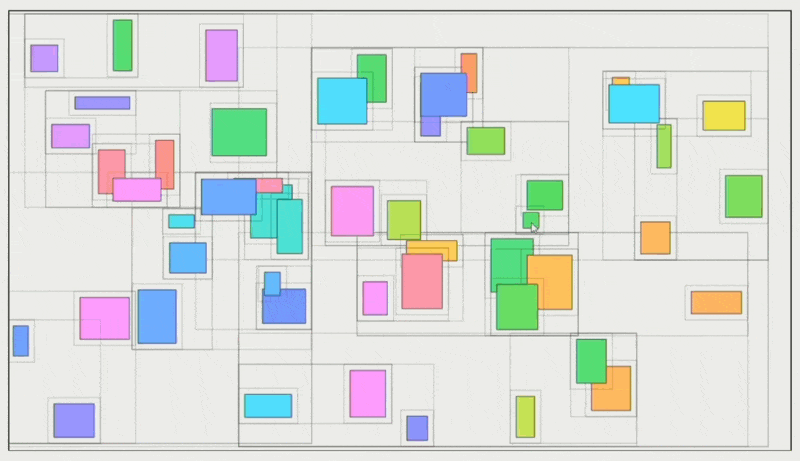
广阶段的目标是找到相交的刚体 AABBs,这表明有可能的重叠刚体对,实现方法有:
-
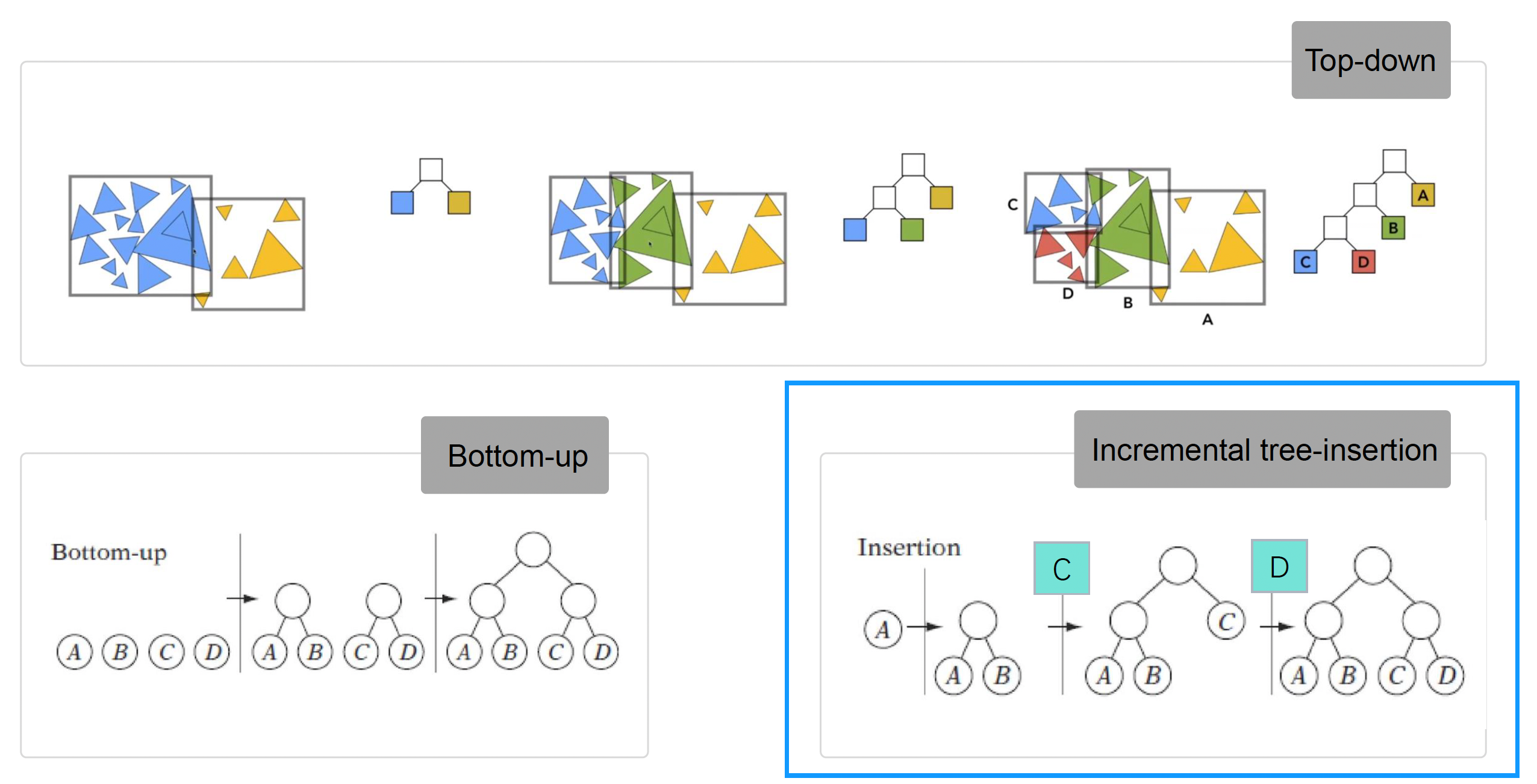
空间划分(space partitioning),比如边界体积层次 (boundary volume hierarchy, BVH) 树;下面列举各种 BVH 树的构建方式
- 优点:环境动态变化时,更新成本很低
-
排序和清理
-
排序阶段(初始化
) :对于每个轴- 初始化场景时,沿着每个轴对 AABBs 的边界排序
- 沿着每个轴检查 AABBs 的边界
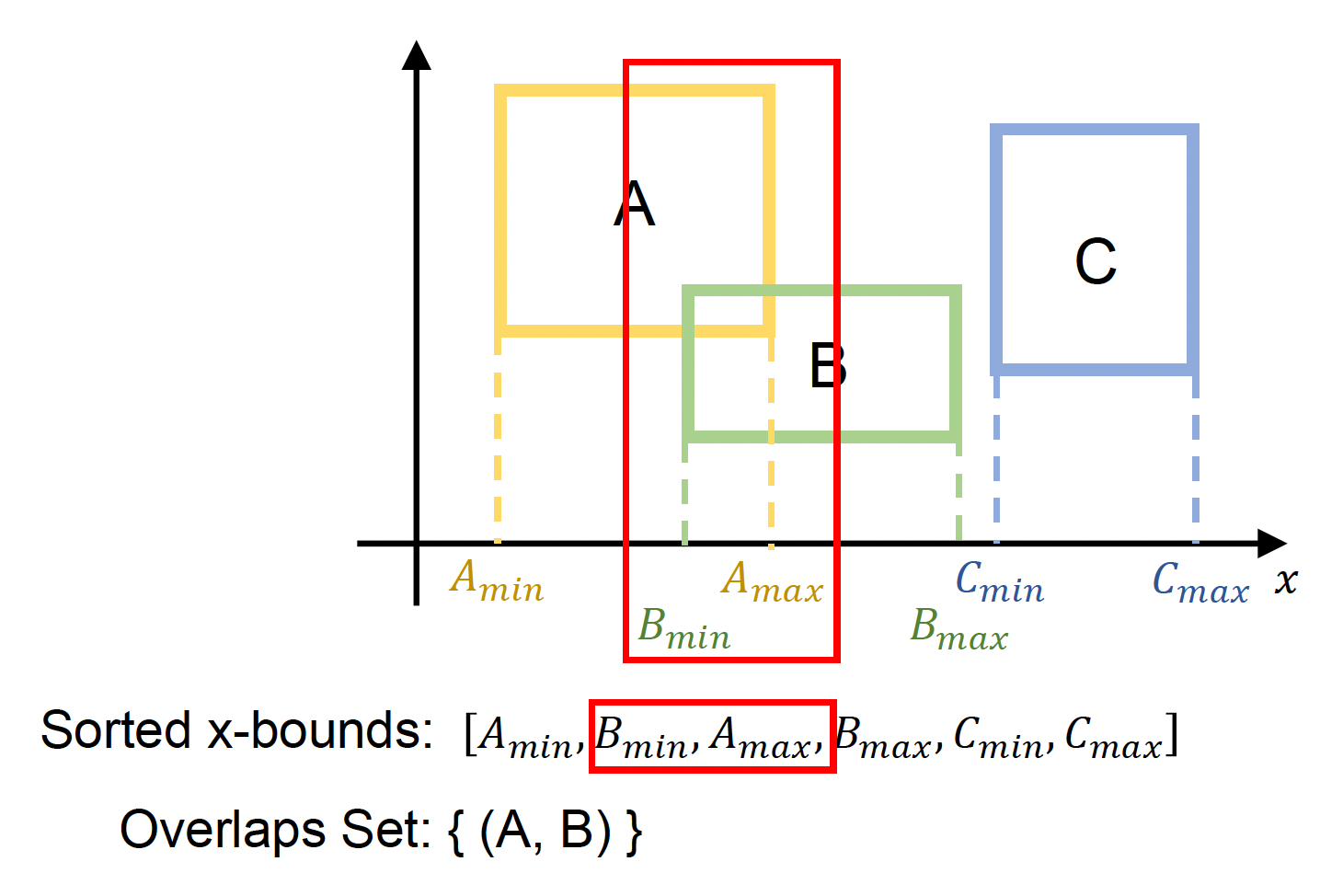
- \(A_{\max} \ge B_{\min}\) 意味着 \(A, B\) 之间可能有重叠
-
清理阶段(更新)
-
只检查边界的交换
- 时间一致性 (temporal coherence)
- 帧与帧之间的局部步骤
-
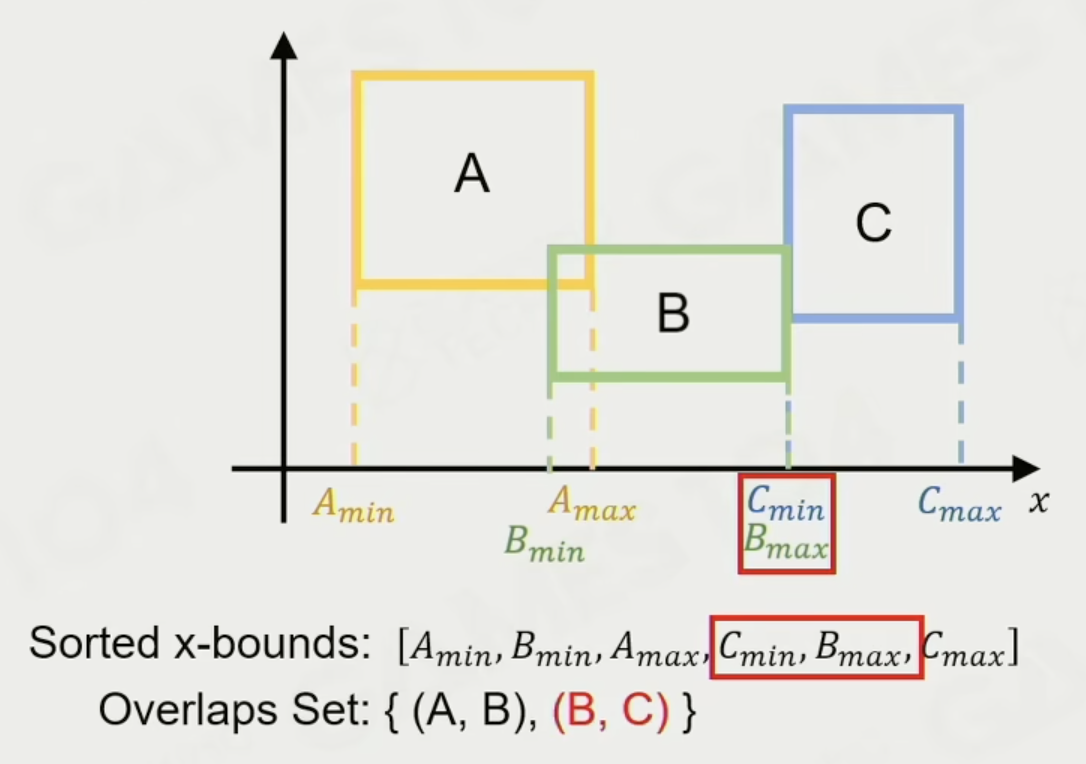
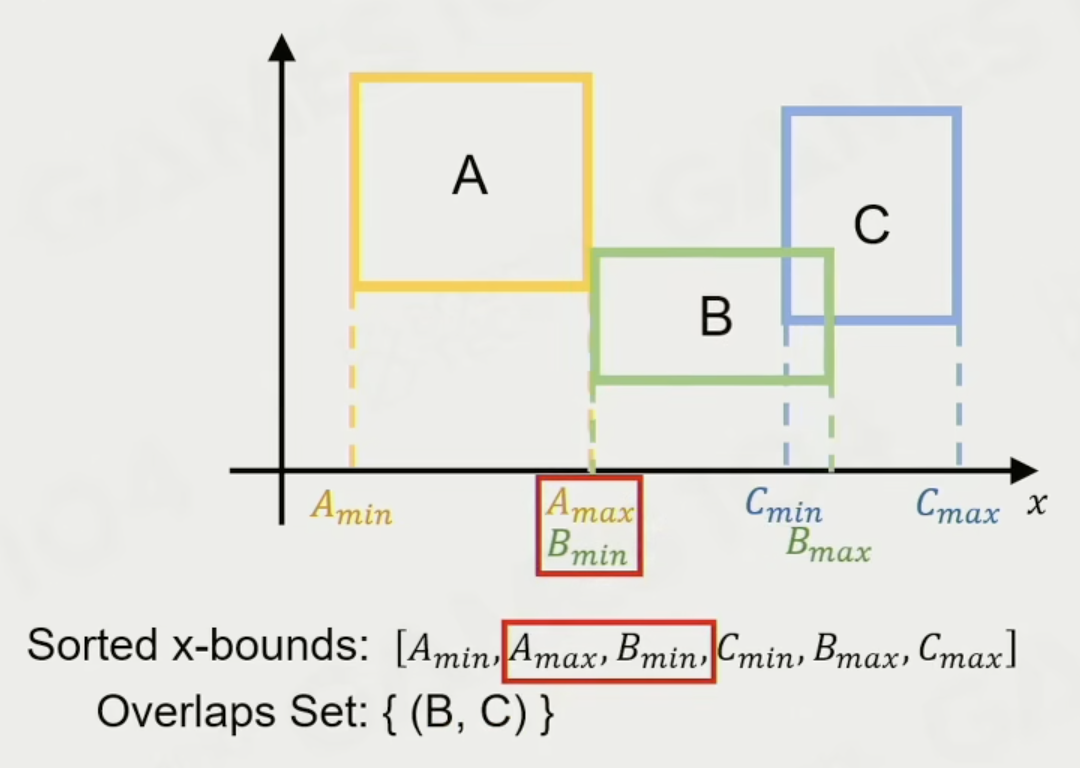
交换 min 和 max 意味着从重叠集合中增加 / 删除潜在的重叠
- 交换 min 和 min,或者 max 和 max 则不会影响重叠集合
-
-
优点:效率非常高(因为大多数物体都是静态的,排好序后也只需调整很少的数字)
-
Narrow Phase⚓︎
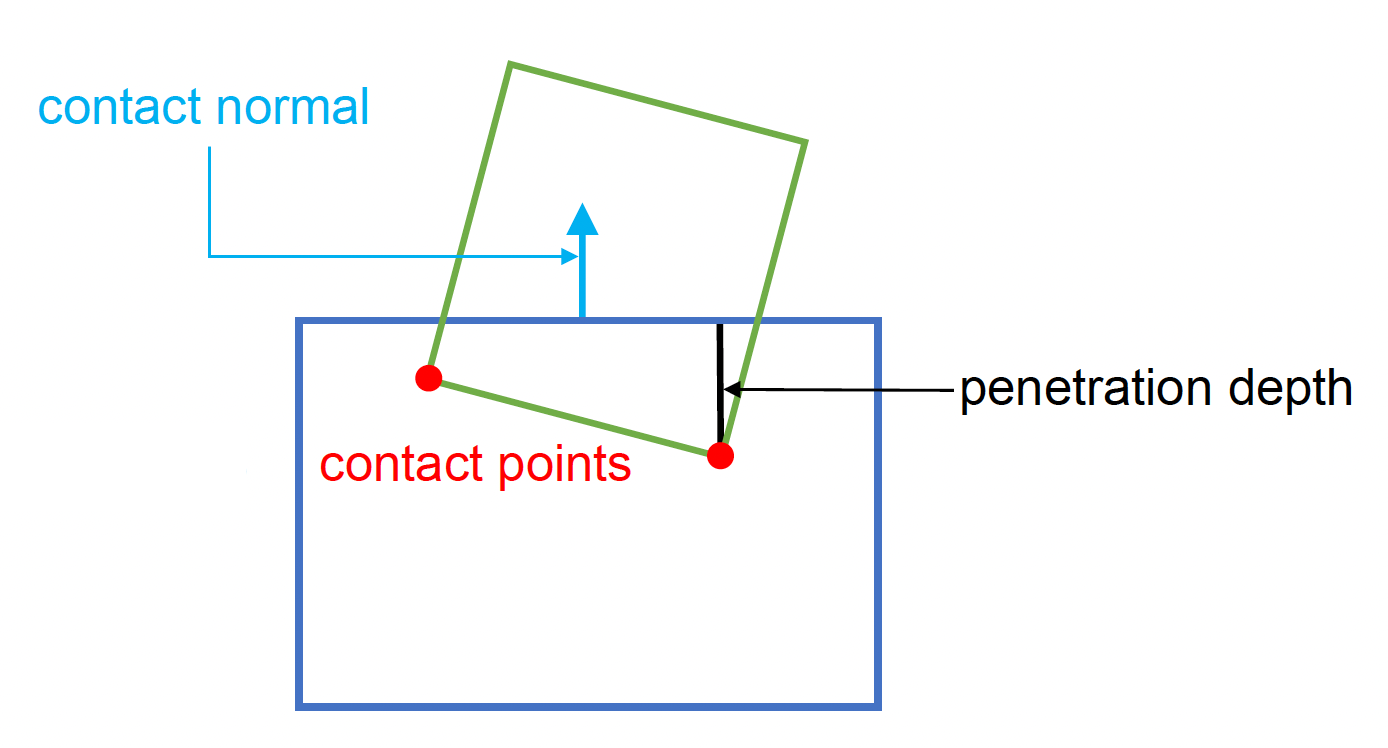
窄阶段的目标是精确检测重叠情况,生成接触信息。接触信息 (contact information) 包括:
- 接触流形 (contact manifold):用一组接触点近似
- 接触法线 (contact normal)
- 穿透深度 (penetration depth)
下面给出窄阶段常用的实现方法。
-
基本形状相交测试(basic shape intersection test)
-
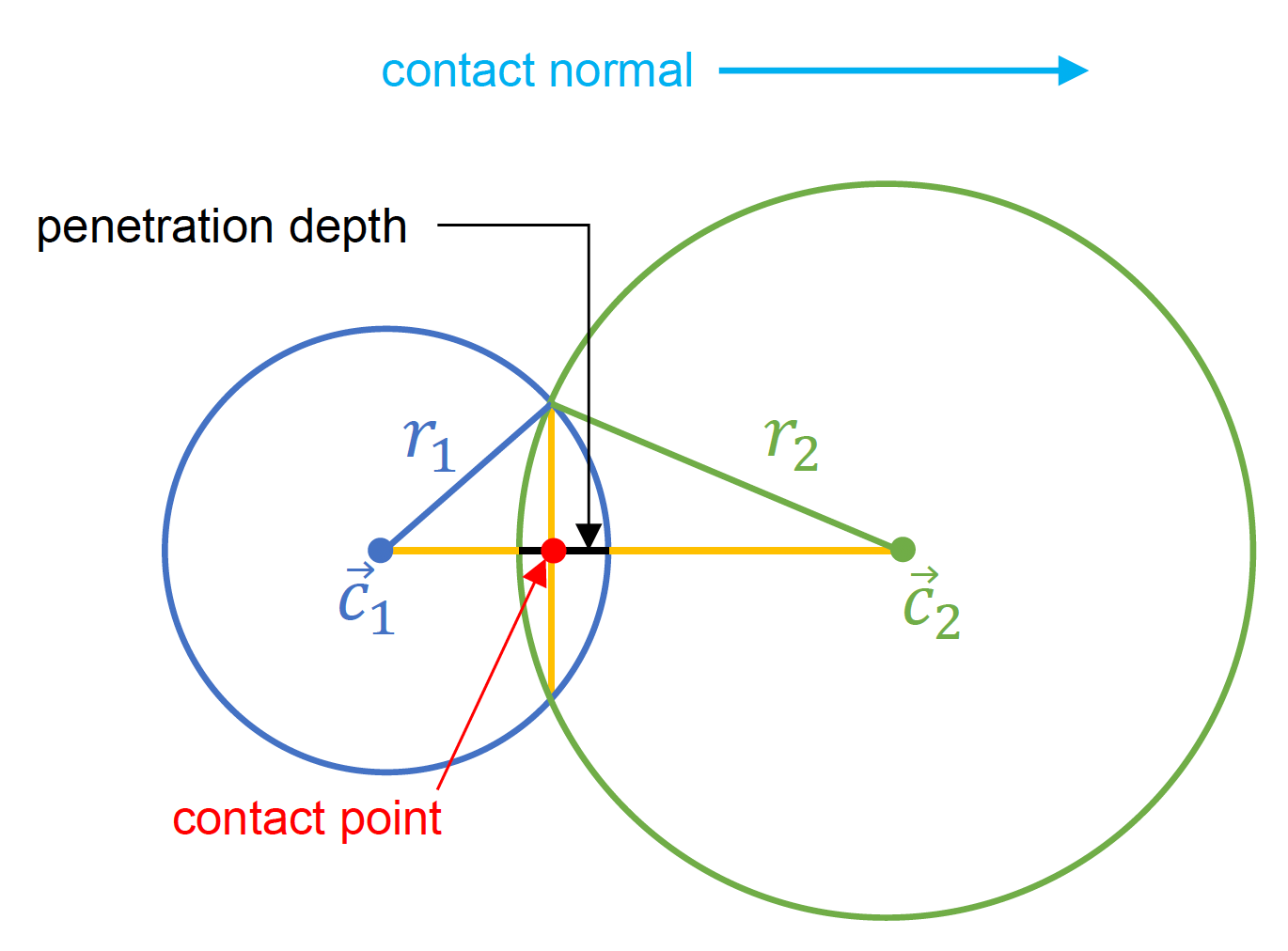
球 - 球测试
- 重叠条件:\(|\vec{c}_2 - \vec{c}_1| - r_1 - r_2 \le 0\)
- 接触信息:
- 接触法线:\((\vec{c}_2 - \vec{c}_1) / |\vec{c}_2 - \vec{c}_1|\)
- 穿透深度:\(|\vec{c}_2 - \vec{c}_1| - r_1 - r_2\)
-
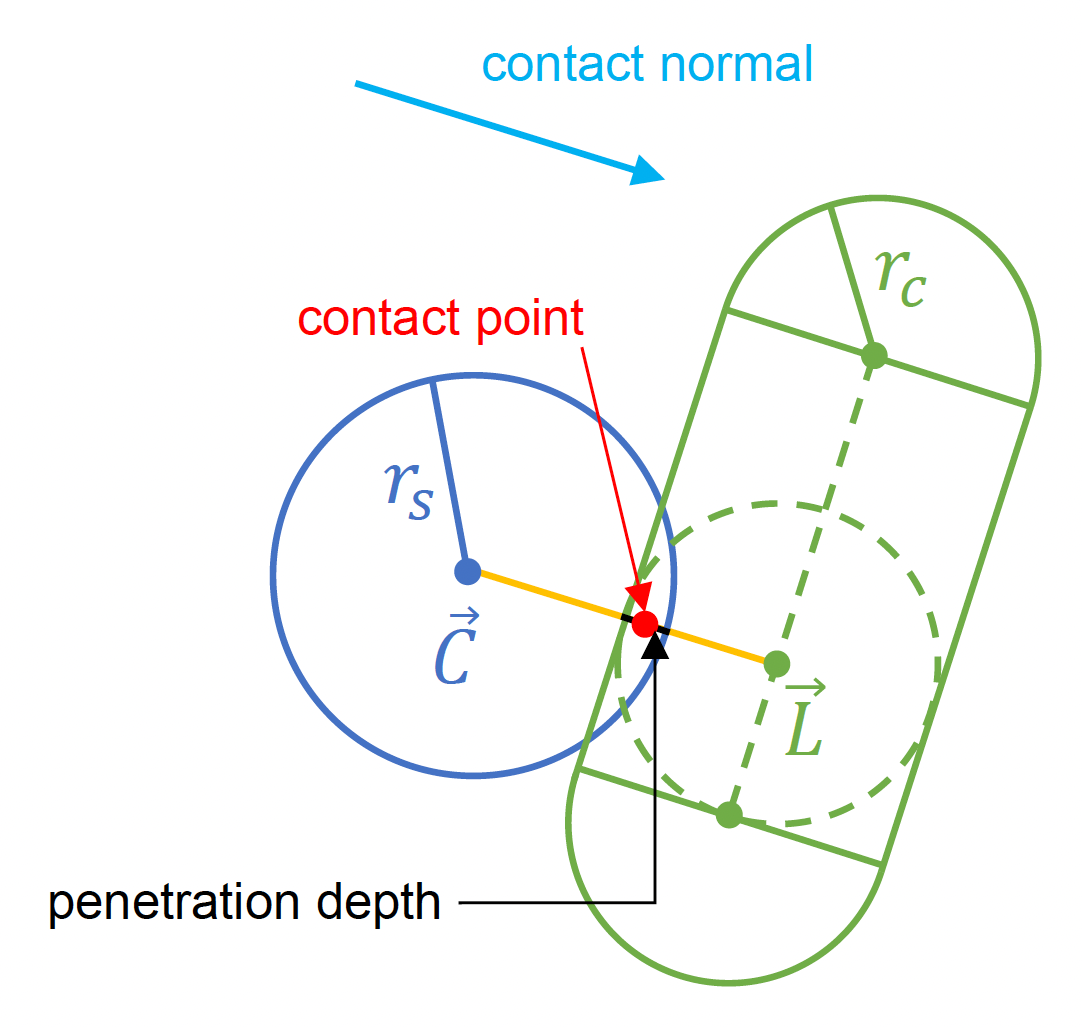
球 - 胶囊测试
其中 \(\vec{L}\) 为在内部胶囊段中离圆最近的点
- 重叠条件:\(|\vec{C} - \vec{L}| - r_S - r_C \le 0\)
- 接触信息:
- 接触法线:\((\vec{C} - \vec{L}) / |\vec{C} - \vec{L}|\)
- 穿透深度:\(|\vec{C} - \vec{L}| - r_S - r_C\)
-
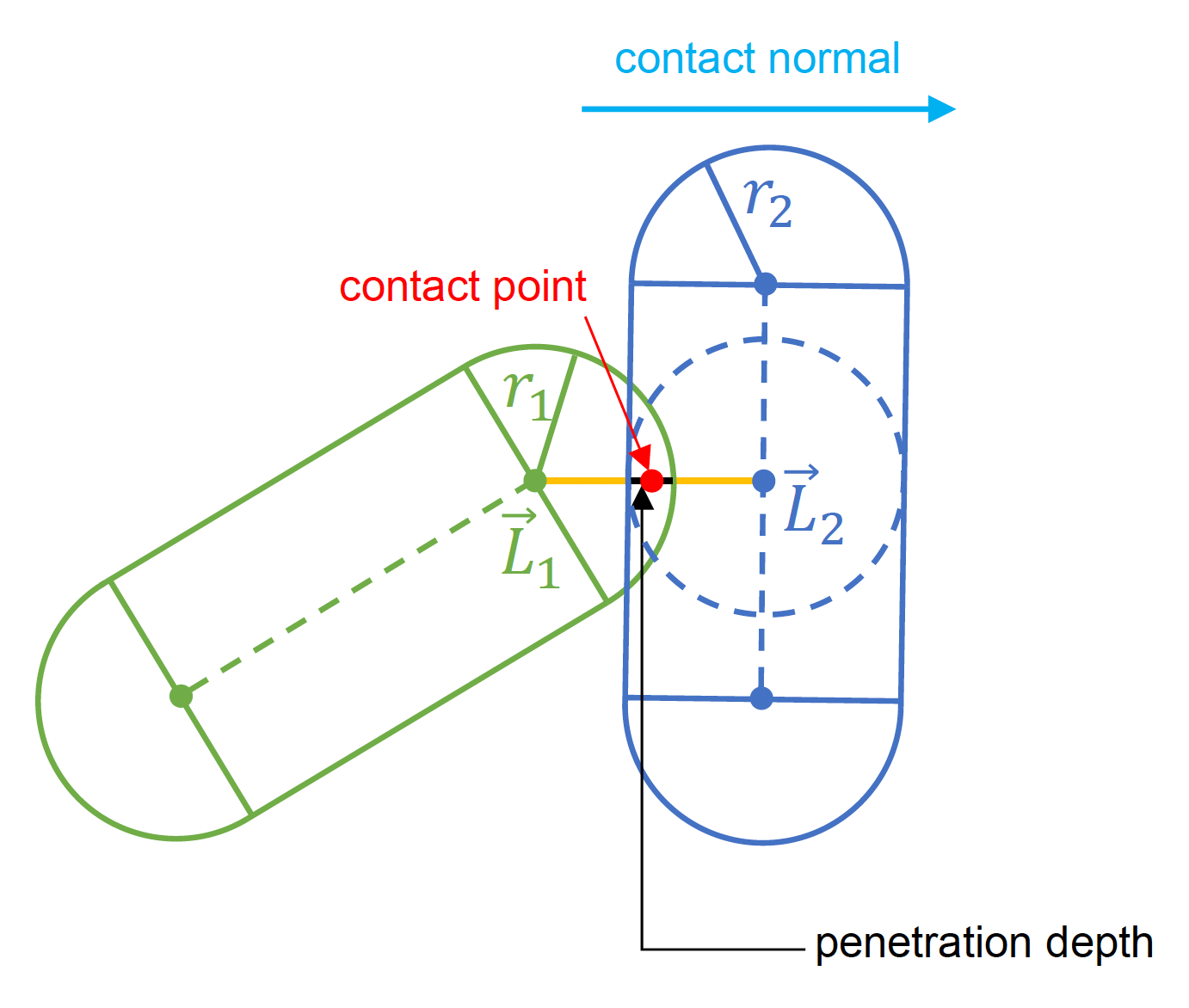
胶囊 - 胶囊测试
其中 \(\vec{L}_1, \vec{L}_2\) 为在两个段之间最近的点
- 重叠条件:\(|\vec{L}_2 - \vec{L}_1| - r_1 - r_2 \le 0\)
- 接触信息:
- 接触法线:\((\vec{L}_2 - \vec{L}_1) / |\vec{L}_2 - \vec{L}_1|\)
- 穿透深度:\(|\vec{L}_2 - \vec{L}_1| - r_1 - r_2\)
-
-
基于闵可夫斯基差的方法(Minkowski difference-based methods)
-
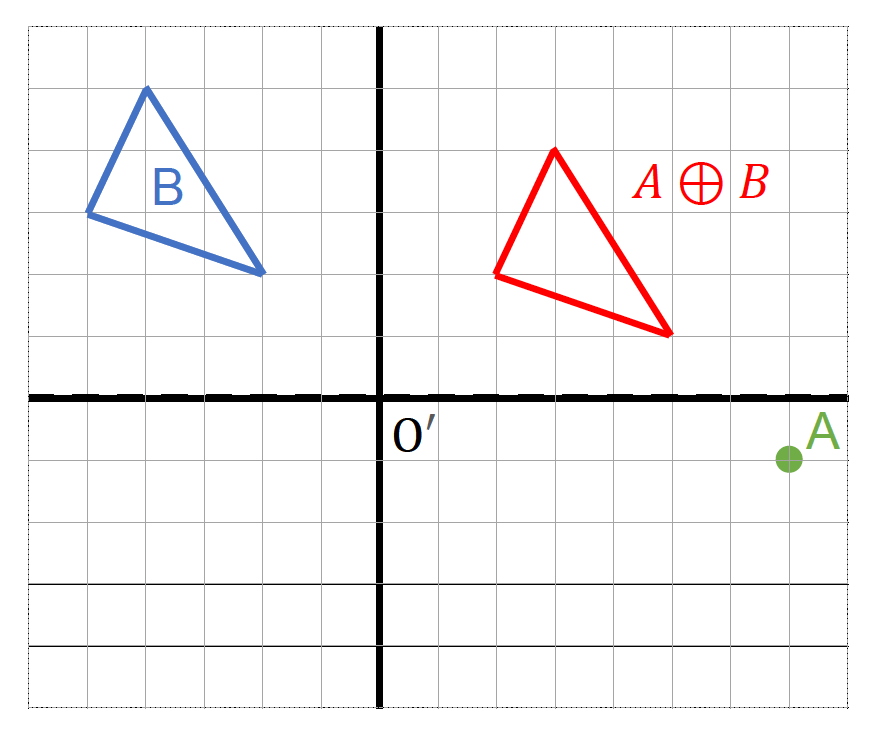
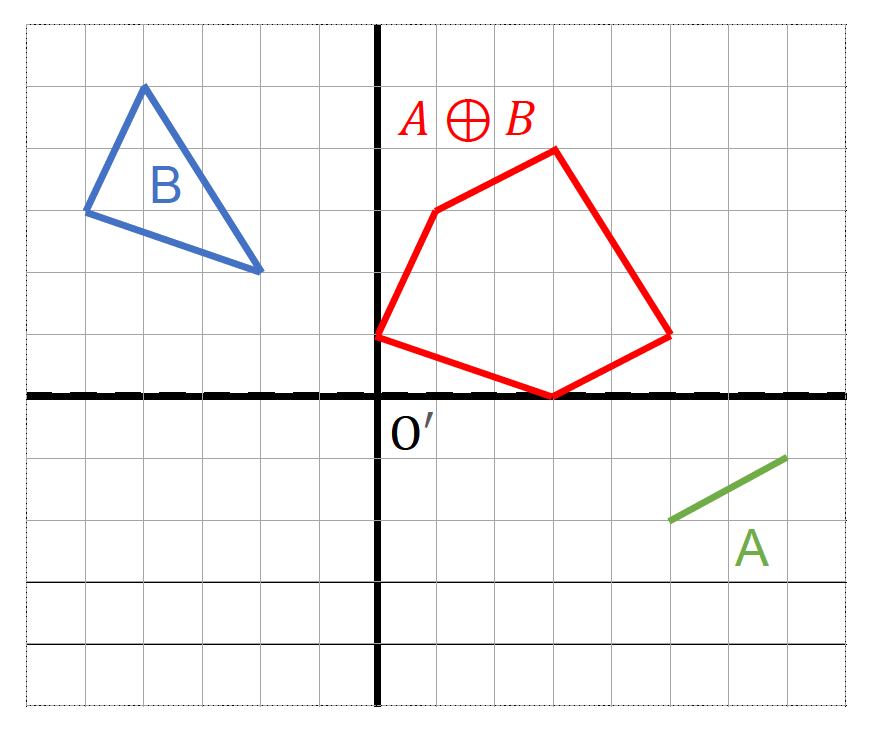
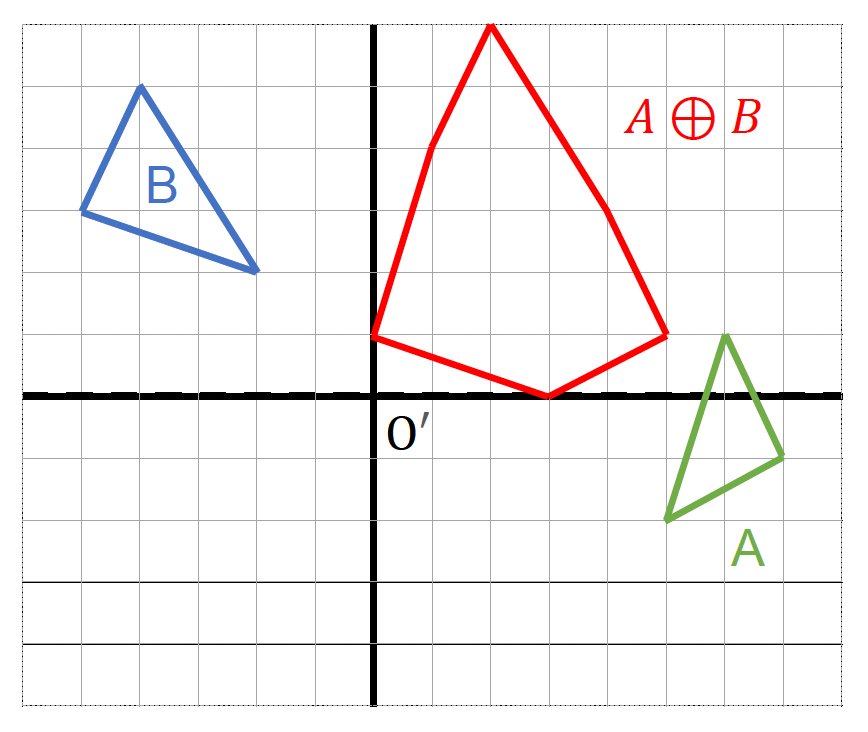
闵可夫斯基和:来自 A 的点 + 来自 B 的点 = 这两个点的闵可夫斯基和
\[ A \oplus B = \{\vec{a} + \vec{b} : \vec{a} \in A, \vec{B} \in B\} \]例子
-
关于凸多边形 (convex polygon)
- 定理:若 \(A, B\) 是凸多边形,那么 \(A \oplus B\) 也是凸多边形
- \(A \oplus B\) 的顶点是 \(A, B\) 的顶点和
-
-
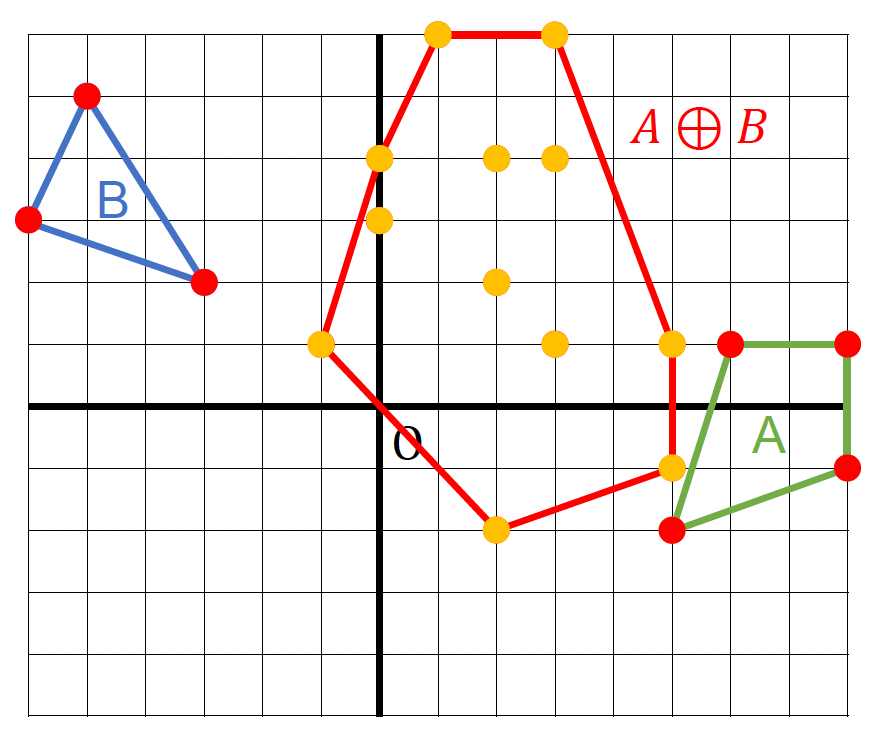
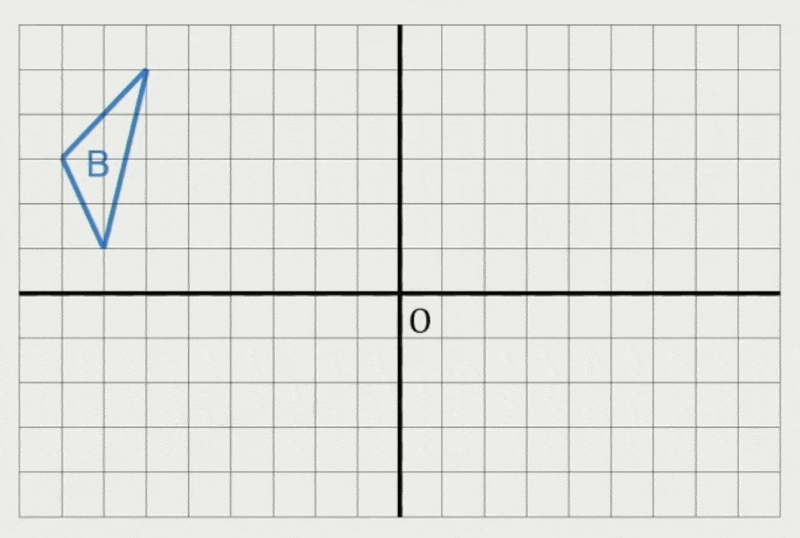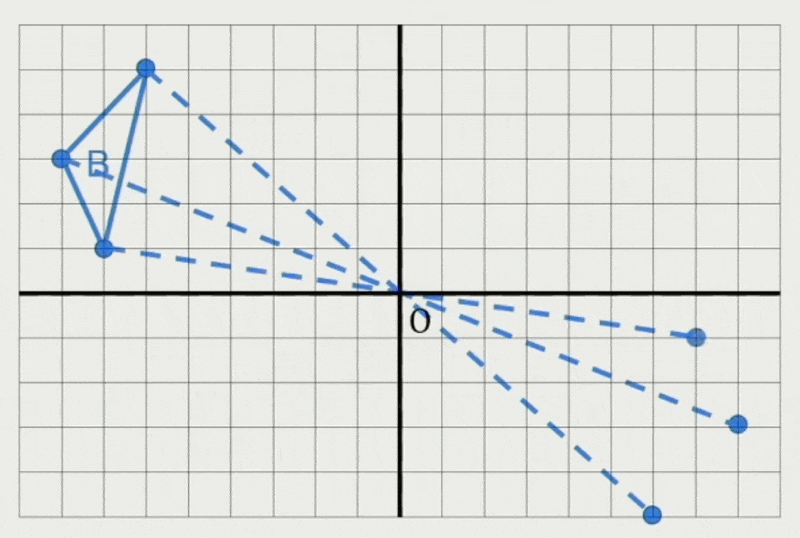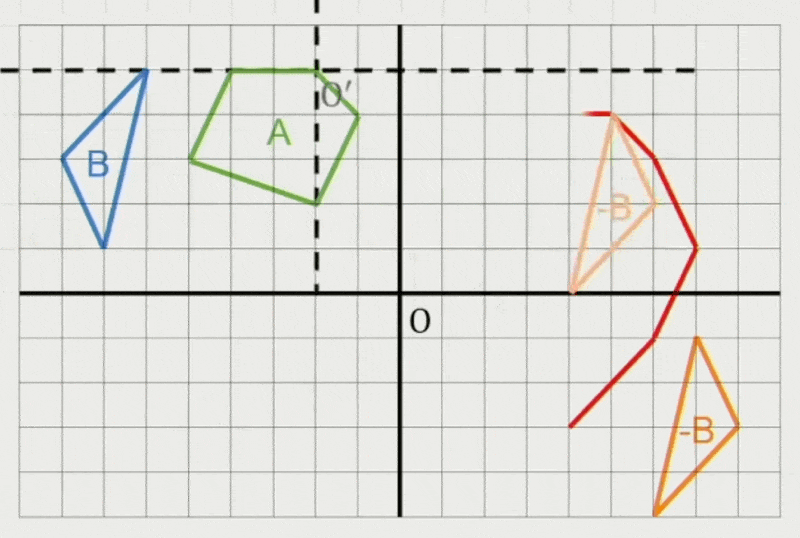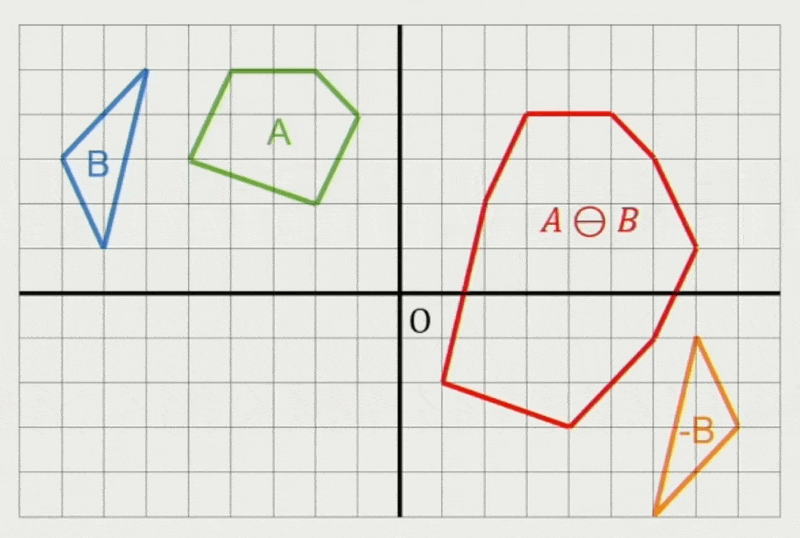
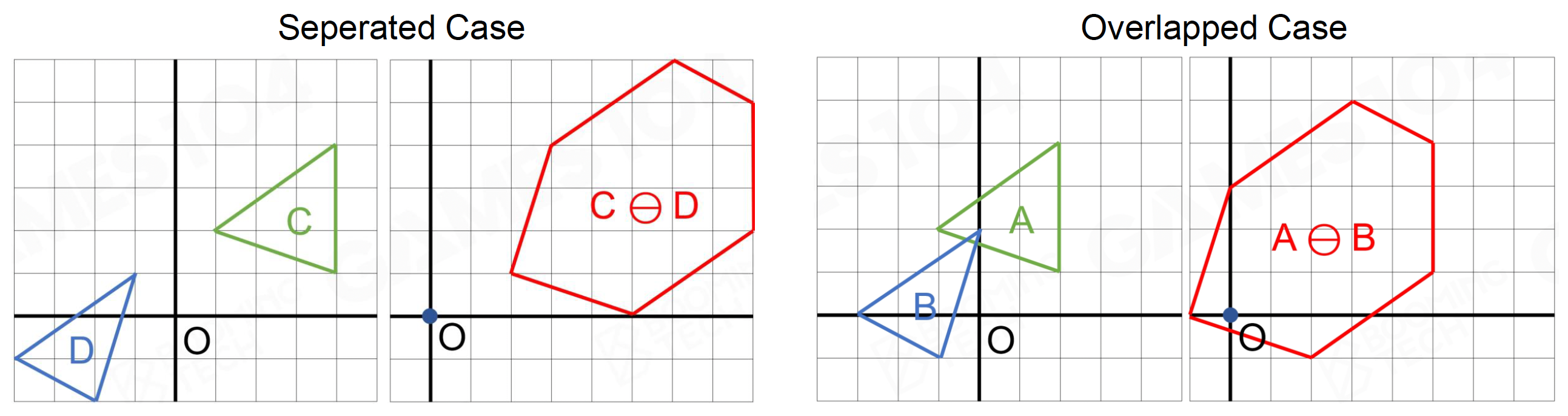
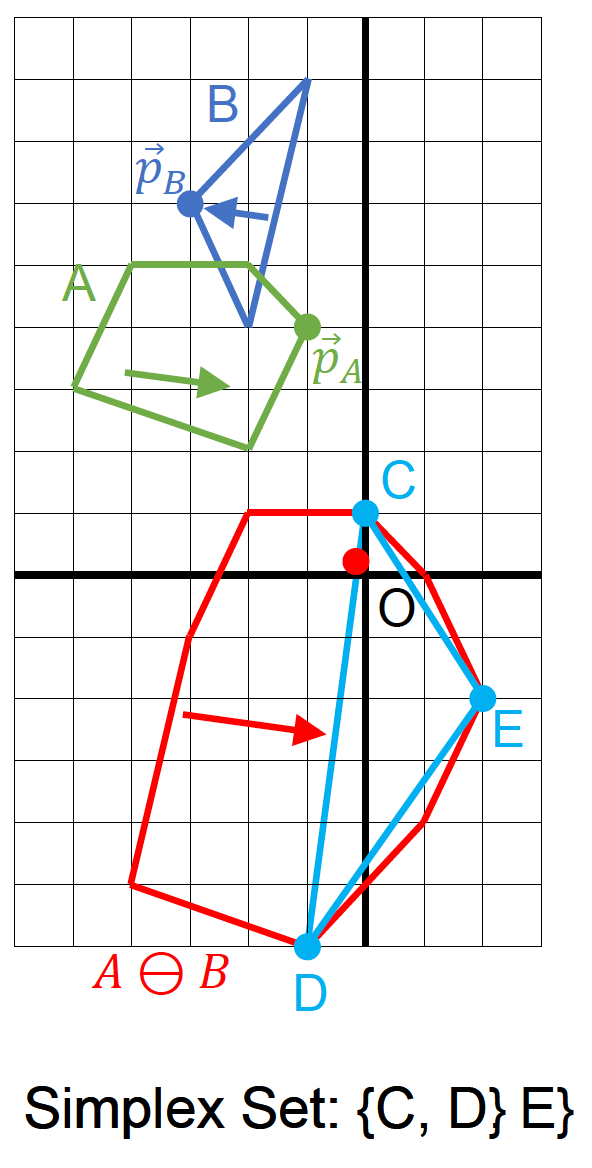
闵可夫斯基差:来自 A 的点 - 来自 B 的点 = 这两个点的闵可夫斯基差
\[ A \ominus B = \{\vec{a} - \vec{b} : \vec{a} \in A, \vec{B} \in B\} \]-
也可以看成 \(A\) 和镜像的 \(B\) 的闵可夫斯基和
\[ A \ominus B = A \oplus (-B) \] -
若 \(A, B\) 相交,那么原点一定在它们的闵可夫斯基差的内部
-
-
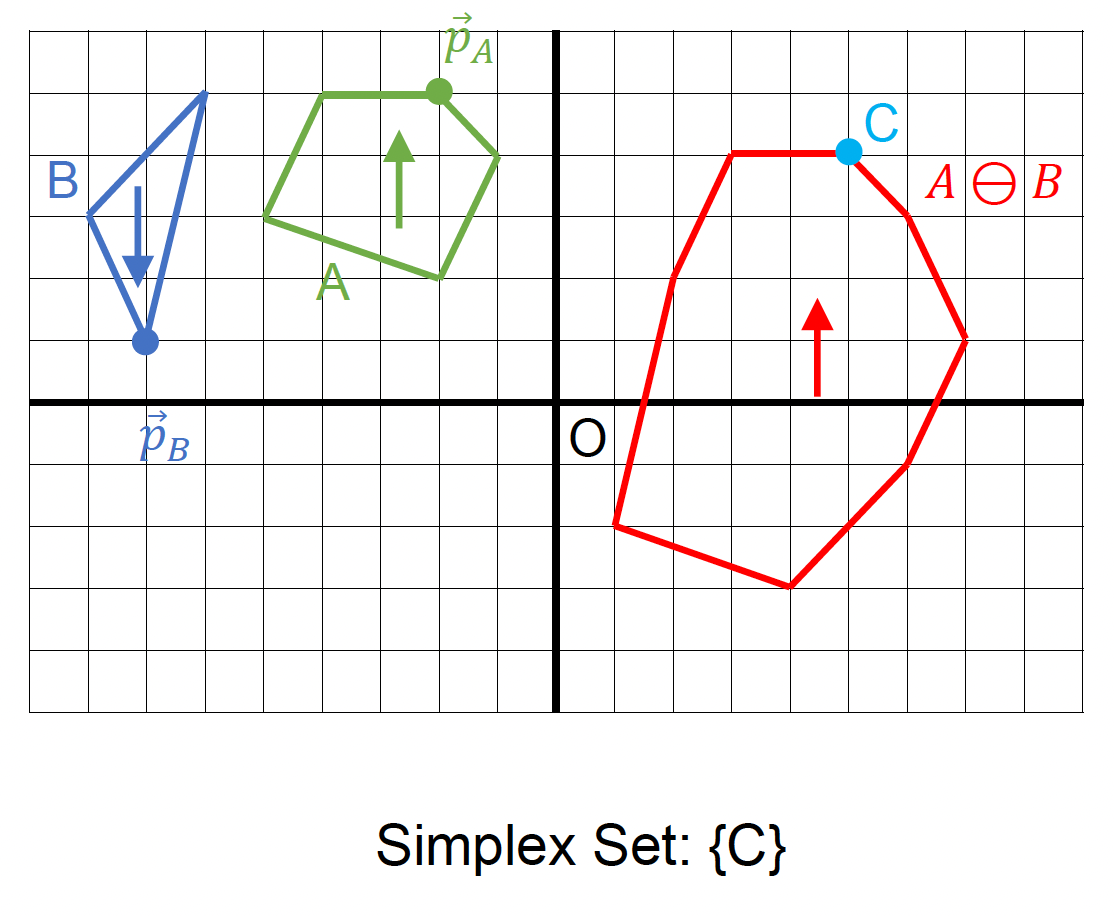
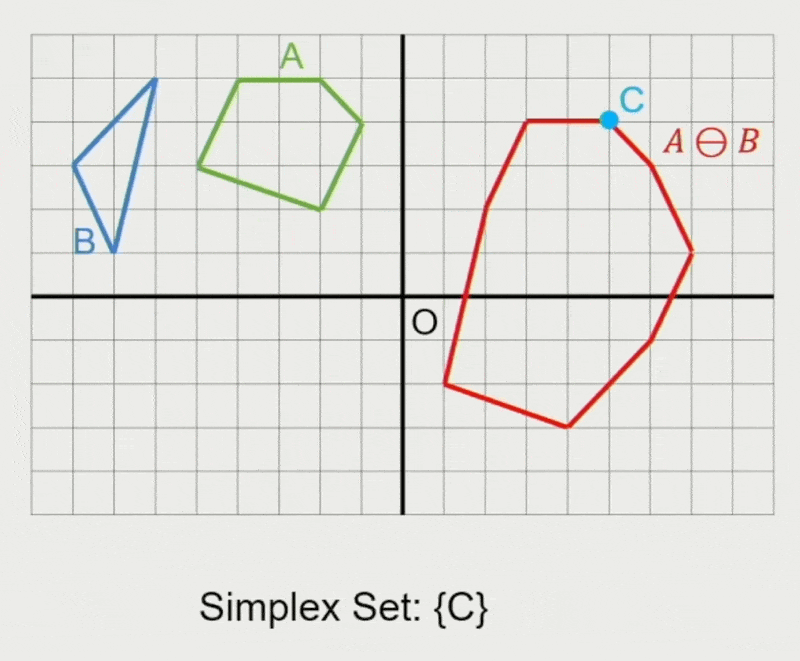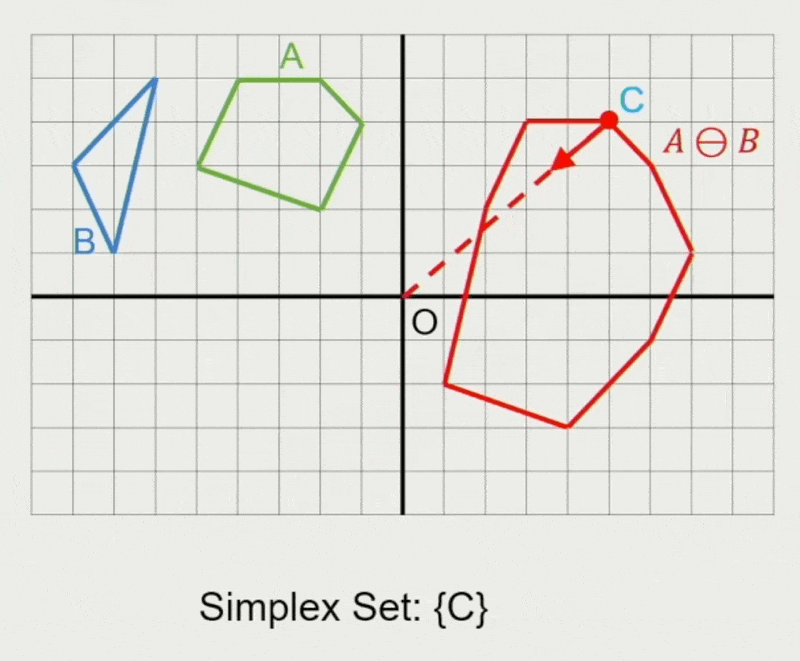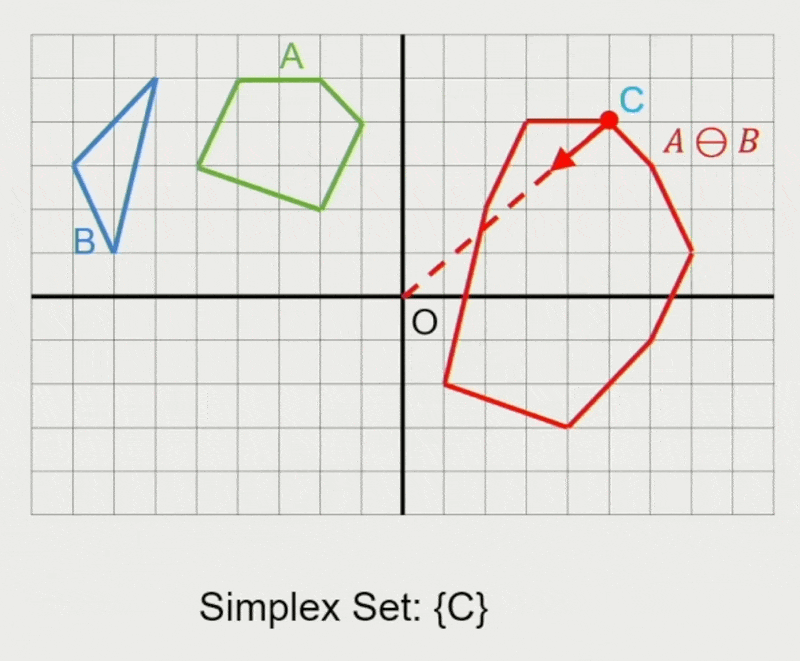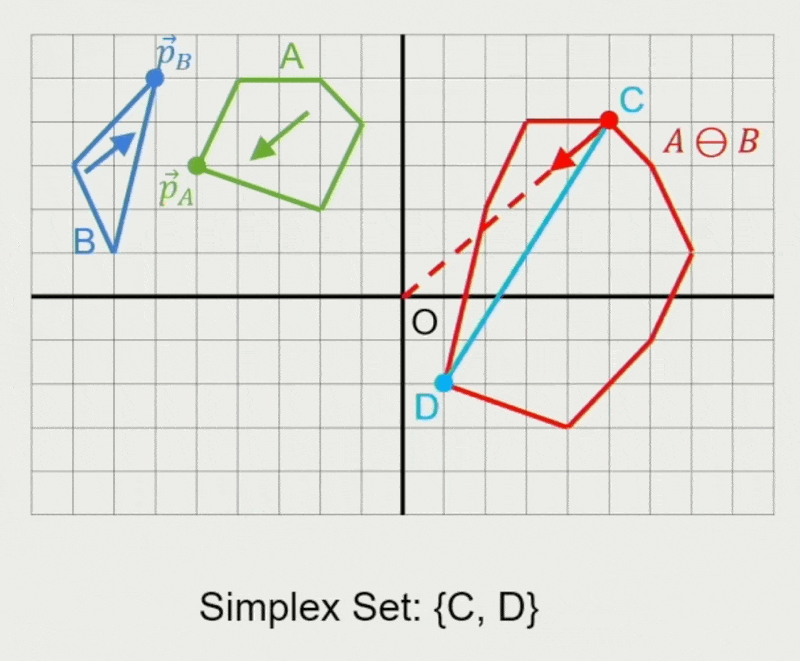
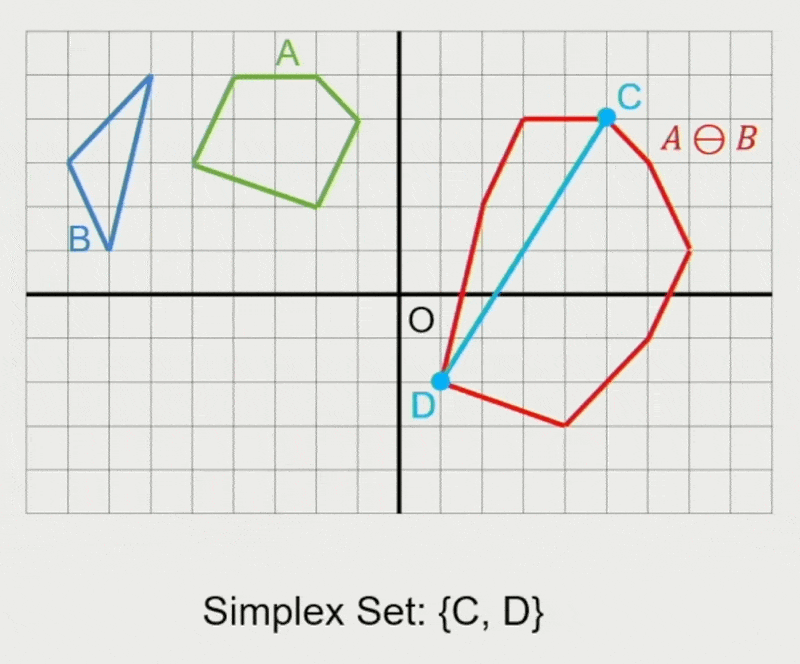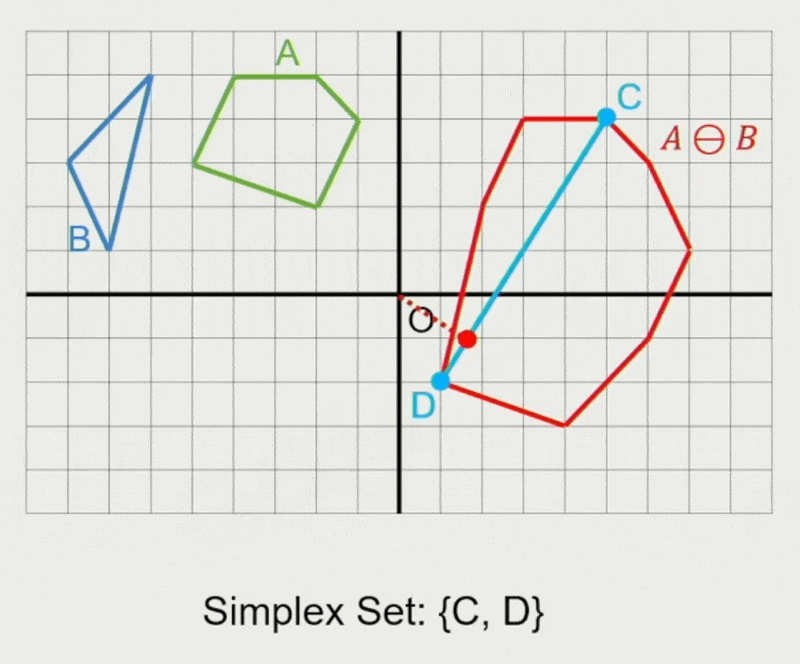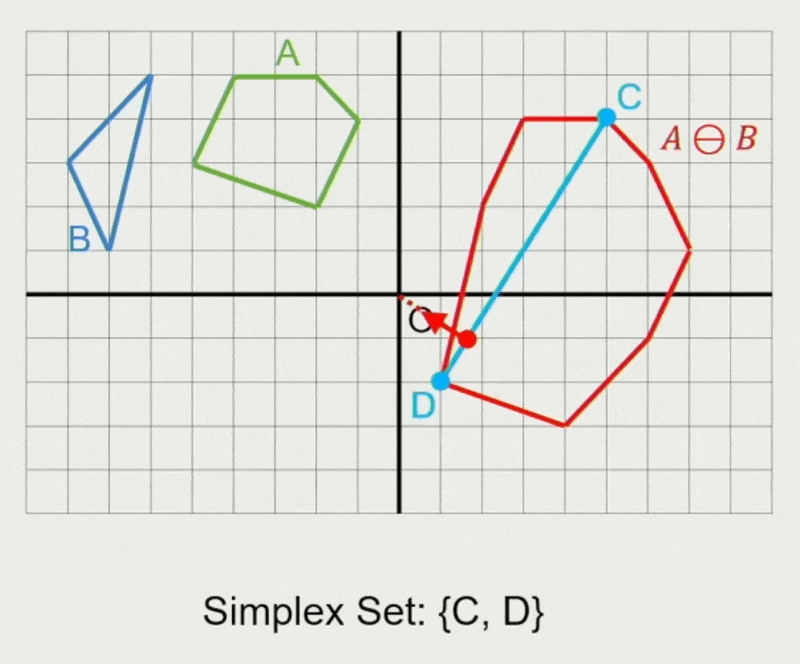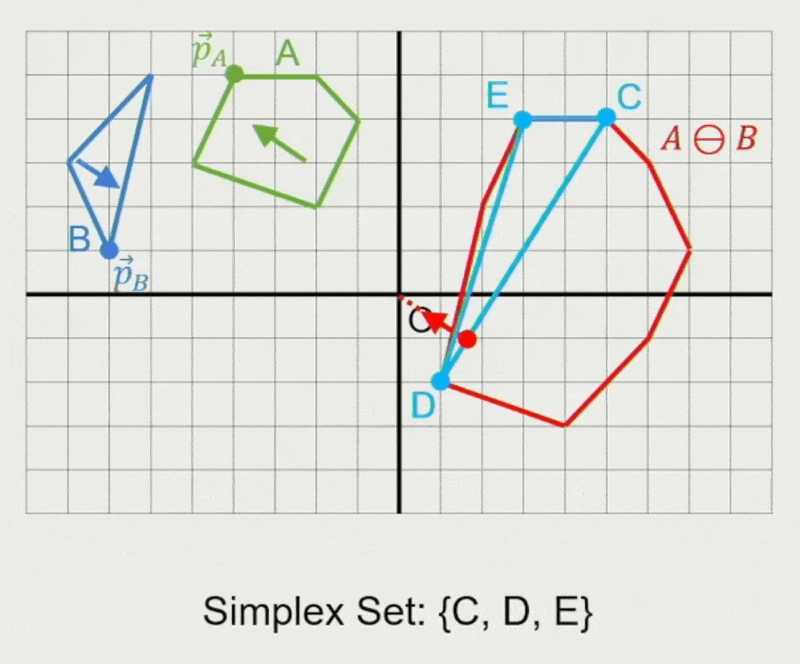
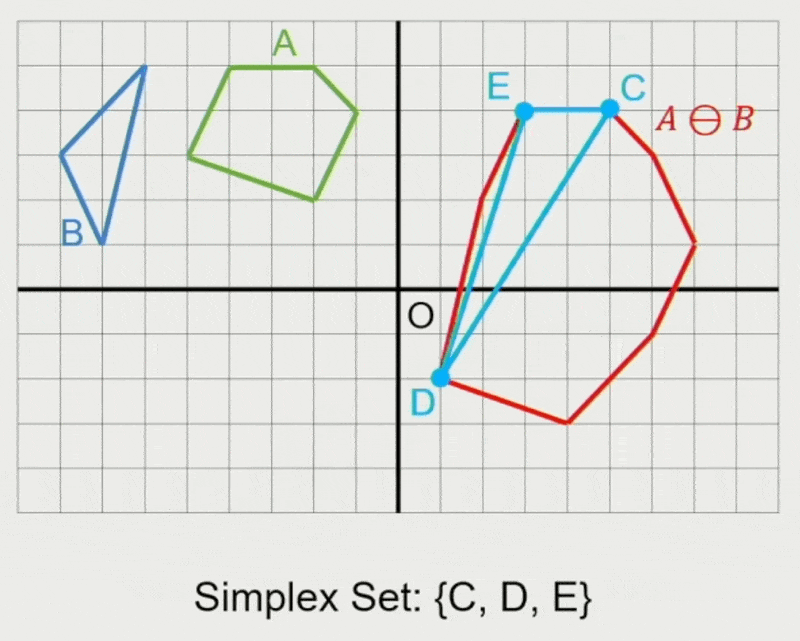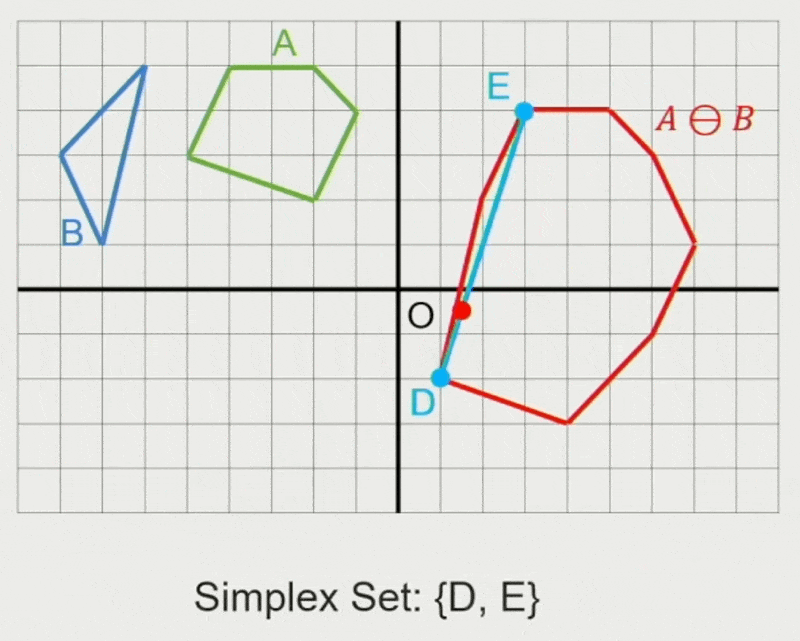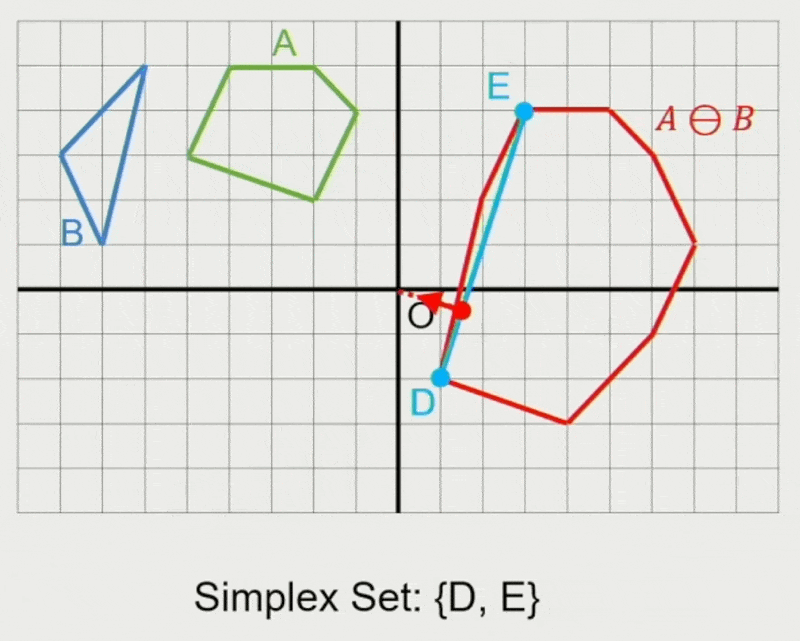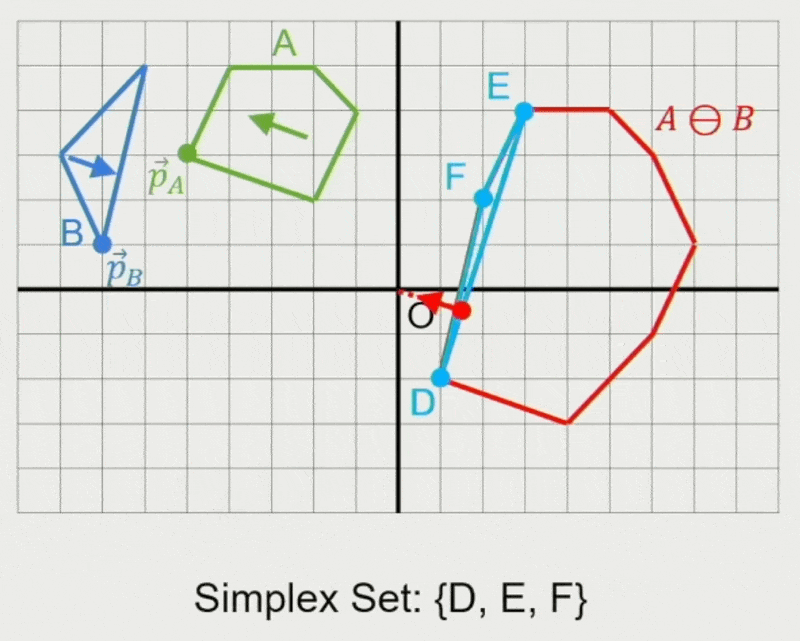
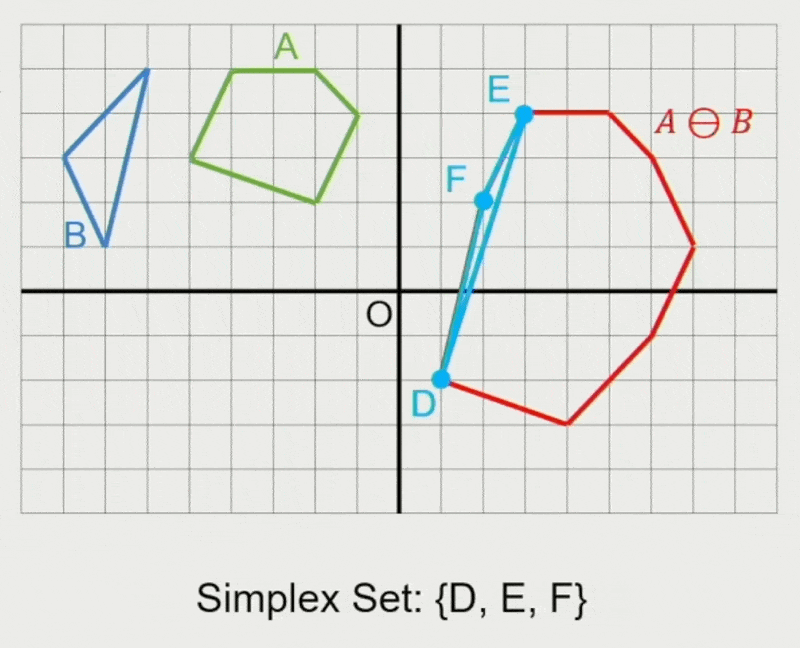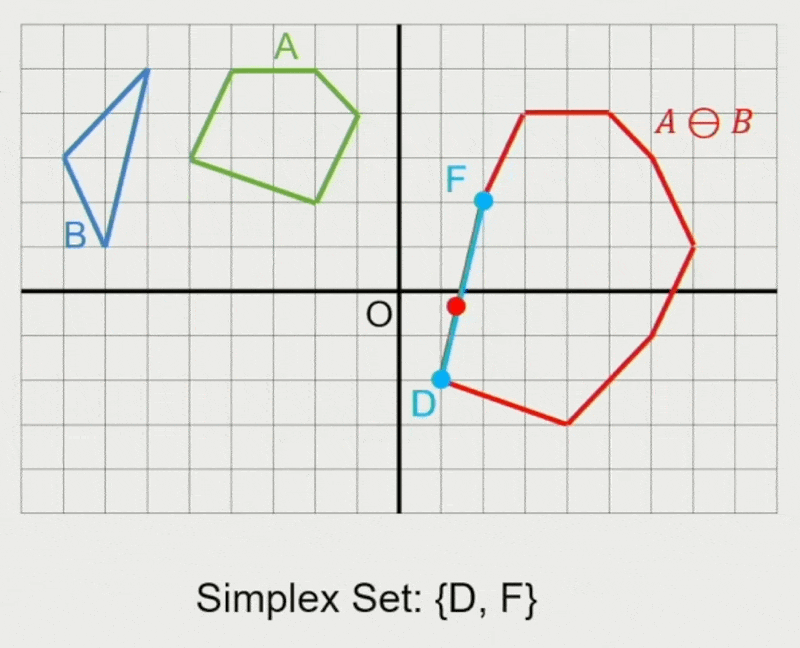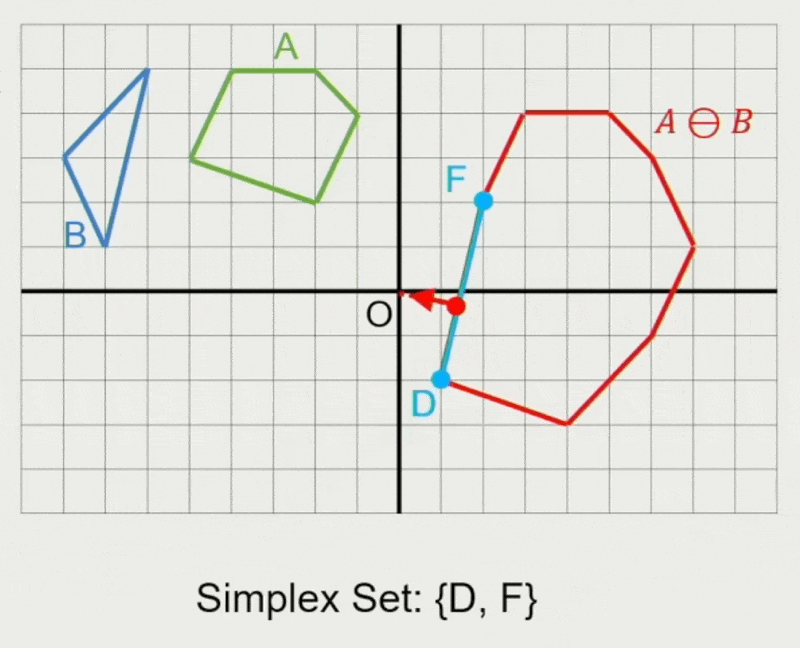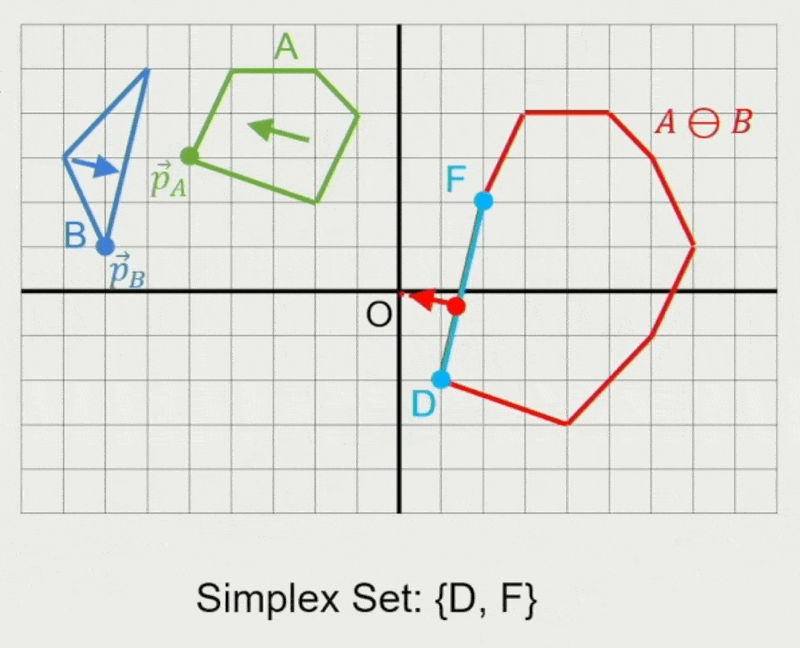
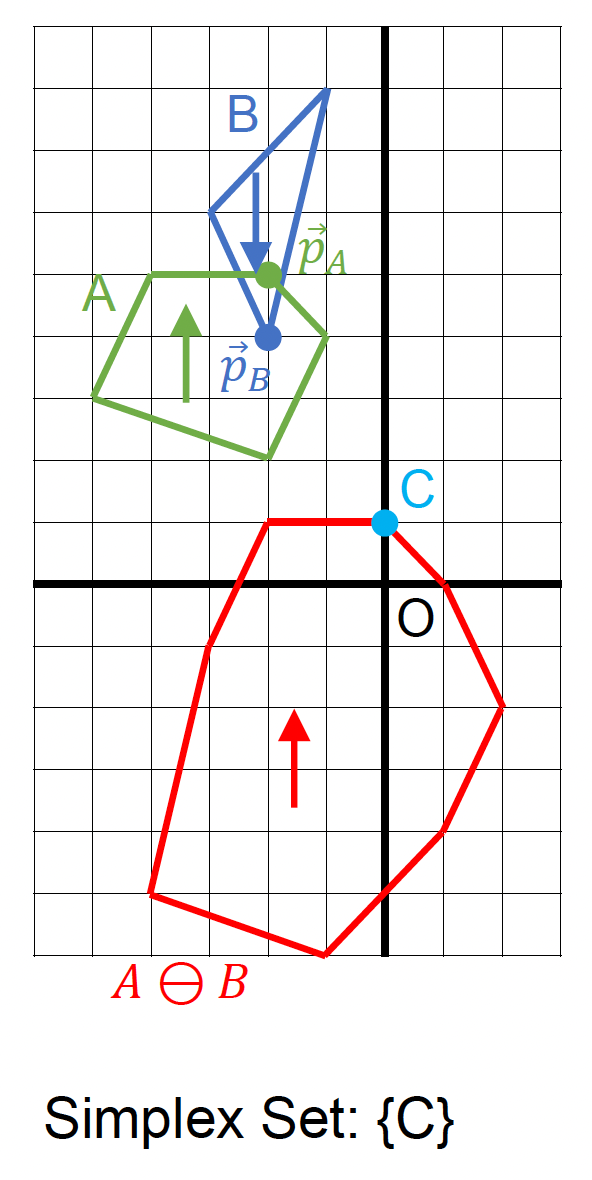
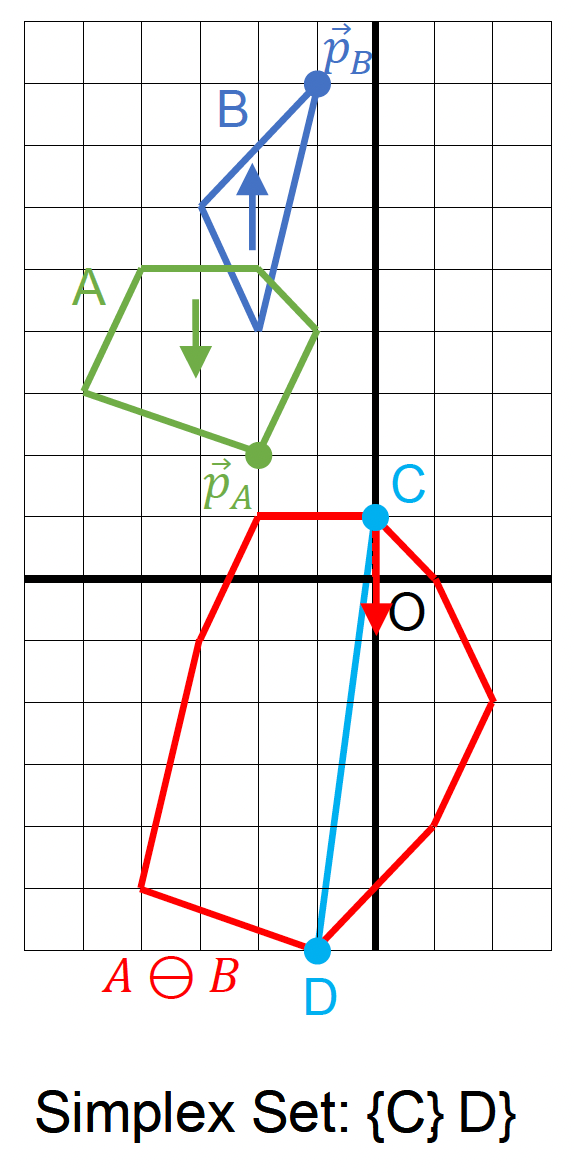
GJK 算法:
- 确定迭代方向
- 检查原点是否在单纯形(simplex) 内
- 在单纯形内找到离原点最近的点
- 若最近距离还能减少,则继续迭代
- 从单纯形中移除对新最近点没有贡献的点
- 寻找支持点 \(\vec{p}_A, \vec{p}_B\)
- 在闵可夫斯基差上向迭代单纯形添加新点 \(\vec{p}_A - \vec{p}_B\)
- 确定迭代方向
-
-
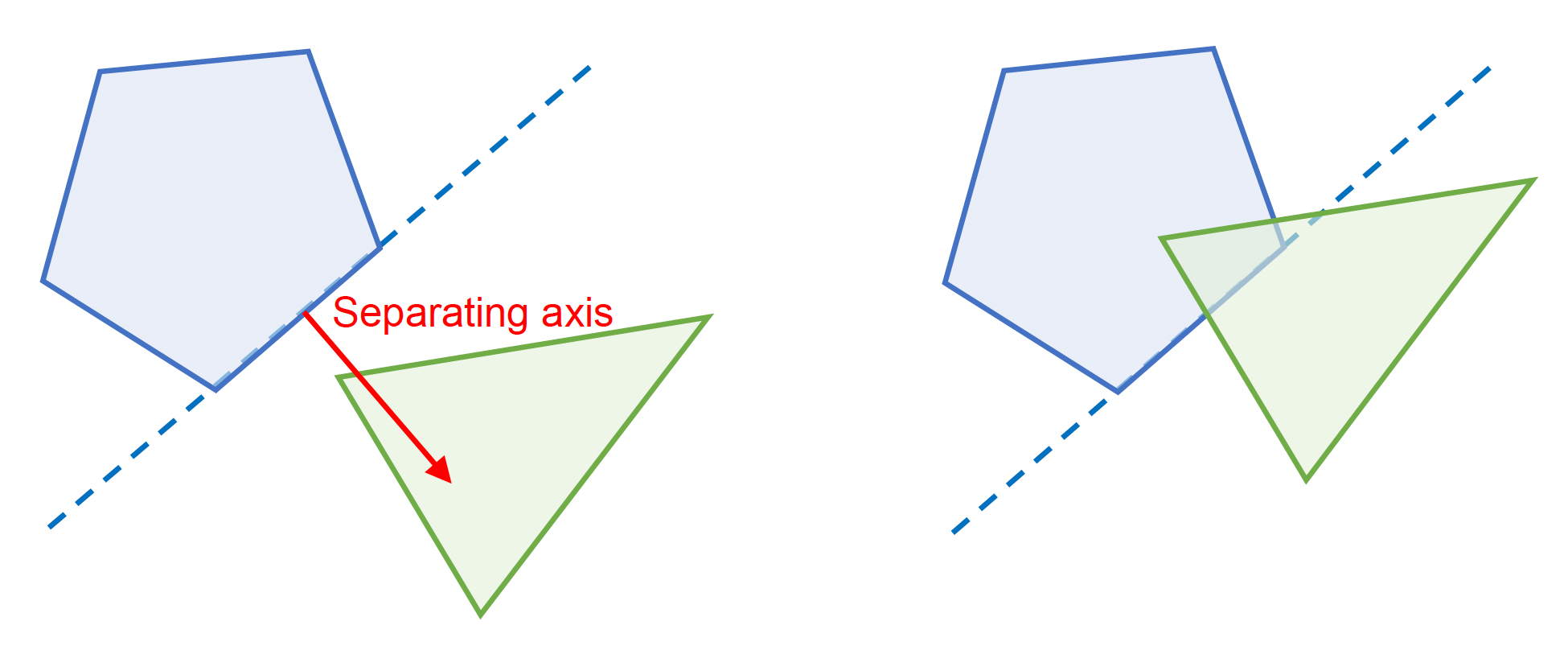
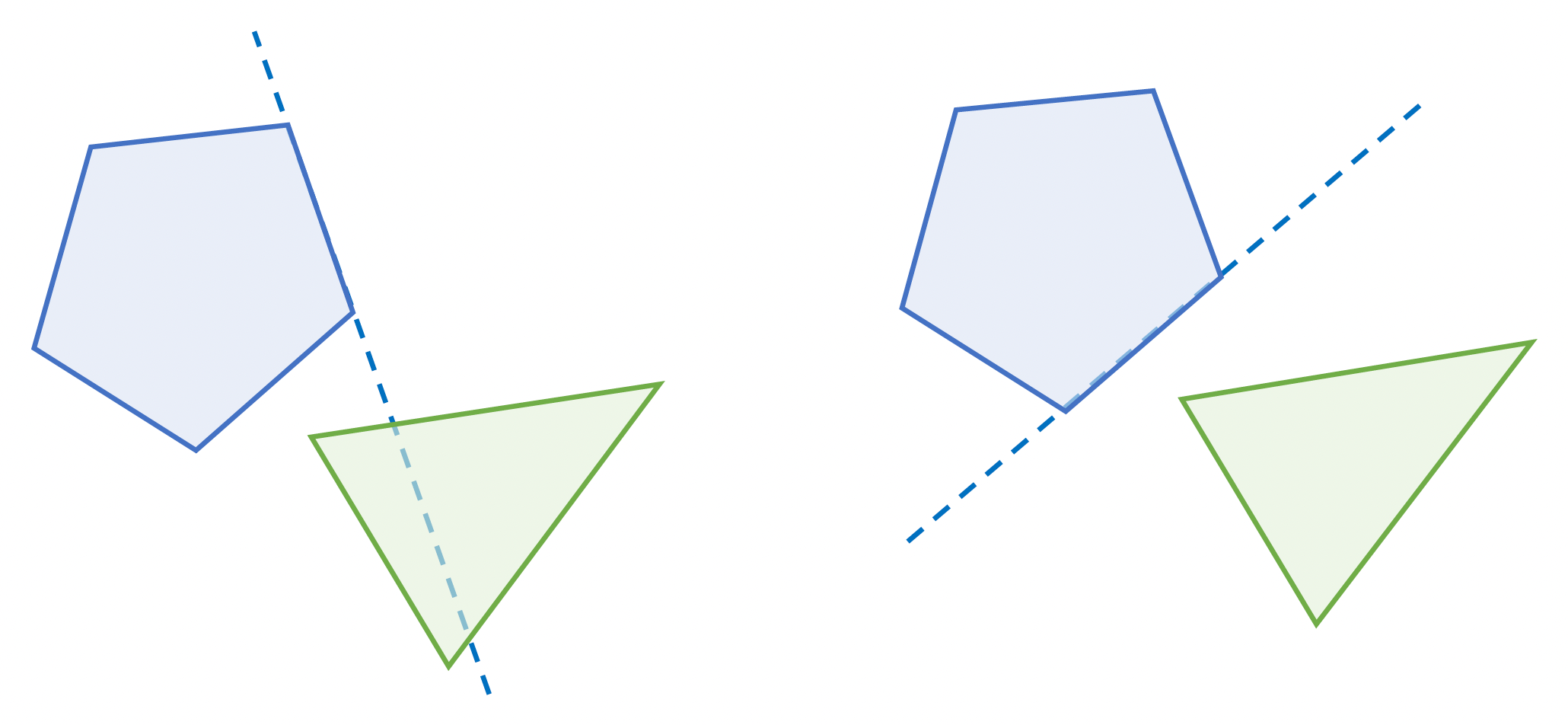
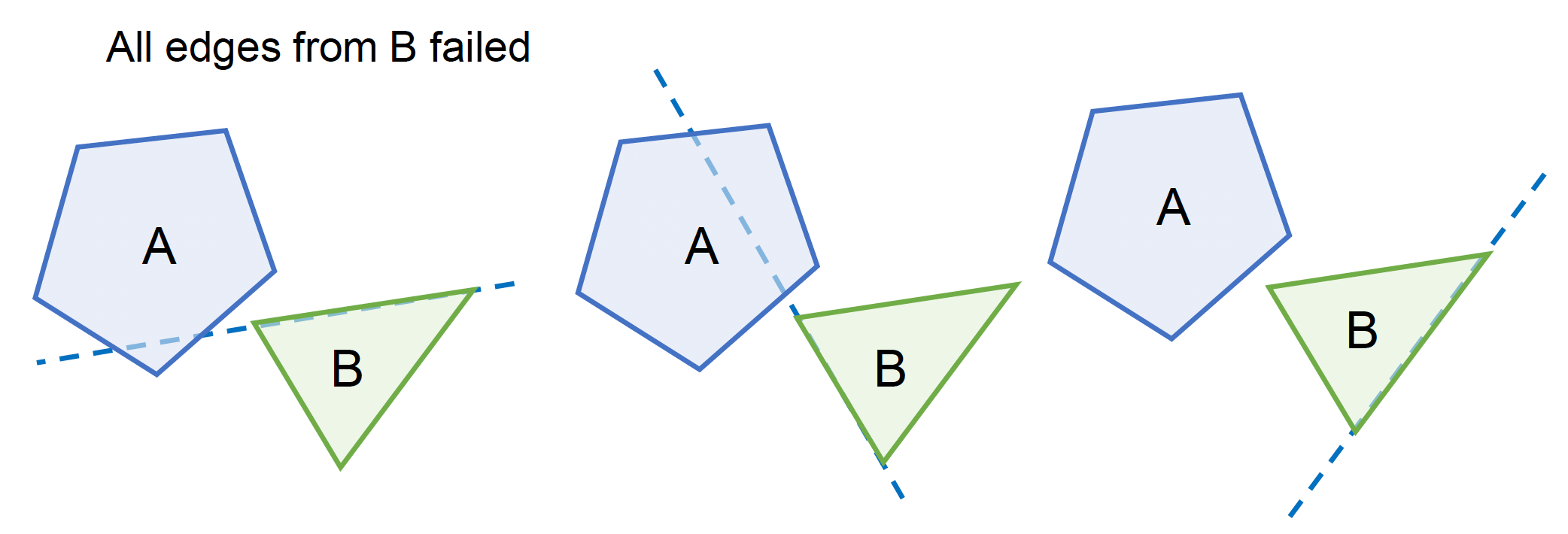
分离轴定理(seperating axis theorem, SAT)
-
由于凸性 (convexity),任何边都可用于分离两个凸多边形
-
另一种理解:在 2D 情况下,一定能找到一条轴,使得两个多边形的顶点在这条轴上的投影是分离的(两个投影顶点集合没有交集)
-
一定要检查所有的边,直到找到一条分离轴
-
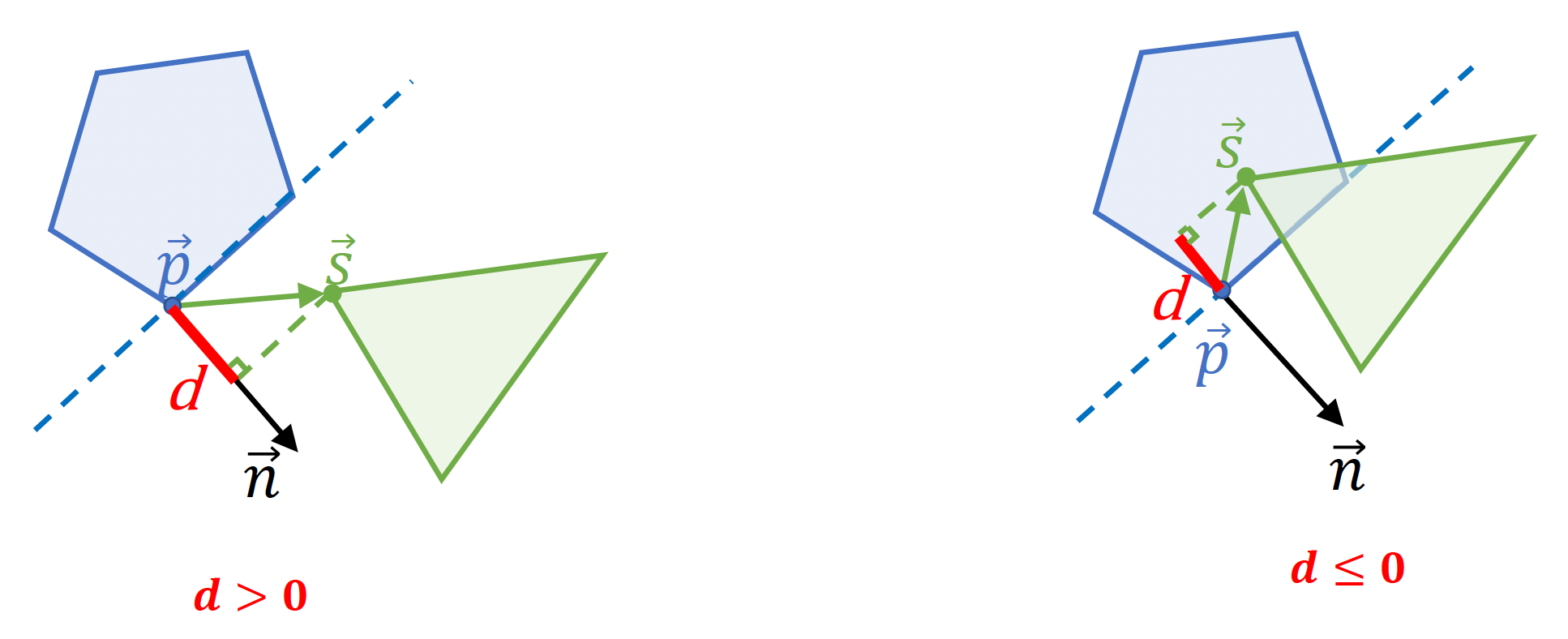
分离标准:\(\textcolor{red}{d} = \vec{n} \cdot (\textcolor{yellowgreen}{\vec{s}} - \textcolor{cornflowerblue}{\vec{p}})\),穿透深度就是 \(|d|\)
-
SAT-2D 算法
- 对 A 的每条边检查 B 的每个顶点
- 对 B 的每条边检查 A 的每个顶点
-
SAT-2D 算法的优化:缓存上一个分离轴
-
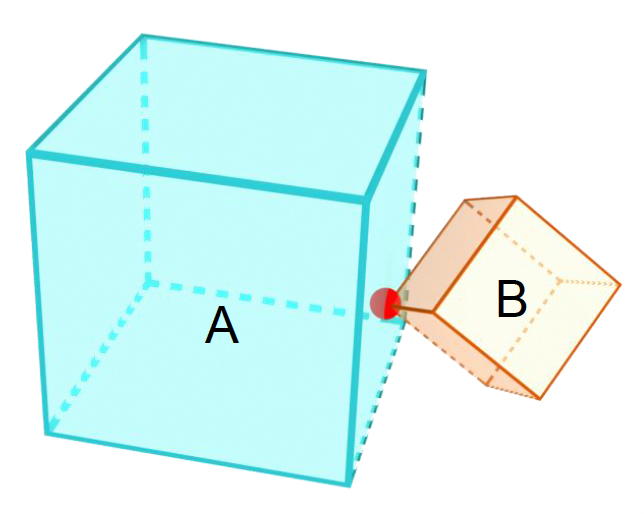
SAT-3D
- 检查 A 的每个面和 B 的每个顶点 -> 分离轴为 A 的面法线
- 检查 B 的每个面和 A 的每个顶点 -> 分离轴为 B 的面法线
- 检查 A 的每条边和 B 的每条边 -> 分离轴为两条边的叉积
-
Collision Resolution⚓︎
有了精确检测碰撞和获取碰撞信息的方法后,下一步就要来解决碰撞问题。
Applying Penalty Force⚓︎
第一种方法是向发生碰撞的两个物体各自施加一个惩罚力(penalty force),将它们推开来。问题在于两个物体会迅速远离,看起来很假,因此现代引擎中很少会用这种方法。
Solving Constraints⚓︎
目前常用的方法是将这个力学问题转为数学上的约束问题,即拉格朗日力学(Lagrangian mechanics)。
- 碰撞约束包括非穿透 (non-penetration)、弹性 (restitution) 和摩擦力 (friction)
- 迭代求解
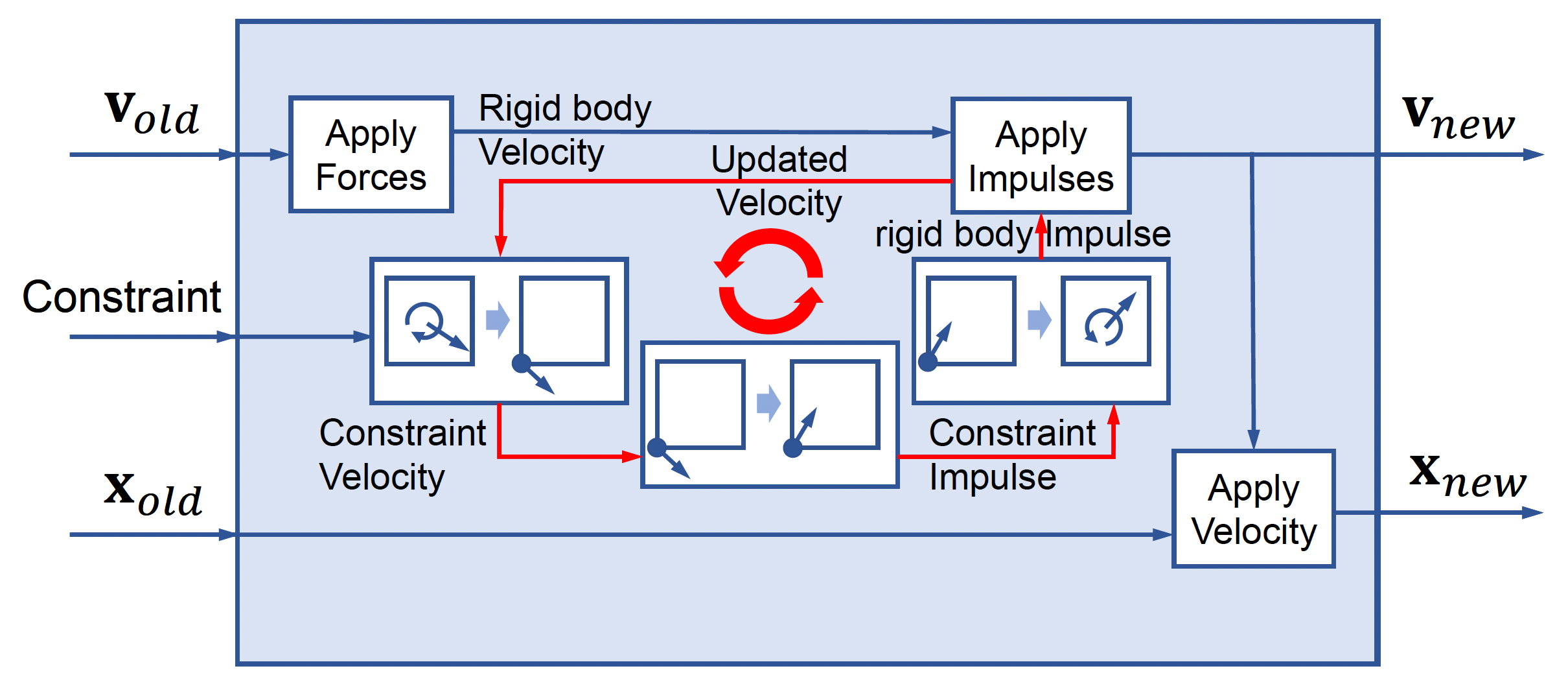
先只考虑求解有关速度的约束:
- 方法
- 顺序冲量 (sequential impulse)
- 半隐式积分 (semi-implicit integration)
- 非线性高斯 - 赛德尔方法 (non-linear Gaussian-Seidel method)
- 特点
- 在很多情况下快速且稳定
- 常用于多数物理引擎
Scene Query⚓︎
场景查询(scene query) 是一种用于检测物体与场景几何体之间空间关系的机制。
Raycast⚓︎
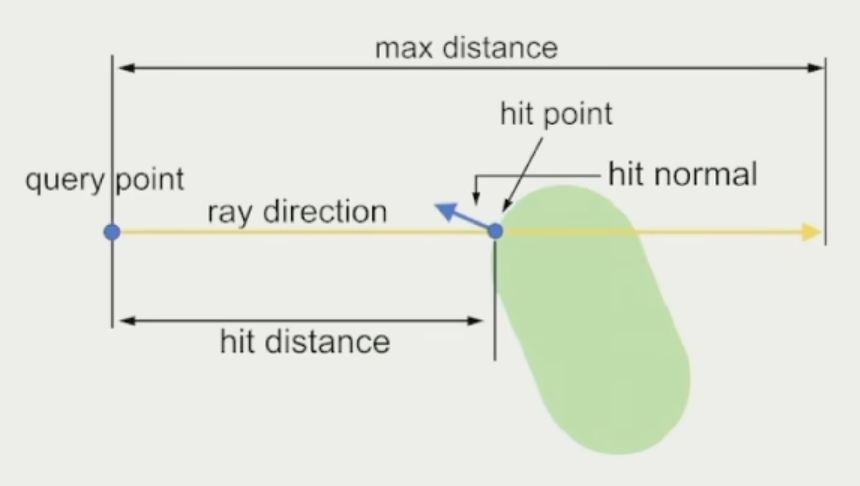
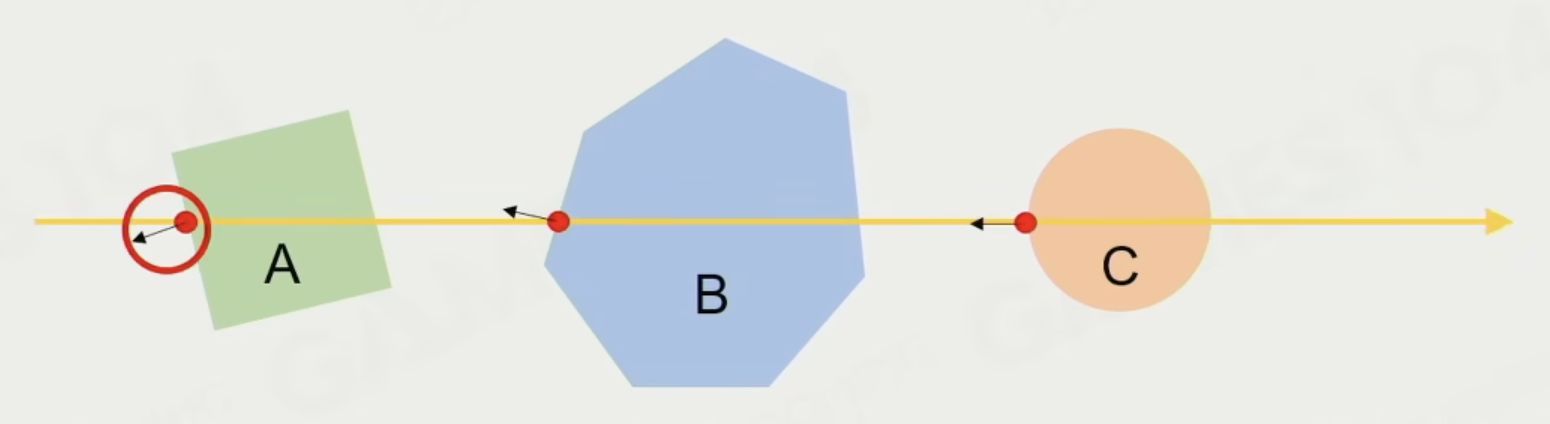
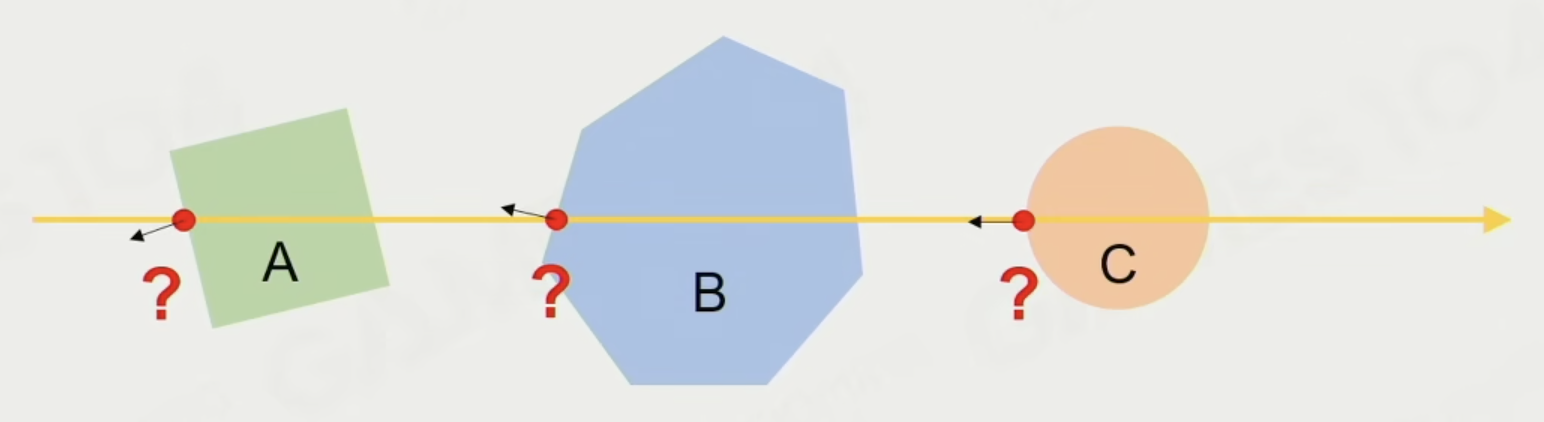
- 射线投射(raycast) 是指将用户定义的射线与整个场景相交
- 可以定义点、方向、距离和查询模式
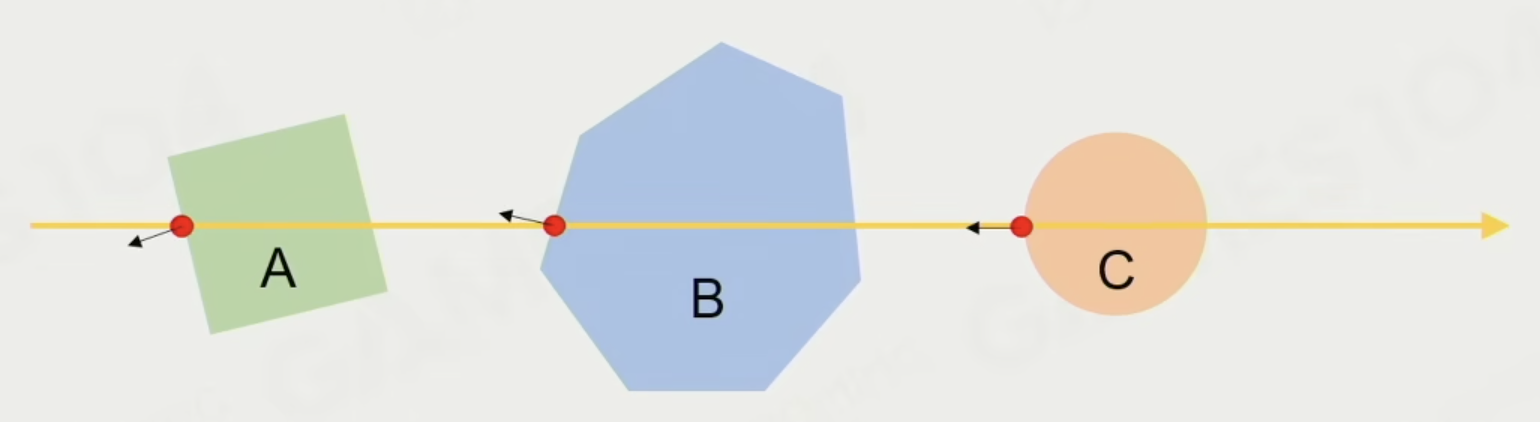
射线投射一般分为以下三类:
-
多命中(multiple hits):寻找所有阻塞命中
-
最近命中(closest hit):寻找所有阻塞命中,选择距离最小的一个
-
任意命中(any hit):任何遇到的命中都行
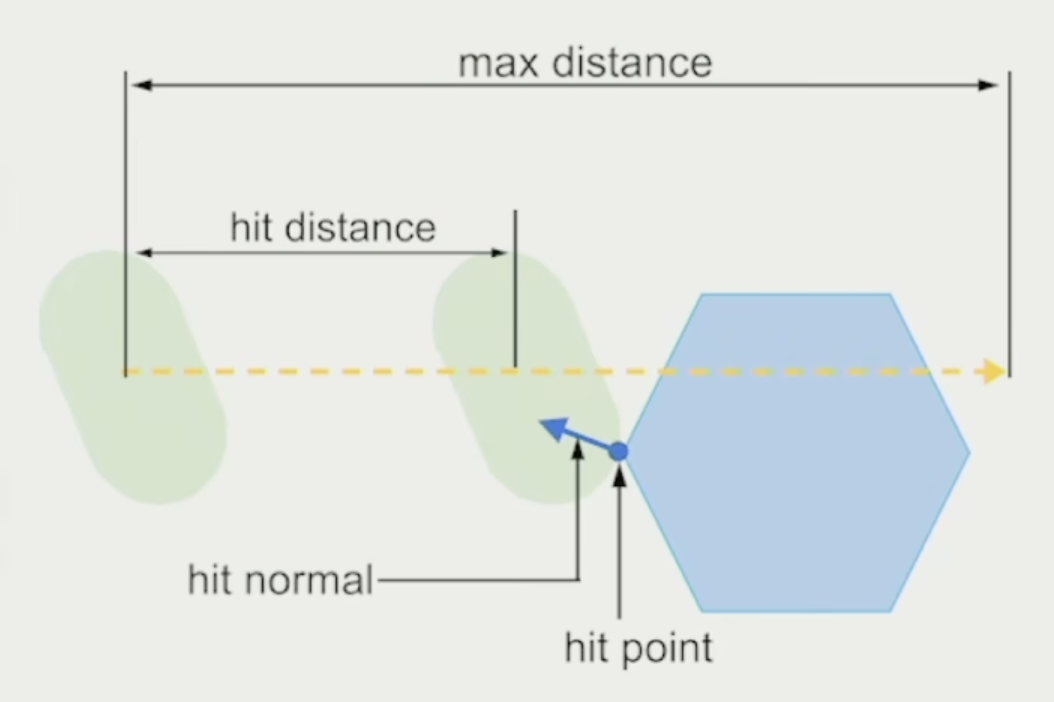
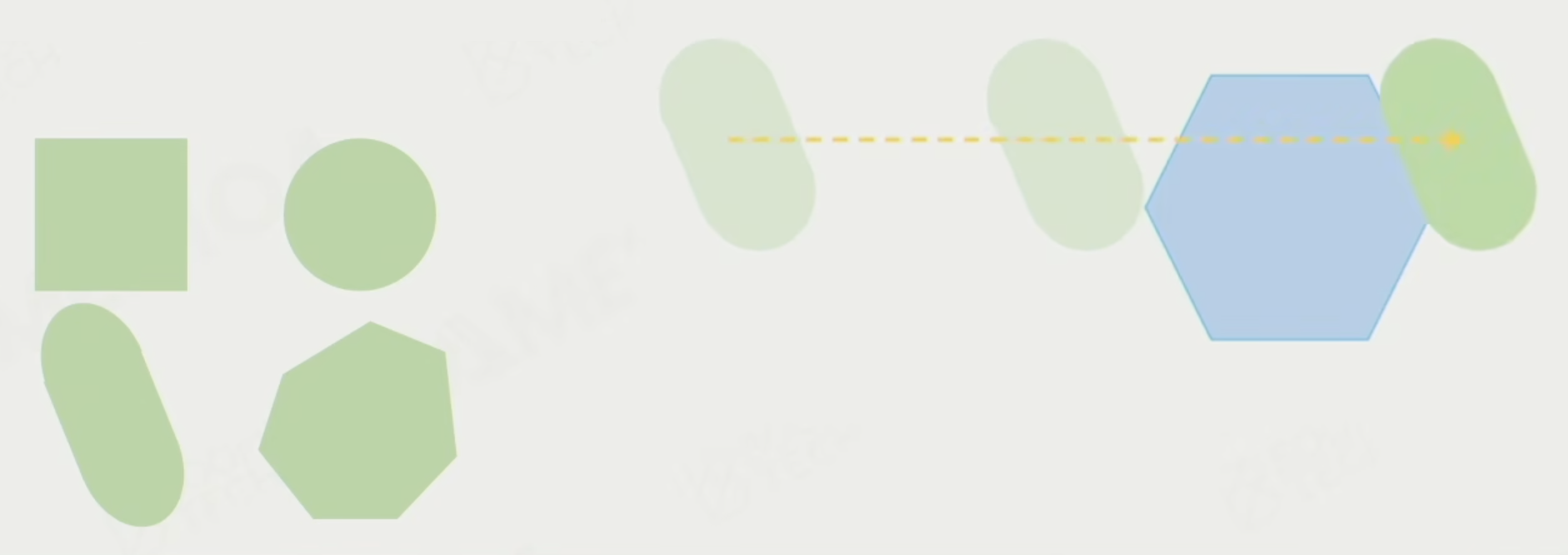
Sweep⚓︎
扫掠(sweep) 在几何上类似于射线投射,但可以定义形状和姿态,包括盒子、球体、胶囊和凸形等。
Overlap⚓︎
重叠(overlap) 查询是指在指定形状包围的区域中搜索场景中的任何重叠对象。指定形状可以是矩形、球体、胶囊和凸形等。
Collision Groups⚓︎
-
参与者具有碰撞组属性
- 玩家:棋子 (pawn)(即可操控角色)
- 障碍物:静态
- 可移动箱子:动态
- 触发框:触发器
-
可以通过场景查询来过滤碰撞组
- 玩家移动查询碰撞组
: (棋子,静态,动态) - 触发器查询碰撞组
: (棋子)
- 玩家移动查询碰撞组
Efficiency, Accuracy, and Determinism⚓︎
Simulation Optimization⚓︎
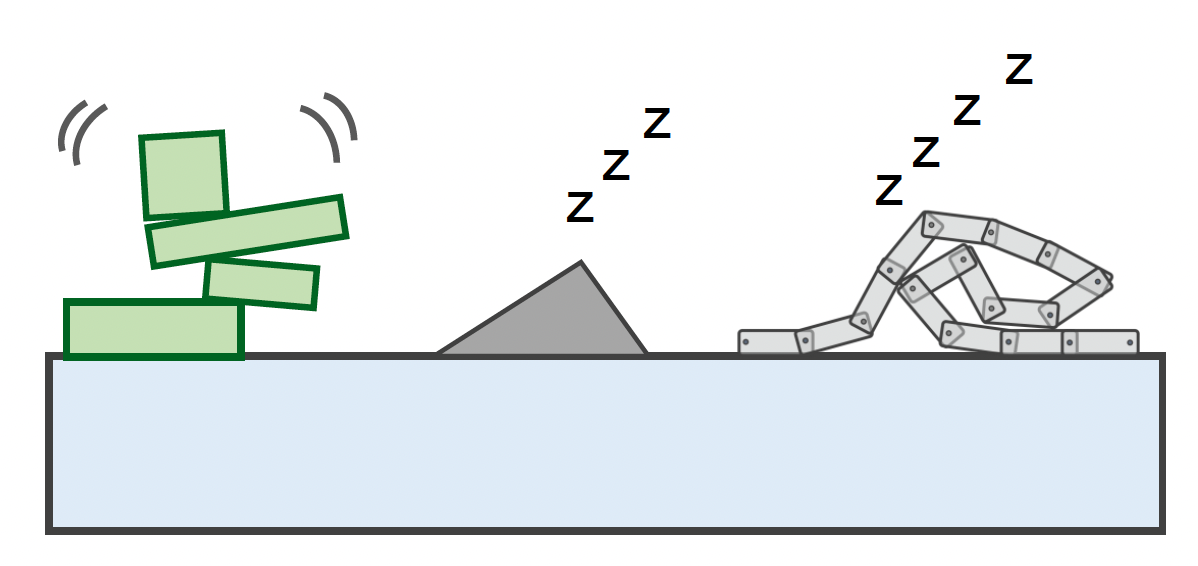
物理世界中会把物体分为一个个的岛屿(island),可简单理解成为物体分组。
- 之所以这么做,是因为要模拟和计算所有的刚体需花费大量资源
-
因此如果一段时间内属于某个岛屿的刚体没有移动,那该岛屿可进入休眠状态,直到再次受到外力作用
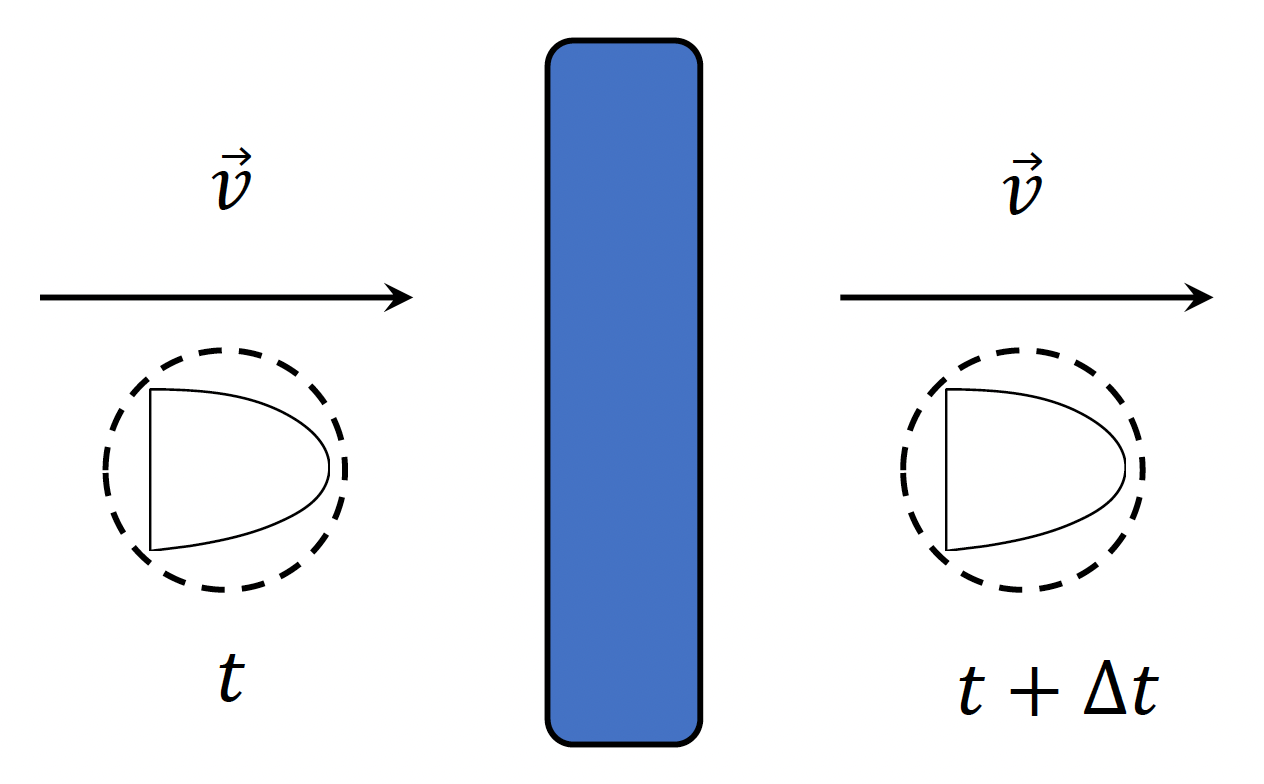
Continuous Collision Detection⚓︎
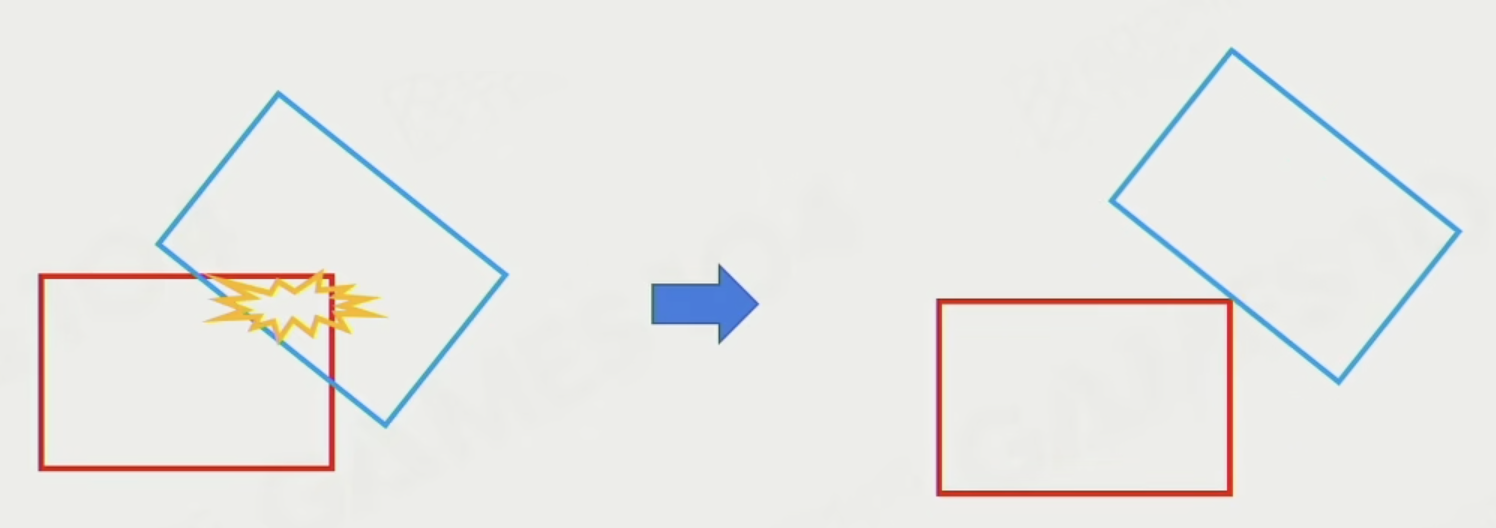
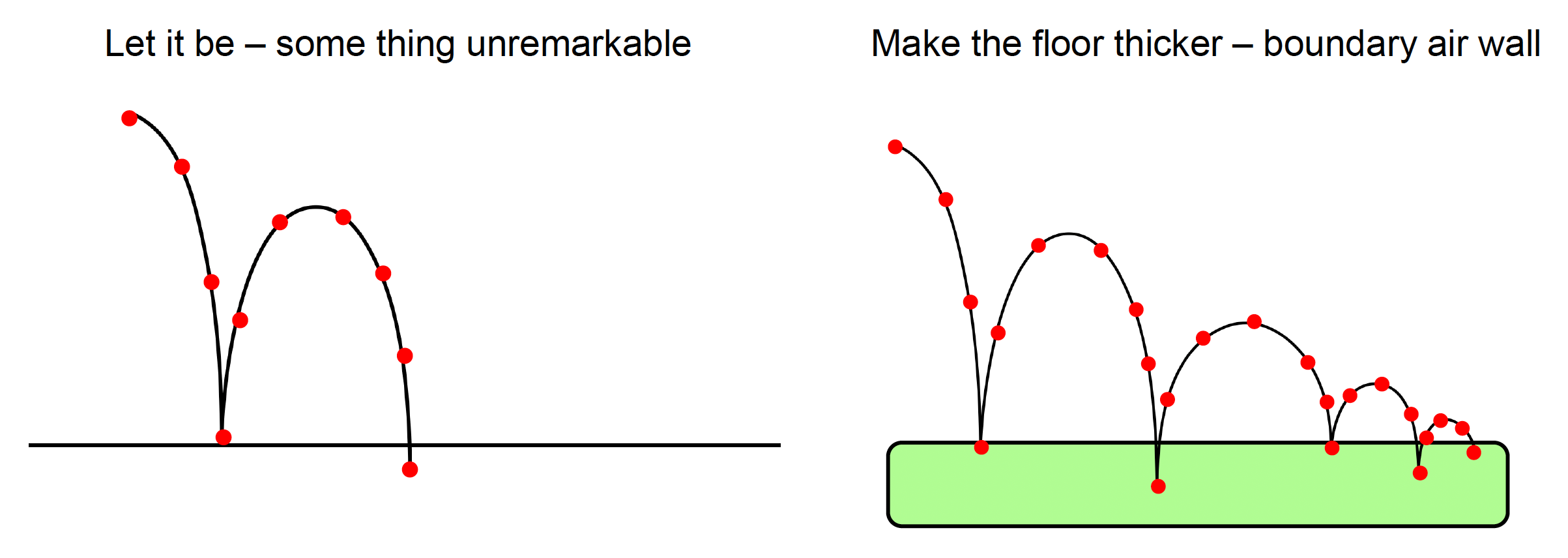
造成这一 bug 的原因就是障碍物太薄 + 角色移动太快,碰撞检测的结果是两者之间没有任何交集,因而导致角色的穿墙。这种现象被称为隧道效应(tunneling)。
-
最简单的方法是把墙体做厚
-
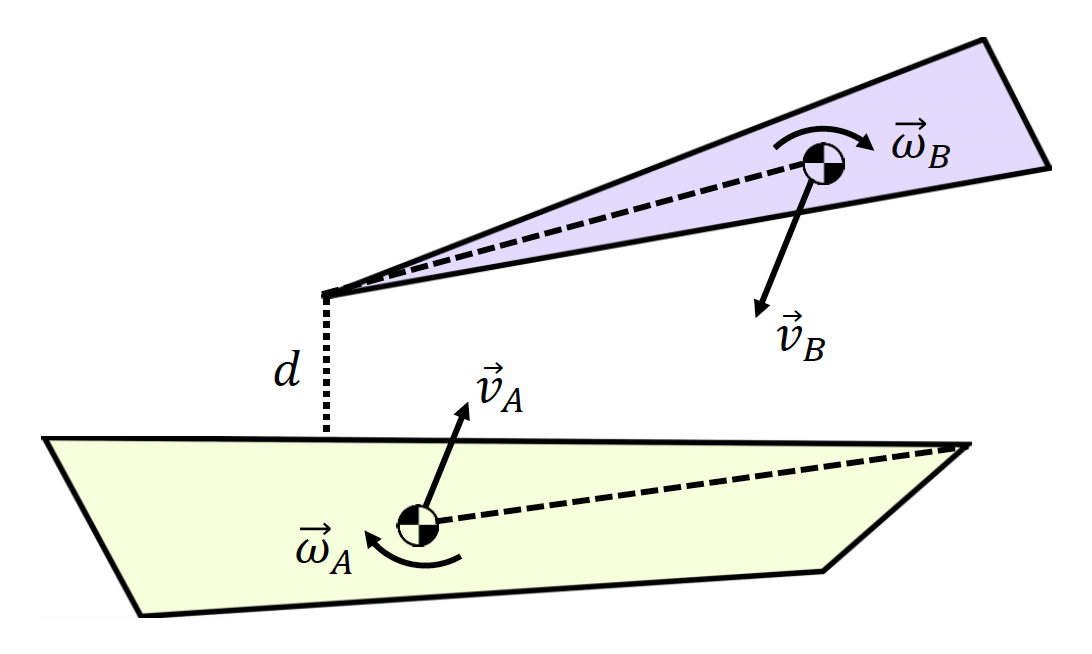
碰撞时间(time-of-impact, TOI
) :一种保守的推进方式- 估算 A 和 B 不会碰撞的“安全”时间子步
- 将 A 和 B 向前推进这一段“安全”子步
- 重复上述步骤,直到两者距离低于某个阈值
Deterministic Simulation⚓︎
多人游戏的挑战
- 游戏中的物理受游戏玩法影响
- 即便是小错误也会产生蝴蝶效应
- 同步状态需要足够的带宽
- 同步输入需要确定性的模拟
相同的旧状态 + 相同的输入 = 相同的新状态。要保证模拟的确定性,需满足以下要求:
- 物理模拟的步长是固定的
- 模拟求解的迭代顺序是一致的
- 浮点数一致性
现代物理引擎实际上花了非常多的力气来解决确定性的问题,比如 UE 的 Chaos。之所以投入这么多,是因为一旦能保证确定性,多个客户端之间就没有必要同步很多复杂的物理状态,只需有相同的输入就能确保这些客户端能看到相同的物理世界。
到目前为止,物理对游戏而言相当重要,也是困难的一件事,不少 3A 大作会在物理方面出一些 bug。
评论区