Lec 1: AVL Trees, Splay Trees and Amortized Analysis⚓︎
约 4536 个字 110 行代码 预计阅读时间 24 分钟
提醒
不论是 AVL 树,还是 Splay 树,它们的原型还是二叉查找树,具备二叉查找树的所有性质。
AVL Trees⚓︎
在 FDS 的学习中,我们知道:对一棵二叉查找树进行多次增删操作,有可能破坏二叉树的平衡性,从而降低查找效率。最糟糕的情况是将一组节点按照升 / 降序插入,这样的话二叉树就会退化成一个链表,访问节点的时间复杂度相应地从 \(O(\log N)\) 降到 \(O(N)\)。
为了提升二叉查找树的查找效率,我们需要保证整棵树的平衡性,AVL 树(以及后面要讲的伸展树)便是不错的解决之道。
定义
- 空的二叉树被认为是平衡的
- 如果树 \(T\) 有左右子树 \(T_L\) 和 \(T_R\),那么满足下列条件的树 \(T\) 才是平衡的:
- \(T_L\) 和 \(T_R\) 是平衡的
- \(|h_L - h_R| \le 1\),其中 \(h_L\) 和 \(h_R\) 分别是 \(T_L\) 和 \(T_R\) 的高度
AVL 树的每个节点都有一个平衡因子(balance factor)\(BF(node) = h_L - h_R\)。根据上面的定义知,它的取值仅有 -1, 0 或 1。
AVL 树的高度
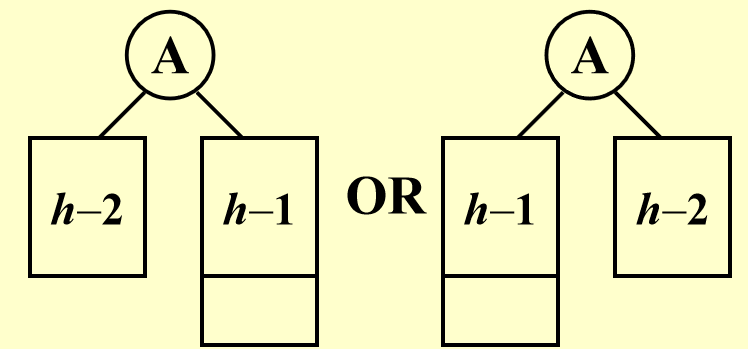
一棵高为 \(h\) 时节点数最小的平衡树的形状如下所示:
由 AVL 树的定义,不难得出关于 AVL 的最小节点数 \(n_h\) 和树高 \(h\) 相关的递推关系式(与斐波那契数列很像
事实上,\(n_h = F_{h + 3} - 1(h \ge -1, F_0 = 0, F_1 = 1)\)。而斐波那契数 \(F_h \approx \dfrac{1}{\sqrt{5}}(\dfrac{1 + \sqrt{5}}{2})^i\),所以:
因而高度 \(h = O(\log n)\)
AVL 树能够保持平衡的关键在于:每次插入或删除一个节点之后,都要检查一下这次操作是否会破坏原来二叉树的平衡性,
- 如果没有被破坏,那么就 OK 了
- 如果被破坏了(以插入操作为例
) :- 先找到离插入节点(被称为trouble maker)最近的异常(\(|BF(tf)| > 1\))节点 \(tf\)(trouble finder)
- 然后通过旋转(rotate) 的方法,将 \(tf\) 旋转到合适的位置,使得原来以 \(tf\) 为根节点的子树继续保持 AVL 树的性质(此时这棵子树不一定以 \(tf\) 为根节点)
注
- 如果有多个 trouble finder,我们只要关注那个离 trouble maker 最近的节点即可,因为只要当以它为根节点的子树恢复为一棵 AVL 树,以它的祖先节点为根节点的树自然也变回 AVL 树。
- 在介绍 AVL 树的旋转操作时,主要对插入操作带来的平衡破坏展开讨论,而对删除操作的分析就一笔带过了
旋转的具体操作与插入节点 (trouble maker) 的位置有密切的关系,共分为四种情况:
- LL:插入的位置位于 trouble finder 的左孩子的左子树上
- RR:插入的位置位于 trouble finder 的右孩子的右子树上
- LR:插入的位置位于 trouble finder 的左孩子的右子树上
- RL:插入的位置位于 trouble finder 的右孩子的左子树上
其中前两种情况和后两种情况分别是镜像对称的,也就是说本质上只有两种不同的旋转方法需要讨论,其中:
- 前两种情况的解决方法被称为单旋(single rotation)
- 后两种情况的解决方法被称为双旋(double rotation)
下面将详细介绍这两种旋转方法。
LL & RR⚓︎
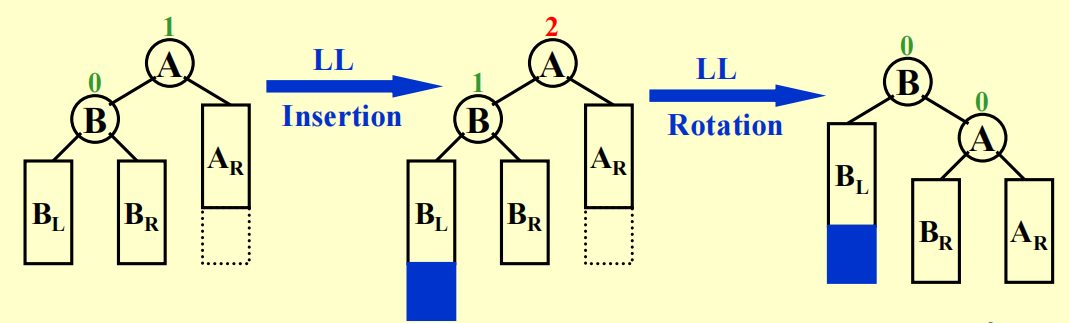
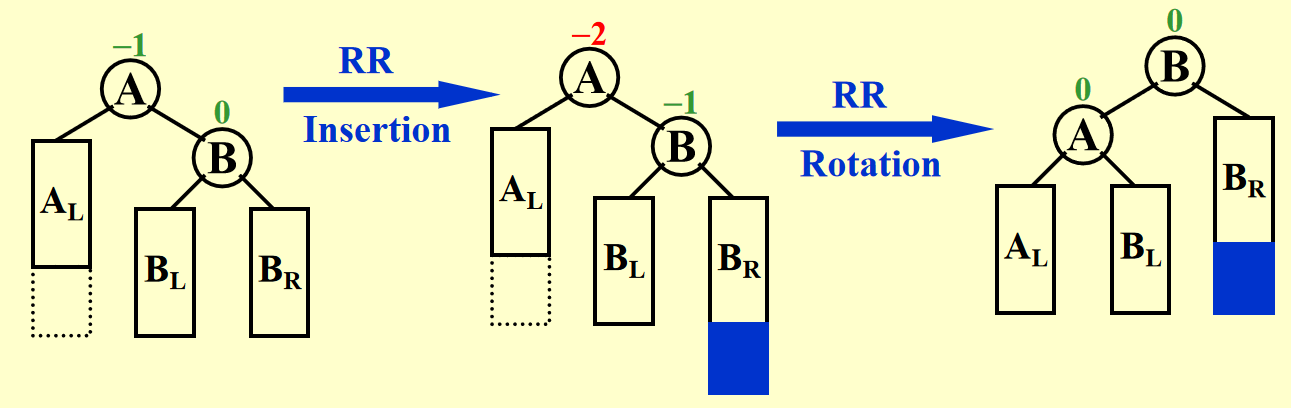
先分析 LL:
过程演示


可以看到,trouble maker(用红色阴影标记,因为不清楚其具体的位置,但它一定在整棵子树最深的位置上)在 trouble finder(用橙色标出)的左孩子的左子树上。
注:根据定义,右子树可以和左孩子的右子树保持一致的高度,但这里画的是高度相差 1 的情况。


如何实现「旋转
- 从初始状态中可以看出,trouble finder 的左孩子的左子树太高了,而 trouble finder 的右子树较矮,因此我们希望“降低”左边的高度,而“提高”右边的高度
- 所以,选择 trouble finder 的左孩子作为新树的根节点(用橙色阴影标出,以下称为 NR
) ,而 trouble finder 则成为它的右孩子 - 而 NR 原来的右孩子则由 trouble finder 接管,成为它的左子树(红色实线表示删除的边,绿色虚线表示新增的边)
- 如图蓝色箭头所示,为了让新树更加美观,应当将 trouble finder “左旋” 下来,但保持这些节点或子树的相对水平位置不变(这样维持了二叉查找树的性质)
有了上面的图示,理解起来应该不算困难。所以 RR 部分的演示我就省略了(其实是我懒得画了 x
一句话总结:LL 用左旋,RR 用右旋。
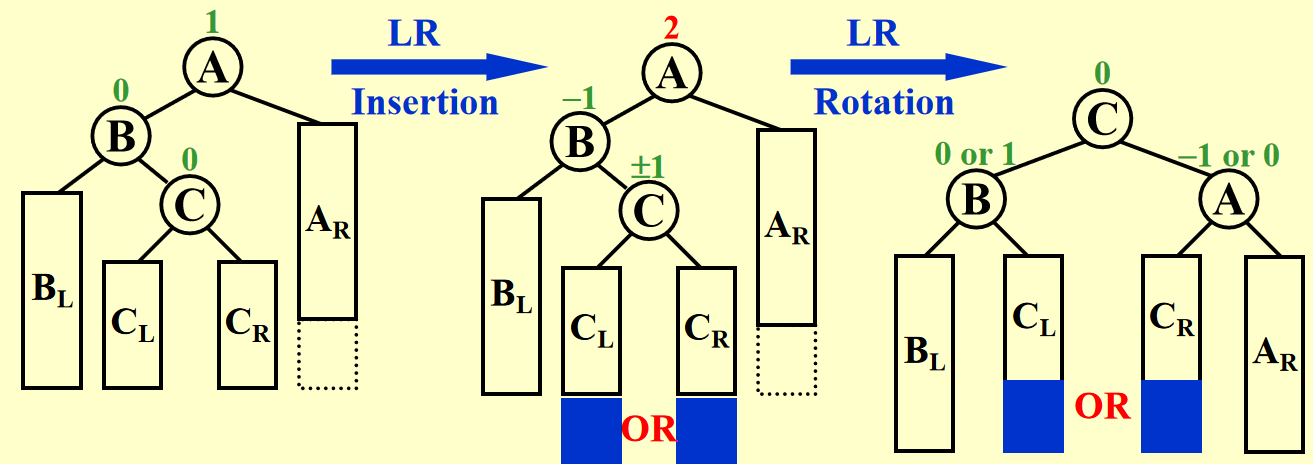
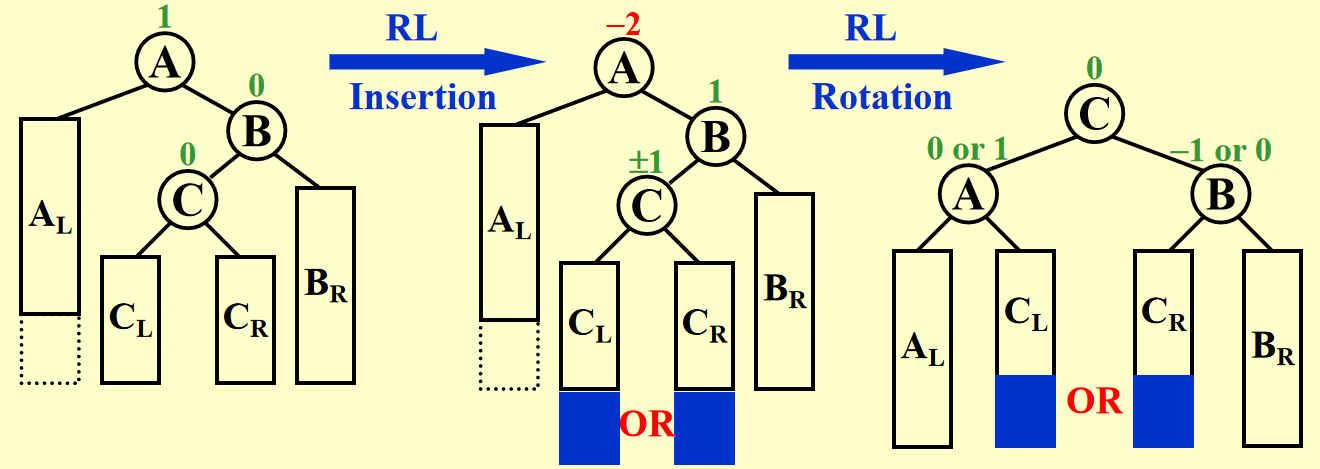
LR & RL⚓︎
这两种情况稍微复杂一些,因为仅靠一次旋转是无法恢复树的平衡的,需要转两次(double rotation)才能成功。而且双旋需要关注三个节点(trouble finder、tf 中有 tm 的儿子节点和孙子节点
过程演示
小问题
第 2 步和第 4 步的蓝色箭头画反了,所以不要管那个蓝色箭头!
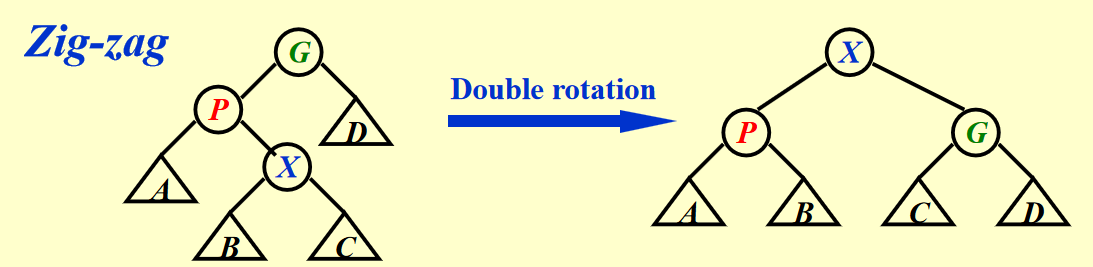
RL 的旋转方法与之类似,只要做一个镜像变换即可,这里也省略具体过程了,仅贴上一张 PPT 的图片:
时间复杂度:\(O(\log N)\),其中 \(N\) 为节点数,即与树的高度成正比(最坏情况是从叶子节点开始,一直调整到根节点
总结
我们应该记住的是两类旋转方法的具体步骤(增加 / 删除边和变换节点的祖先 - 后代关系
我的记忆法(慎看,对我挺有效,但是可能会打乱读者的记忆法)
- LL&RR:将 touble finder 的左 / 右孩子作为新的根节点,trouble finder 退化为这个孩子的右 / 左孩子,然后重新分配子树的归属,在操作过程中保持节点的相对水平位置不变
- LR&RL:左子树右旋 + 整棵树左旋 / 右子树左旋 + 整棵树右旋
关于删除
PPT 没有详细讨论 AVL 树的删除,这里仅仅简单讲几句(对删除操作感兴趣的读者可以看 wiki 的描述
- 先按照普通二叉查找树的删除方法进行删除
- 这一过程中子树的高度发生变化,很有可能破坏 AVL 树的平衡性,这时需要通过上面讲到的旋转方法使其再次回到平衡状态
- 但如果运气差一点的话,旋转完一次还不够,因为这可能破坏了其他子树的平衡,因此需要再次旋转,直至整棵树平衡
- 时间复杂度:\(O(\log N)\)
Implementation by Code⚓︎
节点应该存什么字段
有两种做法:存储节点的高度,或者存储节点的平衡因子 bf,它们各有优劣:
- 高度:简单、清晰;但是如果树过高,占用内存空间较大
- 平衡因子:只需要存三个值,节省内存空间(只需 2 位即可
) ;但是不太便于理解
我们现在不会遇到很高的 AVL 树,所以下面的代码实现使用前者。
代码实现(摘自教材)
#ifndef _AvlTree_H
struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;
AvlTree MakeEmpty(AvlTree T);
Position Find(ElementType X, AvlTree T);
Position FindMin(AvlTree T);
Position FindMax(AvlTree T);
AvlTree Insert(ElementType X, AvlTree T);
AvlTree Delete(ElementType X, AvlTree T);
ElementType Retrieve(Position P);
#endif /* _AvlTree_H */
// Place in the implementation file
struct AvlNode {
ElementType Element;
AvlTree Left;
AvlTree Right;
int Height;
}
AvlTree Insert(ElementType X, AvlTree T) {
if (T == NULL) {
// Create and return a one-node tree
T = (AvlTree)malloc(sizeof(struct AvlNode));
if (T == NULL) {
FatalError("Out of space!!!");
} else {
T->Element = X;
T->Height = 0;
T->Left = T->Right = NULL;
}
} else if (X < T->Element) {
T->Left = Insert(X, T->Left);
if (Height(T->Left) - Height(T->Right) == 2)
if (X < T->Left->Element)
T = SingleRotateWithLeft(T);
else
T = DoubleRotateWithLeft(T);
} else if (X > T->Element) {
T->Right = Insert(X, T->Right);
if (Height(T->Right) - Height(T->Left) == 2)
if (X > T->Right->Element)
T = SingleRotateWithRight(T);
else
T = DoubleRotateWithRight(T);
}
// Else X is in the tree already; we'll do nothing
T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
return T;
}
static Position SingleRotateWithLeft(Position K2) {
// K2: trouble finder
// K1: the left son of K1
Position K1;
K1 = K2->Left;
K2->Left = K1->Right;
K1->Right = K2;
K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;
K1->Height = Max(Height(K1->Left), K2->Height) + 1;
return K1;
}
static Position SingleRotateWithRight(Position K2) {
// K2: trouble finder
// K1: the right son of K1
Position K1;
K1 = K2->Right;
K2->Right = K1->Left;
K1->Left = K2;
K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;
K1->Height = Max(Height(K1->Right), K2->Height) + 1;
return K1;
}
Splay Trees⚓︎
AVL 树虽然能够始终保持树的平衡,但是需要维护每一个节点的高度 / 平衡因子字段,这有些麻烦。在 AVL 树的基础上发展出来的 Splay 树(伸展树)相比 AVL 树更加简单粗暴:
- 它继承了 AVL 树的旋转操作;但是它并不维护节点的高度 / 平衡因子字段,因此它无法保障树的平衡
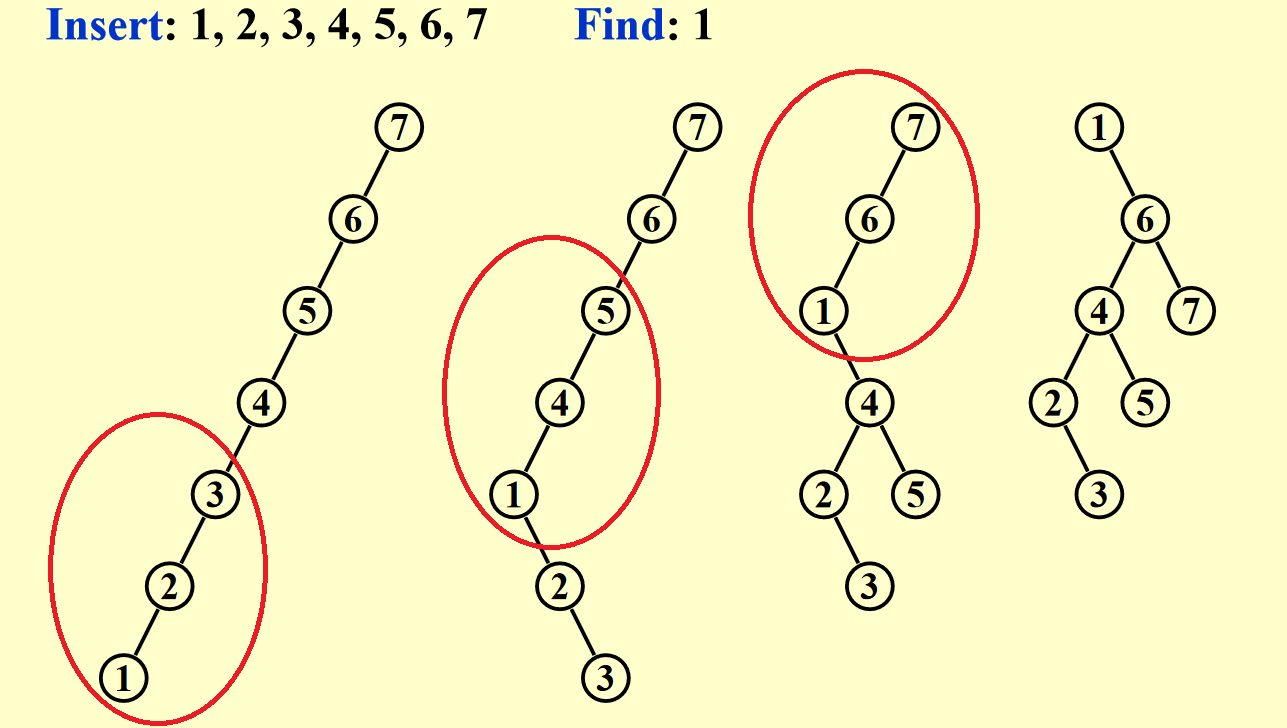
- Splay 树的核心操作在于:每当我们访问一个节点后,就将该节点通过 AVL 树的旋转方法将其调到根节点的位置上。
- 因此它能够保证 \(M\) 次操作(增删查改)的摊还 (amortized) 复杂度为 \(O(M \log N)\)(在摊还分析一节再作具体分析)
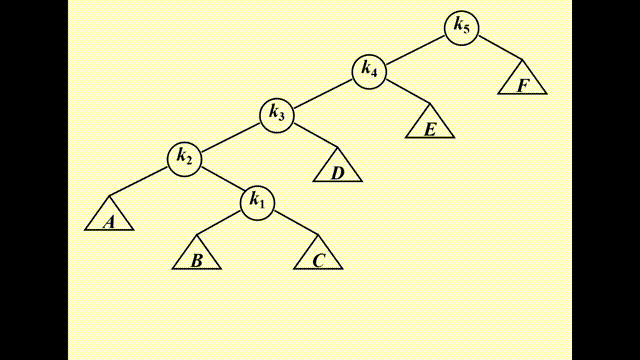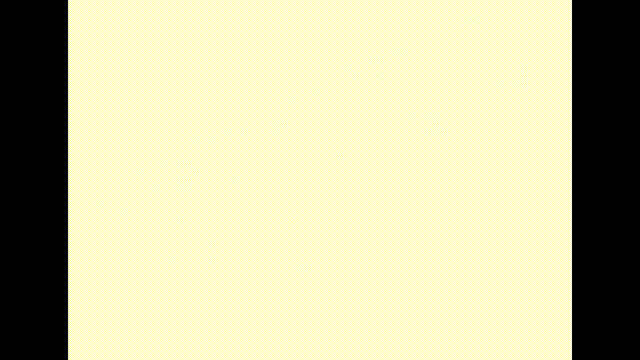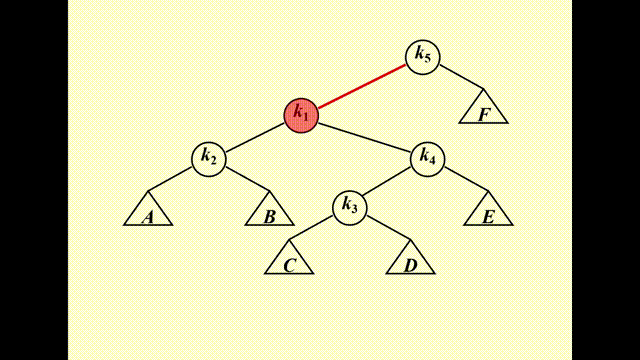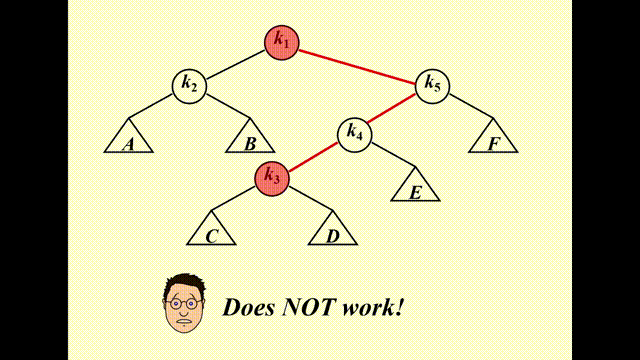
错误示范
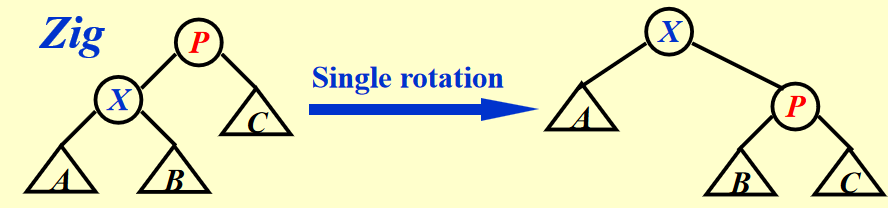
下面介绍正确的操作,分为 3 种情况(其中被访问的节点记作 \(X\),它的父亲和祖父分别记作 \(P\) 和 \(G\)
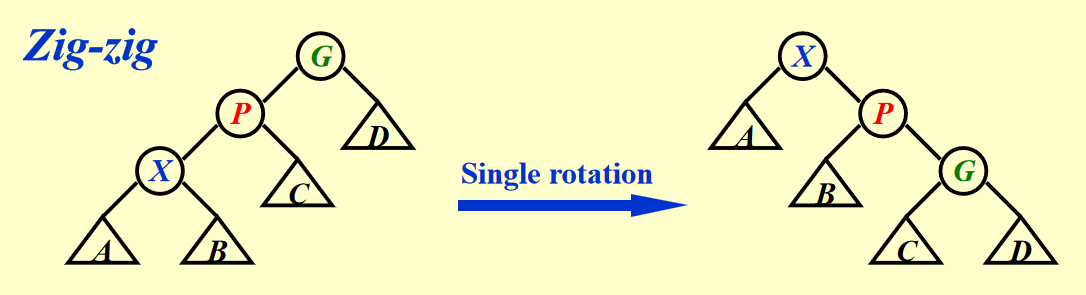
- Case 1:\(P\) 是根节点 -> 旋转 \(X\) 和 \(P\) 即可(AVL 树的单旋)
-
Case 2:\(P\) 是非根节点
- Case 2-1:Zig-zag(\(X, P, G\) 三者不在一条直线上)-> \(X\) 节点转两次(其实就是 AVL 树的 LR 和 RL 情况)
- Case 2-2:Zig-zig(\(X, P, G\) 三者在一条直线上)-> 先转 \(P\) 节点,后转 \(X\) 节点
应用
注
- 在调整的过程中,千万不要和 AVL 树的操作搞混:AVL 树是通过检测树高或平衡因子来决定是否要继续旋转;而 Splay 树是要一直盯着被访问的那个节点来旋转,直到它位于根节点为止
- 在节点数足够多的理想情况下,把被访问的节点移到根节点上之后,路径上大多数节点的高度降至原来的一半左右
Splay 树的插入和删除操作
- 先插入新的节点
- 将该节点通过 Splay 树的旋转操作移动到根节点的位置上
- 访问要删除的节点 \(X\),根据规则,\(X\) 将会作为整棵树的根节点
- 移除 \(X\),这样就剩下两棵子树 \(T_L\) 或 \(T_R\)
- \(FindMax(T_L)\) 或者 \(FindMin(T_R)\),也就是说从两棵子树中找到合适的节点,作为新树的根节点,使新树仍然保持二叉查找树的性质
Splay 树的复杂度涉及到摊还分析,下面将介绍这一知识点(在今后的学习中还会多次用到摊还分析,所以请务必认真阅读下面的内容
Amortized Analysis⚓︎
我们先来理解「摊还」这个词:
- 保证在 \(N\) 个数据上的 \(M\) 次运算的总体复杂度为 \(O(M \log N)\)
- 它考虑的是全局(所有数据)的耗时,因此允许在某些数据的运算上耗时久一些,因为可以用在另一些数据上耗时较短的运算来弥补这个损失
- 区分最坏复杂度,摊还复杂度和平均复杂度
- 最坏:保证单个运算以及整体运算的复杂度不超过某一边界(考虑数据最理想的情况)
- 摊还:保证整体的运算复杂度不超过某一边界,但允许某几次运算可以超过该边界(考虑数据的真实情况)
- 平均:在给定数据分布平均的情况下(是一种理想的假设
) ,保证整体运算的复杂度不超过某一边界注:只有平均复杂度考虑数据分布,前两者并不考虑数据的分布。
通过上面的分析,不难得出以下不等关系:
worst-case bound \(\ge\) amortized-case bound \(\ge\) average-case bound
何时使用摊还分析?
个人的一些见解:当我们难以确定所有的数据分布(比如情况太多了,或者某些情况难以直接分析得到等等)从而无法用平均复杂度分析,且希望得到更精准的复杂度分析时(最坏复杂度假定每次操作都是最坏的,但并不是所有操作都会遇到最坏情况
常见的摊还分析方法有:
- 聚合法(aggregate method)
- 核算法(accounting method)
- 势能法(potential method)
Aggregate Method⚓︎
思路:摊还复杂度 = 所有操作的总时间 / 操作次数,即 \(T_{amortized} = \dfrac{\sum\limits^nT_i}{n}\)
这是最为简单暴力的方法
例子
对于一个栈,创建一个 MultiPop 的方法:依次弹出栈内所有的元素(如果有的话
易知 \(size(S) \le n\)(\(n\) 为数据总数
Accounting Method⚓︎
一句话概括
: “取长补短”
思路:当我们的摊还成本(amortized cost) \(\hat{c}_i\) 高于实际成本(actual cost) \(c_i\) 时,多出来的部分就转化为积分(credit)。如果之后的摊还成本小于实际成本时,可以用之前攒的积分抵消实际的成本(注意:不允许“摊还成本 + 积分 < 实际成本”,不然的话摊还复杂度就沦为下界了
其中 \(\sum\limits^n\hat{c}_i \ge \sum\limits^nc_i\)(确保了摊还复杂度是一个上界
例子
接着上面 MultiPop 的例子,假如我们的实际成本和摊还成本分别如下:
- \(c_i\):
Push:1,Pop:1,MultiPop:min(sizeof(S), k) - \(\hat{c}_i\):
Push:2,Pop:0,MultiPop:0
我们可以这样理解:每次 Push 一个元素的时候,我们用两块钱执行这个只需一块钱的操作,多出来的一块钱存起来作为积分。这样的话,当我们 Pop 一个元素的时候,就不需要花钱,只要花费等价的积分即可。通过上面给出的信息不难判断,每当 Pop 一个元素的时候,我们都会有足够多的积分来消费,所以 MultiPop 的运算我们可以不花一分钱就可以完成。
用符号语言表述:
Potential Method⚓︎
核算法看似非常简单,但它的缺陷在于:我们需要考虑每一步操作的成本和积分,这样就比较繁琐,不利于我们从全局分析问题。而势能法能够克服这一缺陷。
思路:我们将核算法提到的「积分」概念转化为「势能差」概念——即 \(\hat{c}_i - c_i = \Phi(D_i) - \Phi(D_{i-1})\),其中 \(D_i\) 表示经历了 i 次运算后的数据结构,\(\Phi(D_i)\) 表示该数据结构的势能函数(potential function)。经过一些转化,可以得到:
因此,我们只需考虑初始和末尾的势能,确保它们的势能差 \(\Phi(D_n) - \Phi(D_0) \ge 0\) 即可(而通常会令 \(\Phi(D_0) = 0\)
例子
还是接着 MultiPop 的例子,我们假定 \(D_i\) 为经过 i 次操作后的栈,\(\Phi(D_i)\) 表示栈的元素个数,那么易知 \(\Phi(D_i) \ge 0 = \Phi(D_0)\)。
-
Push:\(\Phi(D_i) - \Phi(D_{i-1}) = (sizeof(S) + 1) - sizeof(S) = 1\) \(\Rightarrow \hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1}) = 1 + 1 = 2\) -
Pop:\(\Phi(D_i) - \Phi(D_{i-1}) = (sizeof(S) - 1) - sizeof(S) = -1\) \(\Rightarrow \hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1}) = 1 - 1 = 0\) -
MultiPop:\(\Phi(D_i) - \Phi(D_{i-1}) = (sizeof(S) - k') - sizeof(S) = -k'\) \(\Rightarrow \hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1}) = k' - k' = 0\)
\(\therefore \sum\limits_{i = 1}^n\hat{c}_i = \sum\limits_{i = 1}^nO(1) = O(n) \ge \sum\limits_{i=1}^nc_i \Rightarrow T_{amortized} = \dfrac{O(n)}{n} = 1\)
Analysis for Splay Tree⚓︎
结论:Splay 树的摊还复杂度为 \(T_{amortized} = O(\log N)\)
下面我们用势能法来进行势能分析。
分析
我们假定:
- \(D_i\) = 以被访问的节点为根节点(经过变换后)的新树
- \(c_i\) = 转换过程中所需的实际成本
- zig:\(c_i = 1\)
- zig-zag & zig-zig:\(c_i = 2\)
-
\(\Phi(T) = \sum\limits_{i \in T} \log S(i) = \sum\limits_{i \in T} R(i)\),其中 \(i\) 是 \(T\) 的后代,\(S(i)\) 是以 \(i\) 为根节点的子树的节点数,将其取对数就是 \(i\) 的秩(rank)\(R(i)\)
-
\(R(i) \approx H(i)\)(\(H(i)\) 为树的高度)
为什么不用树的高度作为势能函数
因为很多子树的高度在旋转的时候会发生改变,而大小在旋转的过程中虽然也有不小的变化,但是由于取了对数,所以秩的变化就变得很小了,这便于我们的计算。
下面我们就具体分析 Splay 树的三种情况(记 \(R_k(X)\) 为第 \(k\) 次操作后节点 \(X\) 的秩
- 显然,在旋转前后,以 \(P\) 为根节点的子树的大小变小了,因此 \(R_{k+1}(P) - R_k(P) < 0\)
引理
如果 \(a + b \le c\),且 \(a, b\) 都是正整数,则
证明:
- 根据算术 - 几何不等式 \(\sqrt{ab} \le \dfrac{a+b}{2}\)
- 因此 \(\sqrt{ab} \le \dfrac{c}{2}\)
- 两边平方: \(ab \le \dfrac{c^2}{4}\)
- 再两边取对数,得到上述引理
- 旋转前 \(G\) 的大小和旋转后 \(X\) 的大小相等,所以 \(R_{k+1}(X) = R_{k}(G)\),可以相互抵消
- 旋转后,\(S(X) \ge S(P) + S(G)\),根据上面的引理知,\(\log S(P) + \log S(G) \le 2 \log S(X) - 2\),即 \(R_{k+1}(P) + R_{k+1}(G)\le 2 R_{k+1}(X) - 2\)
- 旋转前,\(P\) 是 \(X\) 的父节点,因此 \(R_k(P) \ge R_k(X)\)
- 通过上述的转换和抵消,可以得到最终的不等式
错误示范
用和推导 zig-zag 类似的方法放缩不等式,可以得到下面的结果:
从放缩的角度看挺不错的,但是后面多出了个常数 2,而我们不知道要执行多少次 zig-zig 旋转操作,所以会带来不确定的数据,这不利于我们的精确分析。
zig 旋转的摊还成本可以带常数,是因为只有一次 zig 操作。
- 旋转后的 X 的大小 = 旋转前的 G 的大小,所以两者对应的秩相抵消
- 观察旋转前的 X 子树和旋转后的 G 子树,不难发现它们加起来的大小 \(\le\) 旋转后的 X 树的大小,所以再次用到上面的引理,可以得到 \(R_{k+1}(G) + R_k(X) \le 2R_{k+1}(X) - 2\)
- \(R_{k+1}(P) \le R_{k+1}(X), R_k(P) \ge R_k(X)\),所以最后部分进行简单的放缩
- 最终我们得到了正确的不等式
现在我们将这三部分并起来,得到最终的摊还成本。但在此之前,我们需要进一步的放缩,便于后续计算:
在最终计算之前,还得先确定这 3 种操作的总次数 \(k\),不难得到:
- 当 \(k\) 为偶数时,每次操作要么是 zig-zig,要么是 zig-zag
- 当 \(k\) 为奇数时,前 \(k-1\) 次操作是 zig-zig 或 zig-zag,最后一次操作是 zig
将所有旋转操作对应的摊还成本加起来:
这样,我们成功证明了 Splay 树的摊还复杂度。
评论区