Lec 6: Backtracking⚓︎
约 2011 个字 65 行代码 预计阅读时间 11 分钟
Introduction⚓︎
要想得到某个问题的解,一种方法是列出所有可能的情况,然后对它们逐一检查并识别出可能的解,这种方法称为暴力 (brute force) 枚举,但它仅在情况数不多的时候是可行的,而且它的效率实在太低了,我们无法保证它能在有限时间内找到正确解。
一种优化的方法是本章将要介绍的回溯法(backtracking),它在检查情况的时候会消除一些不合适的情况(称为剪枝(pruning)
回溯法的大致思路是:
- 假设我们已经得到部分解 \((x_1, \dots, x_i)\),其中 \(x_k \in S_k, 1 \le k \le i < n\)(个人理解:\(S_k\) 表示第 \(k\) 步下的选择集 (S means Stage or (partial) Solution),而 \(x_k\) 便是其中的一个选项)
- 首先将一种可能情况为 \(x_{i+1} \in S_{i+1}\) 加到这个部分解中,并检查新的部分解 \((x_1, \dots, x_i, x_{i+1})\) 是否满足限制条件
- 如果满足条件,继续添加下一种情况到部分解中(重复上一步)
- 但如果 \(S_{i+1}\) 中没有满足要求的选择,那么表示沿 \(x_i\) 往下走是走不通的,那么就删掉 \(x_i\),并且回溯到上一个部分解 \((x_1, \dots, x_{i-1})\),然后从 \(S_i\) 中挑选另外的可能情况 \(x_i'\),以此类推
Template⚓︎
注
如果是初次阅读本笔记,建议先看下面的八皇后问题和 Turnpike 重构问题后再来看该模板,这样印象会更深一点。
代码实现
bool Backtracking (int i) {
Found = false;
if (i > N)
return true; // solved with (x1, ..., xN)
for (each xi in Si) {
// check if satisfies the restriction R
OK = Check((x1, ..., xi), R); // pruning
if (OK) {
Count xi in;
Found = Backtracking(i + 1);
if (!Found)
Undo(i); // recover to (x1, ..., x{i-1})
}
if (Found) break;
}
return Found;
}
注
- 回溯的效率跟可能情况 \(S\) 的规模、约束函数的复杂性、满足约束条件的结点数相关
- 约束函数决定了剪枝的效率,但是如果函数本身太复杂也未必合算
- 满足约束条件的解的数量很难估计,因而对回溯算法的时间复杂度分析很难完成
Examples⚓︎
Eight Queens⚓︎
Description⚓︎
问题描述
将 8 个皇后放在 \(8 \times 8\) 的棋盘上,保证任何两个皇后之间不会相互攻击。其中皇后的攻击条件为:两个皇后位于同一行、同一列或同一对角线上。
下面我们用数学化的语言重新描述这一问题,便于我们设计合适的算法:
- 令 \(Q_i\) 为棋盘上第 \(i\) 行的皇后,\(x_i\) 为 \(Q_i\) 的列索引,\(S_i\) 为 \(x_i\) 可取值的集合
- 限制条件为:
- \(S_i = \{1, 2, 3, 4, 5, 6, 7, 8\}\),其中 \(1 \le i \le 8\)
- 这表明八皇后问题一共有 \(8^8\) 种可能解
- 当 \(i \ne j\) 时,\(x_i \ne x_j\)
- 这表明每个解是 \(1, 2, \dots, 8\) 的排列,所以可能解的个数降到了 \(8!\) 个
- 延伸:对于 n 皇后问题,一共有 \(n!\) 种可能解
- \(\dfrac{x_i - x_j}{i - j} \ne \pm 1\)
- 用于确保“不在同一对角线”的限制条件
- \(S_i = \{1, 2, 3, 4, 5, 6, 7, 8\}\),其中 \(1 \le i \le 8\)
Method⚓︎
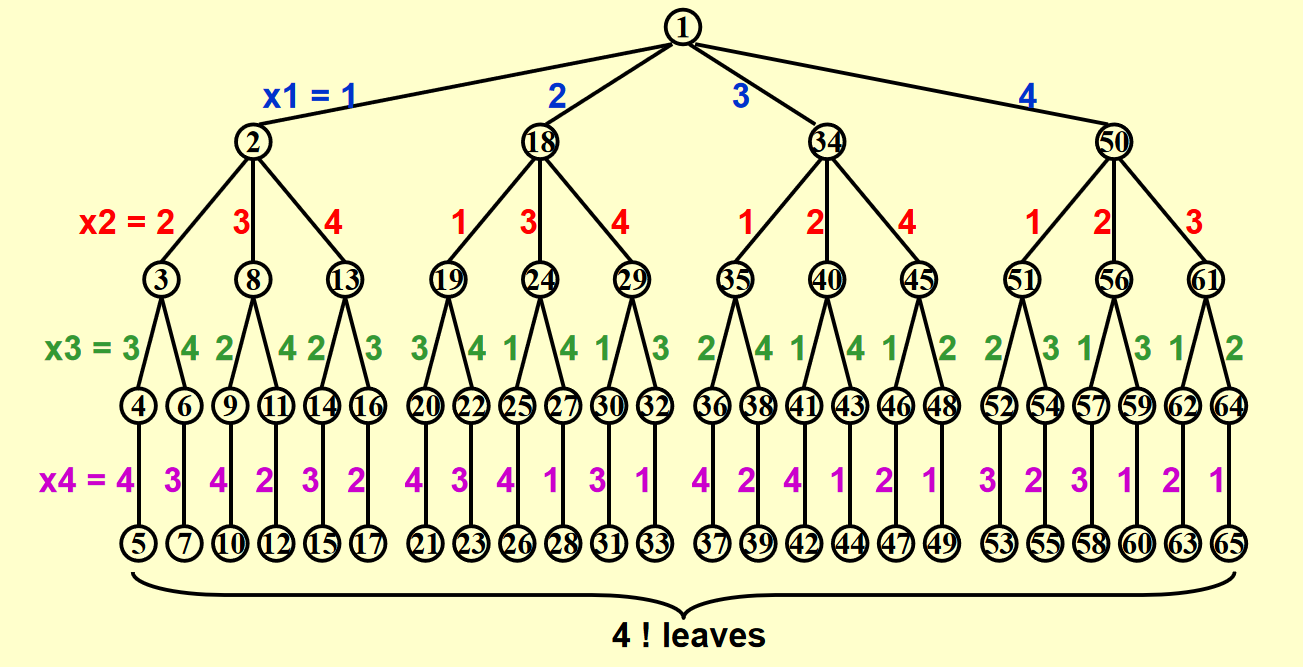
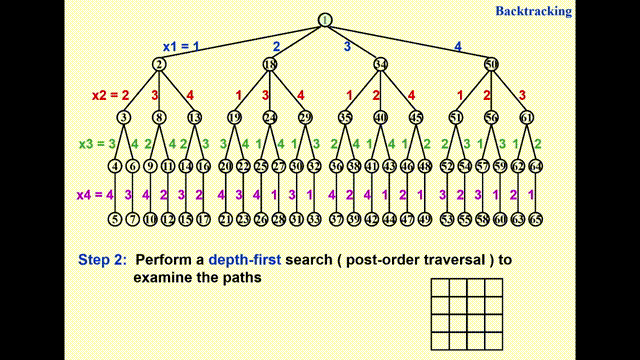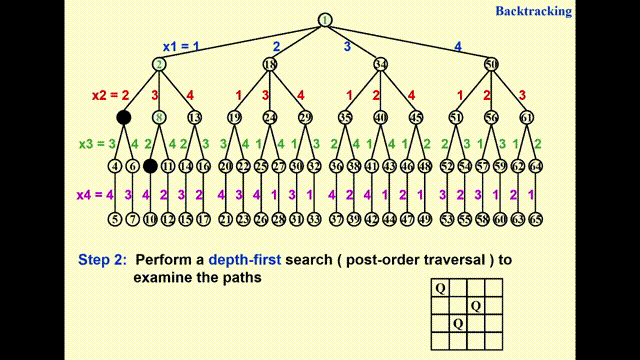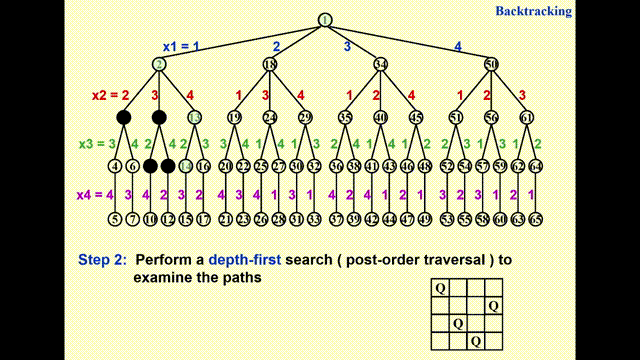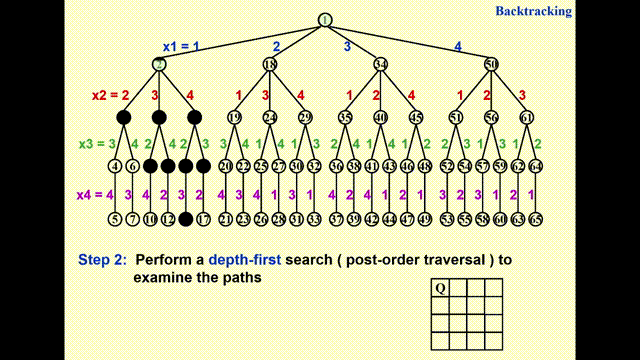
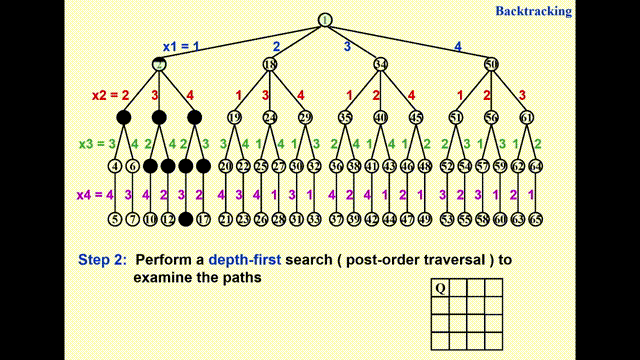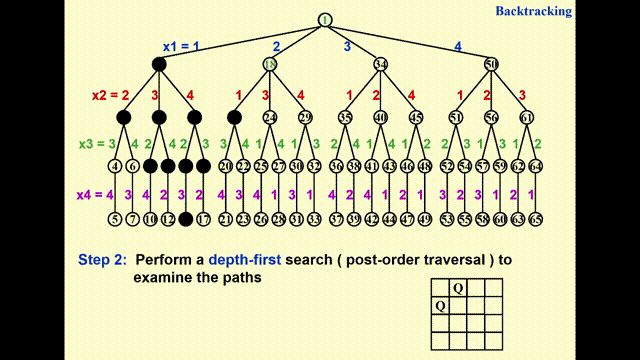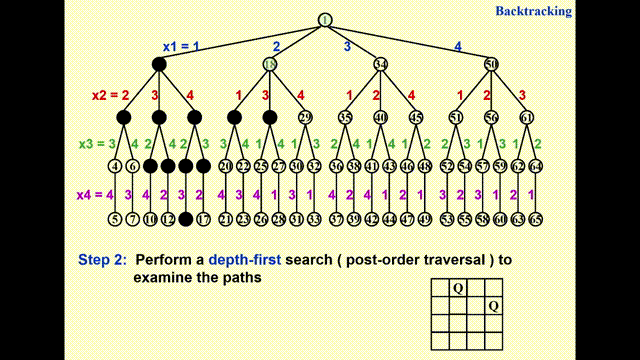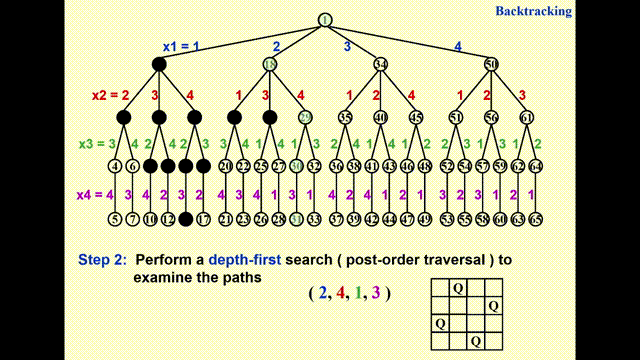
受篇幅限制,列出八皇后问题的所有可行解不太现实,因此下面将以四皇后问题为例介绍解法(八皇后问题的解法与之基本一致,只是规模更大了些
-
构建一棵博弈树(game tree)
- 每一条从根节点到叶子节点的路径即为一种可能的解
- 节点内的数字表示搜索的顺序,深度为 \(i\) 的节点表示第 \(i\) 行上的皇后
- 不难发现,这棵博弈树已经排除了两个皇后同行同列的情况,因此之后只需检验是否在同一对角线即可
- 博弈树只是一个抽象模型,便于我们直观感受和理解回溯法的过程,实际编写程序时无需创建这样的树
-
通过执行深度优先搜索(depth-first search)(后序遍历)来检验每一条可能的路径
补充:n 皇后问题解的个数
Turnpike Reconstruction⚓︎
Description⚓︎
问题描述
背景知识:给定 \(N\) 个在 x 轴上的点,它们的坐标满足 \(x_1 < x_2 < \dots x_N\),并假设 \(x_1 = 0\)。在所有点中任取两点,一共有 \(\dfrac{N(N-1)}{2}\) 种取法,对应有 \(\dfrac{N(N-1)}{2}\) 不同的路径。
问题:给定 \(\dfrac{N(N-1)}{2}\) 条路径,如何重新构造 (reconstruct) 一个点集?
Method⚓︎
例子
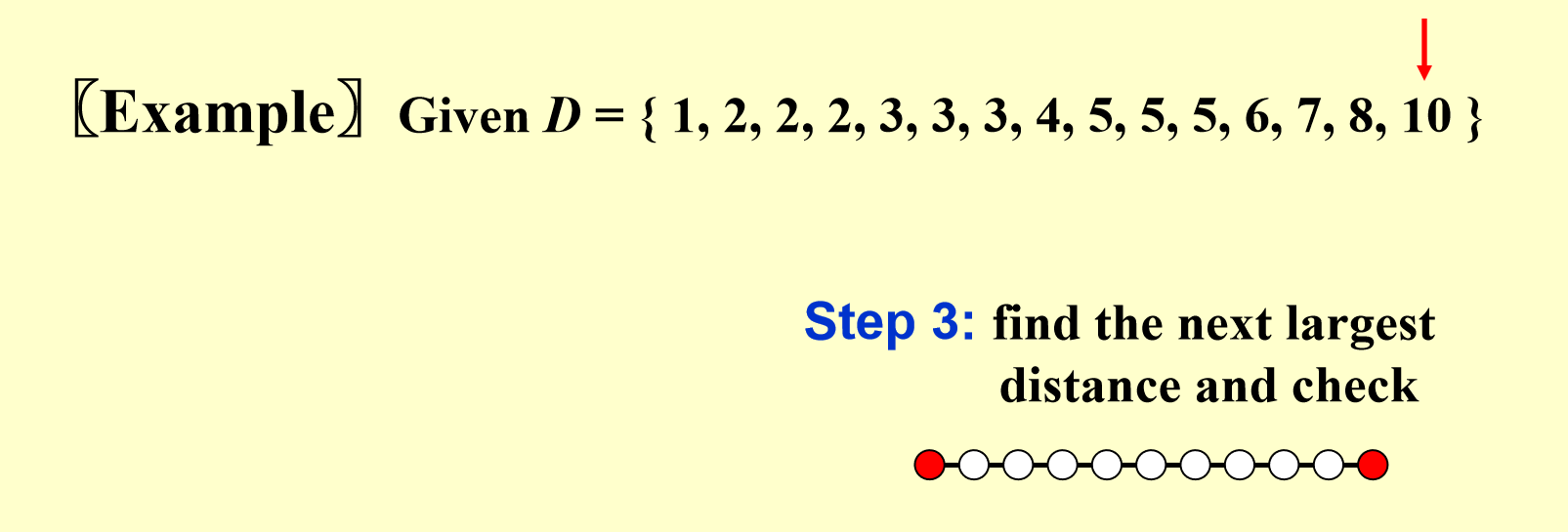
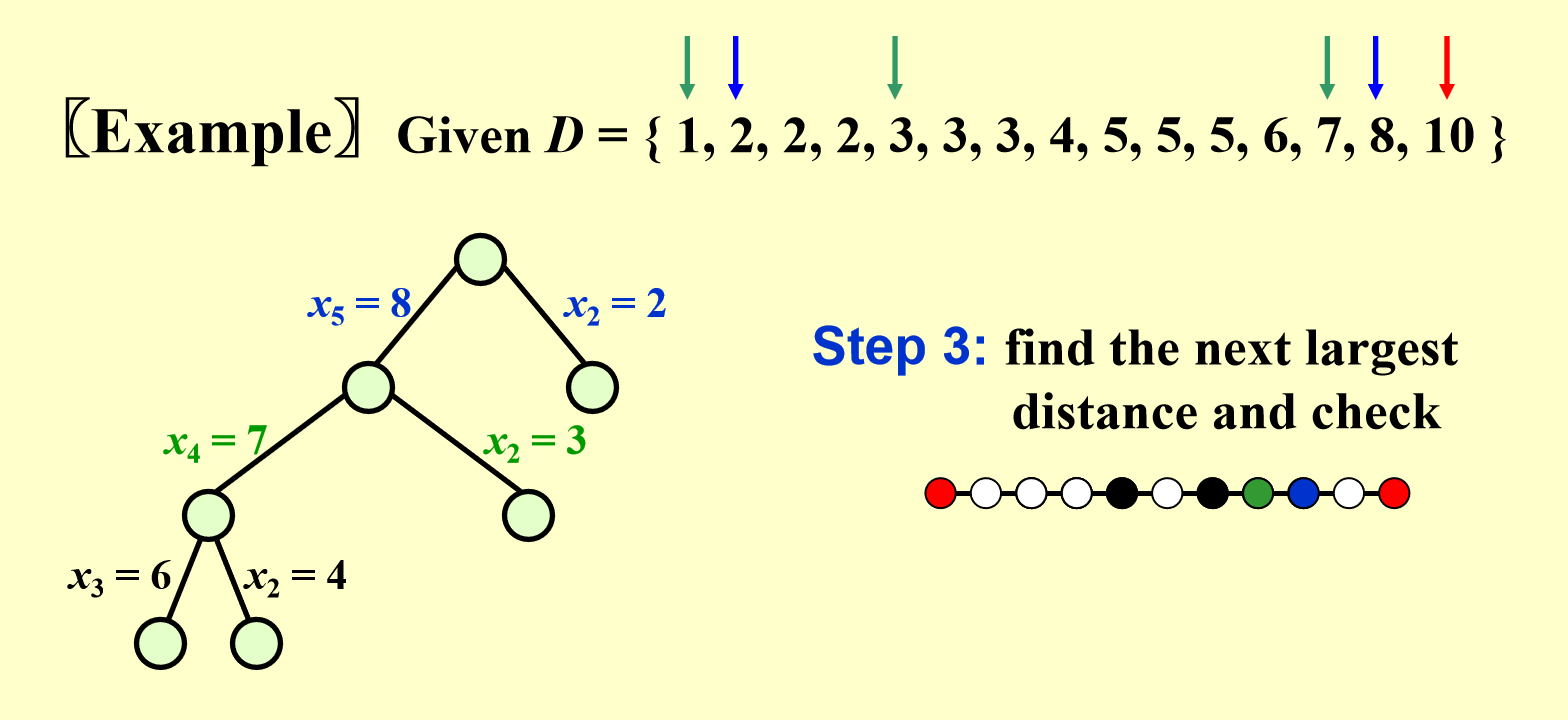
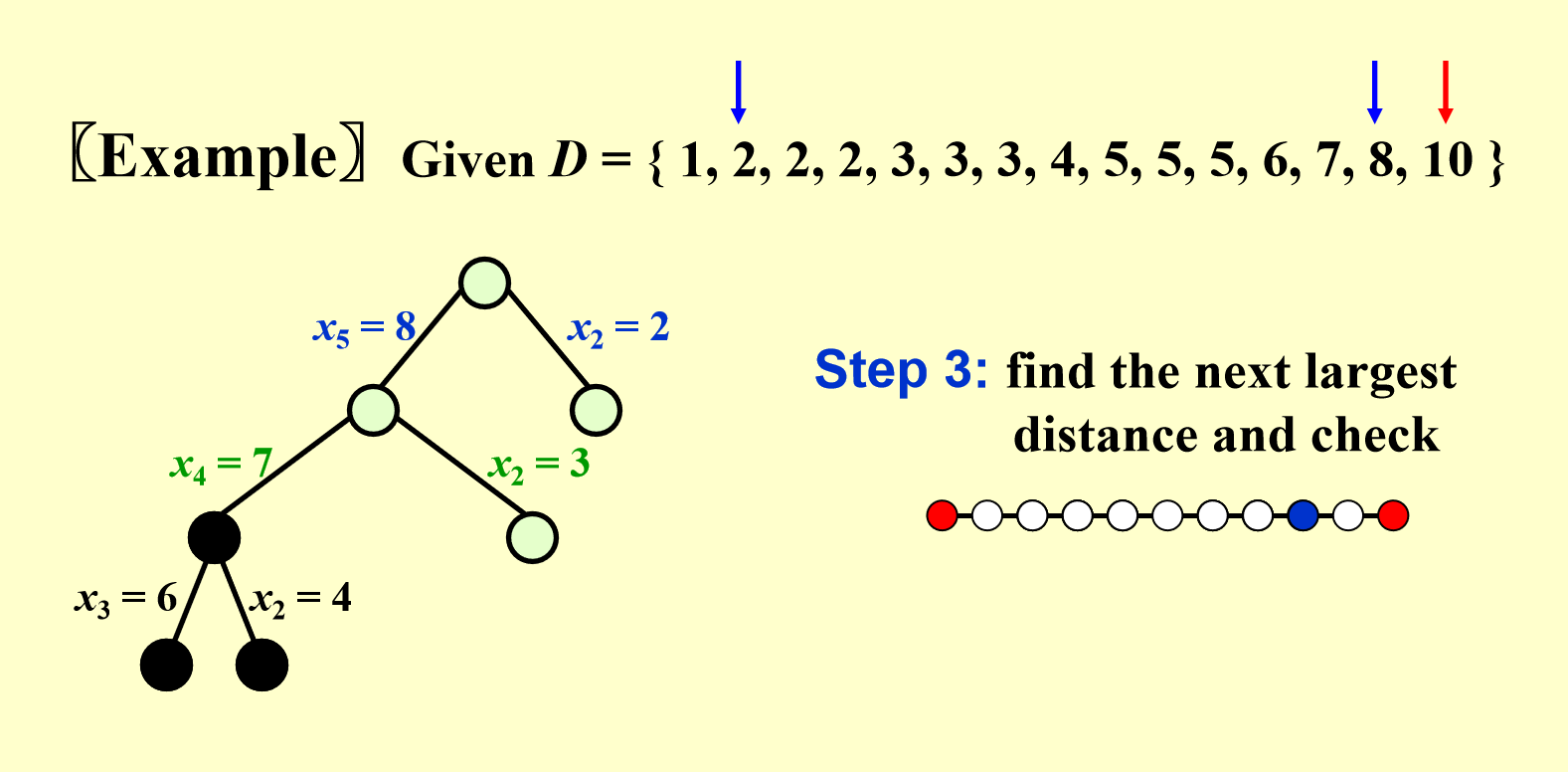
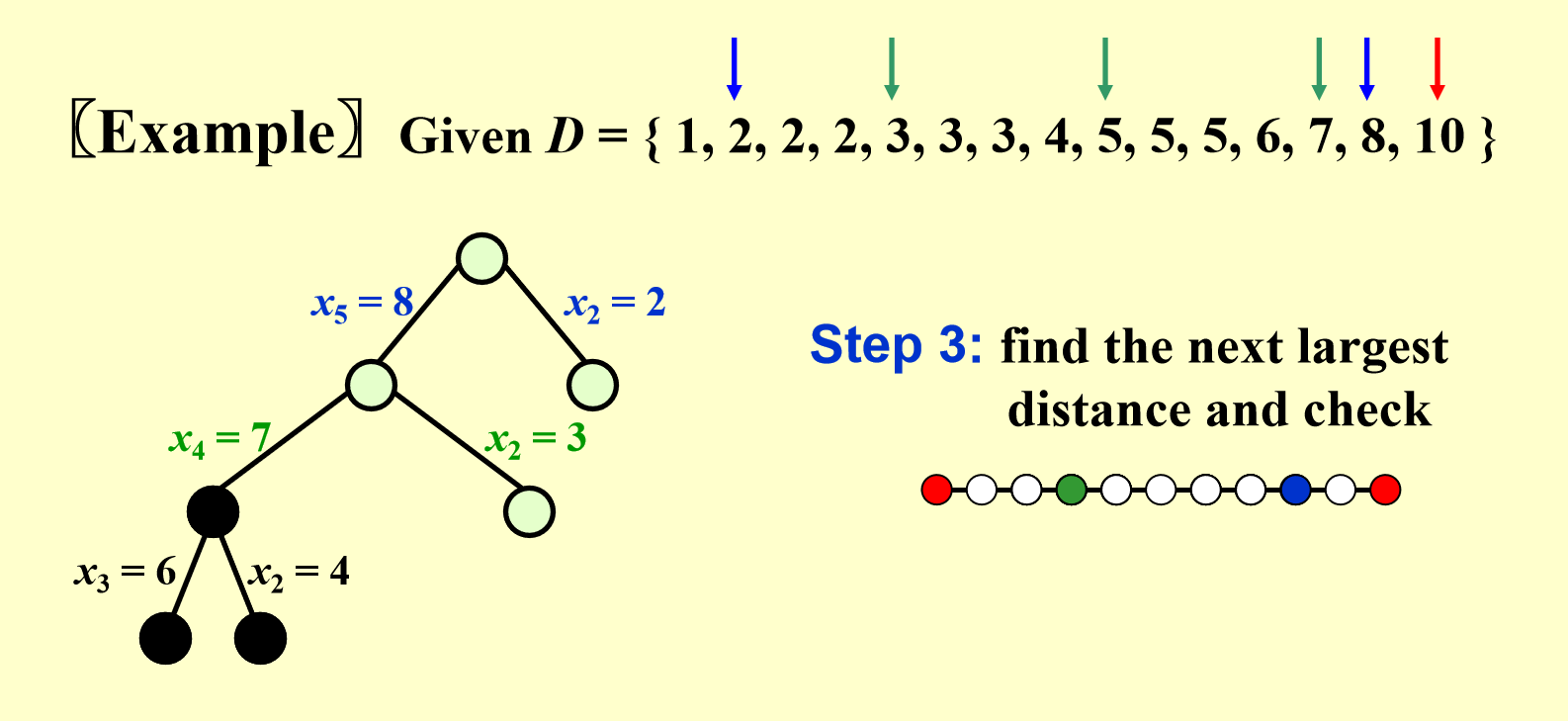
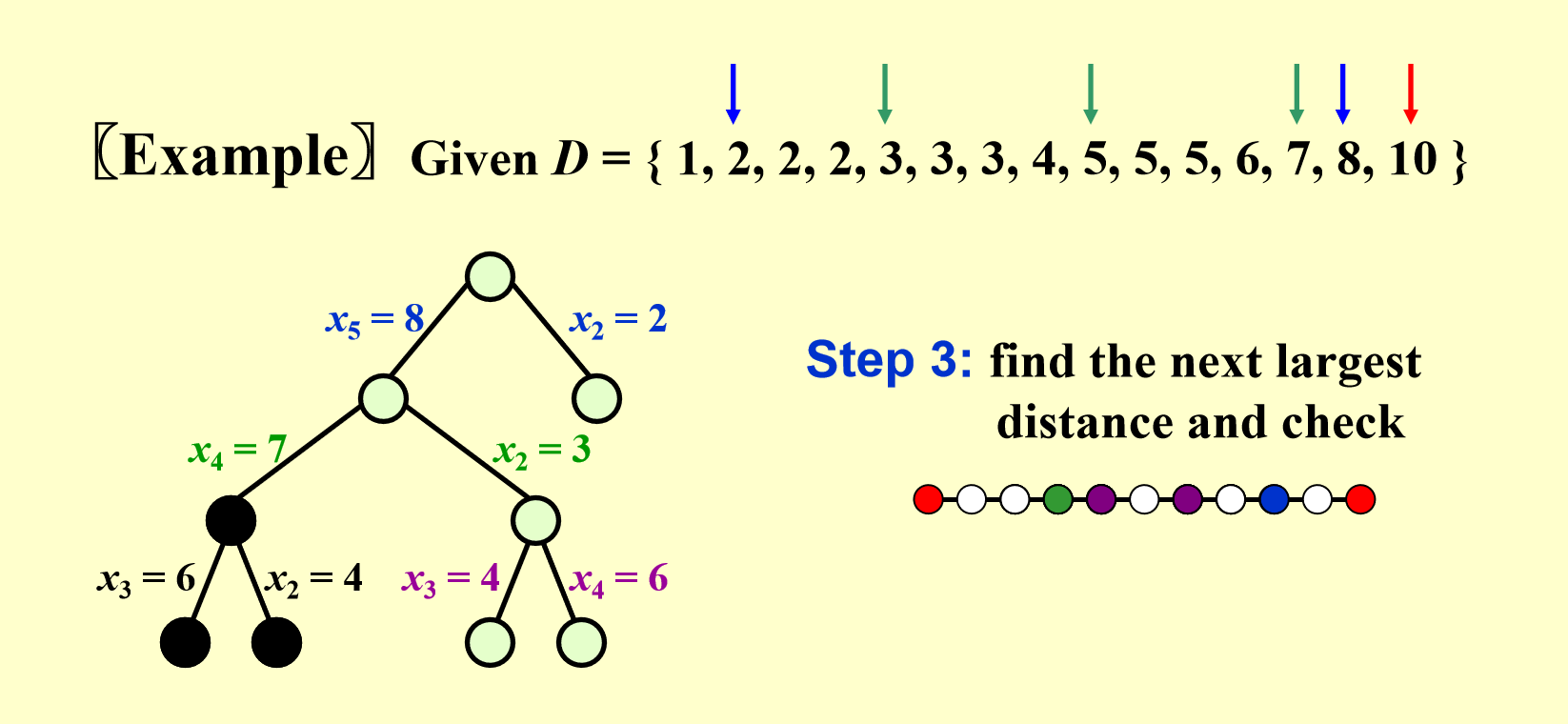
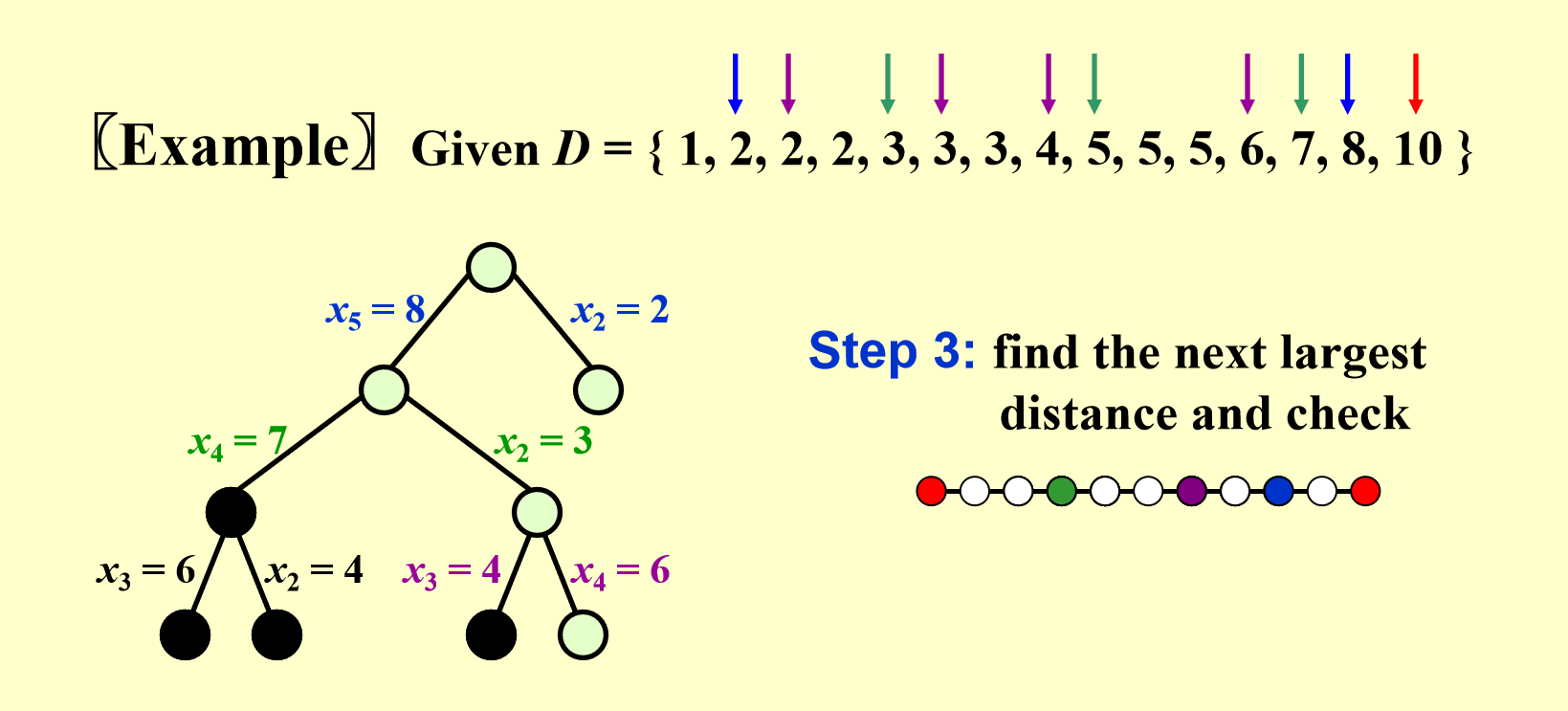
根据距离集 \(D = \{1, 2, 2, 2, 3, 3, 3, 4, 5, 5, 5, 6, 7, 8, 10\}\) 构造点集。
- 解方程 \(\dfrac{N(N-1)}{2} = 15\),解得 \(N = 6\),即一共有 6 个点
- 由于已知 \(x_1 = 0\) 且最长的距离为 10,可以推断最远的点的坐标 \(x_6 = 10\),将 10 从 \(D\) 中删除,表示我们暂时不会用到这个距离
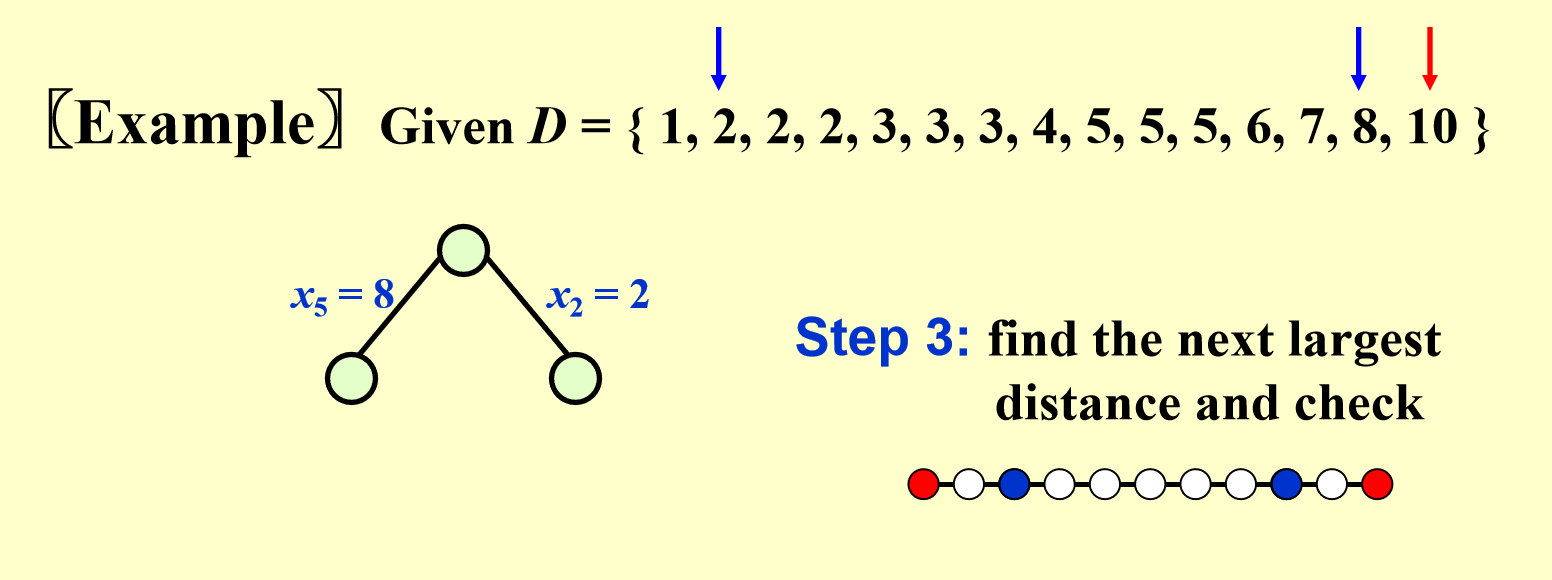
- 继续检查下一个最大的距离,找出当前所有可行点的位置,使用回溯法往下搜索,直到找出正确的解。这里的步骤说不太清楚,还是直接看下面的动画演示吧:
动画演示
- 一共有两种情况:\(x_5 = 8\)(\(x_5 - x_1 = 8\))或 \(x_2 = 2\)(\(x_6 - x_2 = 8\)
) ,根据深度优先搜索,我们先探索左边的分支 - 将距离集中的 1 个 \(2\) 和 \(8\) 删掉,因为新点的加入导致更多距离的出现
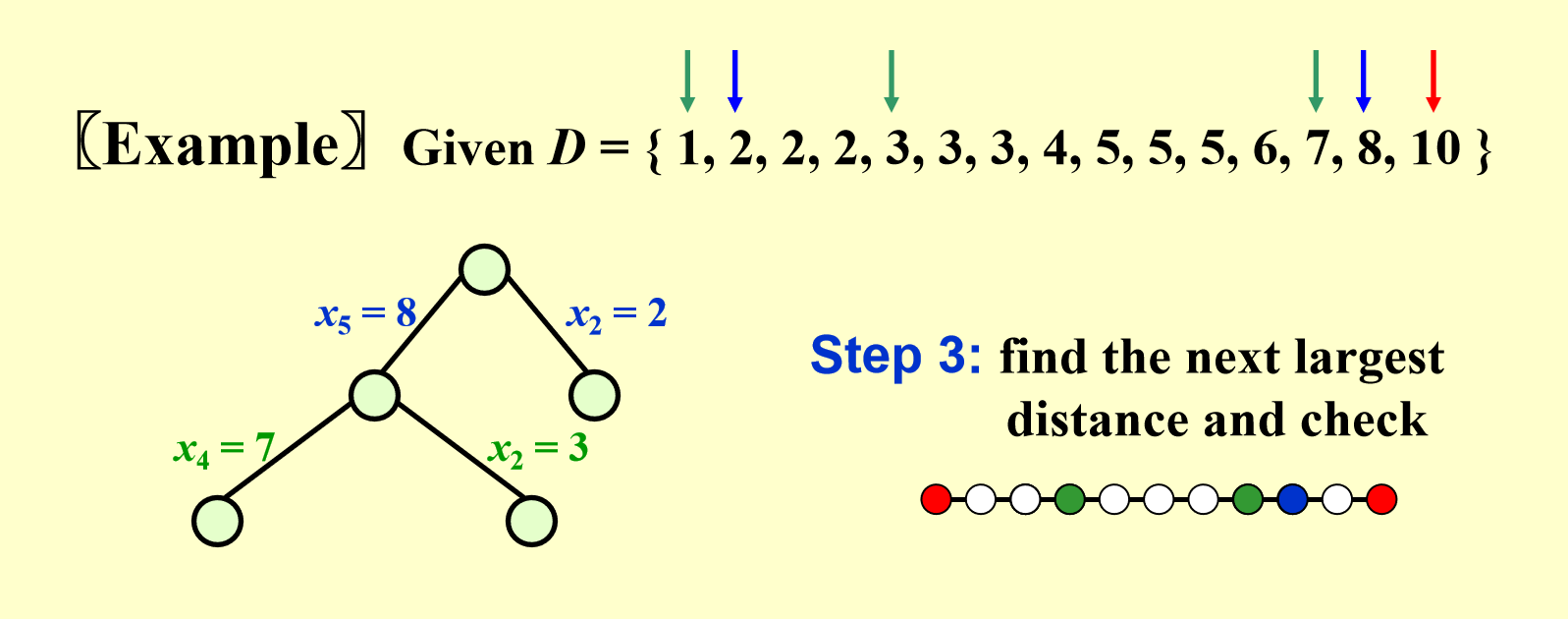
- 一共有两种情况:\(x_4 = 7\)(\(x_4 - x_1 = 7\))或 \(x_2 = 3\)(左边的分支中还没用到 \(x_2\),\(x_6 - x_2 = 7\)
) ,根据深度优先搜索,我们先探索左边的分支 - 将距离集中的 \(1\)、1 个 \(3\) 和 \(7\) 删掉
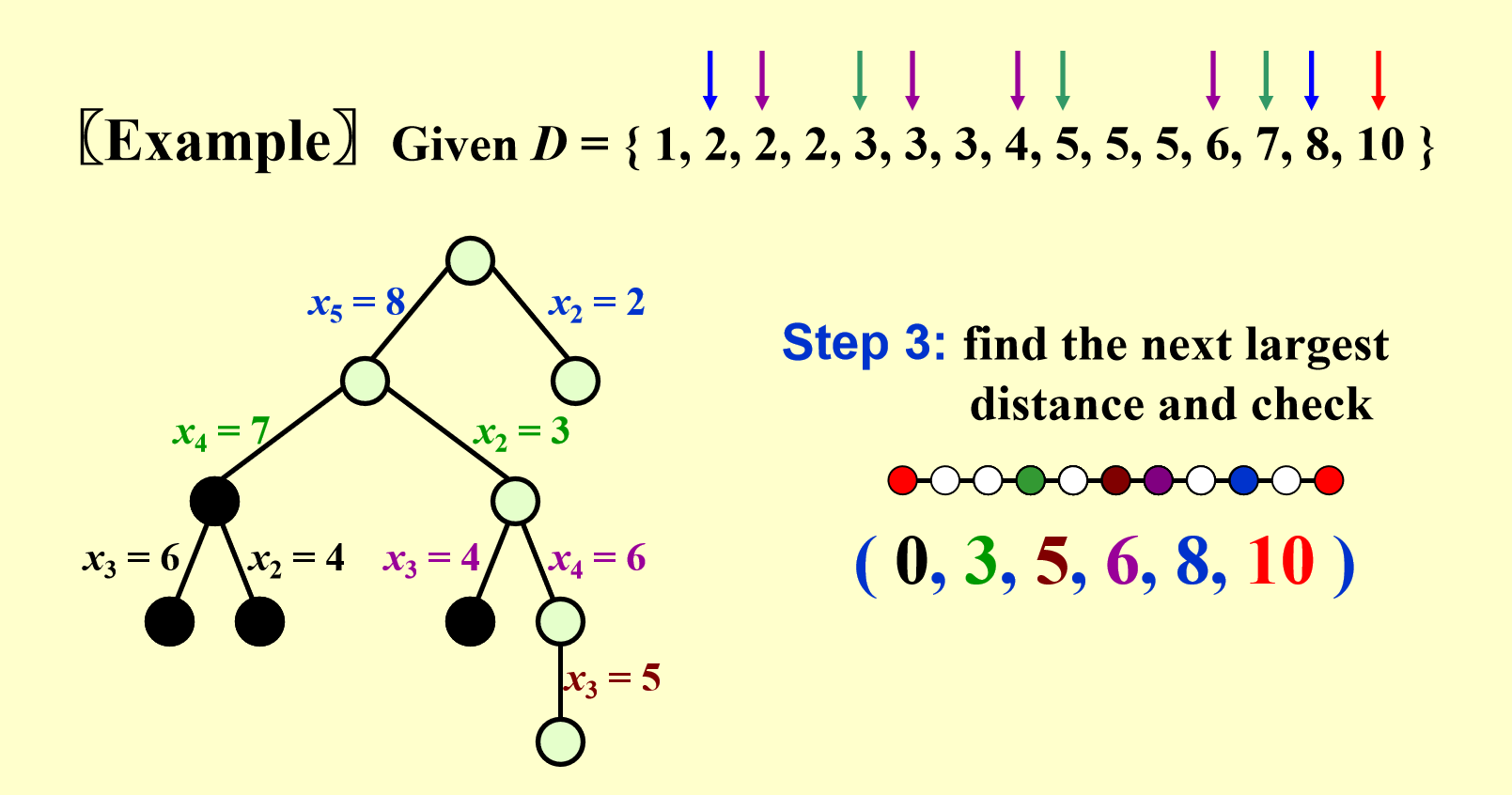
- 一共有两种情况:\(x_3 = 6\)(\(x_3 - x_1 = 6\))或 \(x_2 = 4\)(\(x_6 - x_2 = 6\))
- 经检验,这两种情况均不满足要求
- \(x_3 = 6\) 时,有 \(x_4 - x_3 = x_5 - x_4 = 1\),但距离集中只有 1 个 \(1\),不满足条件
- \(x_2 = 4\) 时,有 \(x_2 - x_1 = x_5 - x_2 = 4\),但距离集中只有 1 个 \(4\),不满足条件
- 所以通过回溯,回到 \(x_2 = 3\) 的分支上,记得恢复点集和距离集中被用掉或被删掉的点或路径
问题:为什么第 3 步不是找“下一个最小的距离”
相较于找最小的距离,找最大的距离所产生的可能性更少(或者解空间更小
代码实现
bool Reconstruct(DistType X[], DistSet D, int N, int left, int right) {
// X[1]...X[left-1] and X[right+1]...X[N] are solved
bool Found = false;
if (is_Empty(D))
return true; // solved
D_max = Find_Max(D);
// option 1: X[right] = D_max
// check if |D_max - X[i]| in D is true for all X[i]'s that have been solved
OK = Check(D_max, N, left, right); // pruning
if (OK) { // add X[right] and update D
X[right] = D_max;
for (i = 1; i < left; i++)
Delete(abs(X[right] - X[i]), D);
for (i = right + 1; i <= N; i++)
Delete(abs(X[right] - X[i]), D);
Found = Reconstruct(X, D, N, left, right - 1);
if (!Found) { // if does not work, undo
for (i = 1; i < left; i++)
Insert(abs(X[right] - X[i]), D);
for (i = right + 1; i <= N; i++)
Insert(abs(X[right] - X[i]), D);
}
}
// finish checking option 1
if (!Found) { // if option 1 does not work
// option 2: X[left] = X[N] - D_max
OK = Check(X[N] - D_max, N, left, right);
if (OK) {
X[left] = X[N] - D_max;
for (i = 1; i < left; i++)
Delete(abs(X[left] - X[i]), D);
for (i = right + 1; i <= N; i++)
Delete(abs(X[left] - X[i]), D);
Found = Reconstruct(X, D, N, left + 1, right);
if (!Found) {
for (i = 1; i < left; i++)
Insert(abs(X[left] - X[i]), D);
for (i = right + 1; i <= N; i++)
Insert(abs(X[left] - X[i]), D);
}
}
// finish checking option 2
} // finish checking all the option
return Found;
}
一些小结论
- 如果将距离集存储在一棵 AVL 树中,且没有回溯发生,那么该算法的时间复杂度为 \(O(N^2 \log N)\),其中 \(N\) 为点数
Games: Tic-tac-toe⚓︎
Description⚓︎
问题描述
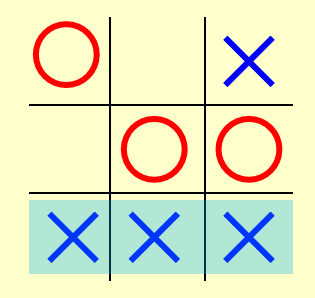
井字棋(tic-tac-toe):在 \(3 \times 3\) 的棋盘上,一位玩家画圈,另一位玩家画叉,轮流下棋。如果某位玩家在棋盘上的所有标记中有 3 个位于同一行、同一列或同一对角线上,则该玩家获胜。
- 一共有 \(3^9\) 种可能的棋局(每个格子上有圈、叉、空三种情况,不考虑获胜后停止下棋的问题)
- 一共有 \(9!\) 种可能的下棋顺序(不考虑当前的棋子是圈还是叉)
Method⚓︎
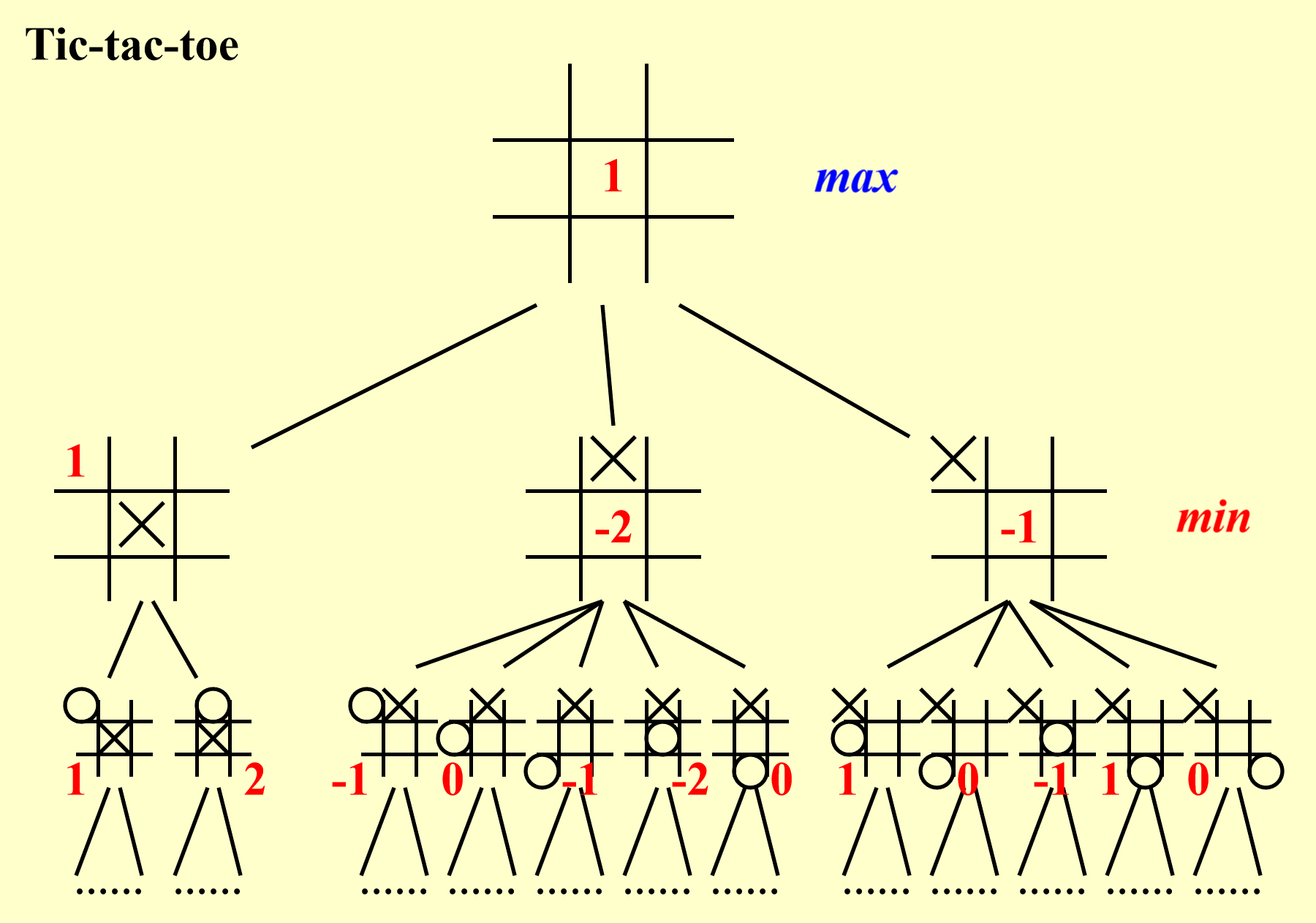
我们采用极小化极大策略(minimax strategy) 来解决井字棋的问题,这一策略对于棋手双方而言都是最佳策略。
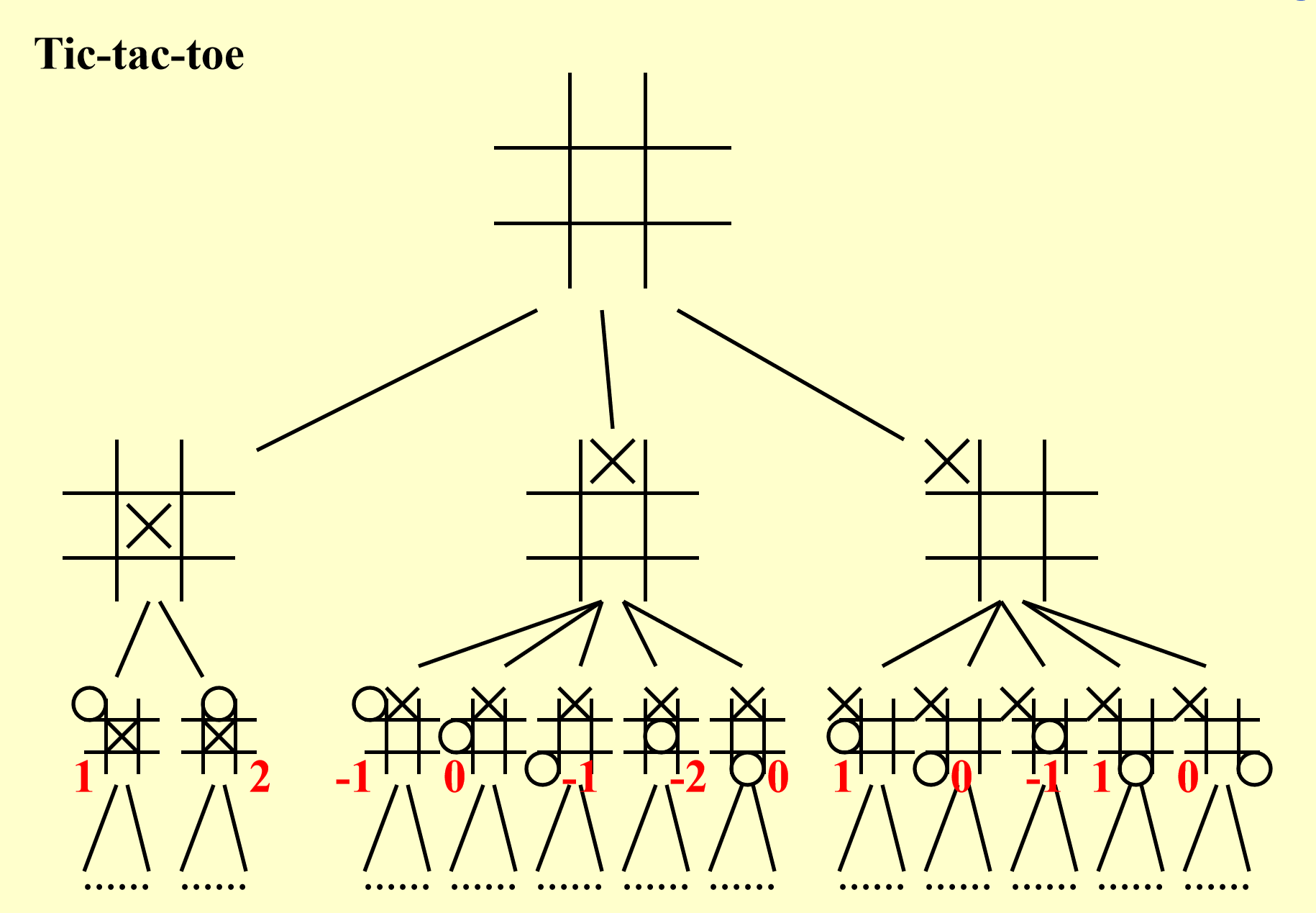
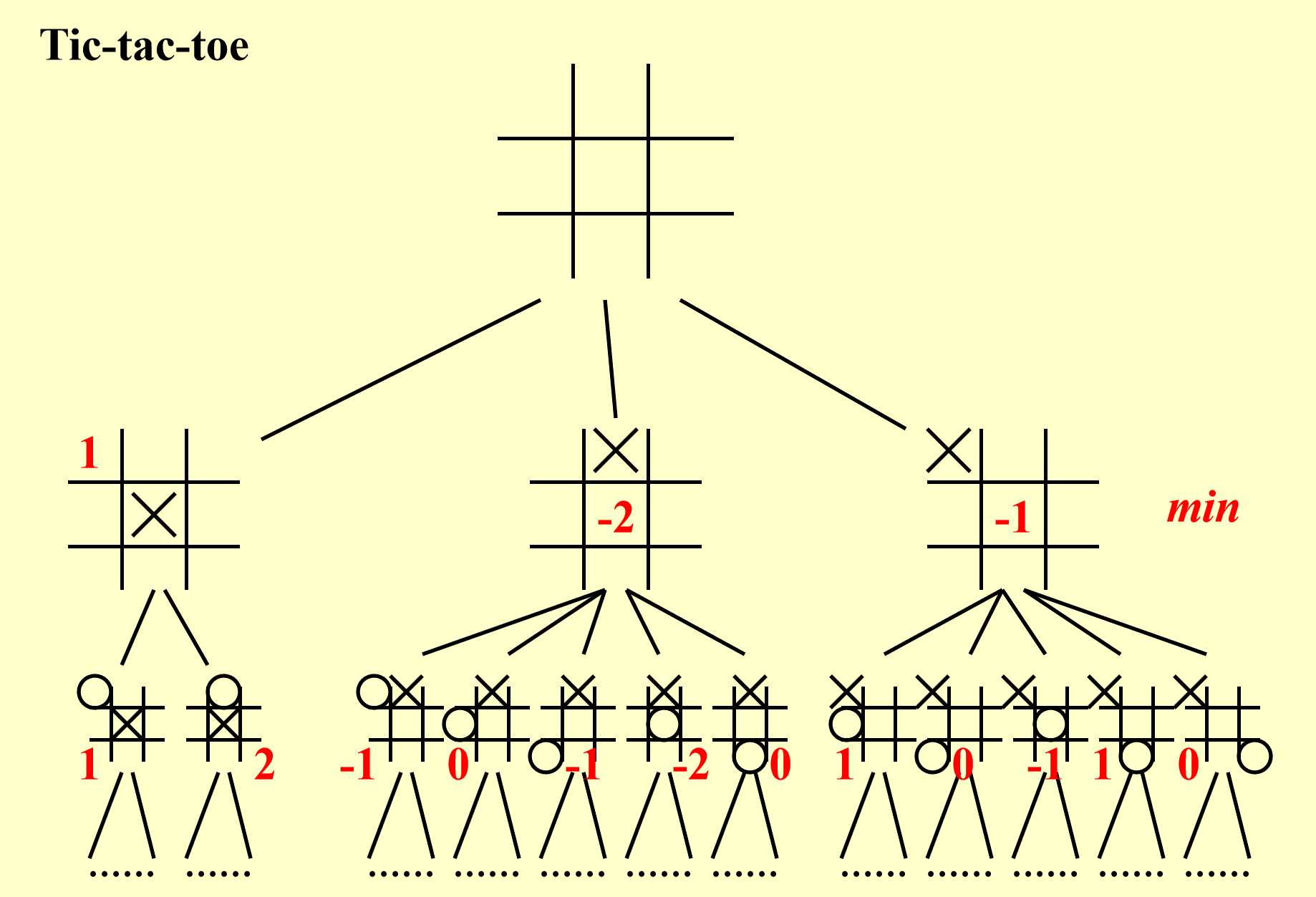
- 使用一个评估函数(evaluation function) 来量化当前棋局 \(P\) 的价值:通常令为 \(f(P) = W_{\text{Computer}} - W_{\text{Human}}\),\(W\) 表示在当前棋局 \(P\) 下可能的获胜情况数
-
假设玩家双方分别是人类和计算机,根据上述评估函数,显然人类倾向于最小化当前棋局 \(P\) 下的价值(goodness)(\(f(P)\) 越小,人类获胜的可能越大
) ,而计算机倾向于最大化 \(P\) 下的价值(\(f(P)\) 越大,计算机获胜的可能越大)
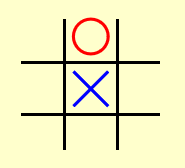
动画演示
- 为了解释的方便,我们不考虑更后面的轮数(实在画不下这么大的博弈树
! ) ,所以从第 2 轮开始分析 - 计算机对应“叉”,人类对应“圈”
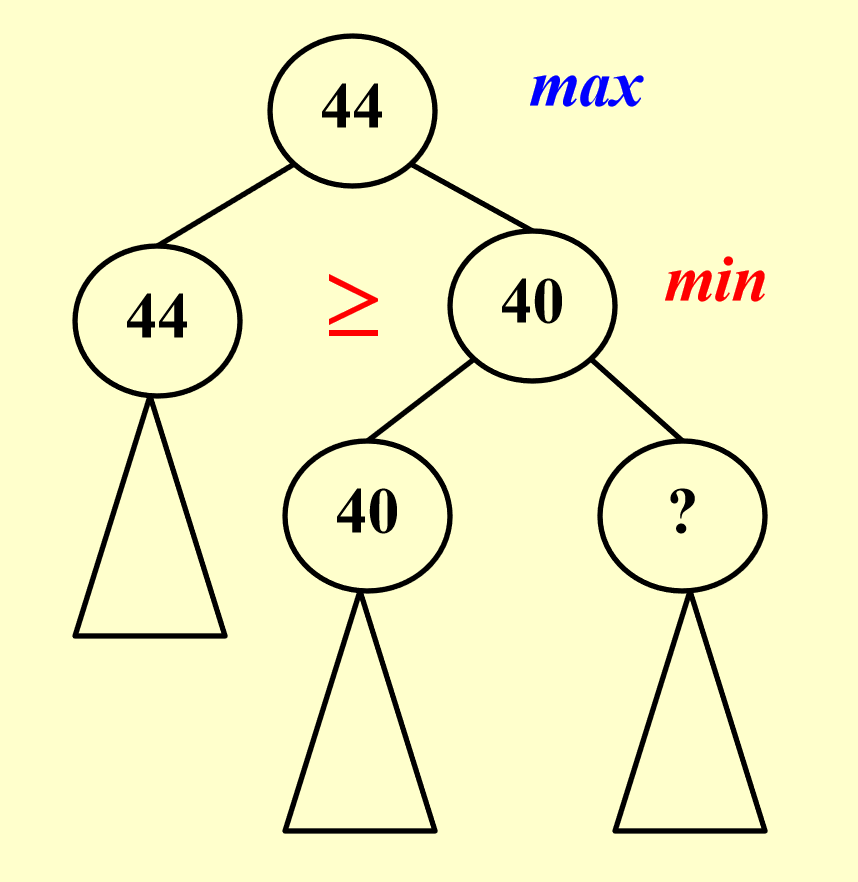
\(\alpha-\beta\) 剪枝:它结合了 \(\alpha\) 剪枝和 \(\beta\) 剪枝,能够将博弈树的搜索规模限制在 \(O(\sqrt{N})\) 个节点(\(N\) 为博弈树的节点数
-
\(\alpha\) 剪枝:对于下列情况,我们不需要再搜索根节点为
?的子树- 若
? >= 40,第二层的节点40不会更新,因为该节点取的是左右孩子的最小值 - 若
? < 40,虽然第二层节点的40会更新,但是不影响第一层的节点,因为第一层节点取的是左右孩子的最大值,而最大值原来就不是这个更新的节点
- 若
-
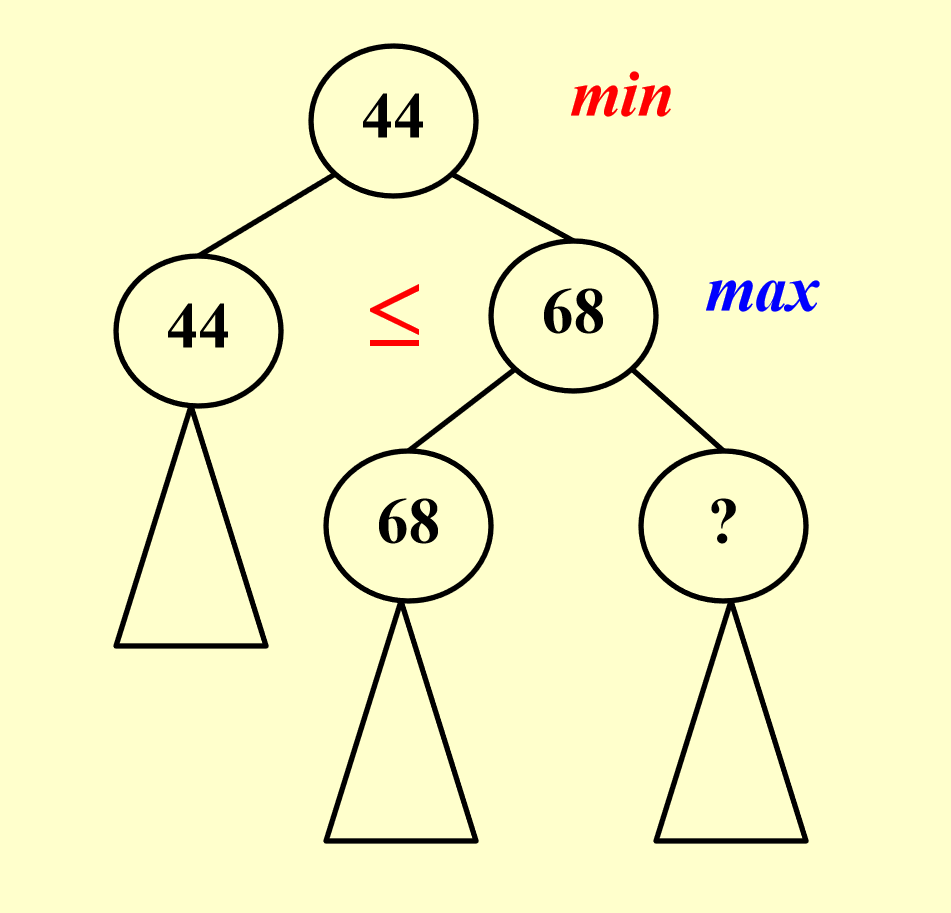
\(\beta\) 剪枝:对于下列情况,我们不需要再搜索根节点为
?的子树- 若
? <= 68,第二层的节点68不会更新,因为该节点取的是左右孩子的最大值 - 若
? > 68,虽然第二层节点的68会更新,但是不影响第一层的节点,因为第一层节点取的是左右孩子的最小值,而最小值原来就不是这个更新的节点
- 若
评论区