Lec 2: Red-Black Trees and B+ Trees⚓︎
约 4799 个字 291 行代码 预计阅读时间 28 分钟
Red-Black Trees⚓︎
注意
在红黑树中
Definition⚓︎
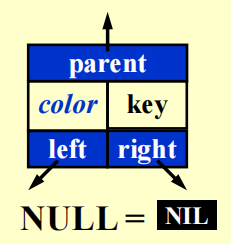
红黑树(red-black trees) 本质上也是一棵二叉查找树,它的目标同 AVL 树一样,也是尽可能地维护二叉查找树的平衡。下图表示的是红黑树的一个节点:
- 节点除了有指向左右孩子的指针外,还额外多了一个指向父节点的指针
- 此外又多了一个存储颜色的字段,占 1 bit 空间(红色 / 黑色)
- 红黑树里的空指针
NULL一般会称为NIL,它代表的是一个外部节点,其颜色为黑色。规定:红黑树的孩子要么是实际存在的节点,要么是个空节点
于是有了以下定义:
定义
红黑树是一棵满足下面几条性质的二叉查找树:
- 每个节点的颜色非黑即红
-
根节点是黑色的
根据 wiki 上的内容,第二条性质并不是必需的。
-
每个叶子节点 (
NIL) 是黑色的注意
- 这里的「叶子结点」并不是指没有孩子的节点,它特指空节点
NIL。而空节点一般不会被画出来的,所以需要记住这一点,否则在对红黑树操作时很容易弄错 - 如果定义中缺少这一性质,那么一棵 skew tree,甚至是链表都有可能符合红黑树的定义
- 这里的「叶子结点」并不是指没有孩子的节点,它特指空节点
-
如果一个节点是红色的,那么它的孩子都是黑色的
- 总结:红色节点要么有两个黑孩子,要么没有孩子,不会出现红色节点相邻的情况,也不会出现红色节点只有一个孩子的情况(否则下面的性质不会满足)
-
- 在红黑树中,实际存在的节点被称为内部节点(internal node),而空节点
NIL被称为外部节点(external node)
对于每个节点,从该节点出发,到它后代叶子节点(即
NIL节点)的所有简单路径包含了相同数量的黑色节点(这是实现红黑树平衡的关键) - 在红黑树中,实际存在的节点被称为内部节点(internal node),而空节点
为了量化红黑树的平衡程度,我们为节点 x 定义一个称为「黑高」(black height) 的字段 \(\mathrm{bh}(x)\):它表示从节点 x 出发到叶子节点 (NIL)的任意简单路径上黑色节点的个数(不包括节点 x)
- 根据定义的性质 5,由于每条简单路径的黑色节点数相同,所以便可以任意选取其中 1 条路径
- 整棵树的黑高等于根节点的黑高
引理:一棵有 \(N\) 个内部节点的红黑树,它的高度至多为 \(2\log (N+1)\)。
- 由该引理知,尽管红黑树相比 AVL 树看起来不是那么平衡,但是它能够确保树高是 \(O(\log N)\) 的,所以红黑树也是一棵相当平衡的树。
证明
我们要证明两个不等式:
- 对于任意节点 \(x\),\(\mathrm{sizeof}(x) \ge 2^{\mathrm{bh}(x)} - 1\)
- \(\mathrm{bh}(Tree) \ge \dfrac{h(Tree)}{2}\)
用归纳法证明
- 当 \(h(x) = 0\) 时,\(x\) 是空节点,所以 \(\mathrm{sizeof}(x) = 2^0 - 1 = 0\)
- 归纳假设:对于满足 \(h(x) \le k\) 的节点 \(x\),该不等式均成立
- 当 \(h(x)=k+1\) 时,\(\mathrm{bh}(child) = \mathrm{bh}(x)\) 或者 \(\mathrm{bh}(x)-1\)
- 因为 \(h(child) \le k\),所以 \(\mathrm{sizeof}(child) \ge 2^{\mathrm{bh}(child)} - 1 \ge 2^{\mathrm{bh}(x)-1}-1\)
- 所以 \(\mathrm{sizeof}(x) = 1 + 2\mathrm{sizeof}(child) \ge 2^{\mathrm{bh}(x)}-1\),得证
由定义知,对于每个红色节点,它的孩子都是黑色的,因此从根节点到叶子结点的所有简单路径上,至少有一半的节点(不包括根节点)是黑色的,即不等式 2 成立
由两个不等式可以得到:
即 \(h \le 2 \log(N+1)\)
Operations⚓︎
Insertion⚓︎
与 AVL 树类似,我们希望插入的节点尽可能不影响红黑树的平衡程度,换言之就是尽可能地不改变红黑树的黑高,因此新插入节点的颜色应该是红色的。
- 如果运气好的话,即新插入节点的父节点是黑色的,我们无需作任何调整
- 但很可能会遇到父节点也是红色的情况,这样需要我们做一定的调整,下面根据课件给出的例子,分情况讨论调整的方法
分析
注意
- 这块内容是红黑树的灵魂部分,所以需要仔细品读和深入理解
- 「调整」一栏的图中,黑色三角形表示以黑色节点为根节点的子树
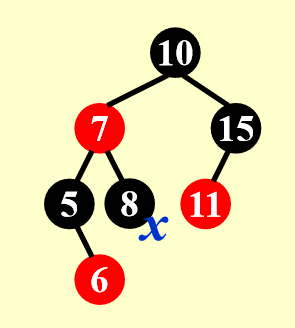
新插入节点的父节点,以及父节点的兄弟节点都是红色的。
新插入节点是其祖父节点(黑色)的 LR 或 RL 孙子节点。
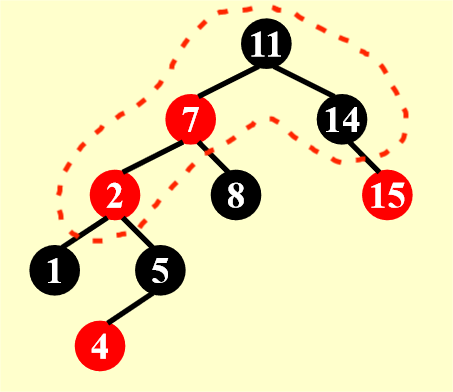
根据前面的分类讨论,我们可以画一个(不是特别标准的)状态图,从全局角度观察整个插入流程(想法来自修佬的笔记)


- 可以看到,在整个调整的过程中,只需要常数次的旋转和染色,就可以使子树恢复合法的红黑树性质(即保持平衡
) 。而最坏的情况是需要不断向上维护子树的平衡,直至根节点为止,因此插入的效率和 AVL 树差不多,均为 \(O(\log N)\)。
注:迭代实现比递归实现速度上略快一点,但不多。
注
在网上搜相关资料的时候,我发现实际上插入分为五种情况,而课件忽略了前两种较为简单的情况,这里就稍微简单地提一下:
- Case 4:向空树插入新节点 -> 将该节点染黑即可
- Case 5:父节点是黑色的 -> 啥也不用动,因为没有与红黑树的性质冲突(其实前面例子刚开始的时候就已展示过这种情况了)
思考
用双旋替代 Case 2 和 Case 3 的调整是否可行?答案是否定的(如果是肯定的话,这里也就不会分两种情况来介绍了
Deletion⚓︎
我们通过「两步走」的方法实现整个删除操作:维护红黑树的平衡 -> 删除树中节点
先来看删除节点(共 4 种情况
- 删除树中的唯一节点 -> 直接删
- 被删除节点有两个孩子 -> 用左子树最大节点或右子树最小节点的值替代被删除的节点的值(注意保持颜色不变
) (具体删除细节见 FDS 相关部分) ,然后将用于替代的节点从原来的位置中删除(根据二叉查找树的性质知,它至多只有一个孩子,因此问题转换为后面两种情况) - 被删除节点没有孩子 -> 直接用
NIL替代(黑色)该节点 - 被删除节点有一个孩子
- 若孩子为红色 -> 该节点为黑色 -> 直接用孩子替代该节点并染黑即可
- 若孩子为黑色 -> 该节点可红可黑
- 该节点为红色 -> 直接用孩子替代该节点
- 该节点为黑色 -> 删除后由于打破最后一条性质,需要重新维护
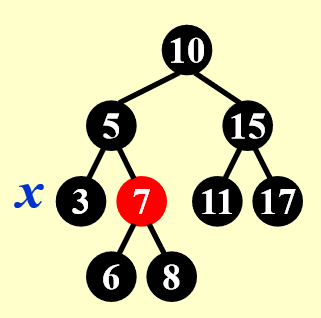
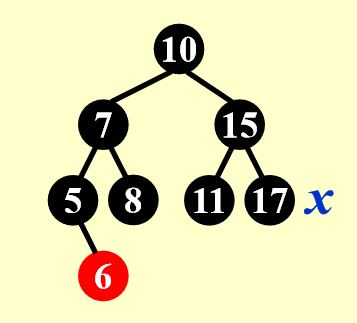
综上所述,再来看最重要(也是最麻烦)的平衡维护。这里用 X 表示当前需要维护的节点(一般是接替黑色的被删节点的孩子NIL节点
分析
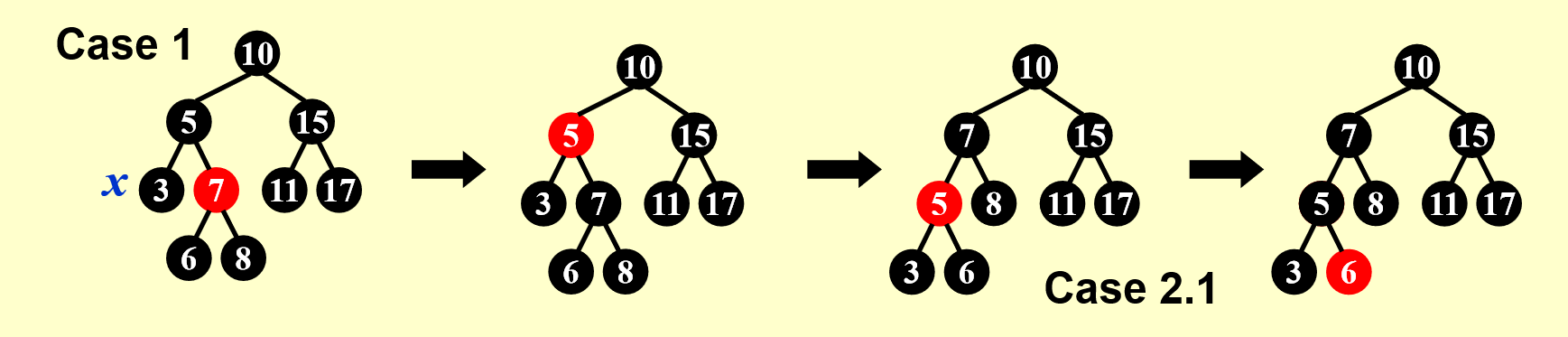
X 的兄弟节点 S 是红色的(则 S 的两个孩子、父节点 P 一定都是黑色的
X 的兄弟及兄弟的两个孩子都是黑色的(不考虑 X 父节点的颜色)
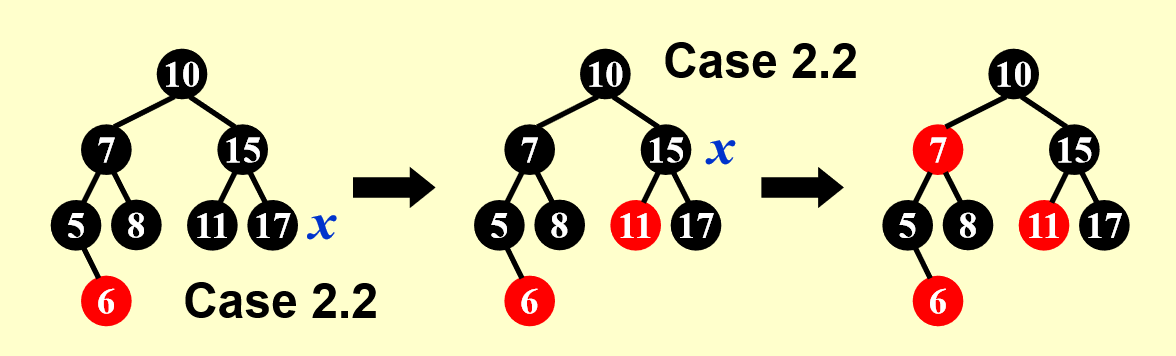
兄弟节点 S 是黑色的;兄弟节点靠近内侧的孩子(LR、RL)是红色的,靠近外侧的孩子(LL、RR)是黑色的;父节点的颜色可红可黑。
再次献上不是很标准的状态图:


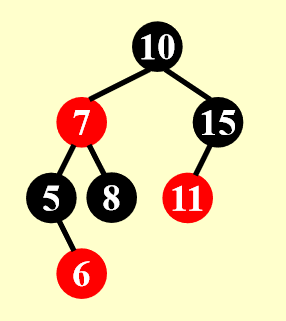
从状态图中,可以发现在删除一个节点并维护平衡的过程中,至多需要 3 次旋转操作,以及 \(O(\log N)\) 次染色操作,因此删除操作的时间复杂度为 \(O(\log N)\)。然而,由于删除操作中只需常数次的旋转,而 AVL 树需要 \(O(\log N)\) 次旋转(旋转比染色耗时更长
例子
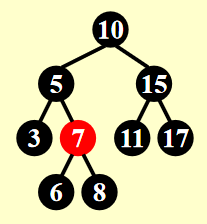
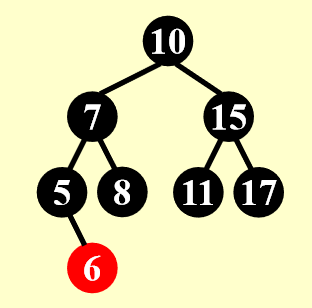
看了前面的理论分析如果你是像我一样第一次学红黑树的话)你应该处于一种似懂非懂的状态。现在尝试阅读下面的例子,看你是否真的理解红黑树的删除过程。
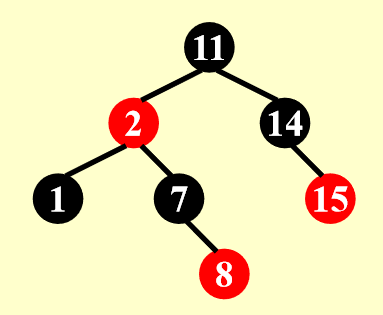
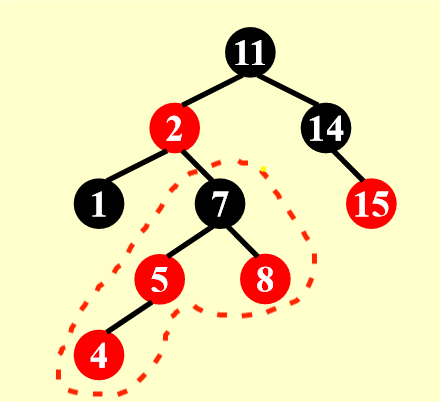
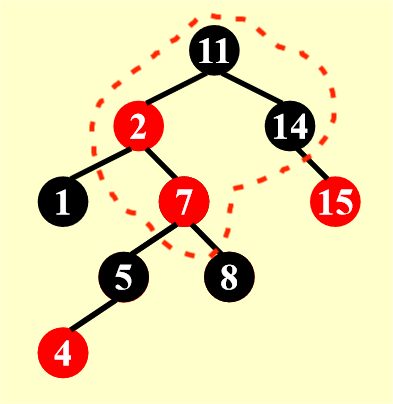
这是一棵红黑树,我们要从中删除若干个节点:
AVL 树 vs 红黑树
AVL 树和红黑树的效率比较(插入 / 删除单个节点所需的旋转次数
| AVL Tree | Red-Black Tree | |
|---|---|---|
| Insertion | \(\le 2\) | \(\le 2\) |
| Deletion | \(O(\log N)\) | \(\le 3\) |
- 事实上,AVL 树的最差高度略低于红黑树,因此如果有频繁的访问操作,推荐使用 AVL 树
- 然而,红黑树的优势在于它的单次删除所需旋转次数是常数级复杂度的,而 AVL 树的删除需要 \(O(\log N)\) 次旋转,所以如果有频繁的删除操作,推荐使用红黑树
- 而且,红黑树的节点只需存储 1 位颜色字段,而 AVL 树至少需要 2 位来存储平衡因子,因此红黑树在空间上更占优势
- 总体而言,红黑树的运行效率比 AVL 树快了大概 10%-20% 左右
B+ Trees⚓︎
B+ 树是 B 树的改良版,广泛应用于关系型数据库和操作系统的文件系统中。
计算机内的大量数据往往是存在磁盘内而非内存里,但磁盘的访问速度比内存慢很多。因此为了加快磁盘的访问速度,可以把数据存储于一段连续的块内,这便是 B+ 树和普通的二叉查找树之间的区别。而且,相比二叉查找树,B+ 树的插入与修改拥有较稳定的对数时间复杂度,因而能够保持数据稳定有序。
定义
\(M\) 阶 (order) B+ 树遵循以下结构上的性质:
- 根节点要么是叶子节点,要么有 \(x\)(\(x \in [2 , M]\)) 个孩子
- 所有非叶子节点(除了根节点)有 \(y\)(\(y \in [\lceil \dfrac{M}{2}\rceil , M]\)) 个孩子
上面的两个下界都是分裂节点时分配到的孩子数
- 所有的叶子位于相同深度的位置上(因为 B+ 树是自底向上构建的,而一般的二叉查找树是自顶向下构建的)
还有以下值得注意的地方:
- 所有数据实际上只存储在叶子节点上,每个叶子节点就是一个块
- 每个内部节点存储指向 \(M\) 个孩子的指针(如果孩子个数少于 \(M\) 个,剩下的指针为空指针
) ,以及 \(M-1\) 个来自除第一棵子树外每棵子树的最小值
Operations⚓︎
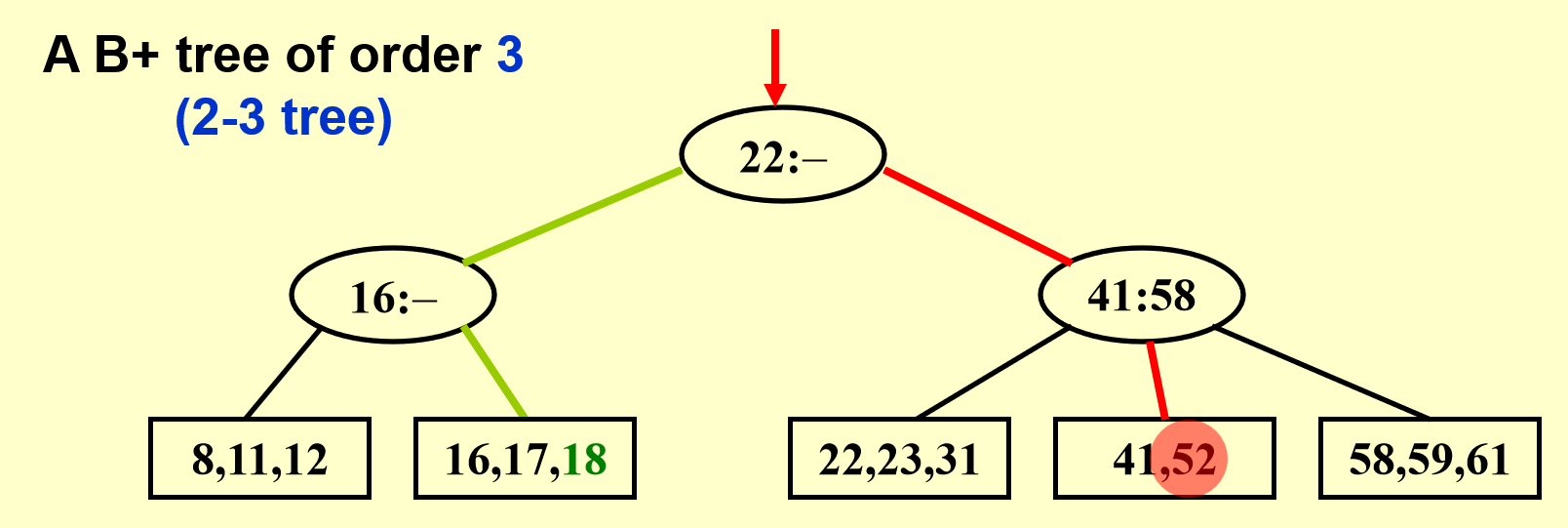
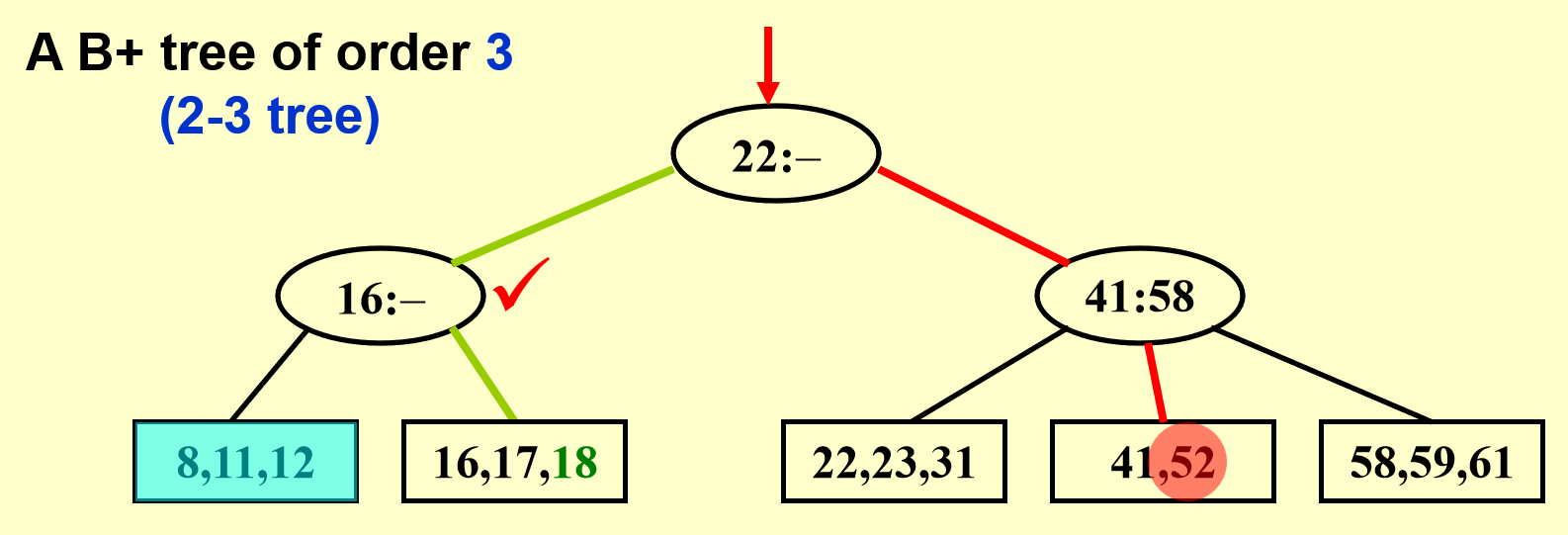
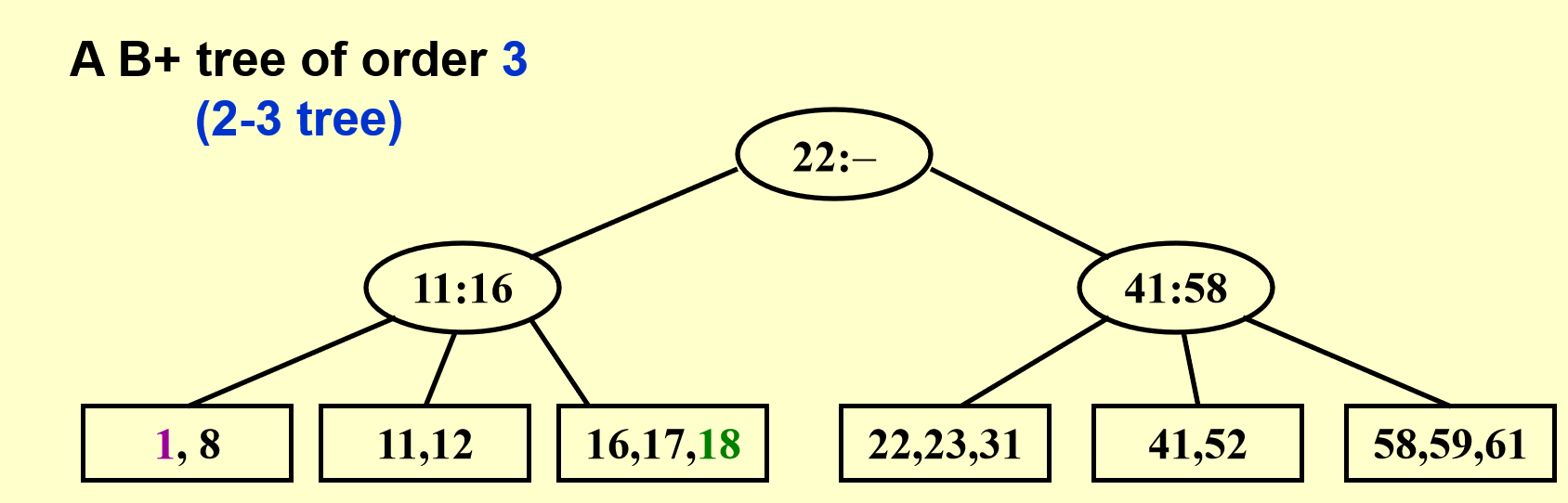
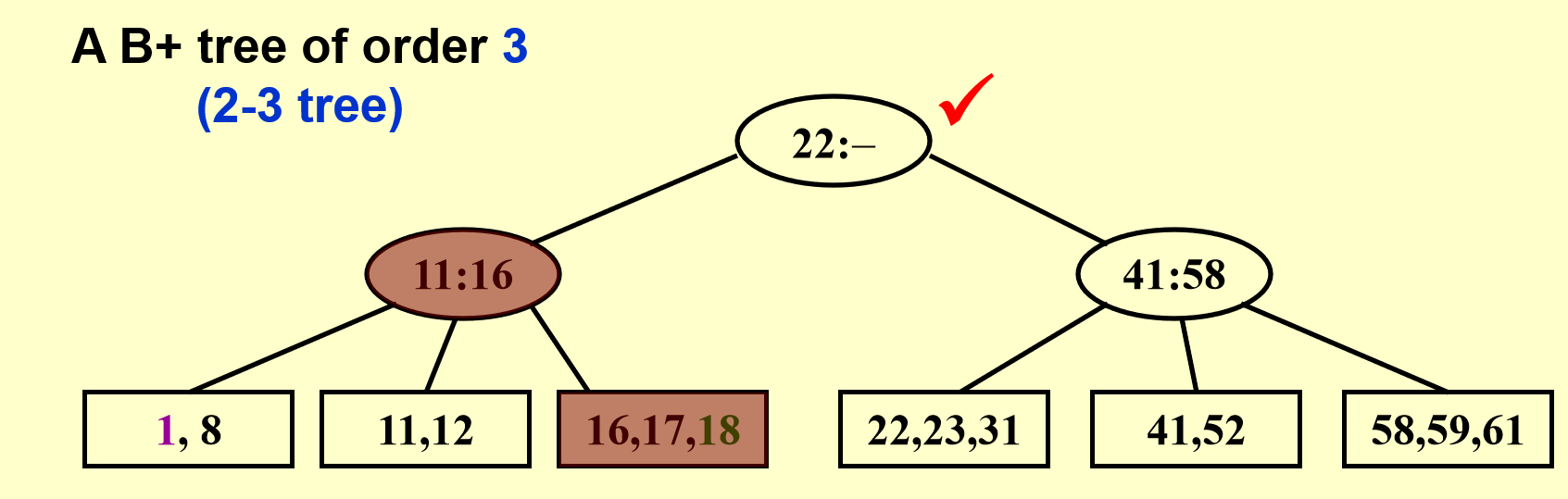
再来看一个例子,从中学习 B+ 树的创建、查找、插入等操作
例子
这是原始数据,由 5 个存储块构成,每个存储块存有 2-3 个数据(不得超过这个范围
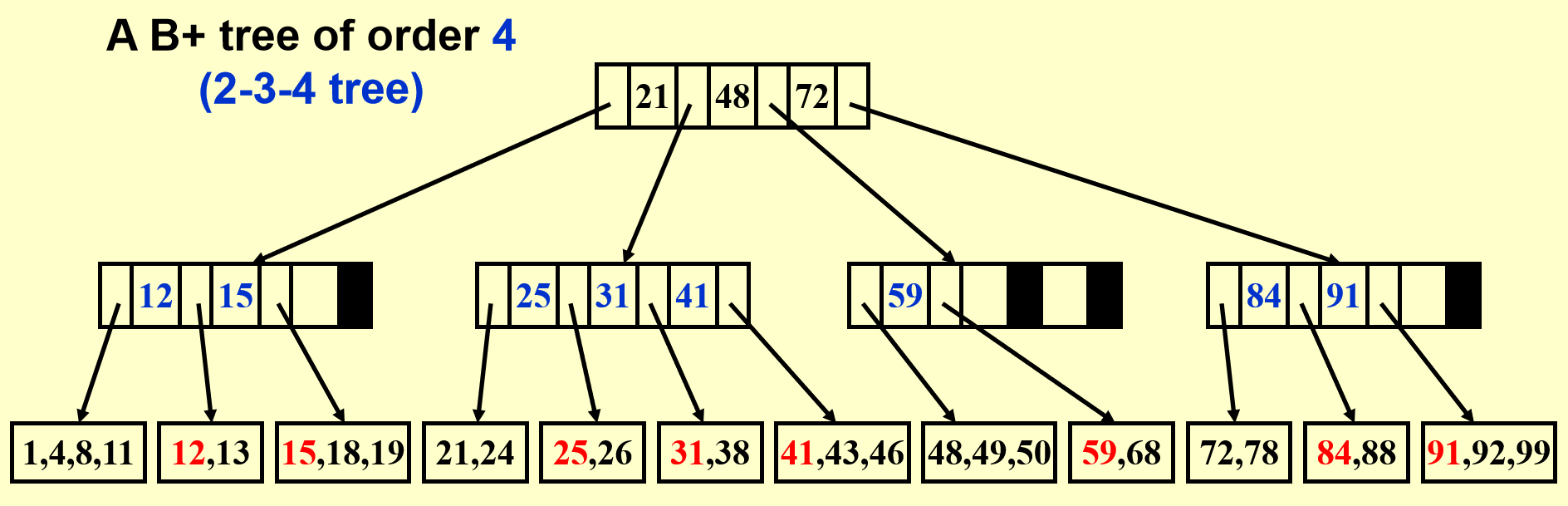
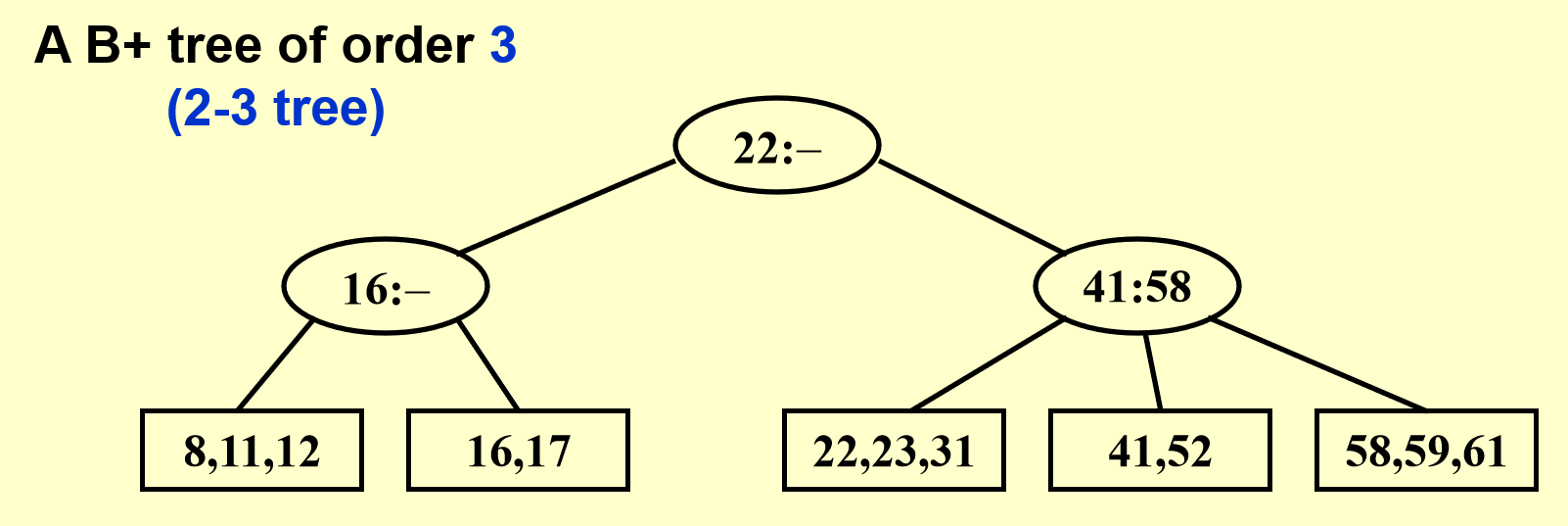
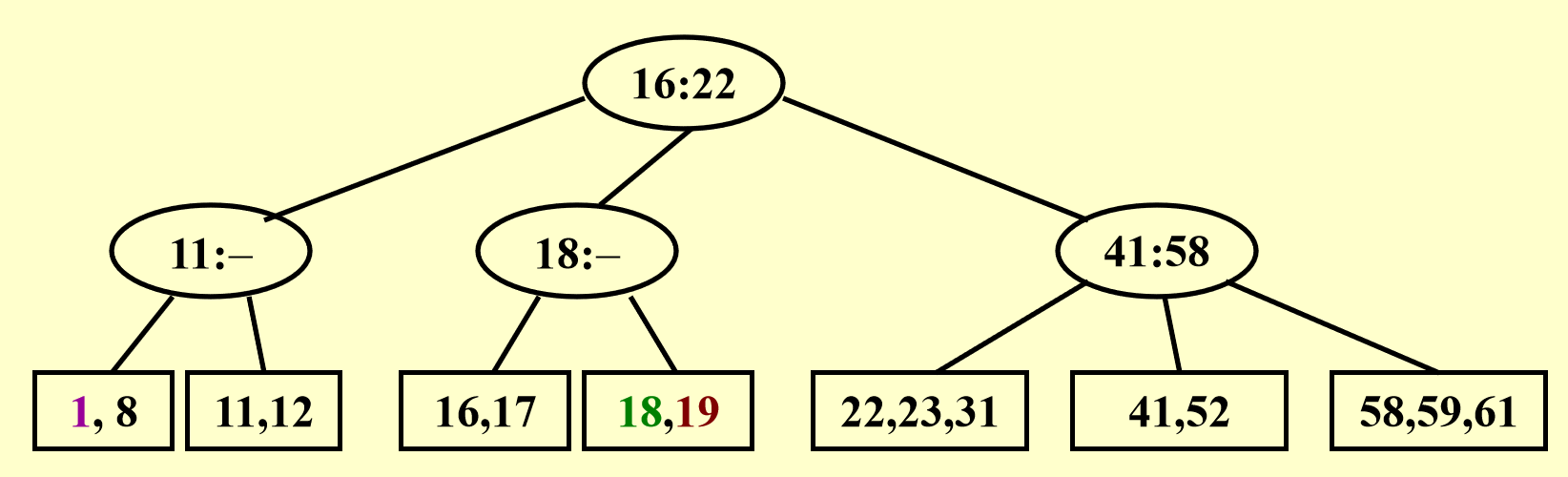
我们先根据这些存储块,自底向上创建一棵三阶 B+ 树:
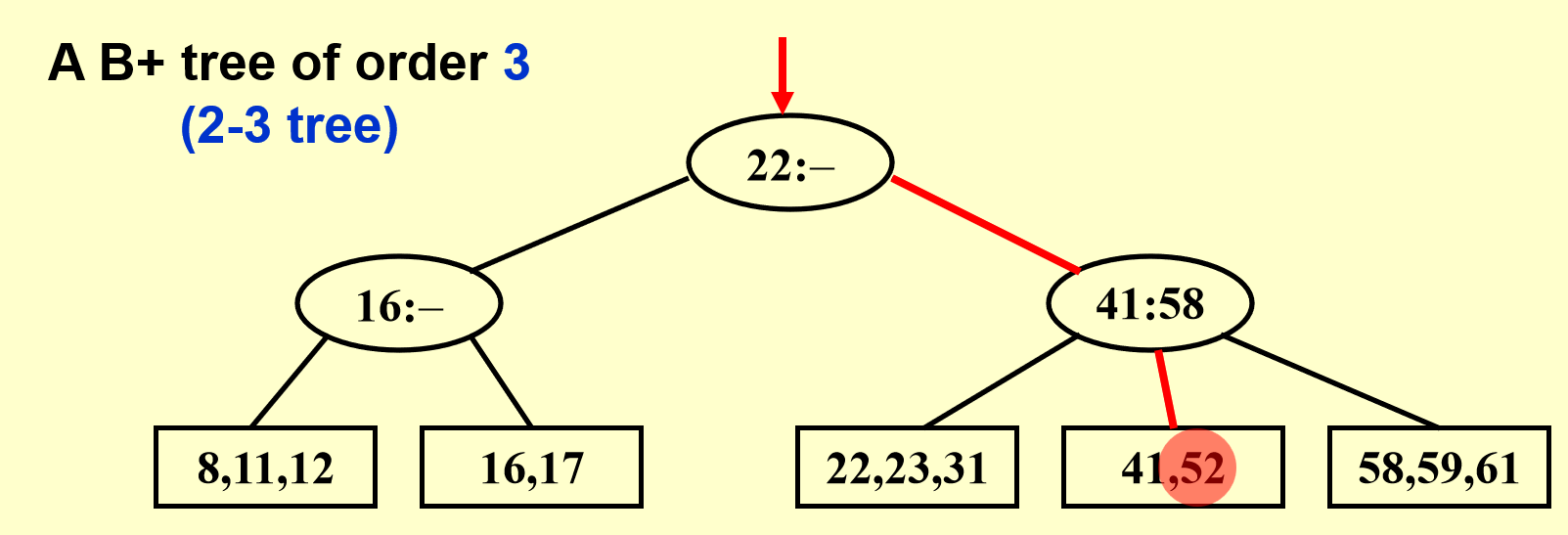
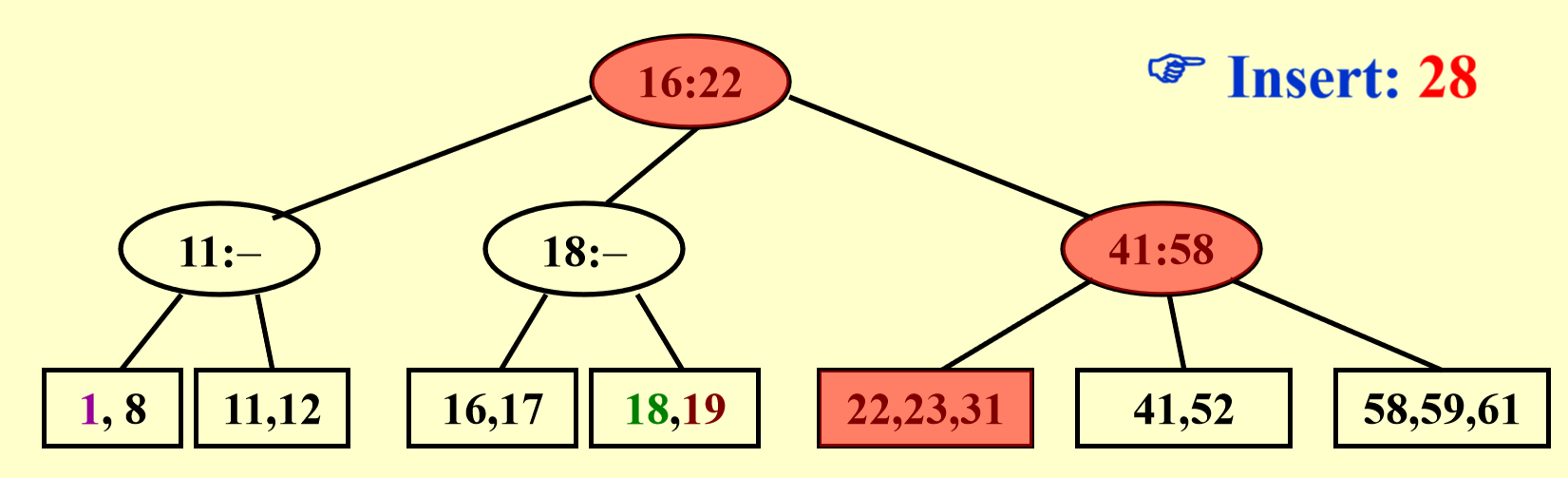
通过查找发现,我们要插入的数据块(蓝色)的数据已满,不能再插入了,那么就看能不能将这个数据块一分为二(每个数据块放 2 个数据
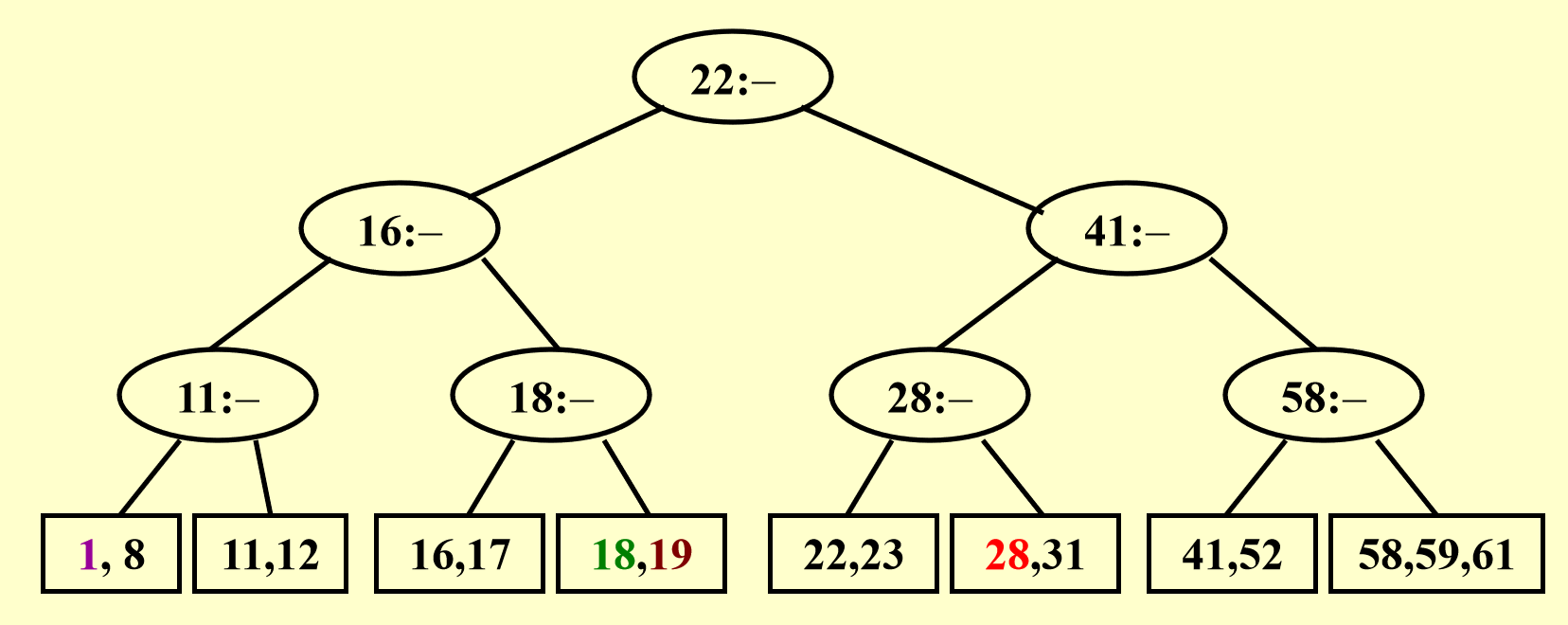
在插入操作中我们运用的是简单的分裂法,这会产生很多的叶子节点(一个个存储块
删除操作与插入类似,但要注意:如果一个根节点失去两个孩子时,要移除这个根节点。
伪代码实现(插入操作)
Btree Insert(ElementType X, Btree T) {
Search from root to leaves for X and find the the proper leaf node;
Insert X;
while (this node has M+1 keys) {
split it into 2 nodes with RoundUp((M+1) / 2) and RoundDown((M+1) / 2) keys respectively;
if (this node is the root)
create a new root with two children;
check its parent;
}
}
对于一棵有 \(N\) 个数据的 \(M\) 阶 B+ 树:
- 深度 \(\mathrm{Depth}(M, N) = O(\lceil \log_{\lceil \frac{M}{2} \rceil} N \rceil)\)
- 插入时间 \(T(M, N) = O(\dfrac{M \cdot \log N}{\log M}) = O(M \log_M N)\)
- 所以阶数 \(M\) 不是越大越好,最合适的取值为 3 或 4
- 查找时间 \(T_{Find}(M, N) = O(\log_M N) \le O(\log N)\)
代码实现
往一棵空树中插入若干数据(输入
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ORDER 3
#define LEAFCUT (ORDER / 2 + 1)
#define NONLEAFCUT (ORDER / 2)
#define SIZE 20000
typedef struct node * Node;
typedef struct node * BplusTree;
struct node {
int size;
int childrenSize;
int data[ORDER + 1];
Node children[ORDER + 1];
Node parent;
};
typedef struct queue * Queue;
struct queue {
int size;
int front;
int rear;
Node data[SIZE];
};
BplusTree Create();
Node Find(int x, BplusTree T, bool * flag);
void Insert(int x, Node node);
void Split(Node node);
void PrintTree(BplusTree T);
Queue CreateQueue();
void Enqueue(Node node, Queue Q);
Node Dequeue(Queue Q);
int cmp(const void * a, const void * b);
int cmpNode(const void * a, const void * b);
BplusTree Tree;
int main() {
int n;
int x;
int i, j, k;
bool isDuplicated = false;
Node tmp;
Tree = Create();
scanf("%d", &n);
for (i = 0; i < n; i++) {
isDuplicated = false;
scanf("%d", &x);
tmp = Find(x, Tree, &isDuplicated);
if (isDuplicated) {
printf("Key %d is duplicated\n", x);
} else {
Insert(x, tmp);
}
}
PrintTree(Tree);
return 0;
}
BplusTree Create() {
BplusTree T = (BplusTree)malloc(sizeof(struct node));
if (T == NULL) {
printf("Failed to create a B+ Tree!\n");
return T;
}
int i;
// T->data = (int *)malloc(sizeof(int) * (ORDER + 1));
for (i = 0; i <= ORDER; i++) {
T->children[i] = (Node)malloc(sizeof(struct node));
}
T->size = 0;
T->childrenSize = 0;
T->parent = NULL;
return T;
}
Node Find(int x, BplusTree T, bool * flag) {
int i;
if (!T) {
return T;
} else if (!T->childrenSize) {
if (T->size) {
for (i = 0; i < T->size; i++) {
if (x == T->data[i]) {
*flag = true;
break;
}
}
}
return T;
}
int pos = -1;
for (i = 0; i < T->size; i++) {
if (x < T->data[i]) {
pos = i;
break;
}
}
if (pos == -1) {
pos = i;
}
return Find(x, T->children[pos], flag);
}
void Insert(int x, Node node) {
int i;
node->data[node->size++] = x;
qsort(node->data, node->size, sizeof(int), cmp);
Split(node);
}
void Split(Node node) {
if (!node->childrenSize && node->size <= ORDER
|| node->childrenSize && node->size < ORDER) {
return;
}
Node lnode, rnode, tmpNode;
int cut;
int i, j;
if (!node->parent) {
tmpNode = Create();
node->parent = (Node)malloc(sizeof(struct node));
Tree = node->parent = tmpNode;
}
lnode = Create();
rnode = Create();
lnode->parent = rnode->parent = node->parent;
if (!node->childrenSize) {
cut = LEAFCUT;
for (i = 0; i < cut; i++) {
lnode->data[i] = node->data[i];
}
lnode->size = cut;
for (j = cut; j < node->size; j++) {
rnode->data[j - cut] = node->data[j];
}
rnode->size = node->size - cut;
} else {
cut = NONLEAFCUT;
for (i = 0; i <= cut; i++) {
if (i != cut)
lnode->data[i] = node->data[i];
lnode->children[i] = node->children[i];
lnode->children[i]->parent = lnode;
}
lnode->size = cut;
lnode->childrenSize = cut + 1;
for (j = cut + 1; j < node->size; j++) {
rnode->data[j - cut - 1] = node->data[j];
}
for (j = cut + 1; j < node->childrenSize; j++) {
rnode->children[j - cut - 1] = node->children[j];
rnode->children[j - cut - 1]->parent = rnode;
}
rnode->size = node->size - cut - 1;
rnode->childrenSize = node->childrenSize - cut - 1;
}
node->parent->data[node->parent->size++] = node->data[cut];
if (node->parent->childrenSize) {
for (i = 0; i < node->parent->childrenSize; i++) {
if (node->parent->children[i] == node) {
node->parent->children[i] = lnode;
break;
}
}
} else {
node->parent->children[node->parent->childrenSize++] = lnode;
}
node->parent->children[node->parent->childrenSize++] = rnode;
qsort(node->parent->data, node->parent->size, sizeof(node->parent->data[0]), cmp);
qsort(node->parent->children, node->parent->childrenSize, sizeof(node->parent->children[0]), cmpNode);
free(node);
Split(node->parent);
}
void PrintTree(BplusTree T) {
int i;
int flag;
Node node;
Queue q;
q = CreateQueue();
Enqueue(T, q);
Enqueue(NULL, q);
while (q->size) {
node = Dequeue(q);
if (!node) {
printf("\n");
if (q->size) {
Enqueue(NULL, q);
}
} else {
printf("[");
for (i = 0; i < node->size; i++) {
if (!i) {
printf("%d", node->data[i]);
} else {
printf(",%d", node->data[i]);
}
}
printf("]");
}
if (node) {
for (i = 0; i < node->childrenSize; i++) {
Enqueue(node->children[i], q);
}
}
}
}
Queue CreateQueue() {
Queue Q = (Queue)malloc(sizeof(struct queue));
Q->size = 0;
Q->front = Q->rear = 0;
return Q;
}
void Enqueue(Node node, Queue Q) {
Q->data[Q->rear++] = node;
Q->size++;
}
Node Dequeue(Queue Q) {
Node returnNode = Q->data[Q->front++];
Q->size--;
return returnNode;
}
int cmp(const void * a, const void * b) {
return *(int *)a - *(int *)b ;
}
int cmpNode(const void * a, const void * b) {
const Node nodeA = *(const Node*)a;
const Node nodeB = *(const Node*)b;
return nodeA->data[0] - nodeB->data[0];
}
评论区