Lec 4: Leftist Heaps and Skew Heaps⚓︎
约 4543 个字 90 行代码 预计阅读时间 24 分钟
注意
下面所涉及到的堆若不做特殊说明,默认为最小堆。
Leftist Heaps⚓︎
Definition⚓︎
引入
在 FDS 中,我们已经学过了堆(优先队列),通过这一数据结构,我们可以在 \(O(1)\) 时间内找到数据集中的最大值或最小值,同时它的插入和删除元素的操作也相当快(\(O(\log N)\)
尽管如此,我们还会用到合并(merge) 操作。在一般的堆中,合并的时间复杂度为 \(\Theta(N)\):
- 首先,要将一个堆(数组)内的数据拷贝到另一个堆(数组)上,需要 \(\Omega(N)\) 的时间
- 之后还得用 \(\mathrm{BuildHeap}\) 的方法整理合并后的堆,需要 \(O(N)\) 的时间
那么,是否存在一种改良的堆,可以提高合并的效率呢?答案便是我们接下来要讲的 leftist heaps。
也许你会想到用指针来提升合并的速度,但这样做会影响到其他运算的效率:我们原来可以用数组索引快速定位到父节点和孩子节点(只需简单的移位和加法操作
) ,用指针的话就会使这种定位变得更加困难。
左偏堆(又称左式堆、左倾堆等)(leftist heaps)
- 它保留了堆的顺序性质,即每个节点一定比它所有的孩子节点大 / 小
- 变化之处在于结构性质:它不再是一棵完全二叉树,而是一棵不平衡的树
除此之外,左偏堆的节点还多了一个名为空指针路径长度(null path length) 的字段,记作 \(\mathrm{Npl}(X)\),表示的是从节点 \(X\) 到没有两个孩子的节点(即叶节点或度为 1 的节点)的最短距离。
- 记 \(\mathrm{Npl}(NULL) = -1\)
- 这个字段用于准确表述左偏堆满足的性质:对于堆上的每个节点,它的左孩子的空指针路径长度不小于它的右孩子的空指针路径长度,因此整棵树会“向左歪”,即左子树的深度更深一些。
-
空指针路径长度的递推关系式为:
\[ \mathrm{Npl}(X) = \min \{\mathrm{Npl}(C) + 1\ \mathrm{for\ all}\ C\ \mathrm{as\ children\ of}\ X\} \] -
因此,空指针路径长度往往是自底向上计算的。
定理
对于一个左偏堆,如果它右侧的路径上有 \(r\) 个节点(即根节点的空指针路径长度为 \(r-1\)
证明(归纳法)
- 当 \(n = 1\) 时,显然成立
- 假设当 \(n \le r\) 时定理成立
- 当 \(n = r + 1\) 时,由于根节点也算在右侧路径的节点数内,所以先将它去掉
- 也就是说右子树的右侧路径上有 \(r\) 个节点,那么根据归纳假设知,右子树的节点数至少为 \(2^r - 1\)
- 再根据左偏树的定义知,左孩子的空指针路径长度不小于它的右孩子的空指针路径长度,因此左子树的节点数也至少为 \(2^r - 1\)
- 那么整个堆的节点数至少为 \(1 + 2 \times (2^r - 1) = 2^{r + 1} - 1\),得证
由这个定理,不难得到以下推论:对于一个具有 \(N\) 个节点的左偏堆,它的右侧路径上至多有 \(\lfloor \log (N + 1) \rfloor\) 个节点。因此,想要减小合并操作所花的时间,我们需要让该操作尽可能地在堆的右侧来完成,因为右侧的堆高为 \(O(\log N)\),那么合并的速度就能接近 \(O(\log N)\) 了。
Operations⚓︎
左偏堆的声明如下:
代码实现
#ifndef _LeafHeap_H
struct TreeNode;
typedef struct TreeNode * PriorityQueue;
// Minimal set of priority queue operations
// Note that nodes will be shared among several
// leftist heaps after a merge; the use must
// make sure to not use the old leftist heaps
PriorityQueue Initialize(void);
ElementType FindMin(PriorityQueue H);
int IsEmpty(PriorityQueue H);
PriorityQueue Merge(PriorityQueue H1, PriorityQueue H2);
#define Insert(X, H) ( H = Insert1((x), H) )
// DeleteMin macro is omitted
PriorityQueue Insert1(ElementType X, PriorityQueue H);
PriorityQueue DeleteMin1(PriorityQueue H);
#endif
// Place in implementation file
struct TreeNode {
ElementType Element;
PriorityQueue Left;
PriorityQueue Right;
int Npl;
};
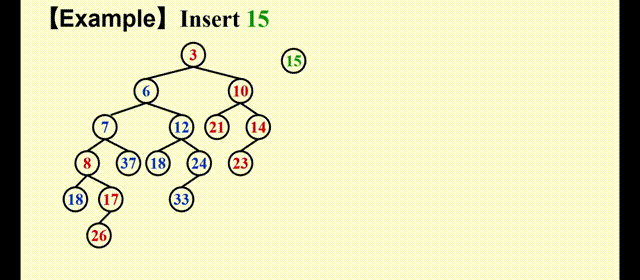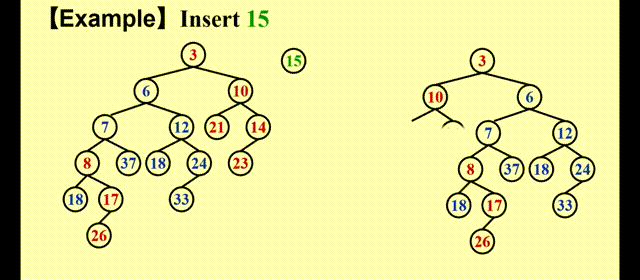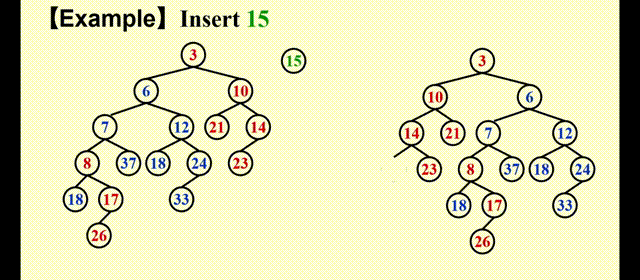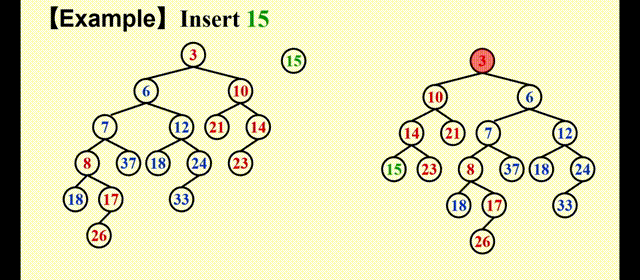
接下来主要介绍左偏堆合并操作的实现。
Merge⚓︎
Recursive Version
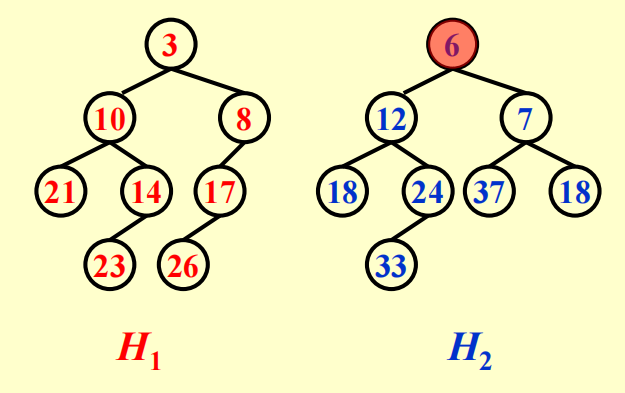
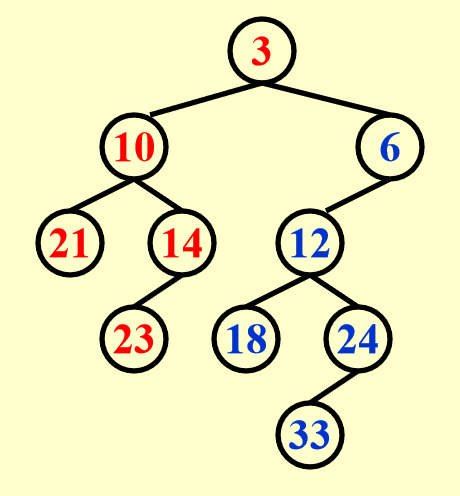
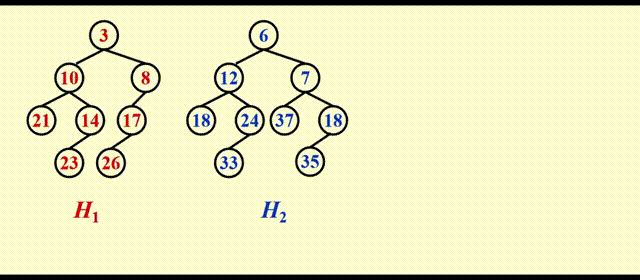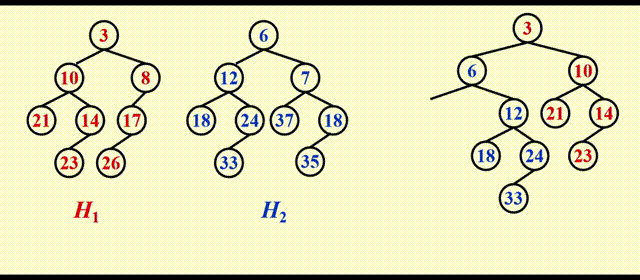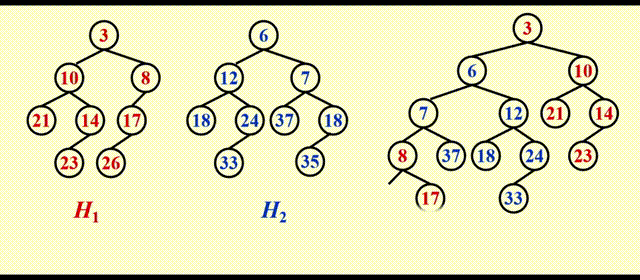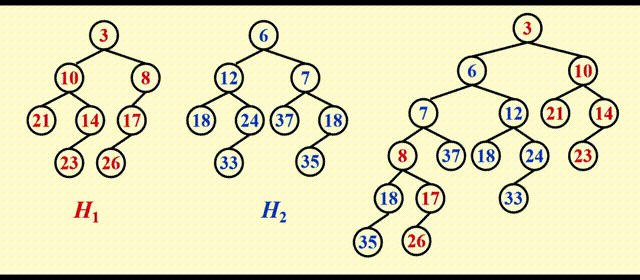
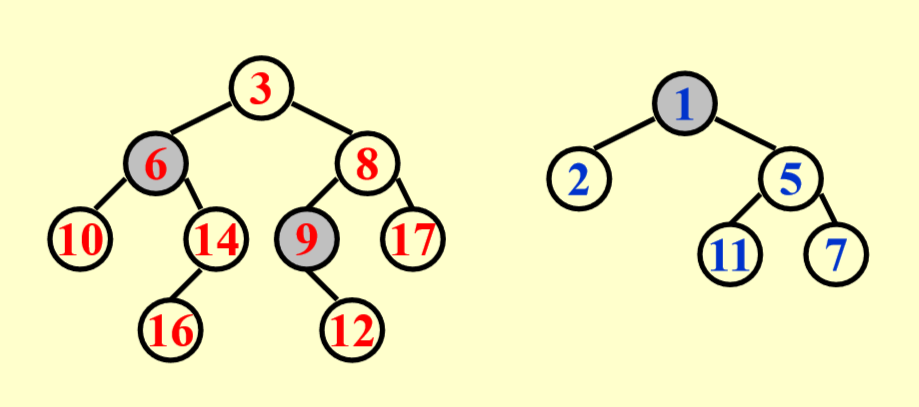
现在我们需要合并这两个左偏堆:
递归版本的合并操作流程如下:
-
合并:
Merge(H1->Right, H2)- 由于 \(H_1\) 的根节点更小,所以我们将 \(H_1\) 的右子树与 \(H_2\) 进行递归地合并
-
附加:
Attach(H2, H1->Right)- 将合并好的堆附加到 \(H_1\) 右子树的位置
-
如有必要,交换左右子树:
Swap(H1->Right, H1->Left)
代码实现
PriorityQueue Merge(PriorityQueue H1, PriorityQueue H2) {
// If one heap is empty, then return another heap
if (H1 == NULL) {
return H2;
}
if (H2 == NULL) {
return H1;
}
// Assure that the left parameter is the heap with smaller root
if (H1->Element < H2->Element) {
return Merge1(H1, H2);
} else {
return Merge1(H2, H1);
}
}
static PriorityQueue Merge1(PriorityQueue H1, PriorityQueue H2) {
if (H1->Left == NULL) { // single node
H1->Left = H2; /* H1->Right is already NULL
and H1->Npl is already 0*/
} else {
H1->Right = Merge(H1->Right, H2); // Step 1 & 2
if (H1->Left->Npl < H1->Right->Npl) {
SwapChildren(H1); // Step 3
}
H1->Npl = H1->Right->Npl + 1; // Important!
}
return H1;
}
问题:要是Merge1()没有更新 \(Npl\) 会出现什么问题?
这样的话,堆上所有节点的 \(Npl\) 字段的值均为初始值 0,那么程序会误以为这个堆始终是一个左偏堆,因而不会有交换两个孩子之类的调整操作,从而得到一个错误的堆。
Iterative Version
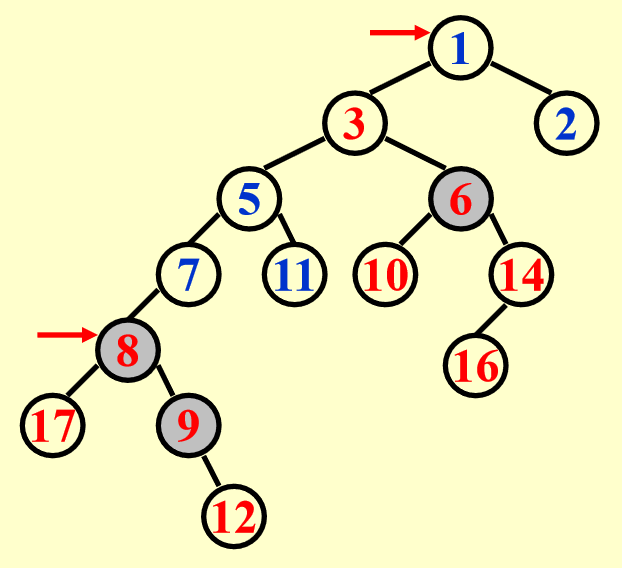
迭代版本的合并操作流程如下(还是以上面那两个堆为例
-
在不改变左孩子的情况下,根据两个堆的右子树进行合并。我的理解是:
- 将根节点较小的堆作为合并的目标堆,然后将目标堆的右子树“拆出来”,作为待比较堆 A,另一个堆作为待比较堆 B
- 比较两个待比较堆,将根节点更小的待比较堆去掉右子树后附加到目标堆的右子树(即最右侧
) ,从而更新目标堆 - 而被抛下的右子树作为新的待比较堆,与另一个待比较堆进入下一轮的 PK。重复进行上述的比较、附加操作,直到只剩下一个目标堆为止
实际上,最开始的目标堆也是一个待比较堆。
动画演示
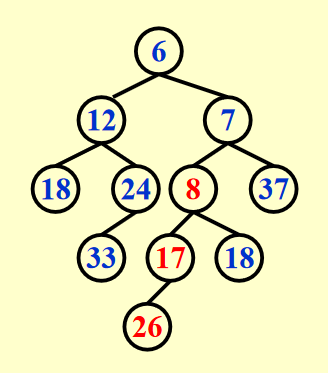
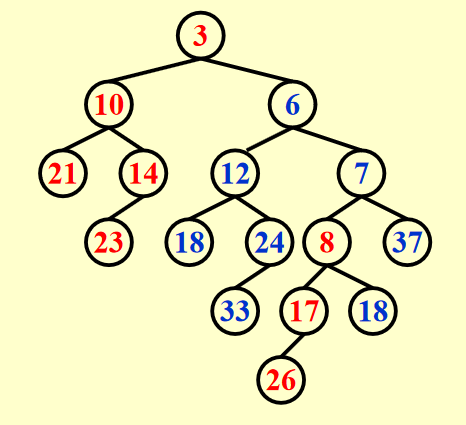
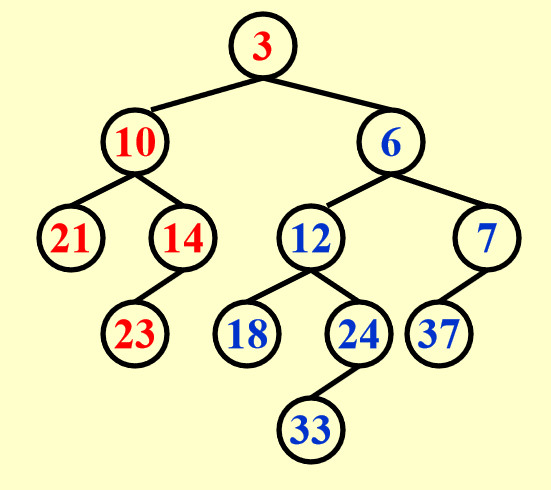
由于 \(H_2\) 的根节点更小,所以将 \(H_2\) 的根节点及其左子树附加在 \(H_1\) 右子树的位置上,这样就形成了新的目标堆。而 \(H_1\) 与 \(H_2\) 原来的右子树则作为新的一组待比较堆。
-
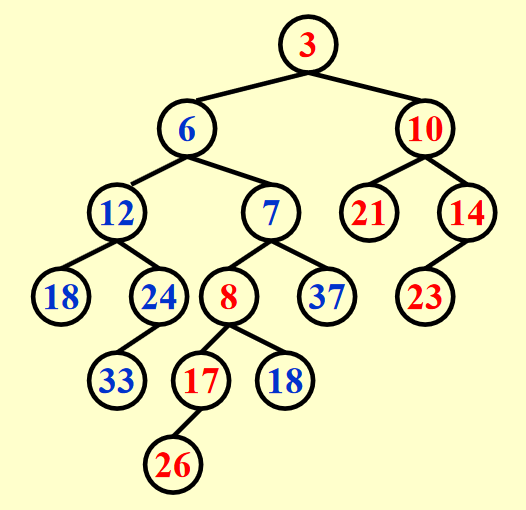
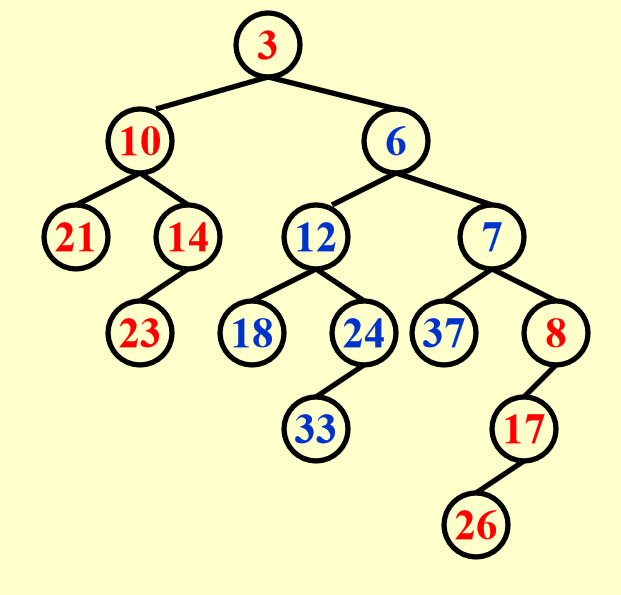
如有必要(左子树空指针路径长度更小时
) ,交换合并后的堆的两个子树
重要提醒
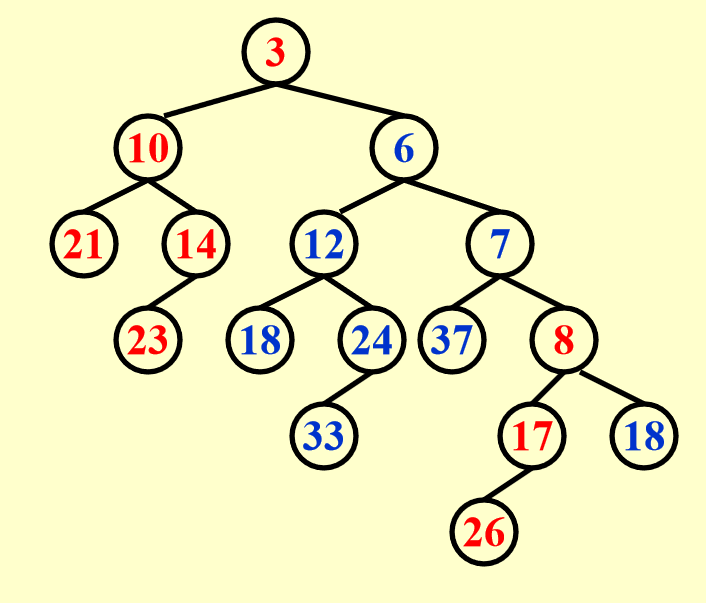
这里可不是说只要交换一次就好了——只要发现堆中存在右子树比左子树规模更大的情况,就应该进行(局部的)调整,因此有可能需要交换多次(上面的例子中就交换了 2 次
代码实现(待补充)
递归实现和迭代实现各有优劣:
- 递归实现的难度较小,代码写起来较为容易,但是不太好让人理解合并的过程
- 迭代实现更为清晰地展现了合并的过程,但是代码编写较为困难
无论是递归实现,还是迭代实现,时间复杂度均为 \(T_P = O(\log N)\)
Insert⚓︎
插入是一种特殊的合并操作,可以理解为只有一个节点的堆与另一个堆进行合并。
代码实现
PriorityQueue Insert1(ElementType X, PriorityQueue H) {
PriorityQueue SingleNode;
SingleNode = (PriorityQueue)malloc(sizeof(struct TreeNode));
if (SingleNode == NULL)
FatalError("Out of Space!!!");
else {
SingleNode->Element = X;
SingleNode->Npl = 0;
SingleNode->Left = SingleNode->Right = NULL;
H = Merge(SingleNode, H);
}
return H;
}
DeleteMin⚓︎
我们可以利用合并操作来删除最小节点:
- 删除根节点,此时会将原来的堆拆作两个子堆
- 合并两个子堆
代码实现
// DleteMin1 returns the new tree;
// To get the minimum, use FindMin
// This is for convenience
PriorityQueue DeleteMin1(PriorityQueue H) {
PriorityQueue LeftHeap, RightHeap;
if (IsEmpty(H)) {
Error("Priority queue is empty");
return H;
}
LeftHeap = H->Left;
RightHeap = H->Right;
free(H);
return Merge(LeftHeap, RightHeap);
}
时间复杂度:\(T_P = O(\log N)\)
DecreaseKey⚓︎
在介绍二叉堆的时候,我们用DecreaseKey()函数使堆中的某个元素移到根节点上,以此提高该元素的优先级。在左偏堆中,这样的操作虽然麻烦一些,但是时间复杂度仍然为 \(O(\log N)\)。
实现步骤:
- 将被操作的节点 \(K\) 及其子树从原来的堆中剔除
- 将刚刚提出来的子树分为 3 部分:节点 \(K\)、左子树和右子树
- 将节点 \(K\) 的值降为整个堆的最小值
- 合并左右子树(\(O(\log N)\)
) ,形成新的子树 \(S\)
- 将 \(S\) 的根节点放回原来堆内节点 \(K\) 的位置,不断调整该子树祖先的 \(Npl\) 值,直到遇到某个不需要改变 \(Npl\) 值的节点为止
- 何时需要调整 \(Npl\) 值
: (待补充)
- 何时需要调整 \(Npl\) 值
- 将节点 \(K\) 插入到这个堆内,它初始的 \(Npl\) 值为 0,通过调整后它会上升至根节点的位置
BuildHeap⚓︎
构建左偏堆的时间复杂度为 \(O(N)\),有以下几种实现方法:
- 递归构建左子树和右子树,然后将根节点“下滤”
- 将每个元素看作单节点的左偏堆,先将它们全部放在一个队列里,然后重复以下操作:让队首的两个堆出队,将它们合并起来后将这个新的堆入队,直到只剩下一个堆为止
另一种构建堆的方法
- 将所有的元素视为只有一个节点的左偏堆,并将这些堆放入一个队列里
- 取出队首的两个堆进行合并操作,然后将合并好的堆放入队列内
- 若队列内还有一个以上的堆,则重复第 2 步,直至队列内仅剩一个堆
结论:
- 在第 \(k\) 个 run 之后(每个元素出队 & 入队 \(k\) 次
) ,形成了 \(\lceil \dfrac{N}{2^k} \rceil\) 个堆,每个堆包含 \(2^k\) 个节点 - 最坏情况:\(N = 2^k\),其中 \(k\) 为整数
- 时间复杂度 \(T(N) = O(\dfrac{N}{2}\log2^0 + \dfrac{N}{2^2}\log2^1 + \dfrac{N}{2^3}\log2^2 + \dots + \dfrac{N}{2^k}\log2^{k-1}) = O(N)\),其中整数 \(k\) 满足 \(N = 2^k\)
Skew Heaps⚓︎
Definition⚓︎
斜堆(skew heaps) 是左偏堆的一种简单形式,它们之间的关系类似 AVL 树和伸展树。斜堆去除了Npl字段,但它像伸展树一样,能够保证在 \(M\) 次连续操作消耗至多 \(O(M \log N)\) 的时间。
斜堆的合并操作的大致思路类似左偏堆,但不同之处在于:由于斜堆不维护Npl字段,因此即将被附加的待比较堆(它的根节点更小,包括最开始的目标堆)在拆开右子树后,需要把待比较堆的左子树换到右子树的位置上,然后再加到目标堆上。也就是说每一次的附加都需要一次交换操作,而不是最后根据Npl的情况来交换。
注意
考虑 Base case:最后仅剩的一个待比较堆,右侧路径上除了最大节点之外都要交换左右子树。
动画演示
这里的动画我就不逐帧分析了,相信大家在学习左偏堆的合并,以及斜堆合并的思路后,应该比较容易看懂这个动画 ~
注
- 斜堆的优势在于:由于不用维护
Npl字段,因此它节省了一定的存储空间,同时也不需要根据Npl判断何时交换堆的两个孩子 - 从 cy 的 PPT 看,递归版和迭代版的演示不能说十分相似,只能说一模一样
- 在最坏情况下,由于右侧路径可以任意长,因此递归实现可能因为栈空间不足而无法实现
- 如何精确决定左偏堆或斜堆的预期右路径长度是一个开放性的问题
- 在最坏情况下,斜堆所有操作(合并、插入、删除最小值等)的时间复杂度均为 \(O(N)\),但摊还复杂度都是 \(O(\log N)\)
Amortized Analysis⚓︎
由于插入和删除本质上还是合并操作,所以这里我们就讨论合并操作的摊还复杂度,结论是:\(T_{\mathrm{amortized}} = O(\log N)\),下面我们就来证明这个复杂度。
证明
摊还分析的三种方法中,势能分析法最为强大,因此我们使用这个方法。势能分析法中最重要的便是确定势能函数:我们令第 \(i\) 次操作后的数据集 \(D_i\) 为目标堆的根节点,势能函数 \(\Phi(D_i)\) 为这个堆上重节点(heavy node) 的个数。
所谓「重节点
为什么势能函数不是右子树的节点个数
我们知道,斜堆会不停地交换左右子树,因而右子树的节点个数有可能会增加,这是不好的情况;但是在好的情况下,右子树的节点个数也不会减少。这导致势能函数只能反映不好情况下堆的变化,而无法体现好的情况,而一个好的势能函数应当同时反映数据结构的好坏,因此简单记录右子树的节点个数不能满足摊还分析的要求。
而重节点个数很好地反映了当前斜堆的情况:情况较差时,重节点个数多;情况较好时,重节点个数少,可用于“抵消”情况较差的情况,因而更适合作为势能函数。
例子
结论:合并后轻重状态发生变化的节点一定位于原来堆上的(最)右侧路径。理由是在斜堆的合并过程中,待比较堆的根节点一定是原来两个堆上(最)右侧路径的节点(理解了斜堆的合并操作后不难想到
因此,我们在势能分析的时候更关注右侧路径上的节点(无论轻重
- 在合并之前,势能函数 \(\Phi_i = h_1 + h_2 + h\),其中 \(h\) 为两个堆内剩余的重节点数
- 在合并之后,势能函数 \(\Phi_{i+1} \le l_1 + l_2 + h\)
- 原因:由上面的结论知,两个堆右侧路径的节点的轻重状态可能会发生改变,最坏的情况是:原来两个堆右侧路径上的节点都是轻节点,合并之后都变成了重节点,所以合并后的堆的重节点个数最多为 \(l_1 + l_2 + h\)
所以,
由于 \(l = O(\log N)\),所以摊还复杂度 \(T_{\mathrm{amortized}} = O(\log N)\)。证毕。
补充:证明 \(l = O(\log N)\)
注:\(l\) 是堆(最)右侧路径的轻节点数
我们可以先证明:对于右侧路径上带有 l 个轻结点的斜堆,至少有 \(2^l - 1\) 个结点。换句话说,如果一个堆有 \(N\) 个节点,那么它右侧路径上的轻节点个数为 \(O(\log N)\),即 \(l = O(\log N)\),所以只要证出前者,后者自然成立。我们采用归纳法证明(证明过程类似左偏堆那个定理的证明
- 当 \(l = 1\) 时,显然成立
- 假设 \(l \le n\) 时,该结论成立
- 那么当 \(l = n + 1\) 时,我们先找到右侧路径的第二个轻节点,根据归纳假设知,以该节点为根节点的子树至少有 \(2^l - 1\) 个节点
- 再找第一个轻节点,由轻节点的定义知,它的左子树节点数一定大于右子树节点数,而上面提到的子树位于它的右子树处,所以以第一个轻节点为根节点的子树至少有 \(2 \times (2^l - 1) + 1 = 2^{l + 1} - 1\) 个节点。那么整个堆的节点个数一定大于 \(2^{l + 1} - 1\),得证
一些小结论
- 向一个空的斜堆依次插入 1~\(2^k - 1\)(\(k > 4\))这几个元素后,得到的堆是一棵满二叉树
自调整(self-adjusting) 的数据结构
自调整数据结构是一类在操作过程中会根据访问或修改的历史信息动态调整自身结构,以提高效率的数据结构。这些数据结构没有固定的形态,能通过自适应性调整,在特定情况下优化常用操作的性能。前面介绍过的伸展树和斜堆均有这种自调整的特性,它们的共同点有:
- 节省空间(因为无需记录额外的平衡信息)
- 访问和更新相关的算法易于理解和实现
- 不考虑因数的情况下,这类算法的效率与对应的平衡版本的数据结构(AVL 树和左偏堆)是相当的
- 局部调整的次数不小于对应的平衡版本的数据结构
评论区