绪论⚓︎
约 1383 个字 预计阅读时间 7 分钟
实验测量与误差分布⚓︎
测量四要素:被测对象、测量程序、测量准确度和计量单位
测量的分类:
- 直接测量
- 间接测量:通过计算实测的量得到欲测的量
- 可靠数字:通过直读获取的准确数字
- 存疑数字:通过估读得到的数字
有效数字:可靠数字 + 1 位存疑数字,其总位数被称为有效位数
误差的表示:
- 绝对误差 = 测量值 - 真值
- 相对误差(百分误差)\(E = \dfrac{|测量值 - 真值|}{真值} \times 100\%\)
- 标准误差(标准差)\(S = \sqrt{\dfrac{1}{n-1}\sum\limits_{i=1}^n|绝对误差|^2}\)
注意
如果真值是不可知的,则无法计算误差。
误差分类:
| 名称 | 主要来源 | 特点 | 处理 | 举例 |
|---|---|---|---|---|
| 系统误差(装置误差) | 装置本身 | 可预知,不可避免 | 见下面 | 见下面 |
| 随机误差(偶然误差) | 环境偶然性 | 无规则涨落,不可避免;存在一定的统计规律 | 可通过多次测量来减小 | 测一本书的厚度 |
| 粗大误差(过失误差) | 粗心大意 | 可避免 | 尽量避免 | 电表没调零就用;读错写错数据 |
| 系统误差 | 定义 | 处理 | 举例 |
|---|---|---|---|
| 已定系统误差 | 在同等条件下,对同一个待测量值进行多次测量,测量值和真值的偏离总是相同的那部分误差分量 | 必须修正 | 电表读数、显微镜的零位误差(仪器本身因素) |
| 未定系统误差 | 已知存在于某个范围,而不知具体数值的系统误差 | 后面会提到 | 仪器的允差(示值误差) |
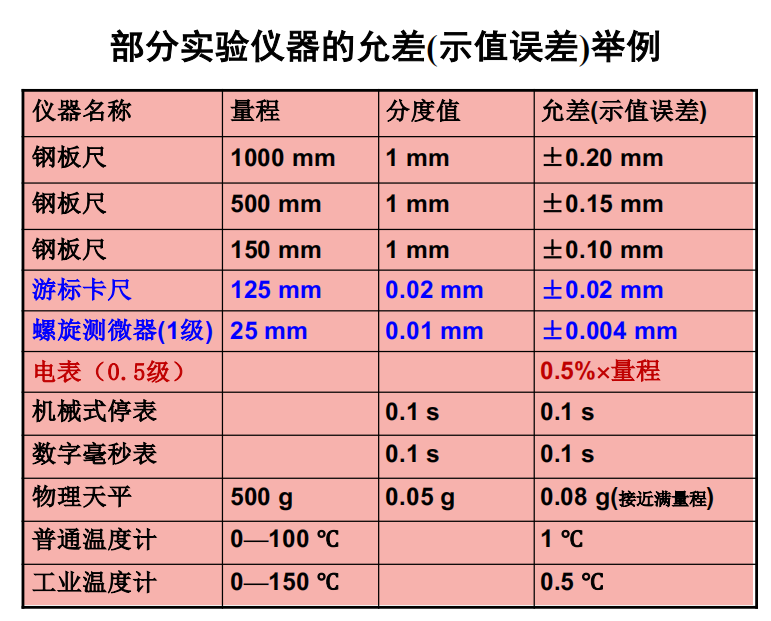
误差的分布:
-
正态分布:测量值的均值 \(\mu\) 看作真值(无穷次测量)
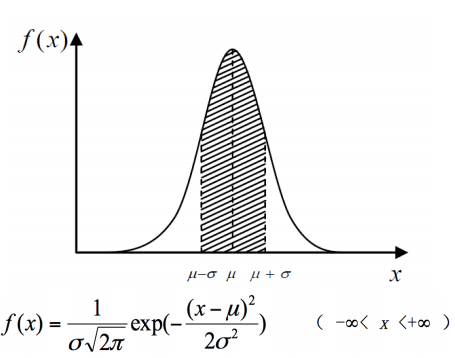
- 特点:单峰性、对称性、有界性、抵偿性
- 消除系统误差后,\(\mu = \lim\limits_{n \rightarrow \infty}\dfrac{1}{n}\sum\limits_{i=1}^nx_i\),被称为数学期望值,表示 \(x\) 出现概率最大的值,作为 \(x\) 的近似真值
- \(\sigma=\lim\limits_{n \rightarrow \infty}\sqrt{\dfrac{1}{n}\sum\limits_{i=1}^n(x_i - \mu)^2}\) 被称为标准差,表现测量值的分散程度:\(\sigma\) 越大,曲线越平坦;\(\sigma\) 越小,曲线越陡峭
- 单次测量值的标准偏差:\(s(x) = \sqrt{\dfrac{1}{n-1}[\sum\limits_{k=1}^n(x_k - \overline{x})^2]}\)
- 平均值的标准偏差:\(s(x) = \sqrt{\dfrac{1}{n(n-1)}[\sum\limits_{k=1}^n(x_k - \overline{x})^2]}\)
-
均匀分布:测量值一定会落在 \((-a, a)\) 区间内
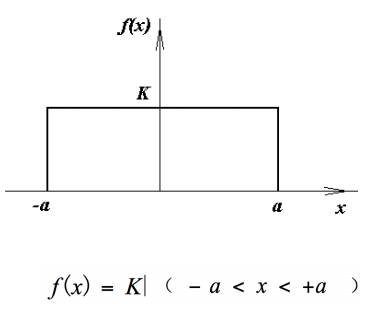
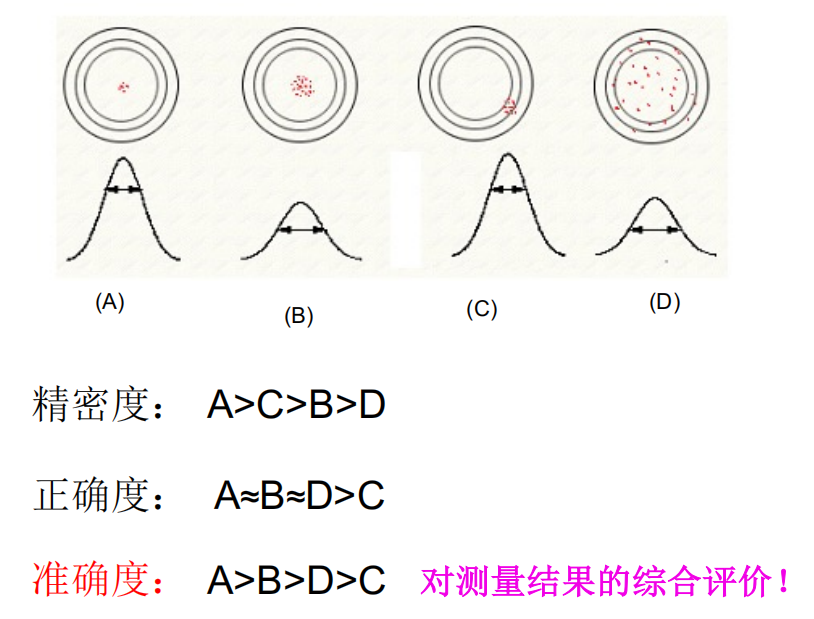
- 精密度:多次重复测量值互相接近的程度
- 正确度:测量平均值接近真值的程度
- 准确度:对上面两个量度的综合评价
误差与不确定度⚓︎
不确定度:由于测量误差存在而对被测量值不能确定的程度,是一定概率下的误差限值。它反映了可能存在的误差分布范围,是一个正值。
不确定度的两个分量:
- A 类分量 \(u_A\):多次重复测量时与随机误差有关的分量
- B 类分量 \(u_B\):与未定系统误差有关的分量。
这两类分量在相同置信概率下用方和根方法合成总不确定度:
\[
u = \sqrt{u_A^2 + u_B^2}
\]
不确定度的类型:
-
直接测量的标准不确定度 \(u\)
- 计算:分为 A 类评定和 B 类评定两部分
- A 类评定:用统计方法评定的不确定度部分
- B 类评定:用其他方法 ......
- 估算过程:
- 测量数据列的平均值:\(\overline{x} = \dfrac{1}{n}\sum\limits_{i=1}^nx_i\)
- 平均值的标准偏差:\(s(\overline{x})=\dfrac{s(x)}{\sqrt{x}}= \sqrt{\dfrac{1}{n(n-1)}[\sum\limits_{k=1}^n(x_k - \overline{x})^2]}\),当 \(6 \le n \le 10\),置信概率为 68.3% 时,可简化认为 \(u_A \approx S(\overline{x})\)
- 根据使用仪器得出 \(u_B\)
- 高斯分布:\(u_B = \dfrac{\delta_仪}{3}\)
- 均匀分布:\(u_B = \dfrac{\delta_仪}{\sqrt{3}}\)
- 总合成不确定度:\(u = \sqrt{u_A^2 + u_B^2}\)
- 最终结果:\(x = \overline{x} + u\)(单位)
- 计算:分为 A 类评定和 B 类评定两部分
-
间接测量的合成标准不确定度 \(u_c\)
- 设 \(y = f(x_1, x_2, \dots, x_i, \dots, x_n)\)
- 不确定度的计算公式
- 公式 1(常用于和差形式的函数
) :\(u_c = \sqrt{\sum\limits_{i=1}^n[\dfrac{\partial f}{\partial x}u(x_i)]^2}\) - 公式 2(常用于积商形式的函数
) :\(\dfrac{u_c}{y} = \sqrt{\sum\limits_{i=1}^n(\dfrac{\partial \ln f}{\partial x})^2[u(x_i)]^2}\)
- 公式 1(常用于和差形式的函数
-
扩展不确定度 \(U\)
有效数字与实验数据处理⚓︎
有效数字的表示法:
- 修约:以修约书代替已知数
- 修约区间:约定的最小变化间距
- 修约规则:“四舍六入五单双”
- 四以下舍掉,六以上进一
- 遇五的话:若前面是奇数就进一,最后一位就变成偶数;若前面是偶数则舍掉
- 有效数值的位数与小数点位置无关,不因使用单位的不同而改变
数值书写的要求:
- 有效数字的位数是由合成不确定度来确定的。测量值的最后一位应与不确定度的最后一位对齐
- 对较大或较小的数值,常采用科学计数法
- 若结果是有间接测量得到的,其有效数字由算出结果的不确定度来确定的。若没有给出各数值的不确定度,由有效数字运算法则确定
数据处理方法:
- 列表法
- 逐差法
- 作图法
- 最小二乘法
评论区
如果大家有什么问题或想法,欢迎在下方留言~