量子测量与量子图灵机⚓︎

约 7775 个字预计阅读时间 39 分钟

量子态演化⚓︎

波函数⚓︎

波函数是量子力学的基本假设，波函数最简单的形式是：$\psi(x) = Ae^{i\left(\frac{p}{\hbar}\right)x}$，它是一种复指数函数，表示了粒子在某位置的概率幅，其绝对值的平方意味着某个时间点自由粒子在某个位置的概率密度
波函数需要满足归一化条件，即对其绝对值的平方进行全空间积分，结果一定是 1

哈密顿量⚓︎

哈密顿量通常表示为 $H$，是一个厄米算符，它对应于系统的能量算符。在量子力学中，系统的状态可以由波函数表示，而哈密顿量作用于波函数上，产生系统的能量和动力学演化。
哈密顿量由两个部分组成：动能项和势能项
- 动能项描述了系统中粒子的运动能量，通常用动量算符和质量来表示
- 势能项则描述了系统中粒子之间的相互作用和受到的外部场的影响，可以是位置算符和外部势场的函数
哈密顿量表达式：

\[ \hat{H} = -\dfrac{h^2}{2m} \nabla^2 + V(\bar{r}) \]
在量子计算中，哈密顿量在描述量子比特的演化和控制中起着关键的作用。通过设计和调整系统的哈密顿量，可以实现量子比特之间的耦合、量子门操作和量子算法的实现。
离散哈密顿量（算符），以量子光学中原子与电磁场相互作用的哈密顿量为例：

\[ \hbar \begin{pmatrix} 0 & \Omega_1 \cos(\omega t + \varphi) \\ \Omega_1 \cos(\omega t + \varphi) & \omega_0 \end{pmatrix} \]
哈密顿量表达式的第一项实则为粒子的动能，第二项是一个空间位置的函数，即势能函数，表示粒子处在不同位置时的势能。

\[ \hat{H} = \hat{T} + \hat{V} = \frac{\mathbf{\hat{p}} \cdot \mathbf{\hat{p}}}{2m} + V(\mathbf{r}, t) = -\frac{\hbar^2}{2m}\nabla^2 + V(\mathbf{r}, t) \]
哈密顿量的本征值是系统能量的可能取值，对应的特征向量是在该能量取值下的状态向量。它们可以用来刻画系统的能级结构、谱线、跃迁概率等性质。

薛定谔方程与量子态演化⚓︎

哈密顿量 $H$ 可以用于表征量子态演化，$H$ 可以和时间有关，也可以独立与时间；若与时间独立（不显含 $t$），则薛定谔方程为：

\[ i\hbar \frac{d|\psi(t)\rangle}{dt} = H |\psi(t)\rangle \]
该方程是一个一阶齐次微分方程，移项后积分，积分的上下限表示波函数从时间 $t_1$ 演化到时间 $t_2$

\[ \begin{aligned} \int_{t_1}^{t_2} \frac{i\hbar}{|\psi(t)\rangle} d|\psi(t)\rangle & = \int_{t_1}^{t_2} H dt \\ i\hbar \left( \ln |\psi(t_2)\rangle - \ln |\psi(t_1)\rangle \right) & = H(t_2 - t_1) \end{aligned} \]

可得：

\[ |\psi(t_2)\rangle = e^{\frac{-iH(t_2-t_1)}{\hbar}} |\psi(t_1)\rangle = e^{\frac{-iH\Delta t}{\hbar}} |\psi(t_1)\rangle \]

设 $t_1 = 0, t_2 = t$，则有：

\[ |\psi(t)\rangle = e^{\frac{-iH\Delta t}{\hbar}} |\psi(0)\rangle = U |\psi(0)\rangle \]

该式表明，量子态从初态到终态的演化可以由一个与 $H$ 有关的算子表示，该算子又被称为时间演化算子 $U$，且 $U$ 一定是幺正的。如果哈密顿量显含时间，则需要更复杂的分析计算，并涉及到时序算子、对易性等原理。

根据量子力学原理，量子态演化过程由两部分组成：

线性演化过程：如果一个物理系统没有被测量，它将按照薛定谔方程以一种确定的、线性的方式演化
非线性的坍缩过程：如果对系统进行一个测量，系统将立即非线性地、随机地从初始的叠加态跃迁到正被测量的可观测量的一个本征态，这时，实验者就会感知到一个确定的观察值，即本征态相应的本征值

与牛顿定律方程描述了低速世界的运动基本规律类似，薛定谔方程也是描述量子系统随时间的演化规律的基本方程。
量子电路中的门，实际上正是通过影响量子系统的“演化”来对量子比特产生逻辑效应。对于量子计算系统，每个量子位都可以处于一种叠加态，这与薛定谔方程中的波函数叠加性质密切相关；薛定谔方程告诉我们粒子可以同时处于多个状态，而量子位也可以处于多个状态的叠加。

总之，薛定谔方程就是量子计算的最底层的理论基础！

量子测量⚓︎

特征值与特征向量⚓︎

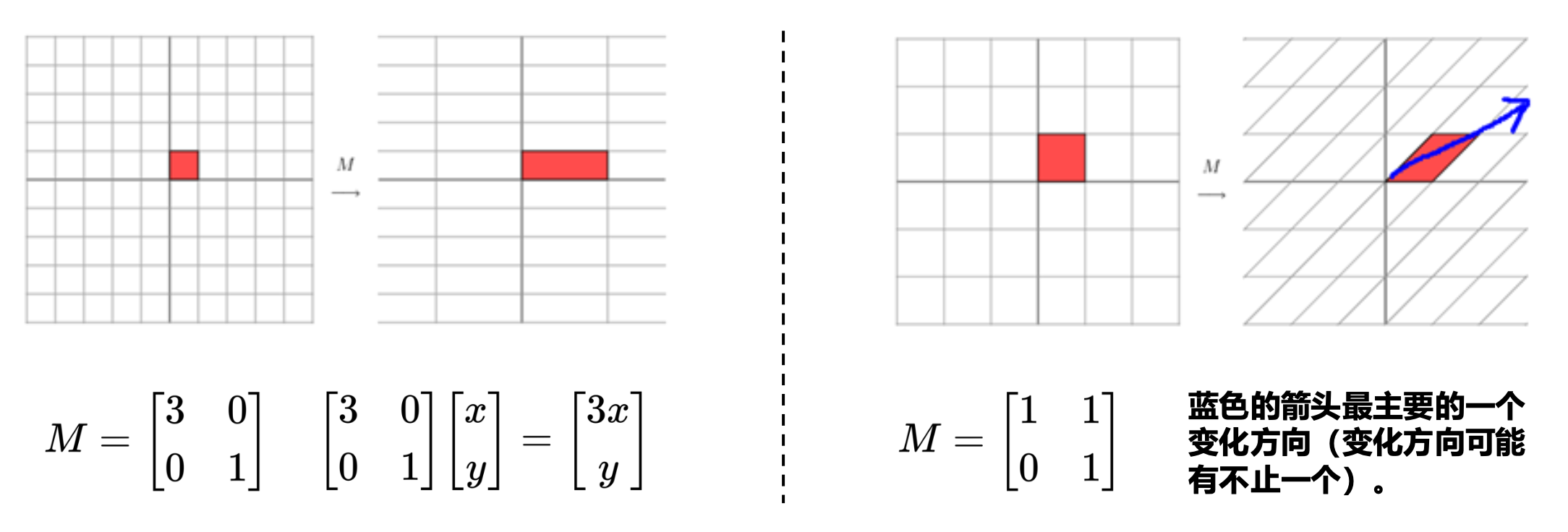
我们知道，矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。

在这个变换的过程中，原向量主要发生旋转、伸缩的变化。
如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。

如果说一个向量 $v$ 是方阵 $A$ 的特征向量，将一定可以表示成下面的形式： $\(Av = \lambda v$\)

这时候，$\lambda$ 就被称为特征向量 $v$ 对应的特征值，特征值分解是将一个矩阵分解成下面的形式： $\(A = Q \Sigma Q^{-1}$\)

其中 $Q$ 是矩阵 $A$ 的特征向量组成的矩阵，$\Sigma$ 是一个对角阵，对角线上的每个元素就是一个特征值。

特征值分解的含义：

分解得到的 $\Sigma$ 矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）
也就是说矩阵 $A$ 的信息可以由其特征值和特征向量表示
对于矩阵为高维的情况下，那么这个矩阵就是高维空间下的一个线性变换。可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前 N 个特征向量，那么就对应了这个矩阵最主要的 N 个变化方向。我们利用这前 N 个变化方向，就可以近似这个矩阵（变换）。

综上，特征值分解可以得到特征值与特征向量，

特征值表示的是这个特征到底有多重要
而特征向量表示这个特征是什么

不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

特征分解⚓︎

特征分解(eigen decomposition)（又称谱分解(spectral decomposition)）是将矩阵分解为由其特征值 $\lambda_i$ 和特征向量 $v_i$ 表示的矩阵 $V = [v_1\ v_2\ \dots\ v_n]$ 之积的方法：

\[ A=V{\begin{bmatrix}\lambda_1&\cdots&0\\\\\vdots&\ddots&\vdots\\0&\cdots&\lambda_n\end{bmatrix}}V^{-1} \]

需要注意只有对可对角化矩阵才可以施以特征分解。特征值的集合 $\{\lambda_i\}$，也称为“谱(spectrum)”。因为厄米矩阵（共轭对称的方阵）属于正规矩阵，根据正规矩阵的性质可知，其可以对角化。

假设 $A$ 是一个复数域正规矩阵，它的特征值为 $\{\lambda_i\}$，标准正交基为 $\{|e_i\rangle\}$ ，那么 $A$ 可以分解为： $$ A=\sum_{i=1}^\mathbf{n}\lambda_i|e_i\rangle\langle e_i| $$

标准正交基和完备性方程⚓︎

标准正交基 $\{|e_i\rangle\}$ 满足如下条件（$i, j$ 相同为 1，不同为 0）：$\langle e_i | e_j \rangle = \delta_{ij}$。

完备性方程： $$ \sum_{\mathrm{i=1}}^\mathrm{n}\lvert e_\mathrm{i}\rangle\langle e_i\rvert=I $$

令 $|x\rangle=\sum_{i=1}^{\mathrm{n}}c_i|e_i\rangle$，由于：

\[ \langle e_j|x\rangle=\sum_{\mathrm{i=1}}^\mathrm{n}c_i\langle e_j||e_\mathrm{i}\rangle=\sum_{\mathrm{i=1}}^\mathrm{n}c_i\delta_{ij}=c_j \]

即：$c_j = \langle e_j | x \rangle$，因此有：

\[ |x\rangle=\sum_{\mathrm{i=1}}^\mathrm{n}c_i|e_\mathrm{i}\rangle=\sum_{\mathrm{i=1}}^\mathrm{n}\langle e_\mathrm{i}|x\rangle|e_\mathrm{i}\rangle=\left(\sum_{\mathrm{i=1}}^\mathrm{n}|e_\mathrm{i}\rangle\langle e_i|\right)|x\rangle \]

由于 $|x\rangle$ 是任意的，因此有 $\sum_{i=1}^n|e_i\rangle\langle e_i|=I$。

例子

问题解答

验证 $|00\rangle=\begin{bmatrix}1\\0\\0\\0\end{bmatrix}|01\rangle=\begin{bmatrix}0\\1\\0\\0\end{bmatrix}|10\rangle=\begin{bmatrix}0\\0\\1\\0\end{bmatrix}|11\rangle=\begin{bmatrix}0\\0\\0\\1\end{bmatrix}$ 是一组标准正交基。

\[ \begin{aligned} & |00\rangle\langle00|+|01\rangle\langle01|+|10\rangle\langle10|+|11\rangle\langle11\\ = & \begin{bmatrix}1\\0\\0\\0\end{bmatrix}[1000]+\begin{bmatrix}0\\1\\0\\0\end{bmatrix}[0100]+\begin{bmatrix}0\\0\\1\\0\end{bmatrix}[0010]+\begin{bmatrix}0\\0\\0\\1\end{bmatrix}[0001]\\ = & \begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}+\begin{bmatrix}0&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}+\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&0\end{bmatrix}+\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}=I \end{aligned} \]

投影算子⚓︎

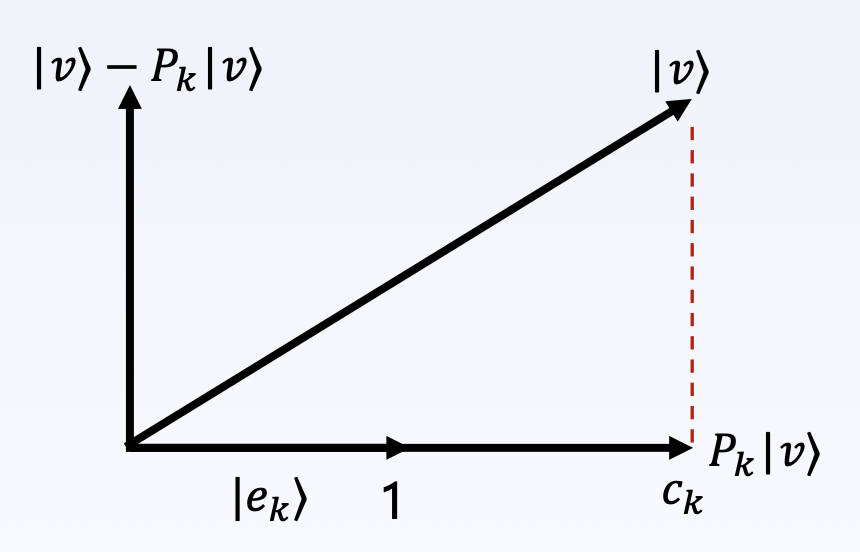
将一个向量 $|v\rangle$ 投影到特定方向，使用单位向量 $|e_k \rangle$ 定义投影算子为：

\[ P_k = | e_k \rangle \langle e_k | \]

这样的投影算子集合 $\{P_k = | e_k \rangle \langle e_k |\}$ 且满足如下性质：

$P_k^2 = P_k$
$P_k P_j = 0 (k \ne j)$
$\sum P_k = I$

综上，$P_k |v \rangle$ 为 $|v\rangle$ 在 $|e_k \rangle$ 上的投影。

例子

若两个基向量为：

\[ \begin{aligned}&|e_1\rangle=H|0\rangle=\frac{1}{\sqrt2}(|0\rangle+|1\rangle)=\frac{1}{\sqrt2}\begin{bmatrix}1\\1\end{bmatrix}\\&|e_2\rangle=H|1\rangle=\frac{1}{\sqrt2}(|0\rangle-|1\rangle)=\frac{1}{\sqrt2}\begin{bmatrix}1\\-1\end{bmatrix}\end{aligned} \]

对应的投影算子为：

\[ \begin{aligned} P_1 & =|e_1\rangle\langle e_1|=\frac{1}{\sqrt{2}}\begin{bmatrix}1\\1\end{bmatrix}\frac{1}{\sqrt{2}}[1\quad1]=\frac{1}{2}\begin{bmatrix}1&1\\1&1\end{bmatrix} \\ P_2 & =|e_2\rangle\langle e_2|=\frac{1}{\sqrt{2}}\begin{bmatrix}1\\-1\end{bmatrix}\frac{1}{\sqrt{2}}[1\quad-1]=\frac{1}{2}\begin{bmatrix}1&-1\\-1&1\end{bmatrix} \end{aligned} \]

由 $P_1, P_2$ 可以验证完备性方程：

\[ \sum_kP_k=\begin{bmatrix}1&0\\0&1\end{bmatrix}=I \]

以及正交条件：

\[ P_1P_2=\begin{bmatrix}0&0\\0&0\end{bmatrix} \]

谱分解的另一种视角⚓︎

回顾前文提到，复数域正规矩阵 $A$ 有谱分解： $$ A=\sum_{i=1}^\mathbf{n}\lambda_i|e_i\rangle\langle e_i| $$

根据投影算子的定义 $P_k = | e_k \rangle \langle e_k |$，因此复数域正规矩阵 $A$ 可以表示为： $$ A = \sum_i \lambda_i P_i $$

因此 $A$ 作用于任何向量，其几何意义如下：相当于该向量，投影到 $A$ 的各特征向量上，然后再以特征值 $\{\lambda\}$ 为系数线性组合起来。

量子测量⚓︎

测量是获取关于量子系统状态的信息的主要方式。测量允许我们从量子系统中获取观测值，以便预测和理解系统的性质，并在量子计算中执行各种程序。

量子测量有很多种方式，如：

一般测量
投影测量 (projective measurements)
POVM 测量 (positive operator-valued measure)

对于选定的观测性质，我们需要执行相应的测量算符。例如，位置测量可以使用位置算符，自旋测量可以使用自旋算符。

每个可能的测量结果都对应一个测量算符的特征值 $\lambda$，由可观测量 $|P|\psi\rangle|^2$ 描述， $P$ 为特征值 $\lambda$ 对应的特征空间上的投影。由于向量做了归一化，测量的状态可以用特征值和特征向量来描述。

投影测量⚓︎

投影测量由一个可观测量(observable) $A$（矩阵）来描述。指标(index) $i$ 表示在实验上可能发生的结果。可观测量 $A$ 是一个待观测系统的状态空间上的厄米算子，它可以写成谱分解的形式： $$ A = \sum_i \lambda_i P_i $$

测量的可能结果与可观测量 $A$ 的特征值 $\lambda_i$ 对应。在对状态 $|\psi\rangle$ 测量之后 , 得到结果 $i$ 概率为： $$ \mathrm{p_{i}=p(\lambda=\lambda_{i})=\langle\psi|P_{i}|\psi\rangle} $$

测量后的态坍缩为：$\dfrac{P_{i}|\psi\rangle}{\sqrt{p_{i}}}$

标准差为：$\Delta(A)=\sqrt{\langle(A-\langle A\rangle)^2\rangle}=\sqrt{\langle A^2\rangle-\langle A\rangle^2}$

量子测量是由投影算子(projection operator) 的集合 $\{P_i\}$ 来描述的。投影算子是一类特殊的厄米算符，它的本征值为 0 或 1，其本征态形成了正交归一的完备基。投影算符具有如下性质： $$ P_m^\dagger P_m=P_m^2=P_m $$

指标 (index) $i$ 表示在实验上可能发生的结果。如果测量前的量子系统处在最新状态 $|\psi\rangle$，那么结果发生的概率为： $$ \mathrm{p}(i)=\langle\psi|P_i^\dagger P_i|\psi\rangle=\langle\psi|P_i|\psi\rangle $$

在投影测量之后，量子态就坍缩到本征态矢 $|\alpha\rangle$ 上。

单比特测量⚓︎

当我们测量单比特量子态 $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ 时，使用的投影算子为：

\[ P_0 = |0\rangle\langle 0| = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, P_1 = |1\rangle\langle 1| = \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} \]

可以证明，这两个算子是自伴的，即： $$ P_0^\dagger = P_0, P_1^\dagger = P_1 $$

而且有： $$ P_0^2 = P_0, P_1^2 = P_1 $$

且满足完备性方程： $$ P_0^\dagger P_0 + P_1^\dagger P_1 = P_0 + P_1 = I $$

当使用 $P_0$ 作用在态矢量上，得到 0 态的概率为：

\[ \mathrm{p}(0) = \langle\psi|P_0^\dagger P_0|\psi\rangle = \langle\psi|P_0|\psi\rangle = \begin{bmatrix} \alpha,\beta \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = |\alpha|^2 \]

测量后的状态为： $$ \frac{P_0 |\psi\rangle}{\sqrt{\mathrm{p}_0}} = \frac{P_0 |\psi\rangle}{\alpha} = \frac{\alpha}{|\alpha|} |0\rangle $$

同理，得到 1 态的概率为：

\[ \mathrm{p}(1) = \langle\psi|P_1^\dagger P_1|\psi\rangle = \langle\psi|P_1|\psi\rangle = \begin{bmatrix} \alpha,\beta \end{bmatrix} \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = |\beta|^2 \]

测量后的状态为：

\[ \frac{P_1 |\psi\rangle}{\sqrt{\mathrm{p}_1}} = \frac{P_1 |\psi\rangle}{\beta} = \frac{\beta}{|\beta|} |1\rangle \]

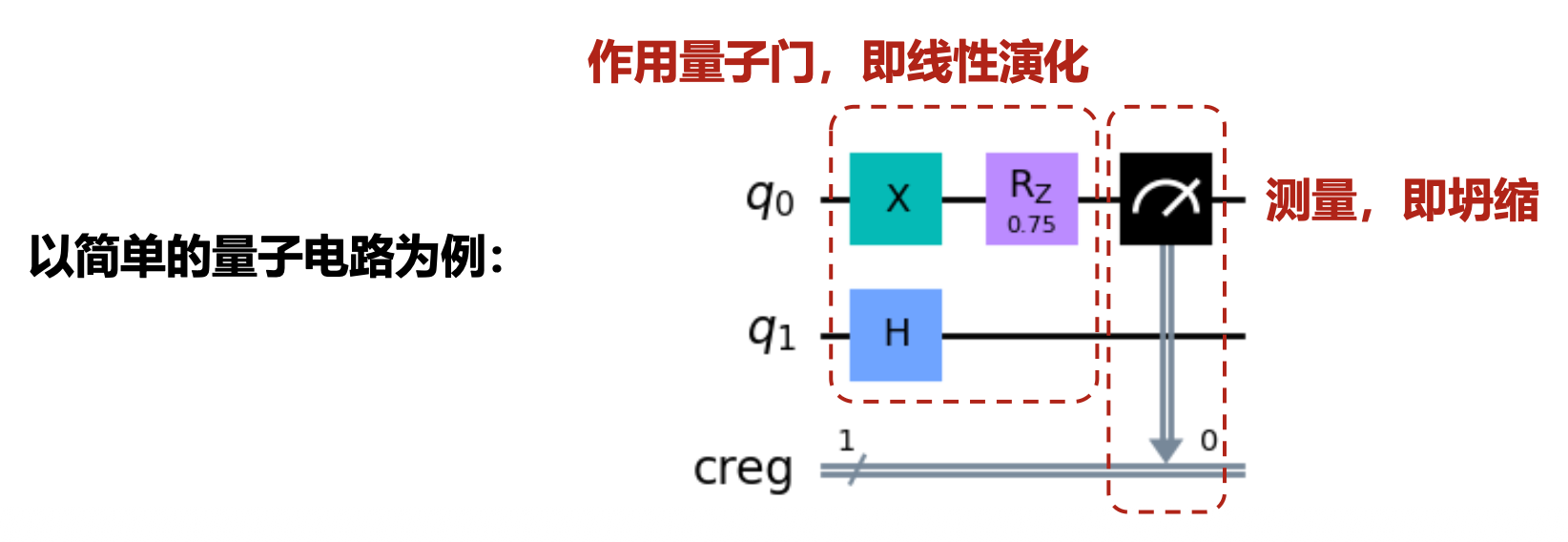
量子线路与测量操作⚓︎

在真实的量子计算机上，最后要对量子系统末态进行测量操作，才能得到末态的信息，因此也把测量操作作为量子线路的一部分，有时也被称为测量门。测量背后的原理就是之前讲到的投影测量。

在量子电路中，用一般使用带仪表符号的门来表示对该量子线路代表的量子比特进行测量操作。
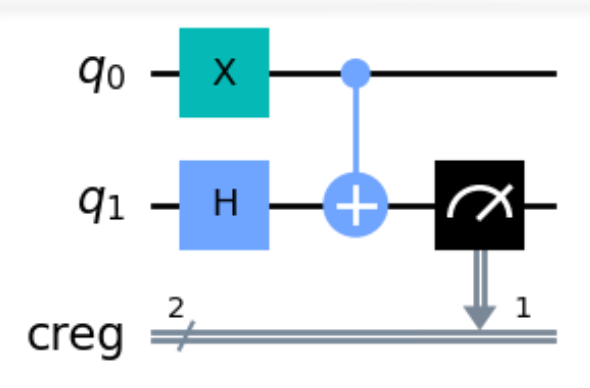
在计算基 $|0\rangle$、$|1\rangle$ 下，测量操作对应的矩阵形式为 :

\[ M_0=|0\rangle\langle0|=\begin{bmatrix}1&0\\0&0\end{bmatrix},M_1=|1\rangle\langle1|=\begin{bmatrix}0&0\\0&1\end{bmatrix} \]

示例

单量子比特线路测量双比特整体测量双比特部分测量

一个简单的单量子比特量子线路如右图所示：

初态为 $|0\rangle$ ，首先经过一个 H 门，演化的到新的态：

\[ |\psi\rangle = H|0\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle) \]

根据单比特测量公式可得：

\[ \begin{aligned} \mathrm{p}(0) & = \langle\psi|P_0^\dagger P_0|\psi\rangle = \langle\psi|P_0|\psi\rangle = \begin{bmatrix} \alpha,\beta \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = |\alpha|^2 \\ \mathrm{p}(1) & = \langle\psi|P_1^\dagger P_1|\psi\rangle = \langle\psi|P_1|\psi\rangle = \begin{bmatrix} \alpha,\beta \end{bmatrix} \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} = |\beta|^2 \end{aligned} \]

因此，测量结果为 0 的概率为 1/2，测量后的状态为 $|0\rangle$；测量结果为 1 的概率为 1/2，测量后的状态为 $|1\rangle$。

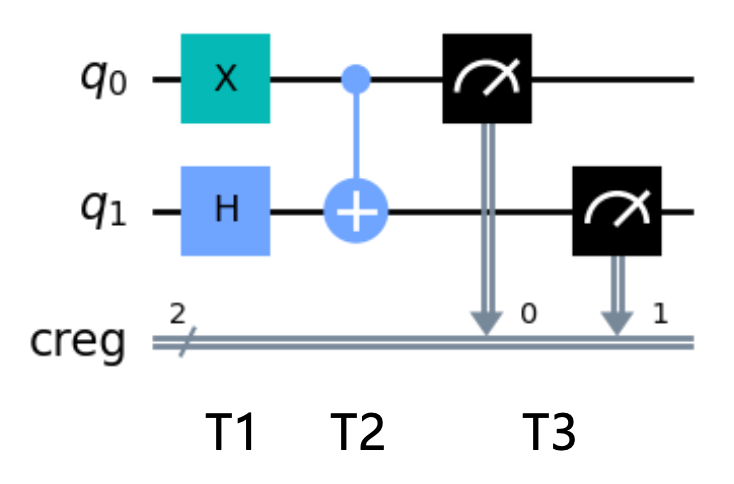
该系统的复合量子态为 $|00\rangle$：

\[ |0\rangle\otimes|0\rangle=|00\rangle=\begin{bmatrix}1\\0\end{bmatrix}\otimes\begin{bmatrix}1\\0\end{bmatrix}=\begin{bmatrix}1\cdot1\\1\cdot0\\0\cdot1\\0\cdot0\end{bmatrix}=\begin{bmatrix}1\\0\\0\\0\end{bmatrix} \]

系统的演化过程：

T1 时刻，分别经过 H 和 X 门，演化为：

\[ \begin{aligned}\left|\psi_{1}\right\rangle&=\left(X\otimes H\right)|00\rangle=\left(\begin{bmatrix}0&1\\1&0\end{bmatrix}\otimes\frac{1}{\sqrt{2}}\begin{bmatrix}1&1\\1&-1\end{bmatrix}\right)|00\rangle\\&=\frac{1}{\sqrt{2}}\begin{bmatrix}0&0&1&1\\0&0&1&-1\\1&1&0&0\\1&-1&0&0\end{bmatrix}\begin{bmatrix}1\\0\\0\\0\end{bmatrix}=\frac{1}{\sqrt{2}}\begin{bmatrix}0\\0\\1\\1\end{bmatrix}=\frac{1}{\sqrt{2}}(|10\rangle+|11\rangle)\end{aligned} \]
T2 时刻，分别经过 CNOT 门，演化为：

\[ |\psi_2\rangle=CNOT|\psi_1\rangle=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}\frac{1}{\sqrt{2}}\begin{bmatrix}0\\0\\1\\1\end{bmatrix}=\frac{1}{\sqrt{2}}(|10\rangle+|11\rangle) \]
T3 时刻，整体测量操作
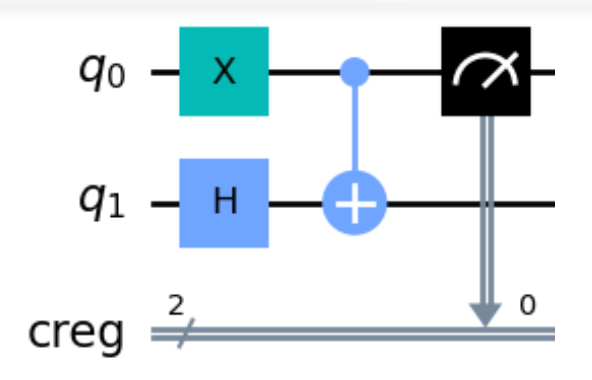
- 使用测量操作 $M_{00} = |00\rangle\langle 00|$，则得到投影到计算基 $|00\rangle$ 下的概率为：
  
  \[ \begin{aligned}P(|00\rangle)&=\langle\psi_2|M_{00}^\dagger M_{00}|\psi_2\rangle=\langle\psi_2|M_{00}|\psi_2\rangle\\&=\frac{1}{\sqrt{2}}\begin{bmatrix}0&0&1&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}\frac{1}{\sqrt{2}}\begin{bmatrix}0\\0\\1\\1\end{bmatrix}\\&=0\end{aligned} \]
  
  根据测量，由于 $P(|00\rangle) = 0$，可知：量子态不可能坍缩在基态 $|00\rangle$ 上面！
- 使用测量操作 $M_{01} = |01\rangle\langle 01|$，则得到投影到计算基 $|01\rangle$ 下的概率为：
  
  \[ P(|01\rangle)=\langle\psi_2|M_{01}^\dagger M_{01}|\psi_2\rangle=\langle\psi_2|M_{01}|\psi_2\rangle=0 \]
  
  根据测量，由于 $P(|01\rangle) = 0$，可知：量子态不可能坍缩在基态 $|01\rangle$ 上面！
- 使用测量操作 $M_{10} = |10\rangle\langle 10|$，则得到投影到计算基 $|10\rangle$ 下的概率为：
  
  \[ P(|10\rangle)=\langle\psi_2|M_{10}^\dagger M_{10}|\psi_2\rangle=\langle\psi_2|M_{10}|\psi_2\rangle=\frac{1}{2} \]
  
  测量之后，量子态坍缩在新态 $|10\rangle$ 上，即 $$ |\psi_3\rangle=\frac{M_{10}|\psi_2\rangle}{\sqrt{P(|10\rangle)}}=|10\rangle $$
- 使用测量操作 $M_{11} = |11\rangle\langle 11|$，则得到投影到计算基 $|11\rangle$ 下的概率为：
  
  \[ P(|11\rangle)=\langle\psi_2|M_{11}^\dagger M_{11}|\psi_2\rangle=\langle\psi_2|M_{11}|\psi_2\rangle=\frac{1}{2} \]
  
  测量之后，量子态坍缩在新态 $|11\rangle$ 上，即 $$ |\psi_3\rangle=\frac{M_{11}|\psi_2\rangle}{\sqrt{P(|11\rangle)}}=|11\rangle $$

如果只对低地址量子比特进行测量，则此时测量对应的测量操作矩阵为：

\[ \begin{aligned}M_0^{q_0}=\sum_{i\in\{0,1\}}M_{0i}=\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}+\begin{bmatrix}0&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}\\M_1^{q_0}=\sum_{i\in\{0,1\}}M_{1i}=\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&0\end{bmatrix}+\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}=\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}\end{aligned} \]
- 因此通过测量，得到测量结果 0 和 1 概率为：
  
  \[ \begin{aligned} P_{q0}(|0\rangle) & = \langle\psi_2| M_0^{q0} |\psi_2\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} = 0 \\ P_{q0}(|1\rangle) & = \langle\psi_2| M_1^{q0} |\psi_2\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} = 1 \end{aligned} \]
- 测量后，量子系统的状态分别变为：
  
  \[ |\psi_3\rangle = \frac{M_1^{q0} |\psi_2\rangle}{\sqrt{P_{q0}(|1\rangle)}} = \frac{1}{\sqrt{2}}(|10\rangle + |11\rangle), c_0 = 1 \]

如果只对高地址量子比特进行测量，则此时测量对应的测量操作矩阵为：

\[ M_{0}^{q_{1}}=\sum_{i\in\{0,1\}}M_{i0}=\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}+\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&0\end{bmatrix}=\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&0\end{bmatrix}\\M_{1}^{q_{1}}=\sum_{i\in\{0,1\}}M_{i1}=\begin{bmatrix}0&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}+\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}=\begin{bmatrix}0&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix} \]
- 因此通过测量，得到测量结果 0 和 1 概率为：
  
  \[ \begin{aligned}P_{q_1}(|0\rangle)=\langle\psi_2|M_0^{q_1}|\psi_2\rangle=\frac{1}{\sqrt{2}}\begin{bmatrix}0&0&1&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&0\end{bmatrix}\frac{1}{\sqrt{2}}\begin{bmatrix}0\\0\\1\\1\end{bmatrix}=\frac{1}{2}\\P_{q_1}(|1\rangle)=\langle\psi_2|M_1^{q_1}|\psi_2\rangle=\frac{1}{\sqrt{2}}\begin{bmatrix}0&0&1&1\end{bmatrix}\begin{bmatrix}0&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}\frac{1}{\sqrt{2}}\begin{bmatrix}0\\0\\1\\1\end{bmatrix}=\frac{1}{2}\end{aligned} \]
- 测量后，量子系统的状态分别变为：
  
  \[ |\psi_3\rangle=\frac{M_0^{q_1}|\psi_2\rangle}{\sqrt{P_{q_1}(|0\rangle)}}=|10\rangle,c_1=0 \\ |\psi_3\rangle=\frac{M_1^{q_1}|\psi_2\rangle}{\sqrt{P_{q_1}(|1\rangle)}}=|11\rangle,c_1=1 \]

量子态区分公设⚓︎

量子测量的原理的一大应用是区分量子系统中不同的量子态。

如果一组态向量是正交的，可以通过为每个态向量分别定义测量算子 $M_i=|\psi_i\rangle\langle\psi_i|$ 对其进行确定性的区分：

\[ p(i)=\langle\psi_i|M_i|\psi_i\rangle=1 \]
如果量子态之间不正交，则可以证明没有量子测量可以精确区分这些状态。

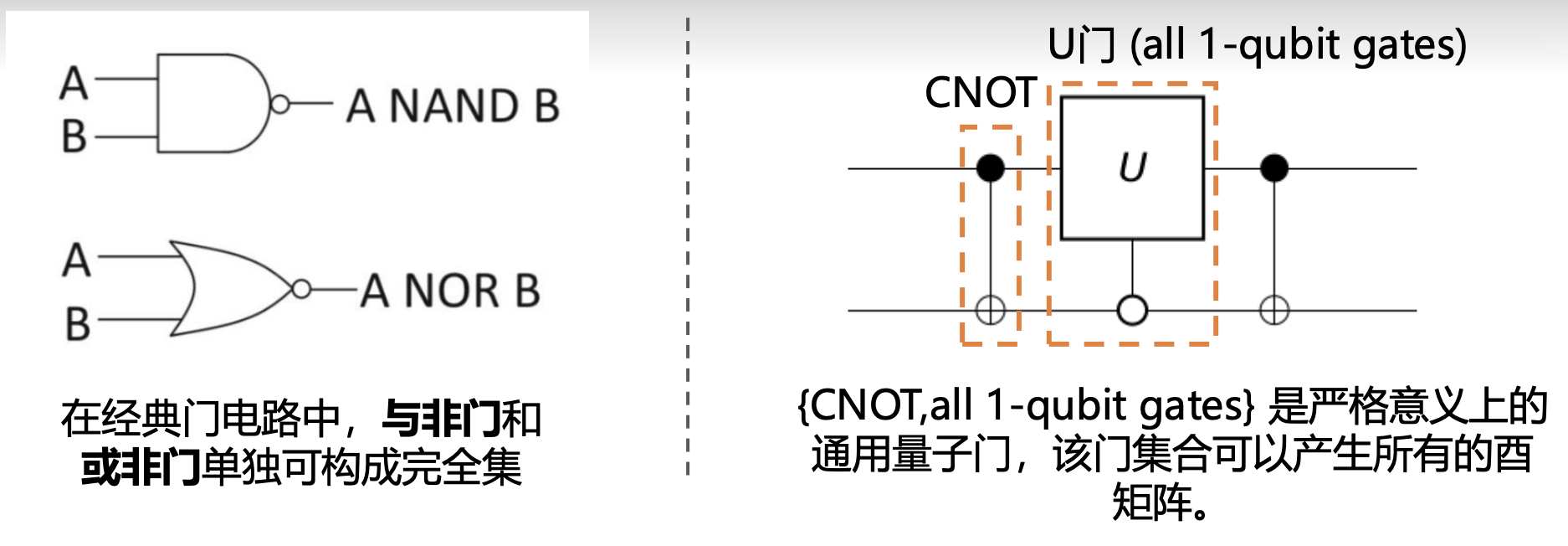
通用量子门⚓︎

通用量子门(universal quantum gate) 是一种能够在量子计算中实现任意量子操作的门。它是量子计算中的基本构建块，类似于经典计算中的逻辑门（如与门、或门、非门等）。

通用量子门可以用来进行任意的量子计算和量子算法。通过将一系列的通用量子门按照特定顺序和参数应用于量子比特上，我们可以进行各种复杂的量子计算操作，包括量子纠缠、量子态制备、量子搜索、量子因子分解等。

以下的门集合是通用的：

单量子比特门和 CNOT 门
通用门的标准集合，由 H 门、相位门、CNOT 门和 $\pi$/8 门构成
H 门、相位门、CNOT 门和 Toffoli 门

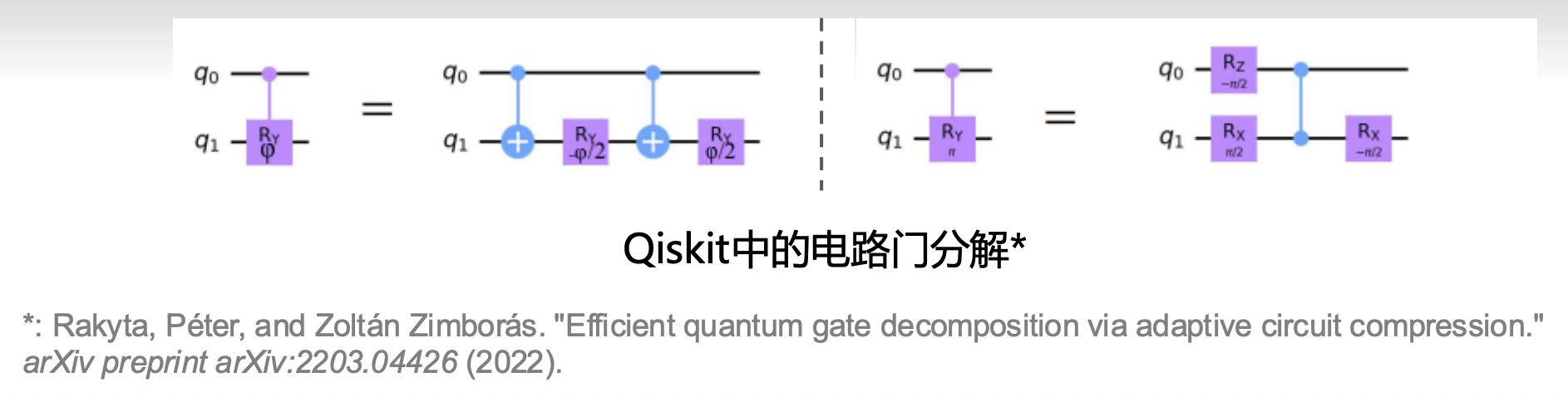
量子门分解⚓︎

通用量子门可以用来对任意的酉操作进行近似，这种近似的方法被称为量子门分解(quantum gate decomposition) 或量子门逼近(quantum gate approximation)
基本思想：将目标酉操作分解为一系列更简单的量子门的乘积，通过合理选择和组合这些基本量子门，并对它们的参数进行调整，我们可以逐步逼近目标酉操作
分解的精度取决于所使用的门集合和逼近方法的复杂程度；通常情况下，使用更多的门和更复杂的门序列可以提供更精确的逼近结果

常见的量子门分解方法包括：

应用基于泰勒级数展开的逼近方法，将目标酉操作近似为一系列基本门的乘积
利用通用量子门集合（如 Hadamard-$\pi$/8-CNOT）中的门进行分解
使用优化算法，例如基于梯度下降的方法，找到适合的门序列和参数来逼近目标酉操作

下面进行证明 Hadamard 门和 $\pi$/8 门可以对任意的单比特酉操作以任意精度近似：

证明

考虑 $T$ 门和 $THT$ 门，其中 $T$ 的作用是在布洛赫球上进行绕 $z$ 轴转 $\pi$/4 角度的操作，而 $THT$ 是绕 $x$ 轴转 $\pi$/4 的角度，将这两个操作组合起来，有： $$ R_z(\pi/4)R_x(\pi/4)=e^{{-i\frac{\pi}{8}Z}e} $$}{8}X}=\cos^2\frac{\pi}{8}I-i[\cos\frac{\pi}{8}(X+Z)+\sin\frac{\pi}{8}Y]\sin\frac{\pi}{8

可以看出这是一个在布洛赫球面上绕轴 $\hat{n}=(\cos\frac{\pi}{8},\sin\frac{\pi}{8},\cos\frac{\pi}{8})$ 旋转 $\theta$ 的操作，其中 $\cos\frac{\theta}{2}=\cos^2\frac{\pi}{8}$。重复进行 $R_{\hat{n}}(\theta)$ 操作可以以任意精度近似任意的 $R_{\hat{n}}(\alpha)$。

量子门分解的代价：

需要注意的是，量子门分解是一种近似方法，因此逼近结果可能不是完美的。分解的精度取决于所选择的门集合、逼近方法以及目标酉操作本身的复杂程度。
对于量子门分解的代价，Solovay-Kitaev 定理阐述了，对任意的单量子比特门，如果要求精度为 $\varepsilon$ 的话，需要 $O(\log^c(1/\varepsilon))$ 多的门。所以对有 $m$ 个门的量子线路以 $\varepsilon$ 为精度的近似需要的通用门的数量级在 $O(m\log^c(m/c))$ 左右。

量子图灵机⚓︎

经典图灵机⚓︎

历史

1936 年，图灵在他的硕士论文《论可计算数及其在判定性问题上的应用》中提出了图灵机模型
1949 年，冯诺伊曼基于此模型造出了世界上第一台通用电子计算机，而后计算机行业开始迅速发展

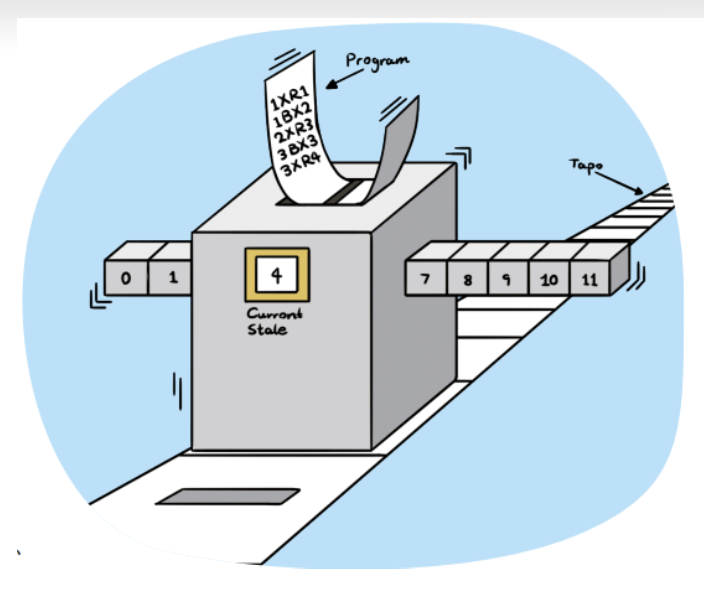
图灵机由以下几个要素组成：

无限长的纸带(tape)：纸带被划分为一个个离散的单元格，每个单元格上可以写入符号
读写头(head)：读写头可以在纸带上水平移动，并读取或写入单元格上的符号
状态集合(states)：图灵机具有一组离散的内部状态，可以根据当前状态和读写头的位置和读取的符号来进行转换
转移函数(transition function)：转移函数定义了在给定状态和读写头读取的符号下，图灵机应该如何改变其状态、移动读写头以及在纸带上写入符号
停机状态(halting state)：图灵机的一种特殊状态，当图灵机进入停机状态时，计算过程终止

量子图灵机⚓︎

历史

在 1980 年和 1982 年，物理学家 Paul Benioff 首次描述了图灵机的量子力学模型
随后量子计算的奠基科学家 Deutsch 在 1985 年撰写的一篇文章进一步发展了量子图灵机的概念，提出量子门可以以类似于传统数字计算二进制逻辑门的方式运行
Deutsch 在 1989 年又提出了更底层的量子电路模型
1993 年，姚期智又证明了每一个量子图灵机都可以用量子电路模拟出来
本世纪以来，量子图灵机逐渐过时，大家提到量子计算时基本默认是量子电路模型，并基于此提出了多种复杂度理论

与经典图灵机基本上类似，区别在于将纸带上的字符与寄存的状态均改为了叠加态的量子比特。量子图灵机的概念模型存在以下问题：

难以保证每一步操作的幺正性
停机问题：量子图灵机一直处于叠加态，不知道什么时候结束
量子图灵机模型只是告诉我们了量子计算机的下限（至少和经典计算机一样快），却并没有真正告诉我们它真正能有多快

直到量子图灵机过时前，人们都一直在讨论这些问题，并未完全解决。

量子电路模型⚓︎

量子电路模型由姚期智在 1993 年提出，是一种基于量子比特和量子门操作的计算框架，用于描述量子计算的过程和算法。

姚期智的量子电路模型基于以下几个关键概念：

量子比特：姚期智的模型使用量子比特 (quantum Bit)，通常简称为 qubit，作为信息的基本单元。与经典比特只能表示 0 或 1 不同，量子比特可以处于 0 和 1 的叠加态，具有更丰富的信息表示能力。
量子门操作：量子门操作是在量子比特上进行的变换操作，类似于经典计算中的逻辑门。姚期智的模型使用一组基本的量子门操作，如 H 门、相位门、CNOT 门等，来对量子比特进行操作和变换。
量子电路：姚期智的模型使用量子电路来表示量子计算过程。量子电路由一系列量子门操作按照特定的顺序组成，类似于经典电路中的逻辑门组合。量子电路描述了量子比特之间的相互作用和信息流动，以及计算过程中的量子门操作序列。
量子测量：量子电路模型允许对量子比特进行测量，以获取计算结果。量子测量将量子比特的状态投影到经典态上，从而获得一个经典的比特值。

在量子电路模型中，每个量子比特可以用一个线路表示，每个量子逻辑门可以用一个符号表示，每个电路可以用一个矩阵表示，它可以清楚地展示量子计算的并行性、可逆性和干涉性，也可以方便地分析量子算法的复杂度和正确性。

量子图灵机和量子电路模型的区别在于：

量子图灵机采用迭代的方式进行计算，通过读写头的移动和纸带上的符号变化来实现状态转换和计算过程；而量子电路模型采用顺序执行的方式进行计算，量子门操作按照特定的顺序应用于量子比特上，因此量子电路模型更加注重描述量子比特之间的相互作用和变换；
量子图灵机是一种通用、底层的计算模型，它提供了一种理论基础和抽象框架，用于研究量子计算的性质和能力；而量子电路模型更加直观和可视化，它提供了一种以量子门操作为基础的计算框架，更加方便和实用。

评论区

如果大家有什么问题或想法，欢迎在下方留言~