量子算法⚓︎
约 5745 个字 8 行代码 预计阅读时间 29 分钟
量子傅里叶变换⚓︎
傅里叶变换⚓︎
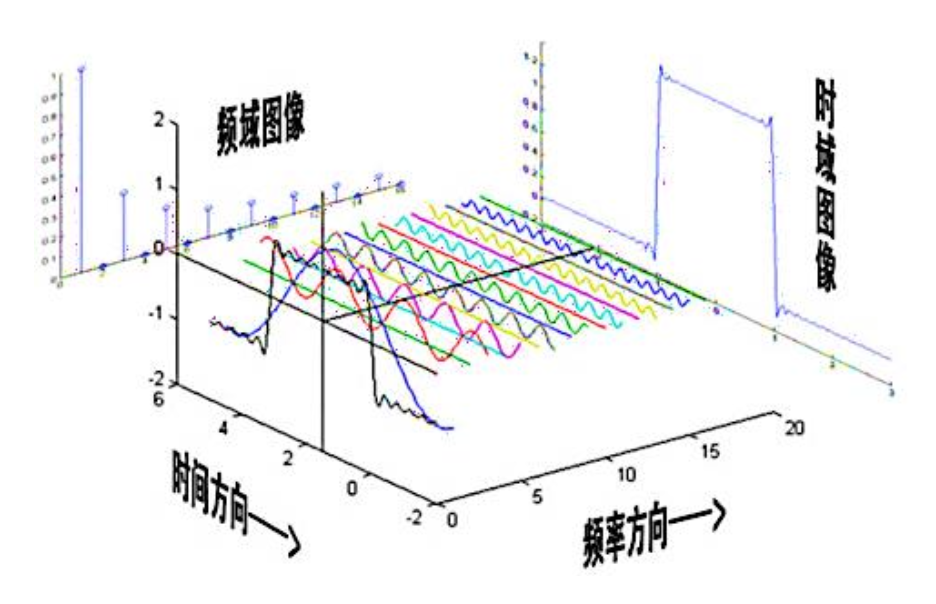
- 通过不同的角度可以发现事物不同的特征,信号也是这样
-
傅里叶变换就是为信号在时域表示和频域表示之间的转换提供了一个桥梁
- 当我们使用傅里叶变换来分析一个音频信号时,我们可以将其看作是时域中的波形
- 经过傅里叶变换后,我们可以将这个信号转换为频域中的频率分量
- 每个峰表示了输入信号中的一个频率分量,其高度表示了该频率在原始信号中的强度
-
傅里叶变换使得人们能从能量的角度看待信号,同时大大简化了信号处理中所需要的计算量
- 傅里叶变换在现代社会中得到了广泛应用,例如手机中的通信模块无时无刻不在进行傅里叶变换
广泛的应用场景:
- 分解信号频率成分,优化信号传输质量
- 声音特效处理与分析,变换声音特征等
- 处理地震信号,了解地质结构
但实际上,傅里叶变换早在 18 世纪就由让 · 巴普蒂斯 · 约瑟夫 · 傅里叶(Baron Jean Baptiste Joseph Fourier)提出,但其真正得到快速发展和广泛使用却已是在 19 世纪 60 年代 FFT(Fast Fourier Transform,快速傅里叶变换)算法发明后,期间间隔了近两百年。
离散傅里叶变换⚓︎
离散傅里叶变换(DFT)是用于将离散信号从时域转换到频域的一种数学工具。它将一系列等间隔采样的信号表示为不同频率成分的组合,用以分析信号的频率特性。DFT 是傅里叶变换在离散情况下的对应形式,特别适用于处理数字信号和有限长度的数据序列。
-
离散傅里叶变换
\[ \{x_j\} \xrightarrow{\text{DFT}} \{y_k\} \\ y_k = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} x_j e^{\frac{2\pi i}{N} \cdot j k} \] -
逆离散傅里叶变换
\[ \{y_k\} \xrightarrow{\text{IDFT}} \{x_j\} \\ x_j = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} y_k e^{-\frac{2\pi i}{N} \cdot j k} \]
量子傅里叶变换⚓︎
量子傅里叶变换(QFT)的作用是将量子态从计算基 \(\{|j\rangle\}\) 映射至频域基 ۧ\(\{|k\rangle\}\) ,其中振幅序列 \(\{x_j\}\) 由 DFT 变换为 \(\{y_k\}\)。 $$ \sum_{k=0}^{N-1} y_k |k\rangle \xleftarrow{\text{QFT}} \sum_{j=0}^{N-1} x_j |j\rangle $$
QFT 作为量子算符即定义为: $$ \text{QFT}|j\rangle = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} \cdot j k} |k\rangle $$
QFT 不仅是 DFT 的量子计算实现,同样是众多量子算法(QPE、Shor)的子模块。
张量积形式⚓︎
为分析基于量子比特的 QFT 算法电路实现,规定以下记法:
- 基态 \(|j\rangle\) 表示为 \(|j_1j_2\cdots j_n\rangle\),即 \(j = 2^{n-1}j_1 + 2^{n-2}j_2 + \cdots + 2^0j_n\)
- 用 \(0.j_1j_2\cdots j_n\) 表示小数 \(2^{-1}j_1 + 2^{-2}j_2 + \cdots + 2^{-n}j_n\)
若使用 \(n\) 个量子比特执行量子傅里叶变换,则共有 \(2^n\) 个基态,\(N = 2^n\)。 $$ \text{QFT}|j\rangle = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} \cdot j k} |k\rangle $$
上述 QFT 算符可写作如下的张量积形式: $$ \text{QFT}|j_1j_2\cdots j_n\rangle = \frac{1}{\sqrt{2^n}} \left( |0\rangle + e^{2\pi i \cdot 0.j_n}|1\rangle \right) \left( |0\rangle + e^{2\pi i \cdot 0.j_{n-1}j_n}|1\rangle \right) \cdots \left( |0\rangle + e^{2\pi i \cdot 0.j_1j_2\cdots j_n}|1\rangle \right) $$
张量积形式有助于构建 \(\text{QFT}\) 的量子电路并证明其酉性。
下面证明 QFT 张量积形式的正确性:
证明
-
将频域基同样展开为二进制表示
\[ \begin{aligned} \text{QFT}|j\rangle & = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} \cdot j k} |k\rangle \\ & = \frac{1}{\sqrt{2^n}} \sum_{k_1=0}^{1} \cdots \sum_{k_n=0}^{1} e^{\frac{2\pi i}{2^n} \cdot j \sum_{l=1}^n k_l 2^{n-l}} |k_1 \cdots k_n\rangle \\ & = \frac{1}{\sqrt{2^n}} \sum_{k_1=0}^{1} \cdots \sum_{k_n=0}^{1} e^{2\pi i j \sum_{l=1}^n k_l 2^{-l}} |k_1 \cdots k_n\rangle \end{aligned} \] -
\(e\) 的指数中的求和拆解至张量积中
\[ \begin{aligned} \text{QFT}|j\rangle & = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} \cdot j k} |k\rangle \\ & = \frac{1}{\sqrt{2^n}} \sum_{k_1=0}^{1} \cdots \sum_{k_n=0}^{1} e^{2\pi i j \sum_{l=1}^n k_l 2^{-l}} |k_1 \cdots k_n\rangle \\ & = \frac{1}{\sqrt{2^n}} \sum_{k_1=0}^{1} \cdots \sum_{k_n=0}^{1} \bigotimes_{l=1}^n e^{2\pi i j k_l 2^{-l}} |k_l\rangle \end{aligned} \] -
交换求和与张量积的运算顺序
\[ \begin{aligned} \text{QFT}|j\rangle & = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} \cdot j k} |k\rangle \\ & = \frac{1}{\sqrt{2^n}} \sum_{k_1=0}^{1} \cdots \sum_{k_n=0}^{1} \bigotimes_{l=1}^n e^{2\pi i j k_l 2^{-l}} |k_l\rangle \\ & = \frac{1}{\sqrt{2^n}} \bigotimes_{l=1}^n \sum_{k_l=0}^{1} e^{2\pi i j k_l 2^{-l}} |k_l\rangle \end{aligned} \] -
展开 \(k_l\) 求和
\[ \begin{aligned} \text{QFT}|j\rangle & = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} \cdot j k} |k\rangle \\ & = \frac{1}{\sqrt{2^n}} \bigotimes_{l=1}^n \sum_{k_l=0}^{1} e^{2\pi i j k_l 2^{-l}} |k_l\rangle \\ & = \frac{1}{\sqrt{2^n}} \bigotimes_{l=1}^n \left( |0\rangle + e^{2\pi i j 2^{-l}} |1\rangle \right) \end{aligned} \] -
根据 \(e^{2 \pi i} = 1\),可将 \(j2^{-l}\) 的整数部分略去
\[ \begin{aligned} \text{QFT}|j\rangle & = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} \cdot j k} |k\rangle \\ & = \frac{1}{\sqrt{2^n}} \bigotimes_{l=1}^n \left( |0\rangle + e^{2\pi i j 2^{-l}} |1\rangle \right) \\ & = \frac{1}{\sqrt{2^n}} \left( |0\rangle + e^{2\pi i 0.j_n} |1\rangle \right) \left( |0\rangle + e^{2\pi i 0.j_{n-1}j_n} |1\rangle \right) \cdots \left( |0\rangle + e^{2\pi i 0.j_1j_2\cdots j_n} |1\rangle \right) \end{aligned} \]
示例
考虑单比特系统下的 QFT 算符
对于计算基 \(|0\rangle, |1\rangle\) 有:
由矩阵形式可知,单比特的 QFT 算符和 H 门等价
考虑对单比特态 \(|\psi\rangle=\alpha|0\rangle+\beta|1\rangle\) 执行 QFT 过程:
其中 \(x_0 = \alpha, x_1 = \beta\),于是有:
同样可知,单比特的 QFT 算符和 H 门等价: $$ \mathrm{QFT}_1|\psi\rangle=\frac{1}{\sqrt{2}}\left(\alpha+\beta\right)|0\rangle+\frac{1}{\sqrt{2}}\left(\alpha-\beta\right)|1\rangle=H|\psi\rangle $$
考虑双比特系统下的 QFT 算符
对于计算基 \(|2\rangle = |10\rangle\) 有 $$ \mathrm{QFT}_2|10\rangle=\frac{1}{2}\left(|00\rangle-|01\rangle+|10\rangle-|11\rangle\right)=\frac{1}{2}\left(|0\rangle+|1\rangle\right)\left(|0\rangle-|1\rangle\right) $$
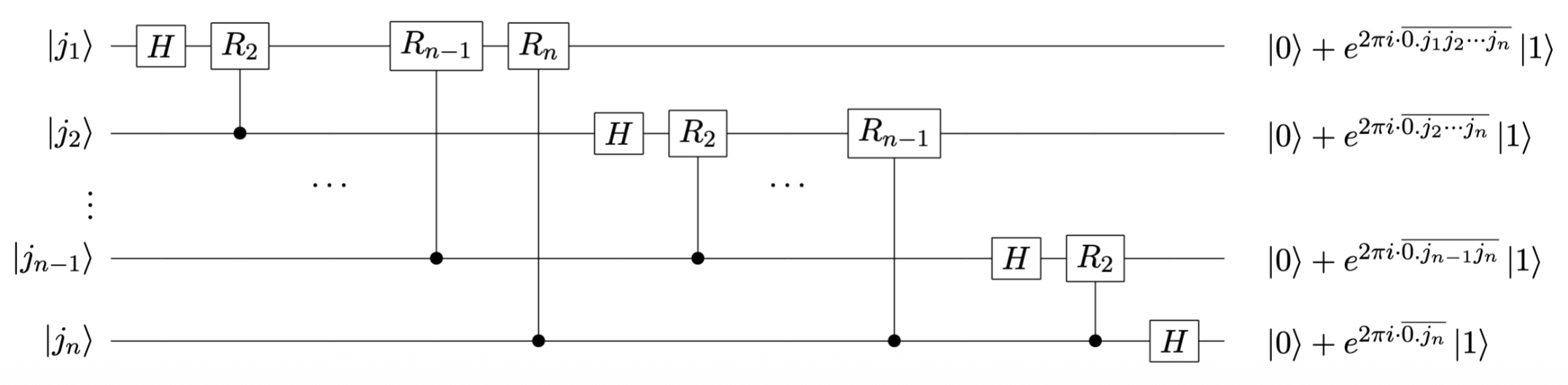
量子电路⚓︎
为构建 QFT 的量子电路,定义如下形式的单比特相位旋转门
QFT 可由如下量子电路实现
- QFT 电路中仅使用了 Hadamard 门和受控旋转门。电路中所有量子门都是酉的,QFT 无疑是酉变换
下面验证 QFT 的量子电路执行过程:
- 当 \(j_1 = 1\) 时, \(e^{2\pi i \overline{0.j_1}} = -1\),否则为 \(1\)。因此,经过一个 \(\text{H}\) 门后系统量子态变为 \(\frac{1}{\sqrt{2}}\left(|0\rangle + e^{2\pi i \overline{0.j_1}}|1\rangle\right)\Big|\overline{j_2\cdots j_n}\Big\rangle\)。
- 当 \(j_2 = 1\) 时,执行受控旋转门 \(R_2\),将 \(|j_1\rangle\) 相位乘以 \(e^{2\pi i \overline{0.0.j_2}}\)。此时,系统量子态变为 \(\frac{1}{\sqrt{2}}\left(|0\rangle + e^{2\pi i \overline{0.j_1j_2}}|1\rangle\right)\Big|\overline{j_2\cdots j_n}\Big\rangle\)。
- 以此类推,执行针对第一个量子比特的所有受控旋转门,此时系统量子态变为 \(\frac{1}{\sqrt{2}}\left(|0\rangle + e^{2\pi i \overline{0.j_1j_2 \dots j_n}}|1\rangle\right)\Big|\overline{j_2\cdots j_n}\Big\rangle\)。
-
同理,执行针对剩余量子比特的所有 H 门和受控旋转门。最终,系统量子态变为
\[ \frac{1}{\sqrt{2^n}}\left(|0\rangle+e^{2\pi i\overline{0.j_1j_2\cdots j_n}}|1\rangle\right)\left(|0\rangle+e^{2\pi i\overline{0.j_2\cdots j_n}}|1\rangle\right)\cdotp\cdotp\cdotp\left(|0\rangle+e^{2\pi i\overline{0.j_n}}|1\rangle\right) \]
对比 QFT 的张量积形式,发现电路末端的态和张量积形式顺序相反,再加一些 SWAP 门即可。
复杂度分析:观察量子电路易知,QFT 的量子门复杂度为 \(O(n^2)\)。
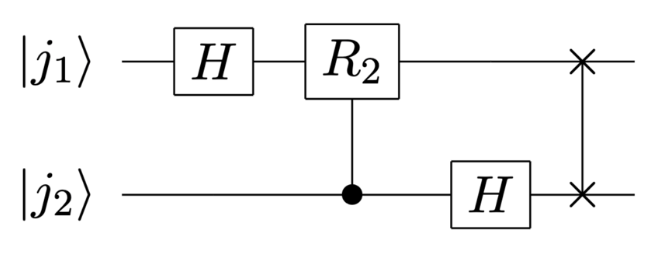
双比特量子电路⚓︎
由上述分析可知,双比特的 QFT 量子电路如下所示:
- 假设对 \(|\psi\rangle = |10\rangle\) 进行 QFT 操作,首先作用 H 门,得到 \(H|10\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) \otimes |0\rangle\)
- 然后作用受控 R 2 门,此时态不变
- 最后对 \(|j_2\rangle\) 作用 H 门,得到 \(\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\)
- 然后 SWAP 门交换量子态,得到 \(\frac{1}{2}(|0\rangle + |1\rangle) \otimes (|0\rangle - |1\rangle)\)
- 最终化简后得到 \(\frac{1}{2}|00\rangle - \frac{1}{2}|01\rangle + \frac{1}{2}|10\rangle - \frac{1}{2}|11\rangle\)
量子相位估计⚓︎
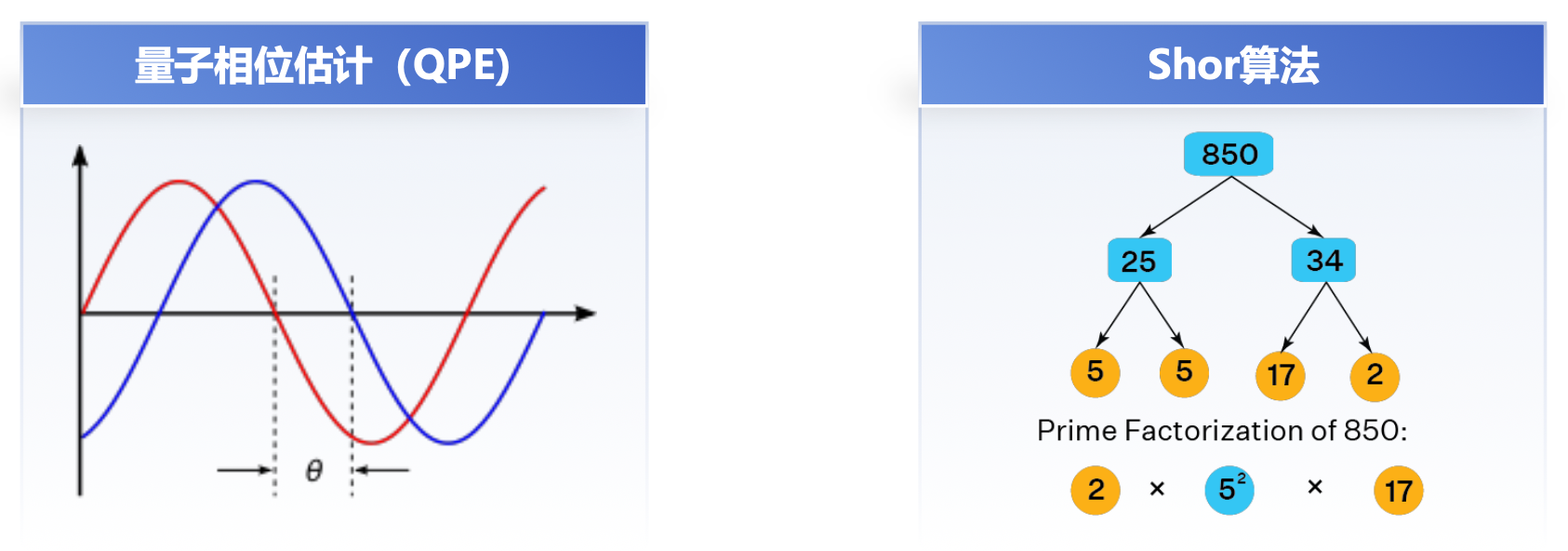
量子相位估计(QPE)用于估计给定量子态的相位信息。它是许多量子算法的核心组成部分,在量子模拟、量子化学和量子机器学习中具有广泛应用。
基本目标:对于一个酉算符 \(U\),已知其本征态 \(|\mu\rangle\),对应本征值为 \(e^{2\pi i \varphi}\),估计相位 \(\varphi\) 的值,其中 \(\varphi \in [0, 1)\)。
算法流程:
- 初始化:准备两个量子寄存器,一个存储相位估计结果,另一个存储本征态 \(|\mu\rangle\)
- 作用 H 门:对用于存储相位的量子比特施加 H 门
- 作用受控 U 门:对每个量子比特执行受控 U 门操作(第 j 个量子比特执行受控 \(U^{2^{j-1}}\) 门)
- 逆 QFT:对相位寄存器进行逆 QFT 操作,将振幅中的相位信息转换为可测量的计算基信息
- 测量:获得相位估计值
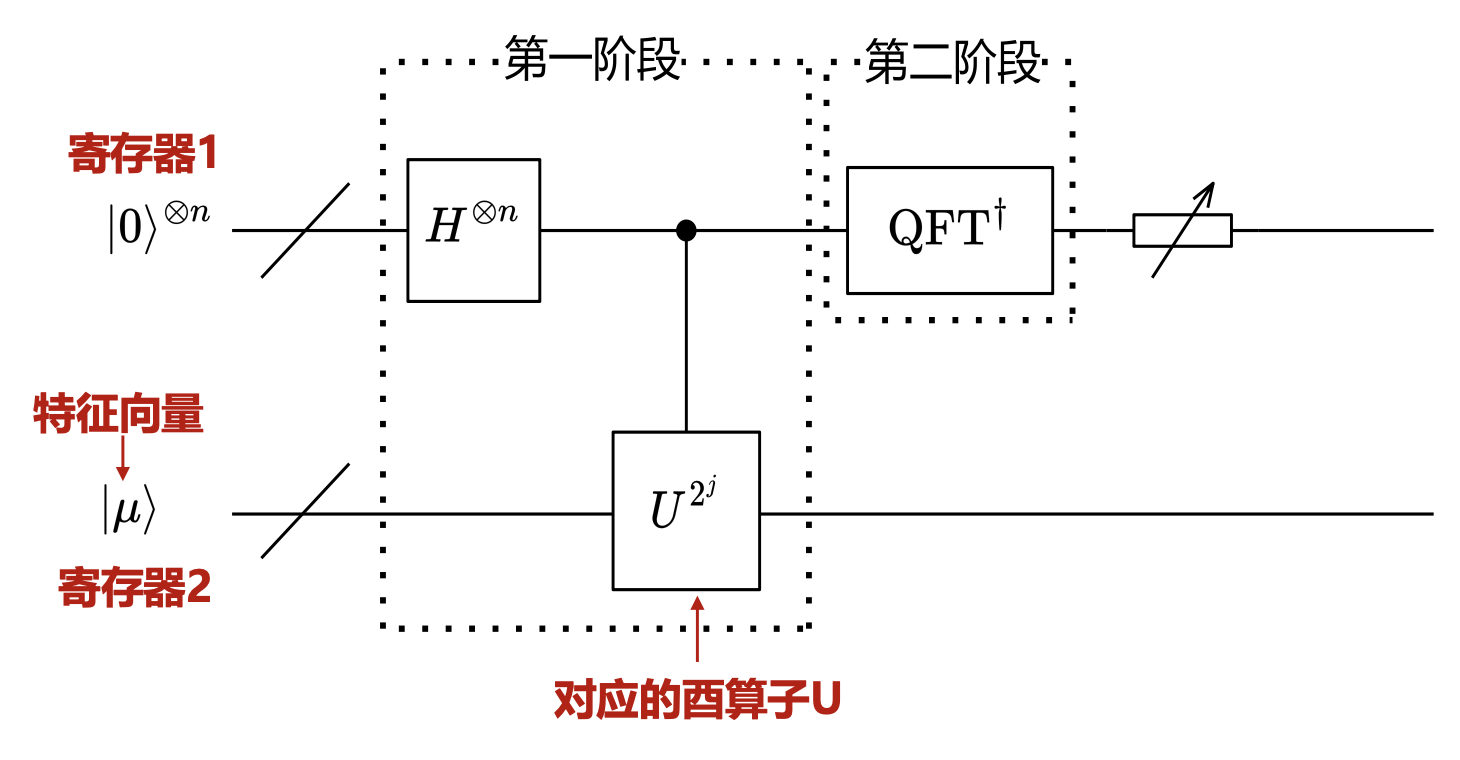
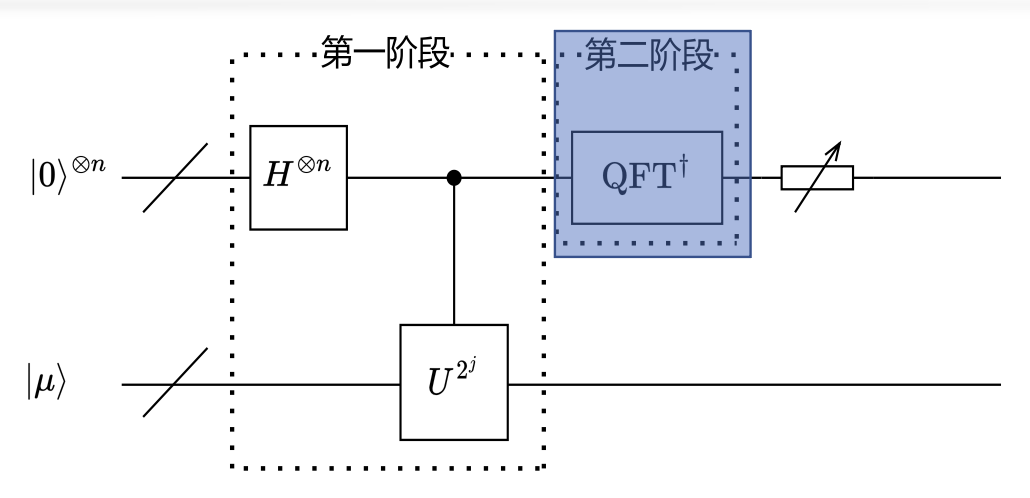
QPE 量子电路⚓︎
- 寄存器 1 用来存储最终的特征值
- 寄存器 2 用来存储输入的特征向量
- 而酉算子 U 通过受控 U 门输入到量子电路中
注:上标 \(\otimes n\) 表示 \(n\) 个比特。
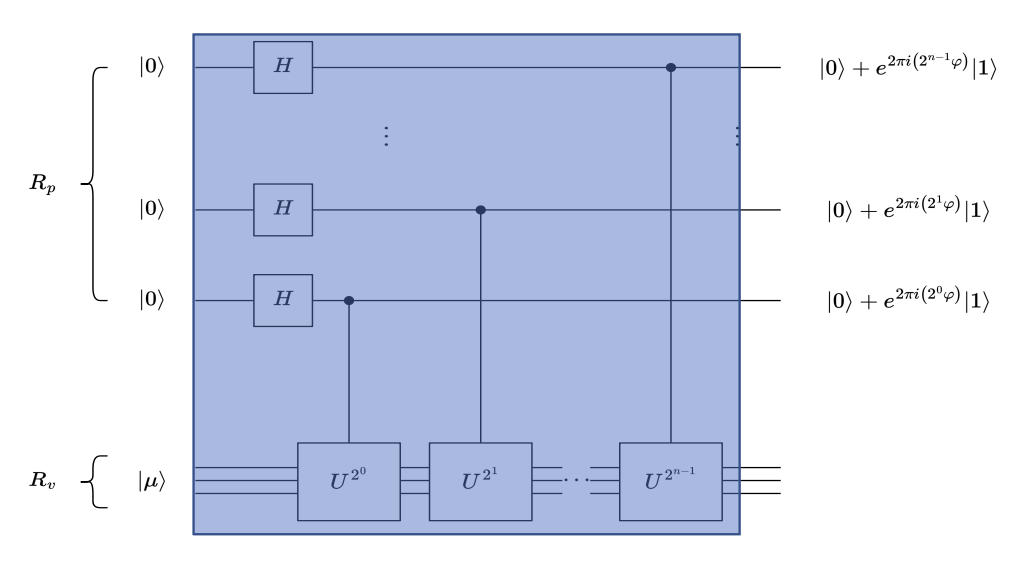
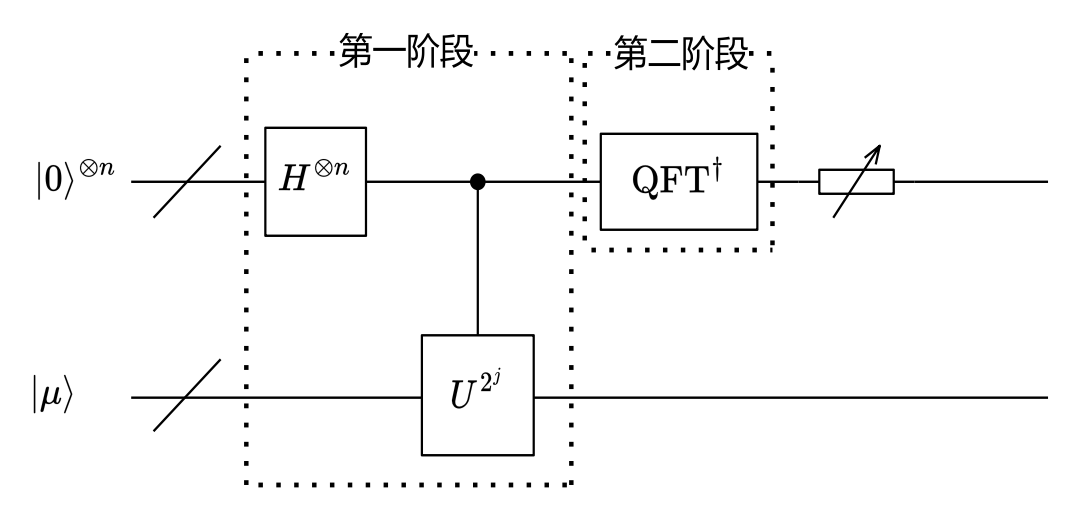
第一阶段⚓︎
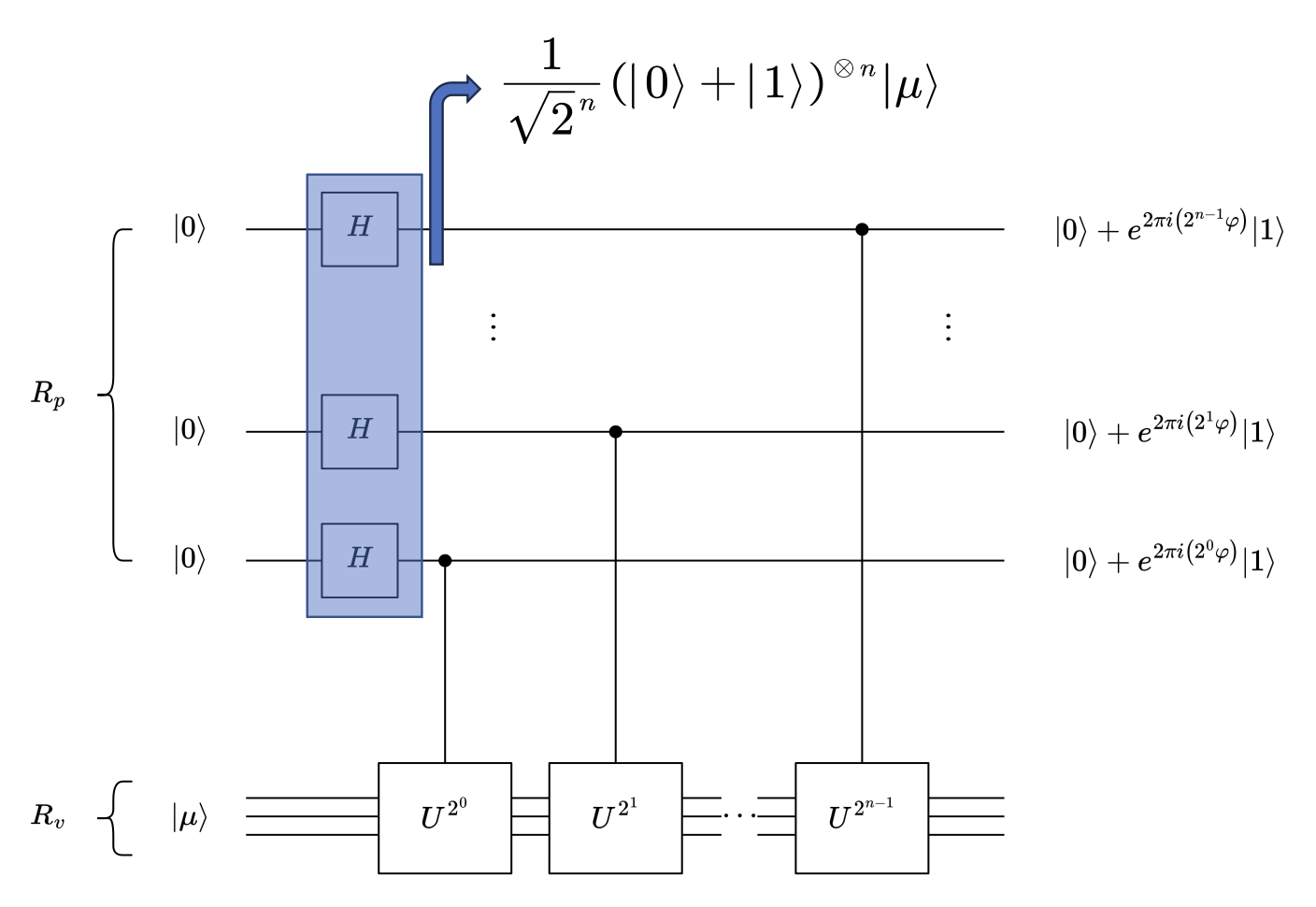
作用 H 门与受控 U 门:
作用 H 门:
作用受控 U 门:
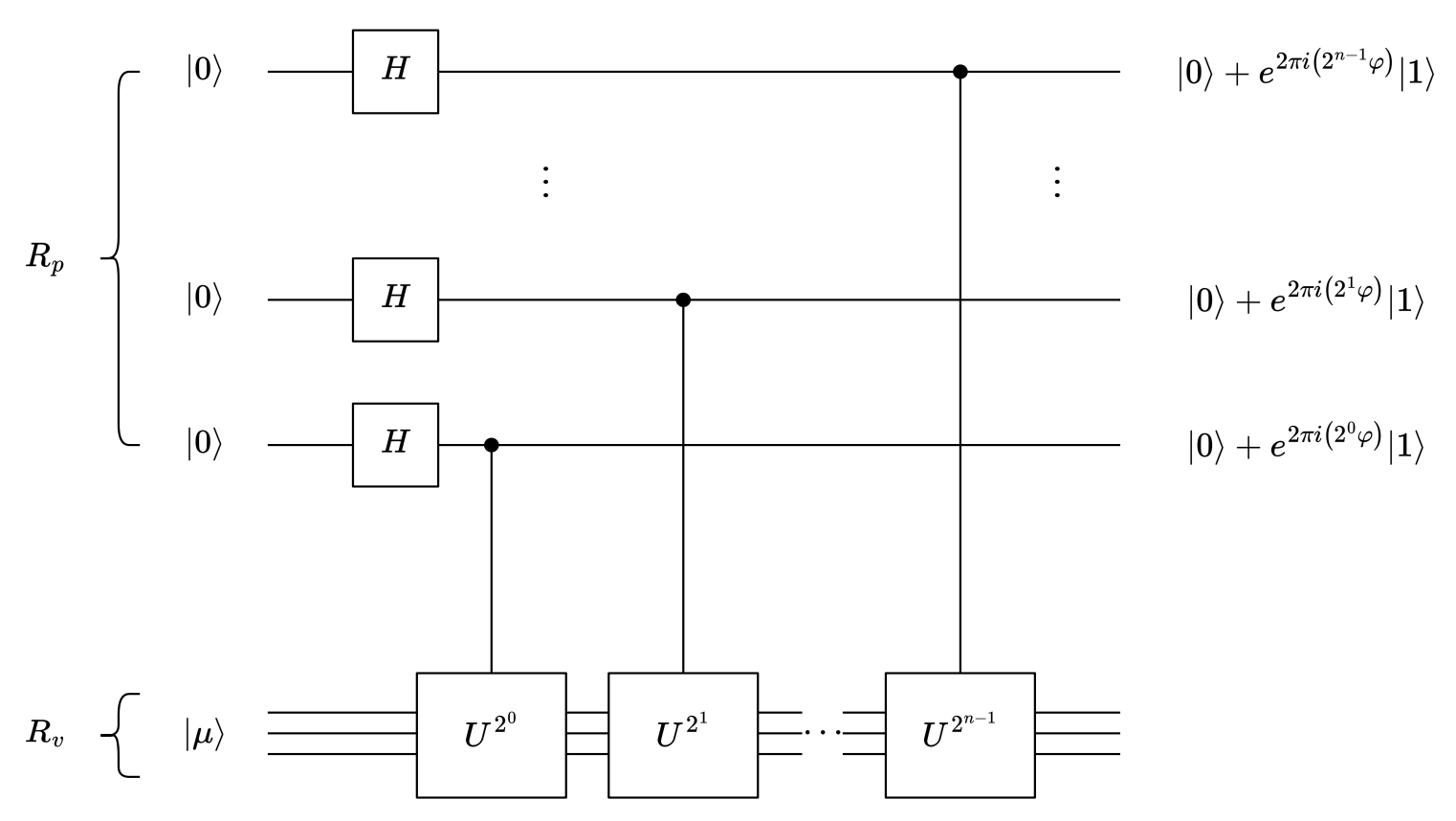
在 \(R_p\) 中,从下往上设置量子态为 \(|j_1\rangle, |j_2\rangle, \ldots, |j_n\rangle\),则有
因为 \(U|\mu\rangle = e^{2\pi i \varphi}|\mu\rangle\),则有
第二阶段⚓︎
- \(\varphi=\overline{0.\varphi_1\varphi_2\cdots\varphi_n}\)
-
QFT 张量积形式: $$ \frac{1}{\sqrt{2^n}} \left( |0\rangle + e^{2\pi i 0.\overline{\varphi_n}} |1\rangle \right) \left( |0\rangle + e^{2\pi i 0.\overline{\varphi_{n-1}\varphi_n}} |1\rangle \right) \cdots \left( |0\rangle + e^{2\pi i 0.\overline{\varphi_1\varphi_2\cdots \varphi_n}} |1\rangle \right) $$
-
作用逆 QFT 电路,即可得到 \(\varphi\)
结果⚓︎
演化过程:
QPE 过程举例⚓︎
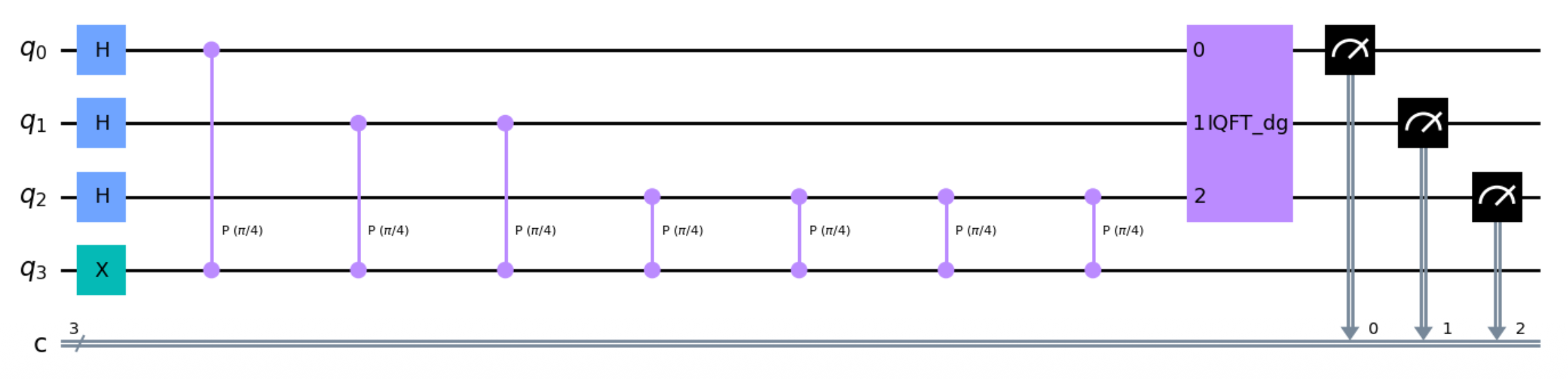
问题:考虑相位旋转门 \(P(\varphi) = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\varphi} \end{bmatrix}\),其本征态之一为 \(|1\rangle\)。取 \(\varphi = \frac{\pi}{4}\),即 \(P\left(\frac{\pi}{4}\right) = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\frac{\pi}{4}} \end{bmatrix}\),求其对应本征值的相位。
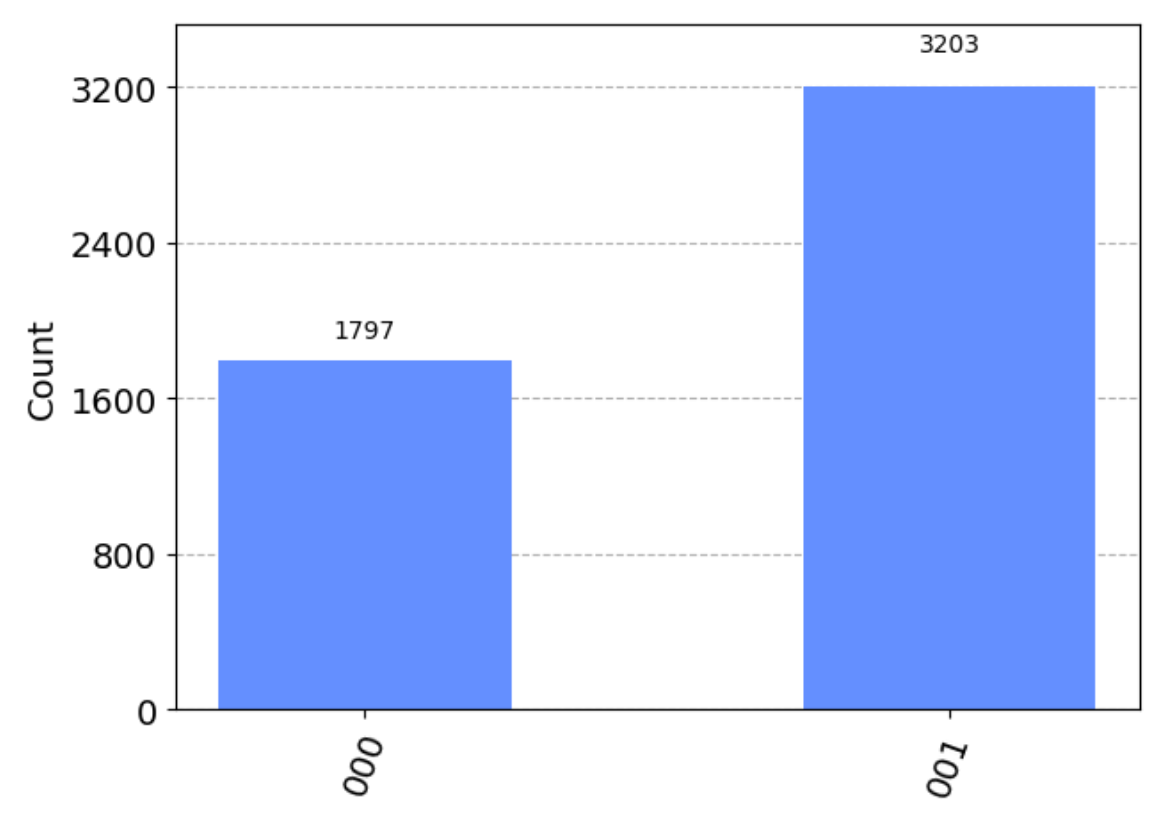
- \(q_0, q_1, q_2\) 作为第一个寄存器估计相位,均初始化为 \(|0\rangle\)
- \(q_3\) 作为第二个寄存器初始化为本征态 \(|1\rangle\)
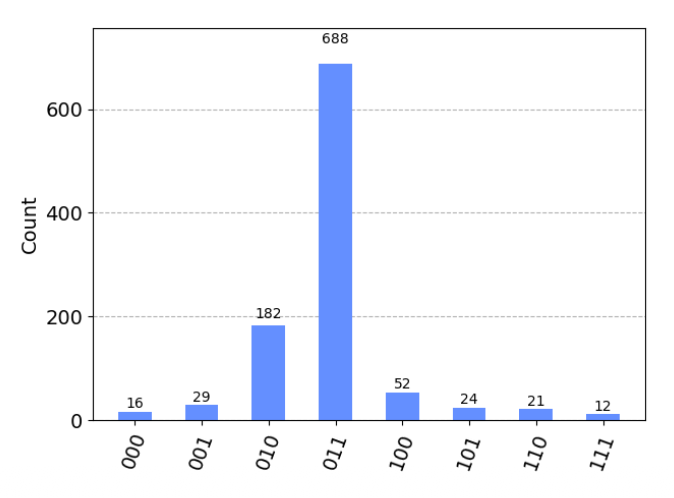
- 运行 QPE 电路,输出相位的三比特估计值为 \(\varphi = (0.001)_2 = \frac{1}{8}\)
- 验证与 \(|1\rangle\) 态本征值理论值相符:\(e^{2\pi i \varphi} = e^{2\pi i \frac{1}{8}} = e^{i \frac{\pi}{4}} = e^{i\varphi}\)
对于相位旋转门 \(P(\varphi) = \begin{pmatrix} 1 & 0 \\ 0 & e^{i\varphi} \end{pmatrix}\)
- 若 \(\varphi = \frac{\pi}{4}\),电路可精确估计出相位 \(\varphi\)
- 若 \(\varphi = \frac{2\pi}{3}\),\(P\left(\frac{2\pi}{3}\right)|1\rangle=e^{i\frac{2\pi}{3}}|1\rangle=e^{2\pi i\varphi}, (011)_2 = \dfrac{3}{8}\),相比更接近
提示
- 将酉矩阵 U 谱分解:\(U = \sum_{j=1}^n \lambda_j |\mu_j\rangle\langle\mu_j|\)
- 任意向量 \(|b\rangle = \sum_{j=1}^n \beta_j |\mu_j\rangle\)
- 执行 QPE 得到 \(\sum_{j=1}^n \beta_j |\varphi_j\rangle|\mu_j\rangle\)
QPE 电路测得相位 \(0\) 和 \(\frac{1}{8}\) 的概率各为 \(\frac{9}{25}\) 和 \(\frac{16}{25}\)。
量子相位估计(QPE)算法用于估计酉算符 \(U\) 的本征态 \(|\psi\rangle\) 对应本征值的相位 \(\phi\),其中 \(U|\psi\rangle = e^{2\pi i\phi}|\psi\rangle\)。假设酉算符 \(U = \begin{bmatrix} e^{i\frac{3}{4}\pi} & 0 \\ 0 & e^{i\frac{5}{4}\pi} \end{bmatrix}\),其本征态为 \(|\psi_0\rangle = |0\rangle\) 和 \(|\psi_1\rangle = |1\rangle\)。请回答以下问题:
- 在 QPE 算法中逆量子傅立叶变换的作用是什么?请写出 \(\text{QFT}^\dagger\) 的具体形式
- 若对量子态 \(|\psi\rangle = \frac{1}{\sqrt{2}}(|\psi_0\rangle + |\psi_1\rangle)\) 执行 3 比特精度的 QPE 算法,推导测量获得的相位估计值的概率分布
- 若对上一小问中的量子态执行 2 比特精度的 QPE 算法,推导测量获得的相位估计值的概率分布
- 逆量子傅立叶变换的作用是将振幅中的相位信息转换为可测量的计算基信息。\(\text{QFT}^\dagger\) 的具体形式为
- \(|\psi_0\rangle\) 和 \(|\psi_1\rangle\) 对应的本征值分别为 \(e^{i\frac{3}{4}\pi}\) 和 \(e^{i\frac{5}{4}\pi}\),对应的相位分别为 \(\phi_0 = \frac{3}{8} = 0.\overline{011}\) 和 \(\phi_1 = \frac{5}{8} = 0.\overline{101}\)。因此,对量子态 \(|\psi\rangle\) 执行 3 比特精度的 QPE 算法,测量获得的相位估计值的概率为
- 若执行 2 比特精度的 QPE 算法,则无法精确估计 \(\phi_0\) 和 \(\phi_1\)。因此与两者相近的相位估计值出现概率较高。对于 \(\phi_0 = 0.\overline{011}\),分别约有 \(\frac{1}{2}\) 的概率估计得 \(0.\overline{01}\) 和 \(0.\overline{10}\);对于 \(\phi_1 = 0.\overline{101}\),分别约有 \(\frac{1}{2}\) 的概率测得 \(0.\overline{10}\) 和 \(0.\overline{11}\)。因此,对量子态 \(|\psi\rangle\) 执行 2 比特精度的 QPE 算法,测量获得的各相位估计值的概率约为
Shor 算法⚓︎
背景⚓︎
对称加密⚓︎
非对称加密⚓︎
非对称加密解决了对称加密密钥分发的问题:
- 非对称加密是单向的,一个人使用一组密钥和公钥
- 密钥由 Bob 自己“制造”并使用,公钥可告诉所有人,所有信息发送方都可使用公钥加密
前置知识
-
同余
- \(a \equiv b \pmod n\):\(a\) 和 \(b\) 除以 \(n\) 的余数相同
- \(ab \equiv 1 \pmod n\):\(b\) 是 \(a\) 模 \(n\) 下的逆元
-
阶:\(a^r \equiv 1 \pmod n\)
- \(a\) 模 \(n\) 的阶:令上式成立的最小正整数 \(r\),记作 \(\text{ord}_n a\)
-
欧拉函数 \(\varphi(n)\) 是与 \(n\) 互质的小于 \(n\) 的整数个数,互质即最大公约数为 1
- 若 \(p\) 是质数,显然有 \(\varphi(p) = p-1\)
- 欧拉函数是积性函数:若 \(\text{gcd}(a, b) = 1\)(\(a, b\) 互质
) ,则 \(\varphi(ab) = \varphi(a)\varphi(b)\) - 若 \(\text{gcd}(a, n) = 1\),则 \(a^{\varphi(n)} \equiv 1 \pmod n\)
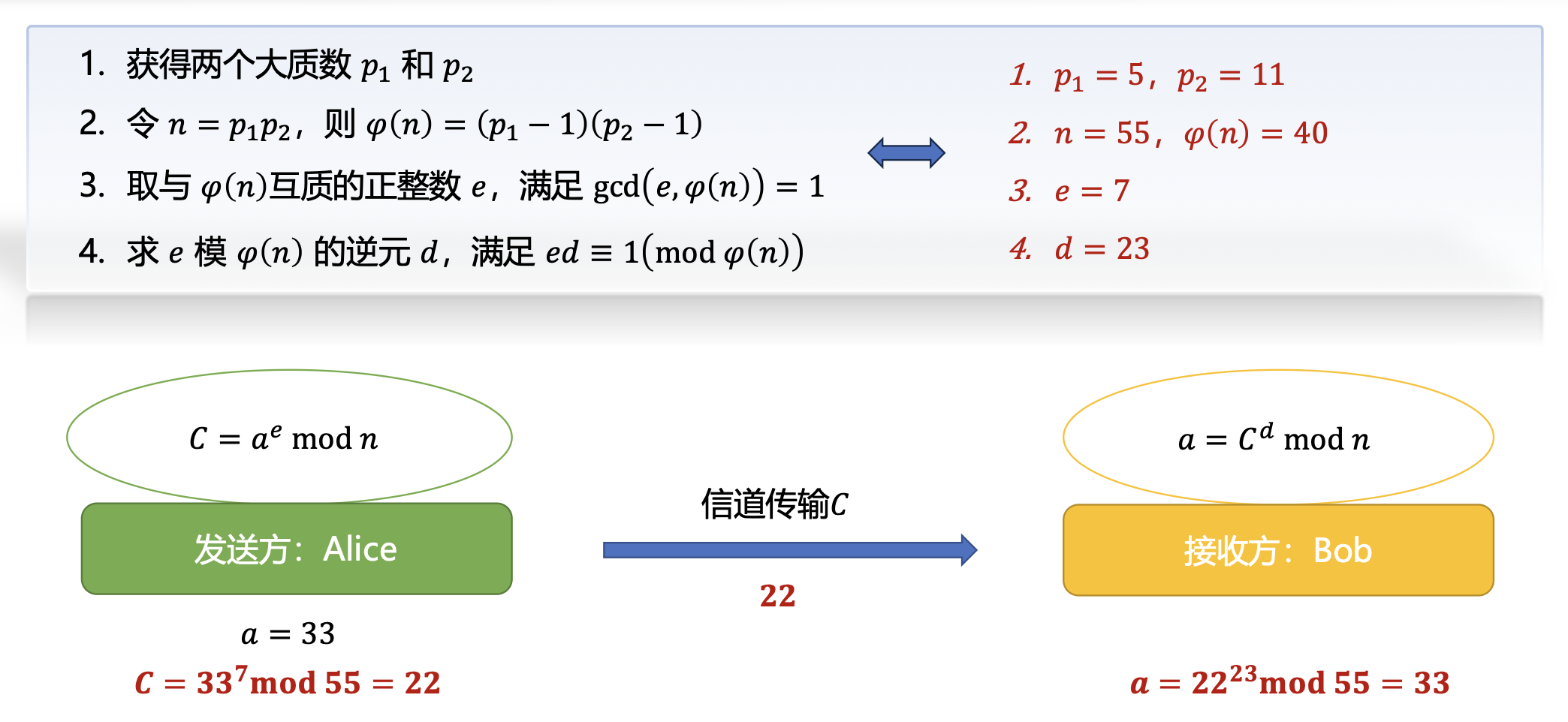
制造公钥(\(n, e\))和密钥(\(n, d\)
- 获得两个大质数 \(p_1\) 和 \(p_2\)
- 令 \(n = p_1p_2\),则 \(\varphi(n) = \varphi(p_1p_2) = (p_1-1)(p_2-1)\)
- 取与 \(\varphi(n)\) 互质的正整数 \(e\),满足 \(\text{gcd}(e, \varphi(n)) = 1, e \neq p_1, p_2\)
- 求 \(e\) 模 \(\varphi(n)\) 的逆元 \(d\),满足 \(ed \equiv 1 \pmod{\varphi(n)}\)
如何破解 RSA?
- 已知公钥 \(n, e\)
- 分解 \(n = p_1 p_2\)
- 计算 \(\varphi(n)\)
- 计算私钥 \(d\)
试除法(传统)
for i in 2, 3, 4, ..., sqrt(n)
while n equiv 0 mod i
n := n / i
add i to ans
if n > 1
add n to ans
return ans
- 尝试用小于 n 的所有可能因数去除目标数,直到找到质因数为止。
- 试除法是传统的分解质因数方法,时间复杂度 \(O(\sqrt{n})\)
- 试除法非常低效,当前常用的 RSA 密钥长度即便使用最快的计算机进行试除法,也会耗费极其长的时间
Shor 算法⚓︎
只有“计算阶”这一步使用量子计算,其余为经典计算。
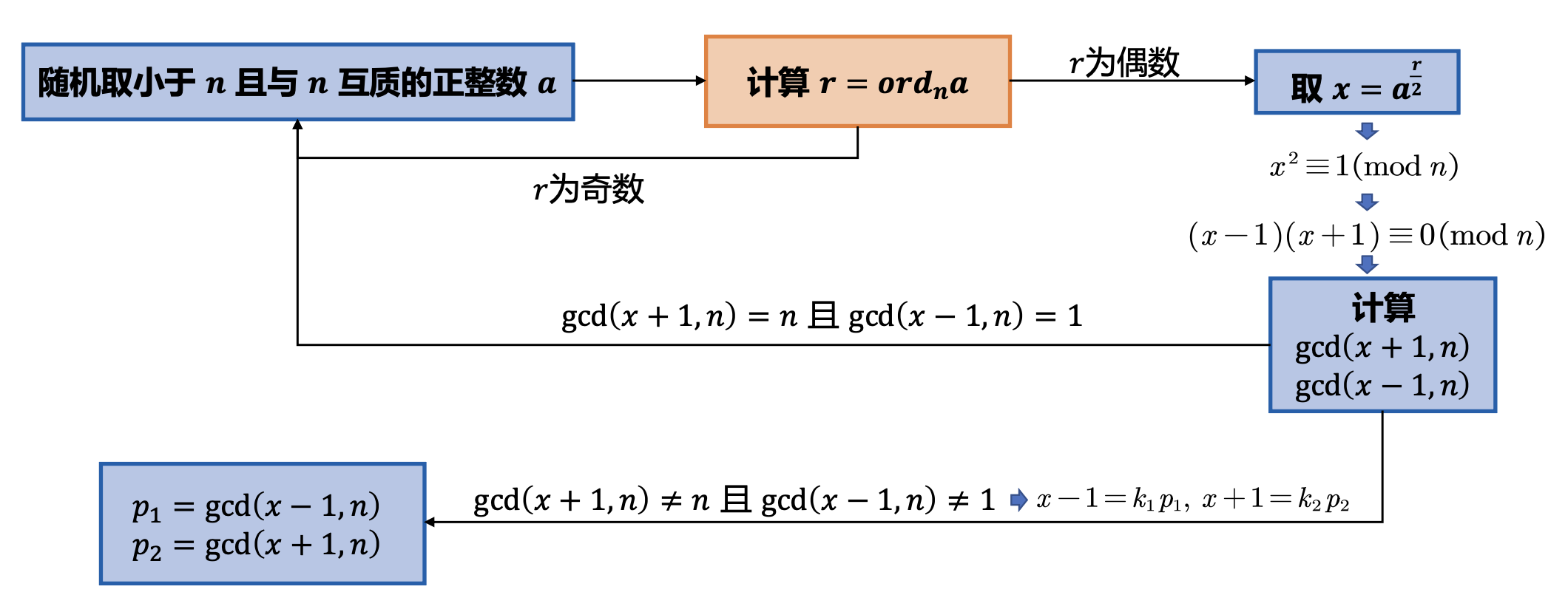
如何使用 Shor 算法求阶?
-
定义酉变换
- \(U|y\rangle=|ay(\mathrm{mod~}n)\rangle\)
- \(U^2|y\rangle=U|ay\left(\mathrm{mod~}n\right)\rangle=|a^2y(\mathrm{mod~}n)\rangle\)
- \(U^t|y\rangle=|a^ty(\mathrm{mod~}n)\rangle\)
-
定义量子态 \(|u_s\rangle\)
\[ |u_s\rangle = \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} e^{-\frac{2\pi isk}{r}} |a^k \pmod N\rangle \]- 性质 1:\(U|u_s\rangle = e^{\frac{2\pi is}{r}} |u_s\rangle\)
- 性质 2:\(\frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} |u_s\rangle = |1\rangle\)
说明
- \(|u_s\rangle\) 是 \(U\) 的特征向量
- \(|1\rangle\) 是 $|u_s\rangle_{s=0}^{r-1} $ 等概率的叠加态,所以根据性质 2 我们可以规避制备 \(|u_s\rangle\)
证明
\[ U|u_s\rangle = \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} e^{-\frac{2\pi isk}{r}} |a^{k+1} \pmod N\rangle = e^{2\pi is} |u_s\rangle \]\[ \begin{aligned} & \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} |u_s\rangle = |1\rangle \iff \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} e^{\frac{2\pi isk}{r}} |u_s\rangle = |a^k \pmod N\rangle \\ & \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} e^{\frac{2\pi isk}{r}} |u_s\rangle = \frac{1}{\sqrt{r}} \sum_{s,l=0}^{r-1} e^{\frac{2\pi isk}{r}} |a^l \pmod N\rangle \end{aligned} \]此时设
\[ \sum_{s=0}^{r-1} e^{\frac{2\pi is(k-l)}{r}} = \begin{cases} r & \text{if } k=l \\ \frac{1-e^{\frac{2\pi i(k-l)}{r}}}{1-e^{\frac{2\pi i(k-l)}{r}}} = 0 & \text{if } k\neq l \end{cases} \]即有 $$ \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} e^{\frac{2\pi isk}{r}} |u_s\rangle = \frac{1}{r} \sum_{s,l=0}^{r-1} e^{\frac{2\pi isk}{r}} |a^l \pmod N\rangle = \frac{1}{r} \sum_{l=0}^{r-1} r\delta_{k,l}|a^l \pmod N\rangle = |a^k \pmod N\rangle $$
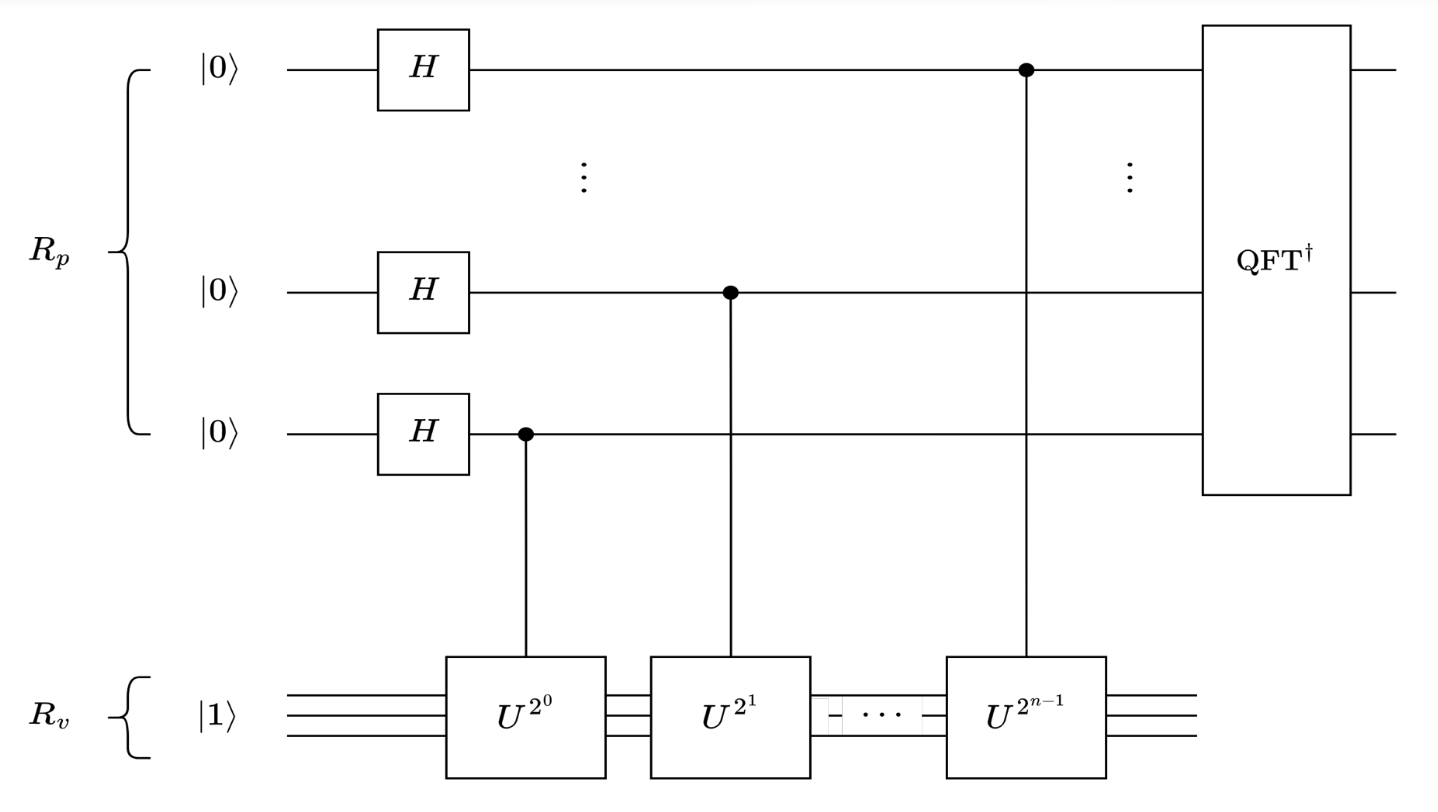
量子电路⚓︎
量子电路说明:
对 \(U\) 和 \(|1\rangle\) 进行 QPE,可等概率测量得到相位 \(\left\{ 0, \frac{1}{r}, \frac{2}{r}, \ldots, \frac{r-1}{r} \right\}\)
U 算子的一种构造方法⚓︎
\(U\) 算子的初步构造方法十分简单:
-
将变换前所有可能的 \(x\) 进行穷举(从 \(0\) 到 \(N-1\) 共有 \(N\) 个数
) ,并一一算出对应的 \(f(x) = a^x \bmod N\) -
对每一个 \(x\),我们都可以写出变换前的态 \(|x\rangle\) 和变换后的态 \(|f(x)\rangle\) 的矩阵表示,将它们进行外乘即可得到每一个 \(x\) 对应的变换矩阵,然后将所有矩阵求和即得到算子 \(U\) 的矩阵表示,即
Grover 算法⚓︎
引入:简单搜索问题举例(寻找因子)
寻找 24 的因子?
通过遍历 1 至 24 所有整数,逐个检验。
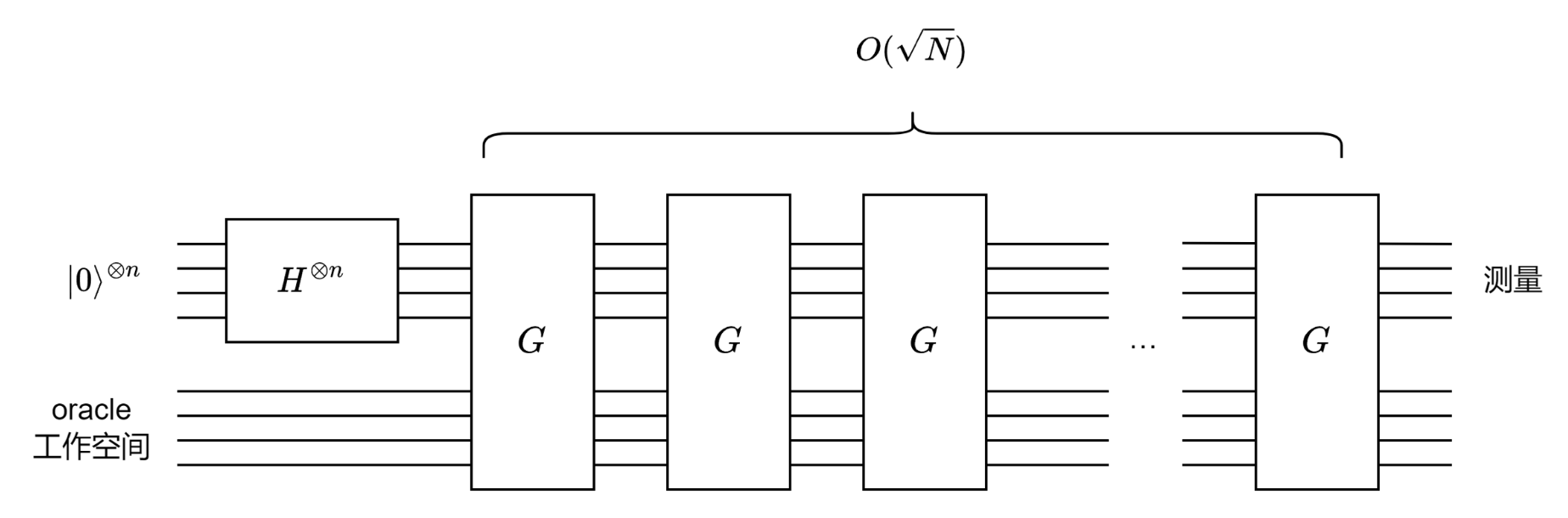
Grover 算法可以将 \(O(N)\) 的经典算法,加速至 \(O(\sqrt{N})\)。
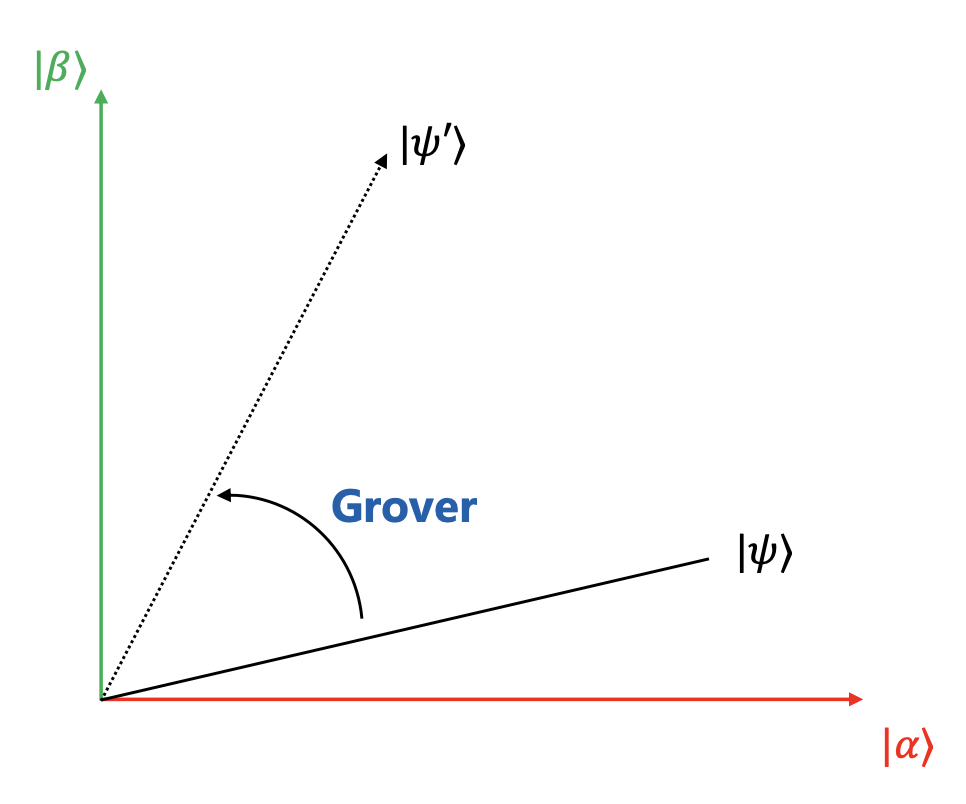
Grover 算法的几何解释:
- \(|\alpha\rangle\) 是所有错解的叠加态
- \(|\beta\rangle\) 是所有正解的叠加态
例子
寻找 24 的因子
- \(|\alpha\rangle\) 处于 5, 7, 9, 10, 13... 的叠加态
- \(|\beta\rangle\) 处于 1, 2, 3, 4, 6... 的叠加态
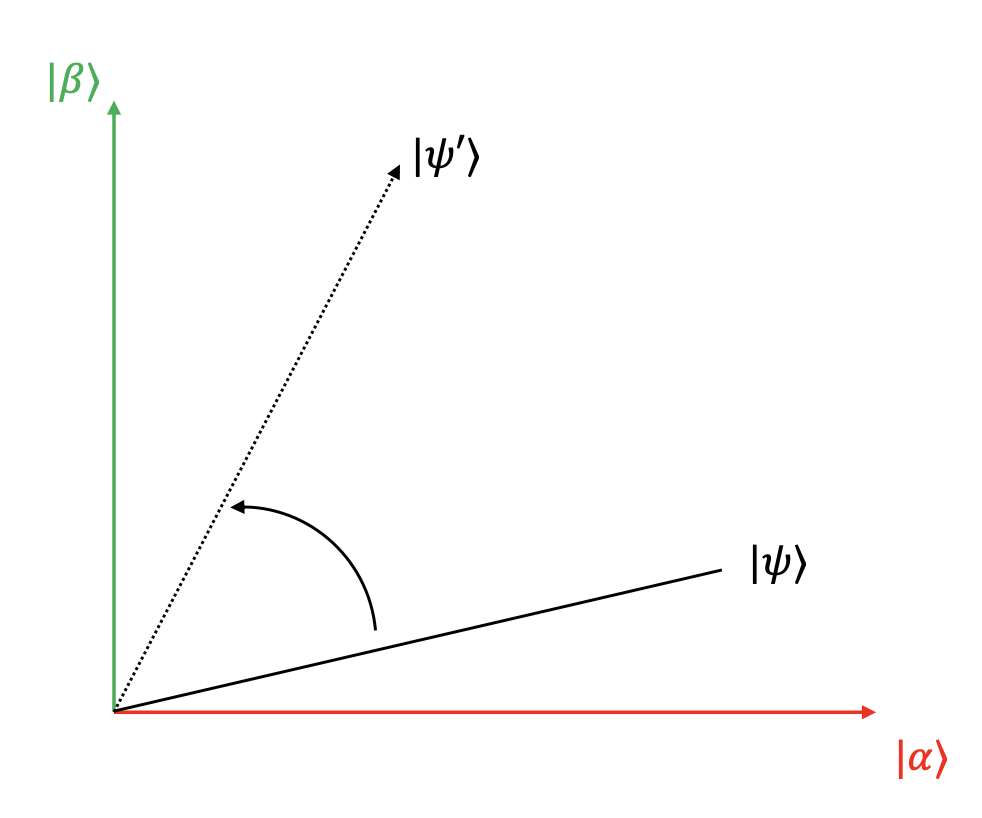
Grover 算法通过旋转初始量子态,使其逐渐接近 \(|\beta\rangle\)。
Oracle⚓︎
- Oracle 是一个黑盒,它不能给出问题的可行解,但能检验某个解是不是正确的
- 几何上的旋转主要通过 Oracle 电路实现
- 不同问题的 Oracle 电路不同,比如检验是否为 \(x\) 因子的电路、检验 \(x\) 是否小于一个常数 \(C\) 的电路,学习 Grover 算法不必纠结 Oracle 电路实现
例子
\(x\) 为正解时 \(f(x) = 1\),否则 \(f(x) = 0\)。
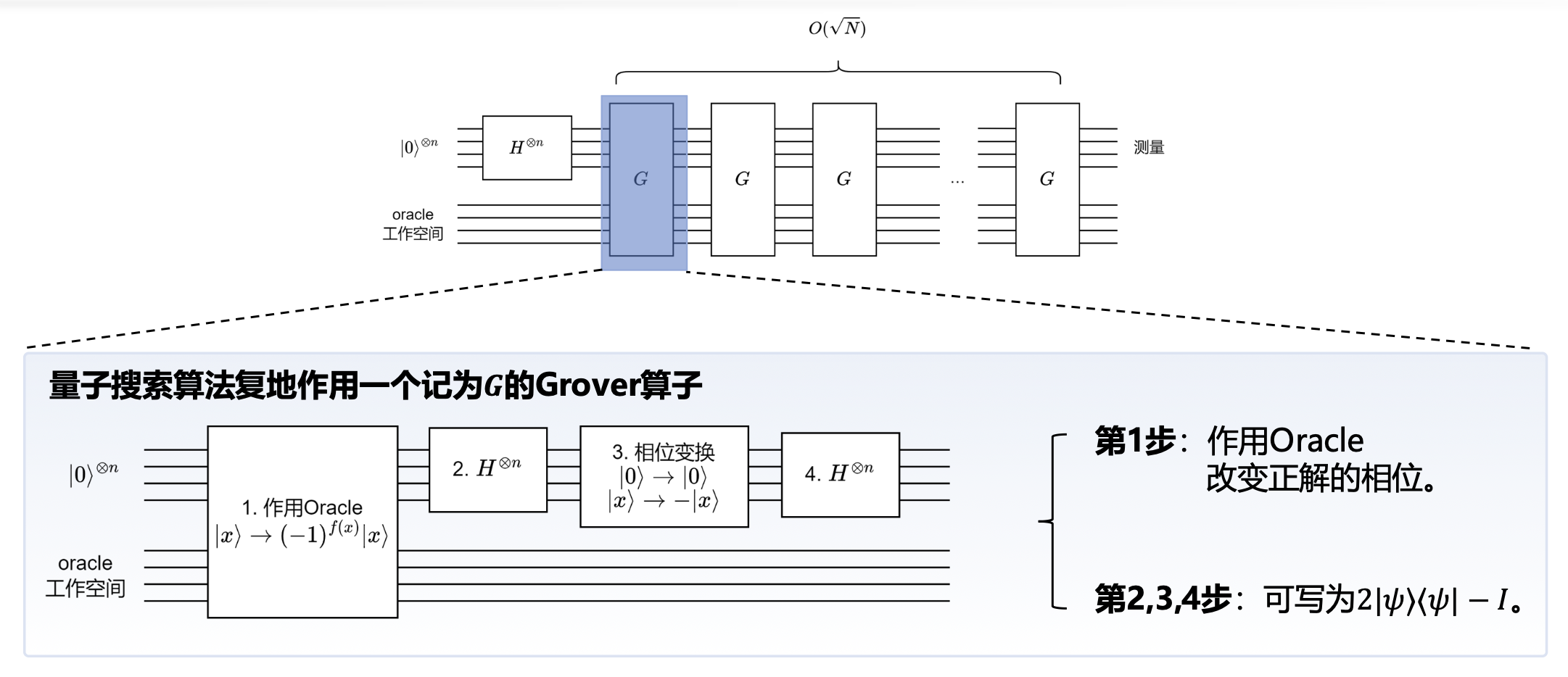
量子电路⚓︎
算法始于状态 \(|0\rangle^{\otimes n}\),用 \(H^{\otimes n}\) 使寄存器处于均匀叠加态:
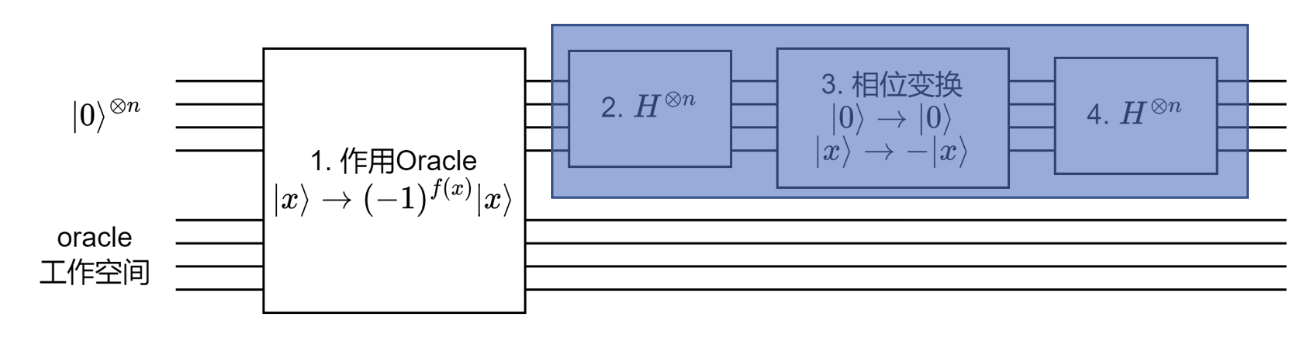
简单证明第 2, 3, 4 步:可写为 \(2|\psi\rangle\langle\psi| - I\)
第 3 步的酉矩阵表示为
于是 \(H^{\otimes n} (2|0\rangle\langle 0| - I) H^{\otimes n} = 2|\psi\rangle\langle\psi| - I\)。
G 迭代的几何意义⚓︎
初始状态:\(|\psi\rangle = \sqrt{\frac{N-M}{N}} |\alpha\rangle + \sqrt{\frac{M}{N}} |\beta\rangle\)
- 待检验的解个数:\(N\)
- 可行解个数:\(M\)
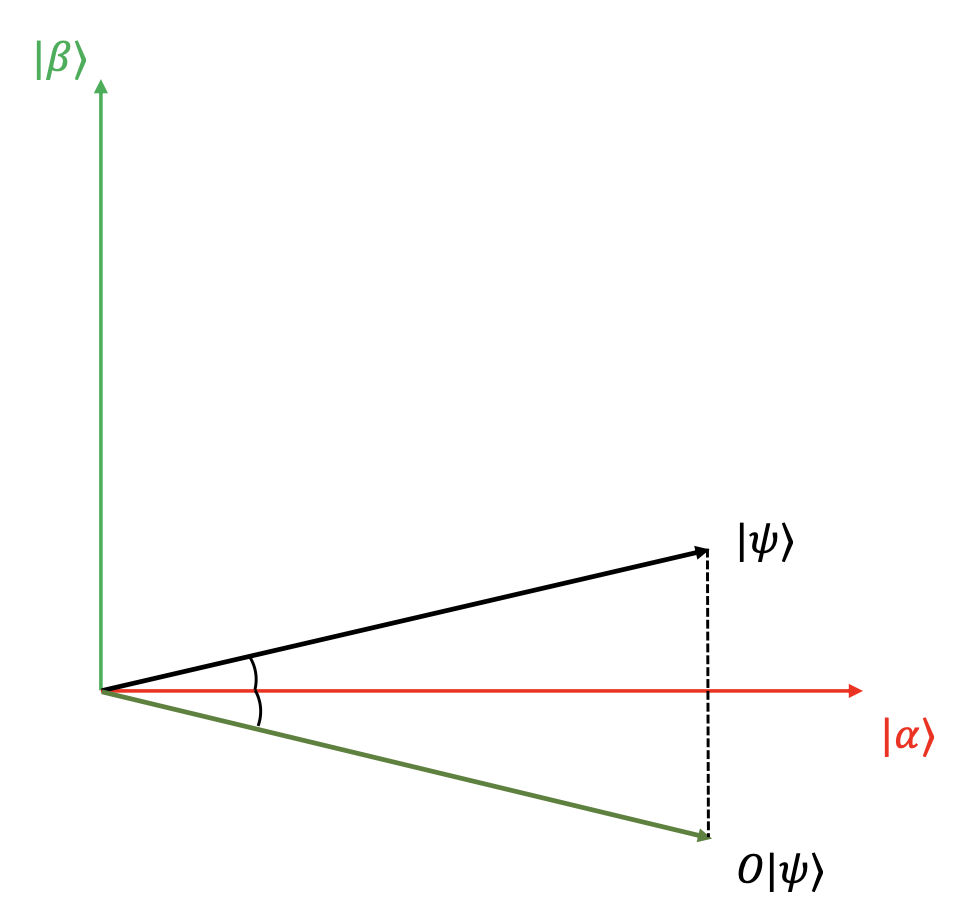
第 1 步:作用 Oracle(算子 \(O\)
- \(O\) 就是以 \(|\alpha\rangle\) 为对称轴做对称操作
-
令 \(a = \sqrt{\frac{N-M}{N}}, b = \sqrt{\frac{M}{N}}\),即有:
\[ O(a|\alpha\rangle + b|\beta\rangle) = a|\alpha\rangle - b|\beta\rangle \] -
在 \(|\alpha\rangle\) 上的投影不变,在 \(|\beta\rangle\) 上的投影翻转
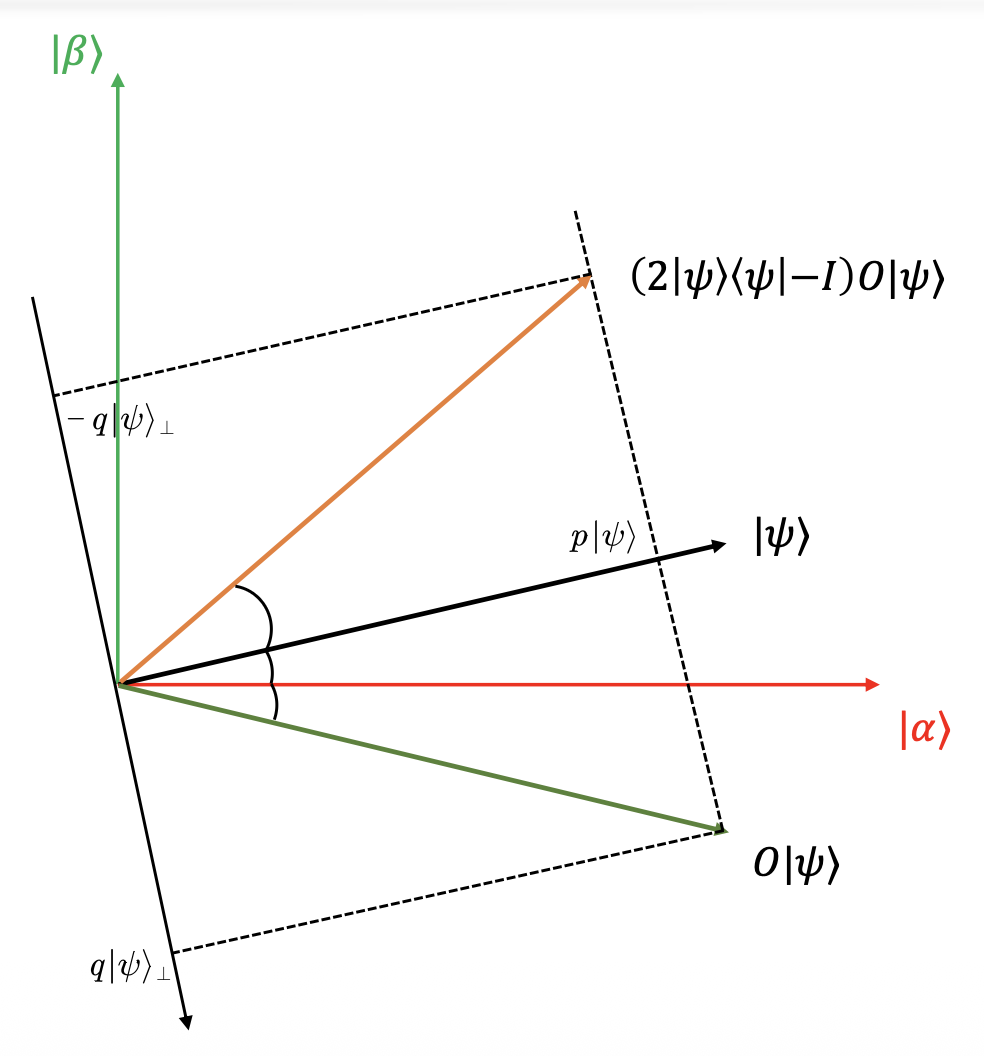
第 2, 3, 4 步:作用 \(2|\psi\rangle\langle\psi| - I\)
- 任意量子态(单位向量)\(|v\rangle = p|\psi\rangle + q|\psi\rangle_{\perp}\)
-
其中 \(|\psi\rangle_\perp\) 表示与 \(|\psi\rangle\) 垂直的分量
\[ (2|\psi\rangle\langle\psi| - I)|v\rangle = p|\psi\rangle - q|\psi\rangle_{\perp} \] -
\(2|\psi\rangle\langle\psi| - I\) 就是以 \(|\psi\rangle\) 为对称轴做对称操作
总结:
- 初始状态为 \(|\psi\rangle = \sqrt{\frac{N-M}{N}} |\alpha\rangle + \sqrt{\frac{M}{N}} |\beta\rangle\)
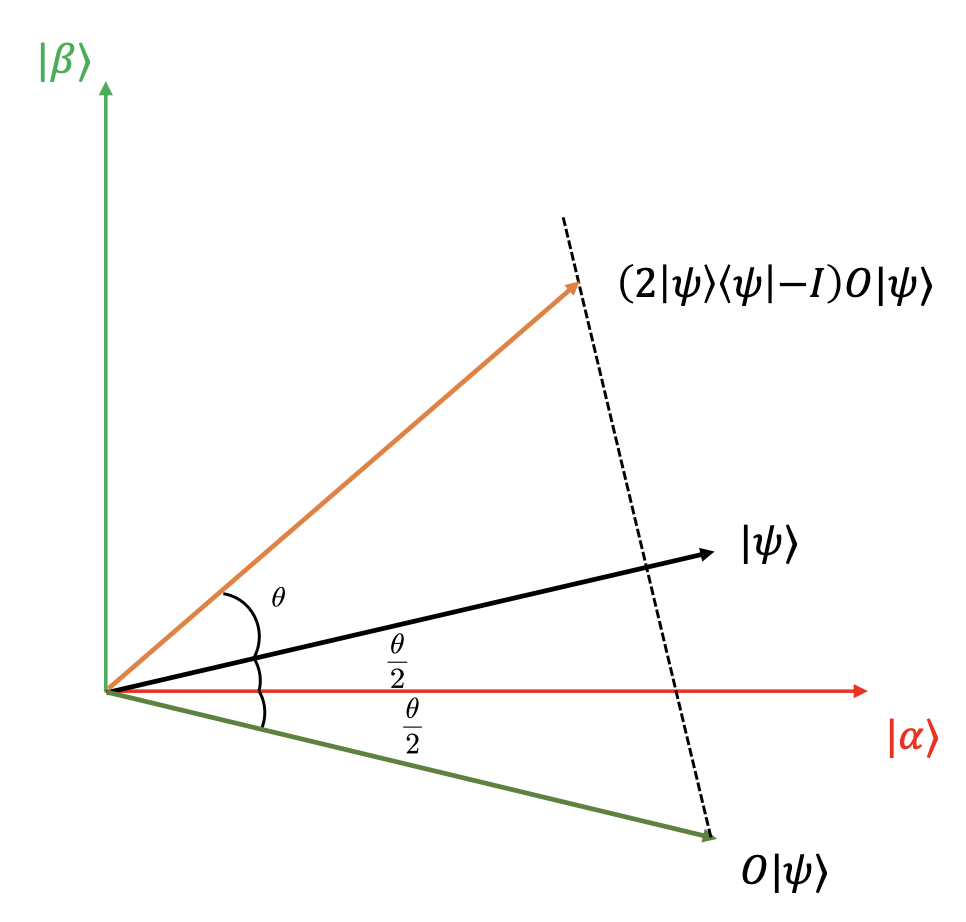
- \(G\) 算子几何意义:先将量子态相对 \(|\alpha\rangle\) 做对称,再将量子态相对 \(|\psi\rangle\) 做对称
- 使用 \(G\) 算子后,量子态向正确解的叠加态旋转
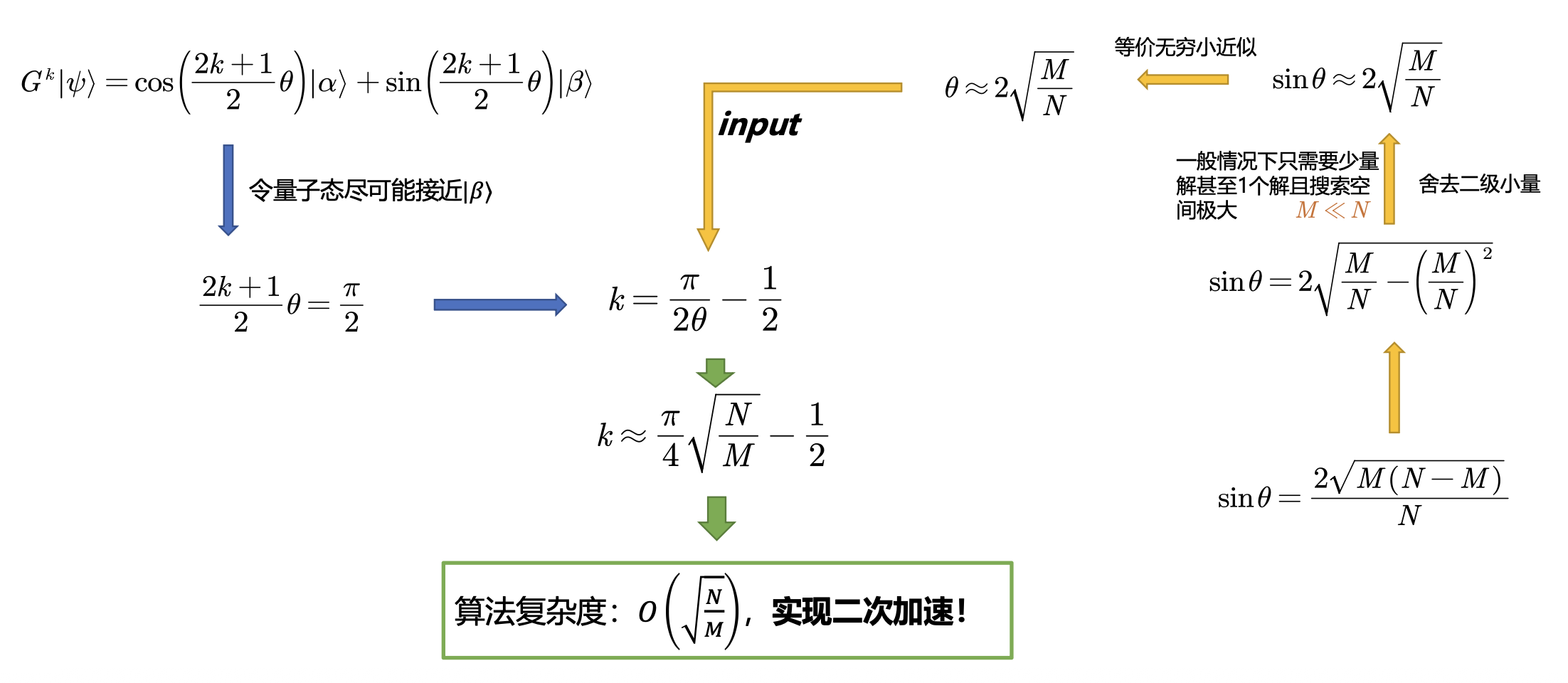
- 可以证明,作用一次 \(G\) 算子,可将量子态向 \(|\beta \rangle\) 旋转角度 \(\theta\),即 \(G^k |\psi\rangle = \cos\left(\frac{2k+1}{2}\theta\right) |\alpha\rangle + \sin\left(\frac{2k+1}{2}\theta\right) |\beta\rangle\)
- \(|\psi\rangle=\sqrt{\frac{N-M}{N}}|\alpha\rangle+\sqrt{\frac{M}{N}}|\beta\rangle\)
- \(\theta=2\arccos\sqrt{\frac{N-M}{N}}\)
- \(\sin\theta=\frac{2\sqrt{M(N-M)}}{N}\)
复杂度分析⚓︎
评论区