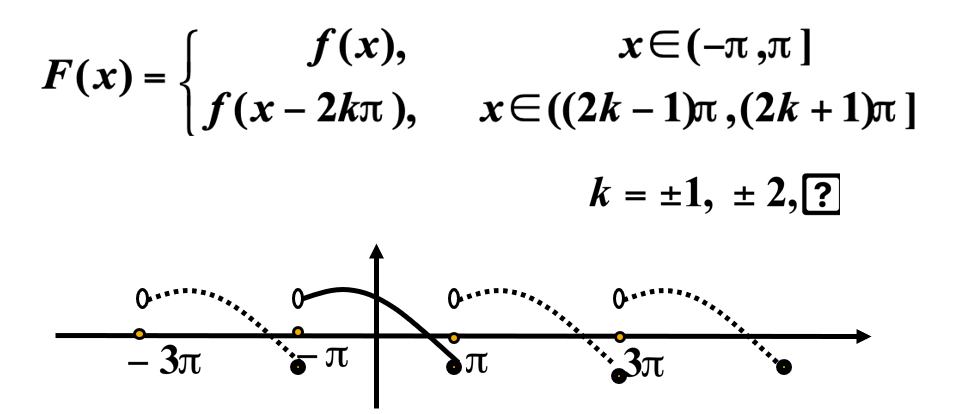Chap 6: Fourier Transform⚓︎
约 2001 个字 预计阅读时间 10 分钟
核心知识
- 傅里叶变换 (FT)
- 连续型 (CFT)
- 离散型 (DFT)
- 快速傅里叶变换 (FFT)
- 2D FT
Mathematic Background⚓︎
背景知识
古今往来,众多数学家一直在寻找用简单函数较好地近似代替复杂函数的途径,除了理论上的需要外,它对实际应用的领域的意义更是不可估量。在微积分发明之前,这个问题一直没有本质上的突破。
英国数学家泰勒在 17 世纪找到了用幂函数的无限线性组合表示一般的解析函数的方法:
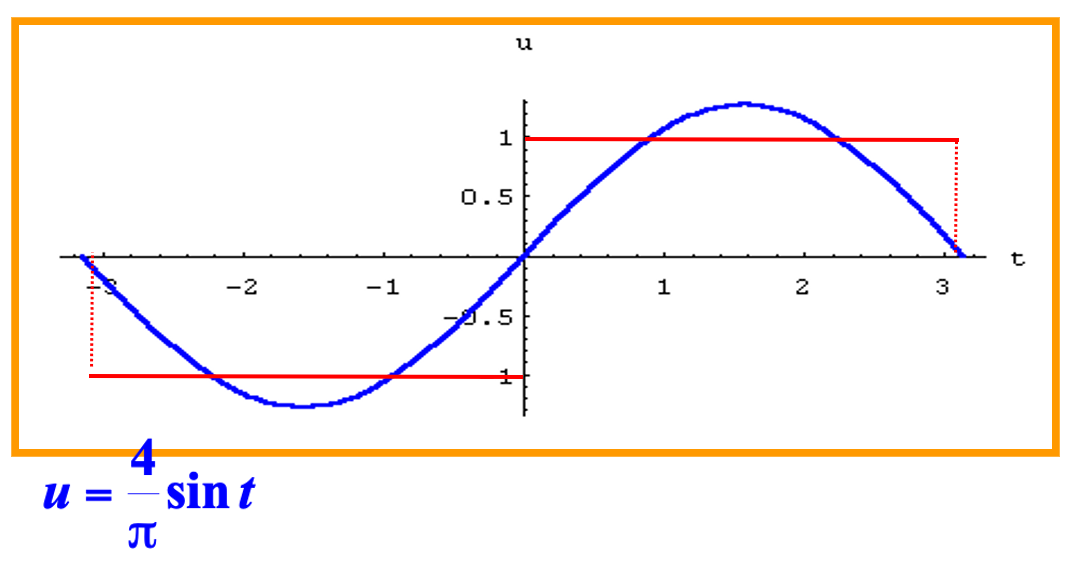
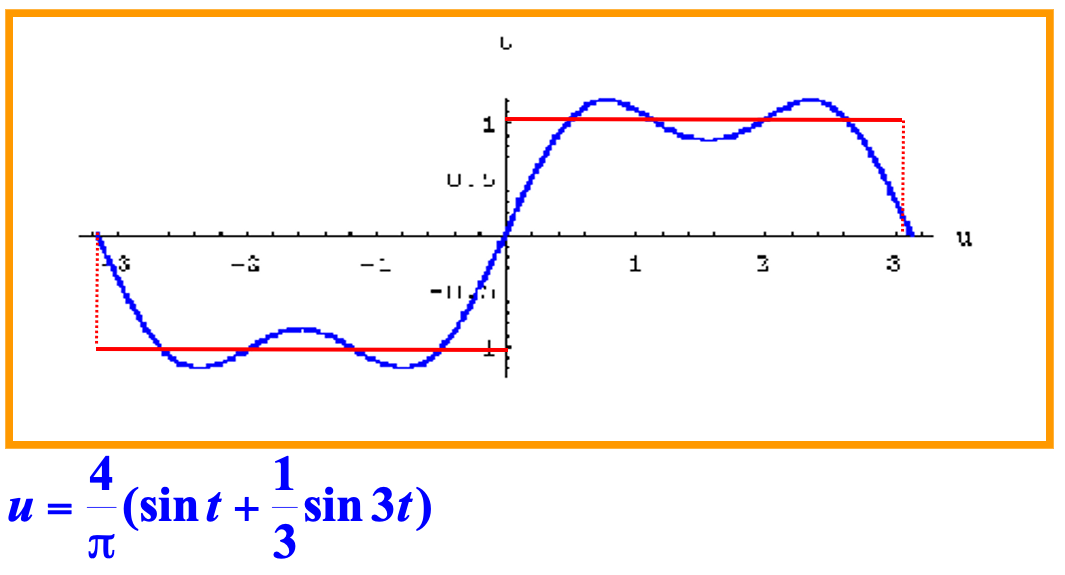
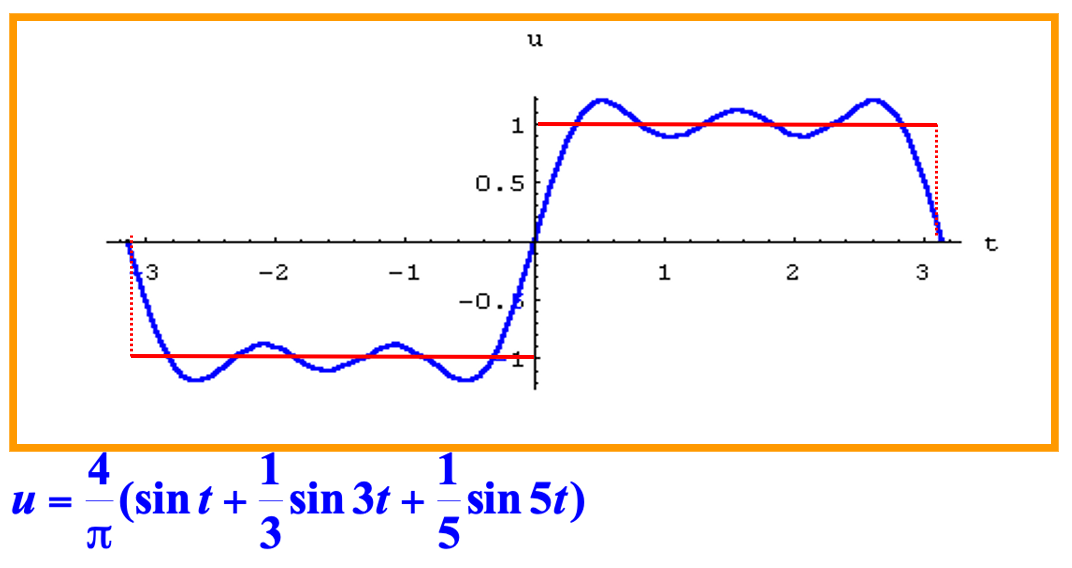
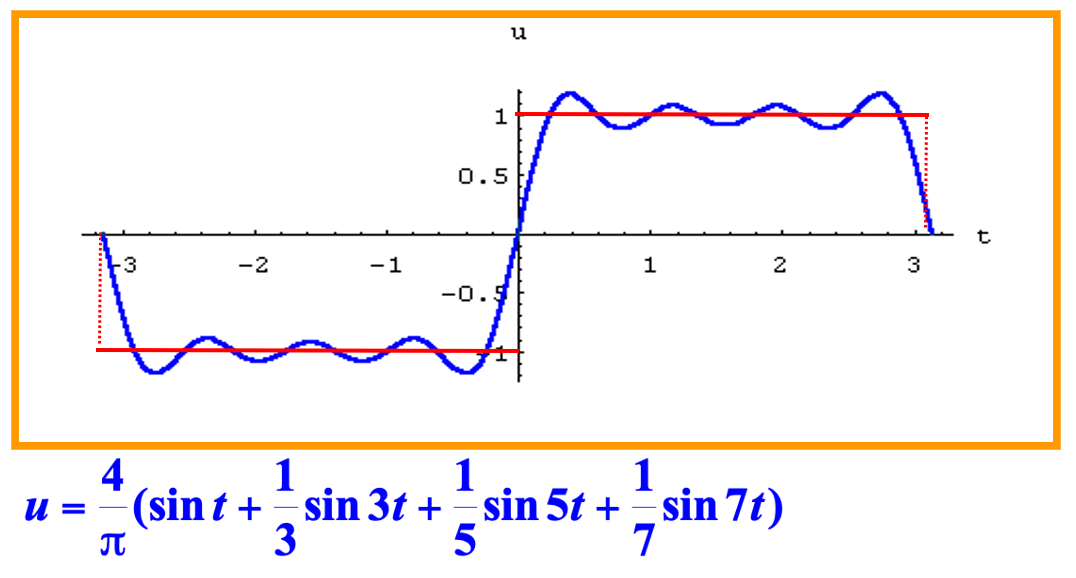
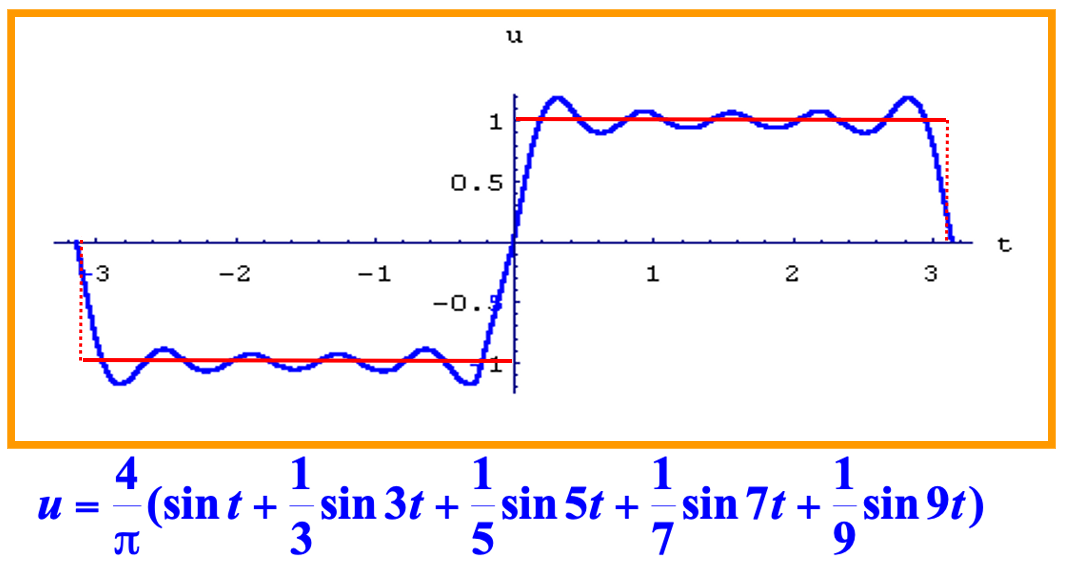
三角函数可以表示一些简单的周期现象,即简谐振动。物理学上可以将一个周期运动分成若干个简谐振动的叠加:
注:课件里还有一些关于复数和三角函数的背景知识介绍,由于这些内容早在高中学过了,所以就不放在笔记里了。
Fourier Series⚓︎
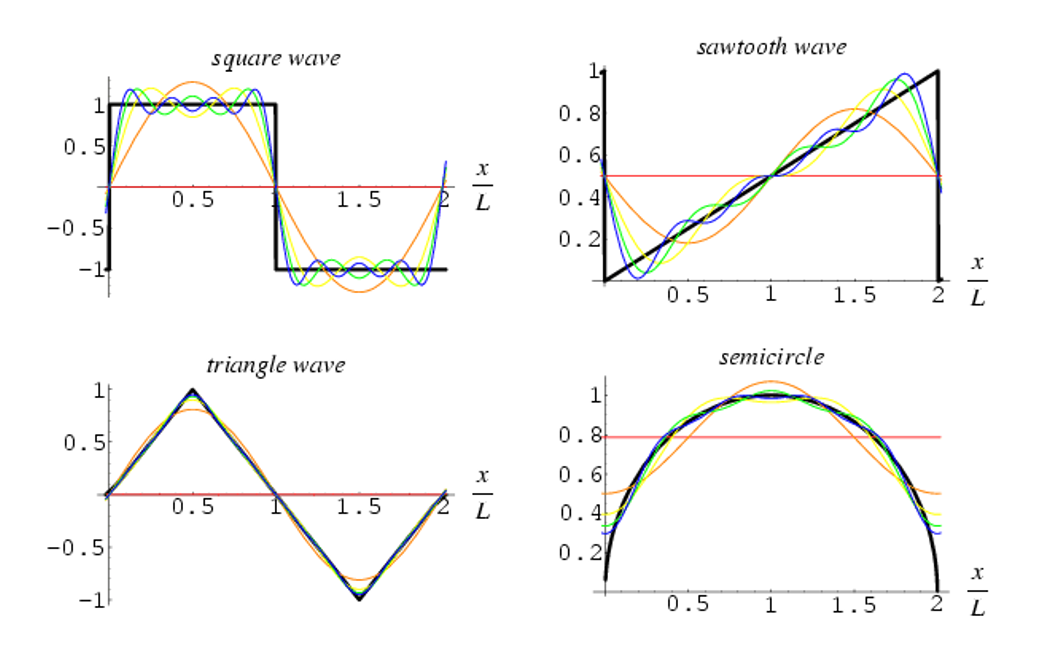
18 世纪中叶,法国数学家傅里叶在研究热传导问题时,找到了三角函数的无限线性组合表示有限区间上的一般函数的方法,即把函数展开成三角级数:
其中:
- \(a_0 = \dfrac{1}{\pi}\int_{-\pi}^{\pi} f(x) \text{d}x\)
- \(a_n = \dfrac{1}{\pi}\int_{-\pi}^{\pi} f(x) \cos (nx) \text{d}x\)
- \(a_n = \dfrac{1}{\pi}\int_{-\pi}^{\pi} f(x) \sin (nx) \text{d}x\)
Fourier Transform⚓︎
傅里叶变换(Fourier transform) 是一种对于在有限区间内的复杂傅里叶级数的泛化。
- 傅里叶分析 = 频率域的分析,频率与 \(\sin (nx), \cos (nx)\) 中的 \(n\) 成正相关
- 傅里叶分析的一个缺点是正弦波和余弦波是无限长的,因此对于特定信号的分析,使用小波 (wavelet) 分析的方法更加合适
-
对于非周期函数 , 如果函数 \(f(x)\) 只在区间 \([-\pi, \pi]\) 上 , 也可展开成傅氏级数(用到周期延拓的方法)
-
应用:
- 生物统计学:假虹膜检测
- 计算机图形学:抗锯齿
Image Transform⚓︎
很多时候,相比在一般的空间域 (spatial domain) 内,在变换域(transformed domain) 内完成图像处理任务可能取得更好的效果。
图像变换的步骤为:
- 转换图像
- 在变换域内执行处理任务
- 通过逆变换 (inverse transform) 将图像还原到原来的空间域内
在变换图像的过程中会用到这些变换核(transformation kernels):
- 前向变换 (forwarding transform):
- 逆变换:
Continuous Fourier Transform⚓︎
图像的频率:
- 低频对应变化缓慢的像素信息,比如连续的表面等
- 高频对应变化迅速的像素信息,比如物体的边缘等
连续型的傅里叶变换是指将一个信号(或函数)从空间域变换到频率域上。
- 前递 FT:\(F(f(x)) = F(u) = \int_{-\infty}^{+\infty} f(x) e^{-\bm{j} 2\pi ux} \text{d}x\)
- 逆 FT(IFT):\(F^{-1}(F(u)) = f(x) = \int_{-\infty}^{+\infty} F(u) e^{\bm{j} 2\pi ux} \text{d}u\)
其中 \(e^{\pm \bm{j} \theta} = \cos \theta \pm \bm{j} \sin \theta\)
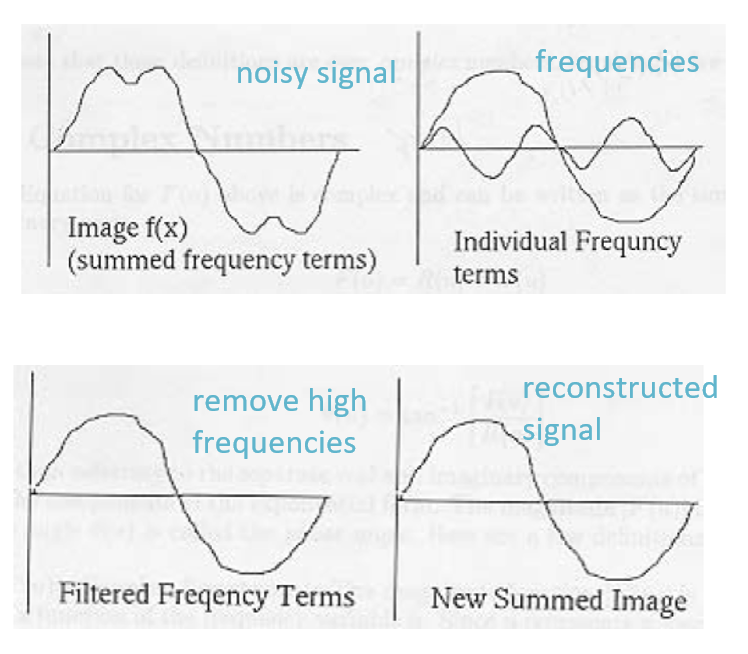
利用连续型 FT 实现频率滤波 (frequency filtering) 的步骤:
- 获得函数 \(f(x)\) 的傅里叶变换 \(F(f(x))\)
- 去除不想要的频率:\(D(F(f(x)))\)
- 还原回原来的信号:\(f(x) = F^{-1}(D(F(f(x))))\)
Discrete Fourier Transform⚓︎
- 前向 DFT:\(F(u) = \sum\limits_{x=0}^{N-1} f(x) e^{-\frac{\bm{j} 2 \pi ux}{N}}, u = 0, 1, \dots, N - 1\)
- 逆 DFT:\(f(x) = \dfrac{1}{N}\sum\limits_{u = 0}^{N - 1}F(u) e^{\frac{\bm{j} 2\pi ux}{N}}, x = 0, 1, \dots, N - 1\)
Fast Fourier Transform⚓︎
由于离散傅里叶变换的计算中有很多重复的内容,如果可以避开这些冗余的计算,就可以加快傅里叶变换的速度。Cooley 和 tukey 于 1965 年提出一种快速傅里叶变换(FFT) 的方法:
- 将原始的 N 点序列依次分解为一系列短序列;
- 求出这些短序列的离散傅立叶变换;
- 组合出所需的变换值;
- 计算量(乘除法
) :\(2N^2 \rightarrow 2N \log N\)
具体来说,处理步骤如下:
- 令 \(W_N^{n, k} = e^{-\frac{\bm{j}2\pi nk}{N}}\),那么原来的 DFT 表示为 \(F(k) = \sum\limits_{n=0}^{N-1}f(n) W_N^{n, k}\)
- 假设 \(N\) 是 2 的正整数幂,令 \(N = 2M\),那么有:
- 通过化简可以得到:
- 若 \(k = M, M + 1, \dots, 2M - 1\),那么:
文字解释:对一个长度为 N 的序列进行傅立叶变换,可以通过将其分成两半计算。对第一部分的计算需要通过计算两个长度为 \(\dfrac{N}{2}\) 长度序列的傅立叶变换式进行,然后利用这两个长度为 \(\dfrac{N}{2}\) 的序列可以得到第二部分的值。
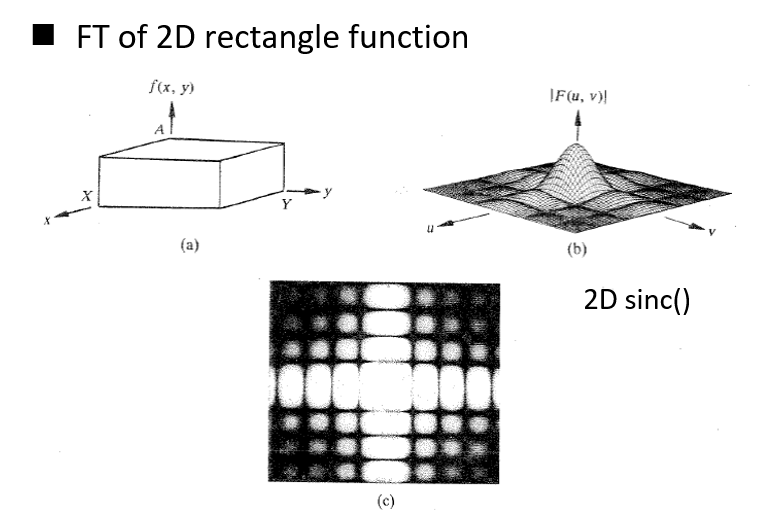
FT in 2D⚓︎
-
连续型:
- 前向 FT:\(F(f(x, y)) = F(u, v) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) e^{-\bm{j} 2\pi (ux + vy)} \text{d}x\text{d}y\)
- 逆 FT:\(F^{-1}(F(u, v)) = f(x, y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} F(u, v) e^{\bm{j} 2\pi (ux + vy)} \text{d}u\text{d}v\)
-
离散型(假设 \(f(x, y)\) 是 \(M \times N\) 的
) :- 前向 FT:\(F(u, v) = \sum\limits_{x=0}^{M-1} \sum\limits_{y=0}^{N-1} f(x, y) e^{-\bm{j}2\pi (\frac{ux}{M} + \frac{vy}{N})}, u = 0, 1, \dots, M - 1, v = 0, 1, \dots, N - 1\)
- 逆 FT:\(f(x, y) = \dfrac{1}{MN} \sum\limits_{u=0}^{M-1} \sum\limits_{v=0}^{N-1} F(u, v) e^{\bm{j}2\pi (\frac{ux}{M} + \frac{vy}{N})}, x = 0, 1, \dots, M - 1, y = 0, 1, \dots, N - 1\)
- 可视化 DFT:一般将 \(|F(u, v)|\) 的值进行可视化,但是一般情况下它的动态范围过大,因此需要进行适当的放缩(利用公式 \(D(u, v) = c \log(1 + |F(u, v)|)\),其中 \(c\) 为常数
) :
例子
评论区