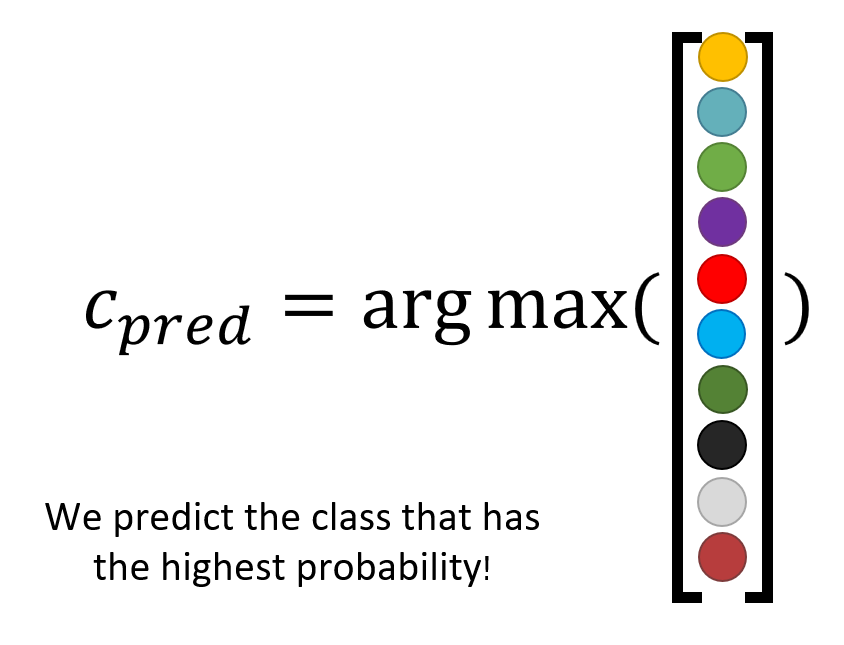Chap 8: Deep Learning⚓︎

Introduction⚓︎

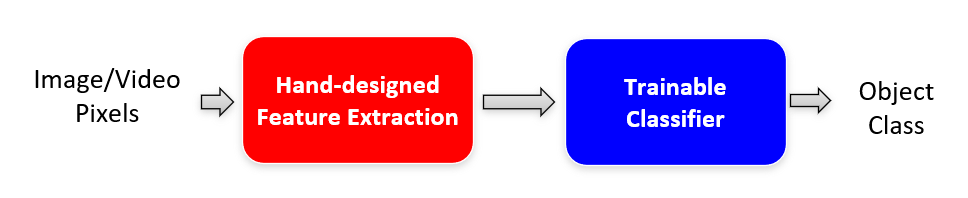
传统的识别方法：

• 特征是不可学习或训练的
  • 然而特征是图像识别取得进步的关键
  • 很多对于特定任务的特征都是手工设计的，但是手工需要专家花费巨大的努力
• 分类符 (classifiers) 一般是可训练的，比如 SVM，HMM 等

学习特征的原因：

• 找到对于具体识别任务中更适合的特征，以取得更好的表现
• 对于难以通过手工设计特征的领域而言，学习特征十分有必要，比如 Kinect、视频、多光谱 (multi-spectrum) 等
• 考虑特征的计算时间：
  • 识别过程中一般需要定义和提取大量的特征点
  • 对于大型的数据集而言，花费时间过长（10s 一张图）

特征学习的模型：

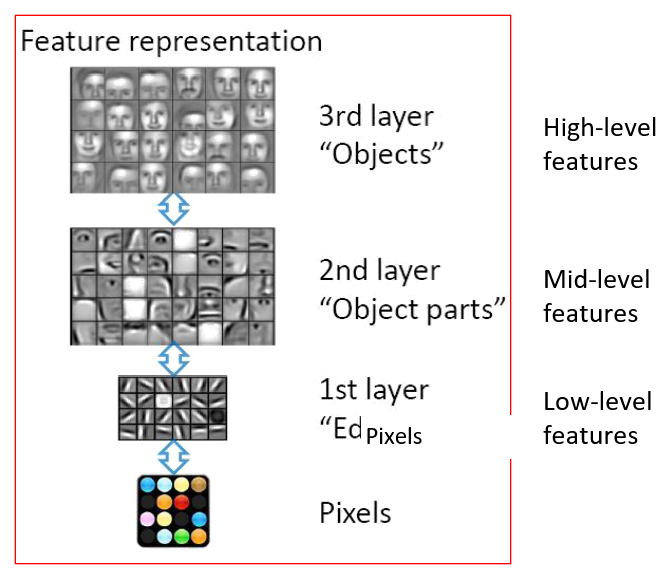
（特征学习 / 深度学习 / 表征学习）关键思想：

• 从数据中学习统计结构和数据的相关性
• 习得的表征 (representation) 可用作识别任务的特征

• 2006 年以来，深度学习在学习特征或表征中越来越流行，原因有：

  • 理论支持：电路设计中的深度 - 广度权衡 (depth-breadth tradeoff)，采用更深层的结构，可以更加高效地表征很多功能

    
    • 深层的结构可被高效地表征
    • 从低层级向高层级的结构传播较为自然
    • 低级的表征可在多个任务间共享

  • 生物学支持：视觉皮层是分层的 (hierarchical)

  • 数据支持：大数据集，方便的收集和存储
  • 硬件支持：GPT、集群

Convolutional Neural Network⚓︎

Basics⚓︎

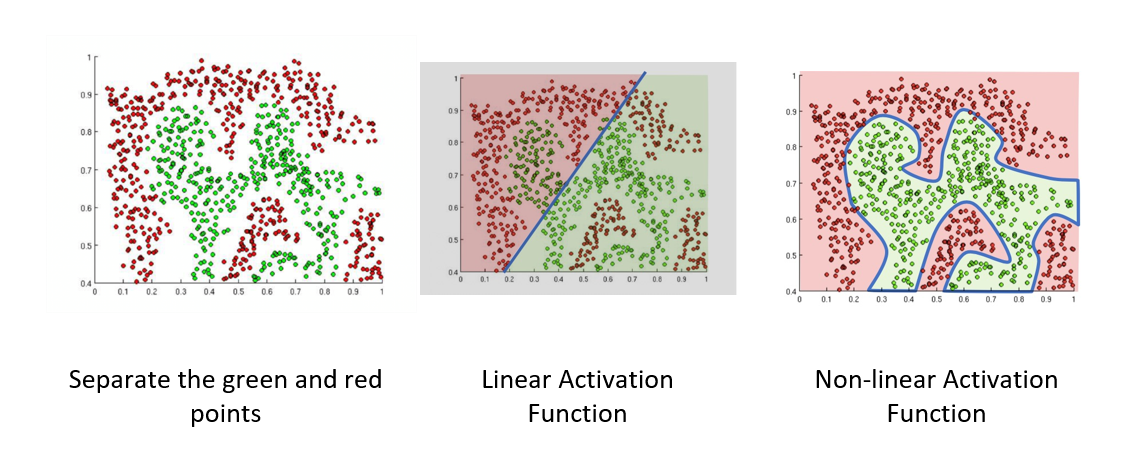
卷积神经网络(convolutional neural network, CNN) 是深度学习中一种著名的方法。

使用 CNN 的原因：

• 是少数能够在监督下训练的深度模型之一
• 易于理解和实现
• 应用广泛：
  • 赢得了很多比赛
  • 被部署于很多实际应用中，包括图像识别、语音识别、Google 和百度的照片标记器 (tagger)
  • 应用于数组数据中（邻近的数据往往是相关的）

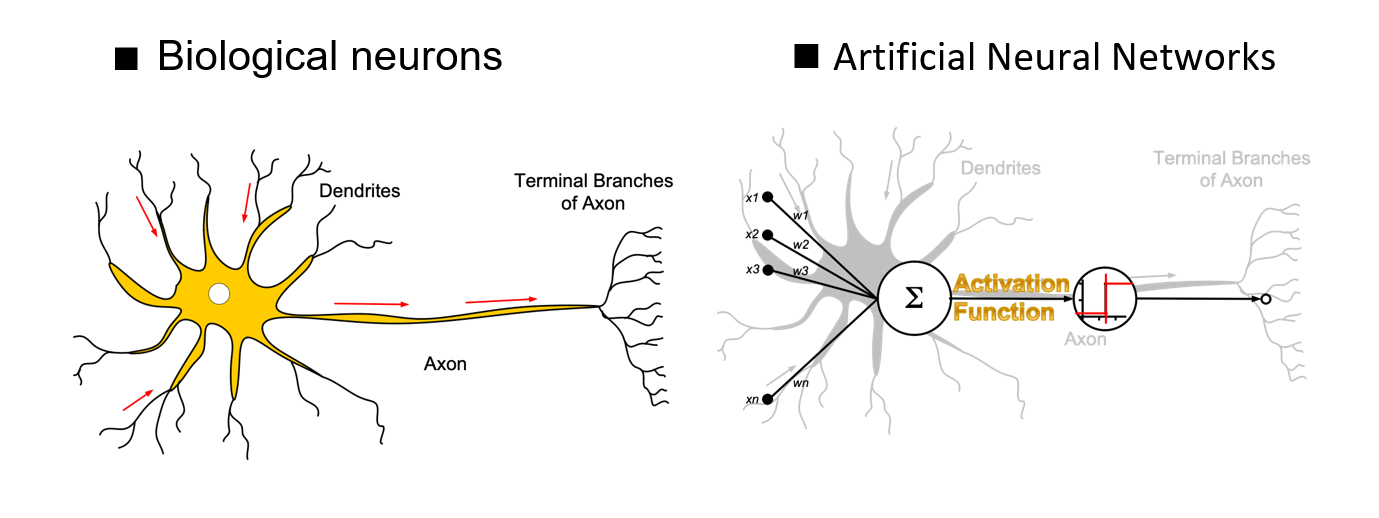
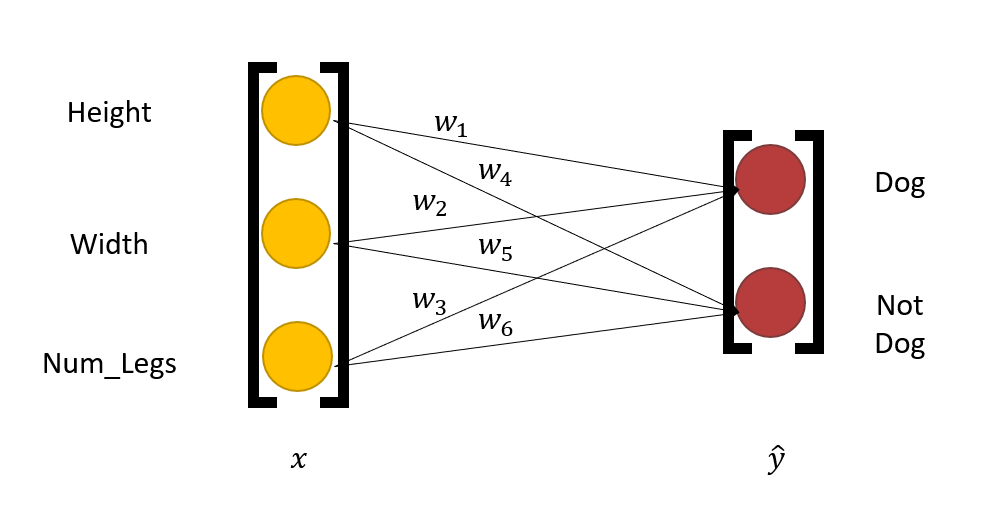
神经元：对突触的观测值连到汇总的地方，并进行加权求和，通过激活函数（归一化后）产生输出，本质上就是一个函数。

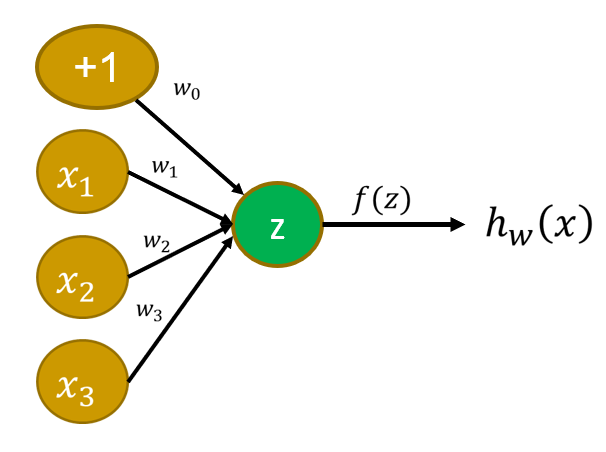
• 输入：\(x_1, x_2, x_3\)
• 输出：\(h_w(x)\)
• 令 \(X = [1\ x_1\ x_2\ x_3]^T, w = [w_0\ w_1\ w_2\ w_3]^T\)，那么 \(z = w^TX = w_0 + w_1x_1 + w_2x_2 + w_3x_3\)
• \(h_w(x) = f(z) = f(w^TX)\)

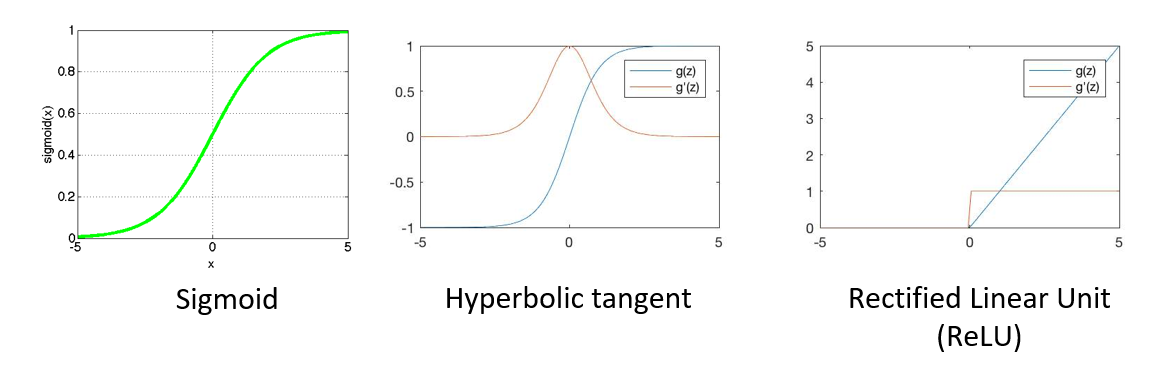
常见的激活函数(activation function) 有：

• S 形 (sigmoid)（逻辑）：\(f(z) = \dfrac{1}{1 + e^{-z}}\)
• 双曲切线 (hyperbolic tangent)：\(f(z) = a \cdot \tanh (b \cdot x)\)
• 平方：\(f(z) = z^2\)
• 线性：\(f(z) = az + b\)
• ReLU：\(f(z) = \max(0, z)\)

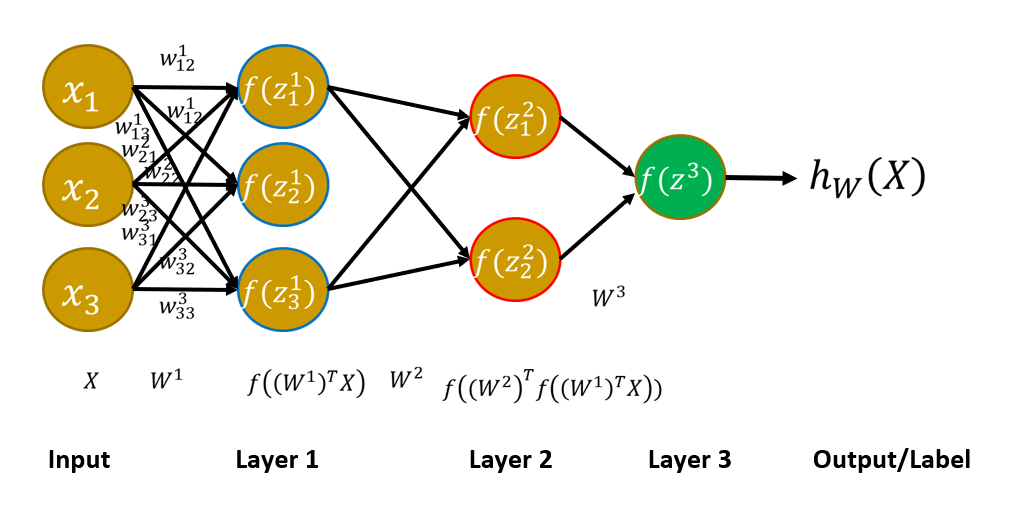
多层神经网络：

求解方法：反向传播(back-propagation, BP)

1. 随机初始化权重，计算 \(h_w(X)\)
2. 计算误差 \(E = (h_w(X) - y)^2\)
3. 根据这个误差值，从最后一层开始向前修改每一层的权重值
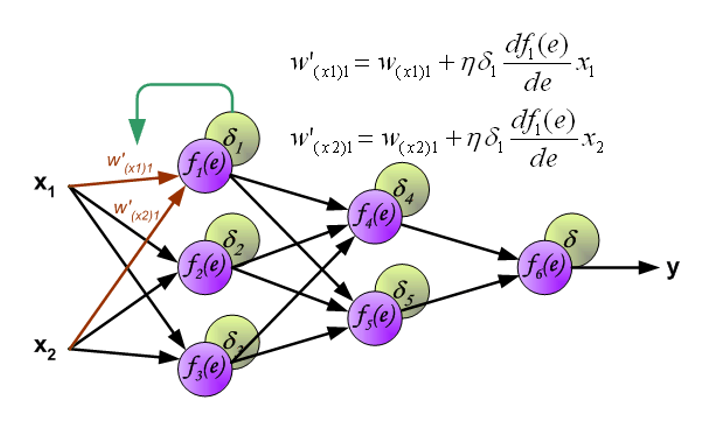
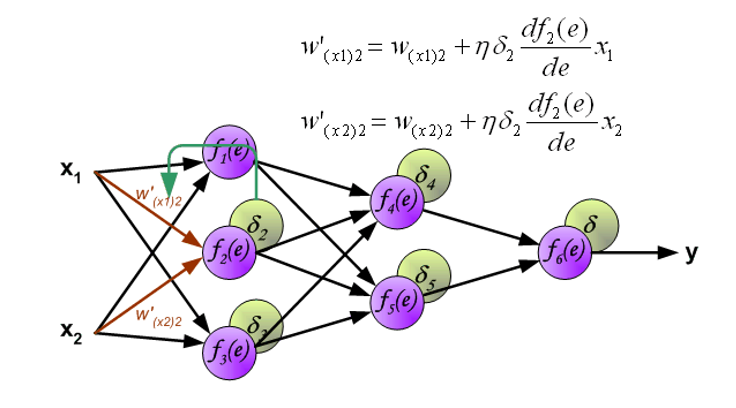
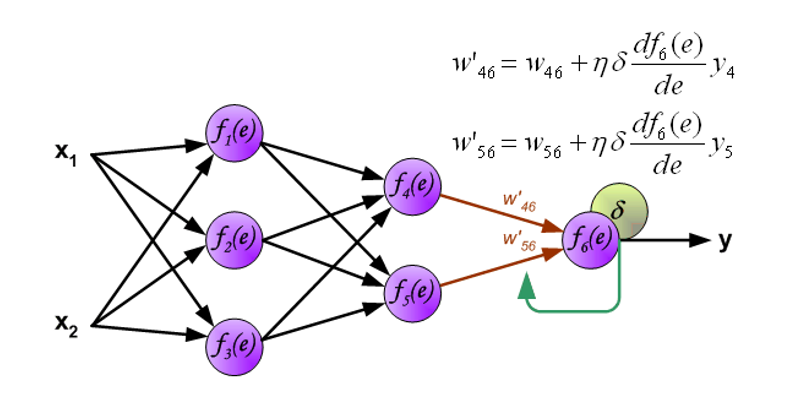
   • 利用递推式 \(W_k = W_{k-1} - \varepsilon \dfrac{\partial E}{\partial w}\)，具体来说，对于第 \(k\) 层的某个权重值 \(w_{ij}\) 而言，\(w_{ij}^{(k)} = w_{ij}^{(k - 1)} - \varepsilon \dfrac{\partial E}{\partial w_{ij}^{(k - 1)}}\)（最后一项由梯度下降法得到，从应试角度来说不必深究其原理）

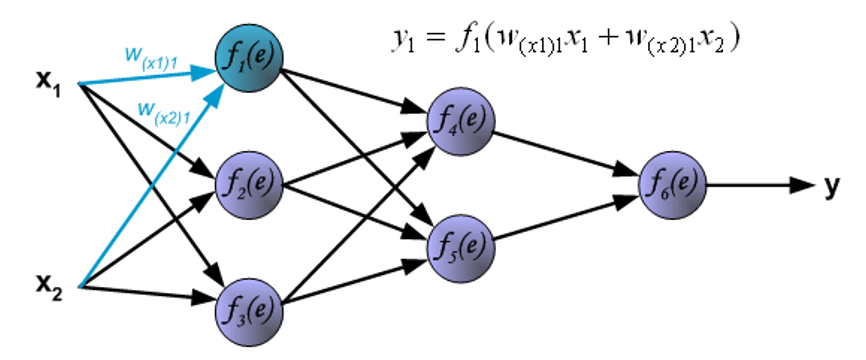
例子

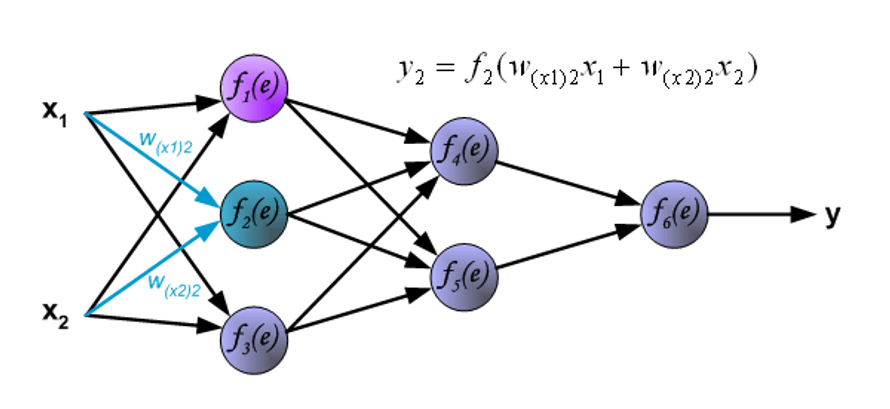
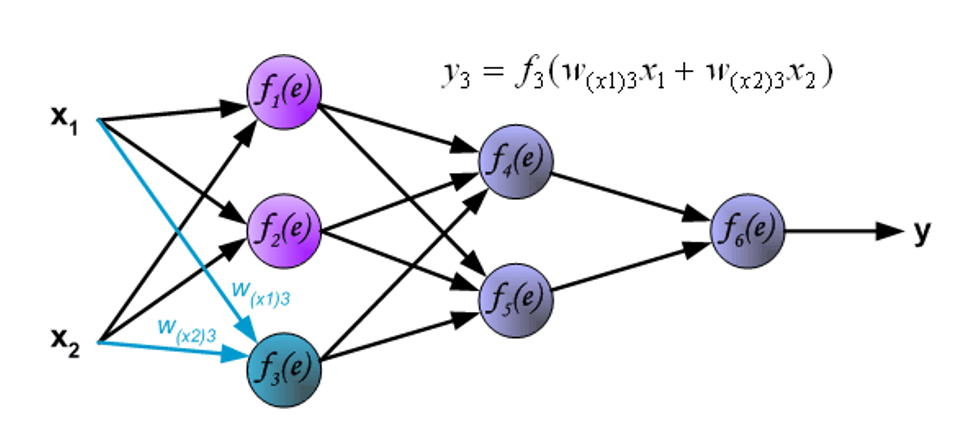
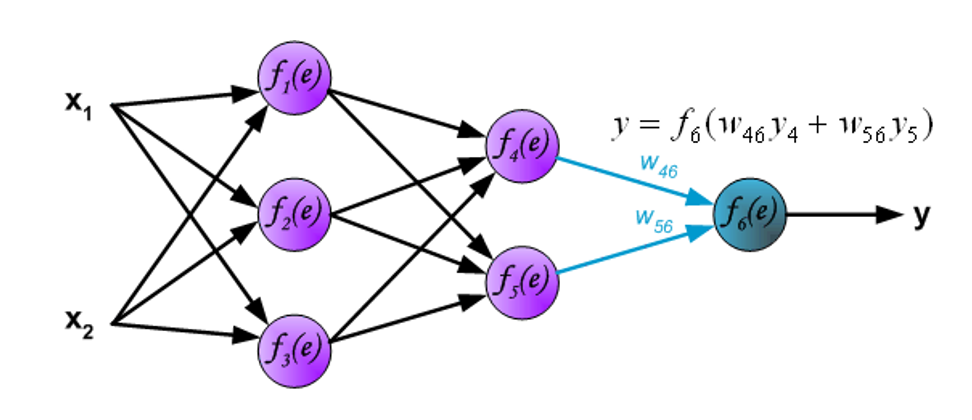
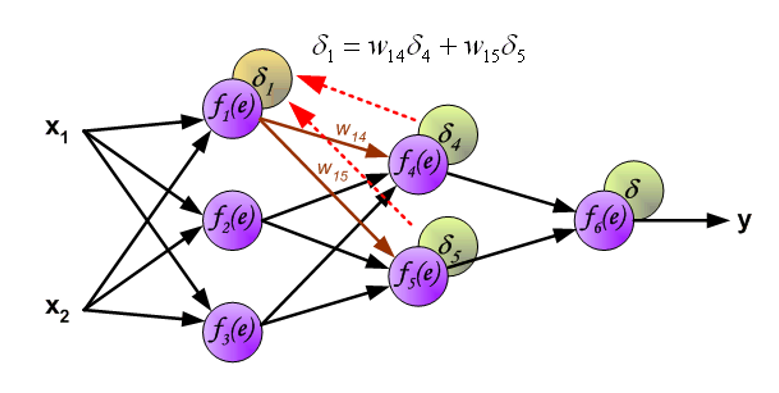
下图展示信号在网络间的传播，\(w_{xm}n\) 表示输入 \(x_m\) 和输入层的神经元 \(n\) 之间的连接的权重，\(y_n\) 表示神经元 \(n\) 的输出信号。

神经元 1 神经元 2 神经元 3

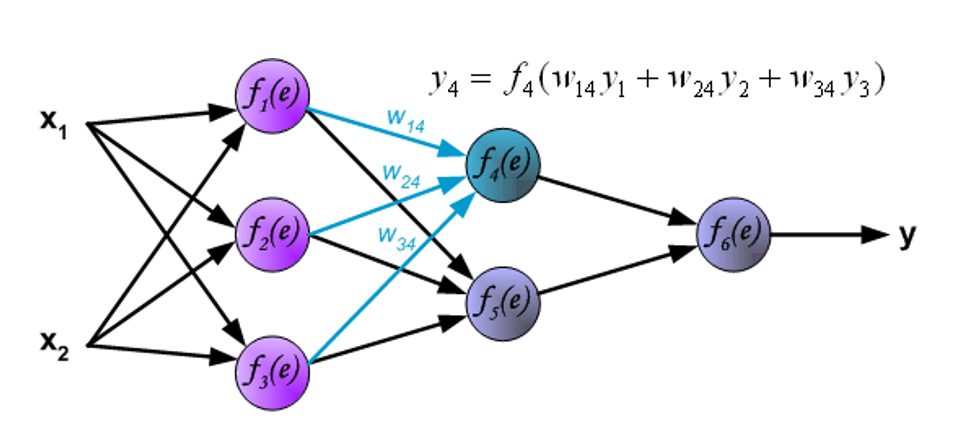
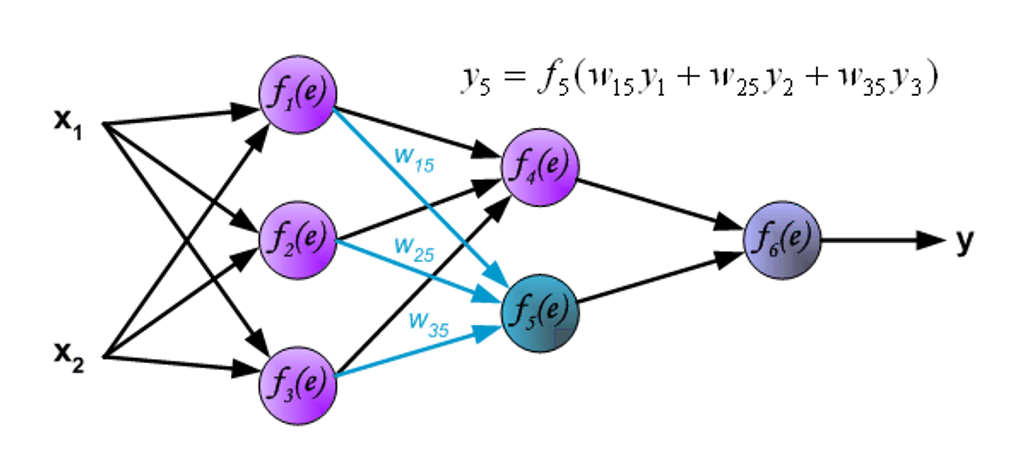
现在进入内层的传播了。\(w_{mn}\) 表示输出神经元 \(m\) 与下一层的输入神经元 \(n\) 之间的连接的权重。

神经元 4 神经元 5

信号被传送到输出层。

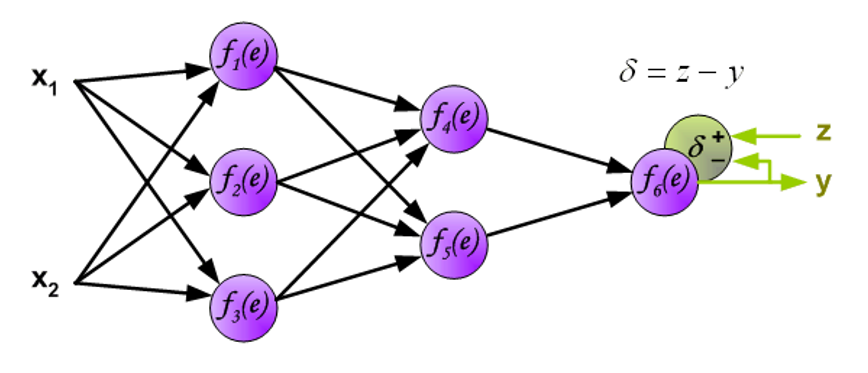
现在将在网络中 \(y\) 的输出信号与预期输出值（目标，来自训练好的数据集）\(z\) 进行比较，它们的差值称为输出层神经元的误差信号 \(d\)。

然后将误差信号反向传递至所有的神经元，此时原来的输出信号将作为输入。

神经元 4 神经元 5

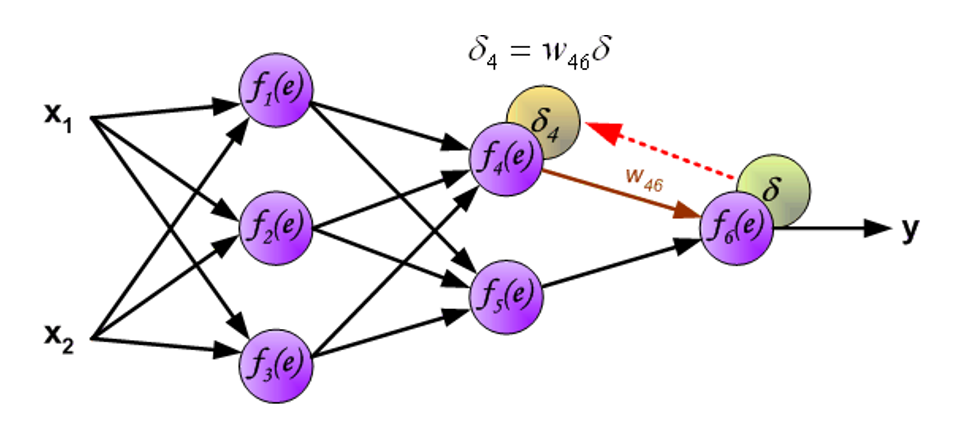
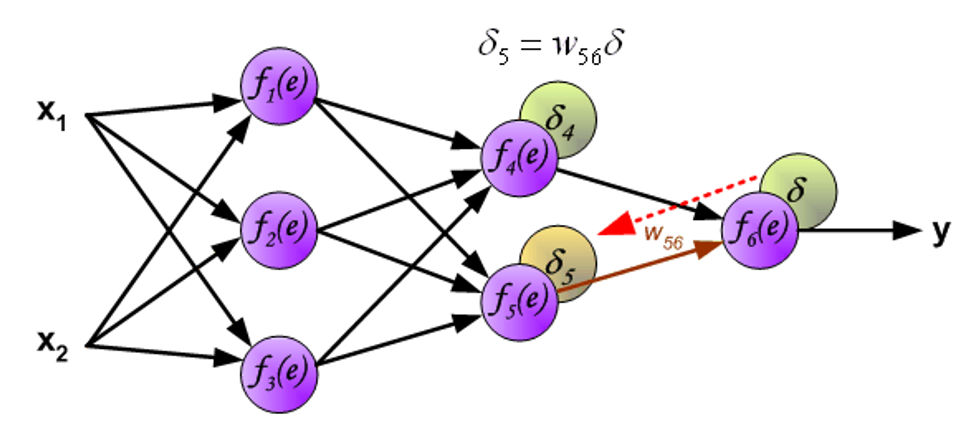
用于反向传递误差的权重系数 \(w_{mn}\) 等于在计算输出值时用到的权重值，改变的只是数据流方向。这种方法可用于所有的网络层。如果被传递的误差来自多个被加入的神经元，那么处理方式如下所示：

当每个神经元的误差计算完毕时，每个神经元输入节点的权重系数可能需要被修改。在下面给出的公式中，\(\dfrac{\text{d}f(e)}{\text{d}e}\) 表示神经元激活函数的导数。

神经元 1 神经元 2 最后

Convolution⚓︎

解决方法：

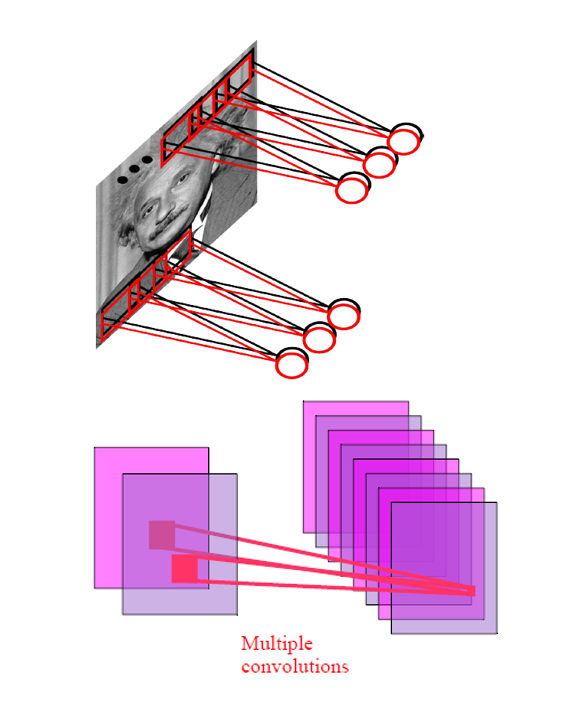
• 卷积：
  • 采用了局部连接，每个神经元其实没有必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部的信息综合起来就得到了全局的信息
  • 权值共享，把每个卷积核当作一种特征提取方式，而这种方式与图像等数据的位置无关。这就意味着，对于同一个卷积核，它在一个区域提取到的特征，由于图像的特征是稀疏的，也能适用于于其他区域

• 池化，降采样，只提取一些重要的特征，经过池化层之后，模型参数会减少很多

• 在图像某个部分有用的特征可能在其他地方也有用（稀疏表征）

例子：\(200 \times 200\) 的图像

• 10 个大小为 \(10 \times 10\) 的滤波器
• 10 张大小为 \(200 \times 200\) 的特征图
• \(400000\) 个内部单元，有 \(10 \times 10\) 个字段 = \(1000\) 个参数

因此计算量得到减小！

为何用 10 个滤波器

• 在每个位置上检测多个图案 (motifs)
• 关注相同区域的一组单元与这块区域对应的特征向量 (feature vector) 是相似的
• 结果是一个 3D 数组，每一个切片是一个特征图

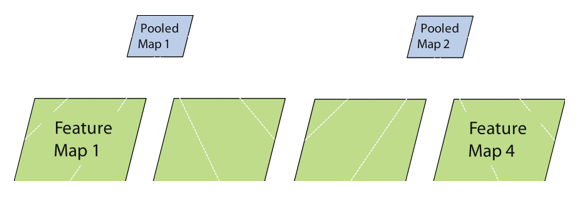
Pooling⚓︎

池化(pooling) 是 CNN 中用于对特征图进行降维和信息提取的操作（降采样），通过减少数据量，提高了模型的计算效率，并保留主要特征，同时增强了特征的不变性（包括平移、旋转、尺度等）。

• 空间池化

  • 池化窗口的区域可以重叠，也可以不重叠
  • 分类：
    • 平均池化：在池化窗口中计算所有元素的平均值作为输出
    • 最大池化：在池化窗口中选择最大值作为输出
  
  • 通常结合二次抽样 (subsample)

• 根据特征图池化

  • 跨特征比较的额外形式
  • 最大池化
  • 应用
    • 找到唯一特征
    • 减少变体
  

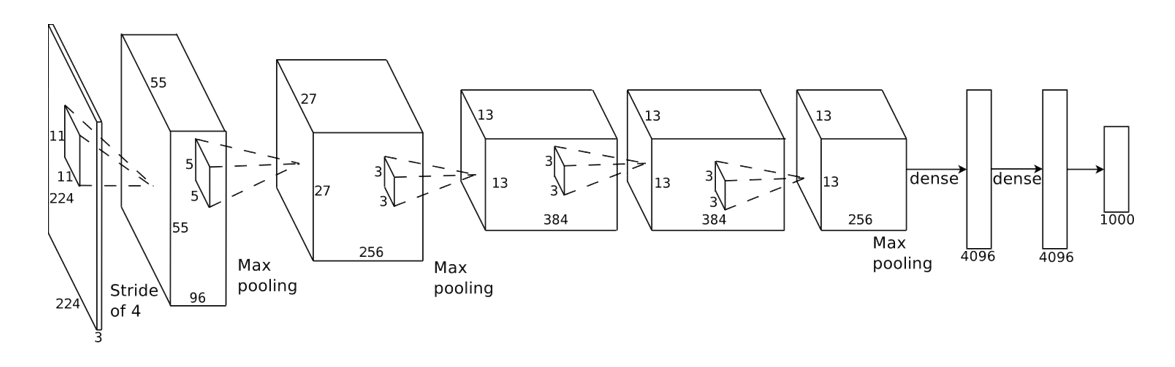
Cuda-convnet⚓︎

• 尽管卷积和池化 / 二次采样能够有效减少变体，但是训练 CNN 耗时太久，因此采用 cuda-convnet 这一改进方法
• 代码：cuda-convnet

• 特征：

  • 用两个英伟达的 GPU，并使用梯度下降法进行训练，需要花一周的时间（@ImageNet）
  • 650,000 个神经元
  • 60,000,000 个参数
  • 七个内含“权重”层
  • 最终的特征层：4096 维
  • 圆圈表示卷积层：使用一组 3D 滤波器对输入进行卷积，然后应用 S 型激活函数
  • 方框表示全连接层：对输入应用线性滤波器，然后应用 S 型激活函数
  

• 过程：

Input -> C1C1 -> C2C2 -> C3C3 -> C4 -> C5C5 -> F6F6 -> F7 -> Output

Convolution-based Classification Algorithm⚓︎

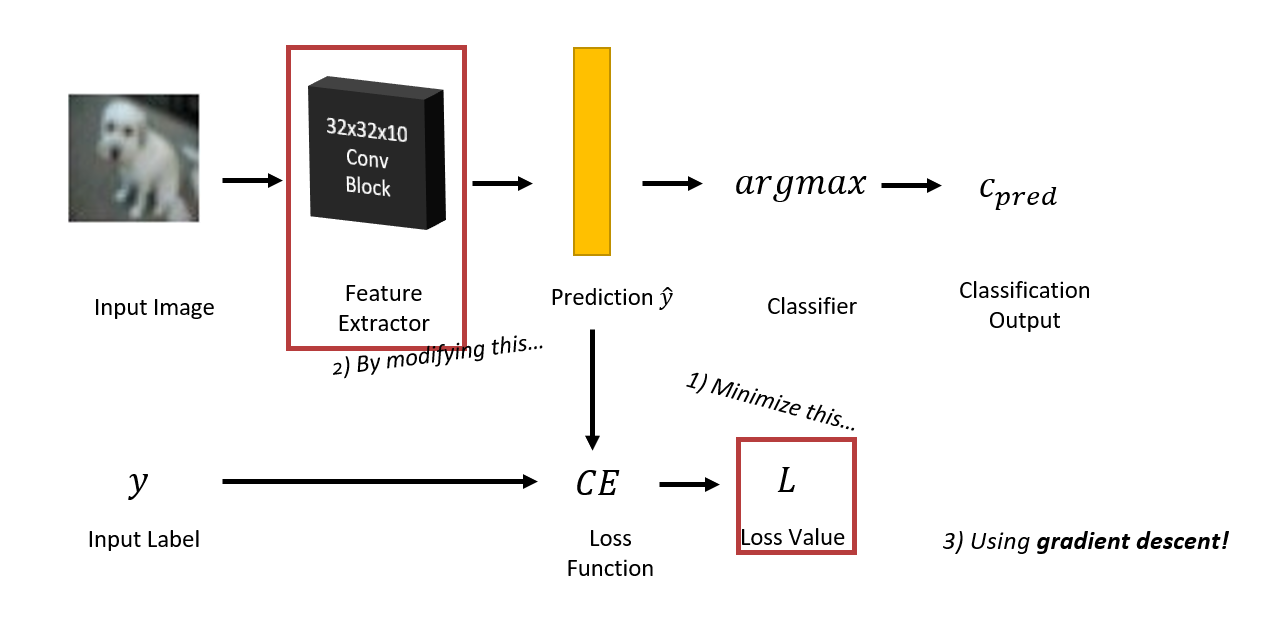
将卷积的特征提取功能与分类算法的图像分类相结合，我们得到了一种基于卷积的分类(classification) 算法。

完整的工作流：

• 分类器会从特征提取器中挑选分数最高的结果作为分类依据

  

• 特征提取器 (feature exactor)

  • 先来看特征提取器的功能：

    
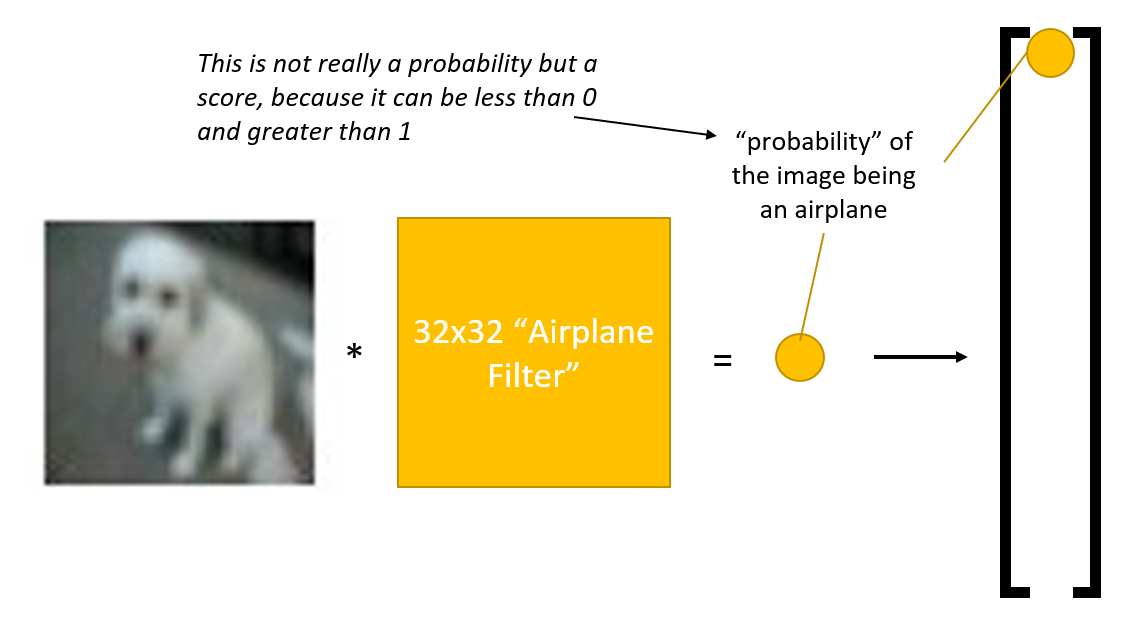
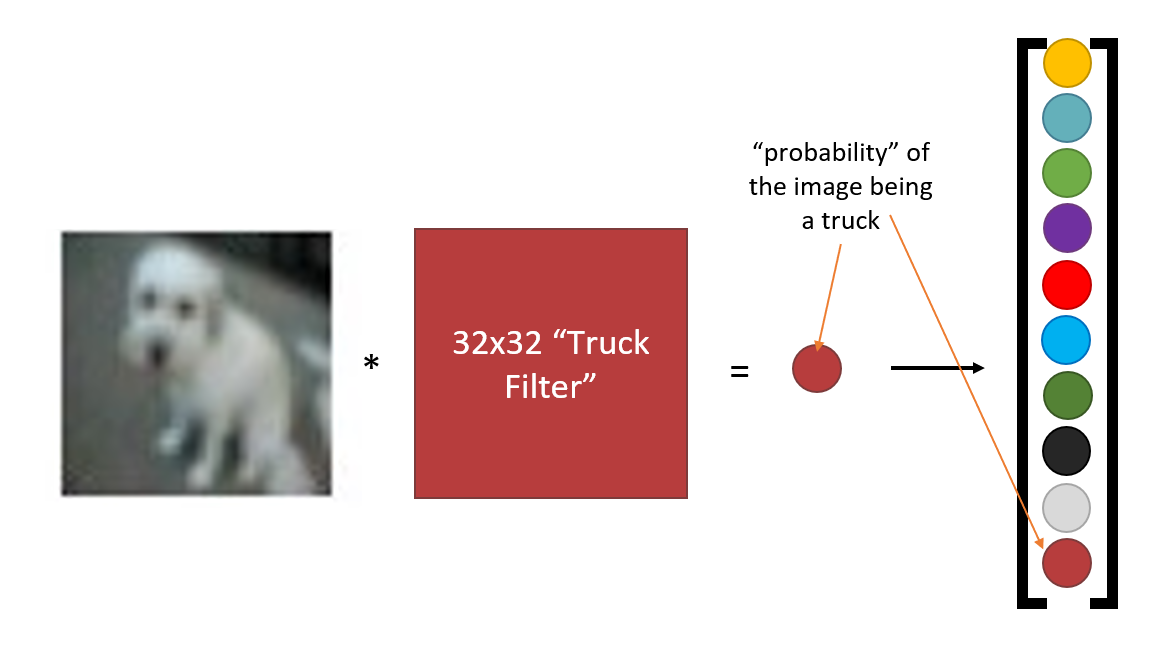
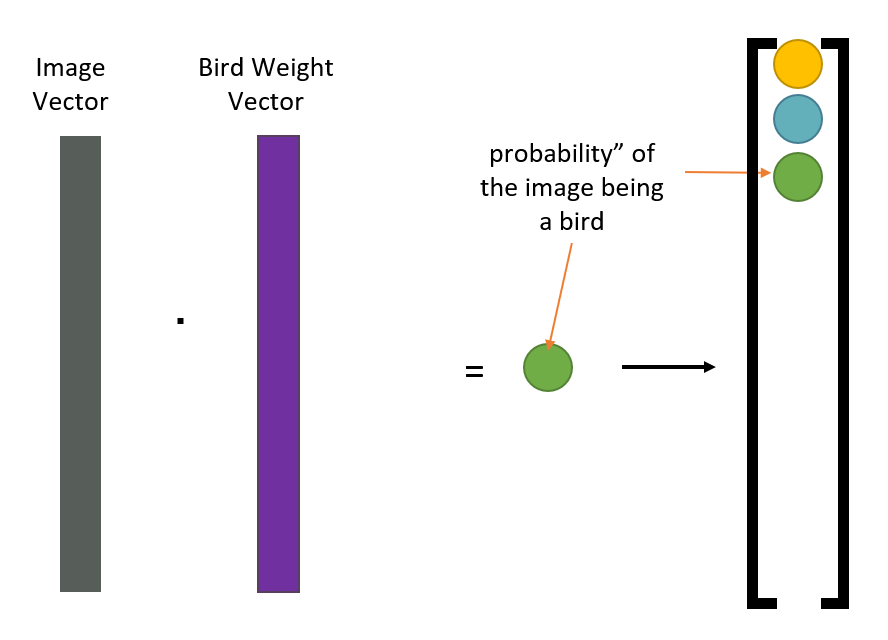
    • 对于一张图片，需要使用多种不同的滤波器，每个滤波器代表一类图像，图片与滤波器的运算结果是一个“概率”值，但是这个“概率”可以 <0 或 >1，因此更确切的说法是“分数”
    • 最终结果（得到一组概率值，构成一个一维向量）：
    

    • 更抽象的理解：

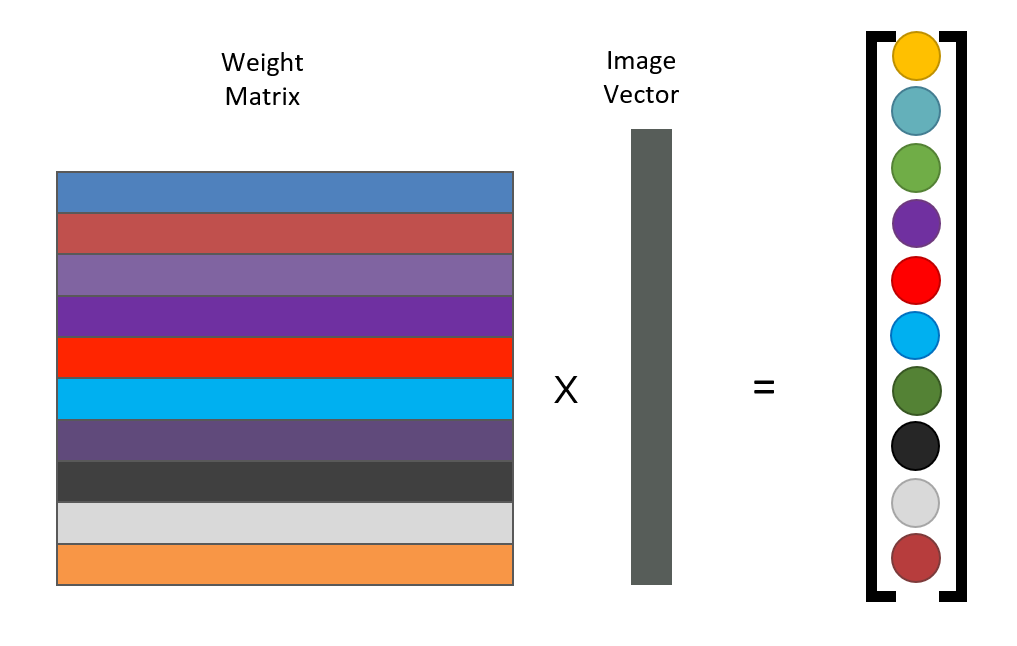
      • 单个滤波器的计算：向量乘法
      
      • 多个滤波器的计算：矩阵乘法
      

      • 用公式表示为：\(Wx = \hat{y}\)

        • \(W\)：由权重向量构成的矩阵
        • \(x\)：图像（向量）
        • \(y\)：由一系列“概率”值的向量
        • \(Wx\) 的计算被称为全连接层(fully-connected layer)
        

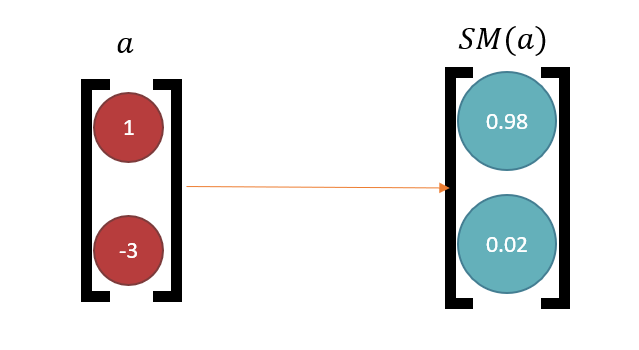
    • 但我们希望能够得到真正的概率（在 0-1 之间），且这些概率之和为 1。解决方案是使用 softmax 函数：\(a(x)_i = \dfrac{e^{x_i}}{\sum_j e^{x_j}}\)，效果如下所示：

    

    原公式变为：\(\hat{y} = SM(Wx)\)

• 我们还希望预测值尽可能接近真实值，即 \(\text{arg max}(\hat{y}) = \text{arg max}(y)\)

  • 解决方案：\(W^* = \text{arg min}(-\sum\limits_{x, y}\log(p_c))\)，其中 \(p_c\) 是 \(\hat{y}\) 是真实值的概率
  • 令损失 \(L = -\log(p_c)\)，当 \(L\) 越大时，\(p_c\) 值越小，即预测值更不准，所以需要尽可能地减小 \(L\)
  • 减小 \(L\) 的方法：梯度下降法(gradient descent)，梯度通过上面介绍过的反向传播 (back propagation) 获得

评论区