Lec 2: Relational Model⚓︎
约 3972 个字 预计阅读时间 20 分钟
核心知识
- 基本概念(一些名词)
- 键:超键、候选键、主键、外键
- 关系代数【重点
! 】 :务必记住各种运算的含义和书写,可以和下面几讲的 SQL 搭配食用
Structure of Relational Databases⚓︎
- 关系型数据库(relational database):一组由单个或多个基于关系模型的关系构成的容器。
-
关系模型(relational model):一种基于关系定义的数据库抽象,以避免维护的开销。
- 它的关键点在于:
- 用简单的数据结构(关系)存储数据库
- 物理存储由 DBMS 实现
- 通过高级语言访问数据,DBMS 会帮我们找到最佳的执行策略
- 结构上,数据库关系及其内容的定义和它们的物理表示独立
- 完整性上,它能够确保数据库满足指定的约束(constraints)
- 操作上,它提供了访问和修改数据库内容的编程接口
- 它的关键点在于:
-
关系(relations):一个无序集合,里面包含了表示实体的属性的联系。
- 关系的数学定义为:对于给定的集合 \(D_1, D_2, \dots, D_n(D_i = a_{ij}|_{j=1 \dots k})\),关系\(r\) 为笛卡尔积 \(D_1 \times D_2 \times \dots \times D_n\) 的子集。
- 笛卡尔积可以用一张二维表表示
- 元组(tuple) 是关系中的一组属性值。关系是一个由 n 元组 (n-tuples) \((a_{1j}, a_{2j}, \dots, a_{nj})\) 构成的集合,其中 \(a_{ij} \in D_i\)
-
属性(attributes)
- 关系内的每个属性都有一个名称
- 每个属性的允许值的集合被称为属性的域(domain)
-
属性值(通常)要求具备原子性(atomic),即不可分割 (indivisible)(满足第一范式 (1st NF))
- 多值 (mutlivalued) 属性、复合 (composite) 属性到不具备原子性
-
特殊值 null 是所有域的成员,它使得很多运算的定义变得复杂,因此在实践中我们希望尽可能地消除它
-
关系是无序的(unordered)
- 元组的顺序没有意义,可按任意顺序被存储
- 同一个关系内,不能存在重复的元组
-
联系(relationship):多个实体之间的关联
Database Schema⚓︎
关系的两大概念:
- 关系模式(relation schema):描述关系的结构,包含了一系列的属性及其对应的域
- 假如有属性 \(A_1, A_2, \dots, A_n\),那么 \(R = (A_1, A_2, \dots, A_n)\) 就是关系模式,而 \(r(R)\) 就是在关系模式 \(R\) 上的一个关系
- 关系模式基本上不太会变化
- 关系实例(relation instance):在某个时刻上,对关系内的数据的快照 (snapshot)
- 关系上的当前值(即关系实例)会在表格中具体指明,且会随着关系的更新而改变
- 关系 \(r\) 的元素 \(t\) 是一个元组,在表格上就是一行的记录;可用 \(t[name]\) 表示 \(t\) 在 \(name\) 属性上的值
Keys⚓︎
键(keys):令 \(K \subseteq R\),有以下几类键:
- 超键(superkey):对于每个可能的关系 \(r(R)\),\(K\) 能识别出唯一的元组。也就是说,对于元组 \(t_1, t_2 \in r\) 且 \(t_1 \ne t_2\),那么 \(t_1.K \ne t_2.K\)
- 候选键(candidate key):最小数量的超键,也就是说候选键的子集无法构成超键
- 主键(primary key):是一种候选键,且由数据库设计者显式选择的键(通常用下划线标出)
- 主键也被称为主键约束(primary key constraints)
- 被选中作为主键的属性的值不能或者很少发生改变
- 如果关系中没有定义主键的话,有些 DBMS 会(通过一个 ID 列)自动创建一个内部的主键
- 外键(foreign key):用于指明来自一个关系的属性映射到另一个关系的元组上
- 假设存在关系 \(r(A, B, C), s(B, D)\),关系 \(r\) 的属性 \(B\) 是参照 \(s\) 的外键,其中 \(r\) 是参照关系(referencing relation),\(s\) 是被参照关系(referenced relation)
- 参照关系中外码的值必须在被参照关系中实际存在或为 null
- 在外键约束中,被参照的属性必须是被参照关系的主键
注意
上述这些键都有可能包含多个属性,不要以为主键一定只包含一个属性!
约束(constraints):用户定义的条件,数据库里的所有实例都必须遵守。
- 能够验证单个元组乃至整个关系的有效性
- DBMS 会阻止任何违背约束的修改
唯一键和参照键是最常用的约束。
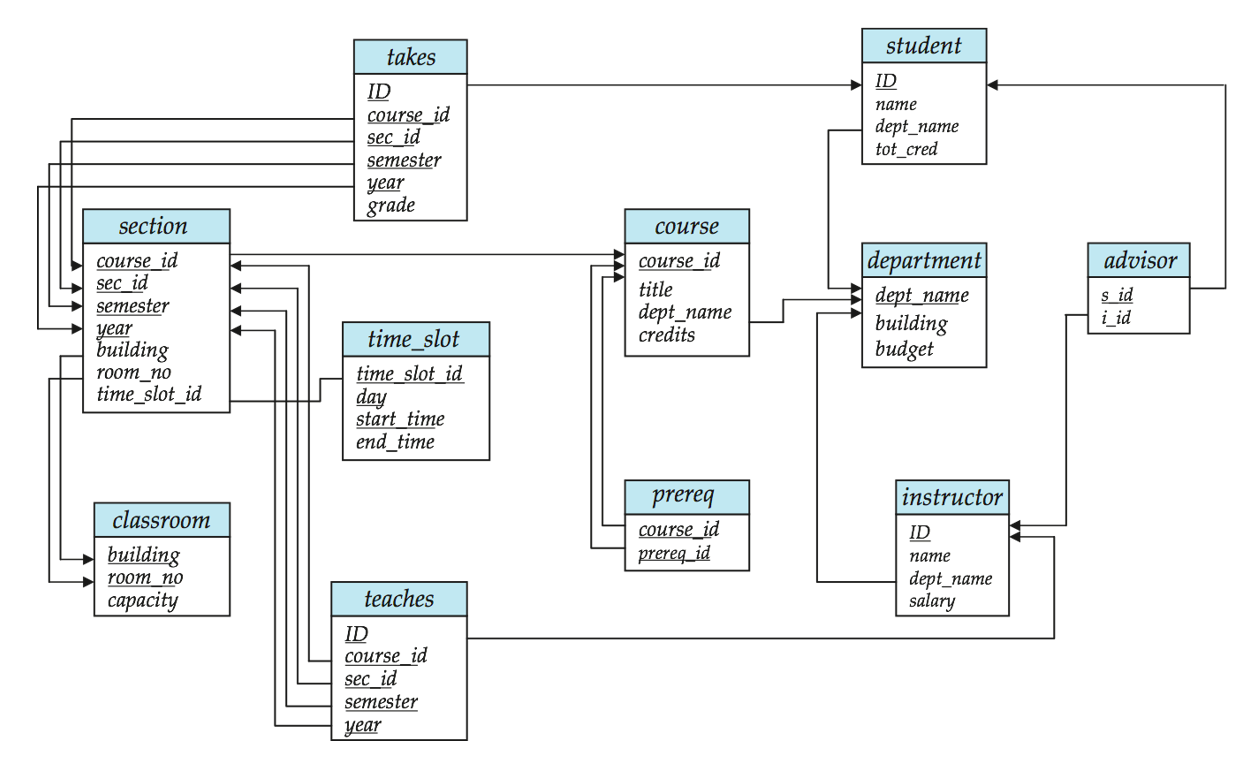
Schema Diagrams⚓︎
在模式图中,
- 主键用下划线表示出来
- 外键约束用一根从参照关系指向被参照关系的箭头表示
- 参照完整性约束用一根双头箭头表示
Relational Query Languages⚓︎
查询语言(query language):用户用于请求数据库信息的语言,可以被归类为:
- 必要查询语言(imperative query language):
- 用户指示系统来执行一些在数据库上的具体操作,以计算预期结果
- 通常有状态变量的概念,随计算过程而更新
- 功能查询语言(functional query language):
- 计算被表示为可能在数据库的数据上,也可能在其他函数的结果上执行操作的函数评估
- 函数没有副作用,因此无需更新程序状态
- 声明查询语言(declarative query language):
- 用户并不通过一系列的函数调用来描述想要的信息,而是通过数学逻辑来描述
“纯”语言 (pure language):简洁而形式化,缺乏语法糖,但是能阐明从数据库获取数据的基本技术。有以下几类纯语言:
- 关系代数(relational algebra):SQL 的基础
- 元组关系演算(tuple relational caculus)
- 域关系演算(domain relational calculus)
Relational Algebra⚓︎
关系代数(relational algebra):用于检索和操纵关系中元组的基本运算(基于集合代数
- 同时也从高层级定义了计算查询的顺序
关系代数的运算符包括:
- 单目运算:
- 选择(select)
- 投影(project)
- 重命名(rename)
- 双目运算:
- 并(union)
- 交(intersection)
- 差(set difference)
- 笛卡尔积(Cartesian product)
- 自然连接(natural join)
- 除(divide)
这些运算符可以形成一条“链”,组成更复杂的运算。
关系运算的优先级
- 投影
- 选择
- 笛卡尔积(乘法)
- 连接、除法
- 交
- 并、差
注
- 数据库系统不允许用户直接用关系代数来编写查询语句
-
虽然在数学中,关系不得有重复的元组,但是数据库系统的表格允许重复元组的出现,除非指定约束来禁止
- 在关系代数中引入多重集(multiset) 的概念,以接纳重复元组的情况,在下一讲中会介绍
-
上述的关系代数运算可以组合在一起,形成关系代数表达式(relational-algebra expression)
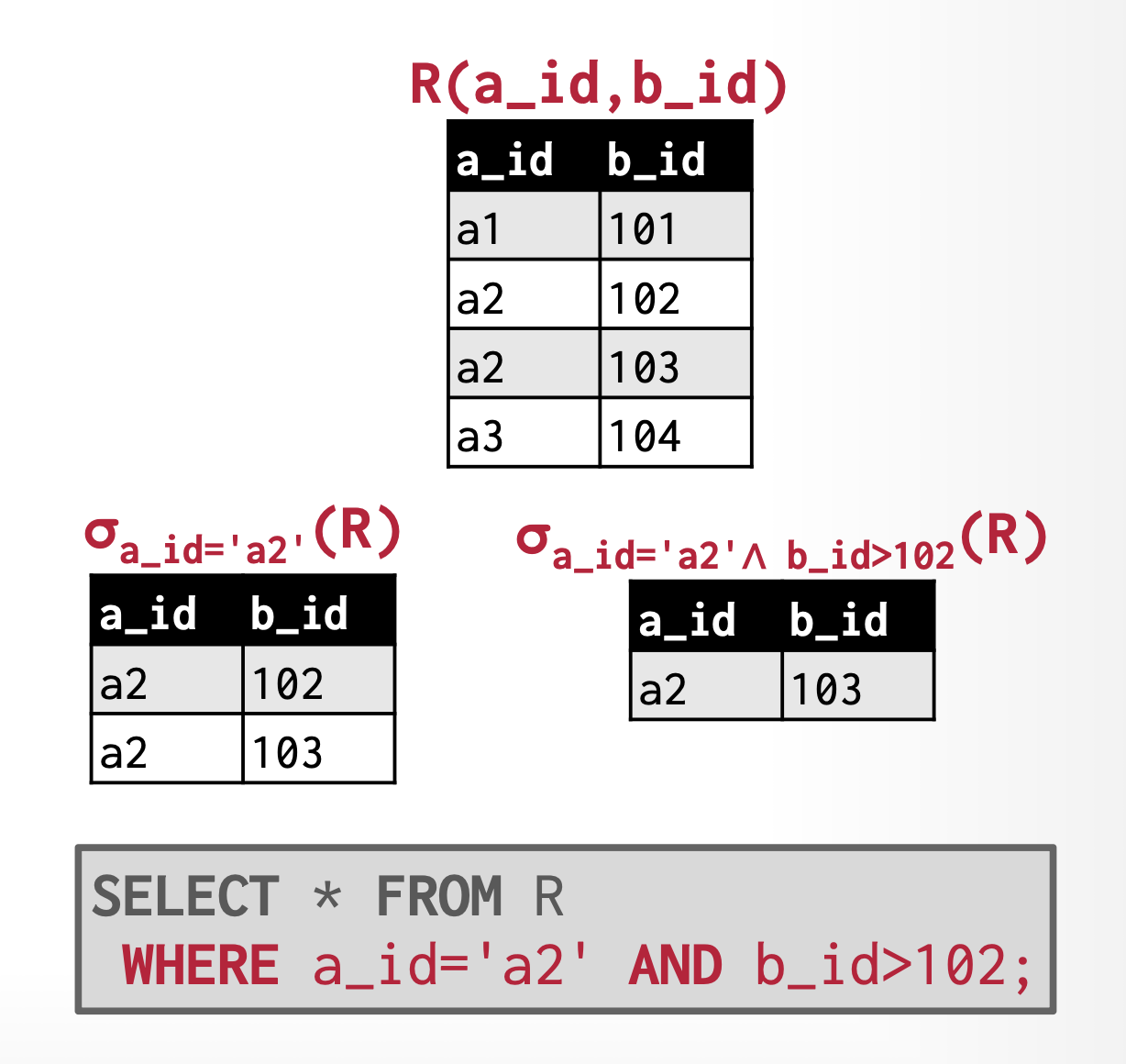
Select⚓︎
- 从关系中找到满足选择谓词的元组子集
- 选择运算记作:\(\sigma_p(r) = \{t\ |\ t \in r \text{ and } p(t)\}\)
- 其中 \(p\) 称为选择谓词(selection predicate),它起到一个过滤器的作用,仅保留那些满足指定需求的元组。可通过连接符 (connectives) 与(\(\wedge\)
) 、或(\(\vee\)) 、非 \(\neg\) 连接多个谓词 - 每个项的格式为:<attribute> op <attribute>/<constant>,其中 op 是比较运算符(\(=, \ne, >, \ge, <, \le\) 中的其中一种)
- 执行选择时,选择条件必须是针对同一元组中相应属性值代入进行比较
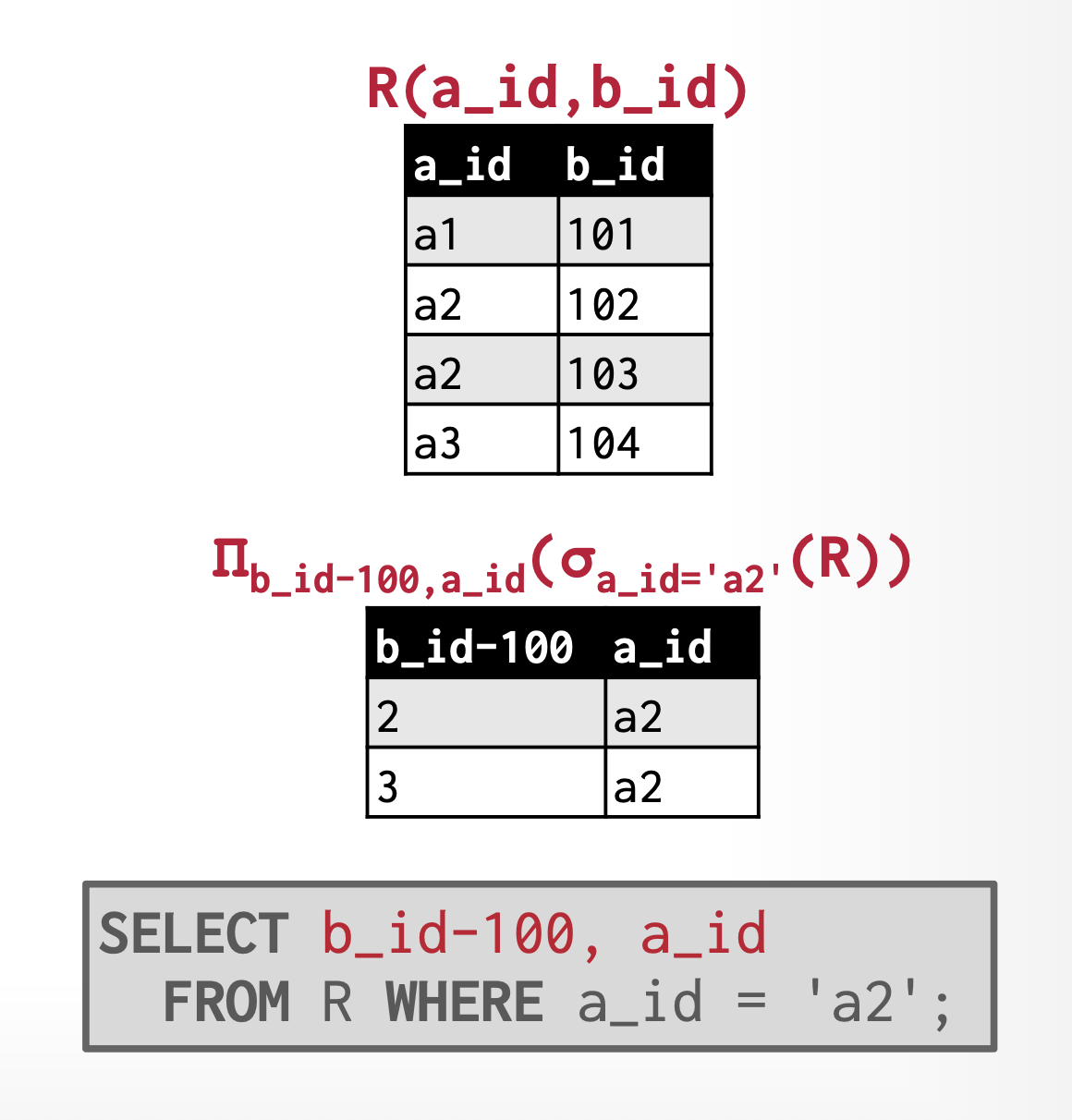
Project⚓︎
- 得到一个关系,其元组仅包含指定的属性,可用于重新排列属性顺序,移除不想要的属性,或者通过操纵值获得派生属性(广义投影)
- 投影运算记作:\(\prod_{A_1, A_2, \dots, A_k}(r)\),其中 \(A_1, \dots, A_k\) 是属性名称
- 运算结果为包含指定的 \(k\) 列关系,那些没有指定的列会被排除在外
- 由于返回的也是关系,所以投影结果中重复行会被自动删除
- 广义的 (generalized) 投影运算允许在投影列表中使用算术表达式,即 \(\prod_{F_1, F_2, \dots, F_n}(E)\)
- 其中 \(E\) 是关系代数表达式,\(F_i\) 是一个包含常数和 \(E\) 的模式中的属性的算术表达式
Cartesian Product⚓︎
- 得到一个集合,里面包含了两个输入关系可能的所有元组组合
- 笛卡尔积记作:\(r \times s = \{\{t, q\}\ |\ t \in r \text{ and } q \in s\}\)
- 若 \(r, s\) 分别有 \(n_1, n_2\) 的元组,那么它们的笛卡尔积有 \(n_1 \cdot n_2\) 个元组
- 若两个关系存在同名属性,那么需要将它们区分开来,可行的方法有:
- 在名称前加上
关系名.的前缀 - 重命名(下面很快会介绍)
- 在名称前加上
Natural Join⚓︎
- 得到一个集合,其中的元组是分别来自两个输入关系的元组的组合,而这两个元组之间必须有一个或多个共同的属性值
- 自然连接记作:\(r \bowtie s\)
-
令 \(r, s\) 的模式分别为 \(R, S\),那么 \(r \bowtie s\) 的结果为一个在模式 \(R \cup S\) 上的关系,按照以下方法获得:
- 考虑分别来自 \(r, s\) 的每一对元组 \(t_r, t_s\)
- 如果 \(t_r, t_s\) 在 \(R \cap S\) 的每个属性上的取值相同,则将元组 \(t\) 加入到结果中,其中 \(t\) 有与 \(t_r\) 在 \(r\) 上,以及 \(t_s\) 在 \(s\) 上相同的值
-
\(r, s\) 必须有共同属性(名称、域对应相同)
- 扩展——Theta 连接(又称条件连接
) ,记作:\(r \bowtie_\theta = \sigma_\theta(r \times s)\),其中 \(\theta\) 是关于模式上属性的谓词
Set Operations⚓︎
要想正确执行集合运算,需要作为操作数的两个关系 \(r, s\) 是可兼容的(compatible),即
- \(r, s\) 必须具备相同的元数(arity)(即相同数量的属性)
- 当属性有相关类型时,对每个 \(i\) 而言,\(r, s\) 的第 \(i\) 个属性的类型必须相同
集合运算包括:并(union)、交(intersection)、差(set-difference)
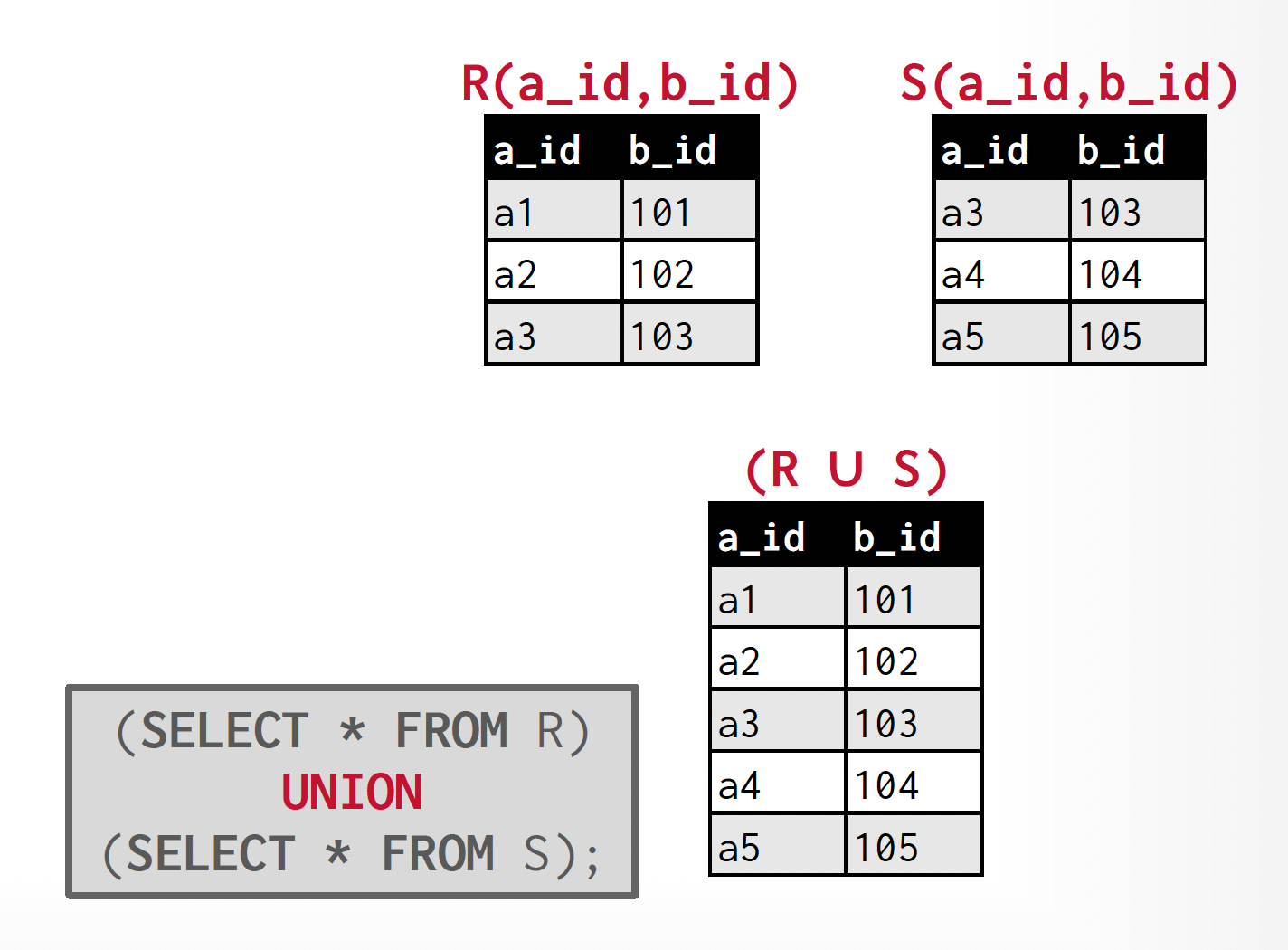
Union⚓︎
- 得到一个关系,包含了所有出现在两个输入关系或其中某个关系中的元组
- 并运算记作:\(r \cup s = \{t\ |\ t \in r \text{ or } t \in s\}\)
- 上述运算的合法条件为:两个关系必须是可兼容的,具体指
Intersection⚓︎
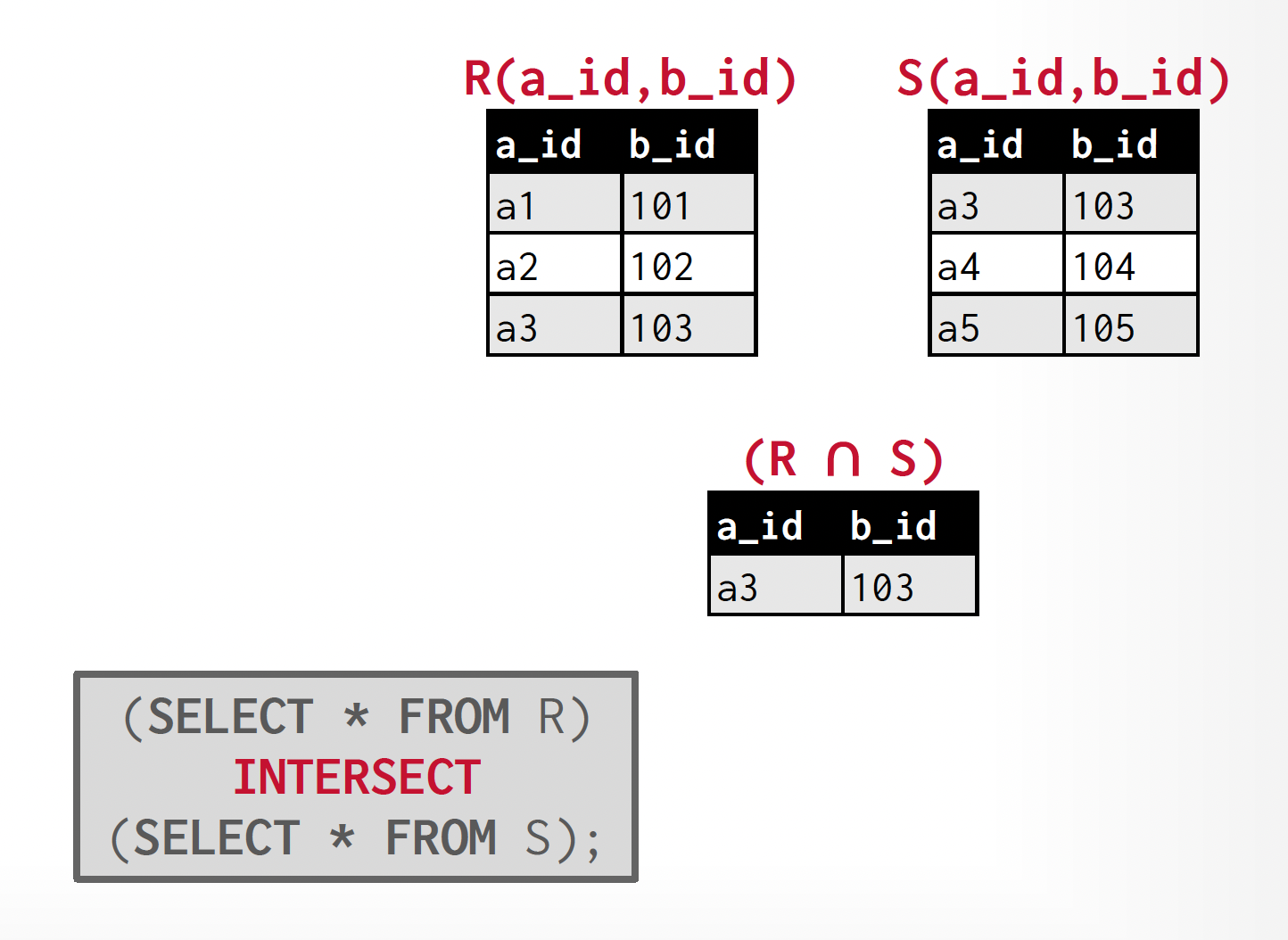
- 得到一个关系,仅包含所有同时出现在两个输入关系中的元组
- 交运算记作:\(r \cap s = \{t\ |\ t \in r \text{ and } t \in s\}\)
- \(r \cap s = r - (r - s)\)
Set Difference⚓︎
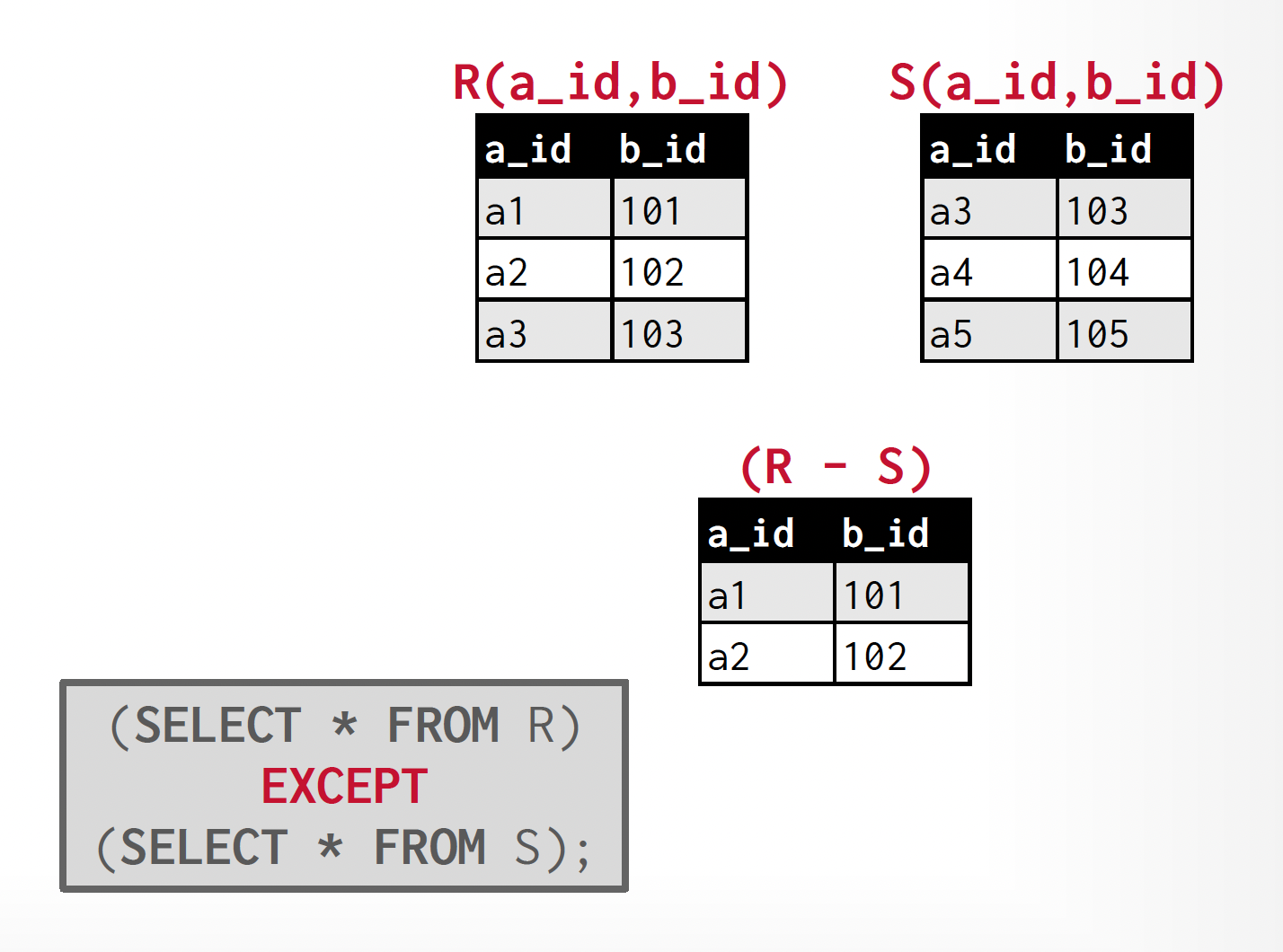
- 得到一个关系,包含出现在第一个输入关系,但不出现在第二个输入关系的元组
- 差运算记作:\(r - s = \{t\ |\ t \in r \text{ and } t \notin s\}\)
Assignment⚓︎
赋值运算符 \(\leftarrow\) 提供了一种表达复杂查询的便捷方法
- 可以将查询写成一个顺序的程序,里面包含了一系列的赋值语句,随后跟上一个表达式,其值作为查询的结果
- 赋值必须用于临时的关系变量,因为如果用在永久变量上的话就是对数据库的修改
Rename⚓︎
- 命名运算记作:\(\rho_X(E)\) 返回在名称 \(X\) 下的表达式 \(E\)
- 如果 \(E\) 的元数为 \(n\),那么 \(\rho_{X(A_1, A_2, \dots, A_n)}(E)\) 返回在名称 \(X\) 下的表达式 \(E\),并且属性名改为 \(A_1, A_2, \dots, A_n\)
- 虽然也可以使用位置序号来表示属性(比如 \(\$1, \$2, \dots\)
) ,但这种方式很不方便,因为它无法直观反映属性的名称
Extended Relational-Algebra-Operations⚓︎
Divide⚓︎
- 除法运算记作:\(r \div s\)
- 性质:令 \(q = r \div s\),那么 \(q\) 是最大的关系,满足 \(q \times s \subseteq r\)
- 定义:\(r \div s = \prod_{R - S}(r) - \prod_{R - S}((\prod_{R - S}(r) \times s) - \prod_{R - S, S}(r))\)
- 解释:
- \(\prod_{R - S, S}(r)\) 仅重排了 \(r\) 的属性
- \(\prod_{R - S}((\prod_{R - S}(r) \times s) - \prod_{R - S, S}(r))\) 找出 \(\prod_{R - S}(r)\) 的 \(t\),满足对于某些元组 \(u \in s, tu \notin r\)
- 另一种表述:\(r \div s = \{t\ |\ t \in \prod_{R - S}(r) \wedge \forall u \in s(tu \in r)\}\)
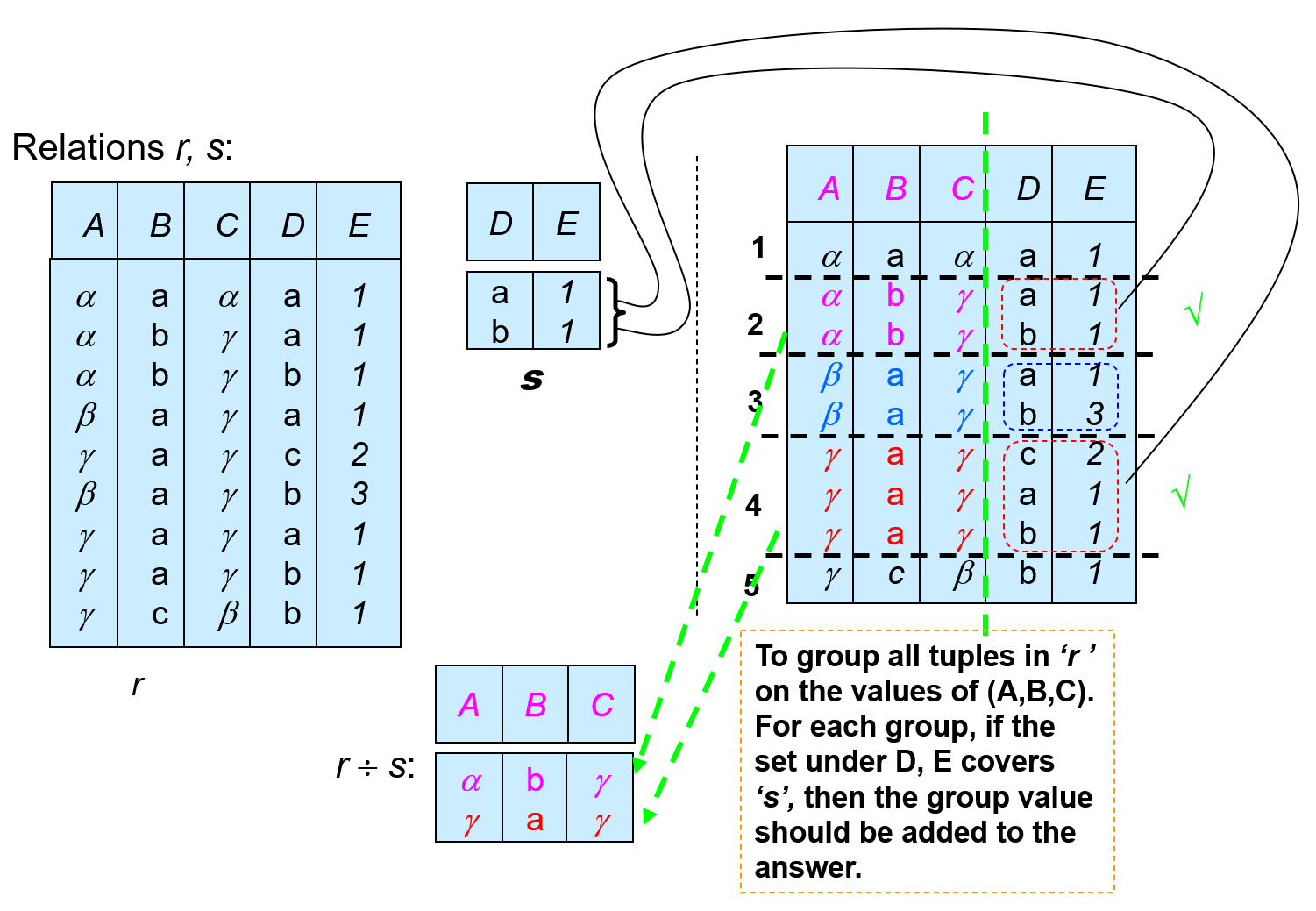
- 还是来看人话吧(
但还是很绕) :\(r \div s\) 结果的模式为 \(R - S\),其元组满足和 \(S\) 的所有的元组组合而成的元组都存在于 \(R\) 中 - 商来自于 \(\prod_{R-S}(r)\),并且其元组 \(t, s\) 所有元组的拼接被 \(r\) 覆盖
- 该运算适用于带有 "for all" 字样的查询语句
Aggregate Functions and Operations⚓︎
- 聚合函数(aggregate function):接受一组值,返回单个值,包括:
- avg:平均值
- min:最小值
- max:最大值
- sum:求和
- count:计数
-
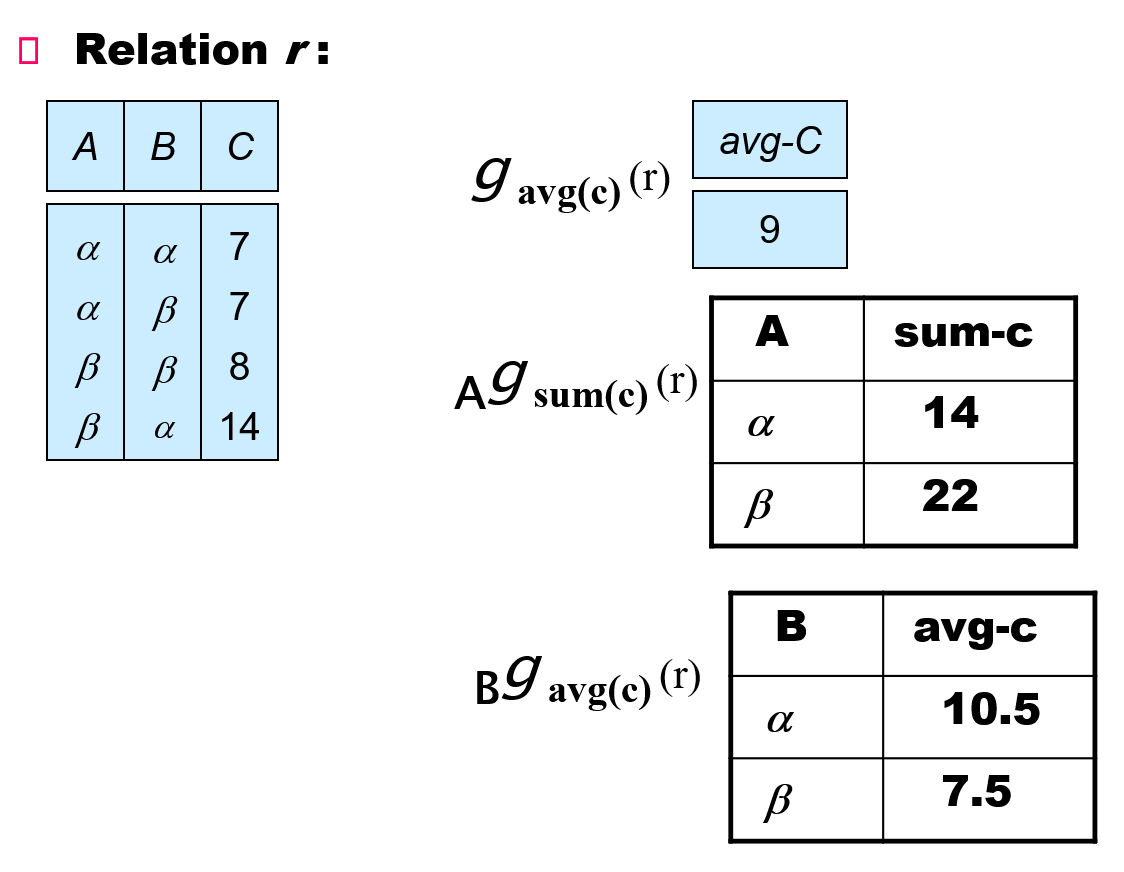
聚合运算(aggregate operation) 的格式为:
\[ _{G_1, G_2, \dots, G_n} {\Large g}_{F_1(A_1), F_2(A_2), \dots, F_n(A_n)}(E) \]其中:
- \(E\) 是任意的关系代数表达式
- \(G_1, G_2, \dots, G_n\) 为一组聚集在一起的属性(可以为空)
- \(F_i\):聚合函数
- \(A_i\):属性名
-
聚合的结果没有名称
- 可以用重命名操作为结果赋予名称
- 方便起见,我们将重命名作为聚合运算的一部分,如下面表达式中的 as 子句
\[ _{G_1, G_2, \dots, G_n} {\Large g}_{F_1(A_1), F_2(A_2), \dots, F_n(A_n) \text{ as new\_name}}(E) \]
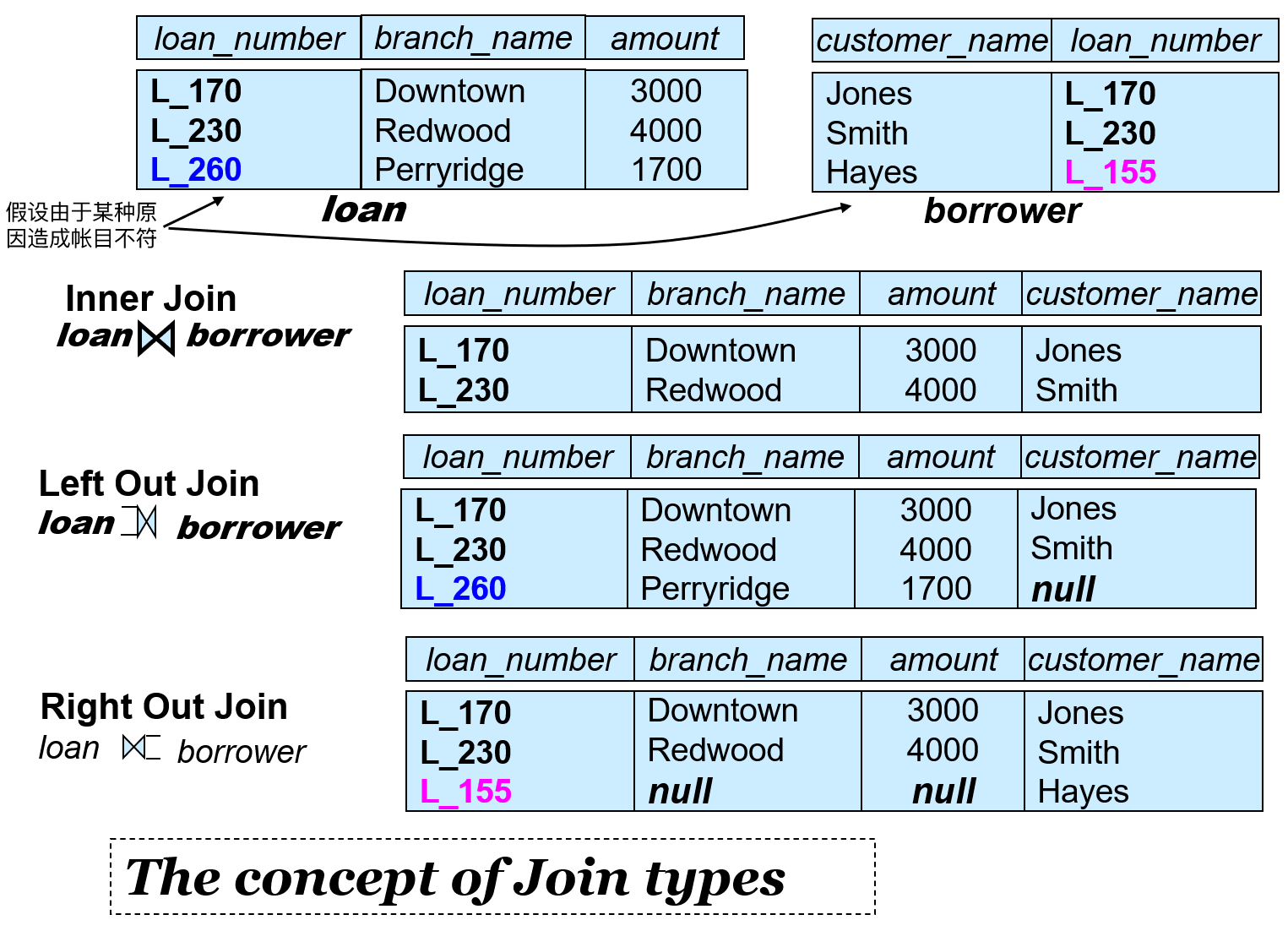
Outer Join⚓︎
- 外连接(outer join) 扩展了传统连接的语义,允许我们保留那些在连接条件上不匹配的元组,从而在查询中获取更完整的信息。
-
外连接分为:
- 左外连接(left outer join) ⟕:
- 先执行一个普通的连接
- 然后保留左边关系中所有元组(即使没在右边关系中找到匹配元组)
- 对于那些没有匹配元组的行,右边关系对应的属性值将用 null 填充
- 右外连接(right outer join) ⟖:
- 先执行一个普通的连接
- 然后保留右边关系中所有元组(即使没在左边关系中找到匹配元组)
- 对于那些没有匹配元组的行,左边关系对应的属性值将用 null 填充
注意:不要搞错左外连接和右外连接的符号朝向!
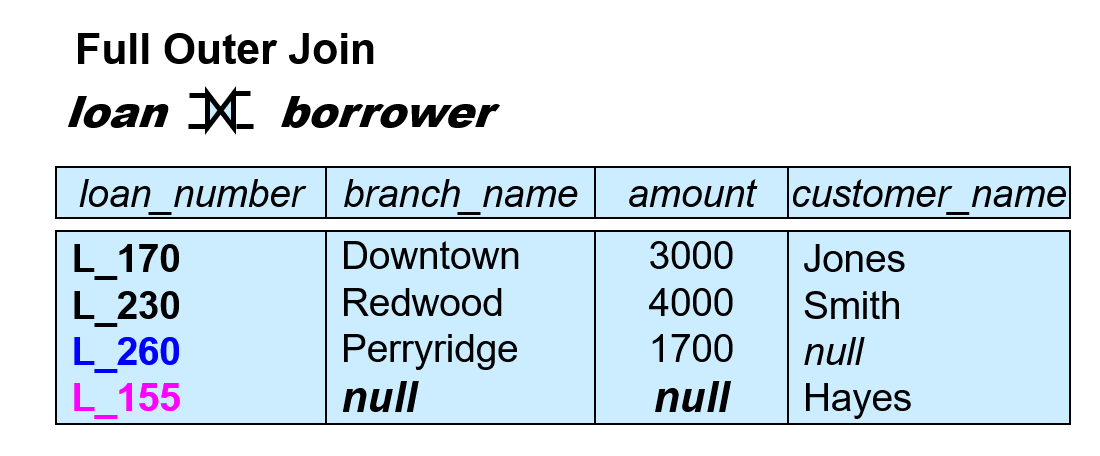
- 全外连接(full outer join) ⟗:左外连接和右外连接结果的并集
- 左外连接(left outer join) ⟕:
Modification of the Database⚓︎
可通过删除 (deletion)、插入 (insertion) 和更新 (updating) 运算修改数据库的内容,这些运算都要用赋值运算符表示。
Deletion⚓︎
- 删除请求的表述与查询类似,除了将选择出来的元组展示给用户的操作,变为从数据库中移除这些元组
- 只能删除一整个元组,不能只删除元组中的部分属性
- 用关系代数表示删除:\(r \leftarrow r - E\),其中 \(r\) 为关系,\(E\) 为关系代数查询
Insertion⚓︎
-
要想在关系中插入数据,我们需要:
- 指明被插入的元组
- 编写一个查询,其结果是一组将被插入的元组
-
用关系代数表示插入:\(r \leftarrow r \cup E\),其中 \(r\) 为关系,\(E\) 为关系代数表达式
- 插入单个元组时,\(E\) 是一个仅包含一个元组的常量关系
Updating⚓︎
- 更新操作可仅改变元组中的某一个值,而无需改变整个元组的值
- 使用广义投影运算来实现:\(r \leftarrow \prod_{F_1, F_2, \dots, F_n}(r)\)
- 其中 \(F_i\) 有两种表示的可能:
- \(r\) 中没有更新的第 \(i\) 个属性
- 如果对应属性要更新,那么 \(F_i\) 是一个包含常量和 \(r\) 的属性的表达式,用于将新的值赋给属性
评论区