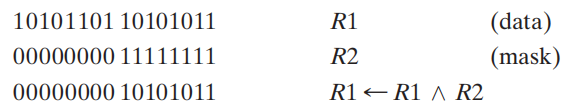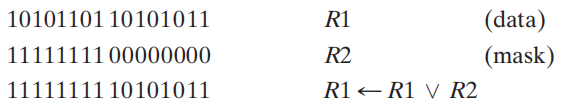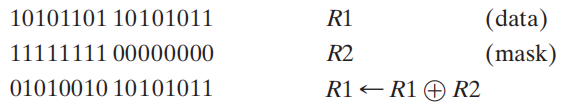Chap 6: Registers and Register Transfers⚓︎

Registers and Load Enable⚓︎

n 位寄存器 (register) 由一组触发器和组合逻辑门构成，用来实现多位数据的存储等操作

• n 位触发器保存一位或多位数据
• 组合逻辑门对数据进行加工

计数器 (counter)：随着时间脉冲的变化，不断在某个固定序列内循环“扫描”的一种寄存器

寄存器和计数器都是时序函数块 (sequential functional blocks)

• 寄存器主要用于存储和操纵信息
• 计数器主要用于序列和控制操作

Example

2 位寄存器 4 位寄存器

这里多了一个清除输入\(\overline{Clear}\)，用于在正式运行前的初始化 ( 寄存器的所有值均置 0)，当 \(\overline{Clear} = 0\) 时，对触发器进行异步复位。在正常运行时，\(\overline{Clear}\) 应保持 1，除非需要复位。这个输入是可选的。

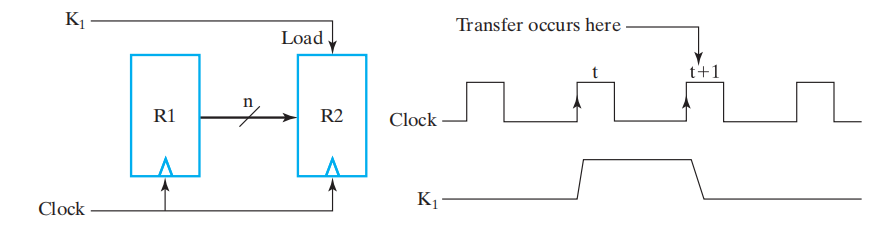
寄存器能在每个时钟周期里加载 (loading)信息：将新的信息传输至寄存器内。如果加载操作在同一时钟脉冲内完成，称之为并行完成。

加载 (load)：控制寄存器的存储和加载的信号：

• load = 1：加载数据输入的值
• load = 0：将值存储至寄存器内

寄存器的符号：

注：由于 Clear 写在方框内部，且外部有个圆圈，因此 Clear 没有取反；但如果 Clear 写在外面，就需要写成 \(\overline{Clear}\)

为了更合理地存储或加载信息，寄存器需要用控制信号实现人为的控制，实现方法如下：

• 用一个信号来阻止寄存器的时钟输入 \(\Rightarrow\) 门控时钟
• 用一个信号，将寄存器的输出反馈至它的输入 \(\Rightarrow\) 控制数据

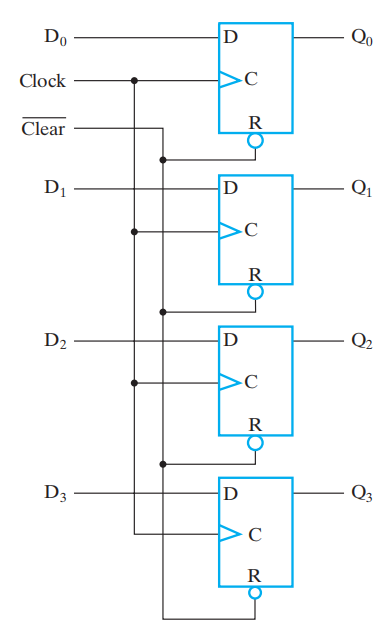
Registers with Clock Gating⚓︎

主时钟生成器 (master clock generator)：提供一个应用于所有触发器和寄存器的时钟脉冲

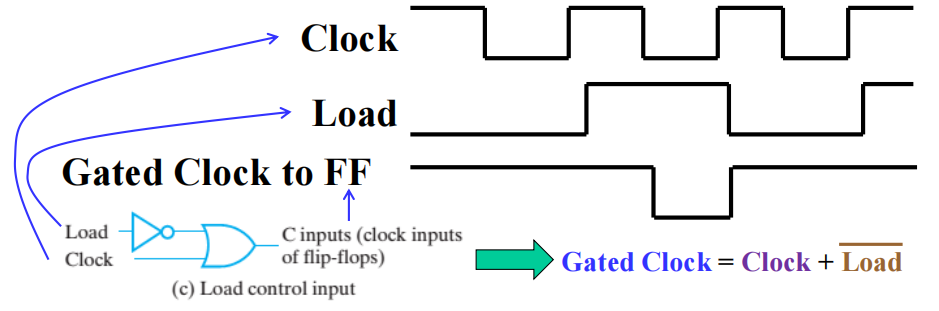
门控时钟 (clock gating)：控制时钟的使用，其中的 \(Load\) 相当于时钟的使能信号，起到“开关”的作用

此时控制信号 \(C = Clock + \overline{Load}\)

• 当 \(Load = 0\) 时，\(C = 1\)，时钟信号失效，寄存器保持原来的数据
• 当 \(Load = 1\) 时，\(C = Clock\)，时钟信号生效，寄存器加载新数据

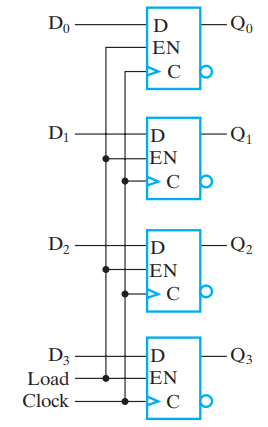
Registers with Load-Controlled Feedback⚓︎

解决方案：

• 保持时钟的连续运行
• 用一个加载控制，在原数据和新数据之间进行选择，即是要保持数据还是加载数据 ( 类似一个 2-1 MUX) 电路实现：

• \(EN = 0\) 时，\(D = Q\)，也就是保持之前的值
• \(EN = 1\) 时，\(D\)加载新的值

这种电路被称为带使能的 D 触发器 (D flip-flop with enable)，可避免时钟移，所以更推荐这个方案。

🌰：带有并行加载的 4 位寄存器

之所以说是“并行加载”的，是因为每个触发器均由一个 \(Load\) 信号控制，因此要么同时保持 4 位数据，要么同时加载 4 位数据

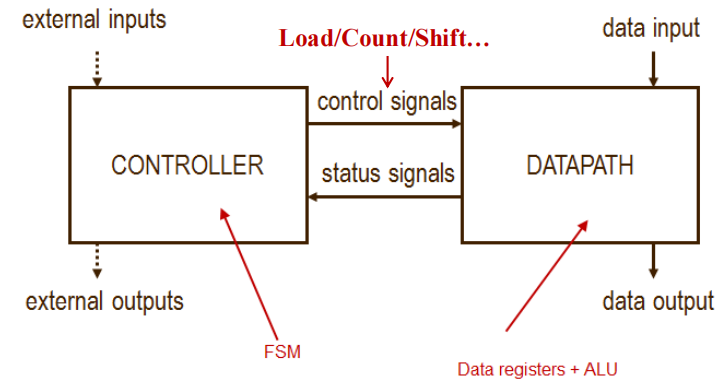
Datapath and Control Signals⚓︎

• 数据通路 (datapath) 是执行数据加工操作 ( 寄存器传输和微操作 ) 的一组函数单元 ( 比如 ALU, MUX)，寄存器和总线
• 控制单元 (control unit) 产生控制信号，告诉数据通路要做什么 ( 决定操作序列 )

Register Transfer Operations⚓︎

寄存器传输操作 (register transfer operations)：对存储于寄存器内的数据进行移动和加工操作，它由以下部分组成：

• 一组寄存器
• 微操作 (microoperations)：对存储于寄存器内的数据进行的基本操作，比如加载 (load)、计数 (count)、移位 (shift)、加 (add)、按位或 (bitwise OR)，等等
• 控制操作：监督系统的操作序列

寄存器传输语言 (register transfer language, RTL)：一种用于描述寄存器传输中的逻辑行为的语言

表示寄存器的图形化符号：

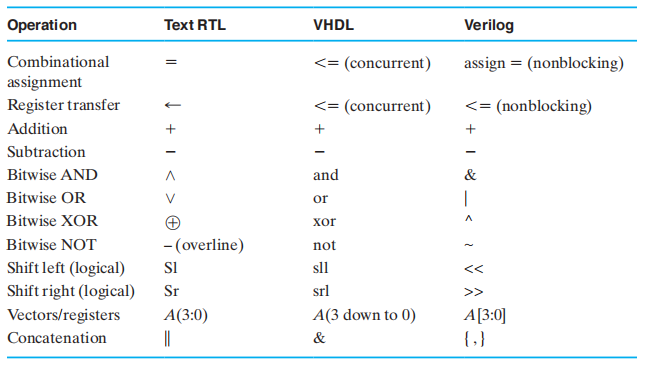
RTL 中的常用表示法：

条件传输 (conditional transfer)

控制表达式 (control expression) 具体说明了运算的逻辑条件：

• if 控制表达式 == 逻辑1 \(\rightarrow\) 执行运算
• if 控制表达式 == 逻辑0 \(\rightarrow\) 不执行运算

If (K1 = 1) then (R2 \(\leftarrow\) R1) 可以简记为： $$ K1: (R2 \leftarrow R1) $$ 其中K1为控制变量，具体说明微操作的条件执行

图示：

而 \(K3: R2 \leftarrow R1, R1 \leftarrow R2\) 表示同时交换R1 和 R2 的值

RTL, VHDL 和 Verilog 的寄存器传输符号

Microoperations⚓︎

微操作 (microoperation) 的 4 种类型：

• 传输 (transfer)：将数据从某个寄存器转移到另一个寄存器内
• 算术 (arithmetic)：对寄存器内的数据执行算术运算
  • 加法 +
  • 减法 -（一般用补码实现，具体操作见 Chap 3）
  • 乘法 *
  • 除法 /
• 逻辑 (logic)：执行按位逻辑运算
  • 逻辑或 \(\vee\)
  • 逻辑与 \(\wedge\)
  • 逻辑异或 \(\oplus\)
  • 非 ( 取反码 ) \(\overline{X}\)
• 移位 (shift)：对寄存器内的数据进行移位

具体描述

算术微操作逻辑微操作移位微操作

注：关注第 2,3 行 ( 反码、补码的表示 )

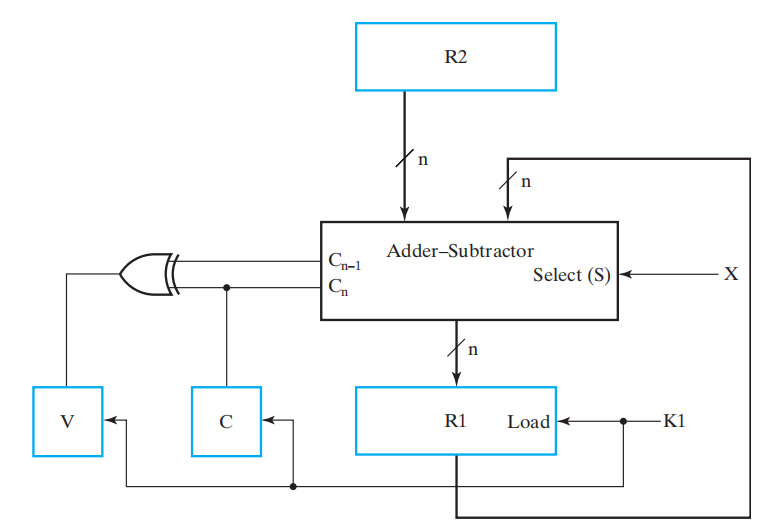
加减法器

回顾 Chap 3 的加减法器设计

\[ \begin{align} \overline{X} \cdot K1: & R1 \leftarrow R1 + R2 \notag \\ X \cdot K1: & R1 \leftarrow R1 + \overline{R2} + 1 \notag \end{align} \]

注：\(X\) 决定运算模式 (0：加法，1：减法 )，\(K1\) 为使能信号

电路实现：

注：溢出 ( 即最高位的进位 )输出会被传输到 V 中 ( 一个触发器 )( 前提是 K1 = 1)

注：对于 n 位的寄存器，一个逻辑微操作需要的门的数量为 n 个

Example

区别一些符号掩码

\[ (K1 + K2):\ R1 \leftarrow R1 \vee R3 \]

注：

• 条件中出现的 '+' 表示“或”运算
• 而 \(R1 \leftarrow R1 + R3\) 中的‘+’表示“加法”微操作
• 用 '\(\vee\)' 表示“或”微操作

• 逻辑与：
  
  我们仅保留了R1的低位部分，高位部分均变成0
• 逻辑或：
  
  我们仅保留了R1的低位部分，高位部分均变成1
• 逻辑异或：R1 的低位部分得到保留，而高位部分全部取反
  

• 具体实现方法见移位寄存器一节
• 移位往往用到“0 填充 (zero fill)”：左移 - 右边补 0，右移 - 左边补 0。这样的位被称为进入位 (incoming bit)
• 移出去的位一般就抛弃掉，这种位被称为移出位 (outgoing bit)
• 有时，需要用 1 个单独的触发器提供要移位的数据，或者获取移位后的数据
• 还有更复杂的移位（翻转，算术运算……），这里就略过了
• 还可以实现多个位的移动，如果通过 1 个变量指定移动的位数，称该变量为移位量 (shift amount)

Register Transfer Structures⚓︎

类别：

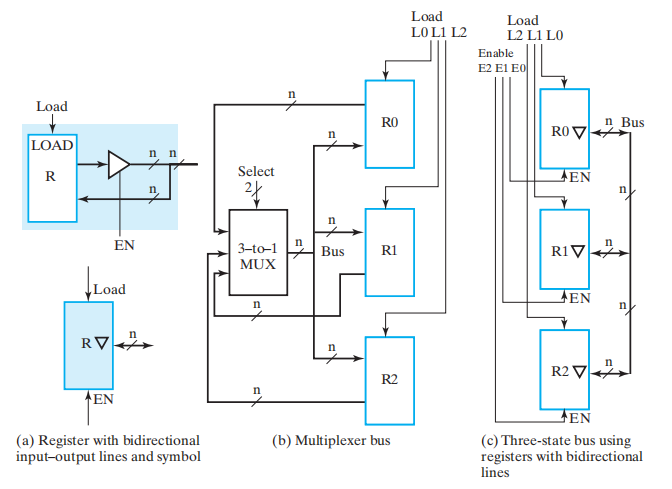
• 基于多路选择器的传输 (multiplexer-based transfer)：由单个 MUX，从多个输入中进行挑选
• 基于总线的传输 (bus-based transfer)：由一个共用的 MUX( 它驱动一条向多个寄存器提供输入的总线 ) 从多个输入中进行挑选
• 三态总线 (three-state bus)：由一个三态门驱动器 ( 其输出与供给多个寄存器的总线相连接 ) 从多个输入中进行挑选

Multiplexer-Based Transfers⚓︎

🌰：

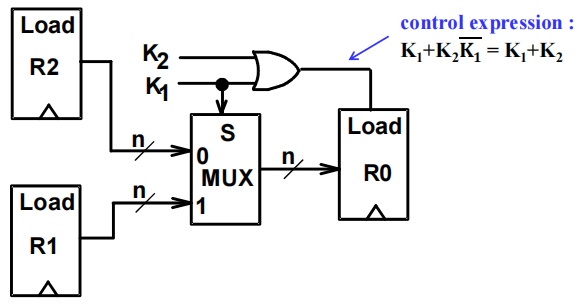
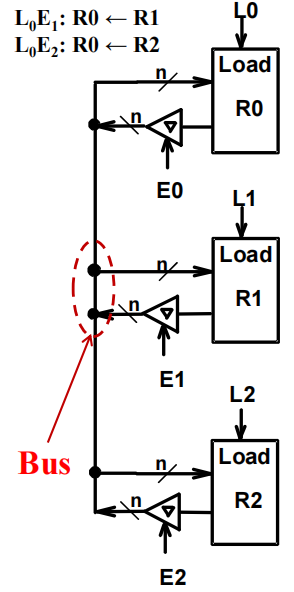
$$ K1: R0 \leftarrow R1 \quad K2\overline{K1}: R0 \leftarrow R2 $$ 框图：

更详细的内部结构图 (4 位寄存器 )：

该类模型的泛化：

• MUX 的信息输入部分中，有 k 个来自专用逻辑的输入，以及 n - k 个来自寄存器或公用逻辑的输入
• 通过一个编码器，将 n 个选择转化为 MUX 的 m 个选择输入
• 缺陷：开销较大

专用逻辑、公用逻辑的概念见后面的小节

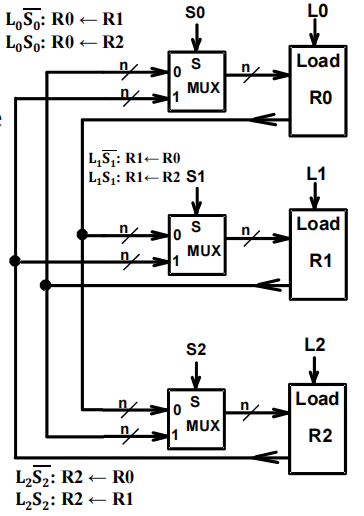
Bus-Based Transfers⚓︎

dedicated MUX-based transfersmultiplexer busthree-state bus

事实上，这种寄存器传输并不是基于总线实现的，放在这里只是为了和后面的设计进行对比

• 每个 MUX 都是某个寄存器的专用逻辑 (dedicated logic)
• 能够实现同步传输

• 由一个 MUX 驱动的单个总线，也就是说该 MUX 是寄存器的共用逻辑 (shared logic)
• 优点：电路更精简，成本更低
• 缺点：同一时间内只能传输一个数据

• 三态门的实现与共用 MUX 本质上是差不多的，因此它也只能一次传一个数据
• 但是三态门的实现降低了成本，因而也更常用
• 这里的符号可以进一步简化，最终可以得到右侧的电路图

• 这里我们用到了使能信号 \(EN\)：当 \(EN = 1\) 时表示输出，当 \(EN = 0\) 时表示输入
• 真正决定是否读入寄存器的是 \(Load\)

Shift Registers⚓︎

移位寄存器 (shift register) 能将数据向 MSB 或 LSB 的位置移动

Serial Shift Register⚓︎

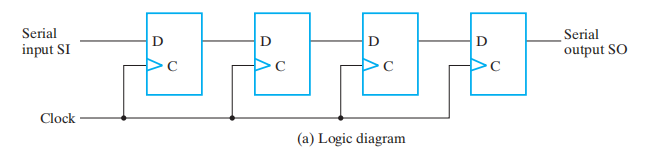
移位寄存器最简单的实现：仅用一组按行排列连接起来的D 触发器构成：

• 串行输入 / 右移输入 (serial input/ shift right input)——数据输入
• 串行输出 (serial output)——数据输出

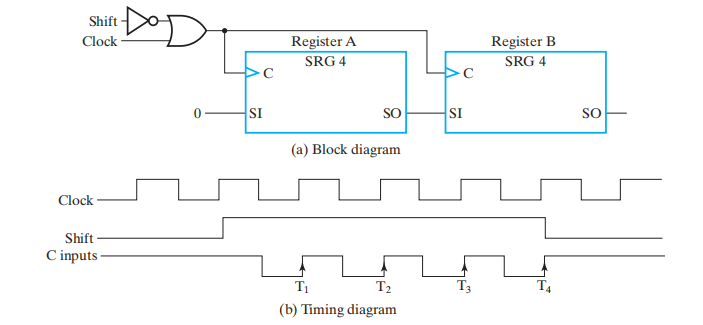
符号：

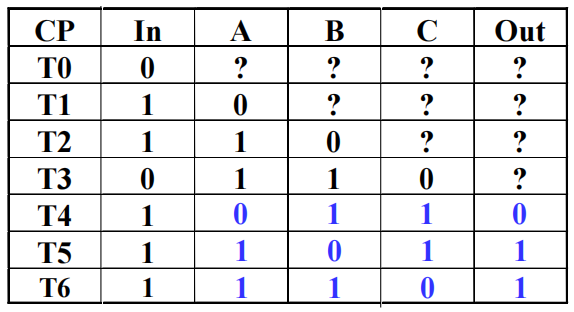
• CP 表示时钟脉冲，\(T_i\) 表示第 i 个时钟周期
• '?' 表示未知状态，

Parallel Load Shift Registers⚓︎

" 并行 " 主要体现在两方面：

• 并行输出 (parallel output)：在同一时钟周期内得到所有触发器的结果
• 并行载入 (parallel load)：在同一时钟周期内对所有触发器载入数据

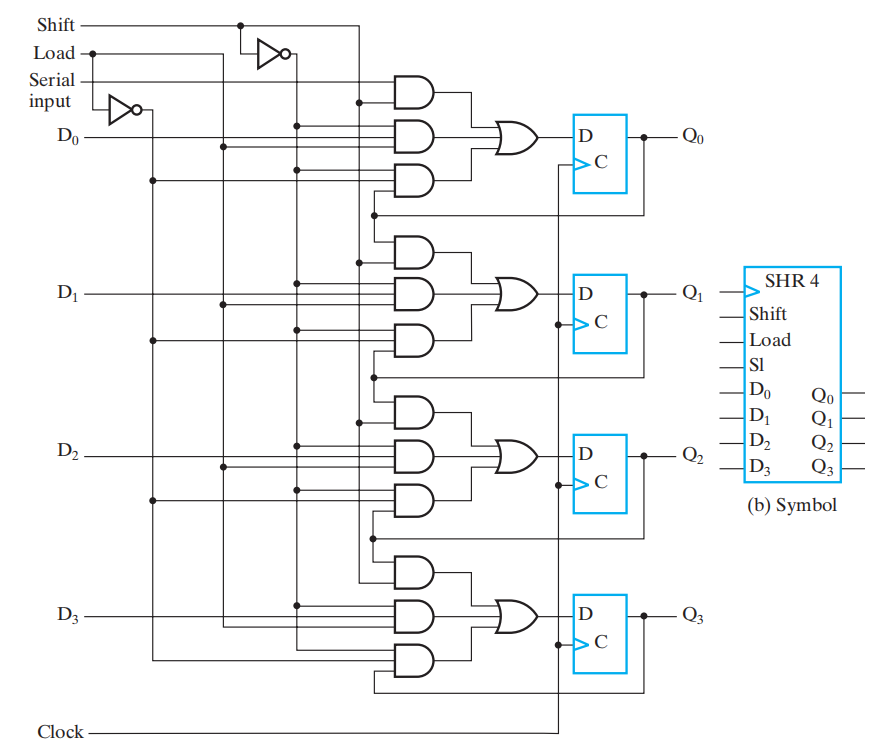
n 位并行加载移位寄存器 (parallel load shift registers)

细节分析

• 观察右侧的触发器，发现其结构大致类似上面的串行移位

• 较麻烦的可能还是分析每个触发器对应的逻辑门，每个与门的功能如下：

  • 第一个与门 \(F_{i1} = \begin{cases}Shift \cdot SI & \text{第一个FF} \\ Shift \cdot Q_{i - 1} & \text{其余FF}\end{cases}\)，当 \(Shift = 1\) 时，寄存器执行移位操作

  • 第二个与门 \(F_{i2} = \overline{Shift} \cdot Load \cdot D_i\)，当 \(\overline{Shift} \cdot Load = 1\) 时，寄存器执行并行加载

  • 第三个与门 \(F_{i3} = \overline{Shift} \cdot \overline{Load} \cdot Q_i\)，当\(\overline{Shift} \cdot \overline{Load} = 1\)时，寄存器保持上次的值

功能表：

Shift Registers with Additional Functions⚓︎

上述移位寄存器只能进行单向移位操作，因此被称为无向移位寄存器 (undirectional SHR)。下面我们将实现一个具备右移、左移、并行加载、保持功能的 SHR，被称为双向移位寄存器 (bidirectional SHR)

这里只展示整个移位寄存器的一部分，不难想到对于寄存器的每一位，我们都要用一个 MUX 进行选择

功能表：

Counters⚓︎

两种常见类型：

• 异步计数器 / 行波计数器 (asynchronous counters/ripple counters)

  • 对于表示最低位的触发器，它的时钟输入与时钟相连
  • 对于表示其他位的触发器，它们的时钟输入与来自上一位的输出相连，因此电路不是同步的
  • 当逐位接近最高位时，由于电路元件自身的延迟，输出发生改变的延迟将会越来越大
  • 优点：低能耗

• 同步计数器 (synchronous counters)

  • 时钟与触发器的时钟输入直接相连
  • 用逻辑实现想要的状态序列

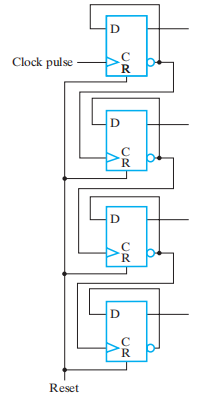
Ripple Counters⚓︎

2 位行波计数器 3 位行波计数器 4 位行波计数器

工作流程：

• 当触发器 A 的时钟输入出现正边沿时，A 取补，即从 0 变成 1 或从 1 变成 0
• 触发器 B 的时钟输入 = \(\overline{A}\)
• 当触发器 A 的输出从 1 \(\rightarrow\) 0 时，触发器 B 的时钟输入就会出现正边沿，此时 B 取补

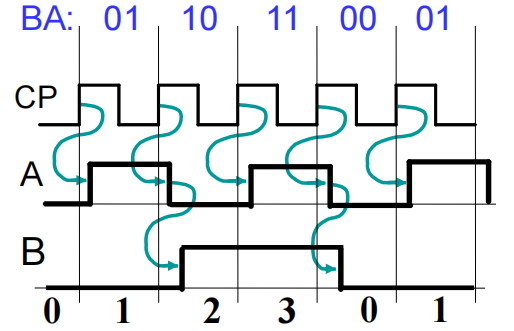
下面的时序图可以更加直观地展示上述内容：

• 蓝绿色箭头表示“工作流程”所述的因果关系
• 对应的状态序列 (B, A) = (0, 0), (0, 1), (1, 0), (1, 1), (0, 0), (0, 1)……

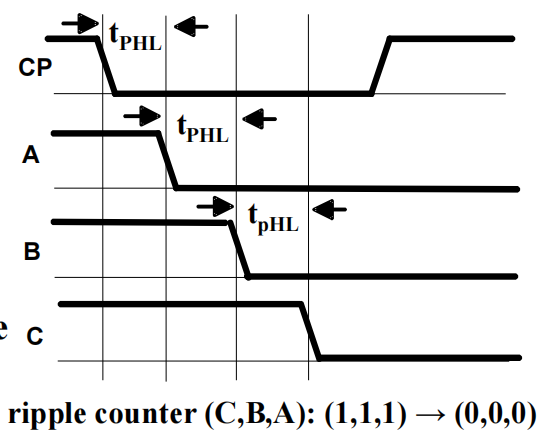
对于 3 位行波计数器，当 C = B = A = 1 时，计数器的状态为 (C, B, A) = (1, 1, 1)，下一次时钟的增加使得 (C, B, A) = (0, 0, 0)。从下面的时序图中，我们发现：

• 时钟 - 输出延迟 \(t_{PHL}\) 导致时钟边沿不断增加的延迟
• 对于 n 为行波计数器，最坏情况的延迟为 \(n \cdot t_{PHL}\)

4 位行波计数器的框图

Synchronous Counters⚓︎

类别

serial gatingparallel gating

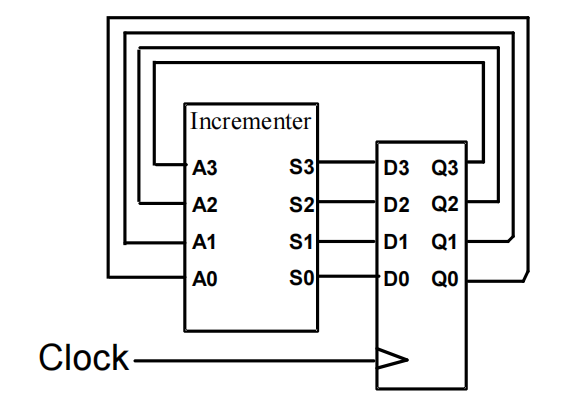
为了消除行波影响，我们让每个触发器使用共同的时钟，并用一个组合电路来生成下一状态。例如对于升计数器 (up-counter)，我们会使用一个自增器 (incrementer)

内部细节：

• 内部逻辑：蓝色方框表示自增器
• 计数使能 (count enable, EN)：迫使与门链的输出均为 0，用来保持状态
• 出进位 (carry out, CO)：自增器的一部分。通过将 CO 与另一个计数器的 EN 端连接，构建一个更大的计数器

上图中，与门链导致“进位链 (carry chain)”的出现，因而产生较长的通路延迟，这种计数器的形式被称为串行门 (serial gating)

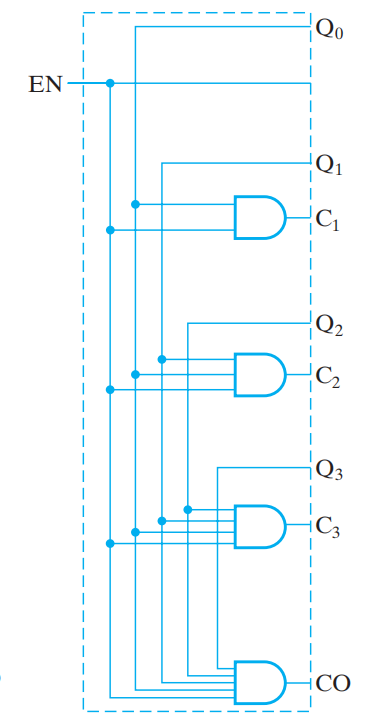
将与门链 \(\Rightarrow\) 并列的与门，我们得到了另一种形式——并行门 (parallel gating)，这种形式减少了通路延迟，类似超前进位。它利用 CO 和 EN 来阻止较长的通路。逻辑图如下 ( 用它替换 serial gating 电路图中蓝框部分的电路 )：

布尔方程：

\[ \begin{align} C1 & = EN \cdot Q_0 \notag \\ C2 & = EN \cdot Q_0 \cdot Q_1 \notag \\ C3 & = EN \cdot Q_0 \cdot Q_1 \cdot Q_2 \notag \\ C4 & = EN \cdot Q_0 \cdot Q_1 \cdot Q_2 \cdot Q_3 \notag \\ \end{align} \]

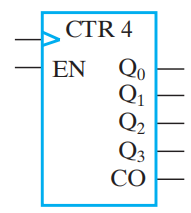
符号：

Other Counters⚓︎

• 降计数器 (down counter)：向下计数
• 升降计数器 (up-down counter)：既可以向上，也可以向下计数，取决于控制输入的值，比如 \(Up/\overline{Down}\)
• 并行加载计数器 (parallel load counter)：能够并行加载可用的值，取决于控制输入 ( 比如 \(Load\))
• 模 n 计数器 (divide-by-n/ modulo n counter)：
  • 对除以 n 的余数进行计数
  • 或者对任意 n 个状态的序列进行计数（根据具体状态分析）
  • BCD 计数器是一个模 10 计数器

Up-Down Binary Counter⚓︎

🌰：4 位升降计数器，有使能输入 EN，选择输入 S(S = 0 时向上数，S = 1 时向下数 )

输入方程：

该方程既能用串行门实现，也能用并行门实现，这里就不给出具体的实现了。

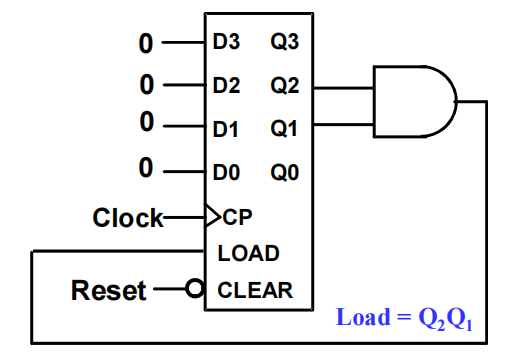
Counter with Parallel Load⚓︎

将并行加载的功能用于计数器内，这样可以给计数器设定一个我们想要的数字

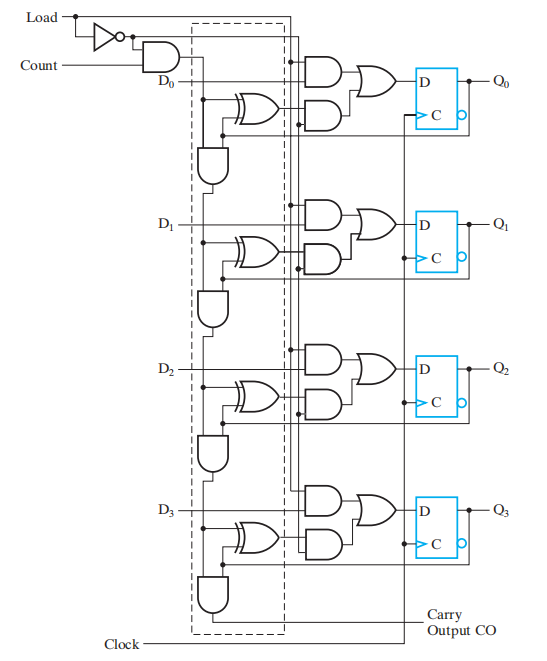
电路实现：

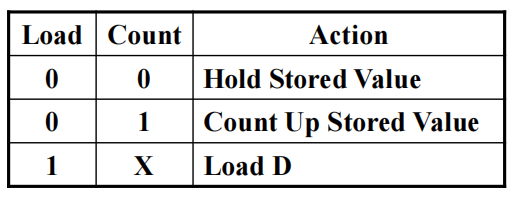
功能表：

注：可以看到 Load 的优先级高于 Count，因为只要 Load = 1，不管 Count 有什么值，计数器执行加载功能

Synchronous BCD⚓︎

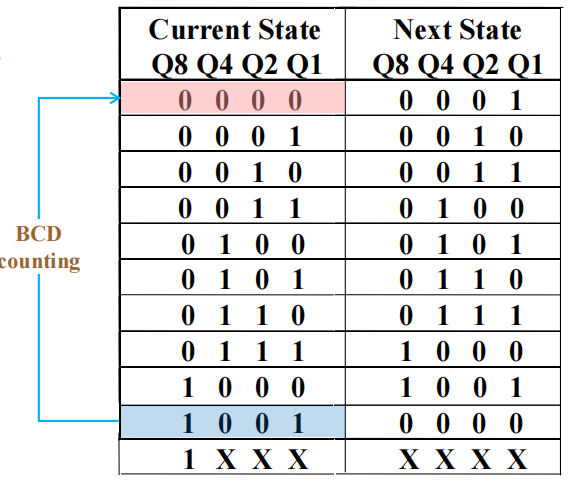
状态表：

注：10-15( 即 1010-1111) 是我们不关心 (don't care) 的情况

使用 K-maps，对下一状态的方程进行两级优化，得到以下方程：

思考

如果计数器的电源受到干扰，或者受到其他影响，使得计数器的状态不在 0000-1001 之间，会出现什么问题呢？

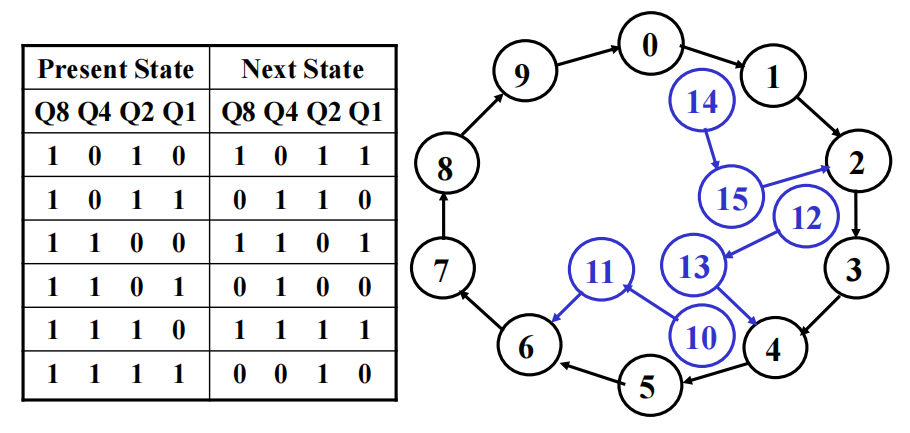
\(\therefore\) 我们需要让计数器具备“自愈能力 (self-healing ability)”，使得它能在 2 个时钟周期内，从异常状态中回到正常状态。利用好那 6 个“不关心”的状态，可以实现这个“自愈能力”，状态表和状态图如下：

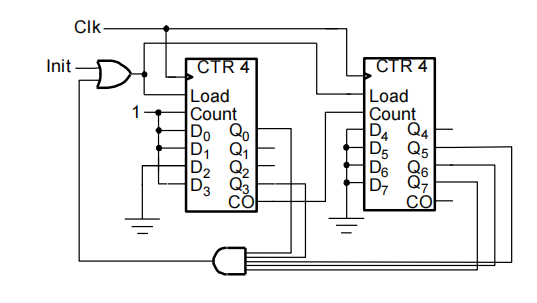
另一种实现方法：并行加载二进制计数器 + 与门

电路实现：

注：当计数到 1001 时，Q0 = Q3 = 1，这使得 Load = 1，计数器执行加载功能，将读入 D(3: 0) 的值，即 0000，从而实现 0-9 之间的计数

例题

问题答案

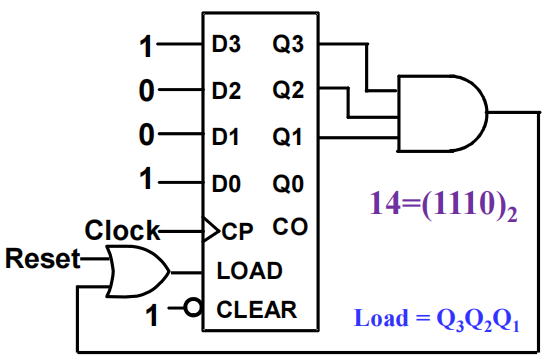
Counting Modulo N⚓︎

下列技术将用到带有异步 / 同步的清空 (clear)，以及 / 或者并行加载 (load) 的 n 位二进制计数器：

• ❌在模 N 计数中，当检测到最后的数N时，进行异步清 0，或者异步加载值 0。然而，这种方法使得数字仅在很短的时间内出现，导致在某些情况下无法正常工作
• ✅在模 N 计数中，当检测到最后的数N - 1时，同步清 0，或者同步加载值 0
• 检测最后的数，使用加载功能提前预设值，满足 == 最后的数 - 预设值 = N - 1==，也就是说计数的范围变成了 [ 预设值，最后的数 ]。实在看不懂的话见下例中第 2 种实现方法

模 7 计数器

常规实现一点改变

注：原理同 BCD 计数器，只是它是数到 6 就要返回 0

预设加载值 9，当数到 14 时，由于 14 - 9 = 7 - 1，因此需要回到 9，计数范围为 \([9, 14]\)

电路实现：

注：

• 预设值是在输入 D(3: 0) 处设置
• 对于该计数器，如果最后的数设为了 15，那么可以利用进位 CO 检测该最后的值 ( 这样就省去一个与门了 )

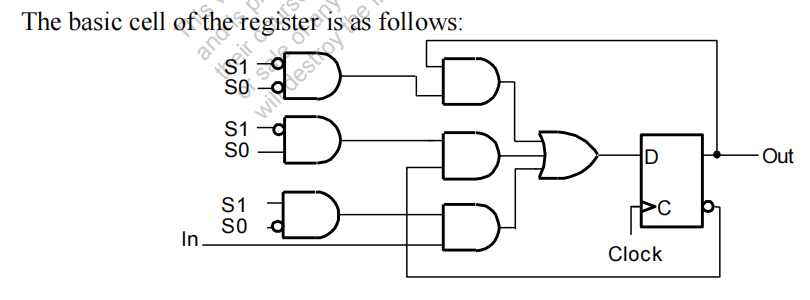
Register Cell Design⚓︎

在组合电路中，我们使用迭代阵列实现复杂的组合电路。同样地，我们可以将这种思想运用到时序电路的设计中——将迭代组合电路和触发器相连接，构建一个双态时序电路，被称为寄存器单元 (register cell)。只要我们构建了一个存储器单元，然后复制 n 份副本，我们就构建出能够执行一个或多个微操作的 n 位寄存器。

由此，我们得到了寄存器设计的步骤：

• ⭐设计具有代表性的寄存器单元
• 复制并连接寄存器单元，构成完整的寄存器
• 修改某几个寄存器单元以解决一些特殊情况或边界问题

寄存器单元设计的方法：

• MUX：使用 n 输入 MUX，以及一系列的传输源和函数

  图片

  • 专用逻辑 (dedicated logic)：实现微操作的组合逻辑被视为寄存器的一部分
  • 共用逻辑 (shared logic)：被多个寄存器共用的，实现微操作的组合逻辑
  • 通过控制信号 \(K_0, K_1, \dots, K_{n-1}\) 的或运算，生成加载使能信号

  • 如何选择来自源，或 / 和传输函数？

    • MUX + 编码器 ( 如图所示 )：控制输入需要被编码
    • n \(\times\) 2 与 - 或门：控制输入不需要被编码

• 时序电路设计

  • 找到状态图或状态表，注意只有两个状态分配后的状态 = 寄存器单元的输出值
  • 运用 Chap 4 介绍的流程来完成单元设计
  • 优化：K-maps(4-6 个变量 )、手动优化或计算机辅助 ( 更多的变量 )

寄存器单元的规范包括：

• 寄存器函数 (register functions)：一般用寄存器传输表示
• 控制输入 (control input)
  • 无编码形式：比如 Load, Shift, Add，1 个时钟周期内至多有 1 个输入为 1，即 (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1)
  • 编码形式：比如 S1, S0，所有的组合为 (00, 01, 10, 11)
• 数据输入 (data input)

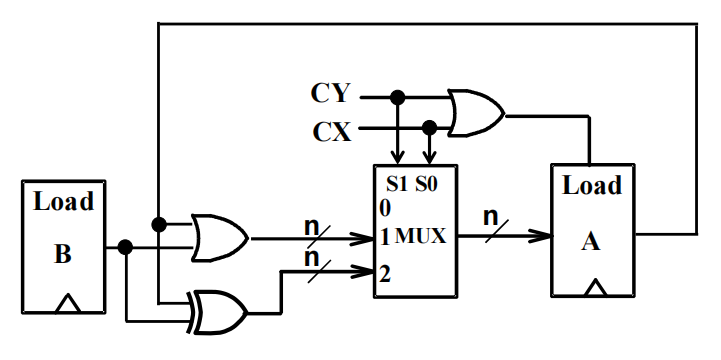
例题

例 1 例 2

题目法一：MUX 法二：时序电路设计

• 寄存器的加载信号：Load = CX + CY
• 由于控制输入的数量少，因此不需要用到编码器，我们直接将控制输入与 MUX 的选择输入连接，得到：S1 = CY, S0 = CX
• 寄存器的数据输入：

\[ \begin{align} D1 & = A_i \leftarrow B_i \vee A_i \quad (CY, CX) = (0, 1) \notag \\ D2 & = A_i \leftarrow B_i \oplus A_i \quad (CY, CX) = (1, 0) \notag \\ \end{align} \]

• 当 Load = 0，即 (CX, CY) = (0, 0) 时，寄存器 A 保持状态

电路实现：

单个元件的门成本 = 19，共享译码器的成本 = 8

状态表：

• 4 个变量将给出状态表的 16 个状态项
• 因为我们不会用到 CX = CY = 1 的条件 ( 即 don't care conditions)，因此实际上我们只关心 12 个项

K-map 化简：

我们得到 SOP 方程为： $$ D_i = CXB_i + CY\overline{A_i}B_i + A_i\overline{B_i} + \overline{CY}A_i $$ 进一步化简(为了减少门成本)，得到： $$ D_i = CXB_i + A_i \oplus (CYB_i) $$ 门输入成本 = 2 + 8 + 2 + 2 = 14，因此比法一更节省成本。而且由于没用到使能信号，成本将进一步减少

题目答案

Control of Register Transfers⚓︎

Introduction to Register Transfer Systems⚓︎

基本元素：

• 一组寄存器：大多数是数据通路，部分为控制单元
• 基本操作 ( 微操作 )：寄存器传输
• 控制：监督寄存器传输序列

Register Transfer System Design Procedure⚓︎

• 写下详细的系统规范 (specification)
• 找出所有的输入信号( 数据、控制、状态 )，所有的输出信号( 数据、控制、状态 )，以及寄存器的数据通路和控制单元
• 找出系统的状态机 (state machine diagram)，包括作为输出的数据通路和控制单元上的寄存器传输
• 找出所有的内部控制和状态信号，用这些信号将状态机中的输出条件和行动分开 ( 包括寄存器传输 )，并将它们用表格表示出来
• 画出数据通路的框图，包括所有的控制、状态输入和输出；如果包括寄存器传输的硬件，画出控制的框图
• 设计出具体的寄存器传输逻辑，用于数据通路和控制
• 设计控制单元逻辑
• 验证数据通路和控制单元结合后的操作是否正确，若失败，调试系统并验证改变后的系统，直至符合预期目标

A Design Example( 涉及到状态机的知识，可以选择性阅读 )

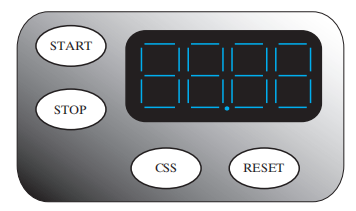
🌰：Dashwatch（一种简单的停表，时间上限为 99.99s）

• 输入：
  • START：将时间复位至 0，随后开始计时
  • STOP：停止计时，在 4 位 BCD 数码管上显示最近的时间
  • CSS：比较、存储和显示最小的时间
  • RESET
• 输出：4 位 BCD 数码管 + 小数点
• 寄存器：
  • 4 位 BCD 计数器 (TM)：每隔 0.01s 向上数
  • 16 位并行加载计时器 (SD)：存储最短的时间

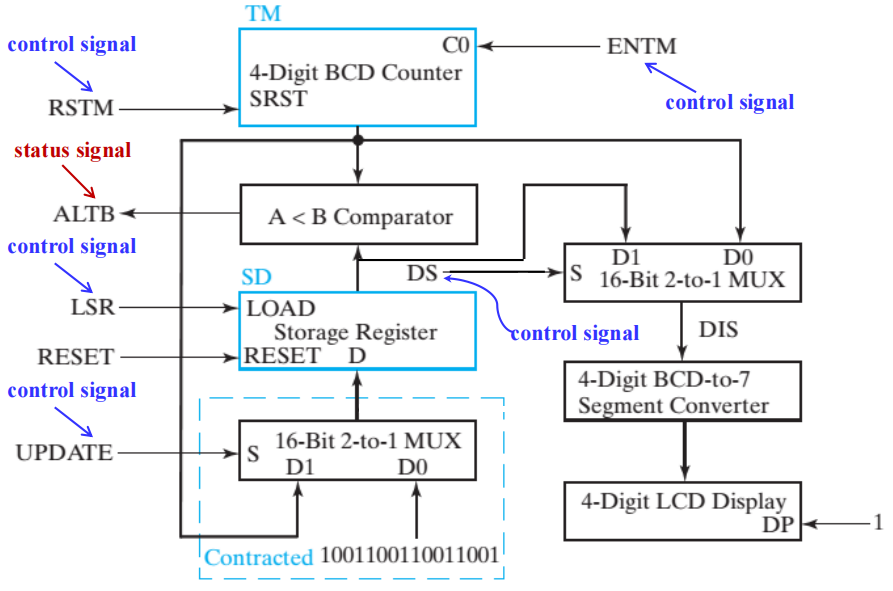
所有的输入、输出和寄存器：

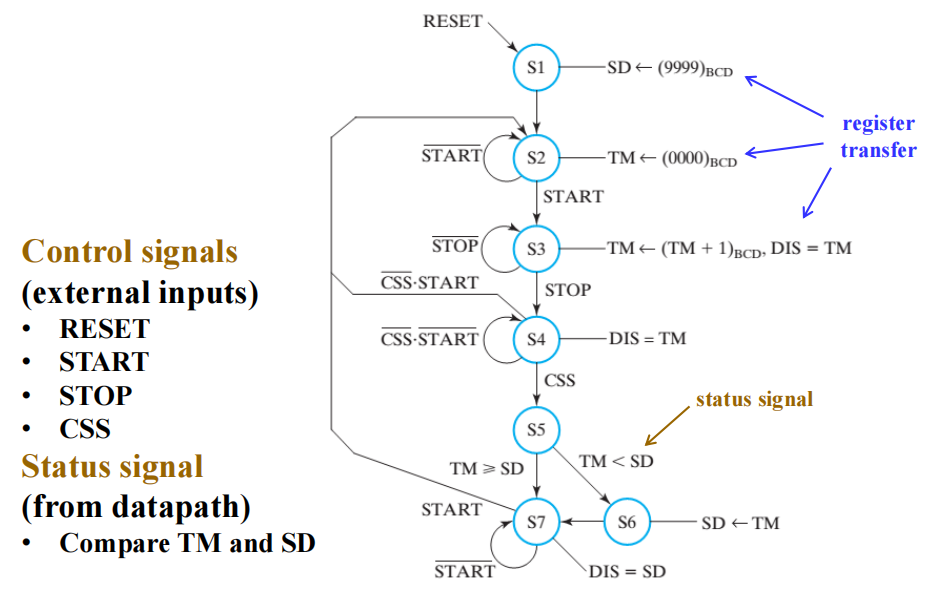
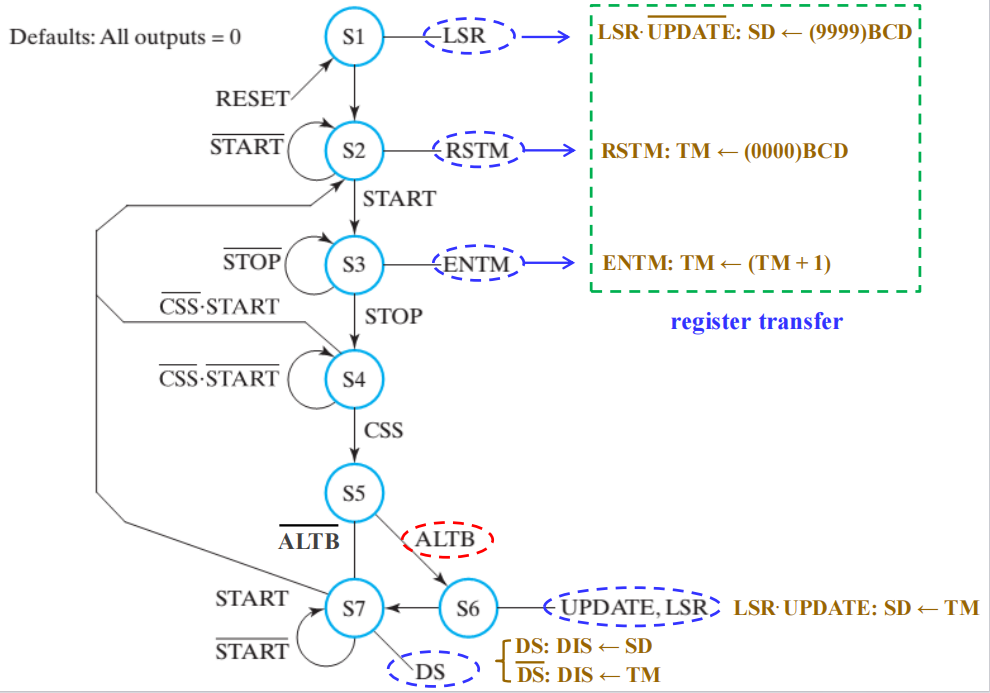
寄存器传输输出的状态机 ( 摩尔型 )

• S1：复位状态，初始化 SD 位 1001100110011001(99.99)，即最大值
• S2：紧随 S1 发生，使 TM = \((0000)_{BCD}\)
• S3：计时状态。按下 START 键后进入计时状态，按下 STOP 键后退出。在该状态下，T 的值在每个时间脉冲内自增 1(0.01s，时钟频率 = 100Hz)，DIS 显示 TM 的值
• S4：决定阶段，从以下 3 个状态中选择 1 个：
  • 比较、存储并显示最短时间
  • 继续显示 TM 的值
  • 重新开始
• S5：比较 TM 和 SD 的值
• S6：如果 TM 更小，TM 的值被加载至 SD 内
• S7：重新开始，并显示 SD 存储的最短时间

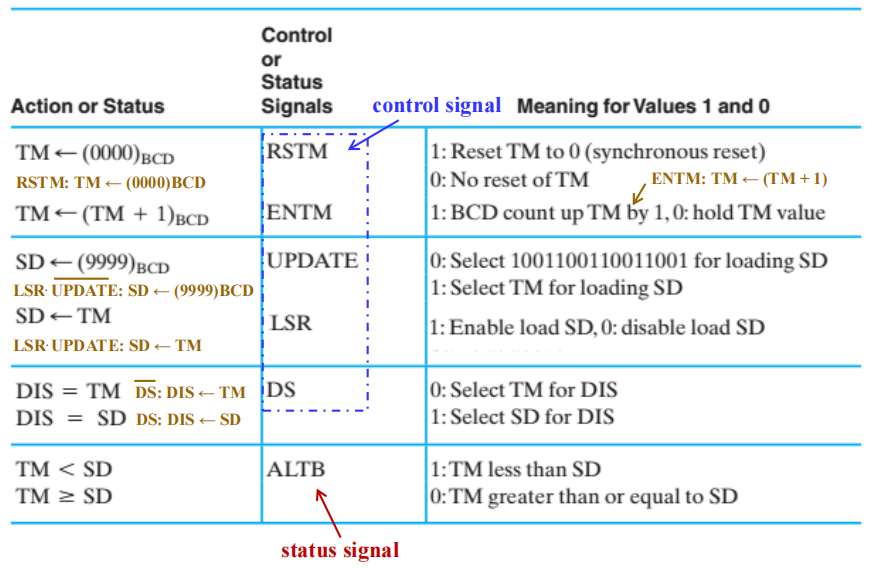
输出控制 / 状态表：

找出内部控制 / 状态信号：

• TM：计时器

  • 复位至 0：RSTM
  • 向上计数的使能信号：ENTM

• SD：最短时间

  • 加载 SD：LSR = 1
  • 选择输入 9999：UPDATE = 0
  • 选择输入 TM：UPDATE = 1

• DIS：显示 (\(B_1, B_0, DP, B_{-1}, B_{-2}\))

  • 选择输入 TM：DS = 0
  • 选择输入 SD：DS = 1

• 比较 TM 和 SD（状态）

  • TM < SD：ALTB = 1
  • TM \(\ge\) SD：ALTB = 0

数据通路：

数据通路的开发细节：

• TM：带有同步复位的 4 位 BCD 计数器

  • 基于先前的 BCD 加法器设计
  • 添加同步复位 SRST
  • SRST = RSTM
  • C0( 进入的进位 ) = ENTM

• A < B 比较器

  • 比较 TM 和 SD
  • 设计从左往右的迭代单元阵列，输出 C0

• SD：标准 16 位并行加载寄存器

  • LOAD = LSR
  • 使用 16 位 2-1MUX，从 \(9999_{BCD}\) 和 TM 中选择并行加载输入 D
  • S = UPDATE

显示逻辑：

• 16 位 2-1MUX
• 4 位 BCD7 段数码管转换器
• 4 位七段数码管显示器 ( 带有小数点 )：小数点控制：DP = 1

取代寄存器传输的控制信号输出的状态机：

使用 D 触发器进行独热码状态分配 (7 位 )，得到下列输入方程：

输出方程为：

\[ \begin{align} LSR & = S1 + S6 \notag\\ RSTM & = S2 \notag\\ ENTM & = S3 \notag\\ UPDATE & = S6 \notag\\ DS & = S7 \notag \end{align} \]

注：课本上还有一个更复杂的例子，我还没来得及看……

Microprogrammed Control⚓︎

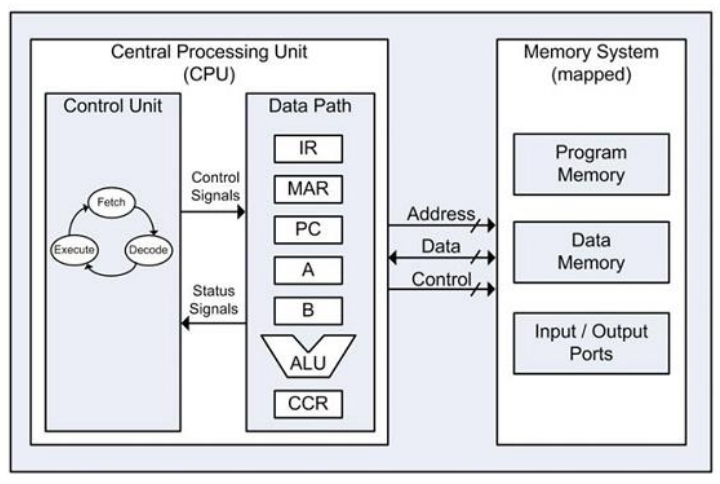
• 不可编程的系统 (non-programmable system)——具体系统
  • 没有编程计数器 (program counter, PC) 或者类似的寄存器
  • 控制单元不进行获取和执行指令的操作，而是基于输入和数据通路的状态位，决定要执行的操作 ( 序列 )
• 可编程的系统 (programmable system)——通用系统
  • 一部分输入由一系列指令 (instruction) 构成，被称为程序 (program)
  • 通常存储于内存，并且由 PC 决定地址
  • 控制单元负责获取和执行指令

Serial Transfers and Microoperations⚓︎

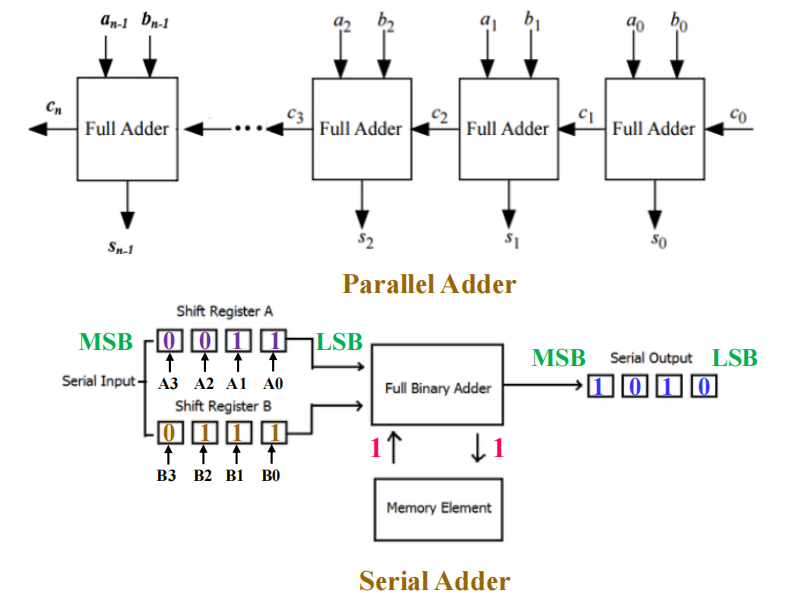
• 当系统在一段时间内只能传递或操作 1 位信息时，称这个系统处于串行模式 (serial mode)
• 与串行传输相对的并行传输 (parallel transfer)：同时传输寄存器的所有位

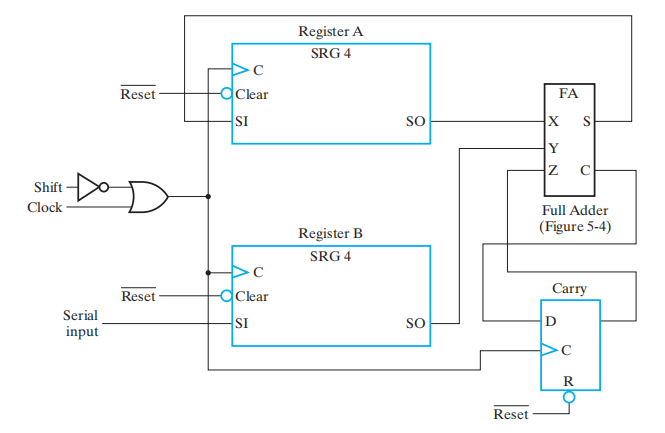
串行传输 ( 移位 )：

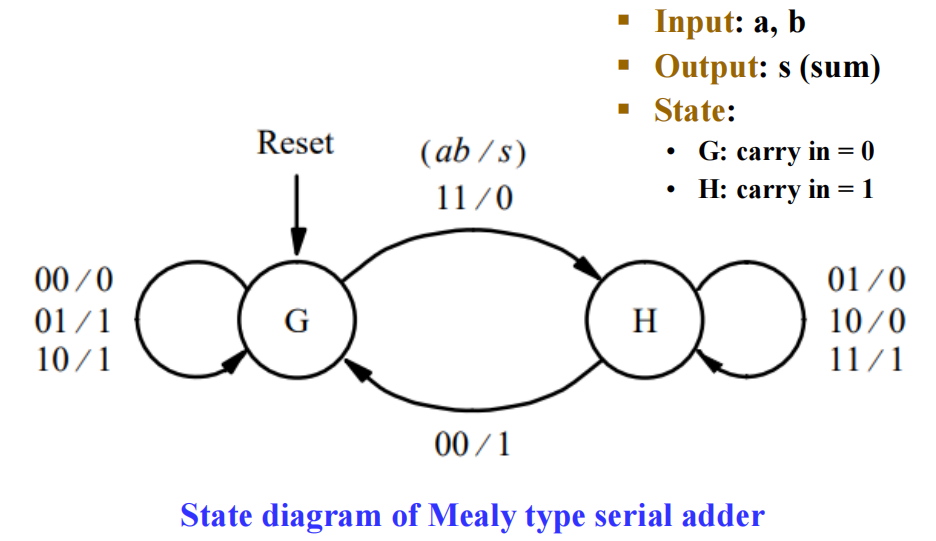
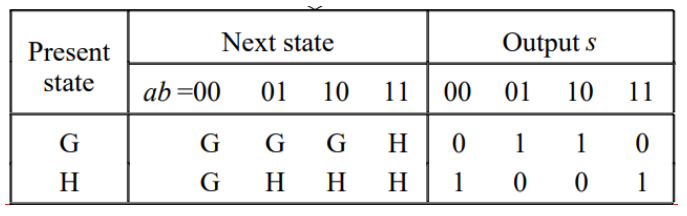
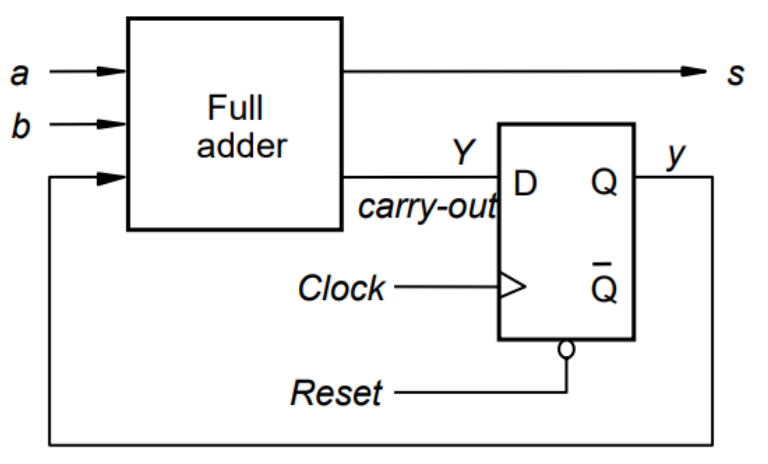
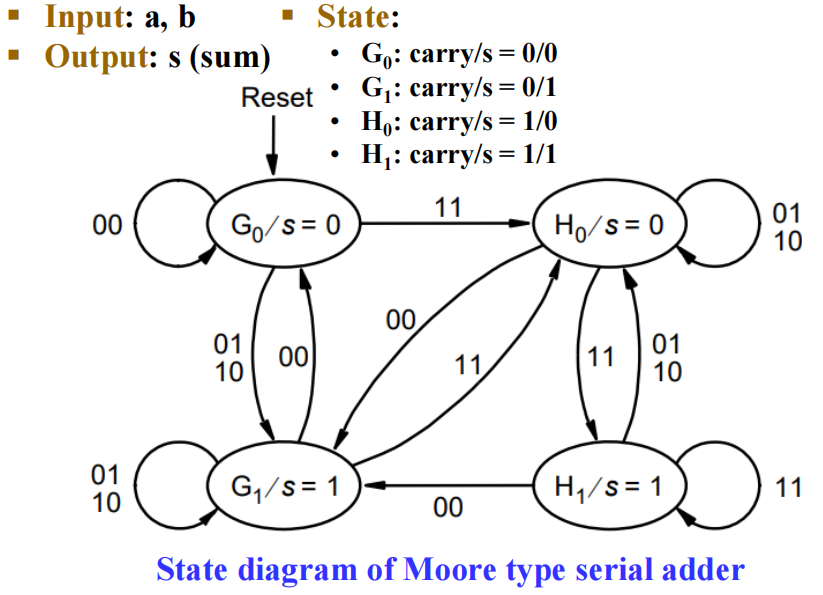
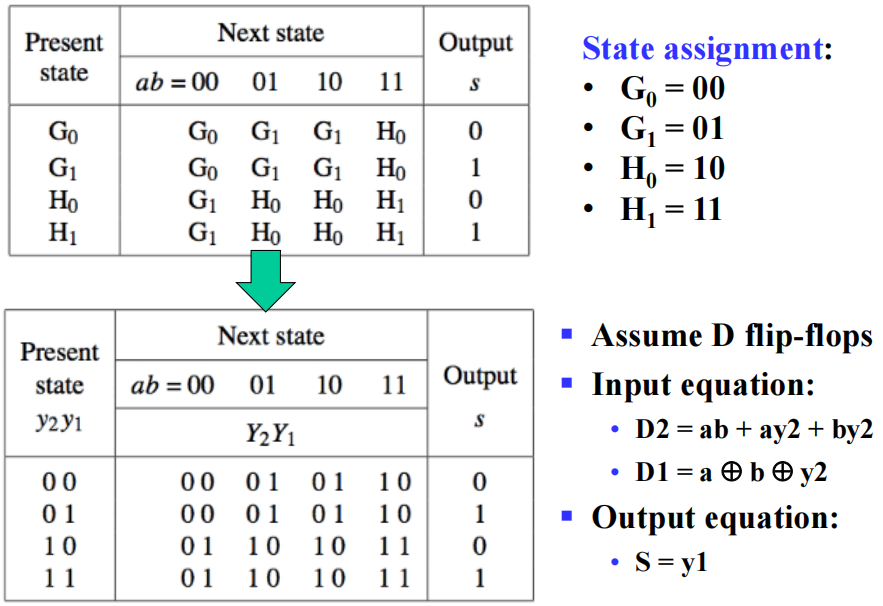
串行加法器 (serial adder)

它是一个时序电路，一次只能执行 1 位二进制加法

用 2 个状态记住进位：

• G：carry in = 0
• H：carry in = 1

米里型摩尔型

状态图：

状态表：

状态分配后的状态表：

化简 ( 略 )

输入方程：\(D = ab + ay + by\) 输出方程：\(S = a \oplus b \oplus y\)

框图：

状态图：

状态表，输入方程和输入方程

框图：

上面 2 个电路仅保存了进位，如果我们想实现 \(A \leftarrow A + B\)，就需要保存 A 的值。教材给出了对应的实现：

评论区