Sets, Relations and Language⚓︎

Sets⚓︎

• 集合
  • 没有重复元素
  • 顺序不重要
• 元素 / 成员
• 单元集 (singleton)：只有 1 个元素的集合
• 空集 \(\emptyset\)
• 子集
• 真子集 (proper subset)
• 判断两个集合是否相等

• 集合运算

  • 并 (union)：\(\bigcup S = \{x : x \in P \text{ for some set } P \in S\}\)
  • 交 (intersection)：\(\bigcap S = \{x : x \in P \text{ for each set } P \in S\}\)
  • 差 (difference)

• 集合的性质：

  • 幂等性 (idempotency)：\(A \cup A = A, A \cap A = A\)
  • 交换律 (commutativity)：\(A \cup B = B \cup A, A \cap B = B \cap A\)
  • 结合律 (associativity)：\((A \cup B) \cup C = A \cup (B \cup C), (A \cap B) \cap C = A \cap (B \cap C)\)
  • 分配律(distributivity)：\((A \cup B) \cap C = (A \cap C) \cup (B \cap C), (A \cap B) \cup C = (A \cup C) \cap (B \cup C)\)
  • 吸收律 (absorption)：\((A \cup B) \cap A = A, (A \cap B) \cup A = A\)
  • 德摩根定律(Demorgan's law)：\(A - (B \cup C) = (A - B) \cap (A - C), A - (B \cap C) = (A - B) \cup (A - C)\)
    • \(A = U\)（全集）的时候可能是我们更加熟悉的形式

• 不相交集 (disjoint)：两个集合无公共元素，即它们的交集为空集

• 幂集(power set)：包含某一集合 \(A\) 所有子集的集合，记作 \(2^A\)
• 划分(partition)：幂集的子集，记作 \(\Pi\)，并且满足：
  • 不包含空集
  • 每个元素（原集合的子集）互不相交
  • \(\bigcup \Pi = A\)

Relations and Functions⚓︎

• 有序对(ordered pair) \((a, b)\)

  • \(a, b\) 为其分量 (component)
  • 和集合 \(\{a, b\}\) 不同，首先要考虑分量的顺序，其次两个分量可以是一样的

• 集合 \(A, B\) 的笛卡尔积(Cartesian product)：记作 \(A \times B\)，所有有序对 \((a, b)\ (a \in A \text{ and } b \in B)\) 构成的集合

• 集合 \(A, B\) 的二元关系(binary relation) 即为 \(A \times B\) 的子集

• 有序元组(ordered tuple) \((a_1, \dots, a_n)\)（其中 \(n\) 为任意自然数）

  • 有序三元组 / 四元组 / 五元组 / 六元组 (ordered triples/quadruples/quintuple/sextuples)

• 序列(sequence) 即未指定 \(n\)（序列长度）的有序 \(n\) 元组

• n 重笛卡尔积(n-folds Cartesian product) \(A_1 \times \dots \times A_n\)：所有有序对 \((a_1, \dots, a_n)\ (a_i \in A_i\ (i = 1, \dots, n))\) 构成的集合
• n 元关系(n-ary relation) 即为 \(A_1 \times \dots \times A_n\) 的子集
  • 1, 2, 3 元关系分别对应 unary/binary/tenary relations

• 集合 \(A\) 到集合 \(B\) 的函数(function) 是 \(A\) 到 \(B\) 的二元关系，并满足以下性质：对于每个元素 \(a \in A\)，恰好存在一个以 \(a\) 为第一元素的有序对
• 一般用 \(f, g, h\) 表示函数
• \(f: A \mapsto B\) 表示从 \(A\) 到 \(B\) 的函数 \(f\)
• 其中 \(A\) 为函数的域(domain)
• \(f(a)\) 为 \(a\) 在 \(f\) 中的像(image)
• 若 \(A'\) 是 \(A\) 的子集，那么定义 \(f[A'] = \{f(a): a \in A'\}\)，称 \(f[A']\) 为 \(A'\) 在 \(f\) 中的像
• \(f\) 的范围(range) 即为域对应的像
• 若函数为 \(f: A_1 \times \dots A_n \mapsto B\)，并且 \(f(a_1, \dots, a_n) = b\)（\(a_i \in A_i \text{ and } b \in B\)），那么称 \(a_1, \dots, a_n\) 为 \(f\) 的参数(auguments)，\(b\) 为 \(f\) 的值(value)

• 对于 \(f: A \mapsto B\)

  • 若对于任意两个不同元素 \(a, a' \in A,\ f(a) \ne f(a')\)，称 \(f\) 是单射的 (one-to-one)
  • 若 \(B\) 的每个元素是 \(A\) 中某些元素的像，称 \(f\) 是满射的 (onto)
  • 若既是单射，又是满射，那么 \(f\) 是双射函数 (bijection)

• 二元关系 \(R \subseteq A \times B\) 的逆(inverse) 记作 \(R^{-1} \subseteq B \times A\)，即 \(\{(b, a) : (a, b) \in R\}\)

  • 但函数的逆不一定是函数，只有当 \(f\) 是双射时才能保证是函数（即反函数 \(f^{-1}\)）
  • \(f^{-1}(f(a)) = a\ (\forall a \in A)\)，\(f(f^{-1}(b)) = b\ (\forall b \in B)\)

Special Types of Binary Relations⚓︎

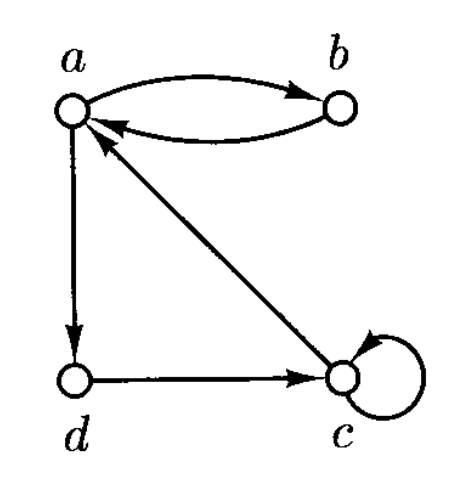
（二元）关系 \(R \subseteq A \times A\) 可以被表示为一张有向图(directed graph)

• \(A\) 的每个元素用一个小圈表示，称为节点(node)
• 而 \((a, b)\) 则用由 \(a\) 到 \(b\) 的箭头表示，称为边(edge)

有向图（\(R \subseteq A \times A\)）的一些性质：

• 自反(reflective)：\((a, a) \in R, a \in A\)

• 对称(symmetric)：当 \((a, b) \in R\) 时，\((b, a) \in R\)

  • 没有形如 \((a, a)\) 对的对称关系可用无向图(undirected graph) 表示

• 反对称(antisymmetric)：当 \((a, b) \in R\) 时，\((b, a) \notin R\)

• 传递(transitive)：当 \((a, b), (b, c) \in R\) 时，\((a, c) \in R\)

同时满足自反、对称、传递的关系被称为等价关系(equivalence relation)。用无向图表示的等价关系由一组集群构成，这些集群就是等价类(equivalence classes)，如下图所示：

通常我们用 \([a]\) 表示包含元素 \(a\) 的等价类，即 \([a] = \{b: (a, b) \in R \text{ or } (b, a) \in R\}\)。

而同时满足自反、反对称和传递的关系被称为偏序(partial order)。假如 \(R \subseteq A \times A\) 是偏序，

• 对于 \(a \in A\)，若满足仅当 \(a = b\) 时 \((b, a) \in R\)，称 \(a\) 为最小值(minimal)
  • 可以这么想：最小值 \(a\) 总是要位于左侧，除非右侧也是 \(a\)
• \(\forall a, b \in A\)，\((a, b) \in A\) 且 \((b, a) \in A\)，那么偏序 \(R\) 就是全序(total order)

二元关系的路径(path) 是一个序列 \((a_1, \dots, a_n)\)（\(n \ge 1\)），满足 \((a_i, a_{i+1}) \in R\)（\(i = 1, \dots, n-1\)）。路径长度就是 \(n\)。

• 对于路径 \((a_1, \dots, a_n)\)，当 \((a_n, a_1) \in R\) 时，该路径就是一个环(cycle)。

Finite and Infinite Sets⚓︎

若存在双射 \(f: A \mapsto B\)，称集合 \(A, B\) 是等势的(equinumerous)。由于双射可逆，因此等势性体现了对称关系。

若集合与 \(\{1, 2, \dots, n\}\)（\(n\) 为自然数）等势，那么该集合是有限的(finite)。而 \(A\) 的基数(cardinality) \(|A|\) 就是 \(n\)（即有限集合的元素个数）。

当集合不是有限的，那就是无限的(infinite)。需要注意的是，不是所有的无限集合是等势的。

若集合与 \(\mathbb{N}\) 等势，那么该集合就是可数无限的(countably infinite)；并且有限和可数无限均属于可数的(countable)，反之就是不可数的(uncountable)。

Three Fundamental Proof Techniques⚓︎

下面介绍三种在各种证明中经常出现的基本原理 (fundamental principle)：

• 数学归纳法(mathematical induction)：令 \(A\) 为一个自然数集合，满足：

  • \(0 \in A\)
  • 对于每个自然数 \(n\)，若 \(\{0, 1, \dots, n\} \subseteq A\)，那么 \(n + 1 \in A\)

  那么 \(A = \mathbb{N}\)

  • 可以用反证法 (contradiction) 证明其正确性

  • 实际上归纳法通常用来证明以下形式的断言：“对于任意自然数 \(n\)，性质 \(P\) 为真。”设集合 \(A = \{n : P \text{ is true of } n\}\)，那么：

    • 在基础步骤(basis step) 中证明 \(0 \in A\)，即 \(P\) 在 \(0\) 上为真
    • 归纳假设(induction hypothesis)：对于固定但任意的 \(n \ge 0\)，\(P\) 在每个自然数 \(0, 1, \dots, n\) 都成立
    • 在归纳步骤中，要利用归纳假设证明 \(P\) 在 \(n+1\) 上为真

    以上便是运用数学归纳法的模板。

  • 具体应用可参考教材列出的例子

• 鸽巢原理(pigeonhole principle)：若 \(A, B\) 是有限集合且 \(|A| > |B|\)，那么 \(A\) 到 \(B\) 的映射不是单射。

  • 通俗版：假设 \(A\) 表示一群鸽子，\(B\) 表示一些鸽巢，那么至少有一个鸽巢会有超过一只的鸽子
  • 可用数学归纳法证明（具体证明见教材，这里只给思路）
    • 基本步骤：证明 \(|B| = 0\) 时成立
    • 归纳假设：\(|B| \le n\) 时均成立
    • 归纳步骤：证明 \(|B| = n + 1\) 时成立

  定理

  令 \(R\) 为有限集合 \(A\) 上的二元关系，\(a, b \in A\)，若 \(R\) 上存在由 \(a\) 到 \(b\) 的路径，那么路径长度至多为 \(|A|\)。

  证明

  用鸽巢原理 + 反证法，其实挺简单的，所以这里不给证明，可参考教材。

• 对角化(diagonalization)：令 \(R\) 为集合 \(A\) 上的二元关系，且令 \(D\) 为 \(R\) 上的对角集合 (diagonal set)，即 \(\{a : a \in A \text{ and } (a, a) \notin R\}\)。\(\forall a \in A\)，令 \(R_a = \{b : b \in A \text{ and } (a, b) \in R\}\)，那么 \(D\) 和所有 \(R_a\) 均不同。

  定理

  幂集 \(2^{\mathbb{N}}\) 是不可数的。

  证明

  假设 \(2^{\mathbb{N}}\) 是可数无限的，也就是说假定存在一种方法可以枚举 \(2^N\) 的所有元素，如： $$ 2^{\mathbb{N}} = {R_0, R_1, R_2, \dots} $$

  （注意这些就是在对角化原理陈述中的集合 \(R_a\)，一旦我们考虑关系 \(R = \{(i,j) : j \in R_i\}\)）。现在考虑（对角）集合 $$ D = {n \in N : n \notin R_n} $$

  \(D\) 是自然数的一个子集，因此它应该出现在枚举 \(\{R_0, R_1, R_2, \dots\}\) 中的某个位置。

  • 但 \(D\) 不可能是 \(R_0\)，因为它在是否包含 0 这一点上与 \(R_0\) 不同（当且仅当 0 不在 \(R_0\) 中时，0 在 \(D\) 中）
  • 同样地，它也不可能是 \(R_1\)，因为它在 1 的归属上不同于 \(R_1\)
  • 以此类推，不得不推出这样一个结论：\(D\) 根本不会出现在这个枚举中，这就和假设产生了矛盾

Closures and Algorithms⚓︎

根据上述定义，我们可以得到一个计算对于任意给定的在有限集合 \(A = \{a_1, a_2, \dots, a_n\}\) 上的二元关系 \(R\) 的自反传递闭包的算法（该算法的正确性来自其对定义的直接实现）：

Initially R^* = emptyset
for i = 1, ..., n do
    for each i-tuple (b[1], ..., b[n]) in A^i do
        if (b[1], ..., b[i]) is a path in R then add (b[1], b[i]) to R^*

显然算法最终会得出正确答案。接下来要研究的问题是：它将在多少步之后终止(terminate)？答案取决于输入关系的规模，即依赖于集合 \(A\) 中元素的数量 \(n\)。因此，我们要寻找一个函数 \(f: \mathbb{N} \mapsto \mathbb{N}\)，使得当 \(n \ge 1\) 时，对于二元关系 \(R \subseteq A \times A, |A| = n\)，算法 \(f(n)\) 步后终止。

正如算法分析中常见的那样，我们允许 \(f(n)\) 是一个粗略的高估 (overestimate)，只要其增长率(rate of growth) 正确即可。下面就来探讨增长率这一话题。

Growth of Functions⚓︎

如果有两个函数 \(f, g: \mathbb{N} \mapsto \mathbb{N}\)，有 \(f \in \mathcal{O}(g), g \in \mathcal{O}(f)\)，那么可以写作 \(f \asymp g\)。容易证明，\(\asymp\) 是一个等价关系。

因此，所有从自然数集合到其自身的函数可通过 \(\asymp\) 划分为不同的等价类中。\(f\) 关于 \(\asymp\) 的等价类就是 \(f\) 的增长率。

Analysis of Algorithms⚓︎

现在对上述算法所需步骤做一个大致的估计：

• 算法需要检验每个序列 \((b_1, \dots, b_i)\)（长度至多为 \(n\)），确定它是否为 \(R\) 的一条路径，若是则将其放入 \(R^*\)
• 每次检验都需要不超过 \(n\) 次的这样的的基本运算：测试 \((a, b)\) 是否在 \(R\) 内，以及将 \((a, b)\) 放入 \(R^*\) 内
• 因此总运算次数不超过 \(n \cdot (1 + n + n^2 + \dots + n^n)\)，即该算法所需时间的增长率为 \(\mathcal{O}(n^{n+1})\)，效率超低！

于是考虑以下更高效的算法，并且可能比前面的算法看起来更为自然和直观：

# reflective
Initially R^* = R union {(a[i], a[i]) : a[i] in A}
# transitive
while there are three elements a[i], a[j], a[k] in A such that 
    (a[i], a[j]), (a[j], a[k]) in R^* but (a[i], a[k]) not in R^* do:
        add (a[i], a[k]) to R^*

算法的正确性不言而喻。那么算法何时停止呢？答案是至多 \(n^2\) 次迭代，因为 \(R^*\) 至多有 \(n^2\) 个二元对。并且由于每次迭代需要 \(\mathcal{O}(n^3)\) 的操作（因为三元组中的每个元素都要被搜一遍），所以整个算法的复杂度为 \(\mathcal{O}(n^5)\)。从原来的指数(exponential) 级降至多项式(polynomial) 级，该算法实现了巨大的提升！

然而这样还不够高效——一个显而易见的问题是该算法会重复遍历已经检查过的三元组。如果能够克服这个问题，算法的复杂度就能降至 \(\mathcal{O}(n^3)\)（每个三元组仅检查一次）。改进思路是将三元组按中间元素的索引升序排序遍历，对应算法如下：

Initially R^* = R union {(a[i], a[i]) : a[i] in A}
for each j = 1, 2, ..., n do
    for each i = 1, 2, ..., n and k = 1, 2, ..., n do
        if (a[i], a[j]), (a[j], a[k]) in R^* but (a[i], a[k]) not in R^* then
            add (a[i], a[k]) to R^*

要想证明该算法的正确性，就需要证明以下陈述：对于每个 \(j = 1, \dots, n\)，在外层循环执行完 \(j\) 次后，\(R^*\) 包含了所有 \((a_i, a_k)\) 对，满足 \(R\) 中从 \(a_i\) 到 \(a_k\) 之间有一条等级(rank)（路径上中间节点的最大索引，不包括起点和终点）不超过 \(j\) 的路径。可通过归纳法证明，具体证明过程见教材 \(P_{37}\)，这里不再赘述。

Closure Properties and Closures⚓︎

任何在有限集合上的闭包性质能在多项式时间内被算出来。假设在有限集合 \(D\) 上有不同元数的关系 \(R_1 \subseteq D^{r_1}, \dots, R_k \subseteq D^{r_k}\)，并有集合 \(A \subseteq D\)。现在要计算 \(A\) 在关系 \(R_1, \dots, R_k\) 下的闭包 \(A^*\)。我们可以通过泛化前面得到的 \(\mathcal{O}(n^5)\) 的传递闭包算法实现在多项式时间内的计算。

Initially A^* = A
while there is an index i, 1 <= i <= k, and r[i] elements a[j[1]], ..., a[j[r[i-1]]] in A^*
    and a[j[r[i]]] in D - A^* such that (a[j[1]], ..., a[j[r[i]]]) in R[i] do:
        add a[j[r[i]]] in A^*

该算法的复杂度为 \(\mathcal{O}(n^{r+1})\)，其中 \(n = |D|\) 且 \(r\) 为 \(r_1, \dots, r_k\) 中最大的数。

Alphabets and Languages⚓︎

计算理论的数学研究必须要从理解符号字符串的数学原理开始。

• 字母表(alphabet)：关于符号(symbol) 的有限集合
  • 和计算理论密切相关的一个字母表是二元字母表(binary alphabet) \(\{0, 1\}\)

• 字符串(string)：来自字母表的有限符号序列

  • 字符串的书写不需要用括号或逗号间隔，而是直接将符号连在一起写，比如 watermelon, 0110011
  • 单个符号等同于用该符号表示的字符串
  • 没有符号的字符串是空字符串(empty string)，记作 \(e\)
  • 一般使用 \(u, v, w, x, y, z\) 和希腊字母表示字符串
  • \(\Sigma^*\)：在字母表 \(\Sigma\) 上的所有字符串集合
  • \(\Sigma^+\)：在字母表 \(\Sigma\) 上的非空字符串集合
  • \(\Sigma^n\)：在字母表 \(\Sigma\) 上的长度为 \(n\) 的字符串集合
  • 字符串 \(w\) 的长度(length) 即序列长度，记作 \(|w|\)
  • 可将字符串看作一个函数 \(w: \{1, \dots, |w|\} \mapsto \Sigma\)；\(w(j)\) 的值就是 \(w\) 在第 \(j\) 个位置上的符号
  • 如果需要区分不同位置上的相同符号，我们将它们称为该符号的不同出现(occurrence)

  • 拼接(concatenation)：将两个来自相同字母表的字符串 \(x, y\) 结合起来，形成新的字符串，记作 \(x \circ y\) 或 \(xy\)

    • 形式上的，当且仅当 \(|w| = |x| + |y|, w(j) = x(j)\ (j = 1, \dots, |x|)\) 且 \(w(|x| + j) = y(j)\ (j = 1, \dots, |y|)\) 时， \(w = x \circ y\)
    • \(w \circ e = e \circ w = w\)
    • 拼接满足结合律，即 \((wx)y = w(xy)\)
    • 当且仅当存在字符串 \(x, y\)，满足 \(w = xvy\)，称字符串 \(v\) 为 \(w\) 的子字符串(substring)；此外还有以下特殊情况：
      • \(w = xv\) -> \(v\) 是 \(w\) 的后缀(suffix)
      • \(w = vy\) -> \(v\) 是 \(w\) 的前缀(prefix)

    • 字符串 \(w^i\) 的定义如下（一种归纳定义(definition by induction)）：

      \[ \begin{aligned} w^0 & = e, \quad \text{the empty string} \\ w^{i+1} & = w^i \circ w, \quad \text{for each } i \ge 0 \end{aligned} \]

  • 反转(reversal)：记作 \(w^R\)

    • 形式的归纳定义为：
      • 若 \(|w| = 0\)，则 \(w^R = w = e\)
      • 若 \(|w| = n + 1 > 0\)，则 \(w = ua\)，其中 \(a \in \Sigma\) 且 \(w^r = au^R\)

• 语言(language)：\(\Sigma^*\) 的任意子集（即字母表 \(\Sigma\) 上任意字符串构成的集合）

  • \(\Sigma^*, \emptyset, \Sigma\) 都是语言

  • 用以下形式表述无限 (infinite) 语言：

    \[ L=\{w\in\Sigma^*:w\text{ has property }P\} \]

  • 若 \(\Sigma\) 是有限字母表，那么 \(\Sigma^*\) 是可数无限的

  • 要想构建双射 \(f: \mathbb{N} \mapsto \Sigma^*\)，首先要确定字母表顺序，即 \(\Sigma = \{a_1, \dots, a_n\}\)，然后可按以下方式枚举 \(\Sigma^*\) 的成员：

    • \(\forall k \ge 0\)，所有长度为 \(k\) 的字符串应在长度为 \(k+1\) 字符串之前被枚举
    • 长度恰好为 \(k\) 的 \(n^k\) 个字符串按词典序(lexicographically) 枚举，即 \(a_{i_1}, \dots, a_{i_k}\) 先于 \(a_{j_1}, \dots, a_{j_k}\) 枚举，其中 \(0 \le m \le k - 1, i_l = j_l\ (l = 1, \dots, m), i_{m+1} < j_{m+1}\)

  • 由于语言本质上是集合，所以可通过集合运算（并、交、差）将语言结合起来

    • \(A\) 的补(complement) 为 \(\bar{A} = \Sigma^* - A\)

  • 语言的拼接(concatenation)：若 \(L_1, L_2\) 为在 \(\Sigma\) 上的语言，那么拼接为 \(L = L_1 \circ L_2 = L_1 L_2\)，其中

    \[ L=\{w\in\Sigma^*:w=x\circ y\text{ for some }x\in L_1\mathrm{~and~}y\in L_2\} \]

  • 克莱尼星号(Kleene star)：记作 \(L^*\)，是通过拼接 0 个或多个来自 \(L\) 的字符串构成的全部字符串的集合，即

    \[ L^*=\{w\in\Sigma^*:w=w_1\circ\cdots\circ w_k\text{ for some }k\geq0\text{ and some }w_1,\ldots,w_k\in L\} \]
    • 如果将字母表看作一种有限语言，那么 \(\Sigma^*\) 的定义和克莱尼星号是一致的

  • \(L\) 在拼接运算下的闭包(closure) 记作 \(L^+ = LL^*\)，即包含 \(L\) 和所有由 \(L\) 内字符串拼接而成的字符串的最小语言

    \[ \{w\in\Sigma^*:w=w_1\circ w_2\circ\cdots\circ w_k\text{ for some }k\geq1\text{ and some }w_1,\ldots,w_k\in L\} \]

评论区