Finite Automata and Regular Expressions⚓︎
约 8935 个字 3 行代码 预计阅读时间 45 分钟
核心知识
- DFA
- NFA
- DFA == NFA
- RE & RL
- RE 的定义
- RL 的运算封闭性:并、拼接、克莱尼星号、补、交
- RL <=> FA
- 泵定理
约定
用 DFA 和 NFA 分别指代确定性有限自动机和非确定性有限自动机。
Deterministic Finite Automata⚓︎
有限自动机(finite automata) 接收字符串输入并以输入纸带(input tape) 的形式传递,之后仅输出一个关于是否认为输入可接受(acceptable) 的指示。更多有关有限自动机(更准确的说,是确定性有限自动机(deterministic finite automata, DFA))操作的细节如下:
- 输入纸带被划分为一个个方格,每个方格表示字符串上的单个符号
- 整个机器的主要部分可看作是在任意时刻处于其中一种内部状态(state)(总的状态数是有限的)的一个“黑盒”
- 这个“黑盒”叫做有限控制(finite control),它借助一个可移动的读头(reading head) 感知输入纸带上任意位置所写的符号
- 一开始,读头置于纸带的最左端方格,有限控制设定为初始状态(initial state)
- 每隔固定的一段时间,自动机从输入纸带上读取一个符号,随后根据当前状态及所读符号进入新状态,读完后读头会向右移动一格
- 上述过程反复进行,直到到达输入字符串的末端时,自动机通过其结束时所处的状态来表示对所读内容的接受与否
- 如果它停在一个最终状态(final state) 集合中的某个状态上,则该输入字符串被视为被接受的(accepted)
- 机器所接受的语言就是它所接受的字符串集合
下面给出 DFA 的形式化定义:
定义
确定性有限自动机是一个五元组 \(M = (K, \Sigma, \delta, s, F)\),其中
- \(K\):状态的有限集合
- \(\Sigma\):字母表
- \(s \in K\):初始状态(start state)
- \(F \subseteq K\):最终状态(final states) 集合
- \(\delta\):转移函数(transition function),一个从 \(K \times \Sigma\) 到 \(K\) 的函数
- 如果 \(M\) 处在状态 \(q \in K\),且从输入纸带上读到符号 \(a \in \Sigma\),那么 \(\delta(q, a) \in K\) 是一个唯一确定的(下一个)状态
- DFA 的配置(configuration) \(C\) 由当前状态 \(q\) 和剩余字符串 \(w\) 决定,即 \(C = (q, w)\)(对于上图,就是 \((q_2, ababab)\))
- 若 \((q, w)\) 和 \((q', w')\) 是 \(M\) 的两个配置,那么 \((q, w) \vdash_M (q', w')\) 当且仅当对于某个符号 \(a \in \Sigma\),有 \(w = aw'\) 并且 \(\delta(q, a) = q'\) 时成立,即 \((q, w)\) 在一步内产生(yields in one step) \((q', w')\)
- 注意实际上 \(\vdash_M\) 是从 \(K \times \Sigma^+\) 到 \(K \times \Sigma^*\) 的一个函数,也就是说,除了形如 \((q, e)\) 的配置外,每个配置都有唯一确定的下一个配置
- 而形如 \((q, e)\) 的配置意味着 \(M\) 已经读完所有输入,因此停止处理
-
用符号 \(\vdash_M^*\) 表示 \(\vdash_M\) 的自反传递闭包;\((q, w) \vdash_M^* (q', w')\) 就表示 \((q, w)\) 在 0 步或多步内产生了 \((q', w')\)
- 当且仅当存在状态 \(q \in F\),使得 \((s, w) \vdash_M^* (q, e)\) 成立时,字符串 \(w \in \Sigma^*\) 被 \(M\) 接受
- 被 \(M\) 接受的语言 \(L(M)\) 是所有被 \(M\) 接受的字符串的集合
-
图形化表示:状态图(state diagram)
例子
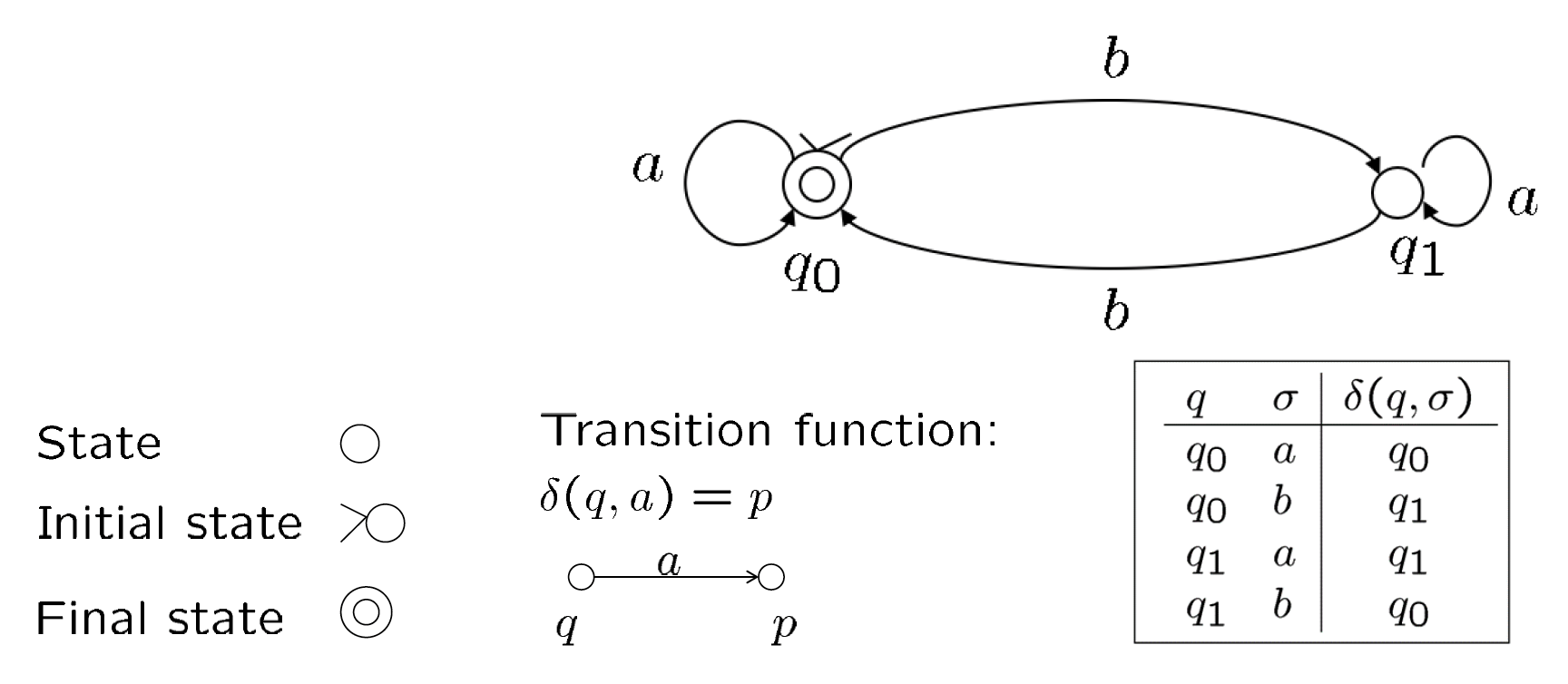
假如确定性有限状态机 \(M = (K, \Sigma, \delta, s, F)\),其中:
而 \(\delta\) 为:
| \(q\) | \(\sigma\) | \(\delta(q, \sigma)\) |
|---|---|---|
| \(q_0\) | \(a\) | \(q_0\) |
| \(q_0\) | \(b\) | \(q_1\) |
| \(q_1\) | \(a\) | \(q_1\) |
| \(q_1\) | \(b\) | \(q_0\) |
不难发现 \(L(M)\) 表示的是有偶数个 \(b\) 的字符串。
除了表格形式外,我们也可以用状态图(state diagram) 表示转移函数,如下所示:
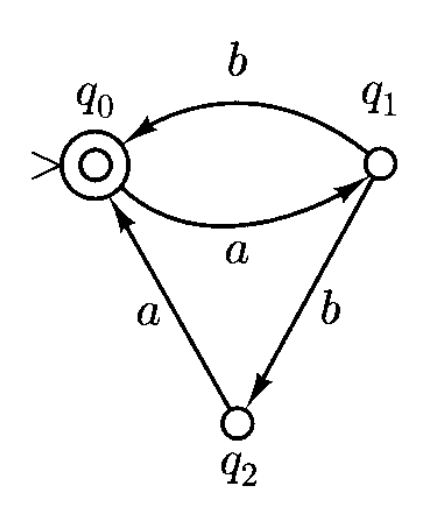
下面设计一个确定性有限状态机 \(M\),它接受语言 \(L(M) = \{w \in \{a, b\}^*: w \text{ does not contain three consecutive b's}\}\),其中:
而 \(\delta\) 为:
| \(q\) | \(\sigma\) | \(\delta(q, \sigma)\) |
|---|---|---|
| \(q_0\) | \(a\) | \(q_0\) |
| \(q_0\) | \(b\) | \(q_1\) |
| \(q_1\) | \(a\) | \(q_0\) |
| \(q_1\) | \(b\) | \(q_2\) |
| \(q_2\) | \(a\) | \(q_0\) |
| \(q_2\) | \(b\) | \(q_3\) |
| \(q_3\) | \(a\) | \(q_3\) |
| \(q_3\) | \(b\) | \(q_3\) |
对应的状态图如下:
可以看到,如果出现连续 3 个 \(b\) 的情况,状态机就会陷入(trap) \(q_3\) 这唯一的非最终状态,因而该字符串无法为自动机接受。我们称 \(q_3\) 为死亡状态(dead state)。DFA 最小化 (minimization)(来自朋辈辅学)
这一块其实教材中提到过,但课件上没有列出,应该不作为考点吧 ...
任意能被 DFA 表示的语言都存在唯一的最小化 DFA。最小化 DFA 的步骤:
- 删除不可达状态
- 合并等价状态:将状态划分为若干等价类
- 接受状态与非接受状态不等价
- 对某一输入符号转移到不同等价类的两个状态不等价
- 从 \(\{K - F, F\}\) 开始,不断划分每个暂定的等价类,直到无法划分
Nondeterministic Finite Automata⚓︎
自动机的非确定性(nondeterminism) 是指状态的改变仅部分取决于当前状态和输入符号。也就是说对于给定的当前状态和输入符号,允许有多种可能的下一状态;自动机可能会选择这些合法的下一状态中的任意一个,而这个选择不受模型的影响。
这种不确定性是对有限状态机的符号化推广 (notational generalization),能够极大简化对自动机的描述。并且稍后我们会看到:每个非确定性有限自动机等价于某个确定性有限自动机。
例子
假如设计一个自动机 \(M\),它能够接受语言 \(L = (ab \cup aba)^*\)。对应的 DFA 和 NFA 的状态图分别如下:
另外,我们允许 NFA 上有带空字符串 \(e\) 的箭头,这能让自动机在不读取任何输入的情况下实现状态转移。
NFA 的形式化定义如下:
定义
非确定性有限自动机(nondeterministic finite automata, NFA) 是一个五元组 \(M = (K, \Sigma, \Delta, s, F)\),其中:
- \(K\):状态的有限集合
- \(\Sigma\):字母表
- \(s \in K\):初始状态
- \(F \subseteq K\):最终状态集合
- \(\Delta\):转移关系(transition relation),一个从 \(K \times (\Sigma \cup \{e\}) \times K\) 的子集
- 元组 \((q, a, p) \in \Delta\) 被称为 \(M\) 的转移(transition)。当 \(M\) 处在状态 \(q\) 且输入符号为 \(a\) 时,\(M\) 会可能会进行 \((q, a, p)\) 或 \((q, e, p)\) 中的任何一种转移
- \(M\) 的配置是 \(K \times \Sigma^*\) 中的一个元素
- 配置间的关系 \(\vdash_M\)(一步内产生)的定义如下:当前仅当存在 \(u \in \Sigma\) 使得 \(w = uw'\),且 \((q, u, q') \in \Delta\) 时,\((q, w) \vdash_M (q', w')\)
- \(\vdash_M\) 不必是函数,因为可能存在一对多的映射
- \(\vdash_M^*\) 是 \(\vdash_M\) 的自反传递闭包;当且仅当 \(\exists\ q \in F\),\((s, w) \vdash_M^* (q, e)\),称字符串 \(w \in \Sigma^*\) 为 \(M\) 接受
例子
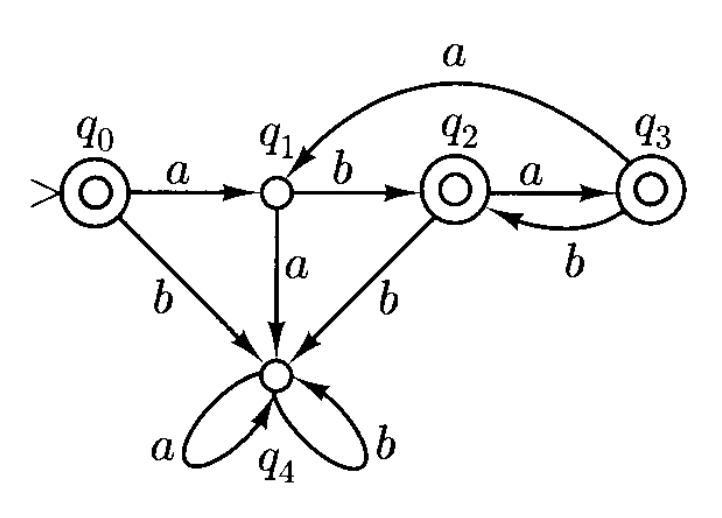
下面设计了一个接受出现模式为 \(bb\) 或 \(bab\) 的字符串的 NFA,其中:
对应的状态图如下:
对于输入 \(bababab\),即有可能陷入 \(q_0\) 状态出不去:也有可能顺利抵达最终状态:
对 NFA 而言,只要存在一种可能到达最终状态的序列,说明对应的字符串是可被接受的,因此 \(bababab \in L(M)\)。
令 \(\Sigma = \{a_1, \dots, a_n\}\ (n \ge 2)\)。考虑以下语言:
也就是说只要字符串包含了字母表内的所有符号就无法被自动机接受,而其他情况均会被接受。这样的 NFA 相对比较容易设计:
- \(K\) 包含 \(n+1\) 个状态 \(\{s, q_1, \dots, q_n\}\)
- 且这些状态均为最终状态,即 \(F = K\)
- \(\Delta\) 仅包含两类转移
- 初始转移(initial transition):\((s, e, q_i)\ (1 \le i \le n)\)
- 主转移(main transition):\((q_i, a_j, q_i)\ (i \ne j)\)
对应的状态图如下(\(n=3\)
值得注意的是,DFA 只是 NFA 的一种特殊类型:在 DFA 中,转移关系是一个从 \(K \times \Sigma\) 映射到 \(K\) 的函数。当且仅当 \(\Delta\) 没有形如 \((q, e, p)\) 的转移,且 \(\forall q \in K, a \in \Sigma\),恰好存在一个 \(p \in K\) 使得 \((q, a, p) \in \Delta\) 时,NFA 就是确定的 (deterministic)。
事实上,虽然看起来 NFA 比 DEA 更强大、更通用,但实际上 NFA 总是可以被转换为等价的 DFA。形式上,对于两个有限自动机 \(M_1, M_2\)(无论是 DFA 还是 NFA
定理
对于每一个 NFA,存在一个等价的 DFA。
注意
建议阅读“证明”的前半部分内容,理解如何根据 NFA 构造等价的 DFA 的方法。
证明
对教材 \(P_{69-72}\) 的翻译,略有删改。
设 \(M=(K,\Sigma,\Delta,s,F)\) 是一个 NFA,我们将构造一个与其等价的 DFA \(M^{\prime}=(K^{\prime},\Sigma,\delta^{\prime},s^{\prime},F^{\prime})\) 。关键思想是将 NFA 看作在任何时刻,不只占据一个状态,而是占据一个状态集合:即,通过到目前为止读取的输入,所有可以从初始状态到达的状态的集合。
以下构造将这一想法形式化:
- \(M^{\prime}\) 的状态集合 \(K^{\prime}\) 将是 \(2^{K}\),即 \(M\) 的状态集合 \(K\) 的幂集
- \(M^{\prime}\) 的最终状态集合 \(F^{\prime}\) 将由 \(K\) 的所有包含至少一个 \(M\) 的终态的子集组成
- \(M^{\prime}\) 的转移函数 \(\delta^{\prime}\) 的定义会稍微复杂一些,基本思想是:\(M^{\prime}\) 在读取输入符号 \(a \in \Sigma\) 上的移动,模仿 \(M\) 在输入符号 \(a\) 上的移动,可能随后跟随 \(M\) 的任意数量的 e- 移动。
为了形式化这个想法,我们需要一个特殊的定义:对于任何状态 \(q \in K\),令 \(E(q)\) 是 \(M\) 的所有可从状态 \(q\) 到达且无需读取任何输入的状态集合。也就是说:
换句话说,\(E(q)\) 是集合 \(\{q\}\) 在关系 \(\{(p,r):\text{there is a transition }(p,e,r)\in\Delta\}\) 下的闭包(称为 \(\varepsilon\)- 闭包
Initially set E(q) := {q};
while there is a transition (p, e, r) in Delta with p in E(q) and r not in E(q) do:
E(q) := E(q) union {r}
该算法保证在最多 \(|K|\) 次迭代后终止,因为 while 循环的每次执行都会向 \(E(q)\) 中添加一个新状态,而最多只有 \(|K|\) 个状态可以被添加。
现在准备形式化地定义与 \(M\) 等价的确定性自动机 \(M^{\prime}=(K^{\prime},\Sigma,\delta^{\prime},s^{\prime},F^{\prime})\)。具体来说:
对于每个 \(Q\subseteq K\) 和每个符号 \(a\in\Sigma\),定义:
也就是说,\(\delta^{\prime}(Q,a)\) 被视为 \(M\) 可以通过读取输入 \(a\)(并且可能随后跟着若干 e- 转移)所能到达的所有状态的集合。
上述构造法所需时间为 \(\mathcal{O}(m \cdot 2^n)\),其中 \(m = |\Sigma|, n = |K|\)。
剩下的任务是要证明 \(M^{\prime}\) 是确定性的并且等价于 \(M\)。
-
证明 \(M^{\prime}\) 是确定性:注意到 \(\delta^{\prime}\) 是单值的,并且根据其构造方式,它在所有 \(Q\in K^{\prime}\) 和 \(a\in\Sigma\) 上都是良好定义的
。 (\(\delta^{\prime}(Q,a)=\emptyset\) 对于某些 \(Q\in K^{\prime}\) 和 \(a\in\Sigma\) 并不意味着 \(\delta^{\prime}\) 不是良好定义的;\(\emptyset\) 是 \(K^{\prime}\) 的一个成员。 ) -
证明 \(M\) 和 \(M^{\prime}\) 是等价的
-
我们现在声称:对于任何字符串 \(w\in\Sigma^{*}\) 和任何状态 \(p,q\in K\),
\[(q,w)\vdash_M^*(p,e)\text{ if and only if }(E(q),w)\vdash_{M^{\prime}}^*(P,e)\]对一些包含 \(p\) 的集合 \(P\) 成立。
-
由此定理将很容易得出:考虑任意字符串 \(w\in\Sigma^{*}\)。那么 \(w\in L(M)\) 当且仅当 \((s,w)\vdash_{M}^{*}(f,e)\) 对于某个 \(f\in F\) (根据定义
) ,当且仅当 \((E(s),w)\vdash_{M^{\prime}}^{*}(Q,e)\) 对于某个包含 \(f\) 的 \(Q\)(根据上述声称) ;换句话说,当且仅当 \((s^{\prime},w)\vdash_{M^{\prime}}^{*}(Q,e)\) 对于某个 \(Q\in F^{\prime}\)。最后一个条件是 \(w\in L(M^{\prime})\) 的定义。 -
我们通过对 \(w\) 进行归纳来证明这个声称:
- 基础步骤:对于 \(|w|=0\)(即 \(w=e\)
) ,我们必须证明 \((q,e)\vdash_{M}^{*}(p,e)\) 当且仅当 \((E(q),e)\vdash_{M^{\prime}}^{*}(P,e)\) 对于某个包含 \(p\) 的集合 \(P\)。第一个陈述等价于说 \(p\in E(q)\)。由于 \(M^{\prime}\) 是确定性的,第二个陈述等价于说 \(P=E(q)\) 且 \(P\) 包含 \(p\);即 \(p\in E(q)\)。这就完成了基础步骤的证明。 - 归纳假设:假设该声称对于所有长度为 \(k\) 或更短的字符串 \(w\) 成立,其中 \(k\ge0\)。
-
归纳步骤:我们证明该声称对于任何长度为 \(k+1\) 的字符串 \(w\) 成立。设 \(w=va\),其中 \(a\in\Sigma\),且 \(v\in\Sigma^{*}\)。
-
对于“仅当”方向,假设 \((q, w)\vdash_{M}^{*}(p,e)\)。那么存在状态 \(r_{1}\) 和 \(r_{2}\) 使得
\[(q,w)\vdash_{M}^{*}(r_{1},a)\vdash_{M}(r_{2},e)\vdash_{M}^{*}(p,e)\]也就是说,\(M\) 从状态 \(q\) 到达状态 \(p\),经过若干次移动(读取了输入 \(v\)
) ,随后一次移动(读取了输入 \(a\)) ,随后若干次移动(未读取任何输入。现在 \((q,va)\vdash_{M}^{*}(r_{1},a)\) 等同于 \((q,v)\vdash_{M}^{*}(r_{1},e)\),并且因为 \(|v|=k\),根据归纳假设,\((E(q),v)\vdash_{M^{\prime}}^{*}(R_{1},e)\) 对于某个包含 \(r_{1}\) 的集合 \(R_{1}\) 成立。由于 \((r_{1},a)\vdash_{M}(r_{2},e)\),存在一个三元组 \((r_{1},a,r_{2})\in\Delta\),因此根据 \(M^{\prime}\) 的构造,\(E(r_{2})\subseteq\delta^{\prime}(R_{1},a)\)。又因为 \((r_{2},e)\vdash_{M}^{*}(p,e)\),可以得出 \(p\in E(r_{2})\),所以 \(p\in\delta^{\prime}(R_{1},a)\)。因此,\((R_{1},a)\vdash_{M^{\prime}}(P,e)\) 对于某个包含 \(p\) 的 \(P\) 成立,从而 \((E(q),va)\vdash_{M^{\prime}}^{*}(R_{1},a)\vdash_{M^{\prime}}(P,e)\)。 -
为了证明另一个方向,假设 \((E(q),va)\vdash_{M^{\prime}}^{*}(R_{1},a)\vdash_{M^{\prime}}(P,e)\),对于某个包含 \(p\) 的 \(P\) 和某个 \(R_{1}\) 使得 \(\delta^{\prime}(R_{1},a)=P\)。现在根据 \(\delta^{\prime}\) 的定义,\(\delta^{\prime}(R_{1},a)\) 是所有集合 \(E(r_{2})\) 的并集,其中对于某个状态 \(r_{1}\in R_{1}\),\((r_{1},a,r_{2})\) 是 \(M\) 的一个转移。由于 \(p\in P=\delta^{\prime}(R_{1},a)\),存在某个特定的 \(r_{2}\) 使得 \(p\in E(r_{2})\),并且对于某个 \(r_{1}\in R_{1}\),\((r_{1},a,r_{2})\) 是 \(M\) 的一个转移。那么根据 \(E(r_{2})\) 的定义,\((r_{2},e)\vdash_{M}^{*}(p,e)\)。同时,根据归纳假设,\((q,v)\vdash_{M}^{*}(r_{1},e)\),因此 \((q, va)\vdash_{M}^{*}(r_{1},a)\vdash_{M}(r_{2},e)\vdash_{M}^{*}(p,e)\)。
-
- 基础步骤:对于 \(|w|=0\)(即 \(w=e\)
-
证毕。
例子
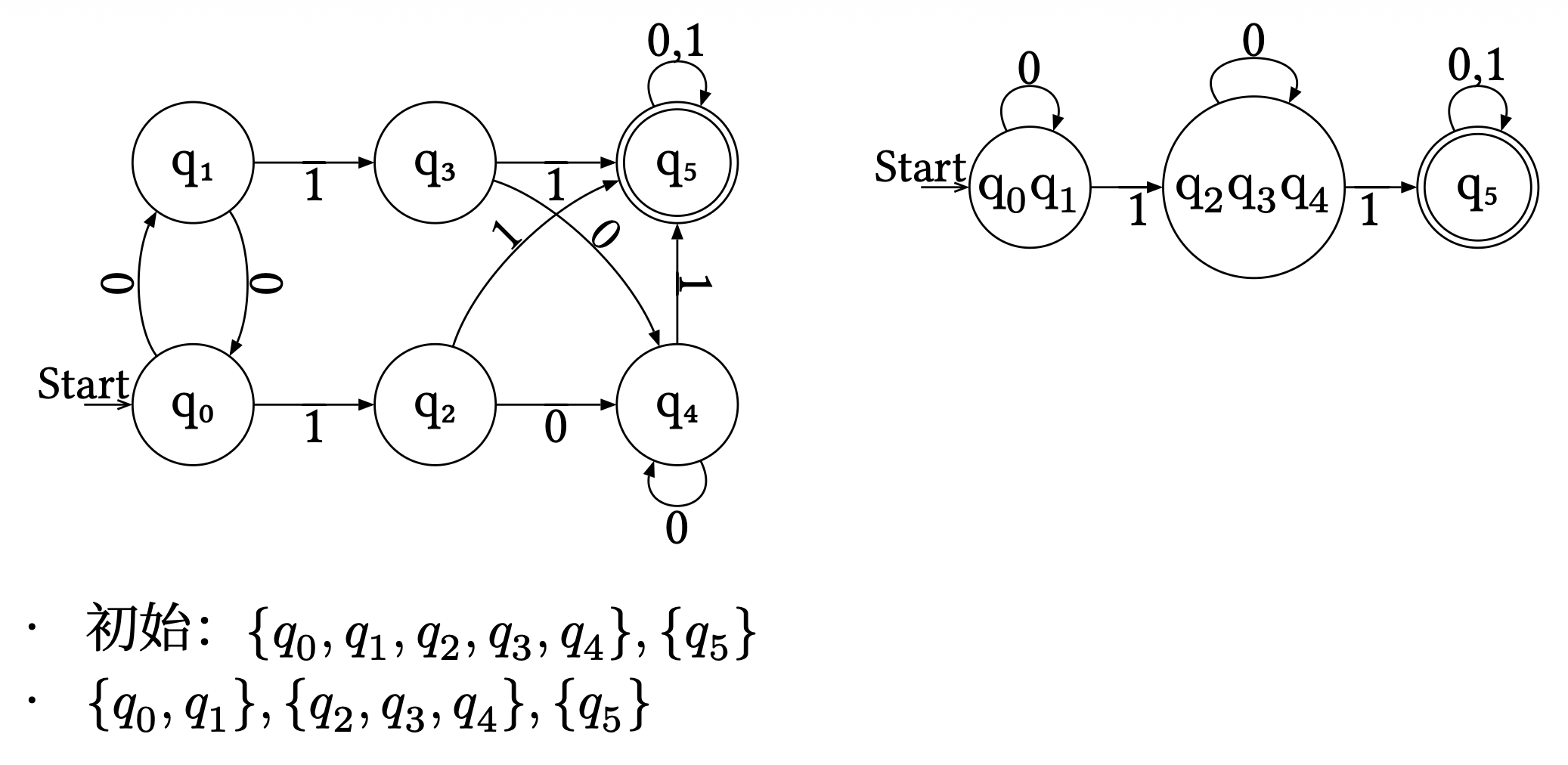
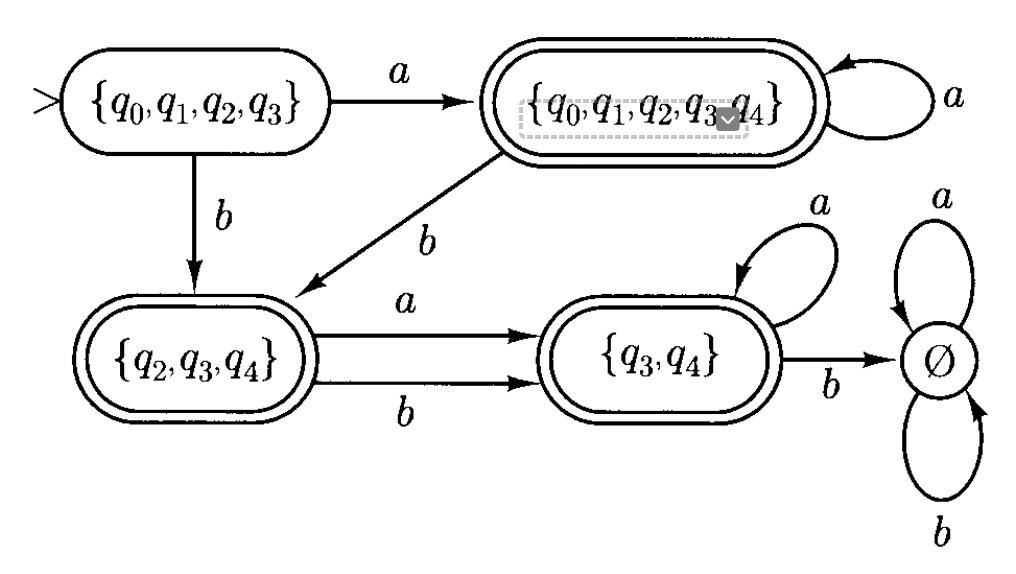
现在利用前面证明过程中给出的算法,将上面的 NFA 转换为等价的 DFA。- 由于 \(M\) 有 \(5\) 个状态,因此 \(M'\) 有 \(2^5 = 32\) 个状态
- 当然其中只有部分状态和 \(M'\) 的运算相关,那些无法从 \(s'\) 到达的状态就是不相关的操作
-
\(E(q)\)
- \(E(q_0) = \{q_0, q_1, q_2, q_3\}\)
- \(E(q_1) = \{q_1, q_2, q_3\}\)
- \(E(q_2) = \{q_2\}\)
- \(E(q_3) = \{q_3\}\)
- \(E(q_4) = \{q_3, q_4\}\)
-
因为 \(s' = E(q_0)\),所以 \((q_1, a, q_0), (q_1, a, q_4), (q_3, a, q_4)\) 都是对 \(q \in s'\) 的转移 \((q, a, p)\),即 \(\delta(q, a) = E(q_0) \cup E(q_4) = \{q_0, \dots, q_4\}\)
- 同理 \((q_0, b, q_2), (q_2, b, q_4)\) 都是对 \(q \in s'\) 的转移 \((q, b, p)\),即 \(\delta(q, b) = E(q_2) \cup E(q_4) = \{q_2, \dots, q_4\}\)
-
重复上述计算,可得到:
\[ \begin{aligned}\delta^{\prime}(\{q_0,q_1,q_2,q_3,q_4\},a)&=\{q_0,q_1,q_2,q_3,q_4\},\\\delta^{\prime}(\{q_0,q_1,q_2,q_3,q_4\},b)&=\{q_2,q_3,q_4\},\\\delta^{\prime}(\{q_2,q_3,q_4\},a)&=E(q_4)=\{q_3,q_4\},\\\delta^{\prime}(\{q_2,q_3,q_4\},b)&=E(q_4)=\{q_3,q_4\},\\\delta^{\prime}(\{q_3,q_4\},a)&=E(q_4)=\{q_3,q_4\},\\\delta^{\prime}(\{q_3,q_4\},b)&=\emptyset,\\\delta^{\prime}(\emptyset,a)&=\delta^{\prime}(\emptyset,b)=\emptyset.\end{aligned} \]
对应的状态图如下:
可以看到 \(\{q_0, q_1, q_2, q_3, q_4\}, \{q_2, q_3, q_4\}, \{q_3, q_4\}\) 是最终状态(因为 \(q_4 \in F\)
Regular Expressions⚓︎
计算理论的中心问题是通过有限规范表示语言。显然有限语言是能穷举出来的,所以仅需考虑无限语言的问题。
一个结论是:无论有多么强大的方法来表示语言,只有可数多个的语言能够被表示出来,只要表示本身也是有限的。所以那些不可数的语言自然无法使用有限表示了。
考虑表达式(expression) 的概念,即描述语言是如何通过前面介绍的运算构建的符号字符串。其中,在 \(\Sigma^*\) 上的正则表达式(regular expression) 是在字母表 \(\Sigma \cup \{(, ), \oslash, \mathsf{U}, *\}\) 的全体字符串,可按以下方式获取:
- \(\oslash\) 和 \(\Sigma\) 的每个成员都是正则表达式
- 若 \(\alpha, \beta\) 都是正则表达式,那么 \((\alpha \beta)\) 也是正则表达式
- 若 \(\alpha, \beta\) 都是正则表达式,那么 \((\alpha \mathsf{U} \beta)\) 也是正则表达式
- 若 \(\alpha\) 是正则表达式,则 \(\alpha^*\) 也是正则表达式
- 只有上述四条均满足时才是正则表达式,否则就不是
正则表达式和它们所表示的语言之间的关系由函数 \(\mathcal{L}\) 构建,使得若 \(\alpha\) 是任意正则表达式,那么 \(\mathcal{L}(\alpha)\) 就是用 \(\alpha\) 表示的语言。函数 \(\mathcal{L}\) 的具体定义如下:
- \(\mathcal{L}(\oslash) = \emptyset, \mathcal{L}(a) = \{a\}\ (\forall a \in \Sigma)\)
- 若 \(\alpha, \beta\) 都是正则表达式,那么 \(\mathcal{L}((\alpha \beta)) = \mathcal{L}(\alpha)\mathcal{L}(\beta)\)
- 若 \(\alpha, \beta\) 都是正则表达式,那么 \(\mathcal{L}((\alpha \mathsf{U} \beta)) = \mathcal{L}(\alpha) \cup \mathcal{L}(\beta)\)
- 若 \(\alpha\) 是正则表达式,那么 \(\mathcal{L}(\alpha^*) = \mathcal{L}(\alpha)^*\)
运算优先级:\(* > \circ > \cup\)
每个能够用一种正则表达式表达的语言能够被无限多个其他正则表达式表示。我们通常会忽略正则表达式中多余的括号(\((, )\)
字母表 \(\Sigma\) 上的正则语言(regular language) 类定义为满足 \(L = \mathcal{L}(\alpha)\) 的全部语言 \(L\),即能被正则表达式表达的全部语言。正则语言也可被看成是一种闭包——在 \(\Sigma\) 上的正则语言类就是以下语言集合(关于并、拼接、克莱尼星号运算)的闭包:
Regular Languages⚓︎
正则语言的另一种定义是被 FA(DFA/NFA)接受的语言。接下来证明被 FA 接受的语言的闭包性质:
定理
被有限自动机接受的语言类在以下运算中是封闭的:
- 并
- 拼接
- 克莱尼星号
- 补
- 交
证明
令 \(M_1 = (K_1, \Sigma, \Delta_1, s_1, F_1), M_2 = (K_2, \Sigma, \Delta_2, s_2, F_2)\)。
令 \(M_1, M_2\) 为 NFA,我们将构造一个 NFA \(M\),满足 \(L(M) = L(M_1) \cup L(M_2)\)。\(M\) 的构造非常简单直观,如下所示:
\(M\) 利用不确定性猜测输入在 \(L(M_1)\) 中还是在 \(L(M_2)\) 中。下面给出形式化的证明:
- 不失一般性地 (Without loss of generality),假设 \(K_1, K_2\) 是不相交集
- 那么 \(M\) 接受语言 \(L(M_1) \cup L(M_2)\) 的定义如下:\(M = (K, \Sigma, \Delta, s, F)\),其中:
- \(s\) 是不属于 \(K_1\) 或 \(K_2\) 的新状态
- \(K = K_1 \cup K_2 \cup \{s\}\)
- \(F = F_1 \cup F_2\)
- \(\Delta = \Delta_1 \cup \Delta_2 \cup \{(s, e, s_1), (s, e, s_2)\}\)
- 也就是说 \(M\) 一开始会任意选取 \(M_1\) 或 \(M_2\) 的初始状态,随后模仿 \(M_1\) 或 \(M_2\) 的行为
- 形式上,若 \(w \in \Sigma^*\),那么 \((s, w) \vdash_M^* (q, e)\ (q \in F)\) 当且仅当 \((s_1, w) \vdash_{M_1}^* (q, e)\ (q \in F_1)\) 或 \((s_2, w) \vdash_{M_2}^* (q, e)\ (q \in F_2)\) 成立
- 因此当且仅当 \(M_1\) 或 \(M_2\) 接受 \(w\) 时,\(M\) 接受 \(w\),于是 \(L(M) = L(M_1) \cup L(M_2)\)
令 \(M_1, M_2\) 为 NFA,我们将构造一个 NFA \(M\),满足 \(L(M) = L(M_1) \circ L(M_2)\)。\(M\) 的构造如下所示:
可以看到,\(M\) 先模拟一段时间的 \(M_1\),之后从 \(M_1\) 的最终状态“跳转”到 \(M_2\) 的初始状态,开始模仿 \(M_2\) 了。
这里省略了形式化的证明。
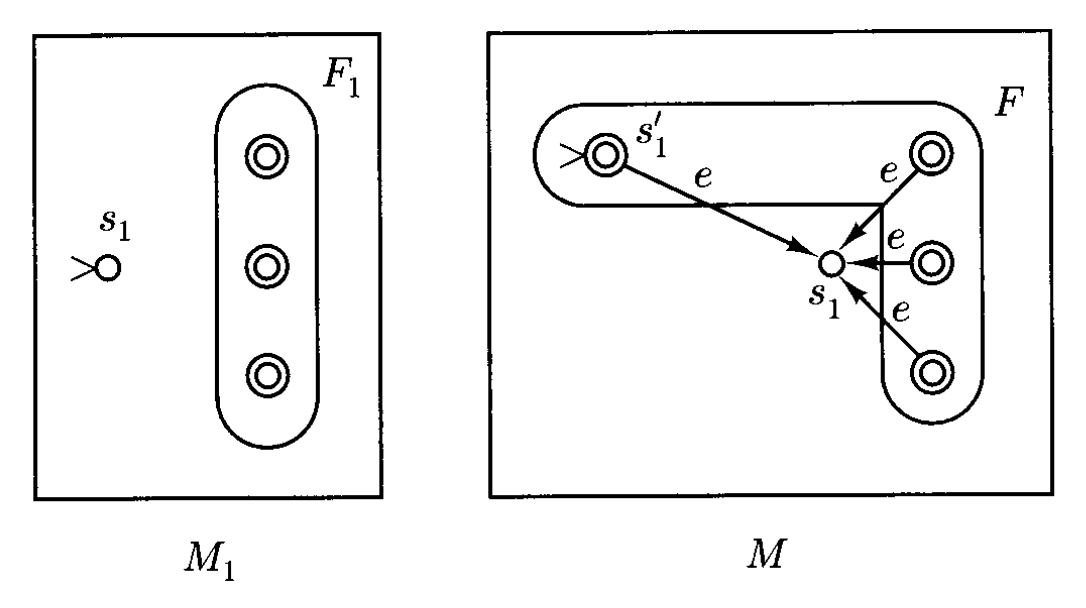
令 \(M_1\) 为 NFA,我们将构造一个 NFA \(M\),满足 \(L(M) = L(M_1)^*\)。\(M\) 的构造如下所示:
- \(M\) 由 \(M_1\) 的状态和 \(M_1\) 的所有转移构成,且任何 \(M_1\) 的最终状态都是 \(M\) 的最终状态
- 此外 \(M\) 有新的初始状态 \(s\),\(s\) 也是一种最终状态,这使得 \(e\) 也能为 \(M\) 所接受
- \(s\) 处存在到 \(M_1\) 的 \(s_1\) 的 e 转移,因此 \(M\) 可模仿 \(M_1\) 的行为
- \(M_1\) 的每个状态都存在一个到 \(s_1\) 的 e 转移,这样一旦读取好 \(L(M_1)\) 的一个字符串后,就能接着继续从初始状态 \(s_1\) 开始了
令 \(M\) 为 DFA。补语言 \(\overline{L} = \Sigma^* - L(M)\) 会被 DFA \(\overline{M} = (K, \Sigma, \delta, s, K - F)\) 接受,即 \(\overline{M}\) 与 \(M\) 相同,除了互换最终状态和非初始状态。
利用德摩根定律,交的封闭性就转换为遵守并的封闭性和补的封闭性,而这些前面都证明过了。
定理
当且仅当为有限自动机所接受时,语言是正则的(regular)。
证明
- 正则语言类是包含空集 \(\emptyset\) 和单元素 \(a\)(其中 \(a\) 是一个符号)的最小语言类,并且在并、拼接和克莱尼星号运算下封闭
- 显然空集及所有单元素确实能被有限自动机接受
- 并且根据上一条定理,有限自动机语言在并、连接和克莱尼星号运算下是封闭的
- 因此,每个正则语言都能被某个有限自动机所接受
- 令 \(M = (K, \Sigma, \delta, s, F)\) 为一个有限自动机(不一定确定
) 。我们将构造一个正则表达式 \(R\),使得 \(L(R) = L(M)\);我们将把 \(L(M)\) 表示为许多(但数量有限的)简单语言的并集 -
设 \(K = \{q_1,..., q_n\}\) 且 \(s = q_1\)
-
对于 \(i, j = 1, \dots, n\) 和 \(k = 0, \dots, n\),定义 \(R(i, j, k)\) 为所有在 \(\Sigma^*\) 中的字符串集合,这些字符串能够驱动 \(M\) 从状态 \(q_i\) 到状态 \(q_j\),而不经过任何编号大于等于 \(k + 1\) 的中间状态
- 也就是说,\(R(i, j, k)\) 是由所有从 \(q_i\) 到 \(q_j\)、等级 (rank) 为 \(k\) 的路径所拼写的字符串集合
-
当 \(k = n\) 时满足:
\[ R(i,j,n)=\{w\in\Sigma^*:(q_i,w)\vdash_M^*(q_j,e)\} \] -
所以 \(L(M)=\bigcup\{R(1,j,n):q_j\in F\}\),关键点在于所有 \(R(i, j, k)\) 集合是正则的,因此 \(L(M)\) 是正则的
-
可通过在 \(k\) 上的归纳法证明 \(R(i, j, k)\) 是正则的
-
\(k=0\):
\[ R(i, j, 0) = \begin{cases}\{a \in \Sigma \cup \{e\} : (q_i, a, q_j) \in \Delta\} \text{ if } i \ne j \\ \{e\} \cup \{a \in \Sigma \cup \{e\} : (q_i, a, q_j) \in \Delta\} \text{ if } i = j\end{cases} \]这些集合都是有限的,因而是正则的
-
归纳步骤
- 假设 \(\forall i, j,\ R(i, j, k - 1)\) 被定义为 \(i, j\) 上的正则语言
-
那么 \(R(i, j, k)\) 可通过包括并、克莱尼星号和拼接的正则操作,结合先前定义好的正则语言来定义,即:
\[ R(i,j,k)=R(i,j,k-1)\cup R(i,k,k-1)R(k,k,k-1)^*R(k,j,k-1) \]该方程说明了要从 \(q_i\) 到达 \(q_j\) 而不经过编号大于 \(k\) 的状态,\(M\) 可以采取以下方式之一:
- 从 \(q_i\) 到 \(q_j\),不经过编号大于 \(k-1\) 的状态;或者
- 先从 \(q_i\) 到 \(q_j\),然后从 \(q_k\) 到 \(q_k\)(零次或多次
) ,接着从 \(q_k\) 到 \(q_j\);在每一步中,都不经过任何编号大于 \(k-1\) 的中间状态
-
因此 \(R(i, j, k)\) 对所有 \(i, j, k\) 而言是正则的,从而完成归纳证明。
一些结论
- 单个正则语言是可数的(语言 \(L \subseteq \Sigma^*\),若 \(\Sigma\) 有限,那么 \(\Sigma^*\) 就是可数的)
- 所有正则语言构成的集合也是可数的
-
对正则语言进行无限次的并/交/拼接运算无法保证结果的正则性
-
正则语言的例子:
- \(L = \{a^*\}\)
- \(L = \{a^* b^*\}\)
- \(L = \{a^m b^n: m, n \ge 0\}\),当 \(m, n\) 之间没有其他关系,或者 \(m, n\) 之间有关系但它们的大小是有限的时候(比如 \(m = n\) 且 \(n < 1000\))满足
- \(L = \{a^n: n \ge 0\}\)(和第一个例子等价)
-
\(L = \{w^R: w \in L_0 \text{ and } L_0 \text{ is regular}\}\)
- 也就是说正则语言 \(L_0\) 中所有字符串的反转构成的集合 \(L\) 也是正则语言(可通过构造 NFA 证明)
-
\(L = \{a^n : n \in \text{Even}\}\)(因为 \(L = (aa)^*\))
-
非正则语言的例子:
- \(L = \{a^m b^n: m, n \ge 0\}\),\(m, n\) 之间有关系,且大小没有限制(比如 \(m > n, m = 2n\))
- \(L = \{a_1^n a_2^n \dots a_k^n\} (k \ge 3)\)
- \(L = \{a^n: n \text{ is Prime}\}\)
- \(L = \{ww^R: w \in \{a, b\}^*\}\)
- 也就是说回文语言不是正则语言(但它是上下文无关语言)
- \(L = \{ww: w \in \{a, b\}^*\}\)
- \(L = \{wcw: w \in \{a, b\}^*\}\)
- \(L = \{w\dddot{w}: w \in \{a, b\}^*\}\),其中 \(\dddot{w}\) 将 \(w\) 中的 \(b\) 替换为 \(a\),\(a\) 替换为 \(b\)
Languages that Are and Are Not Regular⚓︎
尽管目前我们有能够证明语言是正则的强大技术,但我们目前还没展示过如何判断语言不是正则的。下面给出两条为正则语言所具备的,但某些非正则语言不具备的性质:
- 当从左到右扫描字符串时,用于最终判断该字符串是否属于某语言所需的内存容量必须是有限的、预先固定的,并且依赖于该语言本身,而非特定的输入字符串
- 例如,我们可以判断 \(\{a^n b^n: n \ge 0\}\) 不是正则的,因为无法做到构建一个有限状态设备,能在到达 \(a\) 和 \(b\) 的分界处时准确记住它已经看到了多少个 \(a\),并与 \(b\) 的数量进行比较
- 具有无限数量字符串的正则语言通过带有循环的自动机以及包含克林星号的正则表达式来表示
- 这类语言必然拥有具备某种简单重复结构的无限子集,这种结构源于相应正则表达式中的克林星号或有限自动机状态图中的循环。
- 例如,集合 \(\{a^n: n > 1 \text{ is a prime}\}\) 不是正则的,因为质数集合中不存在简单的周期性
这些直观的想法虽然准确,但在用于正式证明时还不够精确。我们现在将证明一个定理,它捕捉了这种直觉的一部分,并轻松推导出某些语言的非正则性作为其直接结果。
泵定理(pumping theorem)
令 \(L\) 为一正则语言,存在整数 \(n \ge 1\)
证明
由于 \(L\) 是正则的,因此它能被 DFA \(M\) 所接受。设 \(n\) 为 \(M\) 的状态数,\(w\) 是长度不小于 \(n\) 的字符串。考虑 \(M\) 在 \(w\) 上运算的前 \(n\) 步: $$ (q_0,w_1w_2\ldots w_n)\vdash_M(q_1,w_2\ldots w_n)\vdash_M\ldots\vdash_M(q_n,e) $$
- 其中 \(q_0\) 是初始状态,\(w_1, \dots w_n\) 是 \(w\) 前 \(n\) 个符号
- 因为 \(M\) 只有 \(n\) 个状态,所以上述计算中存在 \(n+1\) 种配置 \((q_i, w_{i+1}, \dots w_n)\)
- 根据鸽巢原理,存在 \(i, j, 0 \le i < j \le n\) 满足 \(q_i = q_j\)
- 也就是说存在非空字符串 \(y = w_i w_{i+1} \dots w_j\),使得 \(M\) 的状态从 \(q_i\) 重新回到 \(q_i\)
- 因此可以从 \(w\) 中移除 \(y\),或者在 \(w_j\) 之后重复插入多个 \(y\),而 \(M\) 仍然会接受这些字符串,即对于每个 \(i \ge 0\),\(M\) 都会接受 \(xy^iz \in L\) 的情况,其中 \(x = w_1 \dots w_i, z= w_{j+1} \dots w_m\)
可将泵定理看作证明语言是正则的必要不充分条件。我们常用它证明一个语言不是正则的。
总结:正则语言的判定
- 不存在判断任意语言是否正则的通用方法
- 证明语言正则
- 该语言有限
- 构造一个接受该语言的 FA
- 构造一个生成该语言的正则表达式
- 正则语言的闭包性质
- 证明语言非正则
- 泵定理
- 反证
- 不存在接受该语言的 FA
- 正则语言的闭包性质(常用技巧是拿一个已知的正则语言和题目给出的语言取交集,如果交集不是正则的,说明题目给出的语言一定不是正则的(反之不一定
) )
题集
来自朋辈辅学课件
判断 \(L = \{a^i b^j c^k : i + j \not\equiv k \pmod 3, i, j, k \in \mathbb{N}\}\) 是否为正则语言
- 令 \(i \equiv t_1 \pmod 3, j \equiv t_2 \pmod 3, k \equiv t_3 \pmod 3, t_1, t_2, t_3 \in \{0, 1, 2\}\)
- 显然 \((t_1, t_2, t_3)\) 的取值只有有限种
- \(L_{1, t_1} = \{a^{3n_1 + t_1} : n_1 \in \mathbb{N}\}, L_{2, t_2} = \{b^{3n_2 + t_2} : n_2 \in \mathbb{N}\}, L_{3, t_3} = \{c^{3n_3 + t_3} : n_3 \in \mathbb{N}\}\) 均为正则语言
- 对每组 \((t_1, t_2, t_3)\) 的取值,\(L_{1, t_1} \circ L_{2, t_2} \circ L_{3, t_3}\) 为正则语言
- \(L = \bigcup_{t_1 + t_2 \not\equiv t_3 \pmod 3} L_{1, t_1} \circ L_{2, t_2} \circ L_{3, t_3}\) 为有限个正则语言的并集,故 \(L\) 为正则语言
来自朋辈辅学课件
判断 \(L = \{w : w \in \{a, b\}^*, w \ne w^R\}\) 是否为正则语言
- 令 \(L' = \{a, b\}^* - L = \{w : w \in \{a, b\}^*, w = w^R\}\),则 \(L, L'\) 正则性相同
- \(\forall\ p \ge 1\),取 \(w = a^p b a^p \in L'\),则 \(|w| = 2p + 1 \ge p\)
- 任意划分 \(w = xyz\) 使 \(|xy| \le p, |y| \ge 1\),则 \(y = a^k, k \ge 1\)
- 取 \(i = 0\),则 \(xy^iz = a^{p-k} b a^p \notin L'\)
- 因为 \(L'\) 不是正则语言,故 \(L\) 也不是正则语言
来自 zq 的 quiz1
判断是否正确:若 \(L_1 \circ L_2\) 是正则的 , 那么 \(L_1\) 或 \(L_2\) 也是正则的。
❌,理由如下:
- 假设语言 \(A\) 不是正则的,那么 \(\overline{A}\) 也不是正则的
- 显然 \(A \cup \{e\}\) 和 \(\overline{A} \cup \{e\}\) 也不是正则的
-
但 \((A \cup \{e\}) \circ (\overline{A} \cup \{e\}) = \Sigma^*\) 是正则的
\[ \begin{aligned} & (A \cup \{e\}) \circ (\overline{A} \cup \{e\}) \\ = & (A \circ \overline{A}) \cup (A \circ \{e\}) \cup (\overline{A} \circ \{e\}) \cup (\{e\} \circ \{e\}) \\ = & (A \circ \overline{A}) \cup \underbrace{A \cup \overline{A}}_{\Sigma^*} \cup \{e\} \\ = & \Sigma^* \end{aligned} \]
来自 24-25 历年卷
判断是否为正则语言并证明:
- \(\{uv | u, v \in a^+ b^+ \text{ and } |u| = 3|v|\}\)
- \(\{uv | u, v \in \{a, b\}^* \text{ and } |u| = 3|v|\}\)
不是正则的,理由如下:
- 令要求判断的语言为 \(L_1\),令正则语言 \(L_2 = a^+ba^+b\)
- 若 \(L_1\) 是正则的,那么 \(L_1 \cap L_2\) 也一定是正则的
- 可以计算出 \(L' = L_1 \cap L_2 = \{a^{3j+2} b a^j b | j \ge 1\}\)
-
使用泵定理:
- 假设 \(L'\) 是正则的,设泵长度为 \(p\)
- 取字符串 \(s = a^{3p+2} b a^p b \in L'\)
- 根据泵定理,\(s\) 可分解为 \(xyz\),其中 \(|xy| \le p\) 且 \(|y| > 0\);不难发现 \(y\) 一定全由 \(a\) 组成
- 进行泵操作,比如 \(xy^2z\);这显然破坏了原有的数量关系,此时该字符串不会属于 \(L'\),因此 \(L'\) 不是正则语言
-
于是 \(L_1\) 也不会是正则语言
是正则的,理由如下:
- 不难找出等价语言 \(L = \{w \in \{a, b\}^* | |w| = 0\ (\text{mod } 4)\}\),即所有长度为 4 的倍数的字符串集合
- 可构造 DFA 识别 \(L\)(4 个状态,起始和终止状态均为同一个状态,每读取一个符号向前移动一次)
- 因此该语言是正则的
来自 22-23 历年卷
\(L = \{uv2w : u, v, w \in \{0, 1\}^*, |u| = 2|v| + 1 \text{ and } |w| \ne |v| + 2 \}\) 是不是 regular 的(\(uv2w\) 中的 2 是符号)
整理了 Gemini 3 Pro 的回答
- 令 \(x = uv\),那么 \(|x| = 3|v| + 1\)(与 1 模 3 同余
) ,或者 \(|v| = (|x| - 1) / 3\) - 结合第二个条件,得到 \(|w| \ne (|x| - 1) / 3 + 2\),即 \(|x| \ne 3|w| - 5\)
-
于是可以将 \(L\) 重新表述为:
\[ L = \{x2w, x, w \in \{0, 1\}^*, |x| \equiv 1 \text{ mod } 3 \text{ and } |x| \ne 3|w| - 5 \} \] -
取 \(L\) 补集的一部分 \(L' = \{x2w, x, w \in \{0, 1\}^*, |x| = 3|w| - 5 \}\),只要证明 \(L'\) 不是正则的,那么 \(L\) 也就不是正则的
-
利用泵定理:
- 取 \(L'\) 中的字符串 \(s = 0^{3p-5}21^p\),将其划分为 \(xyz\) 组成的字符串,其中 \(|xy| \le p\),\(|y| = k > 0\),显然 \(y\) 一定是由 0 构成的,所以 \(y = 0^k\)
- 取 \(i = 2\),生成的字符串 \(xy^2z\) 有 \(3p - 5 + k\) 个 0,而 1 的数量不变,那么这个新生成的字符串就不属于 \(L'\),那么 \(L'\) 就不可能是正则的,于是 \(L\) 也不是正则的
来自 22-23 历年卷
设计一个 DFA 或者 NFA,接受所有 \(\{0, 1\}^*\) 里最后 4 位至少有一个 1 的字符串,如果不够 4 位还是要求至少有一个 1。要求最多 5 个状态和 8 个转移。
DFA 应该不太可行,于是画了个 NFA,而且 NFA 的结构看上去也很简单
graph LR
%% 定义一个隐藏节点作为起点箭头来源
Start(( )) --> q0
style Start fill:none,stroke:none
%% 状态定义
q0((q0)) -- 0,1 --> q0
q0 -- 1 --> q1(((q1)))
q1 -- 0 --> q2(((q2)))
q2 -- 0 --> q3(((q3)))
q3 -- 0 --> q4(((q4)))
%% 样式定义:双圈表示接受状态
style q1 stroke-width:4px
style q2 stroke-width:4px
style q3 stroke-width:4px
style q4 stroke-width:4px评论区