Sets, Relations and Language⚓︎
约 4838 个字 19 行代码 预计阅读时间 24 分钟
核心知识
只有「字母表和语言」一节是新知识,是一定要看的;而上面的内容都是在回顾离散数学中的基础知识,不会直接考,忘记的话可以阅读一下。
Sets⚓︎
- 集合
- 没有重复元素
- 顺序不重要
- 元素 / 成员
- 单元集 (singleton):只有 1 个元素的集合
- 空集 \(\emptyset\)
- 子集
- 真子集 (proper subset)
- 判断两个集合是否相等
-
集合运算
- 并 (union):\(\bigcup S = \{x : x \in P \text{ for some set } P \in S\}\)
- 交 (intersection):\(\bigcap S = \{x : x \in P \text{ for each set } P \in S\}\)
- 差 (difference)
-
集合的性质:
- 幂等性 (idempotency):\(A \cup A = A, A \cap A = A\)
- 交换律 (commutativity):\(A \cup B = B \cup A, A \cap B = B \cap A\)
- 结合律 (associativity):\((A \cup B) \cup C = A \cup (B \cup C), (A \cap B) \cap C = A \cap (B \cap C)\)
- 分配律(distributivity):\((A \cup B) \cap C = (A \cap C) \cup (B \cap C), (A \cap B) \cup C = (A \cup C) \cap (B \cup C)\)
- 吸收律 (absorption):\((A \cup B) \cap A = A, (A \cap B) \cup A = A\)
- 德摩根定律(Demorgan's law):\(A - (B \cup C) = (A - B) \cap (A - C), A - (B \cap C) = (A - B) \cup (A - C)\)
- \(A = U\)(全集)的时候可能是我们更加熟悉的形式
-
不相交集 (disjoint):两个集合无公共元素,即它们的交集为空集
- 幂集(power set):包含某一集合 \(A\) 所有子集的集合,记作 \(2^A\)
- 划分(partition):幂集的子集,记作 \(\Pi\),并且满足:
- 不包含空集
- 每个元素(原集合的子集)互不相交
- \(\bigcup \Pi = A\)
Relations and Functions⚓︎
Relations⚓︎
-
有序对(ordered pair) \((a, b)\)
- \(a, b\) 为其分量 (component)
- 和集合 \(\{a, b\}\) 不同,需要考虑分量的顺序,而且两个分量可以是一样的
-
集合 \(A, B\) 的笛卡尔积(Cartesian product):记作 \(A \times B\),所有有序对 \((a, b)\ (a \in A \text{ and } b \in B)\) 构成的集合
- 集合 \(A, B\) 的二元关系(binary relation) 即为 \(A \times B\) 的子集
-
有序元组(ordered tuple) \((a_1, \dots, a_n)\)(其中 \(n\) 为任意自然数)
- 有序三元组 / 四元组 / 五元组 / 六元组 (ordered triples/quadruples/quintuple/sextuples)
-
序列(sequence) 即未指定 \(n\)(序列长度)的有序 \(n\) 元组
- n 重笛卡尔积(n-folds Cartesian product) \(A_1 \times \dots \times A_n\):所有有序对 \((a_1, \dots, a_n)\ (a_i \in A_i\ (i = 1, \dots, n))\) 构成的集合
- n 元关系(n-ary relation) 即为 \(A_1 \times \dots \times A_n\) 的子集
- 1, 2, 3 元关系分别对应 unary/binary/tenary relations
Functions⚓︎
- 集合 \(A\) 到集合 \(B\) 的函数(function) 是 \(A\) 到 \(B\) 的二元关系,并满足以下性质:对于每个元素 \(a \in A\),有且仅有一个以 \(a\) 为第一元素的有序对
- 一般用字母 \(f, g, h\) 表示函数
- \(f: A \mapsto B\) 表示从 \(A\) 到 \(B\) 的函数 \(f\)
- 其中 \(A\) 为函数的域(domain)
- \(f(a)\) 为 \(a\) 在 \(f\) 中的像(image)
- 若 \(A'\) 是 \(A\) 的子集,那么定义 \(f[A'] = \{f(a): a \in A'\}\),称 \(f[A']\) 为 \(A'\) 在 \(f\) 中的像
- \(f\) 的范围(range) 即为域对应的像
- 若函数为 \(f: A_1 \times \dots A_n \mapsto B\),并且 \(f(a_1, \dots, a_n) = b\)(\(a_i \in A_i \text{ and } b \in B\)
) ,那么称 \(a_1, \dots, a_n\) 为 \(f\) 的参数(auguments),\(b\) 为 \(f\) 的值(value) -
对于 \(f: A \mapsto B\)
- 若对于任意两个不同元素 \(a, a' \in A,\ f(a) \ne f(a')\),称 \(f\) 是单射的 (one-to-one / injective)
- 若 \(B\) 的每个元素是 \(A\) 中某些元素的像,称 \(f\) 是满射的 (onto)
- 若既是单射,又是满射,那么 \(f\) 是双射函数 (bijection)
-
二元关系 \(R \subseteq A \times B\) 的逆(inverse) 记作 \(R^{-1} \subseteq B \times A\),即 \(\{(b, a) : (a, b) \in R\}\)
- 但函数的逆不一定是函数,只有当 \(f\) 是双射时才能保证是函数(即反函数 \(f^{-1}\))
- \(f^{-1}(f(a)) = a\ (\forall a \in A)\),\(f(f^{-1}(b)) = b\ (\forall b \in B)\)
Special Types of Binary Relations⚓︎
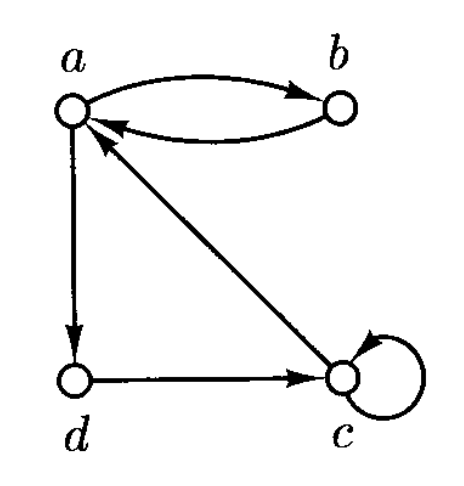
(二元)关系 \(R \subseteq A \times A\) 可以被表示为一张有向图(directed graph)
- \(A\) 的每个元素用一个小圈表示,称为节点(node)
- 而 \((a, b)\) 则用由 \(a\) 到 \(b\) 的箭头表示,称为边(edge)
有向图(\(R \subseteq A \times A\))的一些性质:
- 自反(reflective):\((a, a) \in R, a \in A\)
-
对称(symmetric):当 \((a, b) \in R\) 时,\((b, a) \in R\)
- 没有形如 \((a, a)\) 对的对称关系可用无向图(undirected graph) 表示
-
反对称(antisymmetric):当 \((a, b) \in R\) 时,\((b, a) \notin R\)
- 传递(transitive):当 \((a, b), (b, c) \in R\) 时,\((a, c) \in R\)
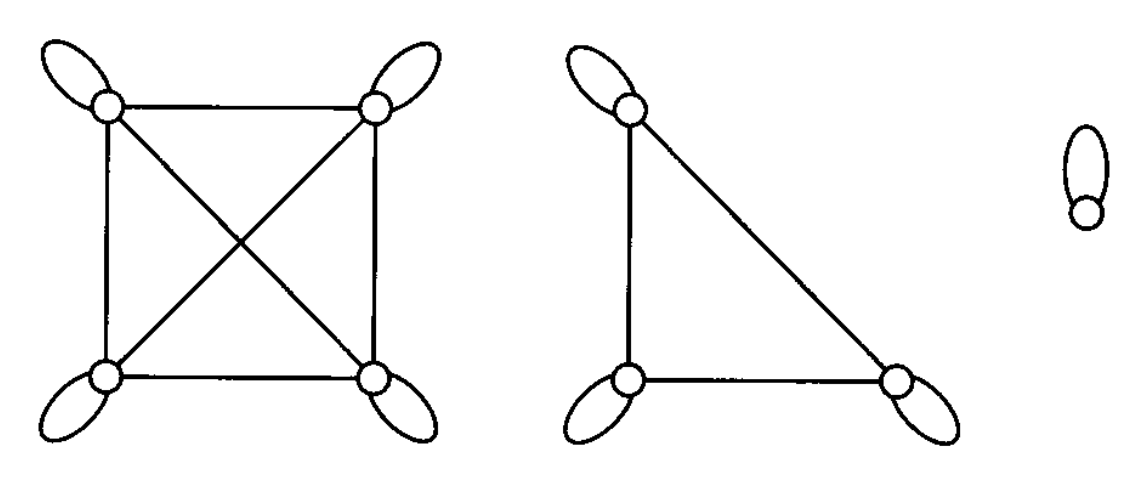
同时满足自反、对称、传递的关系被称为等价关系(equivalence relation)。用无向图表示的等价关系由一组集群构成,这些集群就是等价类(equivalence classes),如下图所示:
通常我们用 \([a]\) 表示包含元素 \(a\) 的等价类,即 \([a] = \{b: (a, b) \in R \text{ or } (b, a) \in R\}\)。
定理
令 \(R\) 为非空集合 \(A\) 的一个等价关系,那么 \(R\) 的等价类构成了 \(A\) 的一个划分。
证明
- 设 \(\Pi = \{[a] : a \in A\}\),需要证明 \(\Pi\) 中的集合非空、互不相交,并且它们的并集覆盖了 \(A\)
- 所有等价类都是非空的,因为根据自反性,\(\forall a \in A, a \in [a]\)
- 要证明互不相交,考虑任意两个不同的等价类 \([a]\) 和 \([b]\),并假设 \([a] \cap [b] \ne \emptyset\)。于是存在一个元素 \(c\) 使得 \(c \in [a]\) 且 \(c \in [b]\)。因此 \((a, c) \in R\) 且 \((c, b) \in R\);由于 \(R\) 是传递的,\((a, b) \in R\);又因 \(R\) 是对称的,\((b, a) \in R\)。现在取任意元素 \(d \in [a]\),则 \((d, a) \in R\),由传递性得 \((d, b) \in R\)。因此 \(d \in [b]\),所以 \([a] \subseteq [b]\)。同理可得 \([b] \subseteq [a]\)。故 \([a]=[b]\)。但这与 \([a]\) 和 \([b]\) 是不同的假设相矛盾。
- 要证明 \(\bigcup \Pi = A\),只需注意到每个 A 中的元素都包含在 \(\Pi\) 的某个集合中——即由自反性可知,对于每个 \(a \in A\) ,有 \(a \in [a]\)
而同时满足自反、反对称和传递的关系被称为偏序(partial order)。假如 \(R \subseteq A \times A\) 是偏序,
- 对于 \(a \in A\),若满足仅当 \(a = b\) 时 \((b, a) \in R\),称 \(a\) 为最小值(minimal)
- 可以这么想:最小值 \(a\) 总是要位于左侧,除非右侧也是 \(a\)
- \(\forall a, b \in A\),\((a, b) \in R\) 或 \((b, a) \in R\),那么偏序 \(R\) 就是全序(total order)
二元关系的路径(path) 是一个序列 \((a_1, \dots, a_n)\)(\(n \ge 1\)
- 对于路径 \((a_1, \dots, a_n)\),当 \((a_n, a_1) \in R\) 时,该路径就是一个环(cycle)。
Finite and Infinite Sets⚓︎
若存在双射 \(f: A \mapsto B\),称集合 \(A, B\) 是等势的(equinumerous),记作 \(A \sim B\)。而等势就是一种等价关系:
- 自反:对于任何集合 \(A\),恒有 \(A \sim A\),因为存在恒等映射 \(Id_A: A \to A\) 为双射
- 对称:若 \(A \sim B\),则 \(B \sim A\),因为 \(A \sim B\) 意味着存在双射 \(f: A \to B\),那么其逆映射 \(f^{-1}: B \to A\) 也一定是双射
- 传递:若 \(A \sim B\) 且 \(B \sim C\),则 \(A \sim C\),因为存在双射 \(f: A \to B\) 和 \(g: B \to C\),它们的复合映射 \(g \circ f: A \to C\) 同样是双射
若集合 \(A\) 与 \(\{1, 2, \dots, n\}\)(\(n\) 为自然数)等势,那么集合 \(A\) 就是有限的(finite);而 \(A\) 的基数(cardinality) \(|A|\) 就是 \(n\)(即有限集合的元素个数
当集合不是有限的,那就是无限的(infinite)。需要注意的是,不是所有的无限集合是等势的。
若集合与 \(\mathbb{N}\) 等势,那么该集合就是可数无限的(countably infinite);并且有限和可数无限均属于可数的(countable),反之就是不可数的(uncountable)。
定理
以下四个命题等价:
- \(A\) 是可数的
- \(A\) 是有限的,且存在一个双射 \(f: A \to \mathbb{N}\)
- 存在单射 \(g: A \to \mathbb{N}\)
- 存在满射 \(h: \mathbb{N} \to A\)
Three Fundamental Proof Techniques⚓︎
下面介绍三种在各种证明中经常出现的基本原理 (fundamental principle):
-
数学归纳法(mathematical induction):令 \(A\) 为一个自然数集合,满足:
- \(0 \in A\)
- 对于每个自然数 \(n\),若 \(\{0, 1, \dots, n\} \subseteq A\),那么 \(n + 1 \in A\)
那么 \(A = \mathbb{N}\)
- 可以用反证法(contradiction) 证明其正确性
-
实际上归纳法通常用来证明以下形式的断言
: “对于任意自然数 \(n\),性质 \(P\) 为真。 ”设集合 \(A = \{n : P \text{ is true of } n\}\),那么:- 在基础步骤(basis step) 中证明 \(0 \in A\),即 \(P\) 在 \(0\) 上为真
- 归纳假设(induction hypothesis):对于固定但任意的 \(n \ge 0\),\(P\) 在每个自然数 \(0, 1, \dots, n\) 都成立
- 在归纳步骤中,要利用归纳假设证明 \(P\) 在 \(n+1\) 上为真
以上便是运用数学归纳法的模板。
-
具体应用可参考教材列出的例子
-
鸽巢原理(pigeonhole principle):若 \(A, B\) 是有限集合且 \(|A| > |B|\),那么 \(A\) 到 \(B\) 的映射不是单射。
- 通俗版:假设 \(A\) 表示一群鸽子,\(B\) 表示一些鸽巢,那么至少有一个鸽巢容纳的鸽子数超过 1
- 可用数学归纳法证明(具体证明见教材,这里只给思路)
- 基本步骤:证明 \(|B| = 0\) 时成立
- 归纳假设:\(|B| \le n\) 时均成立
- 归纳步骤:证明 \(|B| = n + 1\) 时成立
定理
令 \(R\) 为有限集合 \(A\) 上的二元关系,\(a, b \in A\),若 \(R\) 上存在由 \(a\) 到 \(b\) 的路径,那么路径长度至多为 \(|A|\)。
证明
用鸽巢原理 + 反证法,其实挺简单的,所以这里不给证明,可参考教材。
-
对角化(diagonalization):令 \(R\) 为集合 \(A\) 上的二元关系,且令 \(D\) 为 \(R\) 上的对角集合(diagonal set),即 \(\{a : a \in A \text{ and } (a, a) \notin R\}\)。\(\forall a \in A\),令 \(R_a = \{b : b \in A \text{ and } (a, b) \in R\}\),那么 \(D\) 和所有 \(R_a\) 均不同。
定理
幂集 \(2^{\mathbb{N}}\) 是不可数的。
证明
假设 \(2^{\mathbb{N}}\) 是可数无限的,也就是说假定存在一种方法可以枚举 \(2^N\) 的所有元素,如: $$ 2^{\mathbb{N}} = {R_0, R_1, R_2, \dots} $$
(注意这些就是在对角化原理陈述中的集合 \(R_a\),一旦我们考虑关系 \(R = \{(i,j) : j \in R_i\}\)
) 。现在考虑(对角)集合 $$ D = {n \in N : n \notin R_n} $$\(D\) 是自然数的一个子集,因此它应该出现在枚举 \(\{R_0, R_1, R_2, \dots\}\) 中的某个位置。
- 但 \(D\) 不可能是 \(R_0\),因为它在是否包含 0 这一点上与 \(R_0\) 不同(当且仅当 0 不在 \(R_0\) 中时,0 在 \(D\) 中)
- 同样地,它也不可能是 \(R_1\),因为它在 1 的归属上不同于 \(R_1\)
- 以此类推,不得不推出这样一个结论:\(D\) 根本不会出现在这个枚举中,这就和假设产生了矛盾
Closures and Algorithms⚓︎
定义
令 \(R \subseteq A^2\) 为定义在集合 \(A\) 上的有向图,那么 \(R\) 的自反传递闭包(reflective transitive closure) 为关系:
根据上述定义,我们可以得到一个计算对于任意给定的在有限集合 \(A = \{a_1, a_2, \dots, a_n\}\) 上的二元关系 \(R\) 的自反传递闭包的算法(该算法的正确性来自其对定义的直接实现
Initially R^* = emptyset
for i = 1, ..., n do
for each i-tuple (b[1], ..., b[i]) in A^i do
if (b[1], ..., b[i]) is a path in R then add (b[1], b[i]) to R^*
显然算法最终会得出正确答案。接下来要研究的问题是:它将在多少步之后终止(terminate)?答案取决于输入关系的规模,即依赖于集合 \(A\) 中元素的数量 \(n\)。因此,我们要寻找一个函数 \(f: \mathbb{N} \mapsto \mathbb{N}\),使得当 \(n \ge 1\) 时,对于二元关系 \(R \subseteq A \times A, |A| = n\),算法 \(f(n)\) 步后终止。
正如算法分析中常见的那样,我们允许 \(f(n)\) 是一个粗略的高估 (overestimate),只要其增长率(rate of growth) 正确即可。下面就来探讨增长率这一话题。
Growth of Functions⚓︎
定义
假设 \(f: \mathbb{N} \mapsto \mathbb{N}\),\(f\) 的阶数(order)(记作 \(\mathcal{O}(f)\))为所有包含以下性质的函数 \(g: \mathbb{N} \mapsto \mathbb{N}\) 的集合:存在正整数 \(c > 0, d > 0\),\(\forall n \in \mathbb{N}\),\(g(n) \le c \cdot f(n) + d\)。若该不等式对所有 \(n\) 都成立,那么我们可以说 \(g(n) \in \mathcal{O}(f(n))\)(其中常量为 \(c, d\)
如果有两个函数 \(f, g: \mathbb{N} \mapsto \mathbb{N}\),有 \(f \in \mathcal{O}(g), g \in \mathcal{O}(f)\),那么可以写作 \(f \asymp g\)。容易证明,\(\asymp\) 是一个等价关系。
因此,所有从自然数集合到其自身的函数可通过 \(\asymp\) 划分为不同的等价类中。\(f\) 关于 \(\asymp\) 的等价类就是 \(f\) 的增长率。
Analysis of Algorithms⚓︎
现在对上述算法所需步骤做一个大致的估计:
- 算法需要检验每个序列 \((b_1, \dots, b_i)\)(长度至多为 \(n\)
) ,确定它是否为 \(R\) 的一条路径,若是则将其放入 \(R^*\) - 每次检验都需要不超过 \(n\) 次的这样的的基本运算:测试 \((a, b)\) 是否在 \(R\) 内,以及将 \((a, b)\) 放入 \(R^*\) 内
- 因此总运算次数不超过 \(n \cdot (1 + n + n^2 + \dots + n^n)\),即该算法所需时间的增长率为 \(\mathcal{O}(n^{n+1})\),效率超低!
于是考虑以下更高效的算法,并且可能比前面的算法看起来更为自然和直观:
# reflective
Initially R^* = R union {(a[i], a[i]) : a[i] in A}
# transitive
while there are three elements a[i], a[j], a[k] in A such that
(a[i], a[j]), (a[j], a[k]) in R^* but (a[i], a[k]) not in R^* do:
add (a[i], a[k]) to R^*
算法的正确性不言而喻。那么算法何时停止呢?答案是至多 \(n^2\) 次迭代,因为 \(R^*\) 至多有 \(n^2\) 个二元对。并且由于每次迭代需要 \(\mathcal{O}(n^3)\) 的操作(因为三元组中的每个元素都要被搜一遍
然而这样还不够高效——一个显而易见的问题是该算法会重复遍历已经检查过的三元组。如果能够克服这个问题,算法的复杂度就能降至 \(\mathcal{O}(n^3)\)(每个三元组仅检查一次
Initially R^* = R union {(a[i], a[i]) : a[i] in A}
for each j = 1, 2, ..., n do
for each i = 1, 2, ..., n and k = 1, 2, ..., n do
if (a[i], a[j]), (a[j], a[k]) in R^* but (a[i], a[k]) not in R^* then
add (a[i], a[k]) to R^*
要想证明该算法的正确性,就需要证明以下陈述:对于每个 \(j = 1, \dots, n\),在外层循环执行完 \(j\) 次后,\(R^*\) 包含了所有 \((a_i, a_k)\) 对,满足 \(R\) 中从 \(a_i\) 到 \(a_k\) 之间有一条等级(rank)(路径上中间节点的最大索引,不包括起点和终点)不超过 \(j\) 的路径。可通过归纳法证明,具体证明过程见教材 \(P_{37}\),这里不再赘述。
Closure Properties and Closures⚓︎
定义
令 \(D\) 为集合,\(n \ge 0\),\(R \subseteq D^{n+1}\) 为 \(D\) 上 \(n+1\) 元关系。那么对于 \(D\) 的子集 \(B\),若当 \(b_1, \dots, b_n \in B\) 且 \((b_1, \dots, b_n, b_{n+1}) \in R\),那么称 \(B\) 是在 \(R\) 下是封闭的(closed)。任何形如“集合 \(B\) 在关系 \(R_1, R_2, \dots, R_m\) 下是封闭”的性质被称为 \(B\) 的闭包性质(closure property)。
定理
令 \(P\) 为定义在集合 \(D\) 上的关系的一条闭包性质,且 \(A\) 为 \(D\) 的子集,那么存在一个唯一的最小集合 \(B\),满足包含 \(A\) 且具备性质 \(P\)。
任何在有限集合上的闭包性质能在多项式时间内被算出来。假设在有限集合 \(D\) 上有不同元数的关系 \(R_1 \subseteq D^{r_1}, \dots, R_k \subseteq D^{r_k}\),并有集合 \(A \subseteq D\)。现在要计算 \(A\) 在关系 \(R_1, \dots, R_k\) 下的闭包 \(A^*\)。我们可以通过泛化前面得到的 \(\mathcal{O}(n^5)\) 的传递闭包算法实现在多项式时间内的计算。
Initially A^* = A
while there is an index i, 1 <= i <= k, and r[i] elements a[j[1]], ..., a[j[r[i-1]]] in A^*
and a[j[r[i]]] in D - A^* such that (a[j[1]], ..., a[j[r[i]]]) in R[i] do:
add a[j[r[i]]] in A^*
该算法的复杂度为 \(\mathcal{O}(n^{r+1})\),其中 \(n = |D|\) 且 \(r\) 为 \(r_1, \dots, r_k\) 中最大的数。
Alphabets and Languages⚓︎
计算理论的数学研究必须要从理解符号字符串的数学原理开始。
- 字母表(alphabet):关于符号(symbol) 的有限集合,记作 \(\Sigma\)
- 和计算理论密切相关的一个字母表是二元字母表(binary alphabet) \(\{0, 1\}\)
-
字符串(string):来自字母表的有限符号序列
- 字符串的书写不需要用括号或逗号间隔,而是直接将符号连在一起写,比如 watermelon, 0110011
- 单个符号等同于用该符号表示的字符串
- 没有符号的字符串是空字符串(empty string),记作 \(e\)
- 一般使用 \(u, v, w, x, y, z\) 和希腊字母表示字符串
- \(\Sigma^*\):在字母表 \(\Sigma\) 上的所有字符串集合(包括空字符串)
- \(\Sigma^+ = \Sigma^* - \{e\}\):在字母表 \(\Sigma\) 上的非空字符串集合
- \(\Sigma^n = \underbrace{\Sigma \times \dots \times \Sigma}_{\text{length} = n}\):在字母表 \(\Sigma\) 上的长度为 \(n\) 的字符串集合
- 字符串 \(w\) 的长度(length) 即序列长度,记作 \(|w|\)
- 可将字符串看作一个函数 \(w: \{1, \dots, |w|\} \mapsto \Sigma\);\(w(j)\) 的值就是 \(w\) 在第 \(j\) 个位置上的符号
- 如果需要区分不同位置上的相同符号,我们将它们称为该符号的不同出现(occurrence)
-
拼接(concatenation):将两个来自相同字母表的字符串 \(x, y\) 结合起来,形成新的字符串,记作 \(x \circ y\) 或 \(xy\)
- 形式上,当且仅当 \(|w| = |x| + |y|, w(j) = x(j)\ (j = 1, \dots, |x|)\) 且 \(w(|x| + j) = y(j)\ (j = 1, \dots, |y|)\) 时,\(w = x \circ y\)
- \(w \circ e = e \circ w = w\)
- 拼接满足结合律,即 \((wx)y = w(xy)\)
- 当且仅当存在字符串 \(x, y\),满足 \(w = xvy\),称字符串 \(v\) 为 \(w\) 的子字符串(substring);此外还有以下特殊情况:
- \(w = xv\) -> \(v\) 是 \(w\) 的后缀(suffix)
- \(w = vy\) -> \(v\) 是 \(w\) 的前缀(prefix)
-
字符串 \(w^i\) 的定义如下(一种归纳定义(definition by induction)
) :\[ \begin{aligned} w^0 & = e, \quad \text{the empty string} \\ w^{i+1} & = w^i \circ w, \quad \text{for each } i \ge 0 \end{aligned} \]
-
反转(reversal):记作 \(w^R\),其归纳定义为:
- 若 \(|w| = 0\),则 \(w^R = w = e\)
- 若 \(|w| = n + 1 > 0\),则 \(w = ua\),其中 \(a \in \Sigma\) 且 \(w^R = au^R\)
-
语言(language):\(\Sigma^*\) 的任意子集(即字母表 \(\Sigma\) 上任意字符串构成的集合)
- \(\Sigma^*, \emptyset, \Sigma\) 都是语言
-
用以下形式表述无限 (infinite) 语言:
\[ L=\{w\in\Sigma^*:w\text{ has property }P\} \] -
若 \(\Sigma\) 是有限字母表,那么 \(\Sigma^*\) 是可数无限的
-
要想构建双射 \(f: \mathbb{N} \mapsto \Sigma^*\),首先要确定字母表顺序,即 \(\Sigma = \{a_1, \dots, a_n\}\),然后可按以下方式枚举 \(\Sigma^*\) 的成员:
- \(\forall k \ge 0\),所有长度为 \(k\) 的字符串应在长度为 \(k+1\) 字符串之前被枚举
- 长度恰好为 \(k\) 的 \(n^k\) 个字符串按词典序(lexicographically) 枚举,即 \(a_{i_1}, \dots, a_{i_k}\) 先于 \(a_{j_1}, \dots, a_{j_k}\) 枚举,其中 \(0 \le m \le k - 1, i_l = j_l\ (l = 1, \dots, m), i_{m+1} < j_{m+1}\)
-
由于语言本质上是集合,所以可通过集合运算(并、交、差)将语言结合起来
- \(A\) 的补(complement) 为 \(\bar{A} = \Sigma^* - A\)
-
语言的拼接(concatenation):若 \(L_1, L_2\) 为在 \(\Sigma\) 上的语言,那么拼接为 \(L = L_1 \circ L_2 = L_1 L_2\),其中
\[ L=\{w\in\Sigma^*:w=x\circ y\text{ for some }x\in L_1\mathrm{~and~}y\in L_2\} \] -
克莱尼星号(Kleene star):记作 \(L^*\),是通过拼接 0 个或多个来自 \(L\) 的字符串构成的全部字符串的集合,即
\[ L^*=\{w\in\Sigma^*:w=w_1\circ\cdots\circ w_k\text{ for some }k\geq0\text{ and some }w_1,\ldots,w_k\in L\} \]- 如果将字母表看作一种有限语言,那么 \(\Sigma^*\) 的定义和克莱尼星号是一致的
-
\(L\) 在拼接运算下的闭包(closure) 记作 \(L^+ = LL^*\),即包含 \(L\) 和所有由 \(L\) 内字符串拼接而成的字符串的最小语言
\[ \{w\in\Sigma^*:w=w_1\circ w_2\circ\cdots\circ w_k\text{ for some }k\geq1\text{ and some }w_1,\ldots,w_k\in L\} \]
注意
当 \(\Sigma = \emptyset\) 时,还是存在非空的语言 \(L = \{e\}\)。
评论区