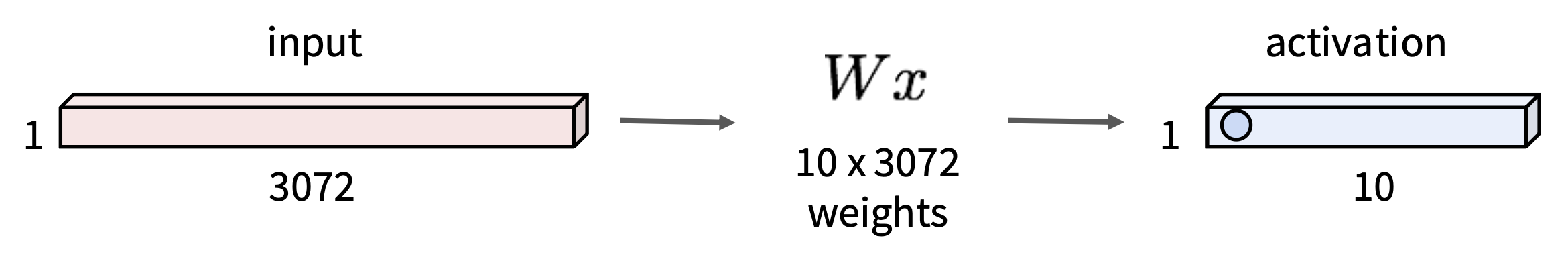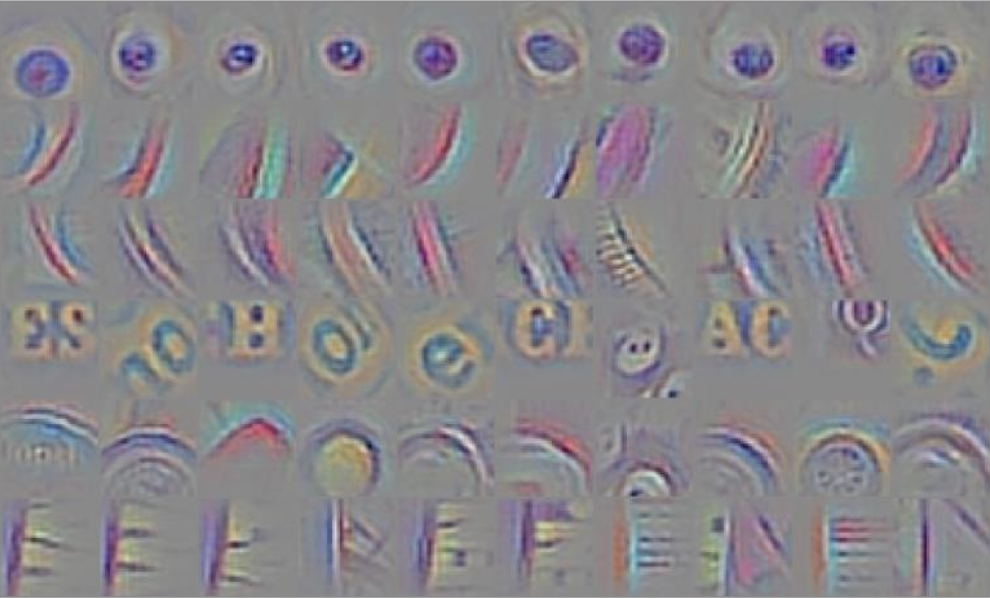Image Classification with CNNs⚓︎
约 2780 个字 4 行代码 预计阅读时间 14 分钟
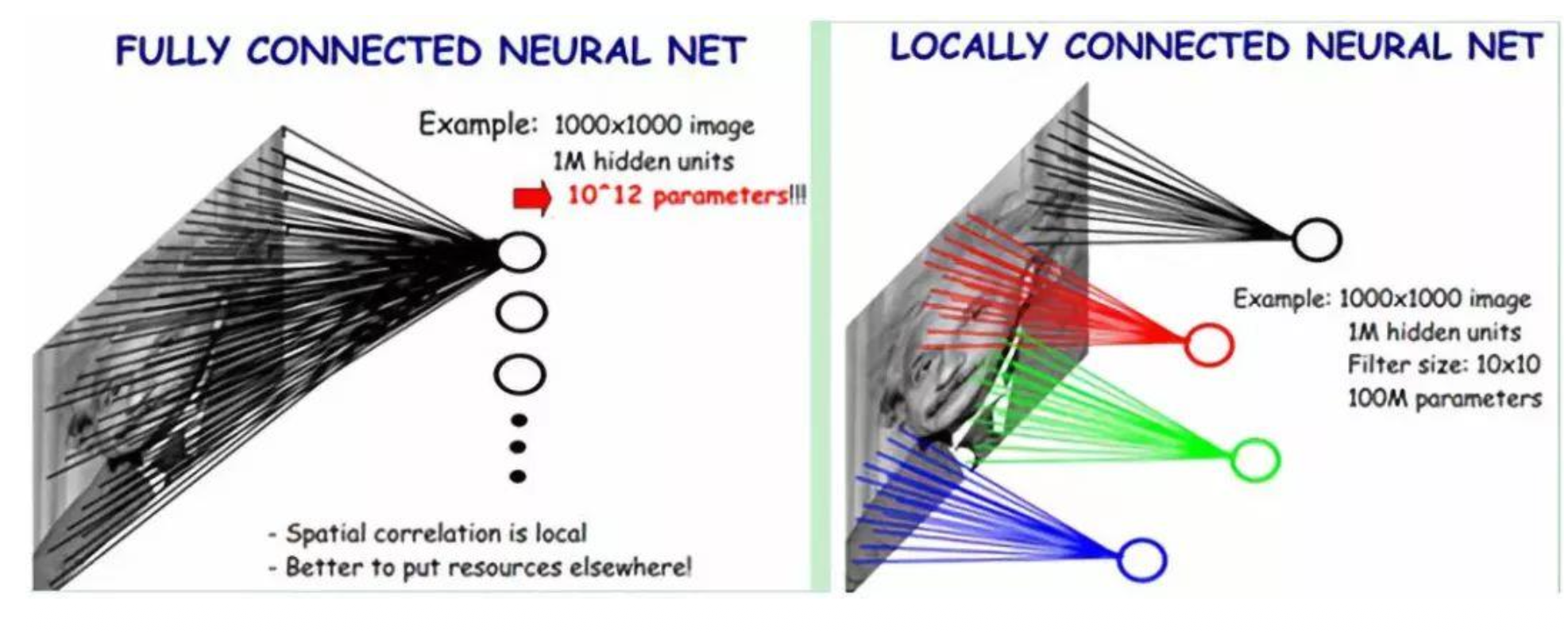
前面讲的(全连接)神经网络有一个问题:由于图像需要被展平为一维向量后再被处理,所以图像原本的空间结构就会被破坏掉;这就成了神经网络永远学不到的东西。所以本讲我们介绍一种专门用于图像和视觉任务的神经网络——卷积神经网络(convolutional neural network, ConvNet / CNN)。
如下图所示,整个网络分成了两部分:
- 卷积(convolution) 和池化(pooling) 算子提取有关 2D 图像结构的特征
- 全连接层在末端构成了多层感知机(MLP)以预测分数
- 通过反向传播 + 梯度下降法可以实现端到端的训练
另一种理解卷积的思路
卷积 = 局部连接性 + 权重共享
-
局部连接性:仅关注图像的局部特征 (local pattern)
-
权重共享
-
能够减少参数量
- 全局连接:7
- 局部连接:9
- 采用权重共享的局部连接:3
-
为何是有效假设?
- 权重表示物体应该看起来是什么样子
- 而不应该改变物体在图像中的位置(移位不变性(shift invariance property))
-
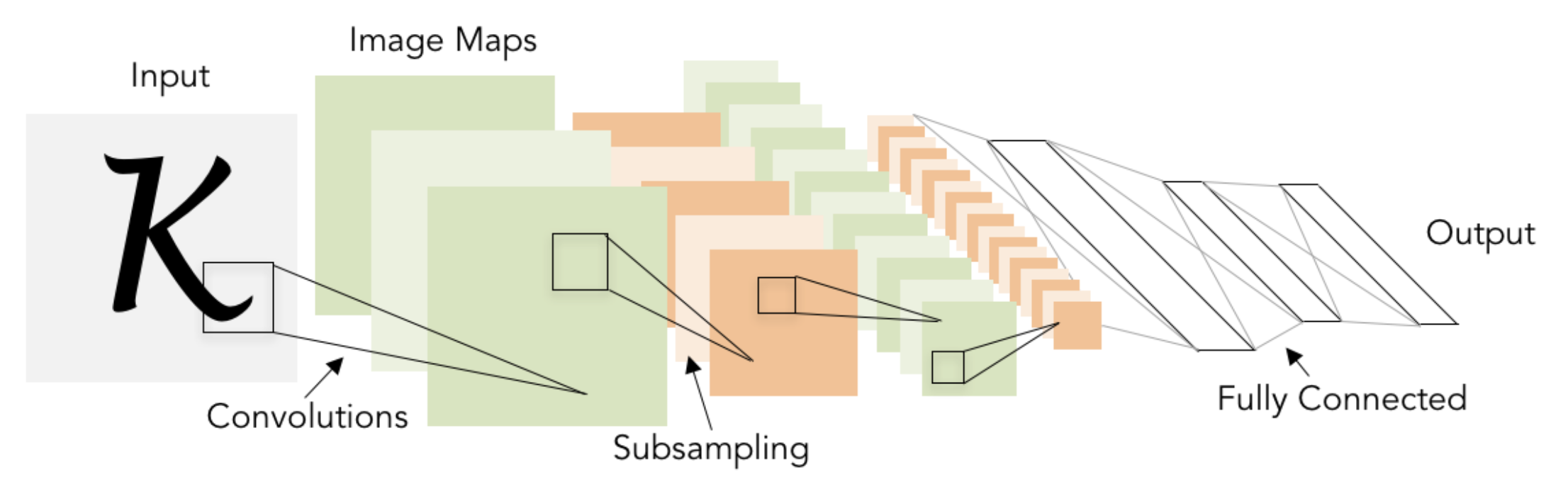
一些关于 ConvNet 的历史
- 杨立昆等人于 1998 年将基于梯度的学习(即上面那幅图)用于文档识别任务中
-
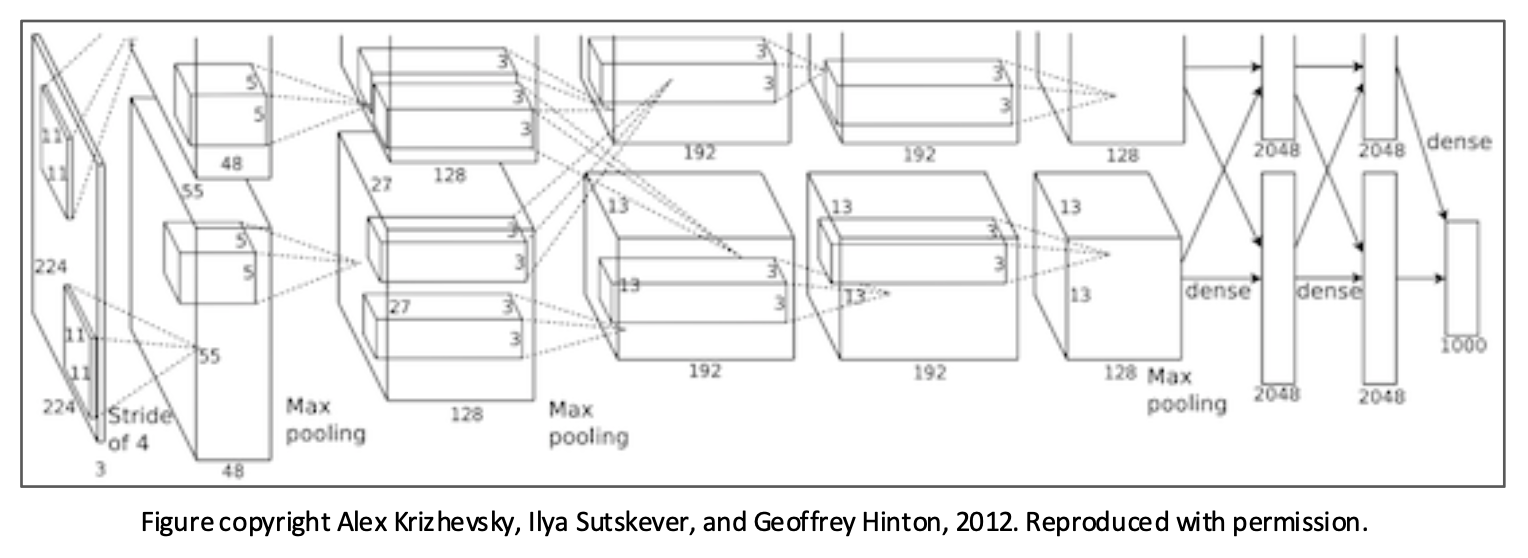
2012 年,ImageNet 挑战赛获胜者 AlexNet 用的就是一种深度卷积神经网络
-
~2012-2020,CNN 几乎支配了全部的视觉任务
-
CS231n 这门课以前也仅专注于 CNN
-
-
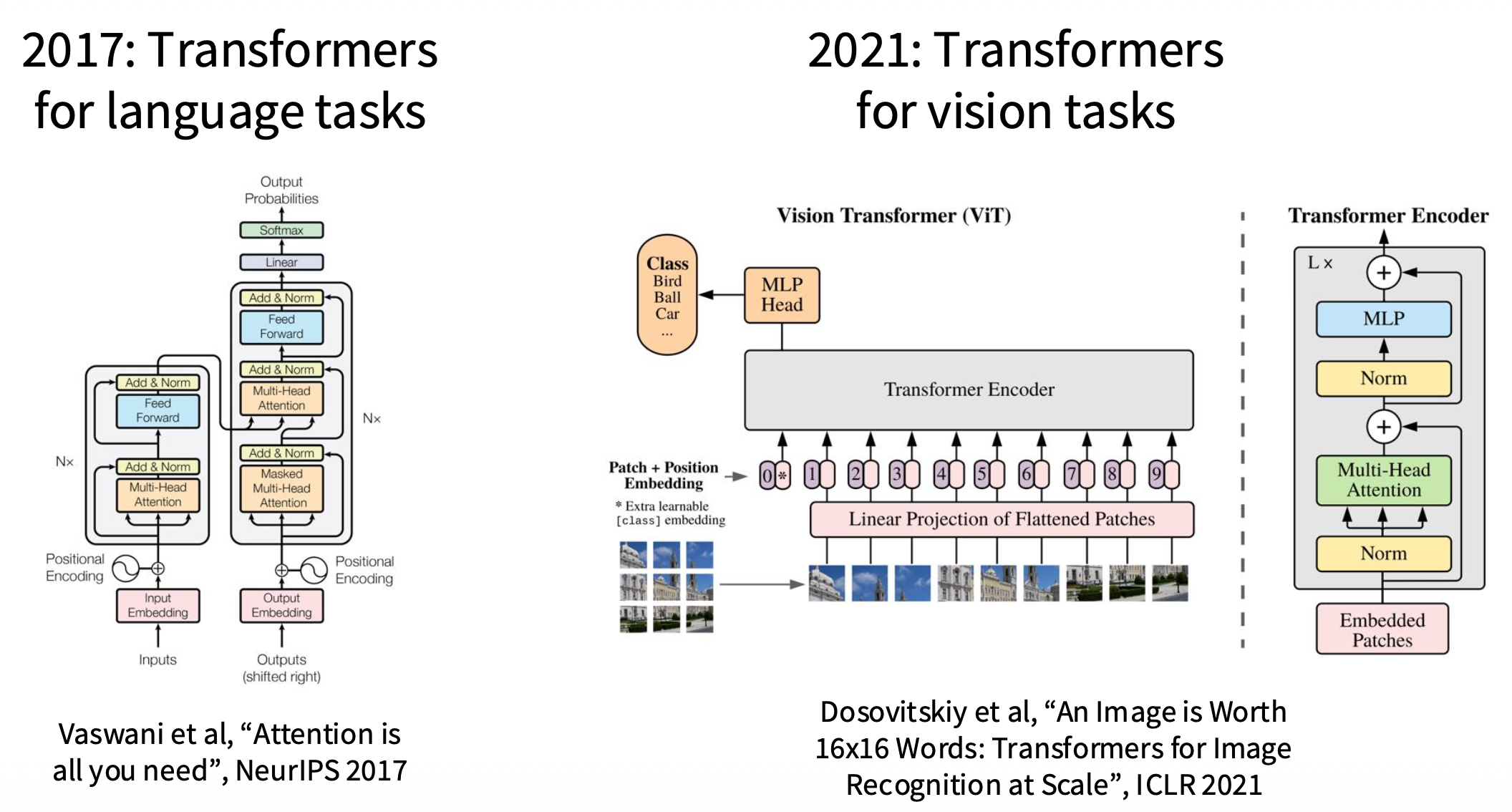
2021- 至今:Transformer 成为主流
Convolution Layers⚓︎
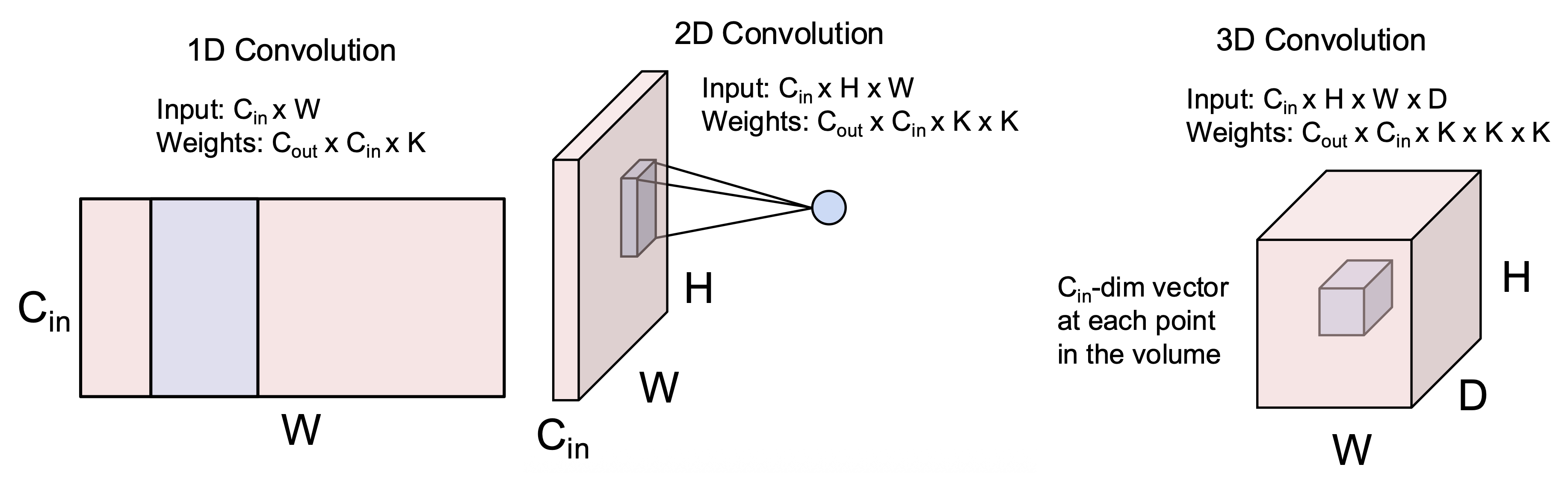
对于一幅大小为 32x32x3 的图像,全连接层在处理前会将其展平为 3072x1 的向量,然后做矩阵 - 向量乘法(\(Wx\)
- 激活向量的每个元素是 \(W\) 中的某行和输入向量的(3072 维的)点积
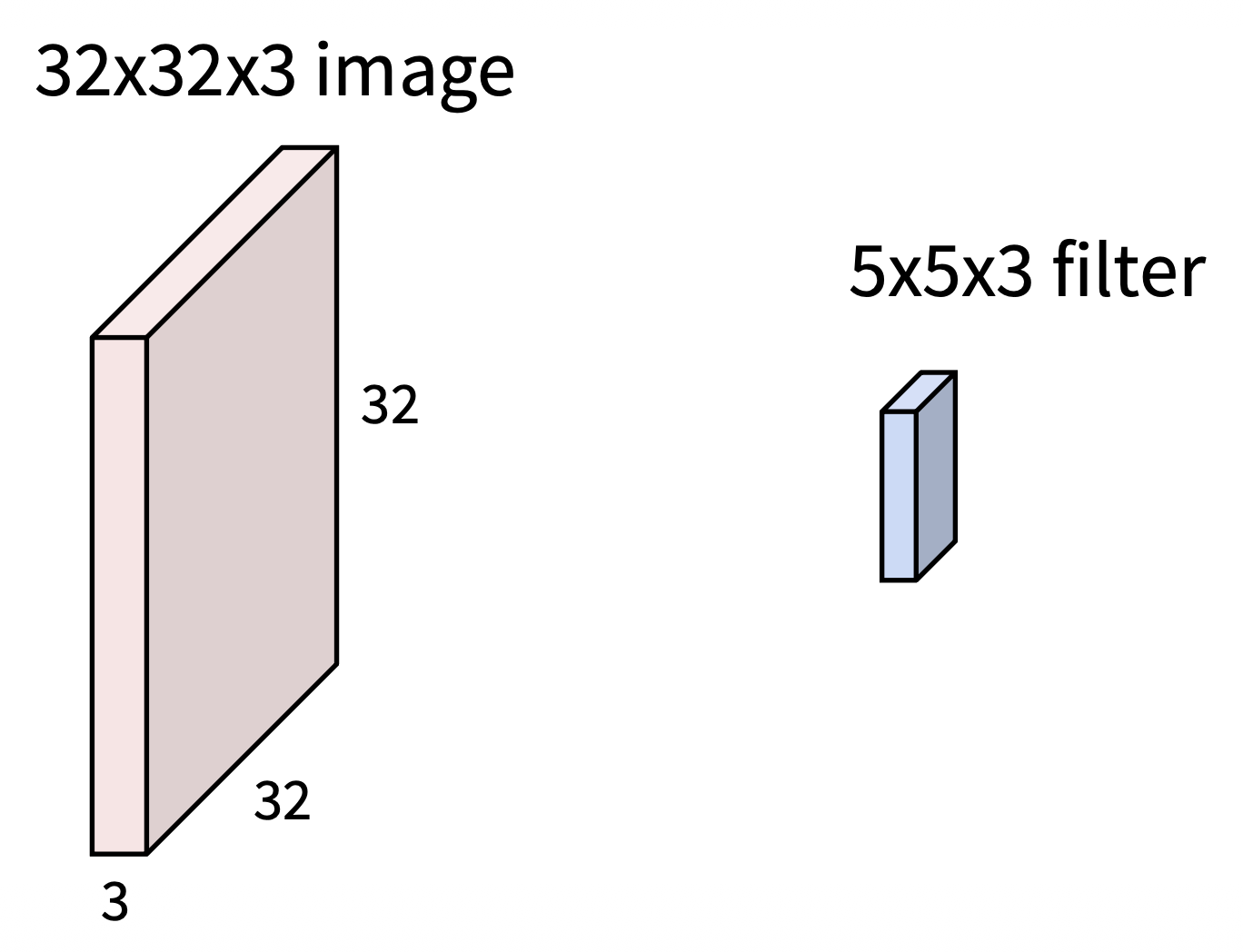
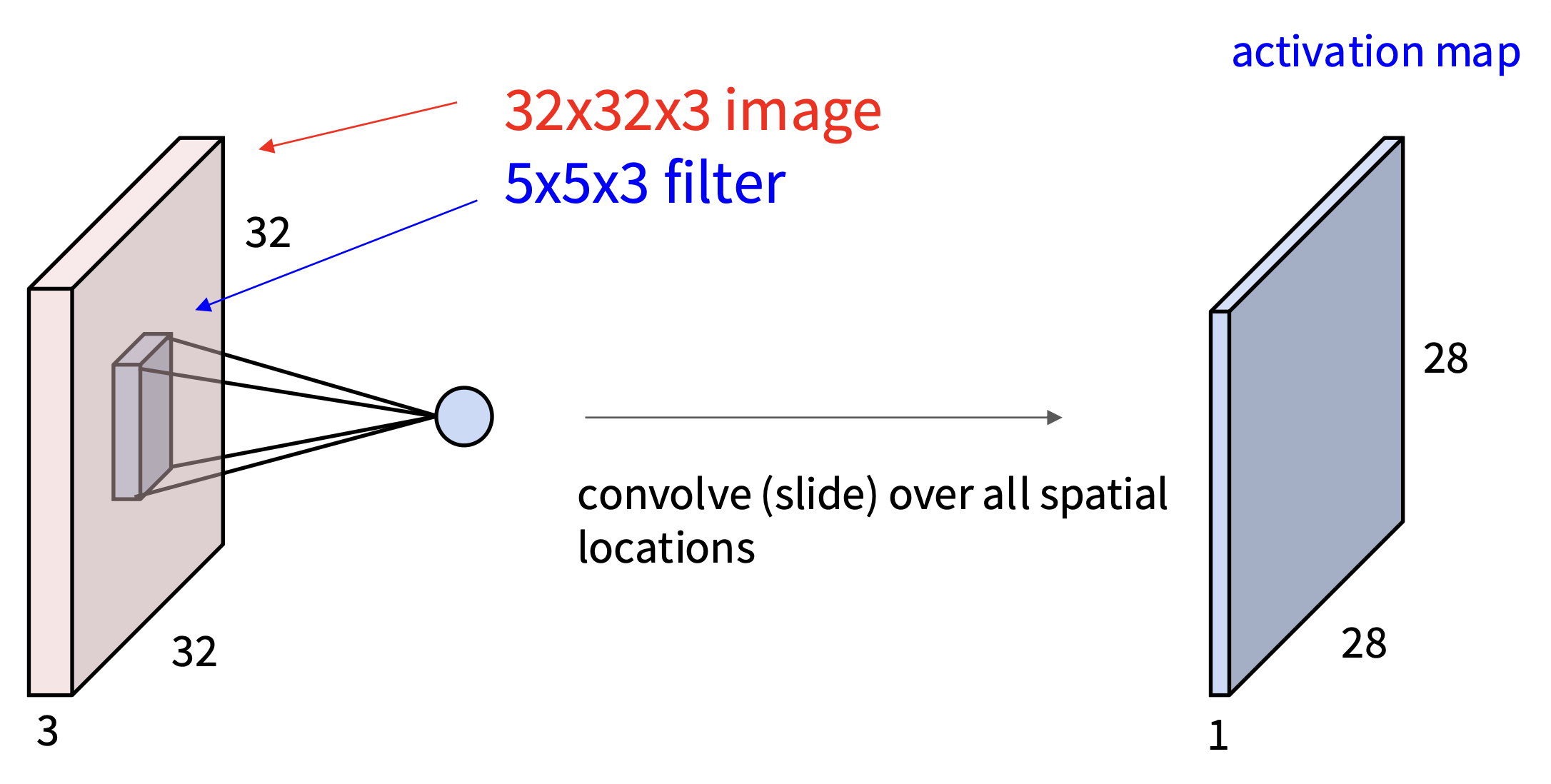
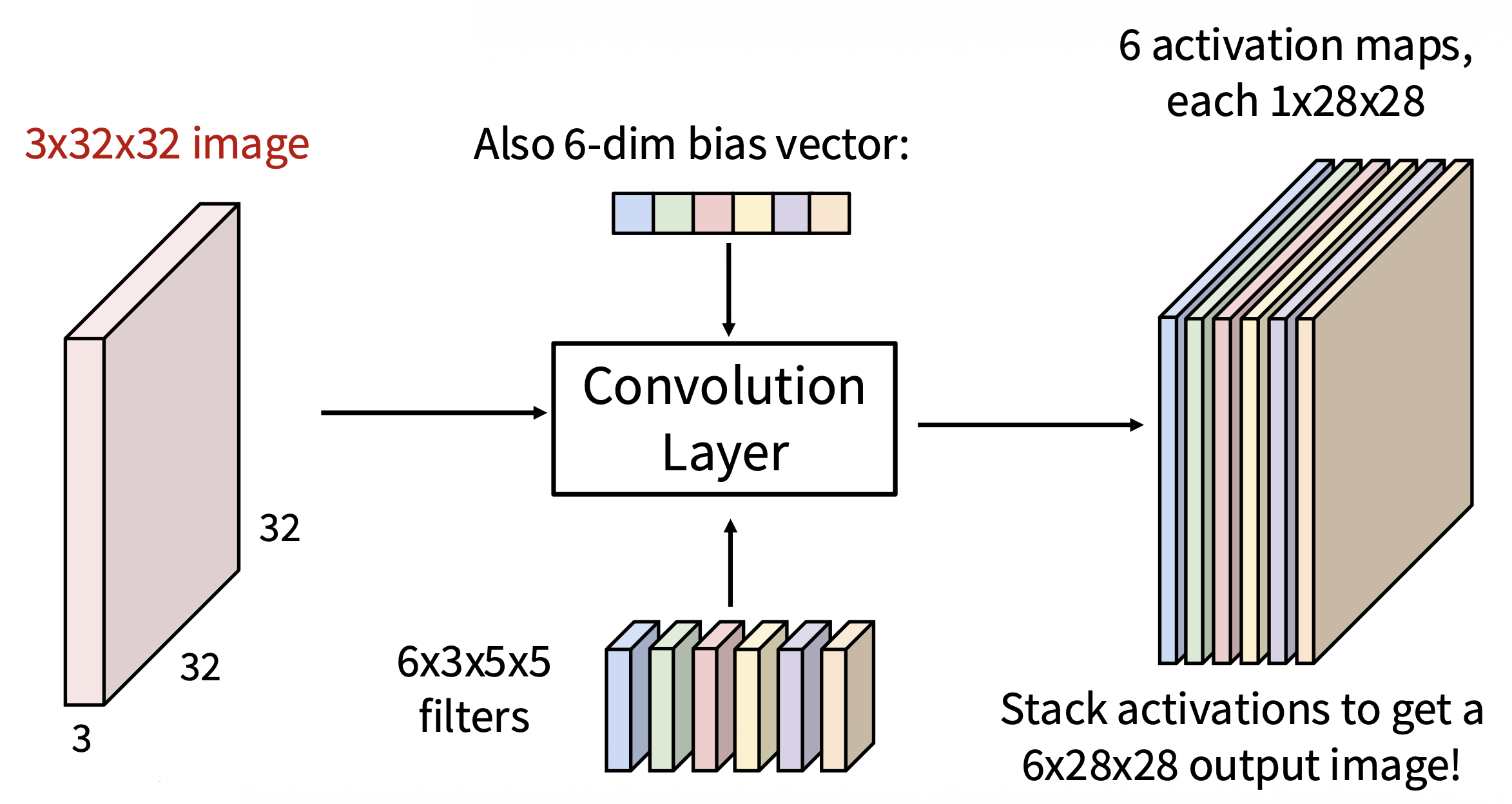
而卷积层则会保留图像原本的空间结构,并且用一个深度(通道数)和图像相同的滤波器(filter)(或叫做卷积核(kernel))\(w\) 对图像做卷积,即滤波器扫过整张图像,计算点积(\(w^T x + b\),矩阵点积是逐元素相乘再求和)
- 滤波器和图像某小块的点积结果是一个数字
-
当滤波器扫过整张图像后,所有卷积的结果会构成一张激活图(activation map)
-
实际应用中,往往有不止一个的滤波器。这里假设用了 6 个滤波器(并且考虑偏移量(构成了一个向量
) ) ,结果如下:可以看到,6 张激活图叠在一起就好像一张大小为 6x28x28 的输出图像
-
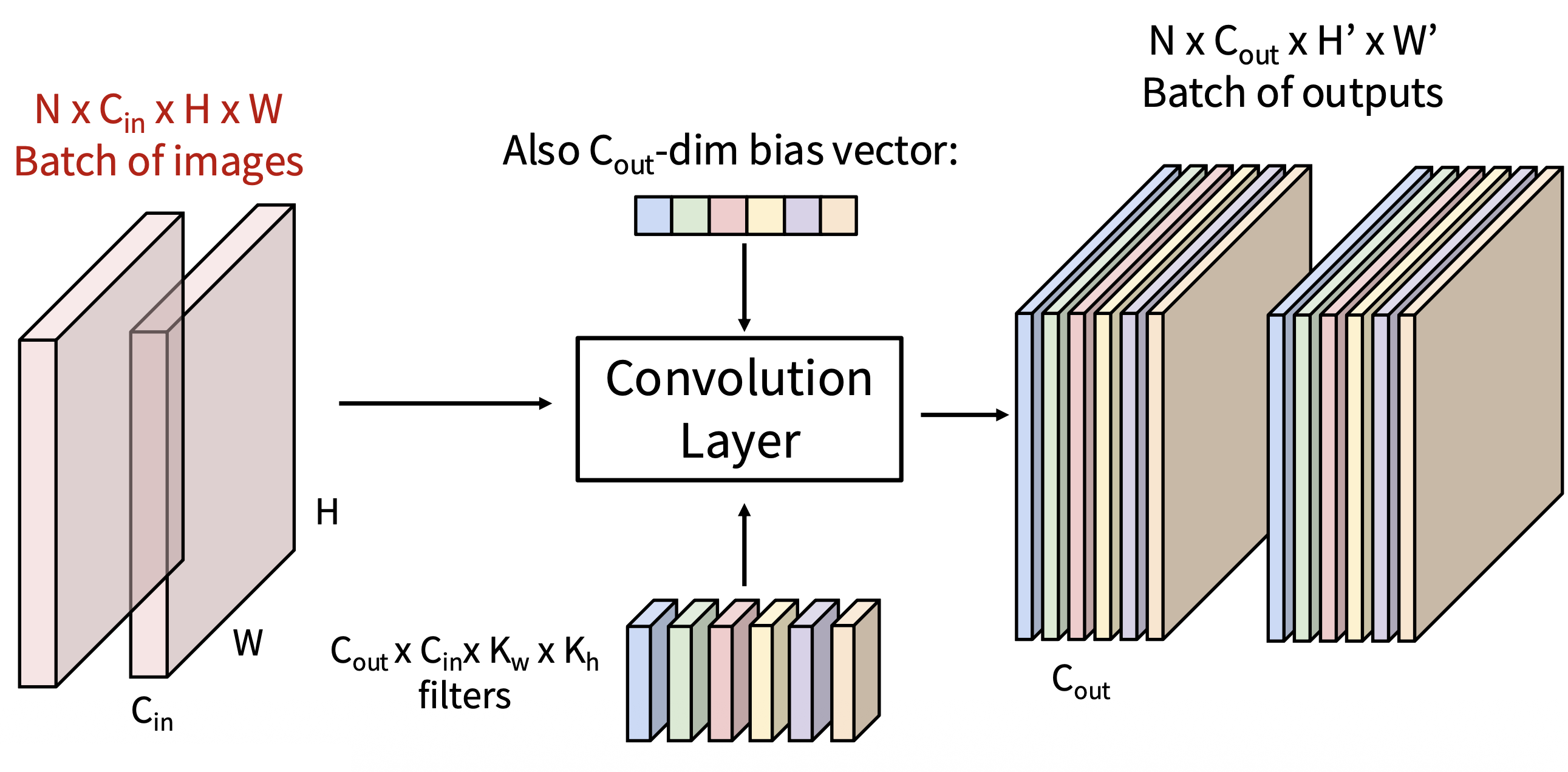
推广上述模型:假设有 N 幅大小为 C in xHxW 的图像,有 C out 个大小为 C in xK w xK h 的滤波器和 C out 维的偏移向量,那么对应有 N 个大小为 C out xH'xW' 的输出
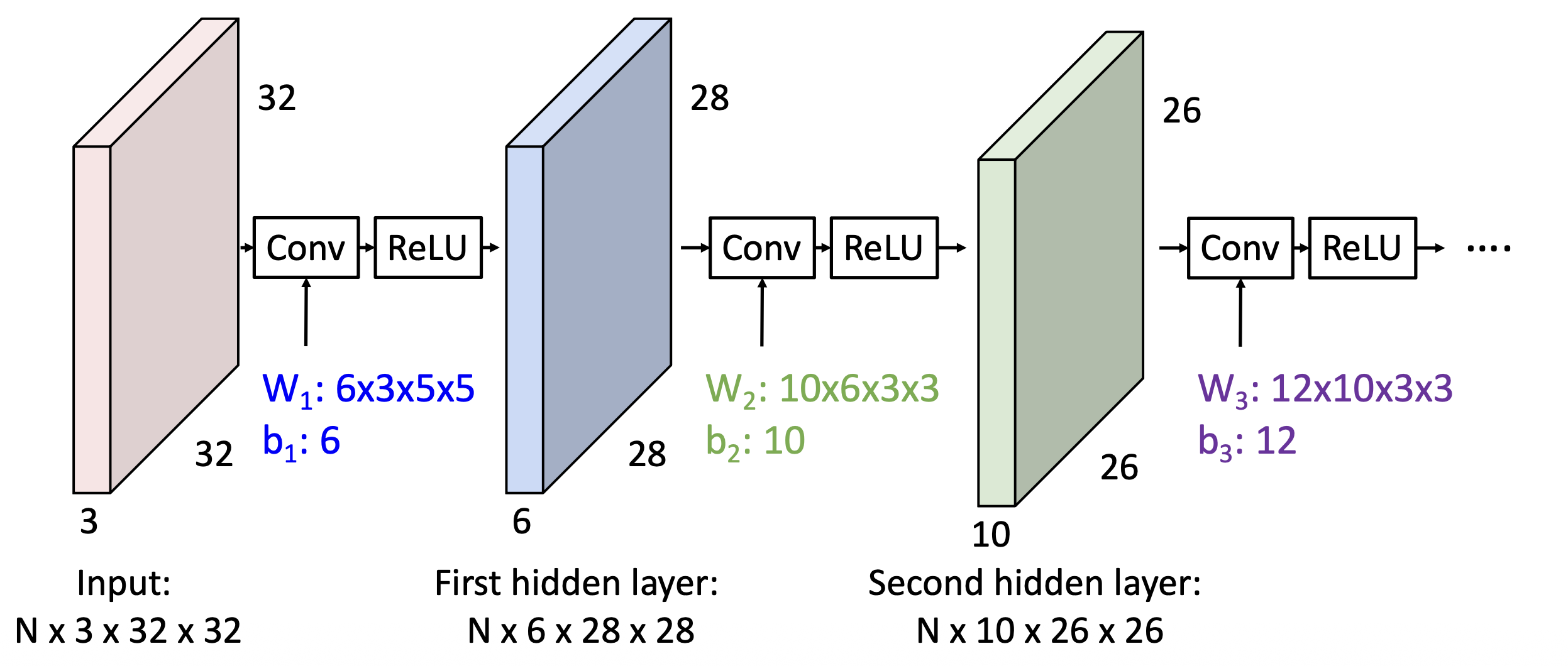
类似全连接层,如果仅是简单地将两个卷积层堆叠起来,我们只会得到另一种卷积。解决这个问题的方法依然是使用激活函数。
What do Conv Filters Learn?⚓︎
-
对于线性分类器,它能学到每个类别的模板
-
对于一般的神经网络(多层感知机
) ,它能学到图像的所有模板 -
对于第一层的卷积滤波器,它能学到一些局部的图像模板(通常学到有方向的边缘、对比色等)
- 下面的例子来自 AlexNet(64 个滤波器,大小为 3x11x11)
-
对于更深的卷积层,我们难以将其学到的东西可视化,但可以肯定的是它们可能学到了更大的图像结构,比如眼睛、字母等
- 下面的例子来自参与 ImageNet 比赛的某个模型的第 6 个卷积层(可视化来自 [Springenberg et al, ICLR 2015])
Spatial Dimension⚓︎
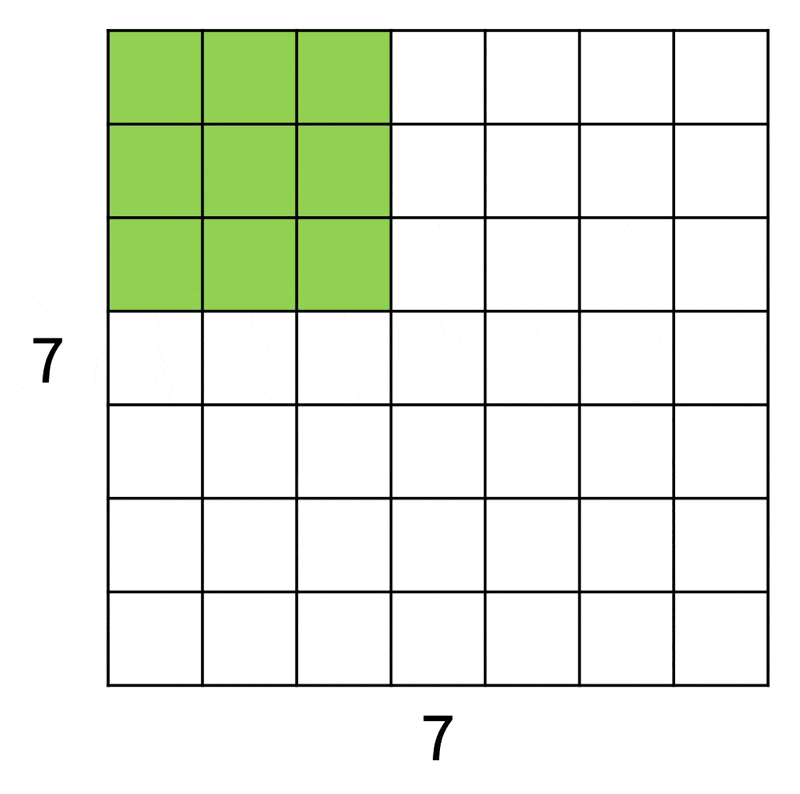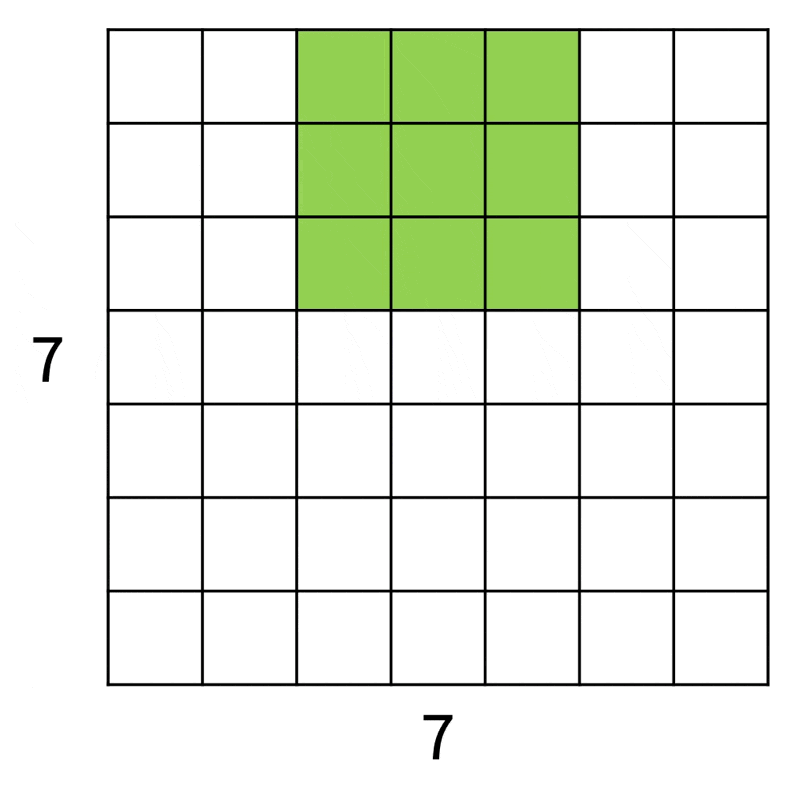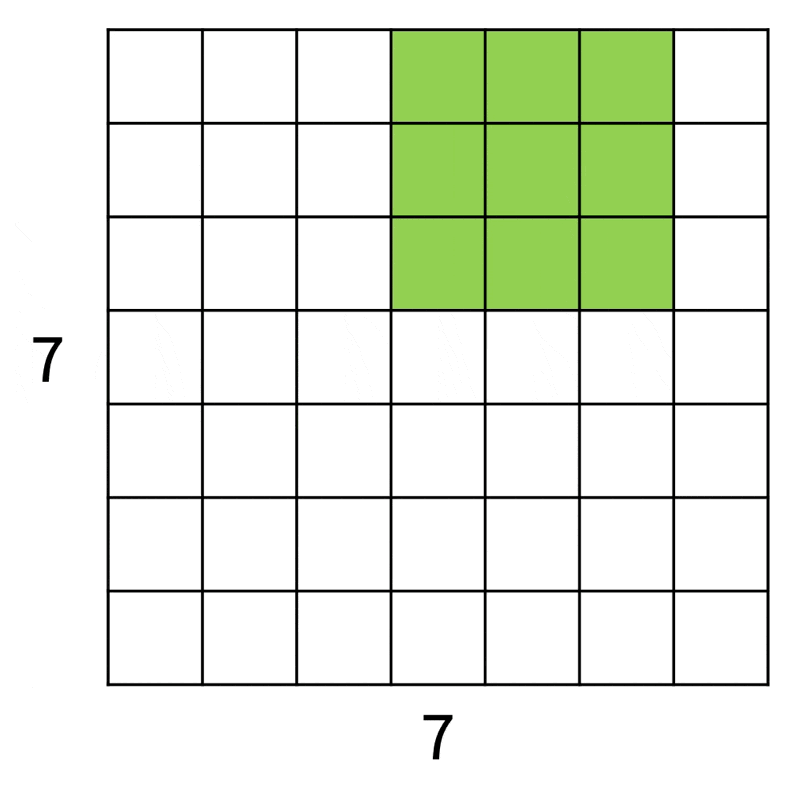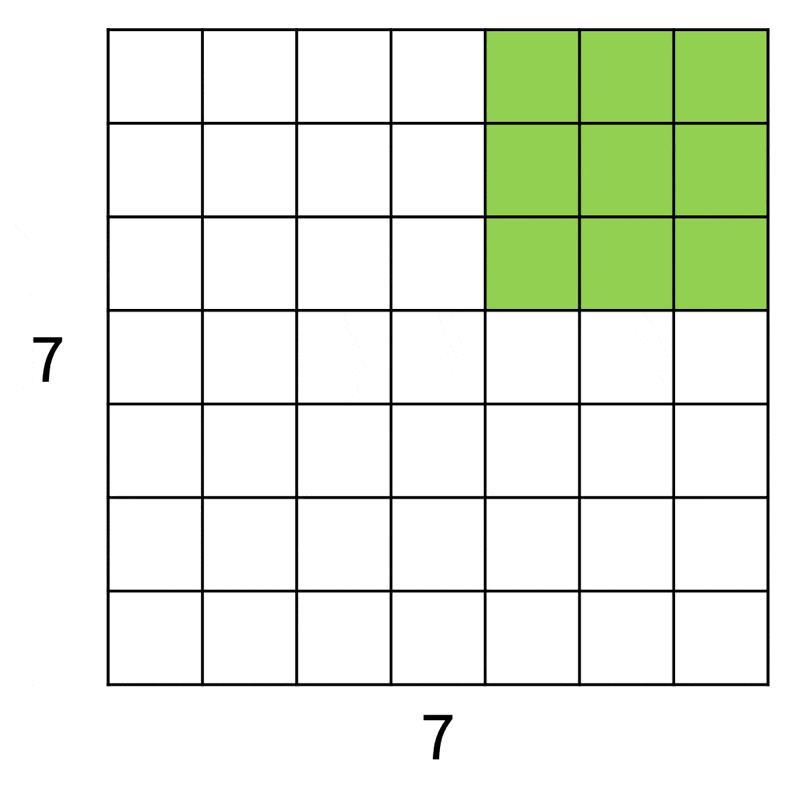
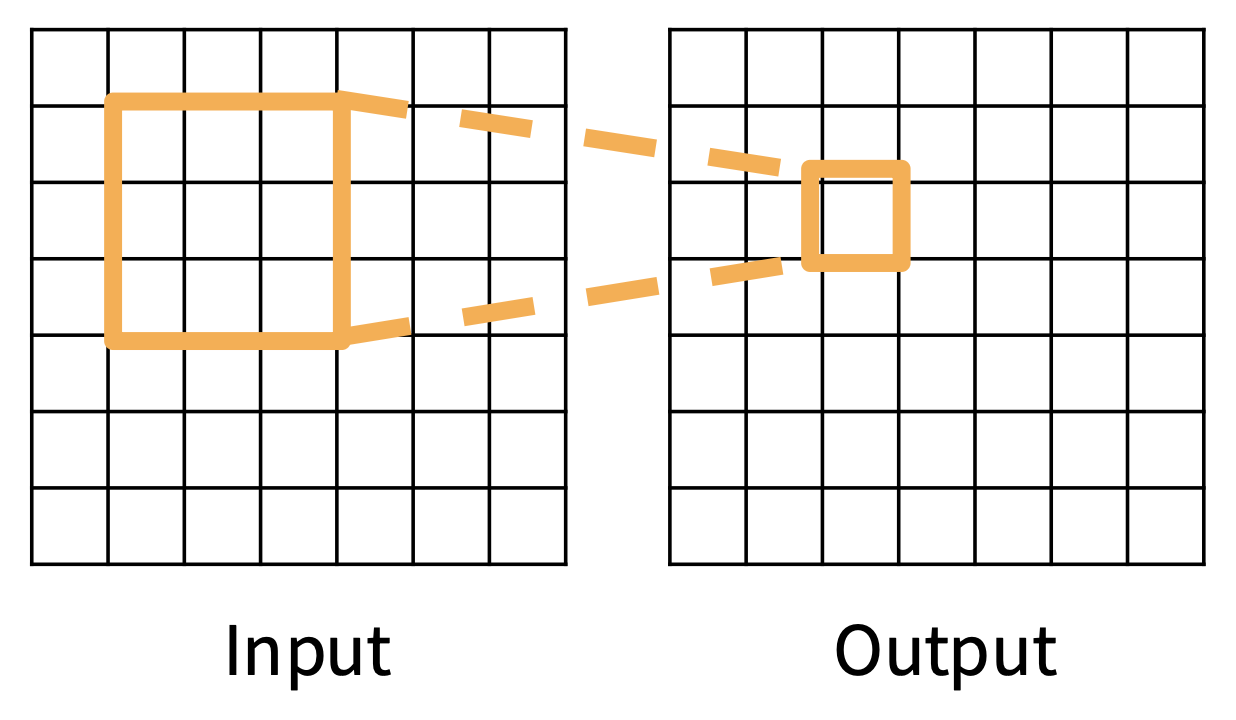
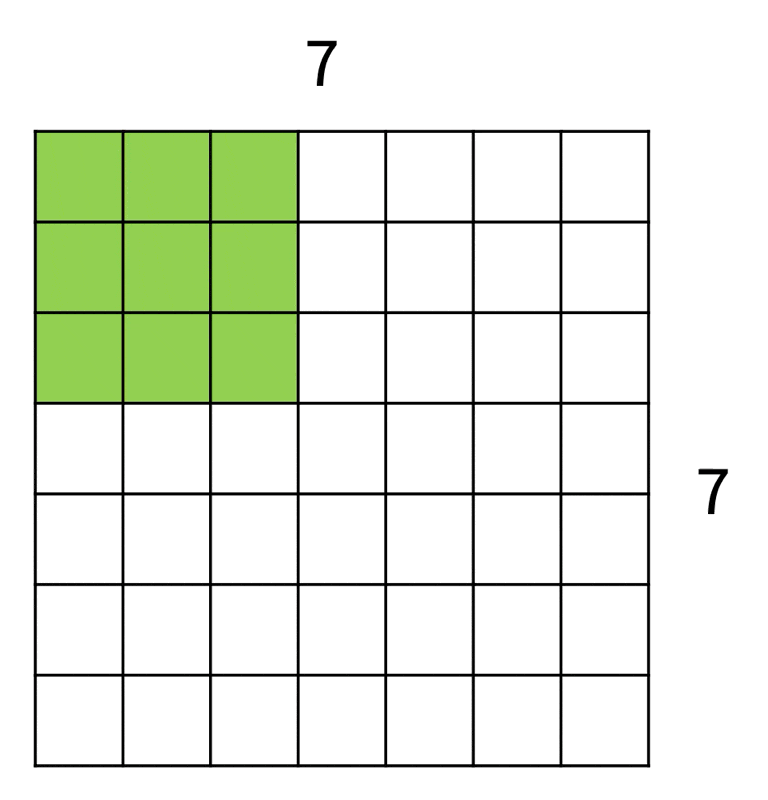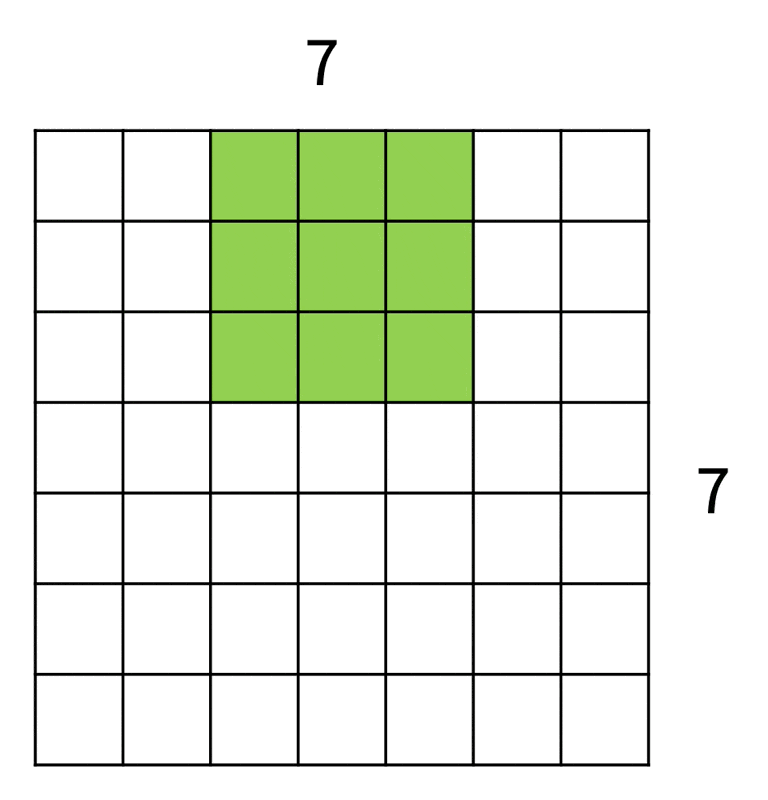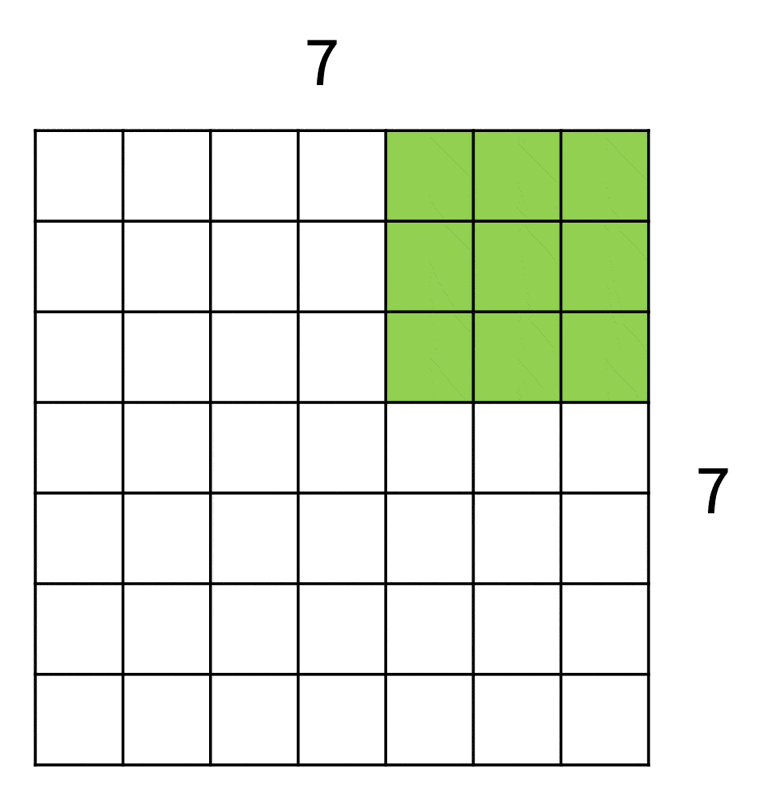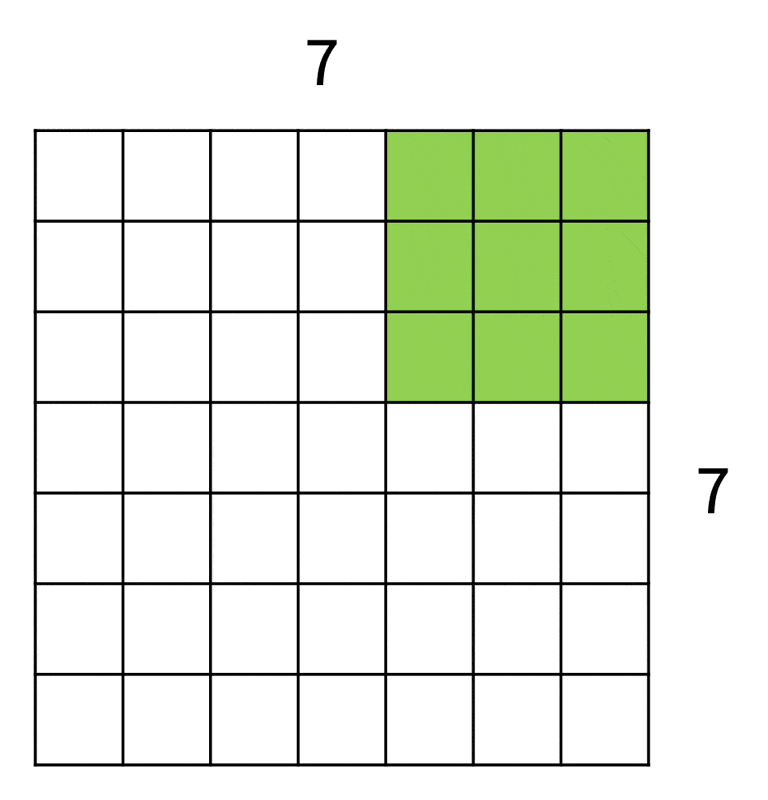
为便于解说和理解,下面从一维角度来看滤波器在图像上的操作:
如上图所示,输入图像大小为 7x7,而滤波器大小为 3x3,因此输出大小为 5x5。
更一般地(仅考虑某一边的大小
- 输入:W
- 滤波器:K
- 输出:W - K + 1
不难发现这样一个问题:每经过一次卷积层
假设填充宽度为 P,那么输出宽度就变成 W - K + 1 + 2P,所以我们通常设置 P = (K - 1) / 2,从而保证输出大小 = 输入大小。
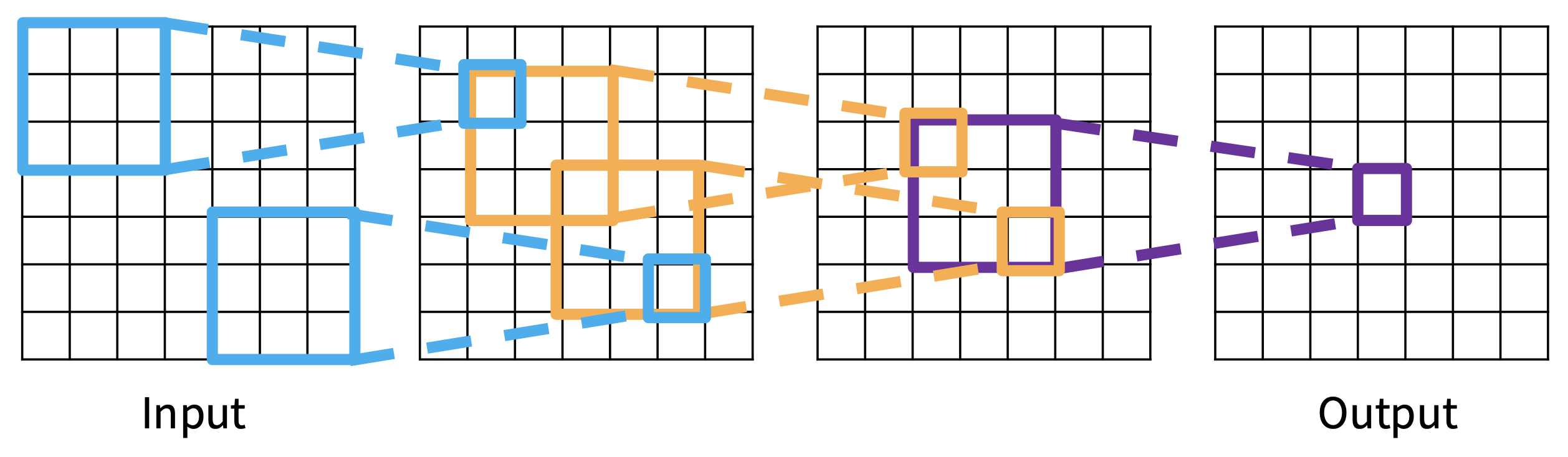
Receptive Field⚓︎
假如卷积核大小为 K,那么输出中的每个元素对应输入中 KxK 大小的感受野(receptive field)。
每次连续的卷积都会使感受野宽度增加 K – 1,因此连续使用 L 层卷积时,感受野宽度变为 1 + L * (K – 1)。
注意区分“输入中的感受野”和“前一层中的感受野”的概念!
这里存在的一个问题是:对于很大的图像,可能需要很多层才能让每个输出“看见”整张图像。解决方案是在网络内做降采样(downsampling)。
Stride Convolution⚓︎
一种降采样方式是增大滤波器的移动步幅(stride)。还是对于 7x7 大小的输入和 3x3 大小的滤波器,假如步幅调整至 2 个单位(原来为 1
推广至一般情况:
- 输入:W
- 滤波器:K
- 填充:P
- 步幅:S
-> 输出:(W - K + 2P) / S + 1
问题
- 输入图像大小:3x32x32
- 10 个 5x5 的滤波器,步幅为 1,填充宽度为 2
请问:
- 输出大小?
- 可学习的参数数量?
- 乘法 - 加法运算次数?
- 输出大小:10x32x32
- 可学习的参数数量:10 * (3 * 5 * 5 + 1 (for bias))
- 乘法 - 加法运算次数:(3 * 5 * 5) * (10 * 32 * 32) = 768K
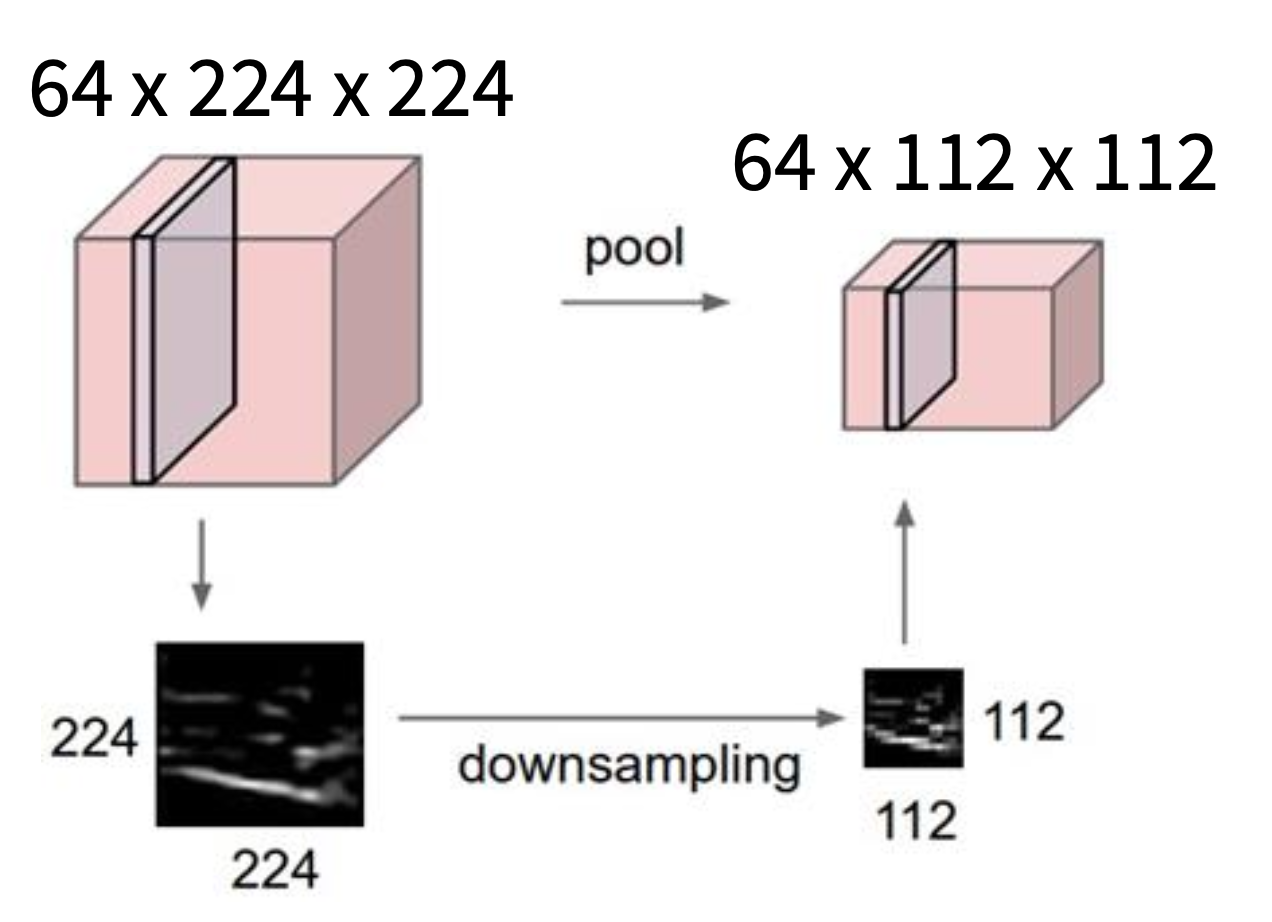
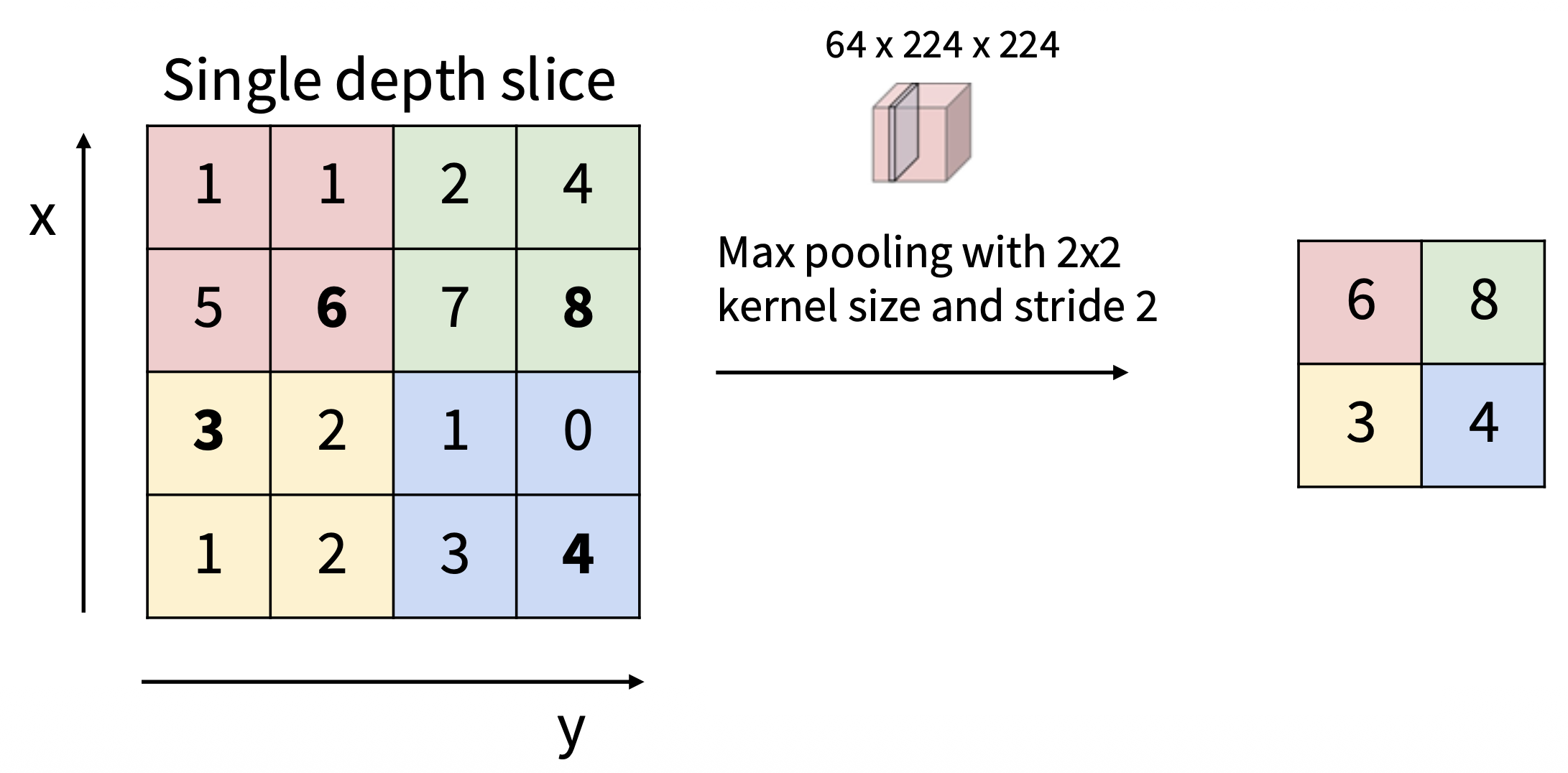
Pooling Layers⚓︎
池化层(pooling layer) 是另一种降采样的方法:对于大小为 CxHxW 的输入,为每个 1xHxW 的平面进行降采样。
超参数:
- 核大小
- 步幅
- 池化函数
常用的池化函数:
-
最大池化(max pooling):选取核内最大值作为输出结果
- 该函数对小的空间位移具有不变性(invariance),并且没有可学习的参数
-
平均池化(average pooling)
池化的意义:
- 聚合空间信息
- 让特征图更小,更易于管理
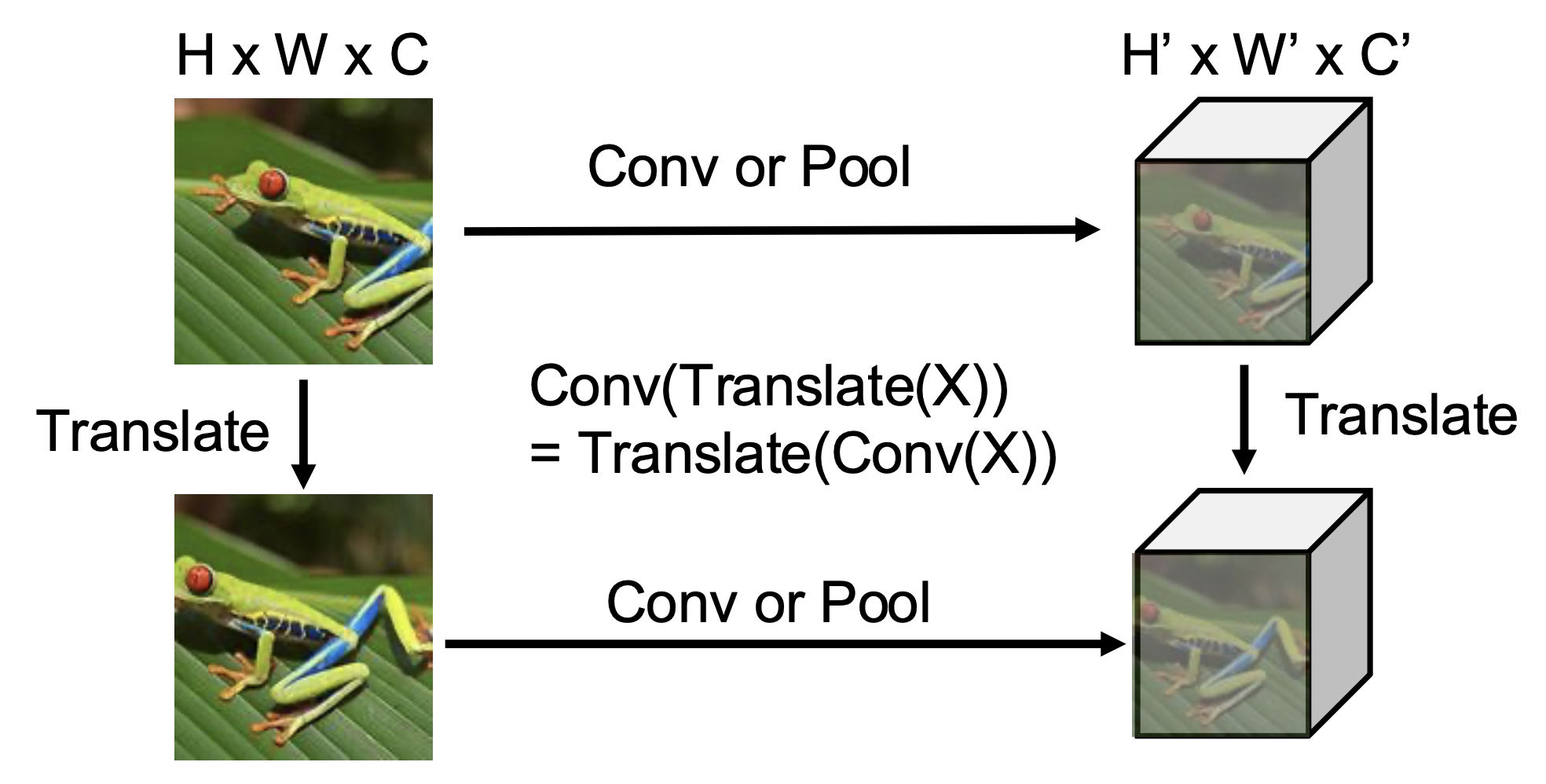
Translation Equivariance⚓︎
卷积和池化之间具有转换等变性(translation equivariance),即:
这一性质对应到我们的直觉上就是:图像的特征不依赖于它们在图像上的位置。
注
经典的 CNN 架构:
LeNet-5
| Layer | Output Size | Weight Size |
|---|---|---|
| Input | 1 x 28 x 28 | |
| Conv (C_out=20, K=5, P=2, S=1) | 20 x 28 x 28 | 20 x 1 x 5 x 5 |
| ReLU | 20 x 28 x 28 | |
| MaxPool(K=2, S=2) | 20 x 14 x 14 | |
| Conv (C_out=50, K=5, P=2, S=1) | 50 x 14 x 14 | 50 x 20 x 5 x 5 |
| ReLU | 50 x 14 x 14 | |
| MaxPool(K=2, S=2) | 50 x 7 x 7 | |
| Flatten | 2450 | |
| Linear (2450 -> 500) | 500 | 2450 x 500 |
| ReLU | 500 | |
| Linear (500 -> 10) | 10 | 500 x 10 |
当我们走进这个网络,可以发现:
- 空间大小在减小
- 但是通道数在增加
- 不过一些现代架构打破了这一趋势(之后会介绍)
Normalization⚓︎
Batch Normalization⚓︎
引入
考虑单个网络层 \(y = Wx\),以下条件会为优化带来困难:
- 输入 \(x\) 不以 0 附近为中心(因而需要较大的偏移量)
- 输入 \(x\) 的每个元素有不同的缩放比例(因而 \(W\) 中的项需要变化很大)
解决思路是迫使输入在每个层上有着很好的缩放比例!
思路:将每一层的输出归一化,使其均值为 0,方差为 1 个单位。这样做是为了减少内部协变量偏移 (internal covariate shift) 并提升优化空间。
可以像这样对一批激活值进行归一化: $$ \hat{x} = \dfrac{x - E[x]}{\sqrt{Var[x]}} $$
由于这是一个可微(differentiable) 函数,因此我们可以将其用作网络中的算子,并通过它进行反向传播。
假如输入为 \(X \in \mathbb{R}^{N \times D}\),那么:
- (每通道的)均值 \(\mu_j=\dfrac{1}{N}\sum_{i=1}^Nx_{i,j}\),形状为 \(D\)
- (每通道的)方差 \(\sigma_j^2=\dfrac{1}{N}\sum_{i=1}^N(x_{i,j}-\mu_j)^2\),形状为 \(D\)
- 归一化后的元素 \(\widehat{x}_{i,j}=\dfrac{x_{i,j}-\mu_j}{\sqrt{\sigma_j^2+\varepsilon}}\),形状为 \(N \times D\)
如果零均值、单位方差的约束过于严格该怎么办呢?于是我们引入了可学习的缩放 (scale) 和偏移 (shift) 参数 \(\gamma, \beta \in \mathbb{R}^D\)。学习 \(\gamma = \mu, \beta = \sigma\) 将恢复恒等函数(在期望上
即便如此,上述方法仍然存在一个问题:上述估计依赖于选定的小批量,而在测试时不能这么做。所以 \(\mu_j, \sigma_j^2\) 的值需要通过在训练过程中获取平均值得到。以均值为例:
mu_test[j] = 0
for each training iteration:
mu[j] = 1 / N * sum(i=1, N, x[i][j])
mu_test[j] = 0.99 * mu_test[j] + 0.01 * mu[j]
方差的计算同理。
由于在测试过程中,批归一化操作成为一个线性算子,因此可以和先前的全连接层或卷积层融合起来。
-
FC:
\[ \begin{align*} x &: N \times D \\ \text{Normalize} &\downarrow \\ \mu, \sigma &: 1 \times D \\ \gamma, \beta &: 1 \times D \\ y &= \frac{(x - \mu)}{\sigma}\gamma + \beta \end{align*} \] -
CNN(空间批归一化,BatchNorm2D
) :\[ \begin{align*} x &: N \times C \times H \times W \\ \text{Normalize} &\downarrow \quad \quad \quad \quad\ \downarrow \quad \ \ \ \downarrow\\ \mu, \sigma &: 1 \times C \times 1 \times 1 \\ \gamma, \beta &: 1 \times C \times 1 \times 1 \\ y &= \frac{(x - \mu)}{\sigma}\gamma + \beta \end{align*} \]
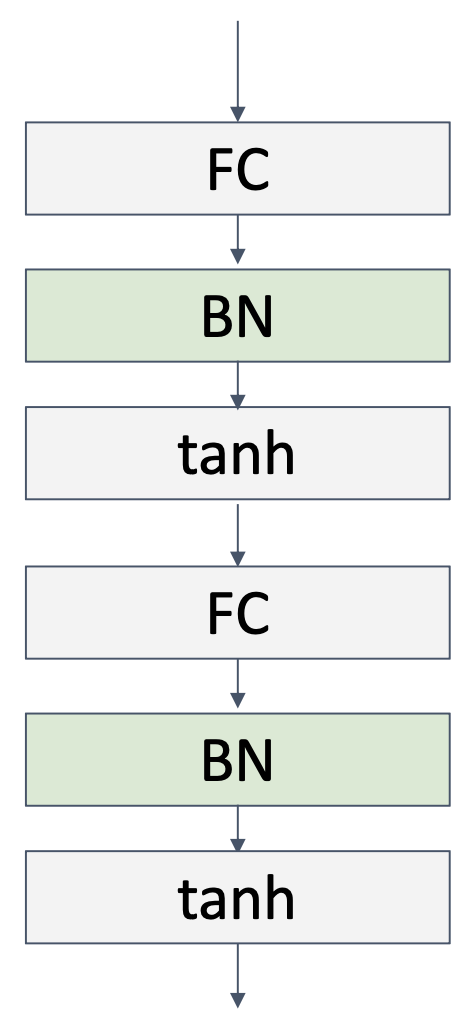
批归一化通常位于 FC 或 CNN 之后,并在非线性 (nonlinearity) 操作前:
优点:
- 使深度网络训练变得容易得多
- 允许更高的学习率,实现更快收敛
- 网络对初始化的鲁棒性增强
- 在训练过程中起到正则化作用
- 测试时零额外开销:可与卷积层融合
缺点:
- (目前)理论上尚未充分理解
- 在训练和测试期间表现不同,这是非常常见的错误来源
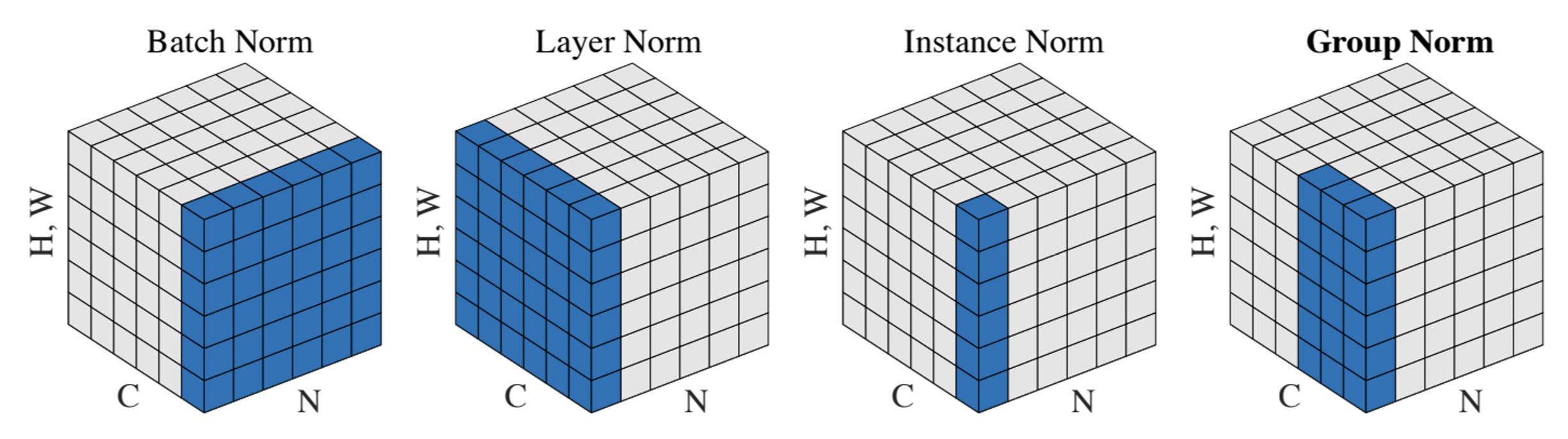
Layer Normalization⚓︎
-
FC 上的批归一化:
\[ \begin{align*} x &: N \times D \\ \text{Normalize} &\downarrow \\ \mu, \sigma &: 1 \times D \\ \gamma, \beta &: 1 \times D \\ y &= \frac{(x - \mu)}{\sigma}\gamma + \beta \end{align*} \] -
FC 上的层归一化(layer normalization),在训练和测试上有相同行为,为 RNN 和 Transformer 所用:
\[ \begin{align*} x &: N \times D \\ \text{Normalize} &\downarrow \\ \mu, \sigma &: N \times 1 \\ \gamma, \beta &: 1 \times D \\ y &= \frac{(x - \mu)}{\sigma}\gamma + \beta \end{align*} \]
Instance Normalization⚓︎
-
CNN 上的批归一化:
\[ \begin{align*} x &: N \times C \times H \times W \\ \text{Normalize} &\downarrow \quad \quad \quad \quad\ \downarrow \quad \ \ \ \downarrow\\ \mu, \sigma &: 1 \times C \times 1 \times 1 \\ \gamma, \beta &: 1 \times C \times 1 \times 1 \\ y &= \frac{(x - \mu)}{\sigma}\gamma + \beta \end{align*} \] -
CNN 上的实例归一化(instance normalization):
\[ \begin{align*} x &: N \times C \times H \times W \\ \text{Normalize} &\downarrow \quad \quad \quad \quad\ \downarrow \quad \ \ \ \downarrow\\ \mu, \sigma &: 1 \times C \times 1 \times 1 \\ \gamma, \beta &: 1 \times C \times 1 \times 1 \\ y &= \frac{(x - \mu)}{\sigma}\gamma + \beta \end{align*} \]
评论区