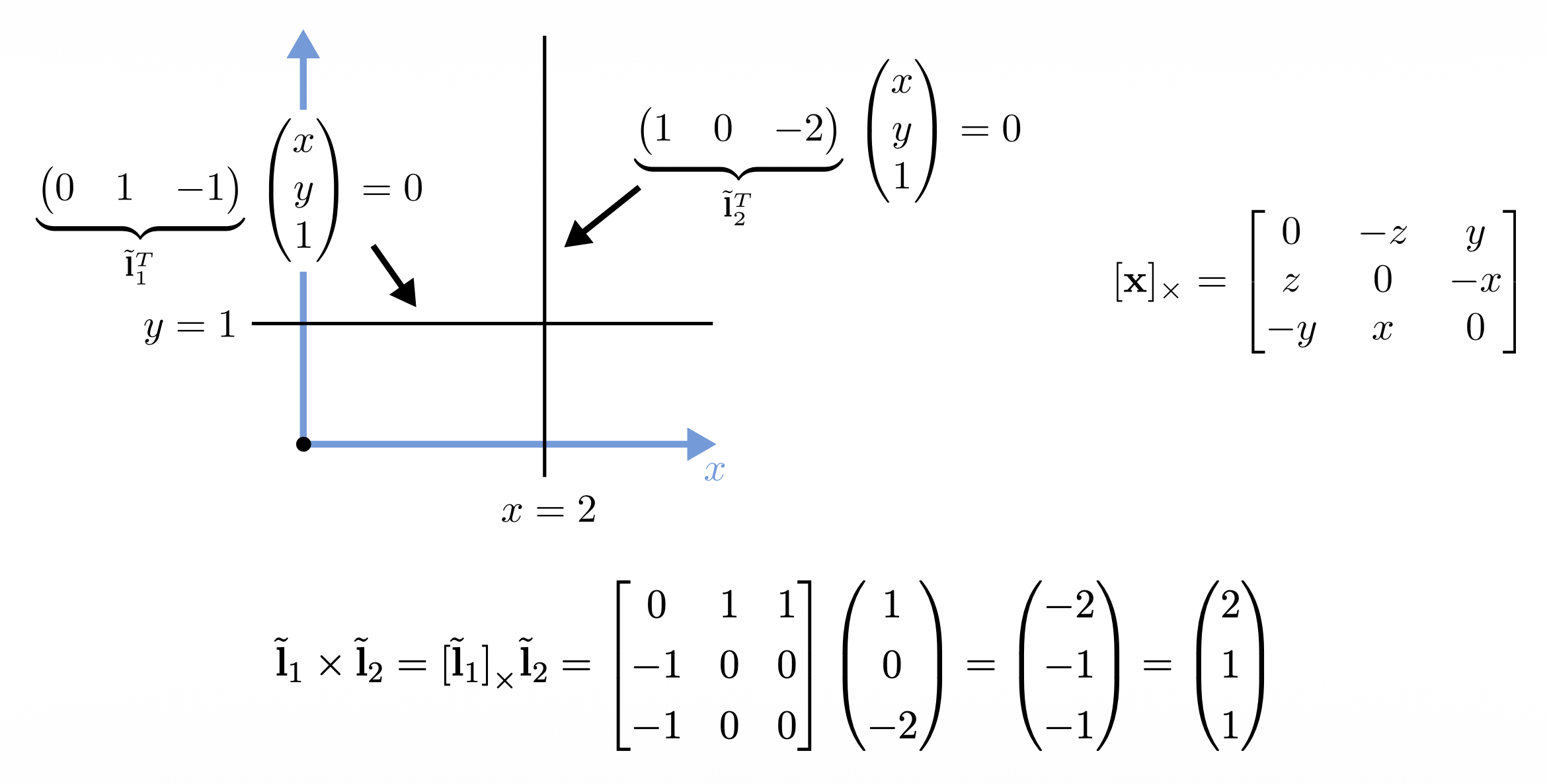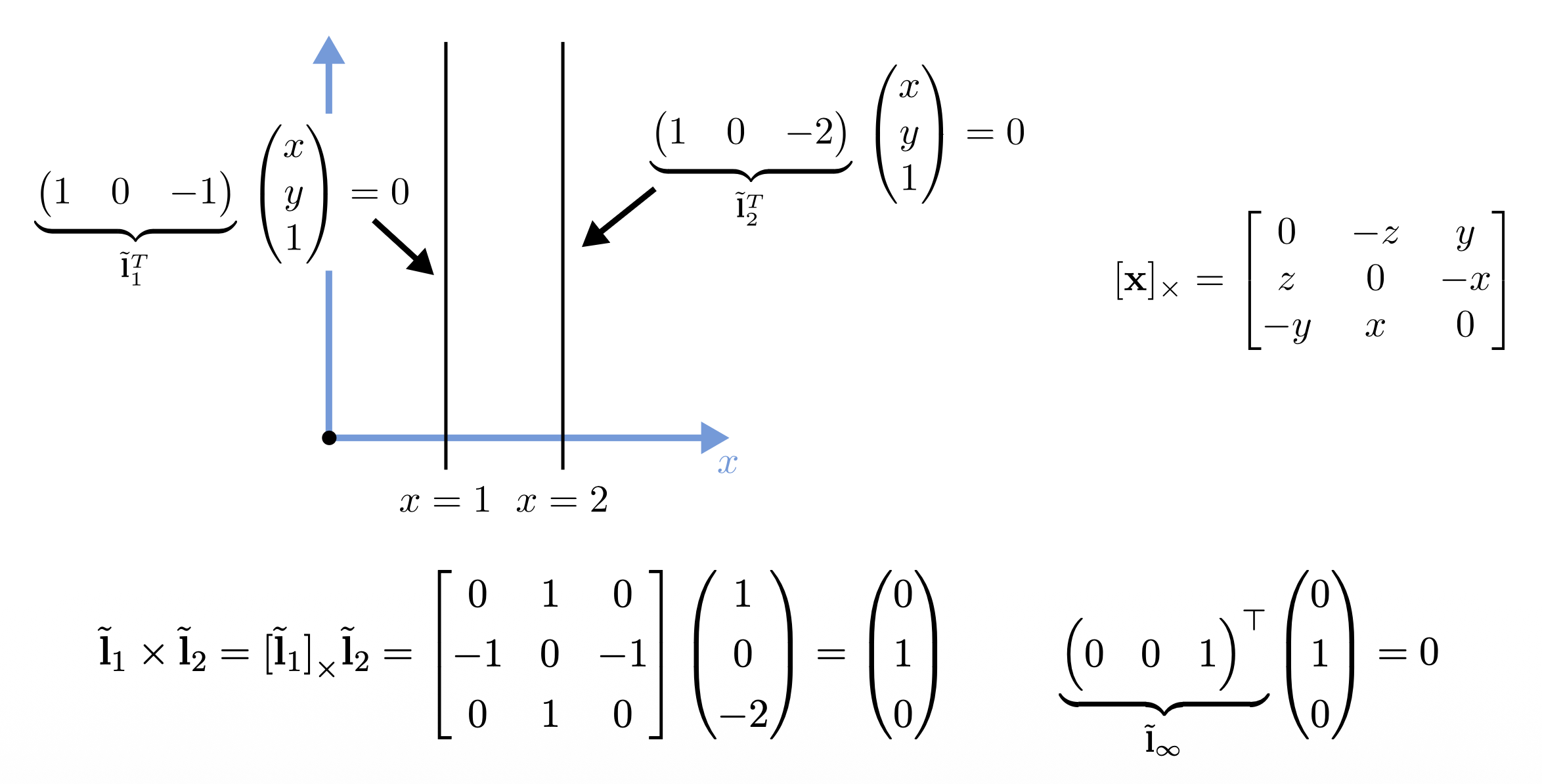Image Formation⚓︎
约 5728 个字 预计阅读时间 29 分钟
核心知识
比较重要的一讲,涉及很多基础理论。
- 相机和镜头(透镜)相关的各种概念,比如视场、光圈、景深等
- 透视投影
- 齐次坐标
- 畸变:透视畸变、径向畸变
- 光度投影:快门、色彩空间、拜耳滤色镜
- 明确不考的:
- 正射投影
- 着色
Primitives and Transformations⚓︎
几何图元(geometric primitives) 是用于描述 3D 形状的基本构建块 (basic building blocks),下面将介绍其中的点(points)、线(lines) 和面(planes),以及一些最基本的变换(transformations)。
2D Primitives⚓︎
Points⚓︎
- 非齐次坐标(inhomogeneous coordinates) 形式:\(\mathbf{x} = \begin{pmatrix}x \\ y\end{pmatrix} \in \mathbb{R}^2\)
- 齐次坐标(homogeneous coordinates) 形式:\(\tilde{\mathbf{x}} = \begin{pmatrix}\tilde{x} \\ \tilde{y} \\ \tilde{w}\end{pmatrix} \in \mathbb{P}^2\),其中 \(\mathbb{P}^2 = \mathbb{R}^3 \backslash \{(0, 0, 0)\}\) 为投影空间(projective space)
注:仅比例不同的齐次向量被认为是相等的,并且它们形成了一个等价类 => 齐次坐标由比例定义
-
非齐次坐标 \(\mathbf{x}\) -> 齐次坐标 \(\tilde{\mathbf{x}}\)
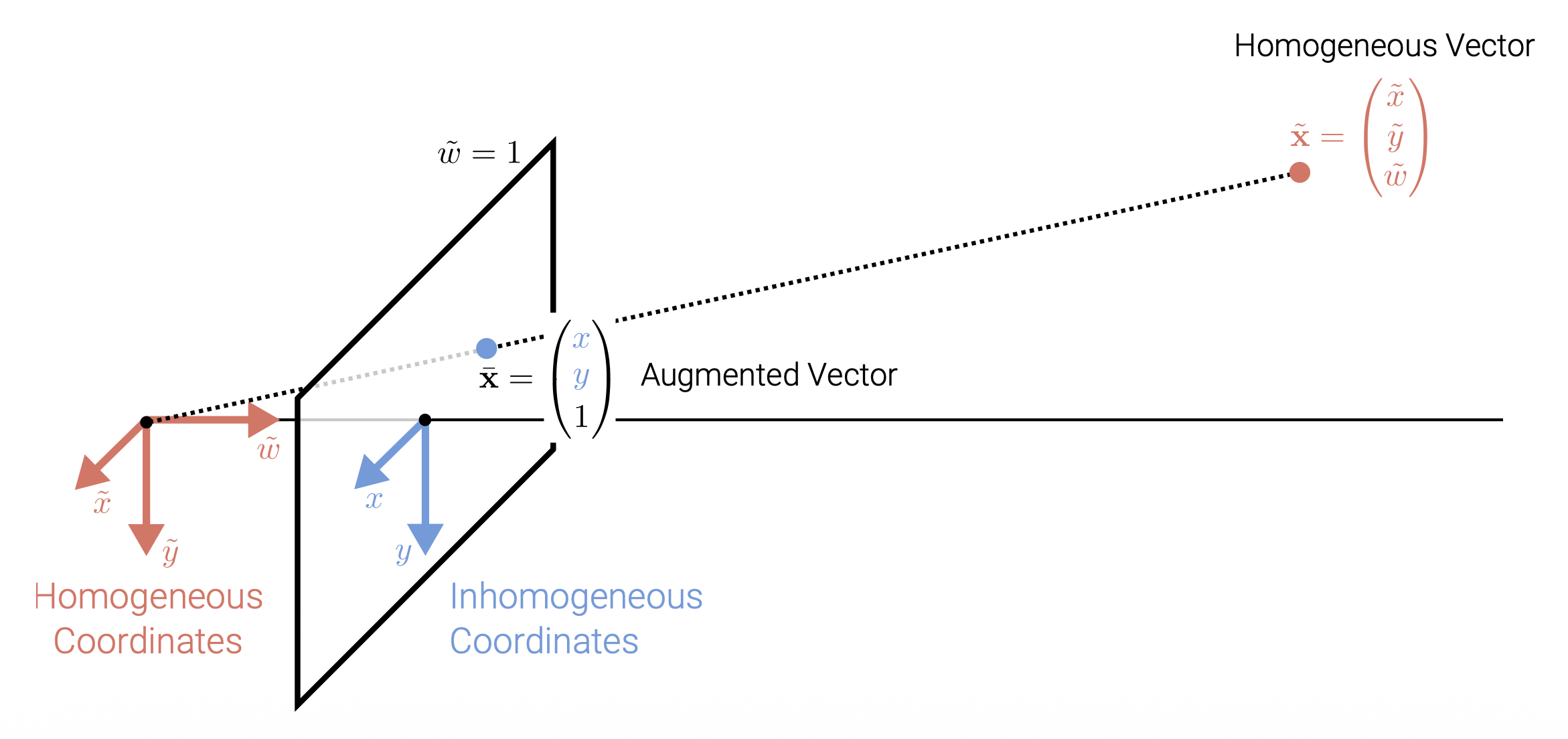
\[ \tilde{\mathbf{x}} = \begin{pmatrix}\tilde{x} \\ \tilde{y} \\ \tilde{w}\end{pmatrix} = \begin{pmatrix}x \\ y \\ 1\end{pmatrix} = \begin{pmatrix}\mathbf{x} \\ 1\end{pmatrix} = \bar{\mathbf{x}} \]其中 \(\bar{\mathbf{x}}\) 为增广向量(augmented vector)。
-
齐次坐标 -> 非齐次坐标
\[ \bar{\mathbf{x}} = \begin{pmatrix}\mathbf{x} \\ 1\end{pmatrix} = \begin{pmatrix}x \\ y \\ 1\end{pmatrix} = \dfrac{1}{\tilde{w}} \tilde{\mathbf{x}} = \dfrac{1}{\tilde{w}} \begin{pmatrix}\tilde{x} \\ \tilde{y} \\ \tilde{w}\end{pmatrix} = \begin{pmatrix}\tilde{x} / \tilde{w}\\ \tilde{y} / \tilde{w}\\ 1\end{pmatrix} \]
最后一个元素 \(\tilde{w} = 0\) 的齐次坐标被称为理想点(ideal points) 或无穷远点(points at infinity)。这样的点不能被表示成非齐次坐标的形式。
二维齐次坐标和非齐次坐标的几何关系:
额外补充的(为方便复习,隐藏这些不必要的内容)
Lines⚓︎
2D 直线可用齐次坐标表示:\(\tilde{\mathbf{l}} = (a, b, c)^T\)
我们可以归一化(normalize) \(\tilde{\mathbf{l}}\),使得 \(\tilde{\mathbf{l}} = (n_x, n_y, -d)^T = (\mathbf{n}, -d)^T\),其中 \(\|\mathbf{n}\|_2 = 1\),其中 \(\mathbf{n}\) 是和直线垂直的法向量,\(d\) 是到原点的距离。
一个例外是无穷远直线(line at infinity) \(\tilde{\mathbf{l}}_\infty = (0, 0, 1)^T\),它经过了所有的理想点。
叉积(cross product) 被表示为斜对称矩阵 (skew-symmetric matrix) 与向量的乘积。
注:之后我们就约定用方括号表示矩阵,圆括号表示向量。
二维直线的算术运算:
- 齐次坐标下,两条直线的交(intersection) 为:\(\tilde{\mathbf{x}} = \tilde{\mathbf{l}}_1 \times \tilde{\mathbf{l}}_2\)
- 同样地,连接两点的直线可以简写为:\(\tilde{\mathbf{l}} = \tilde{\mathbf{x}}_1 \times \tilde{\mathbf{x}}_2\)
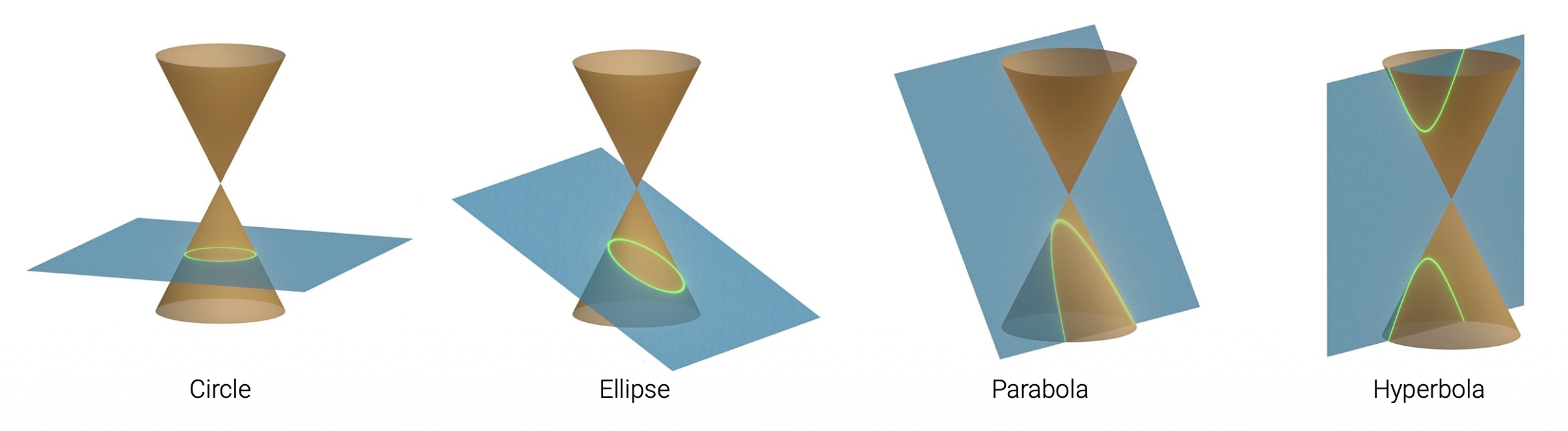
更复杂的代数对象可以使用多项式齐次方程(polynomial homogeneous equations) 来表示。例如,圆锥曲线()(作为平面与三维圆锥的交线)可以用二次方程来表示: $$ {\bar{\mathbf{x}} | \bar{\mathbf{x}}^T \mathbf{Q} \bar{\mathbf{x}} = 0} $$
这对于多视图几何以及相机校准 (camera calibration) 很有帮助。
3D Primitives⚓︎
Points⚓︎
- 非齐次坐标(inhomogeneous coordinates) 形式:\(\mathbf{x} = \begin{pmatrix}x \\ y \\ z\end{pmatrix} \in \mathbb{R}^3\)
- 齐次坐标(homogeneous coordinates) 形式:\(\tilde{\mathbf{x}} = \begin{pmatrix}\tilde{x} \\ \tilde{y} \\ \tilde{z} \\ \tilde{w}\end{pmatrix} \in \mathbb{P}^3\),其中投影空间 \(\mathbb{P}^3 = \mathbb{R}^4 \backslash \{(0, 0, 0, 0)\}\)
Planes⚓︎
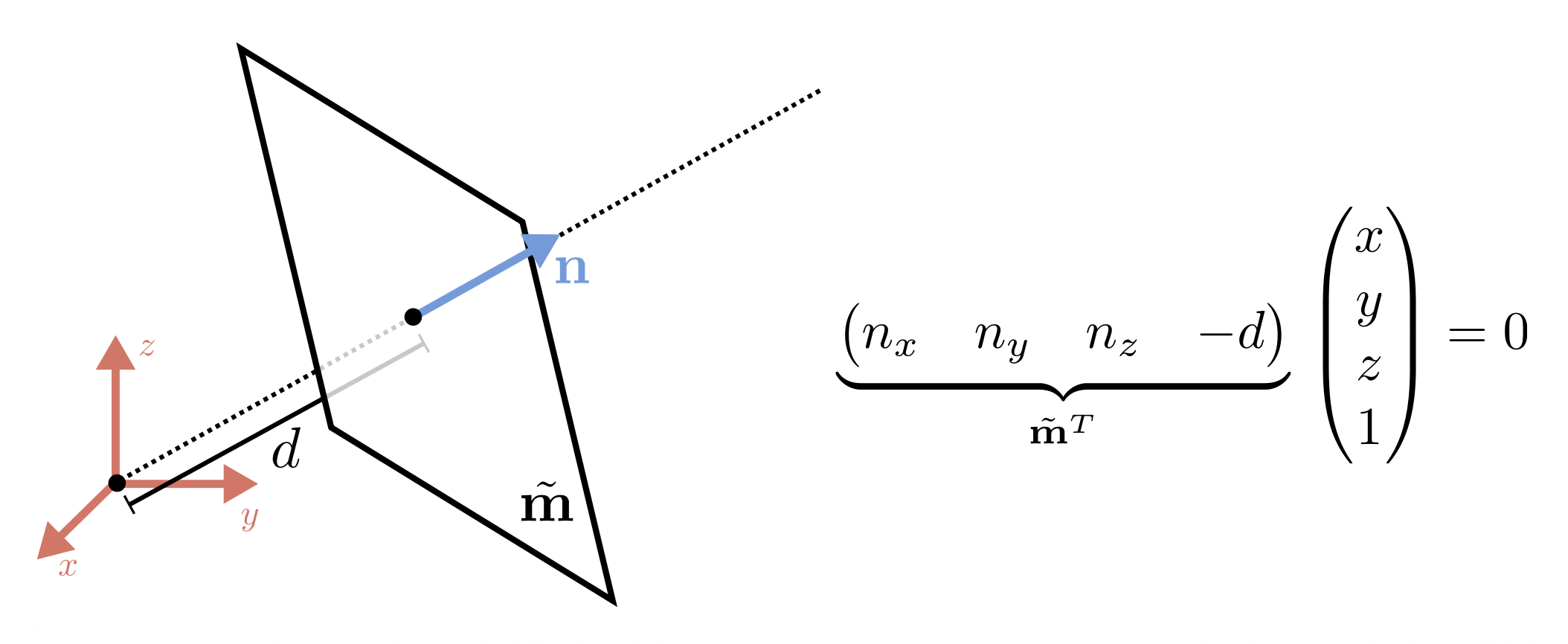
3D 平面可用齐次坐标表示:\(\tilde{\mathbf{m}} = (a, b, c, d)^T\)
再次归一化(normalize) \(\tilde{\mathbf{m}}\),使得 \(\tilde{\mathbf{l}} = (n_x, n_y, n_z, -d)^T = (\mathbf{n}, -d)^T\),其中 \(\|\mathbf{n}\|_2 = 1\),其中 \(\mathbf{n}\) 是和平面垂直的法向量,\(d\) 是到原点的距离。
一个例外是无穷远平面(plane at infinity) \(\tilde{\mathbf{l}}_\infty = (0, 0, 0, 1)^T\),它经过了所有的理想点。
Lines⚓︎
3D 直线的表示不如 2D 直线或 3D 平面优雅。一种可能的表示方法是,将线上的点表示为该线上的两个点 \(p\) 和 \(q\) 的线性组合:
然而,这种表示法使用了 6 个参数来描述 4 个自由度(degree of freedom, DoF)(可以自由变化的数据个数
Quadrics⚓︎
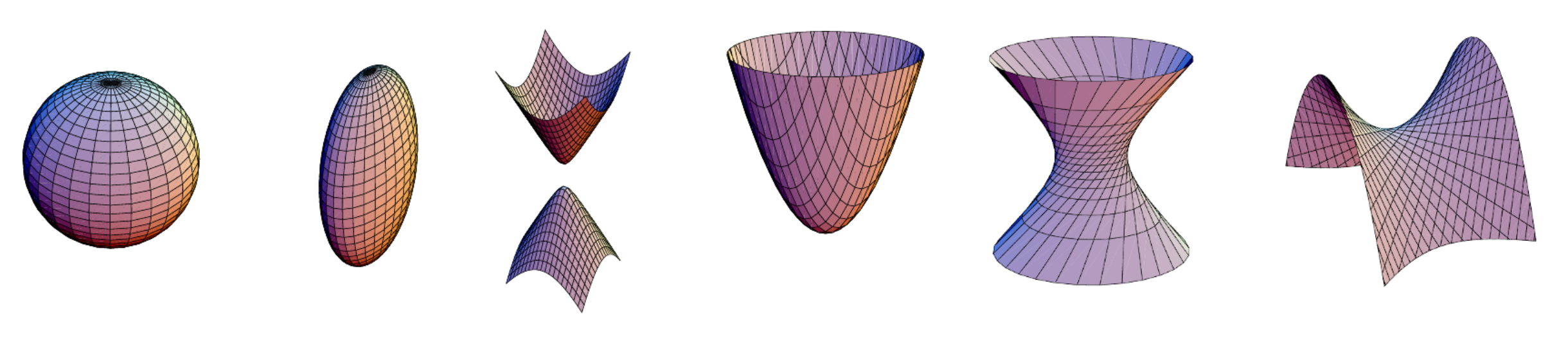
二维圆锥曲线的三维类比是二次曲面(quadric surface)。
这同样在多视图几何研究中非常有用,并且可作为有用的建模基元 (modeling primitives)(比如球体、椭球体、圆柱体等
超二次曲面(superquadrics)(二次曲面的泛化)用于形状抽象和压缩:
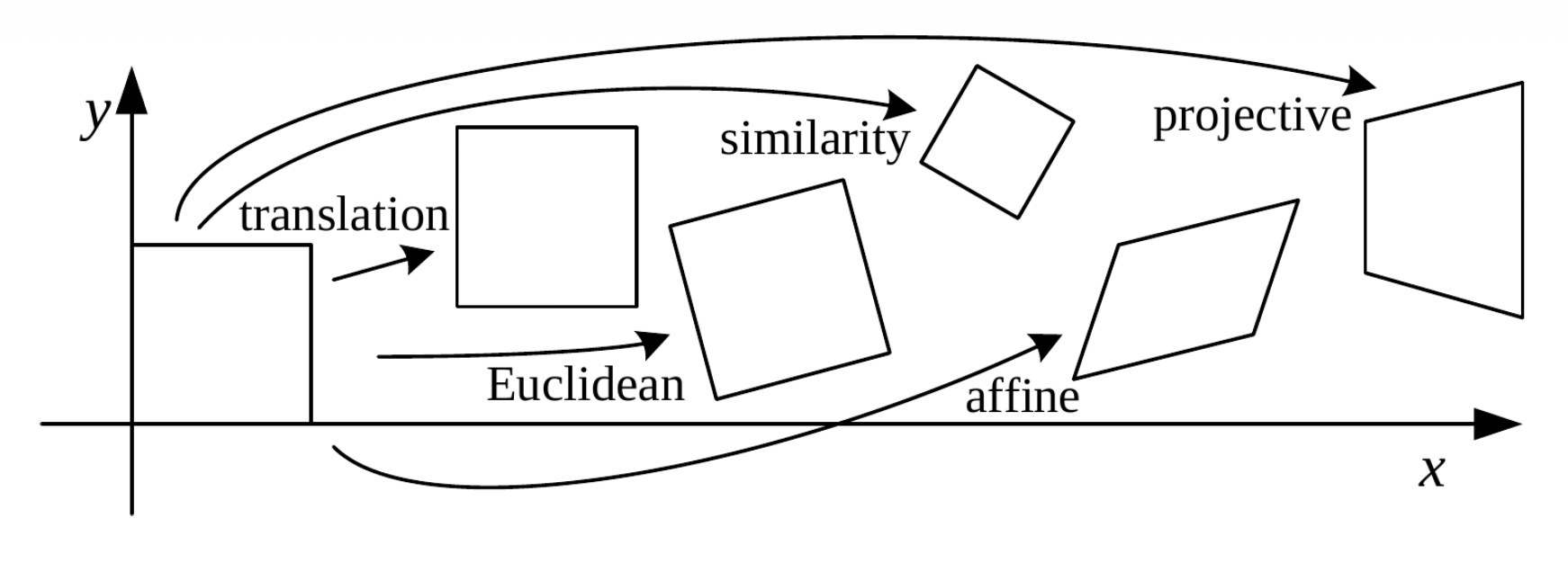
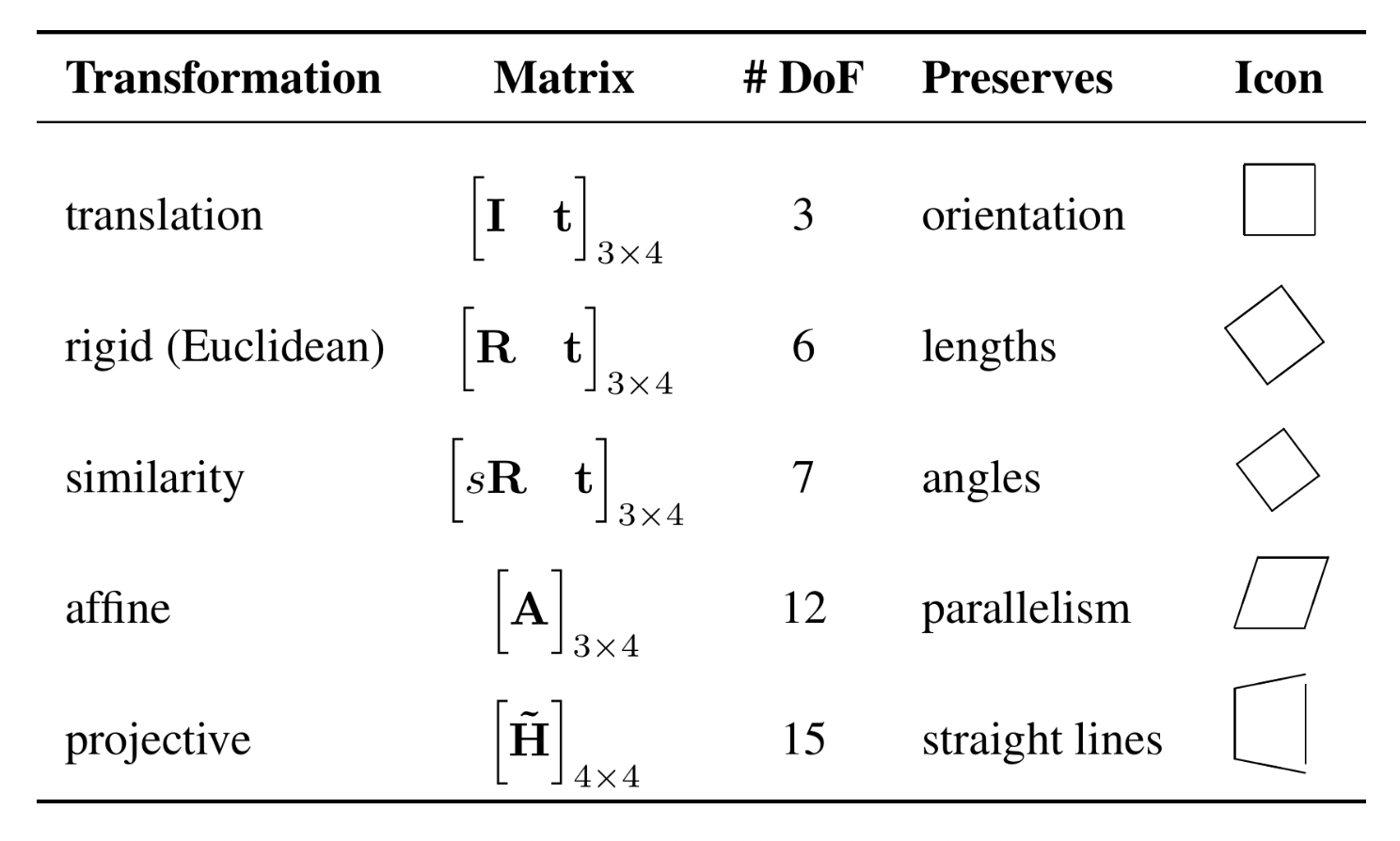
Transformations⚓︎
2D Transformations⚓︎
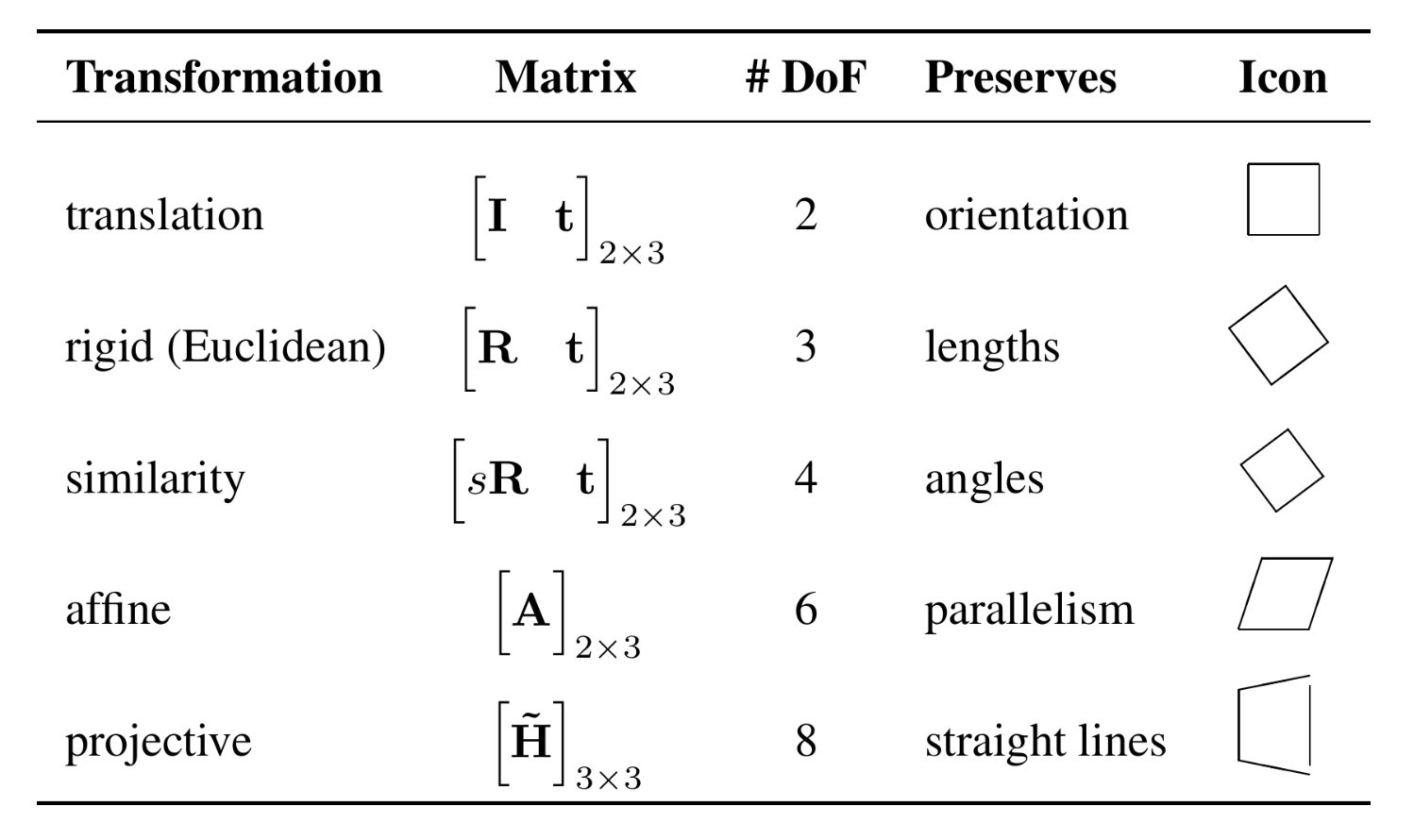
-
平移(translation):对输入的 2D 平移,2 DoF
\[ \mathbf{x}' = \mathbf{x} + \mathbf{t} \quad \Leftrightarrow \quad \bar{\mathbf{x}}' = \begin{bmatrix}\mathbf{I} & \mathbf{t} \\ \mathbf{0}^T & 1\end{bmatrix} \bar{\mathbf{x}} \]- 使用齐次表示法可以链接 / 逆转变换
- 增广向量 \(\bar{\mathbf{x}}\) 能始终被替换为一般的齐次形式 \(\tilde{\mathbf{x}}\)
-
欧几里得(Euclidean) 变换:2D 平移 + 2D 旋转,3 DoF
\[ \mathbf{x}' = \mathbf{Rx} + \mathbf{t} \quad \Leftrightarrow \quad \bar{\mathbf{x}}' = \begin{bmatrix}\mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1\end{bmatrix} \bar{\mathbf{x}} \]- \(\mathbf{R} \in SO(2)\) 是一个正交归一旋转矩阵,满足 \(\mathbf{RR}^T = \mathbf{I}, \det(\mathbf{R}) = 1\)
- 欧几里得变换保留了欧几里得距离
-
相似(similarity) 变换:2D 平移 + 可缩放的 2D 旋转,4 DoF
\[ \mathbf{x}' = s\mathbf{Rx} + \mathbf{t} \quad \Leftrightarrow \quad \bar{\mathbf{x}}' = \begin{bmatrix}s\mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1\end{bmatrix} \bar{\mathbf{x}} \]- \(\mathbf{R} \in SO(2)\) 是一个旋转矩阵,\(s\) 是一个任意的缩放因子
- 相似变换保留了线之间的夹角关系
-
仿射(affine) 变换:2D 线性变换,6 DoF
\[ \mathbf{x}' = \mathbf{Ax} + \mathbf{t} \quad \Leftrightarrow \quad \bar{\mathbf{x}}' = \begin{bmatrix}\mathbf{A} & \mathbf{t} \\ \mathbf{0}^T & 1\end{bmatrix} \bar{\mathbf{x}} \]- \(\mathbf{A} \in \mathbb{R}^{2 \times 2}\) 是一个任意的 \(2 \times 2\) 的矩阵
- 平行线在仿射变换下保持平行
-
投影(projective) 变换:单应性(homography)(一种从一个平面到另一个平面的可逆投影变换
) ,8 DoF\[ \tilde{\mathbf{x}}' = \tilde{\mathbf{H}} \tilde{\mathbf{x}} \quad \left(\bar{\mathbf{x}} = \dfrac{1}{\tilde{x}} \tilde{\mathbf{x}}\right) \]- \(\tilde{\mathbf{H}} \in \mathbb{R}^{3 \times 3}\) 是一个任意的齐次 \(3 \times 3\) 的矩阵(按比例指定)
- 投影变换保留了直线
在协变向量 (co-vector) 上的 2D 变换:考虑任意的 2D 透视变换 \(\tilde{\mathbf{x}}' = \tilde{\mathbf{H}} \tilde{\mathbf{x}}\),变换后的 2D 直线方程由 \(\tilde{\mathbf{I}'}^T \tilde{\mathbf{x}}' = \tilde{\mathbf{I}'}^T \tilde{\mathbf{H}} \tilde{\mathbf{x}} = (\tilde{\mathbf{H}}^T \tilde{\mathbf{I}'}) \tilde{\mathbf{x}} = \tilde{\mathbf{I}}^T \tilde{\mathbf{x}} = 0\),因此得到 $$ \tilde{\mathbf{I}'} = \tilde{\mathbf{H}}^{-T} \tilde{\mathbf{I}} $$
因此,投影变换对一个 2D 直线或 3D 法向量等共向量的作用可以表示为矩阵转置的逆。
3D Transformations⚓︎
将 2D 变换扩展至 3D 上“
- 3D 变换的定义类比 2D 变换
- 3×4 的矩阵通过添加第四行 \(\begin{bmatrix}\mathbf{0}^T & 1\end{bmatrix}\) 来扩展,以实现齐次变换
- 变换保持相似性(平行关系、直线)不变
Direct Linear Transform for Homography Estimation⚓︎
从一组二维对应关系中估计单应性矩阵的方法为:
- 令 \(\mathcal{X} = \{\tilde{\mathbf{x}}_i, \tilde{\mathbf{x}}_i'\}_{i=1}^N\) 表示一个包含 N 个 2D-to-2D 的关于 \(\tilde{\mathbf{x}}' = \tilde{\mathbf{H}} \tilde{\mathbf{x}}\) 对应关系的集合
- 由于对应向量是齐次的,它们方向相同但大小不同,因此上述方程可表示为 \(\tilde{\mathbf{x}}' \times \tilde{\mathbf{H}} \tilde{\mathbf{x}} = \mathbf{0}\)
-
使用 \(\tilde{\mathbf{h}}_k^T\) 表示 \(\tilde{\mathbf{H}}\) 的第 \(k\) 行,这可以被重写为关于 \(\tilde{\mathbf{h}}\) 的线性方程:
\[ \begin{gathered}\underbrace{\begin{bmatrix}\mathbf{0}^T&-\tilde{w}_i^{\prime}\tilde{\mathbf{x}}_i^T&\tilde{y}_i^{\prime}\tilde{\mathbf{x}}_i^T\\\tilde{w}_i^{\prime}\tilde{\mathbf{x}}_i^T&\mathbf{0}^T&-\tilde{x}_i^{\prime}\tilde{\mathbf{x}}_i^T\\-\tilde{y}_i^{\prime}\tilde{\mathbf{x}}_i^T&\tilde{x}_i^{\prime}\tilde{\mathbf{x}}_i^T&\mathbf{0}^T\end{bmatrix}}_{\mathbf{A}_i}\underbrace{\begin{bmatrix}\tilde{\mathbf{h}}_1\\\tilde{\mathbf{h}}_2\\\tilde{\mathbf{h}}_3\end{bmatrix}}_{\tilde{\mathbf{h}}}=\mathbf{0}\end{gathered} \]最后一行与前三行线性相关,可以删除。
-
每个点对应产生两个方程。将所有方程堆叠成一个 \(2N \times 9\) 维的矩阵 \(A\),从而形成以下约束的最小二乘问题(constrained least squares problem)
\[ \begin{aligned}\tilde{\mathbf{h}}^{*}&=\underset{\tilde{\mathbf{h}}}{\operatorname*{\operatorname*{argmin}}}\left\|\mathbf{A}\tilde{\mathbf{h}}\right\|_2^2+\lambda(\left\|\tilde{\mathbf{h}}\right\|_2^2-1)\\&=\underset{\tilde{\mathbf{h}}}{\operatorname*{\operatorname*{argmin}}}\tilde{\mathbf{h}}^T\mathbf{A}^T\mathbf{A}\tilde{\mathbf{h}}+\lambda(\tilde{\mathbf{h}}^T\tilde{\mathbf{h}}-1)\end{aligned} \]其中固定 \(\|\tilde{\mathbf{h}}\|_2 = 1\),因为 \(\tilde{\mathbf{H}}\) 是齐次的(即仅通过比例定义)且我们不关心平凡解 \(\tilde{\mathbf{h}} = 0\)。上述优化问题的解是 \(\mathbf{A}\) 的最小奇异值对应的奇异向量(singular vector)(即分解 \(\mathbf{A} = \mathbf{UDV}^T\) 时 \(\mathbf{V}\) 的最后一列
) 。
上述算法就叫做直接线性变换(direct linear transformation)。
Camera and Lens⚓︎
Pinhole Camera⚓︎
了解成像的第一步是理解相机(camera) 的原理,所以我们先来思考一下如何设计一台相机。一种简单的想法是直接把一片薄膜 (film) 放在物体面前——毫无疑问,该方法以失败告终,因为没法做到物体上一点和薄膜上的点一一映射。
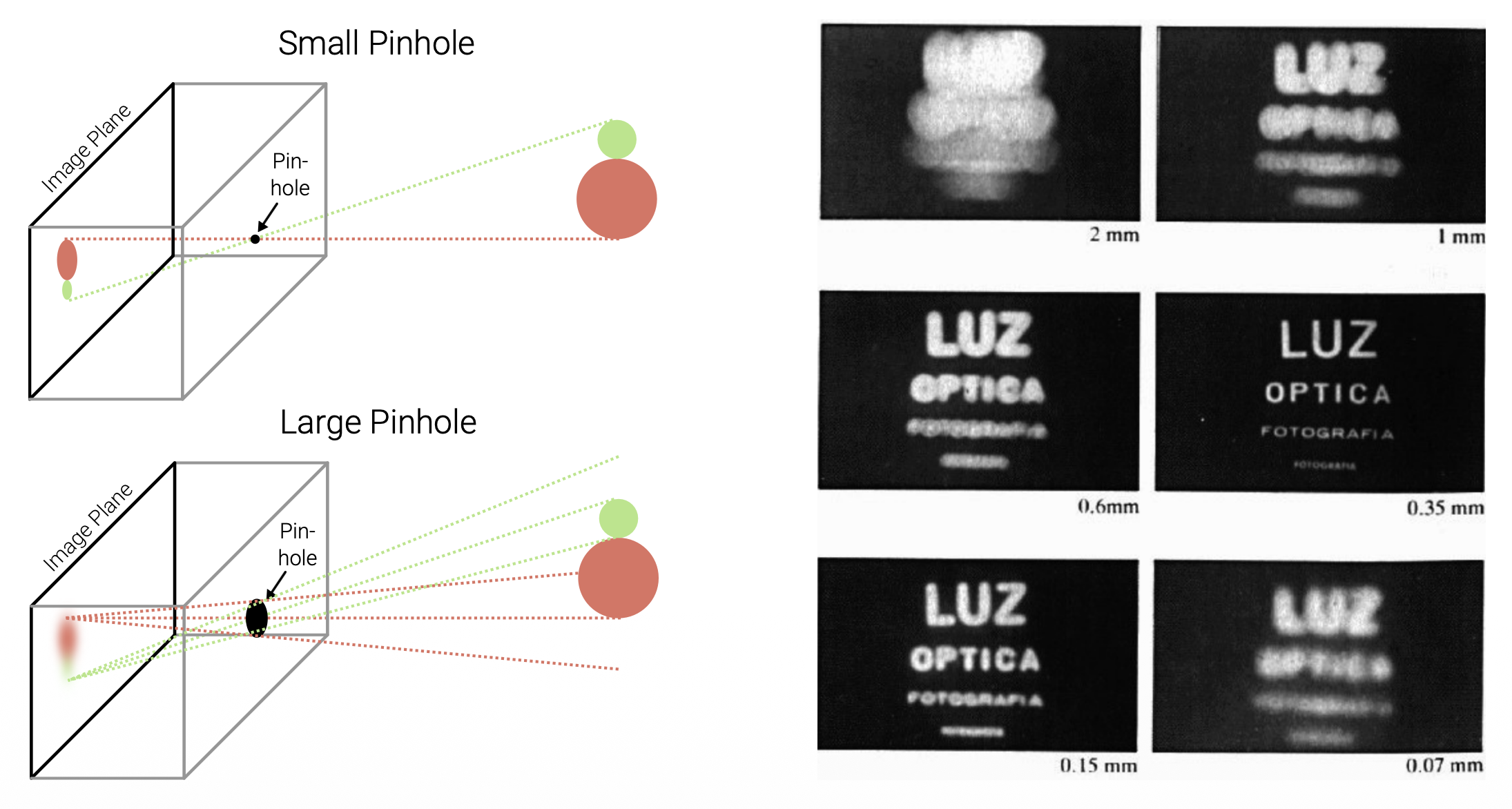
于是我们在物体和薄膜之间加一块挡板,以阻挡大多数的光线,由此得到了一台简陋的针孔相机(pinhole camera)。中间的开口被称为光圈(aperture)。
注:针孔相机的基本原理可追溯至墨子和亚里士多德的年代。
人们发现,光圈越小,成像就越清晰。但我们不会让光圈无止尽地小下去,这是因为:
- 光圈越小,通过的光也就越少,成像就会变得很暗
- 衍射(diffraction) 效应:当光圈尺寸和光的波长相当甚至更小时,通过光圈后会偏离直线传播路径并发生弯曲扩散,自然难以形成清晰的像
Lens⚓︎
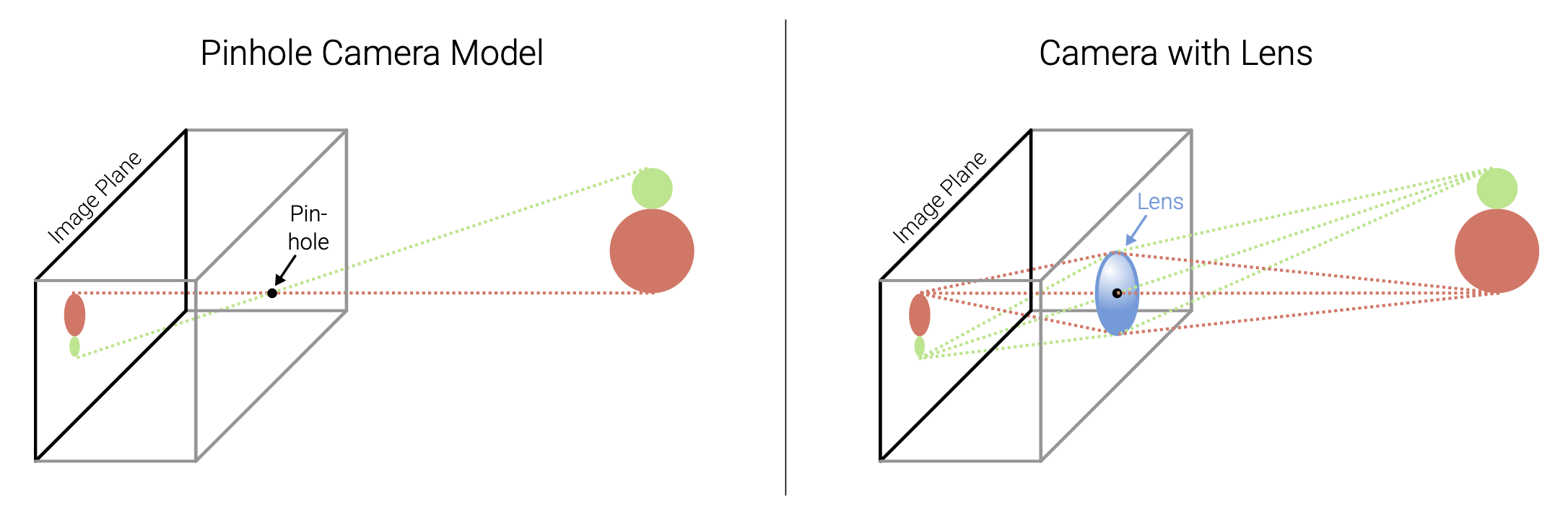
透镜(lens)(或镜头)有着和针孔相同的投影原理,但是它能让更多的光进来,并让这些光汇聚起来。
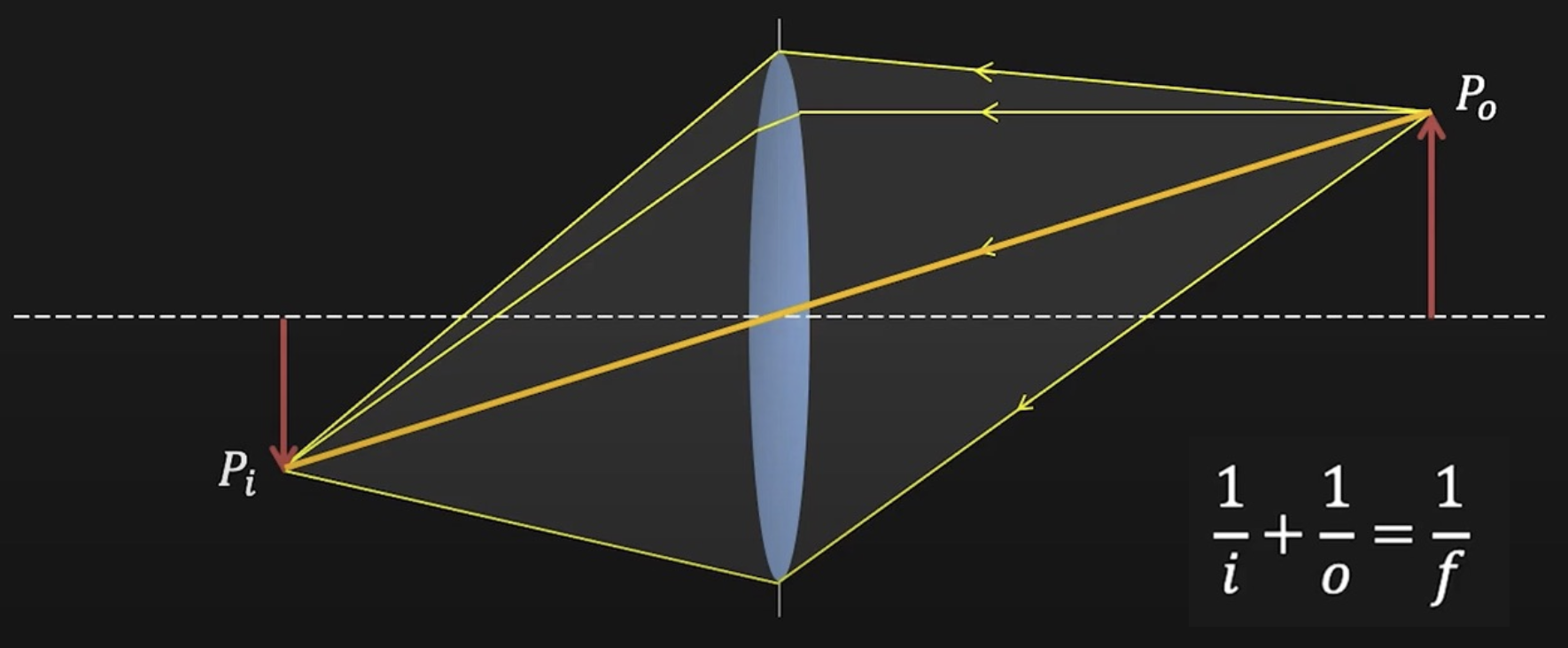
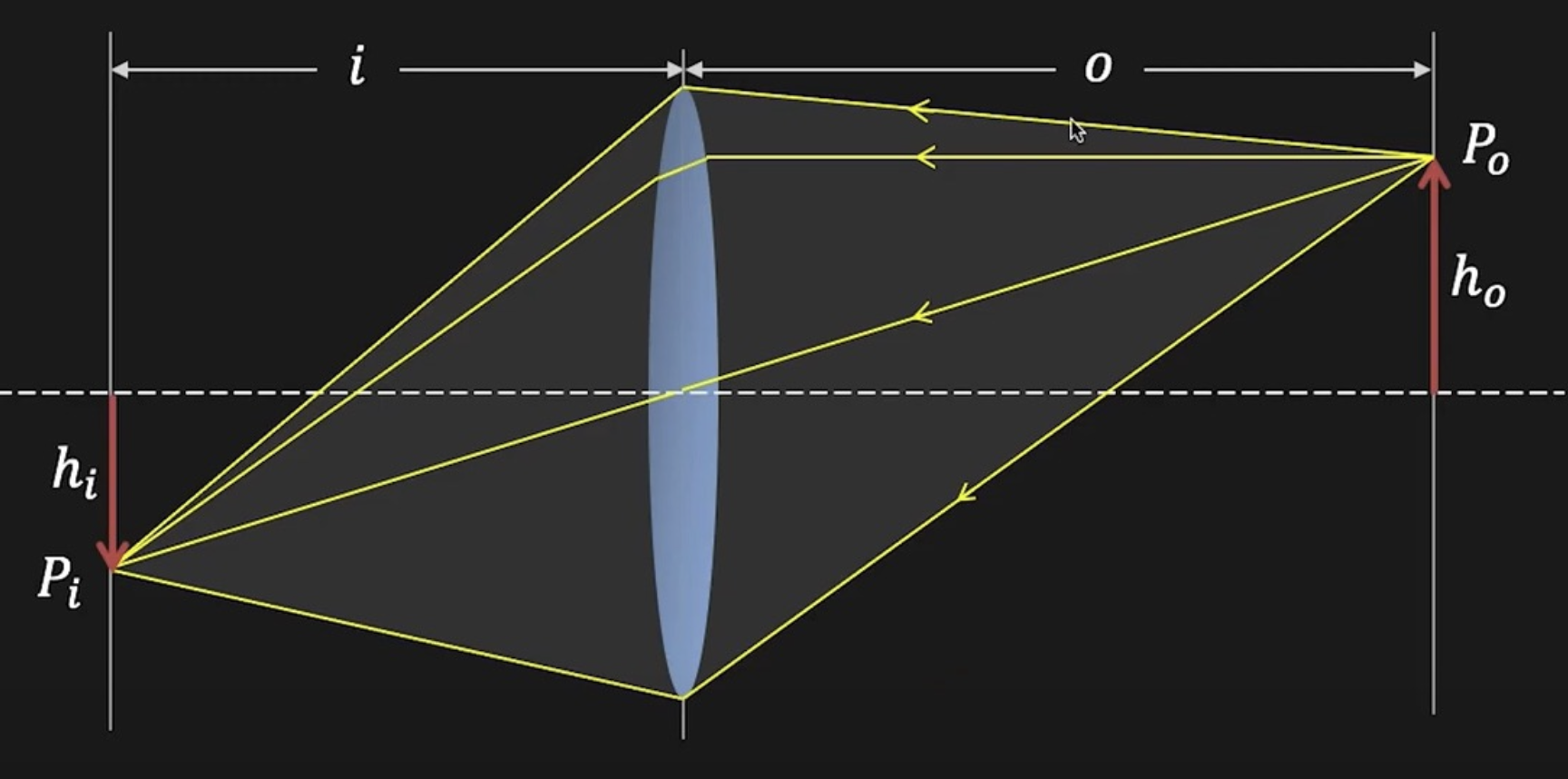
高斯成像公式:\(\dfrac{1}{i} + \dfrac{1}{o} = \dfrac{1}{f}\),其中 \(i, o, f\) 分别为像距、物距和焦距(focal length)。
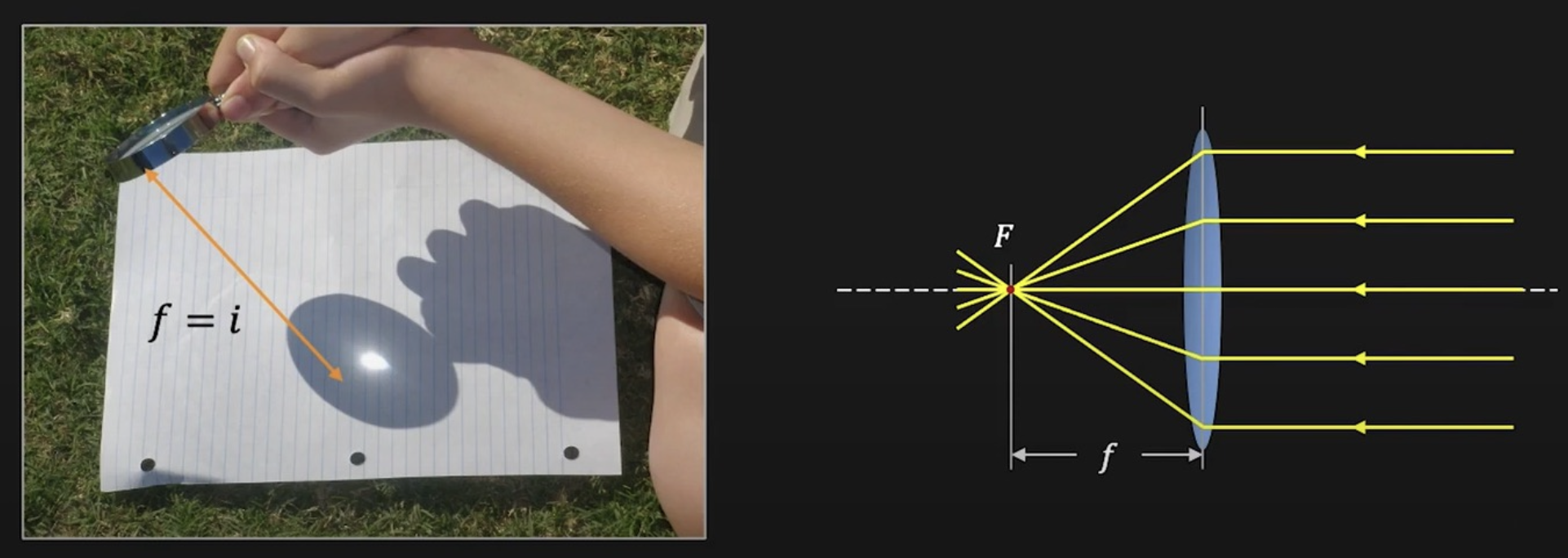
当 \(o = \infty\) 时(对于下图,物体是太阳,离透镜很远很远,可看作无穷远
透镜可用于图像放大(image magnification),放大率为 \(m = \dfrac{h_i}{h_o} = \dfrac{i}{o}\)
相机通过改变焦距来放大图像:
思考
为什么 \(f\) 越大图像越大(即 \(m\) 越大
因此 \(f\) 越大,分子越大,分母越小,\(m\) 显然会变大。
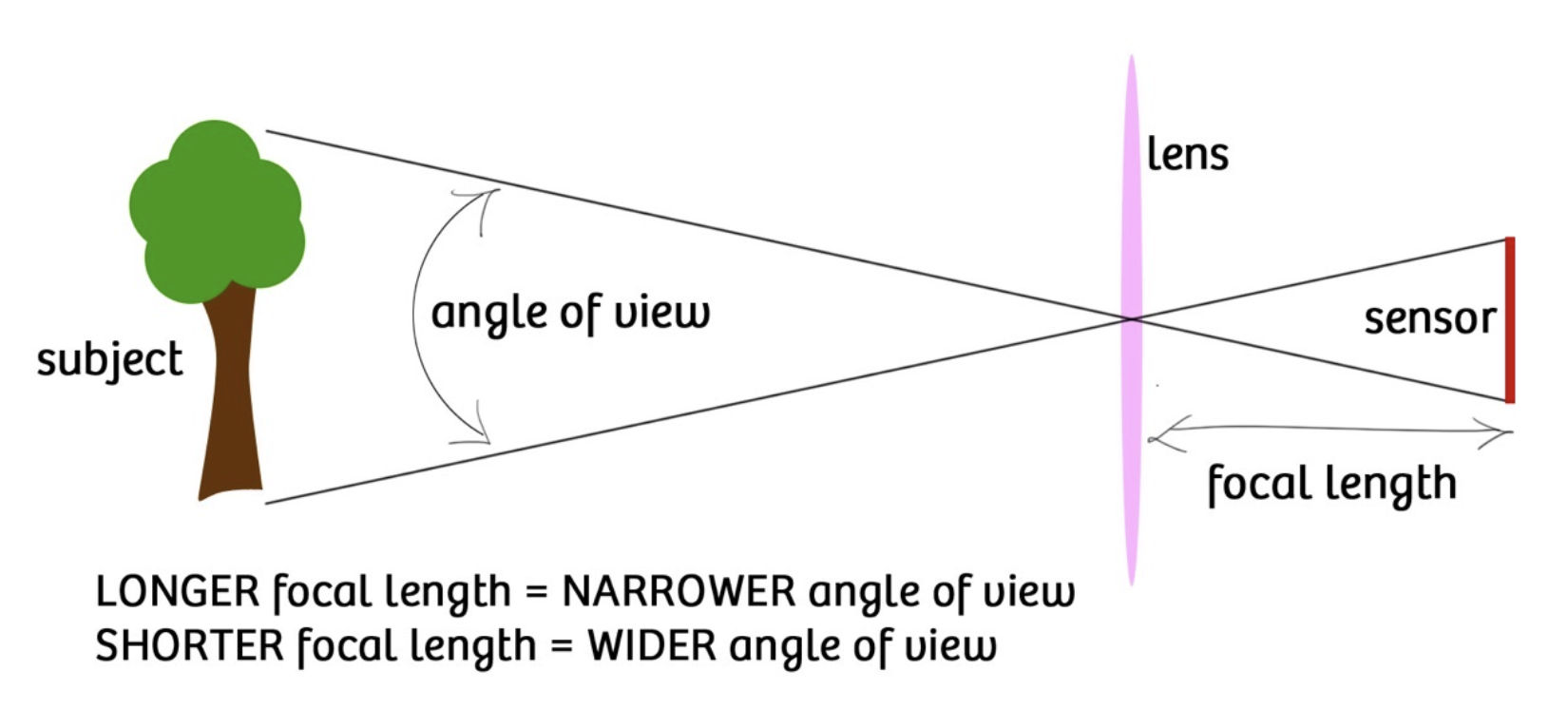
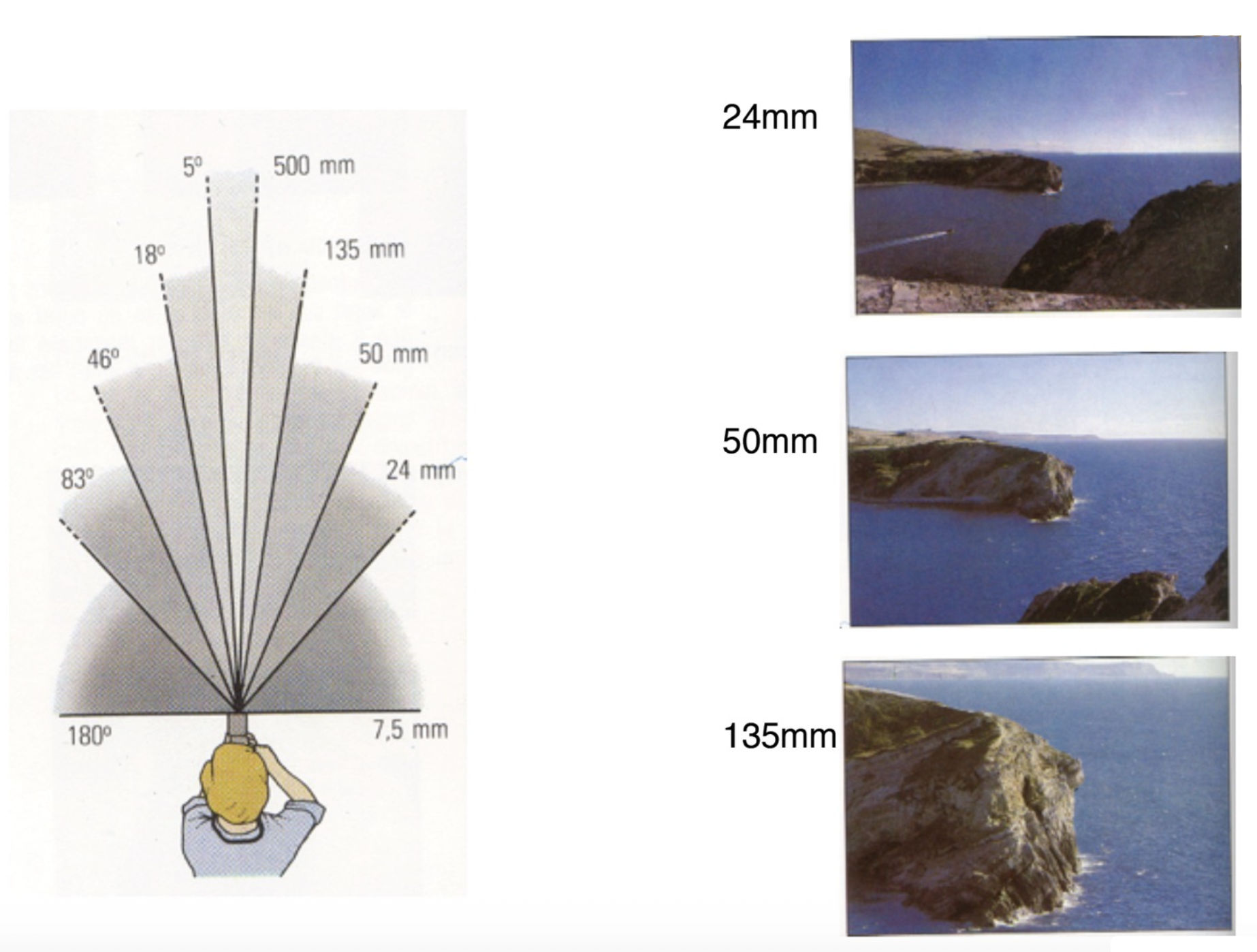
从另一个角度看,调整焦距的同时也改变了视场(field of view, FOV):焦距越长,视角更窄;焦距越短,视角越宽。
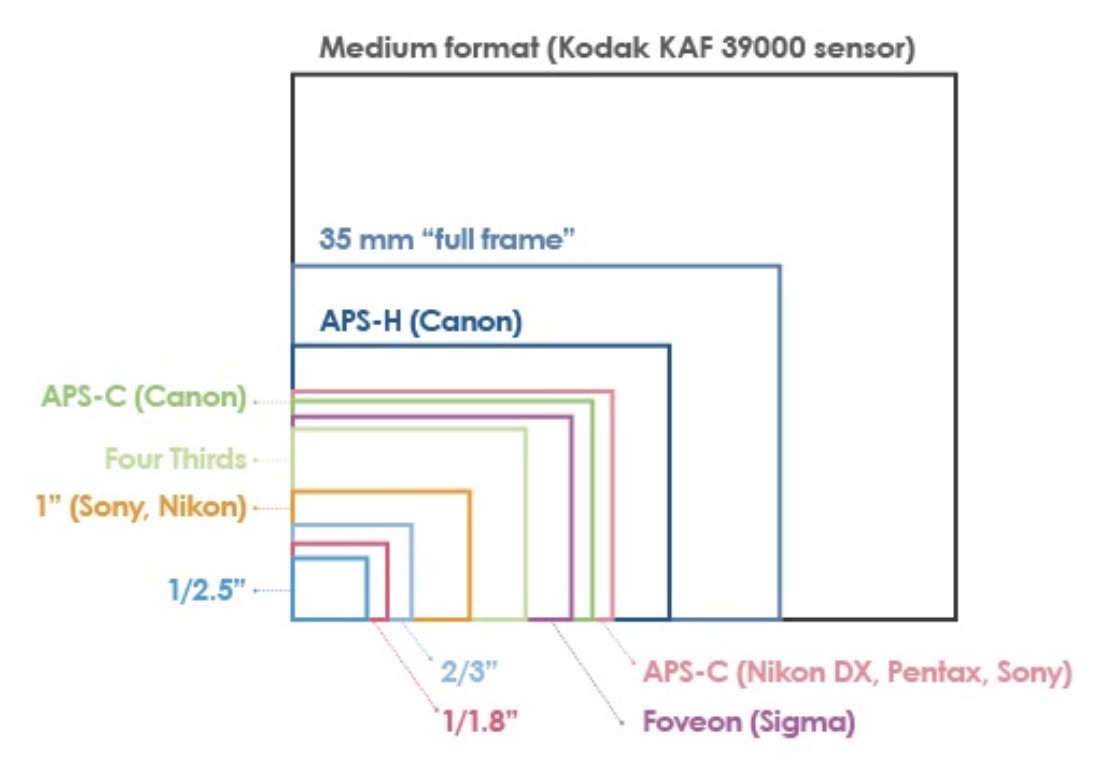
除焦距外,FOV 还取决于传感器的大小。
在相机中,光圈是指镜头的受光区域,一般用镜头直径区分。可通过增减光圈大小来控制图像亮度。
一种更方便的表示光圈的方法是使用一个关于焦距的分数,即 \(D = \dfrac{f}{N}\),其中 \(N\) 为焦比(F-number)。比如对于 50mm 的焦距,当光圈完全打开时,焦比为 1.8(此时光圈直径为 27.8mm
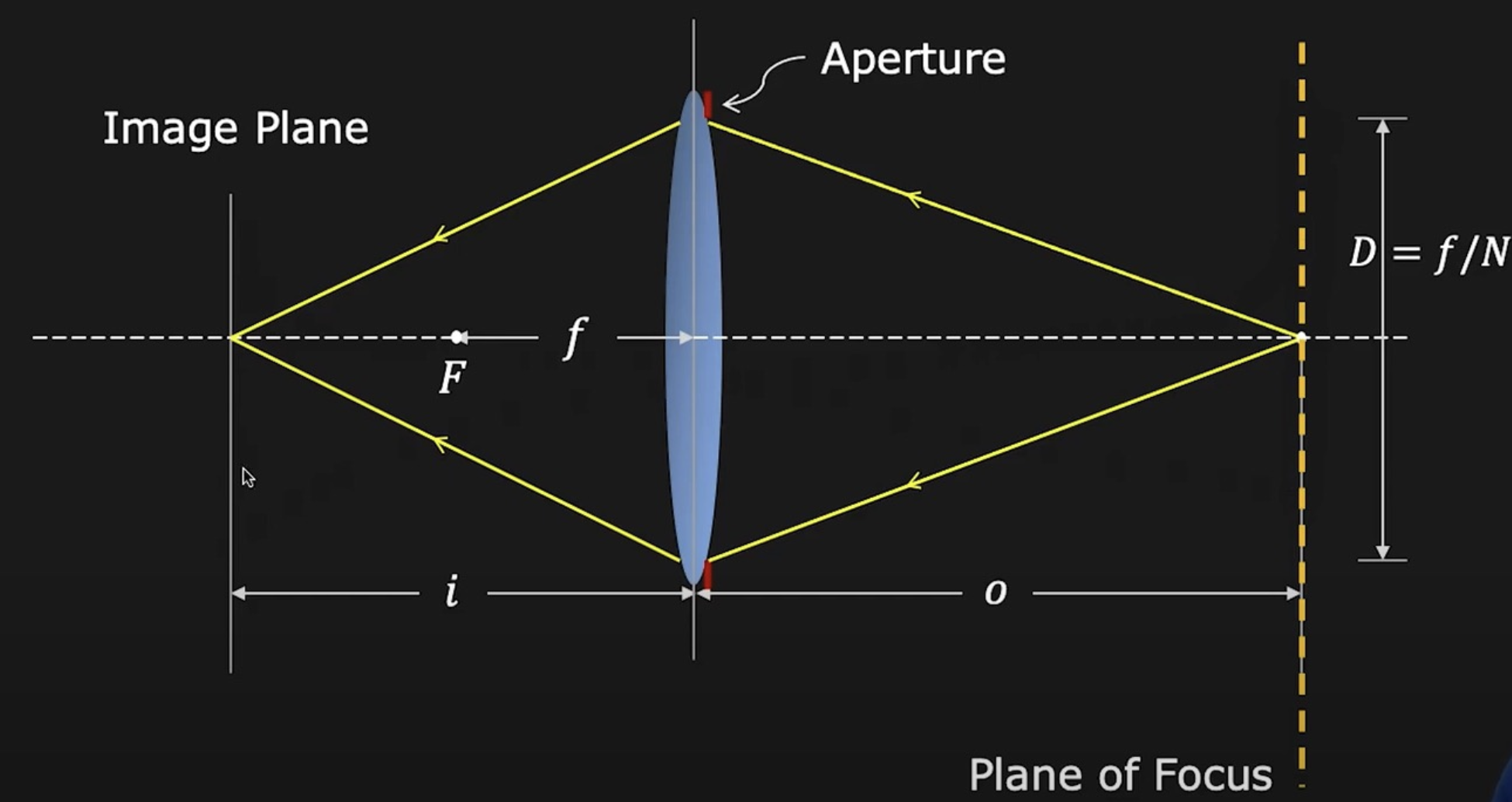
镜头失焦(lens defocus) 问题:
-
假设物体位于黄色虚线处时,物体的光线进入透镜后正好在底片处汇聚成一点,因此成像很清晰
-
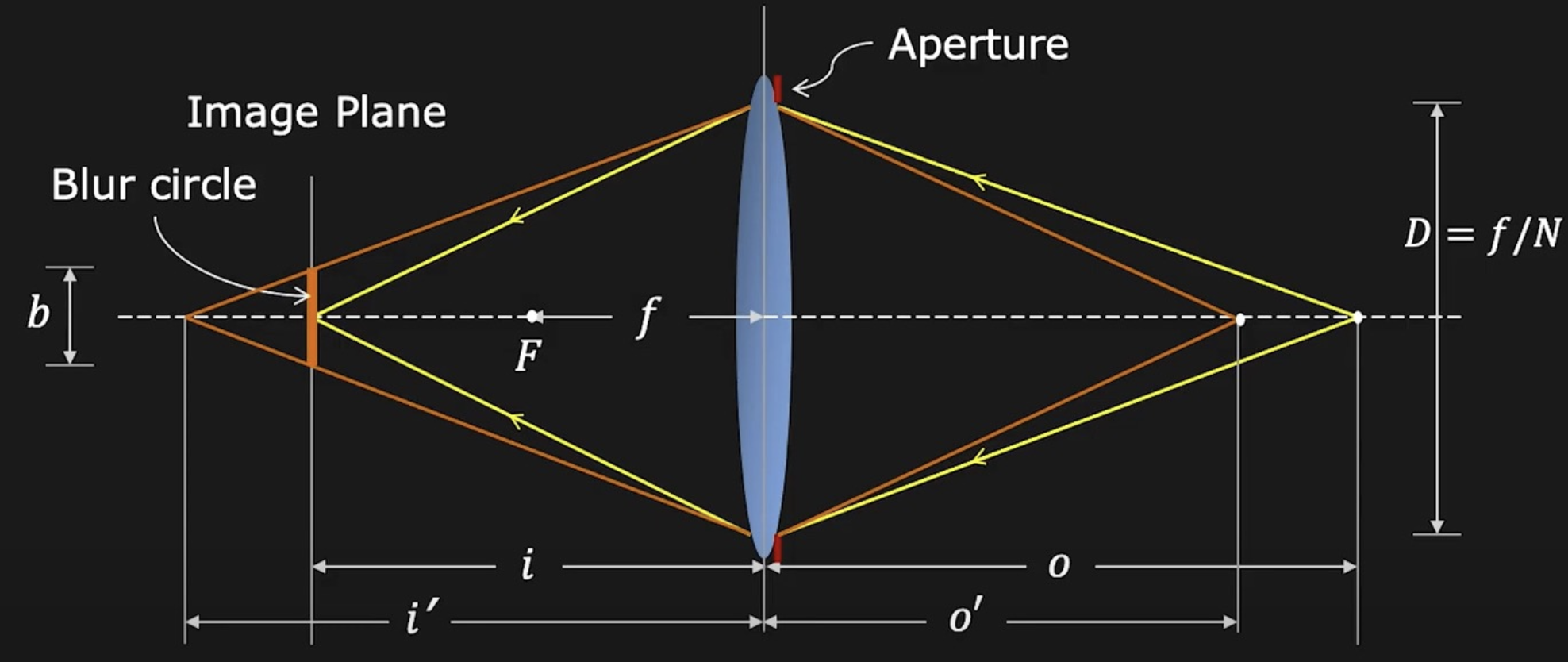
但如果稍微改变物体的位置,比如靠近些,那么对应的像就会远离镜头(同时也远离底片,符合高斯成像公式的约束
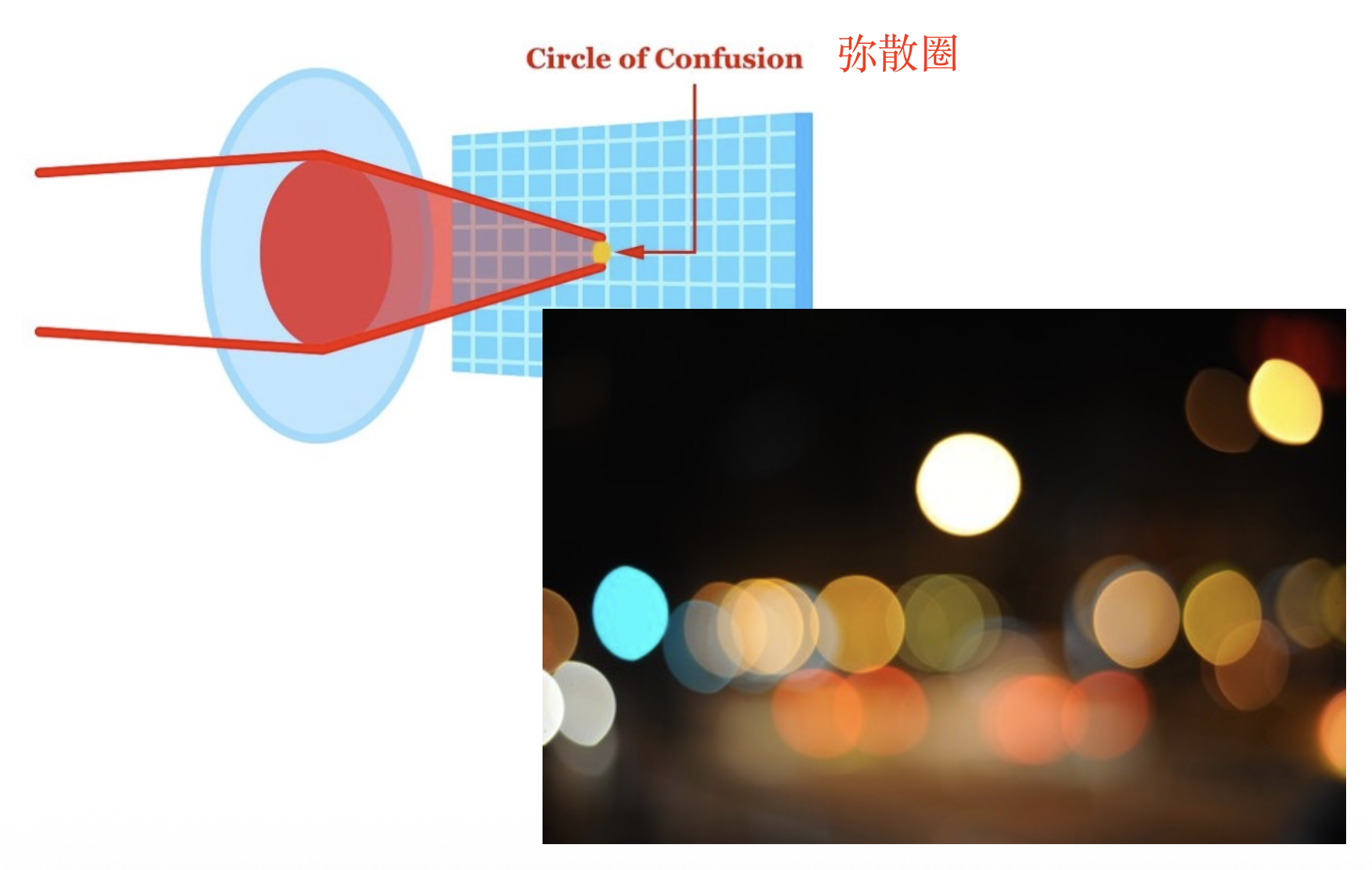
) ,来自物体的光在底片处就会形成一片光斑(模糊圈(blue circle) 或弥散圈(circle of confusion)) ,如图中加粗的橙色实线部分所示
可利用相似三角形解出光斑直径 \(b\):\(\dfrac{b}{D} = \dfrac{|i' - i|}{i'} \Rightarrow b = \dfrac{D}{i'}|i' - i|, b \propto D \propto \dfrac{1}{N}\)
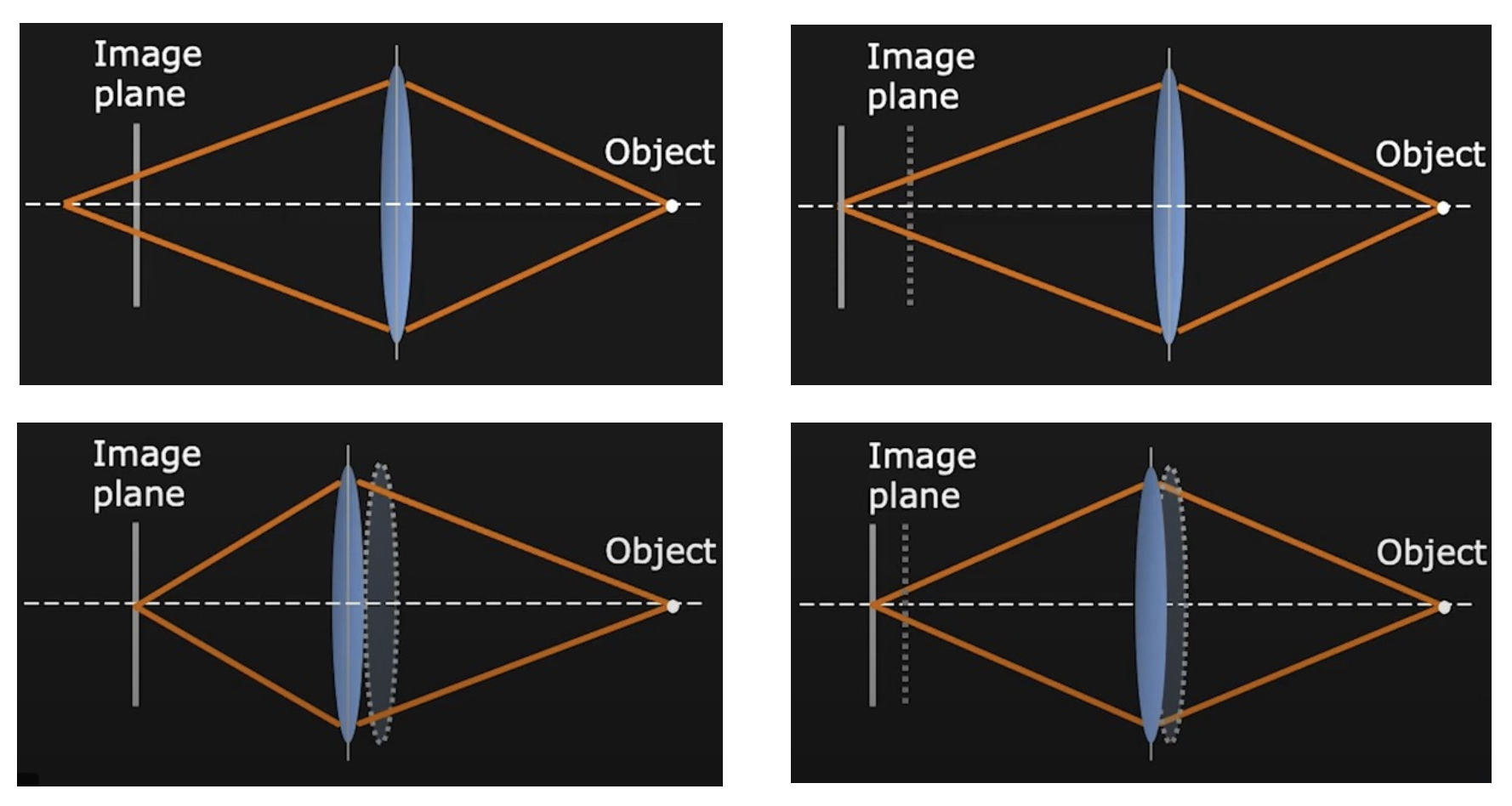
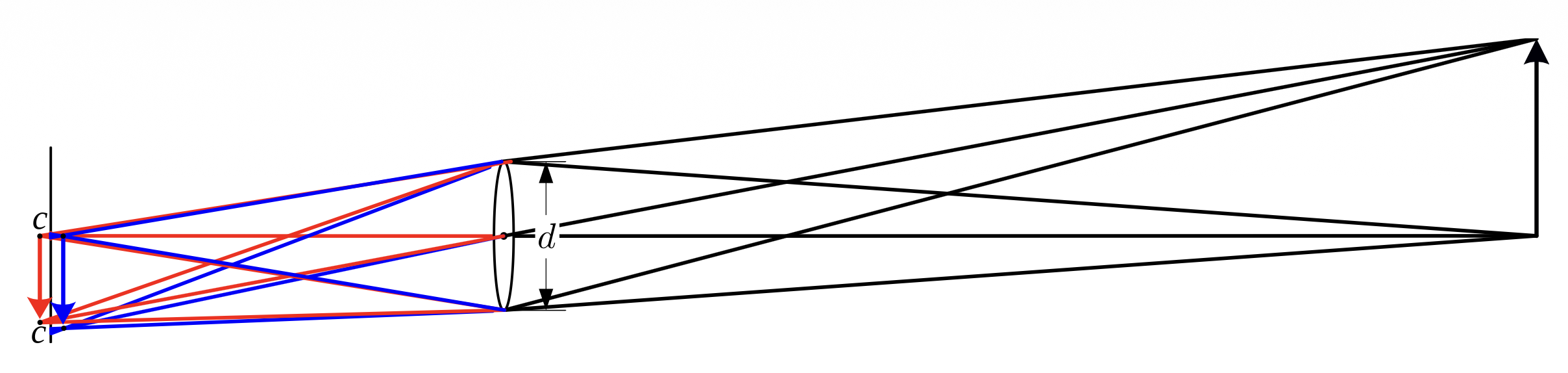
当物体位置不动时,要想对好焦,可以从以下几方面考虑:
- 只移动底片(右上)
- 只移动镜头位置(左下)
- 两者也可同时移动(右下)
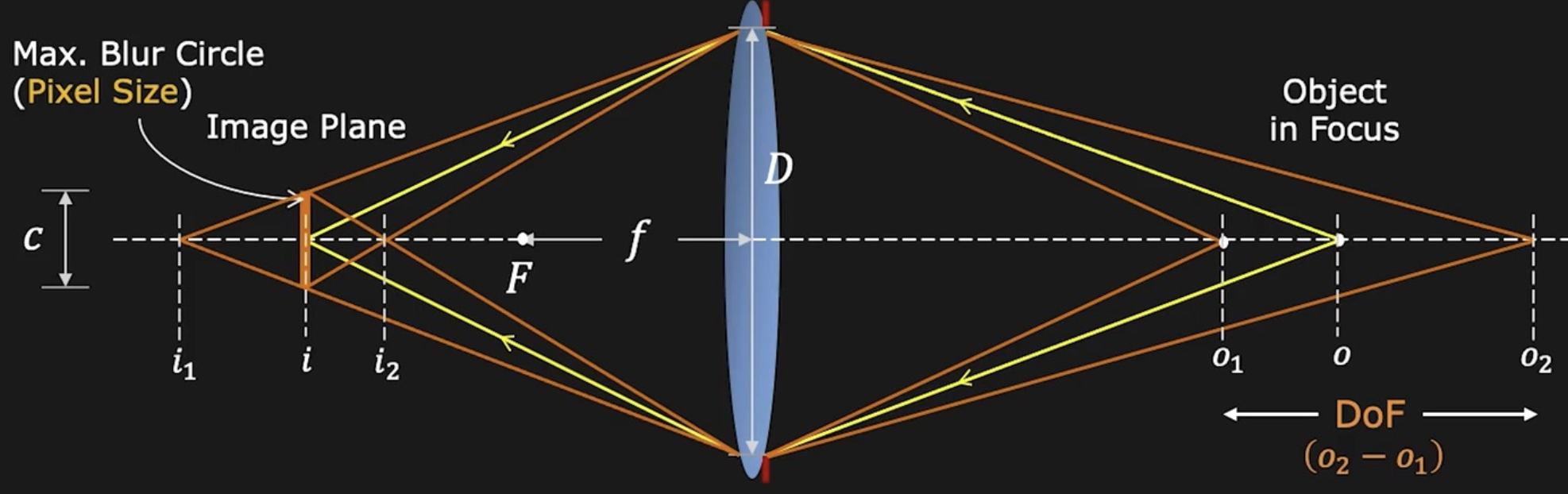
景深(depth of field, DoF):一种物体距离范围,在范围内(即模糊度 \(b\) 小于像素尺寸的范围)的图像能够对好焦。
原理图如下:
- \(c = \dfrac{f^2(o - o_1)}{No_1(o - f)} = \dfrac{f^2(o_2 - o)}{No_2(o - f)}\)
- \(\text{DoF} = o_2 - o_1 = \dfrac{2of^2cN(o - f)}{f^4 - c^2N^2(o - f)^2}\)
- 减小光圈直径(增大焦比)会增加 DoF
色差 (chromatic aberration)
- 玻璃的折射率(index of refraction) 随波长的变化而略有不同
- 因此,简单透镜存在色差问题,这是指不同颜色的光倾向于在略微不同的距离上聚焦(模糊,颜色偏移)
- 为了减少色差和其他类型的像差,大多数摄影镜头都是由不同玻璃元件(具有不同涂层)组成的复合镜头
暗角 (vignetting)
暗角是亮度向图像边缘衰减的趋势,它由两种效果组成:自然暗角和机械暗角。
- 自然暗角(natural vignetting):物体表面和镜头光圈的缩短
- 机械暗角(mechanical vignetting):光束的阴影部分从未达到图像
暗角可以进行校准(即撤销
Geometric Image Formation⚓︎
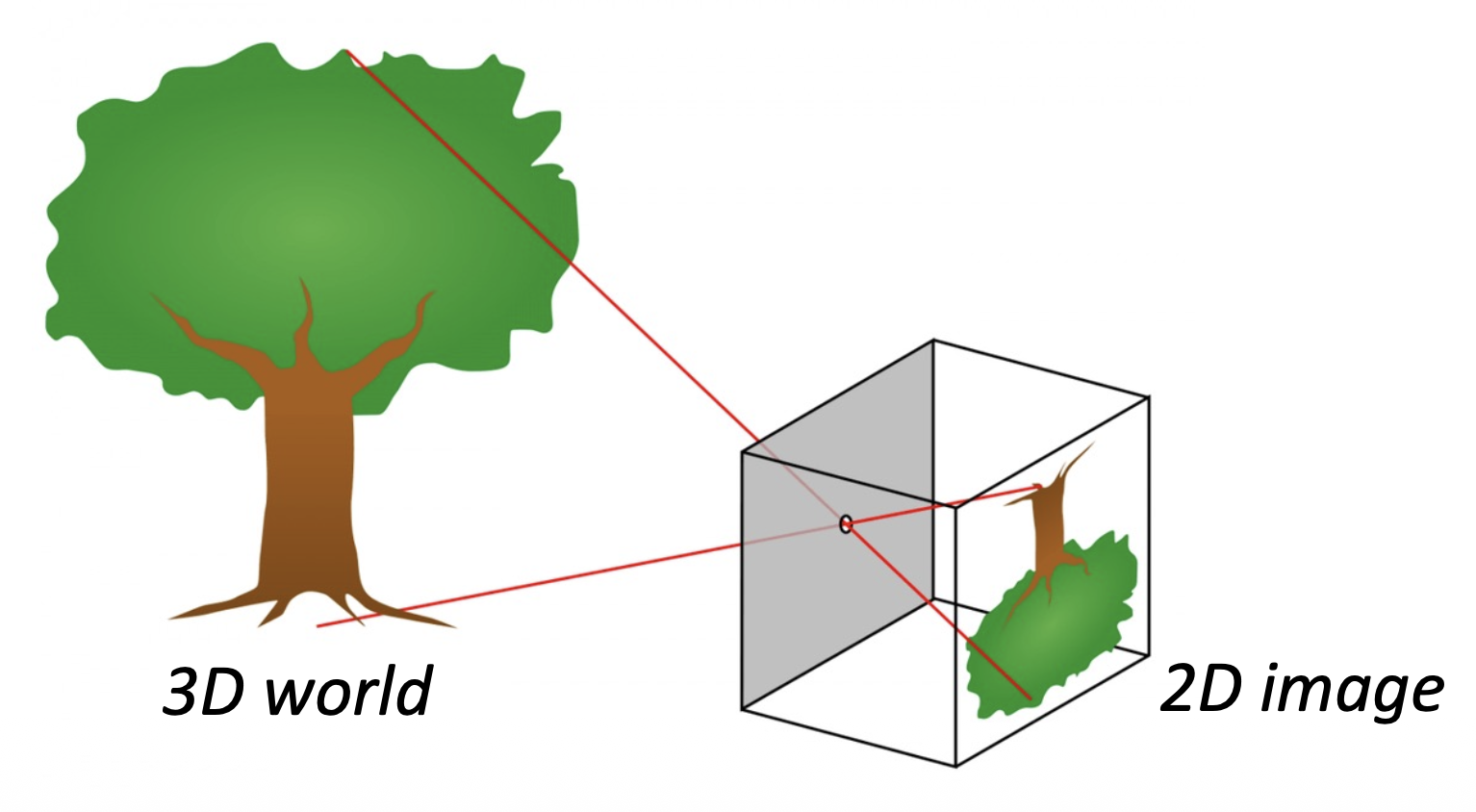
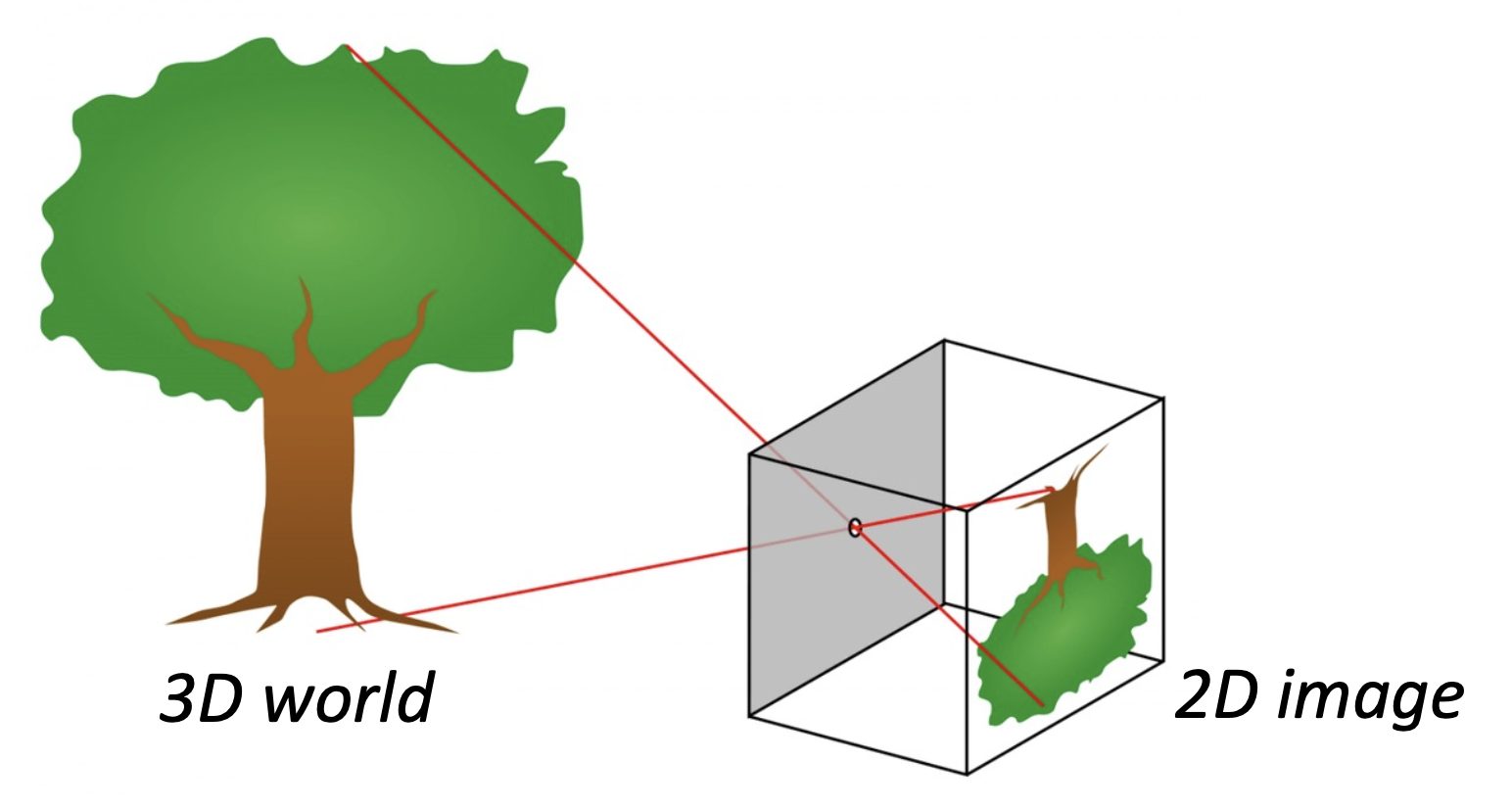
相机模型描述了三维世界和二维图像之间的几何关系。
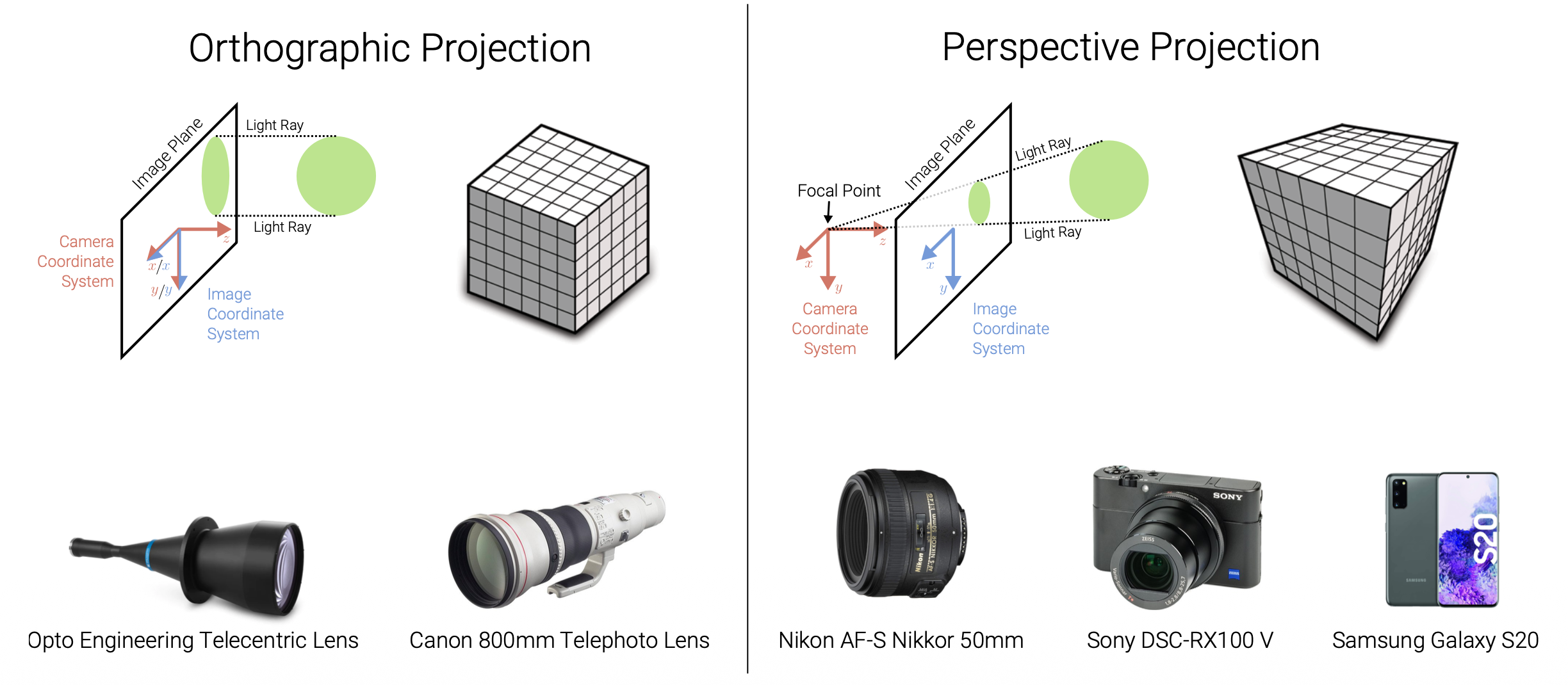
两类投影模型:
- 正射投影(orthographic projection)
- 透视投影(perspective projection)
为便于复习,隐藏了正射投影的部分
Orthographic Projection⚓︎
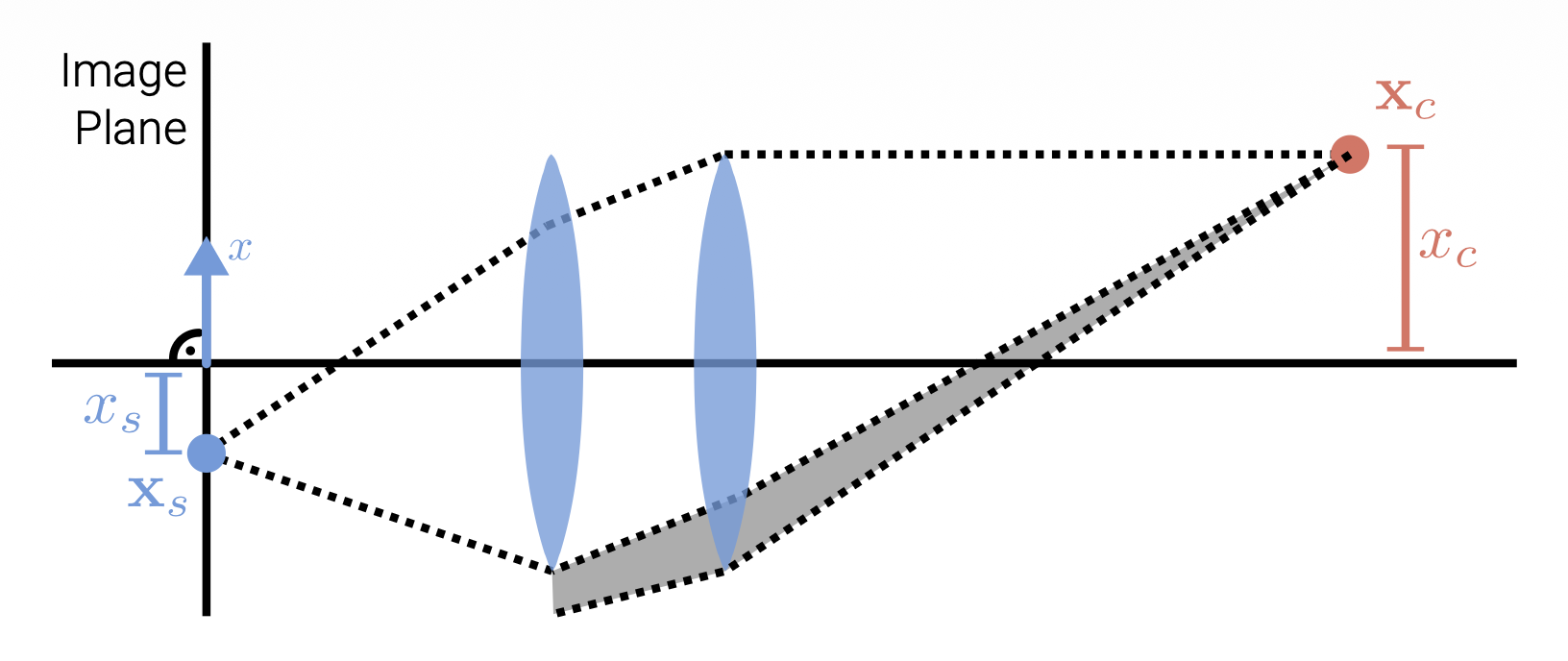
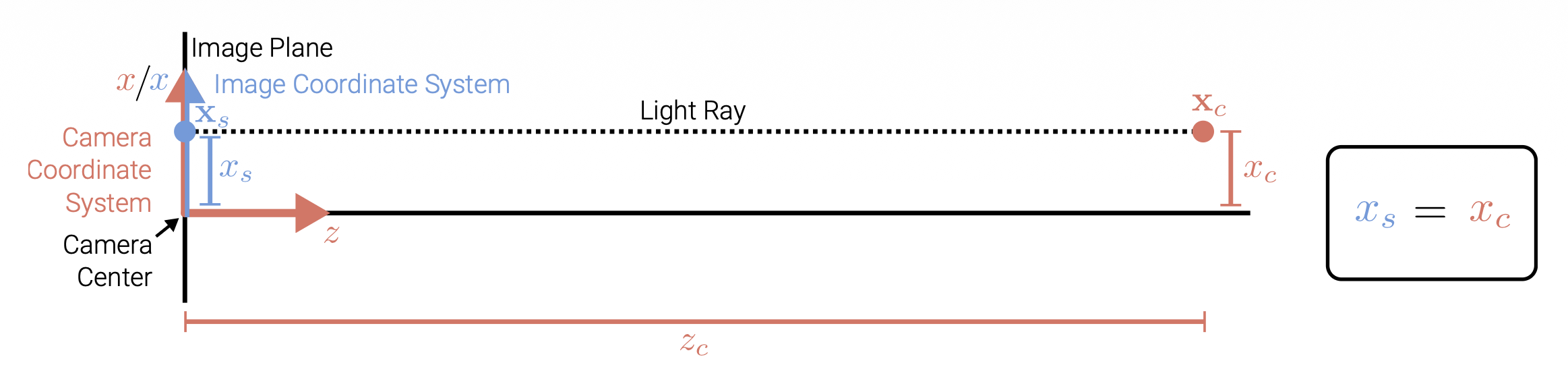
3D 点 \(\mathbf{x}_c \in \mathbb{R}^3\) 到像素坐标 \(\mathbf{x}_s \in \mathbb{R}^2\) 的正射投影(orthographic projection):
- 相机和图像坐标系的 x, y 轴是共享的
- 光线与相机坐标系 z 坐标平行
- 在投影过程中,z 坐标被舍弃,x 和 y 坐标保持不变
- 注:为清晰起见,此处未显示 y 坐标,但其行为和上图的 x 坐标类似
正射投影仅将 3D 点在相机坐标 \(\mathbf{x}_c\) 中的 z 分量丢弃,以获得图像平面(即屏幕)上的对应 2D 点 \(\mathbf{x}_s\)。
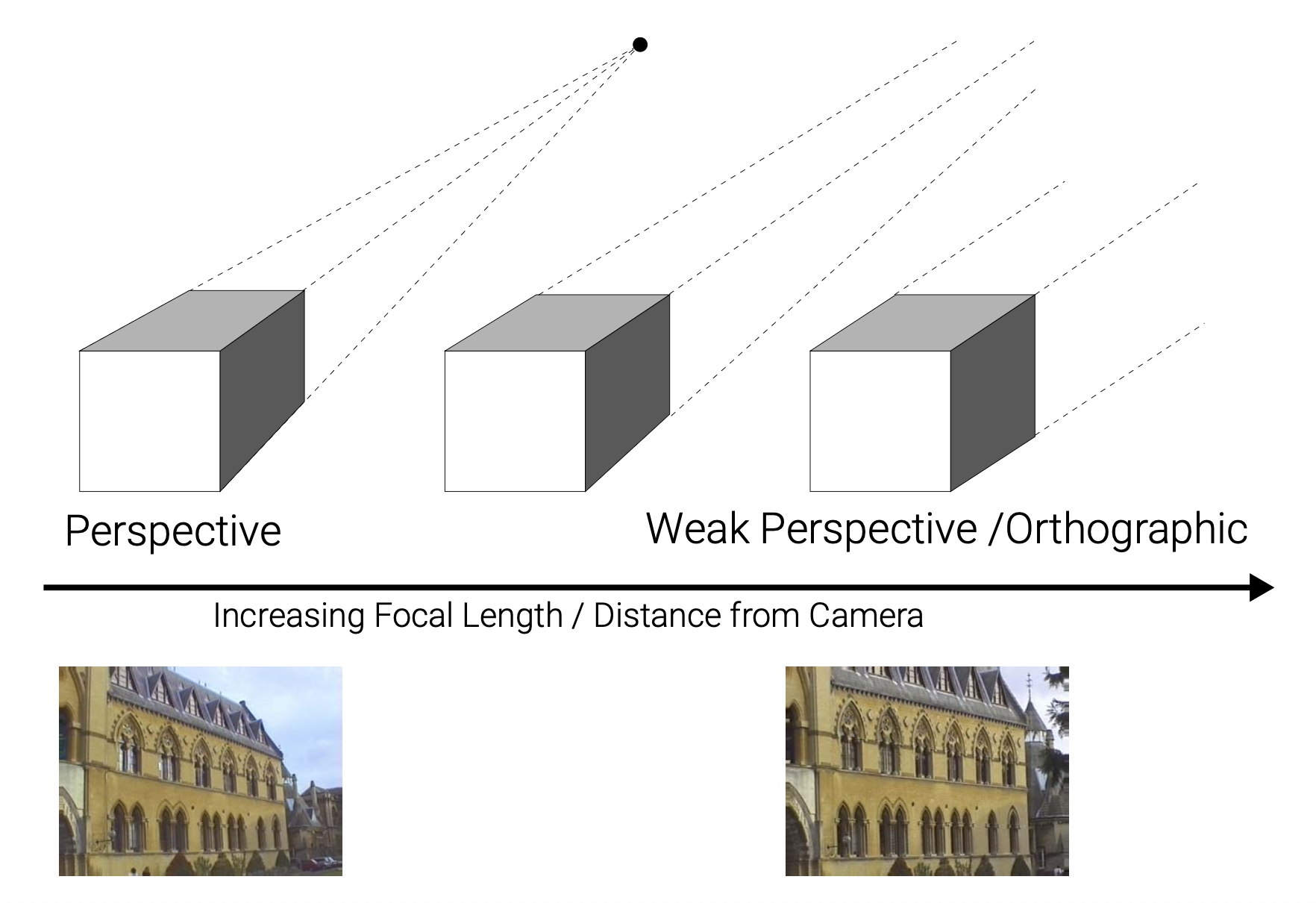
- 对于远心镜头 (telecentric lenses) 而言,正射投影是精确的;而对于长焦镜头 (telephoto lenses) 来说,它是一种近似
- 经过投影后,无法恢复 3D 点到图像的距离
实际上,世界坐标(可能以米为单位测量尺寸)必须进行缩放以适应图像传感器(以像素为单位测量
- 备注:\(s\) 的单位为 px/m 或 px/mm,用于将公制 3D 点转换为像素
- 在正交投影下,结构和运动可以通过因子分解方法(比如通过奇异值分解)同时估计
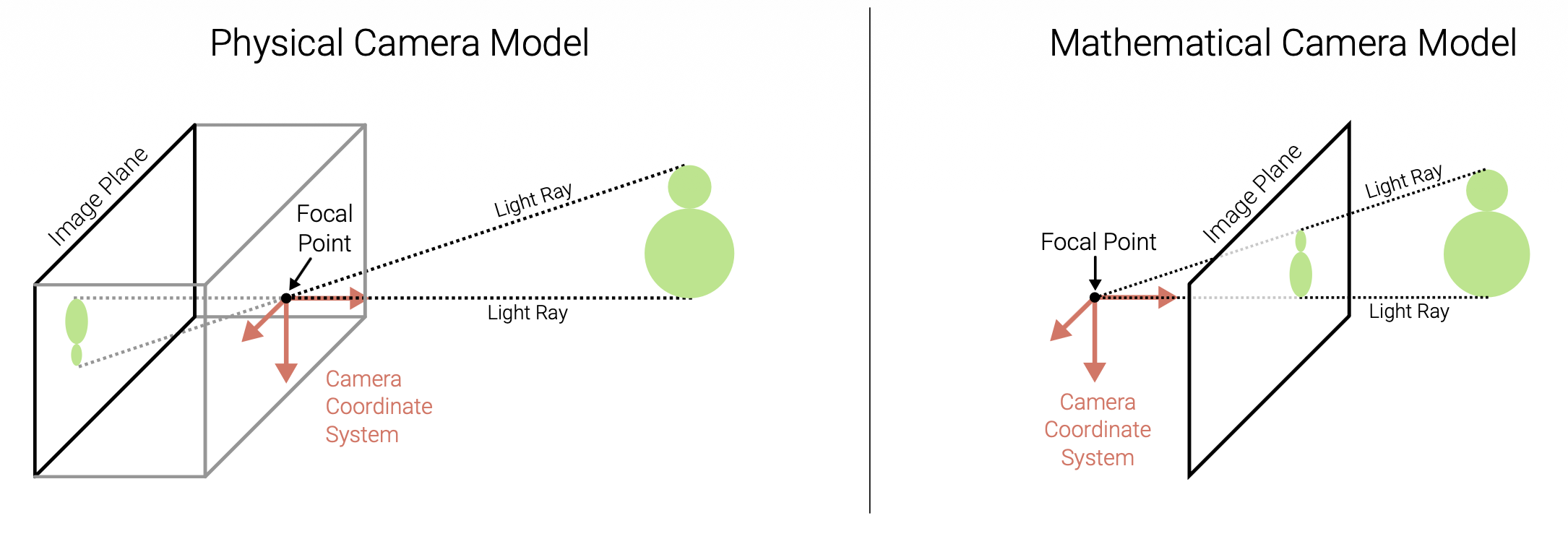
Perspective Projection⚓︎
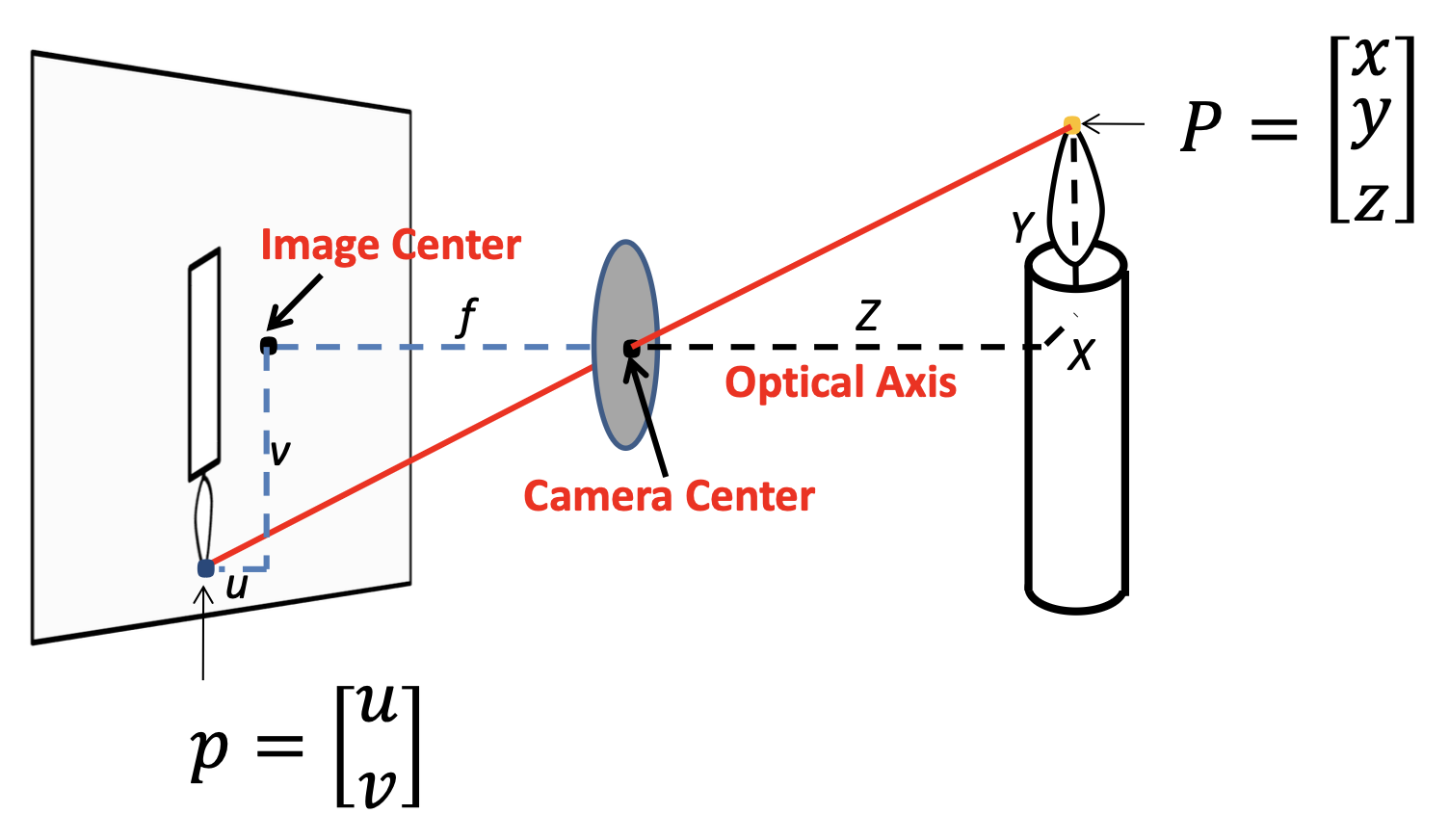
透视投影(perspective projection):三维世界坐标 -> 二维图像坐标
在齐次坐标表示中,透视投影就是一个简单的线性变换(矩阵乘法
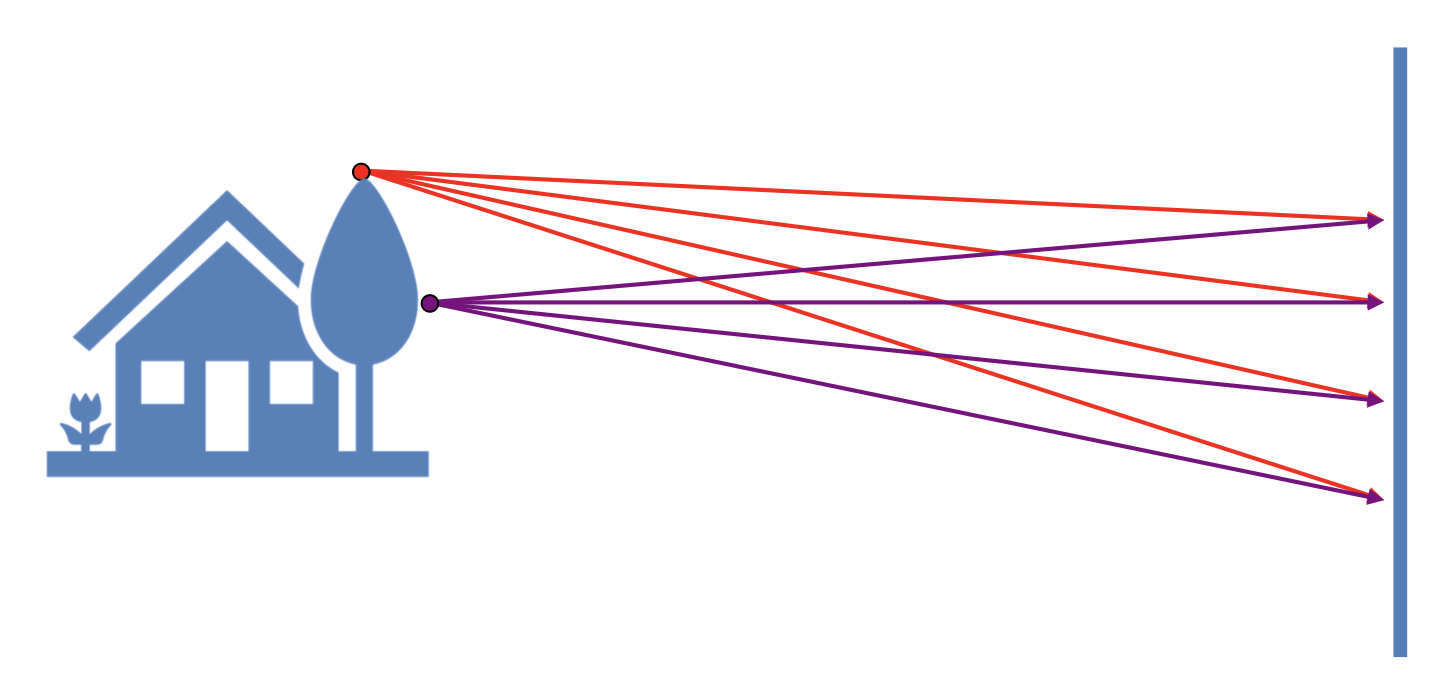
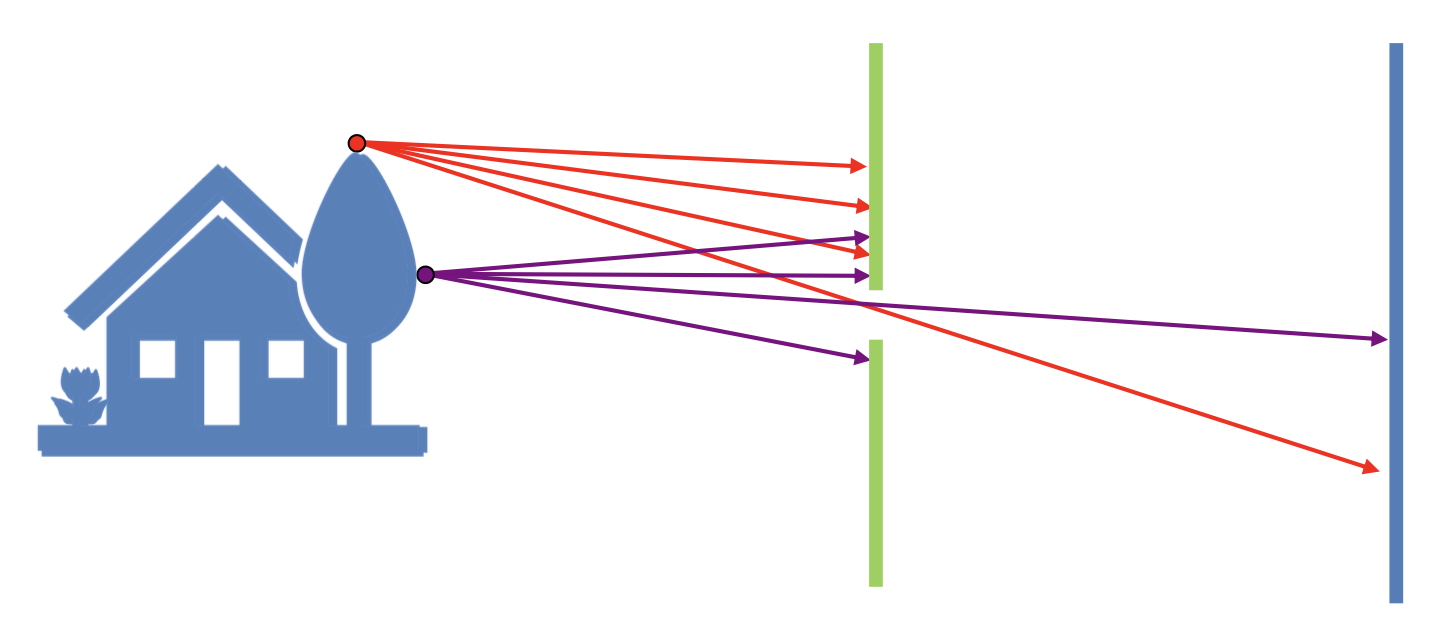
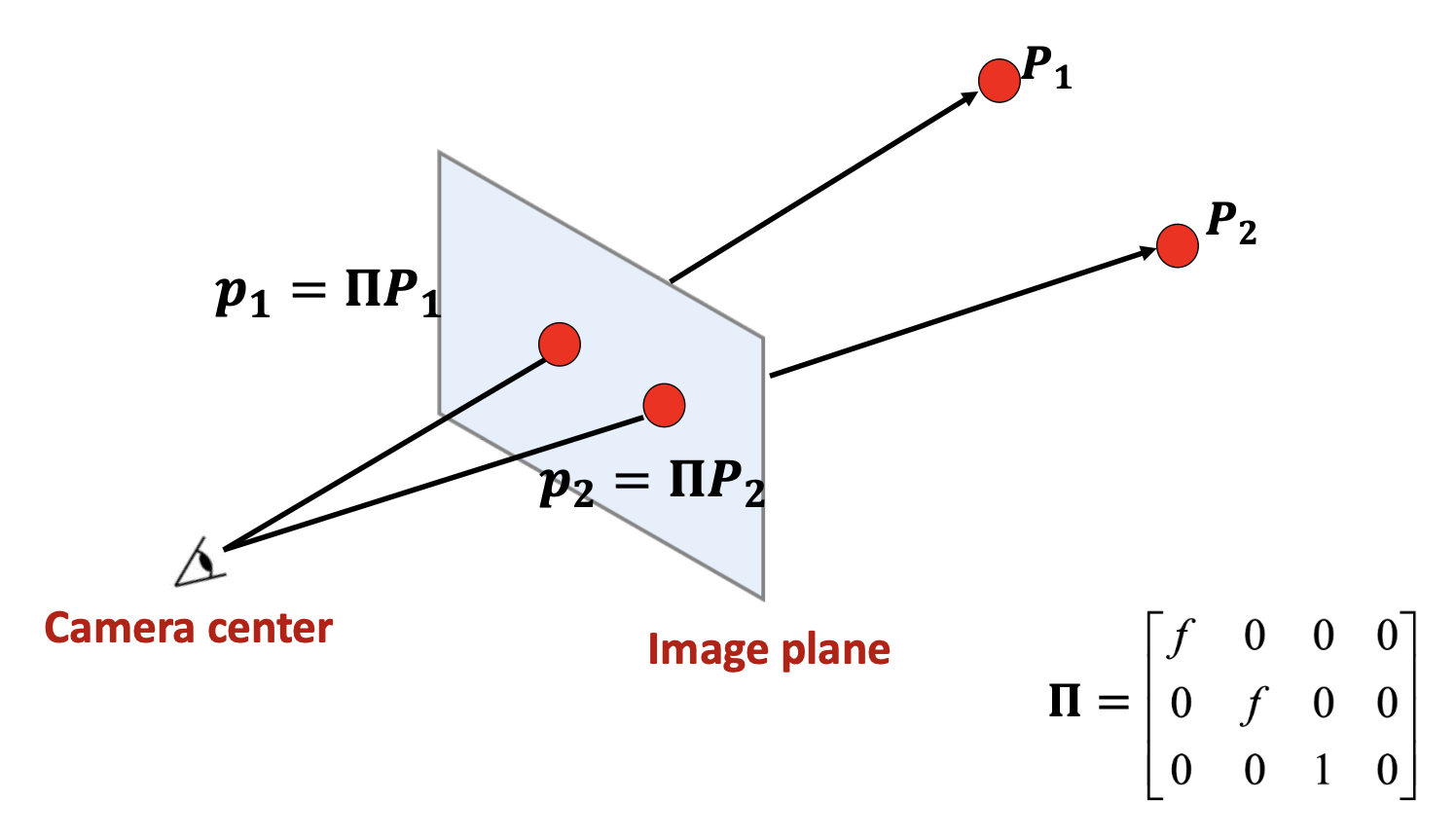
物体上两点在像平面上的透视投影:
Properties⚓︎
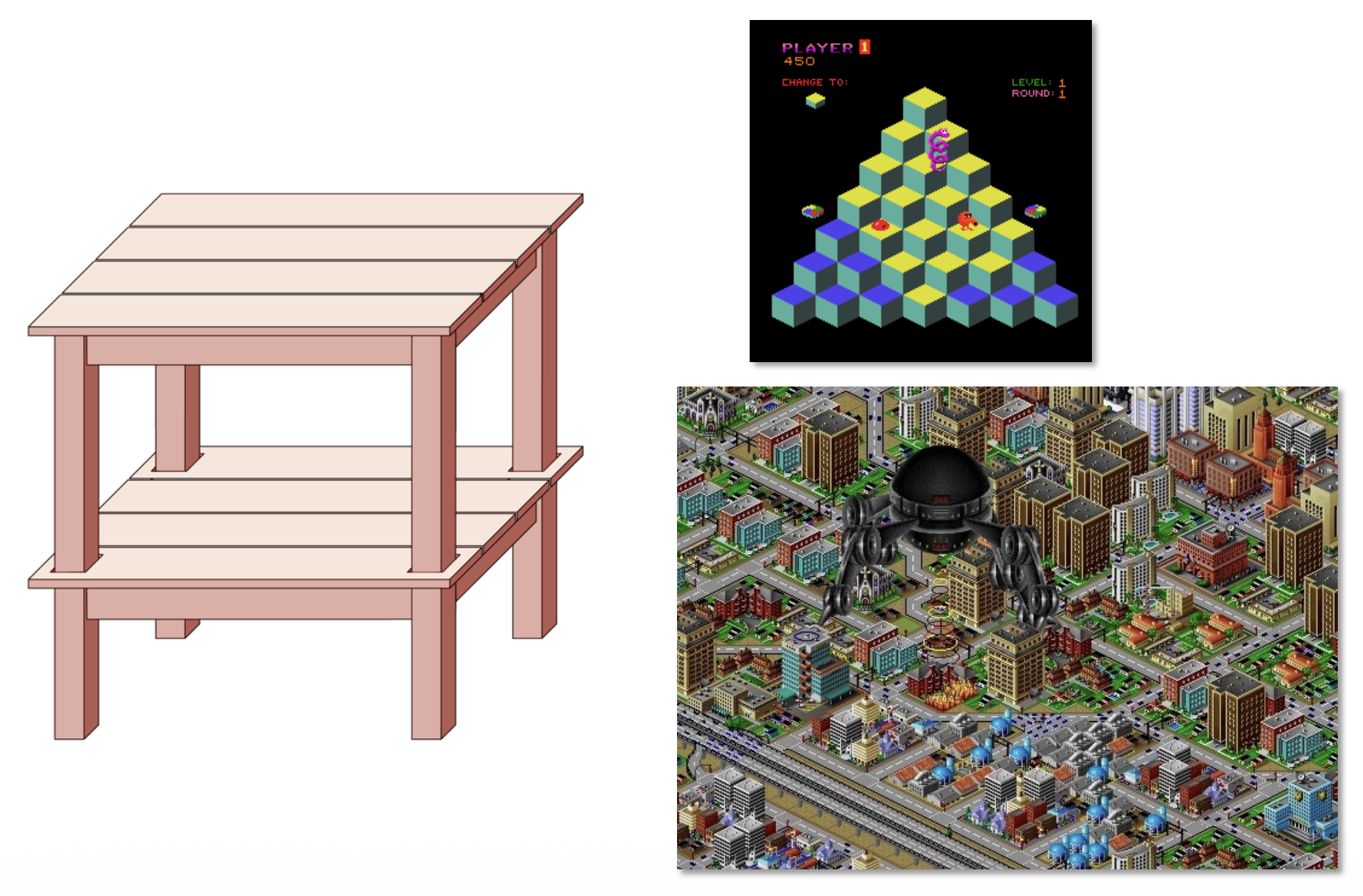
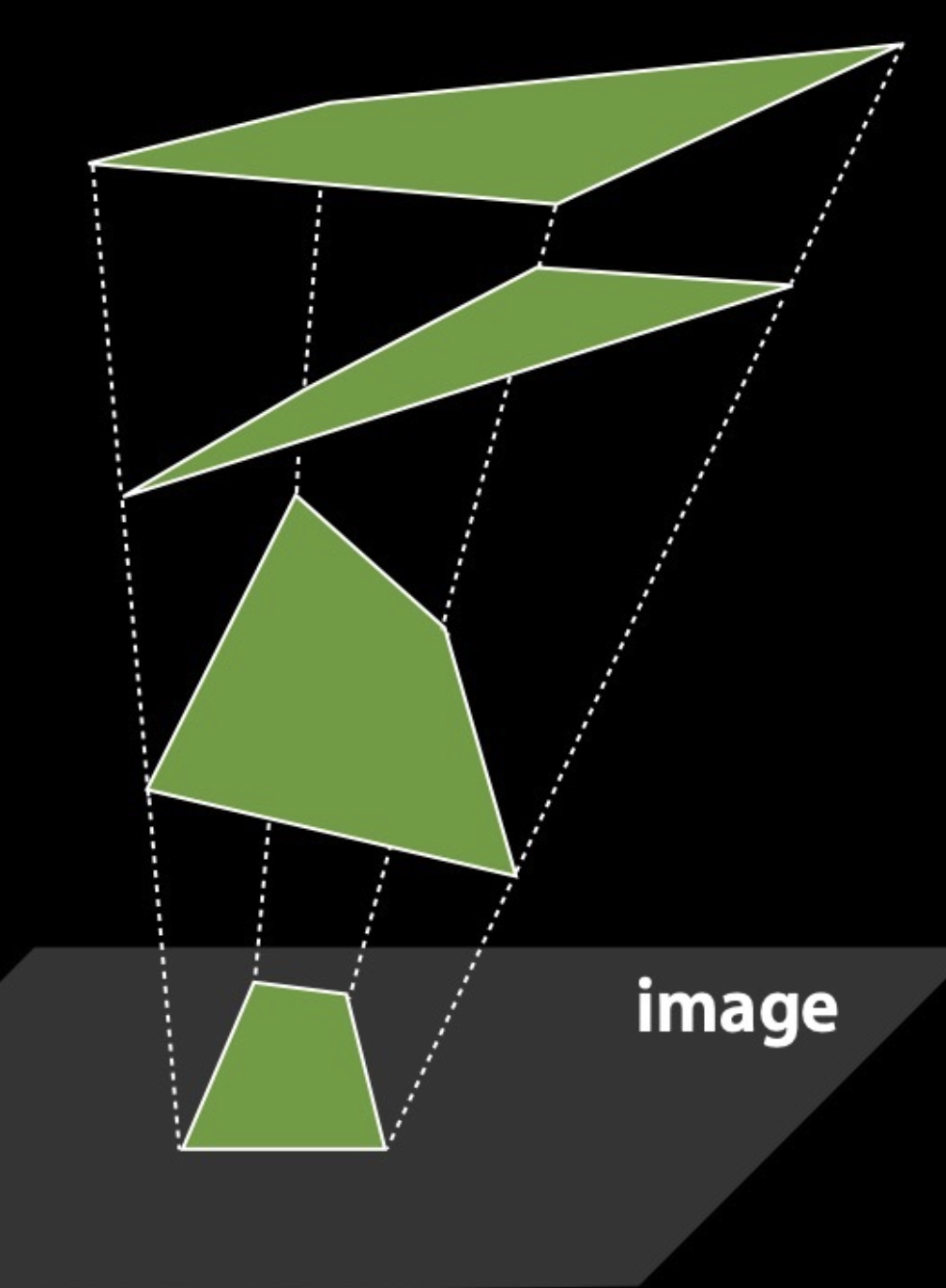
投影可能会很带来一些小麻烦,或者也可以认为是产生一些有意思的错觉。
一个投影可能对应无数种不同的物体形状:
透视投影的性质:
-
保留了直线“直”的性质
-
但是长度和角度关系却被丢失了
-
长度
-
角度
-
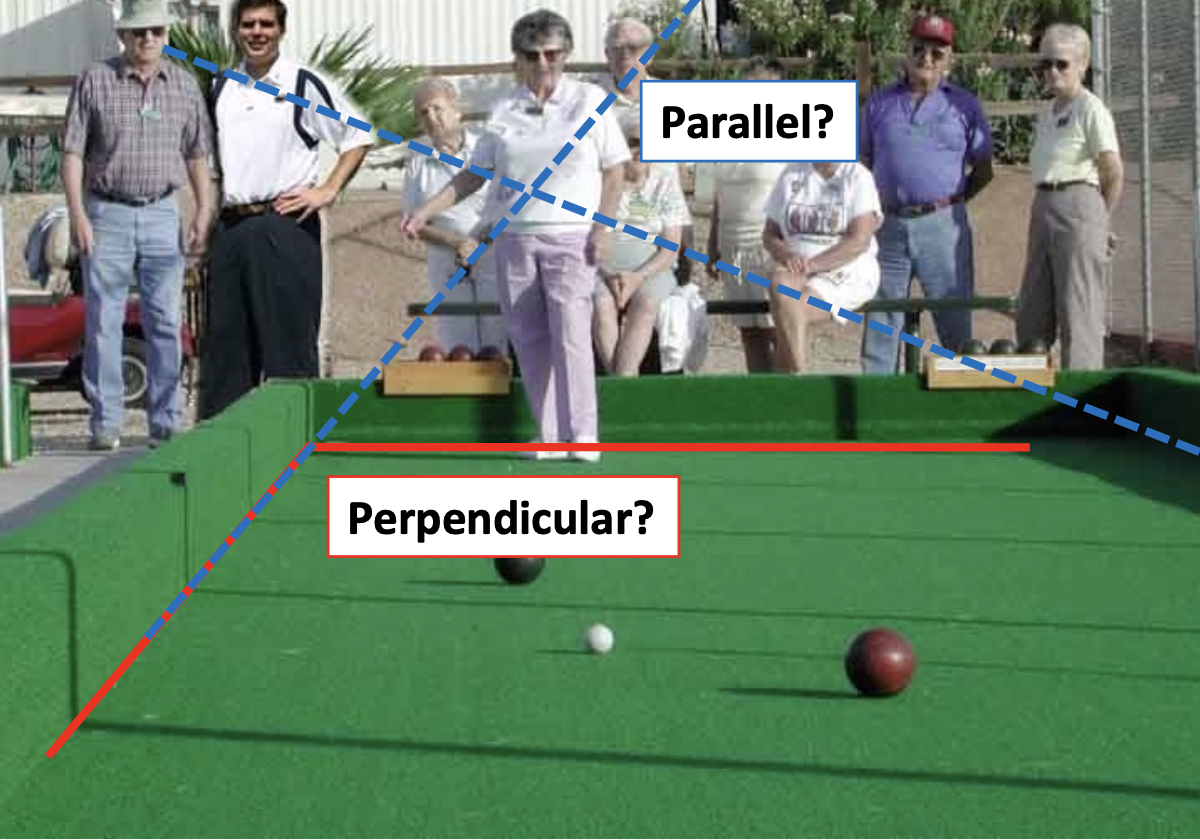
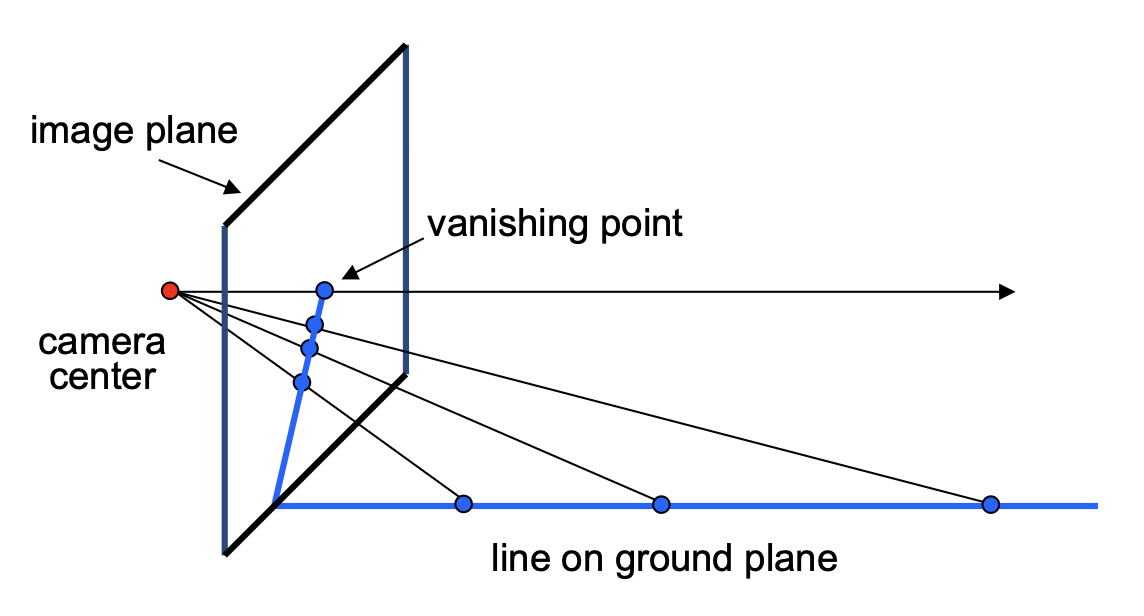
由于角度变化,两条在物理世界平行的线会在图像中汇聚于一点(即灭点(vanishing point)
性质:
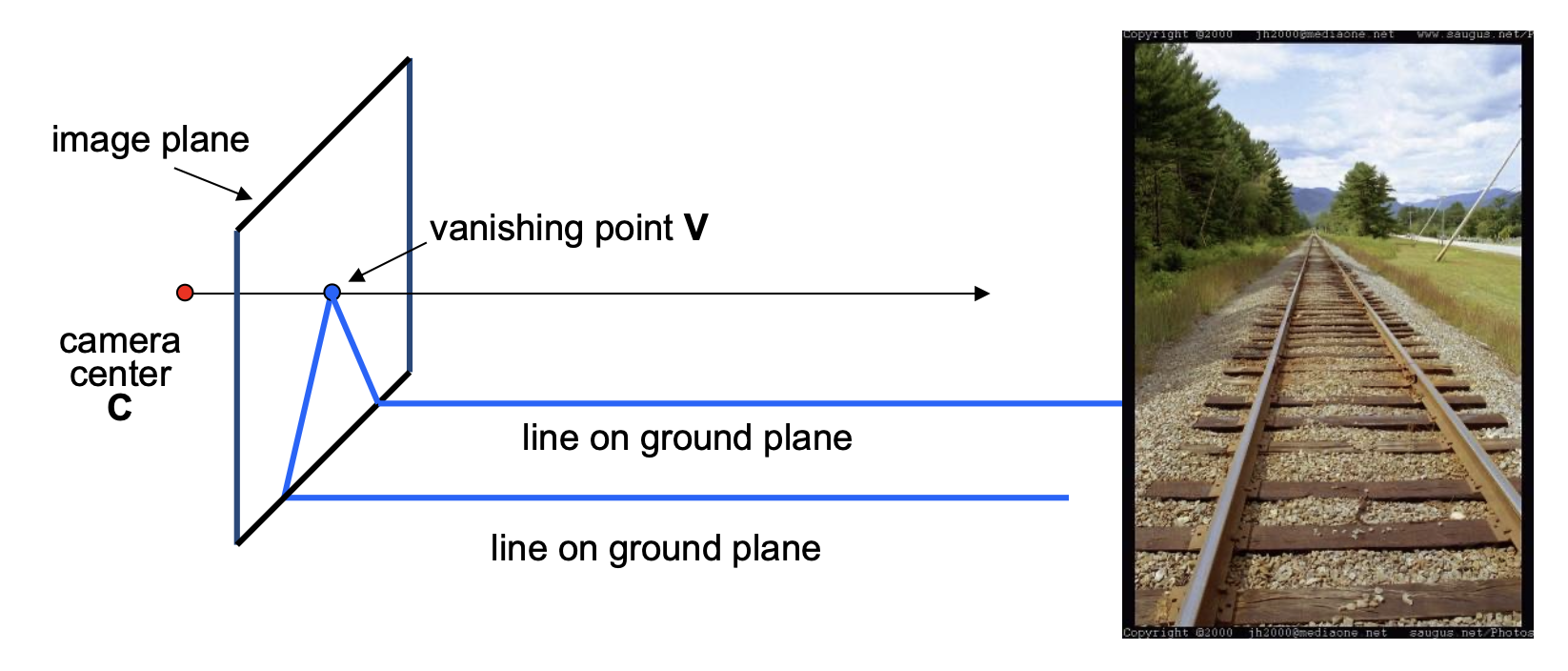
- 任意两条平行线之间都有一个共同的灭点 v
- 来自相机上一点 C 的通过 v 的射线与直线平行
- 因此 v 能够反映直线的方向
- v 可能在图像外,甚至无穷远处
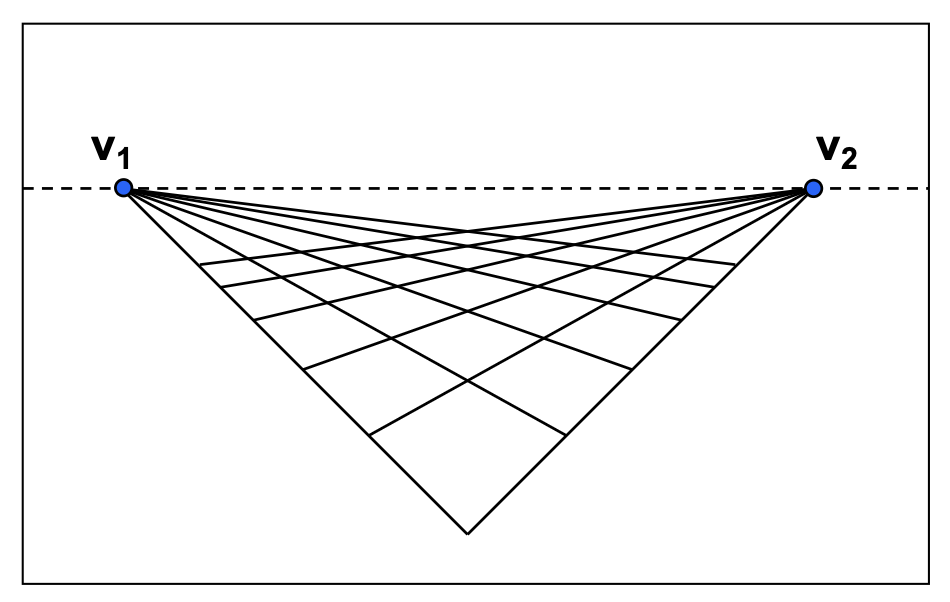
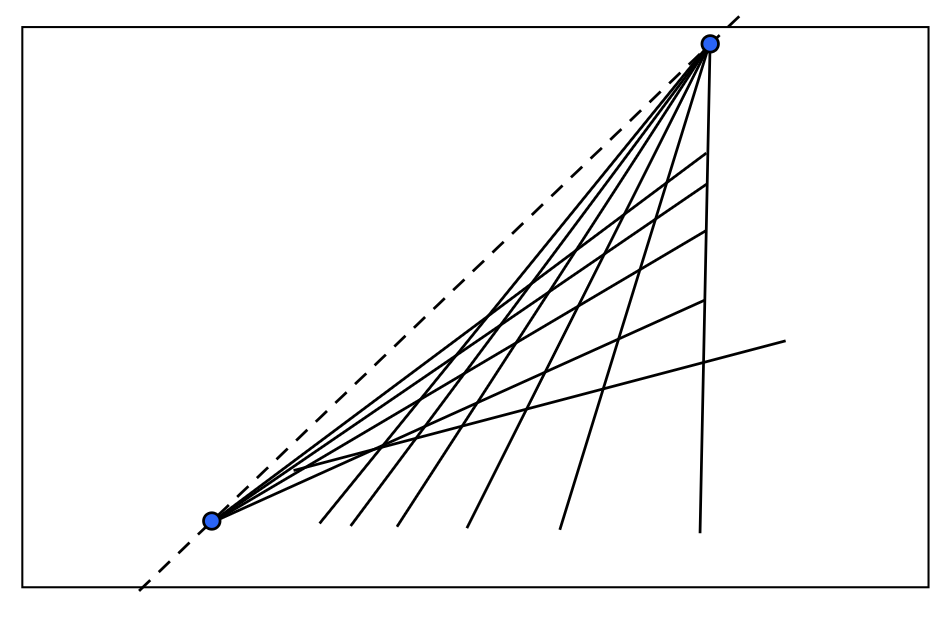
由于平面上任意两条平行线定义了一个灭点,这些灭点的并集就构成了一条灭线(vanishing line)。
需要注意的是,不同的平面会产生不同的灭线,因此灭线包含了平面朝向的信息。
Perspective Distortion⚓︎
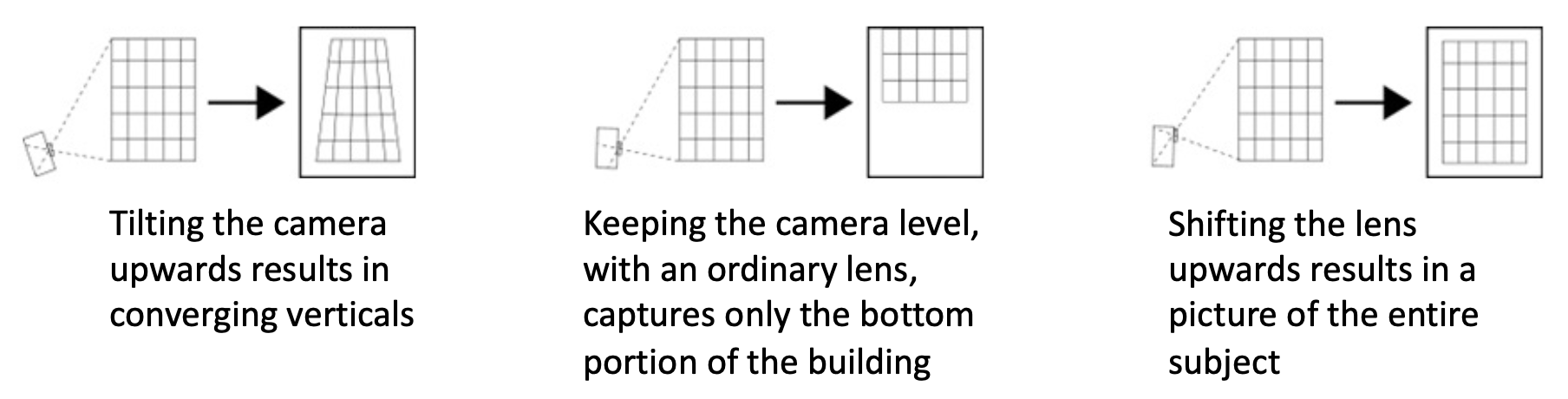
观察左图这幅建筑照片,不难发现建筑物的垂线是歪斜的,延伸后可汇聚于一点。
用更一般的说法来表述:这是一种透视畸变(perspective distortion) 现象,顾名思义是由透视投影引起的。原因便是透视投影会改变物体原有的长度和角度的性质。
我们的预期是得到像右图那样的效果,那么该如何实现呢?解决方案就是使用移轴相机(view camera)(镜头相对于胶片移动
需要注意的是,这一类畸变并不是由镜头的瑕疵引起的。
Radial Distortion⚓︎
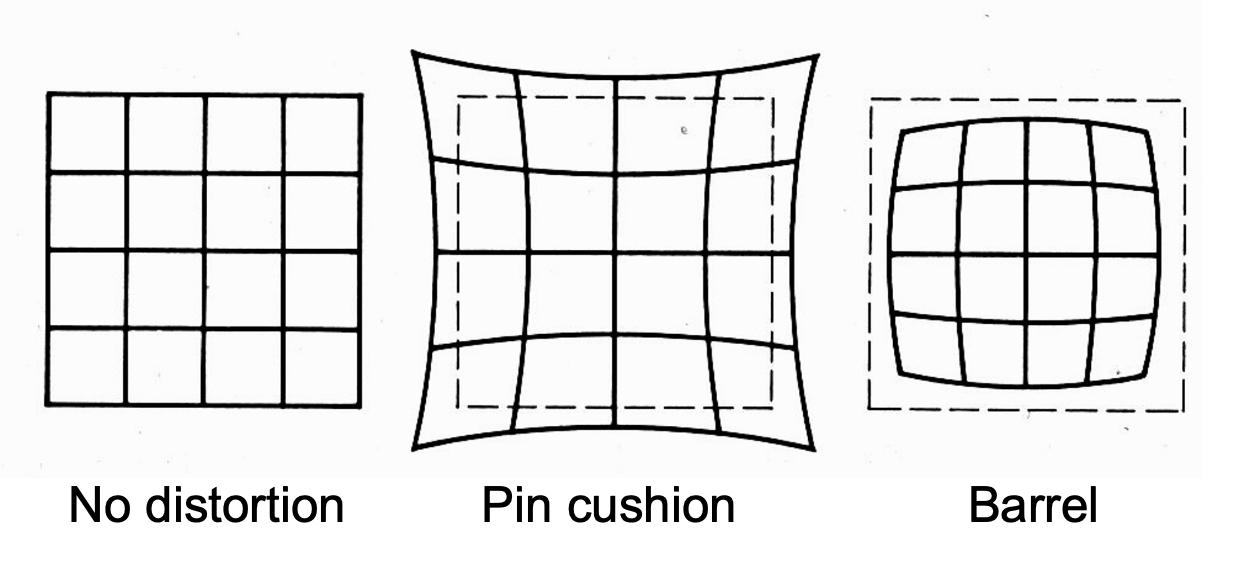
径向畸变(radial distortion) 是另一类畸变。和透视畸变明显不同的一点在于物体的直线性质也没在图像上保持,被扭曲成了各种曲线。径向畸变大致可分为:
- 枕形(pin cushion) 畸变 <- 长焦镜头
- 桶形(barrel) 畸变 <- 广角镜头
- 这类畸变由镜头瑕疵引起
- 对于通过透镜边缘的光线更明显
公式表示:
其中:
- \(x'_n, y'_n\):理想情况下透视投影的坐标
- \(r\):该点离图像中心的距离
- \(\kappa_1, \kappa_2\):和镜头相关的(导致图像畸变的)参数,可以利用标定板计算出来
- 可以利用这些参数实现对畸变图像的校正
例子
Photometric Image Formation⚓︎
光度成像(photometric image formation) 描述了三维世界的物理性质和二维图像的颜色之间的关系。
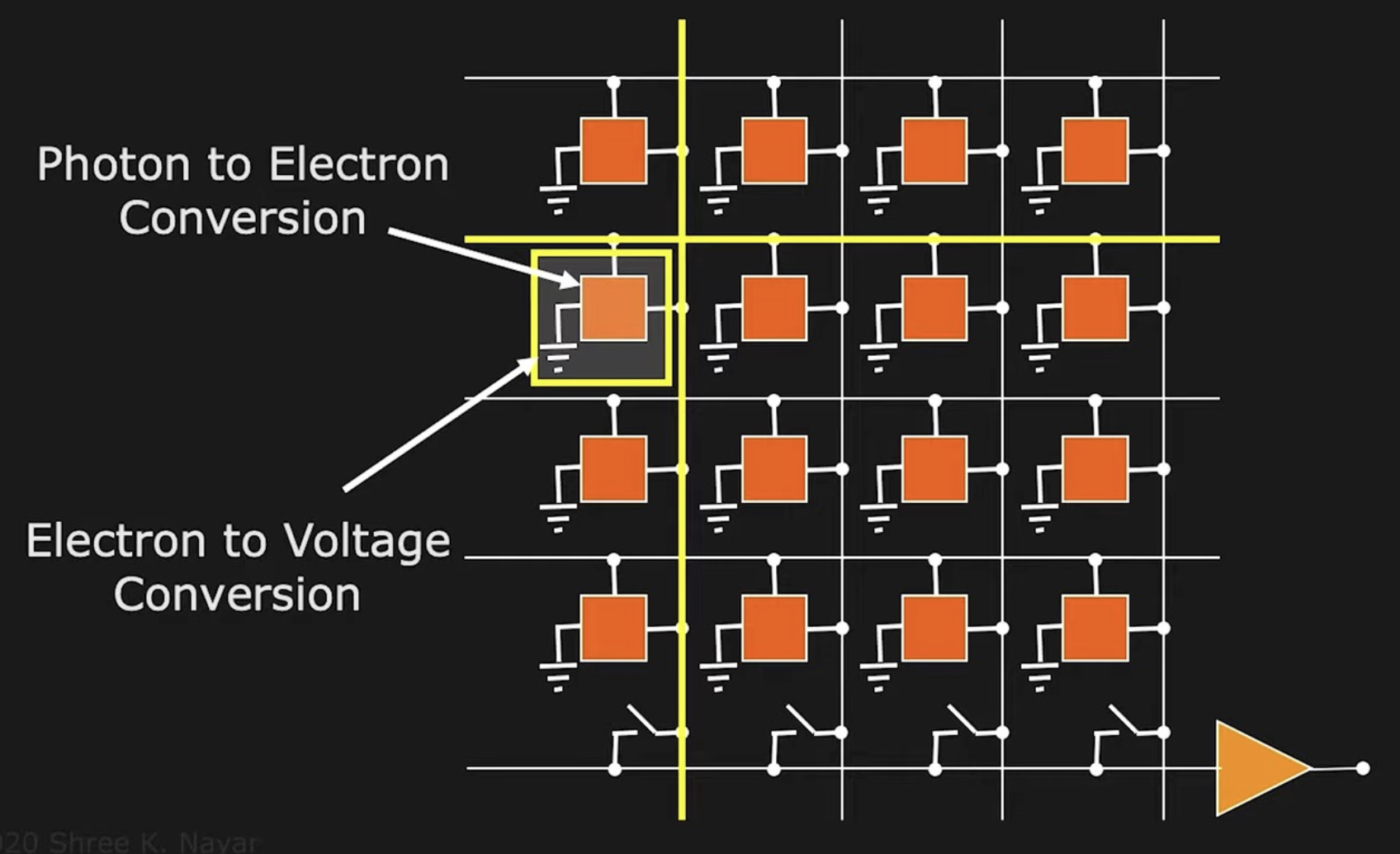
图像传感器:
CMOS(全称互补金属氧化物半导体 (complimentary metal-oxide semiconductor)
Shutter⚓︎
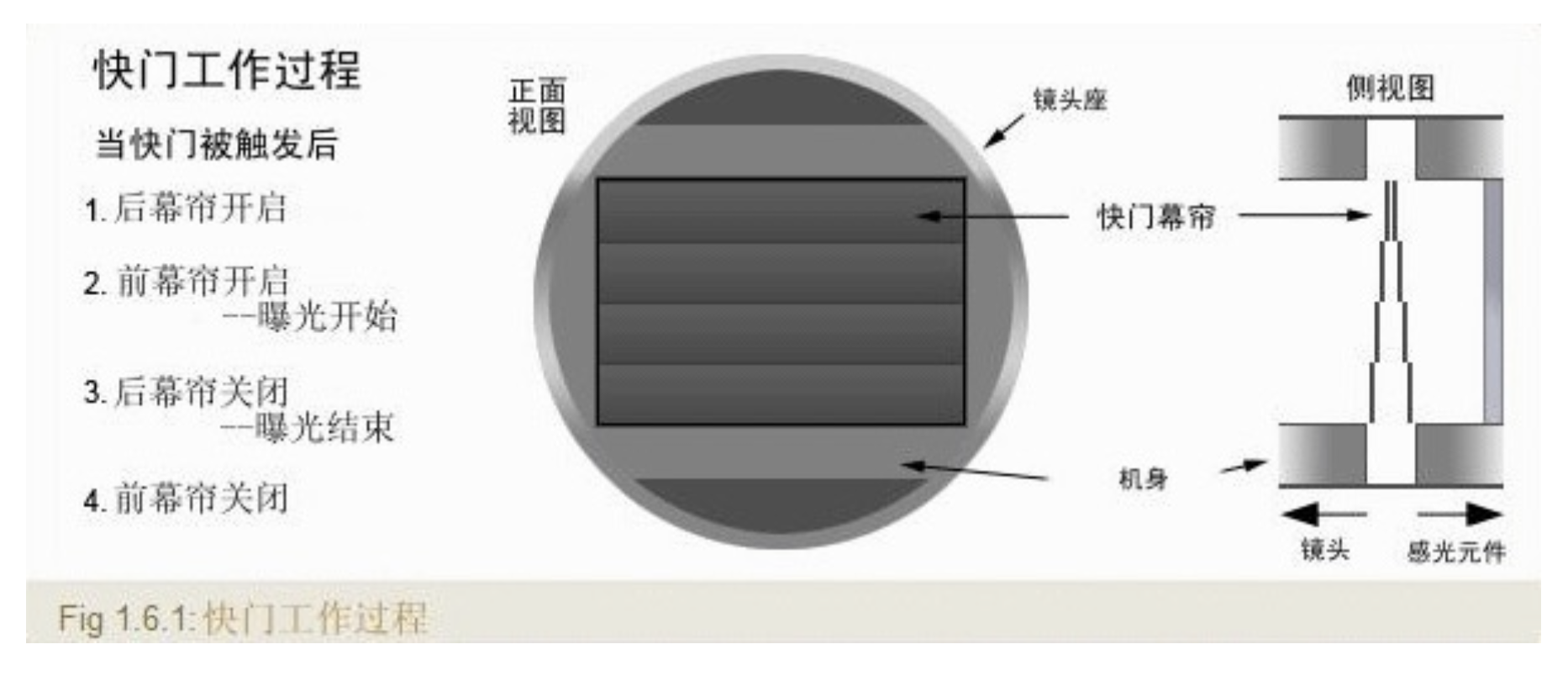
快门(shutter):
- 焦平面快门(focal plane shutter) 位于图像传感器 / 胶片正前方
- 多数数码相机采用机械与电子快门相结合的方式
- 快门速度通过控制曝光时间来改变到达传感器的光量
- 像素值 = 光强在曝光时间内的积分
- 它决定图像是否过曝、欠曝、模糊或出现噪点
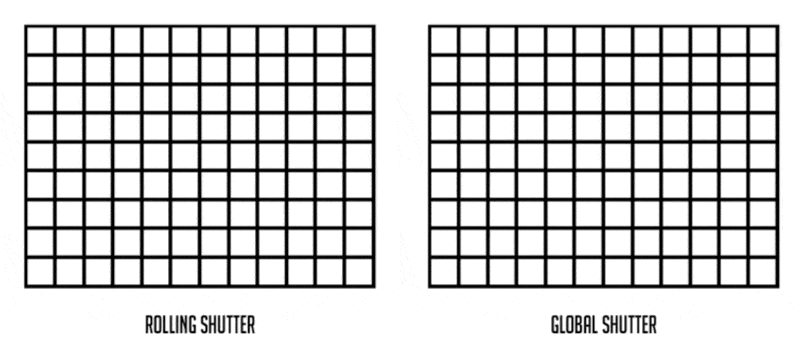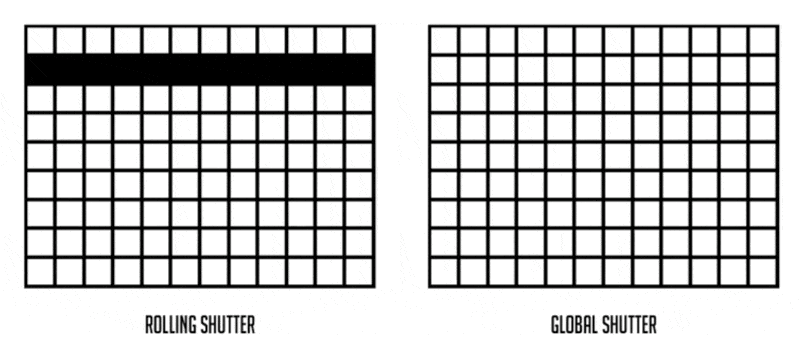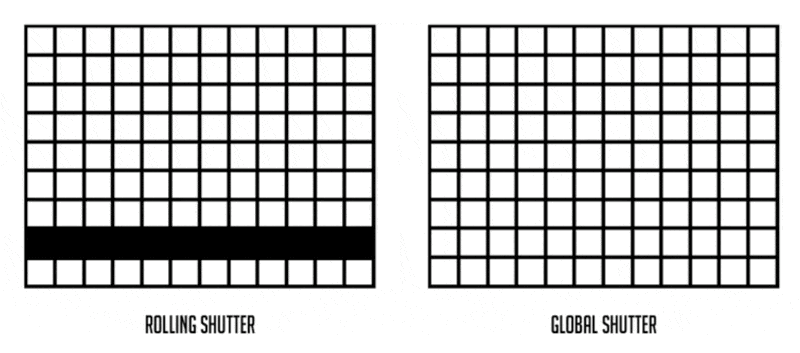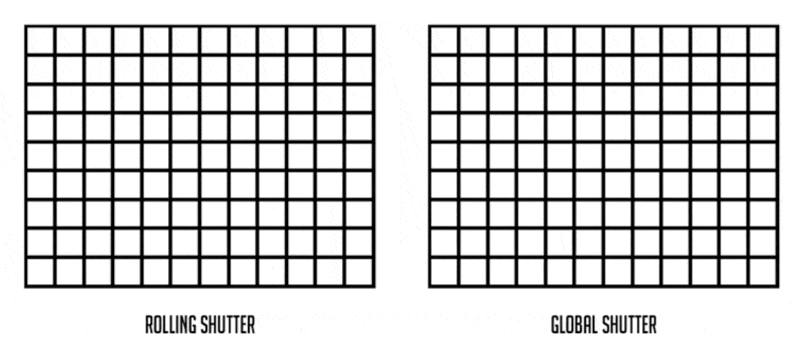
卷帘快门效应(rolling shutter effect):拍摄扇叶或螺旋桨等高速运动的物体时产生的一种图像畸变现象。
更多内容见这篇帖子。
Color Space⚓︎
色彩空间(color space):
-
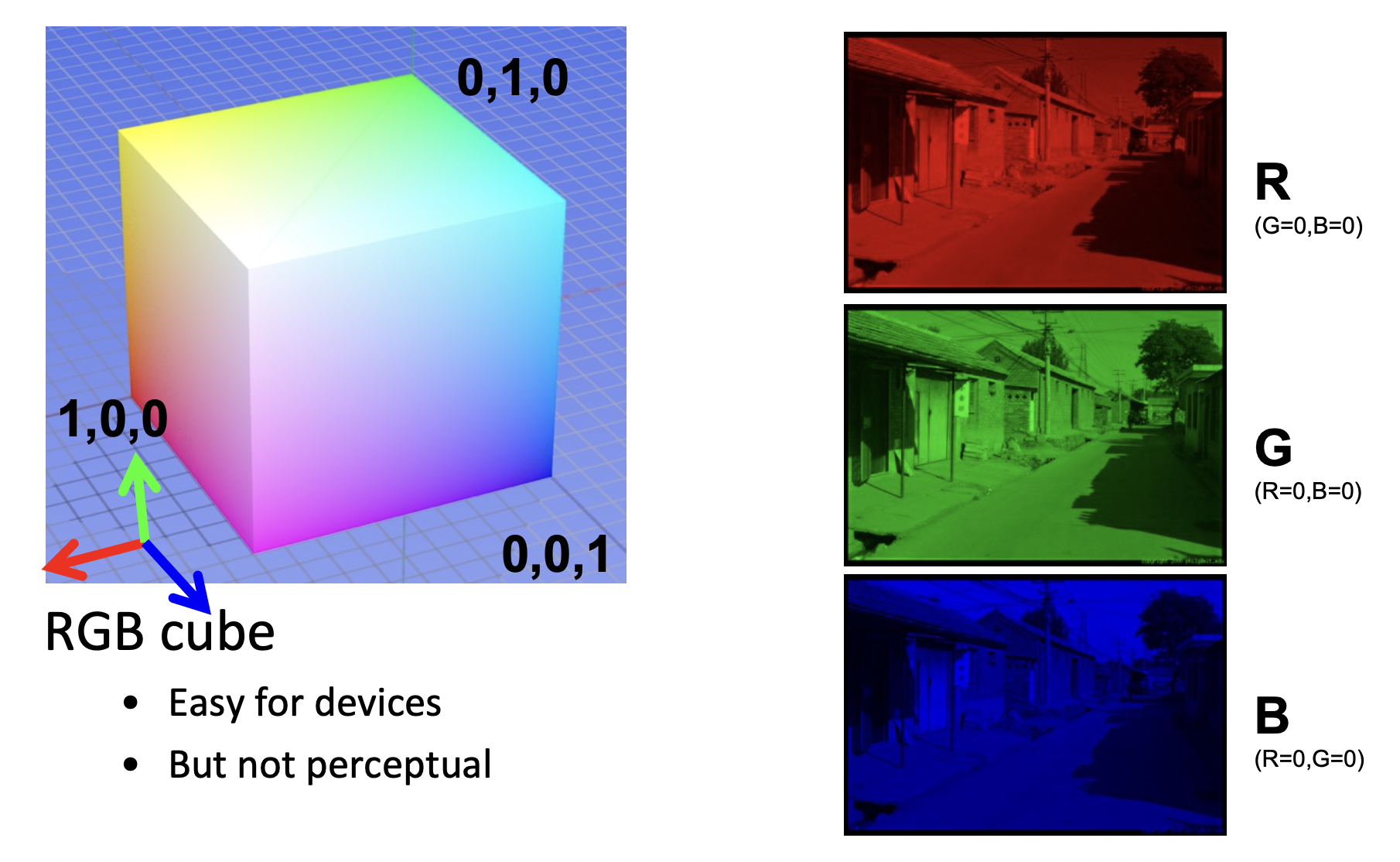
RGB
-
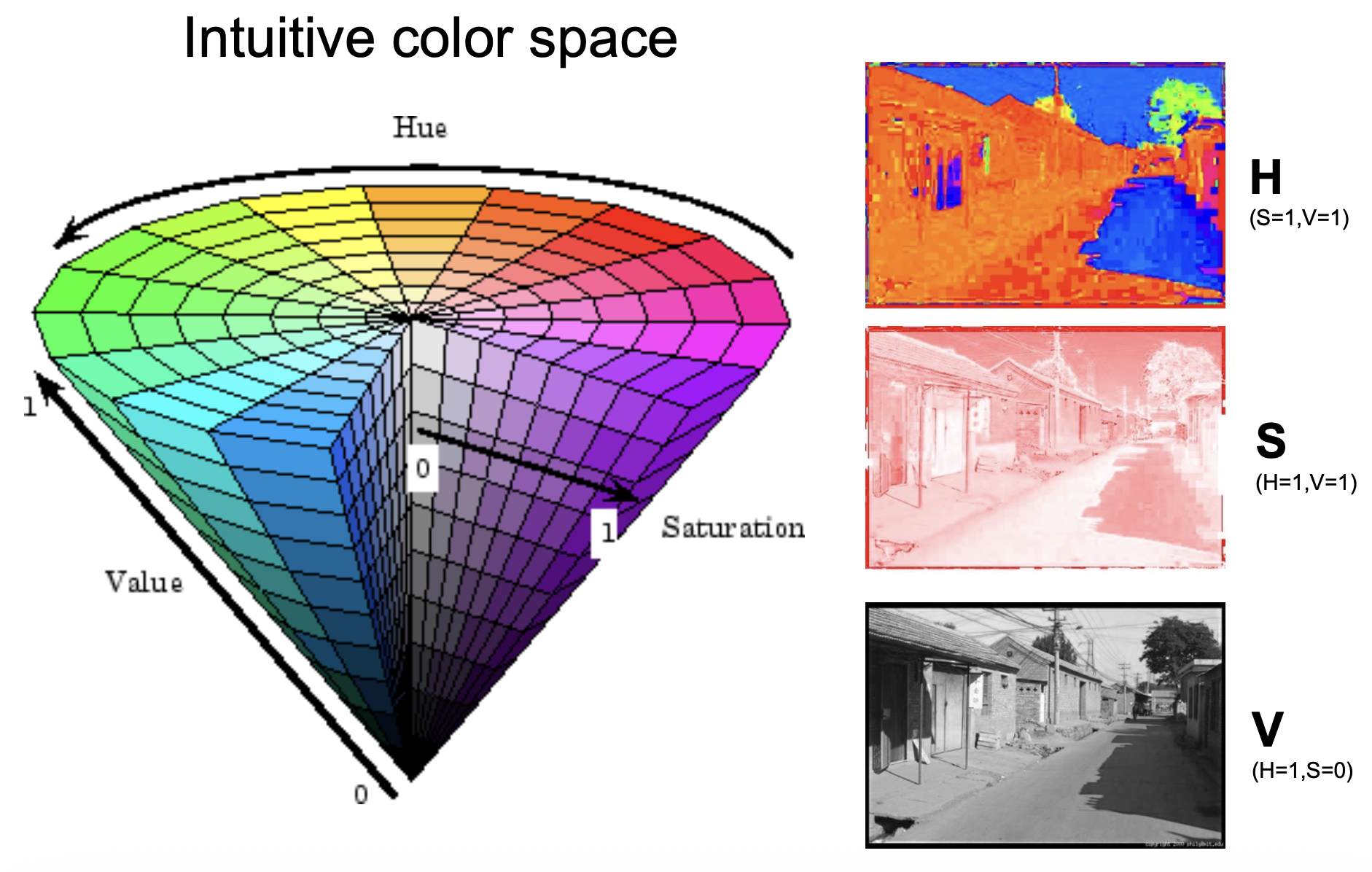
HSV
图像压缩
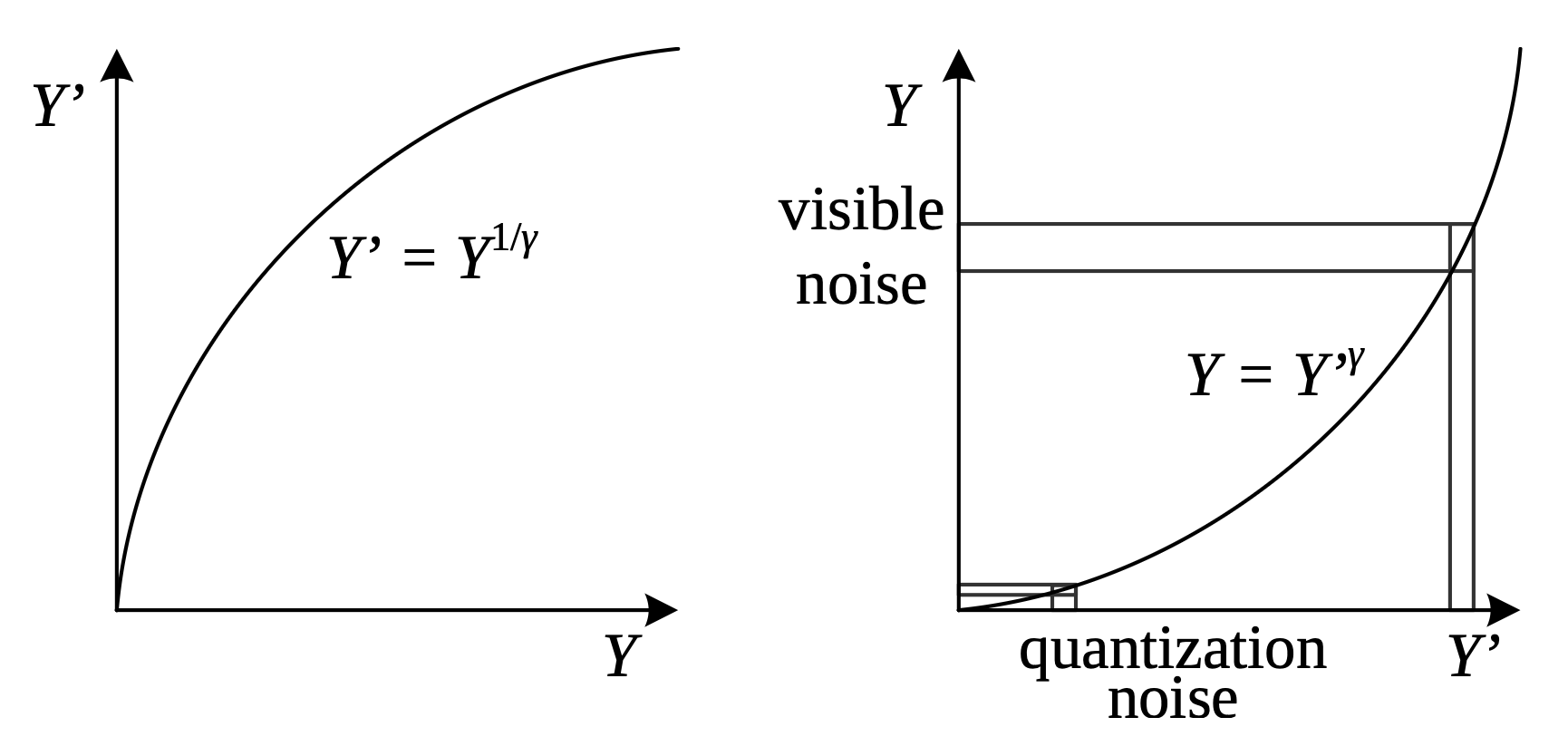
- 通常,亮度 (luminance) 的压缩保真度高于色度 (chrominance)
- 常采用基于(8×8 像素)块状的离散余弦或小波变换
- *离散余弦变换 **(discrete cosine transform, DCT) 是对自然图像主成分分析 (PCA) 的一种近似
- 系数被量化为整数,可通过哈夫曼编码存储
- 近年来,人们开发出基于深度网络的压缩算法
Images in Computer⚓︎
Python 中的图像:
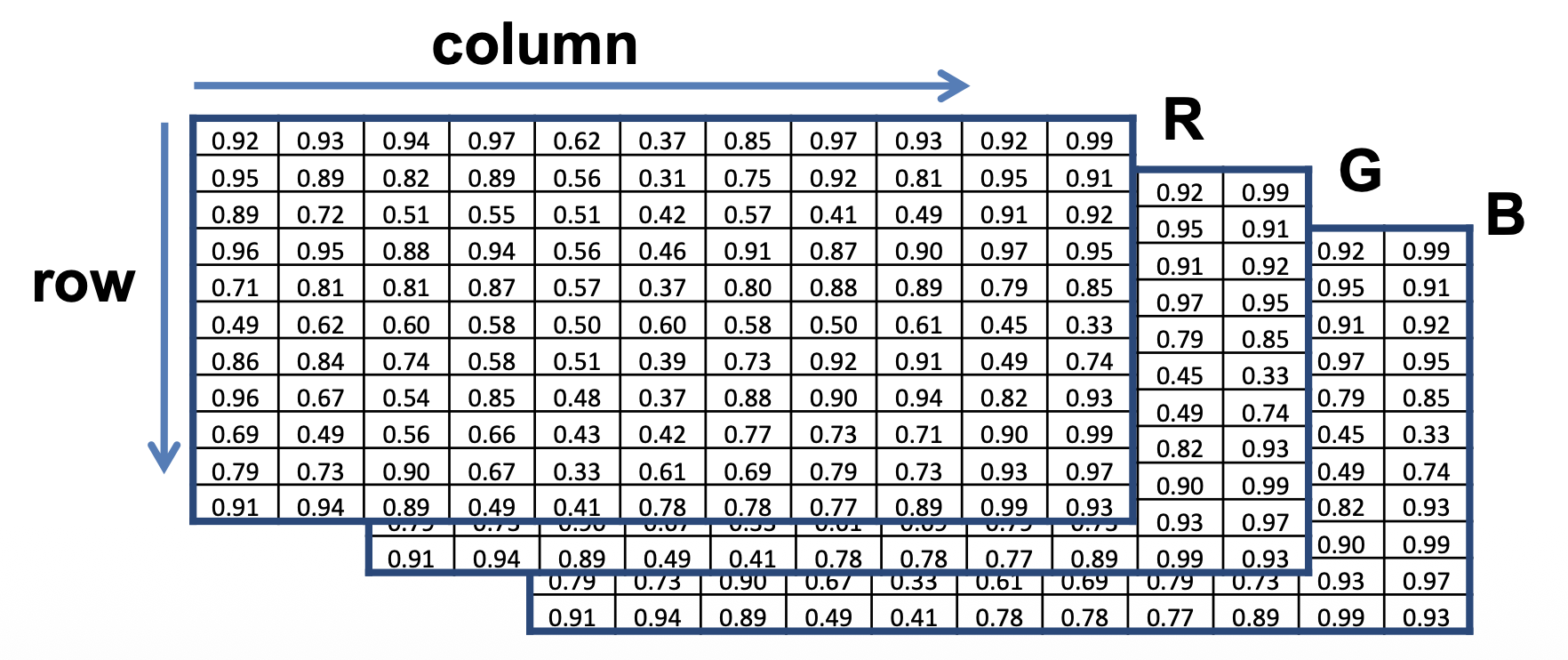
- 用矩阵表示一个图像
- 假设有一个 NxM 的图像叫做
imim(0, 0, 0):左上角的像素在 R 通道的值im(y-1, x-1, b-1):向下 y 个像素,向右 x 个像素的像素在第 b 个通道上的值im(N-1, M-1, 2):右下角的像素在 B 通道的值
Practical Color Sensing: Bayer Filter⚓︎
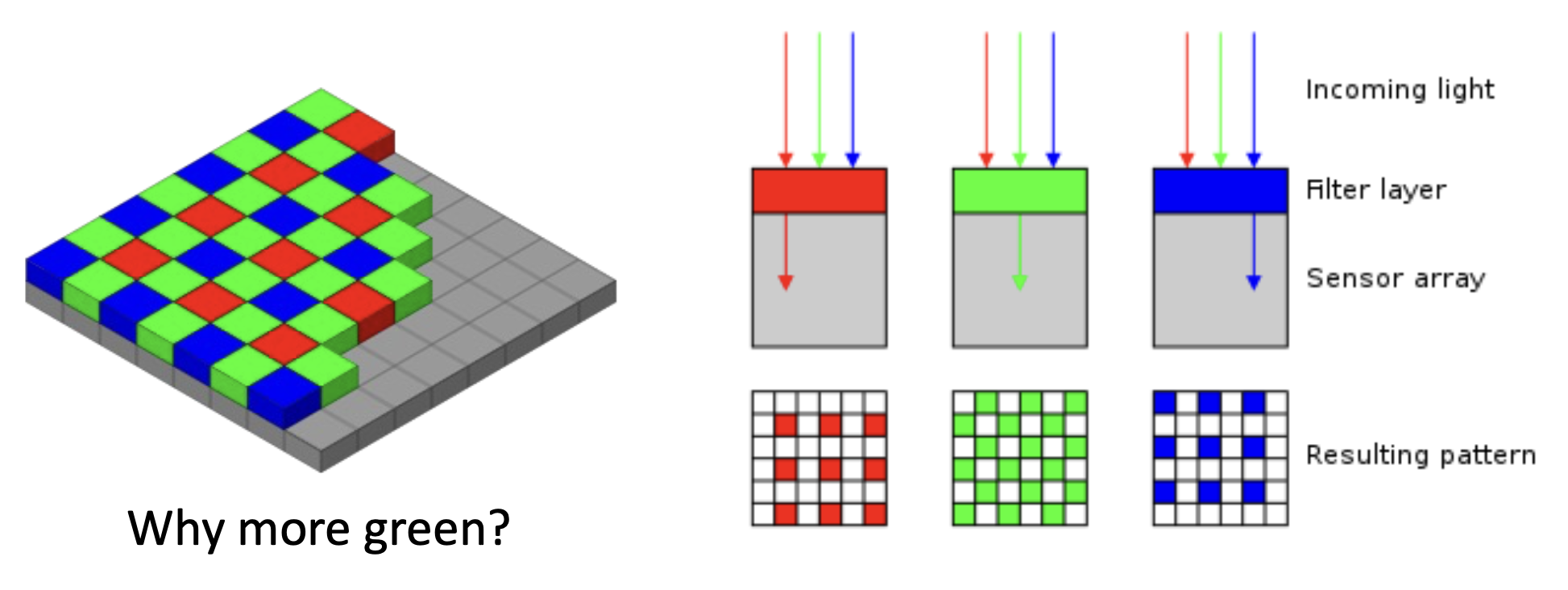
使用拜耳滤色镜(Bayer filter) 实现在单个芯片上的 RGB 感知。
可以看到,在一个 2x2 的单元中包含 1 个红色、1 个蓝色和 2 个绿色像素。之所以绿色更多些,是因为人眼对绿色(所在波长的光)更敏感,因此用更多的绿色就能让人觉得图像更明亮清晰。
Shading⚓︎
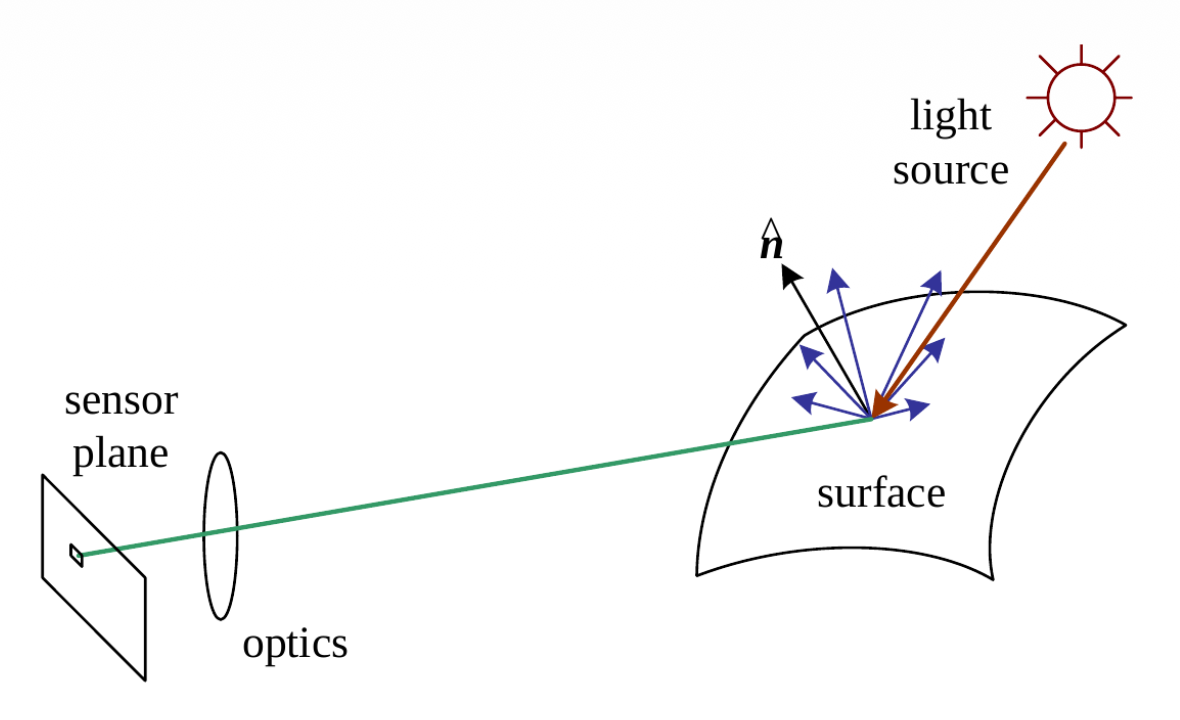
前面探讨的都是单束光线在空间中的传播,现在就从像素强度和色彩的角度来看图像是如何形成的。光线由一个或多个光源发出(emit),并在场景中物体(或介质)的表面反射(reflect) 或折射(refract)(一次或多次
后续详细内容见《计算机图形学》“着色”一节的笔记。
评论区