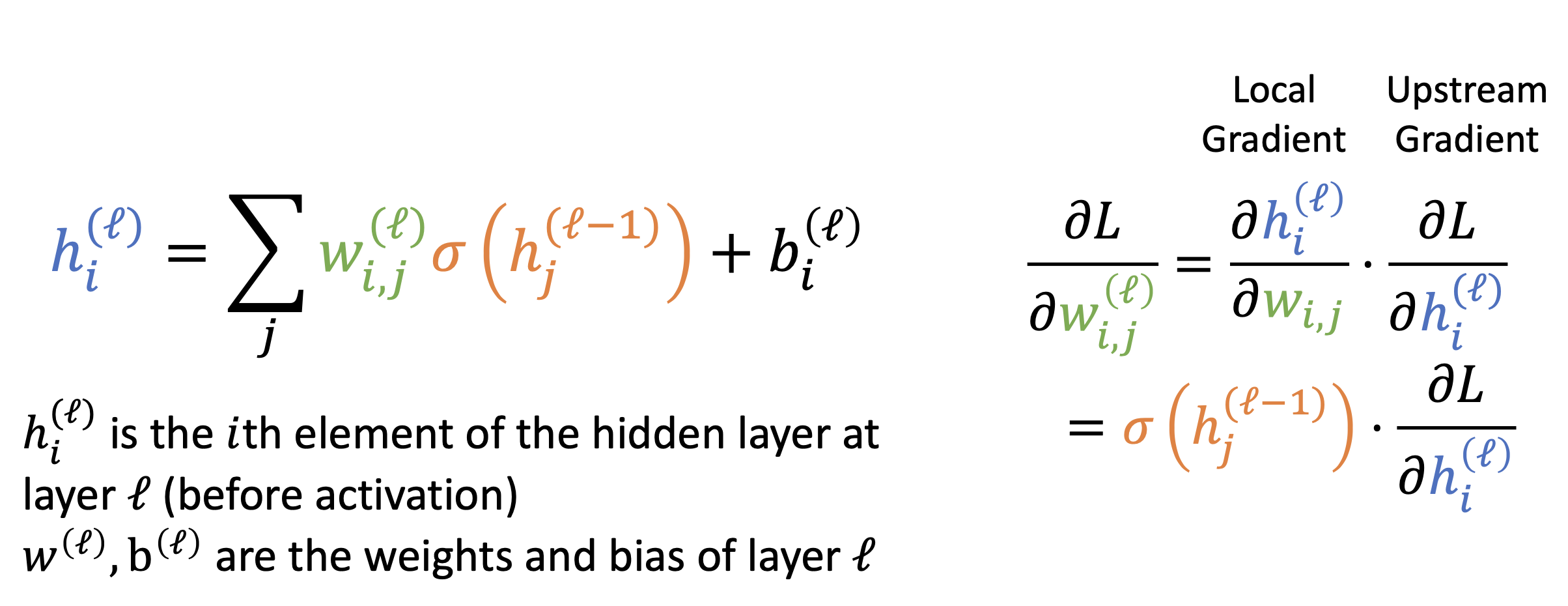CNN Architectures⚓︎
约 5263 个字 110 行代码 预计阅读时间 28 分钟
How to Build CNNs?⚓︎
Layers in CNNs⚓︎
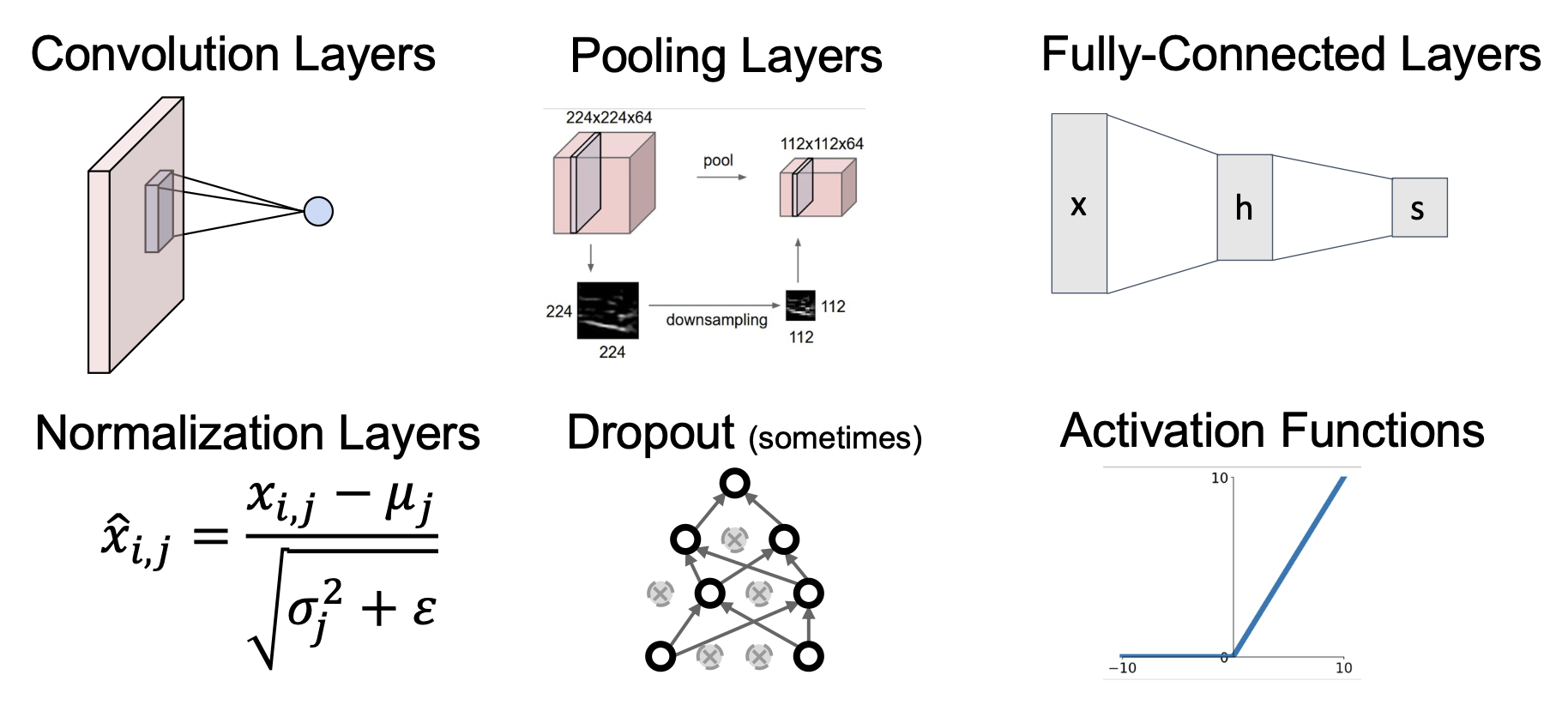
实际上,一个完整的 CNN 包含以下组成部分:
到正则化之前的部分都已经介绍过了,下面就从 Dropout 开始介绍了。
Regularization: Dropout⚓︎
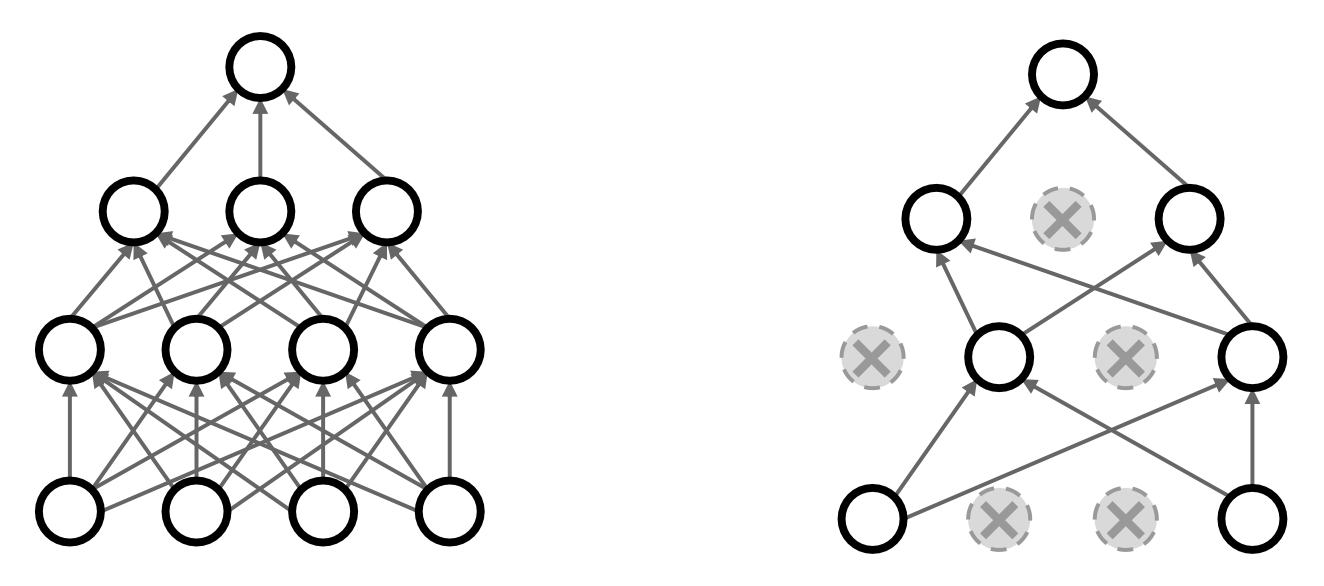
Dropout 的思路是:每一次向前传递时,随机将某些神经元置零(即去除某些神经元
为什么这样是可行的?
-
这迫使网络存在一种冗余的表示,以阻止特征的共适应(co-adaptation)(即神经元之间过度依赖)
-
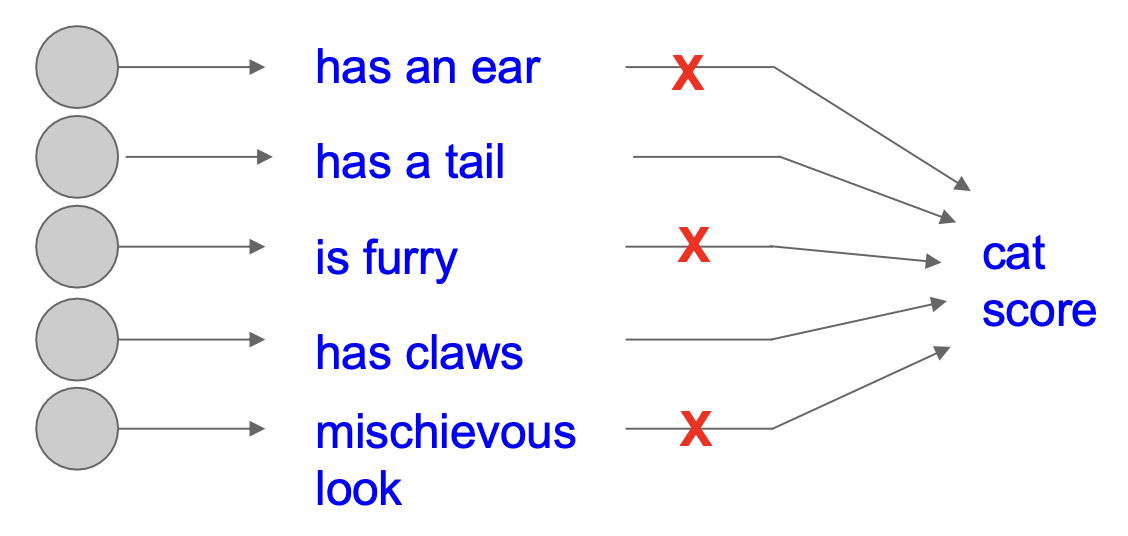
另一种解释:Dropout 是在训练一个很大的(共享参数的)模型集(ensemble),每一个二元任务对应一个模型
- 所以一个有 4096 个神经元的 FC 层就有 2 4096 ~ 10 1023 个可能的任务(而宇宙中的原子也就 ~10 82 的量级啊)
不过在测试时,所有的神经元都要求被激活,因为我们必须缩放激活值,使得对于每个神经元,测试时的输出 = 训练时的期望输出。
下面是加入 Dropout 技术后,训练和预测模型的代码:
""" Vanilla Dropout: Not recommended implementation (see notes below) """
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
""" X contains the data """
""" drop in train time """
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
# first dropout mask
U1 = np.random.rand(*H1.shape) < p
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
# second dropout mask
U2 = np.random.rand(*H2.shape) < p
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
""" scale at test time """
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
out = np.dot(W3, H2) + b3
更常用的方法是“反向 (inverse) Dropout”,即把缩放步骤也放在训练环节,测试时不用做任何改变。
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
# forward pass for example 3-layer neural network
""" drop and scale during training """
H1 = np.maximum(0, np.dot(W1, X) + b1)
# first dropout mask. Notice /p!
U1 = (np.random.rand(*H1.shape) < p) / p
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
# second dropout mask. Notice /p!
U2 = (np.random.rand(*H2.shape) < p) / p
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
""" test time is unchanged! """
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
H2 = np.maximum(0, np.dot(W2, H1) + b2) # no scaling necessary
out = np.dot(W3, H2) + b3
Activation Functions⚓︎
激活函数的目标是向模型引入非线性(non-linearity)。
Sigmoid⚓︎
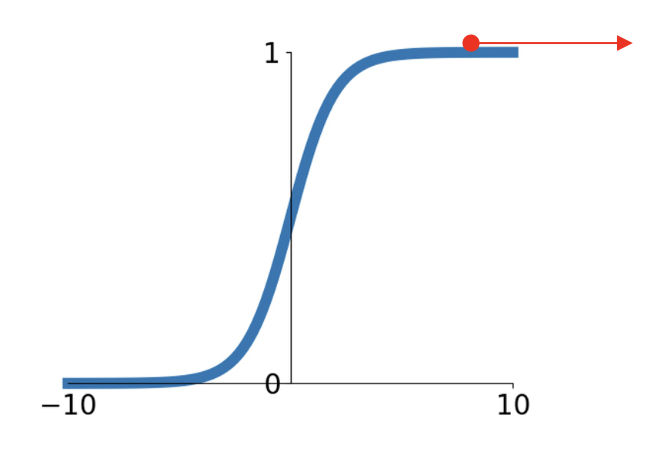
在早期,常用的激活函数是 Sigmoid:\(\sigma(x) = \dfrac{1}{1 + e^{-x}}\)。
- 将数字压缩在 [0, 1] 的范围内
- 这个激活函数在过去很流行,因为它对神经元饱和的“发射速率”(saturating "firing rate") 有一个不错的解释
-
关键问题:
- 绝对值大的正数或负数值会“杀死”梯度 + 多层级的 Sigmoid -> 梯度会变得越来越小(最严重的问题)
-
Sigmoid 的输出并不是以 0 为中心的(输出都是正数)
-
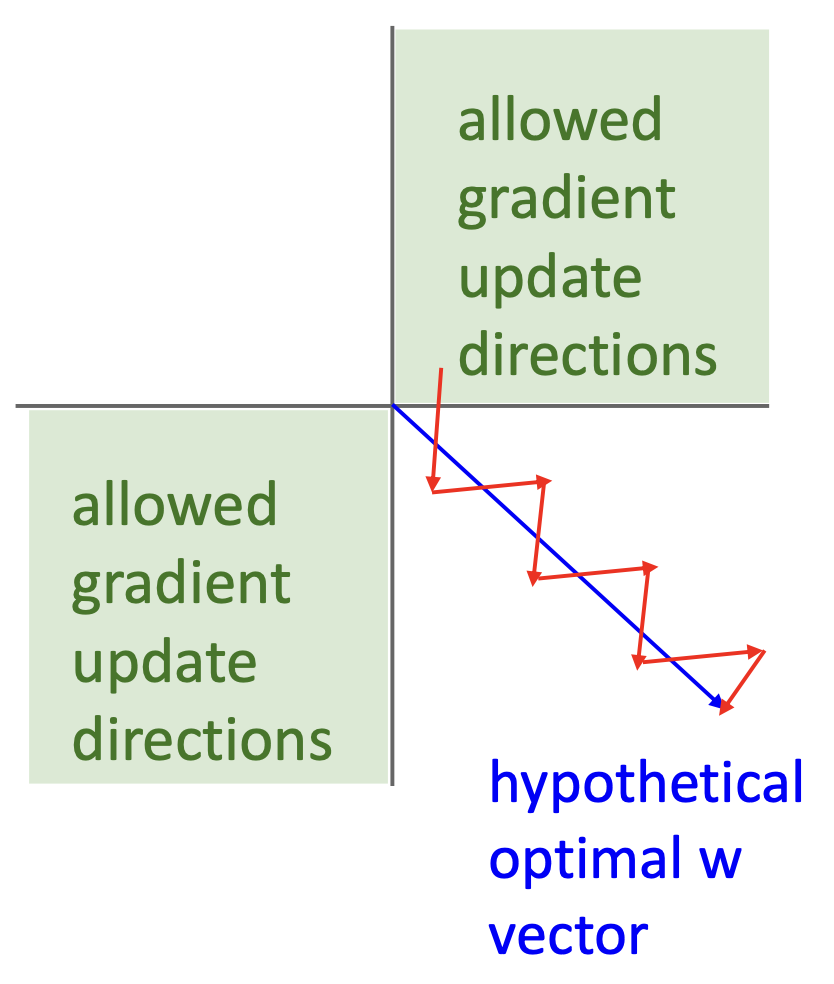
可以看到,所有 \(w^{(l)}_{i, j}\) 的符号和上游梯度 \(\dfrac{\partial L}{\partial h_i^{(l)}}\),这导致 \(w\) 的行上的梯度只能指向某些方向;需要锯齿形 (zigzag) 的移动才能朝其他方向前进
-
实践上这个问题并不是特别糟糕
- 仅对单个样例有影响,可采取小批量 (minibatch) 解决
- 也可用 BatchNorm 来避免这一问题
-
-
指数计算开销有些大
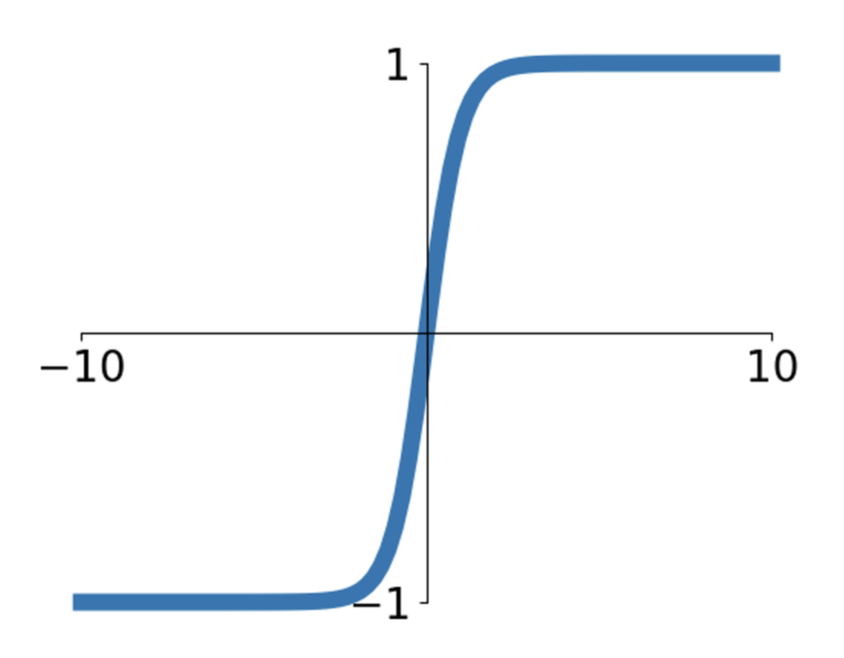
Tanh⚓︎
一种改进措施是采用 Tanh 函数:
- 将范围压至 [-1, 1]
- 优点:以 0 为中心
- 缺点:仍然没能解决梯度在两端被“杀死”的问题
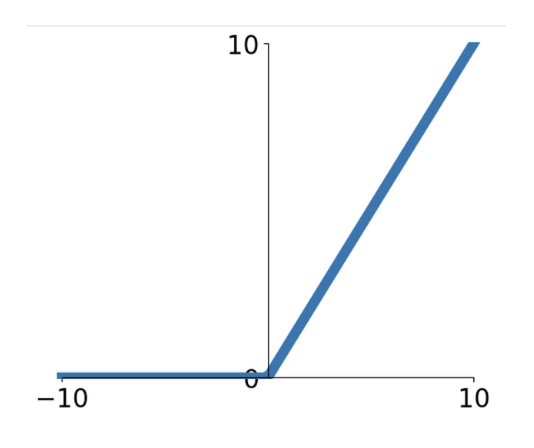
ReLU⚓︎
大概从 AlexNet 出世后,最流行的激活函数莫过于 ReLU(校正线性单元 (rectified linear unit))\(f(x) = \max(0, x)\)。
- 优点:
- 不会在正数区域饱和
- 计算非常高效
- 实践上比 Sigmoid 收敛更快
- 缺点
- 输出不以 0 为中心
-
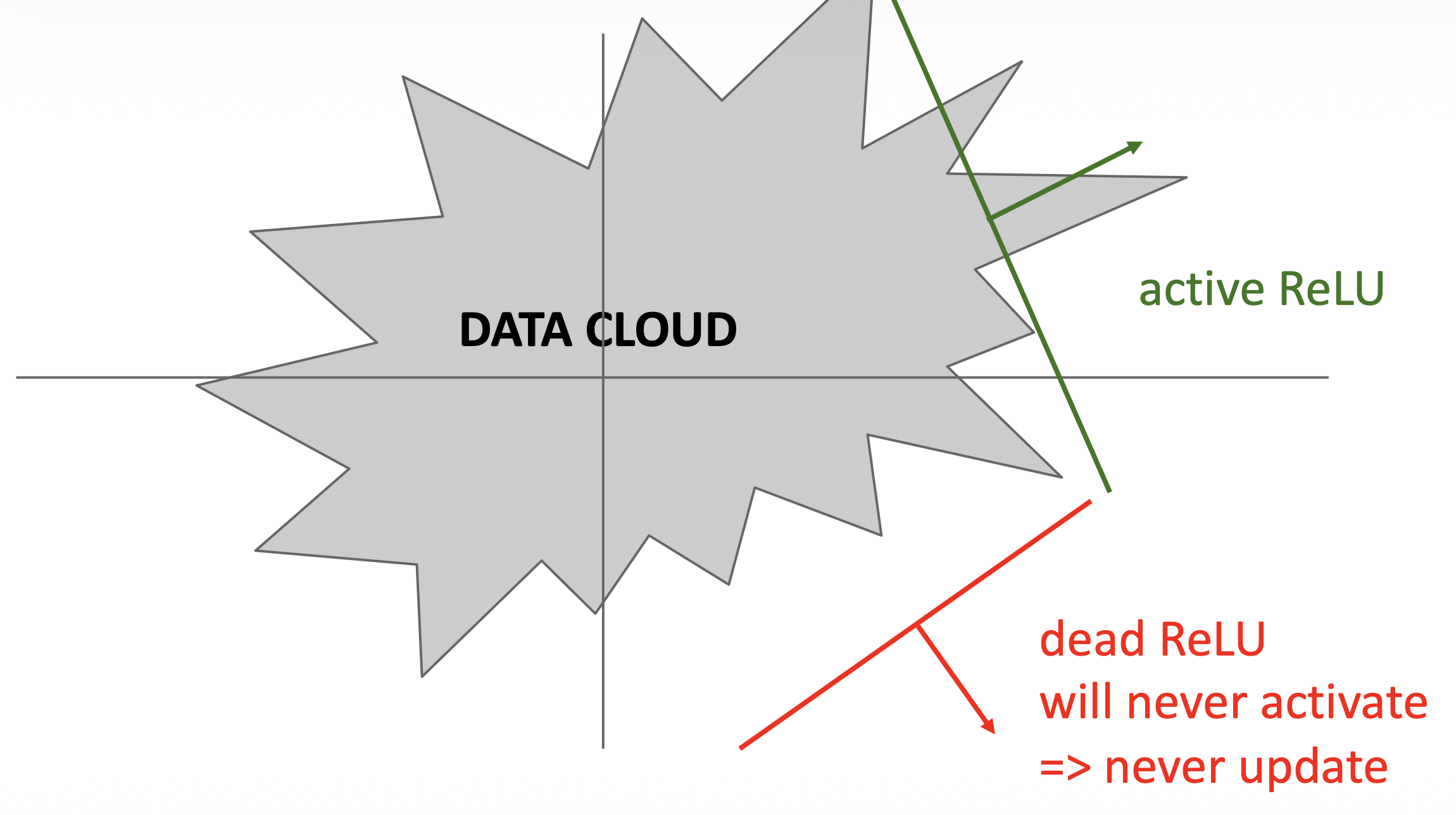
令人不爽的是,ReLU 在 < 0 的时候就寄了
- 有时可用较小的正偏移量(比如 0.01)来初始化 ReLU 神经元
Leaky ReLU and PReLU⚓︎
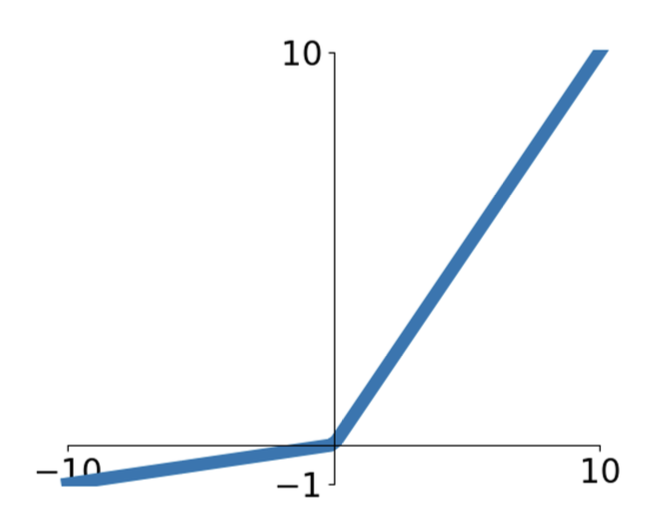
ReLU 的一种变体是 Leaky ReLU \(f(x) = \max(\alpha x, x)\),其中 \(\alpha\) 是超参数,通常设置 \(\alpha = 0.1\)
- 不会饱和
- 计算高效
- 实际上比 Sigmoid / Tanh 收敛得快的多
- 不会像 ReLU 那样在 < 0 时“寄掉”
一种很类似的函数是参数化 (parametric) ReLU(PReLU
ELU and SELU⚓︎
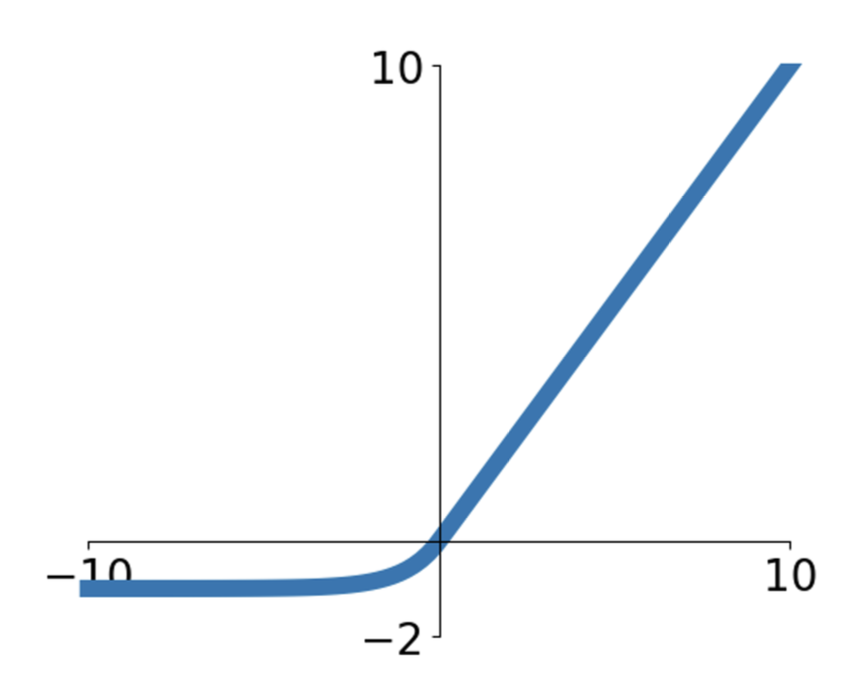
另一种和 ReLU 类似的是 ELU(指数线性单元 (exponential linear unit))\(f(x) = \begin{cases}x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \le 0\end{cases}\)(默认情况下 \(\alpha = 1\))
- 优点:
- 所有 ReLU 的优点
- 更接近 0 均值输出
- 与 Leaky ReLU 相比,增加了负饱和状态下对噪声的鲁棒性
- 缺点:涉及到指数计算
基于 ELU 的一个变体是 SELU(缩放指数线性单元 (scaled exponential linear unit))
其中 \(\alpha = 1.6732632423543772848170429916717, \lambda = 1.0507009873554804934193349852946\)
-
优点:
- 缩放版本的 ELU,在更深的网络上表现更好
- “自归一化(self-normalizing)”的性质,能够在没有 BatchNorm 的情况下训练深层的 SELU 网络
-
缺点:这玩意儿的推导在论文附录占据了 91 页!
GELU⚓︎
最近几年比较流行的一种激活函数是 GELU(高斯误差线性单元 (Gaussian error linear unit)
思路:
- 随机乘以 0 或 1;大值更可能乘以 1,小值更可能乘以 0(数据依赖的 Dropout)
-
取随机结果的期望
-
优点:
- 在 0 附近有非常好的行为
- 其平滑性有利于训练
- 因此在基于 Transformer 的模型中十分常见(BERT、GPT、ViT)
- 缺点:
- 计算开销相比 ReLU 更高
- 绝对值很大的负数仍然存在梯度趋近于 0 的情况
Summary⚓︎
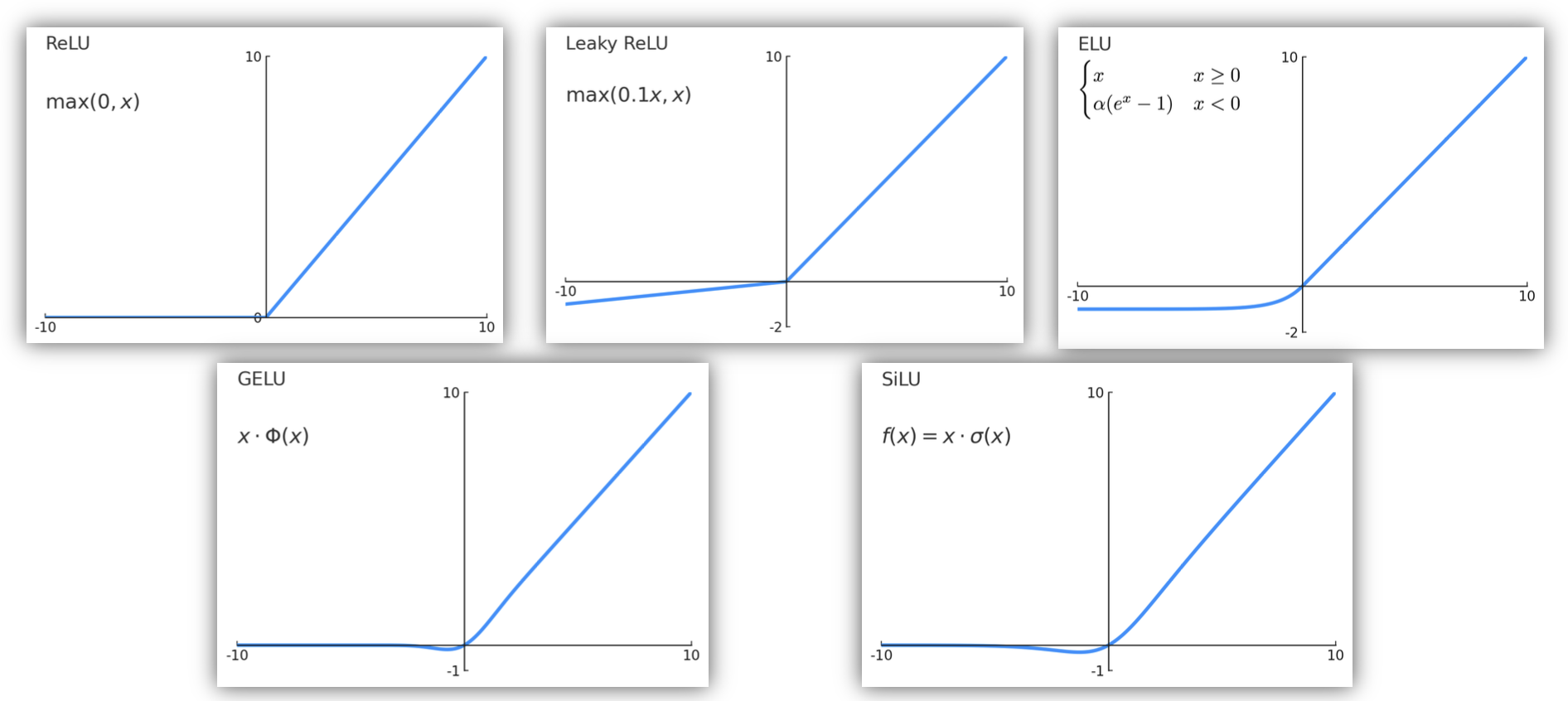
激活函数可不止这几种——下面列举了更多的激活函数:
在 CNNs 中,激活函数通常放置在线性算子(比如前馈 / 线性层,卷积层等)之后。
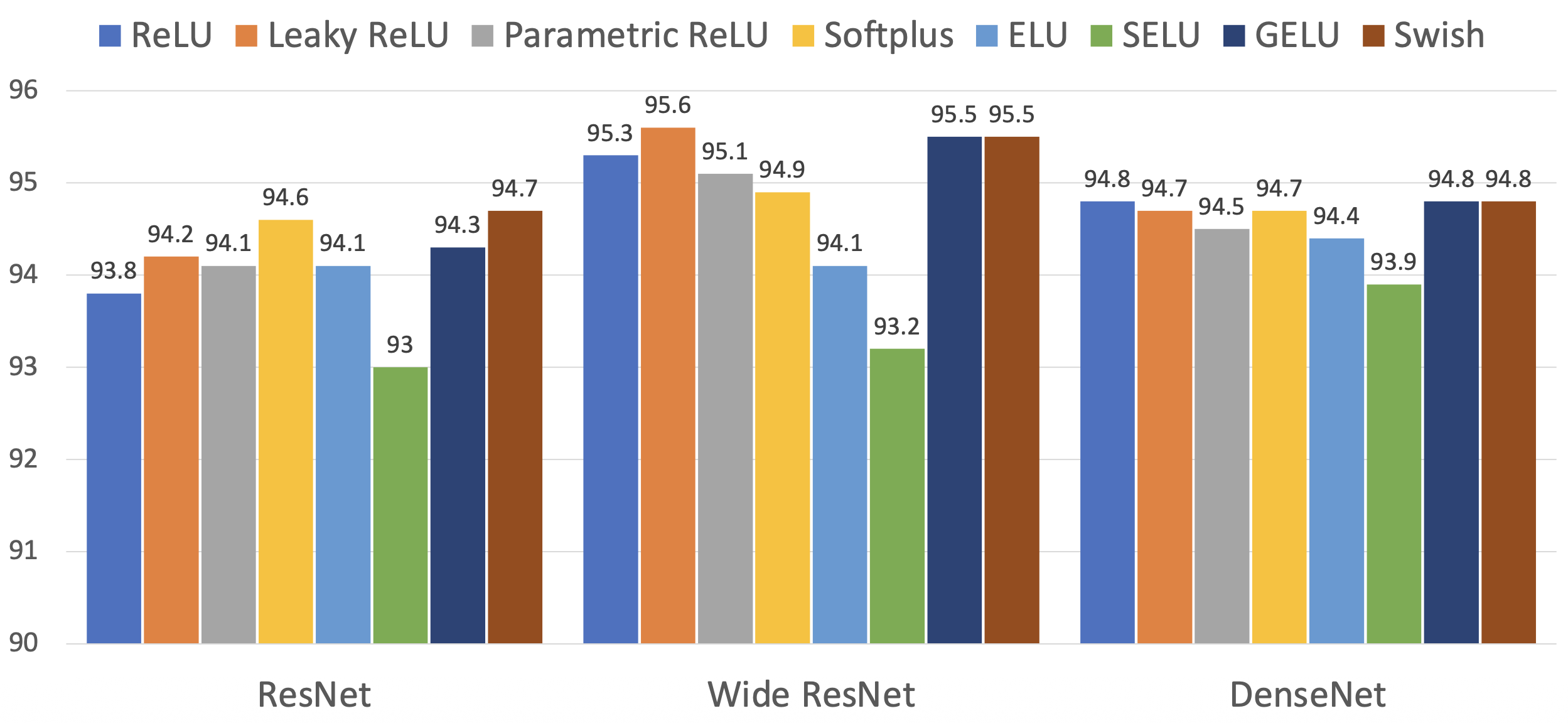
各种激活函数在 CIFAR10 上的准确率
总结
- 不要想太多,就用 ReLU 好了
- 如果需要压榨那最后的 0.1% 的精度,再尝试用 Leaky ReLU / ELU / SELU / GELU
- 不要使用 Sigmoid 或 Tanh
- 一些(非常)最近的结构使用 GeLU 代替 ReLU,但收益微乎其微
CNN Architecture⚓︎
下图展示了各年 ImageNet 大规模视觉识别挑战赛(ILSVRC)获胜模型的层数(折线图)和误差率(柱形图
AlexNet⚓︎
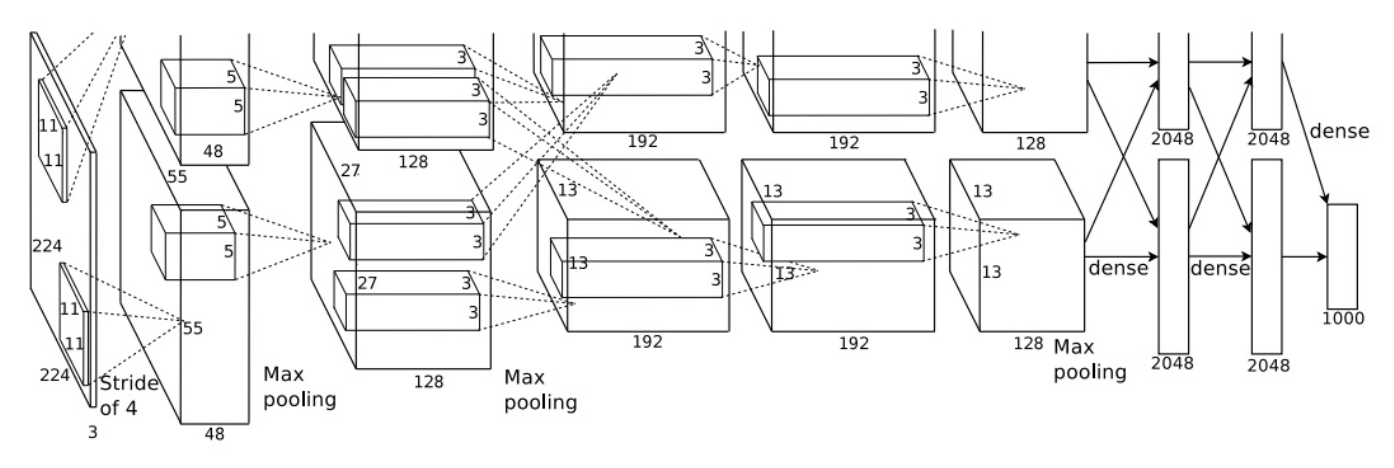
- 输入规模为 227x227
- 5 个卷积层
- 最大池化
- 3 个全连接层
- ReLU 非线性
- 采用局部响应归一化(local response normalization) 技术(不过现在已经被淘汰了)
- 在 2 张 GTX 580 GPU 上训练;由于每个显卡只有 3 GB 内存,所以模型被划分到 2 个 GPU 上
下面给出 AlexNet 的架构图:
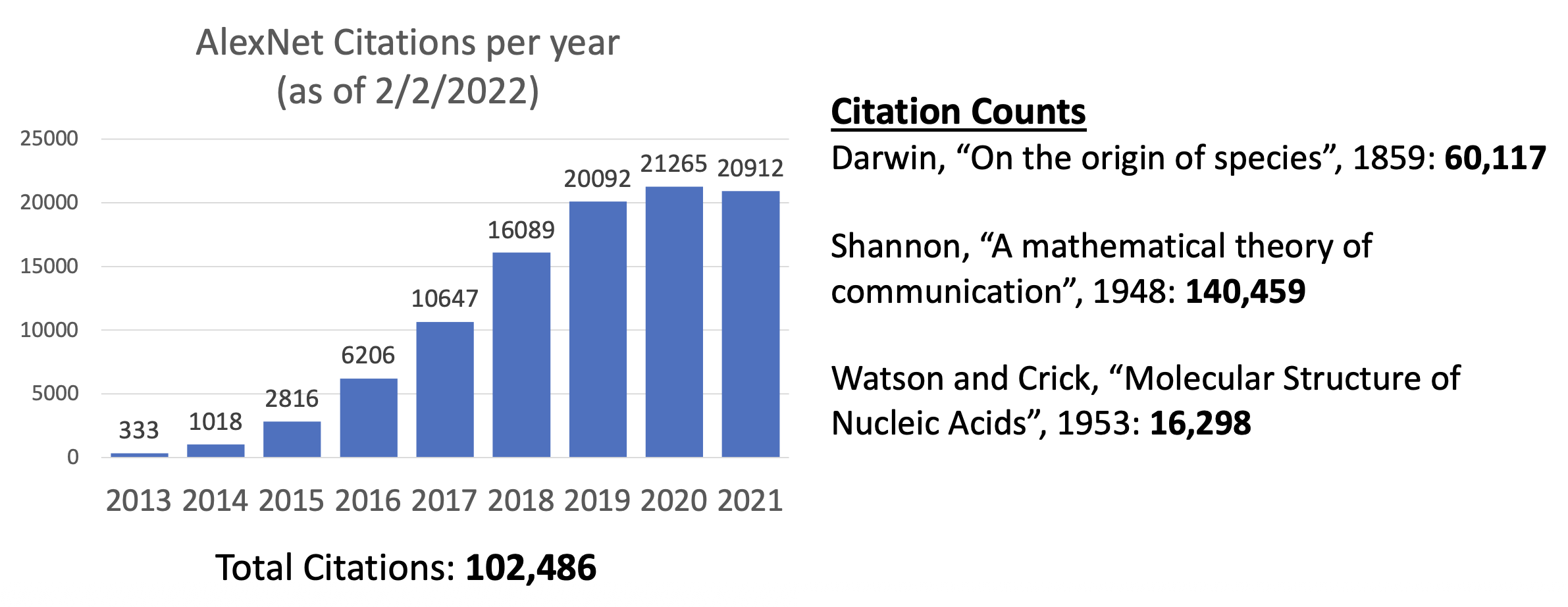
AlexNet 的超绝影响力:
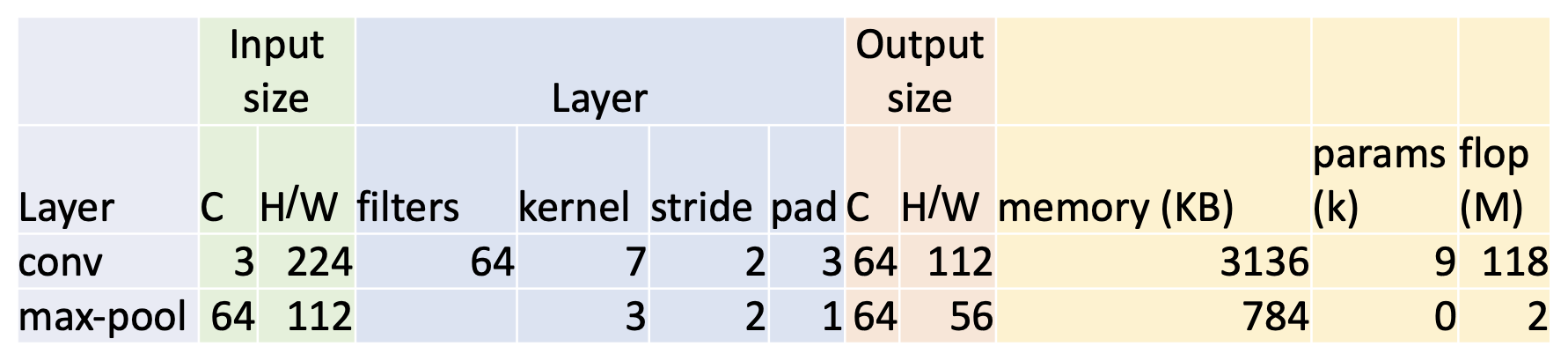
AlexNet 各层参数列表:
-
conv1
- 输出通道数 C' = 滤波器数
- 输出宽 / 高 W'(H') = (W - K + 2P) / S + 1 = (227 - 11 + 2 * 2) / 4 + 1 = 56
-
内存 = 200,704 * 4 / 1024 = 784 B
- 输出元素数 = C' * W' * H' = 64 * 56 * 56 = 200,704
- 每个元素 4B(32 位浮点数)
-
权重数 = 23,296
- 权重形状 = C out * C in * K * K = 64 * 3 * 11 * 11
- 偏移形状 = C out = 64
-
浮点数运算次数 (flop)(乘法 + 加法)= 输出元素数 * 每元素的运算 = (C out * H' * W') * (C in * K * K) = 72,855,552
-
pool1
- 输出通道数 = 输入通道数 = 64
- W' = float((W - K) / S + 1) = 27
-
内存 = C out * H' * W' * 4 / 1024 = 182.25
- 输出元素数 = C out * H' * W'
- 每个元素 4B(32 位浮点数)
-
池化层没有可学习的参数
- 浮点数运算次数 = 输出位置数 * 每个输出位置的运算 = (C out * H' * W') * (K * K) = 419,904 = 0.4 MFLOP
-
flatten
- 输出大小 = C in * H * W = 9216
-
fc6
- 参数个数 = C in * C out + C out = 37,725,832
- 浮点数运算次数 = C in * C out = 37,748,736
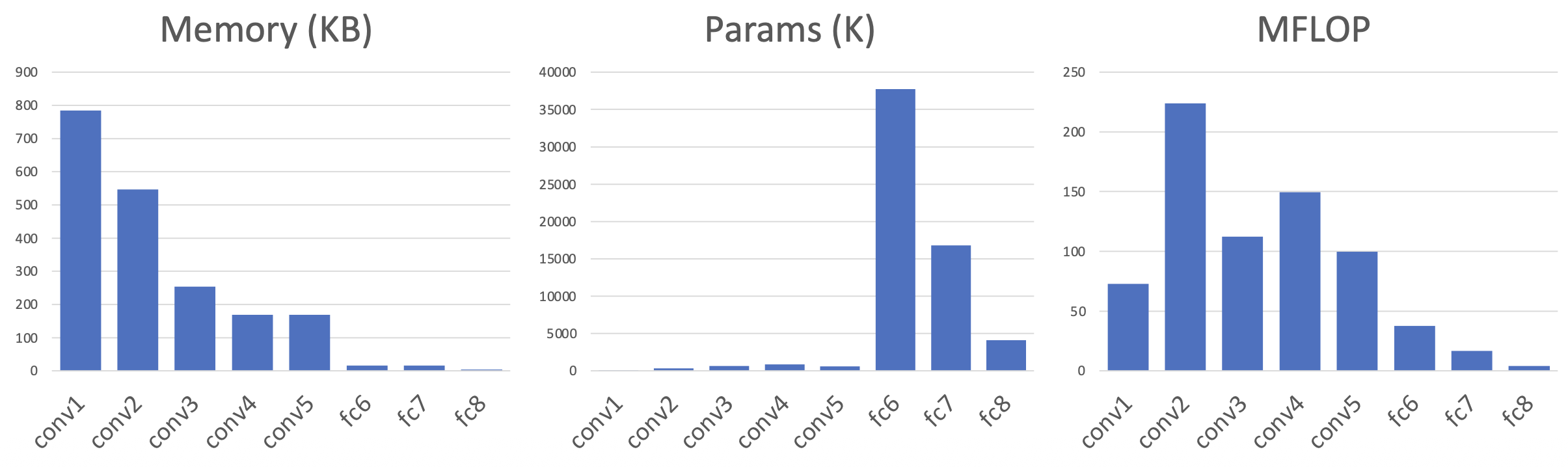
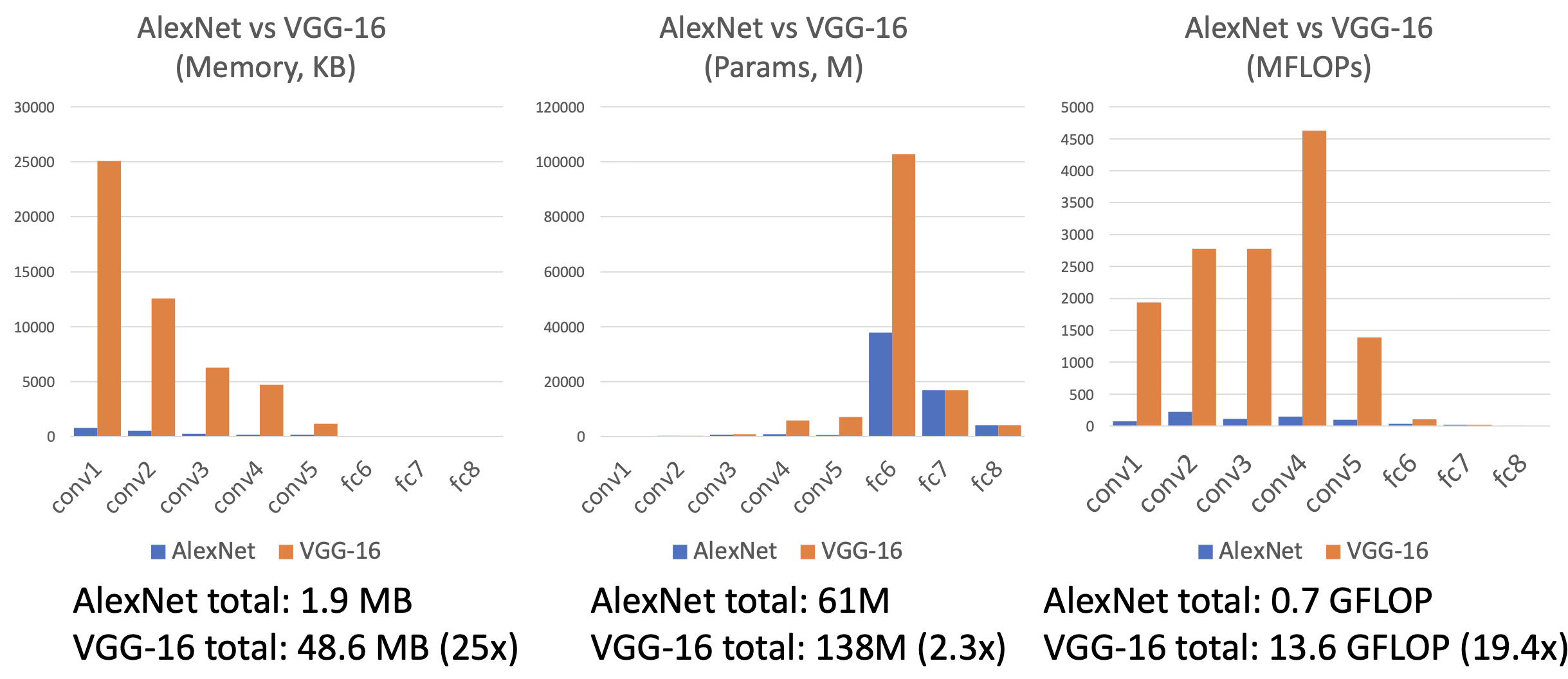
表格中蓝色和绿色列通过不断试错得到;而黄色列的参数则有一些有趣的规律:
- 大多数内存用在前面的卷积层上
- 几乎所有的参数都在全连接层上
- 大多数的浮点运算发生在卷积层中
ZFNet⚓︎
ZFNet 是一个更大的 AlexNet,和 AlexNet 的区别在于:
- CONV1:滤波器大小从(11x11,步幅 4)变为(7x7,步幅 2)
- CONV3, 4, 5:滤波器数从(384,384,256)变到(512,1024,512)
包含更多的试错 ...
通过以上努力,误差率从 16.4% 降至 11.7%
VGGNet⚓︎
相比前两年的 AlexNet,VGGNet 的滤波器更小,但是网络更深。
- 8 层(AlexNet)-> 16-19 层(VGGNet)
- 卷积核的大小统一为 3x3,步幅为 1,填充宽为 1;最大池化核大小统一为 2x2,步幅为 2
- 误差率从前一年的 11.7% 降至 7.3%
- 网络包含 5 个卷积阶段:
- conv-conv-pool
- conv-conv-pool
- conv-conv-pool
- conv-conv-conv-[conv]-pool
- conv-conv-conv-[conv]-pool
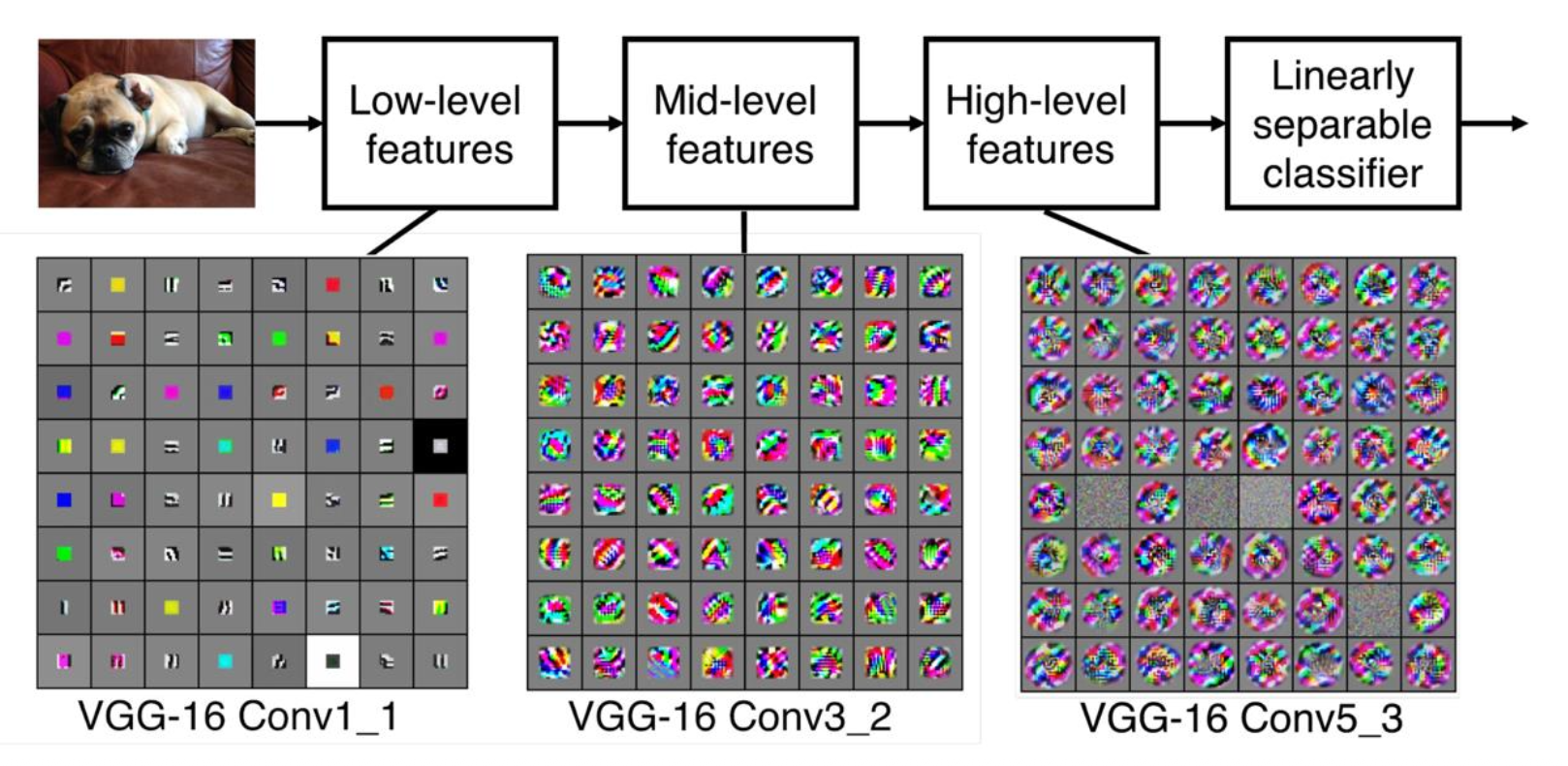
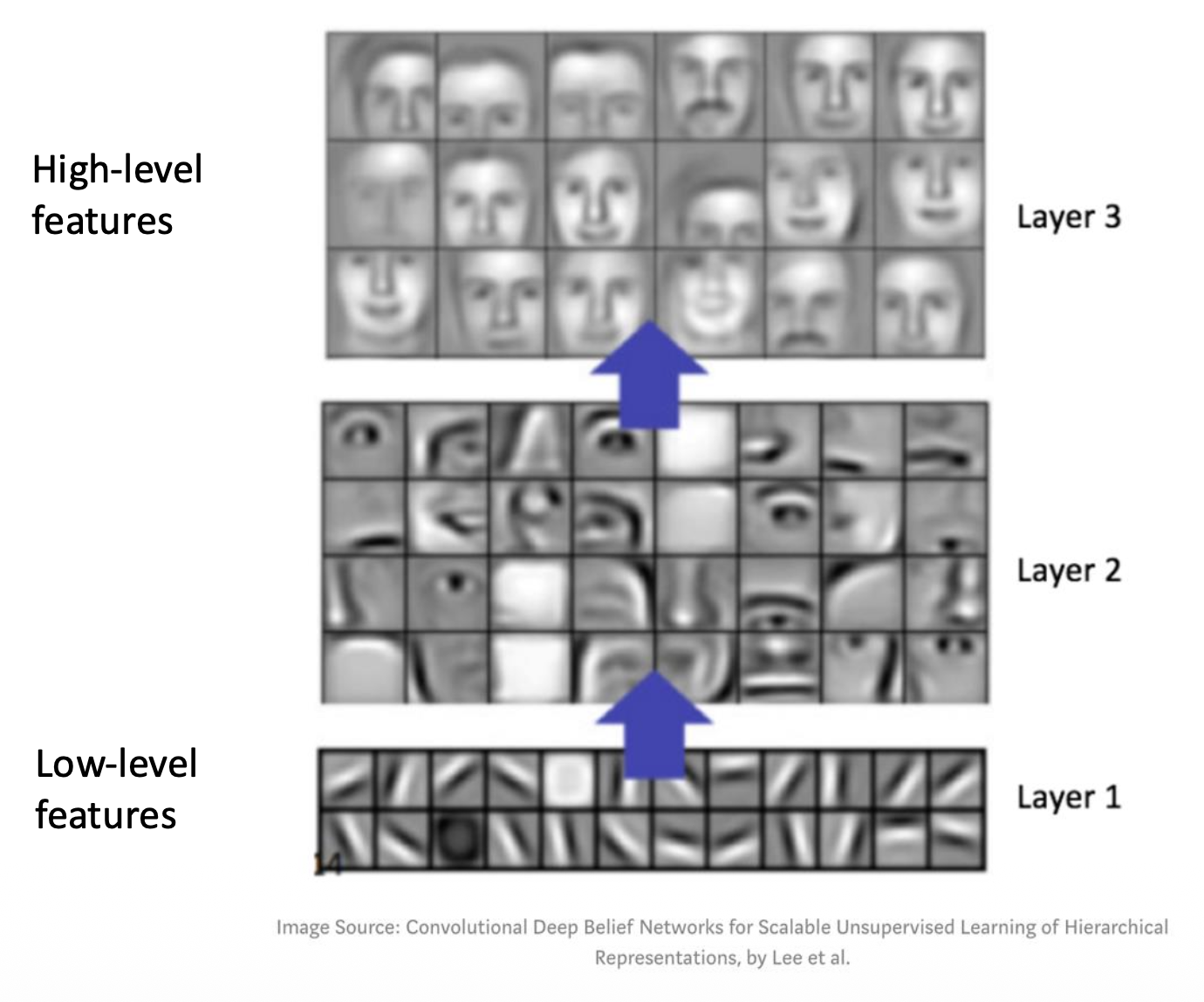
滤波器作为特征提取器:
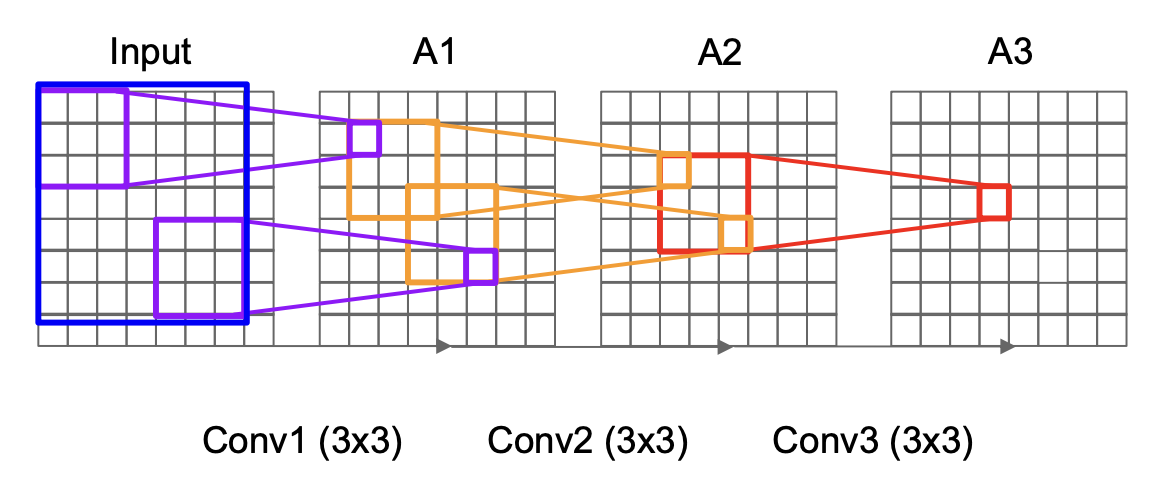
为何能使用更小的滤波器呢?假如有 3 个 3x3 的滤波器(步幅为 1
- 也就是说,只要堆叠 3 个 3x3 的滤波器,就对应一个有相同的有效感受野的 7x7 的滤波器
- 但同时更深,意味着更多的非线性
- 并且用到的参数更少(假设每层通道数为 C
) :3 * (32C2) v.s. 72C2
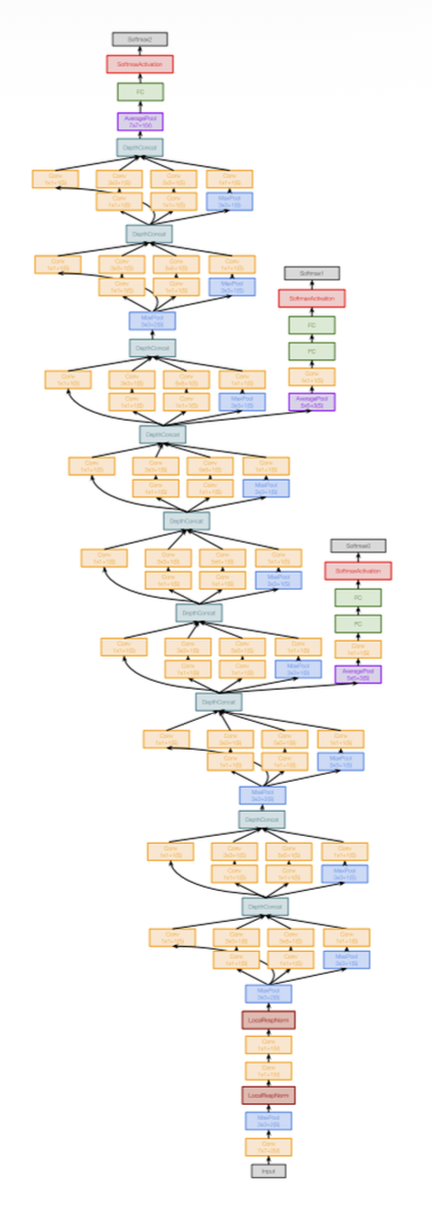
GoogLeNet⚓︎
GoogLeNet 有以下特点:
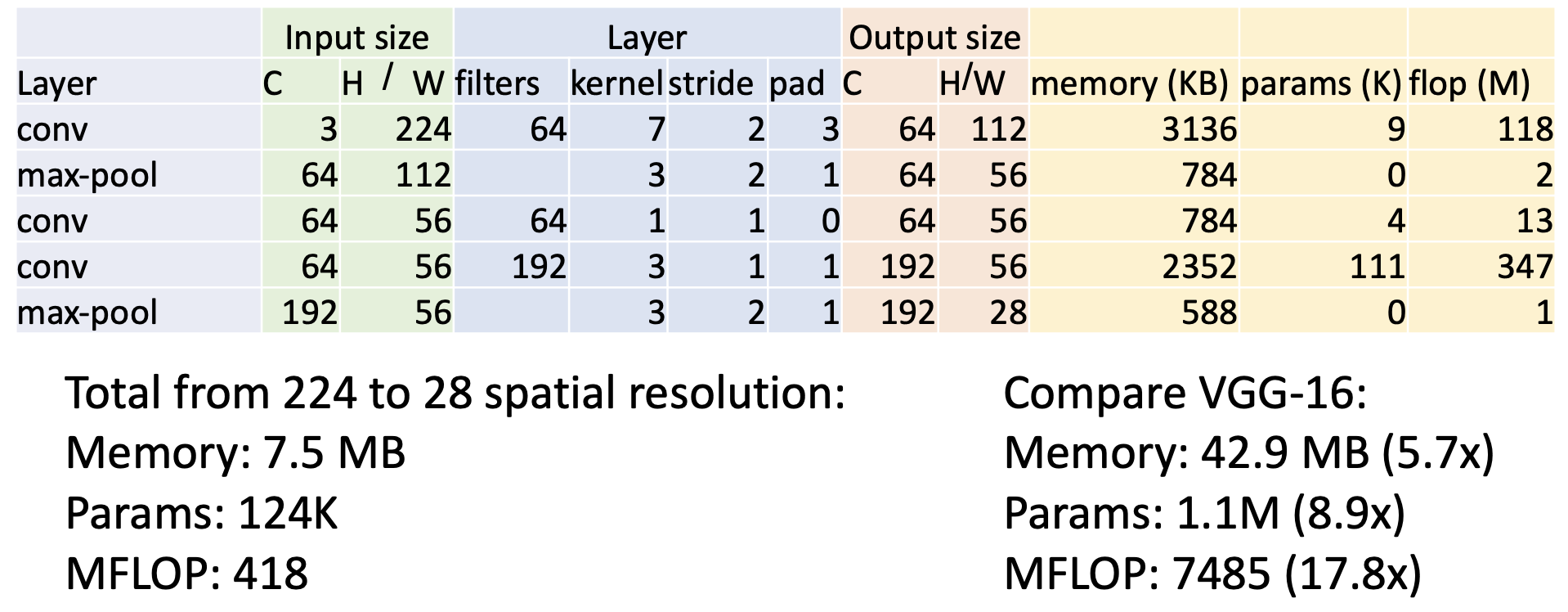
- 注重效率:减少参数量、内存使用和计算量
-
在开始时,主干网络(stem network) 会积极地 (aggressively) 对输入进行降采样(注意到 VGG-16 的大部分计算发生在开始阶段)
-
起始模块(inception module):使用并行分支加载单元
- 局部结构在网络内重复出现多次
- 在开销较大的卷积操作之前使用 1x1 “瓶颈 (bottleneck)”层来减少通道维度
-
全局平均池化(global average pooling):网络末端没有用到大型的全连接层,而是使用全局平均池化来折叠 (collapse) 空间维度,并使用一个线性层来生成类别得分(而 VGG-16 的大多数参数集中在全连接层中)
-
辅助分类器(auxiliary classifiers)
- 使用网络末尾的损失进行训练效果不佳:网络太深,梯度传播不顺畅
- 一种 hack 手段是:在网络的几个中间点附加一些“辅助分类器”,也尝试对图像进行分类并接收损失
- GoogLeNet 在批量归一化之前没,所以有了 BatchNorm 的话就不再需要使用这个技巧
ResNet⚓︎
从 ResNet 开始,模型从深度上有了革命性的突破——从前一年的 22 层,到 ResNet 的 152 层。
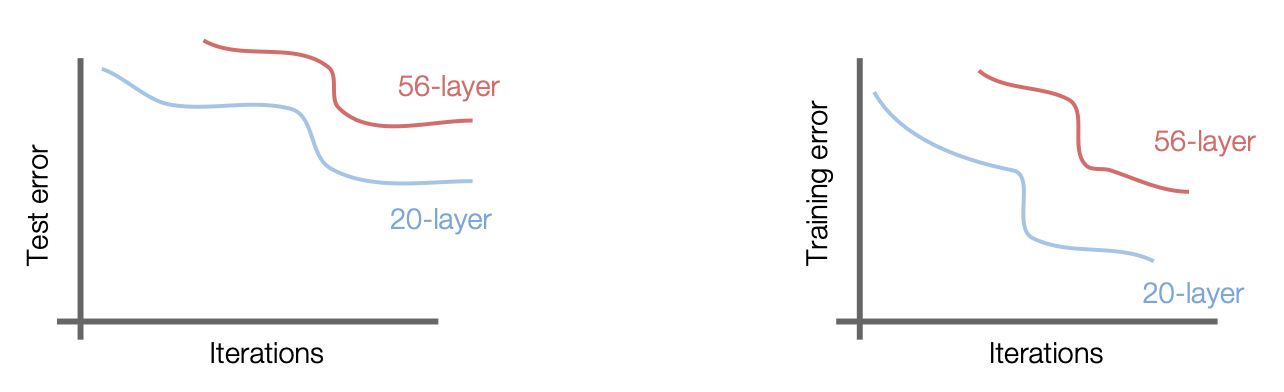
以前,人们通常认为模型越深往往意味着更糟糕的表现。如果只是简单地向 CNN 堆叠更深的层,如下所示,无论是在测试还是在训练时,56 层的网络比 22 层表现更糟;但这也意味着不是由过拟合导致的问题(不然的话 56 层的表现在训练时应和 22 层的差不多
事实上,对于较深模型,其表示能力比较浅模型强大得多(因为有更多的参数
我们提出这样一个假设:此问题是优化问题;更深的模型意味着更难优化。那么如何让较深模型表现得至少和较浅模型一样好呢?一种通过构造的解决方法是复制较浅模型中学习到的层,并将额外的层设置为恒等映射(identity mapping)。
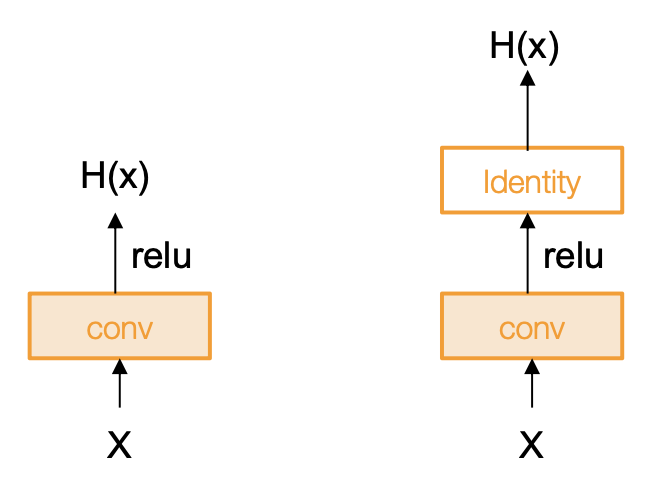
而 ResNet 给出的方案是:使用网络层来拟合残差映射(residual mapping),而不是直接尝试拟合一个期望的底层映射。
- 恒等映射:\(H(x) = x \text{ if } F(x) = 0\)
- 使用层来拟合残差 \(F(x) = H(x) - x\) 而非直接使用 \(H(x)\)
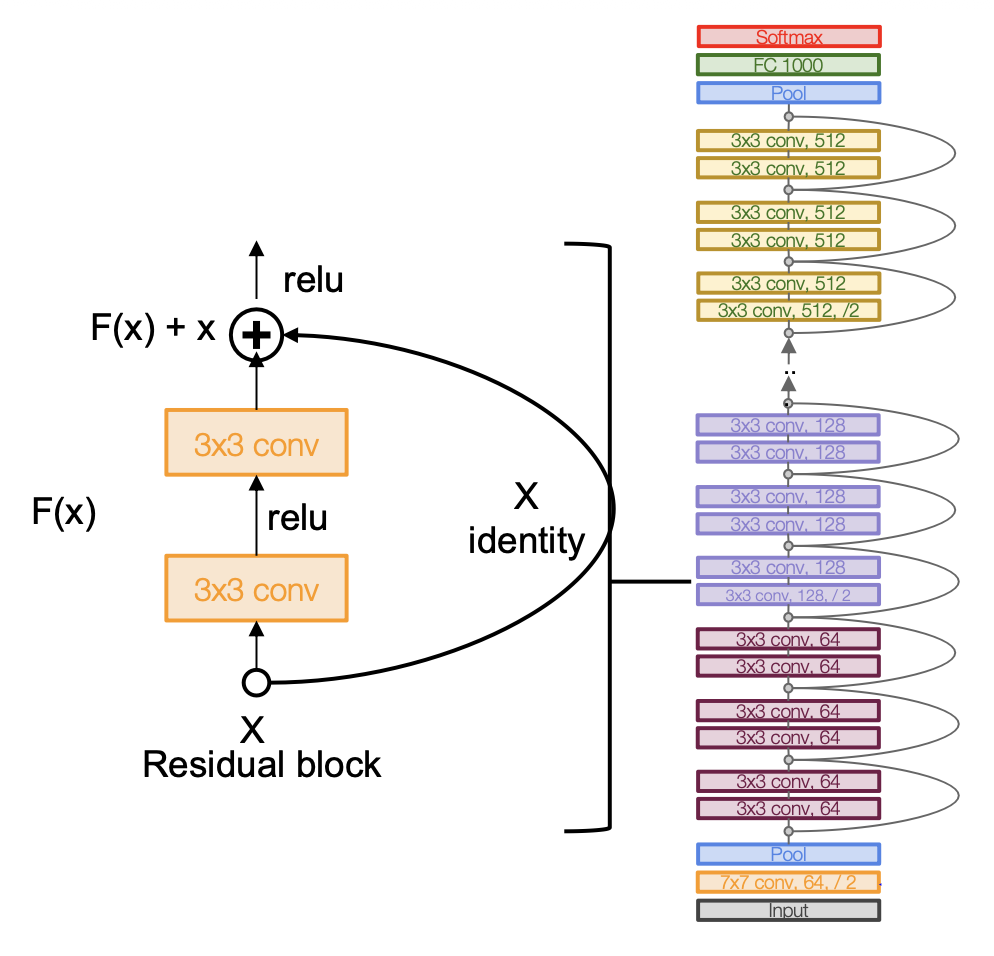
完整的 ResNet 架构如下:
- 堆叠残差块
- 每个残差块有 2 个 3x3 的卷积核
- 周期性地加倍卷积核的数量,使用值为 2 的步幅进行降采样(每一维 / 2
) ,并将激活值减少一半 -
和 GoogLeNet 一样在网络开头设置额外的卷积层(主干网络
) ,在应用残差块之前把输入降采样至原来的 1/4 -
还是类似 GoogLeNet,在网络末端不使用很大的全连接层,而采用全局平均池化和单个的线性层
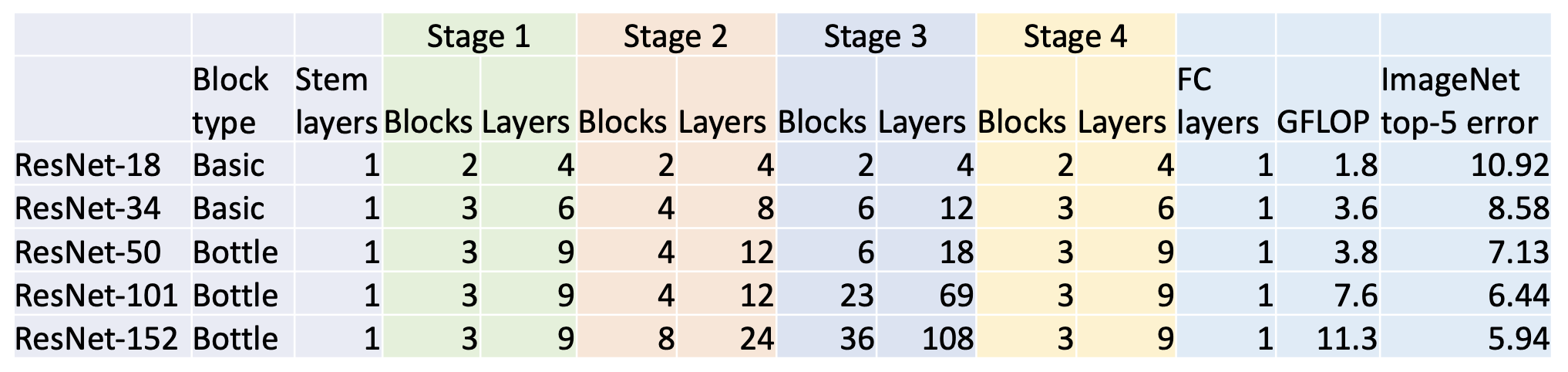
ResNet 被划分为以下阶段:
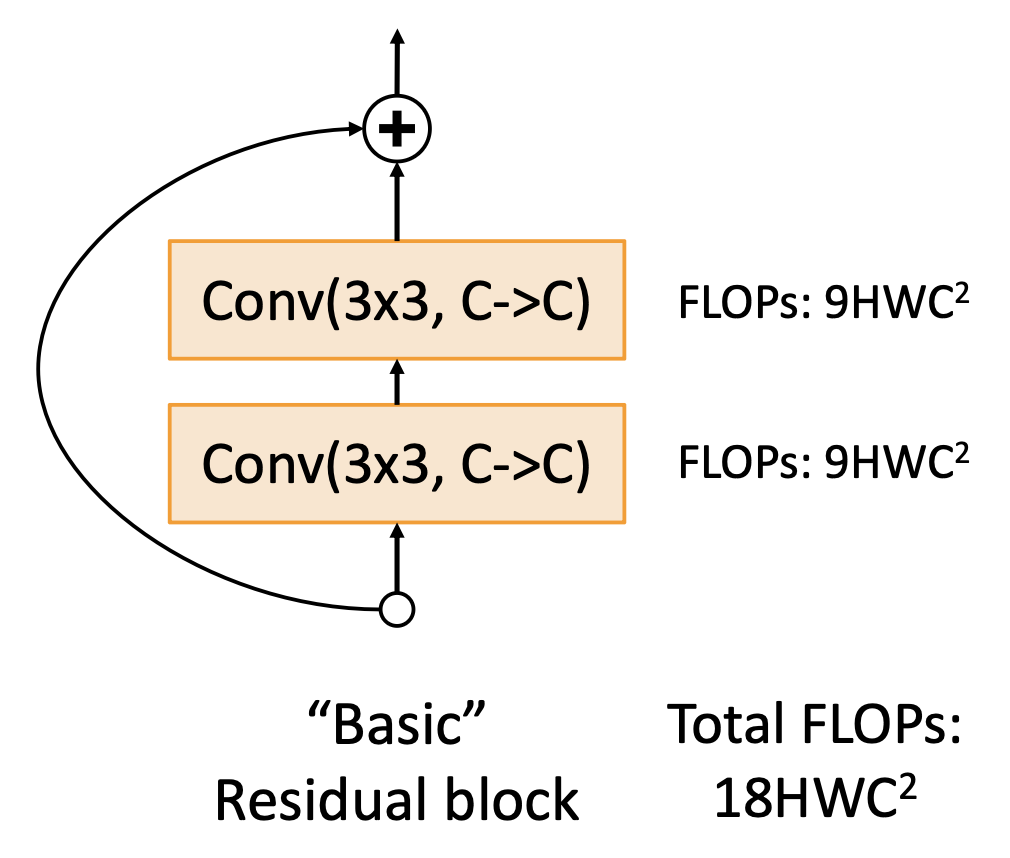
关于残差块:
-
基本块
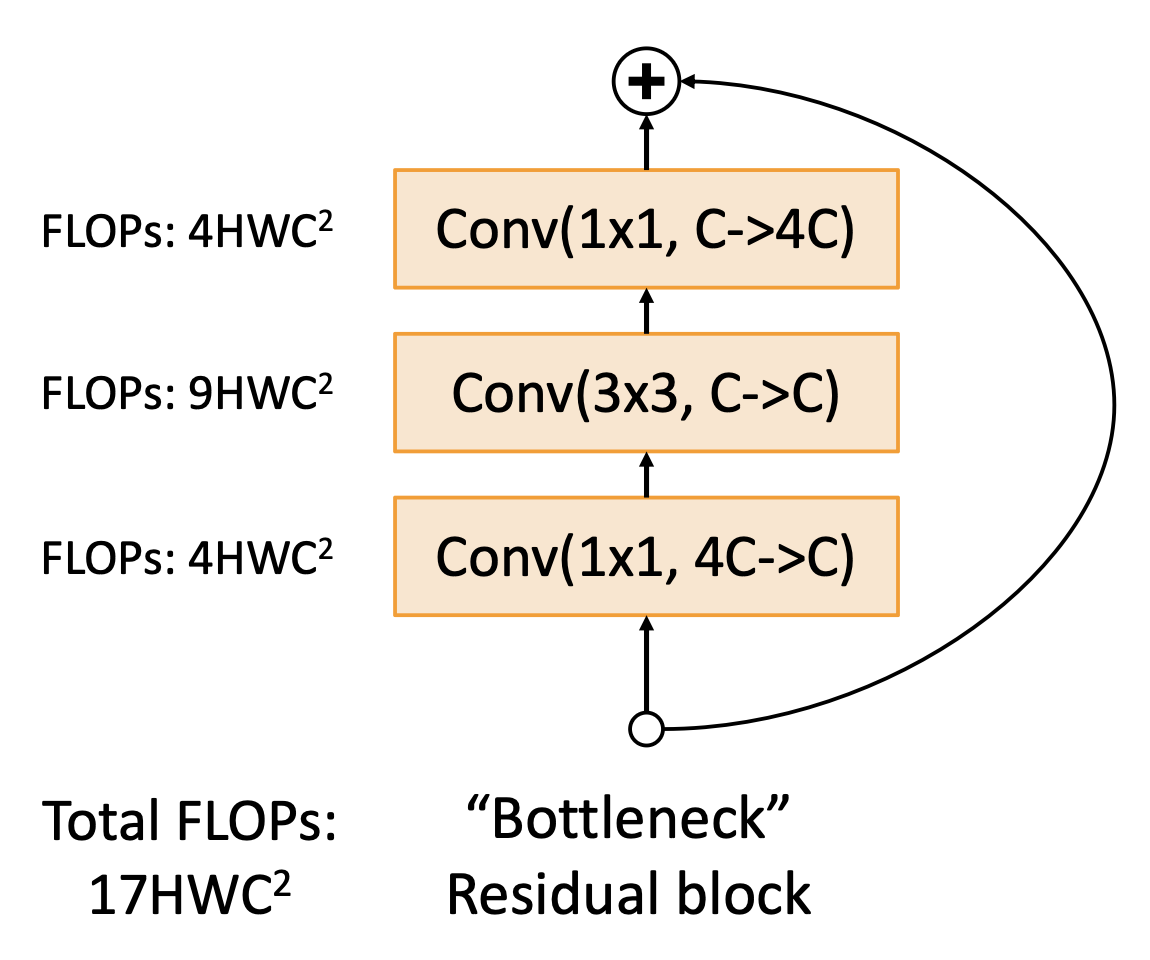
-
“瓶颈”块(更多层,但更少的计算成本)
更深 ResNet-101 和 ResNet-152 模型确实更准确,但是计算量更大:
改善残差块的设计
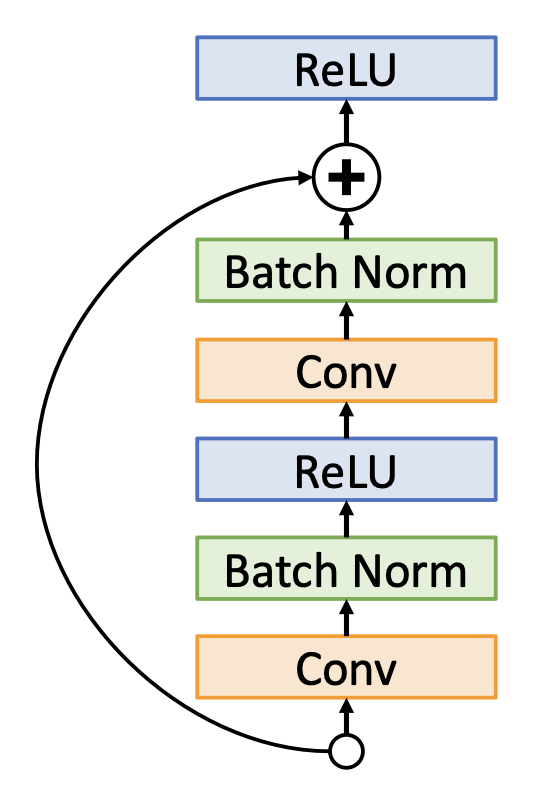
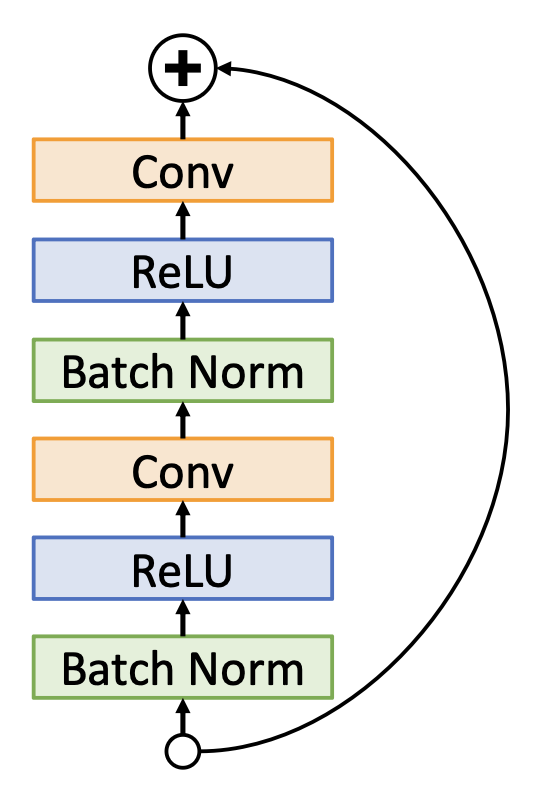
-
原来的残差块:ReLU 在残差块后,实际上无法学习恒等函数,因为输出是非负的
-
预激活(pre-activation) 的残差块:ReLU 在残差块内,可以通过将卷积权重设置为零来学习真实的恒等函数
这一调整在准确率上有了微小的进步,但在实践上用的不多。
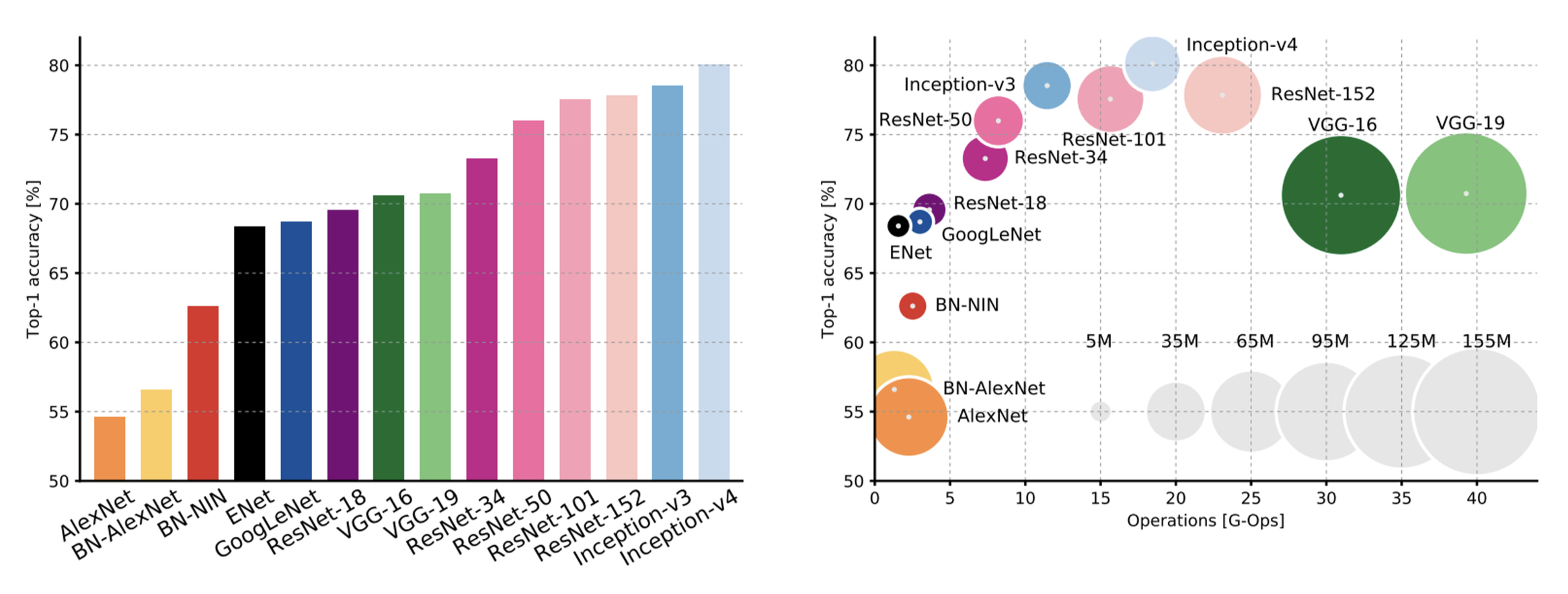
总结:比较各 CNN 架构的复杂性
- Inception-v4:ResNet + Inception
- VGG:内存用的最多,计算量最大
- GoogLeNet:非常高效
- AlexNet:计算量少,参数量也少
- ResNet:简单的设计(
简单在哪) 、中度效率、较高的准确率
Post-ResNet Architectures⚓︎
鸽掉了 hh
Weight Initialization⚓︎
为神经网路层初始化权重也是一门学问。
-
如果值设的太小,在小网络上是 OK 的;但是对于更深的网络层,所有的激活值趋近于 0
-
如果值设的太大,激活值会迅速增加
一种解决方案是 Kaiming / MSRA 初始化:依赖层的大小
dims = [4096] * 7
hs = []
x = np.random.randn(16, dims[0])
for Din, Dout in zip(dims[:-1], dims[1:]):
W = np.random.randn(Din, Dout) * np.sqrt(2 / Din)
x = np.maximum(0, x.dot(W)) # ReLU activation
hs.append(x)
可以看到,现在激活值在每一层都得到很好的缩放!
在残差块中,如果用 MSRA 初始化,那么 Var(F(x)) = Var(x),但随后 Var(F(x) + x) > Var(x),方差会在每个块中增长。解决方案是仅对第一个卷积层用 MSRA 初始化,第二个卷积层使用零初始化,从而 Var(F(x) + x) = Var(x)。
How to Train CNNs?⚓︎
Data Preprocessing⚓︎
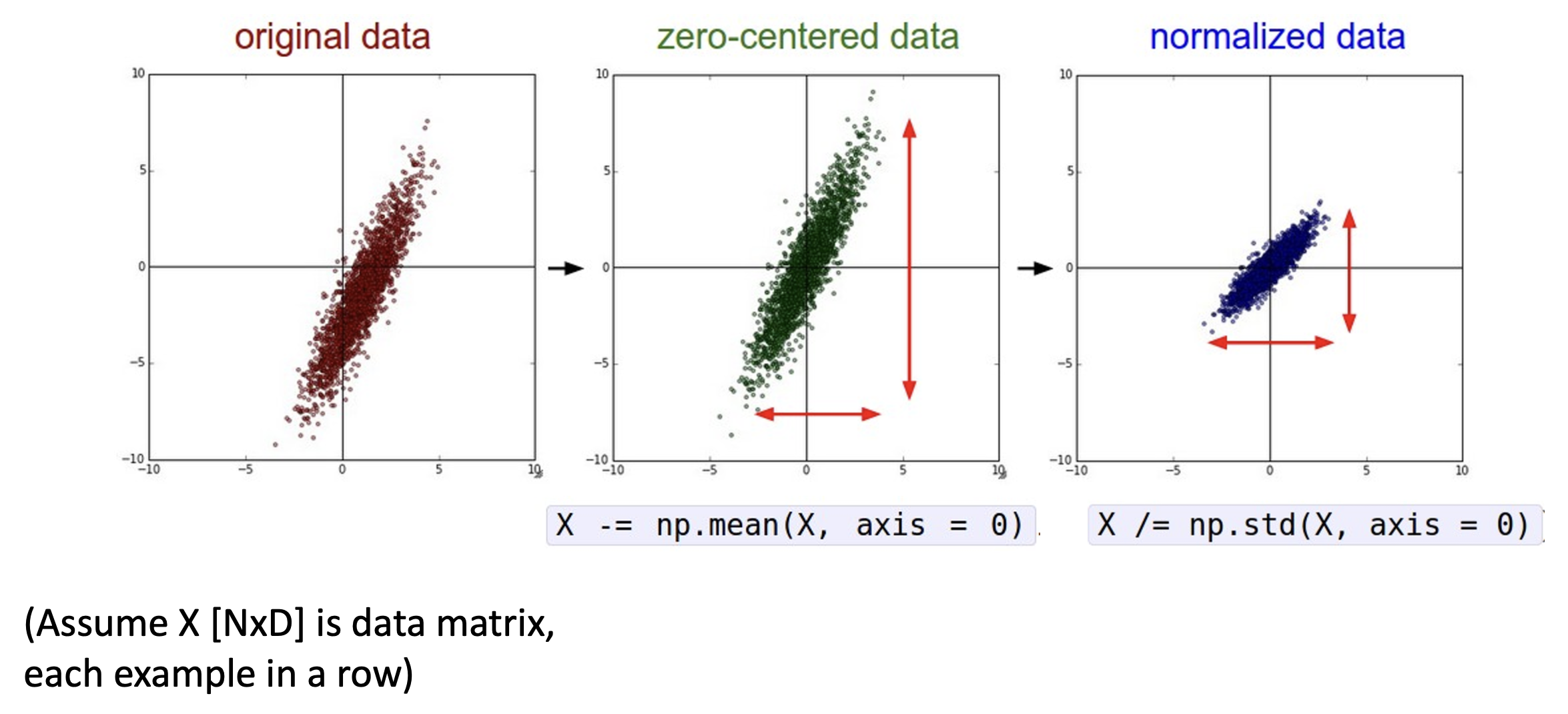
数据预处理时,我们要对图像做归一化(normalization) 处理,即对每一个通道进行中心化和缩放,具体来说:
- 减去每个通道的均值 (per-channel mean)
- 然后除以每个通道的标准差 (per-channel std)
- 需要根据给定的数据集预先计算好各通道的均值和标准差
用代码表示为:
用散点图表示为:
- 归一化前:分类损失对权重矩阵的变化非常敏感,难以优化
- 归一化后:对小权重变化不太敏感,更容易优化
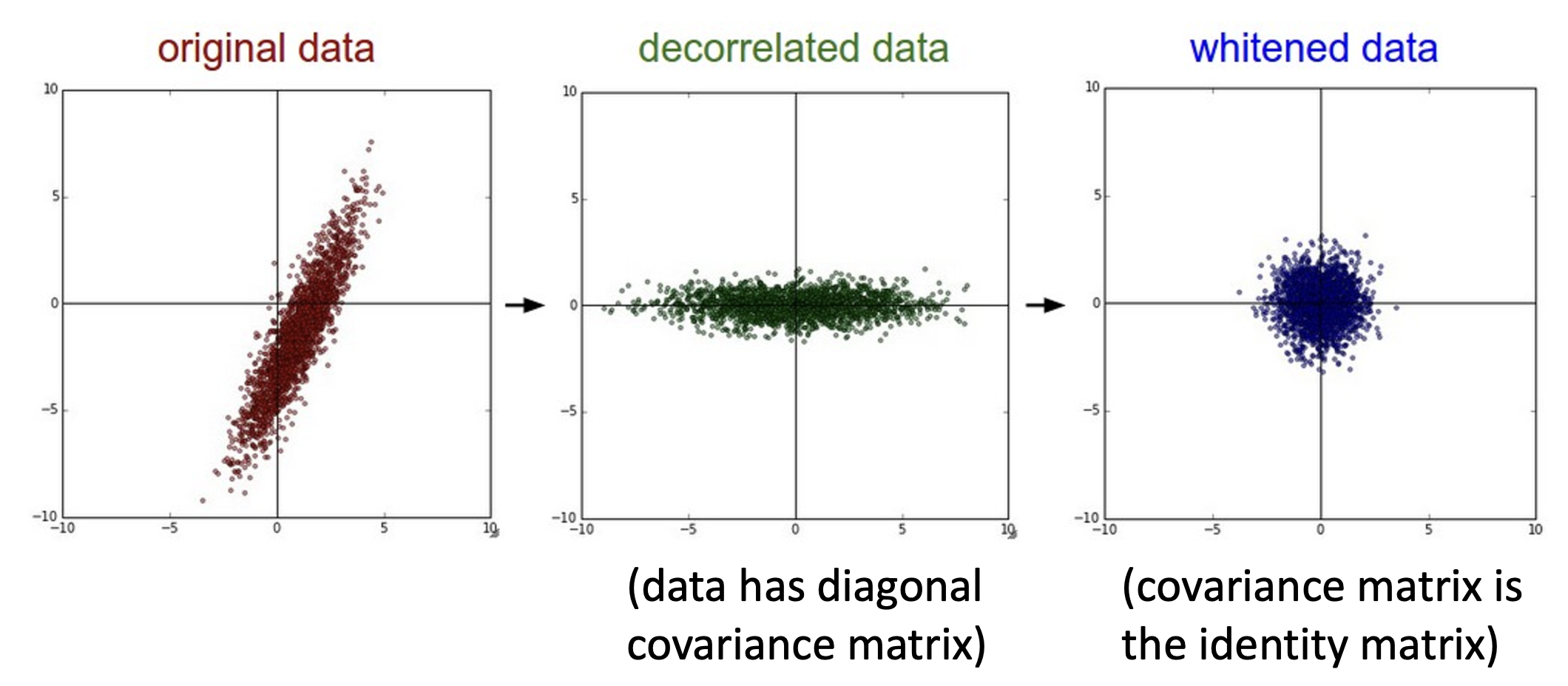
在实践中,可能还会用到数据的主成分分析(PCA)和白化处理(whitening) 技术:
Data Augmentation⚓︎
数据增强(data augmentation) 也是一种正则化方法,简单来说就是基于数据集中原有数据,经过一定变换后构造一些新的数据。
数据增强为模型编码了不变性(invariance),所以设计时需要思考:哪些对图像的改变不应该影响输出?对于不同的任务,该问题的答案也有所不同。
这些变换包括:
-
水平翻转(horizontal flip)
-
随机裁剪和缩放(random crops and scales)(以 ResNet 为例)
- 训练:采样进行随机裁剪或缩放
- 在范围 [256, 480] 中随机选取一个数 L
- 调整训练图像大小,短边长为 L
- 随机从图像裁剪出 224x224 的小块
- 测试:计算一组固定的裁剪后的图像的均值
- 以 5 种比例调整图像大小:{224, 256, 384, 480, 640}
- 对于每个大小,使用 10 种 224x224 的裁剪:4 角 + 中心,+ 翻转
- 训练:采样进行随机裁剪或缩放
-
颜色抖动(color jitter):
- 一种简单的方法是随机调整对比度和亮度
- 更复杂的方法(被用在 AlexNet, ResNet 等模型上
) :- 在训练集中将主成分分析(PCA)用于 [R, G, B] 像素上
- 沿着主成分方向采样“颜色偏移量 (color offset)”
- 将偏移量加在所有训练图像的像素上
-
随机增强(RandAugment):应用各种变换的随机组合
- 几何:旋转、平移、剪切 (shear)
- 颜色:锐化、对比度、亮度、光色分离 (solarize)、色阶分离 (posterize)、颜色
transforms = [ 'Identity', 'AutoContrast', 'Equalize', 'Rotate', 'Solarize', 'Color', 'Posterize', 'Contrast', 'Brightness', 'Sharpness', 'ShearX', 'ShearY', 'TranslateX', 'TranslateY' ] def randaugment(N, M): """Generate a set of distortions. Args: N: Number of augmentation transformations to apply sequentially. M: Magnitude for all the transformations. """ sampled_ops = np.random.choice(transforms, N) return [(op, M) for op in sampled_ops]
以下是一些正则化手段,但又和数据增强关系密切的技术:
-
挖剪(cutout)
- 训练:在图像上随机选择一块区域,将其值置零
- 测试:使用完整的图像
- 该方法在像 CIFAR 这样小的数据集上表现很好,但通常很少在像 ImageNet 这样的大型数据集中使用
-
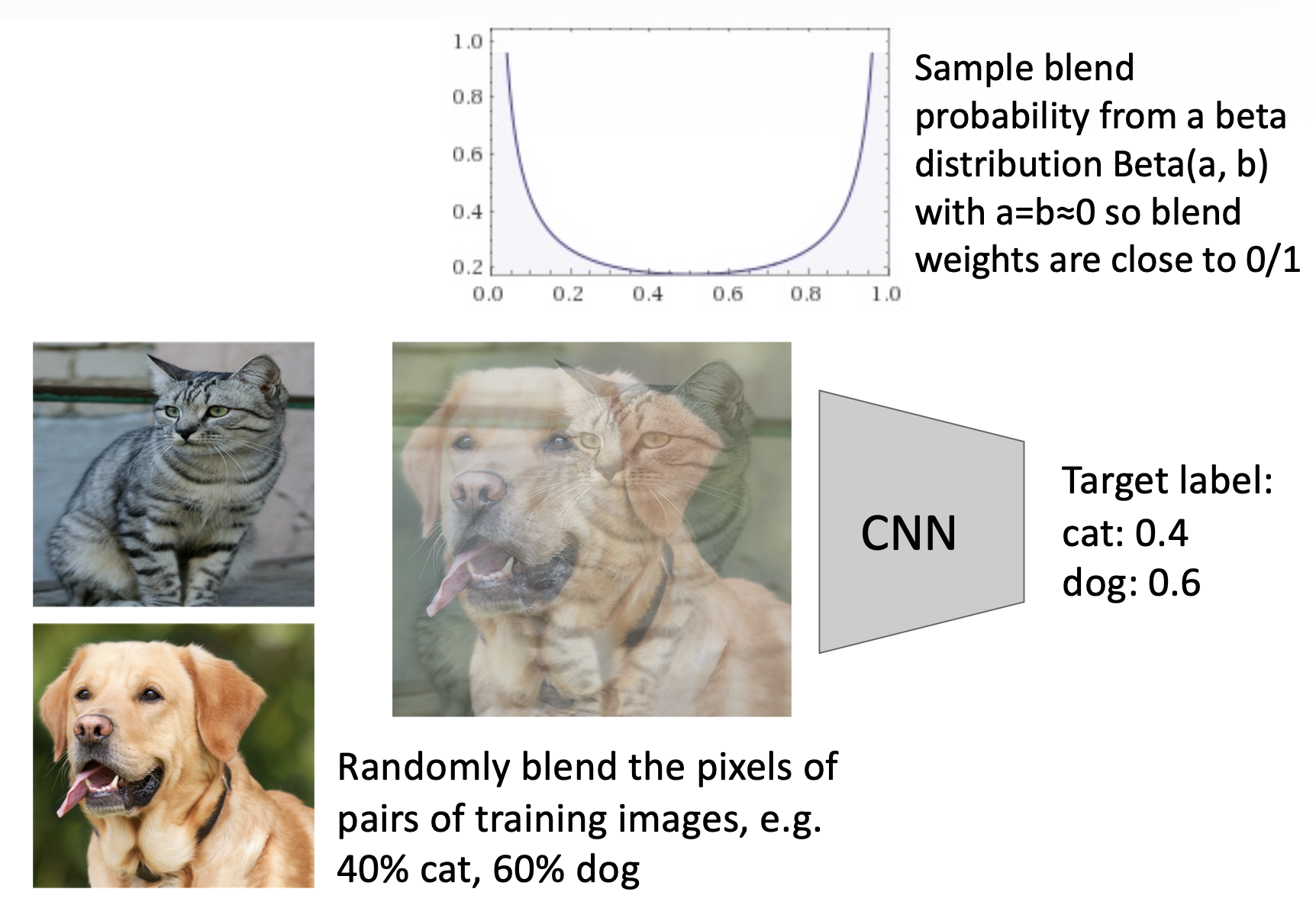
混合(mixup)
- 训练:在随机混合的图像上训练
- 测试:使用原始图像
-
裁剪 + 混合(CutMix)
- 训练:在随机混合的图像上训练
- 测试:使用原始图像
Hyperparameter Selection⚓︎
选择超参数的步骤如下(无需大量 GPUs
-
检查初始损失
- 关闭权重衰减,在初始化时进行合理性检查损失
-
过拟合一个小样本
- 尝试在一小部分训练数据(约 5-10 个小批量)上训练到 100% 的训练准确率
- 调整架构、学习率和权重初始化
- 关闭正则化
- 若损失不下降,说明学习速率太低,初始化效果不佳
- 反之,若损失爆炸到无穷大或 NaN,说明学习率太高,初始化效果不佳
-
找到使损失下降的 LR(学习速率)
- 使用上一步的架构和所有训练数据,开启小权重衰减,然后找到一个学习速率,使得损失在约 100 次迭代内显著下降
- 值的一试的学习速率:1e-1, 1e-2, 1e-3, 1e-4, 1e-5
-
粗糙的超参数网格,训练约 1-5 个周期 (epochs)
- 选择几个学习速率和权重衰减的值,围绕步骤 3 中的有效参数,训练几个模型约 1-5 个周期
- 值的一试的权重衰减:1e-4, 1e-5, 0
-
细化网格,训练时间更长
- 选择步骤 4 得到的最佳模型,在没有学习速率衰减的情况下训练得更久些(约 10-20 个周期)
-
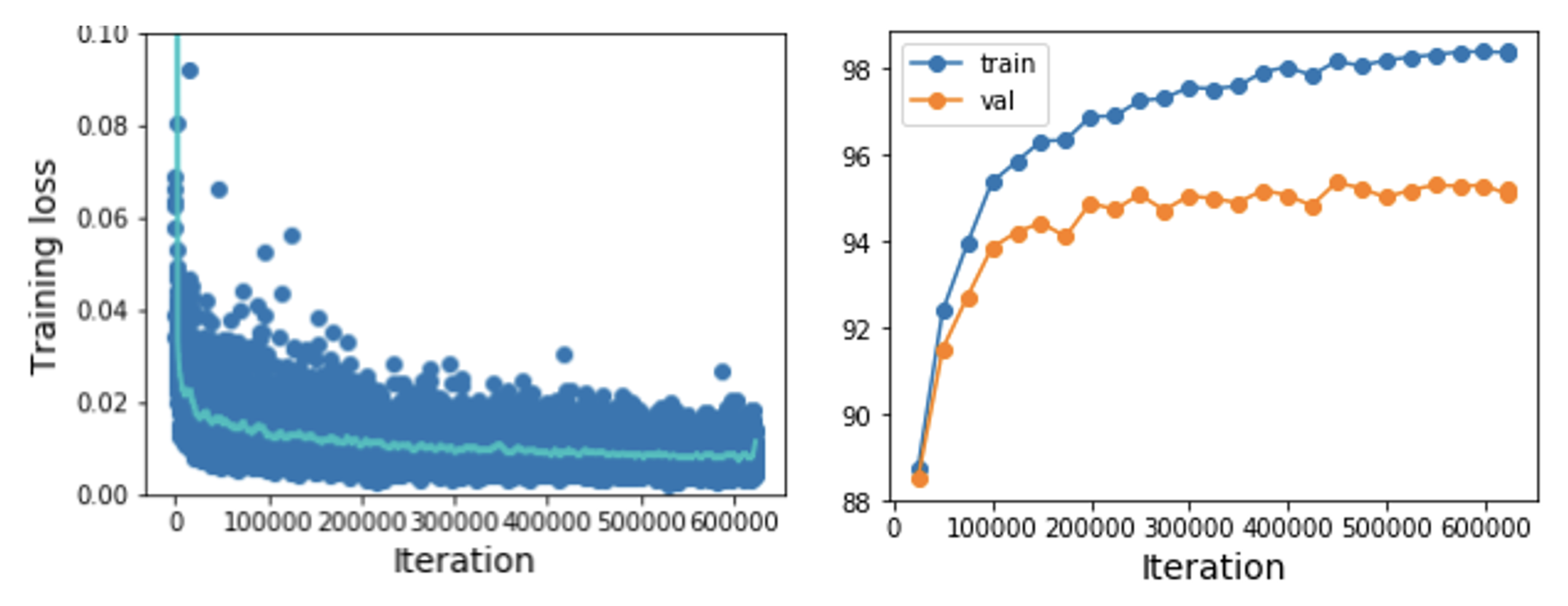
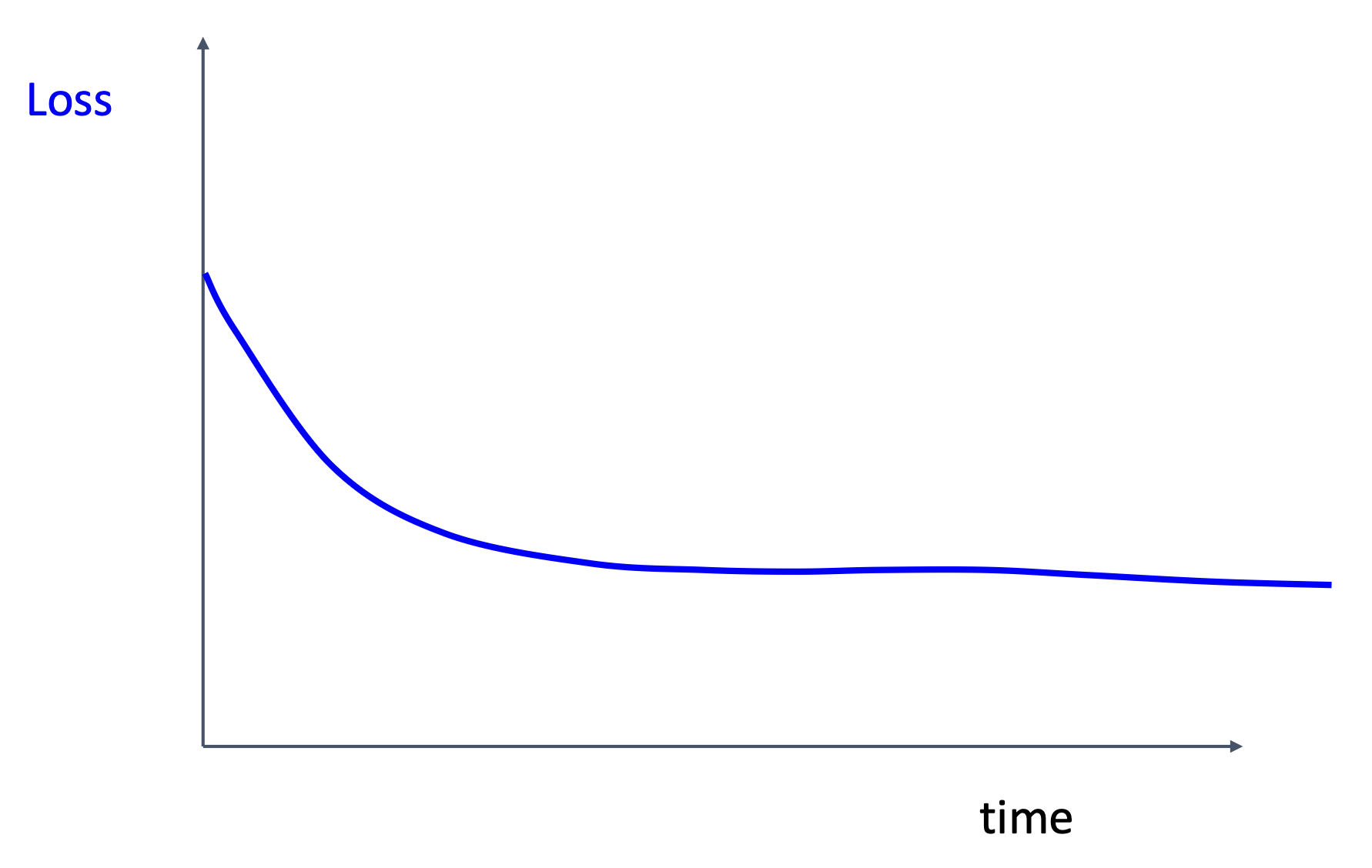
查看损失和准确率曲线
-
损失可能存在噪声,所以使用散点图并绘制移动平均线以更好地观察趋势
-
以下曲线说明很有可能初始化效果不佳
-
如果损失下不去,尝试让学习速率衰减
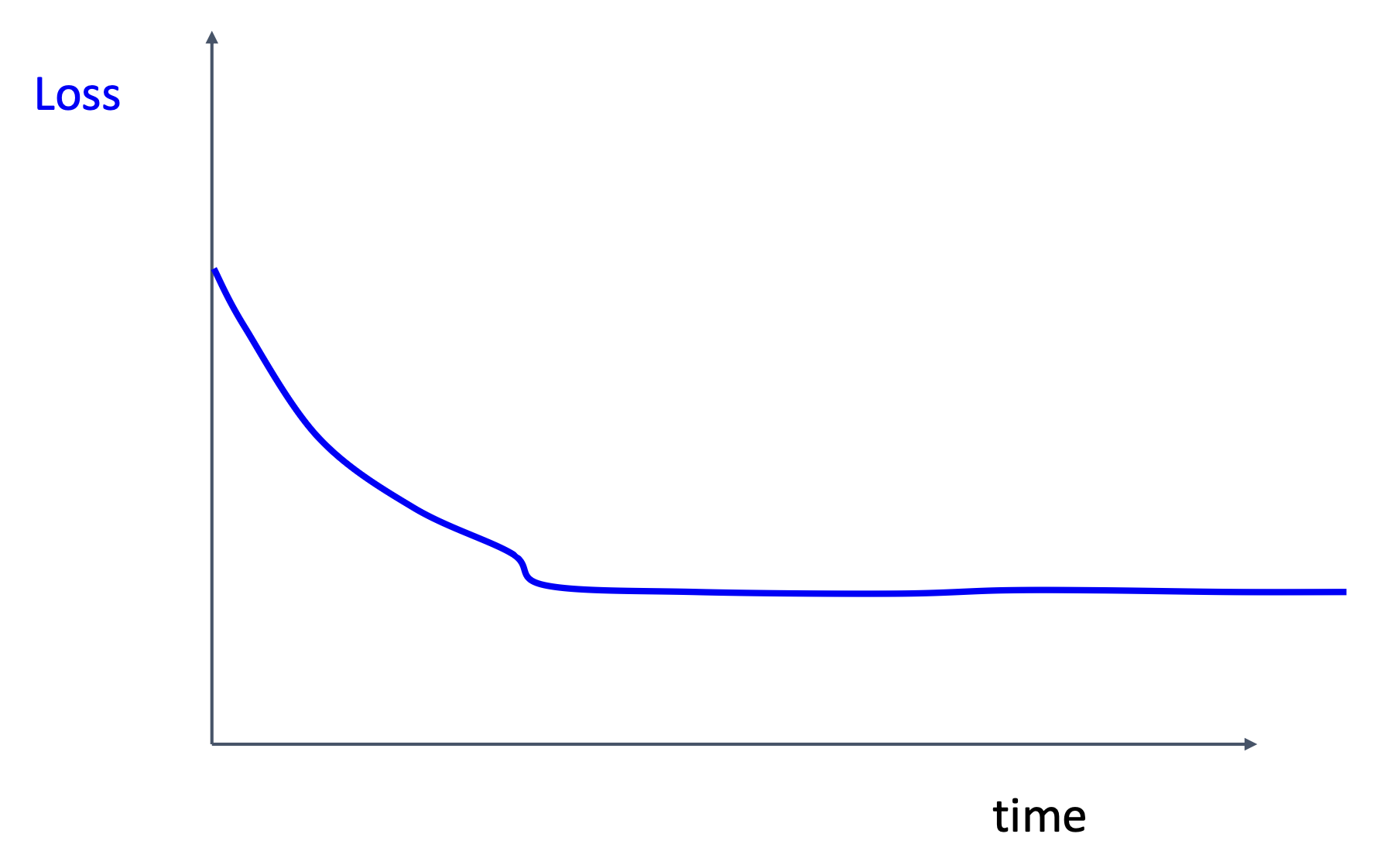
-
当学习速率下降时,损失还在减少,说明学习速率衰减过早
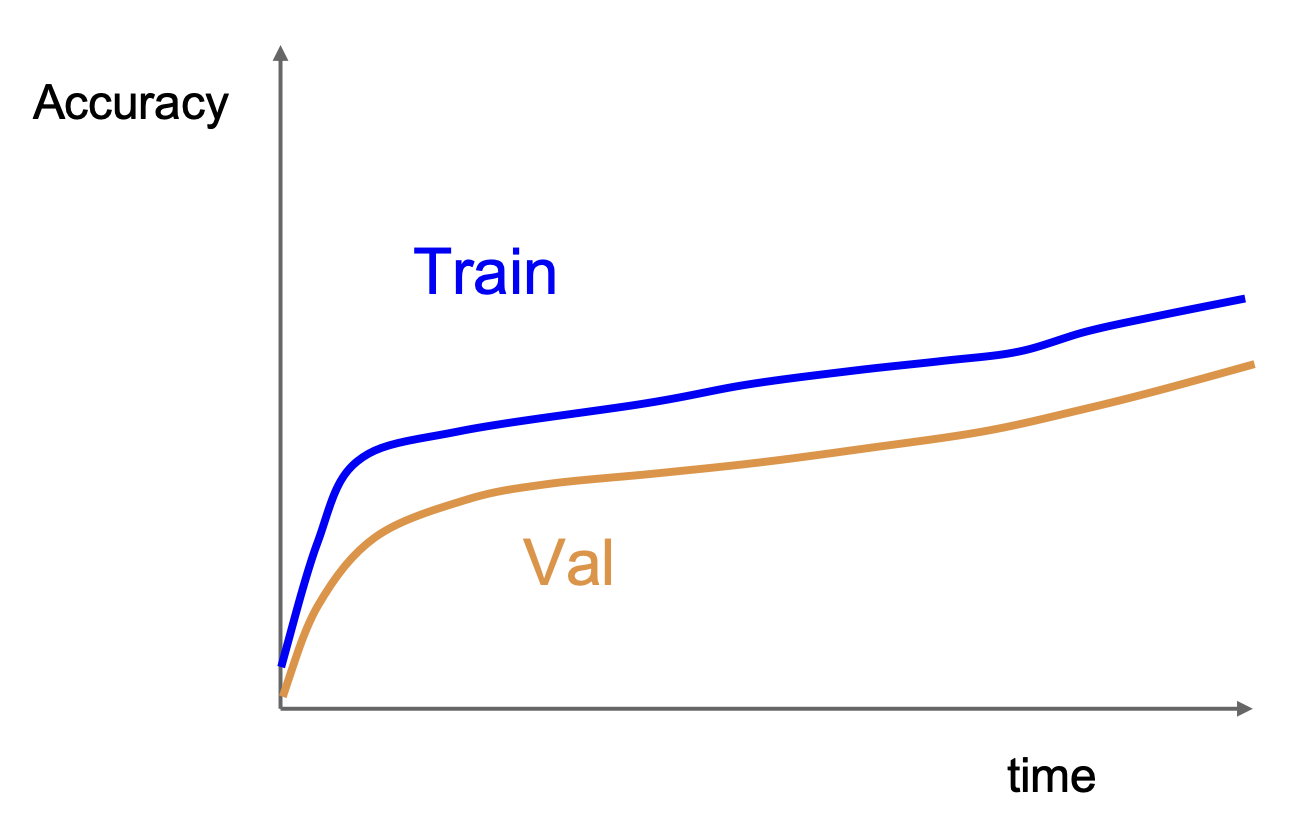
-
如果准确率仍然在上升,说明还需要训练更久
-
训练集和验证集的准确率相差太大,意味着存在过拟合问题,此时需要增加正则化程度或者获取更多数据
-
训练集和验证集的准确率没有差别,意味着欠拟合(underfitting),此时需要训练得更久,或采用更大的模型
-
-
回到第 5 步
超参数选择的方法有:
-
网格搜索(grid search):在超参数网格中评估所有可能的选择
- 例子:
- 权重衰减:[1x10-4, 1x10-3, 1x10-2, 1x10-1]
- 学习速率:[1x10-4, 1x10-3, 1x10-2, 1x10-1]
- 例子:
-
随机搜索(random search):运行许多不同的试验
- 例子:
- 权重衰减:在 [1x10 -4 , 1x10 -1 ] 上对数均匀分布
- 学习速率:在 [1x10 -4 , 1x10 -1 ] 上对数均匀分布
- 例子:
Random Search for Hyper-Parameter Optimization, Bergstra and Bengio, 2012
After Training⚓︎
Model Ensembles⚓︎
模型集成(model ensemble) 的步骤如下:
- 训练多个独立模型
- 测试时,计算这些模型结果的平均值
- 取预测概率分布的平均值,然后选择 argmax
该方法仅得到额外 2% 的性能提升。
模型集成的小技巧:
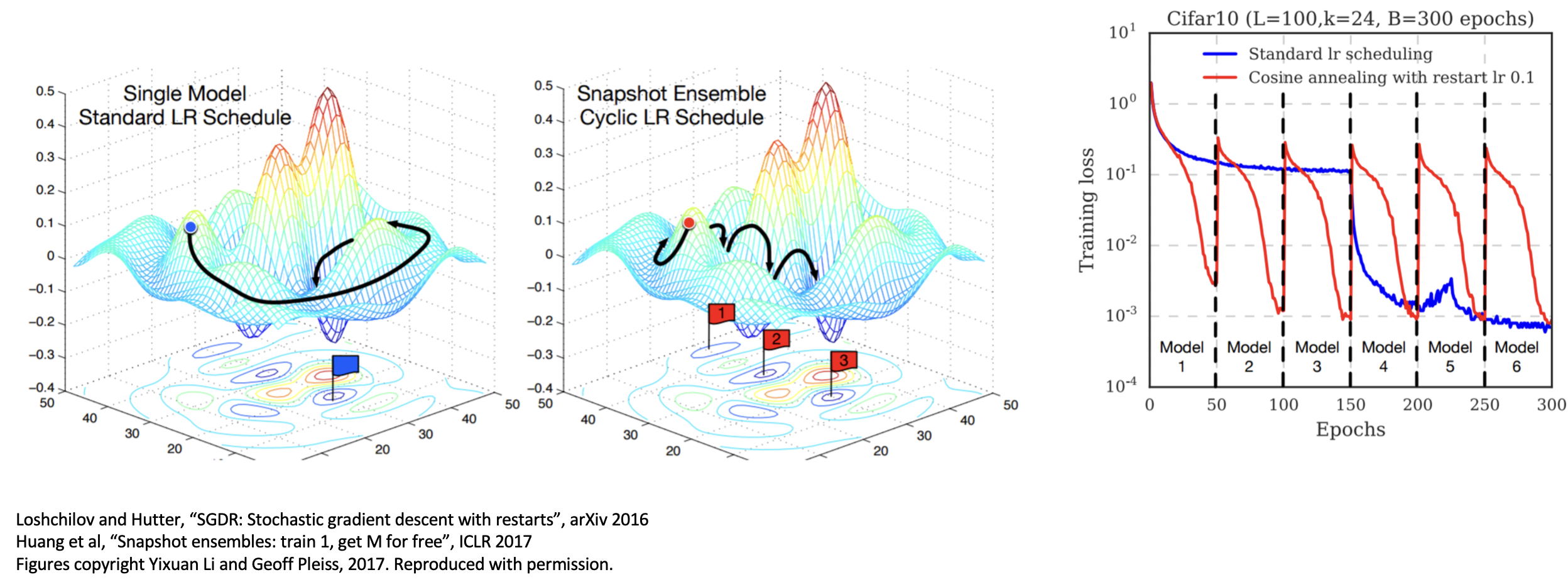
-
在训练时使用单个模型的多份快照,而不要训练独立的模型
- 循环学习速率调度(cyclic learning rate scheduling) 能够让这一技巧发挥得更好
-
保持一个移动的参数向量均值,并在测试时使用,而不是使用真正的参数向量(Polyak 平均)
Transfer Learning⚓︎
迁移学习(transfer learning) 用来解决训练 CNNs 时手边没有很多数据的情况。步骤如下:
- 在 ImageNet 上训练模型
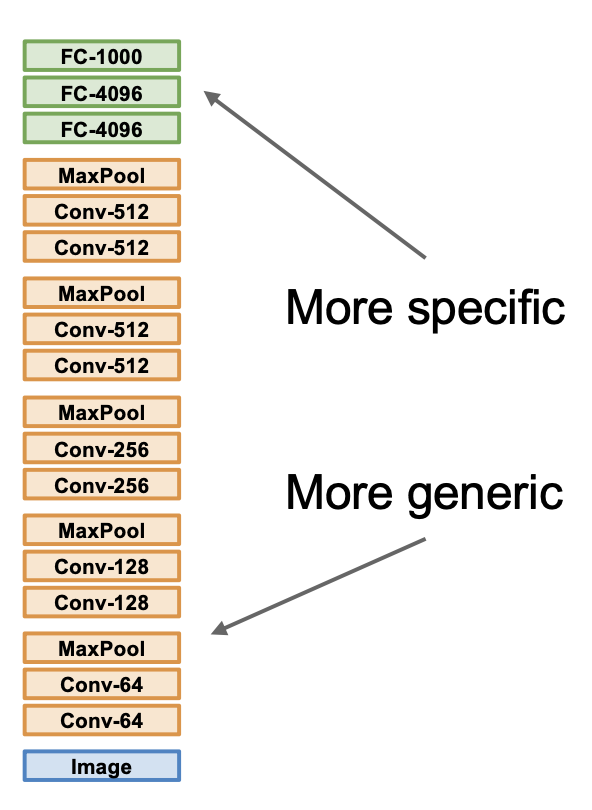
- 由于我们只关心部分数据集上的表现,所以提取上一步训练好的模型,去掉最后的全连接层,冻结和其他数据集相关的权重
- 从预训练模型中初始化,然后进行微调
一些技巧:
- 先进行特征提取训练,然后再进行微调
- 降低学习速率:仅使用在初始训练时 1/10 的学习速率
- 有时通过固定低层来暴露计算
- 在“测试”模式下用 BatchNorm 训练
在迁移学习中,CNN 架构的提升也会为很多下游任务带来提升。
带给我们的启示:如果手边有一些感兴趣的数据,但是 < ~1M 的图像
- 寻找很大的且包含相似图像的数据集,根据该数据集训练一个大模型
- 迁移学习至原来手边的数据集上
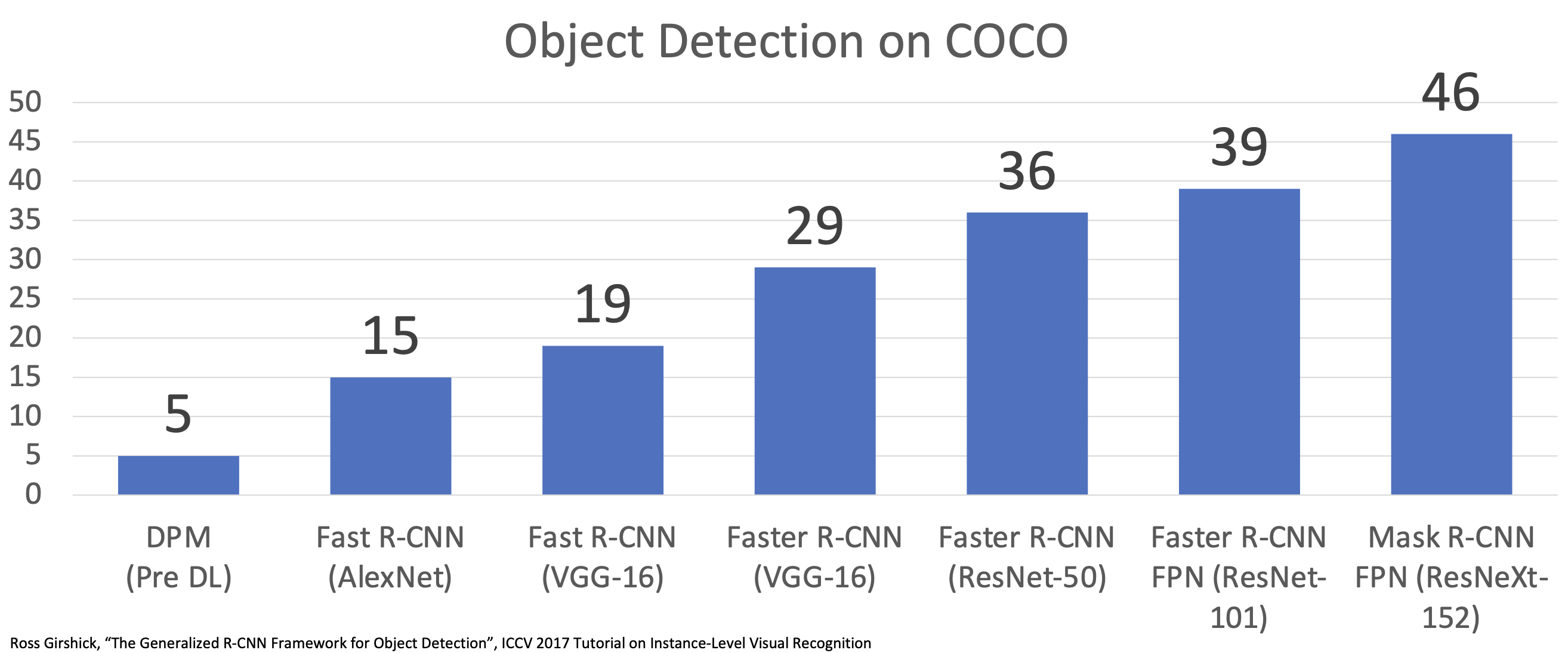
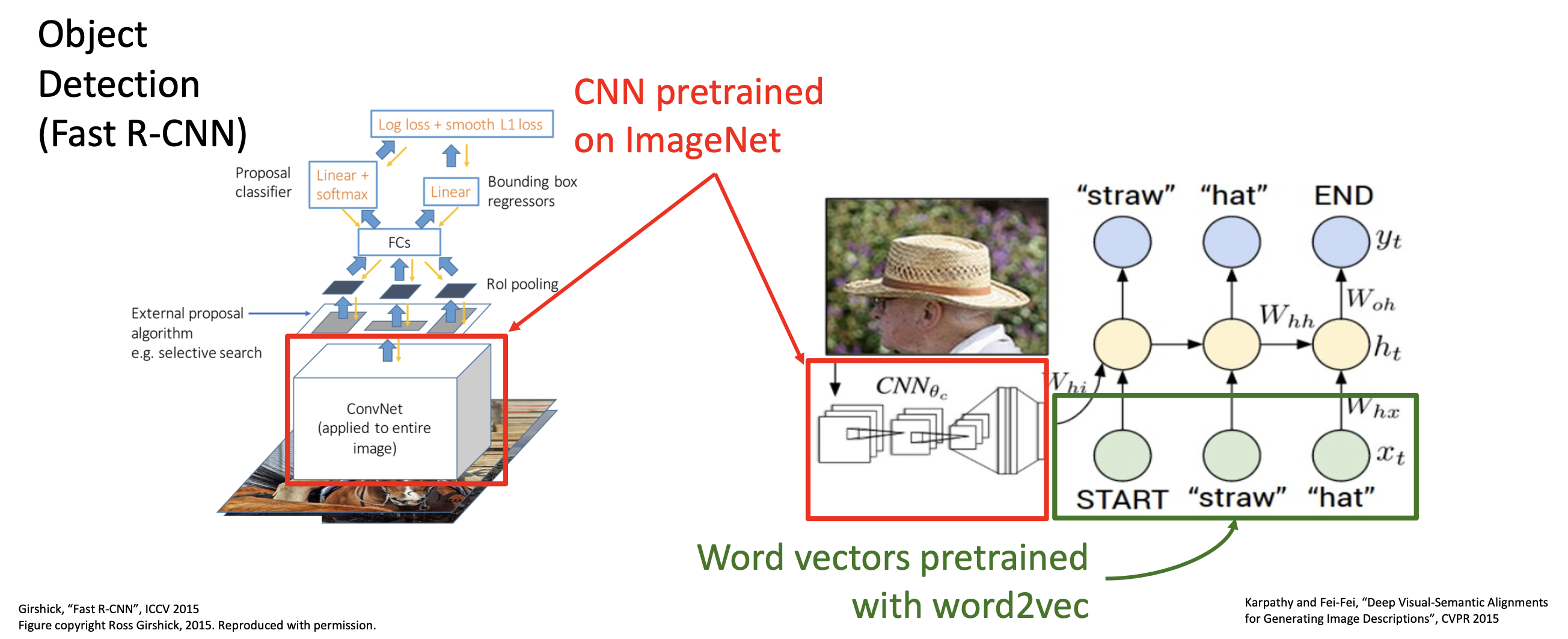
在 CV 中,迁移学习已然成为常态。比如在目标检测(object detection) 任务中,部分模型就是在 ImageNet 上预训练的。
我们可以将这一流程概括为以下步骤:
- 在 ImageNet 上训练 CNN
- 在 Visual Genome 上微调来自步骤 1 的模型,用于目标检测
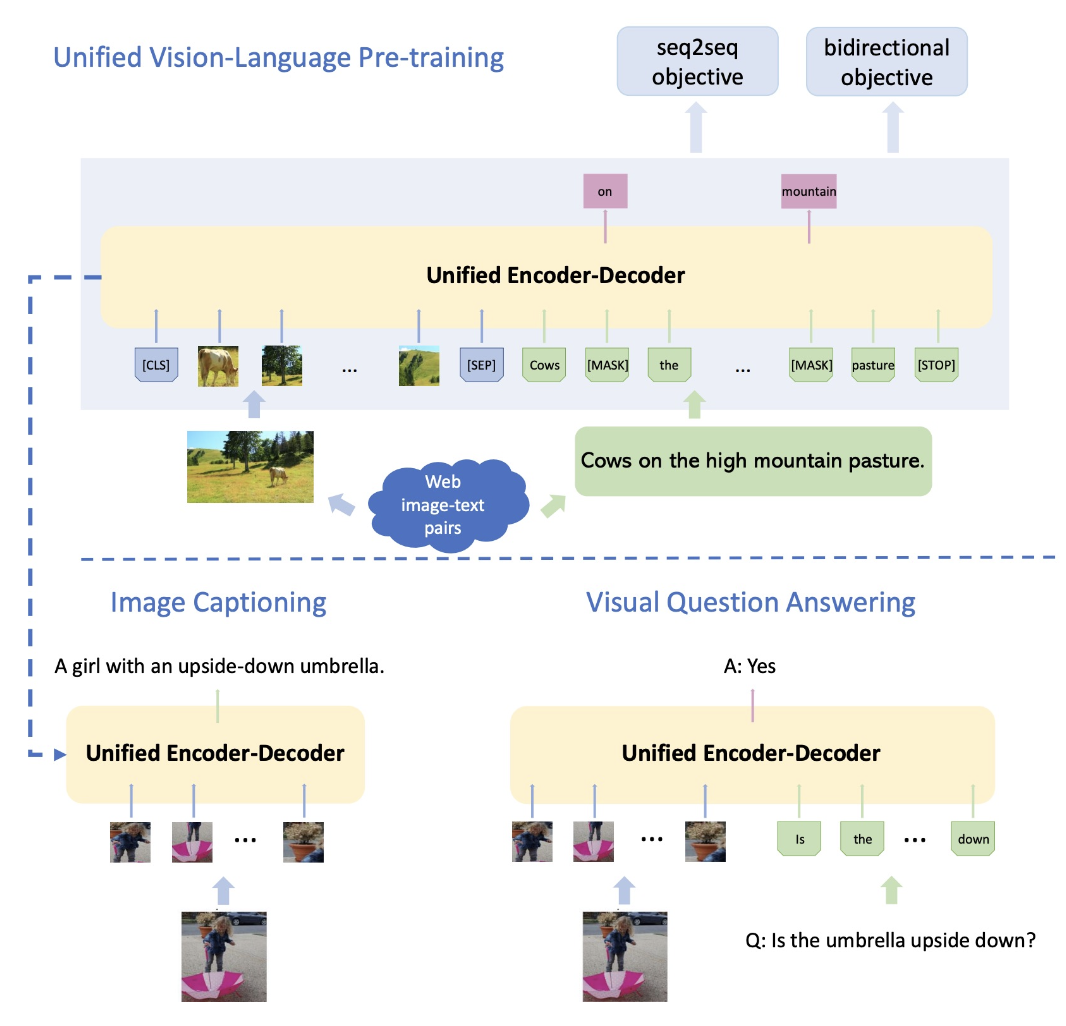
- 在大量文本上训练 BERT 语言模型
- 结合步骤 2 和 3 得到的模型,训练联合的图像 / 语言模型
- 微调步骤 4 得到的模型,用于图像描述、视觉问答等任务
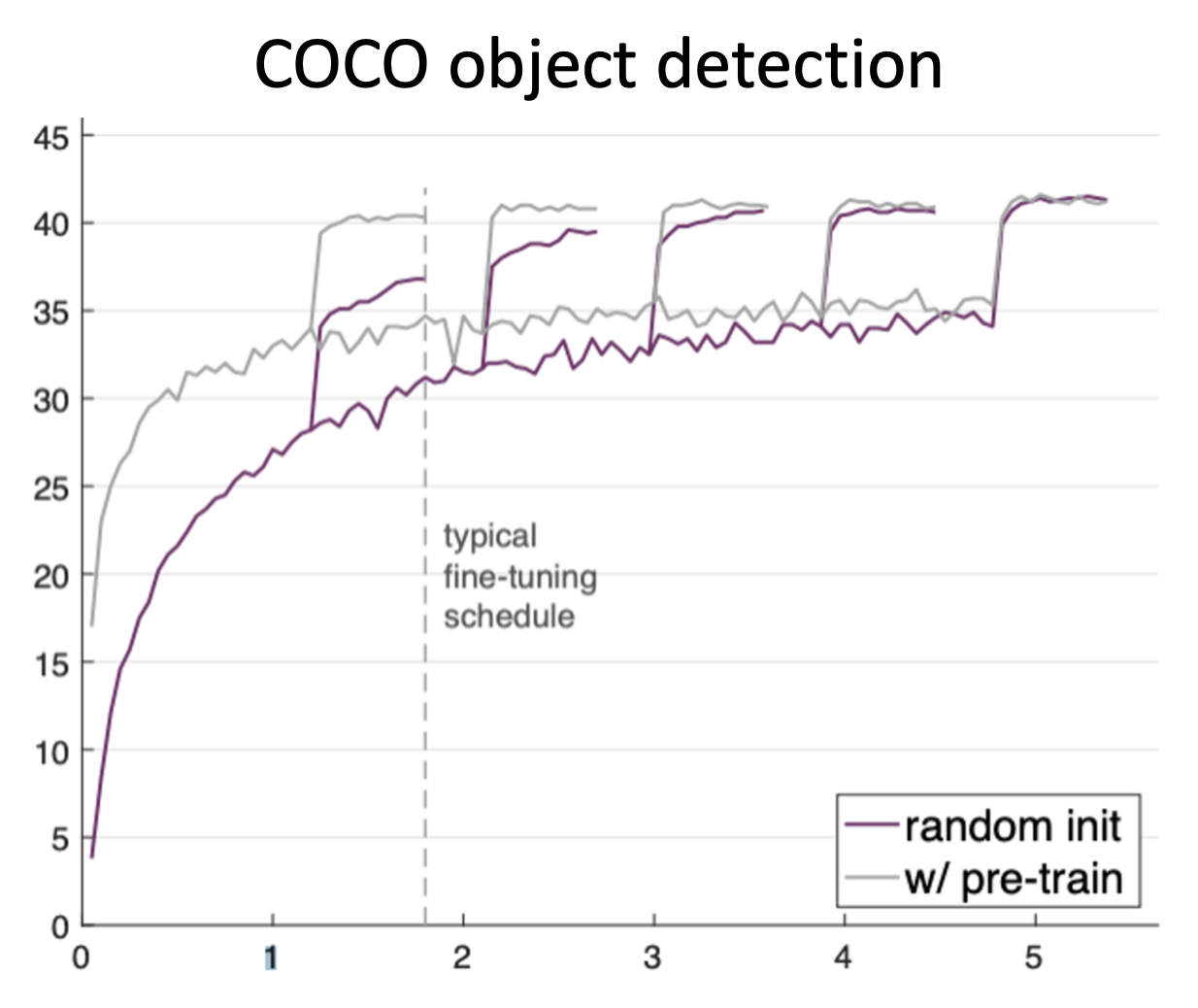
受到质疑
最近有研究发现迁移学习的效果可能并不像我们认为的那么好。在 ImageNet 上从头训练一个模型可以取得和采用预训练模型微调差不多的结果(只要训练时间足够长
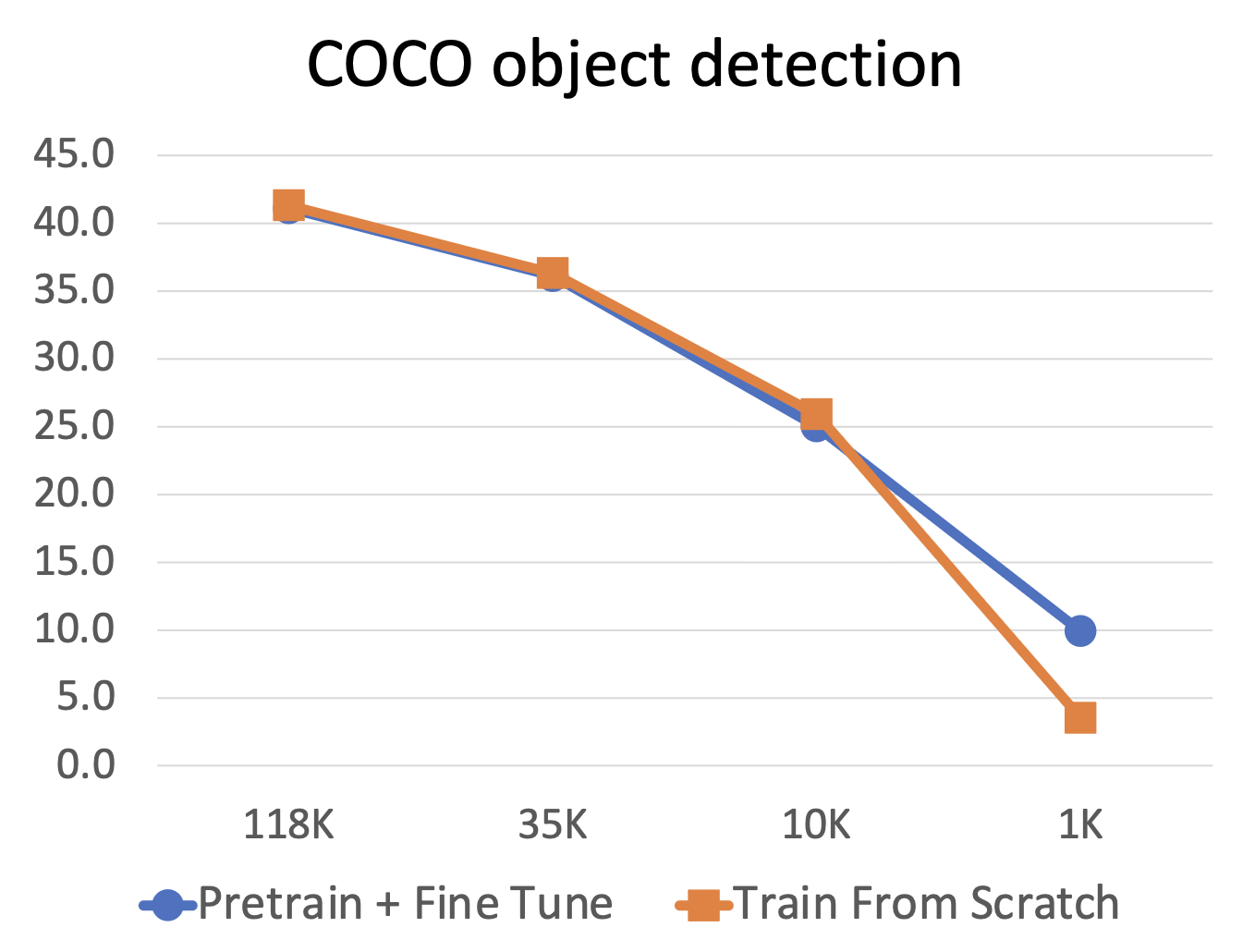
并且只有当数据量很小时,预训练 + 微调才能击败从头训练的策略。也就是说,收集大量数据比预训练更有效。
深度学习框架提供了一个预训练模型家族,所以我们无需训练自己的模型。
- Pytorch:https://github.com/pytorch/vision
- Hugggingface:https://github.com/huggingface/pytorch-image-models
评论区