Recurrent Neural Networks⚓︎

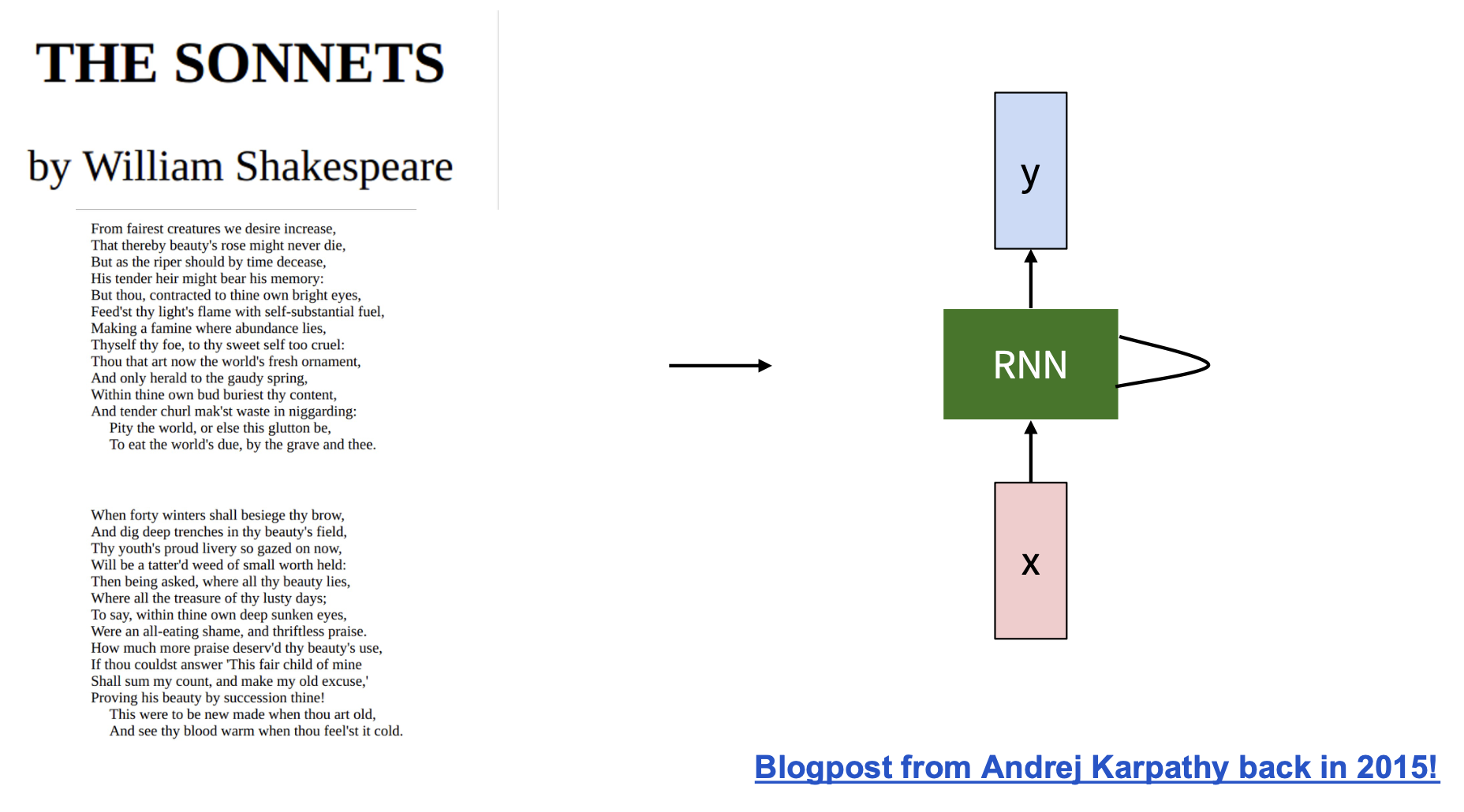
相比一般的神经网络，循环神经网络(recurrent neural network, RNN) 擅长的是处理序列(sequences)。

NNRNN

• 一对多：比如图像字幕（一张图像 -> 一段词序列）
• 多对一：比如行动预测（一段视频帧序列 -> 一个行动类别）
• 多对多：比如
  • 图像字幕（一段视频帧序列 -> 一段词序列）（右二）
  • 帧级别的视频分类（右一）

其实也可作用在非序列数据上

通过一系列“瞥见 (glimpse)”来对图像进行分类：

一块块地生产图像：

与油画模拟器集成，每一个时间步输出新的一笔：

RNN 的关键思想是有一个在序列处理过程中不断更新的“内部状态(internal state)”。

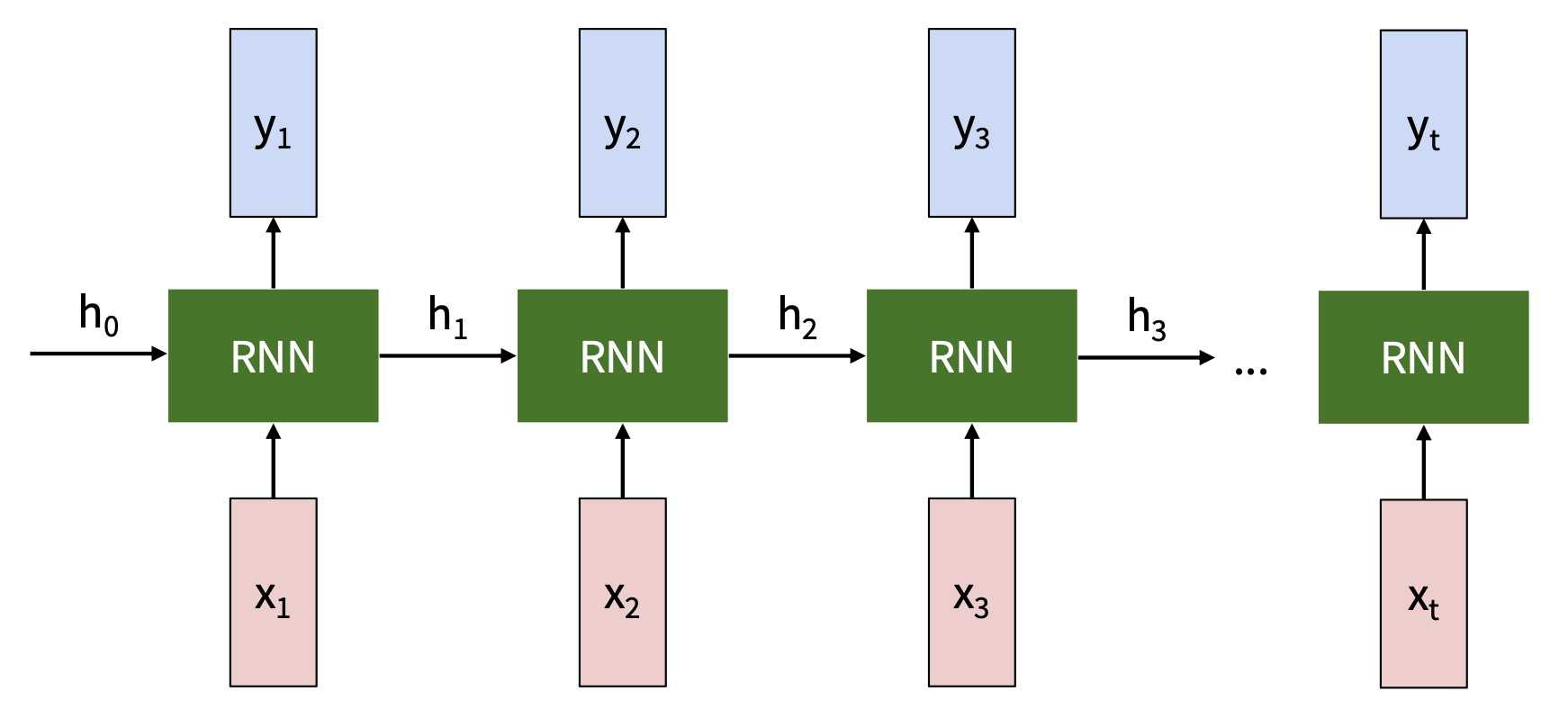
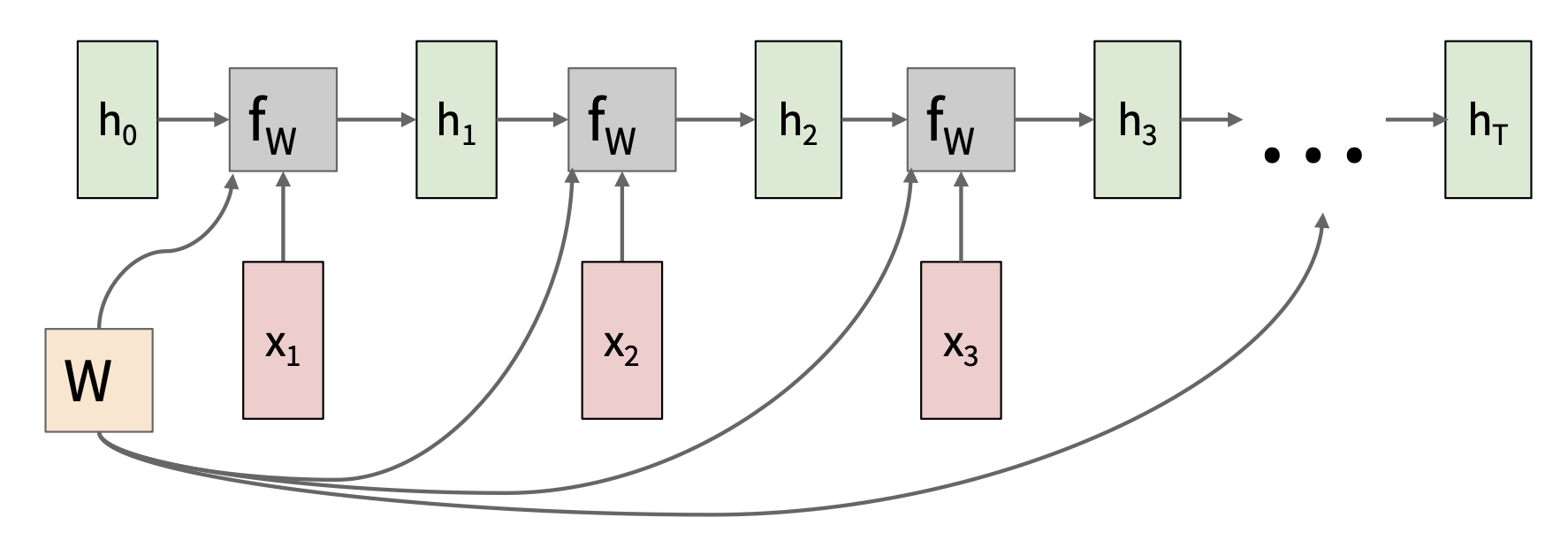
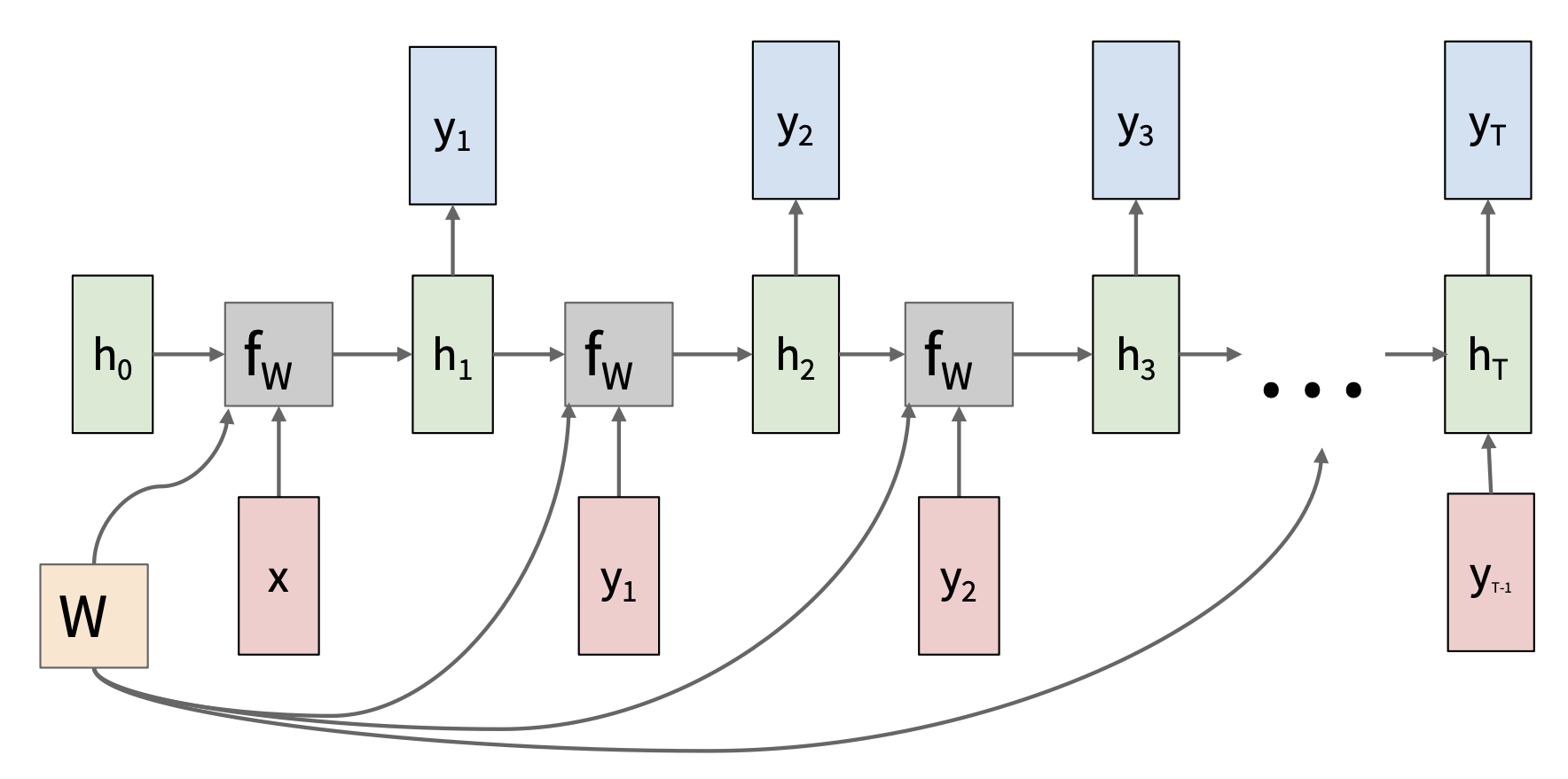
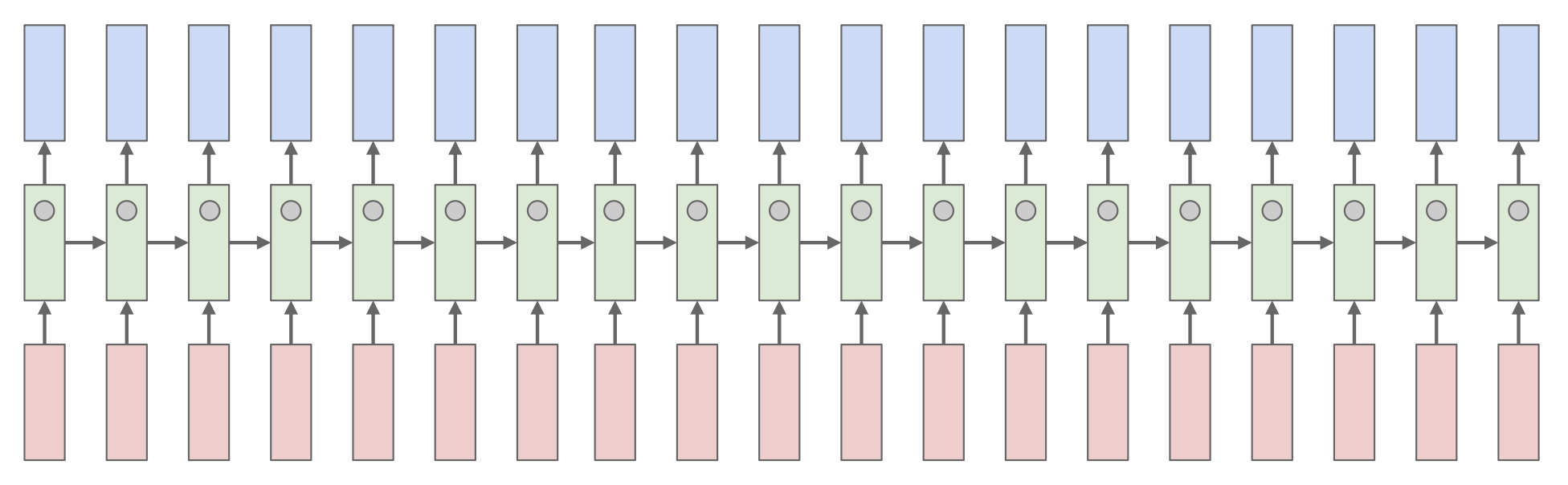
展开后的 RNN：

• 隐含的状态更新：\(h_t = f_W(h_{t-1}, x_t)\)
  • \(h_t\)：新状态
  • \(f_W\)：以 \(W\) 为参数的函数
  • \(h_{t-1}\)：旧状态
  • \(x_t\)：在某一时刻的输入向量
• 输出生成：\(y_t = f_{W_{hy}}(h_t)\)
  • \(y_t\)：输出
  • \(f_{W_{hy}}\)：另一个以 \(W_{hy}\) 为参数的函数
  • \(h_t\)：新状态

注意：每一步都用到相同的函数和参数。

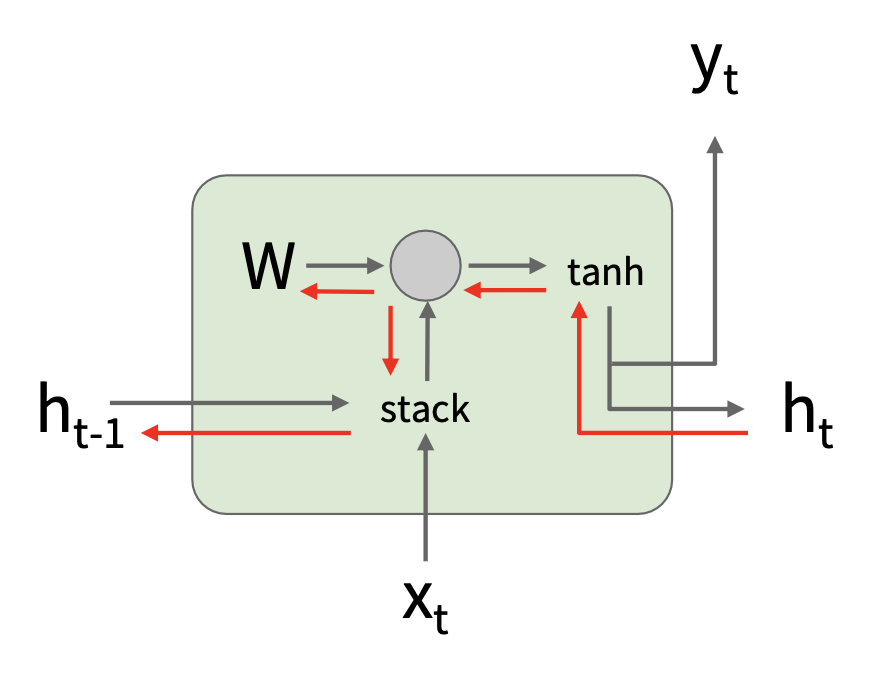
Vanilla RNNs⚓︎

在一个简单的 RNN（Vanilla RNN / Elman RNN）中，

• \(h_t = \tanh (W_{hh}h_{t-1} + W_{xh}x_t)\)
• \(y_t = W_{hy}h_t\)

现在我们手动创建一个 RNN 来检测重复的 1，这是一个多对多的序列建模任务。

• 隐含状态需要捕捉先前的输入和当前的 \(x\) 值
• 简洁起见，令 \(f_W\) 和 \(f_y\) 均为 ReLU 函数，即：
  • \(h_t=ReLU(W_{hh}h_{t-1}+W_{xh}x_t)\)
  • \(y_t=ReLU(W_{hy}h_t)\)
• \(h_t = \begin{pmatrix}\text{Current} \\ \text{Previous} \\ 1\end{pmatrix}\)，初始化 \(h_0 = (0, 0, 1)\)

核心代码段如下（完整代码链接）：

w_xh = np.array([[1], [0], [0]])  # (1)

w_hh = np.array([[0, 0, 0],       # (2)
                 [1, 0, 0],       # (3)
                 [0, 0, 1]])      # (4)

w_yh = np.array([1, 1, -1])       # (5)

x_seq = [0, 1, 0, 1, 1, 1, 0, 1, 1]

h_t_prev = np.array([[0], [0], [1]])

for t, x in enumerate(x_seq):
    h_t = relu(w_hh @ h_t_prev + (w_xh @ x))
    y_t = relu(w_yh @ h_t)
    h_t_prev = h_t

1. 右侧项
   • x = 0 -> [0, 0, 0]
   • x = 1 -> [1, 0, 0]
2. 0 代表左侧项首行（仅用来自右侧项的值）
3. 将“当前”的值从之前的隐藏状态复制过来，成为“之前”
4. 保留底部的 1（有利于输出）
5. max(current + previous - 1, 0)

Computational Graphs⚓︎

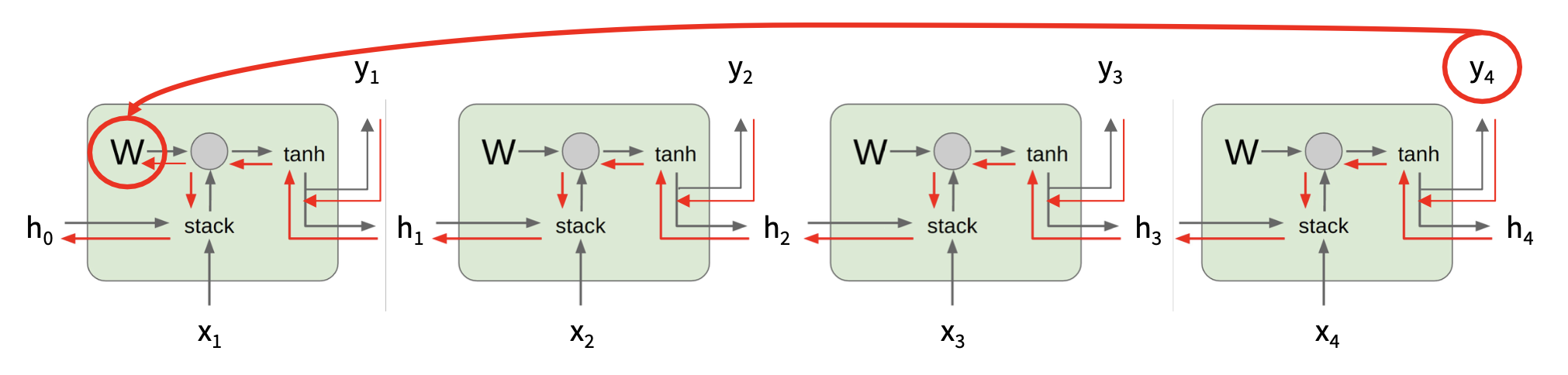
每一步重复使用相同的权重矩阵：

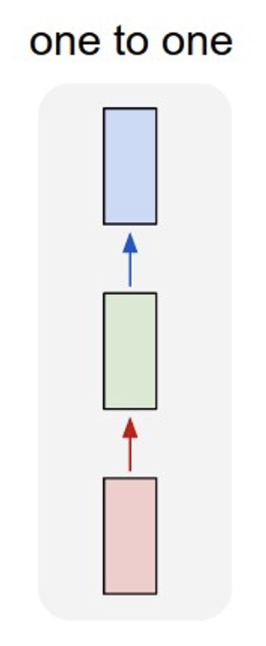
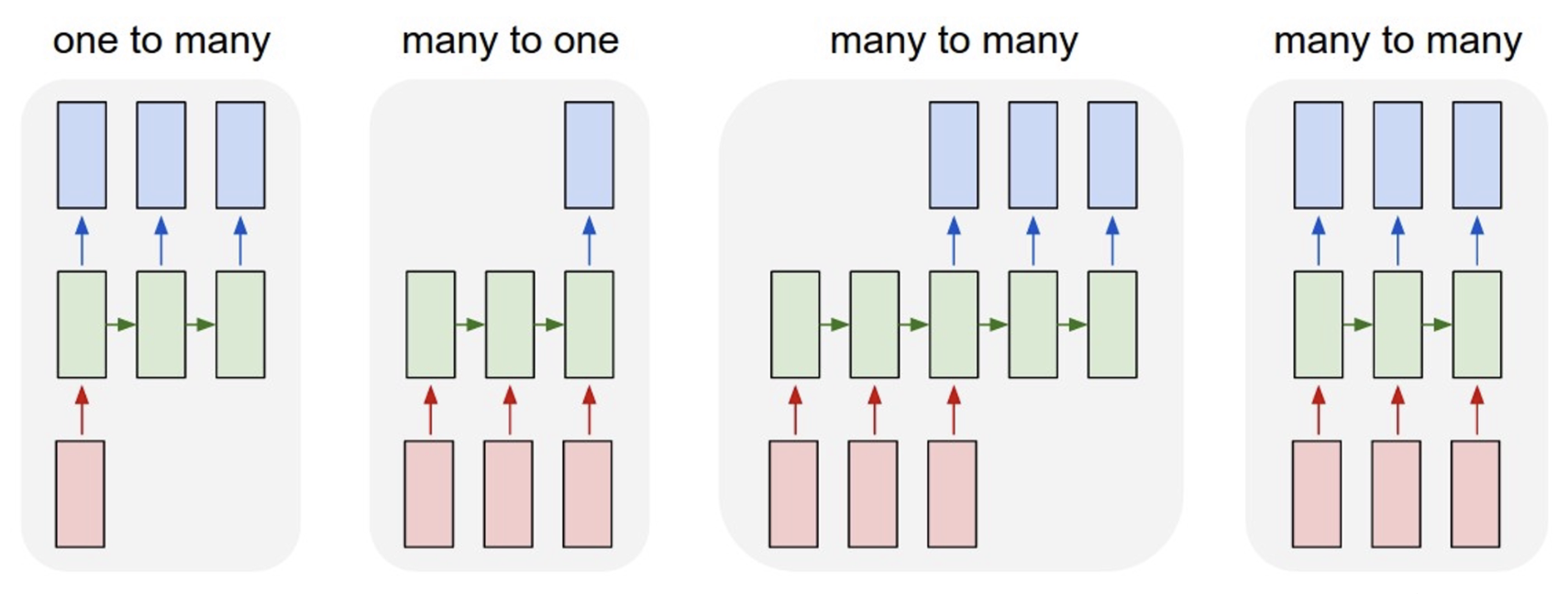
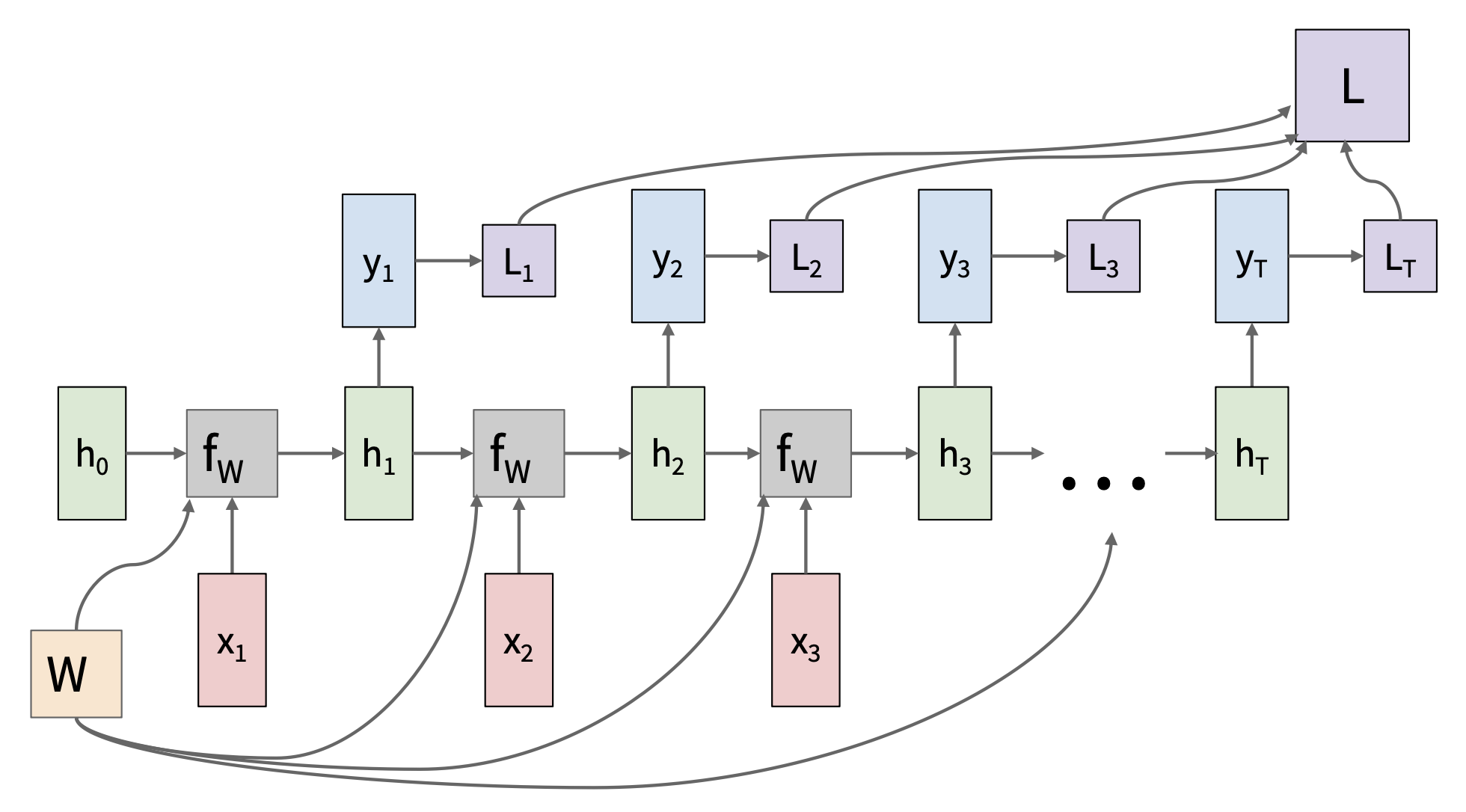
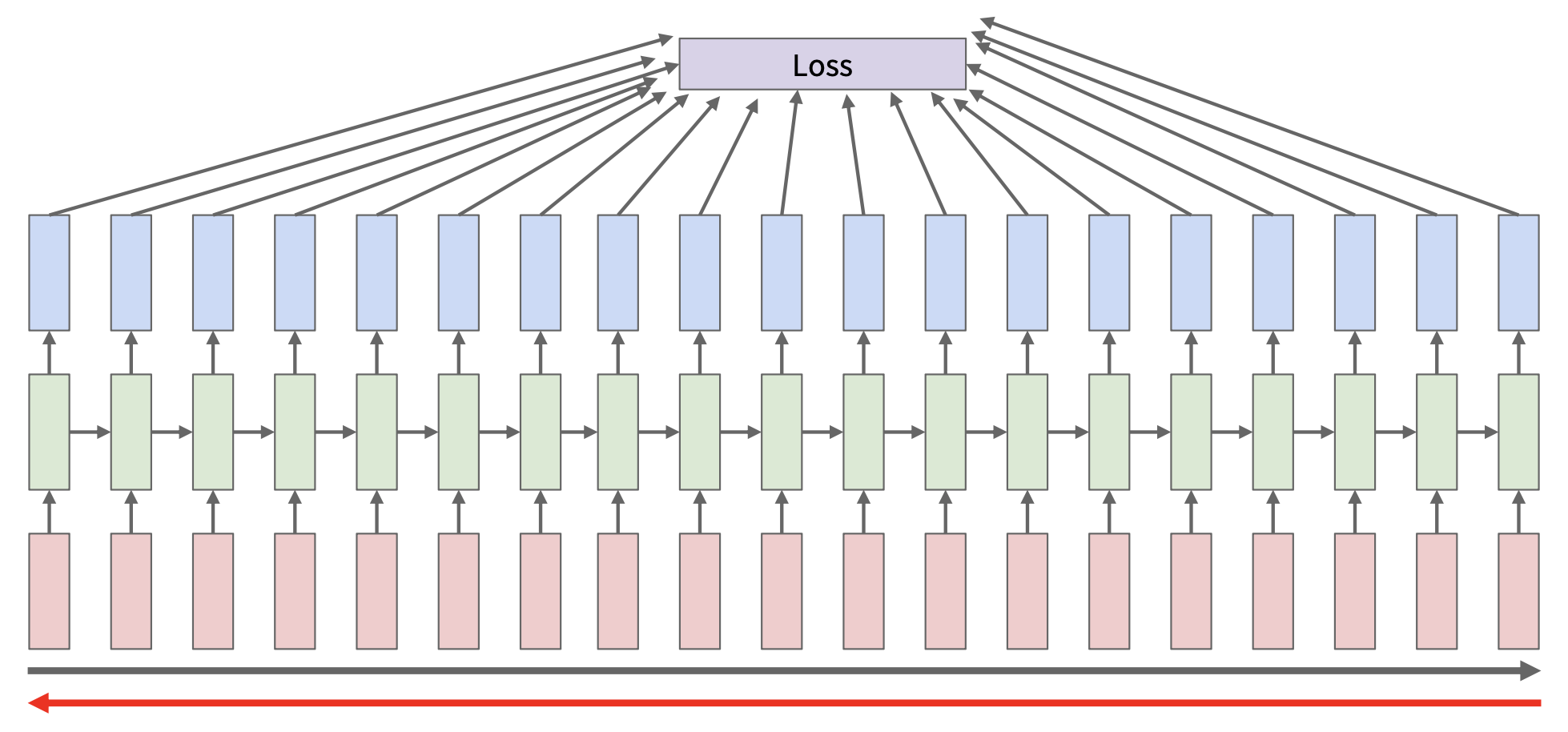
• 多对多：

  

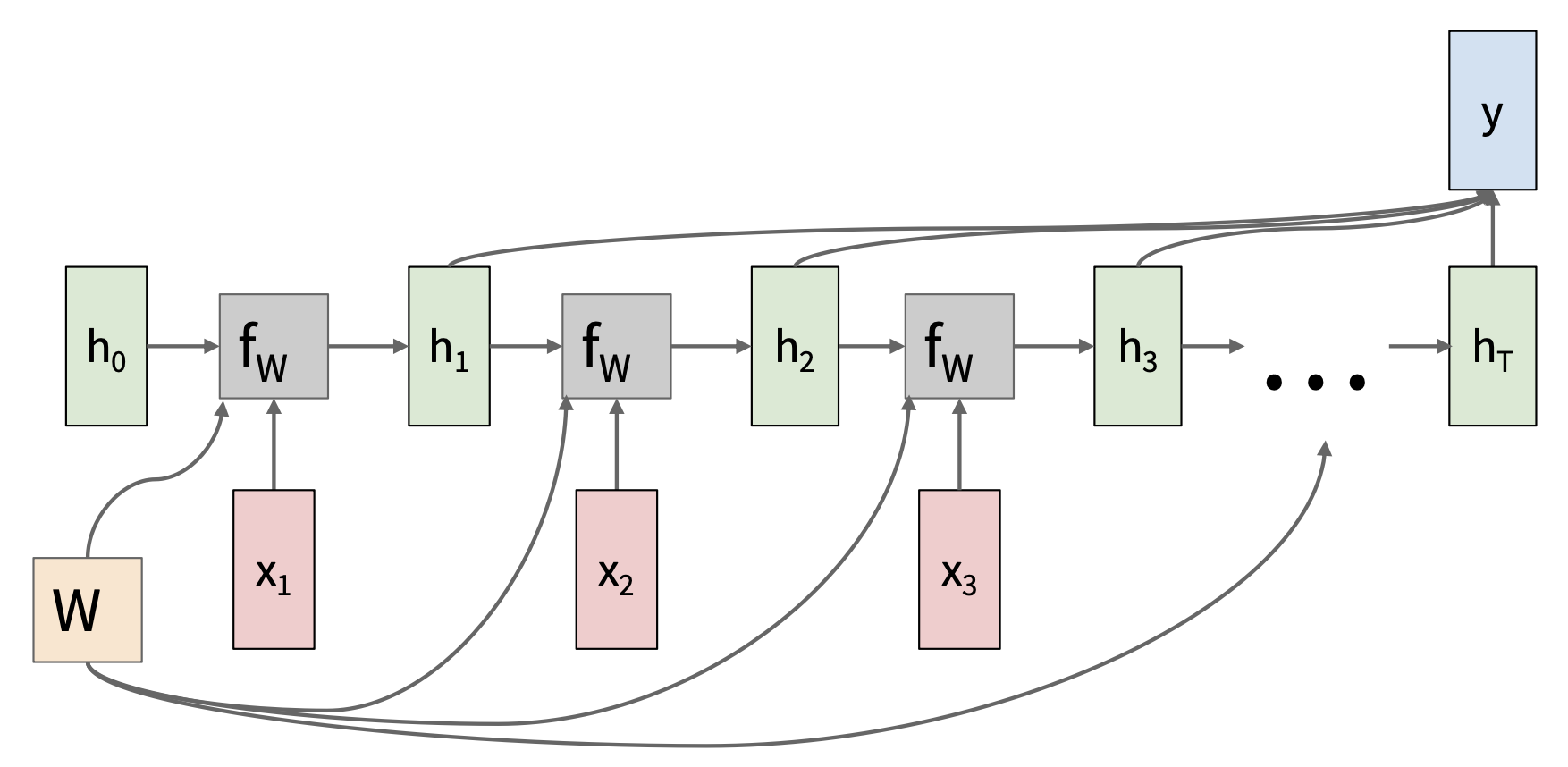
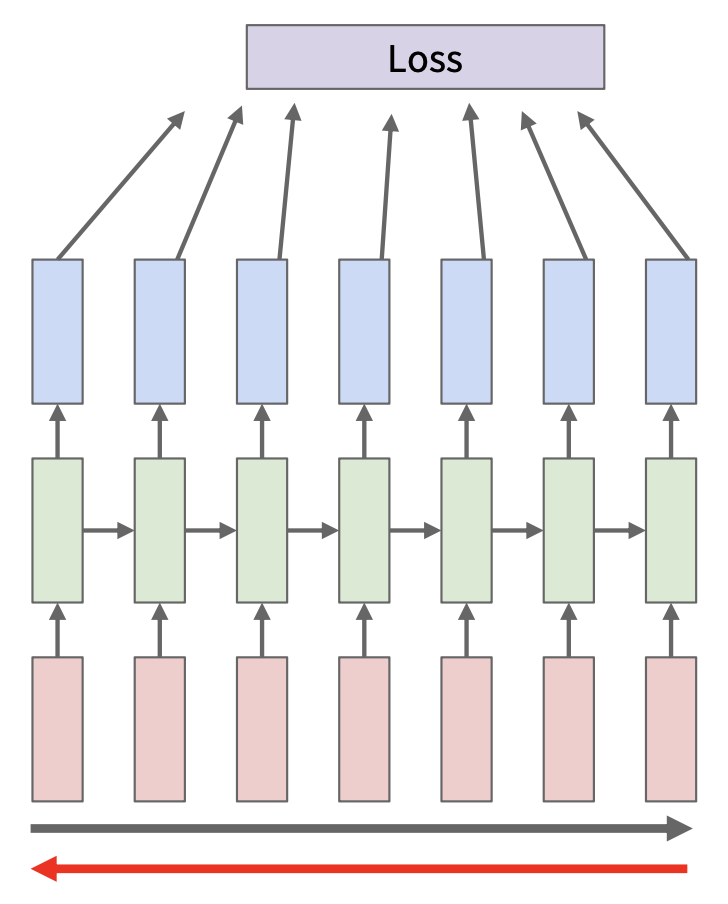
• 多对一：将输入序列编码为单个向量

  

• 一对多：从单个输入向量中产生输出序列

  

Backpropagation⚓︎

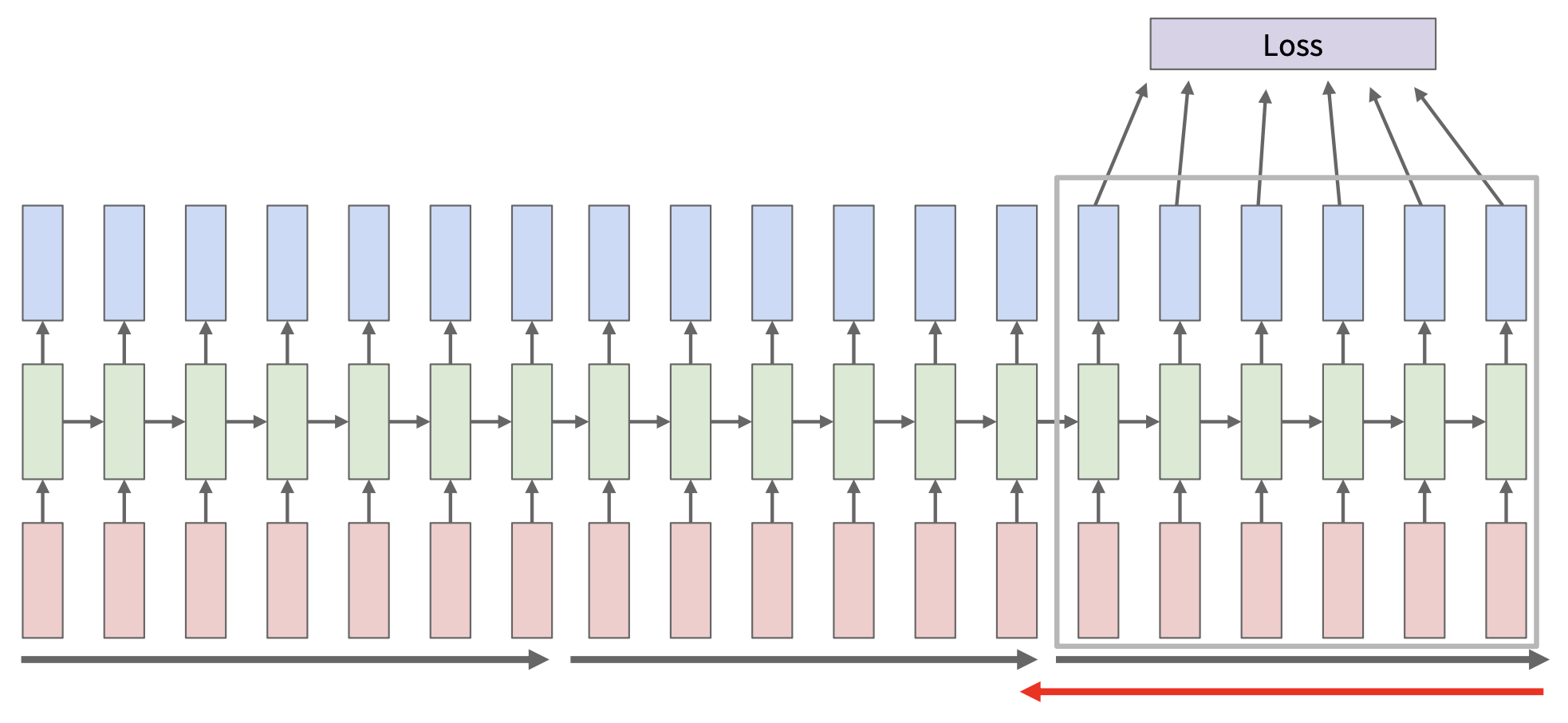
在 RNN 中，向前遍历整个序列以计算损失，然后向后遍历整个序列以计算梯度（反向传播）。

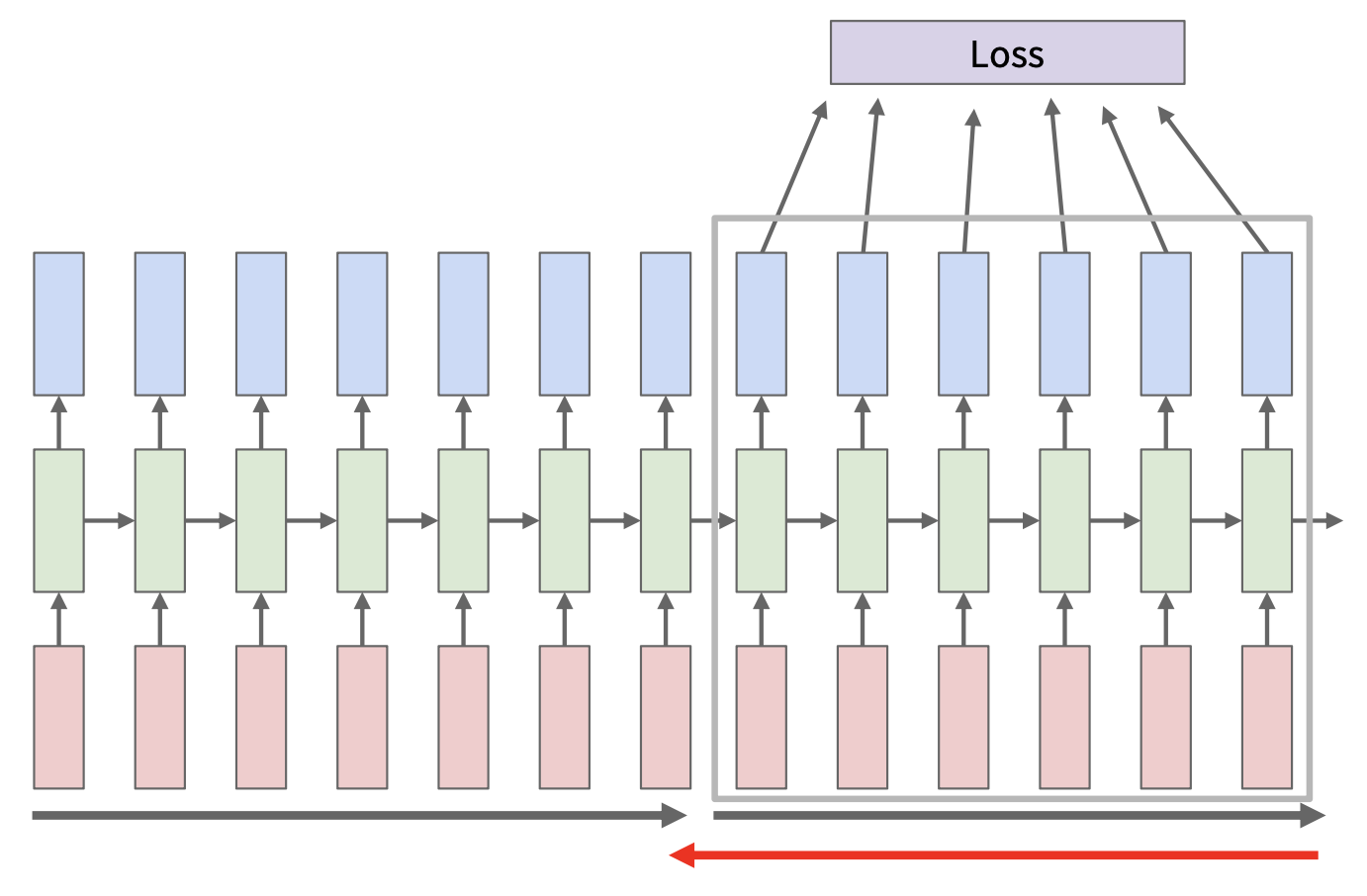
但对 RNN 而言，这样做会在长序列上消耗大量内存。因此在 RNN 上，实际做的是随时间截断的反向传播(truncated backpropagation through time, TBTT)：

• 在序列块(chunks) 中向前和向后遍历计算，而不是一次考虑整个序列
• 永远向前传递隐含状态，但仅在较少的步骤中进行反向传播
• 仍然在每个时间步计算梯度，依赖于上游梯度（每个时间步不再有损失）

Chunk 1Chunk 2Chunk 3

A More Pratical Example⚓︎

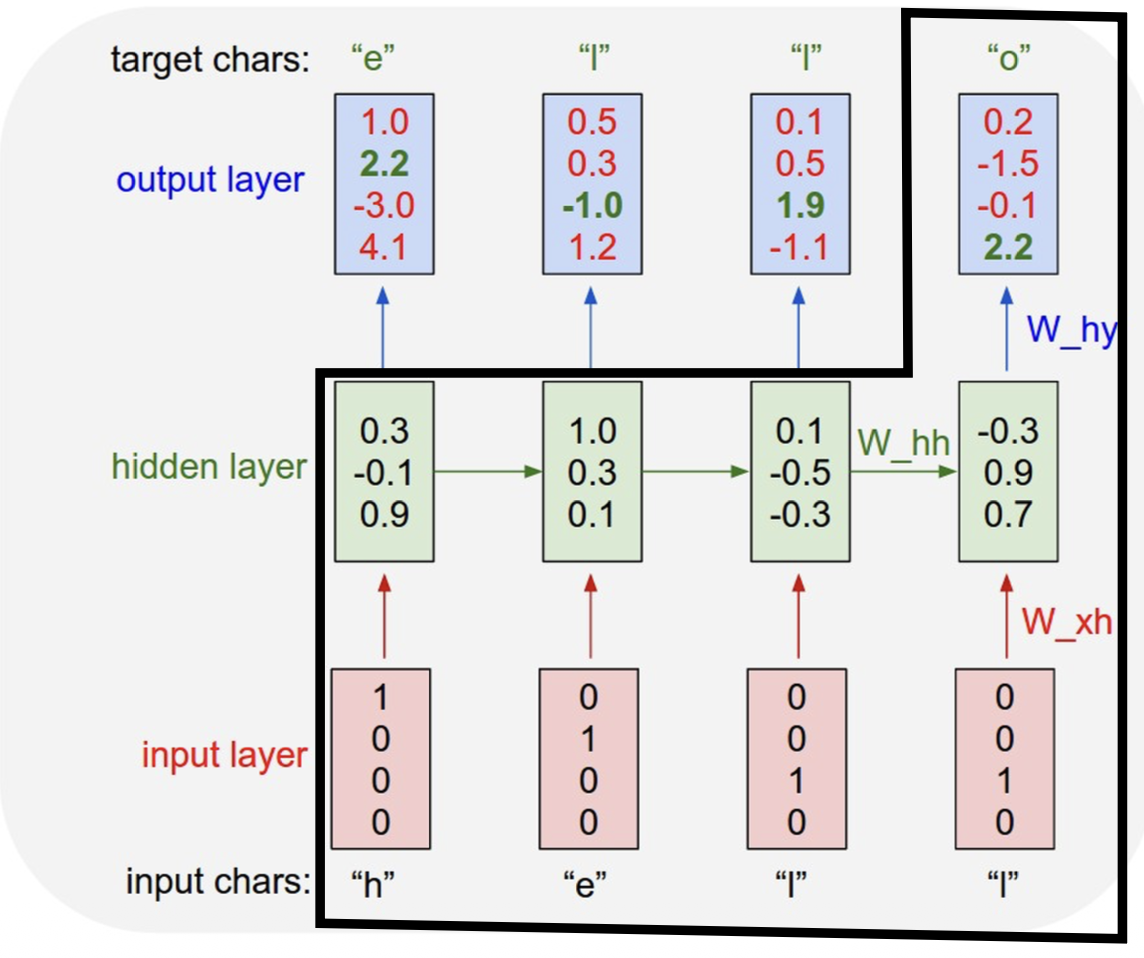
用 RNN 搭建一个字符级的语言模型 (character-level language model)

• 字母表：[h, e, l, o]
• 样例训练序列："hello"
• 给定前 t - 1 个字符，生成第 t 个字符

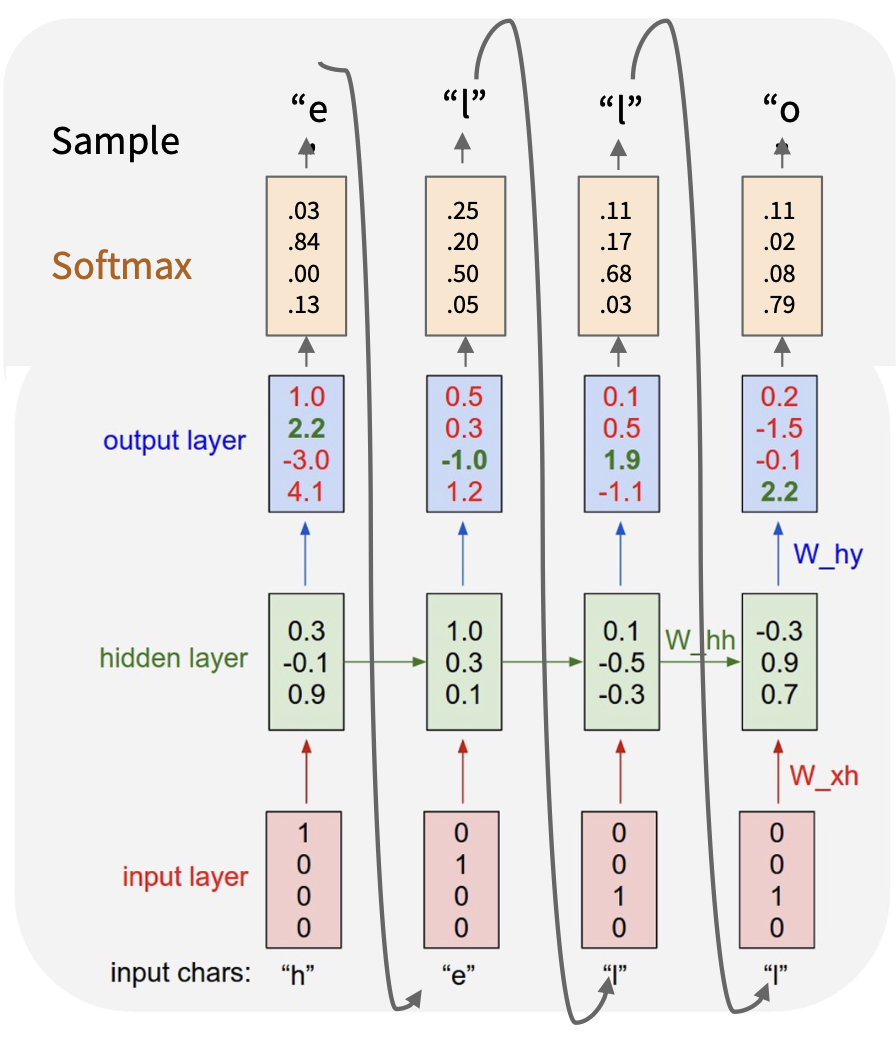
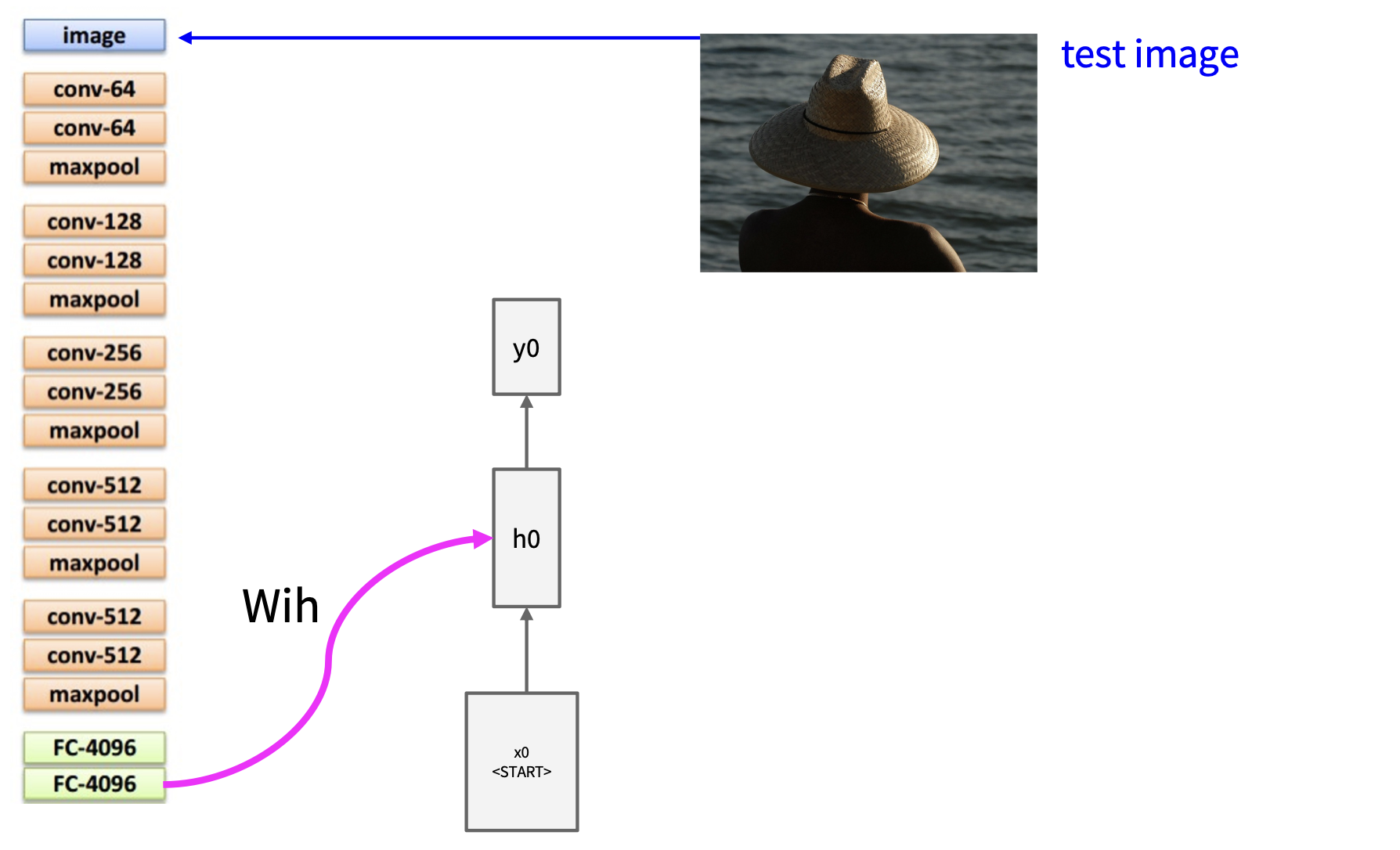
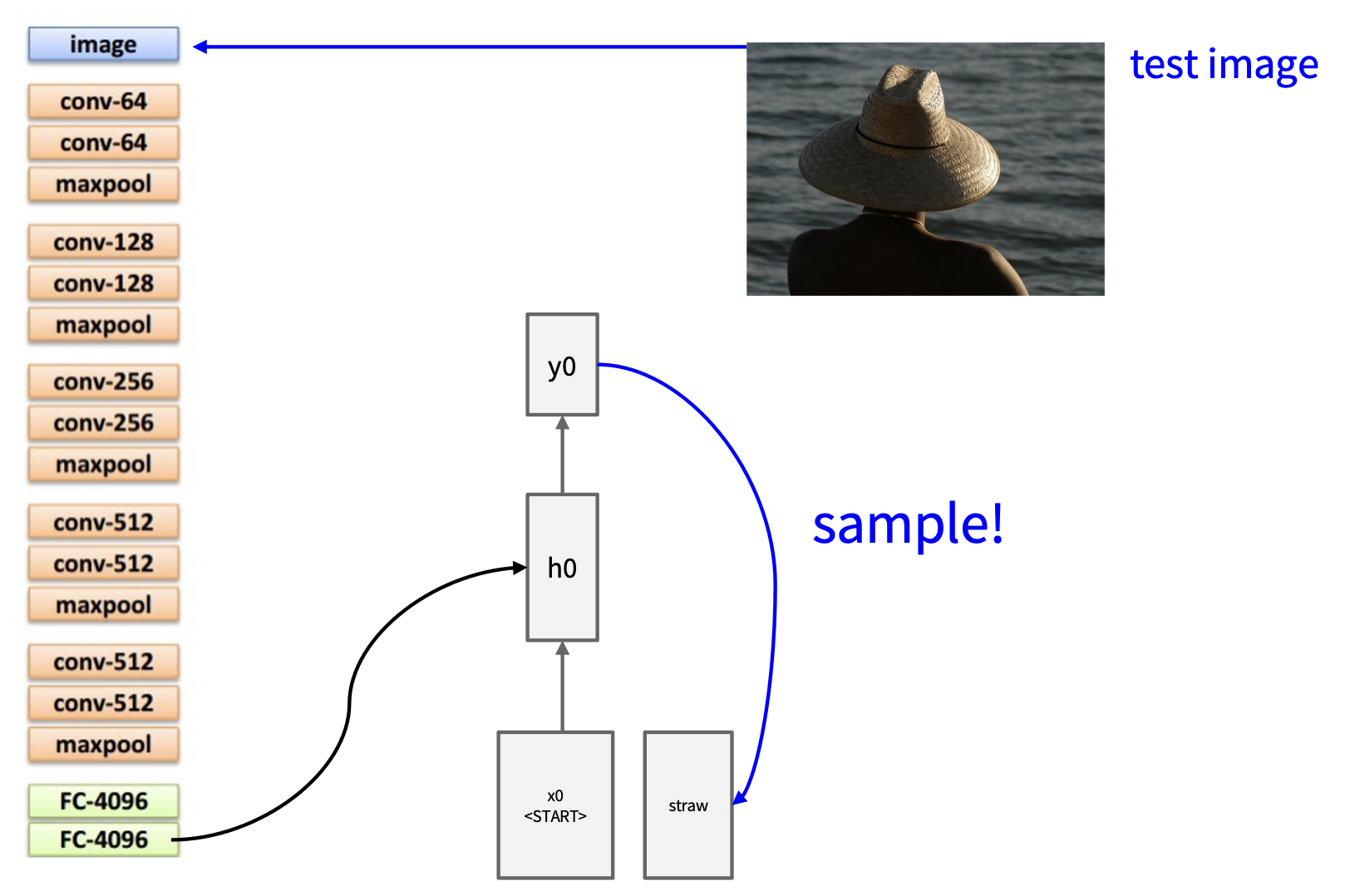
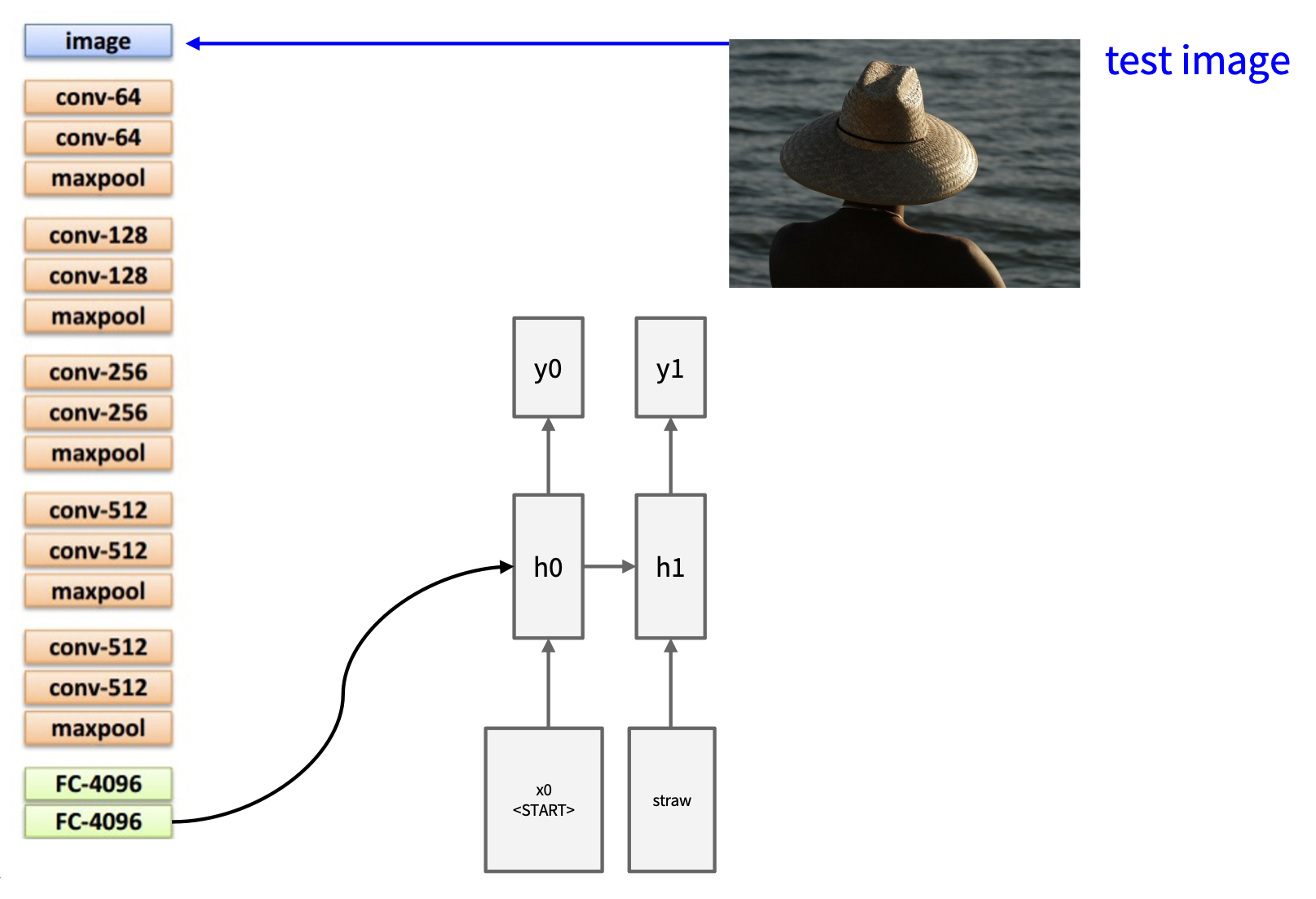
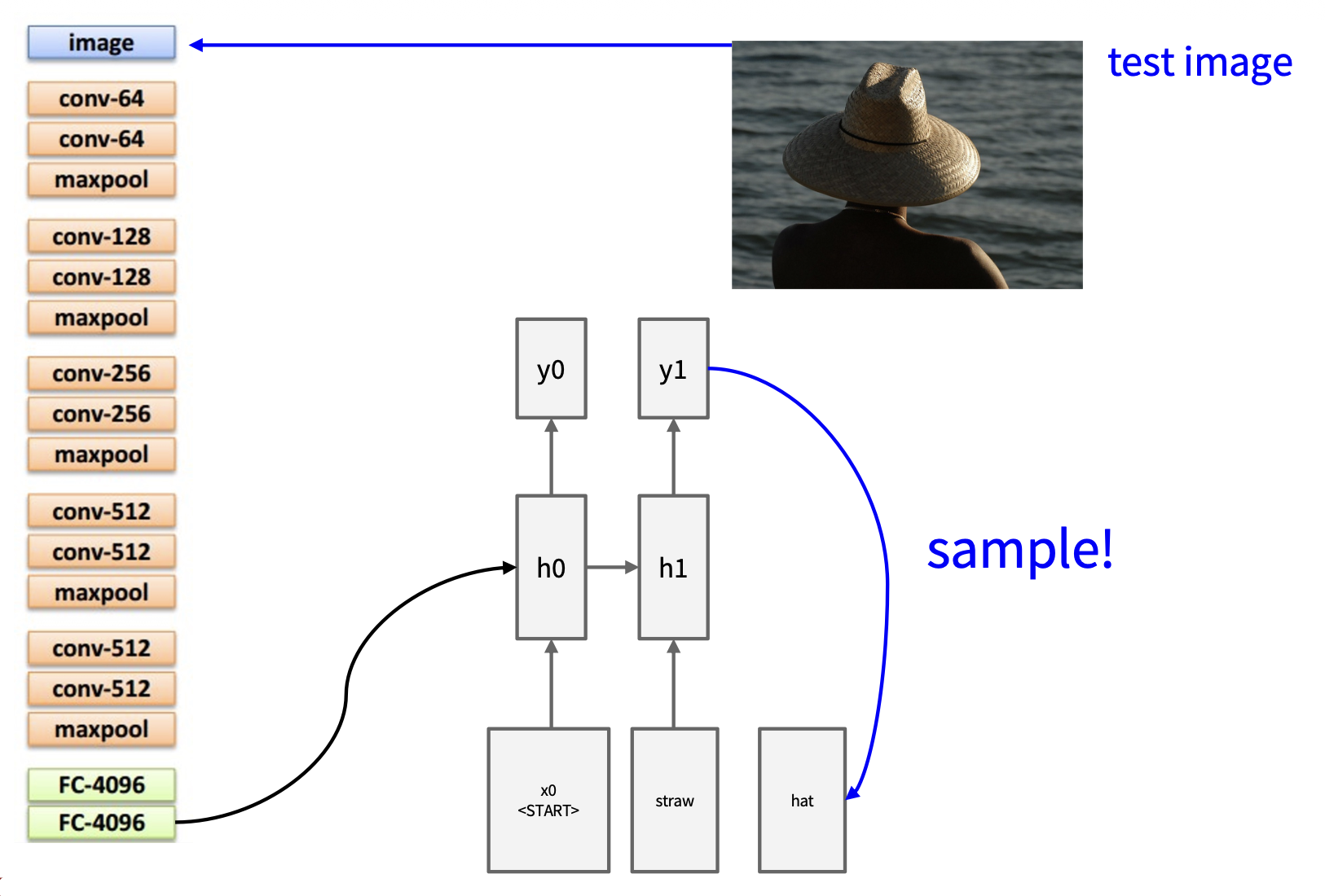
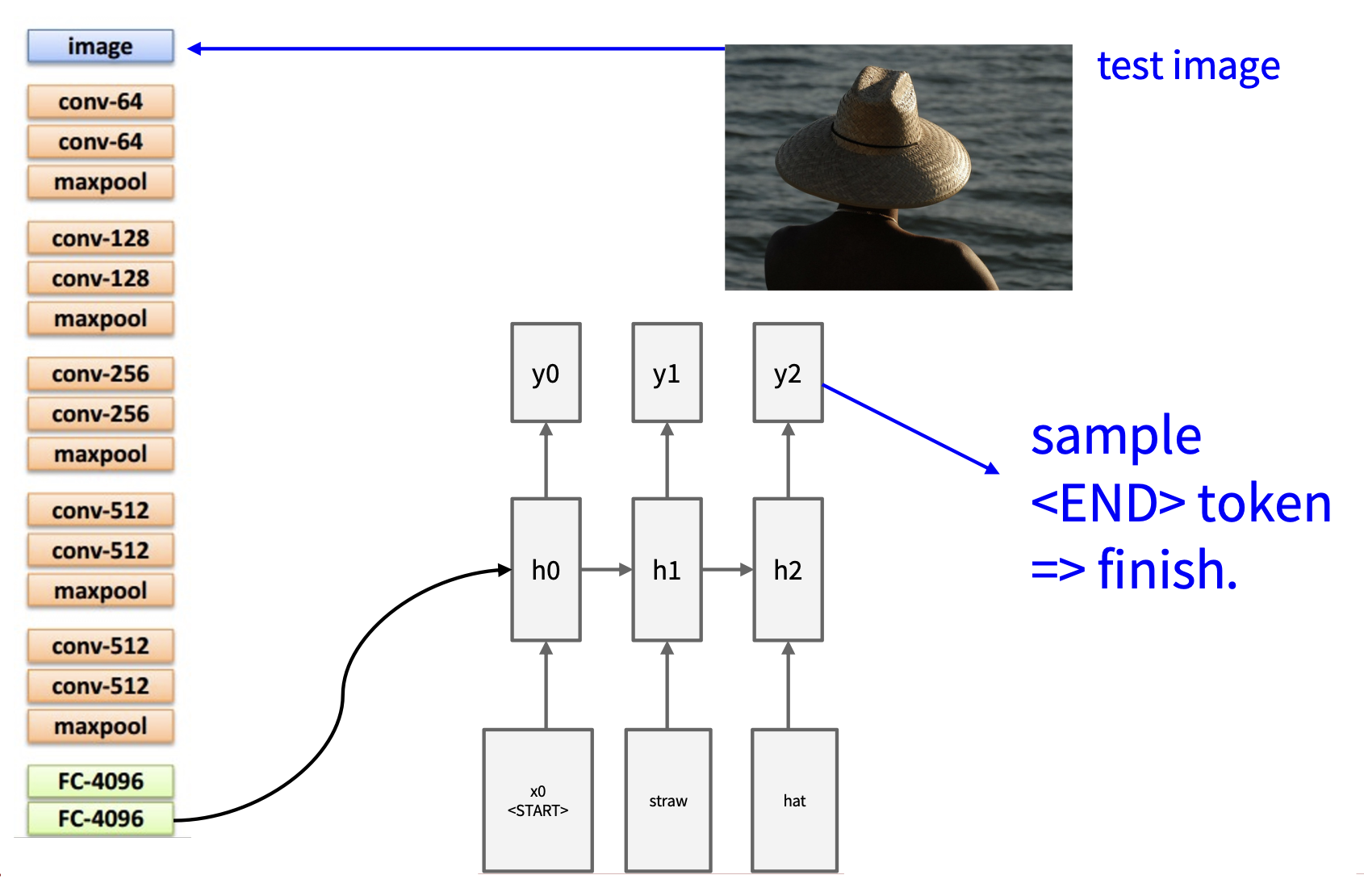
测试时每次仅采样一个字符，将输出反馈给模型（作为下一次的输入）：

矩阵 - 独热向量（输入）乘法的结果是从权重矩阵中提取某一列。

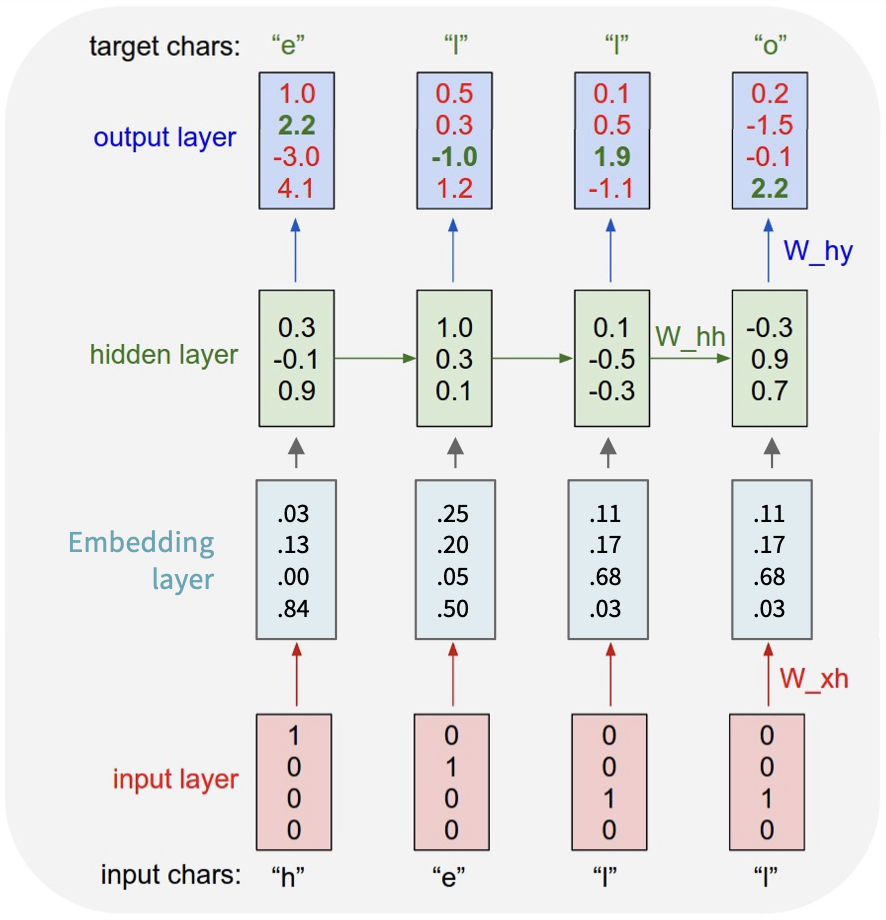
我们通常在输入层和隐藏层之间放置一个单独的嵌入层。

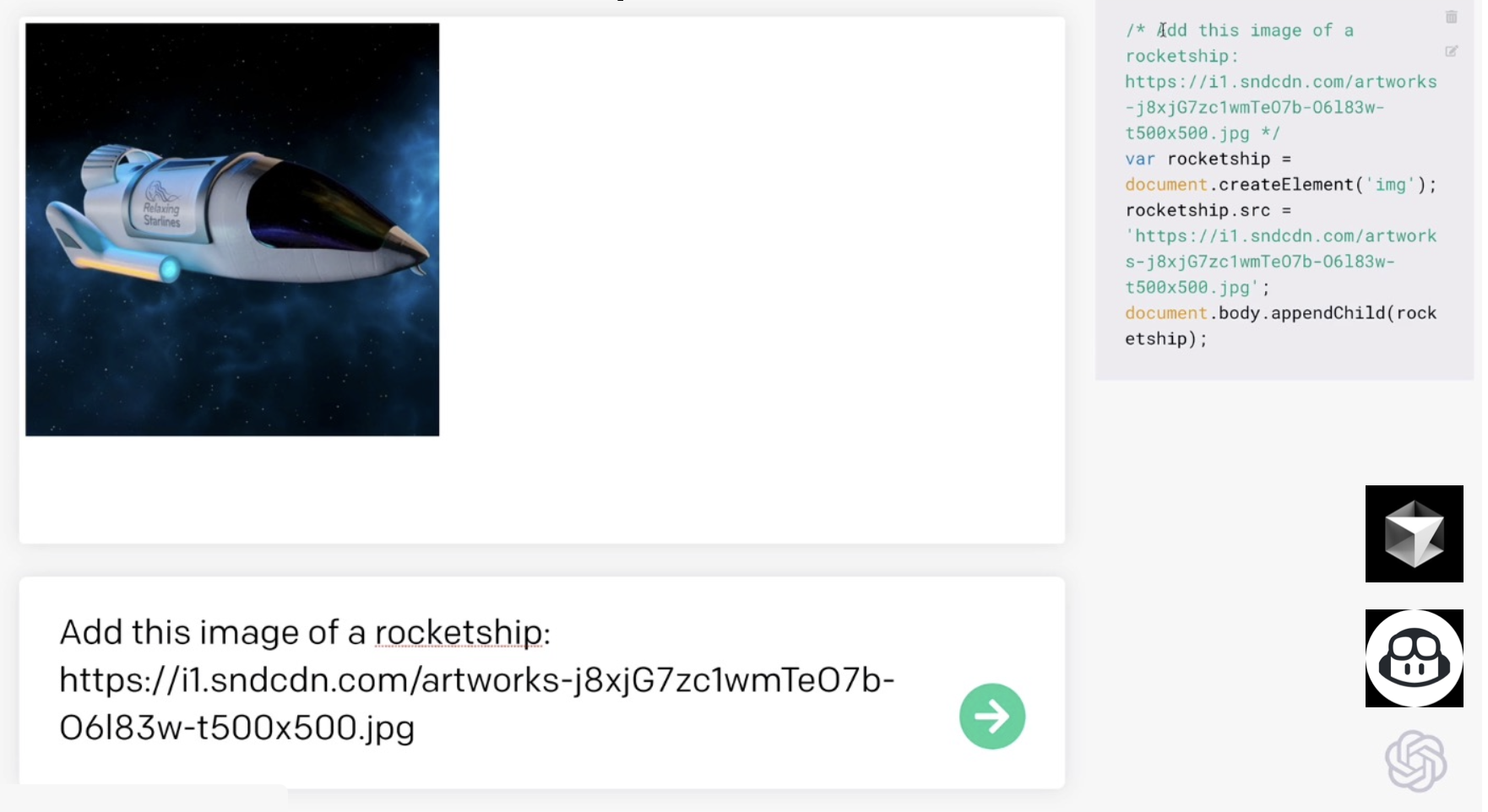
源代码仅 112 行（Python）（链接）

实际应用

文学作品代码

让 RNN 基于莎士比亚的作品训练：

可以看到，随着训练次数的增加，模型生成文本的质量越来越高：

最终成果：

让模型阅读 Linux 源码，最终它能生成这样的 C 代码：

static void do_command (struct seg_file *m, void *v)
{
    int column = 32 << (cmd[2] & 0x80);
    if (state)
        cd = (int) (int_state ^ (in_8(&ch->ch_flags) & Cmd) ? 2: 1);
    else
        seg = 1;
    for (i = 0; i < 16; i++) {
        if (k & (1 << 1))
            pipe = (in_use & UMXTHREAD_UNCCA) +
                ((count & 0x00000000fffffff8) & 0x000000f) << 8;
        if (count == 0)
            sub(pid, ppc_md.kexec_handle, 0x20000000) ;
        pipe_set_bytes(1, 0) ;
    }
    /* Free our user pages pointer to place camera if all dash */
    subsystem_info = &of_changes[PAGE_SIZE];
    rek_controls(offset, idx, &soffset);
    /* Now we want to deliberately put it to device */
    control_check_polarity(&context, val, 0);
    for (i = 0; i < COUNTER; i++)
        seą_puts(s, "policy ");
}

现在的 OpenAI Codex, GitHub Copilot, Cursor IDE 已经具备相当不错的代码生成能力了。

Searching for Interpretable Cells⚓︎

我们将展开后的 RNN 中的隐含状态看作神经网络上的一个个细胞。我们希望能找到那些可解释的(interpretable) 细胞，即有明确功能和目的的细胞，比如说：

• 引用检测细胞

  

• 行长度追踪细胞

  

• if 语句细胞

  

• 注释细胞

  

• 代码深度细胞

  

Applications⚓︎

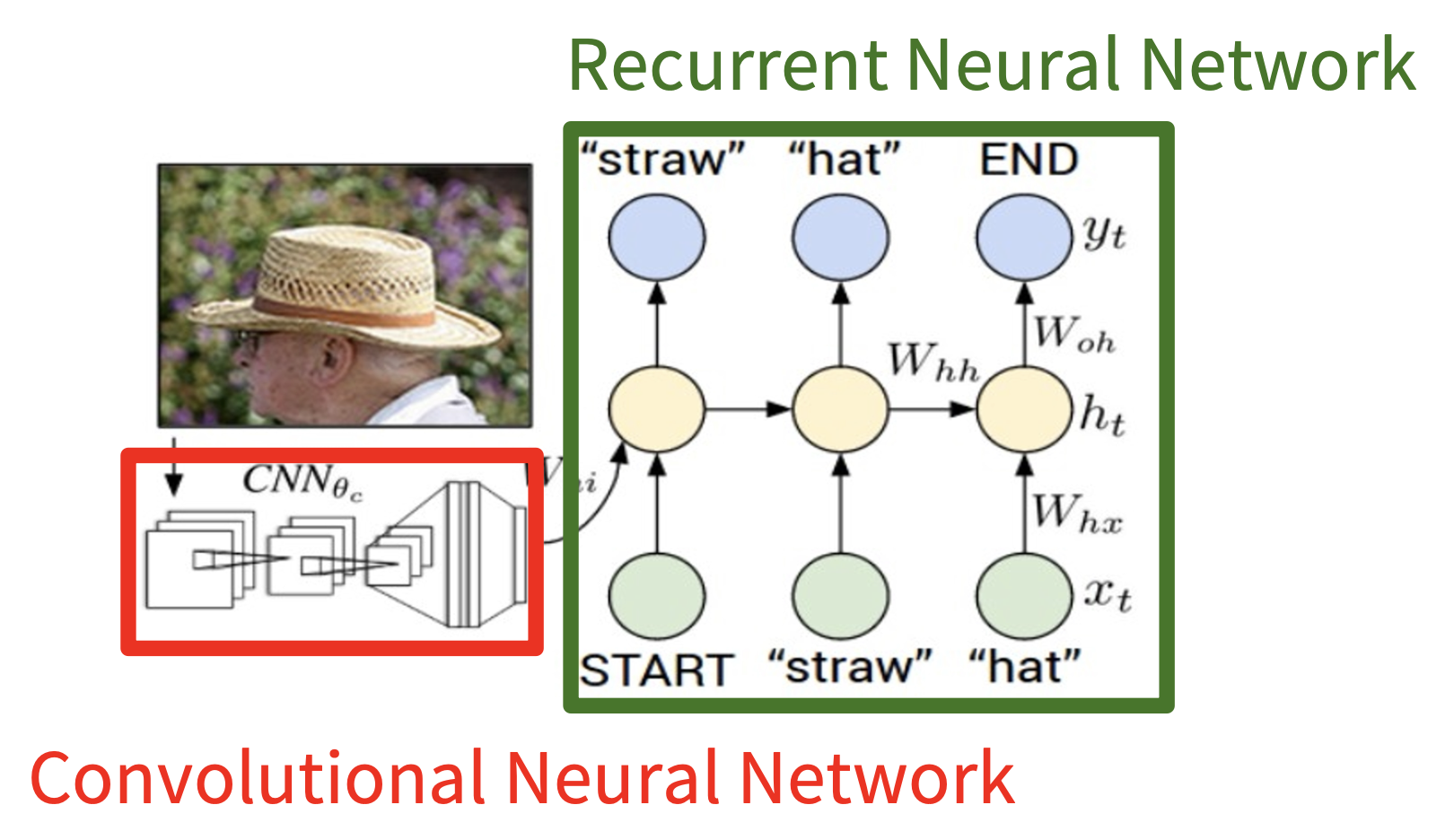
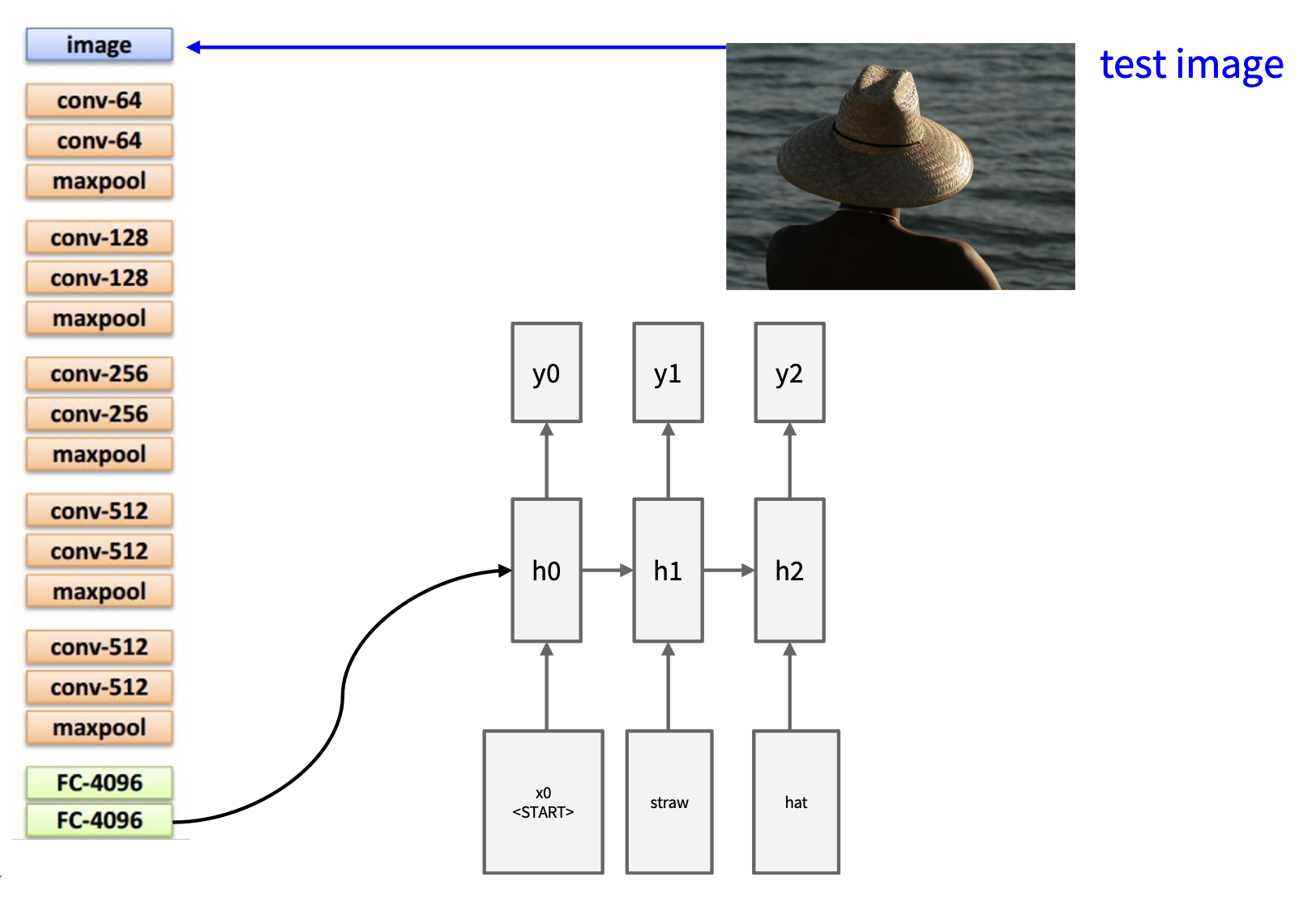
Image Captioning⚓︎

图像字幕的模型同时用到了 CNN 和 RNN。

Step 0Step 1Step 2Step 3Step 4

去掉了最后的全连接层

• 图像经过 CNN 后产生权重矩阵 \(W_{ih}\) 给 RNN
• 而 RNN 的隐含状态方程变为了 \(h = \tanh (W_{xh} \cdot x + W_{hh} \cdot h \textcolor{red}{+ W_{ih} \cdot v})\)

采样前一次输出结果，作为下一次的输入：

同上

若采样发现 token，意味着任务完成，模型停止运行。

结果：

• 成功例子：

  

• 失败例子：

  

Visual Question Answering (VQA)⚓︎

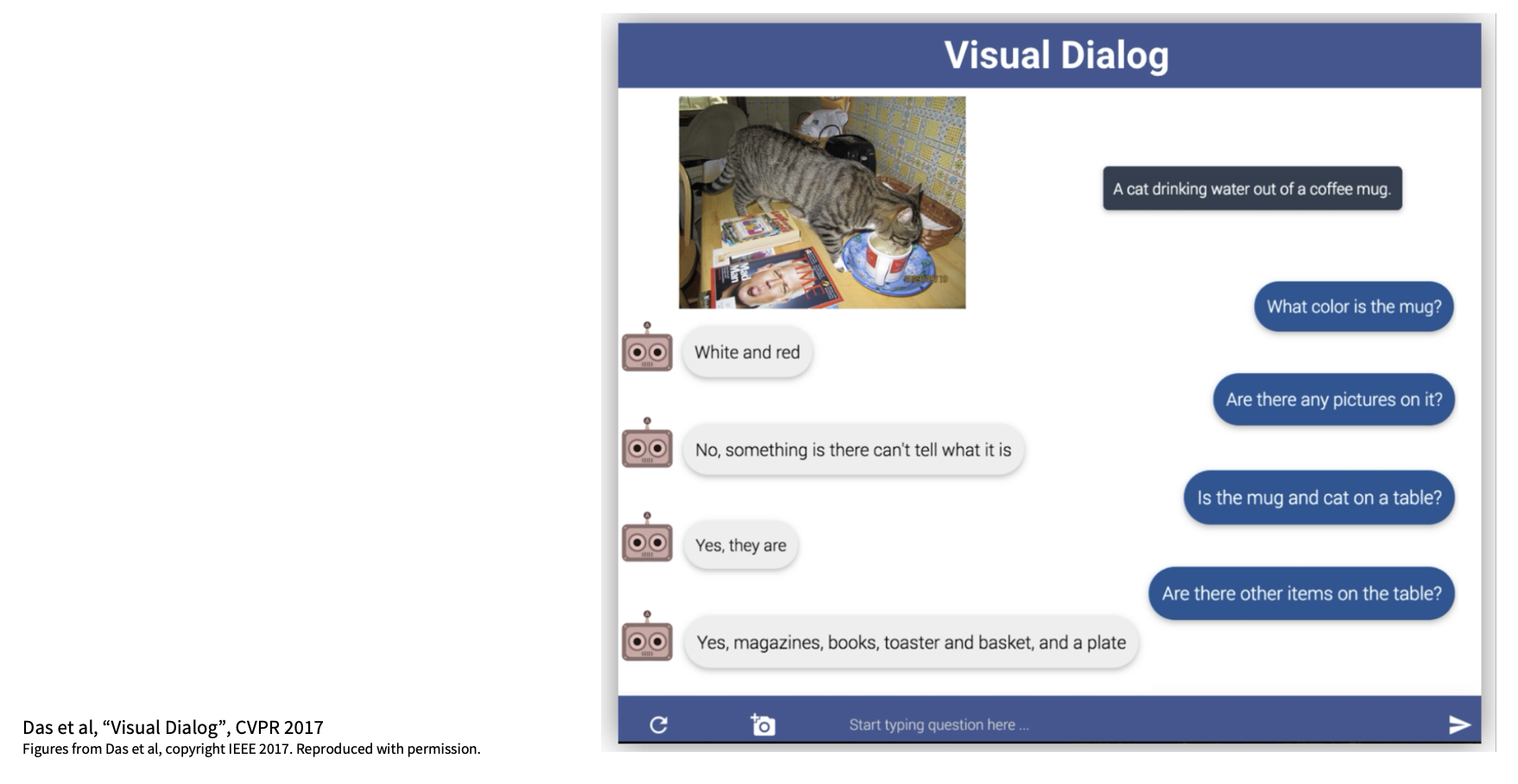
Visual Dialog⚓︎

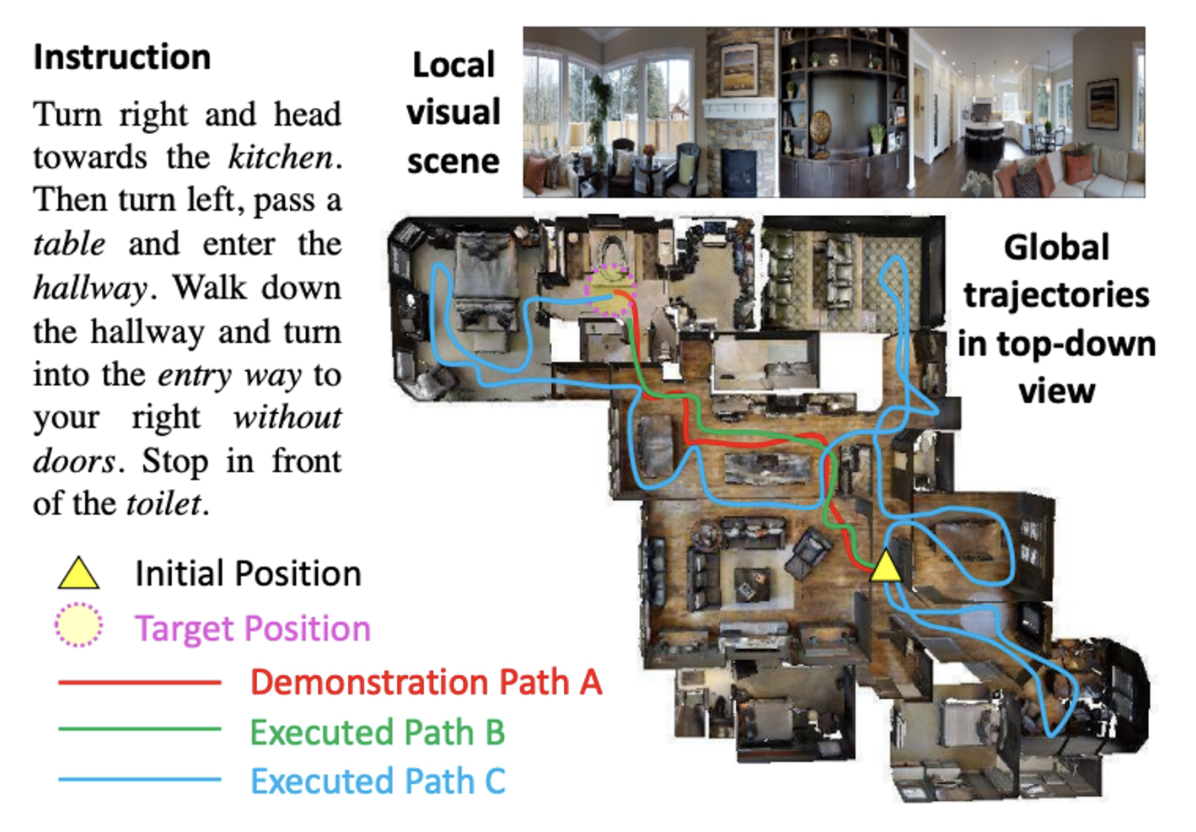
Visual Language Navigation⚓︎

• 智能体将指令编码为语言
• 当视觉输入在一次移动后改变时，用 RNN 生成一系列的移动

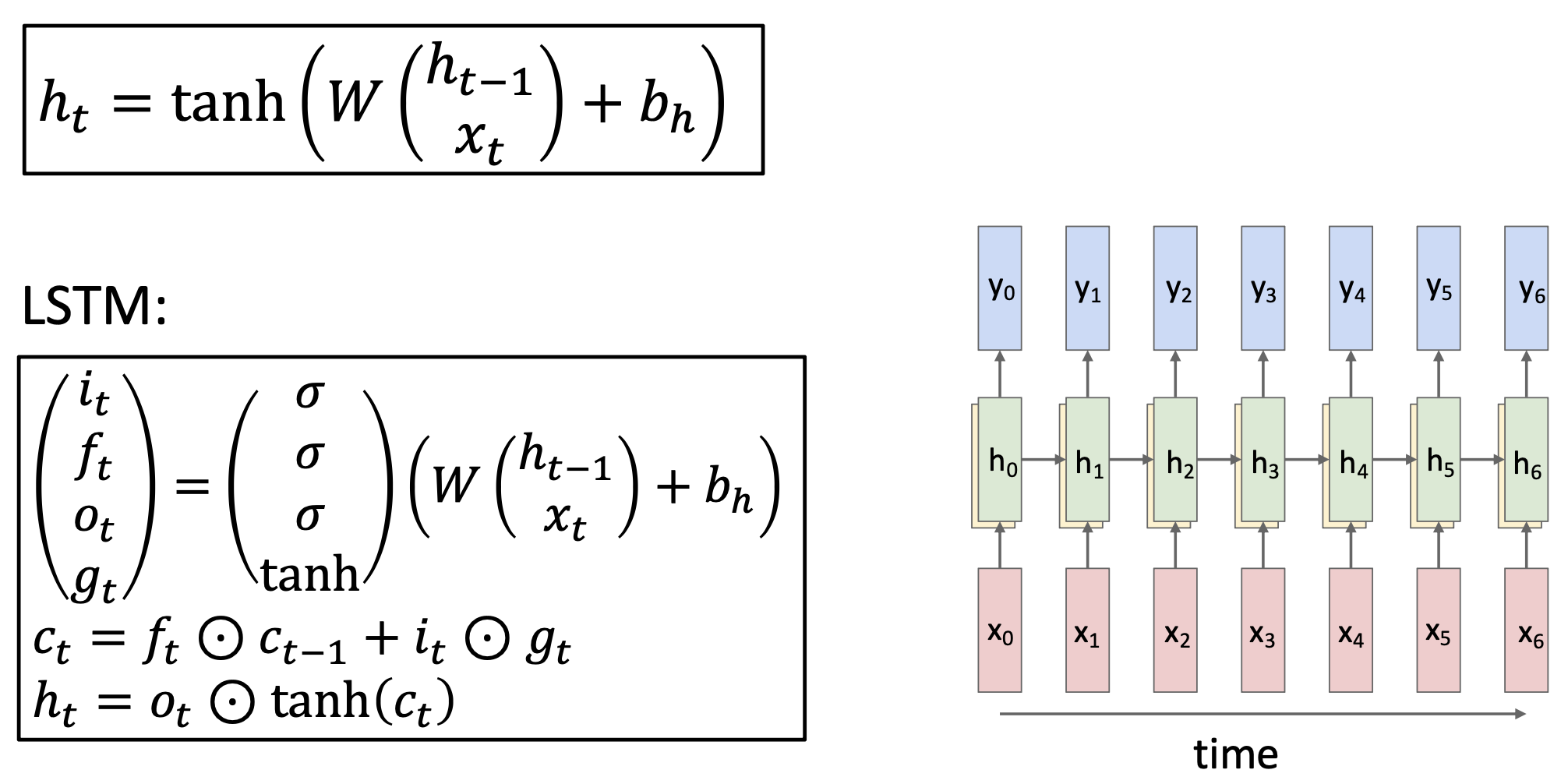
Long Short Term Memory (LSTM)⚓︎

普通 RNN 的问题

普通 RNN 的梯度流：

从 \(h_t\) 到 \(h_{t-1}\) 的反向传播乘以 \(W\)（实际上是 \(W_{hh}^T\)）。因此： $$ \frac{\partial h_t}{\partial h_{t-1}} = \tanh' \left( W_{hh} h_{t-1} + W_{xh} x_t \right) W_{hh} $$

在多个时间步上的梯度：

\[ \begin{align*} \frac{\partial L}{\partial W} &= \sum_{t=1}^{T} \frac{\partial L_t}{\partial W} \\ \frac{\partial L_T}{\partial W} &= \frac{\partial L_T}{\partial h_T} \frac{\partial h_T}{\partial h_{T-1}} \cdots \frac{\partial h_1}{\partial W} = \frac{\partial L_T}{\partial h_T} \left( \prod_{t=2}^{T} \frac{\partial h_t}{\partial h_{t-1}} \right) \frac{\partial h_1}{\partial W} \\ & = \frac{\partial L_T}{\partial h_T} \left( \prod_{t=2}^{T} \tanh' \left( W_{hh} h_{t-1} + W_{xh} x_t \right) \right) W_{hh}^{T-1} \frac{\partial h_1}{\partial W} \end{align*} \]

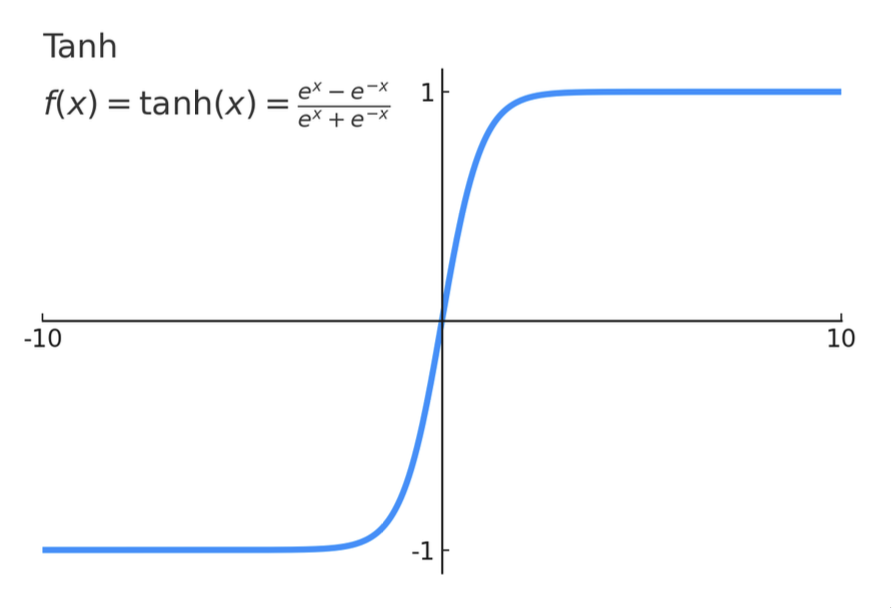
但是根据 \(\tanh'\) 的图像，其值几乎总是 < 1（只有在接近 0 的时候取值较大），所以这样计算出来的梯度值近乎消失 (vanishing gradient)。

若假设没有非线性，考虑 \(W_{hh}^{T-1}\) 的最大奇异值：

• • 解决方案——梯度裁剪(gradient clipping)：若范数过大，则缩放梯度

  > 1 -> 梯度爆炸

  grad_norm = np.sum(grad * grad)
  if grad_norm > threshold:
      grad *= (threshold / grad_norm)
  

• < 1 -> 梯度消失

  • 解决方案：改变 RNN 架构

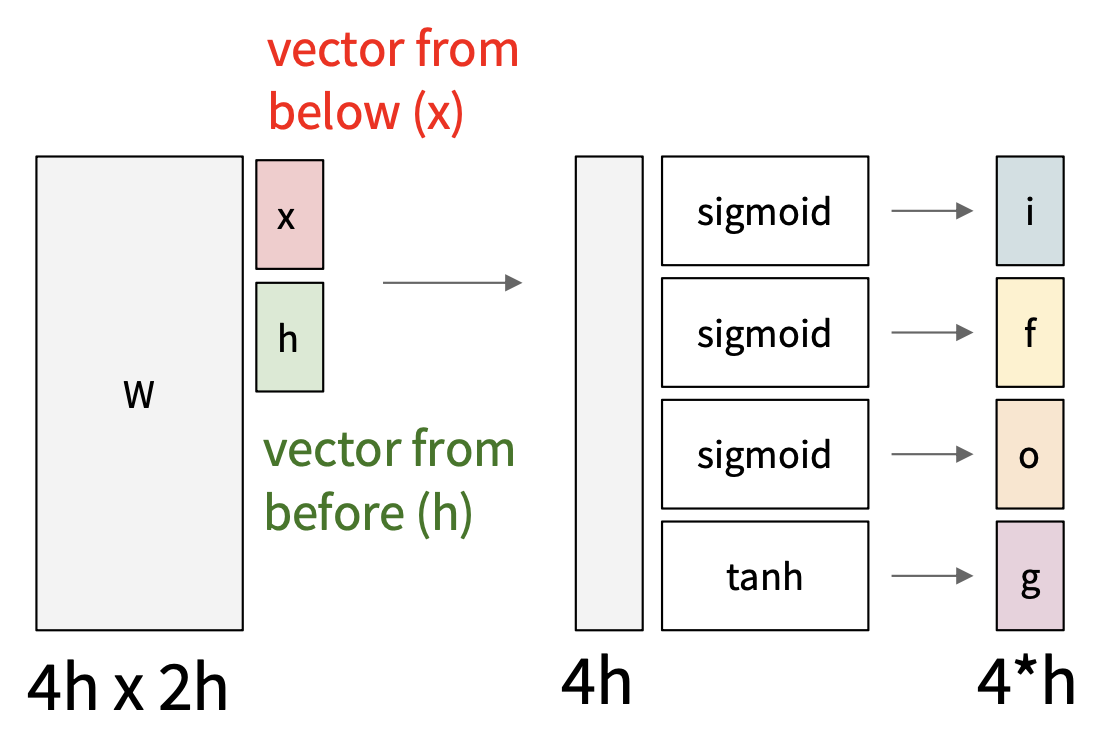
长短期记忆(long short term memory, LSTM) 的方程如下：

其中：

• \(\begin{pmatrix} i \\ f \\ o \\ g \end{pmatrix}\) 表示四个门

  
  • \(i\)：输入门 (input gate)，是否向细胞写入
  • \(f\)：遗忘门 (forget gate)，是否删除细胞
  • \(o\)：输出门 (output gate)，要揭露多少细胞
  • \(g\)：门门 (Gate gate)，向细胞写入多少东西

• \(c_t\) 表示细胞状态

• \(h_t\) 表示隐含状态

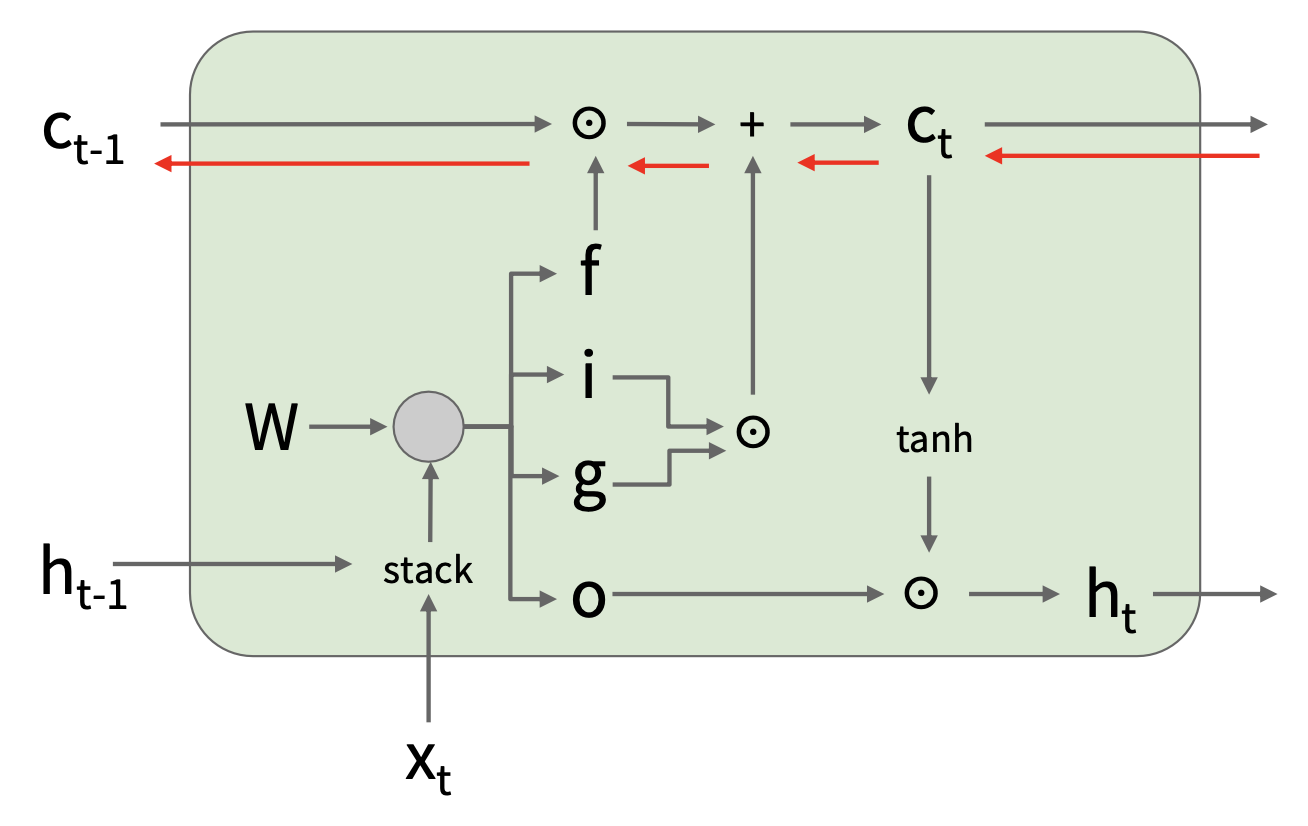
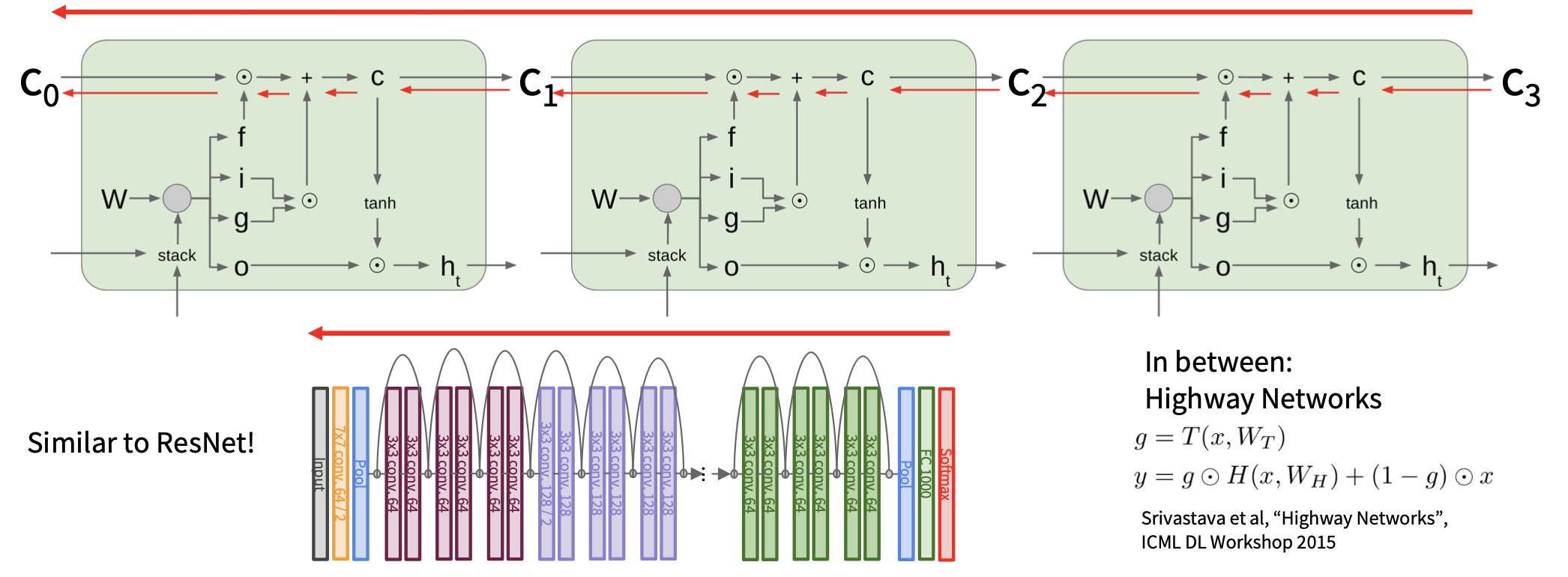
LSTM 的内部结构如下：

从 \(c_t\) 到 \(c_{t-1}\) 的反向传播仅做和 \(f\) 的逐元素乘法，而不是和 \(W\) 的矩阵乘法。

梯度流不可中断！

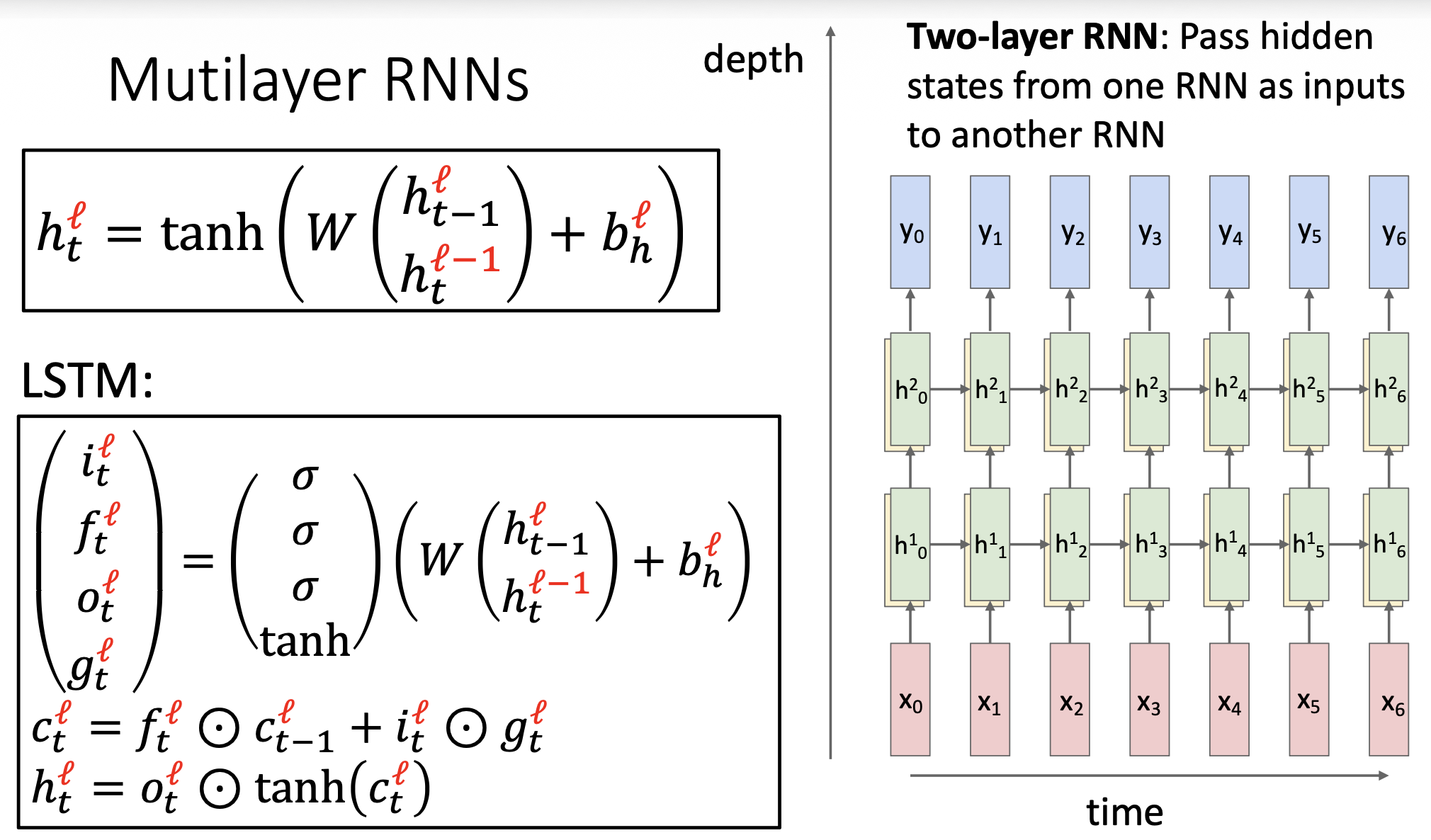
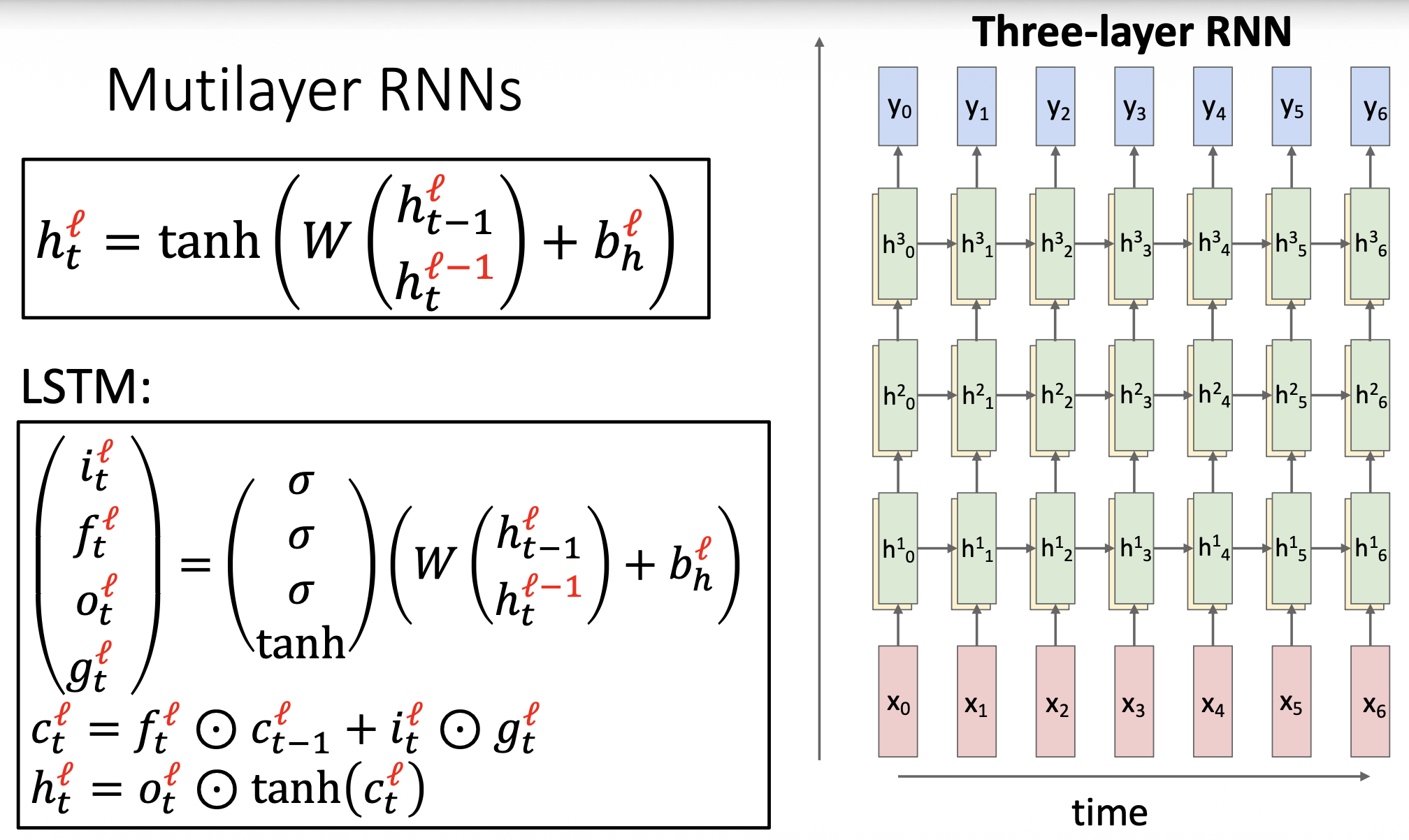
Multilayer RNNs⚓︎

单层 RNNs 多层 RNNs

现代 RNNs

• 有时称为「状态空间模型 (state space models)」
  • 隐含状态
• 主要优势：
  • 无限的上下文长度
  • 计算与序列长度成线性关系

评论区