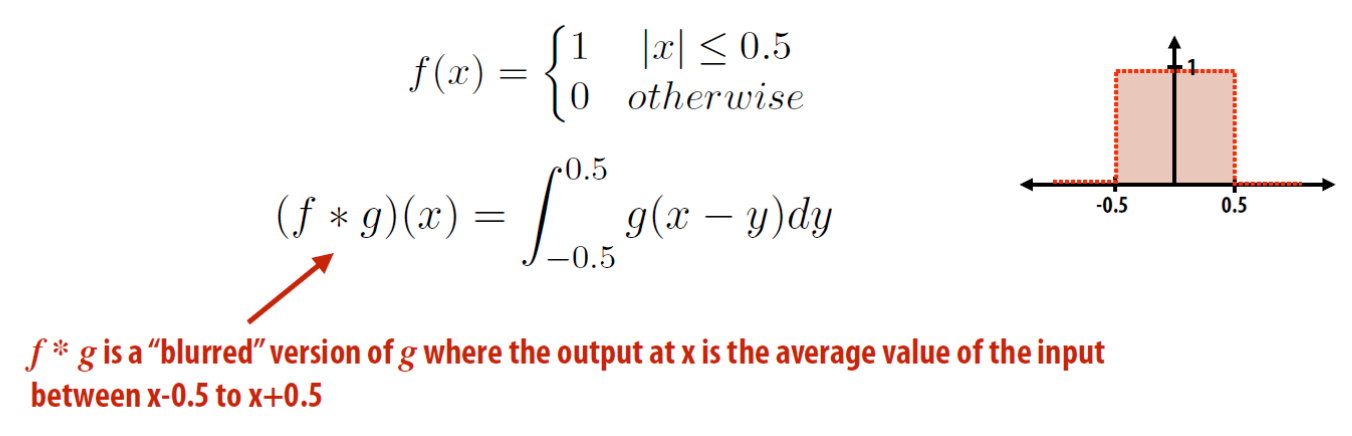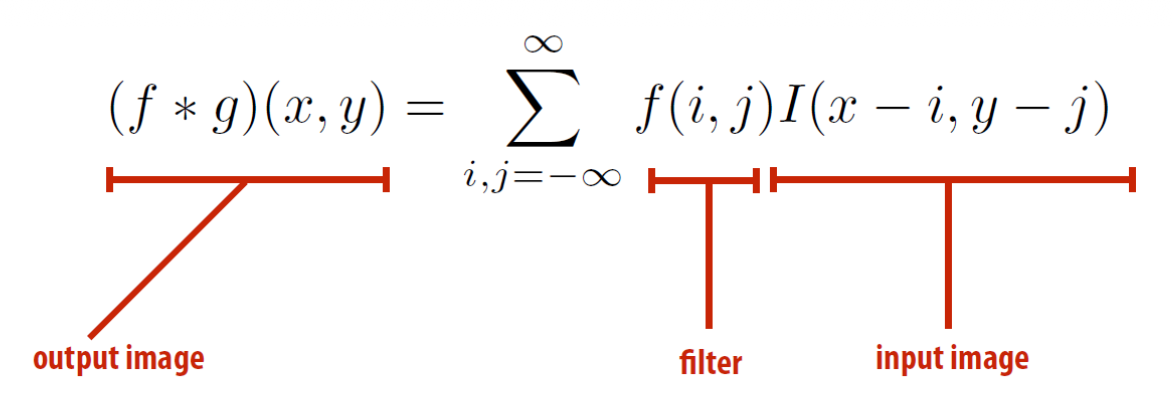Image Processing⚓︎
约 1641 个字 预计阅读时间 8 分钟
核心知识
-
基本图像处理操作:
- 增加对比度、颜色反转
- 模糊:盒滤波、高斯滤波、
双边滤波- 数学原理:卷积
- 锐化:垂直 / 水平边缘检测
-
图像缩放
- 保持宽高比
- 缩小(降采样
) :增加采样率、反走样(先模糊再采样) - 放大(升采样
) :插值
- 缩小(降采样
- 改变宽高比
- 缩小:接缝裁剪
- 放大:接缝插入
- 保持宽高比
-
明确不考的:双边滤波器
Basics⚓︎
常见的一些图像处理操作有:
-
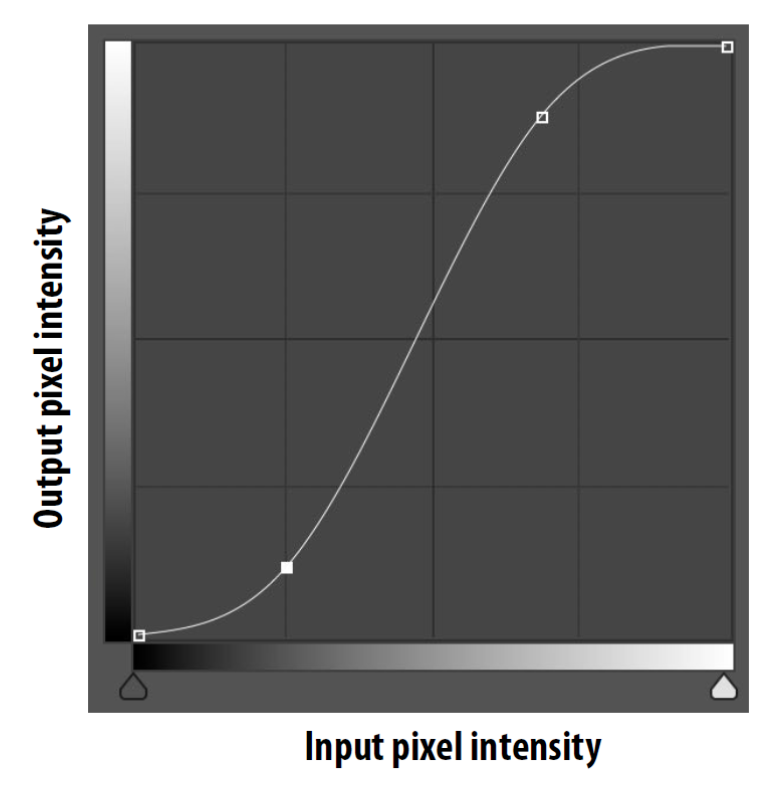
增加对比度(contrast)
-
通过 S 曲线,对每个像素做这样的转换:output(x, y) = f(input(x, y))
-
-
图像(颜色)反转(invert)
- 对每个像素的处理位:out(x, y) = 1 - in(x, y)
-
模糊(blur)
-
利用边缘检测(edge detection) 技术,我们可以实现更“聪明”的模糊(即不会模糊整张图,仍然保留物体边缘特征)
-
-
锐化(sharpen)
下面主要介绍模糊这一操作。在此之前,我们得先理解它的数学基础——卷积(convolution)。
Convolution⚓︎
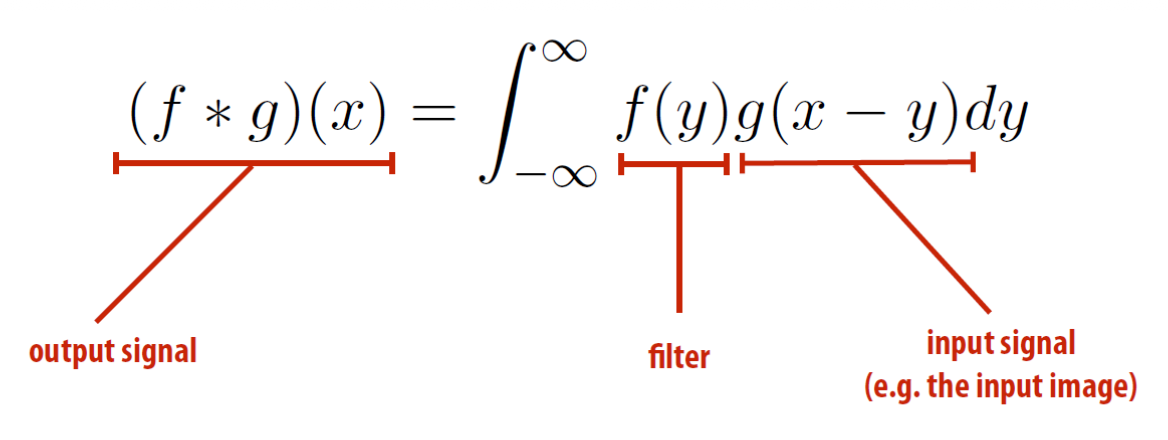
卷积公式如下:
考虑最简单的情况——单位面积的盒状函数 \(f(x)\)——有助于我们理解卷积操作:
\(g(x)\) 是输入图像,得到的输出图像上的每个像素是 \([x - 0.5, x + 0.5]\) 范围内像素的均值,从而起到模糊效果。
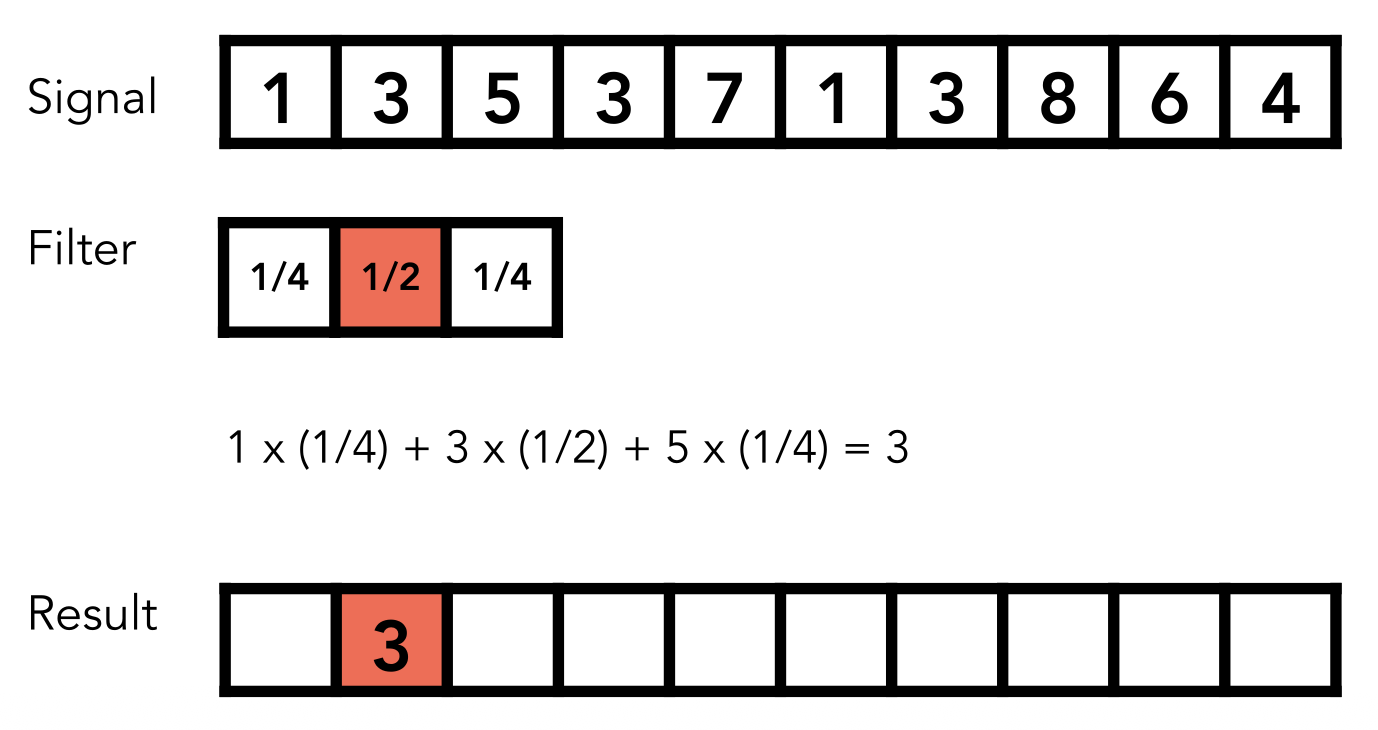
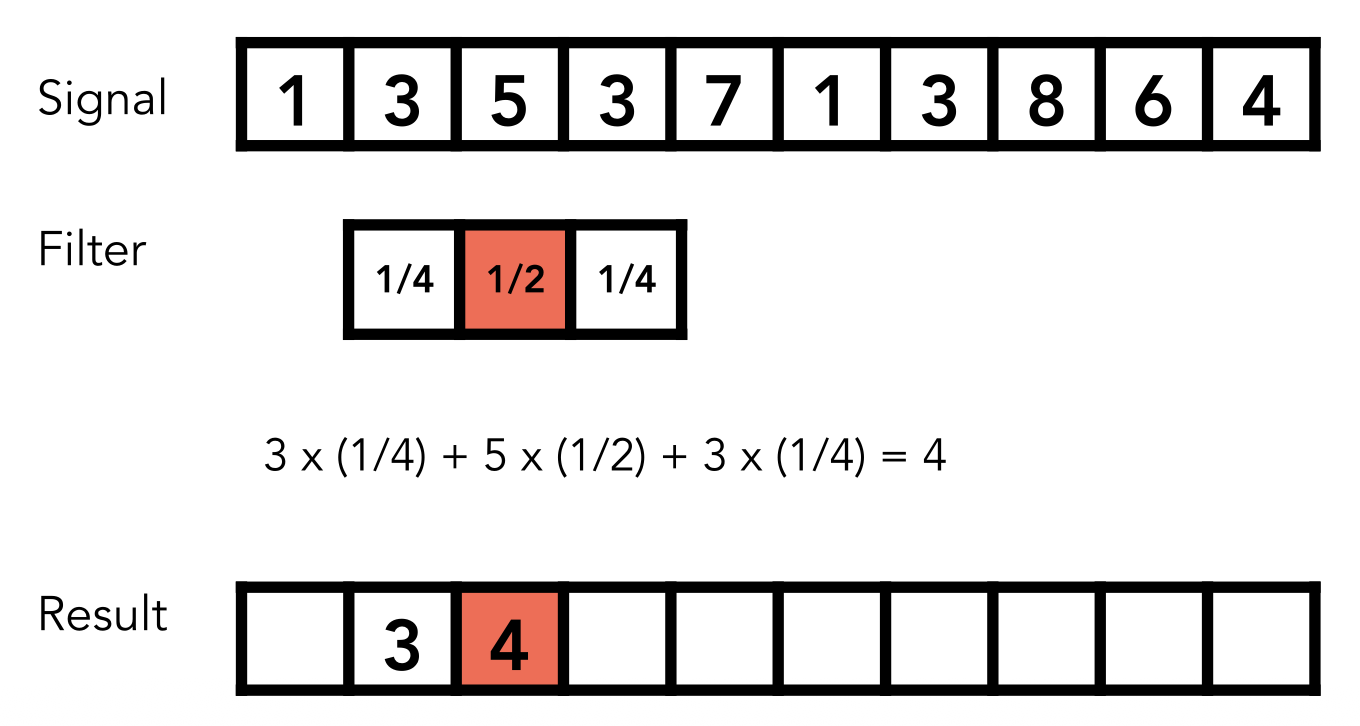
下面从一维角度看这个求均值的过程,可能更好理解些:
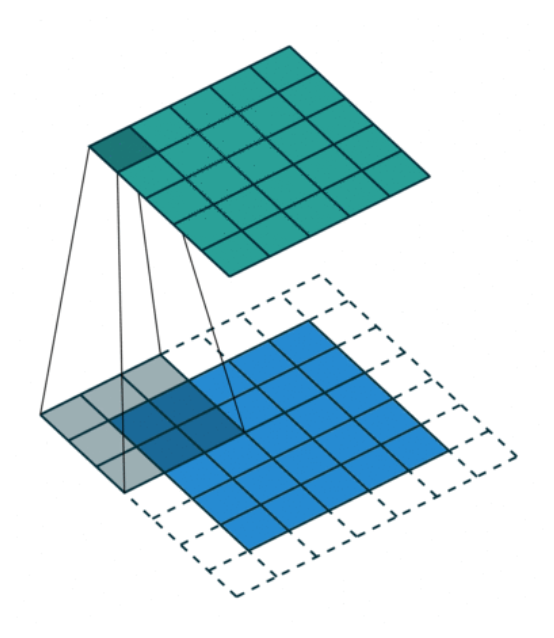
前面给出的卷积公式是连续的。不过对于图像处理,我们只要考虑离散(discrete) 的二维卷积公式就行了,所以公式中的积分可以用累加替换,即:
为方便操作,我们将滤波器(filter) \(f(i, j)\) 限制在 \(-1 \le i, j \le 1\) 的范围内,于是: $$ (f*I)(x,y)=\sum_{i,j=-1}^1f(i,j)I(x-i,y-j) $$
此时 \(f(i, j)\) 可以用一个 \(3 \times 3\) 的矩阵表示,每一个元素的值记作 \(f(i, j) = \mathbf{F}_{i, j}\)(通常称为滤波权重(filter weight) / 滤波核(filter kernel)
我们需要考虑滤波器扫描到图像边界上的特殊情况,因为此时滤波器的一部分不在图像内。一般有以下几种填充手段 (padding):
- 零值
- 边值
- 对称
- ...
Blur⚓︎
Box Blur⚓︎
最简单的盒模糊(box blur)
Gaussian Blur⚓︎
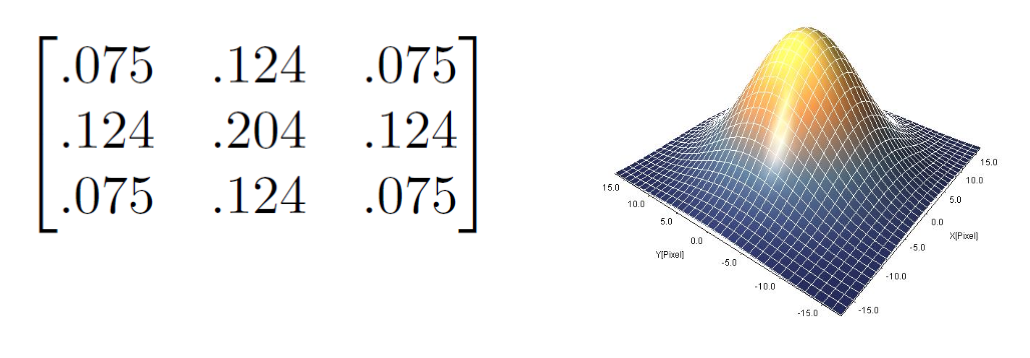
通过 2D 高斯函数获取滤波器的系数:
输出图像的每个像素就是滤波器范围内像素值的加权和,这些邻近像素的贡献随距离增加而衰减(想想正态曲线
滤波器大小为 7x7 的高斯模糊效果如下,可以看到模糊后的图像不会真的糊成一团,图像的原特征还是得到一定保留的(比如砖头间的缝隙等
Sharpening⚓︎
(3x3)锐化的滤波器大致长这样:
效果:
锐化操作的本质是向图像增加高频信号。
- 令 I 为原图像
- 图像中的高频信号:I' = I - Blur(I)
- 锐化后的图像:I = I + I'
Edge Detection⚓︎
以下两个矩阵分别对应检测垂直和水平边(但分别对应水平梯度和垂直梯度)的滤波器:
这些滤波器统称为梯度检测滤波器(gradient detection filter)。以下是这些滤波器的使用效果:
注
我们可以将滤波器视为一种模式的“探测器”(detector),输出图像中的像素值 = 滤波器对输入图像中每个像素周围区域的“响应”(这也是 CV 中的常见解释
Bilateral Filter⚓︎
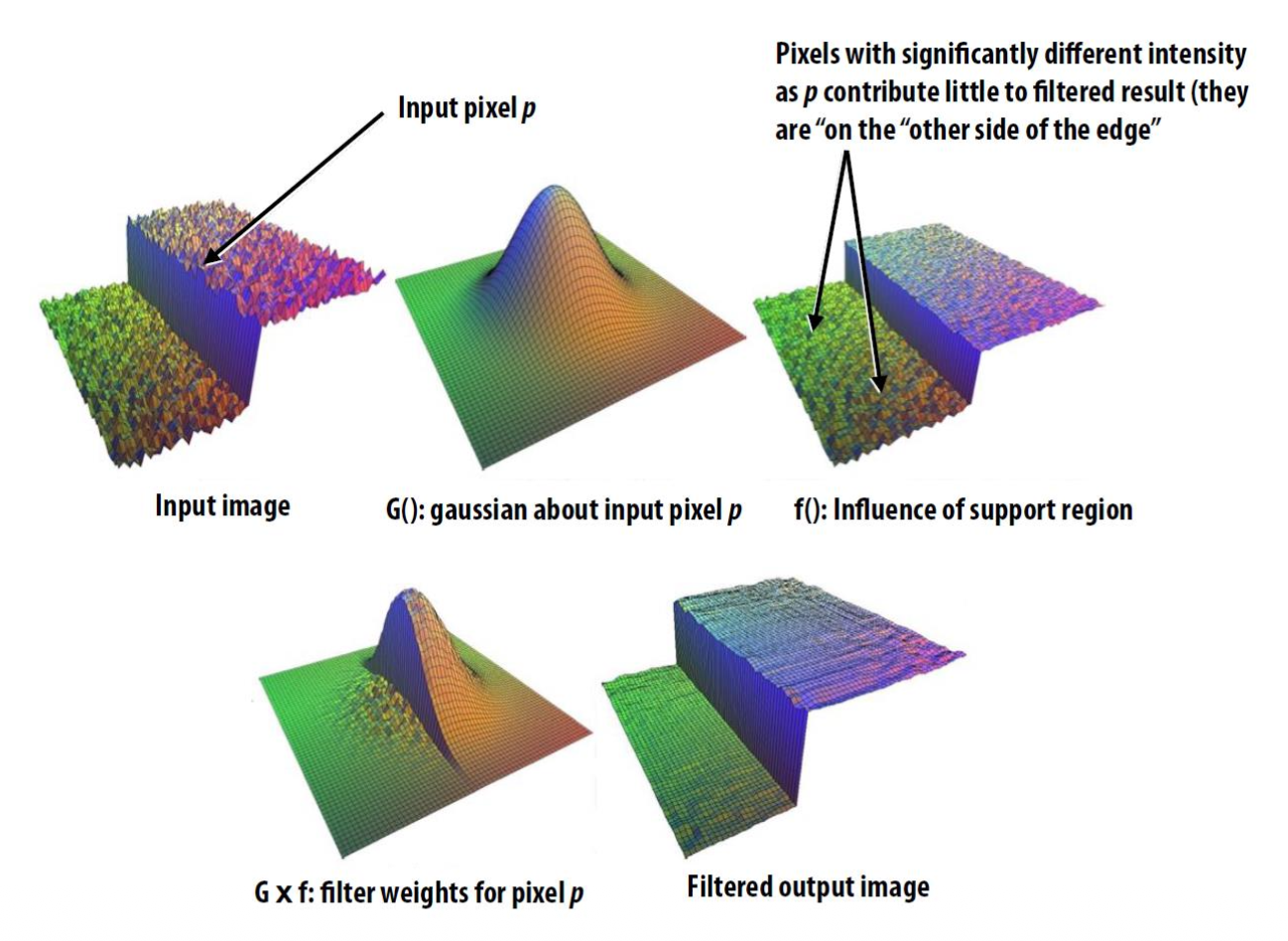
一种更强大但复杂的滤波(模糊)手段叫做双边滤波(bilateral filter),它的作用是在去除图像噪声的同时保留图像原有的边缘特征。
双边滤波的原理图:
滤波核的内容取决于图像内容。
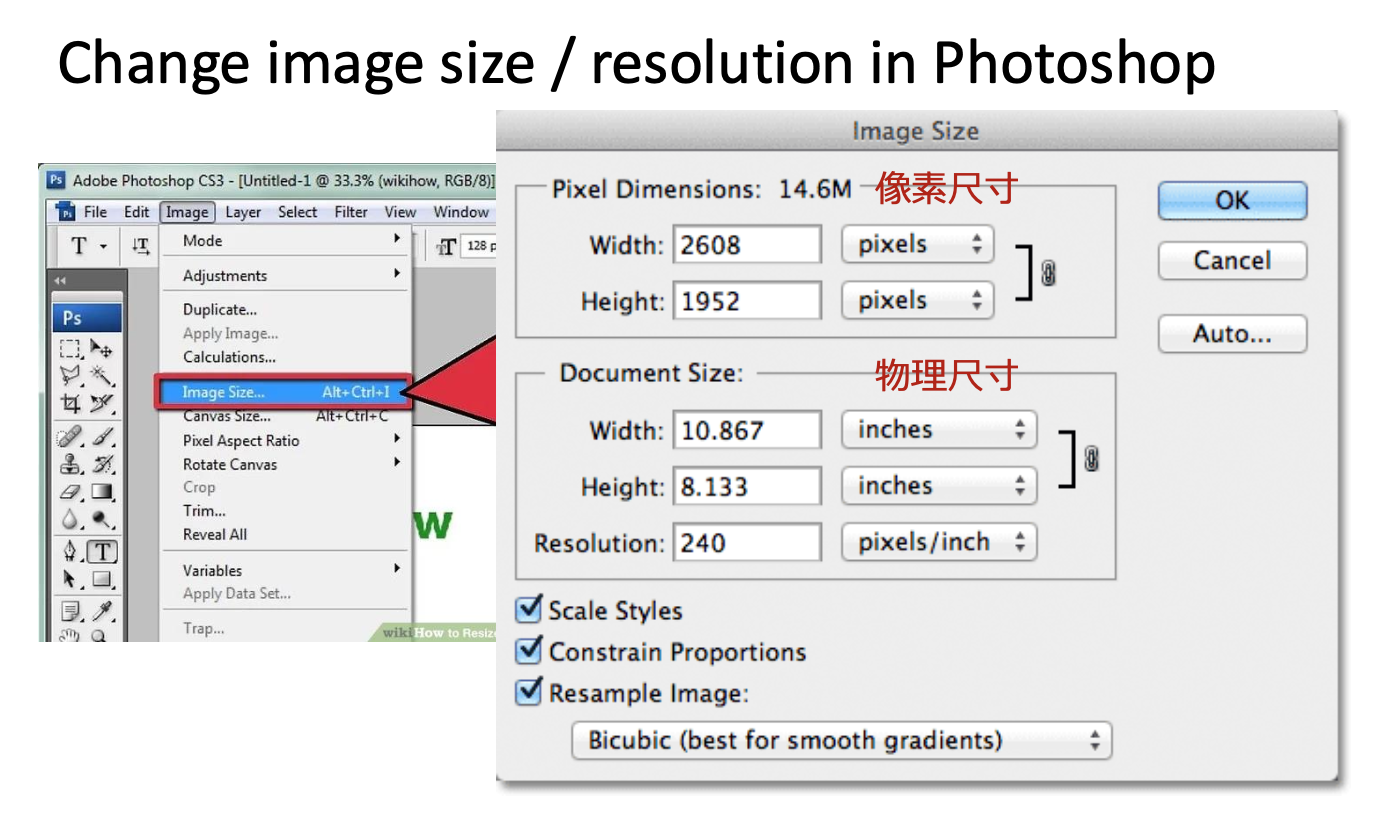
Image Sampling⚓︎
一种对图像的常用操作是缩放(resize)。
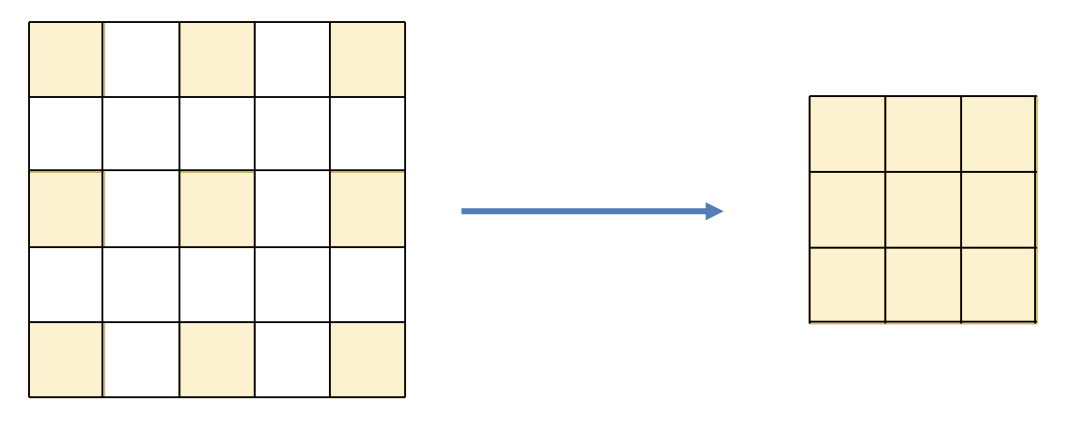
缩放操作涉及到对图像的采样(sampling),比如缩小图像就是一个降采样(down-sampling) 的过程:
后续内容参见笔者的 CG 笔记中关于反走样的介绍。
Image Maginification⚓︎
另一种对图像的缩放就是图像放大(image magnification)。
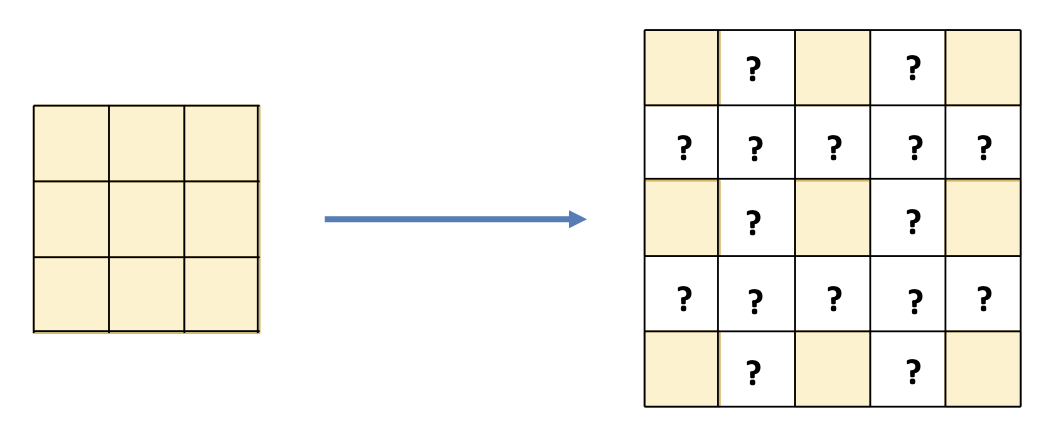
而图像放大的过程本质上是升采样(up-sampling)。
这显然会遇到一个问题:如何插入这些原本不存在的像素呢?解决方案就是插值(interpolation)。
Interpolation⚓︎
下面列举一些常用的插值方式:
-
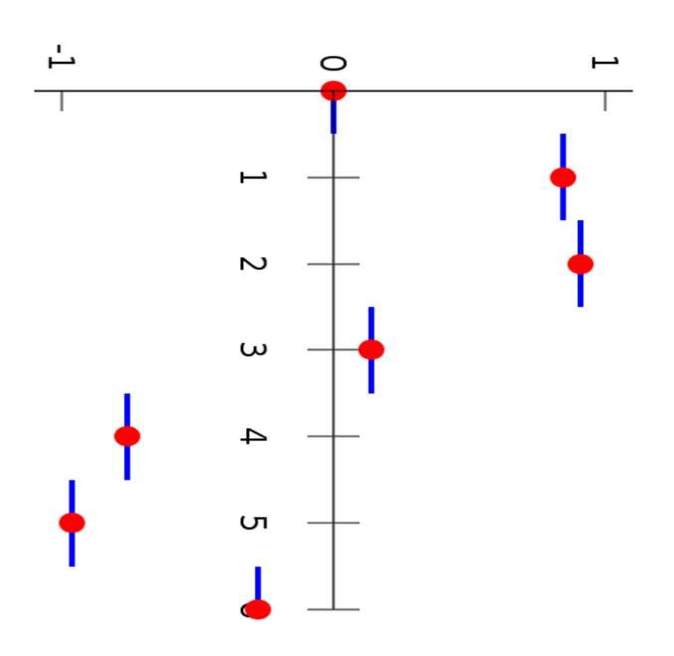
最近邻插值(nearest-neighbor interpolation):不够连续和平滑
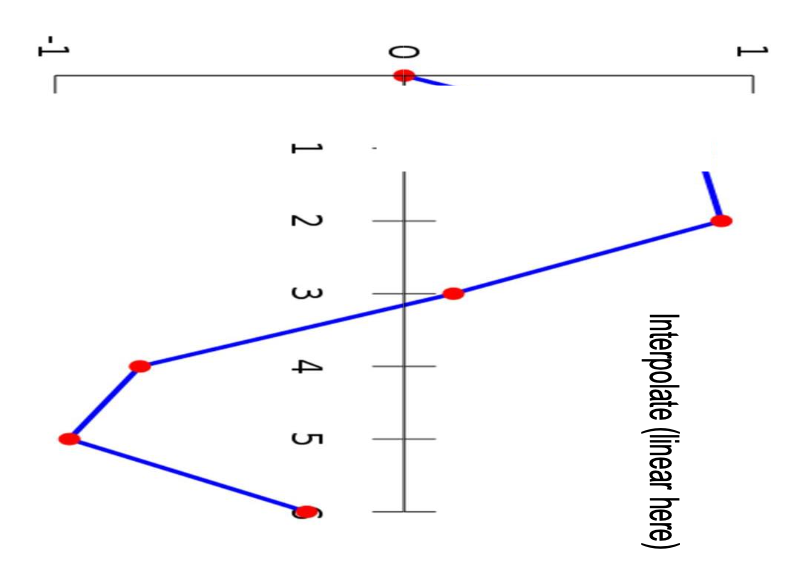
-
线性插值(linear interpolation):连续但不平滑
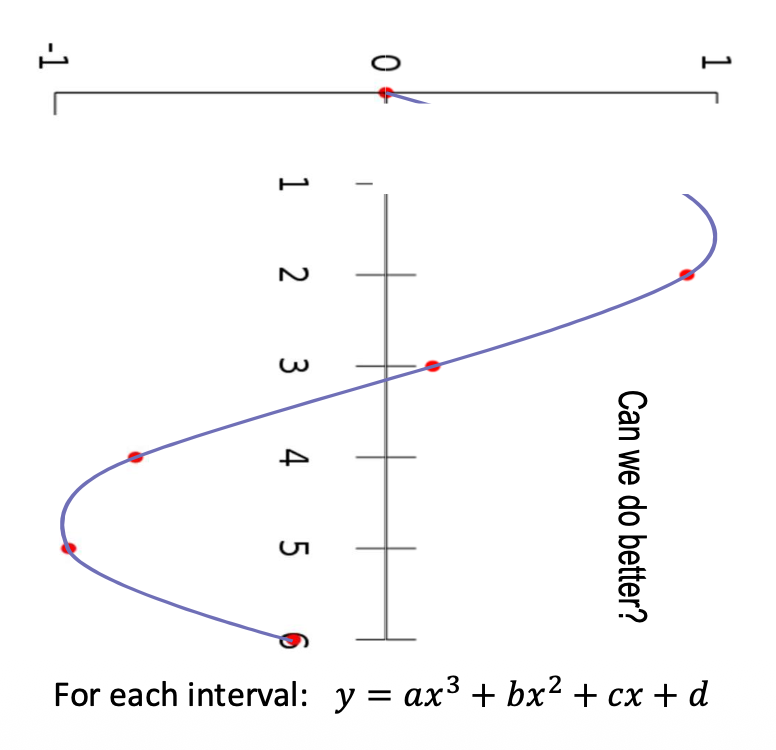
-
三次插值(cubic interpolation):连续且平滑
-
双线性插值(bilinear interpolation)(点击链接后阅读详细内容)
Changing Aspect Ratio⚓︎
有时我们会通过缩放图像(不是剪切 (cropping))来改变图像宽高比(aspect ratio)。但如果处理不当的话可能会导致图像内容的畸变。
这篇论文给出了解决方案:
下面就来阐述其中的思想。
- 问题陈述:我们需要移除图像每行的 n 个像素
- 基本思路:移除“不重要”的像素
那么如何衡量一个像素的重要性呢?
- 一种简单的思路是:构成边缘的像素就是重要像素
- 使用边缘能量(edge energy) 作为衡量指标:\(E(I) = \left|\dfrac{\partial I}{\partial x}\right| + \left|\dfrac{\partial I}{\partial y}\right|\)
- 对图像而言,可利用卷积来求导(回忆前面介绍的边缘检测器)
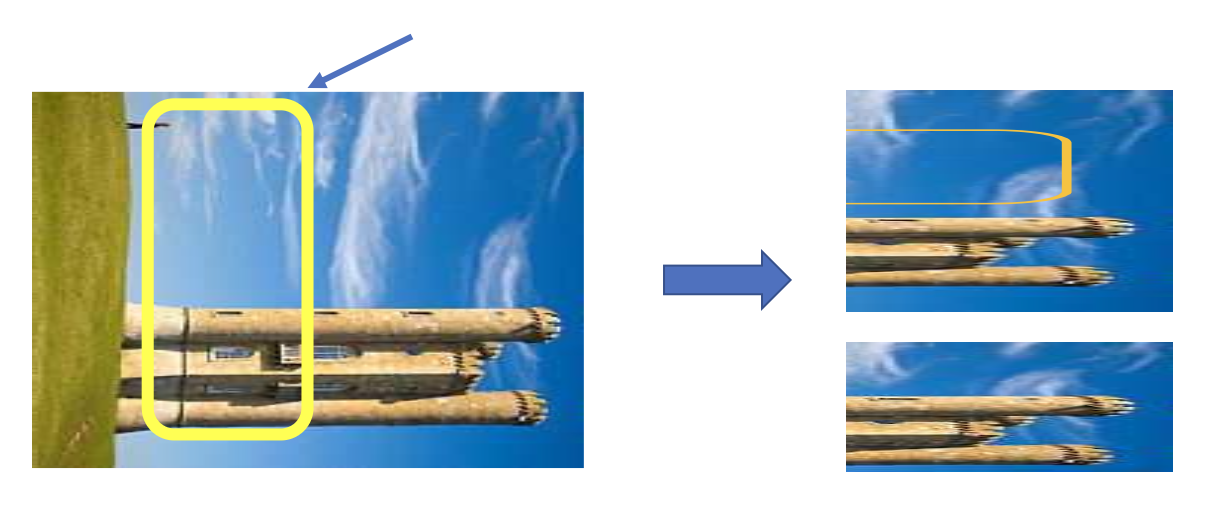
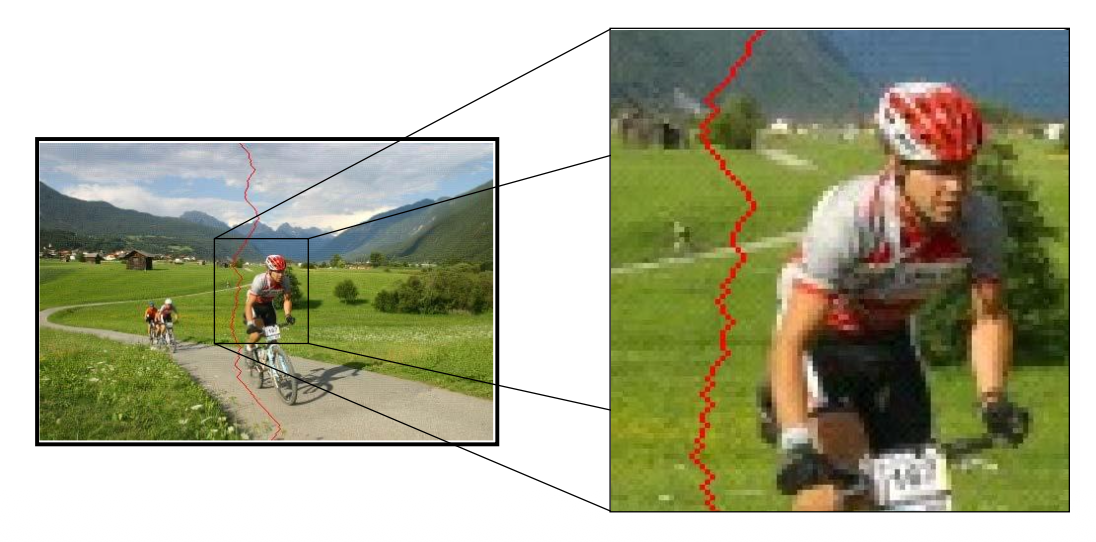
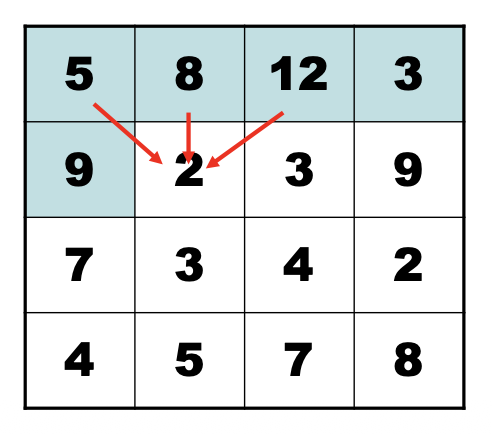
接缝裁剪(seam carving):自顶向下寻找一条使像素边缘能量最小化的连接路径。
若 $\mathbf{M}(i, j) = $ 经过像素 \((i, j)\) 的接缝的最小边缘能量,那么 $$ \mathbf{M}(i,j){=}E(i,j)+\min(\mathbf{M}(i-1,j-1),\mathbf{M}(i-1,j),\mathbf{M}(i-1,j+1)) $$
该计算可通过动态规划完成。
还可通过接缝插入(seam insertion) 来放大图像:
思路:以同样的方法寻找若干条接缝,然后在上面进行插值。
评论区