Structure from Motion⚓︎
约 5865 个字 预计阅读时间 29 分钟
核心知识
本讲内容很多,且涉及到大量数学公式。复习的时候只需理解计算思路,不需要记住繁杂的公式。
- 相机模型:三维点 -> 二维点
- 坐标变换:求解外参矩阵 \(M_{ext}\)(位置 \(\bm{c}_w\) 和朝向 \(R\))
- 透视投影:求解内参矩阵 \(M_{int}\)(焦距 \(f\))
- 图像平面(毫米)-> 图像传感器(像素
) :求解内参矩阵 \(M_{int}\)(像素密度 \(m_x, m_y\) 和主点坐标 \(c_x, c_y\))
- 相机标定:寻找内外参
- 即求解投影矩阵(= 内参矩阵 * 外参矩阵)
- 分解(QR 分解)
- 视觉定位(PnP)
- 运动恢复结构(SfM
) :已知二维点和内参,求外参(相机位置和朝向)和三维点- 数学基础:对极几何、本质矩阵和基础矩阵
- 相对相机位姿估计:求 \(R, \bm{t}\)
- 三角化:已知二维点和内外参,求三维点坐标
- 多帧运动恢复结构:光束法平差
运动恢复结构(structure from motion, SfM):从多张图像中恢复场景的相机位姿和三维结构。
相关应用
下面我们分别来解决以下问题:
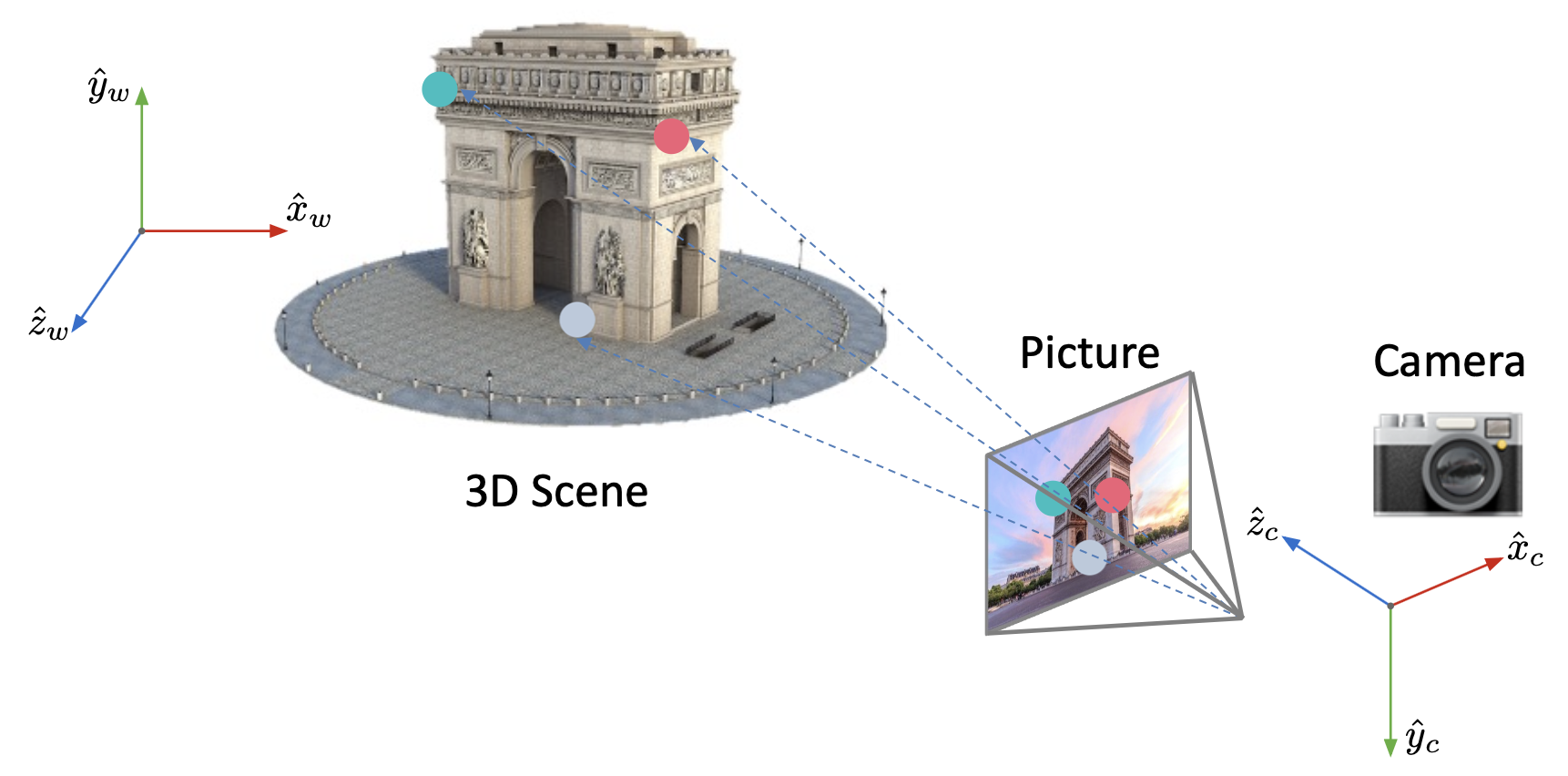
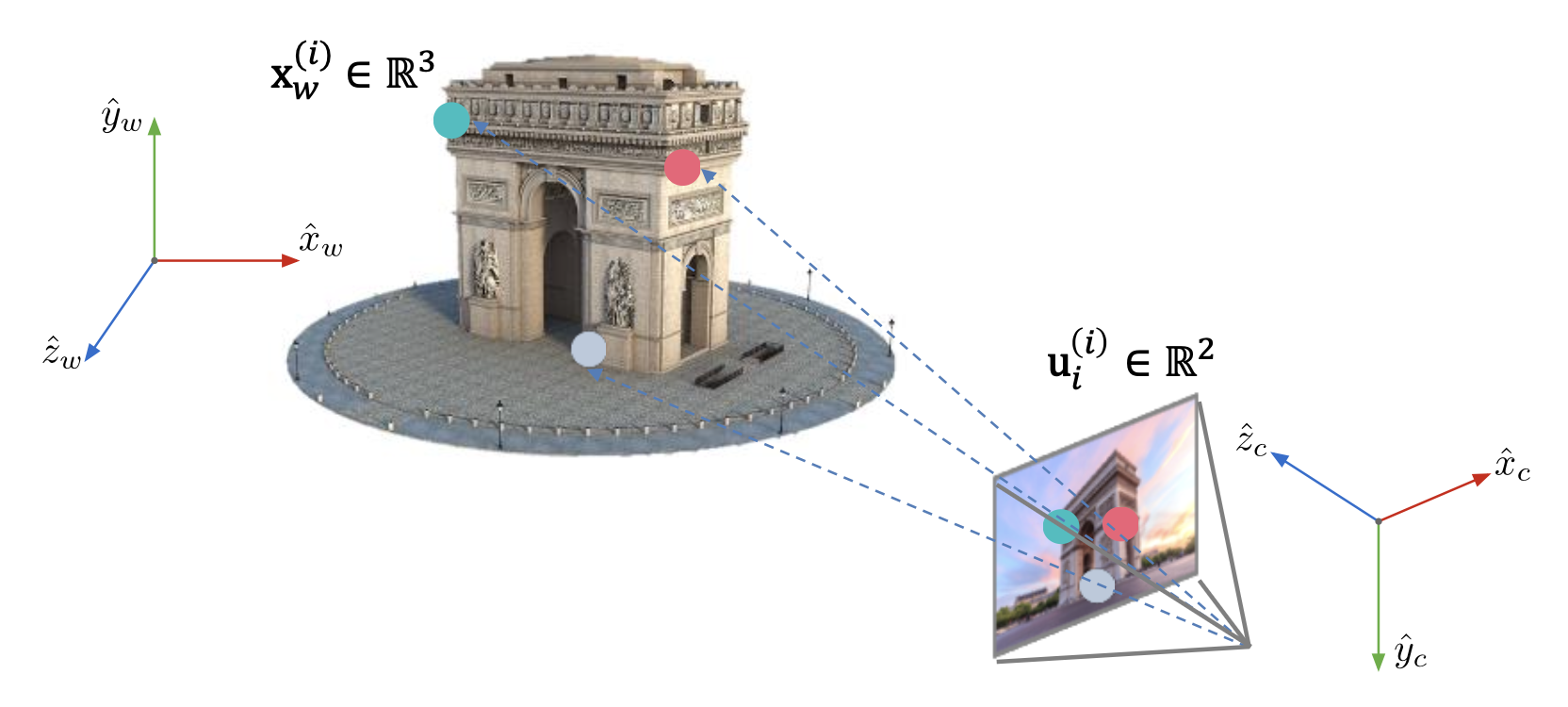
- 相机模型:相机如何将世界中的三维点映射到图像平面上
- 相机标定与位姿估计(camera calibration and pose estimation):如何计算相机相对于世界坐标系的位置和方向
- 运动恢复结构:如何从图像中重建未知的三维结构,即根据场景和多视角(图像)下的相机位姿来计算三维结构
Camera Model⚓︎
Image Formation⚓︎
成像步骤:
- 坐标变换:世界坐标系 -> 相机坐标系
- 透视投影:相机坐标系 -> 二维图像平面
- 图像平面到图像传感器的映射:以毫米为单位的二维坐标 -> 以像素为单位的像素坐标
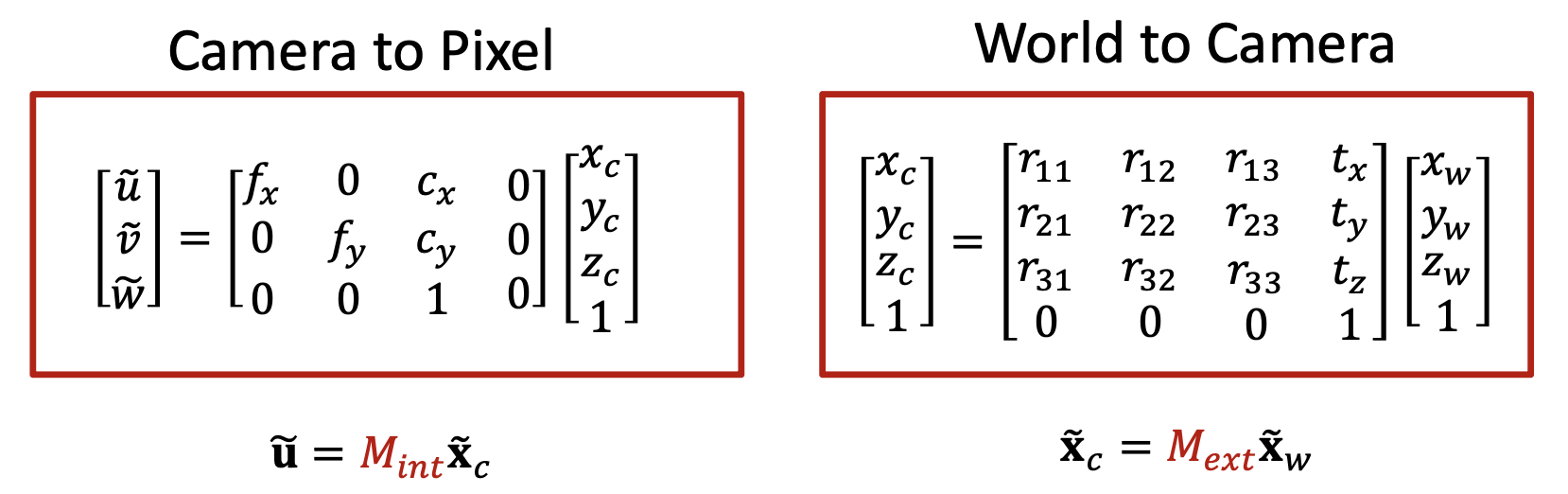
其中第一步需要求解外参矩阵(extrinsic matrix),后两步需要求解内参矩阵(intrinsic matrix)。
Coordinate Transformation⚓︎
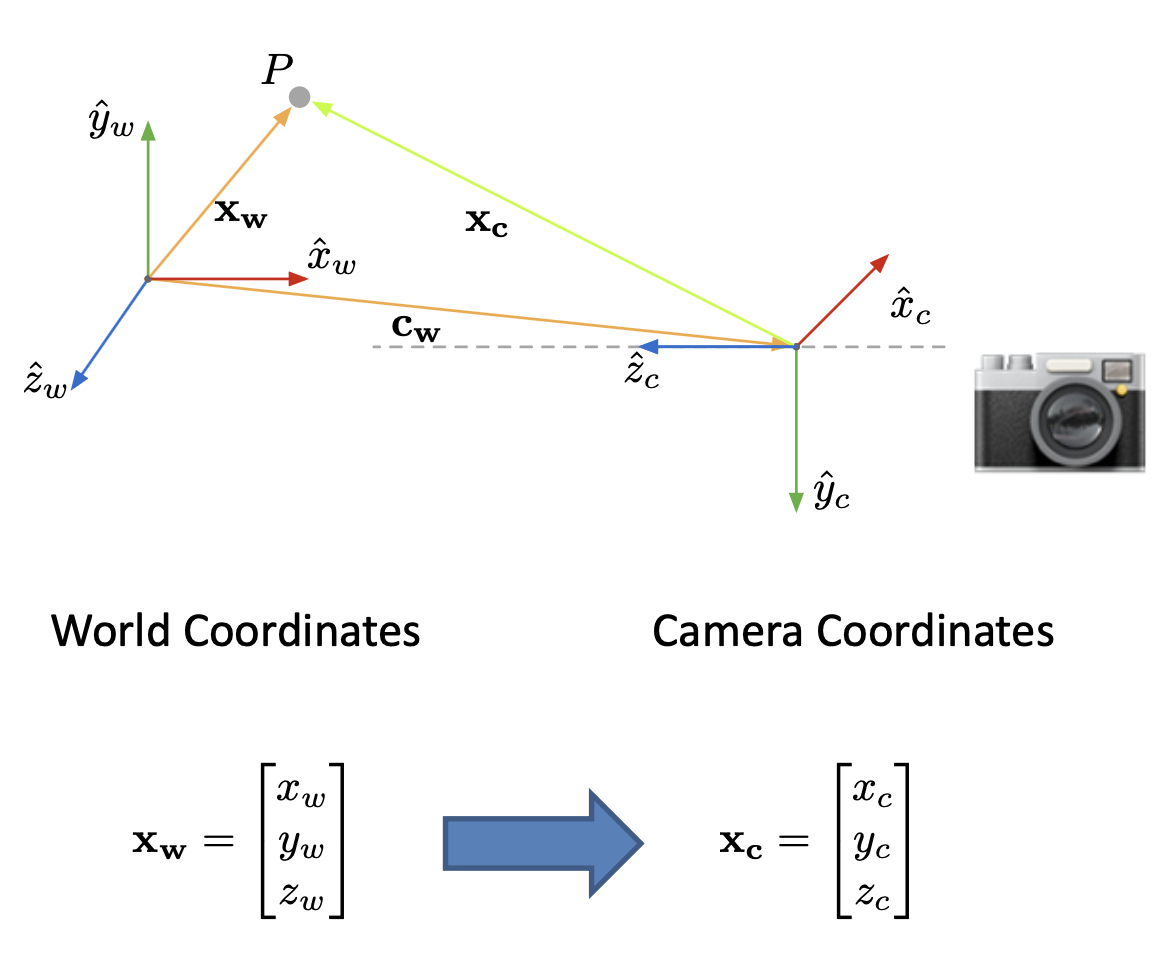
坐标变换的过程如图所示:
相机的外参(extrinsic parameters) 包含:
- 相机在世界坐标系 \(W\) 中的位置(position) \(\bm{c}_w\)
- 相机坐标系在世界坐标系中的朝向(orientation) \(R\)(一个三维旋转矩阵)
其中旋转矩阵 \(R\) 是标准正交的(orthonormal)。
对于给定的相机外参 \((R, c_w)\),点 \(P\) 在相机坐标系中的位置为:
将上述方程重写为齐次坐标的形式:
外参矩阵 \(M_{ext}=\begin{bmatrix}R_{3\times3}&\bm{t}\\\bm{0}_{1\times3}&1\end{bmatrix}=\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_x\\r_{21}&r_{22}&r_{23}&t_y\\r_{31}&r_{32}&r_{33}&t_z\\0&0&0&1\end{bmatrix}\)
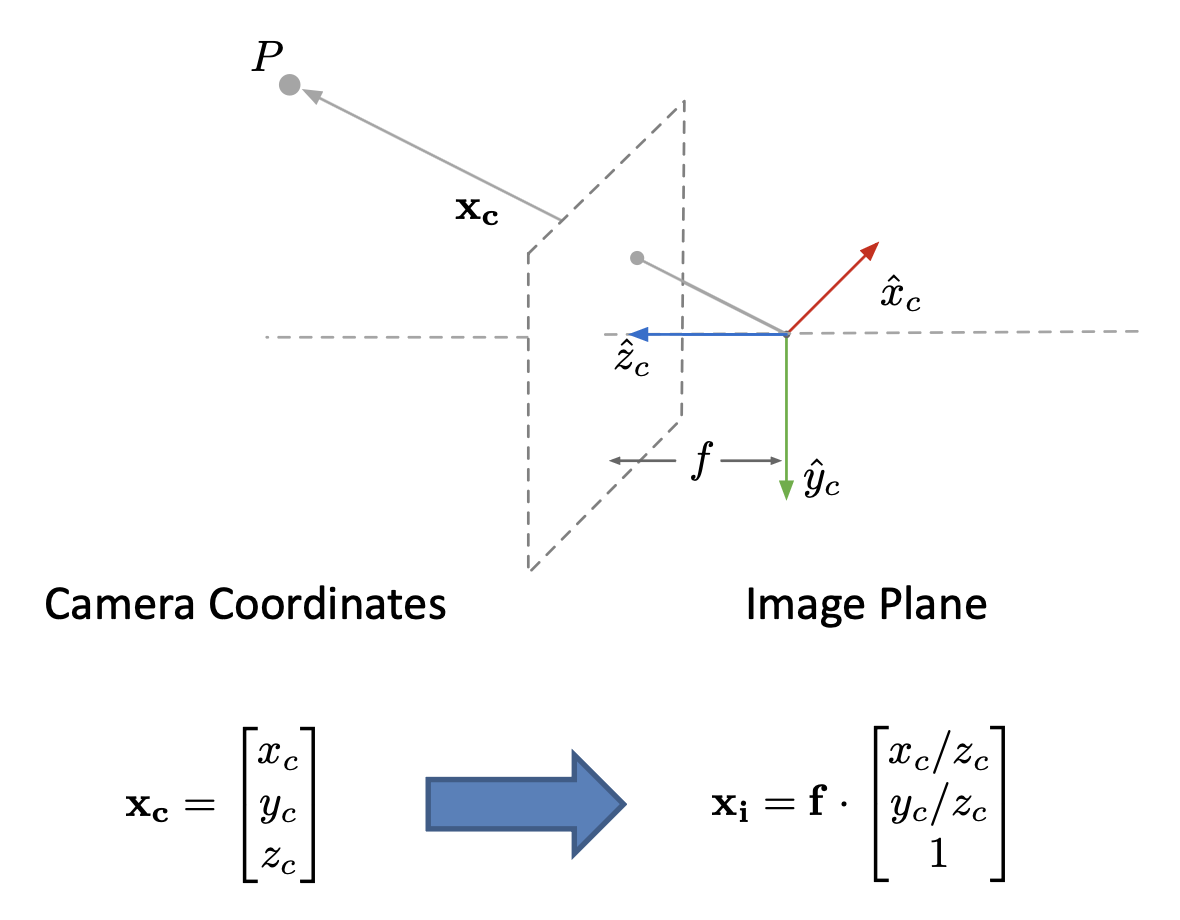
Perspective Projection⚓︎
透视投影的示意图如下:
有关透视投影的具体介绍见「成像」一讲的笔记。
Image Plane to Image Sensor Mapping⚓︎
像素也有可能是矩形的。
若 \(m_x, m_y\) 分别表示 \(x, y\) 方向上的像素密度(pixels/mm
我们通常将图像传感器的左上角作为原点(这样便于索引
转换为齐次坐标形式:
其中 \(f_x = m_x f, f_y = m_y f\)。因此内参矩阵 \(M_{int} = \begin{bmatrix}f_x&0&c_x&0\\0&f_y&c_y&0\\0&0&1&0\end{bmatrix}\)。
Conclusion⚓︎
综上,我们可以得到完整的投影矩阵 \(P\) 了: $$ \widetilde{\bm{u}}=\textcolor{red}{M_{int}M_{ext}}\tilde{\bm{x}}_w=\textcolor{red}{P}\tilde{\bm{x}}_w $$
即:
Camera Calibration⚓︎
相机标定(camera calibration) 指的是寻找内参和外参的过程。
Procedure⚓︎
详细流程如下:
-
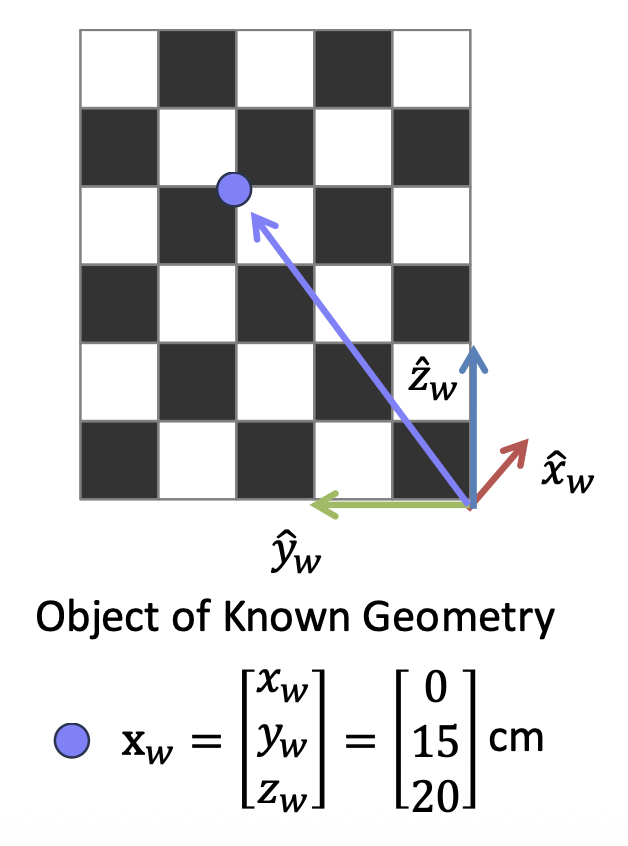
拍摄一个已知几何形状的物体图像(比如标定板(calibration board))
-
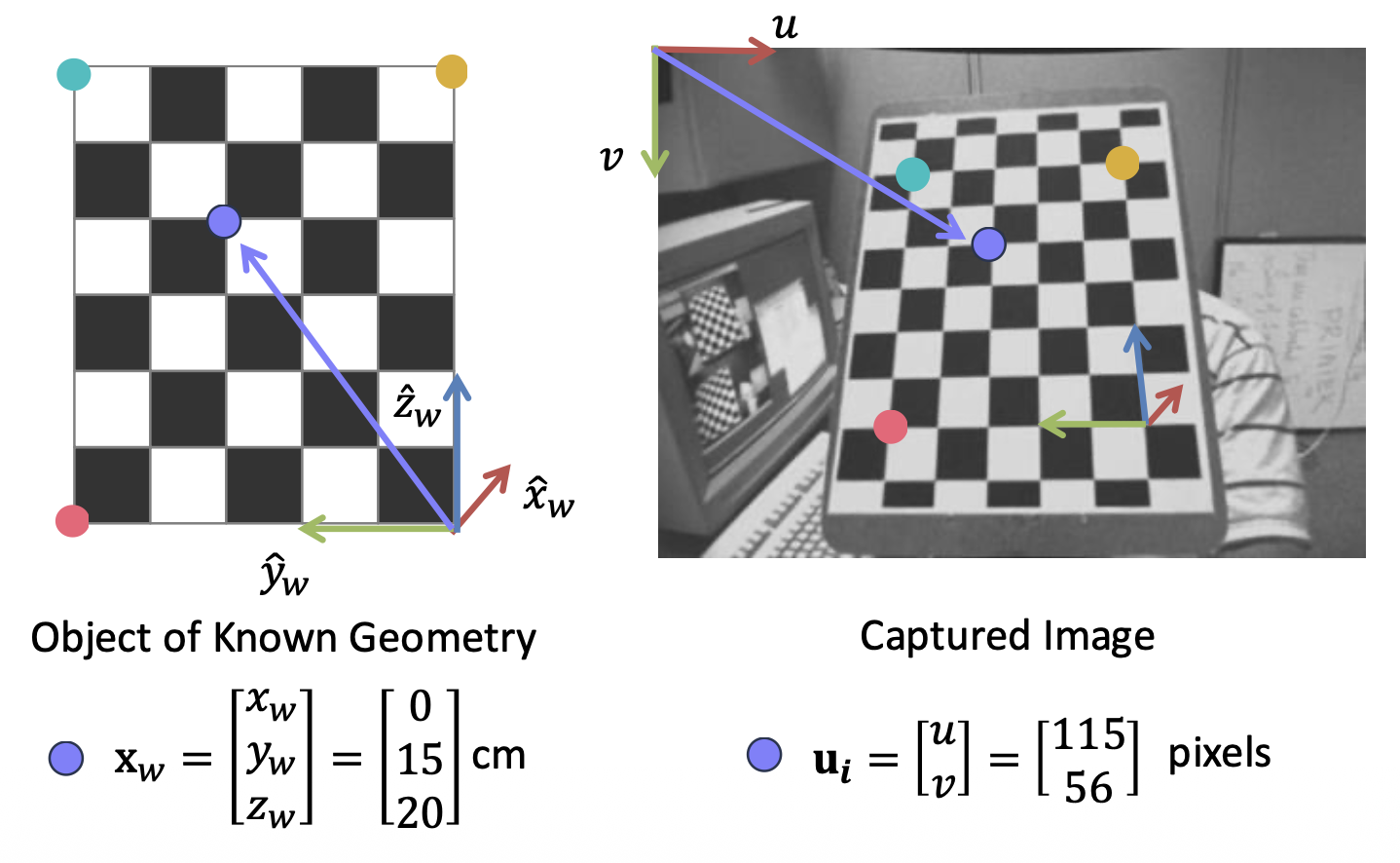
识别三维场景点和图像点之间的对应关系
-
对于场景和图像中每一个对应点 \(i\),有方程:
\[ \underbrace{ \begin{bmatrix} u^{(i)} \\ v^{(i)} \\ 1 \end{bmatrix} }_{\text{Known}} \equiv \underbrace{ \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \end{bmatrix} }_{\text{Unknown}} \underbrace{ \begin{bmatrix} x_w^{(i)} \\ y_w^{(i)} \\ z_w^{(i)} \\ 1 \end{bmatrix} }_{\text{Known}} \]成立。将矩阵乘法扩写为线性方程:
\[ u^{(i)} = \frac{p_{11}x_w^{(i)} + p_{12}y_w^{(i)} + p_{13}z_w^{(i)} + p_{14}}{p_{31}x_w^{(i)} + p_{32}y_w^{(i)} + p_{33}z_w^{(i)} + p_{34}} \\ v^{(i)} = \frac{p_{21}x_w^{(i)} + p_{22}y_w^{(i)} + p_{23}z_w^{(i)} + p_{24}}{p_{31}x_w^{(i)} + p_{32}y_w^{(i)} + p_{33}z_w^{(i)} + p_{34}} \] -
重新安排各元素(已知量放在矩阵 \(A\) 中,未知的投影矩阵参数放在向量 \(\bm{p}\) 中
) :\[ \underbrace{ \begin{bmatrix} x_w^{(1)} & y_w^{(1)} & z_w^{(1)} & 1 & 0 & 0 & 0 & 0 & -u_1x_w^{(1)} & -u_1y_w^{(1)} & -u_1z_w^{(1)} & -u_1 \\ 0 & 0 & 0 & 0 & x_w^{(1)} & y_w^{(1)} & z_w^{(1)} & 1 & -v_1x_w^{(1)} & -v_1y_w^{(1)} & -v_1z_w^{(1)} & -v_1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_w^{(i)} & y_w^{(i)} & z_w^{(i)} & 1 & 0 & 0 & 0 & 0 & -u_ix_w^{(i)} & -u_iy_w^{(i)} & -u_iz_w^{(i)} & -u_i \\ 0 & 0 & 0 & 0 & x_w^{(i)} & y_w^{(i)} & z_w^{(i)} & 1 & -v_ix_w^{(i)} & -v_iy_w^{(i)} & -v_iz_w^{(i)} & -v_i \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_w^{(n)} & y_w^{(n)} & z_w^{(n)} & 1 & 0 & 0 & 0 & 0 & -u_nx_w^{(n)} & -u_ny_w^{(n)} & -u_nz_w^{(n)} & -u_n \\ 0 & 0 & 0 & 0 & x_w^{(n)} & y_w^{(n)} & z_w^{(n)} & 1 & -v_nx_w^{(n)} & -v_ny_w^{(n)} & -v_nz_w^{(n)} & -v_n \\ \end{bmatrix} }_{A\ (\text{Known})} \underbrace{ \begin{bmatrix} p_{11} \\ p_{12} \\ p_{13} \\ p_{14} \\ p_{21} \\ p_{22} \\ p_{23} \\ p_{24} \\ p_{31} \\ p_{32} \\ p_{33} \\ p_{34} \end{bmatrix}}_{\bm{p}\ (\text{Unknown})} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \] -
解出 \(p\)
\[ A \bm{p} = 0 \]
Property of Projection Matrices: Scale⚓︎
已知 \(\begin{bmatrix} \tilde{u} \\ \tilde{v} \\ \tilde{w} \end{bmatrix} \equiv k \begin{bmatrix} \tilde{u} \\ \tilde{v} \\ \tilde{w} \end{bmatrix}\),即:
因此投影矩阵 \(P\) 和 \(kP\) 产生相同的齐次像素坐标。由此我们发现性质:投影矩阵 \(P\) 的定义是尺度(scale) 无关的。
Solving P⚓︎
基于尺度无关的性质,我们可以做其中一种处理:
- 设置好尺度,使得 \(p_{34} = 1\)
- 设置好尺度,使得 \(\|\bm{p}\|^2 = 1\)
我们选择第 2 个选项,并希望 \(A \bm{p}\) 尽可能接近 0,于是得到以下优化目标:
可以证明:矩阵 \(A^TA\) 中对应最小特征值 \(\lambda\) 的特征向量 \(\bm{p}\) 就是方程的解。
最后,重新排列解 \(\bm{p}\) 以形成投影矩阵 \(P\)。
Decomposition⚓︎
现在已经求出 \(P\) 了,接下来我们希望能将 \(P\) 分解为内参矩阵和外参矩阵的乘积,以达成求解内外参的目标。
观察上述方程,发现内参矩阵中存在一个上三角矩阵(记作 \(K\)
对于 \(P\) 的最后一列:
因此:
Visual Localization Problem⚓︎
视觉定位(visual localization) 问题是指给定一张或多张图像,确定相机在特定的三维空间中的位置和姿态(外参)的过程。一般步骤为:
-
寻找三维场景点和二维图像点的对应关系
-
根据这一关系来确定相机的位置
这一问题又经常被称为 PnP(perspective-n-point) 问题(n 是三维点个数;往往假设内参已知
P3P⚓︎
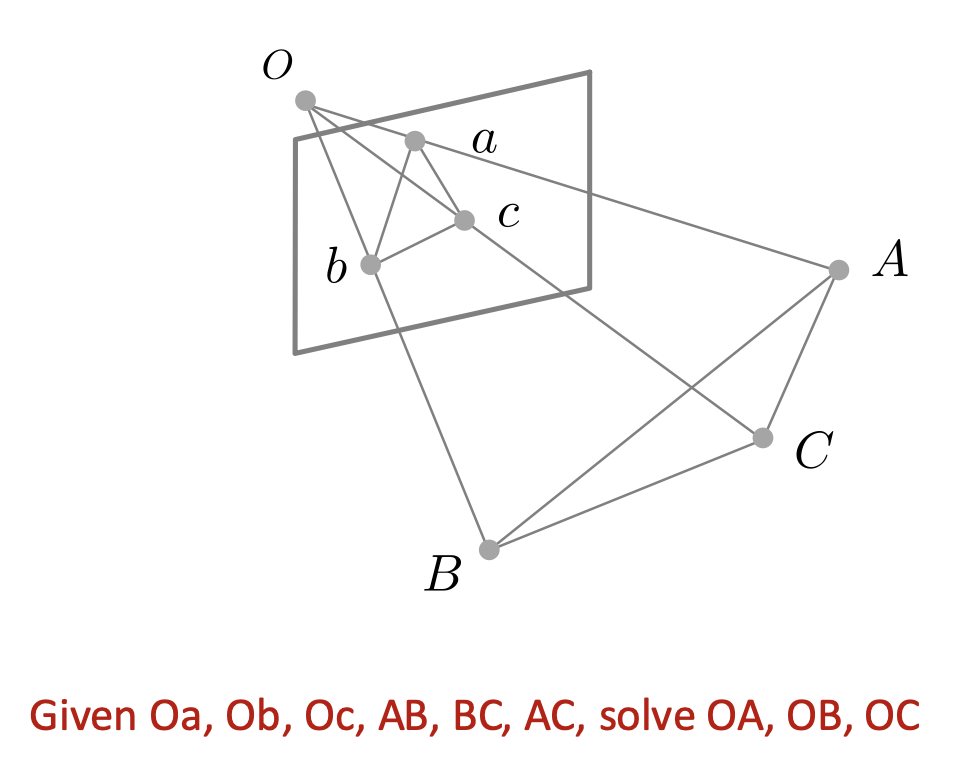
下面使用最小数量的点来求解相机位姿。
-
根据余弦定理
\[ \begin{aligned}OA^2+OB^2-2OA\cdot OB\cdot\cos\langle a,b\rangle&=AB^2\\OB^2+OC^2-2OB\cdot OC\cdot\cos\langle b,c\rangle&=BC^2\\OA^2+OC^2-2OA\cdot OC\cdot\cos\langle a,c\rangle&=AC^2\end{aligned} \] -
除以 \(OC^2\),令 \(x=\frac{OA}{OC},y=\frac{OB}{OC}\)
\[ \begin{gathered}\begin{aligned}x^2+y^2-2xy\cos\langle a,b\rangle=AB^2/OC^2\end{aligned}\\\begin{aligned}y^2+1^2-2y\cos\langle b,c\rangle=BC^2/OC^2\end{aligned}\\\begin{aligned}x^2+1^2-2x\cos\langle a,c\rangle=AC^2/OC^2\end{aligned}\end{gathered} \] -
令 \(v=\frac{AB^2}{OC^2},u=\frac{BC^2}{AB^2},w=\frac{AC^2}{AB^2}\)
\[ \begin{aligned}x^2+y^2-2xy\cos\langle a,b\rangle-v&=0\\y^2+1^2-2y\cos\langle b,c\rangle-uv&=0\\x^2+1^2-2x\cos\langle a,c\rangle-wv&=0\end{aligned} \]
使用 \(v\) 重新组织上述方程,得到:
现在已知量为 \(\cos\langle a,b\rangle,\cos\langle b,c\rangle,\cos\langle a,c\rangle,u,w\),未知量为 \(x, y\),所以问题已经转为求解一个二元二次方程 (binary quadratic equation)。
由于二元二次方程有四种可能解,我们利用一个额外的点来确定最可能的那一个。
PnP⚓︎
PnP 问题更通用的解法是将其转化为一个优化问题,其目标函数为:
- 能够最小化重投影误差(reprojection error)
- 用 P3P 初始化,随后用高斯 - 牛顿法优化
Structure from Motion⚓︎
求解 SfM 问题的步骤:
- 假设对每台相机而言内参矩阵 \(K\) 是已知的
- 寻找一些可靠的对应关系
- 寻找相对相机位置 \(\bm{p}\) 和朝向 \(R\)
- 寻找场景的三维点
Epipolar Geometry⚓︎
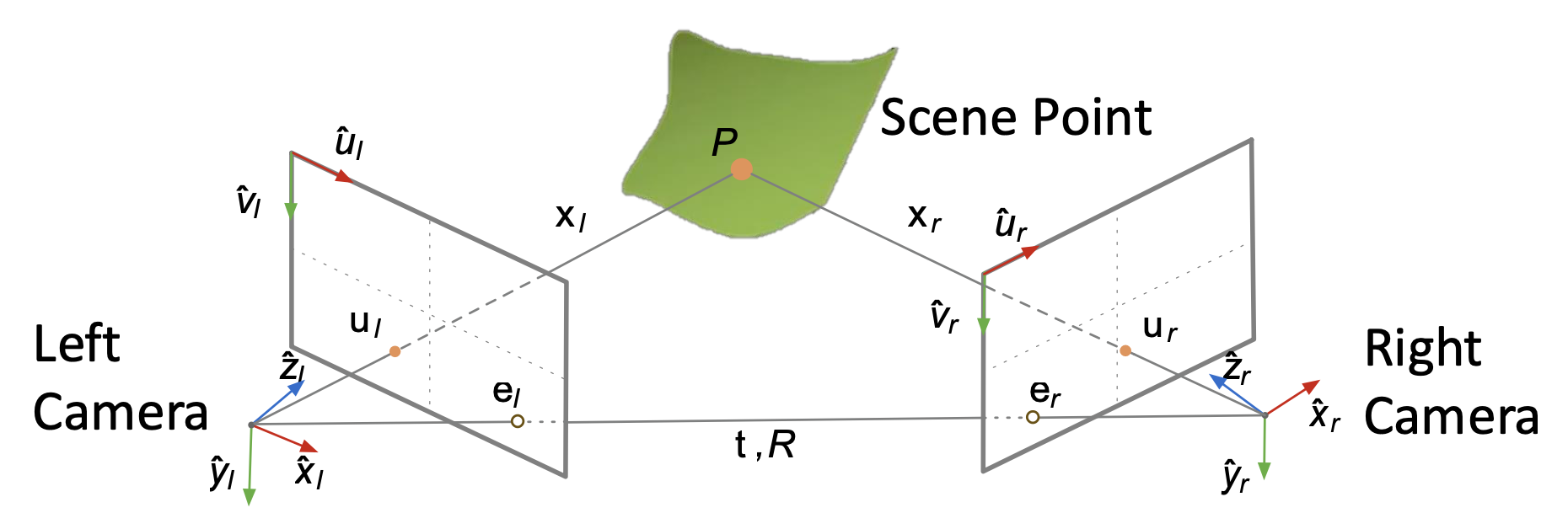
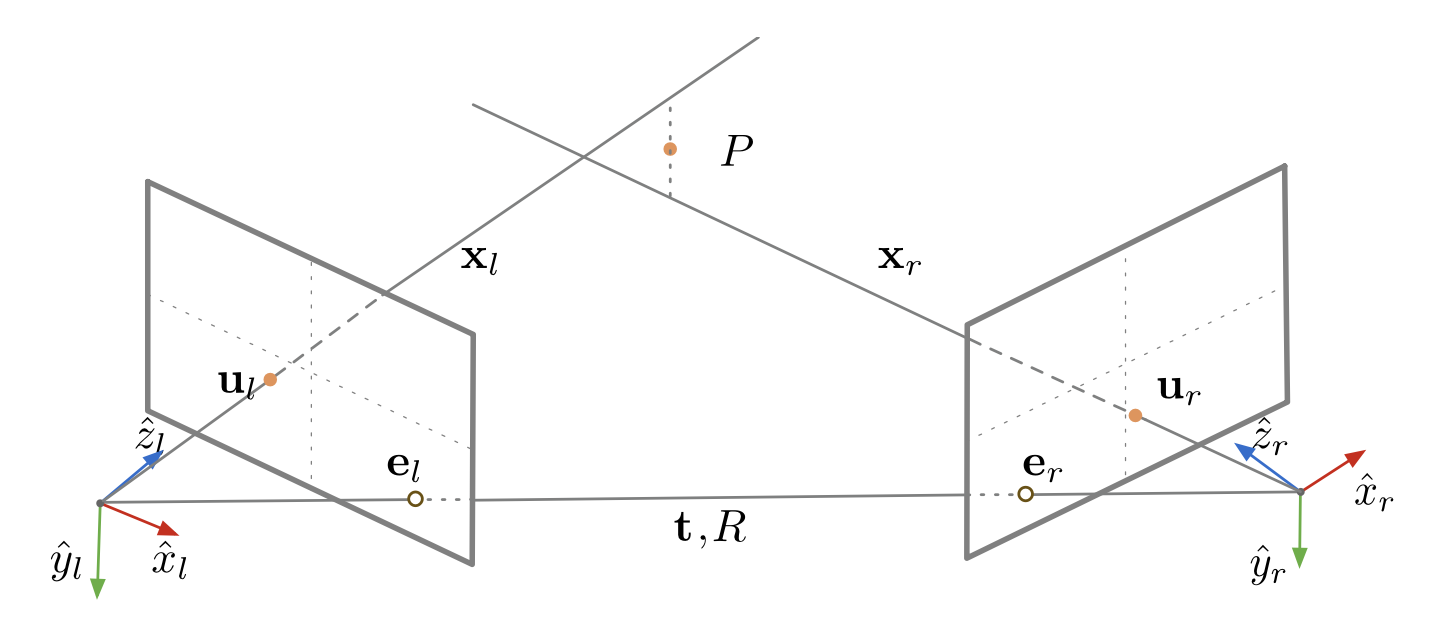
对极几何(epipolar geometry) 描述了三维点在两个视图中的二维投影(\(u_l\) 和 \(u_r\))之间的几何关系。我们需要通过多对二维对应点来求解平移向量 \(\bm{t}\) 和旋转矩阵 \(R\)。
请务必关注图中小字内容,有助于后续理解。看不清的话可点击图片全屏观看。
- 极点(epipole):一个相机的原点 / 针孔在另一个相机视角下的图像点
- 上图的 \(e_l, e_r\) 就是极点(两个相机中心连线和各自像平面的交点)
- 对于给定的相机对,极点是唯一的
- 可简单理解为一台相机在另一条相机拍摄照片中出现的位置(但不一定始终能在照片上出现)
-
场景点 \(P\) 的极平面(epipolar plane):由相机原点(\(O_L, O_r\)
) 、极点(\(e_l, e_r\))以及场景点 \(P\) 共同构成的平面- 每个场景点都位于一个唯一的极平面上
-
对极约束(epipolar constraints):极平面法向量为 \(\bm{n} = \bm{t} \times \bm{x}_l\)
- \(\bm{n}\) 和 \(\bm{x}_l\) 的点乘为 0,即:\(\bm{x}_l \cdot (\bm{t} \times \bm{x}_l) = 0\)
-
写成矩阵形式为:
\[ \begin{align*} \begin{bmatrix} x_l & y_l & z_l \end{bmatrix} \begin{bmatrix} t_y z_l - t_z y_l \\ t_z x_l - t_x z_l \\ t_x y_l - t_y x_l \end{bmatrix} &= 0 \\ \begin{bmatrix} x_l & y_l & z_l \end{bmatrix} \underbrace{ \begin{bmatrix} 0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0 \end{bmatrix} }_{T_\times} \begin{bmatrix} x_l \\ y_l \\ z_l \end{bmatrix} &= 0 \end{align*} \]
由于已知 \(\bm{x}_l = R\bm{x}_r + \bm{t}\),代入上述对极约束条件得到:
Essential Matrix⚓︎
可以将本质矩阵(essential matrix) \(E\) 分解为:\(E = T_\times R\),即:
由于 \(T_\times\) 是斜对称 (skew-symmetric) \((a_{ij} = a_{-ji})\) 且 \(R\) 是标准正交矩阵,所以可利用奇异值分解(singular value decomposition) 从积中解耦出 \(L_\times\) 和 \(R\)。
若 \(E\) 已知,便可计算 \(\bm{t}, R\),所以接下来的问题是如何找到 \(E\)。
解决思路:将场景点相对于左侧相机的三维位置 \((x_l, y_l, z_l)\) 与其相对于右侧相机的三维位置 \((x_r, y_r, z_r)\) 联系起来,得到:
目前我们还不知道 \(\bm{x}_l, \bm{x}_r\),但我们知道在图像坐标中的对应点,即:
-
左侧相机
\[ z_l \begin{bmatrix} u_l \\ v_l \\ 1 \end{bmatrix} = \underbrace{\begin{bmatrix} f_x^{(l)} & 0 & o_x^{(l)} \\ 0 & f_y^{(l)} & o_y^{(l)} \\ 0 & 0 & 1 \end{bmatrix}}_{K_l} \begin{bmatrix} x_l \\ y_l \\ z_l \end{bmatrix} \]解得:
\[ \bm{x}_l{}^T=\begin{bmatrix}u_l&v_l&1\end{bmatrix}\mathrm{z}_l{K_l^{-1}}^T \] -
右侧相机
\[ z_r \begin{bmatrix} u_r \\ v_r \\ 1 \end{bmatrix} = \underbrace{\begin{bmatrix} f_x^{(r)} & 0 & o_x^{(r)} \\ 0 & f_y^{(r)} & o_y^{(r)} \\ 0 & 0 & 1 \end{bmatrix}}_{K_r} \begin{bmatrix} x_r \\ y_r \\ z_r \end{bmatrix} \]解得:
\[ \bm{x}_r=K_r^{-1}z_r\begin{bmatrix}u_r\\v_r\\1\end{bmatrix} \]
代入前面的方程,得到:
注意:场景的深度不影响极线约束,因此可以直接无视方程中的 \(z_l, z_r\)。
将上述方程写为:
中间这个矩阵叫做基础矩阵(fundamental matrix) \(F\)。
基础矩阵作用在齐次坐标上:
可以看到,基础矩阵 \(F, kF\) 描述相同的对极几何,也就是说 \(F\) 的定义与尺度无关。所以通常会给 \(F\) 添加一个约束:\(\|f\|^2 = 1\),即由 \(F\) 的元素构成的向量长度为 1。
Relative Camera Pose Estimation⚓︎
相对相机位姿估计(relative camera position estimation) 是指在左右图像中寻找一组对应的特征点(至少 8 个
- 对于每一个对应关系 \(i\),写出对极约束
-
重新排列项,构成线性方程组
\[ \underbrace{ \begin{bmatrix} u_l^{(1)}u_r^{(1)} & u_l^{(1)}v_r^{(1)} & u_l^{(1)} & v_l^{(1)}u_r^{(1)} & v_l^{(1)}v_r^{(1)} & v_l^{(1)} & u_r^{(1)} & v_r^{(1)} & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ u_l^{(i)}u_r^{(i)} & u_l^{(i)}v_r^{(i)} & u_l^{(i)} & v_l^{(i)}u_r^{(i)} & v_l^{(i)}v_r^{(i)} & v_l^{(i)} & u_r^{(i)} & v_r^{(i)} & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ u_l^{(m)}u_r^{(m)} & u_l^{(m)}v_r^{(m)} & u_l^{(m)} & v_l^{(m)}u_r^{(m)} & v_l^{(m)}v_r^{(m)} & v_l^{(m)} & u_r^{(m)} & v_r^{(m)} & 1 \\ \end{bmatrix} }_{A\ (\text{Known})} % \underbrace{ \begin{bmatrix} f_{11} \\ f_{12} \\ f_{13} \\ f_{21} \\ f_{22} \\ f_{23} \\ f_{31} \\ f_{32} \\ f_{33} \end{bmatrix} }_{\bm{f}\ (\text{Unknown})} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \]即 \(A\bm{f} = 0\)
-
寻找基础矩阵 \(F\) 的最小二乘解:\(A\bm{f}\) 尽可能接近 0 且 \(\|\bm{f}\|^2 = 1\),即(约束为线性最小二乘问题)
\[ \min_{\bm{f}}\|A\bm{f}\|^2\text{ such that }\|\bm{f}\|^2=1 \]之后将解 \(\bm{f}\) 重新组织,构成基础矩阵 \(F\)
-
从已知的左右内参相机矩阵和基础矩阵 \(F\) 计算本质矩阵 \(E\)
\[ E = K_l^T F K_r \] -
从 \(E\) 中提取 \(R, \bm{t}\)(使用奇异值分解)
\[ E = T_\times R \]
Triangulation⚓︎
现在我们已经知道了二维特征点和相机参数,接下来的任务就是确定场景点的三维坐标。
并且我们已知两台相机的相对位置和朝向:
可以得到:
-
左相机图像方程
\[ \begin{align*} \begin{bmatrix} u_l \\ v_l \\ 1 \end{bmatrix} &\equiv \begin{bmatrix} f_x^{(l)} & 0 & o_x^{(l)} & 0 \\ 0 & f_y^{(l)} & o_y^{(l)} & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_r \\ y_r \\ z_r \\ 1 \end{bmatrix} \\ \tilde{\bm{u}}_l &= P_l \tilde{\bm{x}}_r \end{align*} \] -
右相机图像方程
\[ \begin{align*} \begin{bmatrix} u_r \\ v_r \\ 1 \end{bmatrix} &\equiv \begin{bmatrix} f_x^{(r)} & 0 & o_x^{(r)} & 0 \\ 0 & f_y^{(r)} & o_y^{(r)} & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x_r \\ y_r \\ z_r \\ 1 \end{bmatrix} \\ \tilde{\bm{u}}_r &= M_{int_r} \tilde{\bm{x}}_r \end{align*} \]
图像方程:
重新组织项:
从以下方程得到最小二乘解:
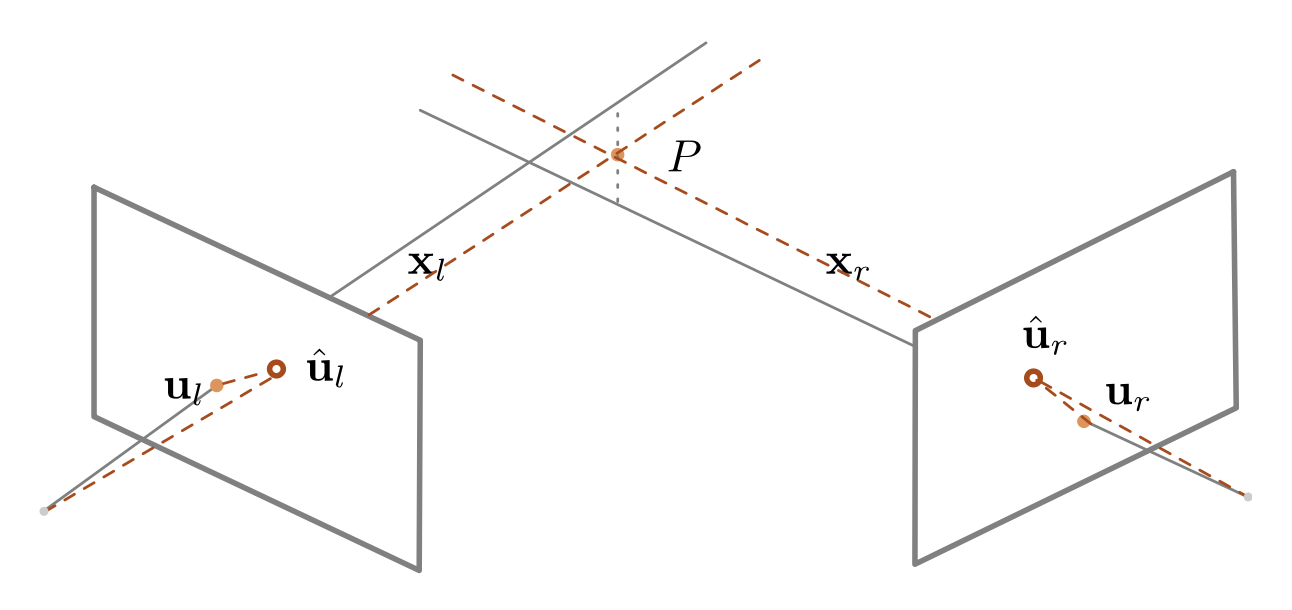
一般情况下,射线 \(\bm{x}_l, \bm{x}_r\) 不会和点 \(P\) 精确相交:
所以需要最小化重投影误差(reprojection error):
我们是否也能优化 \(R, \bm{t}\)(这个问题课上好像直接跳过了😅)
Multi-frame Structure from Motion⚓︎
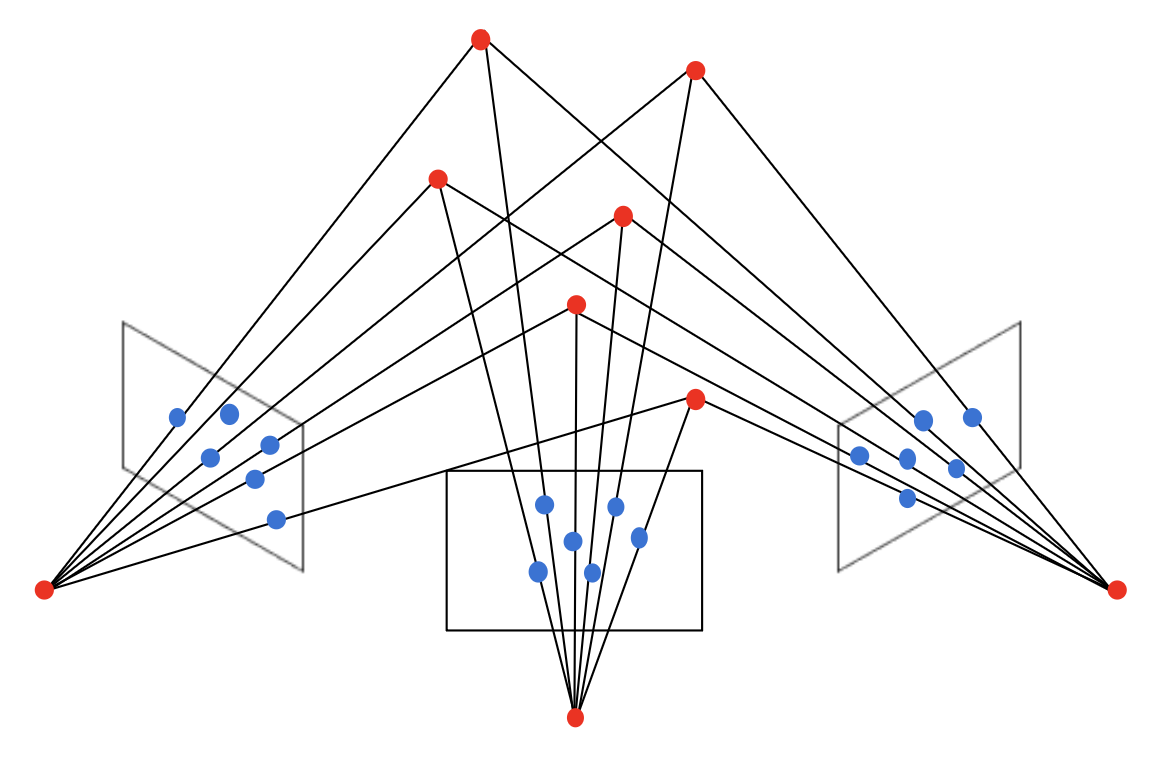
之前讲的都是基于两张不同视角下的图像来计算三维坐标,实际上我们也能根据更多视角下的图像来计算三维结构。
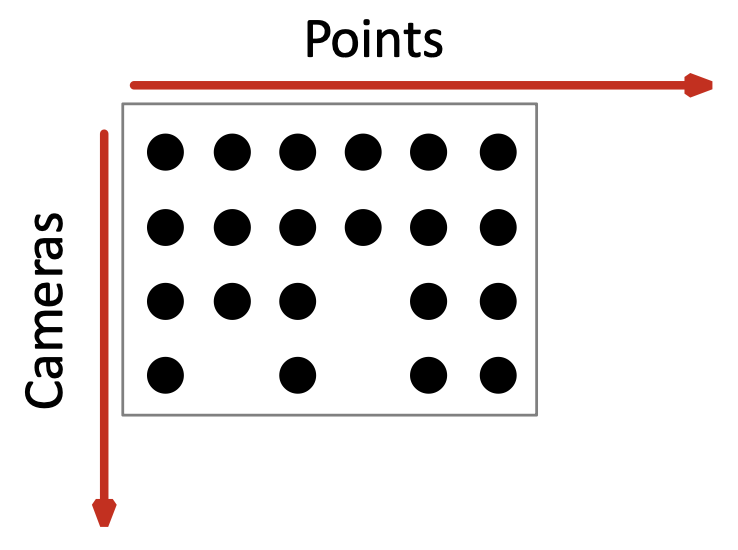
给定 \(m\) 张包含 \(n\) 个三维点的图像:
即从 \(mn\) 个对应的二维点 \(\bm{u}_j^{(i)}\) 估计 \(m\) 个投影矩阵 \(P_{proj}^{(i)}\) 和 \(n\) 个三维点 \(P_j\)。解决该问题的步骤如下:
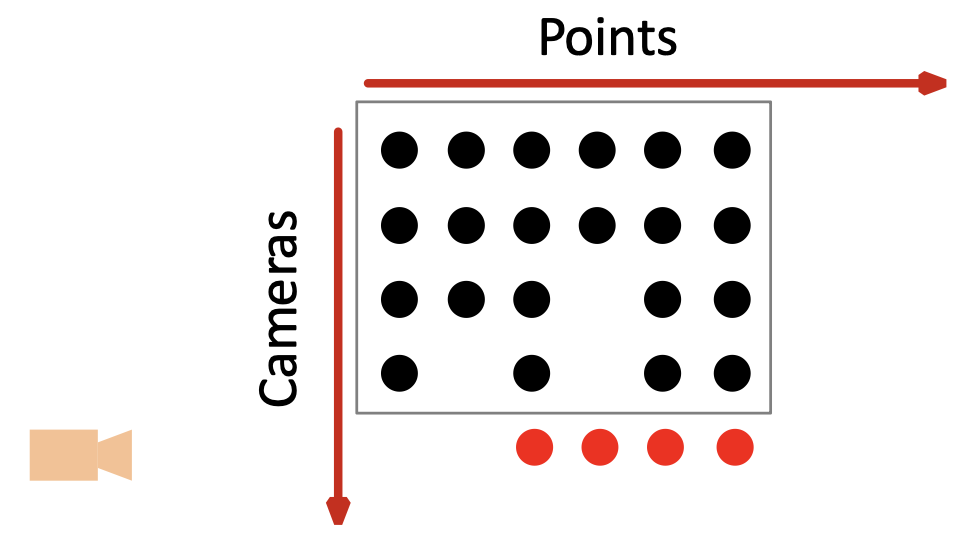
-
初始化相机运动和场景结构
-
对于每个额外的视角
-
确定新相机的投影矩阵,使用其图像中所有可见的已知三维点
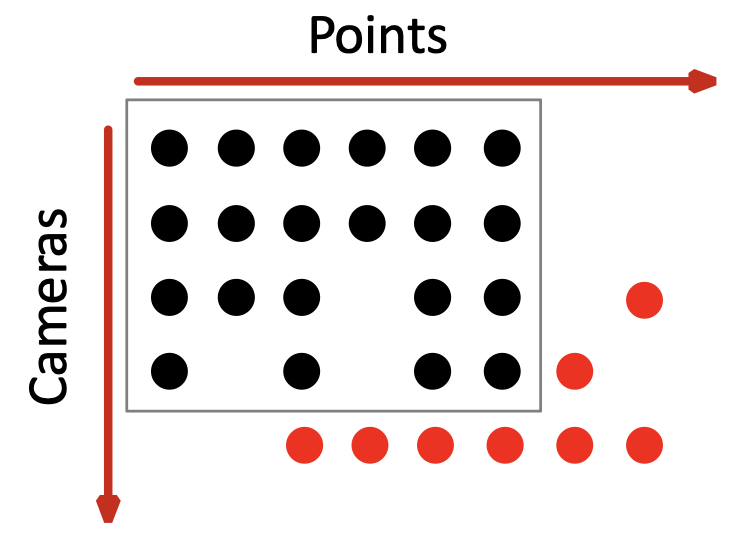
-
优化并扩展结构:计算新的三维点,重新优化该相机也能观察到的现有点
-
-
优化结构与运动:光束法平差(bundle adjustment)
-
光束法平差:通过最小化所有帧的重投影误差来优化三维点和相机参数
\[ E(P_{proj},\bm{P})=\sum_{i=1}^m\sum_{j=1}^n||u_j^{(i)}-P_{proj}^{(i)}\bm{P}_j||^2 \]使用 Levenberg-Marquardt 算法,例如 Google 的 Ceres-Solver
-
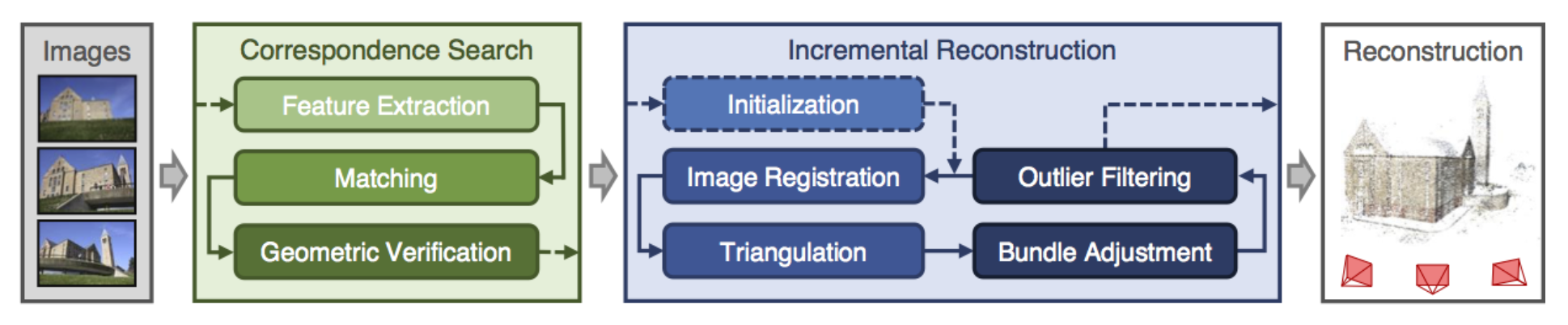
COLMAP⚓︎
COLMAP 是一个通用的运动恢复结构(SfM)和多视图立体(MVS)管道,具有图形和命令行界面。它为有序和无序图像集合的重建提供了一系列功能。
之后的某次实验以及大作业的三维重建选题都会用到这一工具。
增量 SfM 管线:
评论区