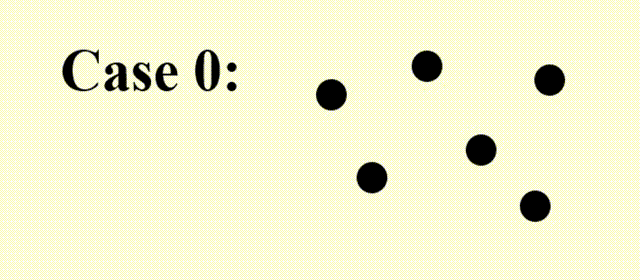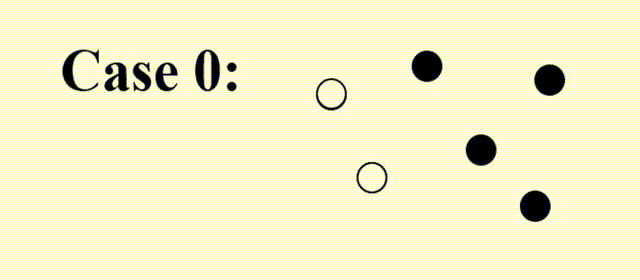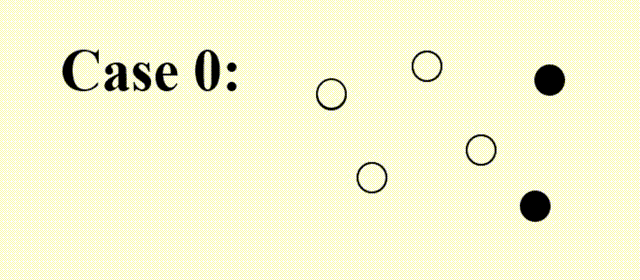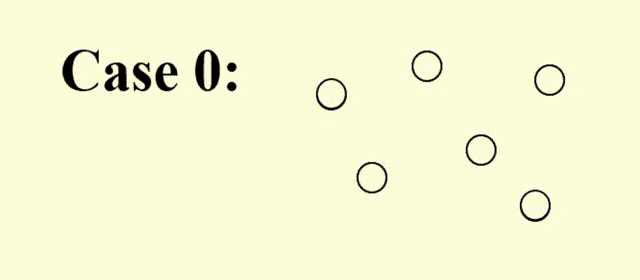Lec 12: Local Search⚓︎
约 5280 个字 51 行代码 预计阅读时间 27 分钟
Introduction⚓︎
我们继续延续上一讲的话题——本讲所介绍的局部搜索(local search) 实际上是近似算法的一大门类,它的大致思路是:通过局部最优解获得全局近似解。
例子
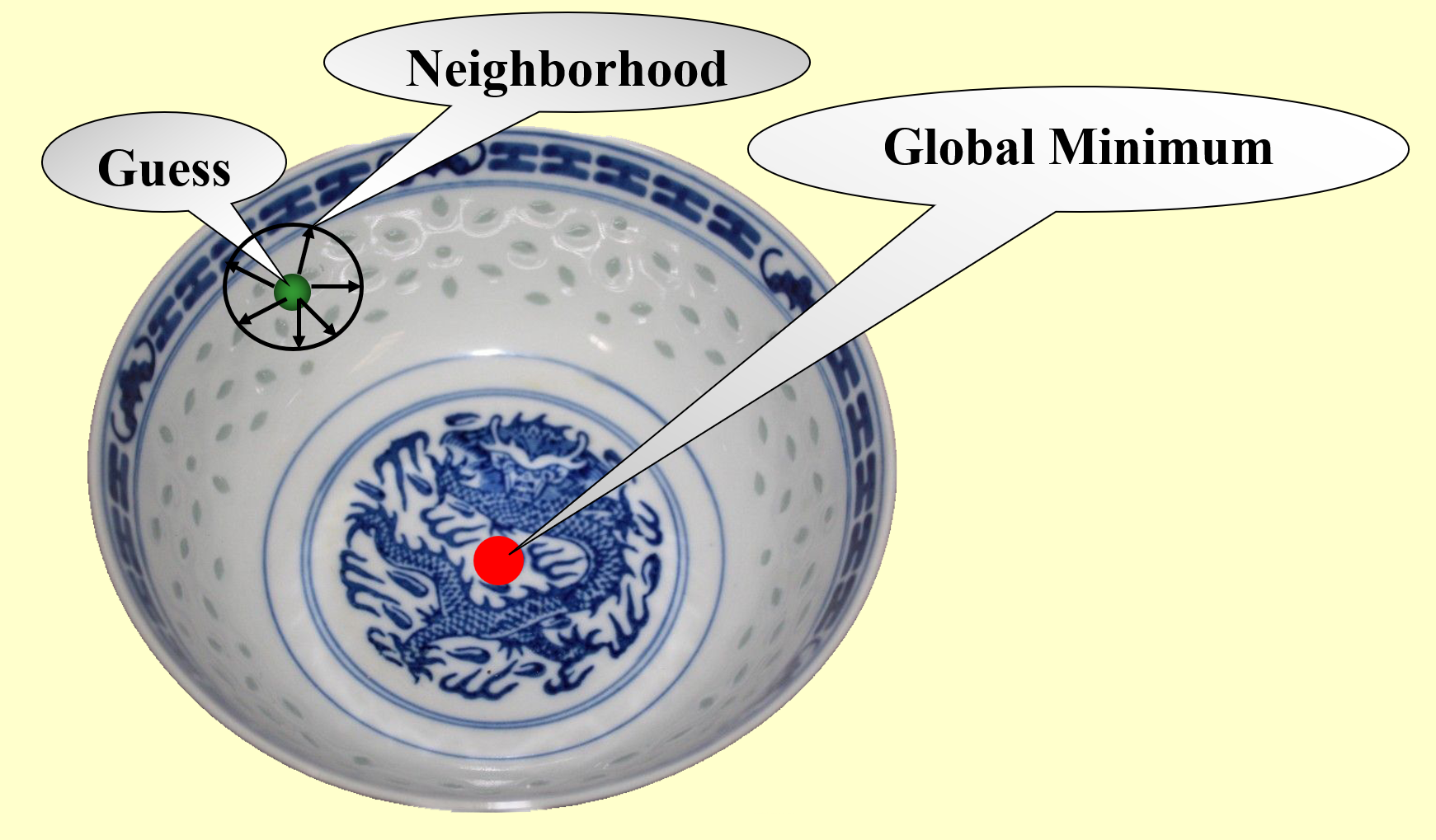
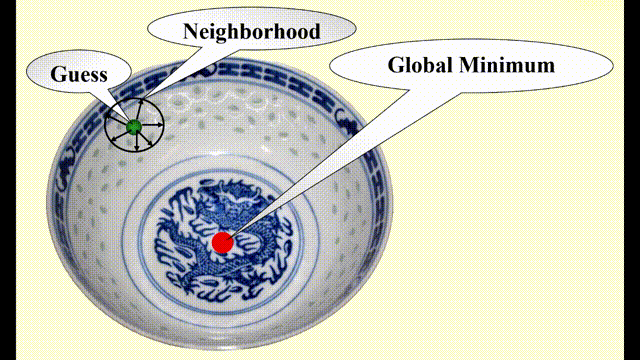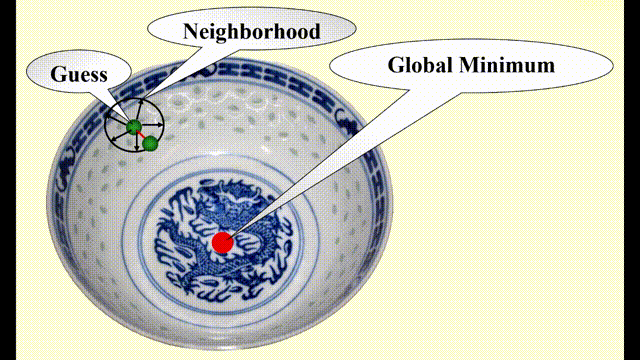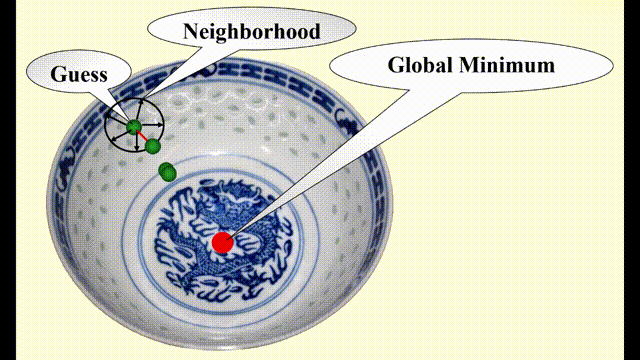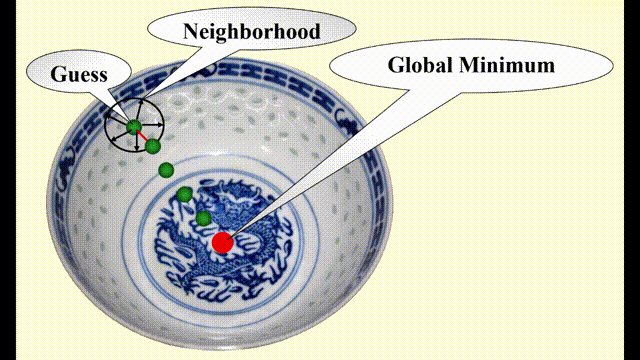
假如要求你使用局部搜索算法来寻找碗的(全局)最低点,如下图所示(图片的违和感太强
- 先在碗中任取一点(称为猜测点 (guess))
- 以该点为中心,在一定范围内(邻居 (neighbor))搜寻该范围内的最低点(局部最优解)
- 接着以这个最低点为中心,在新的范围内搜寻范围内的最低点……
- 以此类推,直到在局部范围内无法再找到更低的点为止,此时发现的最低点应为整个碗的最低点(全局最优解)
思考
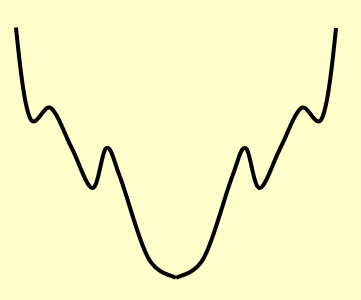
局部搜索算法的设计需要考虑好「局部」的范围,来看下面的例子:
- 局部范围过小:算法可能就会误以为那些“小坑”是最优解,而不会继续搜索下去(陷入了局部最优之中)
- 局部范围过大:算法可能跳过了最优解,最坏的情况下算法可能陷入死循环,因为算法始终无法确定是否不存在更低的点(比如在最低点两边来回跳,就是找不到最低点)
局部搜索的框架结构:
- 局部(local):
- 在一个可行的集合内定义邻居(neighborhoods)
- 局部最优解(local optimum) 是邻居范围内的最优解
- 搜索(search):
- 从一个可行解 \(FS\) 开始,在邻居范围内找到一个更好的解
- 如果没有改进空间,则将当前的局部最优解视为整个问题的“最优解”(不一定是全局最优)
邻居关系(neighbor relation)
- \(S \sim S'\):\(S'\) 是 \(S\) 的邻居解 (neighboring solution),它来自于对原集合 \(S\) 的较小修改
- \(N(S)\):\(S\) 的邻居,即集合 \(\{S': S \sim S'\}\)(包含所有可能的邻居解)
局部搜索算法的伪代码如下:
Solution Type Gradient_descent() {
Start from a feasible solution S in FS; // randomly
// FS: the feasible solution set(for initialization)
MinCost = cost(S);
while (1) {
S` = Search(N(S)); // find the best S' in N(S)
CurrentCost = cost(S`);
if (CurrentCost < MinCost) {
MinCost = CurrentCost;
S = S`;
}
else break;
}
return S;
}
该算法称为“梯度下降法”(gradient descent),顾名思义,就是沿梯度下降的方向不断进行局部的搜索。
- 事实上,即使是局部搜索算法,我们也无法保证搜索操作(
Search())一定能够在多项式时间内完成
思考:贪心算法 vs 局部搜索
- 贪心算法:它是一个“从无到有”构造解的过程,在当前阶段下挑选算法认为最好的选择
- 局部搜索:先给出一个任意解,从这个解出发,每个阶段改变其中的一个邻居元素,看得到的结果是否会更好。由于算法可能陷入局部最优的情况,因此有时无法得到最优解
因此,贪心算法并不是局部搜索的一种特殊情况。
一些结论
- 对于一个优化问题,如果已知某个邻居的局部最优解是全局最优,那么也并不意味着从邻居出发便能一步得到全局最优
下面给出一些用局部搜索算法计算的经典题目,通过这些题目来进一步加深对局部搜索的理解。
Examples⚓︎
Vertex Cover Problem⚓︎
这一问题在上一讲的最后简单提到过,在这里我们来更为深入地了解这类题型 ~
问题描述
该问题有两类问法:
- 判定版本:给定一个无向图 \(G = (V, E)\) 和一个整数 \(K\),该图是否存在一个子集 \(V' \subseteq V\),使得 \(|V| =(\text{or } \le) K\),且满足 \(G\) 中的每条边(一条边有两个端点)至少有一个属于 \(V'\) 的端点
- 最优版本:给定一个无向图 \(G = (V, E)\),请找到一个最小的子集 \(S \subseteq V\),使得 \(E\) 中的任意一边 \((u, v)\),\(u\) 和 \(v\) 至少有一个属于 \(S\)
下面我们考虑的是最优版本的问法。
先定义一些量:
- 可行解集 \(FS\):所有的顶点覆盖
- \(cost(S) = |S|\)
- \(S \sim S'\):每个顶点覆盖 \(S\) 至多有 \(|V|\) 个邻居
搜索步骤:
- 从 \(S = V\) 开始
- 删除或增加一个节点得到新的顶点覆盖 \(S'\)
- 检查 \(S'\) 的成本是否更低
几种 tricky 的情况
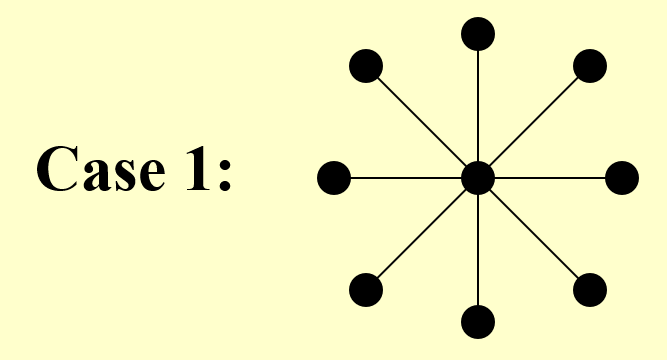
先给个 trivial 的情况练练手。
可以看到,这张图只有顶点没有边,因此最优解就是去掉所有顶点,即 \(S = \emptyset\)。显然,用前面介绍过的梯度下降法能够解决此类情况。
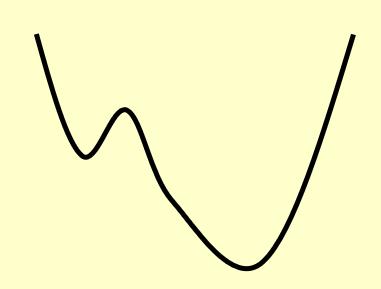
如果用最开始给出的那个碗的例子来类比,对应的碗的剖面大概长这样(很平滑,因此一步步找总能找到最优解
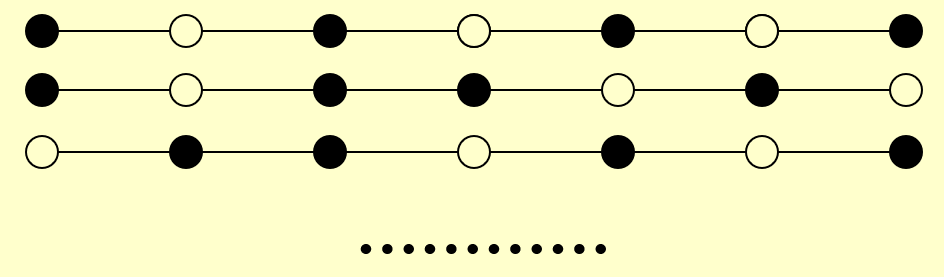
如果我们手工完成的话,这道题相当简单:只需要保留中间那个点,去掉所有其他的点即可。然而,如果算法一开始选择删除的是中间的点,那就寄了——梯度下降法不具备撤销操作,所以这么一删后,无论之后怎么做都无法得到最优解了。
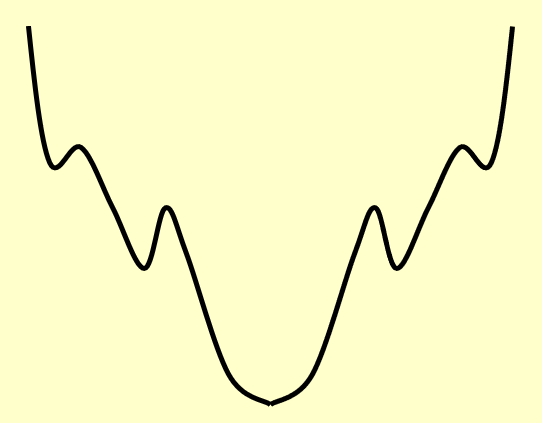
还是用那个碗类比,对应的碗的剖面大概长这样(边上有一小块凹下去的地方,使算法误以为这个局部最优无法得到进一步提升,视其为全局最优,从而得到错误的结果
看过这些 tricky 的例子后,可以发现梯度下降法的一个很大的缺陷是容易陷入局部最优。因此下面给出一个更为强大的算法——Metropolis 算法来解决此题:
SolutionType Metropolis() {
Define constants k and T;
Start from a feasible solution S in FS;
MinCost = cost(S);
while (1) {
S` = Randomly chosen from N(S);
CurrentCost = cost(S`);
if (CurrentCost < MinCost) {
MinCost = CurrentCost;
S = S`;
} else {
With a probability exp(-(CurrentCost - MinCost) / (k * T)), let S = S`;
otherwise break;
}
}
return S;
}
-
再来看前面给出的例子:
- 对于 Case 1,该算法有一定概率可以跳出局部最优,得到正确解
- 而对于 Case 0,有可能在 +1 和 -1 之间无限振荡
-
这一算法与梯度下降法最大的不同之处在于:如果新的顶点覆盖 \(S'\) 的成本更大,它不会马上就被抛弃掉,而是通过某个特殊的概率 \(e^{-\frac{\Delta \text{cost}}{kT}}\) 来决定它是否可以被保留下来(代码高亮部分)
- 这一假设被称为玻尔兹曼分布
- 因此,\(S'\) 既可以来自删掉任意一点后的 \(S\),也可以来自增加任意一点后的 \(S\)(可视为撤销操作)
- 算法中的 \(T\) 表示温度(这个算法来自于统计物理学,因而会涉及到物理量)
- 当 \(T \rightarrow +\infty\) 时,概率 \(e^{-\frac{\Delta \text{cost}}{kT}} \rightarrow 1\),容易引起底部振荡(也就是说无论在何种情况下,\(S'\) 会不断更新)
- 当 \(T \rightarrow 0\),概率 \(e^{-\frac{\Delta \text{cost}}{kT}} \rightarrow 0\),此时该算法接近原始的梯度下降法
- 设计该算法的一大难点在于寻找合适的温度值——这里我们采用模拟退火(simulated annealing) 的算法。该算法的名称来自于冶金学术语“退火”:让材料从很高的温度开始慢慢冷却,使我们有充足的时间在一系列不断减小的中间温度值 \(T = \{T_1, T_2, \dots\}(T_1 \ge T_2 \ge \dots)\) 中找到平衡点 (equilibrium)(即最优解)
补充:二分图上的顶点覆盖问题和匹配问题
Hopfield Neural Networks⚓︎
问题描述
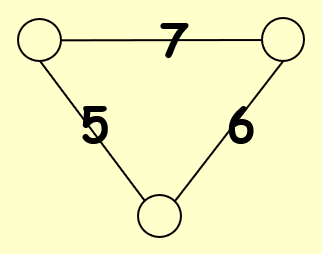
给定一张图(或者称为网络 (network))\(G = (V, E)\),每条边都有一个整数(不论正负)的权重 \(w\),其绝对值 \(|w|\) 称为需求强度 (strength of requirement);每个顶点的取值(称为状态 (state))\(s\) 为 \(\pm 1\)。
对于边 \(e = (u, v)\):
- 如果 \(w_e < 0\),那么 \(u\) 和 \(v\) 具备相同的状态(即都为 -1 或都为 1)
- 如果 \(w_e > 0\),那么 \(u\) 和 \(v\) 具备不同的状态(即一个为 -1,一个为 1)
题目的输出为:网络的一种布局 (configuration)\(S\)——所有顶点的状态集合,每个顶点 \(u\) 都被赋予一个状态 \(s_u\)。
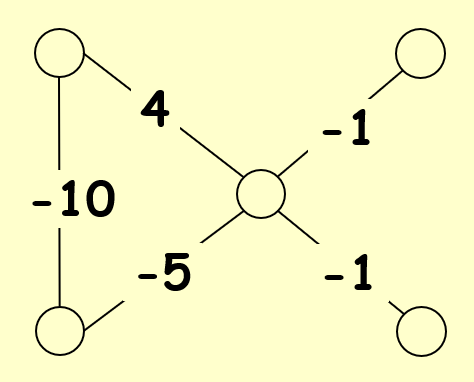
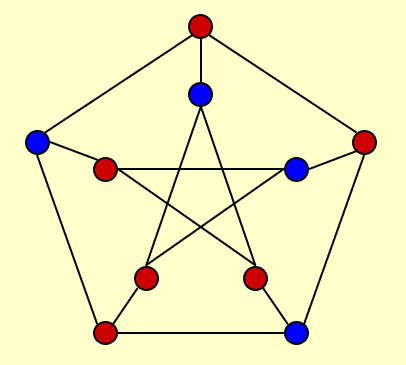
需要注意的是:可能不存在能够满足所有边的需求的布局,比如这张图:
因此,我们需要找到一种足够好的布局,接下来定义一下何谓“足够好”:
-
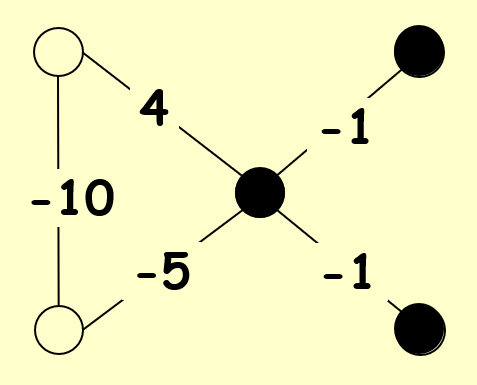
在一种布局中,如果 \(w_e s_u s_v < 0\),称边 \(e = (u, v)\) 是一条好边,否则称其为一条坏边
- \(w_e < 0 \Leftrightarrow s_u = s_v\)
- \(w_e > 0 \Leftrightarrow s_u \ne s_v\)
-
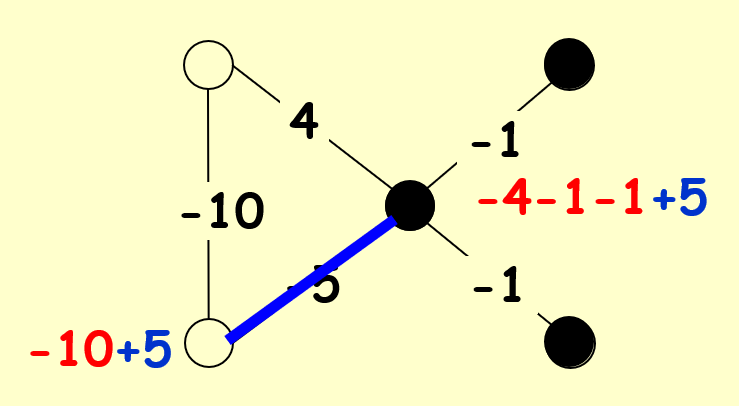
在一种布局中,如果一个顶点的关联 (incident)(即该点作为某条边的端点)好边的总权重不小于关联坏边的总权重,称这个点为满意 (satisfied) 点,即满足:
- 如果一张图的所有顶点都是满意点,那么称这个布局是稳定的 (stable)
下面给出一种寻找稳定布局的算法——状态翻转(state-flipping) 算法:
ConfigType State_flipping() {
Start from an arbitrary configuration S;
while (!IsStable(S)) {
u = GetUnsatisfied(S);
s_u = -s_u;
}
return S;
}
算法非常简单:只要这个布局不是稳定的,算法就会找出不满意点并翻转它的状态,这样就能使其变成满意点(很容易验证
先给个结论:该算法在至多 \(W = \sum_e|w_e|\) 次迭代后终止,下面我们来证明一下:
证明
这里引用摊还分析中的势能函数法来证明该结论。
令势能函数 \(\Phi(S) = \sum_{e \text{ is good}}|w_e|\),当顶点 \(u\) 翻转状态时(\(S\) 会变成 \(S'\))
- 所有与 \(u\) 关联的好边都变成了坏边
- 所有与 \(u\) 关联的坏边都变成了好边
- 其他边保持不变
因此 \(\Phi(S') = \Phi(S) - \sum\limits_{e:e=(u,v) \in E \atop e \text{ is bad}}|w_e| + \sum\limits_{e:e=(u,v) \in E \atop e \text{ is good}}|w_e|\)
由于每次翻转操作针对的是不满意点,因此翻转之后,该等式右边的最后两项权重和之差至少是 1。在最坏的情况下,一个布局的所有边都是坏边,最后都变成了好边,那么所需要的迭代次数就是 \(W\) 了。因此可以得到 \(0 \le \Phi(S) \le W\)。证毕。
下面我们回到局部搜索,从局部搜索算法的角度重新审视这道题:
- 问题:找到最大的 \(\Phi\)
- 可行解集 \(FS\):某种布局
- \(S \sim S'\):\(S'\) 可通过对 \(S\) 的某个顶点的状态翻转后得到
结论:任意一种在状态翻转算法中得到的局部最大的 \(\Phi\) 的最优布局是一种稳定的布局(局部最优 \(\rightarrow\) 全局最优
由于该算法的时间复杂度与边的绝对值权重和相关,而权重的绝对值可以很大很大,因此该算法不是多项式复杂度的,而且至今还未找到多项式时间下(对于 \(n\) 和 \(\log W\),或者仅对于 \(n\) 的)构建稳定布局的算法。
Maximum Cut Problem⚓︎
问题描述
最大割问题(maximum cut problem):给定一张无向图 \(G = (V, E)\),每条边都有一个正整数权重\(w_e\),请找到一种顶点划分 (node partition)\((A, B)\)(即对于所有顶点,要么属于集合 \(A\),要么属于集合 \(B\)
为了使读者更好地理解题目的意思,先给出一种简单的应用:
现在我们从局部搜索的角度审视此题:
- 问题:使 \(w(A, B)\) 尽可能大
- 可行解集 \(FS\):任意划分 \((A, B)\)
- \(S \sim S'\):通过将 \(S\) 中的某个顶点从划分 \(A\) 移动到划分 \(B\),或从划分 \(B\) 移动到划分 \(A\) 来得到 \(S'\)
读者是否有一种似曾相识的感觉——没错,这道题和前面介绍的 Hopfield 神经网络问题十分相似——某个顶点在划分 \(A, B\) 之间的移动对应于顶点状态的翻转(后面直接称这个操作为“翻转”
- 还可以用类似的势能函数来描述这一问题
- 也可以通过前面介绍过的状态翻转算法得到 \(S'\)(单顶点翻转)
然而,我们在前面提到过,这种算法具有一定的局限性,因此需要考虑下面几个问题:
-
局部最优解有多好?
-
先给个结论:令 \((A, B)\) 为一种局部最优的划分,\((A^*, B^*)\) 为一种全局最优的划分,那么 \(w(A, B) \ge \dfrac{1}{2}w(A^*, B^*)\)。换句话说,局部最优解得到的最大割至少是全局最优解的一半。下面给出证明:
证明
因为 \((A, B)\) 是局部最优划分,所以 \(\forall u \in A\),可以得到:
\[ \sum\limits_{v \in A} w_{uv} \le \sum\limits_{v \in B} w_{uv} \]将所有的顶点 \(u \in A\) 累加起来,得到:
\[ \begin{align} 2 \sum\limits_{ \{u, v\} \subseteq A} w_{uv} = \sum\limits_{u \in A} \sum\limits_{v \in A} w_{uv} \le \sum\limits_{u \in A} \sum\limits_{v \in B} w_{uv} = w(A, B) \end{align} \]同理得:
\[ \begin{align} 2 \sum\limits_{ \{u, v\} \subseteq B} w_{uv} \le w(A, B) \end{align} \]\((1) + (2)\) 并化简,得到:
\[ w(A^*, B^*) \le \sum\limits_{ \{u, v\} \subseteq A} w_{uv} + \sum\limits_{ \{u, v\} \subseteq B} w_{uv} + w(A, B) \le 2w(A, B) \]得证。
-
所以,状态翻转算法在本题是一种2- 近似算法
- 相关研究:
- 对于最大割问题,存在一种 1.1382- 近似算法(与 \(\min\limits_{0 \le \theta \le \pi} \dfrac{\pi}{2} \dfrac{1 - \cos \theta}{\theta}\) 相关,
什么鬼) - 若能够证出 \(P = NP\),那么存在一种 \(\dfrac{17}{16}(\approx 1.0625)\)- 近似算法
- 对于最大割问题,存在一种 1.1382- 近似算法(与 \(\min\limits_{0 \le \theta \le \pi} \dfrac{\pi}{2} \dfrac{1 - \cos \theta}{\theta}\) 相关,
-
-
能否在多项式时间内得到结果呢?
- 一种策略是:如果算法找不到有“足够大”提升的解,那么算法就会终止迭代,称这种算法为大提升翻转(big-improvement-flip)。具体来说,该算法挑选那些能够提升至少 \(\dfrac{2\varepsilon}{|V|}w(A, B)\) 割值的顶点来翻转
-
相关结论:
-
算法中止后会返回一个割集 \((A, B)\),满足:\((2 + \varepsilon)w(A, B) \ge w(A^*, B^*)\)
-
因此该算法是一个 \((2 + \varepsilon)\)- 近似算法
证明
根据条件,对于 \(u \in A\),我们可以得到不等式:
\[ \sum\limits_{v \in A} w_{uv} \le \sum\limits_{v \in B} w_{uv} + \dfrac{\varepsilon}{n}w(A, B) \]后续证明过程与前一个证明类似,故不再展开叙述。
-
-
该算法能够在至多 \(O(\dfrac{n}{\varepsilon} \log W)\) 次翻转后终止,其中 \(W = \sum w\)
证明
- 根据前面的证明知,每次翻转后,\(w(A, B)\) 会提升 \((1 + \dfrac{\varepsilon}{n})\) 倍
- 由不等式 \((1 + \dfrac{1}{x})^x \ge 2, \forall x \ge 1\) 知,\((1 + \dfrac{\varepsilon}{n})^{\frac{n}{\varepsilon}} \ge 2, \forall \dfrac{\varepsilon}{n} \ge 1\)
- 我们的目标是最大化 \(w(A, B)\),即令 \(w(A, B) \rightarrow W\),那么由上面的不等式知,要使 \(w(A, B)\) 从最低值 1 出发提升 \(W\) 倍,就需要翻转 \(O(\dfrac{n}{\varepsilon} \log W)\)。得证。
-
-
是否存在一种更好的「局部
」 ?- 一个好的「局部」需要满足:
- 解的邻居需要足够大,使得算法不会陷入局部最优解而“出不来”
- 但解的邻居也不能太大,因为我们希望能够在有限的步数内,在邻居集中高效地寻找最优解
- 要想寻找一个更好的局部解,一个简单的想法是使用前面介绍过的状态翻转算法来翻转 \(k\) 个顶点,这样得到了一个 \(k\) 翻转的邻居关系,
- 若 \((A, B)\) 和 \((A', B')\) 是 \(k\) 翻转的邻居关系,则对于 \(k' > k\),\((A, B)\) 和 \((A', B')\) 也是 \(k'\) 翻转的邻居关系。所以我们可以通过不断增大 \(k\) 找到更好的邻居关系,从而减小近似比
- 但是该方法的搜索空间为 \(\Theta(n^k)\),当 \(k\) 稍微变大时时间复杂度就会变得很大,不太令人满意
- 改进方法——K-L 启发式算法(heuristic),执行步骤如下:
- 第 1 步:对整个顶点集(顶点划分 \((A, B)\))使用状态翻转算法(单顶点的翻转
) ,此时得到的最优解为 \((A_1, B_1)\),被翻转的那个顶点记为 \(v_1\)- 时间复杂度:\(O(n)\)
- 第 k 步:对尚未翻转过的顶点集使用状态翻转算法,此时得到的最优解为 \((A_k, B_k)\),被翻转的顶点有 \(v_1, \dots, v_k\)
- 时间复杂度:\(O(n - k + 1)\)
- 第 n 步:\((A_n, b_n) = (B, A)\)
- 因此,划分 \((A, B)\) 的邻居集为 \(\{(A_1, B_1), \dots, (A_{n - 1}, B_{n - 1})\}\),时间复杂度为 \(O(n^2)\)
- 第 1 步:对整个顶点集(顶点划分 \((A, B)\))使用状态翻转算法(单顶点的翻转
- 一个好的「局部」需要满足:
一些结论
- 最大割的权重和至少是所有边权重和的一半
相关资料:Maximum cut problem
Other Examples⚓︎
以下的例子来自课件之外的内容(作业题 / 历年卷等等
) ,所以写的比较简略和粗糙 ...
扩展
这篇笔记介绍了更多的局部搜索算法!
Minimum Spanning Trees⚓︎
这里给出最小生成树的局部搜索算法的伪代码(摘自作业题
// F: feasible solution
T = any spanning tree in F;
// e: edge in T
// e`: edge in (G - T)
while (there is an edge_swap(e, e`) which reduces Cost(T)) {
T = T - e + e`;
}
return T;
伪代码还算好理解的,就是交换生成树内的一条边和生成树外的一条边,看生成树的边权重和是否减小,若是则交换这两条边。
结论:该算法可以得到在多项式时间内得到最优解。
Schedule Problems⚓︎
怎么又是你
问题描述
类似近似算法中给出的调度问题,机器数量 \(m = 2\),要求的是两台机器 \(A, B\) 完成时间的最小差值,即求 \(\min \{|T_1 - T_2|\}\),其中 \(T_1 = \sum_{j \in A}t_j, T_2 = \sum_{j \in B}t_j\)。
-
该问题是一个 NP Hard 问题,因此采用以下局部搜索算法求得最优解:
- 将任务随机分配给这两台机器,其中机器 \(A\) 接受的任务标号为 \(1, 2, \dots, \dfrac{n}{2}\)
- 规定局部移动为:将任务从一个机器移到另一个机器上。我们只移动那些能够减小 \(|T_1 - T_2|\) 的任务
-
若没有一个任务的时长超过所有任务总时长的一半,则机器 \(B\) 的总时长 \(T_2\) 满足关系:\(\dfrac{1}{2}T_1 \le T_2 \le 2T_1\)
- 若对于某个阶段而言,存在多个可移动的任务,那么我们移动时长 \(t_j\) 最大的任务 \(j\)。在这种情况下,可以证明每个任务最多只会被移动一次,那么该算法的时间复杂度就是 \(O(n)\) 了
- 该算法不一定能够得到最优解
注:这部分内容摘自《Algorithm Design》Chap 12, Exercise 3(作业题里有这题
) 。
评论区