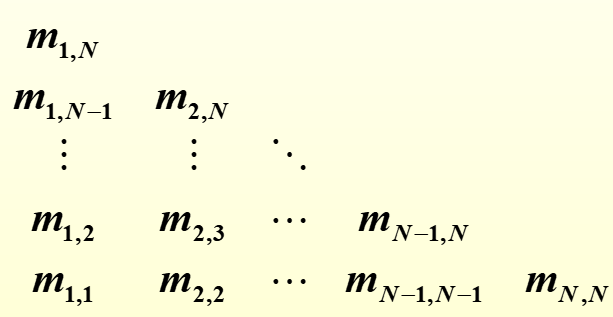Lec 8: Dynamic Programming⚓︎

Theory Background⚓︎

动态规划的概念：

动态规划（dynamic programming, DP）是一个重要的算法范式，它将一个问题分解为一系列更小的子问题，并通过存储子问题的解来避免重复计算，从而大幅提升时间效率。（摘自 Hello 算法）

动态规划的问题特性：

• 重叠子问题：动态规划的子问题是相互依赖的（而分治算法处理的是独立的子问题）
• 最优子结构：原问题的最优解是从子问题的最优解构建得来的
• 无后效性：给定一个确定的状态，它的未来发展只与当前状态有关，而与过去经历的所有状态无关（否则难以用动态规划解决）

满足上述特性的问题用动态规划解决较为合适。

动态规划的基本思想：

• 每个子问题仅解决一次，将得到的解存入一张表中
• 如果某个子问题需要其他子问题的解，可先查表，看是否已经求过解，若是则直接用，否则再计算
• “以空间换时间”——记忆化搜索

注：下面的理论部分建议在阅读完 Examples 一节的前 4 个例子后再来阅读，这样理解会更深刻些。

Examples⚓︎

Climbing Stairs Problem⚓︎

• 假如我们现在站在第 i 个台阶上，因为每步可以上 1 个或 2 个台阶，所以在上一步我们应该站在第 i-1 或第 i-2 个台阶上
• 令爬到第 i 个台阶的方案树为 \(F_i\)，那么很自然地，我们得到了一个递推关系式：\(F_i = F_{i - 1} + F_{i - 2}\)
• 不难发现，这是一个斐波那契数列，因此我们可以采用 FDS 介绍的暴力搜索算法来解决这一问题

然而，也是在 FDS 中，我们已经分析过，这种算法（实际上是递归算法）的时间复杂度是指数级的，有点吓人。之所以速度如此之慢，原因在于几乎所有的子问题都被重复计算了很多次，产生了大量的冗余计算。正在学习 ADS 的我们是时候拿出更高级的算法——动态规划来优化一下了：

• 根据递推关系，要得到 \(F_N\)，只需知道 \(F_{N-1}\) 和 \(F_{N-2}\) 的值
• 那么我们可以在计算过程中仅保留这两个值，即上一次和上上次计算的结果，将它们相加即可得到本次计算的结果，无需存储所有 \(F_i\) 的值（空间复杂度 \(O(N) \rightarrow O(1)\)）
• 然后更新上一次和上上次的值，进入下一轮的计算（\(F(N+1)\)）
• 所以这种方法是自底向上计算的，而递归算法是自顶向下计算的

int Fibonacci(int N) {
    int i, Last, NextToLast, Answer;
    if (N <= 1)
        return 1;
    Last = NextToLast = 1;    // F(0) = F(1) = 1

    for (i = 2; i <= N; i++) {
        Answer = Last + NextToLast;    // F(i) = F(i - 1) + F(i - 2)
        NextToLast = Last;    // update F(i - 1) and F(i - 2)
        Last = Answer;
    }    // end-for

    return Answer;
}

时间复杂度：\(T(N) = O(N)\)

Ordering Matrix Multiplications⚓︎

问题描述

对于多个矩阵的乘法，乘法的顺序相当关键，如果顺序选择不当，会让计算次数变得相当多。

例子

对于一个给定的多矩阵乘法，请找出最优的乘法顺序。

假设我们计算 \(n\) 个矩阵的乘法 \(\mathbf{M}_1 \cdot \dots \cdot \mathbf{M}_n\)，其中 \(\mathbf{M}_i\) 是一个规模为 \(r_{i-1} \times r_i\) 的矩阵。令计算矩阵乘法 \(\mathbf{M}_i \cdot \dots \cdot \mathbf{M}_j\) 的最优成本为 \(m_{ij}\)，那么我们可以得到以下递推关系式：

• 我们需要计算的 \(m_{ij}\) 有 \(O(N^2)\) 个（\(i, j\) 的范围在 \([1, n]\) 之间）
• 根据递推关系式，某个子问题的解一定来自比该子问题规模更小的子问题的解中。因此为了节省计算次数，我们还是自底向上计算：先算最小规模（即 \(i = j\) 时）的 \(m_{ij}\)，再计算更大规模的 \(m_{ij}\)，这样规模较大的子问题可以利用规模较小的子问题的解直接计算，而无需重复计算更小规模的子问题
• 在计算过程中，我们保存了一张形如下三角矩阵的表：

// r contains numbers of columns for each of the N matrices
// r[0] is the number of rows in matrix 1
// Minimum number of multiplications is left in M[1][N]
void OptMatrix(const long r[], int N, TwoDimArray) {
    int i, j, l, L;
    long ThisM;

    for (i = 1; i <= N; i++)
        M[i][i] = 0;
    for (k = 1; k < N; k++)    // k = j - i
        for (i = 1; i <= N - k; i++) {    // For each position
            j = i + k;
            M[i][j] = Infinity;
            for (L = i; L < j; L++) {
                ThisM = M[i][L] + M[L + 1][j] + r[i - 1] * r[L] * r[j];
                if (ThisM < M[i][j])    // Update min
                    M[i][j] = ThisM;
            }    // end for-L
        }    // end for-Left
}

// Compute optimal ordering of matrix multiplication
// c contains number of columns for each of the n matrices
// c[0] is the number of rows in matrix 1 
// Minimum number of multiplications is left in M[1][n] 
// Actual ordering can be computed via 
// another procedure using last_change 
// M and last_change are indexed starting at 1, instead of zero 

void opt_matrix( int c[], unsigned int n, two_d_array M, two_d_array last_change) {
    int i, k, Left, Right, this_M;

    for (Left = 1; Left <= n; Left++)
        M[Left][Left] = 0;
    for (k = 1; k < n; k++)    // k is Right-Left 
        for (Left = 1; Left <= n-k; Left++) {    // for each position 
            Right = Left + k;
            M[Left][Right] = INT_MAX;
            for (i = Left; i < Right; i++) {
                this_M = M[Left][i] + M[i+1][Right]
                + c[Left-1] * c[i] * c[Right];
                if(this_M < M[Left][Right]) {    // Update min
                    M[Left][Right] = this_M;
                    last_change[Left][Right] = i;
                }
            }
        }
}

时间复杂度：\(T(N) = O(N^3)\)

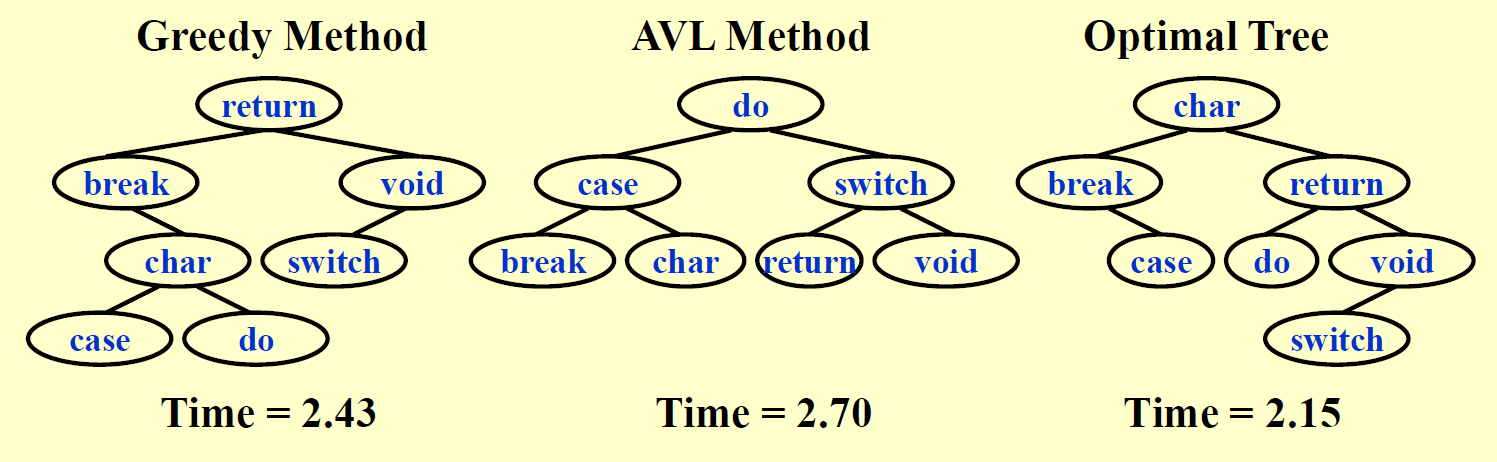
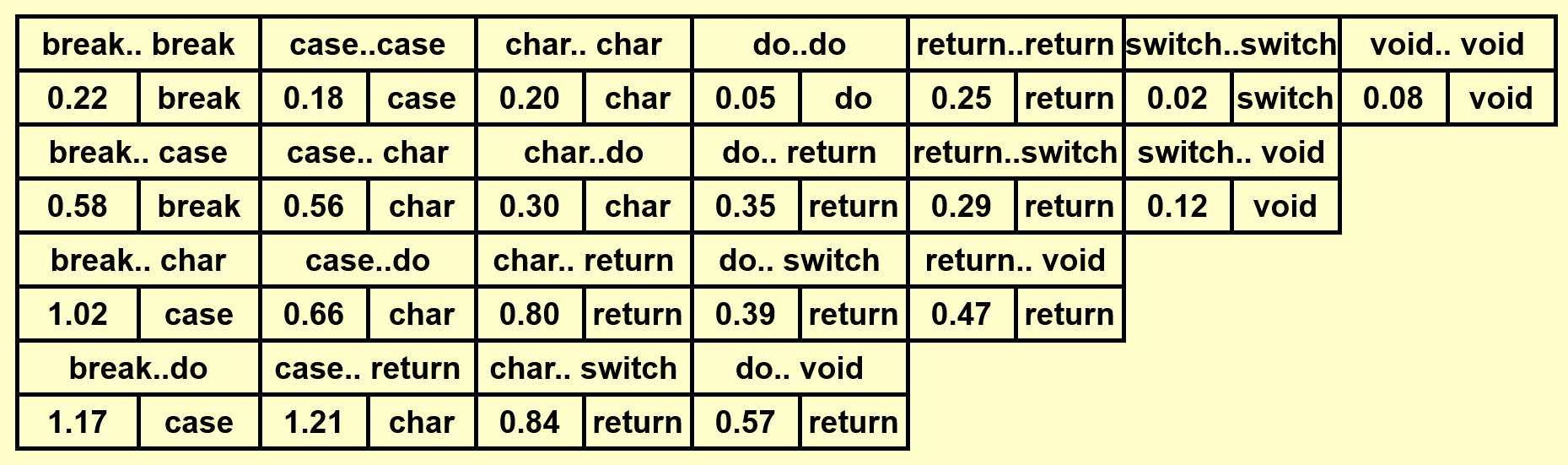
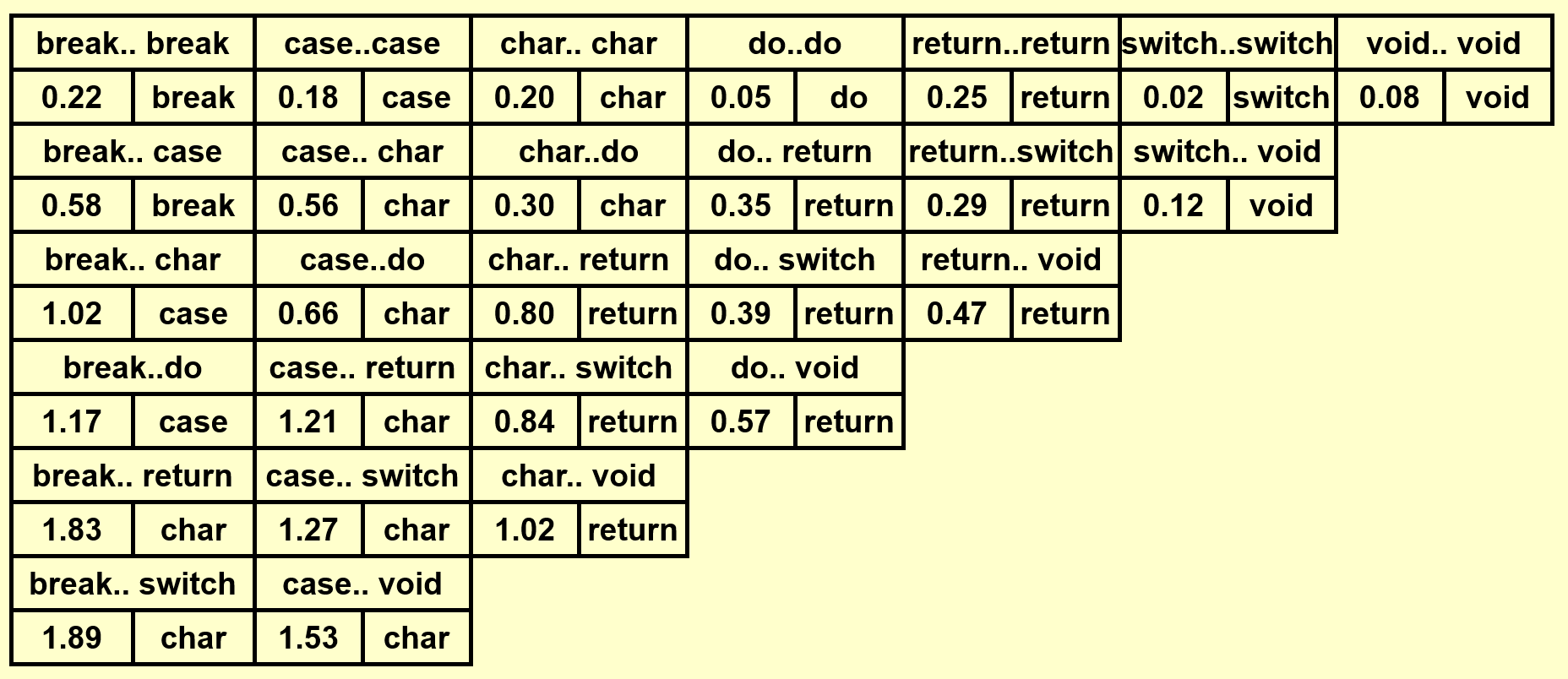
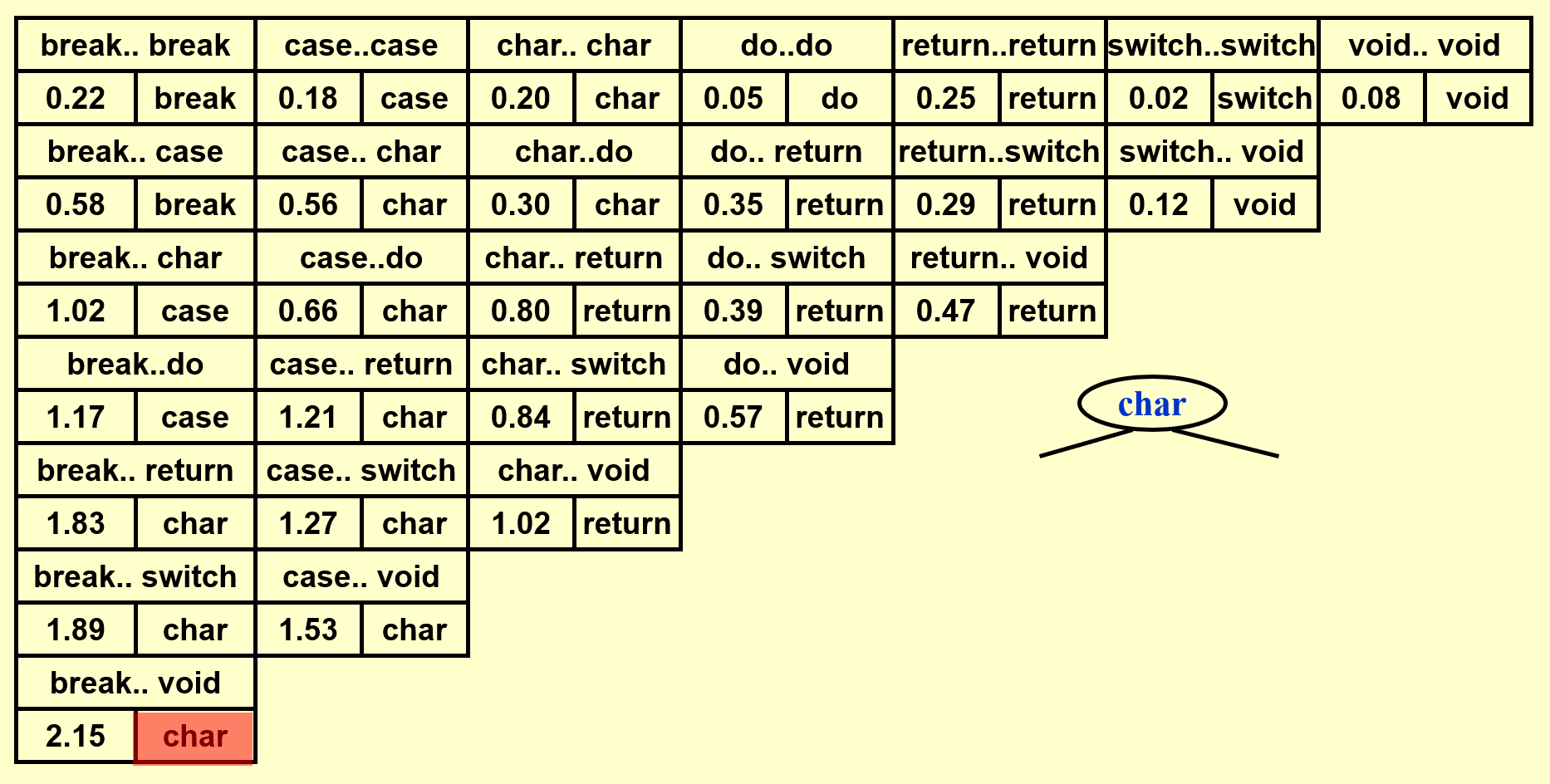
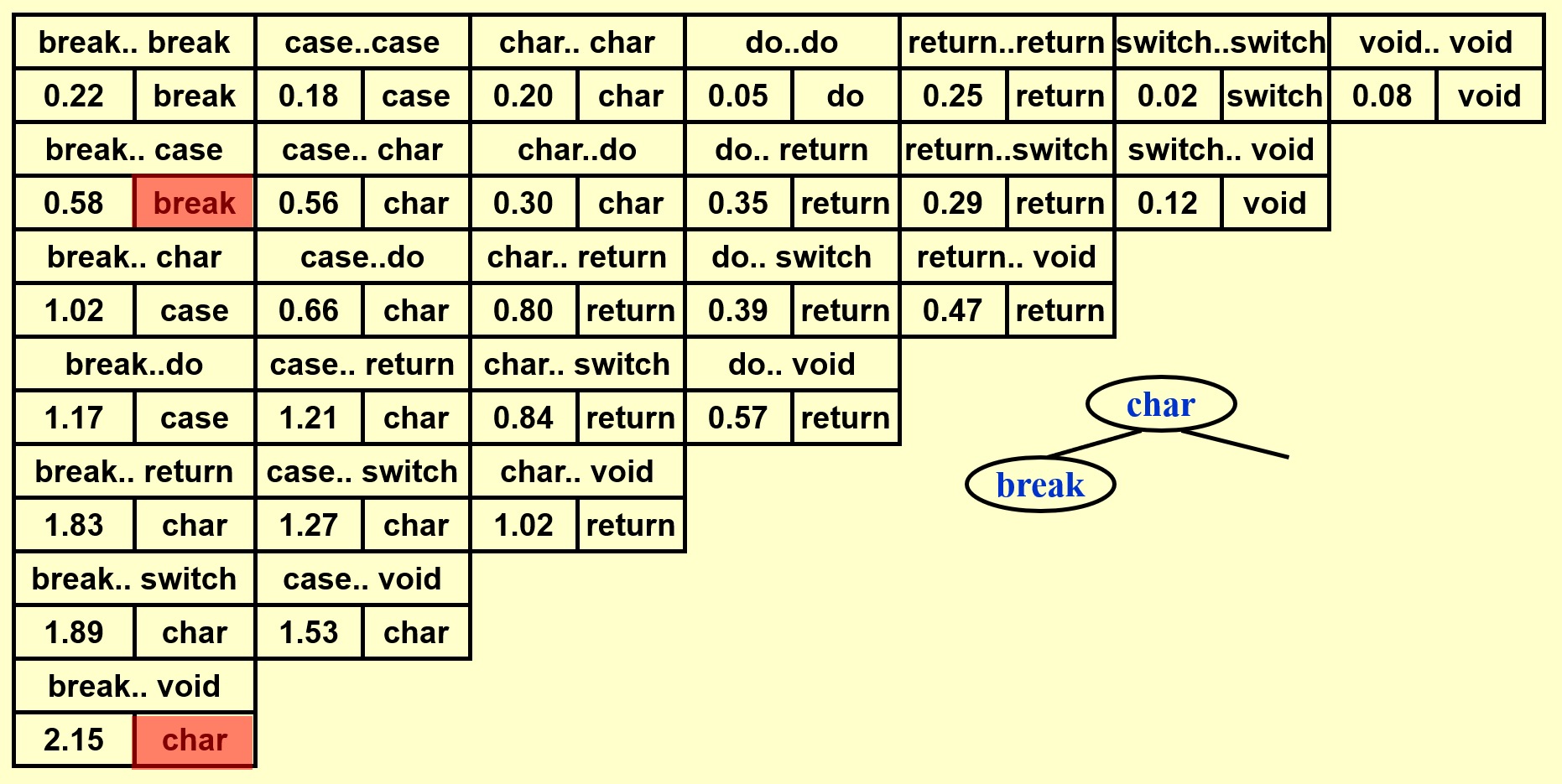
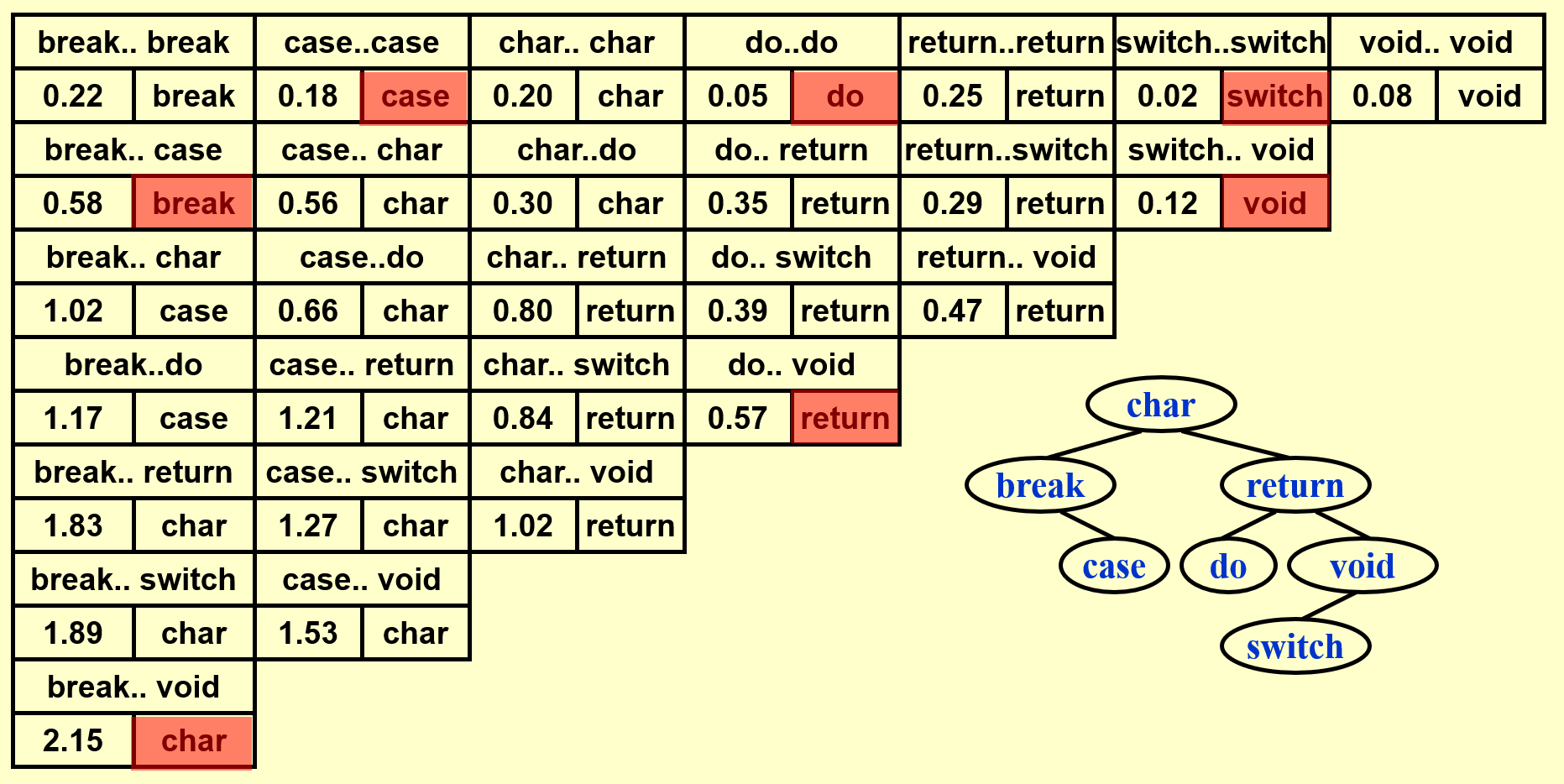
Optimal Binary Search Trees⚓︎

最优二叉查找树(optimal binary search trees, OBST)：一种在二叉查找树上完成静态查找 (static search)（即没有插入和删除操作）操作的最优方法。

例子

问题答案

下面给出一个程序用到的关键词以及对应的词频：

请分别用贪心算法（下一节会讲到，在这里指的是优先插入词频最大的单词）、红黑树来构建二叉查找树。

这里分别给出用贪心算法、红黑树和 OBST 的方法构建出来的二叉查找树，以及对应的 \(T(N)\)：

• 贪心算法之所以慢，是因为它优先考虑词频最大的单词，这可能导致某些高词频的单词被放在深度很大的地方，从而增大了总的查找时间。
• 红黑树之所以慢，是因为它在构建树的过程中仅考虑了黑高，压根没有考虑词频的问题，所以可以看到虽然整棵树挺平衡的，但词频最大的那几个词全在深度最深的地方，使得总查找时间变的很大。

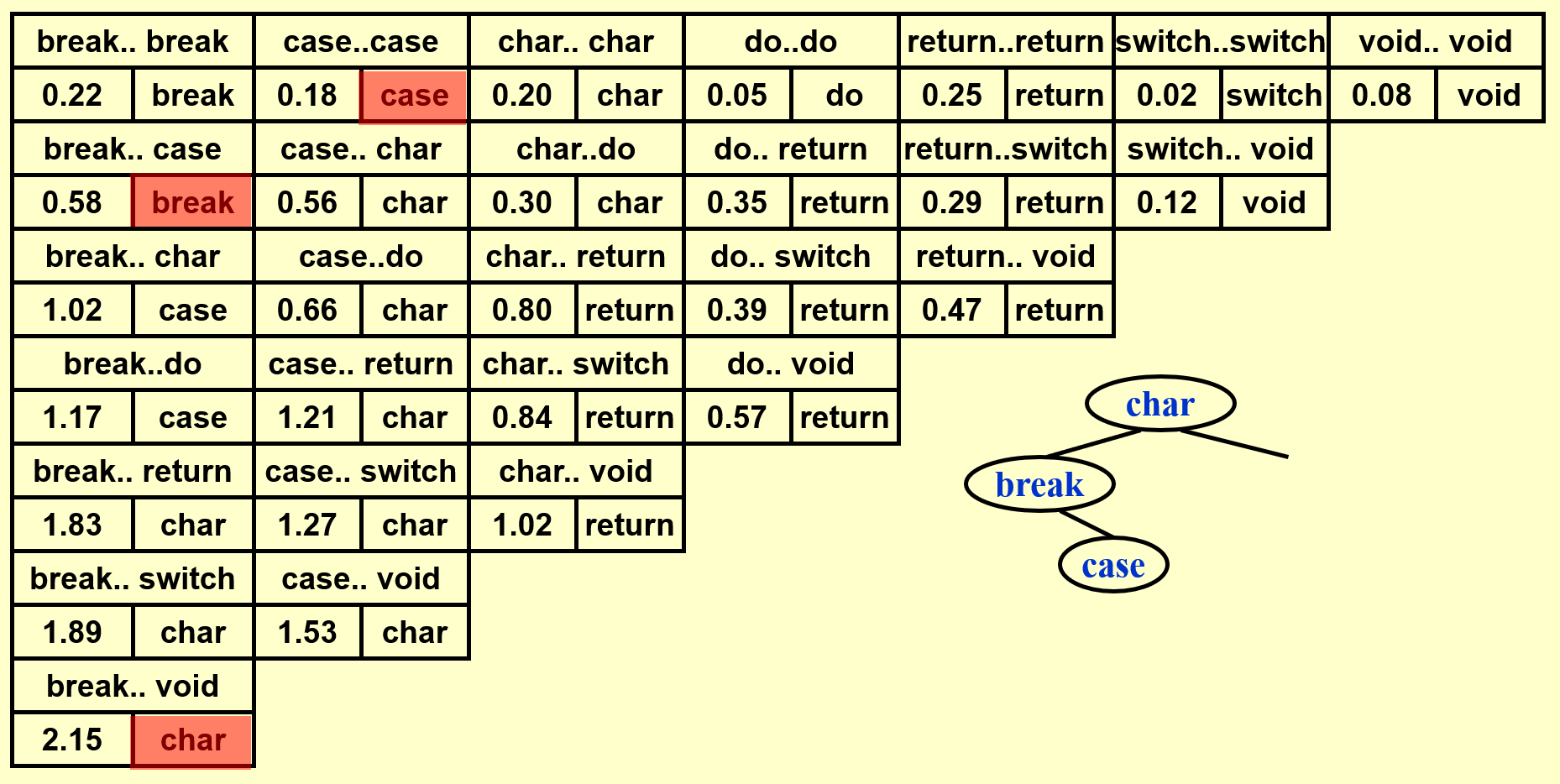
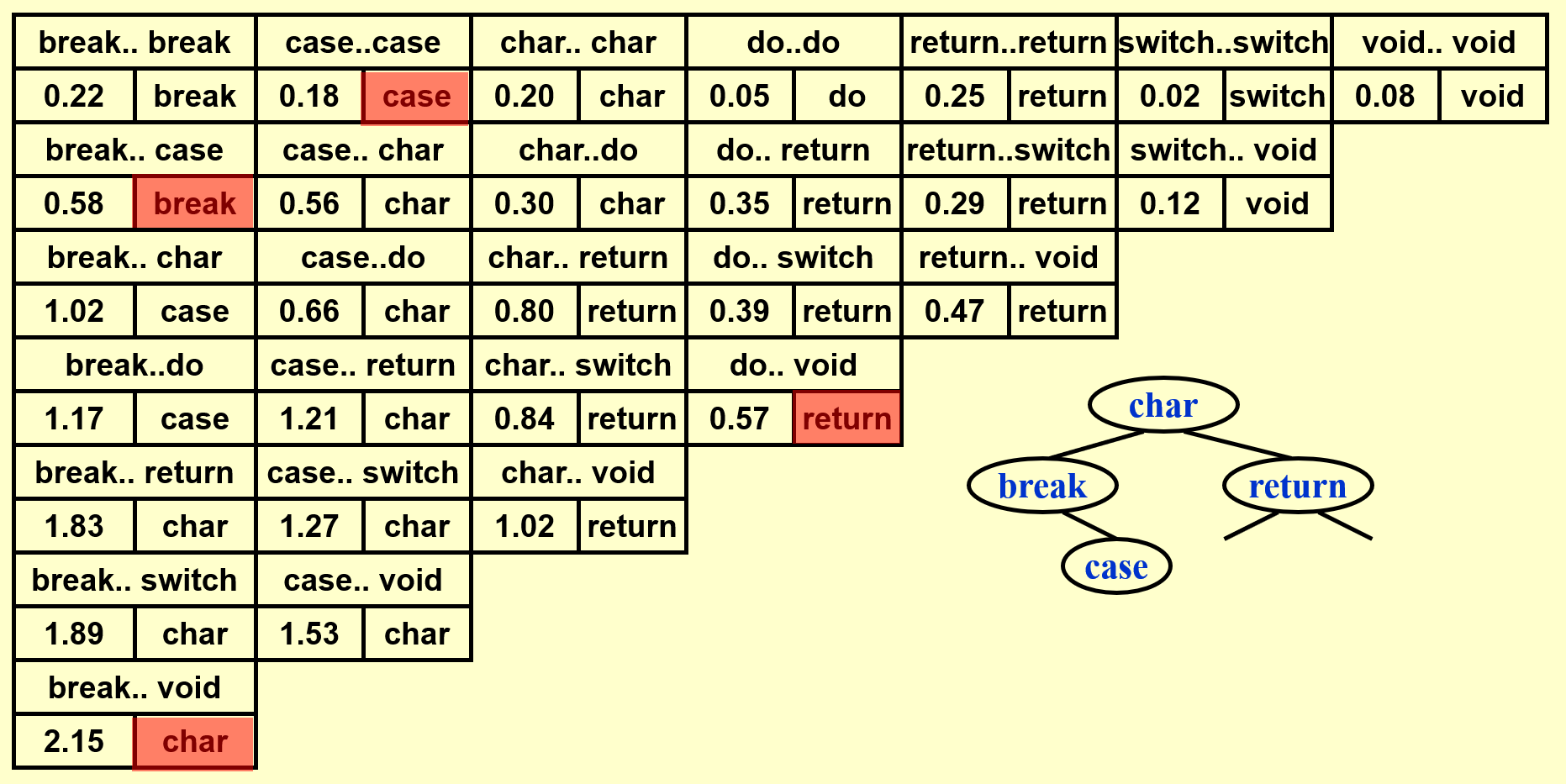
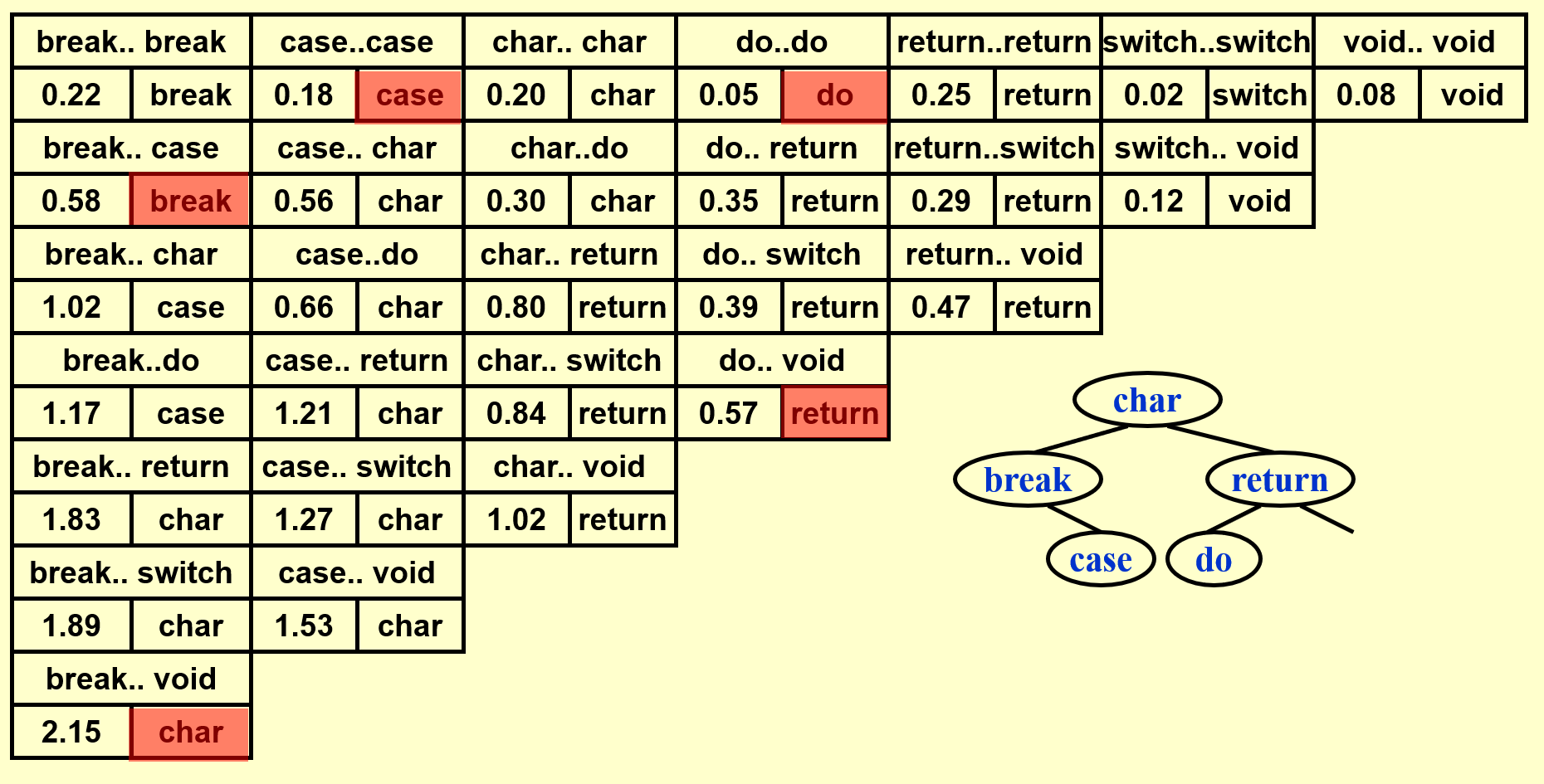
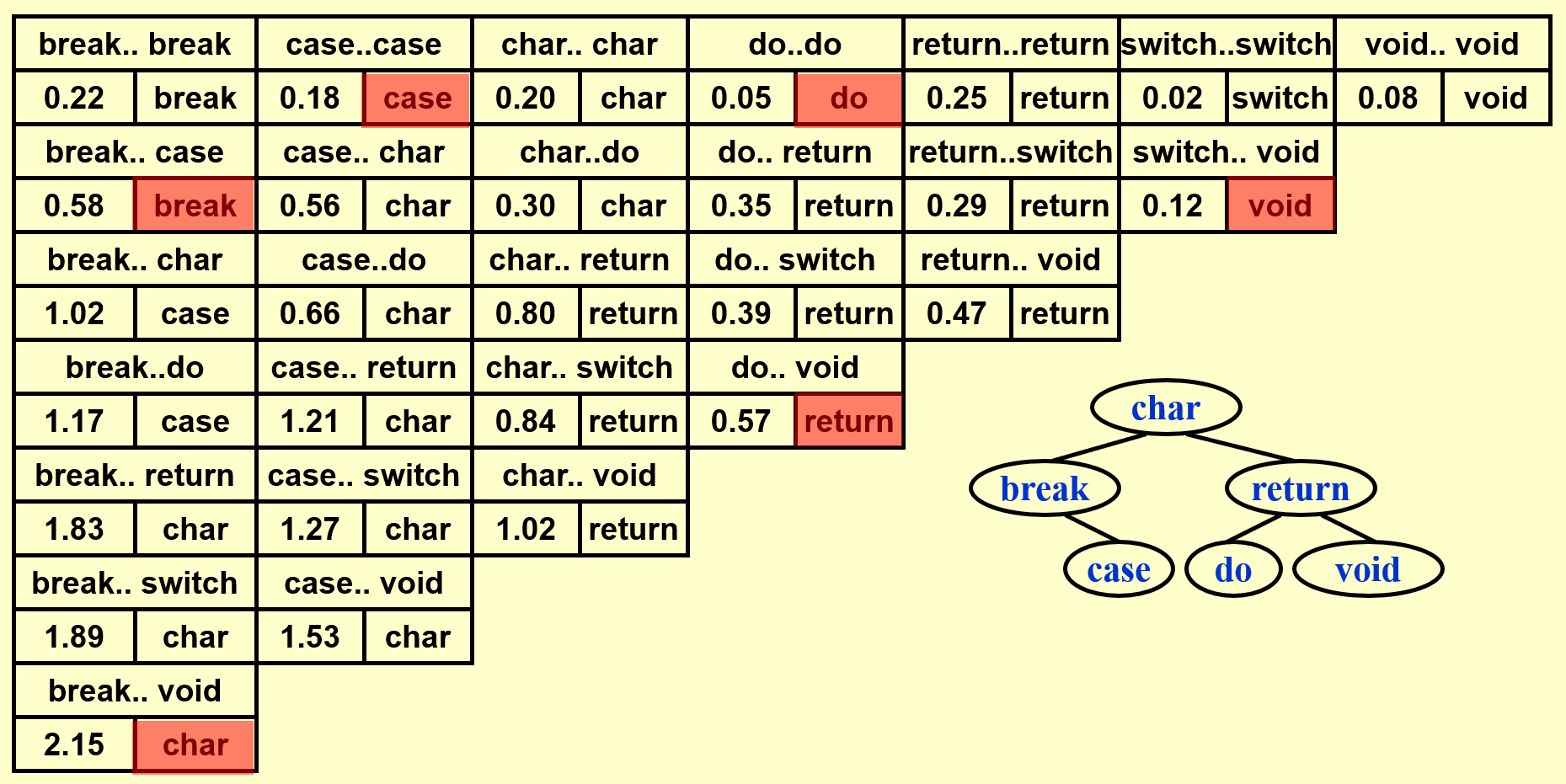
构造 OBST 的解法与计算矩阵乘法的最优顺序类似。先令：

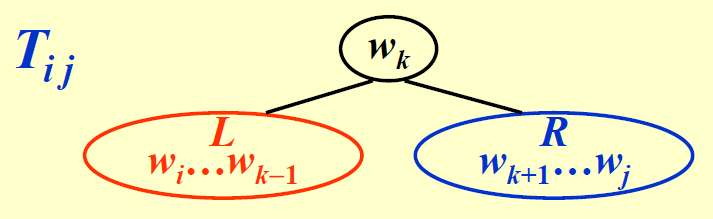
• \(T_{ij}\)：由单词 \(w_i \dots w_j(i < j)\) 构成的 OBST
• \(c_{ij}\)：\(T_{ij}\) 的成本（\(c_{ii} = p_i\)，PPT 上的是错的）
• \(r_{ij}\)：\(T_{ij}\) 的根节点
• \(w_{ij}\)：\(T_{ij}\) 的权重，等于 \(\sum\limits_{k = i}^j p_k\)（\(w_{ii} = p_i\)）

如果令 \(w_k = r_{ij}\)，那么 \(T_{ij}\) 的结构如下所示：

对于这棵树，它的成本为：

若 \(T_{ij}\) 是最优的，那么需要满足 \(c_{ij} = w_{ij} + \min\limits_{i < l \le j}\{c_{i, l - 1} + c_{l + 1, j}\}\)

例子

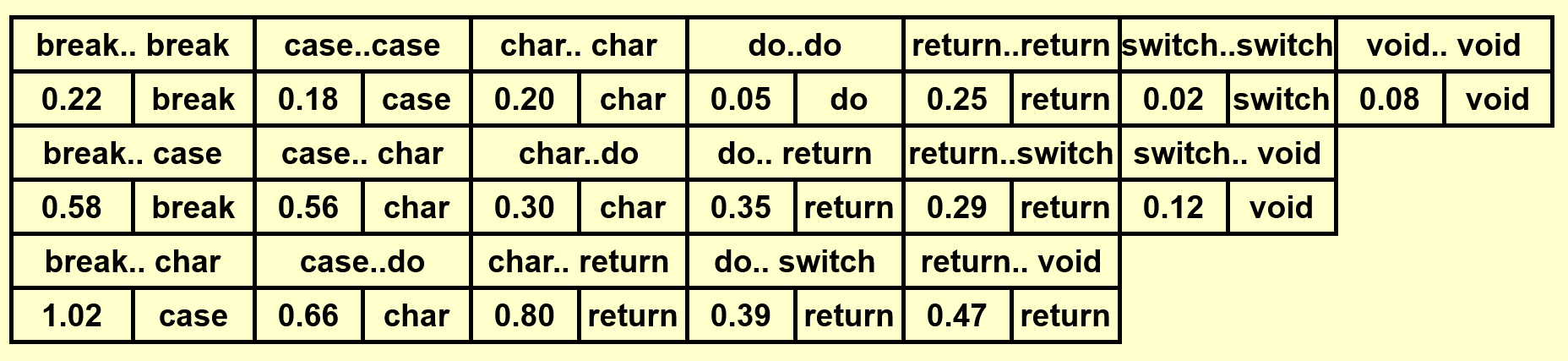
基于上面的那个例子，下面演示如何构建一棵 OBST（这里还是依据自底向上的思想来计算的）：

动画演示

这里只是简单地罗列结果，建议读者先自己动手画一下，然后再来与下面的结果比对。

绘制表格构建 OBST

1 个单词 2 个单词 3 个单词 4 个单词 5 个单词 6 个单词 7 个单词

• 得到完整的表后，先将位于表格最后一行的单词插入树内，作为根节点
• 根据词典序将剩余的单词划分为左右两半，按照中序遍历的顺序逐一插入

Step 1Step 2Step 3Step 4Step 5Step 6Step 7

可以看到 OBST 可以确保词频较大的单词的深度尽可能小，从而有效降低了总的查找时间。

时间复杂度：\(T(N) = O(N^3)\)

注：教材Data Structures and Algorithm Analysis in C第十章课后习题还给出了一个 \(O(N^2)\) 的解法，感兴趣的同学可以自行研究一下。

Floyd Shortest Path Algorithm⚓︎

在 FDS 的课上，我们已经介绍过单源最短路算法——Dijkstra 算法，它的时间复杂度为 \(O(|V|^2)\)（\(|V|\) 为图的顶点数），因此通过该算法计算任意两点间的最短路需要 \(O(|V|^3)\) 的复杂度（每个点都需要用一次该算法）。这种算法在稀疏图上运行较快，对于稠密图而言，更快的算法是下面要讲的Floyd 算法：

先给出定义：

• \(D^k[i][j] = \min\{\text{length of path}\ i \rightarrow \{l \le k\} \rightarrow j\}\)，其中 \(k\) 为当前判断的第 \(k\) 个节点（\(k \in [0, N - 1]\)，共 \(N\) 个待判断的点）
• \(D^{-1}[i][j] = \text{Cost}[i][j]\)（\(k = -1\) 表示 \(i, j\) 之间没有任何节点，即初始状态）

则从顶点 \(i\) 到顶点 \(j\) 之间的最短路径长度为 \(D^{N-1}[i][j]\)。

Floyd 算法的大致思路：从 \(D^{-1}\) 开始，连续得到 \(D^0, D^1, \dots, D^{N-1}\)。如果已经解决了 \(D^{k-1}\)，则此时有两种可能的情况：

• 第 \(k\) 个节点并不在最短路内，即 \(D^k = D^{k - 1}\)
• 第 \(k\) 个节点在最短路内，那么满足 \(D^k[i][j] = D^{k-1}[i][k] + D^{k-1}[k][j]\)

因此有递推关系：\(D^k[i][j] = \min\{D^{k-1}[i][j], D^{k-1}[i][k] + D^{k-1}[k][j]\}, k \ge 0\)

// A[] contains the adjacency matric with A[i][i] = 0
// D[] contains the values of the shortest path
// N is the number of vertices
// A negative cycle exists iff D[i][i] < 0

void AllPairs(TwoDimArray A, TwoDimArray D, int N) {
    int i, j, k;
    for (i = 0; i < N; i++)    // initialize D
        for (j = 0; j < N; j++)
            D[i][j] = A[i][j];

    for (k = 0; k < N; k++)      // add the kth vertex into the path
        for (i = 0; i < N; i++)
            for (j = 0; j < N; j++)
                if (D[i][k] + D[k][j] < D[i][j])    // update shortest path
                    D[i][j] = D[i][k] + D[k][j];
}

// Compute All-Shortest Paths 
// A[] contains the adjacency matrix 
// with A[i][i] presumed to be zero 
// D[] contains the values of shortest path 
// |V| is the number of vertices 
// A negative cycle exists iff 
// d[i][j] is set to a negative value
// Actual Path can be computed via another procedure using path 
// All arrays are indexed starting at 0 
void all_pairs( two_d_array A, two_d_array D, two_d_array path ) {
    int i, j, k;
    for( i = 0; i < |V|; i++ ) // Initialize D and path 
        for( j = 0; j < |V|; j++ ) {
            D[i][j] = A[i][j];
            path[i][j] = NOT_A_VERTEX;
        }
    for( k = 0; k < |V|; k++ )
        // Consider each vertex as an intermediate 
        for( i = 0; i < |V|; i++ )
            for( j = 0; j < |V|; j++ )
                if( d[i][k] + d[k][j] < d[i][j] ) {    // update min 
                    d[i][j] = d[i][k] + d[k][j];
                    path[i][j] = k;
                }
}

时间复杂度：\(T(N) = O(N^3)\)，但是在稠密图中表现较好。

注：离散数学提到过与 Floyd 算法等价的算法——Warshall 算法，用于计算传递闭包。

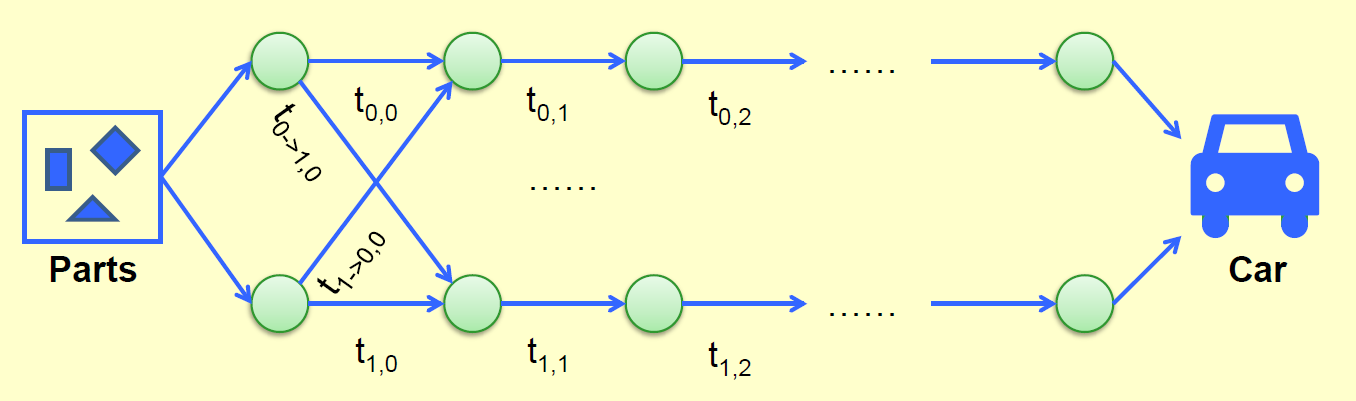
Product Assembly⚓︎

问题描述

产品组装 (product assembly) 问题，有以下条件

• 一辆车的生产需要用到两条组装线
• 每个阶段会用到不同的工艺（时间，即不同的节点值）
• 在各阶段中，可以随时切换组装线

现在要求你求出最短的组装总时间。

下面我们严格按照 Background 提到的解题步骤来解决这一问题：

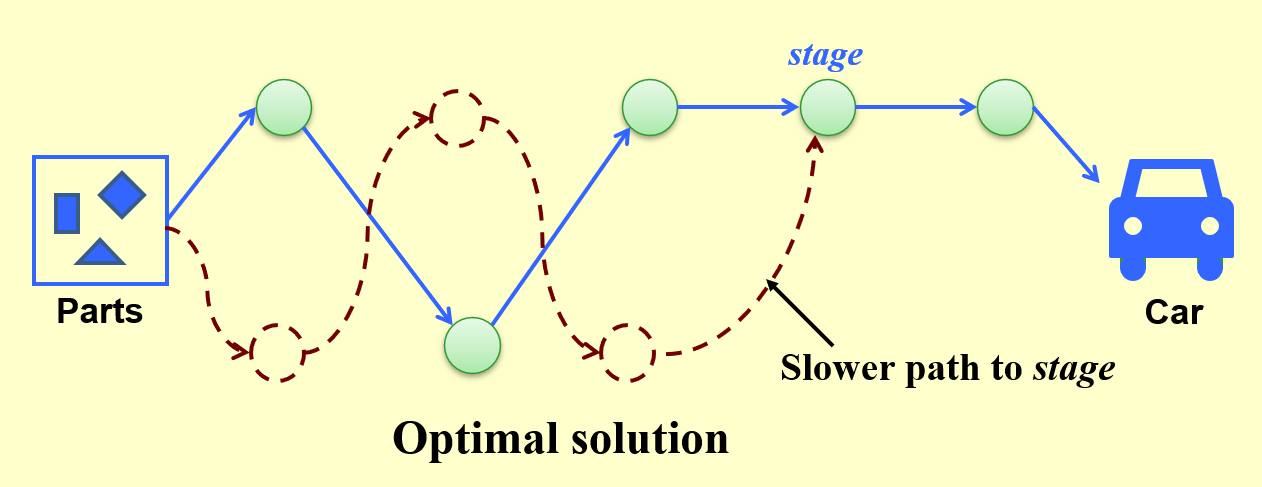
1. 定义状态

   
   • 这张图给出了在stage阶段时的最优解（绿点 + 蓝线）
   • 红色虚线表示虽然有一条同样能在stage阶段到达同一个点的路径，但这条路径所花的时间更差，因此被 pass 掉了

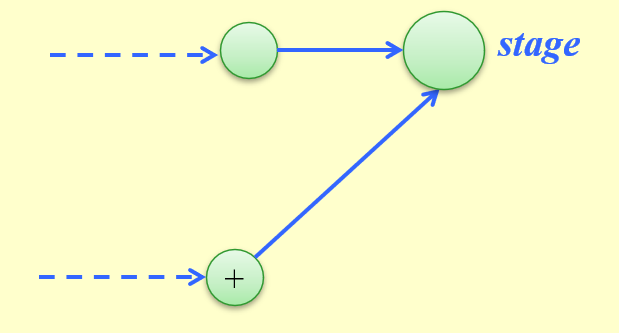
2. 递归地定义最优解的值

   
   • 可以看到，在stage阶段时，我们有两种到达对应点的路径：要么来自第一条组装线，要么来自第二条组装线
   • 因此，我们不难得出以下递推关系式：
   \[ \begin{align} f[line][stage] & = \min\{f[line][stage - 1] + t_{process}[line][stage - 1] \notag \\ & , f[1 - line][stage - 1] + t_{transit}[1 - line][stage - 1]\} \notag \end{align} \]

   其中 \(f[line][stage]\) 表示在stage阶段时，在第line条组装线上的最优时间，\(t_{process}[line][stage]\) 表示在同一条组装线上进入stage阶段所需的时间，\(t_{process}[line][stage]\) 表示从不同组装线上进入stage阶段所需的时间。

3. 确定好计算的顺序。这里直接看代码：

   代码实现

   // Initialization
   f[0][0] = 0; 
   f[1][0] = 0;
   // Outer loop: start from the first stage, end with the last stage
   for (stage = 1; stage <= n; stage++) {
       // Inner loop: test each line and find the minimum path
       for (line = 0; line <= 1; line++) {
           f[line][stage] = min(f[line][stage - 1] + t_process[line][stage - 1], f[1 - line][stage - 1] + t_transit[1 - line][stage - 1]);
       }
   }
   // The solution comes from the last stage of two lines
   Solution = min(f[0][n], f[1][n]);
   

4. 重构解决问题的策略。这里要求输出最短时间的组装顺序，代码如下所示：

   代码实现

   f[0][0] = 0; 
   f[1][0] = 0;
   
   // L[line][stage]: record the source of the stage, either 0 or 1(the number of assembly lines) 
   L[0][0] = 0;
   L[1][0] = 0;
   
   for (stage = 1; stage <= n; stage++) {
       for (line = 0; line <= 1; line++) {
           f_stay = f[line][stage - 1] + t_process[line][stage - 1];
           f_move = f[1 - line][stage - 1] + t_transit[1 - line][stage - 1];
           if (f_stay < f_move) {
               f[line][stage] = f_stay;
               L[line][stage] = line;
           } else {
               f[line][stage] = f_move;
               L[line][stage] = 1 - line;       
           }
       }
   }
   
   // save the optimal path in plan[]
   line = f[0][n] < f[1][n] ? 0 : 1;
   for (stage = n; stage > 0; stage--) {
       plan[stage] = line;
       line = L[line][stage];
   }
   

Knapsack Problem⚓︎

背包问题这块内容主要参照 Hello 算法和 OI Wiki 来写的。

背包问题(knapsack problem) 可能是最常见的动态规划入门题，大致的问题描述为：

背包问题的有多种类型，包括：

• 0-1 背包问题(0-1 knapsack problem)
• 完全背包问题(unbounded knapsack problem)
• 多重背包问题(bounded knapsack problem)

0-1 Knapsack Problem⚓︎

0-1 背包问题在原问题上多了一个限制：每个物品只能选一次。

解题步骤：

1. 定义状态

   • 观察发现，放入物品会改变背包内物品的总价值和背包容量，因此需要记录的量为前 \(i\) 个物品在容量为 \(c\) 的背包中的最大价值，用符号化的语言表示为 \(dp[i, c]\)，那么要求的就是 \(dp[n, cap]\)
   • 用一张 \((n + 1) \times (cap + 1)\) 的表来记录状态

2. 推导状态转移方程

   • 当我们对物品 \(i\) 做出决策时，需要考虑两种情况
     • 不放入物品：\(dp[i, c] = dp[i - 1, c]\)，背包容量和价值均不变
     • 放入物品：\(dp[i, c] = dp[i - 1, c - w_{i - 1}] + v_{i - 1}\)，背包容量减少，价值增加

   • 因此完整的状态转移方程为：

     \[ dp[i, c] = \max\{dp[i - 1, c], dp[i - 1, c - w_{i - 1}] + v_{i - 1}\} \]

3. 确定计算顺序

   • 首先确定一下边界条件：当无物品或背包容量为 0 时最大价值为 0，即状态表首列 \(dp[i, 0]\) 和首行 \(dp[0, c]\) 均等于 0
   • 根据状态方程知，当前状态是根据它上方和左上方的状态推出来的，因此只需正向循环遍历这张状态表即可

下面展示对应的代码实现：

int knapsack_01(int weight[], int val[], int n, int cap) {
    int i, j;
    int dp[MAXN][MAXCAP];

    for (i = 0; i <= n; i++) 
        for (j = 0; j <= cap; j++)
            dp[i][j] = 0;

    for (i = 1; i <= n; i++) {
        for (j = 1; j <= cap; j++) {
            if (weight[i - 1] > c) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + val[i - 1]);
            }
        }
    }

    return dp[n][cap];
}

• 时间复杂度：\(O(n \cdot cap)\)
• 空间复杂度：\(O(n \cdot cap)\)

事实上，这种算法在空间上还可以再优化（\(O(n \cdot cap) \rightarrow O(n)\)）：

• 观察发现，第 i 行状态表的状态来自于第 i-1 行状态表的状态；且遍历第 i 行时第 i-1 行的状态已经算好了，因此我们尝试将状态表从二维降到一维
• 这时就不能正向遍历了，因为在原来的状态表中，当前状态依赖于它上面的和左上角的状态；如果压缩成一维，左上角的状态就被压到了左边，而左边的状态即上一个状态已经更新过了，所以正向遍历就失效了，因此采取倒序遍历的策略

int knapsack_01(int weight[], int val[], int n, int cap) {
    int j;
    int dp[MAXN][MAXCAP];

    for (j = 0; j <= cap; j++)
        dp[j] = 0;

    for (i = 1; i <= n; i++) {
        for (j = cap; j >= 1; j--) {
            if (weight[i - 1] <= c) {
                dp[j] = max(dp[j], dp[c - weight[i - 1]] + val[i - 1]);
            }
        }
    }


    return dp[cap];
}

Unbounded Knapsack Problem⚓︎

完全背包问题则解放了 0-1 背包的限制：每个物品可以重复选取（无数次）。

• 解题思路与 0-1 背包问题类似，唯一的区别在于状态转移方程中，选取物品的时候不需要改变 i 值，因为物体可以重复选取
• 对于空间压缩，由于当前状态依赖于上面和左边的状态，因此将数组压缩成一维后，正向遍历就能正确解决问题

// 与上面代码的唯一区别在于内部循环的遍历顺序发生改变
int knapsack_ub(int weight[], int val[], int n, int cap) {
    int j;
    int dp[MAXN][MAXCAP];

    for (j = 0; j <= cap; j++)
        dp[j] = 0;

    for (i = 1; i <= n; i++) {
        for (j = 1; j <= 1; j++) {
            if (weight[i - 1] <= c) {
                dp[j] = max(dp[j], dp[c - weight[i - 1]] + val[i - 1]);
            }
        }
    }

    return dp[cap];
}

Bounded Knapsack Problem⚓︎

多重背包问题有了更复杂的限制：物品 \(i\) 最多只能选取 \(k_i\) 次。

• 此时状态转移方程为：

  \[ dp[i, c] = \max\limits_{0 \le k \le k_i}\{dp[i - 1, c], dp[i - 1, c - w_{i - 1} \cdot k] + v_{i - 1} \cdot k\} \]

  也就是说，对于每种物品，我们需要加一层遍历来决定选取多少的这一类的物品，因此时间复杂度就提升至 \(O(n \cdot cap \cdot \max\{k_i\})\)，但空间复杂度没有改变

• 事实上该算法还可以进一步优化，甚至可以将时间复杂度降到线性

这里就不列出相应的代码了（笔者偷懒了，逃 x）

评论区