Lec 13: Randomized Algorithms⚓︎

Introduction⚓︎

用算法解决问题时，什么东西是能被随机化 (randomize) 的呢？

• 数据的随机化：传统的算法可根据随机生成的输入数据得到结果
  • 由于数据是随机的（可以理解为数据是等概率分布的），因此对这种算法的分析称为平均情况分析(average-case analysis)
• 算法的随机化：算法在处理最坏情况的输入时会做出随机的决策
  • 我们称这样的算法为随机化算法(randomized algorithm)，这便是本讲将会介绍的话题 ~

为何需要随机化？

• 事实上，我们可以将那些始终能够得到正确答案的、高效可确定 (efficient deterministic) 的算法（就是传统意义上的算法）视为随机化算法的一种特殊情况
• 随机化算法的分类：
  • 高效性：只需在较高概率下得到正确解的高效随机化算法
  • 确定性：只需在预期效率内始终得到正确解的随机化算法

为了便于下面的分析，我们先定义了一些量：

• \(Pr[A]\)：事件 \(A\) 发生的概率
• \(\overline{A}\)：事件 \(A\) 的补(complement)，可以得到：\(Pr[A] + Pr[\overline{A}] = 1\)
• \(E[X]\)：随机变量 \(X\) 的期望(expectation)
  • \(E[X] = \sum\limits_{j = 0}^{\infty} j \cdot Pr[X = j]\)

Examples⚓︎

Hiring Problems⚓︎

int Hiring(EventType C[], int N) {
    // candidate 0 is the least-qualified dummy candidate
    int Best = 0;
    int BestQ = the quality of candidate 0;
    for (i = 0; i <= N; i++) {
        Qi = interview(i);    // Ci
        if (Qi > BestQ) {
            BestQ = Qi;
            Best = i;
            hire(i);          
            // Ch
        }
    }
    return Best;
}

Offline Algorithm⚓︎

下面我们来考虑数据随机分布的情况：

• 假设候选者是按随机的能力顺序依次面试的，且规定：前 \(i\) 个候选者等可能地具备最佳能力
• 令 \(X\) 为雇佣人数，那么 \(E(X) = \sum\limits_{j=1}^N j \cdot Pr[X = j]\)，接下来需要确定 \(Pr[X = j]\) 的值
• 令 \(X_i = \begin{cases}1 & \text{if candidate } i \text{ is hired} \\ 0 & \text{if candidate } i \text{ is NOT hired}\end{cases}\)，那么 \(E[X_i] = Pr[\text{candidate } i \text{ is hired}] = \dfrac{1}{i}\)
• 那么 \(E[X] = E[\sum\limits_{i=1}^N X_i] = \sum\limits_{i=1}^N E[X_i] = \sum\limits_{i=1}^N \dfrac{1}{i} = \ln N + O(1)\)
• 所以总成本为 \(O(C_h \ln N + NC_i)\)

基于上面给出的简单版本的代码，只需稍加修改，便可得到一个更为高效的随机化算法：

int Hiring(EventType C[], int N) {
    // candidate 0 is the least-qualified dummy candidate
    int Best = 0;
    int BestQ = the quality of candidate 0;

    randomly permute the list of candidates; 

    for (i = 1; i <= N; i++) {
        Qi = interview(i);    // Ci
        if (Qi > BestQ) {
            BestQ = Qi;
            Best = i;
            hire(i);          
            // Ch
        }
    }
    return Best;
}

我们仅需在处理数据前先对数据进行随机排列(permute)，即可得到随机排序的数据（而不再是一个假设），从而避免了最坏情况；但缺点在于随机排列数据需要额外的时间成本。

接下来我们来设计这个随机排列算法，大致思路是：为数组A[]的每个元素A[i]预先赋予一个随机的优先值P[i]，然后对数组进行排序。代码实现如下：

void PermuteBySorting (ElemType A[], int N) {
    for (i = 1; i <= N; i++) 
        // makes it more likely that all priorities are unique
        A[i].P = 1 + rand() % (N * N * N);
    Sort A, using P as the sort keys;
}

结论：假定数组元素的优先级都是唯一的，那么该算法能够产生一个基于原输入数据的均匀随机排列(uniform random permutation)（即等可能地从所有可能的排列中选取其中一种排列）。

Online Algorithm⚓︎

之前介绍的算法都是离线算法 (offline algorithm)，即正式处理数据前需要知道所有的输入数据，它虽然能够确保计算结果总是正确的，但是效率并不是很高。现在我们考虑一种更高效的在线算法(online algorithm)，代码如下所示：

int OnlineHiring(EventType C[], int N, int k) {
    int Best = N;
    int BestQ = -Infinity;

    for (i = 1; i <= k; i++) {
        Qi = interview(i);
        if (Qi > BestQ) BestQ = Qi;
    }

    for (i = k + 1; i <= N; i++) {
        Qi = interview(i);
        if (Qi > BestQ) {
            Best = i;
            break;
        }
    }

    return Best;
}

该算法的大致思路是：

• 先面试前 k 个候选者，找到他们之中最高的能力值，但并不会雇佣他们；
• 然后面试后面的候选者，以先前确定的最高能力值作为阈值筛选这些候选者，如果高于这个阈值，就雇佣这个人并不再面试后面的人。

对于该算法，我们需要探讨两个问题：

• 对于给定的 \(k\)，我们能雇佣到能力最高的候选者的概率是多少？

  • 记 \(S_i\) 为事件“第 i 位候选者的能力最佳”
  • 如何让事件 \(S_i\) 发生的：\(\{A \cap B\}\)
    • 事件 \(A\)：能力最佳的人在位置 \(i\)
    • 事件 \(B\)：位置为 \(i\) 的候选人被雇佣。此时前 i-1 个人里面，能力最佳的人出现在位置 1~k 之间，这样的话位置 k+1~i-1 之间的候选者不会被雇佣，从而确保第 i 个人被雇佣
    • 两个时间是独立的

  • 计算概率：

    \[ \begin{align} Pr[S_i] & = Pr[A \cap B] = \underbrace{Pr[A]}_{\frac{1}{N}} \cdot \underbrace{Pr[B]}_{\frac{k}{i - 1}} = \dfrac{k}{N(i - 1)} \notag \\ Pr[S] & = \sum\limits_{i=k+1}^N Pr[S_i] = \sum\limits_{i=k+1}^N \dfrac{k}{N(i-1)} = \dfrac{k}{N} \sum\limits_{i=k}^{N-1}\dfrac{1}{i} \notag \end{align} \]

  • 根据不等式 \(\int_k^N \dfrac{1}{x} \text{d}x \le \sum\limits_{i=k}^{N-1} \dfrac{1}{i} \le \int_{k-1}^{N-1} \dfrac{1}{x}\text{d}x\)，最终可以得到：

  \[ \dfrac{k}{N} \ln(\dfrac{N}{k}) \le Pr[S] \le \dfrac{k}{N} \ln (\dfrac{N - 1}{k - 1}) \]

• 最佳的 \(k\) 值（即能够得到最大的概率）是多少？

  • 根据前面的分析，可以将该问题转化为：求函数 \(f(k) = \dfrac{k}{N} \ln (\dfrac{N}{k})\) 的最大值下对应的 \(k\) 值
  • 对该函数求导，得 \(\dfrac{\text{d}}{\text{d}k}[\dfrac{k}{N} \ln (\dfrac{N}{k})] = \dfrac{1}{N} (\ln N - \ln k - 1) = 0\)，解得 \(k = \dfrac{N}{e}\)
  • 结论：通过上述算法雇佣到能力最佳的候选者的概率至少为 \(\dfrac{1}{e}\)

Randomized Quicksort⚓︎

在 FDS 中，我们介绍的快速排序(quicksort) 是一种确定性 (deterministic) 的排序，它的时间复杂度为：

• \(\Theta(N^2)\)：最坏情况下的运行时间
• \(\Theta(N \log N)\)：平均情况下的运行时间

确定性的快排是基于每种输入排列是等可能分布的假设，因此它没有很好地处理最坏情况。要想避免最坏情况，可以用本讲学到的随机化算法来解决。随机化快排的关键在于——随机且均匀地挑选支点(pivot)，挑选原则为：

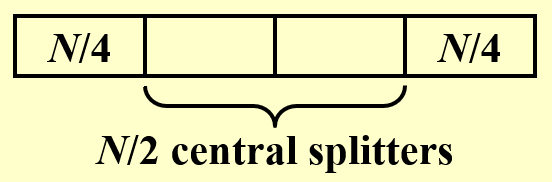
• 中心分离点(central splitter)：一种较好的支点，它分开数据集后使得每个子集至少包含 \(\dfrac{N}{4}\) 的数据

  • 这样就可以消除支点出现在数据两端（相当于没有分）的最坏情况
  

• 修改后的快速排序：在递归前始终能够选出一个中心分离点

结论：寻找中心分离点的预期迭代次数至多为 2

• 解释：根据上面的示意图，不难发现从所有数据中随机选出合适中心分离点的概率为 \(\dfrac{1}{2}\)（中间的一半数据），因此即使第 1 次挑选失败后，第 2 次就能选出正确的中心分离点

分析随机化快排的时间复杂度：

• 记子问题 \(S\) 的类型(type) 为 \(j\)（个人理解为类型 = 快排的趟数），可以得到不等式：\(N(\dfrac{3}{4})^{j+1} \le |S| \le N(\dfrac{3}{4})^j\)

  • \(\dfrac{3}{4}\) 表示的是选择了最边上的中心分离点的情况，此时数据被分为了 \(\dfrac{1}{4}N\) 和 \(\dfrac{3}{4}N\) 两部分，我们更关心每趟快排后最大的子问题 \(S\)

• 结论：对于类型 \(j\)，至多有 \((\dfrac{4}{3})^{j+1}\) 个子问题

  • 解释：这里用到了上面不等式的左半边——因为对于第 \(j\) 趟下的快排，最大子问题的最小规模为 \(N(\dfrac{3}{4})^{j+1}\)，因此子问题最多有 \(\dfrac{N}{N(\frac{3}{4})^{j+1}} = (\dfrac{4}{3})^{j+1}\) 个

• 期望 \(E[T_{\text{type } j}] = O(N(\dfrac{3}{4})^j) \times (\dfrac{4}{3})^{j+1} = O(N)\)

• 不同类型的个数（快排趟数）为 \(\log_{\frac{4}{3}}N = O(\log N)\)
• 结合上面两条，随机化快排的时间复杂度为稳定的 \(O(N \log N)\)（即使在最坏情况下也是这个复杂度）

「类型」这个称呼好怪啊 ...

RandQSort(A, L, R) {
    if (L < R) {
        i = random(L, R);
        swap(A[i], A[R]);
        p = Partition(A, L, R);
        RandQSort(A, L, p - 1);
        RandQSort(A, p + 1, R);
    }
}

Other Examples⚓︎

摘录一些来自作业题 / 历年卷上的例子。

• 链表删除操作的随机化算法

  • 题目描述：给定 N 个节点的链表，要求删除链表中所有的节点
  • 算法：每一步我们随机挑选链表的一个节点，然后删去其后面的所有节点；重复上述步骤，直到链表为空

  • 预期删除次数：\(\Theta(\log N)\)，下面给出证明：

    证明

    • 给链表节点按顺序标号为 \(1 \dots N\)
    • 选择第 \(k\) 个节点，那么从它开始到后面的 \(N - k + 1\) 个节点都会被删除

    • 每一步中，预期删除的节点数为：

      \[ \sum\limits_{k=1}^N (\dfrac{1}{N} \cdot (N - k + 1)) \approx \dfrac{N + 1}{2} \]

      也就是说，每次预期能够删除现有链表中一半的节点

    • 于是不难得出，删除次数为 \(\Theta(\log N)\)

• 跳跃表 (skip list)

  • 推荐看这篇博客，介绍得相当清晰，适合新手学习
  • 查找、插入、删除的时间复杂度均为 \(O(\log N)\)

评论区