Lec 14: Parallel Algorithms⚓︎
约 4289 个字 89 行代码 预计阅读时间 23 分钟
Introduction⚓︎
实际上,我们在前面所学的所有算法都属于顺序算法(sequential algorithms),这类算法的特点是每步只完成一个操作。要想提升算法的速度,除了可以设计更快的算法(降低时间复杂度)外,还可以采用并行的方法。
所谓并行(parallelism),就是指每一步能够同时完成多个操作。有以下几类并行方式:
- 指令级并行:在一个 CPU 内,多条指令可以同时执行,包括了计组课程中提到过的流水线 CPU、乱序、多发射等(后面两者将会在体系课程中详细介绍
) 。 - 数据级并行:将相同的操作数同时应用于一些数据项,比如 SIMD(single instruction, multiple data) 架构(也会在体系课程中详细介绍)
- 线程级并行:通过多个线程同时执行任务来提高程序的并发性能,线程独立运行但共享同一进程的资源,以实现高效计算。
- 本讲所要介绍的并行算法(parallel algorithms) 属于此类,常用的并行算法模型有:
- 并行随机访问机(parallel random access machine, PRAM)
- 工作 - 深度(work-depth, WD)(
还是记英文好)
- 本讲所要介绍的并行算法(parallel algorithms) 属于此类,常用的并行算法模型有:
PRAM Model⚓︎
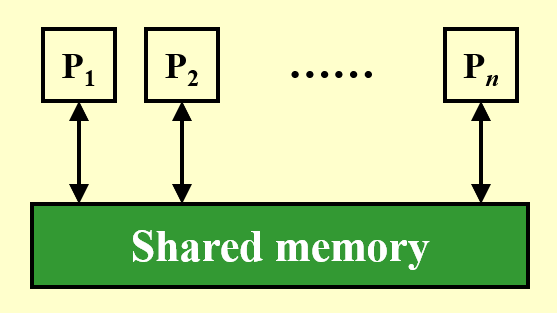
下面给出 PRAM 模型的图示:
- \(P_1, \dots, P_n\) 表示 \(n\) 个处理器,它们同时访问一块共享内存
- 每个处理器与共享内存间的双向箭头表示单位时间内对内存的访问(包括读、写、计算等操作)
- 具体来说,向上的箭头表示读取,向下的箭头表示写入
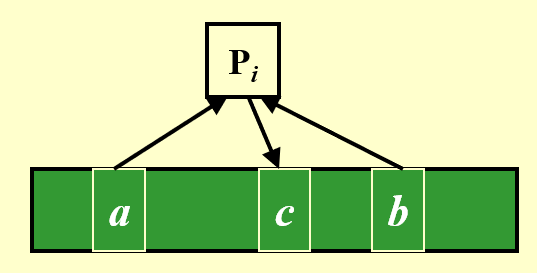
例子
不难发现,这个模型存在一个问题:如果多个处理器同时访问同一块内存(冲突发生
- 专一读取 -- 专一写入 (exclusive-read exclusive-write, EREW):顾名思义,同一时间内不允许多个处理器访问(读 / 写)同一块内存
- 并发读取 -- 专一写入 (concurrent-read exclusive-write, CREW)
- 并发读取 -- 并发写入 (concurrent-read concurrent-write, CRCW),此时还有三种不同的写入规则:
- 任意(arbitrary) 规则:任意选择一个处理器进行写入操作
- 优先级(priority) 规则:选择编号最小的处理器(规定编号越小优先级越高)进行写入操作
- 共同(common) 规则:只有当所有处理器的写入数据是一致的时候,才会执行写入操作
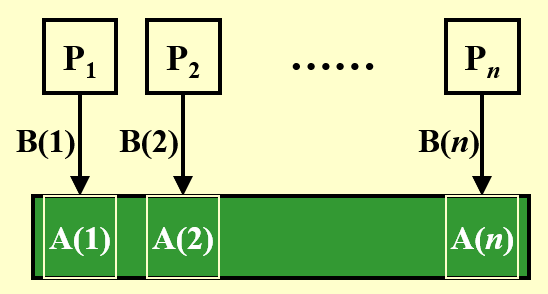
例子:求和问题
- 输入:\(A(1), A(2), \dots, A(n)\)(来自内存的数据)
- 输出:\(A(1) + A(2) + \dots + A(n)\)
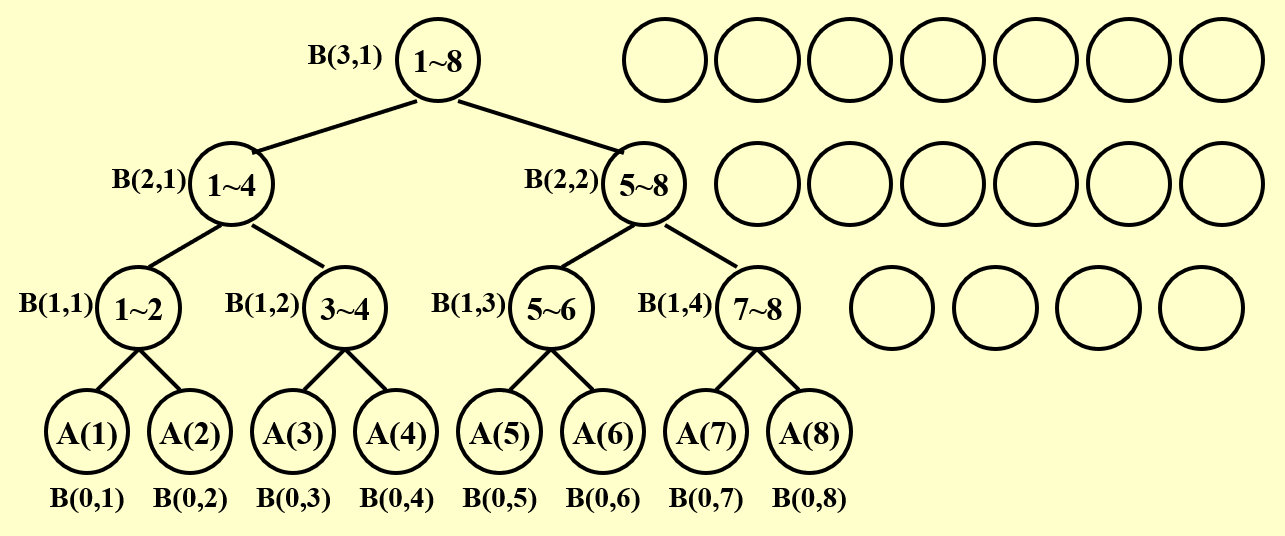
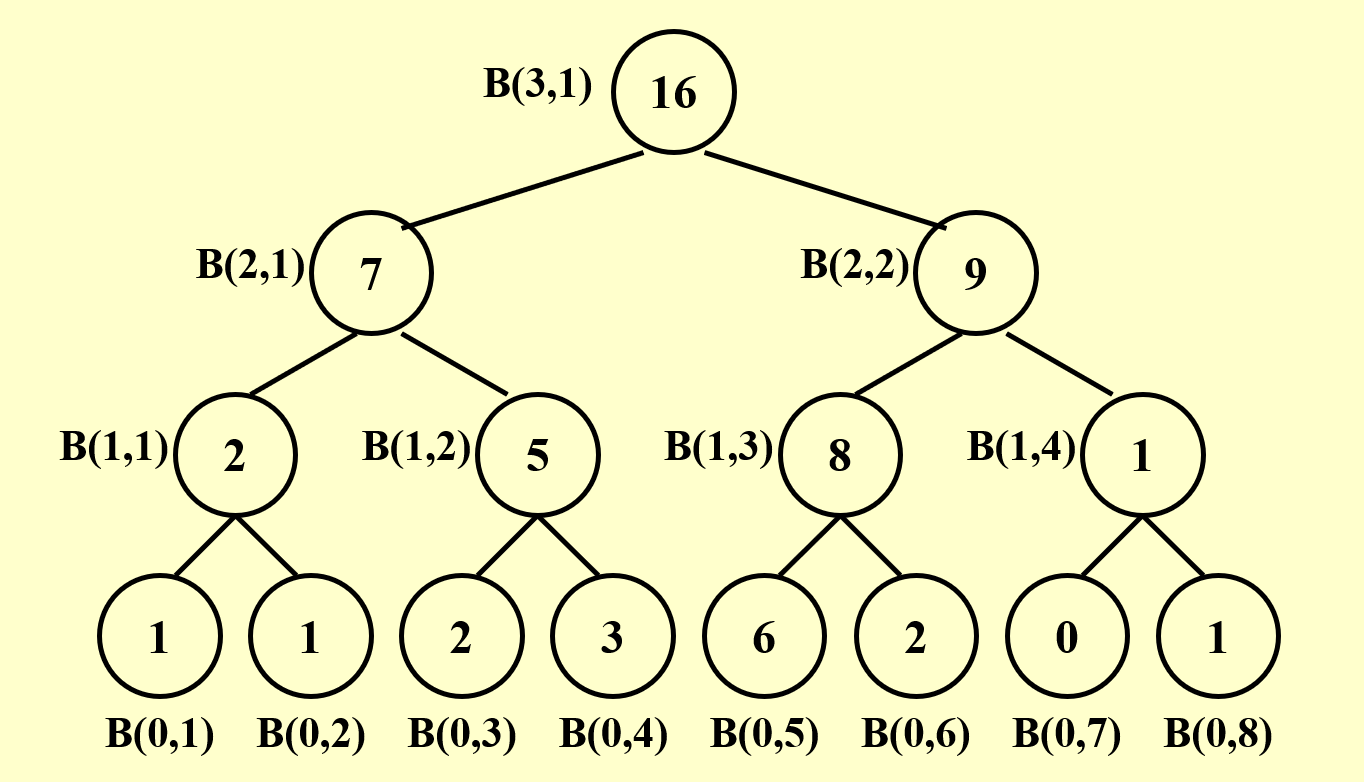
下面给出用 PRAM 模型计算此题的过程图示:
- 最底层表示初始情况,每层表示并行算法的每个步骤
- 每层都有 8 个处理器,空白圆圈表示空闲的处理器
- 观察发现,整个过程中所有工作的处理器构成了一棵满二叉树
- 因此层数为 \(\log n\),即该算法在 \(\log n\) 时间内完成
- \(B(h, i)\) 表示第 \(h\) 步中第 \(i\) 个处理器的计算结果
- 有以下关系式成立:\(B(h, i) = B(h - 1, 2i - 1) + B(h - 1, 2i)\)
伪代码如下所示:
for P_i, 1 <= i <= n pardo
B(0, i) := A(i)
for h = 1 to log(n) do
if i <= n / 2^h:
B(h, i) := B(h - 1, 2 * i - 1) + B(h - 1, 2 * i)
else
stay idle
if i = 1:
output B(log(n), 1)
else:
stay idle
- 关于高亮部分:上层的节点需要知道下层的两个节点值才能计算。由于外层循环是并行计算的,这也就意味着这棵树上同一层的节点是同时算出来的,因此高亮部分的操作是可行的。
- 时间复杂度:\(T(n) = \log n + 2\)
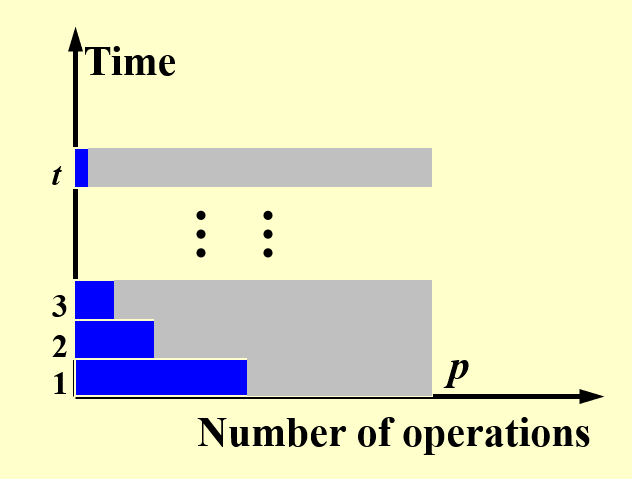
根据上面对例子的分析,我们可以得出关于操作数量和时间之间的关系图:
- 横轴上的最大值为 \(p\),等于用到过的处理器的最大数量
- 纵轴上的最大值为 \(t\),表示总的运行时间
- 每个横条表示一个阶段(单位时间
) ,蓝色部分表示工作的处理器,灰色部分表示空闲的处理器
PRAM 模型的缺陷
- 该模型无法揭示算法和实际使用的处理器个数之间的关系
- 对于上个例子,假如有 100 个处理器,但实际上只用了 8 个处理器,所以更多的处理器并不能使执行速度进一步加快
- 该模型需要指定哪个处理器处理哪部分的指令,这时就需要知道一些可能不太必要的细节(
? )
WD Model⚓︎
接着上面的例子
如果用的是 WD 模型,那么伪代码将会改写为如下形式:
for P_i, 1 <= i <= n pardo
B(0, i) := A(i)
for h = 1 to log(n) do
for P_i, i <= n / 2^h pardo
B(h, i) := B(h - 1, 2 * i - 1) + B(h - 1, 2 * i)
for i = 1 pardo
output B(log(n), 1)
与 PRAM 的不同之处在于高亮的两个语句,这里用到的是并行处理的方式(pardo
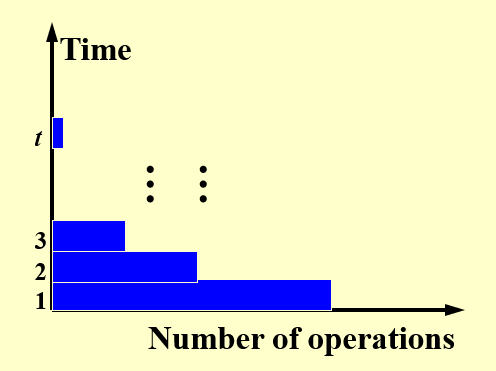
因此对应的操作数量和时间之间的关系图变成了:
由于没有了那些灰色区域(不工作的处理器
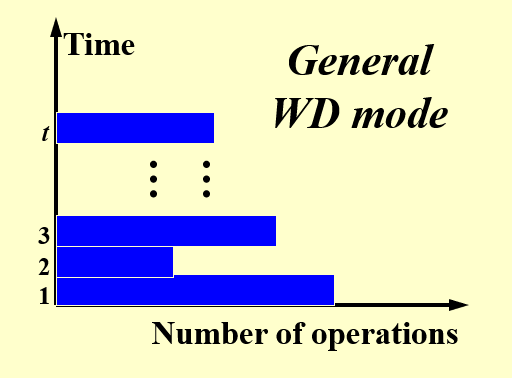
可以看到,每个时间段处于工作状态的处理器数量,即工作量是不一样的,且没有任何规律可言。
Measurement⚓︎
衡量 PRAM 模型下并行算法的性能的一些指标:
- \(W(n)\):工作量(workload),即运行并行算法所需的总操作数目
- \(T(n)\):最坏情况下的运行时间
- \(P(n) = \dfrac{W(n)}{T(n)}\):所需处理器的数量
- 当所需处理器数量 \(p \le \dfrac{W(n)}{T(n)}\) 时,所需时间为 \(\dfrac{W(n)}{p}\)
- 使用任意数量为 \(p\) 的处理器时,所需时间为 \(\dfrac{W(n)}{p} + T(n)\)
后面那三个指标实际上是渐进等价的(asymptotically equivalent),即对于任意大的 \(n\),这三者位于同一复杂度下。
又回到上面的例子(求和问题)
- \(T(n) = \log n + 2\)
- \(W(n) = n + \dfrac{n}{2} + \dfrac{n}{2^2} + \dots + \dfrac{n}{2^k} + 1 = 2n\),其中 \(2^k = n\)
WD 表示法充分性定理(WD-presentation sufficiency theorem):用 WD 模型表示的算法能够被任意 \(P(n)\) 个处理器在 \(O(\dfrac{W(n)}{p} + T(n))\) 时间内实现,此时采用与 WD 表示法相同的并发写入规则
结论(类似上面的定理,但至少是我看得懂的)
采用 WD 模型的并行算法,\(p( > 0)\) 个处理器的并行执行时间范围为:
其中 \(W\) 为工作量,\(D\) 为(分析并行算法时用的满二叉树)深度,也就是单个处理器最坏情况下的执行时间。
证明
来自 wyy 的讲义
- 下界是显然的,故不做赘述
- 对于上界
- 工作量 \(W = \sum\limits_{i=1}^D W_i\),其中 \(W_i\) 为每个时间阶段内的工作量
- 而每个阶段的执行时间为 \(\lceil \dfrac{W_i}{p} \rceil\)(向上取整,不足一个完整任务应视为一个完整任务)
- 故总时间 \(T_p = \sum\limits_{i=1}^D \lceil \dfrac{W_i}{p} \rceil = \sum\limits_{i=1}^D (\lfloor \dfrac{W_i - 1}{p} \rfloor + 1) \le \sum\limits_{i=1}^D ( \dfrac{W_i - 1}{p} + 1) = \dfrac{W - D}{p} + D\)
虽然 PRAM 模型和 WD 模型本质上没有太大的区别,但是 WD 模型可以反映算法与处理器数量之间的关系,因此效果会更好。
误区
- 并行算法的运行时间和工作量并不一定始终比(解决同一问题的)顺序 / 串行算法来的小
Examples⚓︎
Prefix-Sums⚓︎
问题描述
- 输入:\(A(1), A(2), \dots, A(n)\)
- 输出:\(\sum\limits_{i=1}^1A(i), \sum\limits_{i=1}^2A(i), \dots, \sum\limits_{i=1}^nA(i)\)
解决这个问题的方法与前面的求和问题是类似的,首先还是借助一棵平衡二叉树模型来分析:
我们可以先计算求和问题,为之后前缀和问题的解决打下基础。
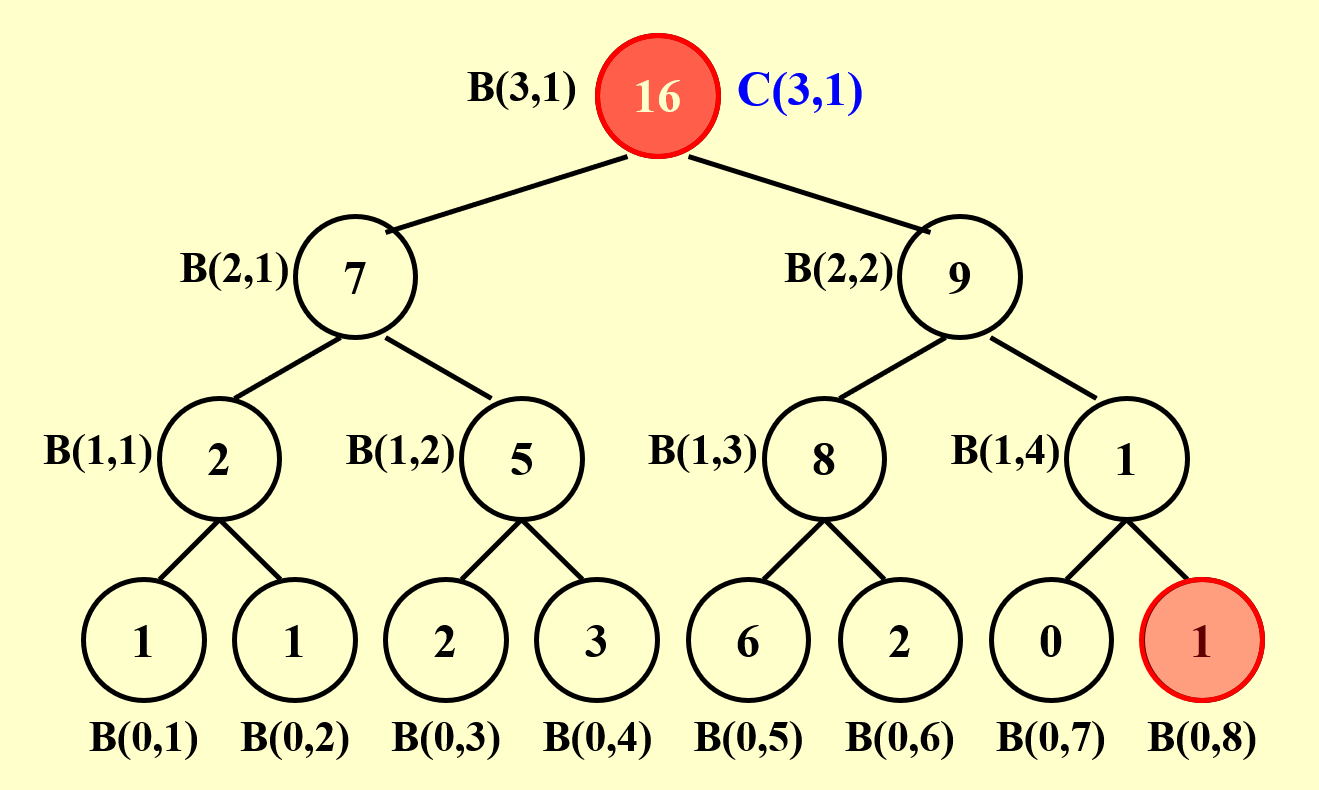
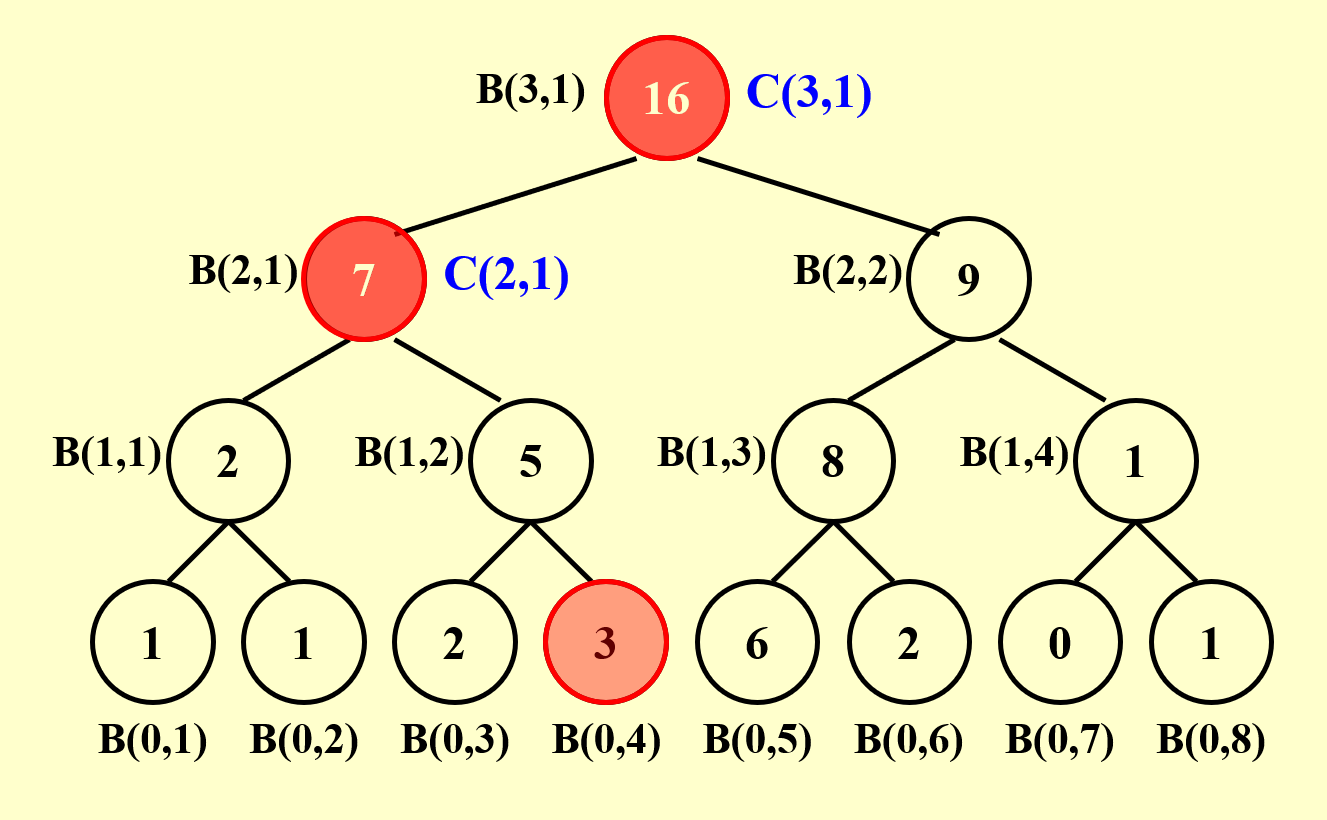
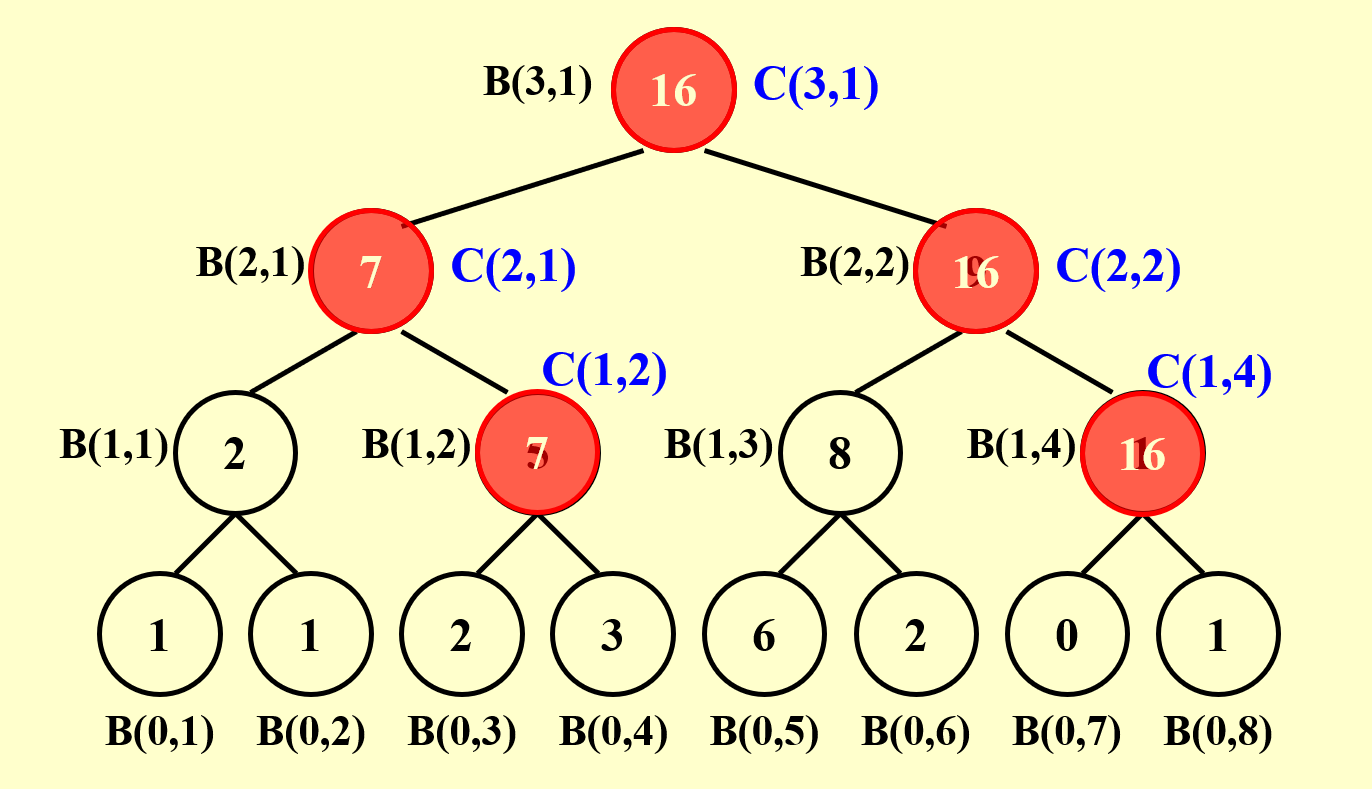
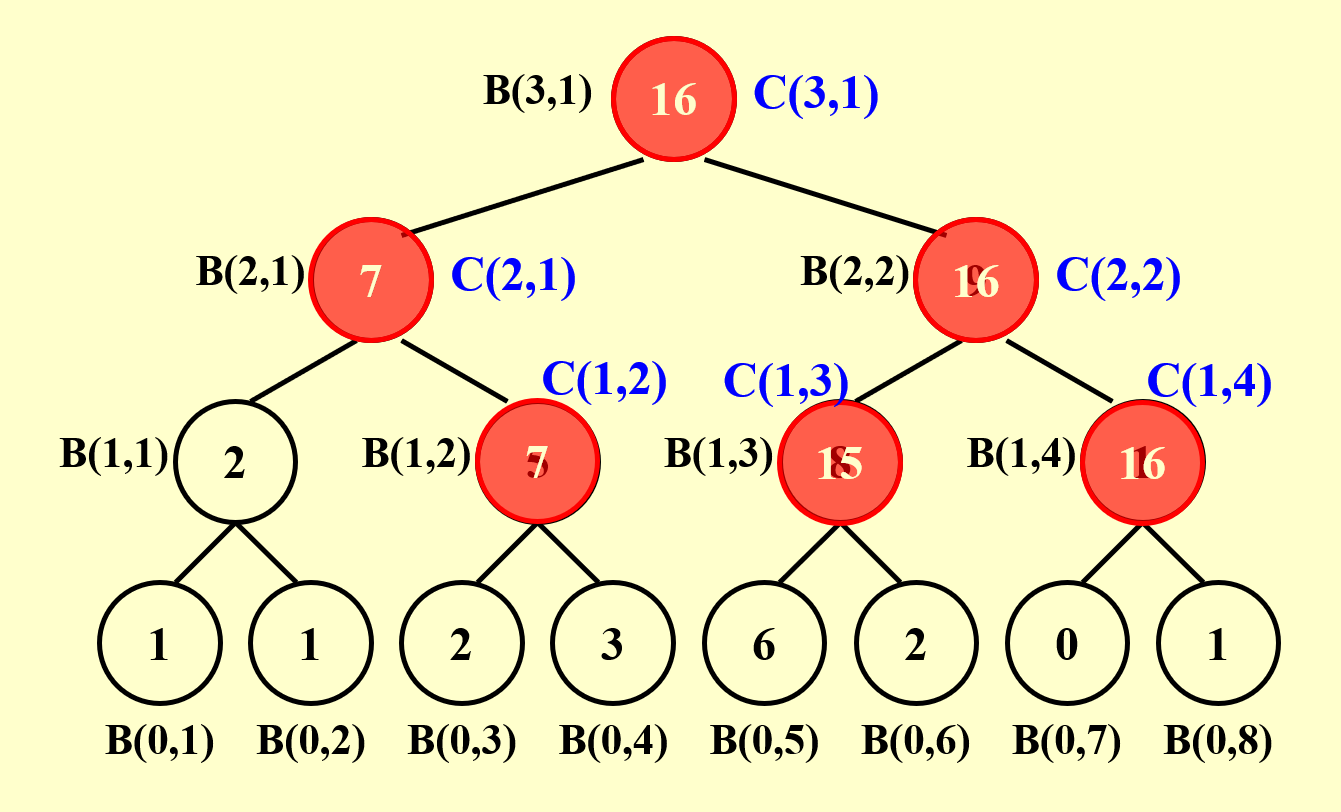
接下来,我们规定前缀和\(C(h, i) = \sum\limits_{k=1}^\alpha A(k)\),其中 \((0, \alpha)\) 表示二叉树的节点 \((h, i)\) 最右侧路径上的叶子节点的位置。要得到 \(C(h, i)\) 的值,需要分以下情况讨论:
总结一下:我们先自底向上计算求和问题,然后根据求和问题的结果自顶向下计算前缀和问题,这两趟计算都用到了并行算法。
伪代码如下所示:
代码实现
// Same as summation problem
for P_i, 1 <= i <= n pardo
B(0, i) := A(i)
for h = 1 to log(n)
for i, 1 <= i <= n / 2^h pardo
B(h, i) := B(h - 1, 2 * i - 1) + B(h - 1, 2 * i)
// Now calculate the prefix sum problem
for h = log(n) to 0
for i even, 1 <= i <= n / 2^h pardo
C(h, i) := C(h + 1, i / 2)
for i = 1 pardo
C(h, 1) := B(h, 1)
for i odd, 3 <= i <= n / 2^h pardo
C(h, i) := C(h + 1, (i - 1) / 2) + B(h, i)
for P_i, 1 <= i <= n pardo
Output C(0, i)
- 时间复杂度:\(T(n) = O(\log n)\)
- 工作量:\(W(n) = O(n)\)
补充:变种问题——求前缀最小值
顾名思义,\(\forall i \in [1, n]\),求序列 \(A(1), A(2), \dots, A(i)\) 中的最小值。下面直接给出并行算法的伪代码:
伪代码
for i, 1 <= i <= n pardo
B(0, i) = A(i)
for h = 1 to log(n)
for i, 1 <= i <= n / 2^h pardo
B(h, i) = min(B(h - 1, 2 * i - 1), B(h - 1, 2 * i))
for h = log(n) to 0
for i even, 1 <= i <= n / 2^h pardo
C(h, i) = C(h + 1, i / 2)
for i = 1 pardo
C(h, 1) = B(h, 1)
for i odd, 3 <= i <= n/2^h pardo
C(h, i) = min(C(h + 1, (i - 1)/2), B(h, i))
for i, 1 <= i <= n pardo
Output C(0, i)
与求前缀和的算法相比,几乎一模一样(高亮行是唯一的区别
- 时间 \(T = O(\log N)\)
- 工作量 \(W = O(N)\)
Merging⚓︎
问题描述
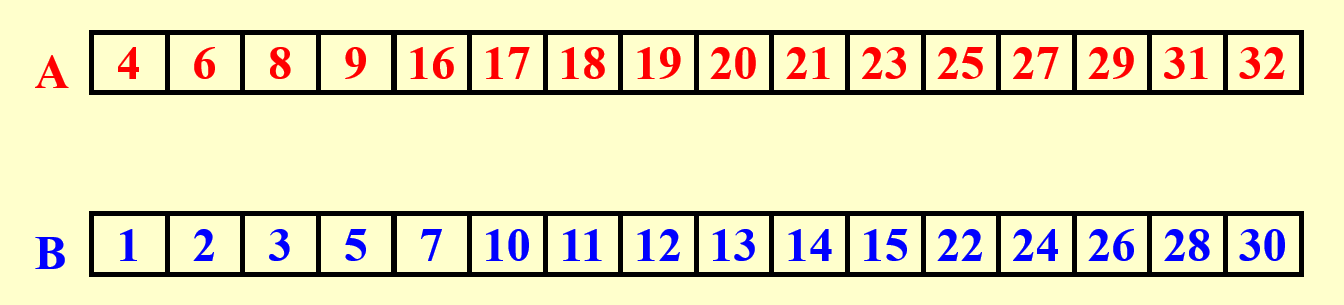
合并两个非递减的数组 \(A(1), A(2), \dots, A(n)\) 和数组 \(B(1), B(2), \dots, B(m)\) 至另一个非递减的数组 \(C(1), C(2), \dots, C(n + m)\)。
为了简化后面的分析,我们规定:
- 数组的索引从 1 开始
- 数组 \(A, B\) 之间没有重复元素
- 令 \(n = m\)
- \(\log n, \dfrac{n}{\log n}\) 的结果均为整数
即使没有这个规定,后面的分析也同样适用于一般的情况。
解决该问题用到的关键方法:划分(partition)。下面介绍一下划分的范式 (paradigm):
- 划分:将输入数据划分为 \(p\)(很大的数字)个独立的小任务,每个小任务的规模大致为 \(\dfrac{n}{p}\)
- 实际的工作:并发执行这些小任务,对于每个小任务使用(顺序)算法来解决
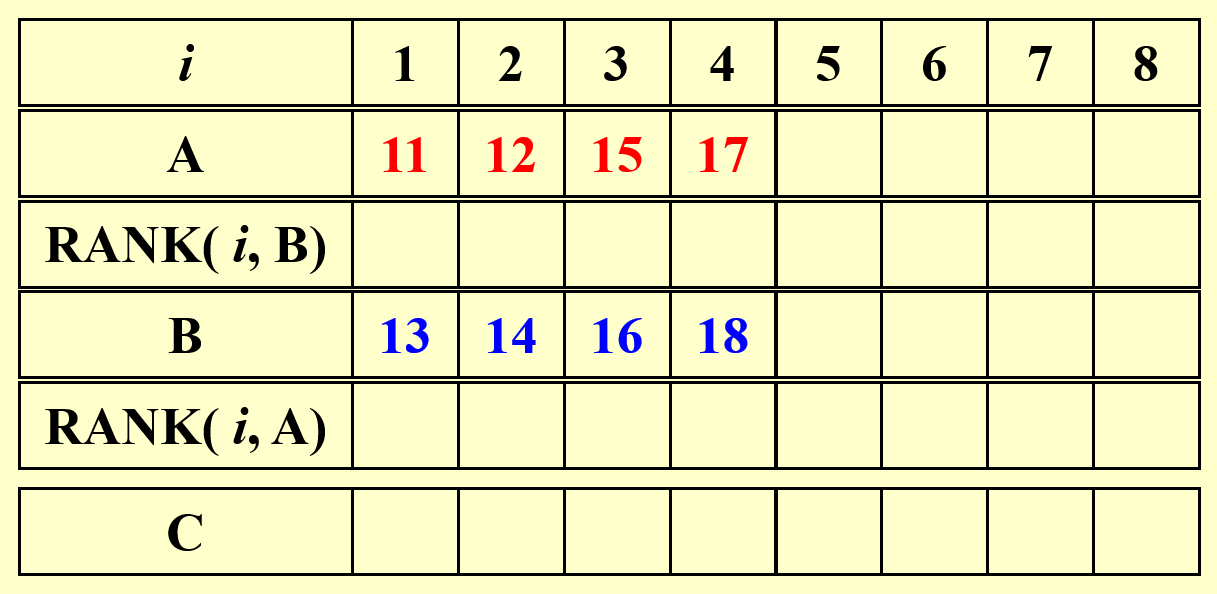
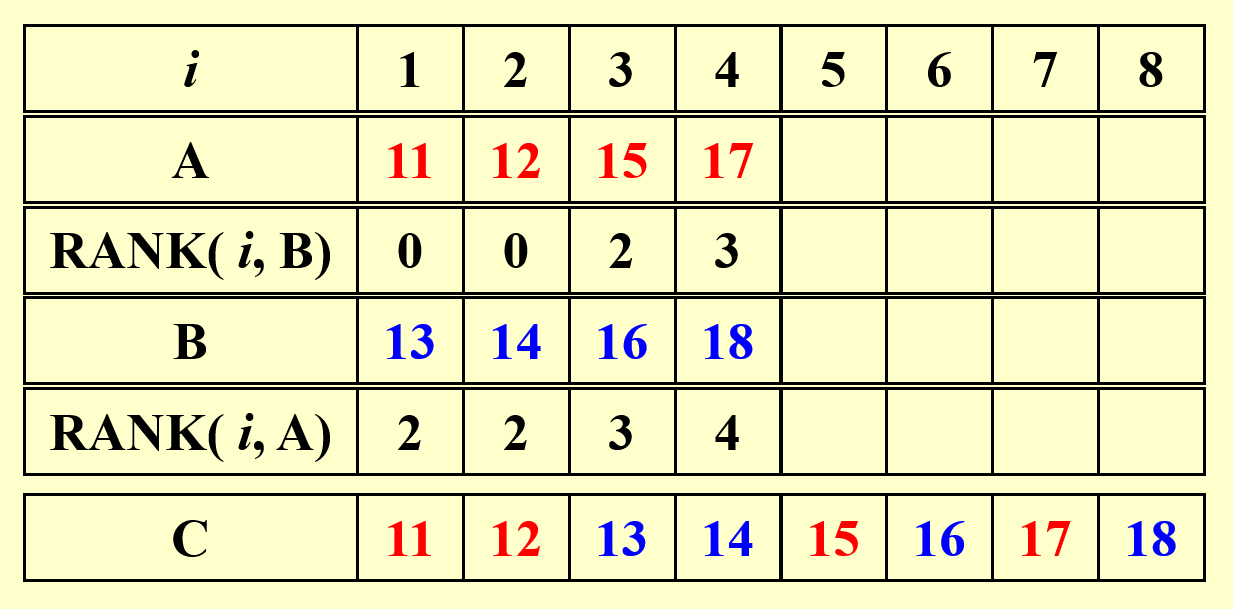
我们可以将合并问题进一步转化为排行问题 (ranking),规定数组 \(B\) 中第 \(j\) 个元素在数组 \(A\) 中的排行为:
那么排行问题可以被描述为 \(\text{RANK}(A, B)\),此时需要计算的东西为:\(\forall 1 \le i \le n\),计算 \(\text{RANK}(i, B)\) 和 \(\text{RANK}(i, A)\)。伪代码如下所示:
代码实现
结论:根据排行问题给出的解,合并问题(不是排行问题)可以在 \(O(1)\) 时间内得到结果,且工作量为 \(O(n + m)\)。所以该算法的速度非常快,但是工作量没有得到优化。
具体解决排行问题的方法
- 时间复杂度:\(T(n) = O(\log n)\)
- 工作量:\(W(n) = O(n \log n)\)
- 用到的处理器数:\(p = n\)
但这些方法都不太好 ......
改进方案:并行排行(parallel ranking)
- 假设 \(n = m\),且确保 \(A(n + 1), B(n + 1)\) 比 \(A(n), B(n)\) 都要大
-
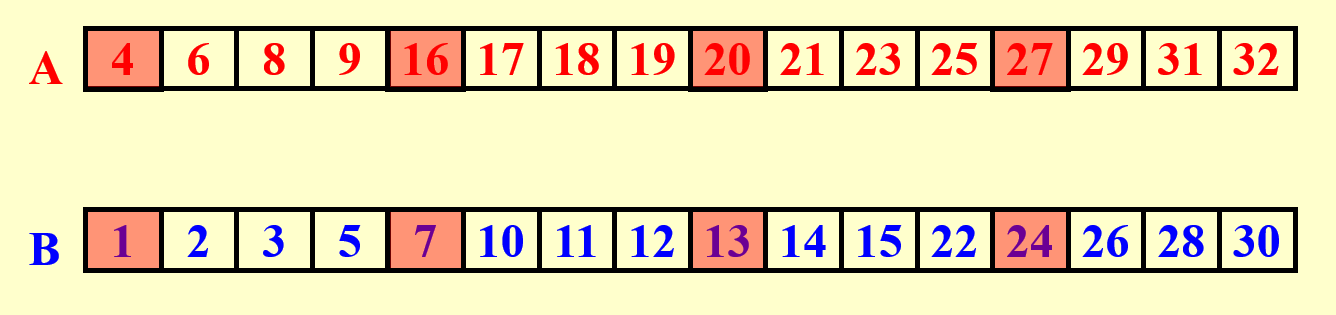
第一步:划分,令处理器数量 \(p = \dfrac{n}{\log n}\),对 \(1 \le i \le p\),有:
- \(A_{\text{Select}}(i) = A(1 + (i - 1)\log n)\)
- \(B_{\text{Select}}(i) = B(1 + (i - 1)\log n)\)
- 计算每一个(根据上面两个式子)被选中的排行
-
第二步:实际排行
- 划分以后,整个问题被分为至多有 \(2p\) 个规模为 \(O(\log n)\) 的子问题
分析:
-
划分:
- 时间:\(T = O(\log n)\)
- 工作量:\(W = O(p \log n) = O(n)\)
-
实际排行:
- 时间:\(T = O(\log n)\)
- 工作量:\(W = O(p \log n) = O(n)\)
-
总结:
- 时间:\(T = O(\log n)\)
- 工作量:\(W = O(p \log n) = O(n)\)
Maximum Finding⚓︎
问题描述
从 \(n\) 个元素中找到最大值
Naive Ideas⚓︎
一些朴素的解题方法
伪代码就不给了,结论为:
- 时间:\(T(n) = O(\log n)\)
- 工作量:\(W(n) = O(n)\)
伪代码如下所示:
代码实现
- 时间:\(T(n) = O(1)\)
- 工作量:\(W(n) = O(n^2)\)
问题
由于是并行比较 \(O(n^2)\) 对元素,因此不可避免地会出现多个处理器访问相同元素的冲突。
解决方案:PRAM 模型 -CRCW 策略 - 共同规则(当所有处理器写入相同的数据时才能进行写入操作)
Doubly-Logarithmic Paradigm⚓︎
我们利用前面提到过的划分范式来改进并行算法。
根据上一种算法想到的划分方式
我们看到,上一种算法中还有一个问题是:虽然时间降为常数级了,但是工作量变成二次的了。所以我们希望通过划分来降低工作量。因此,我们先尝试将问题划分为 \(\sqrt{n}\) 个规模为 \(\sqrt{n}\) 的子问题:
- \(A_1 = A(1), \dots, A(\sqrt{n}) \quad \Rightarrow M_1\)
- \(A_2 = A(\sqrt{n} + 1), \dots, A(2 \sqrt{n}) \quad \Rightarrow M_2\)
- ......
- \(A_{\sqrt{n}} = A(n - \sqrt{n} + 1), \dots, A(n) \quad \Rightarrow M_{\sqrt{n}}\)
最后从每个子问题得到的最大值 \(M_1, M_2, \dots M_{\sqrt{n}}\) 中选取最大值为 \(A_{max}\)
分析:
- 对于每个子问题,采用顺序算法找最大值,因此所需时间为 \(T(\sqrt{n})\),工作量为 \(W(\sqrt{n})\)
- 从这些子问题的最大值寻找整个问题的最大值时,采用两两比较的方式,因此所需时间为 \(T(1)\),工作量为 \(W((\sqrt{n})^2) = O(n)\)
-
由于是并行解决 \(\sqrt{n}\) 个子问题,因此对于总问题而言,有以下递推式成立:
- \(T(n) \le T(\sqrt{n}) + c_1\)(\(c_1 = O(1)\))
- \(W(n) \le \sqrt{n}W(\sqrt{n}) + c_2 n\)(\(c_2 = O(n)\))
-
根据递推式,最终解得:
- 时间:\(T(n) = O(\log \log n)\)
- 工作量:\(W(n) = O(n \log \log n)\)
可以看到,虽然工作量下降了,但是所需时间却变多了,因此这种改进方法还是不太好。
再来看一种称为双对数范式(doubly-logarithmic paradigm) 的划分。我们假设 \(h = \log \log n\) 为整数,此时 \(n = 2^{2^h}\)。现在将问题划分为 \(\dfrac{n}{h}\) 个规模为 \(h\) 的子问题:
- \(A_1 = A(1), \dots, A(h) \quad \Rightarrow M_1\)
- \(A_2 = A(h + 1), \dots, A(2h) \quad \Rightarrow M_2\)
- ......
- \(A_{\frac{n}{h}} = A(n - h + 1), \dots, A(n) \quad \Rightarrow M_{\frac{n}{h}}\)
最后从每个子问题得到的最大值 \(M_1, M_2, \dots M_{\frac{n}{h}}\) 中选取最大值为 \(A_{max}\)
分析:
- 对于每个子问题,所需时间为 \(T(h)\),工作量为 \(W(h)\)
- 根据对之前划分的分析,最终解得:
- 时间:\(T(n) = O(h + \log \log \dfrac{n}{h}) = O(\log \log n)\)
- 工作量:\(W(n) = O(h \cdot \dfrac{n}{h} + \dfrac{n}{h} \log \log \dfrac{n}{h}) = O(n)\)
相比前一种划分而言,这次终于将工作量压到了线性复杂度,但是还是没能保住原来常数级的时间。
Random Sampling⚓︎
我们采用更为高效的划分范式:随机采样(random sampling),其具体步骤如下:
- 这里采用的是PRAM 模型 -CRCW 策略 - 任意规则(任意选择处理器进行写入操作)
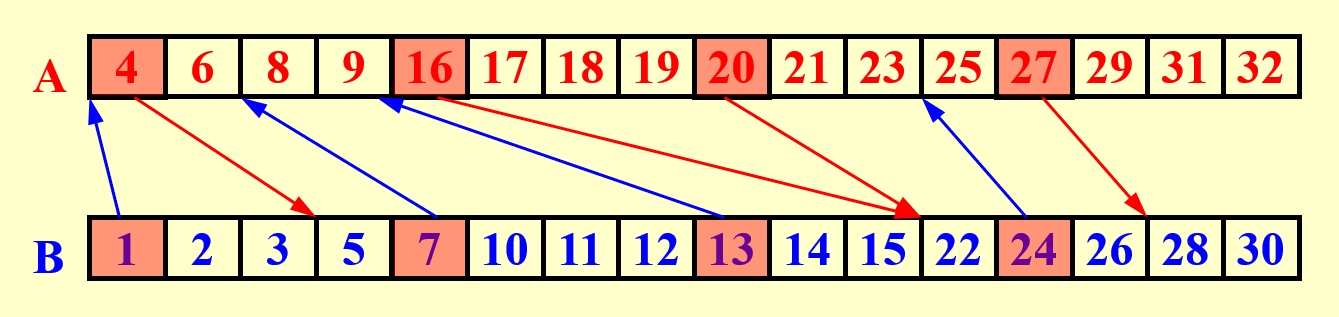
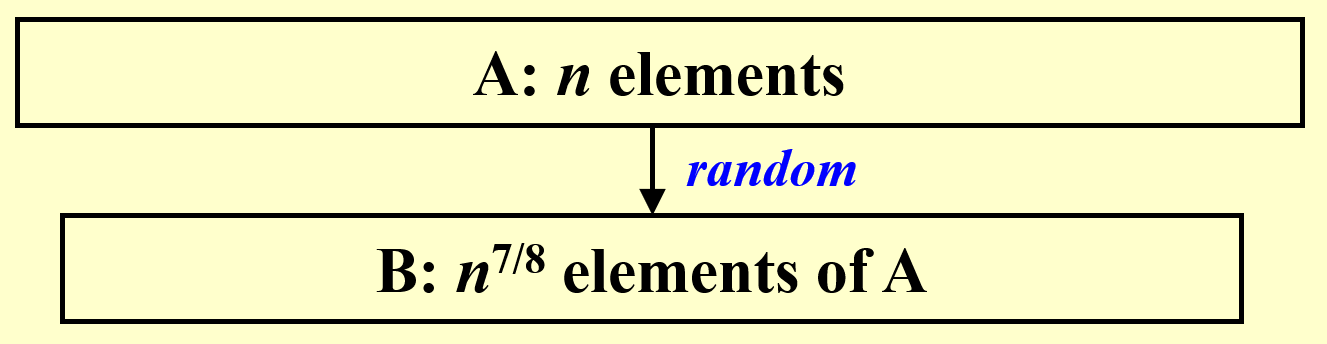
- 先从数组 \(A\) 中的 \(n\) 个元素中挑选 \(n^{\frac{7}{8}}\) 个元素出来,形成数组 \(B\)
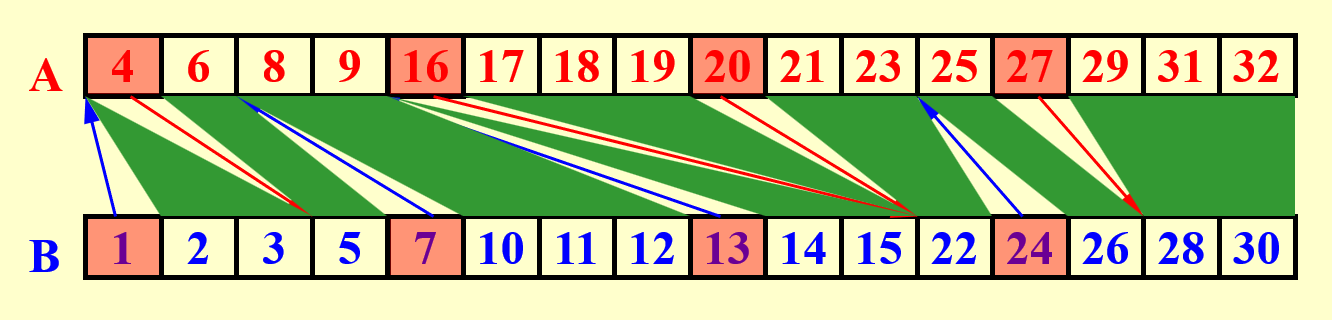
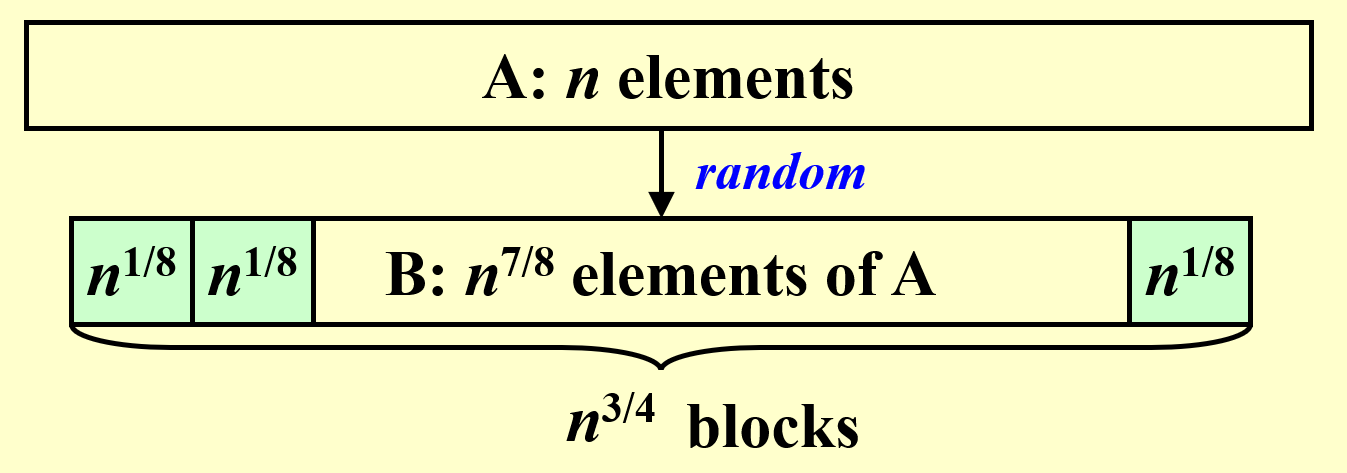
- 将数组 \(B\) 划分为多个大小为 \(n^{\frac{1}{8}}\) 的小块,因此有 \(n^{\frac{3}{4}}\) 个这样的小块。然后对每个小块求出最大值,通过两两比较的方式得到了 \(n^{\frac{3}{4}}\) 个局部最大值
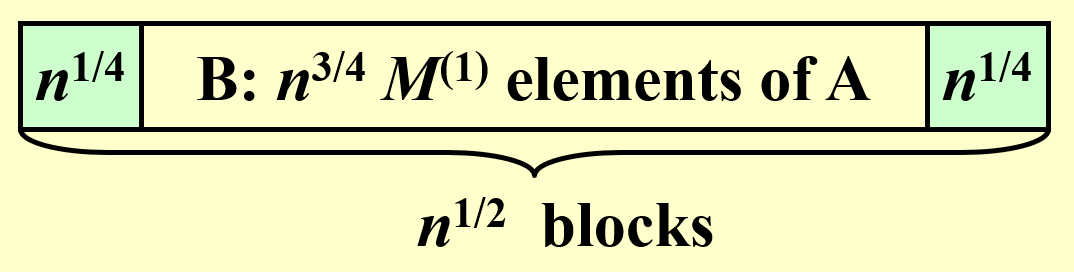
- 接下来将这些最大值划分为 \(n^{\frac{1}{2}}\) 个大小为 \(n^{\frac{1}{4}}\) 的小块,然后对每个小块求出最大值,进而通过两两比较的方式得到所有 \(n^{\frac{7}{8}}\) 个元素的最大值
分析:
-
第 1 次划分:
- 时间:\(M_i^{(1)} \sim T = O(1) \Rightarrow T(n) = O(1)\)
- 工作量:\(W_i = O((n^{\frac{1}{8}})^2) = O(n^{\frac{1}{4}}) \Rightarrow W(n) = O(n)\)
-
第 2 次划分:
- 时间:\(M_i^{(2)} \sim T = O(1) \Rightarrow T(n) = O(1)\)
- 工作量:\(W_i = O((n^{\frac{1}{4}})^2) = O(n^{\frac{1}{2}}) \Rightarrow W(n) = O(n)\)
-
总结:
- 时间:\(M(n^{\frac{7}{8}}) \sim T = O(1)\)
- 工作量:\(W_i = O(n)\)
伪代码:
while (there is an element larger than M) {
for (each element larger than M)
Throw it into random place in new B(n^{7/8})
Compute a new M;
}
注意
由于是随机挑选的,因此这个算法并不保证始终得到正确结果,但是得到正确结果的概率相当大(失败概率为 \(O(\dfrac{1}{n^c})\),其中 \(c\) 为正常数;或者也可以记作 \(O(n^c)\),但此时 \(c\) 为负常数
评论区