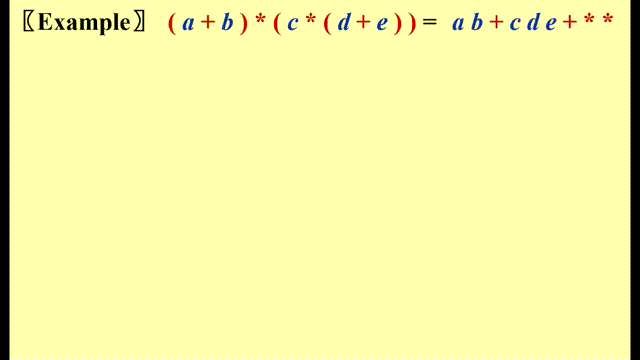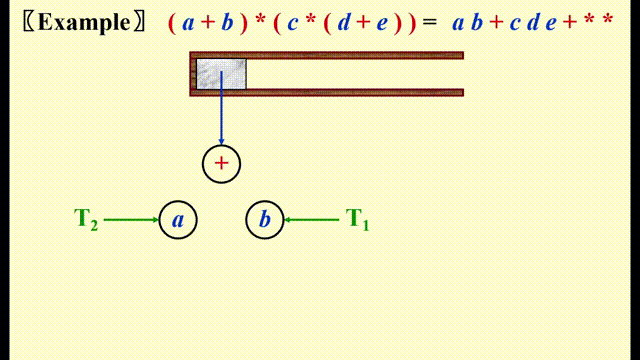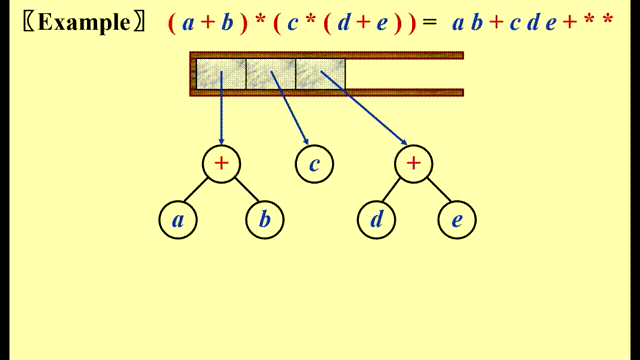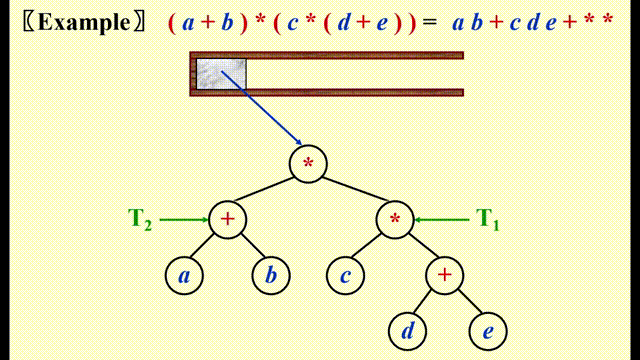Chap 4: Trees⚓︎
约 2679 个字 259 行代码 预计阅读时间 17 分钟
核心知识
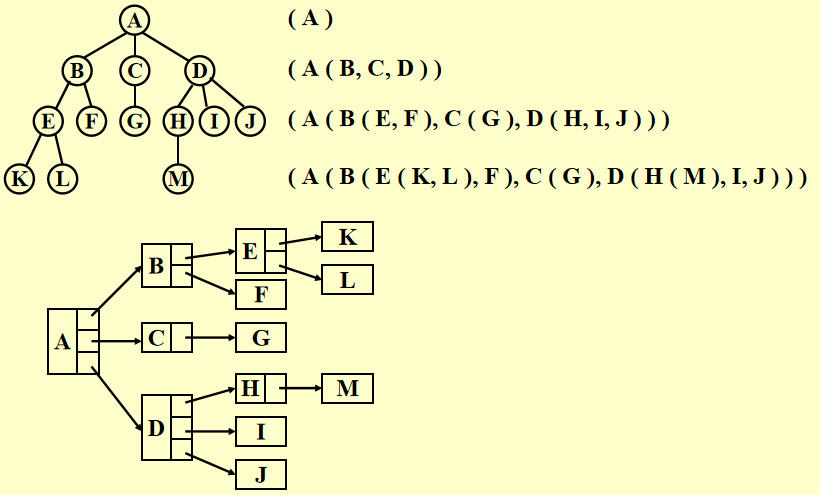
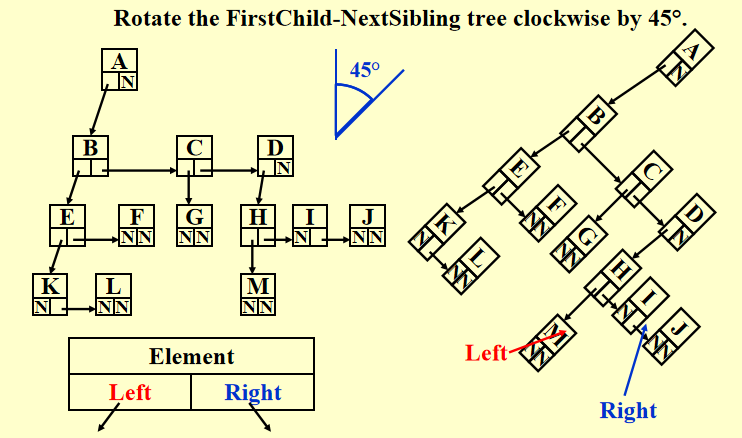
- 树的表示法:first-child-next-sibling
- 二叉树
- 性质
- 树的遍历:前、中、后、层
- 线索二叉树
- 应用:文件系统、表达式树
- 二叉搜索树
- 各种操作,重点是插入和删除
注:更多理论部分的知识可参见离散数学同名章节
Preliminaries⚓︎
Definitions⚓︎
-
树 (trees):它是一组节点,可以为空,如果不为空:
- 包含 1 个根节点 (root) \(r\)
- 有 0 个或多个子树 (subtrees) \(T_1, \dots, T_k\),每个子树的根节点都和 \(r\) 通过一条边 (edge)连接
注:
- 子树之间不会相互连接,因此每个节点都是某个子树的根节点
- 对于一棵有 \(N\) 个节点的树,它有 \(N - 1\) 条边
- 度 (degree):
- 一个节点的度指的是它所有子树的个数
- 一棵树的度为 \(\max\limits_{\text{node } \in \text{ tree}}\{\text{degree(node)}\}\)
- 父节点 (parent):有子树的节点
- 孩子节点 (children):父节点子树的根节点
- 兄弟节点 (siblings):有共同父节点的孩子节点
- 叶子节点 (leaf):度为 0 的节点
- 从 \(n_1\) 到 \(n_k\)路径 (path):一个包含节点 \(n_1, n_2, \dots, n_k\) 唯一的序列,满足 \(n_i\) 是 \(n_{i+1}\) 的父节点 (\(1 \le i < k\))
- 路径长度 (length):路径上边的条数
- 顶点 \(n_i\) 的深度 (depth):从根节点出发到 \(n_i\) 的路径长度,规定 \(\mathrm{depth}(root) = 0\)
- 顶点 \(n_i\) 的高度 (height):从 \(n_i\) 到叶子结点的最长路径长度,规定 \(\mathrm{height}(leaf) = 0\)
- 祖先 (ancestor):从该节点到根节点的路径上所有的节点
- 后代 (descendant):该节点所有子树的节点
- 内部节点 (internal vertices):有孩子节点的顶点
Implementation⚓︎
List Representation⚓︎
缺陷:每个节点的空间大小取决于它有多少个子树,这样实现起来就很麻烦
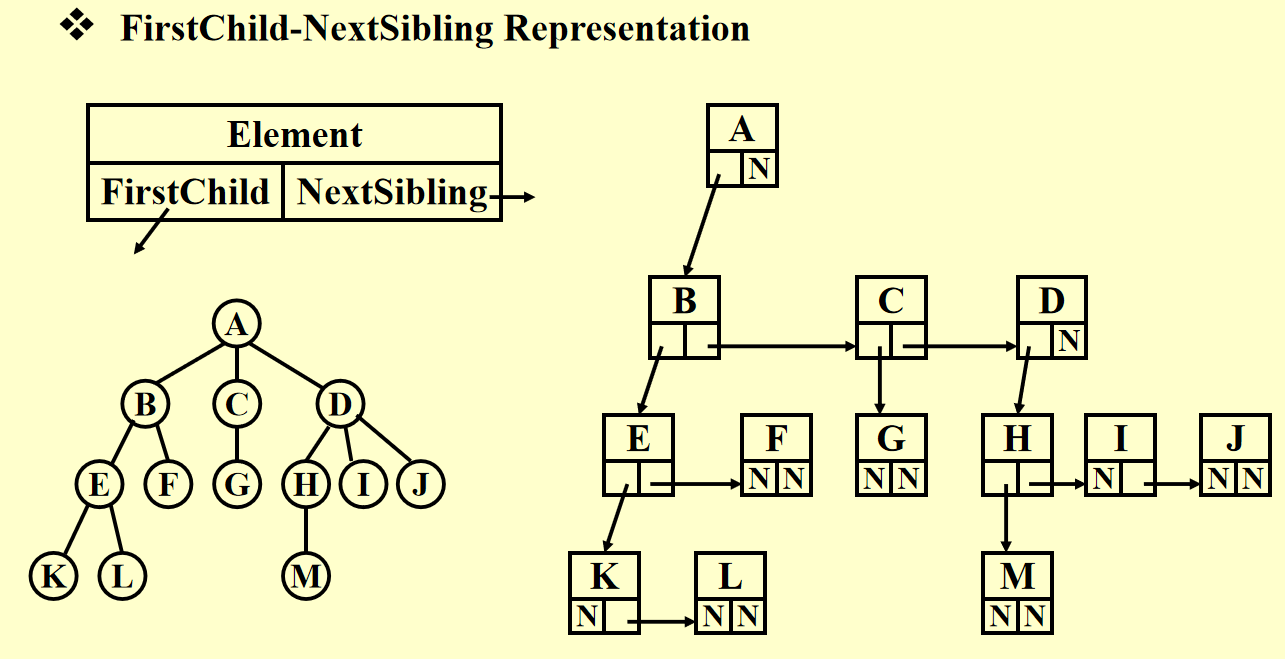
FirstChild-NextSibling Representation⚓︎
注:对于同一棵树,这种表示并不唯一,因为孩子的顺序可以是任意的
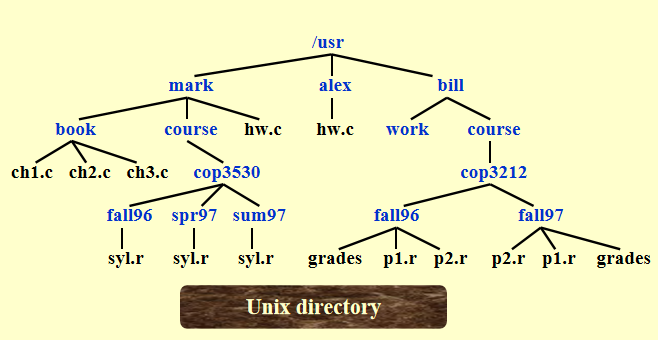
Application(File System)⚓︎
Unix 文件树 \(\Rightarrow\) DOS 目录列表
注意:在 UNIX 系统中位于深度 \(d_i\) 的文件,在转化为 DOS 系统的表示法时需要将它们的名字缩进 \(d_i\) 倍的多个空格
代码实现(前序遍历
static void ListDir(DirOfFile D, int Depth)
{
if (D is legitimate entry)
{
PrintName(D, Depth);
if (D is a directory)
for (each child C of D)
ListDir(C, Depth + 1);
}
}
Depth 变量是不应该被用户看到的内部变量,需要隐藏起来。一种解决方法是像下面那样定义另外一个函数,隐藏Depth 接口
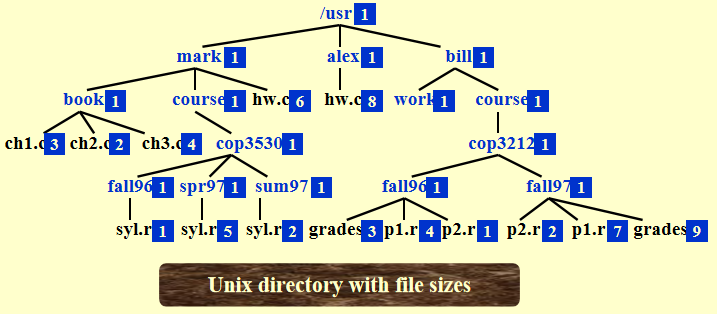
计算目录大小:
代码实现(后序遍历,时间复杂度 \(O(N)\))
static int SizeDir(DirOrFile D)
{
int TotalSize;
TotalSize = 0;
if (D is a legitimate entry)
{
TotalSize = FileSize(D);
if (D is a directory)
for (each child C of D)
TotalSize += SizeDir(C);
} // end if D is legal
return TotalSize;
}
Binary Trees⚓︎
二叉树 (binary tree):每个节点拥有不超过两个孩子的树
补充:一般树(左图)的后序遍历 = 由上述方法得到的二叉树(右图)的中序遍历
Expression Trees(syntax trees)⚓︎
- 先将中缀表达式 -> 后缀表达式
-
然后类似后缀表达式求解的方法,遇到运算符时,将栈内的两个操作数弹出,与运算符构建一棵树,对应关系如下:
- 左子树:栈顶下面的元素
- 根节点:运算符
- 右子树:栈顶元素
将这棵树压入栈中,重复上述步骤直到遍历完整个表达式
代码实现
// from my work of project 2
Tree ExpTree(Queue q)
{
Tree ans; // The final expression tree
Stack s; // The stack for tree construction, containing the nodes or the trees
PtrToNode node, op1, op2, new; // node for all element in the queue; op1 and op2 are operands;and new is a new tree
PtrToQueue cur = q->front->next; // Starting from the second element, for the queue has a dummy header
s = CreateStack(); // Initialization
while (cur != NULL) // Traversing all the element in the queue
{
node = CreateNode(cur->var); // Creating node for every element in the queue
if(isalnum(cur->var[0]) || cur->var[0] == '-' && isalnum(cur->var[1])) // If it's an operand, push it into the stack
{
Push1(node, s);
// printf("%s\n", str);
}
else // If it's a operator,
{
op2 = Top1(s); // Obtaining the top two operands from the stack
Pop(s);
op1 = Top1(s);
Pop(s);
new = CreateTree(node, op1, op2); // Creating an expression (sub)tree
Push1(new, s);
}
cur = cur->next;
}
ans = Top1(s); // The remaining tree in the stack is the answer
return ans;
}
Tree Traversals⚓︎
树的遍历 (tree traversals):对树的每个节点都访问一次,时间复杂度为 \(O(N)\)
前序遍历 (preorder traversal)
后序遍历 (postorder traversal)
void postorder(tree_ptr tree)
{
if (tree)
{
for (each child C of tree)
postorder(C);
visit(tree);
}
}
层序遍历 (levelorder traversal)
void levelorder(tree_ptr tree)
{
enqueue(tree);
while (queue is not empty)
{
visit(T = dequeue());
for (each child C of T)
enqueue(C);
}
}
补充: “之”字形遍历
可以认为是“层序遍历 pro”:第 0 层(根节点)从右往左、第 1 层从左往右、第 2 层从右往左 ...,也就是说每层遍历完后都要改变一次遍历方向
实现方法:用 2 个栈,一个存从左往右遍历的节点,一个存从右往左遍历的节点
中序遍历 (inorder traversal)
// Recursion
void inorder(tree_ptr tree)
{
if (tree)
{
inorder(tree->Left);
visit(tree->Element);
inorder(tree->Right);
}
}
// Iteration(using stack)
void iter_inorder(tree_ptr tree)
{
Stack S = CreateStack(MAX_SIZE);
for (;;)
{
for (; tree; tree = tree->left)
Push(tree, S);
tree = Top(S);
Pop(S);
if (!tree)
break;
visit(tree->Element);
tree = tree->Right;
}
}
注
- 知道前序或者后序遍历 + 中序遍历,可以确定唯一的一棵树
- 知道前序遍历 + 后序遍历,一般情况下无法确定树的形状
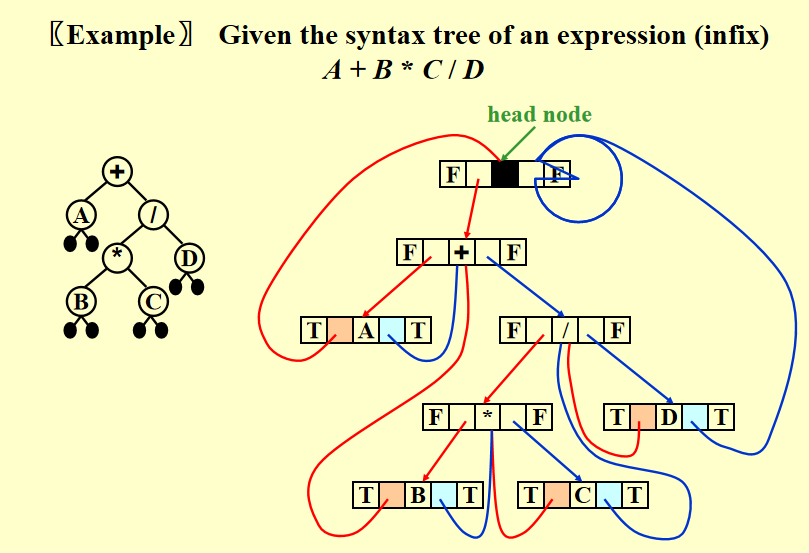
Threaded Binary Trees⚓︎
对于一般的二叉树,它的叶子节点的左右指针指向 NULL,这浪费了很多空间。而线索二叉树 (threaded binary trees)很好地利用了闲置的节点,具体规则如下:
- 如果
Tree->Left为空,将它指向中序遍历中的前一个节点 - 如果
Tree->Right为空,将它指向中序遍历中的后一个节点 - 有一个头节点(dummy node),使得最左边和最右边孩子分别指向这个节点的左右孩子
// 结构声明
typedef struct ThreadedTreeNode *PtrTo ThreadedNode;
typedef struct PtrToThreadedNode ThreadedTree;
struct ThreadedTreeNode
{
int LeftThread; // if it is True, then Left
TreadedTree Left; // is a thread, not a child ptr
ElementType Element;
int RightThread; // if it is True, then Right
ThreadedTree Right; // is a thread, not a child ptr
}
例子
可以看到,我们从 dummy head node 出发,重复“左线索 \(\rightarrow\) 右线索 \(\rightarrow\) 左线索 \(\rightarrow\) 右线索 \(\dots\)”的遍历过程,最后回到 dummy head node ,这样我们可以对整棵树进行一趟完整的中序遍历。
注
虽然这里默认使用中序遍历的定义,但我们也可以将其修改成前序或者后序遍历的版本 ( 比如对于后序遍历版的线索二叉树,某个节点空出来的左子树指向它在后序遍历中的前一个节点,空出来的右子树指向它在后序遍历中的后一个节点 )
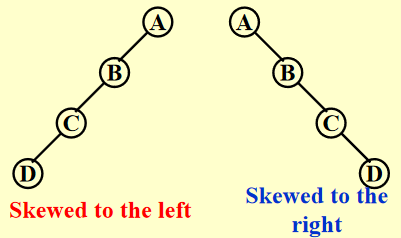
Special Cases⚓︎
- 歪斜二叉树 (skewed binary trees):
- 完全二叉树 (complete binary trees):
Properties⚓︎
-
第 \(i\) 层 (\(i \ge 1\)) 最多拥有 \(2^{i - 1}\) 个节点;深度为 \(k\) 的二叉树最多有 \(2^{k+1} - 1\) 个节点 (\(k \ge 1\))
-
对于非空的二叉树,\(n_0 = n_2 + 1\),其中 \(n_0\) 是叶子节点个数,\(n_2\) 是度为 2 的节点个数
证明
注:该证明可推广至 n 叉树
- 令 \(n_1\) 为度为 1 的节点,\(n\) 为节点总数,则 \(n = n_0 + n_1 + n_2\)
- 令 \(B\) 为边的条数,则 \(n = B + 1\),而且不难发现 \(B = n_1 + 2n_2\)
- 联立上述三个方程,可以得到 \(n_0 = n_2 + 1\)(\(n_1\) 被消掉了 )
推论 1:对于一棵完全二叉树,易知 \(n_1 = 0\) 或 \(1\)。由 \(n_0 = n_2 + 1\) 知 :
- 完全二叉树有奇数个节点时,\(n_1 = 0\)
- 完全二叉树有偶数个节点时,\(n_1 = 1\)

Binary Search Tree⚓︎
Definition⚓︎
二叉搜索树 (Binary Search Tree)是一棵二叉树,它可以是空树,如果非空,则遵循以下规则:
-
每个节点有一个整数的键 (key),每个键互不相同
这里这么定义是为了方便后面的操作,实际上键不必是整数,键也可以相同
-
非空左子树的键必须小于根上的键
- 非空右子树的键必须大于根上的键
- 左右子树也是二叉搜索树
注
- 对二叉搜索树的同一层从左往右遍历,得到的键的序列是有序的
- 通过对二叉搜索树的中序遍历得到的元素序列是有序的
- 给出一棵二叉搜索树的前序或者后序遍历,根据二叉搜索树的定义,我们应当可以还原出这棵树
- 对于一棵完全的二叉搜索树,它最小的节点一定是叶子节点,最大的就不一定了
ADT⚓︎
Objects:拥有 0 个或多个元素的有限有序表
Operations:
SearchTree MakeEmpty(SearchTree T);Position Find(ElementType X, SearchTree T);Position FindMin(SearchTree T);Position FindMax(SearchTree T);SearchTree Insert(ElementType X, SearchTree T);SearchTree Delete(ElementType X, SearchTree T);ElementType Retrieve(Position P);
Implementations⚓︎
预先处理
// 声明部分
#ifndef _Tree_H
struct TreeNode;
typedef struct TreeNode * Position;
typedef struct TreeNode * SearchTree;
SearchTree MakeEmpty(SearchTree T);
Position Find(ElementType X, SearchTree T);
Position FindMin(SearchTree T);
Position FindMax(SearchTree T);
SearchTree Insert(ElementType X, SearchTree T);
SearchTree Delete(ElementType X, SearchTree T);
ElementType Retrieve(Position P);
#endif // _Tree_H
// 写在执行文件部分
struct TreeNode
{
ElementType Element;
SearchTree Left;
SearchTree Right;
}
// 初始化处理(用到后序遍历),时间复杂度 O(logN)
SearchTree MakeEmpty(SearchTree T)
{
if (T != NULL)
{
MakeEmpty(T->Left);
MakeEmpty(T->Right);
free(T);
}
return NULL;
}
Find⚓︎
代码实现(递归版)
Position Find(ElementType X, SearchTree T)
{
if (T == NULL)
return NULL; // not found in an empty tree
if (X < T->Element) // if smaller than root
return Find(X, T->Left); // search left subtree
else if (X > T->Element) // if larger than root
return Find(X, T->Right); // search right subtree
else // if X == root
return T; // found
}
- 时间复杂度 \(T(N)\) 和空间复杂度 \(S(N)\) 都等于 \(O(d)\),其中 \(d\) 为树 \(X\) 的深度
- 函数开始时应先判断树是否为空,如果少了这句,后面就会发生段错误(在不存在的树中获取元素,这是未定义的)
- 这里的递归函数是尾递归 (tail recursions),因此系统会自动将递归优化为循环
代码实现(迭代版)
FindMin⚓︎
代码实现
FindMax⚓︎
代码实现
FindMin() 和 FindMax 函数的时间复杂度均为 \(O(d)\),\(d\) 为树的深度
Insert⚓︎
思路
执行过程类似 Find
- 如果找到了该节点,可以不做任何处理,也可以给它的计数器 +1(如果节点有计数字段的话)
- 否则将最后遇到的非空节点视为新节点的父节点,然后将新节点插入
NULL的位置上
代码实现
SearchTree Insert(ElementType X, SearchTree T)
{
if (T == NULL) // Create and return a one-node tree
{
T = (SearchTree)malloc(sizeof(struct TreeNode));
if (T == NULL)
FatalError("Out of space!!!");
else
{
T->Element = X;
T->Left = T->Right = NULL;
}
} // End create a one-node tree
else
{
if (X < T->Element)
T->Left = Insert(X, T->Left);
else if (X > T->Element)
T->Right = Insert(X, T->Right);
// Else X is in the tree already, we'll do nothing
}
return T; // Don't forget this line!!
}
时间复杂度:\(O(d)\)
思考
可不可以这样简化一下插入函数——将函数返回类型改为void,然后在第一个else中不采用赋值语句,最后也不返回T
NO!!!
如果最后没有在树中找到要插入的节点,那么就需要新建一棵子树。如果建完这棵树后没有返回,那么这棵子树的父节点无法与它建立联系,这棵子树与原来的树就是断开的,因此建了也等于白建。
Delete⚓︎
这是二叉搜索树中最难处理的部分。我们要处理有三种情况:
- 叶子结点
- 有一个孩子
- 有两个孩子
具体分析
其中前两种情况的实现较为简单,最后的情况较为复杂
- 删除叶子节点:直接将它的父节点连接到空节点上
- 删除度为 1的节点:用该节点的子节点替换它自身
-
删除度为 2的节点:
-
用该节点左子树的最大节点或右子树的最小节点(挑一种)替换它自身
解释:以右子树最小节点为例,将其作为新的父节点,因为它既满足比左子树所有节点大(右子树的节点 > 左子树的节点
) ,又满足比新的右子树所有节点小(它原本就是右子树最小的节点) -
从子树中删除用来替换的节点
注意用来替换的节点的度不超过 1
-
代码实现
// 这里删除度为 2 的节点时采用拿右子树最小节点替换的方法
SearchTree Delete(ElementType X, SearchTree T)
{
Position TmpCell;
if (T == NULL)
Error("Element not found");
else
{
if (X < T->ELement) // Go left
T->Left = Delete(X, T->Left);
else if (X > T->Element) // Go right
T->Right = Delete(X, T->Right);
else // Found element to be deleted
{
if (T->Left && T->Right) // Two children
{ // Replace with smallest in right subtree
TmpCell = FindMin(T->Right);
T->Element = TmpCell->Element;
T->Right = Delete(T->Element, T->Right);
} // End if
else // One or zero child
{
TmpCell = T;
if (T->Left == NULL) // Also handles 0 child
T = T->Right;
else if (T->Right == NULL)
T = T->Left;
free(TmpCell); // End else 1 or 0 child
}
}
}
return T;
}
时间复杂度:\(O(h)\),\(h\) 是树的高度。显然,这种删除的操作效率不高
改进方法:如果删除操作用的不多,可以采用 lazy deletion 的方法——为每个节点添加一个 flag 字段,来标记节点是否被删除。因此我们不必通过释放节点的空间的方式来删除节点;而且如果我们重新插入已经删除的节点,也不需要使用 malloc() 分配内存,从而提高程序的效率。
Average-Case Analysis⚓︎
通过计算发现,树的所有节点的平均深度为 \(O(logN)\)(证明过程见教材 \(P_{108}\))
二叉搜索树的大小取决于插入的顺序和删除操作
- 插入:如果顺序不够随机(最坏的情况:升 / 降序
) ,则树会退化成一个链表,因此最坏情况的时间复杂度为 \(O(N)\) - 删除:以替换为右子树最小节点为例,过多的删除操作会导致右子树不断缩小,左子树的规模会大于右子树,破坏了树的平衡
评论区