Chap 2 Algorithm Analysis⚓︎

约 1328 个字 137 行代码预计阅读时间 8 分钟

核心知识

时间、空间复杂度

~~这章貌似没什么东西，可以重点看看递归吧~~

算法 (algorithm)：完成特定任务的有限步指令。所有的算法都具备以下特征：

输入 (input)：0 个或多个输入
输出 (output)：至少有 1 个输出
确定性 (definiteness)：每条指令都是明确的
有限性 (finiteness)：不管什么在什么情况下，算法需要在经过有限步后终止
有效性 (effectiveness)：每条指令足够简单可行，原则上使用纸和笔便能表达出来。

注

程序由编程语言书写，但不必在有限步内完成，比如操作系统的时钟
算法能由以下方法描述：
- 人类语言 (human languages)
- 流程图 (flow charts)
- 编程语言 (programming languages)
- 伪代码 (pseudo-code)

What to Analyze⚓︎

我们需要分析算法的时间和空间复杂度 (time & space complexity)

在分析复杂度前，我们作出以下假设：

每条指令按顺序执行
每条指令很简单，且执行一条指令仅花费一个时间单元
规模是整数且是固定的，并且假设有无限的内存

通常，我们分析以下两种时间复杂度，它们的输入规模均为 $N$：

$T_{avg}(N)$：平均时间复杂度
$T_{worst}(N)$：最差时间复杂度

Asympotic Notation⚓︎

Definition⚓︎

此部分知识（大 $O$、大 $\Omega$、大 $\Theta$ 表示法及其相关规则）在离散数学的 3.2 节中讲得更为详细，请移步此处。但这里还介绍了小 $o$ 表示法：

$T(N) = o(p(N))$：当 $T(N) = O(p(N))$ 且 $T(N) \ne \Theta(p(N))$

参考资料：Big-O Cheat Sheet

General Rules⚓︎

for 循环 (FOR LOOPS)：for 循环的运行时间不超过“循环体内部语句 $\times$ 迭代次数”
嵌套 for 循环 (NESTED FOR LOOPS)：在一组嵌套循环内的一条语句的执行时间为 “该语句 $\times$ 所有的 for 循环规模的乘积”
连续的语句 (CONSECUTIVE STATEMENTS)：简单地相加
条件语句 (IF/ELSE)：对于下面代码块
```
if (condition) S1;
else S2
```
它的运行时间不会超过“测试条件 + S1 和 S2 中运行时间的最长者”
递归 (RECURSION)：我们从斐波那契数的例子下手分析：

关于斐波那契数

空间复杂度：$O(N)$。理解递归的堆栈调用（串行程序）：比如要算 $Fib(N)$，一定是先算完$Fib(N - 1)$ 再算 $Fib(N - 2)$ ，不会同时计算两者，所以是线性复杂度
准确的时间复杂度：$T = \Theta((\dfrac{1 + \sqrt 5}{2})^n)$，利用离散数学教的线性齐次递推关系求解

在计算递归的时间复杂度中，我们常常建立关于时间复杂度的递推关系。下面举几个常见的递推关系：

线性齐次递推关系
形如 $T(N) = T(N / a) + b$，则 $T(N)$ 大致为 $O(\log N)$（严谨的形式可参见主定理）

补充 ( 不做要求 )：主定理

Compare the Algorithms⚓︎

问题

如何求解最大连续子列和？

下面给出了 4 种算法，时间复杂度逐一减小

Algorithm 1⚓︎

时间复杂度：$O(N^3)$

int MaxSubsequenceSum(const int A[ ], int N)
{
    int ThisSum, MaxSum, i, j, k;

    MaxSum = 0;
    for (i = 0; i < N; i++)
        for (j = i; j < N; j++)
        {
            ThisSum = 0;
            for (k = i; k <= j; k++)// 这里浪费了时间，不需要重新从i开始
                ThisSum += A[k];

            if (ThisSum > MaxSum)
                MaxSum = ThisSum;
        }
    return MaxSum;
}

Algorithm 2⚓︎

时间复杂度：$O(N^2)$

int MaxSubsequenceSum(const int A[ ], int N)
{
    int ThisSum, MaxSum, i, j, k;

    MaxSum = 0;
    for (i = 0; i < N; i++)
    {
        ThisSum = 0;
        for (j = i; j < N; j++)
        {
            ThisSum += A[j];

            if (ThisSum > MaxSum)
                MaxSum = ThisSum;
        }
    }
    return MaxSum;
}

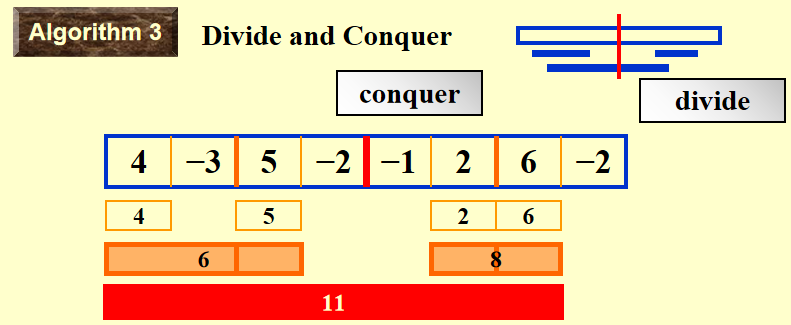
Algorithm 3⚓︎

时间复杂度：$O(NlogN)$

采用分治 (divide-and-conquer) 算法，只需递归比较左半边子列、右半边子列和中间的子列，选择其中最大的作为最大值。

示意图：

static int MaxSubSum(const int A[ ], int Left, int Right)
{
    int MaxLeftSum, MaxRightSum;
    int MaxLeftBorderSum, MaxRightBorderSum;
    int LeftBorderSum, RightBorderSum;
    int Center, i;

    // Base Case
    if (Left == Right)
        if (A[Left] > 0)
            return A[Left];
        else
            return 0;

    // 处理左右两半
    Center = (Left + Right) / 2;
    MaxLeftSum = MaxSubSum(A, Left, Center);
    MaxRightSum = MaxSubSum(A, Center + 1, Right);

    // 处理中间部分
    // 从中间开始左半部分
    MaxLeftBorderSum = 0;
    LeftBorderSum = 0;
    for (i = Center; i >= Left; i--)
    {
        LeftBorderSum += A[i];
        if (LeftBorderSum > MaxLeftBorderSum)
            MaxLeftBorderSum = LeftBorderSum; 
    }
    // 从中间开始右半部分
    MaxRightBorderSum = 0;
    RightBorderSum = 0;
    for (i = Center + 1; i <= Right; i++)
    {
        RightBorderSum += A[i];
        if (RightBorderSum > MaxRightBorderSum)
            MaxRightBorderSum = RightBorderSum; 
    }

    return Max3(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum); // 自定义函数，比较3个数的大小
}

时间复杂度分析：

\[ \begin{align} \text{Base case: }\ T(1) = 1 \quad & T(N) = 2T(N/2) + O(N) \notag \\ \therefore T(N) & = 2T(N/2) + cN \notag \\ & = 2[2T(N/2^2) + cN/2] + cN \notag \\ & = 2^kO(1) + ckN \quad \text{where } N/2^k = 1 \notag \\ & = O(NlogN) \notag \end{align} \]

Algorithm 4⚓︎

时间复杂度：$O(N)$

采用在线 (on-line) 算法：随着程序的运行，在任意时间阶段内计算当前情况下的解

int MaxSubsequenceSum(const int A[ ], int N)
{
    int ThisSum, MaxSum, j;

    ThisSum = MaxSum = 0;
    for (j = 0; j < N; j++)
    {
        ThisSum += A[j];

        if (ThisSum >= MaxSum)
            MaxSum = ThisSum;
        else if (ThisSum < 0)
            ThisSum = 0;
    }
    return MaxSum;
}

Logarithm in the Running Time⚓︎

下面分析的三种算法，它们的时间复杂度均为 $O(\log N)$

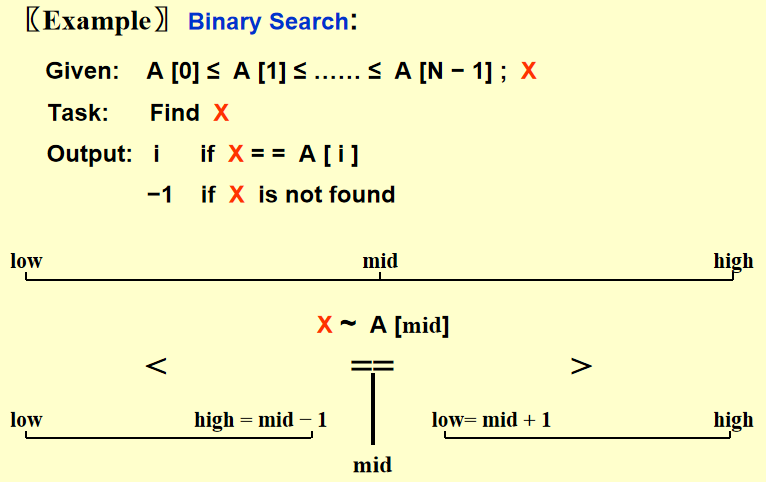
Binary Search⚓︎

使用前提：列表已排好序

分析：

代码实现：

int BinarySearch(const ElementType A[ ], ElementType X, int N)
{
    int Low, Mid, High;

    Low = 0;
    High = N - 1;
    while (Low <= High)
    {
        Mid = (Low + High) / 2;
        if (A[Mid] < X)
            Low = Mid + 1;
        else if (A[Mid] > X)
            High = Mid - 1;
        else
            return Mid;
    }
    return NotFound;  // NotFound被定义为-1
}

Euclid’s Algorithm⚓︎

又称辗转相除法，用于求解两个数的最大公约数 (greatest common divisor, gcd)

参考：离散数学相应章节

分析

要求解两个数 $M, N(M \ge N)$ 的最大公约数，先算出两者相除得到的余数，然后用小的数 $N$ 除以余数得到新的余数，以此类推，当较小数为 0 时结束。此时剩下的非 0 数（即较大数）即为最大公约数。

要说明它的时间复杂度为 $O(logN)$，先证明下面这个定理： $$ \text{If }M > N\text{ ,then }M\text{ mod }N < M / 2 $$

提示：分 $N \le M/2$ 和 $N > M/2$ 两种情况讨论，易证，故略去证明过程

有了这个定理后，自然而然就能得到其时间复杂度在 $O(logN)$ 左右。事实上，实际的复杂度还略微低一些。

代码：

unsigned int Gcd(unsigned int M, unsigned int N)
{
    // 这里已经假设 M > N了
    unsigned int Rem;

    while (N > 0)
    {
        Rem = M % N;
        M = N;
        N = Rem;
    }
    return M;
}

Exponentation⚓︎

long Pow(long X, unsigned int N)
{
    if (N == 0)
        return 1;
    // 6、7两行可以不写，因为前后的代码可以应对该情况
    if (N == 1)   // 6
        return X; // 7
    if (IsEven(N))  // int IsEven(int N){return N % 2 == 0}
        return Pow(X * X, N / 2);
    else
        return Pow(X * X, N / 2) * X;
}

最后注意递归程序的书写问题，错误的书写会影响效率，甚至导致死循环（见书上反例）

Checking Your Analysis⚓︎

如果程序过于复杂，无法直接看出时间复杂度（这种情况常常发生），那么下面的方法会帮到我们：

\[ \text{When }T(N) = O(f(N)) \text{ , check if } \lim\limits _{N \rightarrow \infty} \frac{T(N)}{f(N)} \approx \text{ Constant} \]

如果是常数的话，说明我们估计的时间复杂度 $O(f(N))$ 基本正确

评论区

如果有什么问题或想法，欢迎大家在下方留言~