Chap 7: Sorting⚓︎
约 3326 个字 260 行代码 预计阅读时间 20 分钟
核心知识
本来这里应该整理一张表格,表示每种排序的时间复杂度和适用情况等等,但因时间问题来不及整理,之后会补上。
核心知识就看目录的二级标题吧,实在没时间了(悲)
Preliminaries⚓︎
void X_sort(ElementType A[], int N)
N必须是合法的整数- 方便起见,假设数组元素都是整数
- 基于比较的排序 (comparison-based sorting):假定存在
<,>运算符,且它们是唯一能够用于输入数据的运算符 - 仅考虑内部排序 (internal sorting)(即整个排序能在主内存中完成)
注:教材中未提到选择排序和冒泡排序,但考试会考。若忘记了它们的原理,自己上网搜。
Insertion Sort⚓︎
插入排序 (insertion sort)的大致原理
重复 N - 1 趟排序,从 P = 1 到 P = N - 1 。排序前已知 0~P-1 位置上的元素是有序的。对于第 P 趟排序,我们将位置 P 上的元素向前 P 个元素移动,直到发现正确的位置。这样保证每趟排序结束后位置在 0 ~ P 上的元素是有序的。
代码实现
void InsertionSort(ElementType A[], int N)
{
int j, P;
ElementType Tmp;
for (P = 1; P < N; P++)
{
Tmp = A[P] // the next coming card
for (j = P; j > 0 && A[j - 1] > Tmp; j--)
A[j] = A[j - 1];
// shift sorted cards to provide a position for the new coming card
A[j] = Tmp; // place the new card at the proper position
} // end for-P-loop
}
- 最坏情况:输入的
A[]是逆序的,\(T(N) = O(N^2)\) - 最好情况:输入的
A[]是顺序的,\(T(N) = O(N)\) - 平均情况:\(\Theta(N^2) = \sum\limits_{i = 2}^Ni = 2 + 3 + 4 + \dots + N\)
A Lower Bound for Simple Sorting Algorithms⚓︎
定义:一个数组中数字的逆序对 (inversion)是一个有序对 \((i, j)\),满足 \(i < j\) 且 \(A[i] > A[j]\)
观察发现:数组中逆序对的个数 = 其插入排序过程中的交换次数
证明:交换两个相邻的元素,就可以消去数组中的一个逆序对
所以,插入排序的时间复杂度还可以表示为 \(T(N, I) = O(I + N)\),其中 \(I\) 是原始数组中逆序对的个数。观察发现,当列表已经排过序了,那么这次排序的速度就会很快。
定理 1:对于包含 N 个不同数字的数组,它的平均逆序对个数为 \(\dfrac{N(N-1)}{4}\)
定理 2:任何通过交换相邻元素实现的排序算法,平均时间复杂度为 \(\Omega(N^2)\)
由这些定理,我们知道:可以通过在每次交换中消除多个逆序对的方式来提升排序效率
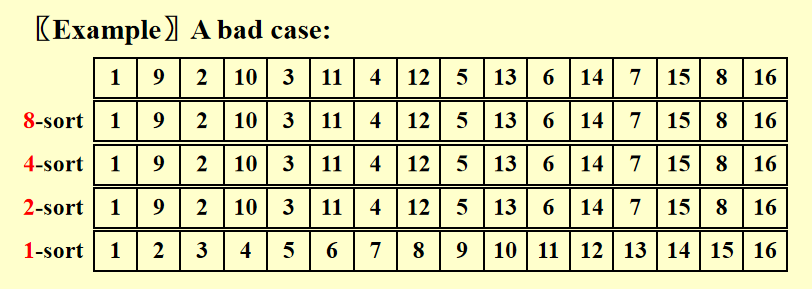
Shellsort⚓︎
希尔排序 (shellsort)的大致原理
- 这种算法比较相隔一定距离的元素
- 比较的间隔在算法运行时将不断减小,直到最后比较的是相邻元素
因此这种排序也被称为缩小增量排序 (diminishing increment sort),它是不稳定的排序
关键概念
-
增量序列 (increment sequence):\(h_1 < h_2 < \dots < h_t(h_1 = 1)\),它决定了希尔排序的运行时间
-
\(h_k\)-sort:阶段 \(k = t, t - 1, \dots, 1\) 的排序。\(h_k\)-sort 后,可以确保序列 A 中 \(\forall i,\ A[i] \le A[i + h_k]\)
- \(h_k\)-sorted 的序列,经历了 \(h_{k-1}\)-sort 后,保持 \(h_k\)-sorted
- 具体做法:对某个位置为 i 的元素,在位置为 \(i, i - h_k, i - 2h_k, \dots\) 的元素中进行插入排序,因此 1 个 \(h_k\)-sort 包含 \(h_k\) 次独立的插入排序
希尔增量序列 (Shell's increment sequence):
代码实现
void Shellsort(ElementType A[], int N)
{
int i, j, increment;
ElementType Tmp;
for (increment = N / 2; increment > 0; increment /= 2)
// h sequence
for (i = increment; i < N; i++)
{ // insertion sort
Tmp = A[i];
for (j = i; j >= increment; j -= increment)
if (Tmp < A[j - increment])
A[j] = A[j - increment];
else
break;
A[j] = Tmp;
} // end for-l and for-increment loop
}
定理:使用希尔增量的希尔排序的最坏运行时间为 \(\Theta(N^2)\)
注:证明部分见书本 \(P_{224}\)
改进版:希巴德增量序列 (Hibbard's increment sequence)
此时可以保证增量的两两互质
定理:使用希巴德增量的希尔排序的最坏运行时间为 \(\Theta(N^{\frac{3}{2}})\)
注:证明部分见书本 \(P_{225}\)
补充
- \(T_{\text{avg-Hibbard}}(N) = O(N^{\frac{5}{4}})\)
- 塞奇威克 (Sedgewick) 的最佳序列是 {1, 5, 19, 41, 109, …},这些项要么来自 \(9 \times 4^i - 9 \times 2^i + 1\),要么来自 \(4^i - 3 \times 2^i + 1\)
- \(T_{avg}(N) = O(N^{\frac{7}{6}})\)
- \(T_{worst}(N) = O(N^{\frac{4}{3}})\)
虽然希尔排序非常简单,但是它的分析相当复杂。它适用于排序中等大的输入序列 ( 成千上万的规模 )
Heapsort⚓︎
算法 1:
Algorithm 1:
{
BuildHeap(H); // O(N)
for (i = 0; i < N; i++)
TmpH[i] = DeleteMin(H); // O(log N)
for (i = 0; i < N; i++)
H[i] = TmpH[i]; // O(1)
}
缺陷:使用了额外的数组,占用了更多的空间(拷贝不影响时间复杂度)
如何改进
观察发现,每使用 1 次 DeleteMin 函数,堆的规模缩小 1,而我们可以利用这个本该废弃的空间,来存放 DeleteMin 得到的最小的数。但按照这个方法,我们得到的是一个递减序列;如果要得到递增序列,需要构建最大堆并使用 DeleteMax 函数。由此,我们得到了算法 2。
算法 2:
代码实现
// 这里的 PercDown 函数与 Chap 6 给出的稍有不同(索引的标注发生变化)
#define LeftChild(i) (2 * (i) + 1)
void PercDown(ElementType A[], int i, int N)
{
int Child;
ElementType Tmp;
for (Tmp = A[i]; LeftChild(i) < N; i = Child)
{
Child = LeftChild(i);
if (Child != N - 1 && A[Child + 1] > A[Child])
Child++;
if (Tmp < A[Child])
A[i] = A[Child];
else
break;
}
A[i] = Tmp;
}
void Heapsort(ElementType A[], int N)
{
int i;
for (i = N / 2; i >= 0; i--) // BuildHeap
PercDown(A, i, N);
for (i = N - 1; i > 0; i--) // DeleteMax
{
Swap(&A[0], &A[i]);
PercDown(A, 0, i);
}
}
- 索引的标注从 0 开始(不同于 Chap 6)
- 堆排序是一种不稳定的算法
定理:对 N 个不同项的随机排列进行堆排序,平局比较时间为 \(2N \log N - O(N \log \log N)\)
注:证明见书本 \(P_{229-230}\)
尽管堆排序给出了最佳平均时间 \(O(N \log N)\),实际上它比使用 Sedgewick 增量序列的希尔排序更慢
Mergesort⚓︎
归并排序 (merge sort):时间复杂度 \(O(N \log N)\),它采用递归算法,是一种稳定的算法

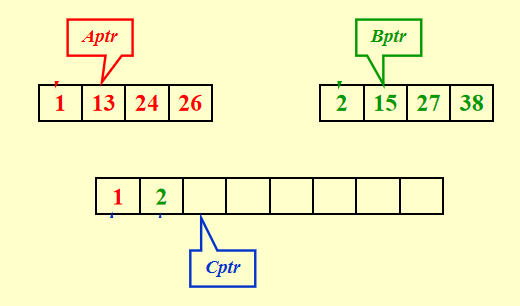
时间复杂度:\(T(N) = O(N)\),\(N\) 为 2 个列表的元素个数总和
代码实现
void MergeSort(ElementType A[], int N)
{
ElementType *TmpArray;
TmpArray = (ElementType *)malloc(N * sizeof(ElementType));
if (TmpArray != NULL)
{
MSort(A, TmpArray, 0, N - 1);
free(TmpArray);
}
else FatalError("No space for tmp array!!!");
}
void MSort(ElementType A[], ElementType TmpArray[], int Left, int Right)
{
int Center;
if (Left < Right)
{
Center = (Left + Right) / 2;
MSort(A, TmpArray, Left, Center);
MSort(A, TmpArray, Center + 1, Right);
Merge(A, TmpArray, Left, Center + 1, Right);
}
}
// Lpos = start of left half, Rpos = start of right half
void Merge(ElementType A[], ElementType TmpArray[], int Lpos, int Rpos, int RightEnd)
{
int i, LeftEnd, NumElements, TmpPos;
LeftEnd = Rpos - 1;
TmpPos = Lpos;
NumElements = RightEnd - Lpos + 1;
while (Lpos <= LeftEnd && Rpos <= RightEnd) // main loop
if (A[Lpos] <= A[Rpos])
TmpArray[TmpPos++] = A[Lpos++];
else
TmpArray[TmpPos++] = A[Rpos++];
while (Lpos <= LeftEnd) // Copy rest of first half
TmpArray[TmpPos++] = A[Lpos++];
while (Rpos <= RightEnd) // Copy rest of second half
TmpArray[TmpPos++] = A[Rpos++];
for (i = 0; i < NumElements; i++, RightEnd--)
// Copy TmpArray back
A[RightEnd] = TmpArray[RightEnd];
}
注
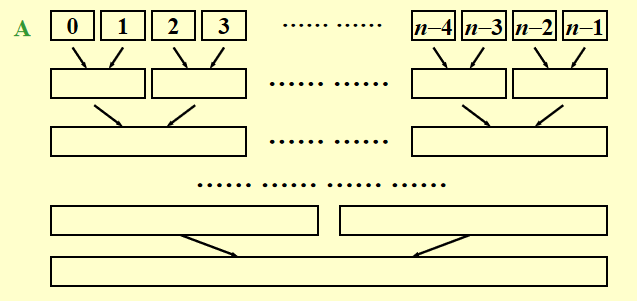
- 归并排序体现了分治 (divide-and-conquer)思想:
MSort为“分”,Merge为“治” - 如果每次调用
Merge,TmpArray会被局部声明,那么空间复杂度 \(S(N) = O(N \log N)\) - 事实上,大量的时间被用于使用
malloc函数建立TmpArray
Analysis⚓︎
时间复杂度分析(利用递推关系
注:另一种证明法见书本 \(P_{233-234}\)
归并排序需要线性大小的额外内存,且拷贝数组会降低速度,因此在内部排序中这种方法不太好用,但是在外部排序 (external sort)(ads 会讲)中很合适
补充:迭代版本
代码实现
可以用来打印每一趟归并排序后的结果
void merge_sort( ElementType list[], int N )
{
ElementType extra[MAXN]; /* the extra space required */
int length = 1; /* current length of sublist being merged */
while( length < N ) {
merge_pass( list, extra, N, length ); /* merge list into extra */
output( extra, N );
length *= 2;
merge_pass( extra, list, N, length ); /* merge extra back to list */
output( list, N );
length *= 2;
}
}
void merge_pass( ElementType list[], ElementType sorted[], int N, int length );
{
int i, j;
int ptr_l, ptr_r, ptr;
ptr = 0;
for (i = 0; i < N; i += 2 * length)
{
ptr_l = i;
ptr_r = i + length;
while (ptr_l < i + length && ptr_r < i + 2 * length && ptr_r < N)
{
if (list[ptr_l] <= list[ptr_r])
sorted[ptr++] = list[ptr_l++];
else
sorted[ptr++] = list[ptr_r++];
}
while (ptr_l < i + length)
sorted[ptr++] = list[ptr_l++];
while (ptr_r < i + 2 * length && ptr_r < N)
sorted[ptr++] = list[ptr_r++];
}
}
void output( ElementType list[], int N )
{
int i;
for (i=0; i<N; i++) printf("%d ", list[i]);
printf("\n");
}
个人感觉迭代版归并排序就像增量不断增大的希尔排序
Quicksort⚓︎
The Algorithm⚓︎
快速排序 (quicksort)(以下简称快排)是目前已知实际上最快的排序算法,它也是一种分治递归算法,时间复杂度为 \(O(N\log N)\)
伪代码模版:
void Quicksort(ElementType A[], int N)
{
if (N < 2) return;
pivot = pick any element in A[] // ?
Partition S = A[] - {pivot} into two dijoint sets: // ?
A1 = {a in S | a <= pivot} and A2 = {a in S | a >= pivot}
A = Quicksort(A1, N1) + {pivot} + Quicksort(A2, N2);
}
图示:
思考
- 我们如何选取
pivot(支点) ,真的可以“随机”挑选吗? - 如何将数组(可以看作集合)“划分 (
partition)”为 2 个子数组(子集) ?
Picking the Pivot⚓︎
Pivot = A[0]
最坏情况:
- 数组
A[]已提前排好序 A[]是逆序的
则所有的元素要么全部放入 A1,要么全部放入 A2,因此浪费了 \(O(N^2)\) 的时间做无意义的事
Pivot = random select from A[]
然而随机数生成的“成本”较高
Pivot = median(left, center, right)
挑选数组中最左边、中间、最右边三个元素的中数,这不仅消除了最坏情况 ( 输入前已排好序 ),还节省了 5% 的运行时间
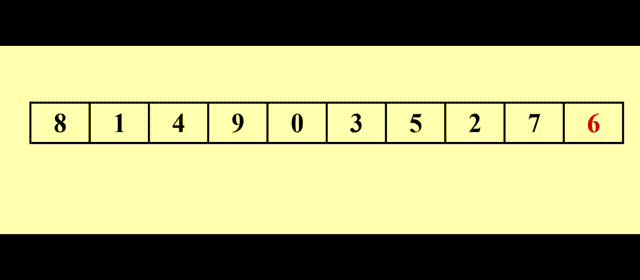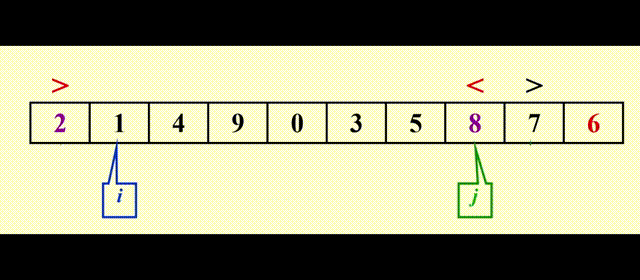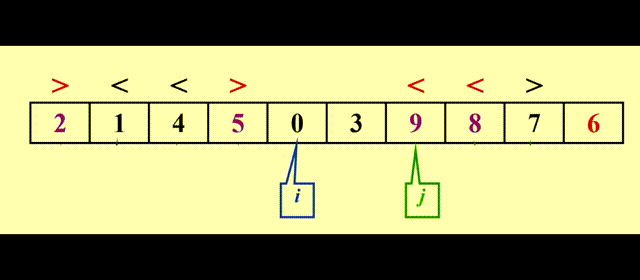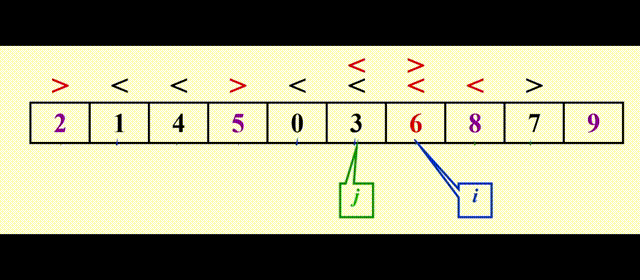
Partitioning Strategy⚓︎
- 初始状态:我们将
Pivot与最后一个元素交换,即把Pivot放入最后;i从第一个元素开始,j从倒数第二个元素开始 -
当
i < j时,- 若
i所指元素比Pivot小,i++,否则停止,等待交换 - 若
j所指元素比Pivot大,j--,否则停止,等待交换 - 当
i和j都停下来了,交换i, j所指元素
这样,数组中比
Pivot小的元素在左边,比Pivot大的元素在右边 - 若
当 key == Pivot 时(key 为数组中的某个值,也就是说数组中有不止一个与 Pivot 相等的元素)
- ⭐同时停止
i和j:- 较坏的情况:1, 1, 1, ……, 这时快排就会进行许多无意义的交换
- 然而,这确保整个序列能够被划分均匀
- 时间复杂度:\(T(N) = O(N \log N)\)
- ❌
i和j均不停止:- 出现子序列划分不均的问题
- 如果所有元素都相等,时间复杂度 \(T(N) = O(N^2)\)
所以,我们选择前一种方案
Small Arrays⚓︎
- 问题:当数组规模较小 (\(N \le 20\)) 时,快排比插排慢
- 解决方案:当 N 较小时,采用另一种更有效的算法(比如插排)
Implementation⚓︎
代码实现
void Quicksort(ElementType A[], int N)
{
Qsort(A, 0, N - 1);
// A: the array
// 0: Left index
// N - 1: Right index
// Return median of Left, Center, and Right
// Order these and hide the pivot
}
void Qsort(ElementType A[], int Left, int Right)
{
int i, j;
ElementType Pivot;
if (Left + Cutoff <= Right) // if the sequence is not too short
{
Pivot = Median3(A, Left, Right); // select pivot
i = Left; // (1)
j = Right - 1; // (2)
for (;;)
{
while (A[++i] < Pivot) {} // scan from left
while (A[--j] > Pivot) {} // scan from right
if (i < j)
Swap(&A[i], &A[j]); // adjust partition
else break; // partition done
}
Swap(&A[i], &A[Right - 1]); // restore pivot
Qsort(A, Left, i - 1); // recursively sort left part
Qsort(A, i + 1, Right); // recursively sort right part
} // end if - the sequence subarray
else
InsertionSort(A + Left, Right - Left + 1);
}
ElementType Median3(ElementType A[], int Left, int Right)
{
int Center = (Left + Right) / 2;
if (A[Left] > A[Center])
Swap(&A[Left], &A[Center]);
if (A[Left] > A[Right])
Swap(&A[Left], &A[Right]);
if (A[Center] > A[Right])
Swap(&A[Center], &A[Right]);
// Invariant: A[Left] <= A[Center] <= A[Right]
Swap(&A[Center], &A[Right - 1]);
// only need to sort A[Left + 1] .. A[Right - 2]
// 因为我们已经知道 A[Left] 比 pivot 小,A[Right] 比 pivot 大
// 所以回到 Qsort 函数后,我们无需改变 A[Left] 和 A[Right] 的顺序
return A[Right - 1]; // Return pivot
}
问题
为什么 (1) 和 (2) 不能分别替换为:i = Left + 1; j = Right - 2; 呢?
这样会漏掉 A[Left + 1] 和 A[Right - 2] 两个元素的判断,这显然是错误的
Analysis⚓︎
快排时间复杂度的递推关系式:
- 最坏情况:每次快排挑选的支点都是最小的元素
- 最好情况:支点为中间元素
- 平均情况:假设 \(\forall i,\ T(i)\) 的平均时间为 \(\dfrac{1}{N}[\sum\limits_{j = 0}^{N - 1}T(j)]\)
An Example⚓︎
代码实现
// Places the kth smallest element in the kth position
// Because arrays start at 0. this will be index k-1
void Qselect(ElementType A[], int k, int Left, int Right)
{
int i, j;
ElementType Pivot;
if (Left + Cutoff <= Right)
{
Pivot = Median3(A, Left, Right);
i = Left; j = Right - 1;
for (;;)
{
while (A[++i] < Pivot) {}
while (A[--j] > Pivot) {}
if (i < j)
Swap(&A[i], &A[j]);
else
break;
}
Swap(&A[i], &A[Right - 1]);
if (k <= i)
Qselect(A, k, Left, i - 1);
else if (k > i + 1)
Qselect(A, k, i + 1, Right);
}
else
InsertionSort(A + Left, Right - Left + 1);
}
时间复杂度:
- 最坏情况:\(O(N^2)\)
- 平均情况:\(O(N)\)
总结:各种排序中的 "run" 到底是什么
历年卷中出现过很多关于排序的 "run" 问题:问第 k 次 run 后列表里的元素排序是什么?题目中的 run 可能和我们的直觉认识相冲突,为此我整理了一下常见排序的一次 run(表述不太清楚,欢迎大家的提议和改进
- 选择、冒泡、插入:一遍外层循环
- 希尔排序:一次 \(h_k\)-sort
- 归并排序(以迭代版为例
) :对于整张列表,每 \(2^k\) 个元素进行归并排序,直到排完所有元素后的结果 - 快排:对于整张列表,找到当前能找的所有支点 (pivot) 后的结果(如果不理解,可以回顾一下前面介绍的原理,以及对应的题目)
Sorting Large Structures⚓︎
- 问题:交换大型结构的成本较高
- 解决方案:添加指向结构的指针,然后交换指针,这种方法被称为间接排序 (indirect sorting)。之后若有需要,也可以利用指针进行直接的交换。
表排序 (table sort)
要点
- 我们用
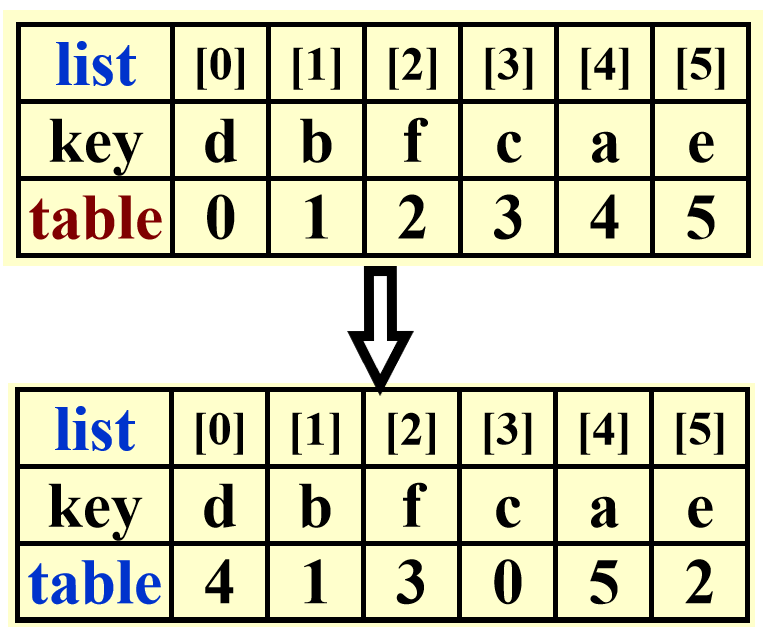
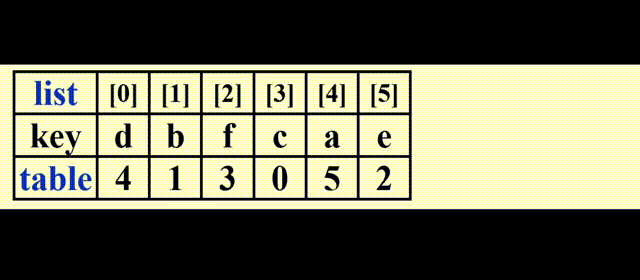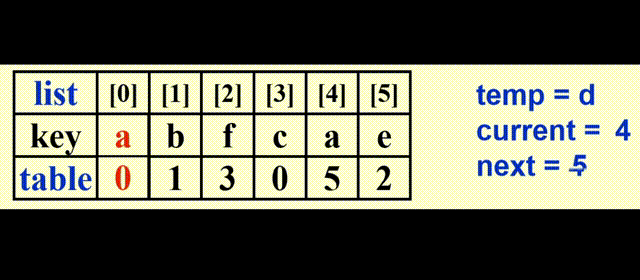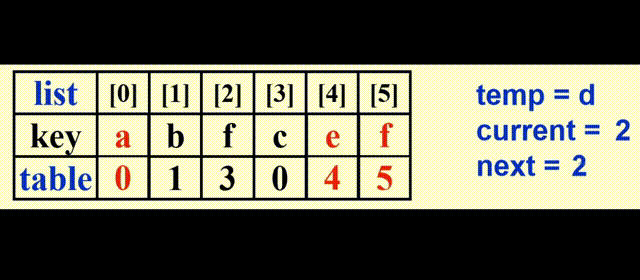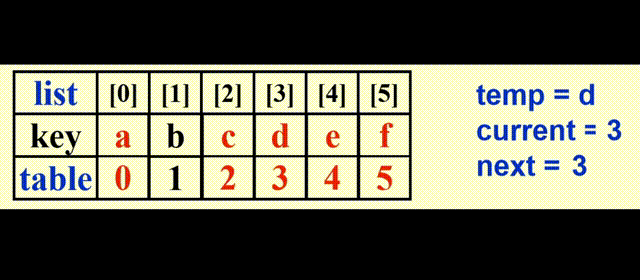
table[]数组存储指针。注意这里的指针不是 C 语言的指针类型,而是数组list[]的索引。初始化为table[i] = i - 对
list[]的内容进行间接排序:我们只需移动指针即可(自己选择一种排序方法排序) - 如何输出排好序的列表:
list[table[0]], list[table[1]], ..., list[table[n-1]]
上图为初始状态,下图为间接排序后的列表
物理排序
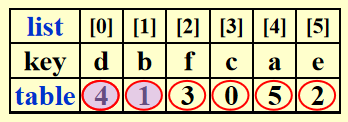
观察 Table 的值,发现这 n 个值的排列是由一些不相交的“环”构成(类似并查集list 进行物理排序(真正地交换元素)
下图打阴影的部分表示 2 个环的“根节点”
最坏情况:有 \(\lfloor \dfrac{N}{2} \rfloor\) 个环,需要 \(\lfloor \dfrac{3N}{2} \rfloor\) 次移动
时间复杂度:\(T = O(mN)\),其中 m 为结构体的大小
General Lower Bound for Sorting⚓︎
定理:任何基于比较进行排序的算法,其最坏情况的计算时间为 \(\Omega(N \log N)\)
证明
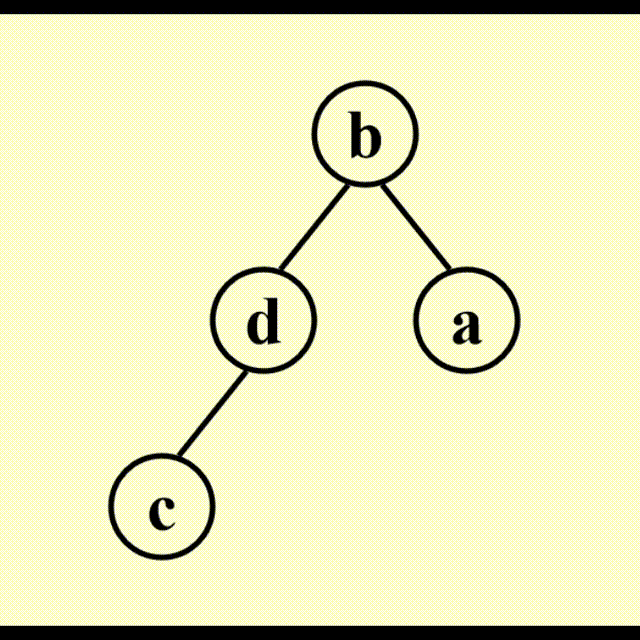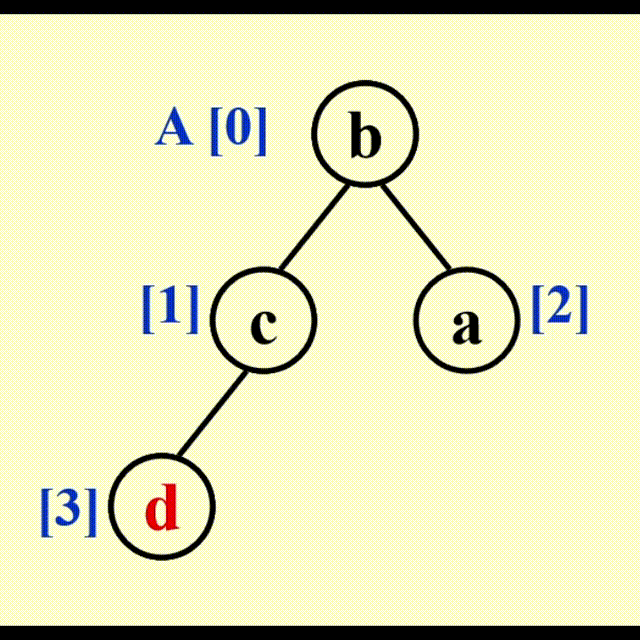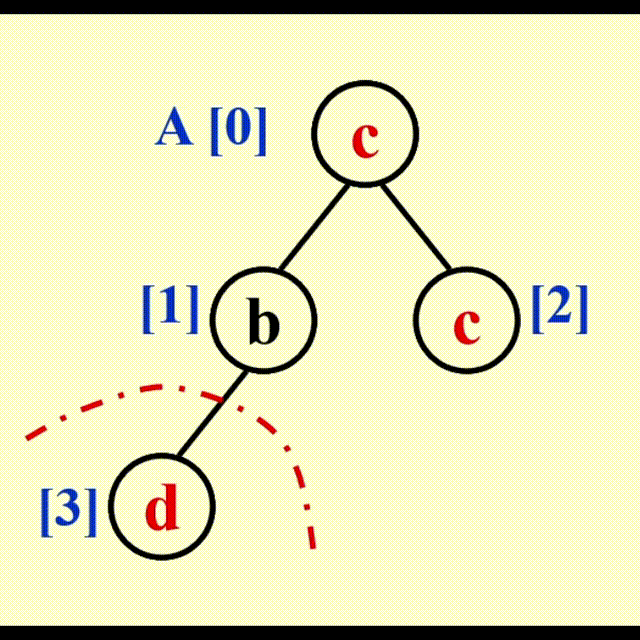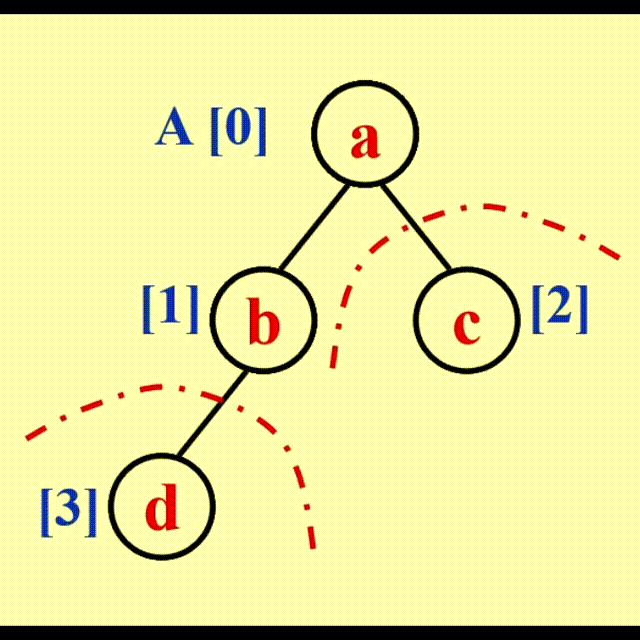
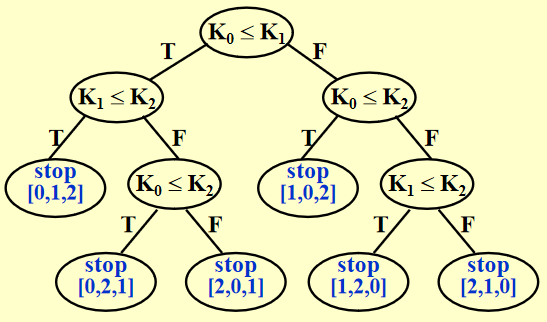
利用决策树 (decision tree)
排序 N 个元素会产生 N! 中不同的可能情况,因此决策树至少有 N! 个叶子节点。若树的高为 k,那么 \(N! \le 2^{k-1}\),所以 \(k \ge \log(N!) + 1\)
\(\because N! \ge (\dfrac{N}{2})^{\frac{N}{2}}\),即 \(\log_2 N! \ge \dfrac{N}{2}\log_2(\dfrac{N}{2}) = \Theta(N \log_2 N)\)
\(\therefore T(N) = k \ge c \cdot N \log_2 N\)
下面我们介绍的排序算法并不是基于比较的
Bucket Sort⚓︎
问题
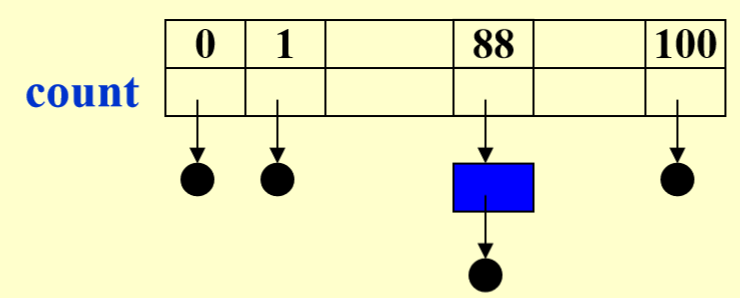
假设有 N 个学生,每个学生有一个在 0-100(因此有 M = 101 可能的不同分数)之间的成绩,那么如何在线性时间内根据他们的乘积进行排序?
图示:
伪代码:
Algorithm
{
initialize count[];
while (read in a student's record)
insert to list count[stdnt.grade];
for (i = 0; i < M; i++)
{
if (count[i])
output list count[i];
}
}
时间复杂度:\(T(N, M) = O(M + N)\)
当 \(M \gg N\) 时,比如 N = 10, M = 1000,如果还想在线性时间内完成排序,桶排序就不太靠谱了——而下面介绍的基数排序将胜任这一问题
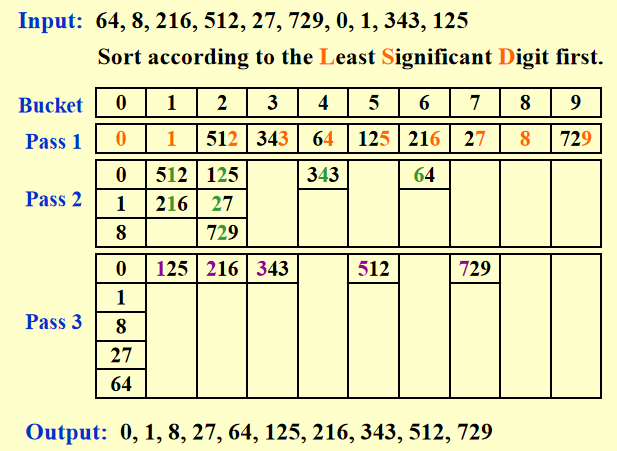
Radix Sort⚓︎
例子
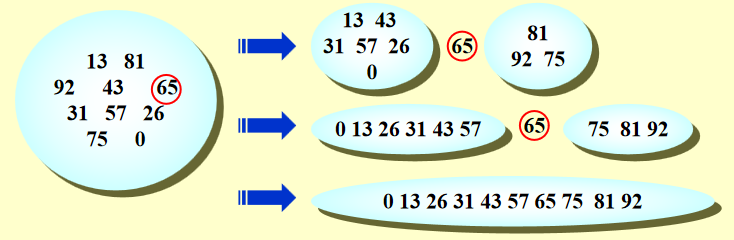
对完全立方数进行排序,采用最低位优先 (least significant digit first)的策略
每一趟后的顺序按从左往右、从上往下的方向读取,比如 Pass 2 后的顺序为:0, 1, 8, 512, 216, 125, 27, 729, 343, 64
时间复杂度:\(T = O(P(N + B))\),其中 \(P\) 为排序的趟数 (pass),N 为元素个数,B 为桶数
分析
假设记录 \(R_i\) 有 r 个键:
- \(K_i^j\):\(R_i\) 的第 j 位
- \(K_i^0\):\(R_i\) 的最高位
- \(K_i^{r-1}\):\(R_i\) 的最低位
对于包含记录 \(R_0, \dots, R_{n-1}\) 的列表,如果满足:
也就是说:\(K_i^0 = K_{i+1}^0, \dots, K_i^l, = K_{i+1}^l, K_i^{l+1} < K_{i+1}^{l+1},\ l < r - 1\) ,则称该列表具有词典序
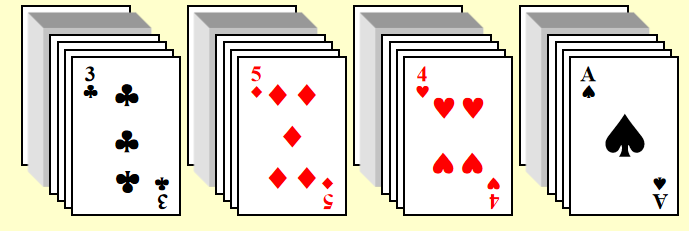
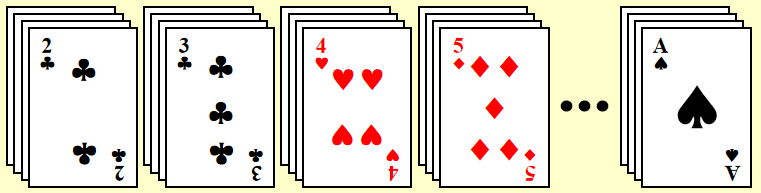
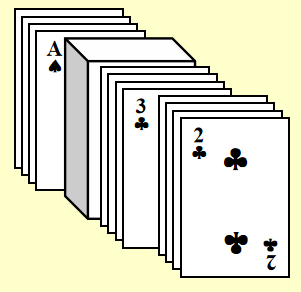
例子
对于一副扑克牌(52 张
评论区