Mistakes in My Homework and Tests⚓︎
Chap 3⚓︎
Question 1:
If a queue is implemented by a circularly linked list, then the insertion and deletion operations can be performed with one pointer rear instead of rear and front.
Answer: T
分析
见下面评论区的回复(学了 ADS 后再看这道题,好像没有整理的必要 (x))
Chap 4⚓︎
Question 1:
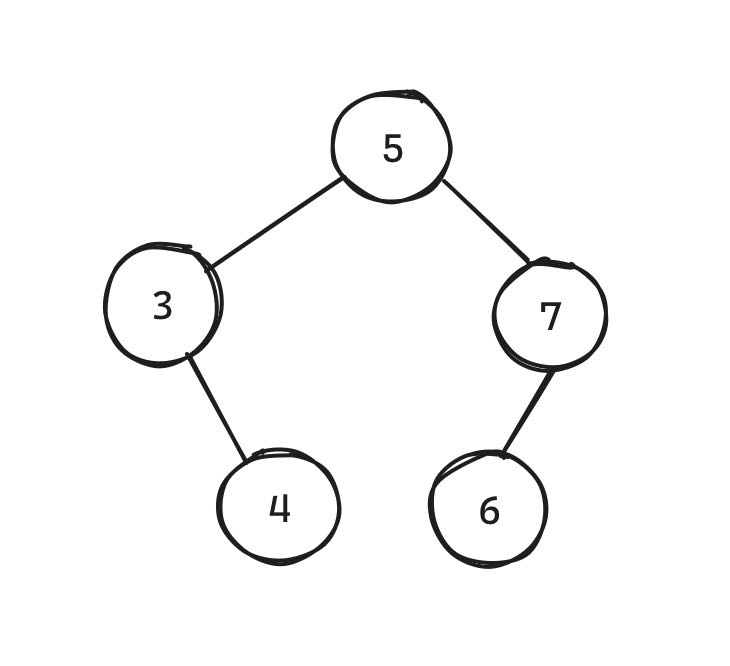
Answer: F
如图所示,5 不必是 4 和 6 的直接父亲,也可以是它们的祖先:
Question 2:
Answer: A
分析
利用离散数学得到的公式:\(n = mi + 1\),可计算内部顶点 i 的个数为 20 个。令这 20 个内部顶点相互连接,使树“退化”为一个类似链表的样子,此时树的高度为 20(算上 1 层叶子节点)
Question 3:
Answer: B
分析
对于节点 \(i\),它的父节点的索引为 \(\lfloor \dfrac{i}{2} \rfloor\)。
对这 2 个节点不断除以 2,列出它们所有祖先节点的索引并比较,最先发现的共同祖先即为题目要求的答案
Question 4:
Answer: T
分析
- 任何树都可以用 FirstChild-NextSibling 表示法来表示
- 而用 FirstChild-NextSibling 表示法得到的树顺时针旋转 45° 就是一棵二叉树了
- 二叉树就可以用一维数组来表示
感谢 @xk0576 同学的分享!
Question 5:
14 distinct binary search trees can be created from 4 distinct keys
Answer: T
分析
问 n 个不同顶点最多构造多少棵不同的 BST,就用卡特兰数做
\(n = 4\),所以 \(C_4 = 14\)
推荐阅读:卡特兰数的 N 种用法
Chap 5⚓︎
Question 1:
Answer: D
分析
- 若没有冲突,平均查找时间为 \(O(1)\)
- 若出现冲突,最坏情况下平均查找时间为 \(O(N)\)
但我们不知道冲突发生的频率和其他情况,因此无法确定总的平均查找时间
Question 2:
Answer: B
分析
不要想太多!
- 线性探测中,篮子个数 b = TableSize,篮子容量 s = 1
- 冲突发生在 7 上(它与 18 冲突
) ,此时已有 5 个元素已放在散列表内 - \(\lambda = \dfrac{5}{11} \approx 0.45\)
Question 3:
Answer: D
Chap 6⚓︎
Question 1:
What is the minimum number of comparisons between heap elements required to construct a max heap of 5 elements using the \(O(n)\) BuildHeap(array)?
A. 2 B. 4 C. 5 D. 3
Answer: B
Chap 7⚓︎
Question 1:
Answer: D
分析
- 第一趟 (run) 快排后,确定一个元素的位置
- 第二趟 (run) 快排后,
- case 1: 若第一趟快排确定的是两边的元素,则本趟确定一个元素的位置
- case 2: 若第一趟快排确定的是中间的元素,则本趟确定两个元素的位置
因此,两趟排序后能够确定 2-3 个元素的位置,我们先找出每个选项中位置正确的元素(加粗表示
- A. 5, 2, 16, 12, 28, 60, 32, 72
- B. 2, 16, 5, 28, 12, 60, 32, 72
- C. 2, 12, 16, 5, 28, 32, 72, 60
- D. 5, 2, 12, 28, 16, 32, 72, 60
可以看到,A 和 B 满足 case 1,C 满足 case 2,而 D 均不满足,因此选 D
这题很考验对快排的理解,如果做不出来应当再巩固相应知识
Chap 8⚓︎
Question 1:
Answer: B
分析
将 16 个元素看成顶点,6 个等价关系看成边,等价类看成连通分量,这样比较容易理解——题目就转化为至少有多少连通分量
每条边(等价关系)连接两个顶点(元素
补充:至多有 16 个等价类,因为任意两个元素之间可以没有任何等价关系
Chap 9⚓︎
Question 1:
Answer: B
Question 2:
Answer: A
分析(q1 & q2)
先读题,q1 问至少有多少个连通分量,而 q2 问至多有多少个连通分量。
q1: 20 条边最多连接 21 个顶点(利用环
q2: 12 条边最少少连接 6 个顶点(利用完全图
Question 3:
Answer: B
分析
还是先读题:题目要求 G不连通
利用完全图的知识,35 条边最少连接 9 个顶点,因此还需再加 1 个顶点,才能使整张图是不连通的,所以共 10 个顶点
Question 4:
Answer: C
分析
见下方评论区回复,建议读者自己画画图推导一下,感觉还是挺简单的(当时的我可能大脑一团浆糊吧)
Question 5:
Answer: C
分析
这个邻接矩阵是对称的,因此表示的是一张无向图,画出来,将每个选项一一带进去验证一下
C 的正确顺序应该是:V5, V1, V3, V6, V2, V4
Question 6:
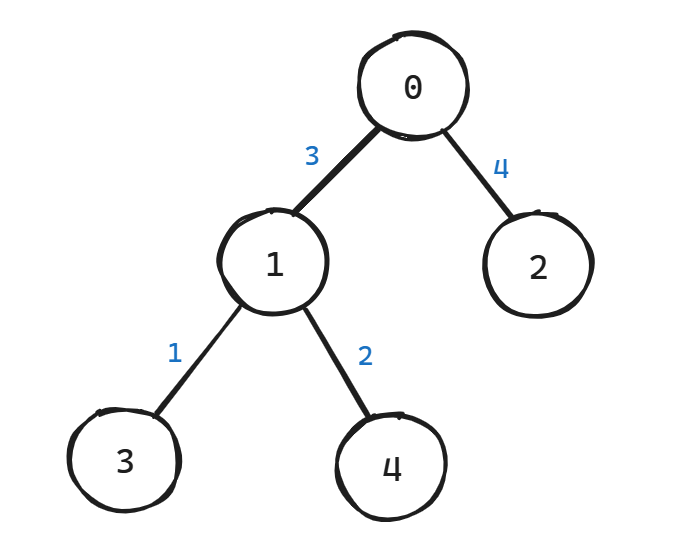
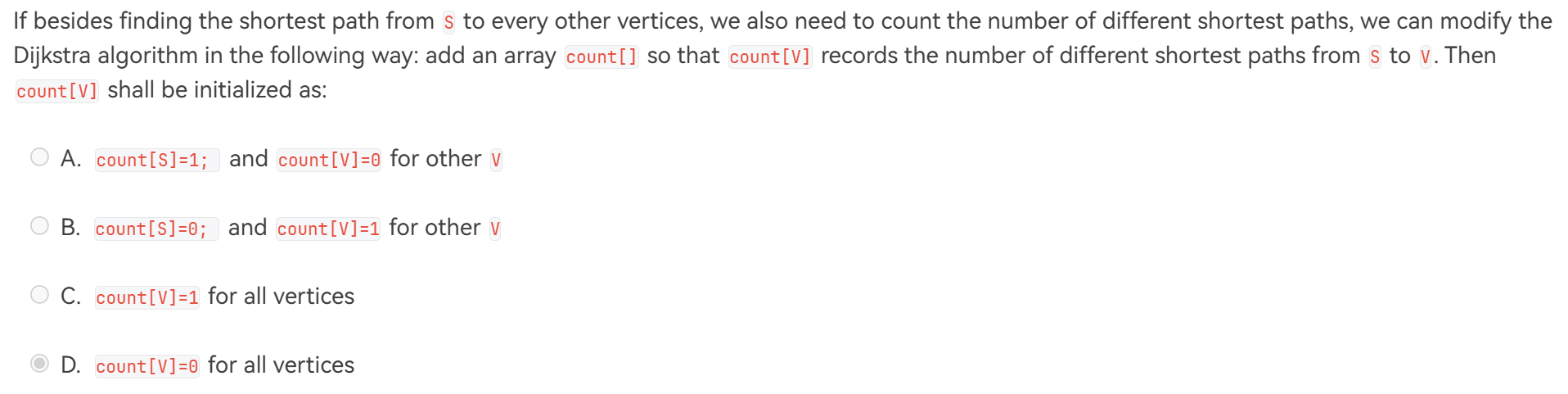
Answer: A
分析
从起点 S 到起点 S 算一条路径,因此初始化count[S] = 1,否则的话根据历年卷(2020-2021)对应的实现代码,与它相邻的顶点的count的值就为 0,这样传递下去后所有的count都为 0 了。
其他顶点的count初始化为 0 就行了,不用多想
Question 7:
To find the minimum spanning tree of graph G(V,E) by Prim’s algorithm, it is possible that the first collected edge is the longest one in E where each edge’s length is different.
Answer: T
分析
假设 |E| = |V| - 1,所有的边都是生成树的边,那么先挑哪一条边都无所谓了
评论区