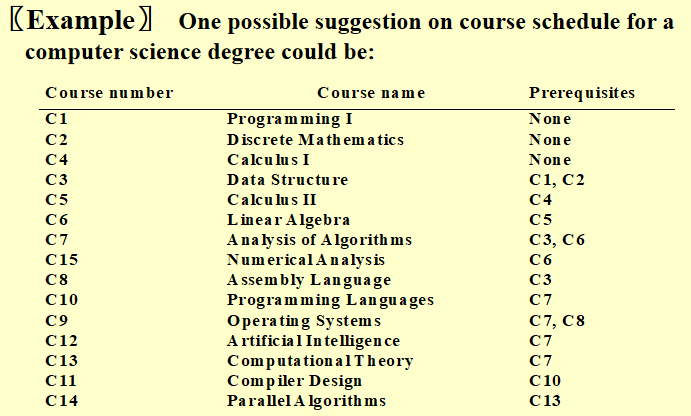
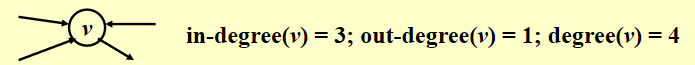Chap 9: Graph Algorithm⚓︎
约 7091 个字 493 行代码 预计阅读时间 42 分钟
核心知识
- 图的定义、性质、表示法
- 拓扑排序(AOV 网)
- 最短路问题
- 无权
- 带正边权:Dijkstra 算法
- 有负边权
- AOE 网
- 网络流
- 解题:流量图、残量图
- 最小生成树 (MST)
- Prim 算法
- Kruskal 算法
- 深度优先搜索 (DFS)
- 基本算法
- 关节点(割点
) 、双连通分量 - 欧拉路、欧拉环
详细的图论知识见离散数学同名章节
Definitions⚓︎
- G(V, E):\(G\) 表示图 (graph),\(V = V(G)\) 表示关于顶点 (vertices)的有限非空集合,\(E = E(G)\) 表示关于边 (edges/arcs)的有限集合
- 无向图 (undirected graph):\((v_i, v_j) = (v_j, v_i)\) 表示相同的边
- 有向图 (directed graph, digraph):\(<v_i, v_j> \ne <v_j, v_i>\)
-
完全图 (complete graph):图上任意两点间都有一条边
-
无向图:\(V = n \quad E = C^2_n = \frac{n(n - 1)}{2}\)
-
有向图:\(V = n \quad E = P^2_n = n(n - 1)\)
-
-
邻接 (adjacent)
-
无向图:如果 \((v_i, v_j)\) 存在,则称 \(v_i, v_j\) 是邻接的
-
有向图:如果 \(<v_i, v_j>\) 存在,则称 \(v_i\) to \(v_j\) 是邻接的,或者说 \(v_j\) from \(v_i\) 是邻接的
-
-
子图 (subgraph) \(G' \subset G\),\(V(G') \subseteq V(G)\) 且 \(E(G') \subseteq E(G)\)
- 从 \(v_p\) 到 \(v_q\) 的路径 (path)(\(\subset G\)):\(\{v_p, v_{i1}, v_{i2}, \dots, v_{in}, v_q\}\),满足 \((v_p, v_{i1}), (v_{i1}, v_{i2}), \dots, (v_{in}, v_q)\) 或者 \(<v_p, v_{i1}>, <v_{i1}, v_{i2}>, \dots, <v_{in}, v_q> \subset E(G)\)
- 路径的长度 (length):路径上边的条数
- 简单路径 (simple path):对于上述路径,\(v_{i1}, v_{i2}, \dots, v_{in}\) 是不同的 ( 不会多次经过同一顶点 )
- 环 (cycle):对于一条简单路径,起点与终点相同,即 \(v_p = v_q\)
-
连通 (connected)
-
无向图:
- 对于两个顶点 \(v_i, v_j\) 而言,如果它们之间存在一条路径,则称它们是连通的
- 对于整张无向图 \(G\) 而言,如果图内任意两点之间相互连通,则称整张图是连通的
对于 \(n\) 个顶点的无向图,最少需要 \(n - 1\) 条边来实现整张图的连通
- 无向图 \(G\) 的(连通)分量 (component):极大连通子图(一张图中可能有多个连通分量)
- 树是连通且无环 (acyclic) 的图
-
有向图:
- 有向无环图 (directed acyclic graph, DAG)
- 强连通 (strongly connected)有向图 \(G\):对于 \(V(G)\) 中的每对顶点 \(v_i, v_j\),存在从 \(v_i\) 到 \(v_j\) 以及从 \(v_j\) 到 \(v_i\) 的有向路径
-
弱连通 (weakly connected)有向图:在不考虑方向的情况下(即无向图
) ,整张图是连通的(即对于 \(V(G)\) 中的每对顶点 \(v_i, v_j\),存在从 \(v_i\) 到 \(v_j\)** 或 ** 从 \(v_j\) 到 \(v_i\) 的有向路径)对于 \(n\) 个顶点的弱连通有向图,最少需要 \(n - 1\) 条边来实现整张图的连通
-
强连通分量 (strongly connected component):极大强连通子图
- 弱连通分量 (weakly connected component):极大弱连通子图
-
-
度 (degree):\(\mathrm{degree}(v)\),与顶点 v 相连的边数
对于一个有向图 \(G\) 而言,度分为入度 (in-degree)和出度 (out-degree),例如:
假如 \(G\) 有 \(v\) 个顶点和 \(e\) 条边,那么 \(e = \dfrac{\sum\limits_{i = 0}^{n - 1}d_i}{2}\),其中 \(d_i = \text{degree}(v_i)\)(握手定理)
对于有向图而言,所有顶点入度之和 = 所有顶点出度之和
Representation of Graph⚓︎
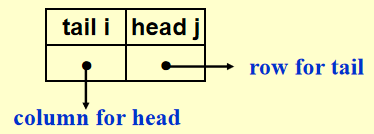
法一:邻接矩阵 (adjacency matrix)
对于一张具有 \(n(n \ge 1)\) 个节点的图 \(G(V, E)\),定义邻接矩阵 \(adj\_mat [i] [j]\) 为
所以也就有:
不难看出,如果 \(G\) 是无向的,则该邻接矩阵是对称的,因此浪费了一半的空间和时间(复杂度:\(\Theta(|V|^2)\)
改进措施:通过将下三角矩阵存入一维数组中,节省了一半的空间
\(adj\_mat[n(n+1)/2] = \{a_{11}, a_{21}, \dots, a_{n1}, \dots, a_{nn}\}\),其中 \(a_{ij}\) 的索引为 \(\dfrac{i(i-1)}{2} + j\)
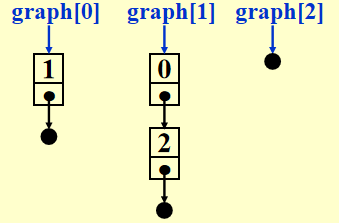
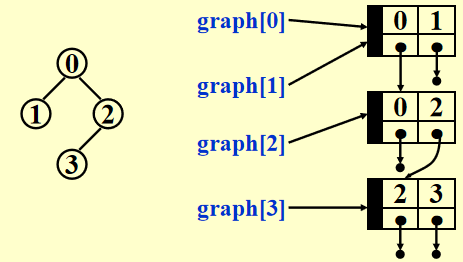
法二:邻接表 (adjacency lists)
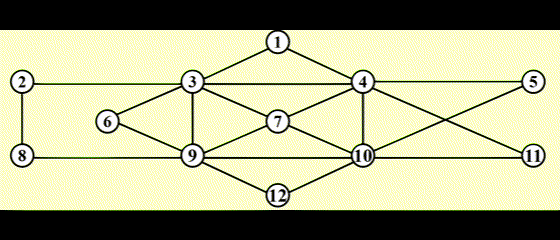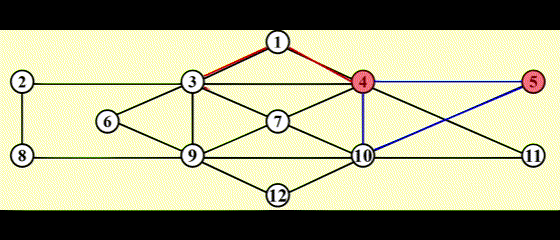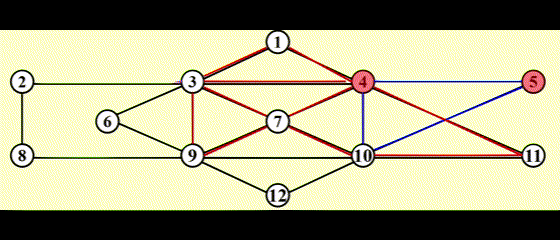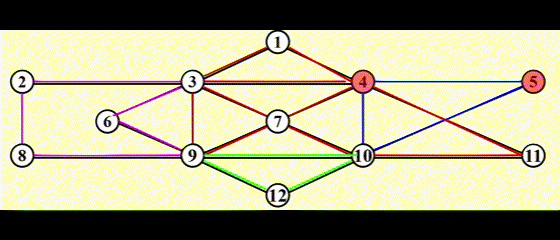
例子
如何存储这张图?
对于无向图 \(G\),邻接表的空间 \(S = n\) 个头 + \(2e\) 个节点 = \((n + 2e)\) 个指针 + \(2e\) 个整型
时间复杂度 \(T = E(G) = O(|V| + |E|)\),适用于稀疏 (sparse) 图(\(|E| < \Theta(|V|^2)\)) 中
注:事实上,邻接表可以胜任各种图的存储
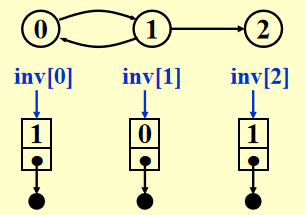
如何计算某个顶点的度
Degree(i) = graph[i] 中节点的个数
我们需要找到 in-degree(i)
-
法 1
: “逆转”邻接链表 -
法 2:用多链表 (multilist)表示邻接矩阵 \(adj\_mat[i][j]\)
众所周知,多链表实现相当复杂,因此更推荐法 1
补充
有时顶点的值不一定是整数,也有可能是字符串,这时需要维护一张从字符串映射到整数索引的表格,在图中用索引代替字符串
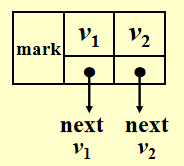
法三:邻接多重表 (adjacency multilist)
注:这个不作要求,了解即可
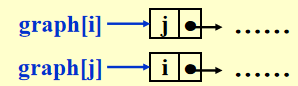
在之前的邻接表里,对于每条边 \((v_i, v_j)\),我们会有两个节点:
通过改进,将这两个节点结合到一起:
于是就有如下表示方法(mark 表示某一条边
最终效果:
观察发现,在没有考虑 mark 存储的情况下,这种表示法的占用空间与邻接表完全一样。虽然它的空间复杂度略微高了点,但是在某些情况下(比如检验某条边后还要检验下一条边)比较有利。
有时,我们会遇到带权边 (weighted edges)的情况,处理方式如下:
- 邻接矩阵:\(adj\_mat[i][j] = \text{weight}\)
- 邻接表 / 邻接多重表:为每个节点添加权重的字段
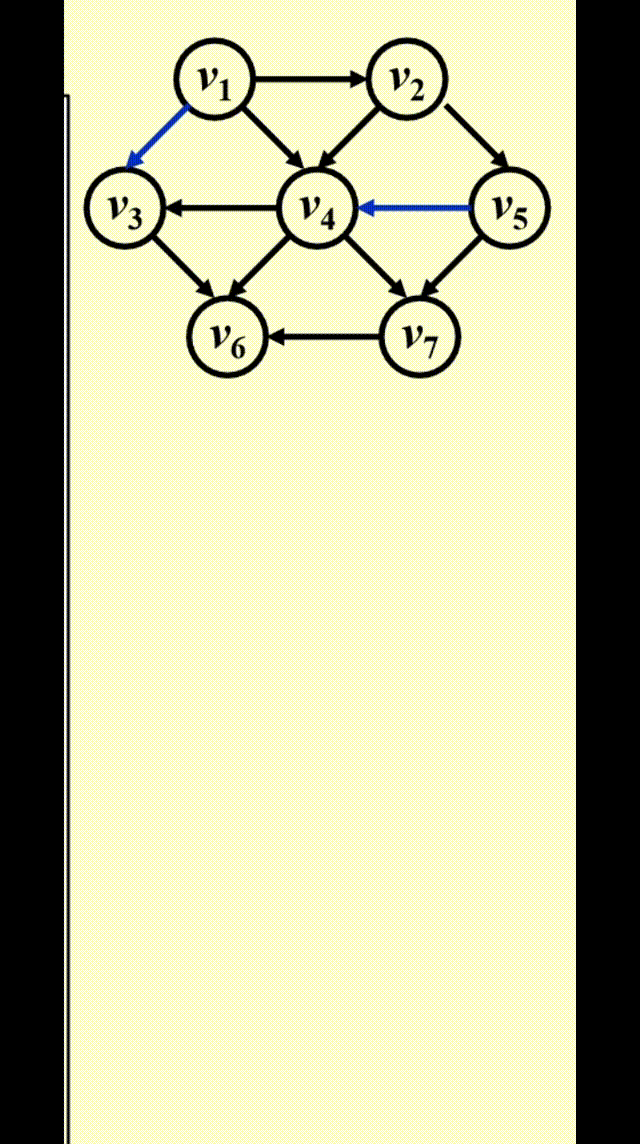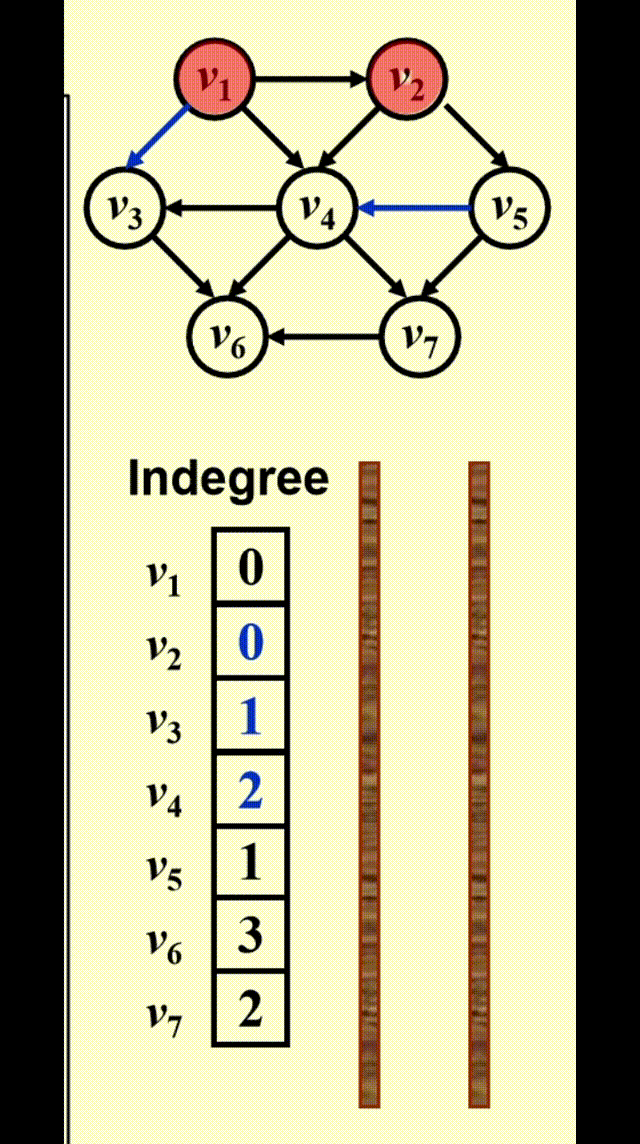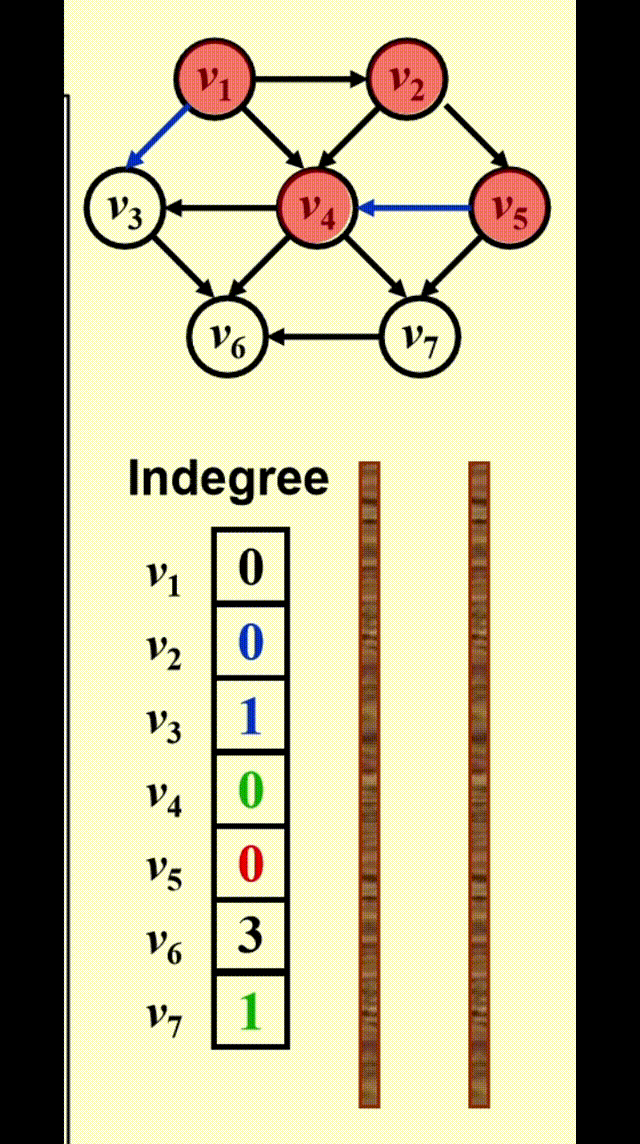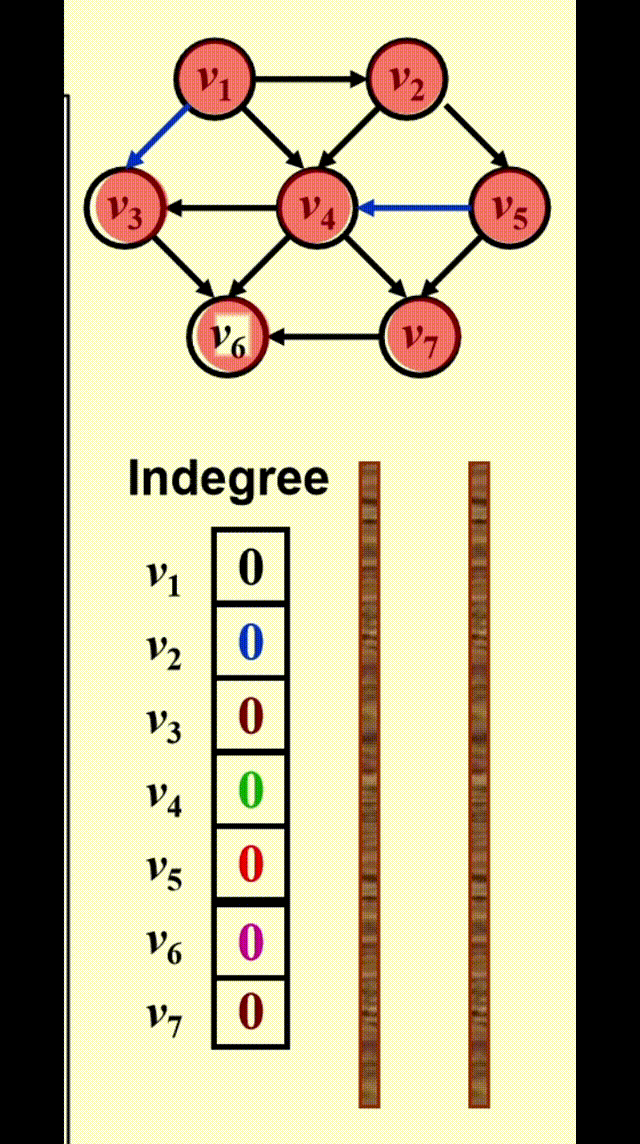
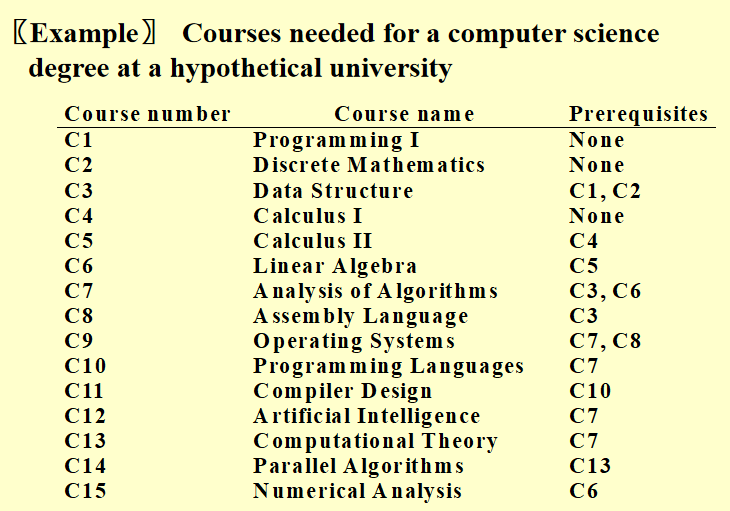
Topological Sort⚓︎
AOV 网 (activity on vertex network):对于有向图 \(G\),\(V(G)\) 表示活动,\(E(G)\) 表示位次关系

- 如果从 \(i\) 到 \(j\) 有一条路径,则称 \(i\) 是 \(j\) 的前任 (predecessor)
- 如果 \(<i, j> \in E(G)\),则称 \(i\) 是 \(j\) 的直接前任 (immediate predecessor)。称 \(j\) 是 \(i\) 的 (直接)后任 ((immediate) successor)
可行的 AOV 网必须是一个有向无环图 (DAG)
补充阅读:AOE 网
偏序 (partial order)是一种具有以下性质的关系
- 反自反性 (irreflexive)(不存在 \(i \rightarrow i\))
- 反对称性 (anti-symmetric)(\((i \rightarrow j) \wedge (j \rightarrow i) \Rightarrow i = j\))
- 传递性(\(i \rightarrow j, j \rightarrow k \Rightarrow i \rightarrow k\))
说明
- 这里的偏序指的是严格偏序,因此和离散数学定义的偏序略有区别
- 如果具有自反性,就会出现要做一件事 \(i\) 之前要完成 \(i\) 的怪圈,因此❌
拓扑序 (topological order)是一张图的顶点的线性顺序,满足:对于任意两个顶点 \(i, j\),如果 \(i\) 是 \(j\) 的前任,则在线性顺序中 \(i\) 要出现在 \(j\) 之前
注:
- 拓扑序不一定是唯一的
- 如果拓扑序中一个顶点出现在另一个顶点的前面,它们之间不一定存在路径
- 可以用拓扑序检验有向图是否存在环
代码实现
// version 1
void Topsort(Graph G)
{
int Counter;
Vertex V, W;
for (Counter = 0; Counter < NumVertex; Counter++)
{
V = FindNewVertexOfDegreeZero(); // O(|V|)
if (V == NotAVertex)
{
Error("Graph has a cycle");
break;
}
TopNum[V] = Counter; // or output V
for (each W adjacent from V)
indegreep[W]--;
}
}
FindNewVertexOfDegreeZero():扫描Indegree[]数组,找到入度为 0 且未赋予拓扑序的顶点,如果没有找到顶点,那么表明图中出现了环- 每处理完一个顶点 V 后,就需要让从 V 出发与 V 邻接的顶点的入度 -1,相当于在图上移除了顶点 V 以及它的所有出边
- 时间复杂度:\(T = O(|V|^2)\) 👎
改进方法:将所有未赋予拓扑序的、度为 0 的顶点放入特殊的盒子(比如队列或 *栈)里
代码实现
// version 2, using queue ADT
void Topsort(Graph G)
{
Queue Q;
int Counter = 0;
Vertex V, W;
Q = CreateQueue(NumVertex);
for (each vertex V)
if (indegree[V] == 0)
Enqueue(V, Q);
while (!isEmpty(Q))
{
V = Dequeue(Q);
TopNum[V] = ++Counter; // assign next
for (each W adjacent from V)
if (--indegree[W] == 0)
Enqueue(W, Q);
} // end-while
if (Counter != NumVertex)
Error("Graph has a cycle")
DisposeQueue(Q); // free memery
}
时间复杂度:\(O(|E| + |V|)\)
Shortest Path Algorithms⚓︎
给定一张有向图 \(G(V, E)\),以及成本函数 \(c(e)\),\(e \in E(G)\),从源 (source)到目的地 (destination)的路径 \(P\) 的长度 (length) 为 \(\sum\limits_{e_i \subset P}c(e_i)\)(也被称为带权路径长度 (weighted path length))
Single-Source Shortest-Path Problem⚓︎
问题
给定一张权重图 \(G(V, E)\),以及一个可区分的顶点 \(s\),寻找从 \(s\) 到 \(G\) 中所有其他顶点的最短权重路径

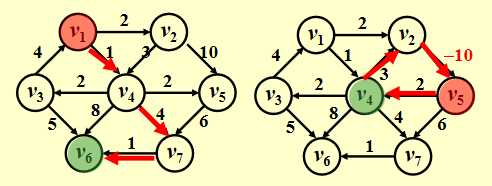
- 右图存在负的边,这样最短路的长度可以是无穷小。因此在这种情况下,最短路是未定义的,因为陷入了死循环。这种循环被称为负值环 (negative-cost cycle)
- 从 \(s\) 到 \(s\) 的最短路径被定义为 0
- 现在,还没有一种最短路算法的速度快于找到从 \(s\) 到所有顶点的路径的算法
Unweighted Shortest Paths⚓︎
在这种情况下,所有边的权重 = 1
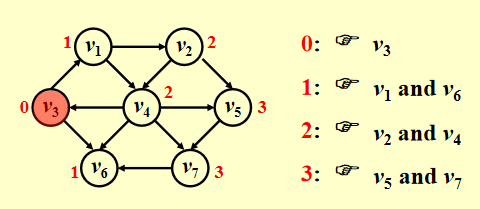
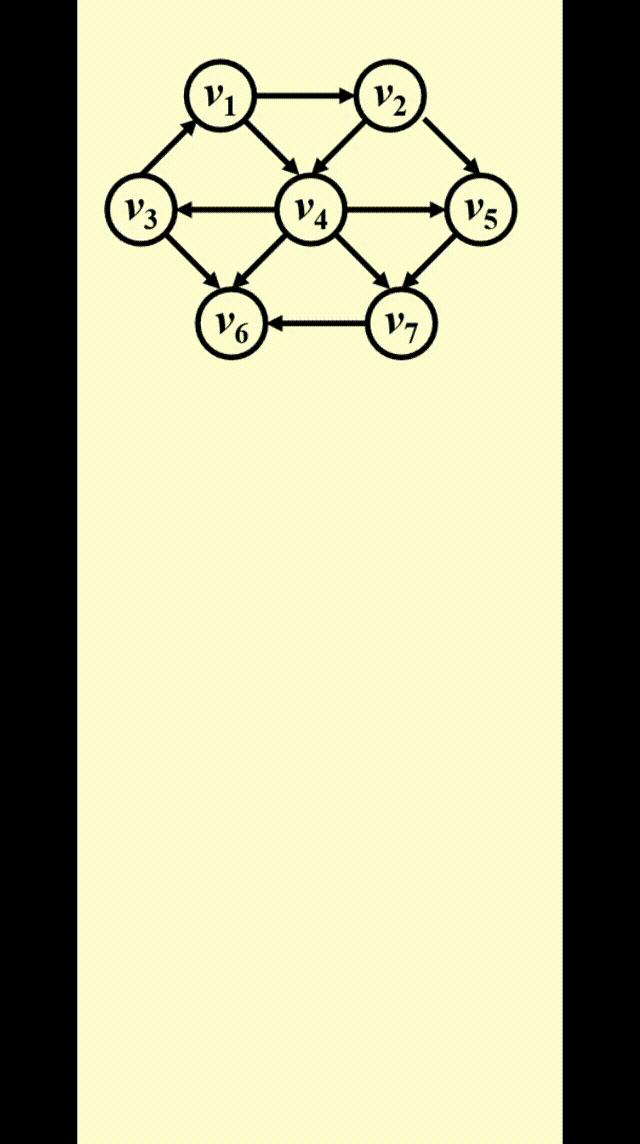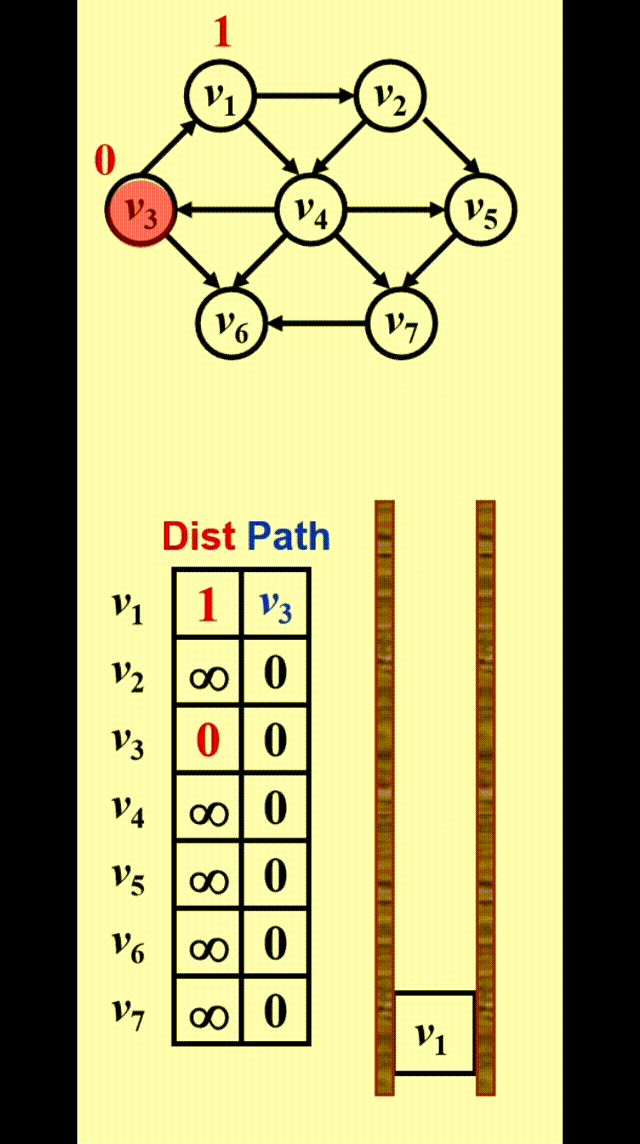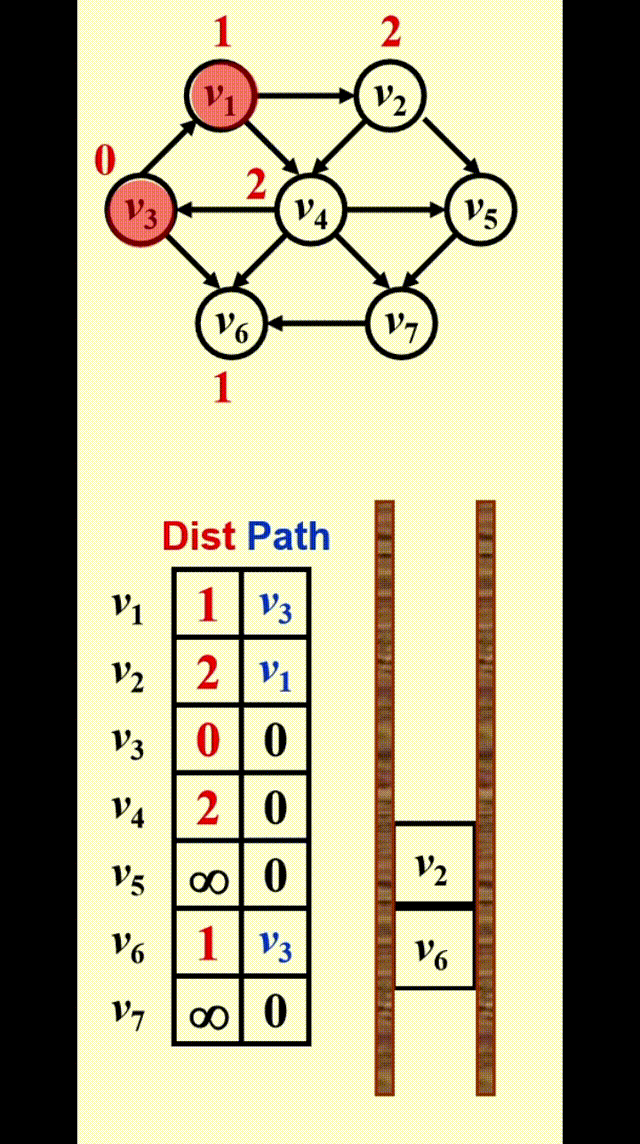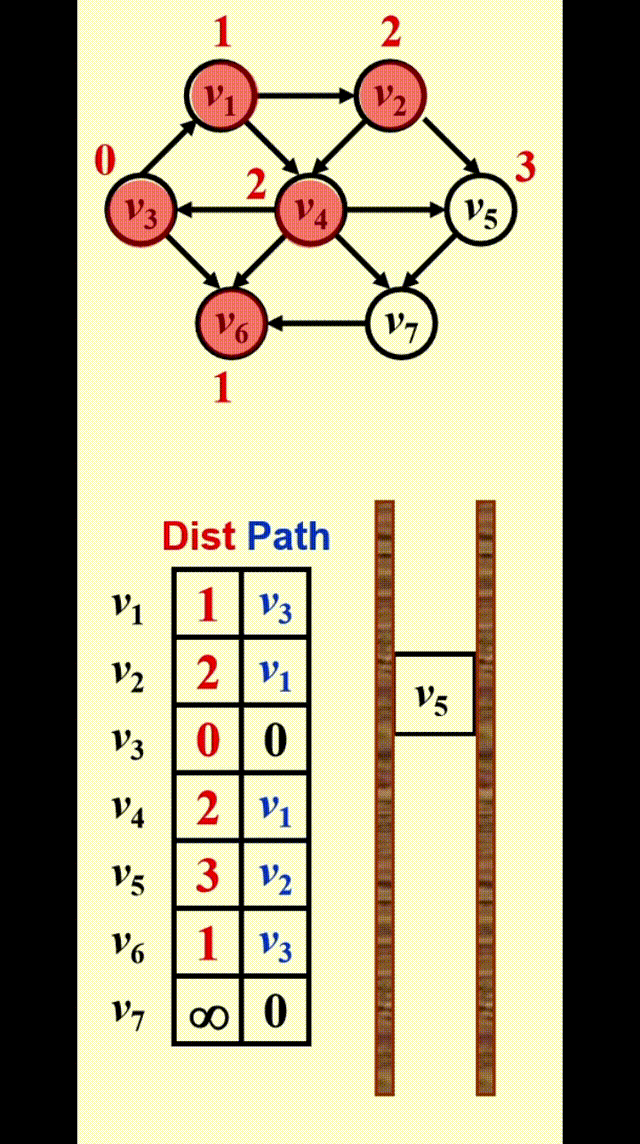
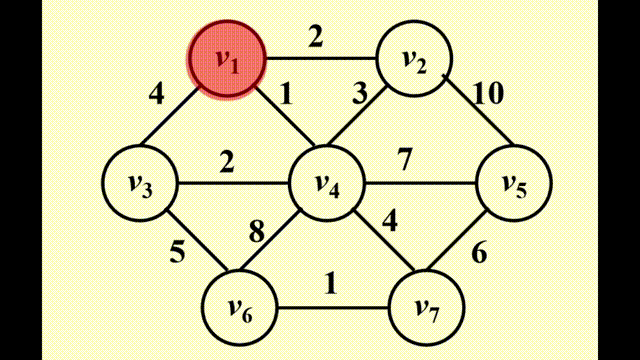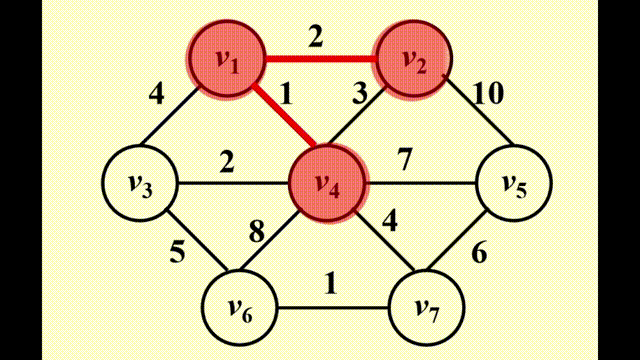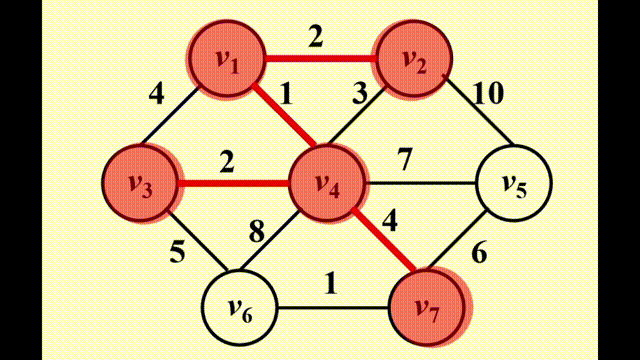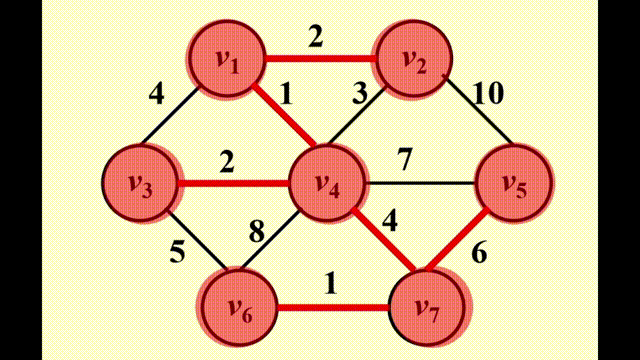
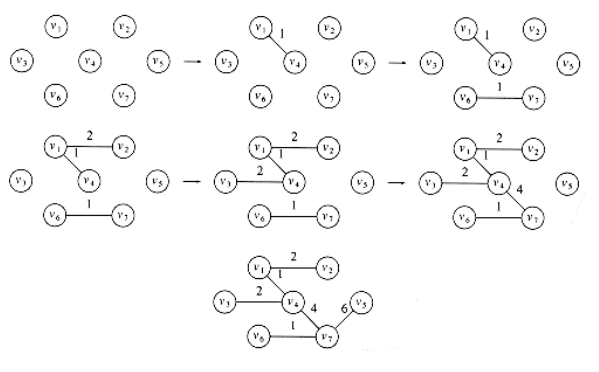
如图所示,为了找到从 \(v_3\) 出发到其他顶点的所有最短路径:
- 先找到与 \(v_3\) 邻接的顶点,记从 \(v_3\) 到这些顶点的最短路径为 1
- 然后再从这些顶点出发,找到与它们邻接的顶点。如果新找到的顶点还没有相应的最短路径,那就记这些顶点的最短路径为 2
- 重复步骤 2,直至所有顶点的最短路径都已找到
这种方法被称为宽度优先搜索 (breadth-first search, BFS):该方法一层层地处理顶点:最近的顶点最先处理,最远的顶点最后处理。这和树中的层序遍历类似
宽度优先搜索的示意图:
实现
-
Table[i].Dist::= 从 \(s\) 到 \(v_i\) 的距离 \(= \begin{cases}\infty & \text{if } v_i \ne s \\ 0 & \text{if } v_i = s\end{cases}\) -
Table[i].Known::= \(\begin{cases}1 \quad \text{if } v_i \text{ is checked} \\ 0 \quad \text{if not}\end{cases}\)
- 其实没有必要设这个字段 ( 因为
Table[i].Dist同时具备标记功能 ),写在这里只是提醒一下要做一下标记- 在初始化中,所有顶点的
Table[i].Known = 0,包括起始顶点,因为没有任何顶点被处理过
Table[i].Path::= 记录路径上 \(v_i\) 的前一个顶点,以便打印整条路径
代码实现
// version 1
void Unweighted(Table T)
{
int CurrDist;
Vertex V, W;
for(CurrDist = 0; CurrDist < NumVertex; CurrDist++)
{
for (each vertex V)
if (!T[V].Known && T[V].Dist == CurrDist)
{
T[V].Known = true;
for (each W adjacent to V)
if (T[W].Dist == infinity)
{
T[W].Dist = CurrDist + 1;
T[W].Path = V; // (*)
}// end-if Dist == Infinity
} // end-if !Known &&Dist == CurrDist
} // end-for CurrDist
}
这个算法显然没什么效率,因为外层循环要循环 NumVertex - 1 次才结束,即使所有的顶点早就处理过了。虽然可以增加一个额外的判断提前结束循环,但这并没有影响最坏情况的运行时间,比如:
起始点为 \(v_9\),第一次循环要找 CurrDist == 0 的顶点(即 \(v_9\)
时间复杂度 \(T = O(|V|^2)\)👎
可以发现,如果顶点 \(V\) 未被标记,但 \(d_v \ne \infty\),那么 \(d_v = CurrDist\) 或 \(d_v = CurrDist + 1\),因此没有必要像上面那个算法一样扫描整个表来找到合适的顶点。
改进思路
用两个箱子,一个箱子放未标记的 \(d_v = CurrDist\) 的顶点,另一个箱子放未标记的且 \(d_v = CurrDist + 1\) 的顶点。那么,原来扫描整张表的操作可以变成:从第 1 个箱子找任一顶点 \(V\),等到 (*) 那行代码执行完后,将 \(W\) 放入第 2 个箱子。等到外层 for 循环一轮结束后,第 1 个箱子为空,将第 2 个箱子的顶点转移到第 1 个箱子,进行下一轮循环。
事实上,我们只需要一个队列就能完成上述改进思路:
这里不用
Known字段是因为Dequeue就代表顶点已经被处理过了,不会再回到队列里
代码实现
// version 2
void Unweighted(Table T)
{
// T is initialized with the source vertex S given
Queue Q;
Vertex V, W;
Q = CreateQueue(NumVertex);
MakeEmpty(Q);
Enqueue(S, Q); // Enqueue the source vertex
while (!IsEmpty(Q))
{
V = Dequeue(Q);
T[V].Known = true; // not really necessary
for (each W adjacent to V)
if (T[W].Dist == Infinity)
{
T[W].Dist = T[V].Dist + 1;
T[W].Path = V;
Enqueue(W, Q);
} // end-if Dist == Infinity
} // end-while
DisposeQueue(Q); // free memory
}
可以看到,这和拓扑排序的算法很像
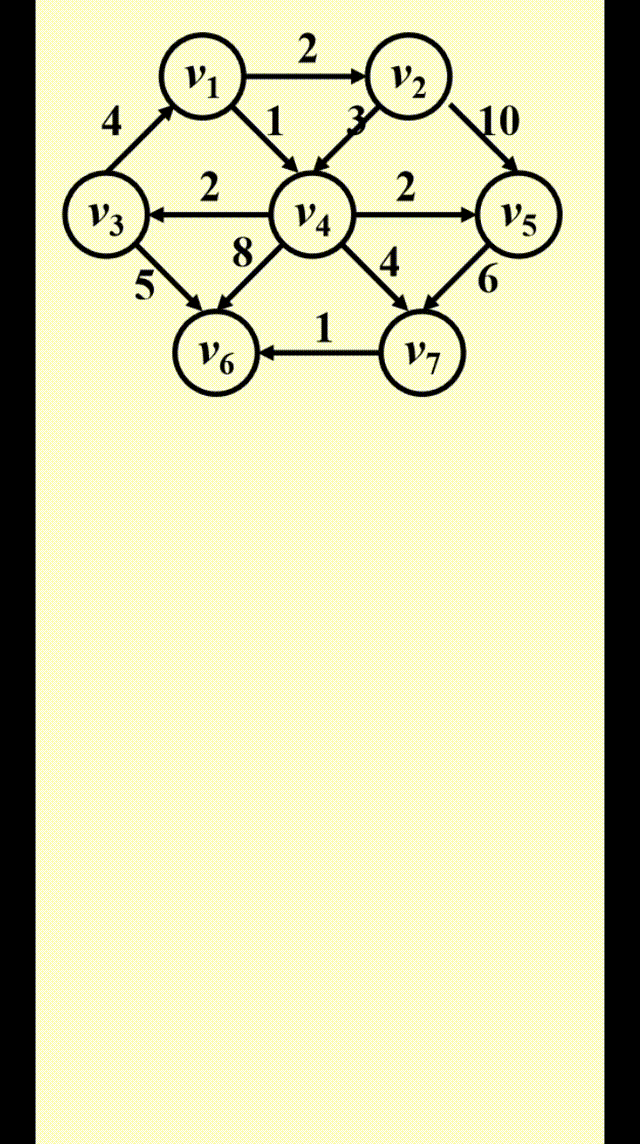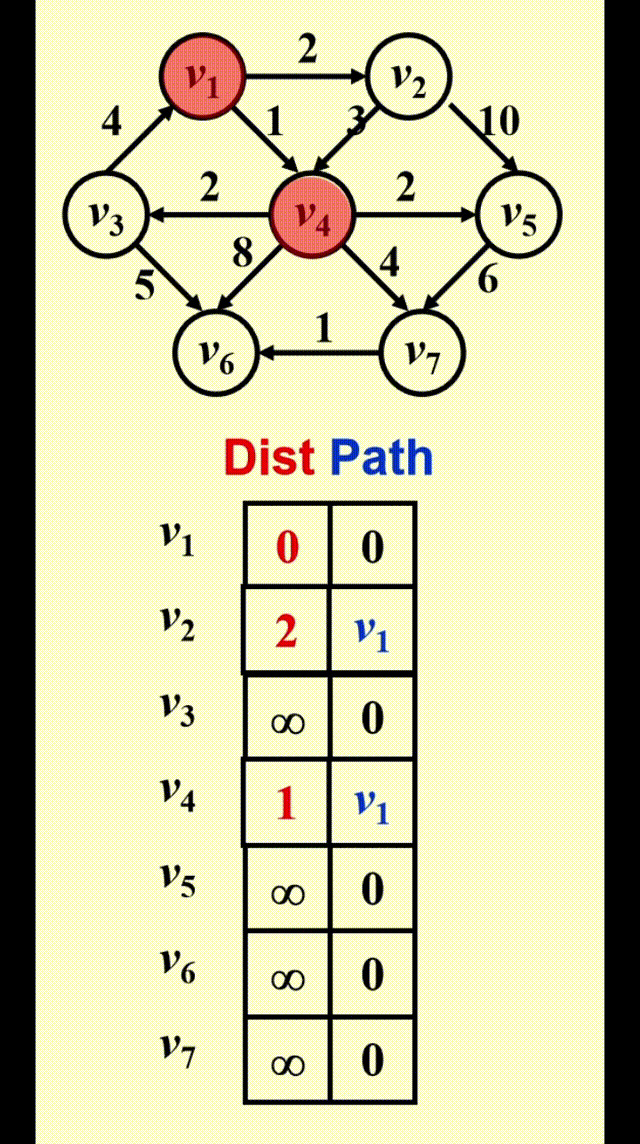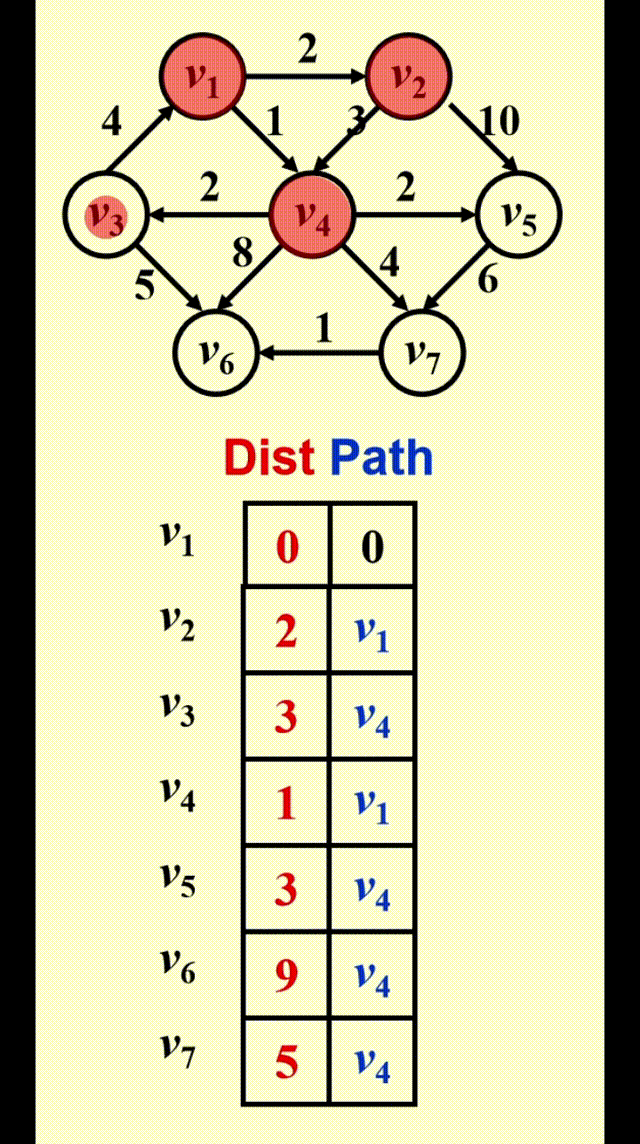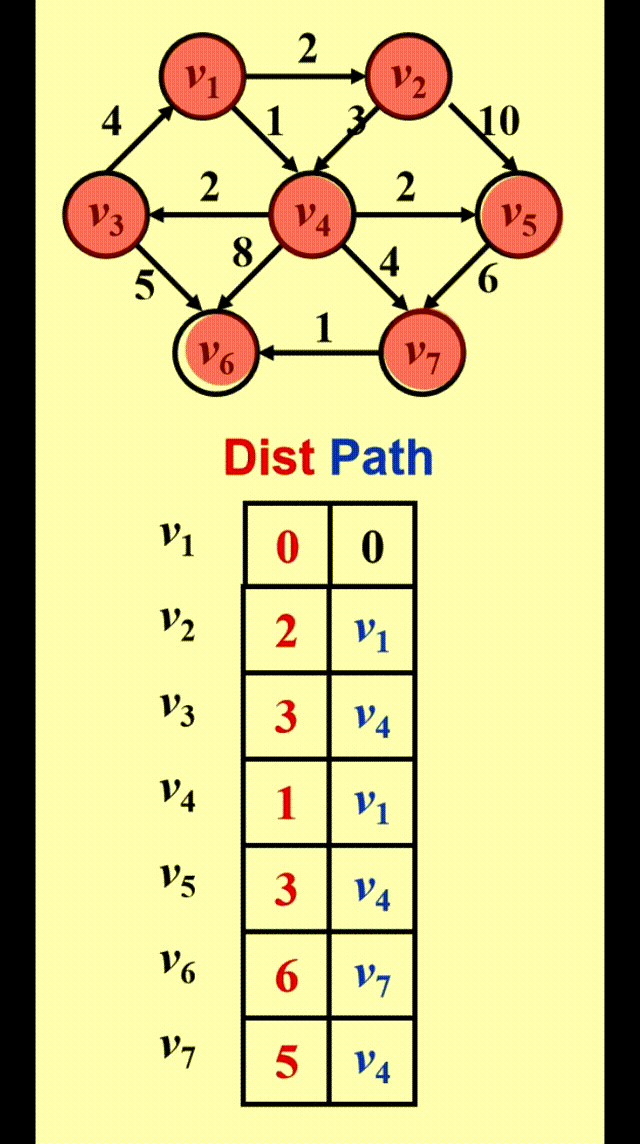
Dijkstra's Algorithm(for weighted shortest paths)⚓︎
Dijkstra 算法的思路
令 \(S =\) {\(s\) 和已找到最短路径的顶点 \(v_i\) 的集合 }。对于 \(\forall u \notin S\),定义distance[u] = 路径 \(\{s \rightarrow (v_i \in S) \rightarrow u\}\) 的最小长度
- Dijkstra 算法按阶段执行,在每个阶段中,挑选一个顶点 \(v\),保证它是所有未被标记的顶点中路径长度 \(d_v\)最短的那个顶点(如果有多个最短路径长度,则任意挑选顶点)
- 对于从顶点 \(v\) 出发的邻接顶点 \(w\),\(d_w = \min(d_w, d_v + c_{v, w})\)
- 标记顶点 \(v\),即令 \(v \in S\)
- 然后对于剩余未被标记的顶点,重复上述操作,直至所有顶点均被标记
不难发现,这是一种贪心算法
预备工作
// Declarations for Dijkstra's algorithm
typedef int Vertex
struct TableEntry
{
List Header; // Adjacency list
int Known;
DistType Dist;
Vertex Path;
};
// Vertices are numbered from 0
#define NotAVerTex (-1)
typedef struct TableEntry Table[NumVertex];
// Initialization
void InitTable(Vertex Start, Graph G, Table T)
{
int i;
ReadGraph(G, T);
for (i = 0; i < NumVertex; i++)
{
T[i].Known = False;
T[i].Dist = Infinity;
T[i].Path = NotAVerTex;
}
T[Start].dist = 0;
}
// Print shortest path to V after Dijkstra has run
// Assume that the path exists
void PrintPath(Vertex V, Table T)
{
if(T[V].Path != NotAVertex)
{
PrintPath(T[V].Path, T);
printf(" to");
}
printf("%v", V) // %v is pseudocode
}
代码实现
void Dijkstra(Table T)
{
Vertex V, W;
for(;;) // O(|V|)
{
V = smallest unknown distance vertex;
if (V == NotAVertex)
break;
T[V].Known = true;
for (each W adjacent to V)
if (!T[W].Known)
if(T[V].Dist + Cvw < T[W].Dist) // 这步操作被称为“松弛”
{
Decrease(T[W].Dist to T[V].Dist + Cvw);
T[W].Path = V;
} // end-if update W
} // end-for(;;)
} // now work for edge with negative cost
Dijkstra 算法的运行时间取决于我们如何寻找距离最短且未被标记的顶点
方法
- 仅仅简单扫描一遍整张表来找到 \(d_v\) 最小的顶点 \(v \rightarrow O(|V|)\);而且外层循环遍历所有顶点,因此时间复杂度为 \(O(|V|^2)\)
- 每条边最多会更新一次,时间复杂度为 \(O(|E|)\),而且与顶点的遍历是独立的
- 因此 \(T = O(|V|^2 + |E|)\),适用于稠密图(此时复杂度相当于线性复杂度)
将距离保存在堆里,调用 DeleteMin 来找到未标记的最小顶点,并且之后不去管它。
那么如何实现算法中的 Decrease(T[W].Dist to T[V].Dist + Cvw); 呢?
DecreaseKey() \(\rightarrow O(\log |V|)\),因此 \(T = O(|V|\log |V| + |E| \log |V|) = O(|E|\log |V|)\),适用于稀疏图
但是,因为堆不能有效支持 Find 操作,当 \(d_i\) 的值发生改变时,它的位置需要维护和更新,用二叉堆实现起来有些麻烦。
如果用到配对堆 (pairing heap),情况就会改善,这种改进不做要求
将更新后的 \(d_w\) 插入堆中,这样的话堆内就会出现多个表示同一顶点的距离。因此在 V = smallest unknown distance vertex; 这一句中,要重复使用 DeleteMin,直到未标记的点出现(标记过的点就扔掉不用DeleteMin 操作,因此在实际运行中可能会变慢。
其他改进方法:斐波那契堆 (Fibonacci heap)
具体实现
void Dijkstra(VType s, Table T, int n) // Finding all the shortest paths
{
VType V, W; // V: the current vertex; W: the vertex adjacent to V
Heap H; // A heap maintaining the shortest unknown vertex
Vertex cur, tmp; // cur: obtaining the information of all adjacent vertice regarding V; tmp: containing new previous vertex adjacent to W
int len, cnt = n; // len: the distance of T[V].dist + the distance between V and W; cnt: used to terminate the loop
H = InitHeap(n, s); // Initialization of the heap
while (cnt > 0)
{
V = DeleteMin(H); // Obtaining the shortest unknown vertex
T[V].Known = 1; // Marking it
cnt--;
cur = G[V]; // Getting all adjacent successors
while (cur != NULL) // Traversing all successors
{
W = cur->vertex; // The current successor
if (!T[W].Known) // If W isn't marked, then try to update it
{
len = T[V].Dist + cur->length; // New distance
if (len < T[W].Dist) // If the new distance is shorter than the previous one, then update it
{
T[W].Dist = len;
if (pos[W] == 0) // If W hasn't been in the heap, then insert it into the heap
Insert(W, len, H);
else // If W is in the heap, then update the distance of W and update the whole heap
DecreaseKey(pos[W], len, H);
T[W].Path = NULL; // Clearing out all previous vertice, because we find the new optimal one
tmp = (Vertex)malloc(sizeof(struct node)); // Insert the new one into the T[W].Path
tmp->vertex = V;
tmp->next = T[W].Path;
T[W].Path = tmp;
}
else if (len == T[W].Dist) // If the new distance is equal to the old one, then just involve the new solution
{
tmp = (Vertex)malloc(sizeof(struct node)); // The same operations
tmp->vertex = V;
tmp->next = T[W].Path;
T[W].Path = tmp;
}
}
cur = cur->next; // Finding the next one
}
}
}
Graphs with Negative Edge Costs⚓︎
如果出现负的边成本,那么我们就不能在使用Known字段标记是否已经处理过某个顶点,因为有可能在第一次处理该顶点之后,又发现更小的路径长度(因为负的边
一种尝试❌
给所有边加上一个相同的正常数,使得所有边的成本为正数
分析:这样做的话,原本包含边数较多的路径,它的成本增长就明显多于边数较少的路径,这就有可能改变最短路径的取法。
然而,若所有边的权重都乘上一个相同的正常数,这不影响最短路的结果
我们用“无权重最短路算法 + Dijkstra 算法”来解决这一问题:
代码实现
void WeightedNegative(Table T)
{
Queue Q;
Vertex V, W;
Q = CreateQueue(NumVertex);
MakeEmpty(Q);
Enqueue(S, Q); // Enqueue the source vertex
while (!IsEmpty(Q)) // each vertex can dequeue at most |V| times
{
V = Dequeue(Q);
for (each W adjacent to V)
if (T[V].Dist + Cvw < T[W].Dist) // no longer once per edge
{
T[W].Dist = T[V].Dist + Cvw;
T[W].Path = V;
if (W is not already in Q)
Enqueue(W, Q);
} // end-if update
} // end-while
DisposeQueue(Q); // free memory
} // negative-cost cycle will cause indefinite loop
- 时间复杂度:\(O(|E| \cdot |V|)\)
- 如果出现负值环,该算法将会陷入无限循环。因此,记录每个顶点的出队次数,发现有顶点出队次数多于 \(|V|\) 次时,就终止程序,这样可以避免这一问题
Acyclic Graphs⚓︎
如果图是无环 (acyclic),我们可以按照拓扑序选择顶点,因为当选择某个顶点后,它的距离不可能因为它前面顶点的入边而减少,这样只需执行一趟算法即可。
时间复杂度 \(T = O(|E| + |V|)\),不需要优先队列
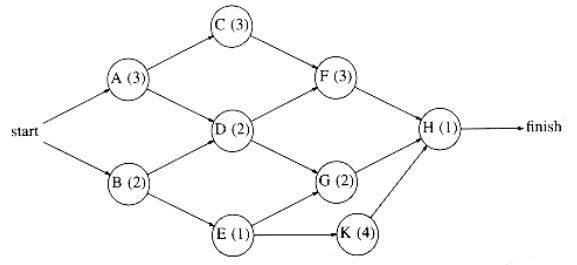
应用:关键路径分析 (critical path analysis)
- AOV 网:每个顶点表示一个活动,且包括需要完成该活动的时间。边 (v, w) 表示 w 完成之前,v 必须完成
-
AOE 网 (activity on edges networks)
表示方法:
注:必要时需要添加 dummy edges 和 dummy nodes,避免错误或缺少的依赖关系产生
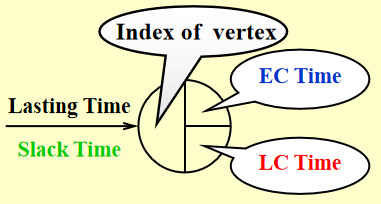
- \(EC[j]\):节点 \(v_j\) 最早的完成时间
- \(LC[j]\):节点 \(v_j\) 最晚的完成时间
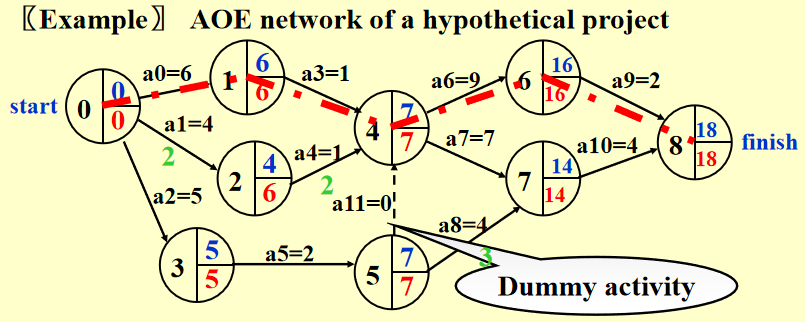
🌰
注:蓝字表示 EC,红字表示 LC,绿字表示空闲时间(后面会讲到)
-
计算 EC:找到第一个事件到最后一个事件之间最长的路
注: 图如果是有环的,因为正成本环 (positive-cost cycles)的存在,这种算法无法实现。然而这里已经规定是无环图,所以无需担心
从起点 \(v_0\) 开始,对于任意的 \(a_i = <v, w>\),我们有
\[ EC[0] = 0 \quad EC[w] = \max\limits_{(v,w) \in E} \{EC[v] + C_{v, w}\} \]按拓扑序计算
-
计算 LC:从终点 \(v_8\) 开始,对于任意的 \(a_i = <v, w>\),我们有
\[ LC[8] = EC[8] \quad LC[v] = \min\limits_{(v,w) \in E} \{LC[v] - C_{v, w}\} \]按逆向拓扑序计算
-
\(<v, w>\) 的空闲时间 (slack time) = \(LC[w] - EC[v] - C_{v, w}\)
- 关键活动 (critical activity):空闲时间为 0 的活动
- 关键路径 (critical path):所有边的空闲时间均为 0 的路径
All-pairs Shortest Path Problem⚓︎
对图中任意一对顶点 \(v_i, v_j(i \ne j)\),要求它们的最短路径,有以下方法:
- 使用 \(|V|\) 次单源算法(比如 Dijkstra
) ,时间复杂度 \(T = O(|V|^3)\),在稀疏图中运行较快 - 用 Chap 10 给出的算法,时间复杂度 \(T = O(|V|^3)\),在稠密图中运行较快,这里就略过了我也不知道是什么算法 (doge)
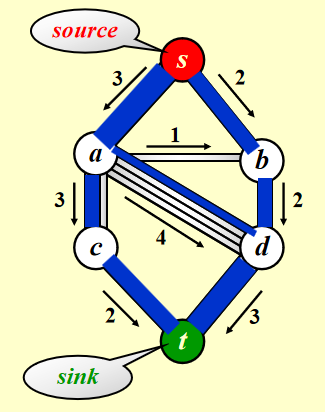
Network Flow Problems⚓︎
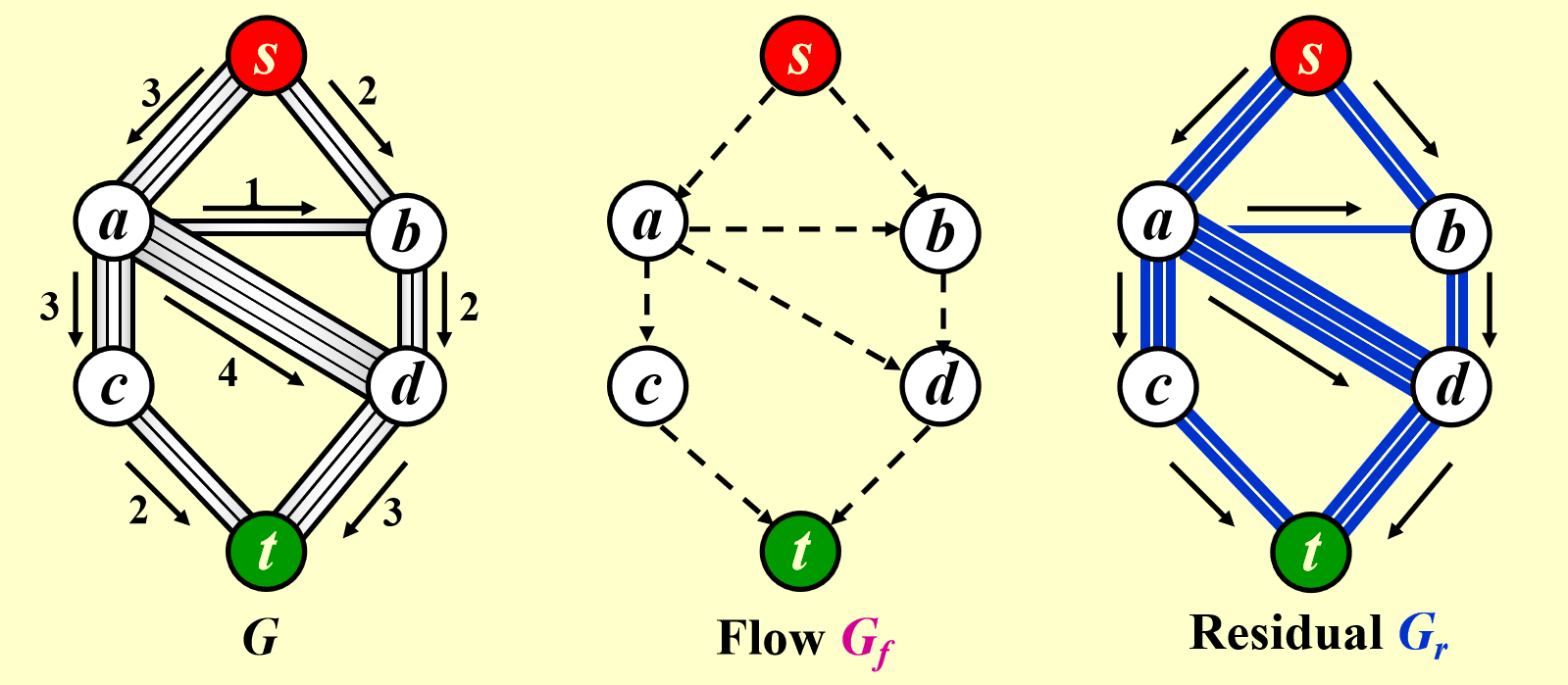
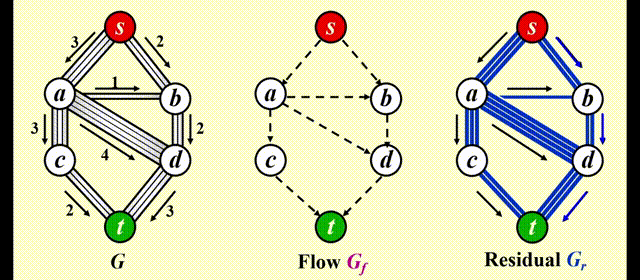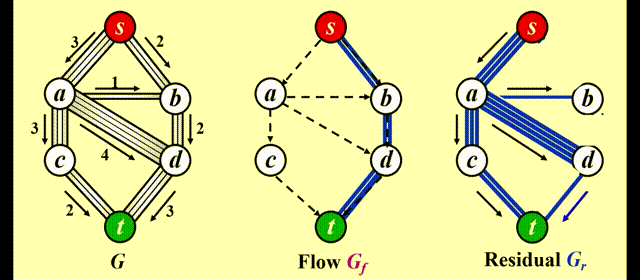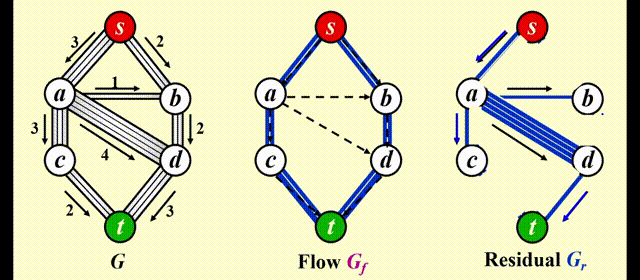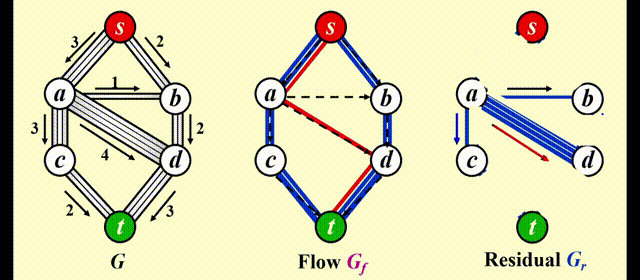
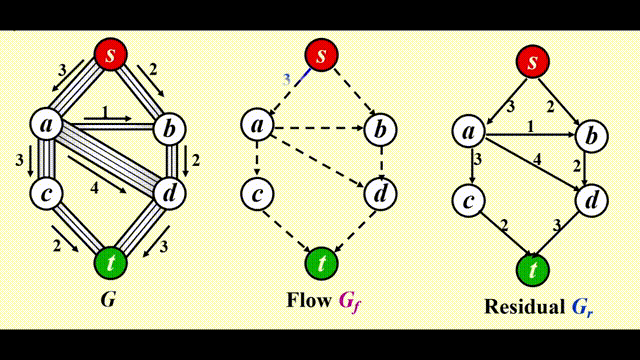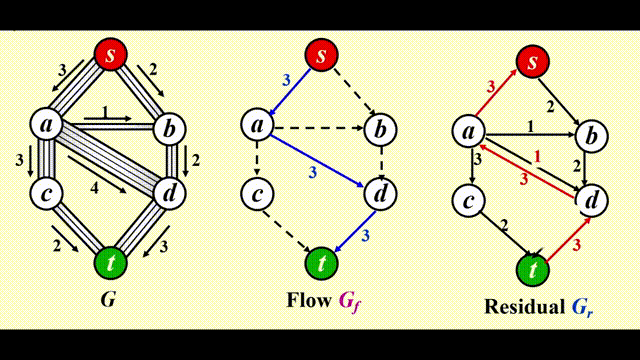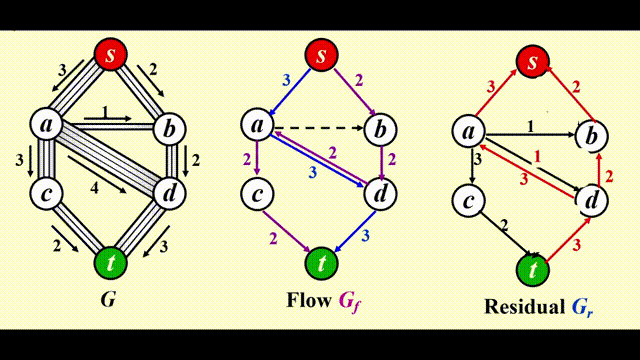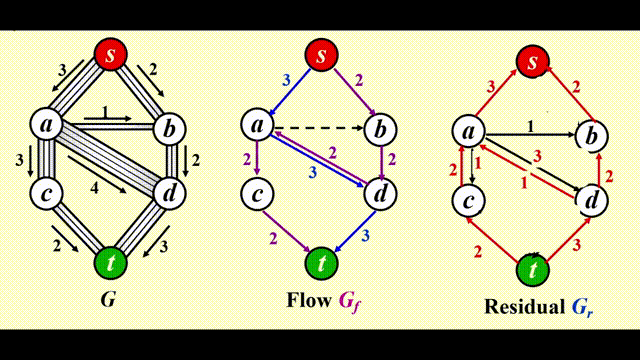
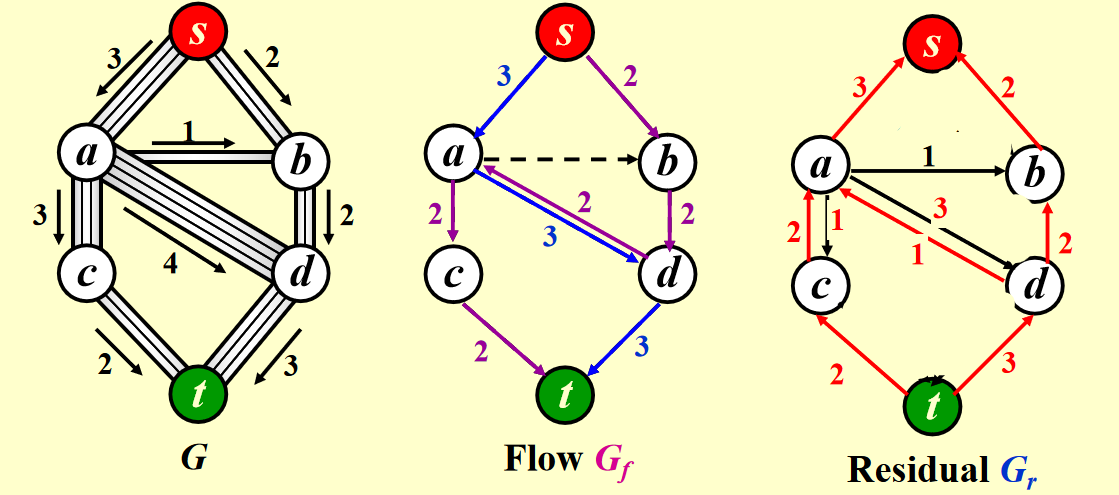
考虑下面的管道网络:
- 这是一个有向图 \(G(V, E)\),每条边的容量 (capacity)为 \(c_{v, w}\),经过该边的流量 (flow)不得超过它的容量
- 我们称起点 s 为源点 (source),终点 t 为汇点 (sink)
- 对于所有顶点 \(v \notin \{s, t\}\),总流入 = 总流出,即 \(\text{Total coming in}(v) \equiv \text{Total going out}(v)\),也就是说顶点不具备存储的能力
🎯:确定从 s 到 t 的最大流 (maximum-flow)
Simple Algorithm⚓︎
注:使用这个算法时,我们需要 3 张图:
- 原图 \(G\)
- 流量 (flow) 图 \(G_f\):表示算法运行的每个阶段中已经得到的流量,初始情况下每条边的流量均为 0
- 残量 (residual) 图 \(G_r\):表示对于图中的每条边,还剩下多少流量可以被添加
步骤
- 在残量图 (residual graph) \(G_r\) 中找一条 \(s \rightarrow t\) 的简单路径,该路径被称为增广路径 (augmenting path)
- 增广路径的流量为路径上的所有边中最小的流量,用该流量更新流量图 (flow graph) \(G_f\)
- 更新 \(G_r\),并移除流量为 0 的边
- 如果 \(G_r\) 中还存在 \(s \rightarrow t\) 的路径,回到步骤 1,否则终止程序
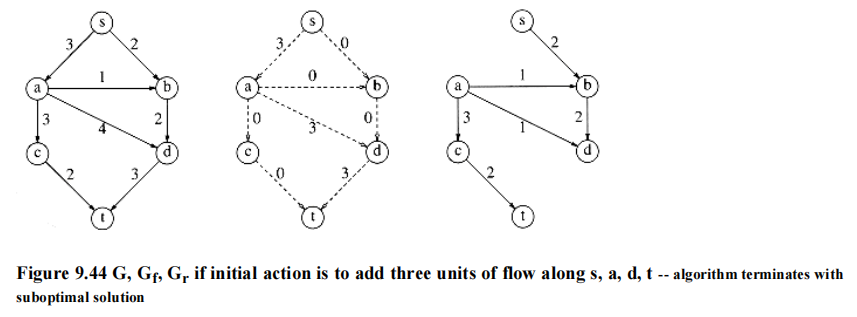
问题
如果我们采用贪心的策略,对于上图,我们会先选择 \(s \rightarrow a \rightarrow d \rightarrow t\),这样得到的流量为 3,如下图所示。然而,这样做的话我们就无法再找到第 2 条路径,因此总流量为 3,不满足要求。因此我们需要改进上述算法。
Solution⚓︎
改进
让算法具备撤销 (undo)决策的能力:对于流量图 \(G_f\) 中的每条边 (v, w),它的流量为 \(f_{v, w}\),在残量图中添加一条反向的边 (w, v),它的流量也为 \(f_{v, w}\)
令 \(f\) 表示图 \(G = (V, E)\) 的流量,则残差图的边的权重为:
最终效果:
注:如果边的容量是有理数,那么该算法在终止时总能得到一个最大流(图有环的话也可以)
Analysis⚓︎
前提:所有边的容量为整数
我们可以利用无权最短路径算法来找到增广路径
时间复杂度 \(T = O(f \cdot |E|)\),\(f\) 表示最大流量
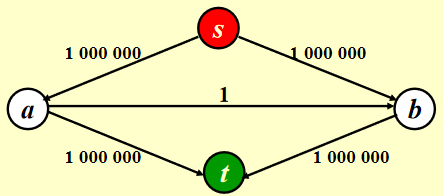
但对于以下特殊情况:
如果我们随机挑选增广路径,挑到一条包括 \(a \rightarrow b\) 的路径,就会产生问题:
Random augmentations could continually augment along a path that includes the edge connected by a and b. If this were to occur repeatedly, 2,000,000 augmentations would be required, when we could get by with only 2.
解决方法
在选择增广路径时,总是挑选对流量提升最大的路径
如何实现:稍微改变一下 Dijkstra 算法
时间复杂度:
在选择增广路径时,挑选边最少的增广路径
时间复杂度:
Supplements⚓︎
- 更优的算法,时间复杂度可以将至 \(O(|E||V|\log(|V|^2/|E|))\) 和 \(O(|E||V| + |V|^{2 + \epsilon})\)
- 对于某些特殊情况,时间复杂度还可以降低:如果除了源点和汇点外的所有顶点的入边容量为 1,或者出边容量为 1,那么最优算法的时间复杂度为 \(O(|E||V|^{\frac{1}{2}})\)
- 更复杂的问题:最小费用流问题 (min-cost flow problem)——每条边不仅有容量,还要考虑单位流量的费用。🎯:要找到所有最大流量中的最小成本
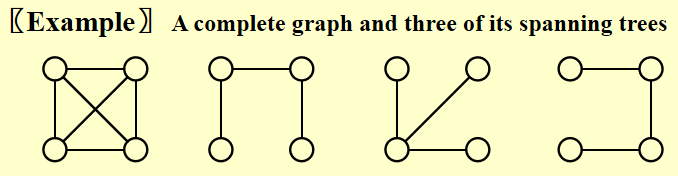
Minimum Spanning Tree⚓︎
定义:图 \(G\) 的生成树 (spanning tree)是一棵包含所有顶点 \(V(G)\)(但不一定包含所有边)的树
🌰:
如何理解最小生成树 (minimum spanning tree)?
-
“树”:无环且边的数量为 |V| - 1
因此当图的边数 < |V| - 1 时,该图不存在最小生成树
-
“最小”:保证生成树的所有边的权重和最小
- “生成”:覆盖所有的顶点
- 最小生成树存在的充要条件是图 \(G\) 是连通的
- 如果在生成树中添加一条边,就会形成一个环
- 最小生成树是并不一定是唯一的,但最小生成树的总权重是唯一的
如何求解?——贪心算法 (greedy algorithm),每一步都采取最优策略,但有以下限制:
- 必须使用图里面的边
- 必须用到 \(|V| - 1\) 条边
- 不能出现环
Prim's Algorithm⚓︎
方法:生成一棵树,与 Dijkstra 算法非常相似,适用于稠密图中
- 初始情况下,先将一个顶点作为树的根放入树内
- 在每个阶段,添加边 (u, v),满足 (u, v) 的权重是来自已有生成树的顶点 u 和来自生成树外的 v 之间的所有边中权重最小的那条,且不产生环,然后将新的顶点 v 添加至树里
- 重复上述步骤,直至所有顶点均在生成树内
与 Dijkstra 不同之处在于:
-
要保存两类值 \(d_v\) 和 \(p_v\):
- \(d_v\):连接 \(v\) 和已知顶点的最短路的权重
- \(p_v\):最后一个导致 \(d_v\) 改变的顶点
-
更新规则更加简单:对于已经选入树内的顶点 \(v\),它的邻接顶点 \(w\) 满足 \(d_w = \min(d_w, c_{w, v})\)
注:由于这是无向图,因此需要用到两张邻接表存储图
时间复杂度:
- 不用堆(适用于稠密图
) :\(O(|V|^2)\) - 二叉堆(适用于稀疏图
) :\(O(E\log|V|)\)
代码实现
/*
* Function: prim
* --------------
* Find a minimum spanning tree for the given undirected
* graph by using Prim's algorithm
*
* w_adj_mat: the weighted adjacency matrix
* n: the number of vertices
*
* returns: the total edge weights of the MST
*/
int prim(int w_adj_mat[MAX][MAX], int n)
{
int dist[MAX]; // distance from vertex i to the known part
int prev[MAX]; // for tracing the edges of MST
int known[MAX]; // 1 if the vertex i is checked, 0 if not
// initialization
for (int i = 0; i < n; i++)
{
dist[i] = INFINITY;
prev[i] = -1;
known[i] = 0;
}
dist[0] = 0; // start from vertex 0
for (int k = 0; k < n; ++k)
{
// choose the vertex closest to the known part
int min_d = INFINITY;
int min_v = -1;
for (int i = 0; i < n; i++)
{
if (!known[i] && dist[i] < min_d)
{
min_d = dist[i];
min_v = i;
}
}
// relaxation of vertices adjacent to the chosen one
known[min_v] = 1;
for (int i = 0; i < n; i++)
{
if (!known[i])
{
if (w_adj_mat[min_v][i] && dist[i] > w_adj_mat[min_v][i])
{
dist[i] = w_adj_mat[min_v][i];
prev[i] = min_v;
}
}
}
}
// total edge weights
int total_w = 0;
for (int i = 1; i < n; ++i)
total_w += dist[i];
return total_w;
}
Kruskal's Algorithm⚓︎
方法:维持一片森林(一组树
- 初始情况下,有 \(|V|\) 棵单个节点构成的树
- 添加一条边,可以合并两棵树。当算法结束时,应当只剩下一棵树。因此,我们很自然地想到使用并查集的算法
-
挑选边(这里假设挑选边 \((u, v)\) )时要注意的细节:
- 如果 u, v 在同一个集合内,则不能添加这条边(否则会出现环)
- 否则加入这条边,使用
Union算法将两个集合合并起来 - 用堆维护未被检验过的最小的边,每当检验一条边时,使用
DeleteMin算法
图示:
伪代码实现:
void Kruskal(Graph G)
{
T = { };
while (T contains less than [V] - 1 edges && E is not empty)
{
choose a least cost edge(v, w) from E; // DeleteMin
delete(v, w) from E;
if ((v, w) does not create a cycle in T)
add(v, w) to T; // Union/Find
else
discard(v, w);
}
if (T contains fewer than [V] - 1 edges)
Error("No spanning tree");
}
正式代码实现
void Kruskal(Graph G)
{
int EdgesAccepted;
DisjSet S;
PriorityQueue H;
Vertex U, V;
SetType Uset, Vset;
Edge E;
Initialize(S);
ReadGraphIntoHeapArray(G, H);
BuildHeap(H);
EdgeAccepted = 0;
while (EdgesAccepted < NumVertex - 1)
{
E = DeleteMin(H); // E = (U, V)
Uset = Find(U, S);
Vset = Find(V, S);
if (Uset != Vset)
{
// Accept the edge
EdgesAccepted++;
SetUnion(S, Uset, Vset);
}
}
}
由于每条边要存 3 个字段,因此用指针数组存储边可能更加高效。
时间复杂度:\(T = O(|E|\log |E|) = O(|E| \log |V|) \quad (|E| = O(|V|^2))\)
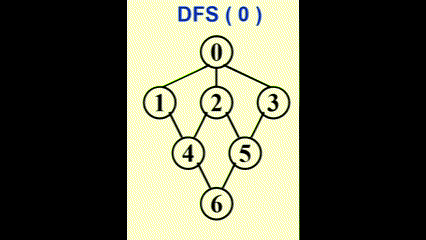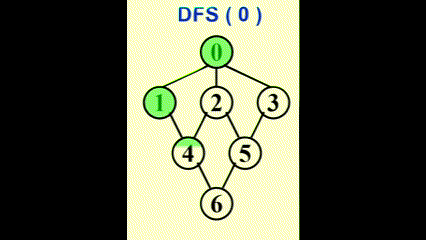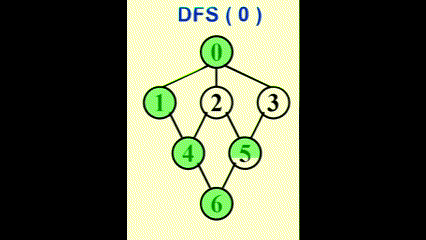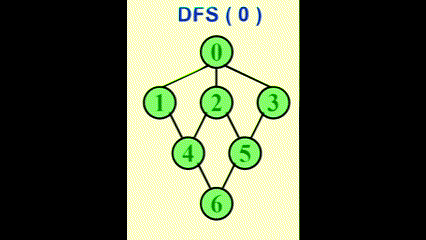
Applications of Depth-First Search⚓︎
深度优先搜索 (depth-first search, DFS)是一种前序遍历的泛化
- 树:时间复杂度 \(T = O(|E|)\ (|E| = \Theta(|V|))\)
- 图:注意要避免环 (cycles),所以访问过的顶点就要对其标记,然后接着访问未访问过的顶点。
- 如果无向图不连通,或者有向图不是强连通的,那么用一次 DFS 无法访问所有顶点,需要对未标记的顶点再用一次 DFS,直至所有顶点都被标记。因此,时间复杂度为 \(O(|E| + |V|)\)
示意图:
代码模板(递归版)
注
DFS 也可以用迭代方法实现,具体来说我们可以用一个栈来存放正在探索的路径上的顶点,当要探索另一条路径时,就把不在该路径上的节点从栈内弹出,然后放入在该路径上的节点。
Undirected Graphs⚓︎
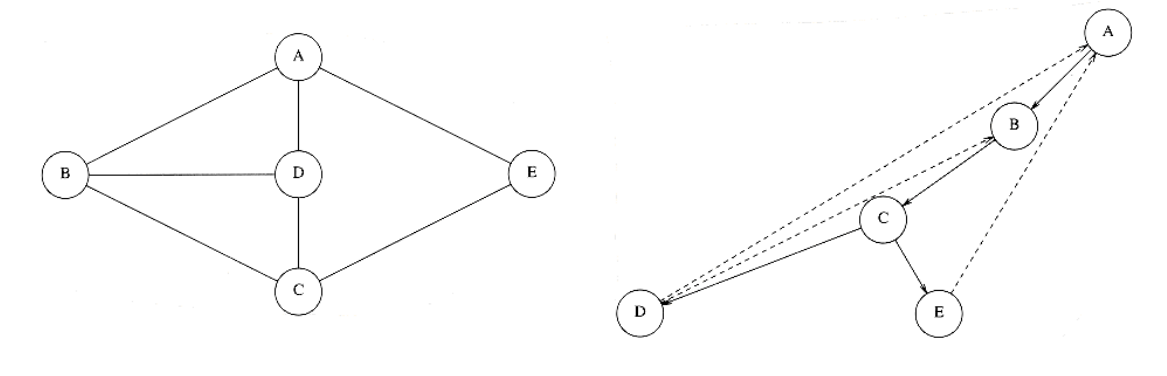
当且仅当 1 次 DFS 能够遍历所有顶点时,无向图是连通的
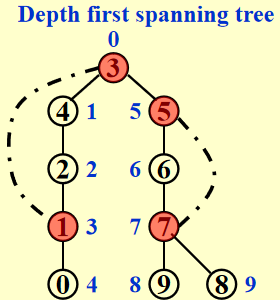
我们可以使用深度优先生成树 (depth-first spanning tree)来形象展示 DFS 的过程。当我们发现某条边 (v, w) 中的 w 已被标记过,用虚线画出这条边,称作“回边 (back edge)”,表示这条边不包含于生成树里,如图所示:
如果无向图不连通,则可以生成深度优先生成森林 (depth-first spanning forest)
代码实现:
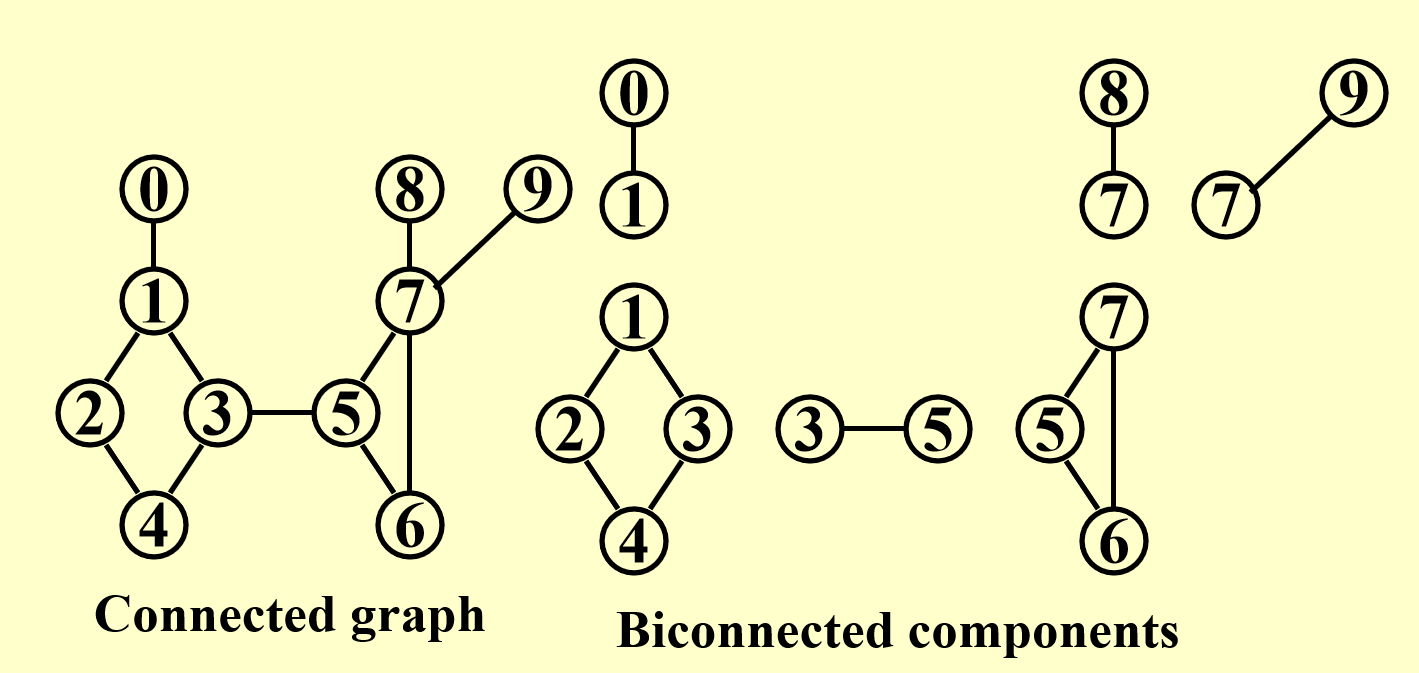
Biconnectivity⚓︎
-
当
G' = DeleteVertex(G, v)至少有 2 个连通分量时,称v为关节点 (articulation point)或者割点 (cut vertex)换句话说,关节点的移除能够破坏图的连通性
-
没有关节点的连通图
G被称为双连通图 (biconnected graph)注:之所以被称为双连通图,是因为至少需要移除两个及以上的顶点,才能形成有多个连通分量的子图
-
双连通分量 (biconnected component):极大双连通子图
注:没有一条边会同时出现在多个双连通分量中。因此 E(G) 被双连通分量划分,而双连通分量又被关节点划分
问题
寻找无向连通图 G 中的双连通分量的个数 = 关节点的个数 + 1
解决方法
如果题目给出一张图,叫我们找出所有关节点,这只要对每个顶点进行判断(假设移除某个顶点后,会不会多一些连通分量
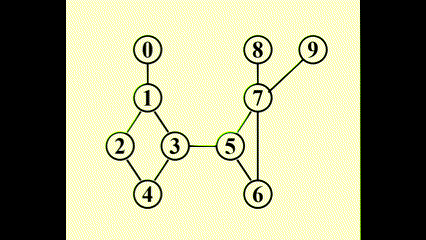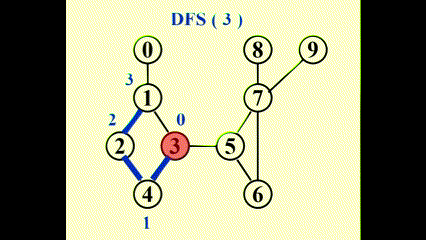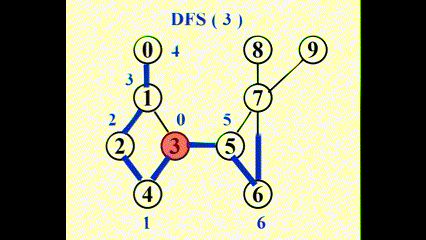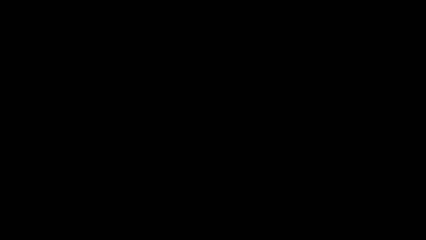
用到的变量:
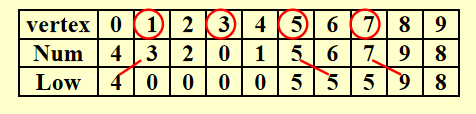
Num(v):顶点 v 的 DFS 序号Low(v):生成树中顶点 v 的所有孩子节点以及 v 回边上的顶点中Num的最小值 (\(\min(Num(w_i))\))(用到后序遍历)
-
使用深度优先搜索 (depth first search)得到 G 的生成树
我们得到:
回边 (back edges)(u, v):在图中而不在生成树内的边 (u, v),它反映了 u 和 v 之间有祖辈和后辈的关系。如果 u 是 v 的祖先,则
Num(u) < Num(v);反之Num(u) > Num(v)Low(u)的计算公式:\[ \begin{align} Low(u) = & \min\{Num(u), \min\{Low(w)\ |\ w \text{ is a child of }u\} \notag \\ & , \min\{Num(w)\ |\ (u, w) \text{ is a back edge}\}\} \notag \end{align} \]表格(记录了
Num(v)和Low(v)) : -
找到 G 内的关节点
- 当且仅当根节点至少有 2 个孩子时,根节点为关节点
- 当且仅当除根节点外的顶点 u至少有 1 个孩子,且该孩子与它的祖先之间没有回边(即
Low(child) >= Num(u))时,u 为关节点
代码实现
// Assign Num and compute Parents
void AssignNum(Vertex V)
{
Vertex W;
Num[V] = Counter++;
Visited[V] = ture;
for each W adjacent to V
if (!Visited[W])
{
Parent[W] = V;
AssignNum(W);
}
}
// Assign Low; also check for articulation points
void AssignLow(Vertex V)
{
Vertex W;
Low[V] = Num[V]; // Rule 1
for each W adjacent to V
{
if (Num[W] > Num[V])
{
AssignLow(W);
if (Low[W] >= Num[V])
printf("%v is an articulation point\n", v);
Low[V] = Min(Low[V], Low[W]); // Rule 3
}
else if (Parent[V] != W)
Low[V] = Min(Low[V], Num[W]); // Rule 2
}
}
// Testing for articulation points in one depth-first search
void FindArt(Vertex V)
{
Vertex W;
Visited[V] = True
Low[V] = Num[V] = Counter; // Rule 1
for each W adjacent to V
{
if (!Visited[W])
{
Parent[W] = V;
FindArt(W);
if (Low[W] >= Num[V])
printf("%v is an articulation point\n", v);
Low[V] = Min(Low[V], Low[W]); // Rule 3
}
else if (Parent[V] != W)
Low[V] = Min(Low[V], Num[W]); // Rule 2
}
}
Euler Circuits⚓︎
- 欧拉路 (Euler tour):在笔不离纸的情况下,图上的每条边均被遍历一遍(一笔画)
- 欧拉环 (Euler circuit):在笔不离纸的情况下,图上的每条边均被遍历一遍,且最后回到起点的位置
判断方法:
- 无向图:
- 当且仅当图是连通的,且每个顶点的度为偶数时,存在欧拉环
- 当且仅当图是连通的,且仅有两个顶点的度为奇数时,存在欧拉路
- 有向图:
- 当且仅当图是弱连通的,且每个顶点的出度 = 入度时,存在欧拉环
- 当且仅当图是弱连通的,且有且仅有一个顶点的出度 = 入度 + 1,有且仅有一个顶点的入度 = 出度 + 1,其余顶点的出度 = 入度时,存在欧拉路
利用DFS寻找欧拉环:
- 用链表维护路径
- 对于每个邻接表,维护一个指向最后被扫描的边
- 时间复杂度 \(T = O(|E| + |V|)\)
补充:哈密顿环 (Hamilton cycle)
无向图中能够访问所有顶点的环。
代码实现
#include <stdio.h>
#include <stdlib.h>
#define SIZE 201
#define PSIZE 2001
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
int AdjV;
PtrToAdjVNode Next;
};
typedef struct Vnode{
PtrToAdjVNode FirstEdge;
} AdjList[SIZE];
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv;
int Ne;
AdjList G;
};
typedef PtrToGNode LGraph;
void HCycle(LGraph g, int p[ ]);
int main()
{
int n, m, k, q;
int i, j;
int v1, v2;
int path[PSIZE];
LGraph Graph;
PtrToAdjVNode cur1, cur2;
Graph = (PtrToGNode)malloc(sizeof(struct GNode));
scanf("%d%d", &n, &m);
Graph->Nv = n;
Graph->Ne = m;
for (i = 0; i < n; i++)
{
Graph->G[i].FirstEdge = NULL;
}
for (i = 0; i < m; i++)
{
scanf("%d%d", &v1, &v2);
cur1 = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
cur1->AdjV = v2;
cur1->Next = Graph->G[v1 - 1].FirstEdge;
Graph->G[v1 - 1].FirstEdge = cur1;
cur2 = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
cur2->AdjV = v1;
cur2->Next = Graph->G[v2 - 1].FirstEdge;
Graph->G[v2 - 1].FirstEdge = cur2;
}
scanf("%d", &k);
for (i = 0; i < k; i++)
{
scanf("%d", &q);
for (j = 0; j < q; j++)
scanf("%d", &path[j]);
if (q != Graph->Nv + 1)
printf("NO\n");
else
HCycle(Graph, path);
}
return 0;
}
void HCycle(LGraph g, int p[ ])
{
int i;
int flag[SIZE];
PtrToAdjVNode cur;
if (p[0] != p[g->Nv])
{
printf("NO\n");
}
else
{
for (i = 0; i < g->Nv; i++)
flag[i] = 0;
for (i = 1; i < g->Nv + 1; i++)
{
if (flag[p[i - 1] - 1] == 1)
{
printf("NO\n");
return;
}
cur = g->G[p[i - 1] - 1].FirstEdge;
while (cur != NULL && cur->AdjV != p[i])
cur = cur->Next;
if (cur == NULL)
{
printf("NO\n");
return;
}
flag[p[i - 1] - 1] = 1;
}
printf("YES\n");
}
}
评论区