跳转至

Chap 5: Hashing⚓︎

约 2199 个字 210 行代码 预计阅读时间 14 分钟

核心知识
  • 散列函数
  • 单独链表法
  • 开放地址
    • 线性探测
    • 二次探测
    • 双重散列法
  • 再散列
引入：插值排序 (interpolation sort)

在 Chap 7 中，我们介绍了一些基于比较的排序算法，这类算法的最优时间复杂度为 \(O(n \log n)\)，然而这不是排序算法的极限——插值排序为我们提供了时间复杂度仅为 \(O(1)\) 的方法，其本质为基于公式的搜索 (search by formula)。

题目：从有序列表 f[l].key, f[l+1].key, ..., f[u].key 中找到特定的 key

General Idea⚓︎

简单表 (symbol table) ADT

  • Objects：一组 " 名称 + 属性 " 对的集合，集合中的每个名称是唯一的

  • Operations：

    • SymTab Create(TableSize)
    • Boolean IsIn(symtab, name)
    • Attribute Find(symtab, name)⭐
    • SymTab Insert(symtab, name, attr)⭐
    • SymTab Delete(symtab, name)

散列表 (hash tables)

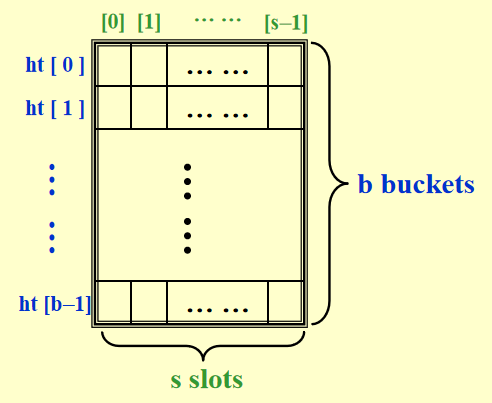
对于每个标识符 x，我们定义一个散列函数 (hash function) f(x)，用来表示 x 在 ht[] 的位置，即下图中包含 x 的篮子 (bucket) 的索引

  • T 表示标识符的总数
  • n 表示 ht[] 中（即已排好序的）标识符的总数
  • 标识符密度 (identifier density) = \(\dfrac{n}{T}\)
  • 加载密度 (loading density)\(\lambda = \dfrac{n}{s \cdot b}\)

散列表的常见问题

  • 冲突 (collision)：2 个不同的标识符放入相同的篮子内，即 \(f(i_1) = f(i_2)\) 且 \(i_1 \ne i_2\)
  • 溢出 (overflow)：某个（些）篮子的空间已满，无法安置新的标识符

    注：当篮子容量 s = 1 时，冲突和溢出同时发生

Example

若没有溢出，散列表的主要操作的时间复杂度均为常数级，即：

\[ T_{search} = T_{insert} = T_{delete} = O(1) \]

Hash Function⚓︎

散列函数 f 的性质：

  • f(x) 必须容易计算，且能最小化冲突的可能
  • f(x) 不能有 " 偏见 "，能够将所有的键平均分配至散列表内，也就是说： \(\forall x,\ \forall i\)，\(f(x) = i\) 的概率为 \(\dfrac{1}{b}\)。这样的散列函数被称为统一散列函数 (uniform hash function)

一些散列函数

\[f(x) = x\ \%\ TableSize\]

x 为整数

这不是一个好的散列函数，因为用这种函数很容易发生冲突。然而，若我们让 \(TableSize\) 为一个质数，且令所有的键尽可能随机，冲突就不那么容易发生了

\[f(x) = (\sum x[i])\ \%\ TableSize\]

x 为字符串

这是前一种函数的变种，用于字符串的情况，\(\sum x[i]\) 为所有字符的 ASCII 码之和。这种方法也很简单，也很容易产生冲突

\[f(x) = (x[0] + x[1] * 27 + x[2] * 27^2)\ \%\ TableSize\]

x 为长度为 3 的英文字符串（全大写或全小写）（27 = 26 个字母 + NULL( 空 )）

这是对前一种函数的改良，把每个字符串表示为一个唯一的 27 进制数。这确实能完全避开冲突，然而实际长度为 3 的英语单词的个数远少于散列表的篮子个数，从而导致空间的巨大浪费

\[f(x) = (\sum x[N - i - 1] * 32^i)\ \%\ TableSize\]

如果我们将 27 改成 32，则用左移 5 位的运算替代乘以 26 的运算，效率更高 ( 移位的速度大于乘法 )。由于是左移位，所以需要稍微调整一下散列值的表示，如下图所示

代码： 

Index Hash3(const char *x, int TableSize)
{
    unsigned int HashVal = 0;
    while (*x != '\0')
        HashVal = (HashVal << 5) + *x++;
    return HashVal % TableSize;
}
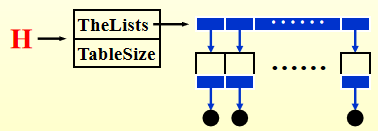
缺点：若字符串 x 太长，那么最先进入散列值的字符会被左移到边界外面，因此我们需要谨慎挑选 x 的字符

Separate Chaining⚓︎

单独链表法 (separate chaining)：将所有散列值相同的键放入同一张链表中

注：这种方法又被称为开散列法 (open hashing)

代码实现
  • 初始化
struct ListNode;
typedef struct ListNode * Position;
struct HashTbl;
typedef struct HashTbl * HashTable;

struct ListNode
{
    ElementType Element;
    Position Next;
};
typedef Position List;

/* List *TheList will be an array of lists, allocated later */ 
/* The lists use headers (for simplicity), */ 
/* though this wastes space */ 
struct HashTbl
{
    int TableSize;
    List * TheLists;
};
  • 创建空表
HashTable InitializeTable(int TableSize)
{
    HashTable H;
    int i;
    if (TableSize < MinTableSize)
    {
        Error("Table size too small");
        return NULL;
    }
    H = (HashTable)malloc(sizeof(struct HashTbl)); // Allocate table
    if (H == NULL) 
        FatalError("Out of Space!!!");
    H->TableSize = NextPrime(TableSize);  // Better be prime
    H->TheLists = malloc(sizeof(List) * H->TableSize);  // Array of lists
    if (H->TheLists == NULL)   
        FatalError("Out of space!!!"); 
    for(i = 0; i < H->TableSize; i++) 
    {   // Allocate list headers
        H->TheLists[i] = malloc(sizeof(struct ListNode)); // Slow! 
        if ( H->TheLists[i] == NULL )  
            FatalError("Out of space!!!"); 
        else    
            H->TheLists[i]->Next = NULL;
    } 
    return H; 
}
散列表示意图

注意：散列表的开头，以及每个篮子都是有 " 空头 " 的，这主要是为了删除操作的方便。若没有删除操作，则最好不要用空头，这样可以节省空间

  • 从散列表中找键
Position Find(ElementType Key, HashTable H)
{
    Position P;
    List L;

    L = H->TheLists[Hash(Key, H->TableSize)];

    P = L->Next;
    // Identical to the code to perform a Find for List ADT
    while (P != NULL && P->Element != Key) // Probably need strcmp
        P = P->Next;
    return P;
}
  • 将键插入散列表内（放在篮子的最上（前）面）
void Insert(ElementType Key, HashTable H)
{
    Position Pos, NewWell;
    List L;
    Pos = Find(Key, H);
    if (Pos == NULL) // Key is not found, then insert
    {
        NewCell = (Position)malloc(sizeof(struct ListNode));
        if (NewCell == NULL)
            FatalError("Out of space!!!");
        else
        {
            L = H->TheLists[Hash(Key, H->TableSize)];
            NewCell->Next = L->Next;
            NewCell->Element = Key; // Probably need strcpy
            L->Next = NewCell;
        }
    }
}

注：

  • 不好的一点是该函数用了两次 Hash() 函数，所以这里需要改进一下
  • 我们要让 TableSize 尽可能接近键的数量，即让加载密度 \(\lambda \approx 1\)
  • 这里仅考虑所有键都不同的情况，若出现相同的键，要么选择无视，要么增加一个额外的字段记录重复的次数

Open Addressing⚓︎

开放地址 (open addressing)：通过寻找下一个空的单元来解决冲突，这样我们就不必使用指针了。

注：这种方法又被称为闭散列法 (close hashing)

模版：

Algorithm: insert key into an array of hash table
{
    index = hash(key);
    initialize i = 0  // the counter of probing
    while (collision at index)
    {
        index = (hash(key) + f(i)) % TableSize;
        if (table is full) break;
        else i++;
    }
    if (table is full)
        ERROR("No space left");
    else
        Insert key at index;
}
其中，f(i)为冲突解决函数，初始状态为 f(0) = 0。通常用于 \(\lambda < 0.5\) 的情况。

正如 while 循环所示，若使用一次冲突解决函数后，冲突仍然发生，那就继续使用冲突解决函数，直至冲突解决，或发现无法解决直接退出。

Linear Probing⚓︎

最简单的冲突解决函数为线性探测 (linear probing)：f(i) = i，它仅是一个线性函数

Example

对比前面的例子，可以发现：虽然加载密度得到不小的提升，但是平均搜索时间比较长。

线性探测中预期探测次数关于加载密度的表达式：

\[ p = \begin{cases}\dfrac{1}{2}(1 + \dfrac{1}{(1 - \lambda)^2}) & \text{for insertion and unsuccessful searches}\\ \dfrac{1}{2}(1 + \dfrac{1}{1 - \lambda}) & \text{for successful searches}\end{cases} \]

对于上面的例子，p = 1.36。虽然很小，但是在最坏情况下 p 会很大。

线性探测的问题：基本聚集 (primary cluster)

线性探测将位置不匹配的键安放至后面最近的空内，这样做会形成区块 (cluster)，使得散列表分布不均匀，导致即使表的空间看起来挺空的，但是某些地方聚集了一堆元素。

随机冲突解决策略 (random collision resolution strategy)
  • 不成功的探测次数：\(\dfrac{1}{1 - \lambda}\)
  • 成功探测的平均次数 = 不成功的探测次数

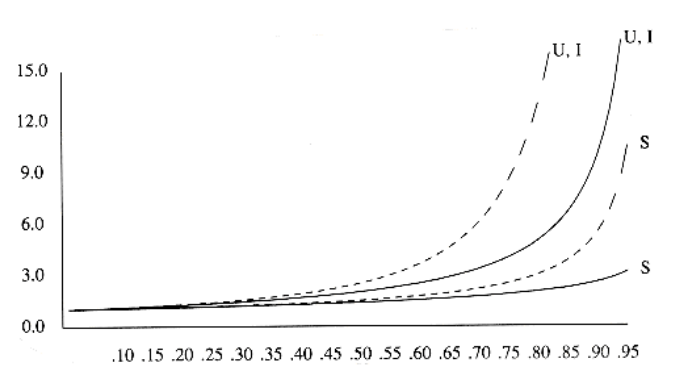
线性探测与随机策略的效率比较（其中 S 表示成功的搜索，U 表示不成功的搜索，I 表示插入）

Quadratic Probing⚓︎

二次探测 (quadratic probing) 的函数为：\(f(i) = i^2\)

定理：若使用二次探测，且表的大小是一个质数，则当表至少有一半的空余空间时，新的元素总是能够被成功插入。

证明

只要证明前 \(\lfloor \dfrac{TableSize}{2} \rfloor\) 个可替代的位置是不同的，也就是说，\(\forall\ 0 < i \ne j \le \lfloor \dfrac{TableSize}{2} \rfloor\)，我们有：

\[ (h(x) + i^2)\ \%\ TableSize \ne (h(x) + j^2)\ \%\ TableSize \]

反证法：假设 \(h(x) + i^2 \equiv h(x) + j^2 (\text{mod }\ TableSize)\)，那么可以得到 \((i + j)(i - j) \equiv 0(\text{mod } TableSize)\)，即 (i + j) 或 (i - j) 能够被质数 TableSize 整除，但这显然是不可能的，推出矛盾，因此定理成立。

注

若表的大小是一个形如 4k + 3 的质数，则使用二次探测 \(f(i) = \pm i^2\) 来探测整张表

代码实现
  • 声明
#ifndef _HashQuad_H

typedef unsigned int Index;
typedef Index Position;

struct HashTbl;
typedef struct HashTbl *HashTable;

HashTable InitializeTable(int TableSize);
void DestroyTable(HashTable H);
Position Find(ElementType Key, HashTable H);
void Insert(ElementType Key, HashTable H);
ElementType Retrieve(Position P, HashTable H);
HashTable Rehash(HashTable H);
// Routine such as Delete and MakeEmpty are omitted

#endif // _HashQuad_H

// Place in the implementation file

enum KindOfEntry {Legitimate, Empty, Deleted};

struct HashEntry
{
    ElementType Element;
    enum KindOfEntry Info;
};

typedef struct HashEntry Cell;

// Cell * TheCells will be an array of HashEntry cells, allocated later
struct HashTbl
{
    int TableSize;
    Cell * TheCells;
};
  • 初始化
HashTable InitializeTable(int TableSize)
{
    HashTable H;
    int i;

    if (TableSize < MinTableSize)
    {
        Error("Table size too small");
        return NULL;
    }

    // Allocate table
    H = (HashTable)malloc(sizeof(struct HashTbl));
    if (H == NULL)
        FatalError("Out of Space!!!");

    H->TableSize = NextPrime(TableSize);

    // Allocate array of Cells
    H->TheCells = (Cell *)malloc(sizeof(Cell) * H->TableSize);
    if (H->TheCells == NULL)
        FatalError("Out of Space!!!");

    for (i = 0; i < H->TableSize; i++)
        H->TheCells[i].Info = Empty;

    return H;
}
  • 寻找位置
Position Find(ElementType Key, HashTable H)
{
    Position CurrentPos;
    int CollisionNum = 0;
    CurrentPos = Hash(Key, H->TableSize);
    while (H->TheCells[CurrentPos].Info != Empty && 
            H->TheCells[CurrentPos].Element != Key) 
    {
        CurrentPos += 2 * ++CollisionNum - 1;  // 1
        if (CurrentPos >= H->TableSize)        // 2
            CurrentPos -= H->TableSize;      
    }
    return CurrentPos;  // 3
}

注

若交换 while 循环内的两个判断条件，程序很有可能出现段错误，因为没有先判断是否有元素

  1. 这里用到二次探测函数的递推关系：\(F(i) = F(i - 1) + 2i - 1\)，避免使用乘法，从而提高效率
  2. 这块语句替换了原来的模除运算，提高了效率；但是若 CurrentPos 大于 2 倍的 TableSize，就无法实现模除的功能了（因此使用前确保 CurrentPos 不超过 2 倍的 TableSize）
  3. 返回可插入的位置
  • 插入元素
void Insert (ElementType Key, HashTable H)
{
    Position Pos;
    Pos = Find(Key, H);
    if (H->TheCells[Pos].Info != Legitimate)  // Ok to insert here
    {
        H->TheCells[Pos].Info = Legitimate;
        H->TheCells[Pos].Element = Key; // Probably need strcpy
    }
}

注

  • 如果有过多的插入和删除操作，插入的效率会显著降低
  • 尽管二次探测解决了基本聚集的问题，但它会导致二次聚集：通过散列函数被分配到相同位置的键，探测到相同的可替代的位置。

Double Hashing⚓︎

双散列 (double hashing)的函数：\(f(i) = i * \mathrm{hash}_2(x)\)，其中 \(\mathrm{hash}_2(x)\) 为第 2 个散列函数

  • \(\mathrm{hash}_2(x) \ne 0\)
  • 确保所有位置都能被探测到

较好的散列函数：\(\mathrm{hash}_2(x) = R - (x \% R)\)，其中 R 为小于 TableSize 的质数

注

  • 若双散列函数能正确执行，那么由模拟结果知，预期的探测次数和随机冲突解决策略的大致相同
  • 二次探测不需要使用第二个散列函数，因此在实践中更简单、更快

Rehashing⚓︎

在二次探测中，我们有时会用到“再散列 (rehashing)”的技巧

何时使用再散列

  • 被占用的表空间达到一半时
  • 插入失败时
  • 散列表的加载因数达到特定值时

具体做法：

  • 建立一张额外的表，大小是原来的两倍
  • 遍历原来的整张散列表中未删除的元素
  • 使用新的散列函数，将遍历到的元素插入新的表中

如果表内有 N 个键，则时间复杂度 \(T(N) = O(N)\)

代码实现 
HashTable ReHash(HashTable H)
{
    int i, OldSize;
    Cell * OldCells;

    OldCells = H->TheCells;
    OldSize = H->TableSize;

    // Get a new, empty table
    H = InitializeTable(2 * OldSize);

    // Scan through old table, reinserting into new
    for (i = 0; i < OldSize; i++)
        if (OldCells[i].Info == Legitimate)
            Insert(OldCells[i].Element, H);

    free(OldCells);

    return H;
}

评论区

如果大家有什么问题或想法，欢迎在下方留言~