Chap 1: Digital Systems and Information⚓︎

Information Representation⚓︎

• 模拟信号 (analog signals)：在值和时间上都是连续 (continuous) 的信号
• 数字信号 (digital signals)：在值和时间上都是离散 (discrete) 的信号

Digital System⚓︎

数字系统 (digital system)：获得一组离散的信息输入和离散的内部信息输入 (系统状态 (system state))，产生一组离散的信息输出。

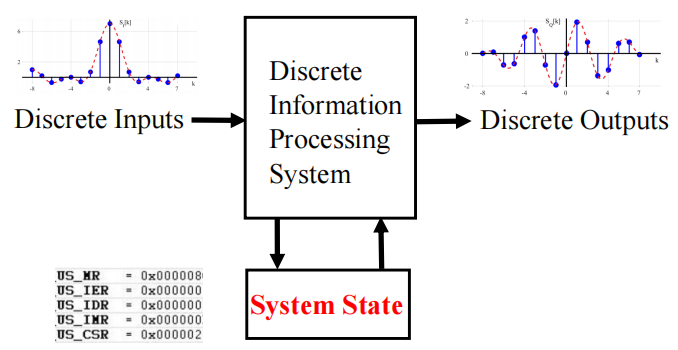
用框图表示：

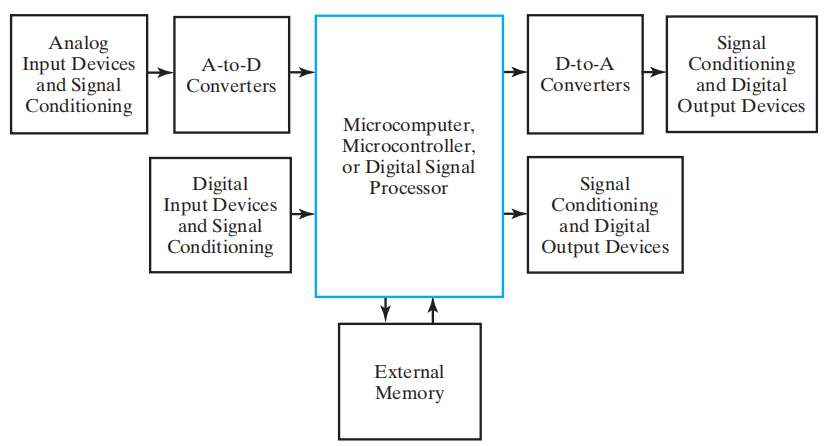
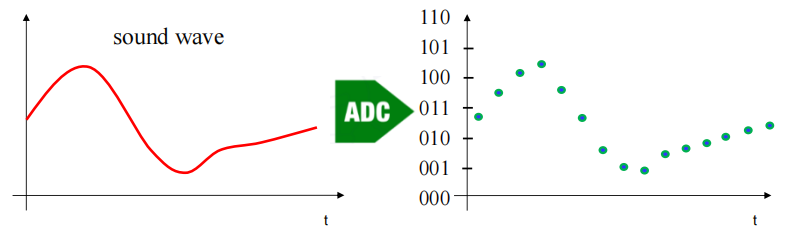
模数转换器 (Analog-to-Digital Converters, ADC)：将模拟信号转换为数字信号，为模拟世界的传感器和数字世界的信号处理搭起了桥梁。

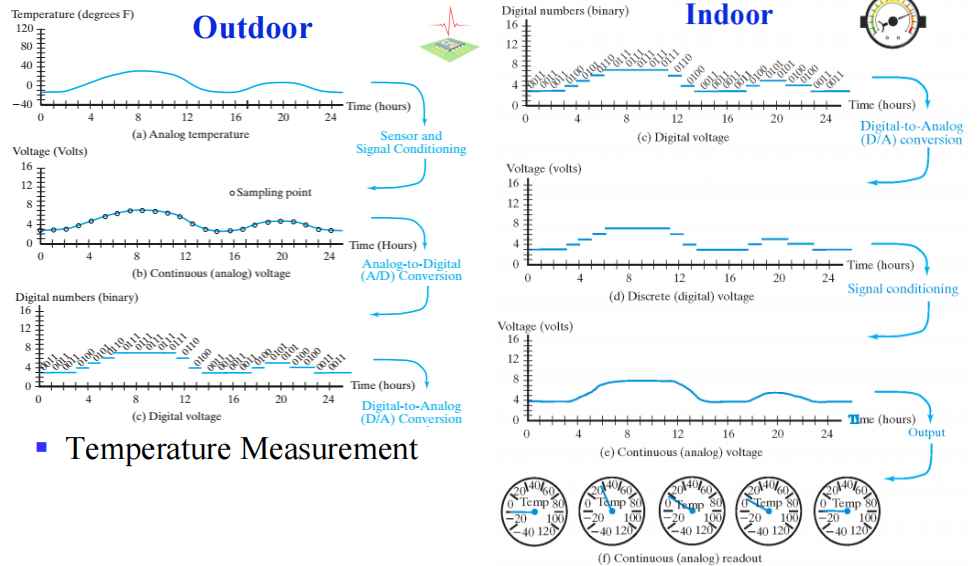
温度测量和显示

Signals⚓︎

在现实世界中，信息变量由物理量表示；而在数字系统中，我们往往取这些变量的离散值——而二进制 (binary) 值是最流行的表示方法，它可以表示物理量的值或值的范围。它通常被表示为：

• 数字 0 和 1
• 符号 False(F) 和 True(T)
• 符号 Low(L) 和 High(H)
• Off 和 On

  注：这里我们用到的是正逻辑 (positive logic)，即用 0 表示 F、L 和 Off，用 1 表示 T、H 和 On

之所以使用二进制，包括以下原因：

• 电子元件的本质——两种状态：比如开关的断开 (0) 和闭合 (1)，晶体管的导通 (1) 和不导通 (0)
• 最少数量的必要电路：使得空间、能耗、成本也达到最小

1 位信号——电压

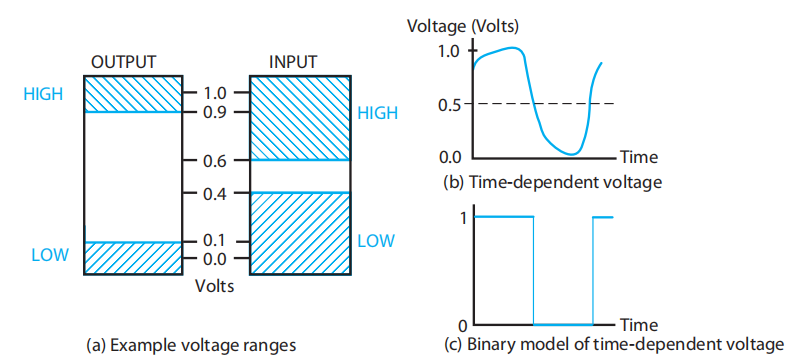
左图中间白色的区域被称为临界区域 (threshold region)

• 落在临界区域上的电压是未定义的，其结果为非法的状态，这通常表示为浮动 (floating)。如果输出引脚处在浮动状态，由于它的值可能在 HIGH 和 LOW 之间任意跳跃，所以无法确定它的输出信号
• 可以发现，输入和输出的电压容差 (voltage tolerance)( 蓝色区域 ) 是不同的，而且输入宽度大于输出，这是为了确保电路在电压变化及不期望的“噪音”电压中能够正常工作。这种输入和输出范围的不同被称为噪音容限 (noise margin)

Number Systems⚓︎

以 \(r\) 为基底 (base/radix) 的数可以被表示成

• 由数字组成的字符串： $$ A_{n-1}A_{n-2}\dots A_1A_0.A_{-1}A_{-2}\dots A_{-m+1}A_{-m}, \quad 0 \le A_i < r $$

  注："." 被称为分隔符 (radix point)，\(A_{n - 1}\) 被称为最高位 (most significant digit, msd)，\(A_{-m}\) 被称为最低位 (least significant digit, lsd)

• 幂级数

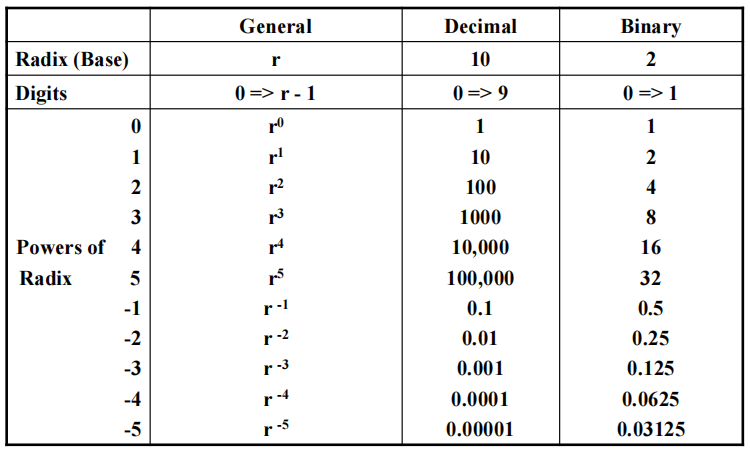
特殊的 2 次幂：

• \(2^{10}\)：K(Kilo)
• \(2^{20}\)：M(Mega)
• \(2^{30}\)：G(Giga)
• \(2^{40}\)：T(Tera)

Arithmetic Operations⚓︎

Binary Arithmetic⚓︎

加、减、乘法的详细内容略过，因为这些东西已经讲了无数遍了 ......

Addition⚓︎

注意进位 (carry) 问题

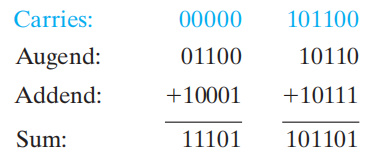
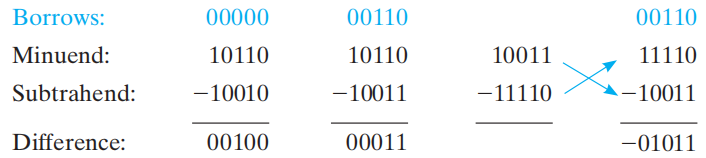
Subtraction⚓︎

注意借位 (borrow) 问题

Multiplication⚓︎

不同基底对应的值

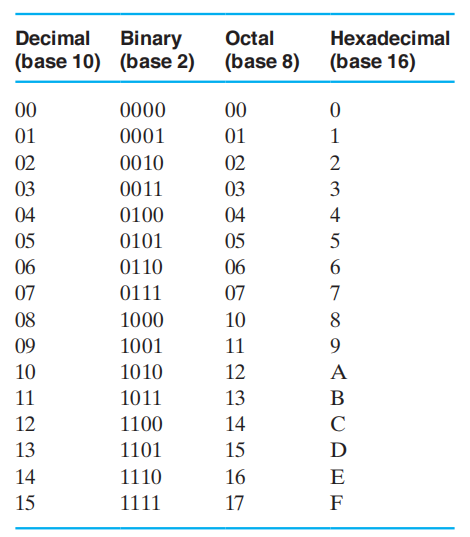
注：如果感觉 \(r(r \ne 10)\) 进制计算很别扭的话，可以先将所有数字都转化为十进制，然后将计算后的结果转化回 \(r\) 进制

Conversion⚓︎

• 二进制 \(\rightarrow\) 十进制：\(\sum(\text{digit} \times \text{respective power of 2})\)

• 十进制 \(\rightarrow\) 二进制

  • 法一

    • 原数减去最大的 2 次幂，使得剩余部分仍为正数，并记录该幂
    • 重复上述步骤，记录所有减过的幂，直到剩余部分为 0
    • 将“1”放在减过的幂的对应位置上，其他位置放“0”

  • 法二（通法）

    • 转换整数部分：重复用新的基底除该数，并保存余数。该数转化为新基底的形式即为刚才所得余数的逆序。如果新的基底大于 10，将大于 10 的余数用 A, B 等表示
    • 转换小数部分：重复用新的基底乘该数，并保存整数部分。该数转化为新基底的形式即为刚才所得余数的顺序。如果新的基底大于 10，将大于 10 的余数用 A, B 等表示
    • 用分隔符 ( 小数点 ) 将前面的结果结合起来

🌰：将 \((725.678)_{10}\) 用二进制表示

关于小数部分的转换 通过重复的乘法，小数部分会出现以下结果：

• 变成 0( 精确值 )
• 出现重复的数字( 不准确值 )

解决方法：具体说明保留多少位或截断数字

补充阅读

为什么十进制小数无法被精确编码为二进制？

——通过求解丢番图方程 (Diophantine equation) 解释

• 八进制 (Octal) \(\leftrightarrow\) 二进制：1 位八进制 = 3位二进制

• 十六进制 (Hexadecimal) \(\leftrightarrow\) 二进制：1 为十六进制 = 4位二进制

  注：二进制转八 / 十六进制的时候可能需要在二进制数里填充 0

• 八进制 \(\leftrightarrow\) 十六进制：将二进制作为过渡的平台

Decimal Codes⚓︎

Binary Numbers and Binary Coding⚓︎

信息类型：

• 数字：用来表示需要的数据范围，进行简单直接的计算（比如算术运算），与二进制数联系紧密
• 非数字：更大的灵活性 ( 无需算术运算 )，不与二进制紧密联系。因此，我们可以用任意二进制的组合 ( 被称为编码 )，使任意的数据得到唯一的编码。

给定 \(n\) 位二进制数 ( 被称为位)，二进制编码 (binary code) 是从一组要被表示的元素到 \(2^n\) 个二进制数的子集的映射 (mapping)

给定 \(M\) 个需要用二进制数编码的元素，最小数量位\(n\) 满足 \(2^{n - 1} < M \le 2^n\)，因此 \(n = \lceil \log_2 M \rceil\)

拓展到基底为 \(r\) 的情况，\(n\) 为 \(r\) 进制数可以表示 \(r^n\) 个不同的元素，因此可以表示 \(M < r^n\) 个元素

常见的编码方式

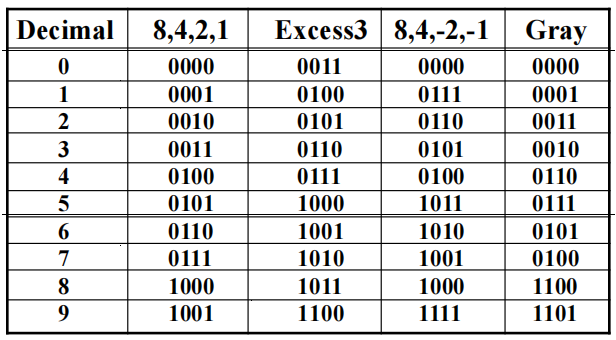
补充：独热码 (one-hot code)，一种只用 1 位表示每个状态的编码，比如 4 位二进制数可以表示四种状态：0001,0010,0100,1000

Binary Coded Decimal(BCD)⚓︎

BCD 码又称8421 码(8, 4, 2, 1 是权重 )，因此 BCD 是权重码 (weighted code)。它是最简单的，最直接的关于十进制数的二进制编码，使用与二进制数相同的幂，但它只使用前 10 个数字 (0-9)。

算术运算（这里只讨论加法）：还是要注意进位问题

🌰：

Excess 3 Code and 8, 4, -2, -1 Code⚓︎

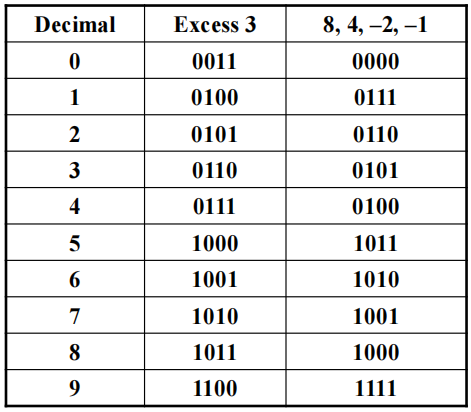
注意到：

• Excess 3 = BCD + 3
• Excess 3 码与 8,4,-2,-1 码是互补码 (complement code)

Alphanumeric Codes⚓︎

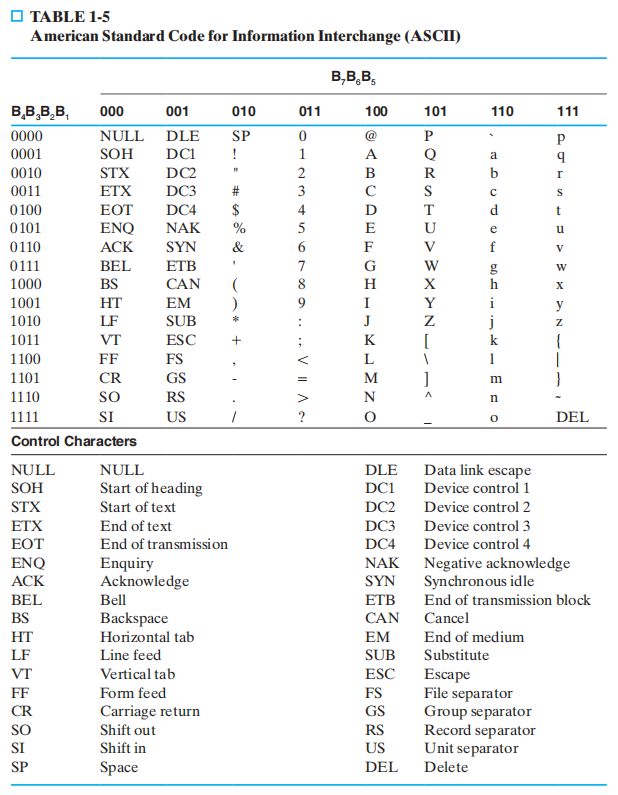
ASCII(American Standard Code for Information Interchange) 字符码：用 7 位表示字符数据，包括：

• 94 个图形打印字符

• 34 个非打印字符：分为 3 类

  • 格式控制字符 (format effector)
  • 信息分隔字符 (information separators)
  • 通信控制字符 (communication control characters)

    ASCII 码的第 8 位（最高位）用来表示奇偶 (parity) 校验码

性质：

• 字符0-9 的十六进制值对应十六进制的 \((30)_{16}-(39)_{16}\)
• 大写字母 A-Z 对应 \((41)_{16}-(5A)_{16}\)
• 小写字母 a-z 对应 \((61)_{16}-(7A)_{16}\)

  因此，大小写字母的 ASCII 码转换只需 翻转第 5 位

Error-Detection⚓︎

错误侦测 (error detection) 通常用于通道编码 (channel coding) 中

拓展知识：Shannon Capacity Theorem/Limit

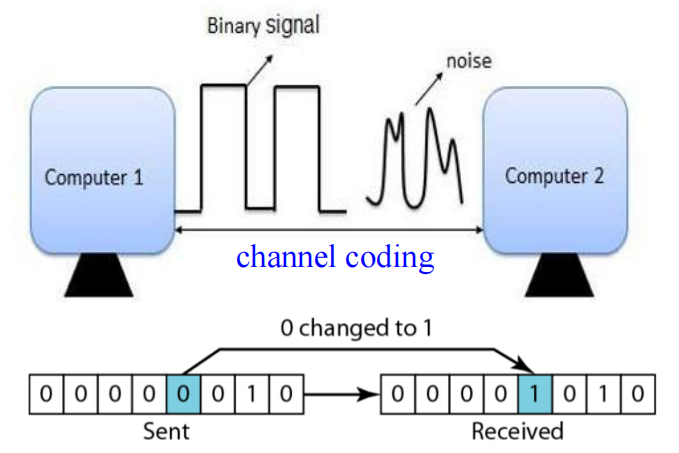
错误侦测的方法：

• 冗余 (redundancy)( 比如多余信息 ) 由额外的位构成，可以被并入到二进制码中，以此来侦测和纠正错误，比如循环冗余校验 (Cyclic Redundancy Check, CRC)

• 奇偶校验位 (parity) 是添加在编码单词上的额外的位，使得整个编码包含 1 的个数是奇数或者偶数。它能够侦测所有单个位的错误和一些多位错误

  • 偶校验 (even parity)：整个编码包含 1 的个数是偶数
  • 奇校验 (odd parity)：整个编码包含 1 的个数是奇数

🌰：

• 校验和 (Checksum)

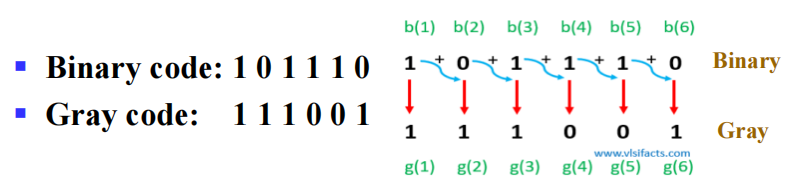
Gray Codes⚓︎

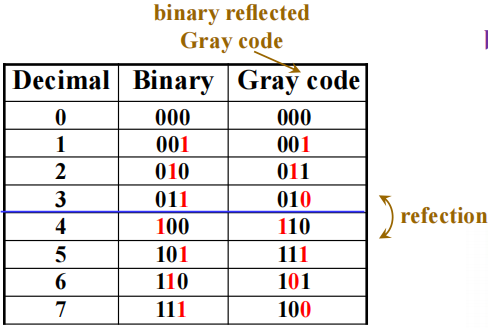
注：格雷码 (Gray code) 的特殊之处在于：相邻的两个数只有1 位的差异。观察表格发现，格雷码的前半部分和后半部分有反射 ( 翻转 )(reflection) 的关系

🌰光轴编码器 (Optical Shaft Encoder)

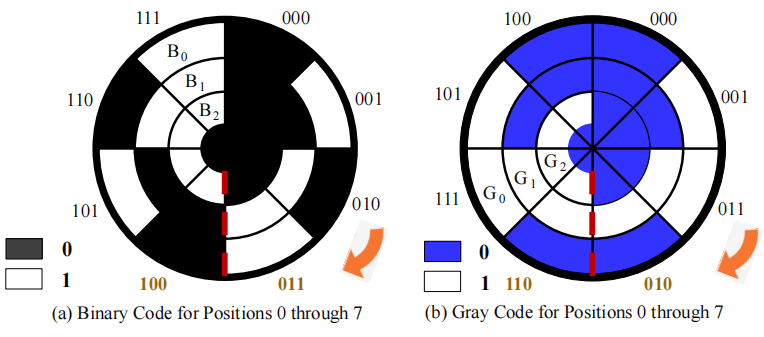
如果光线经过红色虚线 ( 边界 ) 处，左边用二进制码表示的情况就会出现问题（被称为偏斜 (skew)）, 下图所示红色部分的数字都有可能是最终的输出结果：

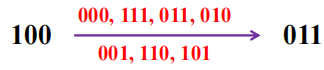
而格雷码就可以避免这种错误的输出可能

二进制转格雷码：

• 用1表示最高位，索引值越大表示位数越低
• \(g(i)\) 表示索引为 \(i\) 的格雷码对应的数字， \(b(i)\) 表示索引为 \(i\) 的二进制码对应的数字

🌰：

Appendix⚓︎

The Digital Computer⚓︎

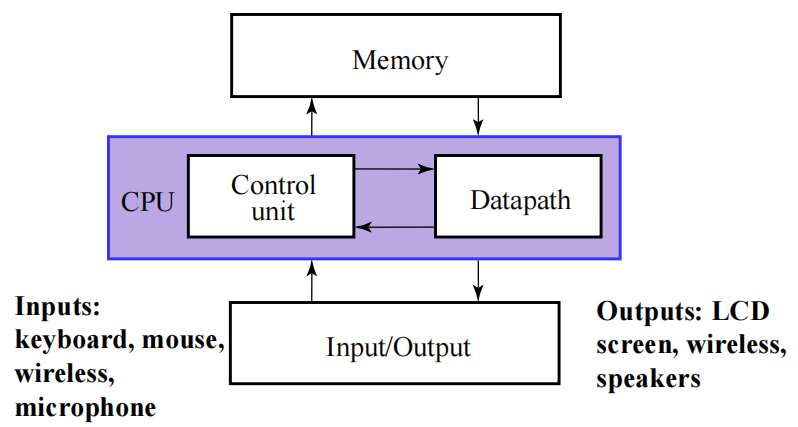
• 内存 (memory)：存储程序的输入、输出和中间数据

• 中央处理器 (central processing unit, CPU)

  • 数据通路 (datapath)：执行由程序指定的算术和其他数据处理运算
  • 控制单元 (control unit)：监督在各种单元间的信息流

• 输入设备 (input device)：将由用户提供的程序和数据传输到内存的设备

• 输出设备 (output device)：将计算结果呈现给用户的设备

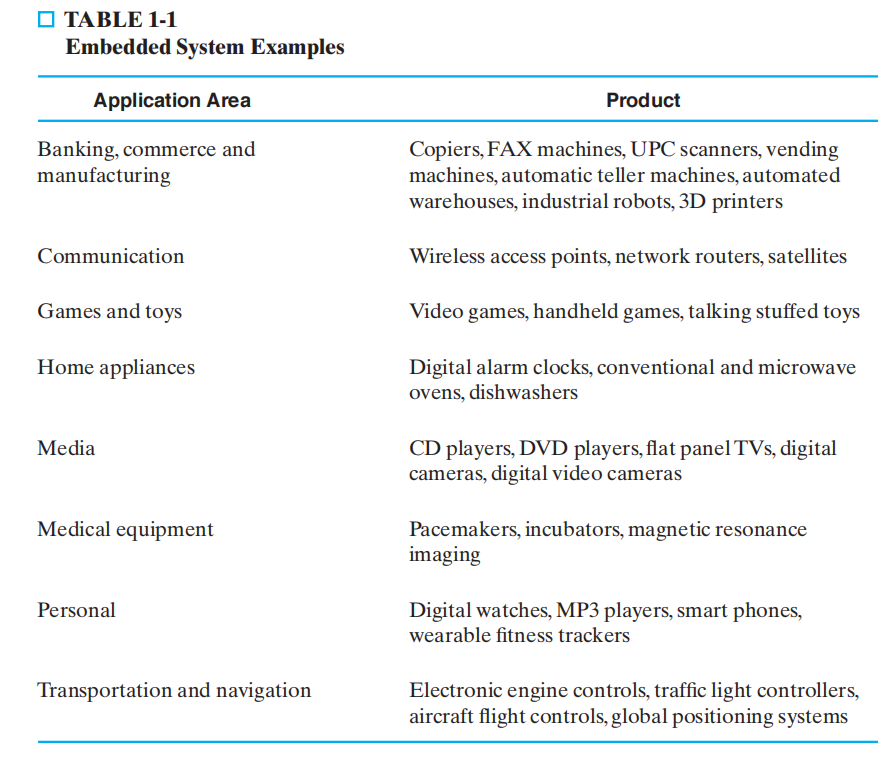
Embedded System⚓︎

More on Generic Computer⚓︎

处理器 (processor) 的类型：

• 中央处理器 (CPU)
• 浮点处理单元 (floating-point unit, FPU)：执行浮点计算，可以用来处理很大或很小的数字
• 存储管理单元 (memory management unit, MMU)：使得对于 CPU 的可用内存比 RAM 的实际内存更大
• 内部缓存 (internal cache)

Abstration Layers in Computer System Design⚓︎

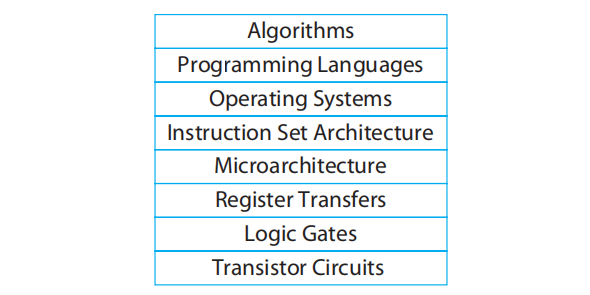
这体现了“自顶向下 (top down)”的设计思想，即从较高的层次来说明整个系统，然后它的设计被分解为连续的更小的块，直到这些块简单到可以直接运行的程度。最后连接这些块，形成整个系统。

这种分层抽象隐藏了系统中各个元件的执行细节，这样设计者可以专注于用来解决问题的那部分元件；而且低层抽象的改变不会影响高层的抽象（比如你写的 c 代码放到别的电脑也能跑）。

高层抽象的提升空间往往高于低层抽象

Unicode⚓︎

注：具体内容见 wikipedia

评论区