Chap 4: Sequential Circuits⚓︎
约 9814 个字 预计阅读时间 49 分钟
核心知识
- 锁存器
- \(SR\) 锁存器、\(\overline{SR}\) 锁存器、带时钟的锁存器——有不确定的状态
- \(D\) 锁存器——空翻问题
- 触发器
- 脉冲触发式:主从触发器——一次性采样问题
- 边沿触发式
- 直接输入
- 时序电路分析
- 输入、输出方程
- 状态表
- 状态图
- 等价状态
- 时序电路设计
- 状态分配
- 时间分析
- 触发器
- 整个时序电路
Sequential Circuit Definition⚓︎
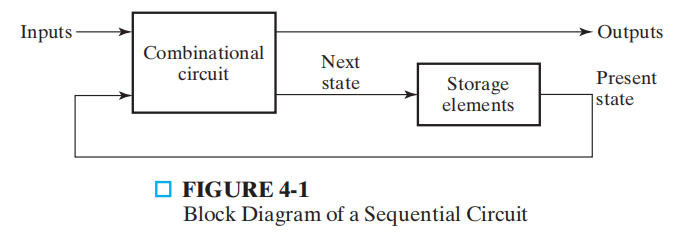
时序电路 (sequential circuit):输出不仅取决于当前的输入,也取决于之前的输入的电路。
时序电路可以用一张状态图 (state diagram) 表示,它由在任意给定时间内的有限数量的状态表示,且状态随着外部输入的变化而变化。
时序电路包括:
-
存储元件 (storage elements):能够存储二进制信息的电路,而这种在任意给定时间内存储的二进制信息被称为在那个时刻的状态 (state)。
-
组合逻辑:
-
输入
- 来自外部的信号
- 来自存储元件的信号,被称为状态 (state),或当前状态 (present state)
-
输出
- 来自外部的信号
- 来自存储元件的信号,被称为下一状态 (next state)
-
Types of Sequential Circuits⚓︎
根据存储元件观察输入信号的时间和内部状态改变的时间,将时序电路分为:
-
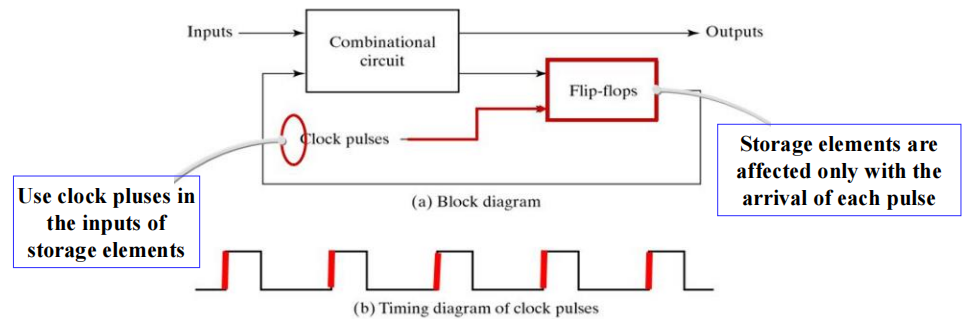
同步 (synchronous):
- 这种电路的行为可由它在离散时间内的信号来定义 ( 人话:随外部时钟脉冲变化)
- 存储元件观察输入信号的时间,并且仅随时间信号 ( 来自时钟生成器 (clock generator) 的 时钟脉冲 (clock pulse)) 的变化而改变状态。因此它又被称为时钟时序电路 (clocked sequential circuits)。因此,这种电路能够在电路的延迟下也能正常工作,而且相对来说比较容易设计出来。
-
异步 (Asynchronous)
- 这种电路的行为依赖于某一时刻的输入信号以及输入信号在连续时间内变化的顺序 ( 人话:不随外部时钟脉冲变化)
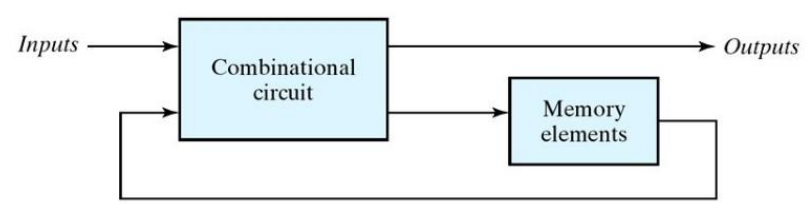
- 这种电路的行为依赖于某一时刻的输入信号以及输入信号在连续时间内变化的顺序 ( 人话:不随外部时钟脉冲变化)
Storage Elements⚓︎
存储信息的方式多种多样,这可以通过逻辑电路实现,比如缓冲器 (buffer)。假设缓冲器具有 \(t_G\) 时间的延迟,那么在 \(t\) 时刻进行输入,将会在 \(t + t_G\) 时刻得到输出,也就是说,信息被存储了 \(t_G\) 时间。
但是,我们希望信息存储的时间是不定的 (indefinite),应该比一个或多个门的延迟更长一些。因此,我们对缓冲器进行改装:将它的输入与输出相连接。假如输入为 0,那么在 \(t_G\) 时间过后缓冲器将会输出 0;然后这个 0 又回到输入,又过了 \(t_G\) 时间后被输出……如此往复,最终实现一直保存 0 的功能 ( 输入为 1 同理 )。
这个例子说明可以通过将具有延迟的逻辑电路构成闭环 (closed loop)的方式来实现存储功能,同时要确保回路中没有逆转信号。一个缓冲器通常由两个非门构成的。
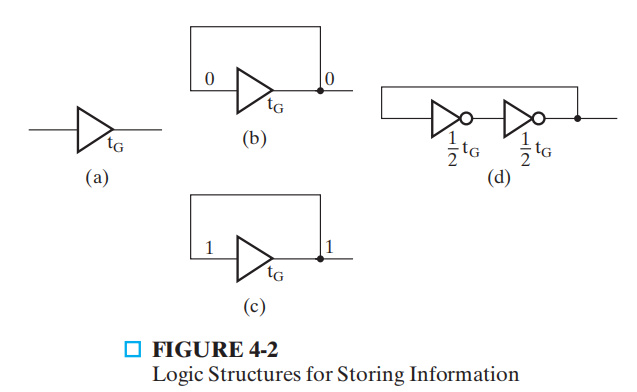
然而,上述方法虽然常用,但它存在一个明显的问题:因为没有额外的输入来控制电路,我们无法改变缓冲器存储的信息。如果我们用或非门或者与非门,就可以改变这一现状,后面讲到的异步存储电路锁存器 (latches) 就是这么构建的。
引入
通常来说,很多复杂的异步时序电路很难设计,因为它们的行为高度依赖门的延迟和改变输入的时间。因此,大多数设计者会选择同步时序电路。尽管如此,有些异步时序电路是必需的,比如我们需要用异步的锁存器来构建同步电路触发器 (flip-flops)。
触发器是能够存储一位信息的二进制存储元件,并具有时间特征 ( 在 Flip-Flop Timing 一节定义 )。它仅根据时钟脉冲来改变状态,也就是说,如果没有时钟脉冲,即使触发器的输出改变了电路的输入,它的输出仍然不变,相当于组合逻辑电路与触发器的回路之间被“切断”了。触发器有 1 个或 2 个输出,一个用于输出存储的正常值,另一个可选的输出存储值的补。最常用的触发器是\(D\) 触发器。在深入学习触发器之前,我们先了解锁存器的工作原理。
Latches⚓︎
\(SR\) and \(\overline{SR}\) Latches⚓︎
锁存器 (latches) 有以下特征:
- 两个稳定的状态,即
0,1 - 可以长期保存给定的状态值
- 在特定条件下可以改变状态,比如置位 (set)
1或复位 (reset)0
由两个或非门的交叉耦合 (cross-coupling) 构成,如图所示:
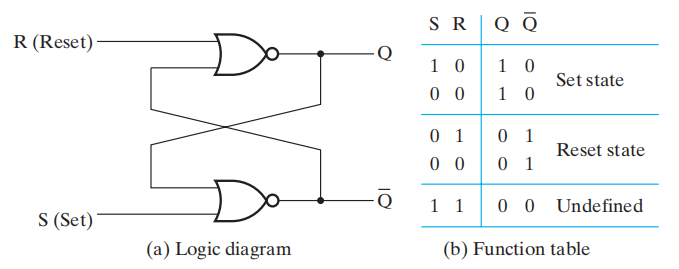
- 其中,输入\(S\) 用于置位 (set),\(R\) 用于复位 (reset)
- 当输出\(Q = 1, \overline{Q} = 0\) 时,被称为置位状态 (set state);当 \(Q = 0, \overline{Q} = 1\) 时,被称为复位状态 (reset state)
- 如果 \(S = R = 1\)( 同时输入 1),那么就会产生未定义的 (undefined) 的状态 ( 两个输出均为 0,但我们希望两个输出是互补的 )
- 如果 \(S = R = 0\) 时,锁存器处于置位或复位状态,取决于最近的一次输入
\(SR\) 锁存器的行为可以由下面的仿真波形图表述:
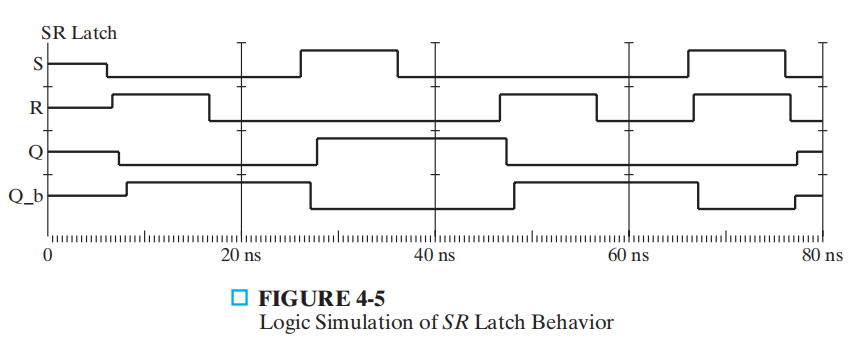
由两个与非门的交叉耦合构成,如图所示:
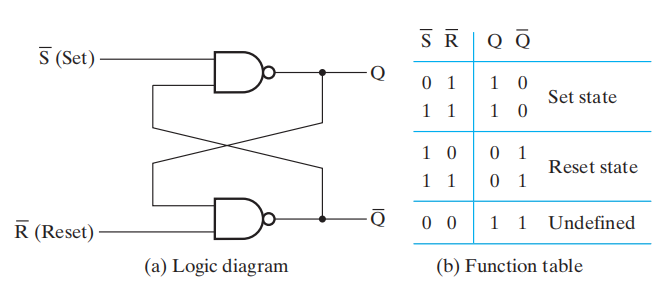
注意:这种锁存器的输入信号要取补
总结
- \(SR\) 锁存器由或非门构成 \(\rightarrow\) 对
0敏感 \(\rightarrow\) 同时为0是保持状态 - \(\overline{SR}\) 锁存器由与非门构成 \(\rightarrow\) 对
1敏感 \(\rightarrow\) 同时为1是保持状态
补充知识——不稳定的锁存器行为 ( 考试应该不做要求 )
-
振荡 (oscillation)
\(\overline{S} = \overline{R} = 0\) 不能作为输入,因为:
- 如果两个门具有 相同的延迟,那么它们将会同时输出 0。将 0 反馈至输入端就会同时输出 1,然后又同时输出 0,如此往复。这种振荡行为被称为critical race,它将会永远持续下去
- 如果两个门具有 不同的延迟,那么锁存器就会改变状态。然而,我们不清楚锁存器会进入什么状态,因此锁存器的下一个状态是未定义的
-
亚稳态 (metastable state)
\(\overline{S} = \overline{R} = 1\),\(\overline{S}-\overline{R}\) 锁存器等价于这种电路图:
考虑两个非门的传输特征: 中间的点代表亚稳态。任何信号的微小变化都会得到加强,且电路会离开亚稳态
中间的点代表亚稳态。任何信号的微小变化都会得到加强,且电路会离开亚稳态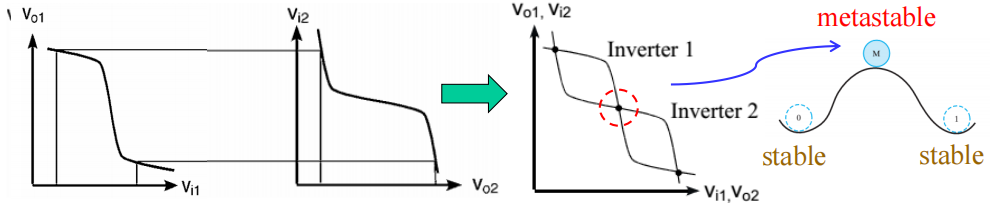
如何避免这些不稳定状态呢?
- 不要同时将 \(R, S\) 从 0 改变至 1,这样可以避免振荡行为。一种方法是不能让它们同时为 0
- 一旦改变一个输入后,就不要再改变它,直到电路完成信号传输并达到稳定状态。这样可以避免亚稳态行为。
时钟 \(SR\) 锁存器 (clocked \(SR\) latches):在原先 \(\overline{SR}\) 锁存器的基础上增加两个与非门和一个控制输入 (control input)\(C\) 得到的,这个输入作为另外两个输入的使能信号
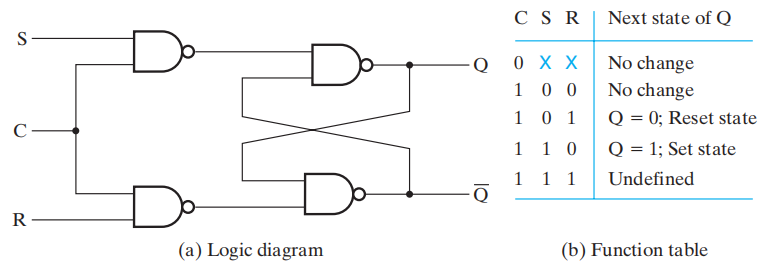
- 它与基本的 \(SR\) 锁存器具有相同的时序行为,除了它只在 \(C\) 为高电平时正常运行
- 基本的 \(\overline{SR}\) 锁存器是异步时序电路,而时钟 \(SR\) 锁存器是同步时序电路
- 这种带控制输入的 \(SR\) 锁存器是构建其他类型的锁存器和触发器的基础
\(D\) Latch⚓︎
如上所述,当 \(S = R = C = 1\) 时,锁存器的状态是未定义的。为了消除这种情况 ( 即 \(S, R\) 不同时为 1),我们采用 \(D\) 锁存器,如图所示。
这种触发器只有两个输入:\(D\)(data) 和 \(C\)(control)。可以发现,\(D\) 充当 \(S\) 的地位,而它的补 \(\overline{D}\) 则充当 \(R\) 的地位,这样就避免同时为 1 的情况。
但这样也消除了同时为 0 的情况,而这种情况本来表示保持状态不变。然而,当 \(C = 0\) 时 ( 禁用 ),锁存器依然能够实现保持状态;只有当 \(C = 1\) 时,数据输入 \(D\) 才能起作用。
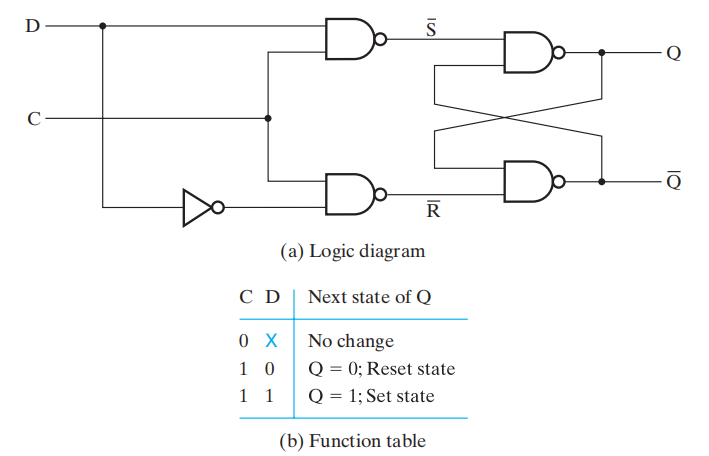
D 锁存器的问题:空翻
触发 (trigger):控制输入的值的改变使得触发器内的锁存器的状态也发生改变
有时钟脉冲的 \(D\) 锁存器,在 \(C\) 达到高电平 (logic-1 level) 时会被触发。在这种情况下,锁存器是透明的 (transparent),因为当控制输入为 1 时,我们可以从它的输出中“看到”它的输入。
如上图所述,触发器的输出与组合电路之间有一个反馈回路。因此,触发器的数据输入部分来自它自身或者其他触发器的输出 ( 这里假定所有锁存器采用相同的时钟脉冲 )。当我们用锁存器构建触发器时,就会产生一个严重的问题:由于锁存器间的相互连接( 某个锁存器的输出 \(\overline{Q}\) 可能是另一个锁存器的输入 \(D\)),当控制输入 \(C = 1\) 时,就会发现锁存器的状态将会不断改变,而不是只改变 1 次,直到 \(C = 0\) 时才停止变化。所以,当所有锁存器由一个共同的时钟信号触发时,不能将它们直接相互连接。之所以会发生这个问题,正是因为锁存器透明的性质。
Flip-Flops⚓︎
为了阻止 " 透明 " 带来的问题,我们采用触发器的设计。在触发器内,在一个输出改变之前,输入与输出间的通路应当断开。有 2 种实现方法:
-
脉冲触发式触发器 (pulse-triggered flip-flop):
- 当有时钟脉冲时,触发器可以修改第 1 个锁存器的值,且保持第 2 个锁存器的值
- 当没有时钟脉冲时,触发器可以改变第 2 个锁存器的值,且保持第 1 个锁存器的值
这里是正脉冲触发式触发器
-
边沿触发式触发器 (edge-triggered flip-flop):
- 只有当时钟脉冲发生 0-1 或者 1-0 的转变时,触发器被触发
- 在其他任何时间内,触发器的状态将保持不变 ( 无论是否有脉冲 )。
注:边沿触发式触发器速度更快,而且它的设计限制更少,因此就更常用
Pulse-Triggered Flip-Flop⚓︎
\(SR\) 主从触发器 (\(S-R\) Master-Slave Flip-Flop):将两个 \(SR\) 锁存器构成
注意两个锁存器的控制输入是互补的关系
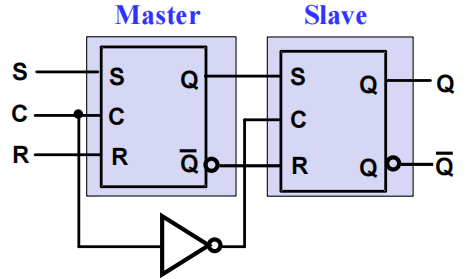
- 当 \(C = 1\) 时,触发器中第一个锁存器,即主 (master) 锁存器的值可以改变,但无法改变第二个锁存器的状态
- 当 \(C = 0\) 时,触发器中第二个锁存器,即从 (slave) 锁存器将主锁存器的输出作为输入,产生相应的输出,此时主锁存器的状态保持不变
- 因此,原来锁存器中输入到输出之间的持续连接,被触发器中交替的时钟值打破
时序图:
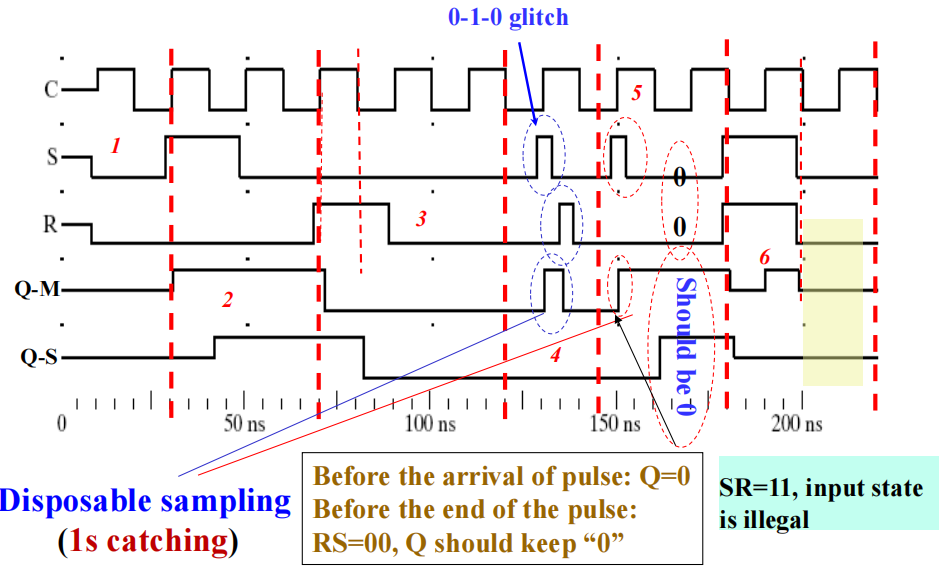
- 可以看出,触发器的输出变化因为脉冲宽度而变慢。
- 当时钟为高电平时,\(R\) 或 \(S\) 的0-1-0 glitch( 短暂跳变到 1) 会被主锁存器发现,因此主锁存器的值发生意外的改变,而这个异常数据会被写入到从锁存器中,这种行为被称为一次性采样 (1‘s catching)
注:一次性采样很可能是由 \(SR\) 主从触发器有 2 种保持的状态:\(C = 0\),和 \(C = 1, S = R = 0\) 导致的。比如:\(C = 1\) 时,\(Q = 0, S = 0, R = 0\) 处于保持状态。若 \(S\) 发生 0-1-0 的跳变,则 \(Q\) 的值从 0 变成 1,也就是说异常的数据被写入主锁存器内。
Edge-Triggered Flip-Flop⚓︎
边沿触发式触发器 (edge-triggered flip-flop) 忽视处在稳定电平的时钟脉冲,仅当时钟信号发生转变时而被触发。
\(D\) 主从触发器 (\(D\) Master-Slave Flip-flop)
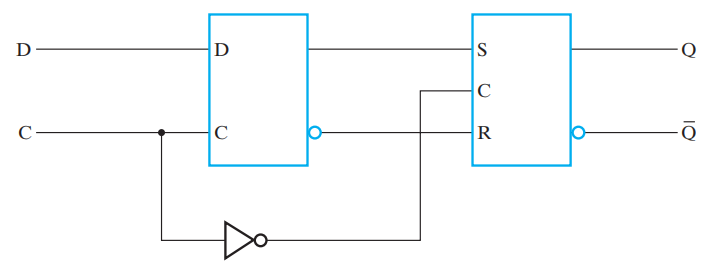
注:在 \(SR\) 主从触发器的基础上,将主锁存器换成了 D 锁存器,其余部分不变
\(D\) 主从触发器避免了上述的一次性采样问题。它输出的改变与脉冲结束时的下降沿 (negative edge) 有关,因此它又被称为下降沿触发的触发器 (negative-level triggered flip-flop),即 1-0 的转变会触发触发器
注:它的原理和下面介绍的触发器类似,因此这里就不解释了
上升沿触发的 \(D\) 触发器 (Positive-Edge-Triggered \(D\) Flip-flop)
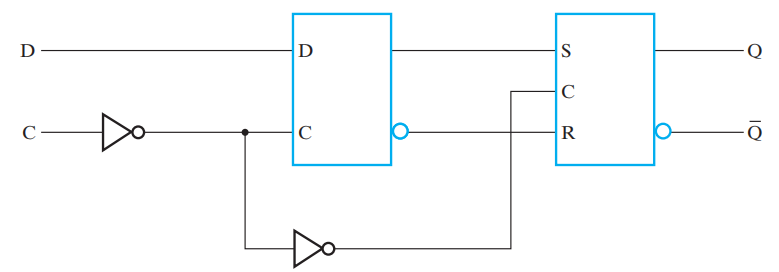
分析
这种触发器在 0-1 的转变,即上升沿 (positive edge) 处会触发触发器。它也是一种主从触发器。与上面的触发器不同的是,它的时钟输入上多了个非门,因此:
- 当时钟输入 \(C = 0\) 时,主锁存器处于使能状态并且是透明的,因此能够接受 \(D\) 的输入;而从锁存器就被禁用了,并保持之前的状态
- 当上升沿出现时,\(C\) 开始变成 1,这时主锁存器被禁用了,它的值被固定了;而从锁存器就拷贝了主锁存器的状态
- 当保持 \(C = 1\) 时,由于主锁存器被禁用,因此两个锁存器的状态均保持不变
- 当下降沿处显示,\(C\) 开始变成 0,主锁存器恢复使能,而从锁存器被禁用了,因此从锁存器仍然保存之前的状态
所以说这个触发器是由上升沿触发的。
注
通常,电路中所有的触发器都会采用同一种类型的。如果采用不同的类型,就要考虑采用不同的时钟脉冲,确保所有触发器的输出能够同时改变,从而正常运行。后面的章节若不做特殊说明,均采用同一类型的触发器。
注意到 \(D\) 触发器没有保持状态,我们可以通过下列方法 " 添加 " 保持状态:
- 时钟门控 (clock gating):禁用输入 \(C\) 的时钟脉冲。虽然节省成本,但会延迟时钟脉冲,这种延迟被称为时钟偏移 (clock skew)。因此避免采用这种方法
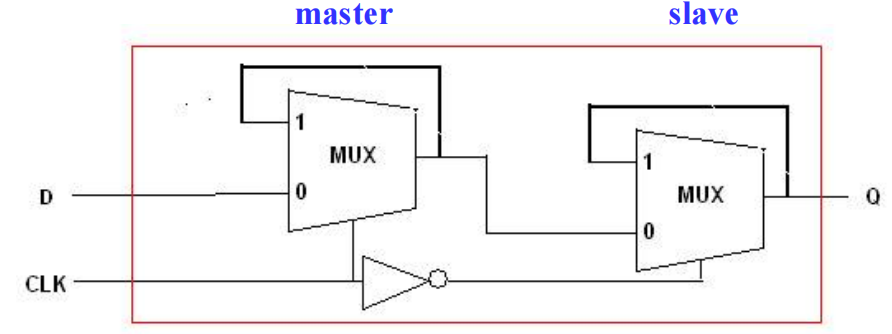
- 保持时钟脉冲不受干扰,并使用多路选择器,将输出连接到输入 \(D\)
Standard Graphics Symbols⚓︎
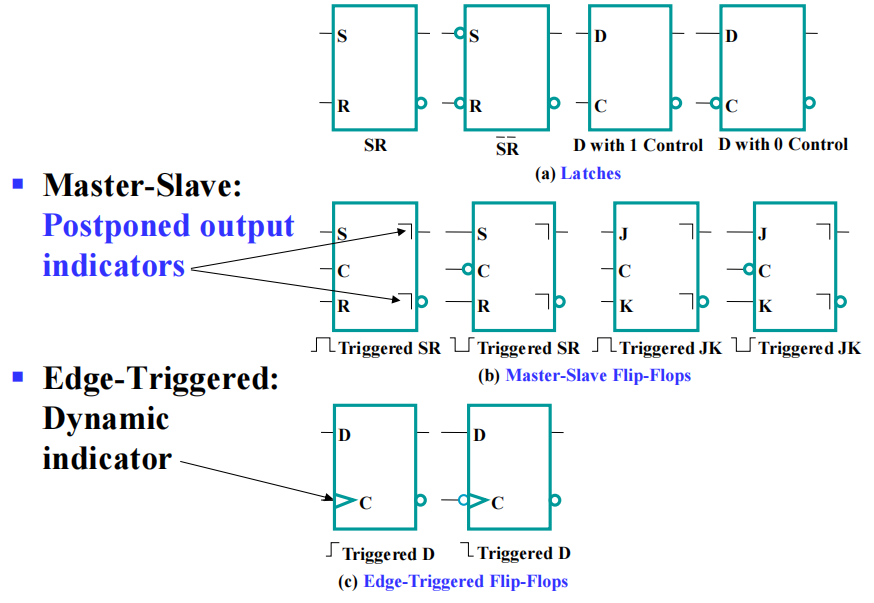
注:
- 输入或输出引脚处的圈表示取补
- 第二行中,第 1、3 个触发器名称左边的记号表示正脉冲,第 2、4 个触发器的记号表示负脉冲
- 第三行中,第 1 个触发器名称左边的记号表示上升沿,第 2 个触发器的记号表示下降沿
- 第二行的输出引脚旁边有 \(\daleth\) 记号,它是延迟输出标识符 (postponed output indicator),表示输出将会在脉冲结束后改变
- 第三行的输出引脚旁边有 \(\vartriangleright\) 记号,它是动态 ( 输入 ) 标识符 (dynamic input),表示触发器响应的是时钟脉冲的转变
Direct Inputs⚓︎
触发器通常提供特殊的输入,用于异步的置位和复位
- 直接输入 / 预置 (direct input/preset):用于异步置位 S 的输入
- 直接复位 / 清空 (direct output/clear):用于异步复位 R 的输入 如果没有这些输入,触发器在刚通电时的状态是任意的。因此,通过这些直接输入,我们可以提前初始化触发器的状态,从而使触发器在通电后能够正常运行
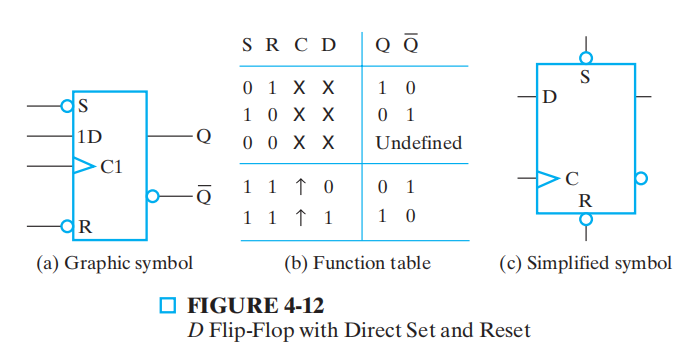
注:
- 控制输入被标记为 \(Cn\),表示它可以控制标记为 \(nD\) 的数据输入
- 没有标上数字的 \(S, R\) 表明它们不受控制输入控制。可以看出,它们是低电平活跃的,因此它们的行为类似 \(\overline{SR}\) 锁存器( 异步时序电路 )
- 函数表中的 \(\uparrow\) 表示 \(C\) 处于上升沿
Flip-Flop Timing⚓︎
- 建立时间 (setup time)\(t_s\):在时钟边沿前,输入 \(S, R\) 或 \(D\) 必须保持稳定状态的最小时间,这样数据才能成功被存入触发器内
- 脉冲触发式触发器:等于时钟脉冲宽度 ( 如果在这段时间修改数据,就会出现一次性采样的问题 )
- 边沿触发式触发器:通常比时钟脉冲宽度小得多,因此它的速度更快
- 保持时间 (hold time)\(t_h\):在时钟边沿后,输入 \(S, R\) 或 \(D\) 必须保持稳定状态的最小时间,这样数据才能可靠地被时钟采样
因此在 \(t_s\) 和 \(t_h\) 的时间段内,我们不能改变触发器的输入!
- 时钟脉冲宽度 (clock pulse width)\(t_w\):确保主锁存器能够有足够时间正确获取输入
-
传播延迟 (propogation delay)\(t_{p-}\):与门电路中的同名参数类似,但它测量从触发时钟边沿到输出稳定之间的时间。因为触发器输出的改变将会被触发器输入的控制分开,因此最小传播延迟应当长于保持时间
- \(t_{PHL}\):高电平 \(\rightarrow\) 低电平
- \(t_{PLH}\):低电平 \(\rightarrow\) 高电平
- \(t_{pd} = \max(t_{PHL}, t_{PLH})\)
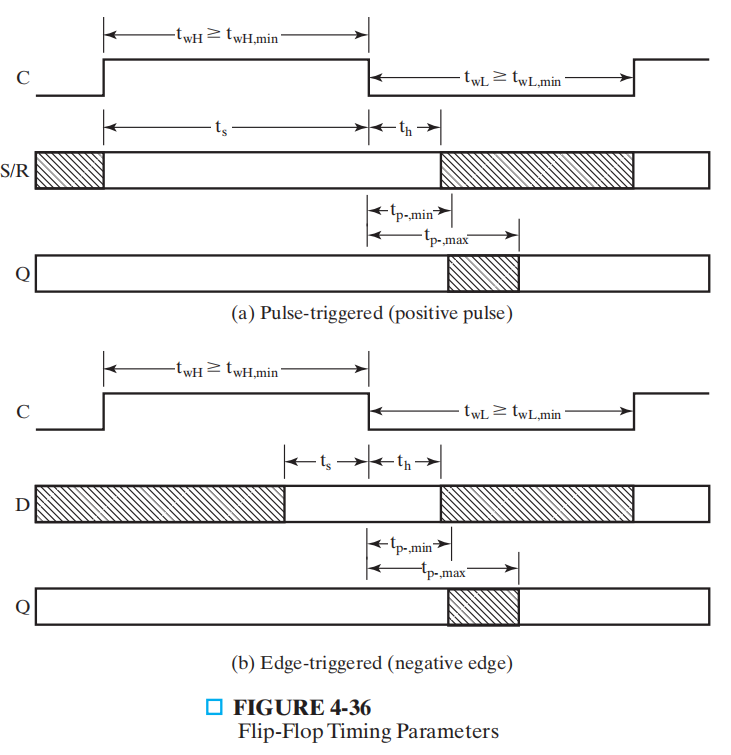
注:阴影部分表示我们可以改变数据的时间段
例题

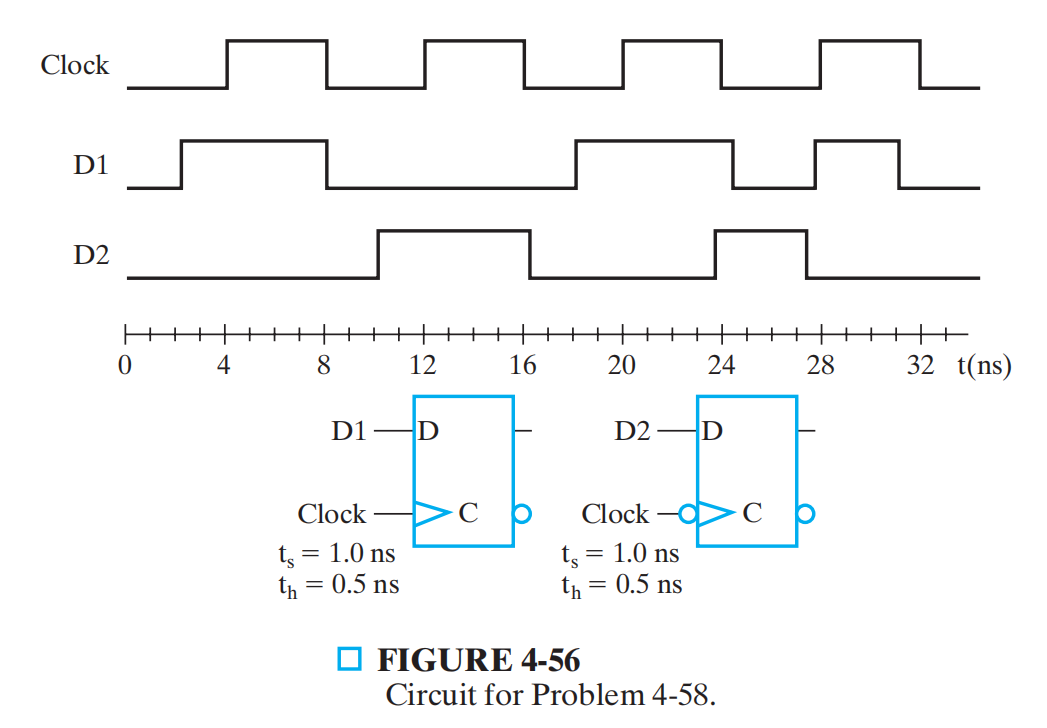
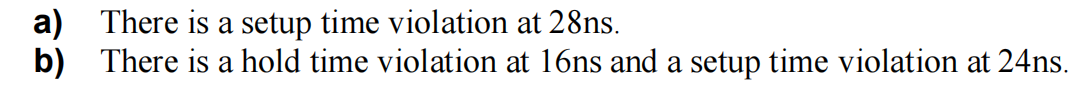
总结
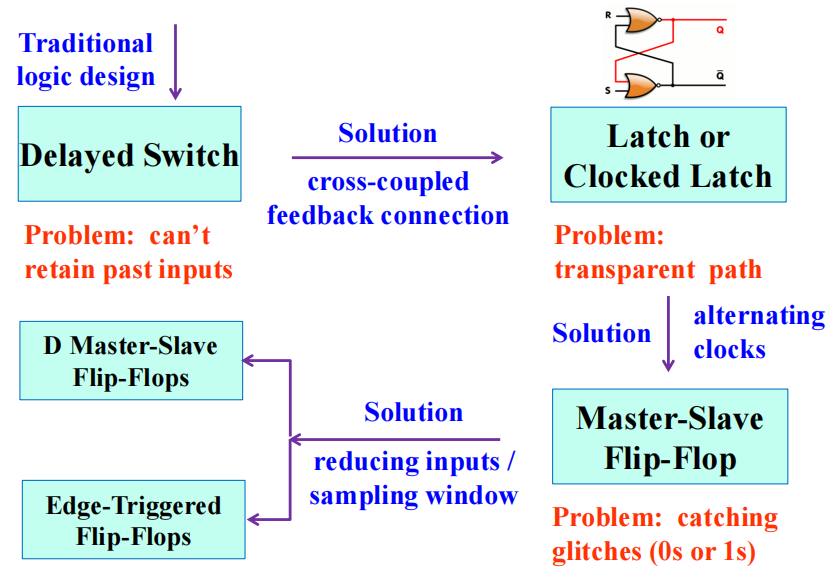
Sequential Circuits Analysis⚓︎
通用模型:
- time(t) 时刻的当前状态被存储在一组触发器中
- time(t) 时刻的下一状态的输入,是关于当前状态 (t) 和 ( 有时 ) 输入 (t) 的布尔函数
- time(t+1) 时刻的下一状态是下一状态输入 (t) 的布尔函数
- time(t) 时刻的输出,也是关于当前状态 (t) 和 ( 有时 ) 输入 (t) 的布尔函数
所以," 状态 " 可以简单理解为触发器的输出
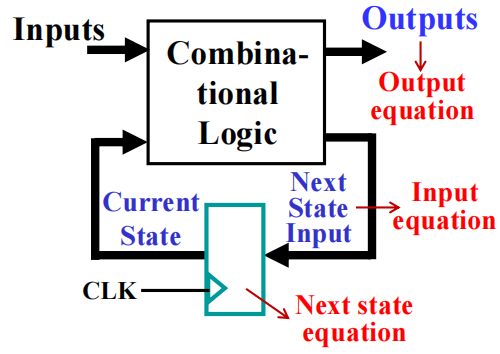
时序电路分析:对于给定的时序电路,说明对应的逻辑图的过程。它包括:
- 从状态表 (state table)、状态图 (state diagram) 和输入、输出布尔方程中得到时序电路的功能
- 找到时间限制,使得时序电路能够避免亚稳态,从而使电路运行无误
步骤
- 得到输入、下一状态以及输出的方程
-
得到状态表(带有状态的真值表
) :- 输入:电路输入,触发器的当前状态
- 输出:电路输出,触发器的下一状态
-
列出时序电路的下一状态
- 得到状态图
- 分析电路性能
- 验证电路正确性,检查自我恢复能力 (self-recovery capability),画出时间参数

Input Equations⚓︎
触发器的输入方程:
- 用 D 表示触发器的输入,用下标表示特定的触发器的输出
- 有多少个触发器,就有多少输入方程
🌰;
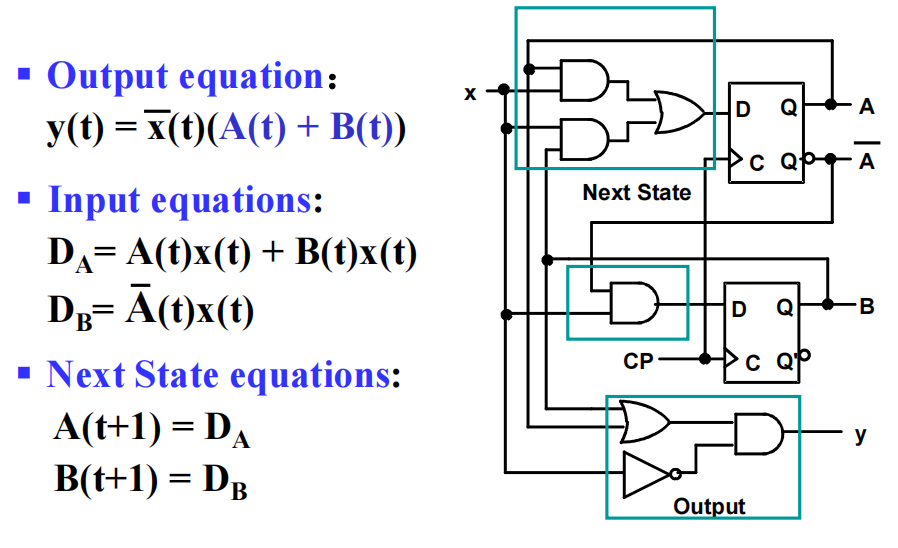
State Tables⚓︎
状态表 (state table) 是一个包含多变量的表格,分为以下 4 个部分:
- 输入:t 时刻的输入组合
- 当前状态:t 时刻的状态值
- 下一状态:t+1 时刻 ( 即下一时刻 ) 的状态值 ( 基于当前状态和输入 )
- 输出:t 时刻的输出值,即关于当前状态和 ( 有时 ) 输入的函数
注:从真值表的角度看,输入部分为输入和当前状态,输出部分为输出和下一状态
🌰( 接着上面的例子 ) 我们从输入、下一状态、输出方程中得到以下状态表;
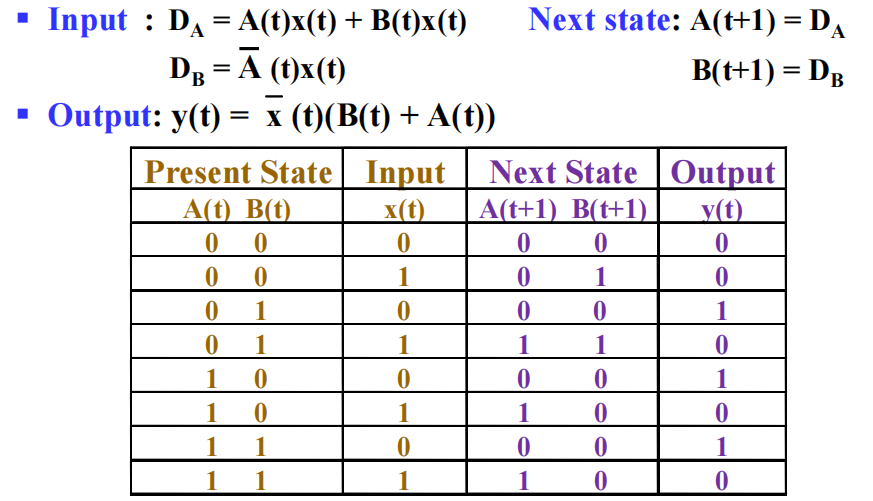
注:对于一个具有 m 个触发器和 n 个输入的时序电路,它的状态表一共有 \(2^{m+n}\) 行。下一状态共有 m 列
状态表的另一种形式——二维表。它能够较好地匹配 K-map,可以看到表格中的当前状态是按照格雷码顺序排列的:
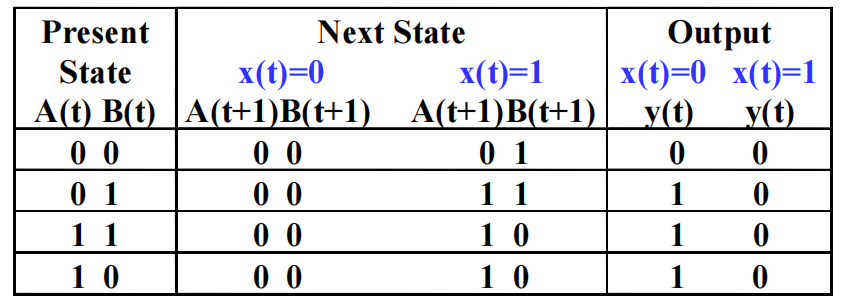
State Diagrams⚓︎
时序电路的功能还可以用状态图 (state diagram) 表示,它由以下部分组成:
- 用圆圈表示状态,圆圈内部写有当前状态的名称
- 用有向边表示从当前状态到下一状态的状态过渡 (state transition)
- 有向边上的标签表示导致某种状态过渡的输入
-
根据输出表示方法的不同,我们有以下 2 类:
- 米里型 (Mealy type):当输出依赖于状态和输入时,输出写在有向边上(输入和输出的标签用斜杠 (/) 区分)
- 摩尔型 (Moore type):当输出仅依赖于状态时,输出写在圈内
具体介绍
输出是仅关于状态的函数,因此在状态图中与状态一起写在圈内
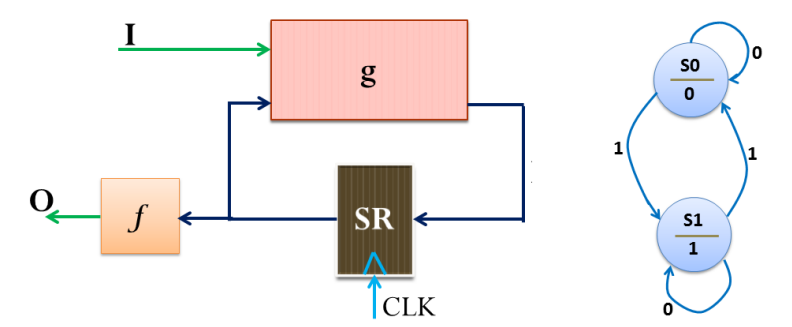
输出是关于输入和状态的函数,因此在状态图中位于状态过渡的弧上
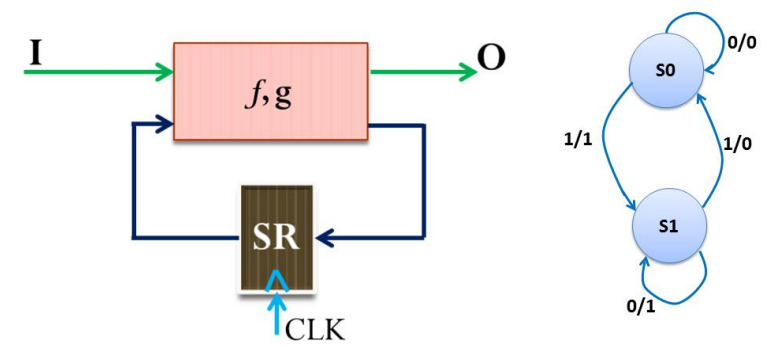
🌰( 还是接着之前的例子 ) 从二维的状态表中得到(米里型)状态图:
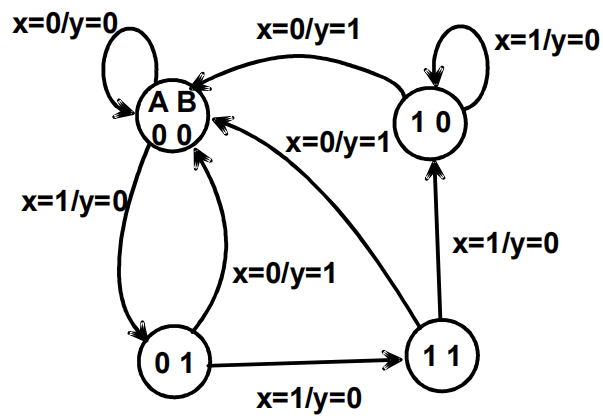
状态表 vs 状态图
- 状态表:更容易从逻辑图和输入方程中得到
- 状态图:更形象地展现不同状态间转变的过程,方便人们理解电路的运作方式
Equivalent States⚓︎
如果两个状态对于每个可能的输入,都得到相同的输出 ( 包括下一状态 ),则称这两个状态是等价的 (equivalent)。等价的两个状态可以进行合并,达到化简的目的。
注:状态的减少不一定减少成本,因为门成本取决于组合逻辑电路和触发器的总成本。尽管如此,合并等价的状态为设计、验证和测试带来内在的好处
Example
接着上面的例子,圈内的数字用字母编号表示
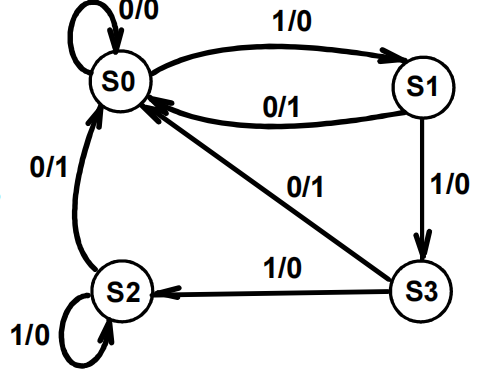
观察S2和S3,当它们的输入相同时,下一状态和输出均相同
- 输入 0,下一状态为 S0,输出为 1
- 输入 1,下一状态为 S2,输出为 0
所以,S2 和 S3 是等价的。因此,我们可以对状态图进行化简,见 " 化简 1"
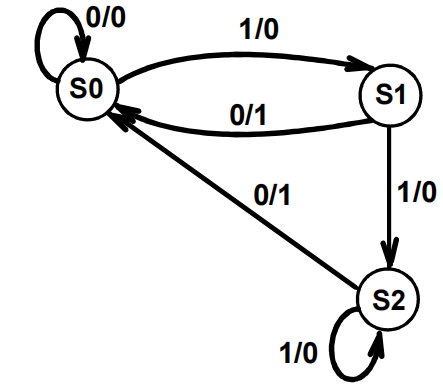
对于这张新的状态图,我们观察S1和S2,发现它们也是等价的,因为:
- 输入 0,下一状态为 S0,输出为 1
- 输入 1,下一状态为 S2,输出为 0
以我们又可以对状态图化简,最终的化简结果如 " 化简 2" 所示:
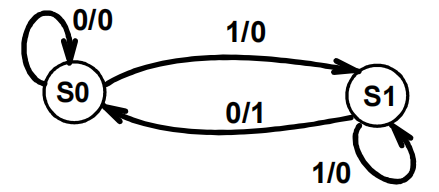
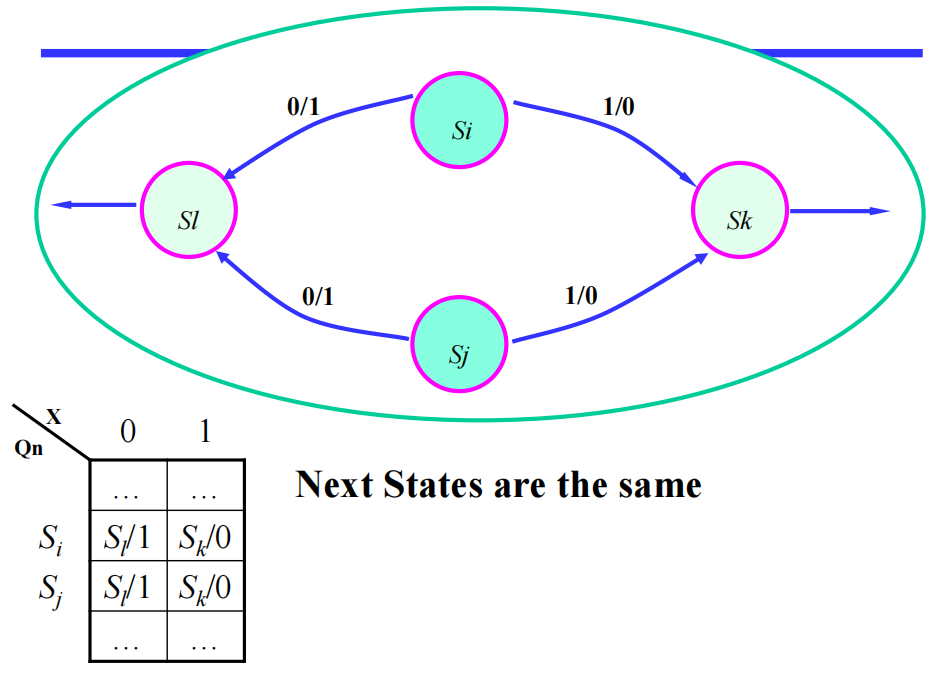
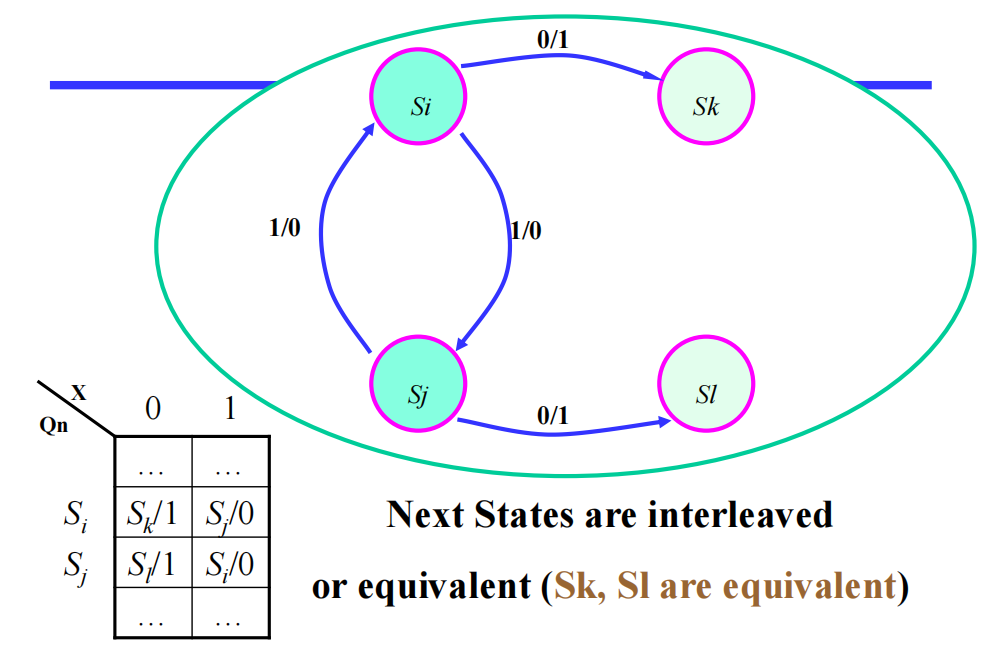
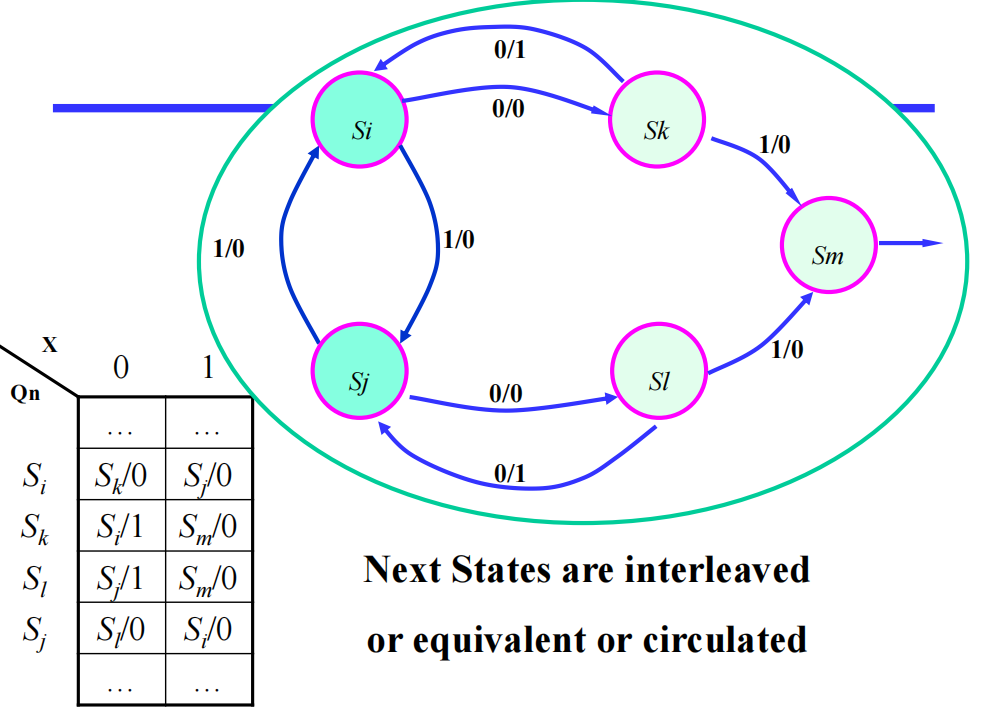
等价状态的类型 ( 前提:对于所有输入,输出都是一样的 ):
- 相同的下一状态
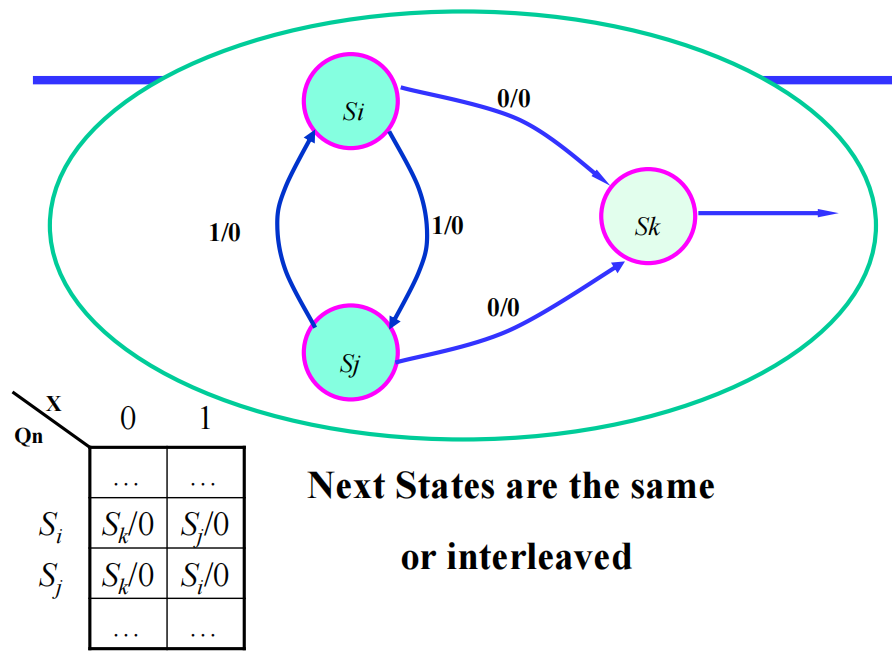
- 交错 (interleaved)的下一状态
- 循环 (circular)的下一状态
Example
Sequential Circuit Simulation⚓︎
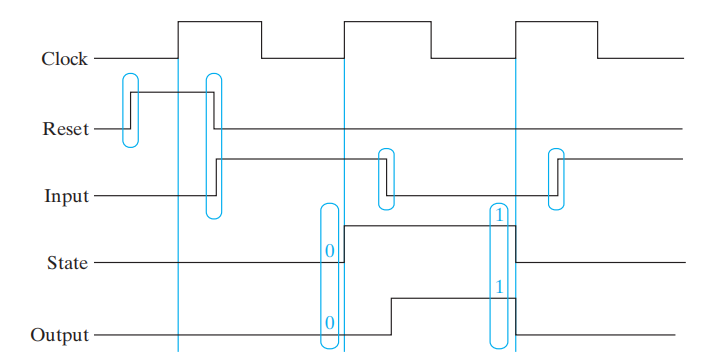
时序电路的仿真 ( 模拟 ) 需要考虑:
- 输入序列中必须出现一组特定的模式 (pattern),包括随时间应用的输入模式和时钟脉冲
- 开始仿真前,需要初始化一个确定的状态,即复位信号 (reset signal)
- 通过观测状态,验证正确性。一个简单的方法是,对每一个状态信号添加一个输出 ( 就像调试 C 代码时添加一些
printf()语句 ) -
随时间应用的输入和对输出的观察与正时钟边沿有关
- 功能仿真 (functional simulation):验证电路的功能,假设电路元件没有延迟或延迟很小。有的仿真器使用一个很小的延迟,以便于观测信号改变的顺序,但如果这个延迟不够小,就会导致问题
- 时间仿真 (timing simulation):验证电路是否正常运作 ( 考虑时间 ),此时考虑电路元件的实际延迟
Timing Analysis of Sequential Circuits⚓︎
时序电路的时间分析的🎯:找到电路的最大延迟 \(\rightarrow\) 最大时钟频率\(f_{\max}\)( 或者最小时钟周期\(t_p\))
Why?
如果时钟周期过短,在建立时间开始前,从电路传到触发器的数据可能来不及改变。
有下列时间参数:
- \(t_p\):时钟周期
- \(t_{pd, FF}\):触发器的传播延迟——从到达时钟边沿,到触发器的输出开始稳定之间的时间
- \(t_{pd, COMB}\):组合逻辑的延迟——从触发器的输出到触发器的输入之间的通路上,组合逻辑的总延迟
- \(t_s\):触发器的建立时间——在时钟事件发生前,数据输入应该保持稳定的时间
- \(t_{slack}\):松弛时间——时钟周期中额外的时间
注:
- 中间 3 个时间限制均来自电路通路
- 注意到触发器的保持时间 \(t_h\) 并不在讨论范围内,但它和其他情况的时间限制方程有关
- 到达一个或多个触发器的时钟信号有延迟,被称为时钟偏移 (clock skew),这会影响 \(f_{\max}\)
时序电路的时间通路 (timing paths):
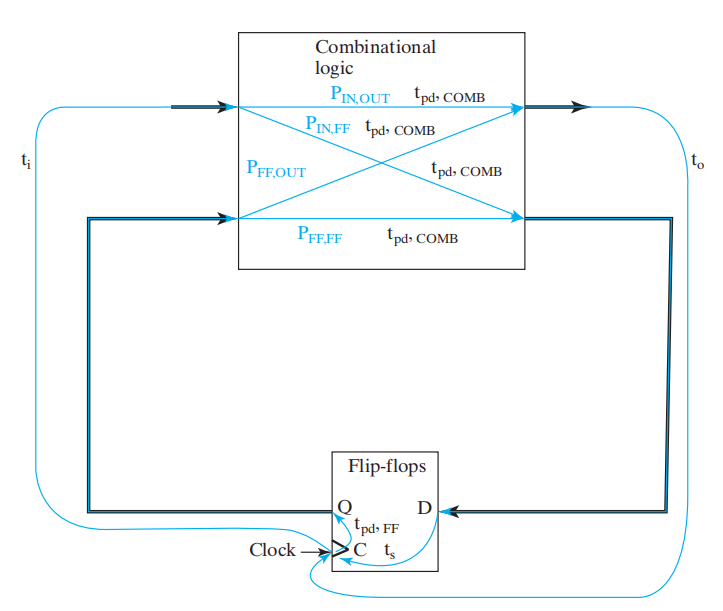
下列时序图标注了上述的时间参数:
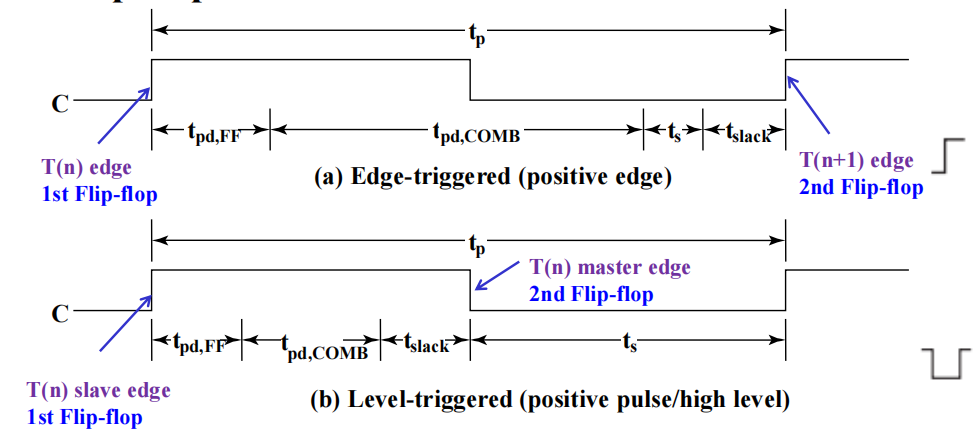
我们可以得到时间方程: $$ t_{pi} \ge t_{slack} + (t_{pd, FF} + t_{pd, COMB} + t_s) $$ 若\(t_{slack} \ge 0\),则 $$ t_p \ge \max(t_{pd, FF} + t_{pd, COMB} + t_s) = t_{p, \min} $$ 这对从触发器输出到触发器输入间的所有通路都是适用的
注:虽然我们可以用 \(t_{PHL}\) 和 \(t_{PLH}\) 来代替 \(t_{pd}\),使时间分析更加准确,但这样就需要额外考虑通路的逆向。因此为了方便,我们统一采用 \(t_{pd}\)
例题
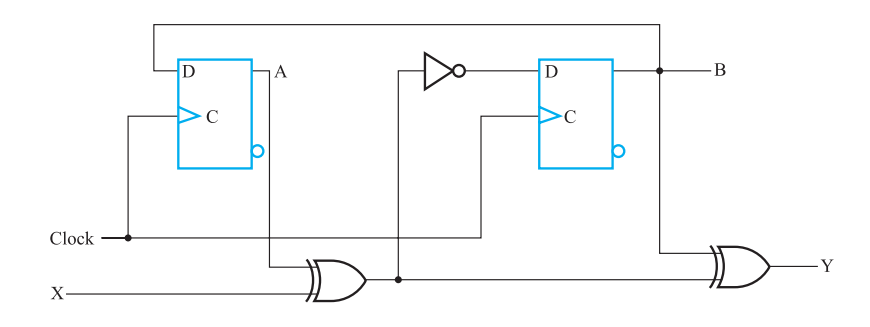
对下列电路进行时间分析:
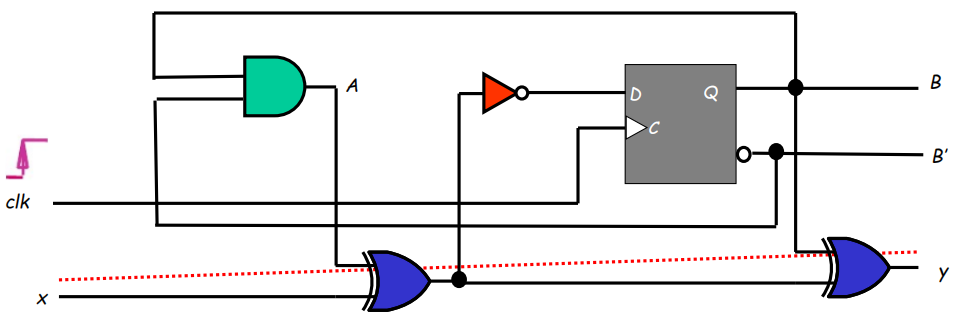
其中:
- \(t_{pd, NOT} = 0.5ns\)
- \(t_{pd, FF} = 2.0ns\)
- \(t_{pd, XOR} = 2.0ns\)
- \(t_s = 1.0ns\)
- \(t_{pd, AND} = 1.0ns\)
- \(t_h = 0.25ns\)
求:
- 外部输入 \(\rightarrow\) 输出之间的最大延迟
- 外部输入 \(\rightarrow\) 正边沿
- 正边沿 \(\rightarrow\) 输出
- 正边沿 \(\rightarrow\) 正边沿
- 外部输入 \(\rightarrow\) 输出之间的最大延迟:\(t_{pd, XOR} + t_{pd, XOR} = 4.0ns\)
- 外部输入 \(\rightarrow\) 正边沿:\(t_{pd, XOR} + t_{pd, NOT} + t_s = 3.5ns\)
- 正边沿 \(\rightarrow\) 输出:\(t_{pd, FF} + t_{pd, AND} + t_{pd, XOR} + t_{pd, XOR} = 7ns\)
- 正边沿 \(\rightarrow\) 正边沿:\(t_{pd, FF} + t_{pd, AND} + t_{pd, XOR} + t_{pd, NOT} + t_s = 6.5ns\)
所以最大延迟为 6.5ns,最大频率为 \(f_{max} = \frac{1}{6.5 \times 10^{-9}} \approx 154MHz\)
( 来自教材习题 )



Sequential Circuit Design⚓︎
时序电路设计的流程如下:

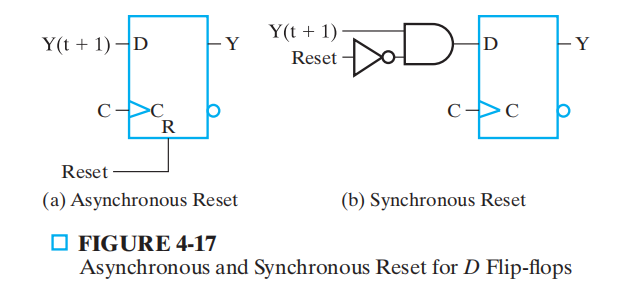
为了确定电路的初始状态 ( 即复位状态 ),我们需要用到复位信号,有异步和同步之分:
注:如果用的是异步复位 ( 直接输入 ),这违反了触发器的同步性质
序列识别器
注:这里的序列识别器用来识别序列 1101
- 输入:\(x(t) \in \{0, 1\}\)
- 输出:\(z(t) \in \{0, 1\}\)
- 函数:\(z(t) = \begin{cases}1 & \text{if } x(t-3, t) = 1101 \\ 0 & \text{otherwise}\end{cases}\)
某个给定的序列

特殊情况:1101101,
可以发现序列的首尾均出现了 1101,而且它们是重叠的,即 1101 101 和 110 1101
时序电路的设计:
-
对于正确的序列:
- 开始于初始状态( 即复位状态 )
- 添加一个状态,表明识别到所要识别序列中的第 1 个符号
- 当连续识别到正确的符号时,就连续添加状态
-
对于错误的序列:
- 最终状态代表输入序列 ( 可能小于最终输入值 ) 的出现
- 添加状态过渡弧,表明当前符号不在所要识别序列时发生的情况
- 对于所有非识别序列输入,添加其他的弧,表明代表那种错误序列出现时的状态过渡
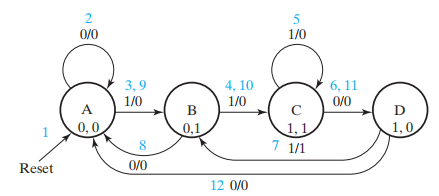
先找到正确序列情况下的状态图 ( 较为容易 ),这里我们列出了所有 4 个状态
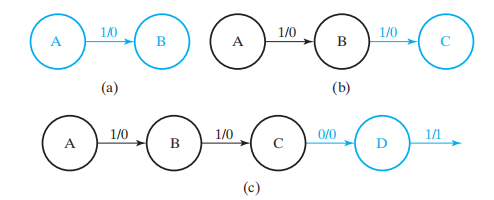
思考
当处于 D 状态时,如果我们输入 1,应该回到哪个状态?( 最右边的箭头该指向哪?)
还是举这个例子:1101101,可以发现第 1 个 1101 中最后一个 1,可以作为第 2 个 1101 中第一个 1,因此 D \(\rightarrow\) B。也就是说,我们重新利用了之前的状态,而不是盲目地添加新状态
除此之外,我们得考虑错误序列的情况,最终的状态图如下所示:
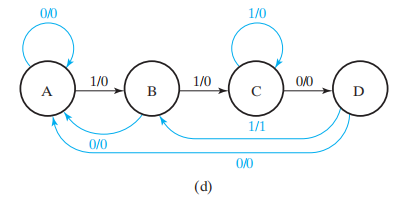
从状态图中,我们很容易地得到状态表
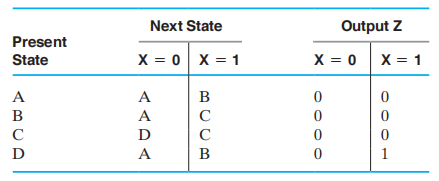
- 在摩尔型中,输出与状态相关
- 我们需要添加额外的状态 E,它对应的输出为 1
E 虽然与 B 很相似,但它的输出为 1,因此与 B 不同
- 因此,摩尔型相比米里型有更多的状态
“Moore is More”
状态图:
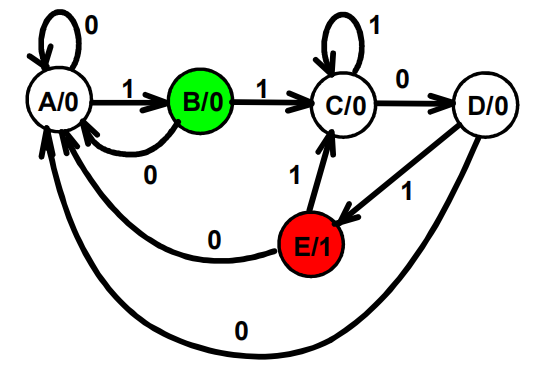
状态表:
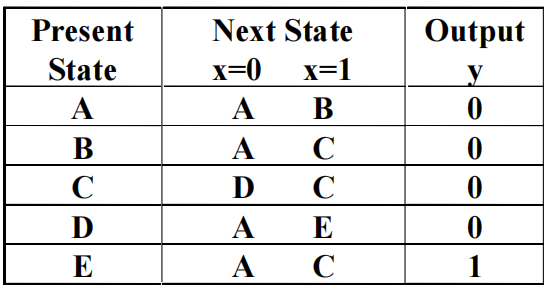
然而,虽然前面说过 B 和 E“不一样”,但如果我们在将带有 E 的状态图转变回米里型:
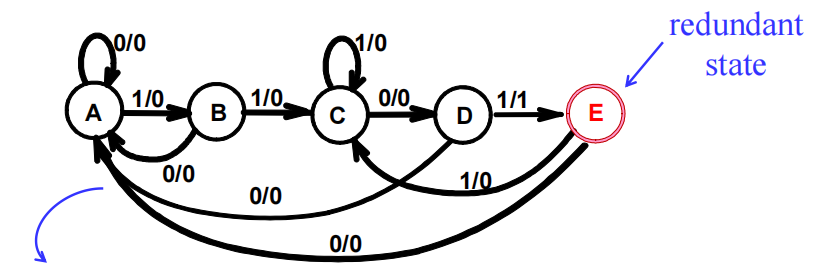
再画出对应的状态表:
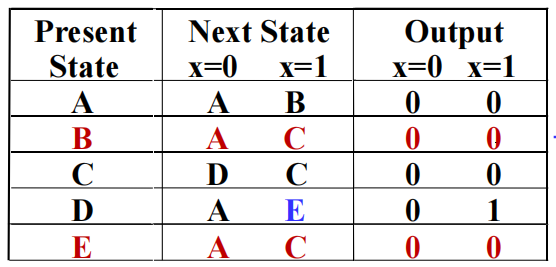
不难发现,B 和 E 其实是等价的,所以我们可以进一步化简:
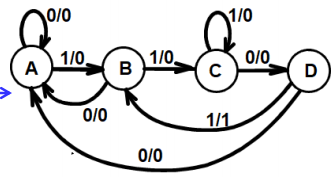
一切回到了原点😂
The Design Procedure⚓︎
- 规范 (specification)
- 构思 (formulation):得到状态图或状态表
- 状态最少化 (state minimization):最小化状态的数量
- 状态分配 (state assignment):为状态分配二进制码
- 找到触发器的输入方程 (flip-flop input equation determination):选择触发器的类型,从表中的“下一状态”一项中得到触发器的方程
- 找到输出方程 (output equation determination):从表中的“输出”一项中得到输出方程
- 优化 (optimization)
- 工艺映射 (technology mapping):从方程中得到电路,并映射到指定的触发器和门
- 验证 (verification):验证最终设计的正确性
Specification⚓︎
说明形式:
- 书面描述
- 数学描述
- HDL
- 表格描述
- 方程描述
- 描述运算的图 ( 不只是结构 )
Formulation⚓︎
🎯:找到状态图
在电路说明时,我们用状态来记住关于过去的输入序列的有意义的性质,这对于预测未来的输出值至关重要
State Minimization(Reduction)⚓︎
通过减少或最小化状态的总数,所需的触发器数量也随之减少。 我们可以通过消除等价状态 (equivalent states) 来减少状态总数。
等价定理 (equivalence theorem):对于每个状态表,存在一个唯一的等价表,使得状态的数量最小
如何做 ?
- 手工:观察、implication chart
- 算法:Hopcroft, Moore, Brzozowski
🌰:
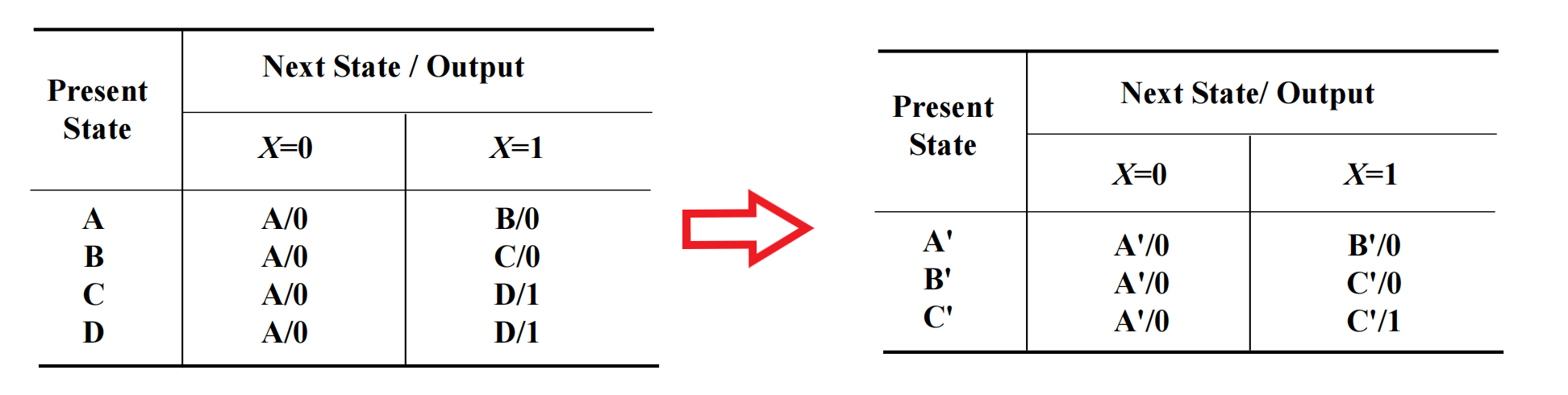
注:可以借鉴离散数学的等价类的知识,我们得到了 3 个等价类:{A}, {B}, {C, D},分别记作 A', B', C'
补充:Implication Chart
按顺序比较两个等价状态
- 如果发现等价状态,在对应位置上打 \(\surd\)
- 如果状态不相等,打 \(\times\)
- 如果需要进一步比较,列出下一状态的对
🌰:
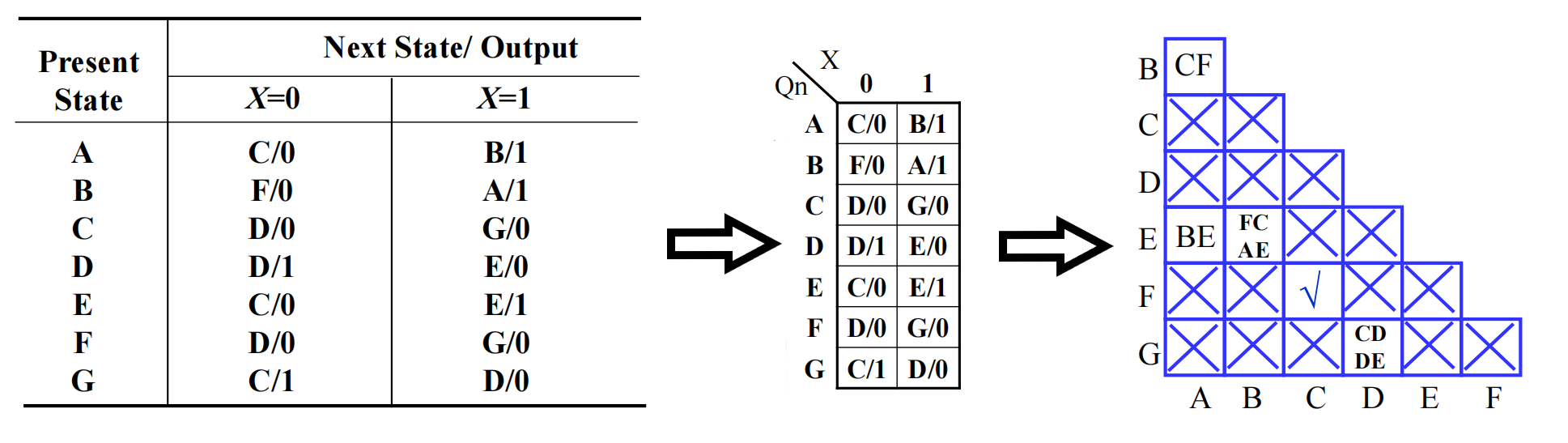
- 在进一步的比较中,发现 CD,DE 不是等价的,因此 DG 不是等价的
- 这样,我们得到:
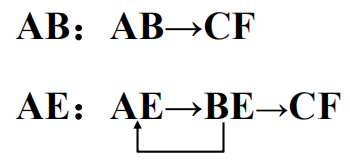
- 找到最大的等价类:(A, B, E), (C, F), (D), (G),标记这 4 个状态位 a, b, c, d
State Assignment⚓︎
我们需要将所有 \(m\) 个状态赋上一个唯一的编码,编码的长度 \(n \ge \lceil \log_2 m \rceil\)。这样会产生 \(2^n - m\) 个无用的状态
方法:计数顺序分配、格雷码分配、独热码分配
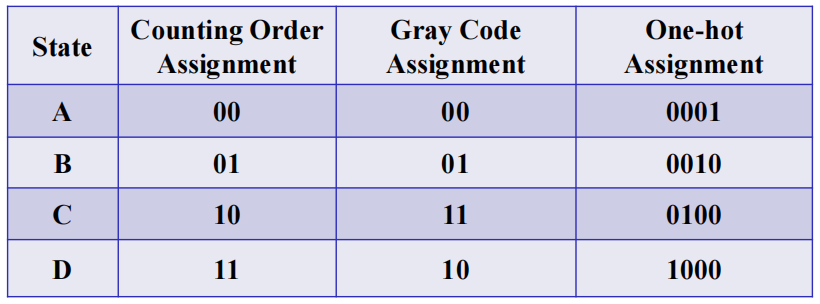
Example
对于前面的 1101 序列识别器,我们采用上述 3 种方法进行状态分配,得到以下状态表:

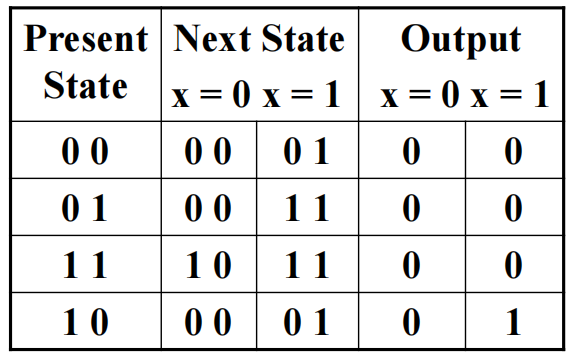
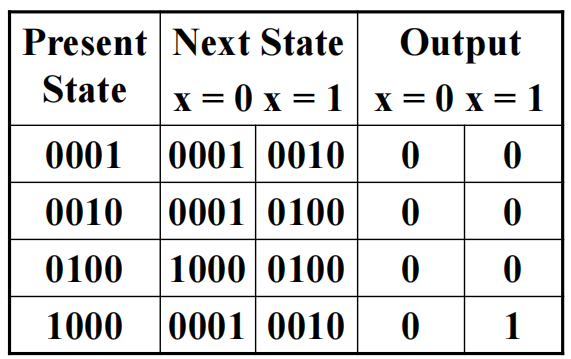
注:独热码的优劣:
- 优:得到更简单、更快速的逻辑,便于调试和分析
- 劣:触发器的成本会提高 (m 个状态需要 m 位独热码,也就需要 m 个触发器 ),这样就产生 \(2^m - m\) 个没有用到过的编码
不难发现,不同的分配会产生不同的输入、输出函数,也会影响电路的复杂度。状态分配的目标是:
- 决定编码的长度
- 找到最佳或近似最佳的状态分配 当N 很大时,找到最佳分配是件很困难的事;而且状态分配的性能也取决于触发类型。实际上,我们采用工程方法进行状态分配,这需要用到启发性的规则 (heuristic rules)
Flip-Flop Input and Output Equation Determination⚓︎
Example
对于前面的序列识别器,我们分别用上述三种方法进行状态分配:
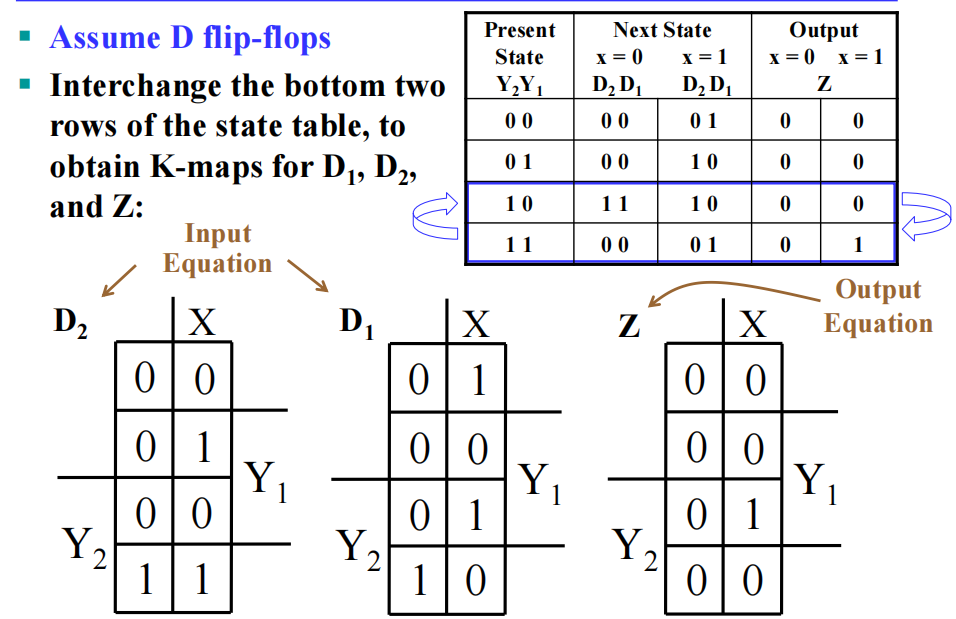
由卡诺图,我们得到: $$ D_2 = Y_2\overline{Y_1} + X\overline{Y_2}Y_1 \quad D_1 = \overline{X}Y_2\overline{Y_1} + X\overline{Y_2Y_1} + XY_2Y_1 \quad Z = XY_2Y_1 $$ 门输入成本 = 22
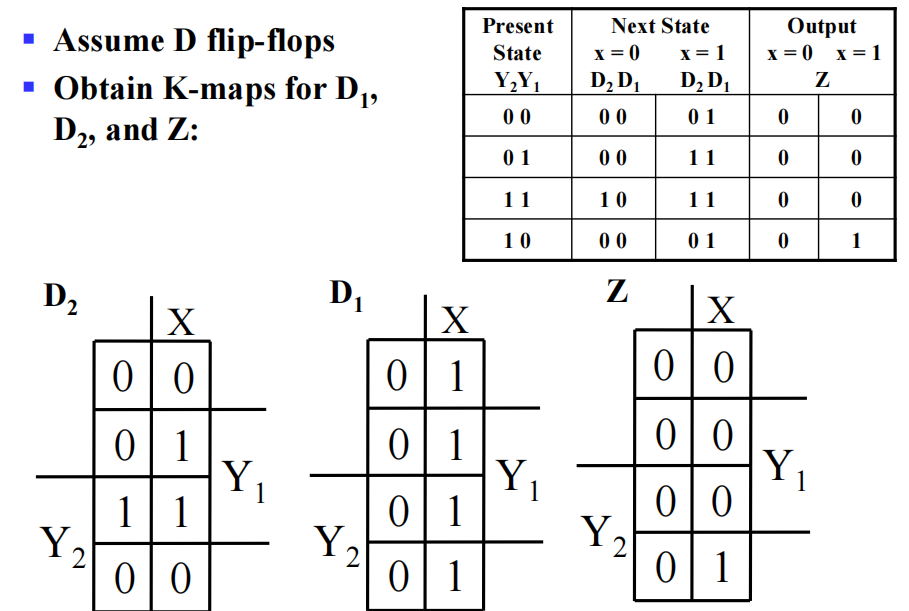
由卡诺图,可以得到:$$ D_2 = Y_2Y_1 + XY_1 \quad D_1 = X \quad Z = XY_2\overline{Y_1} $$ 门输入成本 = 9
电路图:
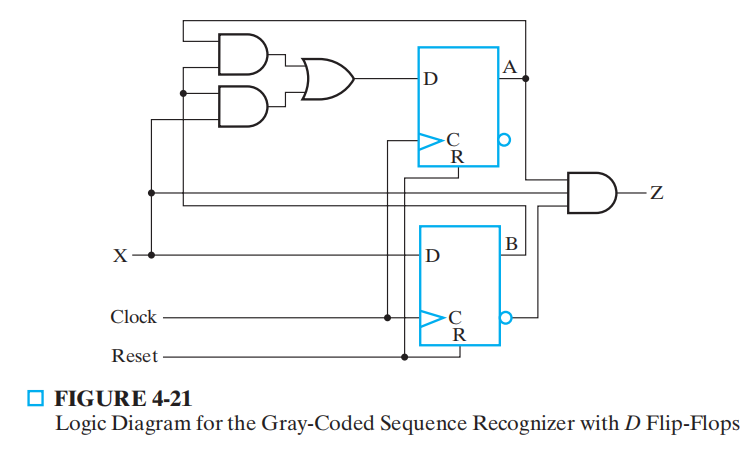
( 没有卡诺图,注意有 4 个输入方程 )
门输入成本 = 17
电路图:
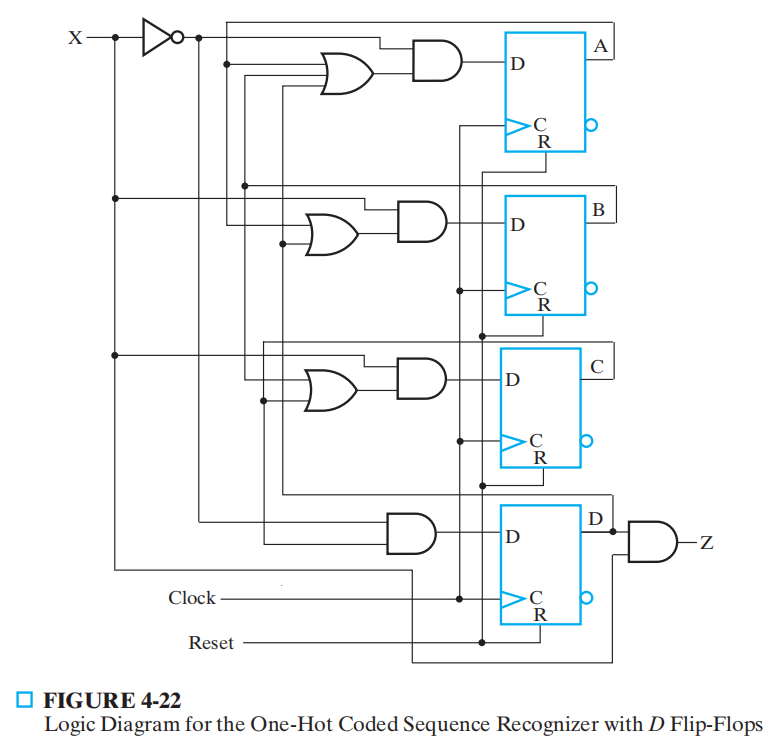
Technology Mapping⚓︎
🌰( 接着上面的例子,我们选取最优的格雷码分配 ):
假设我们的库中只有 D 触发器和与非门 ( 包括非门,至多 4 输入 ),那么我们需要技术映射,电路图如下:
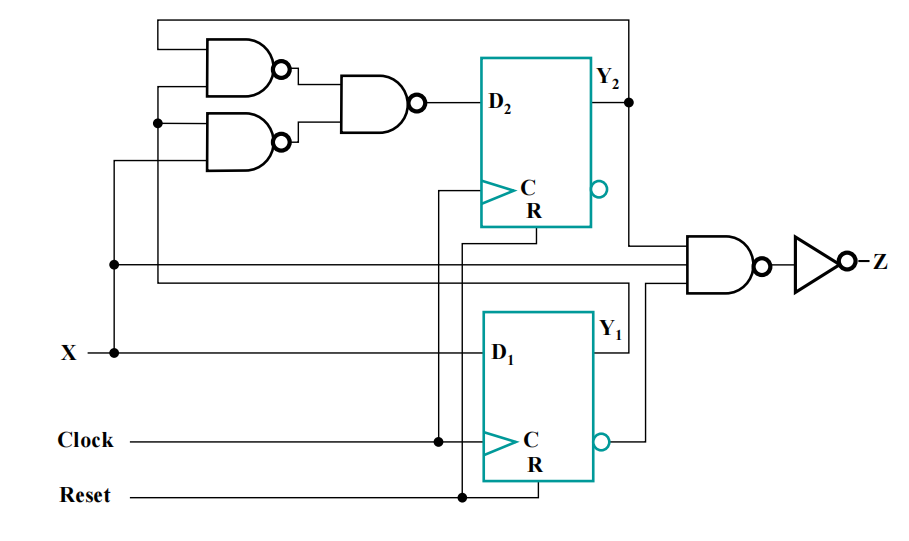
Designing with Unused States⚓︎
对于没有用到的状态,我们把它当作不关心的情况 (don't-care conditions),然后就在 k-map 的相应位置上打上 '\(\times\)',利用这些 '\(\times\)' 进行化简
Example

在实现中,我们如何应对未使用的状态?
- 对于未使用的状态,需要说明它对应的输出,这样,来自未使用的状态及其状态过渡的行为就不会是有害的
- 为未使用的状态添加额外的输出,表明电路进入不正确的状态
- 对于未使用状态下的下一状态行为需要指定,以确保电路能在不使用复位的情况下回到正常的运行
Verification⚓︎
- 手工模拟 (manual verification):手工地将所有的输入组合都试一遍,看结果是否符合预期
- 仿真验证 (verification with simulation):只要准备好输入组合的序列和时钟,剩下的过程交给计算机自动处理,结果以时序图 ( 波形图 ) 的形式呈现
🌰:验证“1101”序列识别器的正确性:
- 手工模拟
- 仿真验证
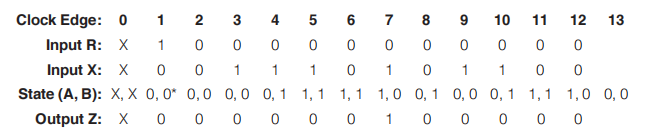
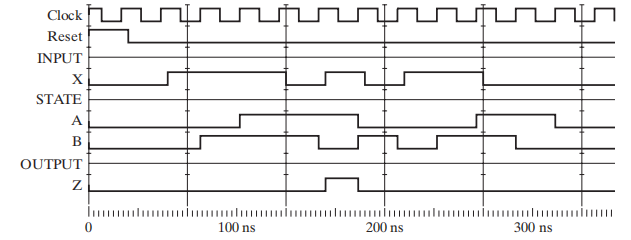
设计 1 个 2 位模 3 累加器
定义:
- 模 n 加法器 (modulo n adder):\(a +_m b = (a + b)\ \mathbf{mod}\ m\)
- 累加器 (accumulator):随时间变化累加输入之和的电路,初始为 0
规范:
- 输入:\((X_1, X_0)\)
- 被存储的和:\((Y_1, Y_0)\)
- 输出:\((Z_1, Z_0)\)
状态图 (摩尔型):
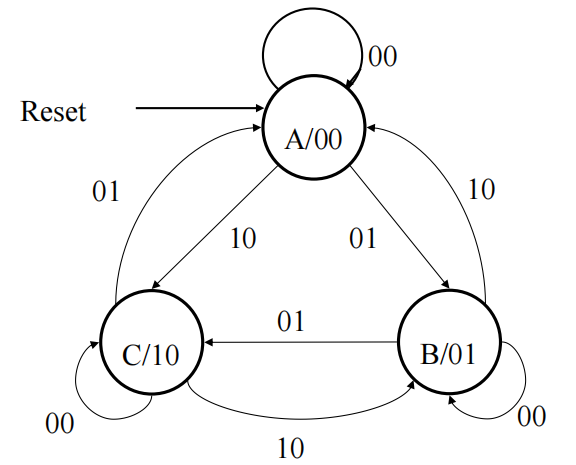
状态表:
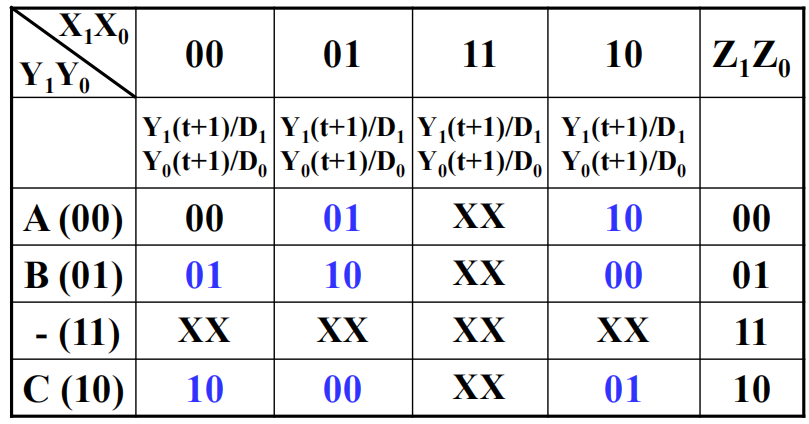
注:可以看到,表中的编码按格雷码顺序排列,方便后面用 K-map 化简
状态分配:\((Y_1, Y_0) = (Z_1, Z_0)\)
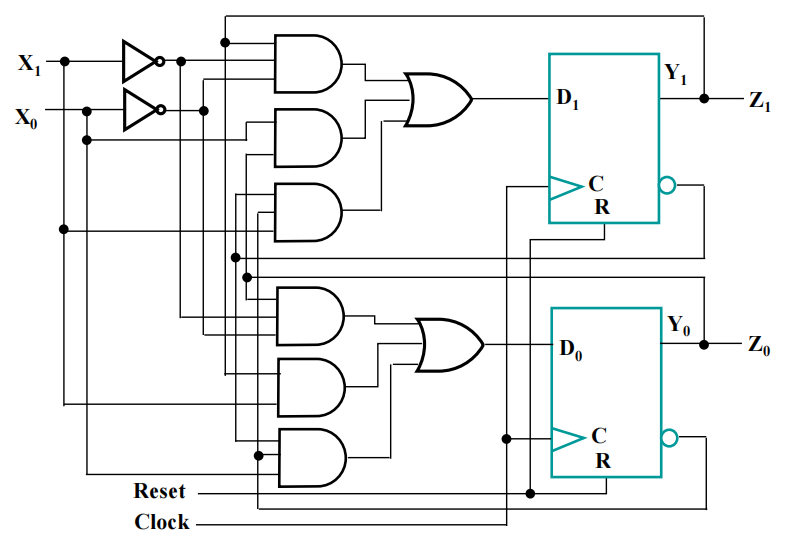
利用 K-map 找到 D 触发器最优的输入方程:
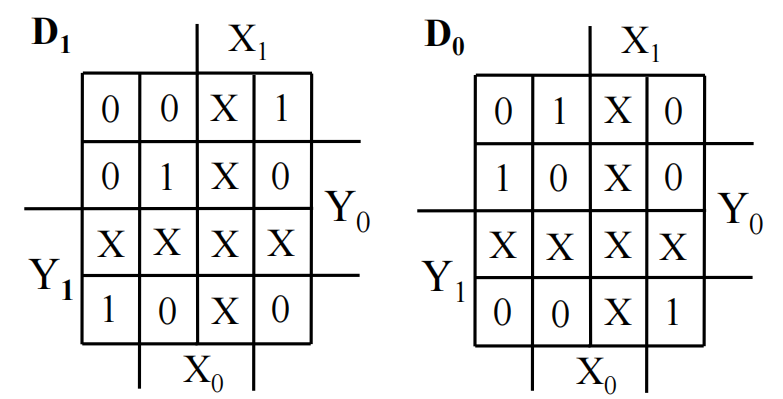
State Machine Design⚓︎
这一节内容在课件里没有详细讲述,而且考试不要求,所以这里就稍微提一下 (
写的很水),具体内容见修佬的笔记
可略过
-
传统的状态图 (traditional state diagram) 的局限,导致其不适用于大型电路:
- 对于 n 个输入变量,必须指定 \(2^n\) 个输入组合,即使下一状态或输出仅取决于部分输入
- 对于 m 个输入变量,必须指定 \(2^m\) 个输入组合,即使仅有部分的输出受状态和输入的影响
-
状态机 (state-machine diagram)
- 使用摩尔型来指定输出
- 通过布尔表达式和方程来替代输入、输出组合的枚举
通用状态机模版:
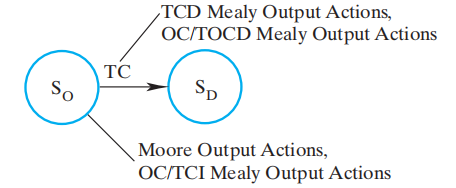
状态机模型主要分为 3 部分:输入条件、过渡、输出行为
- 输入条件 (input condition):表述为关于输入变量的布尔表达式或方程
- 过渡条件 (transition condition, TC):在过渡弧上的输入条件
- 输出条件 (output condition, OC):当值为 1 时,导致输出行为产生的输入条件
-
无条件过渡 (unconditional transition):无视输入值,总是发生于下一个时钟的过渡 ( 内在传输条件 = 1)
-
摩尔输出行为 (Moore output actions):仅取决于状态,即无条件的
- 过渡条件独立的米里输出行为 (transition-condition independent(TCI) Mealy output action)
- 过渡条件依赖的米里输出行为 (transition-condition dependent(TCI) Mealy output action)
- 过渡和输出条件依赖的米里输出行为 (transition and output-condition dependent(TOCD) Mealy output action):取决于状态、过渡条件和输出条件
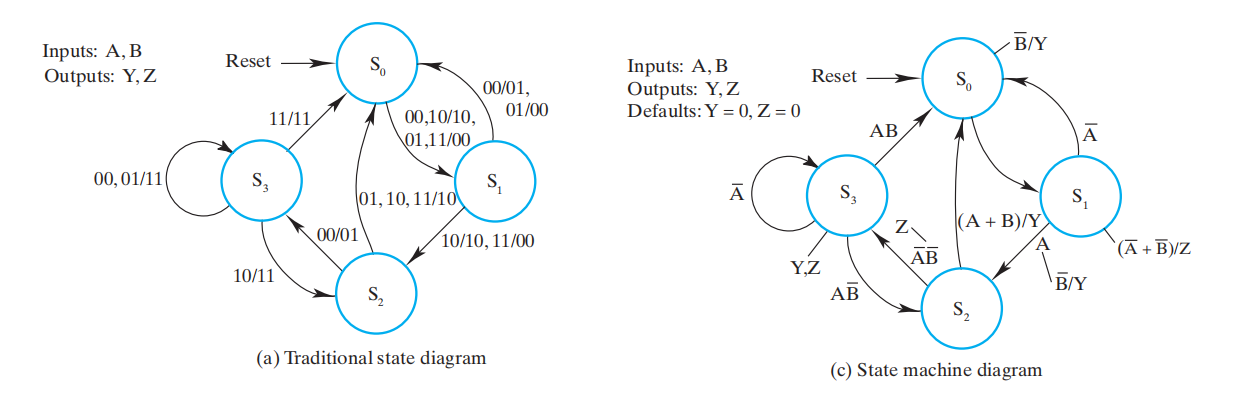
🌰:
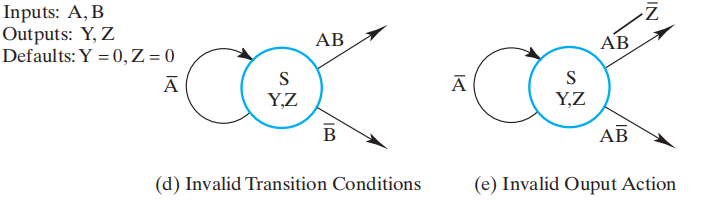
-
传统状态图
- 输入:\(\overline{AB} + \overline{A}B = \overline{A}\)
- 输出:\(Z = \overline{AB}\)
-
状态机
- 输入:\(A\overline{B} + AB = A\)
- 输出:\(Y = A\overline{B}\)
不正确的状态图:
用 Verilog 实现状态机 ( 略 )
Limitations of Finite State Machines⚓︎
- 在无限序列,比如 \([0]^*[1]^+\) 之类的序列里,只能使用有限的状态来识别特定的序列模式
Example
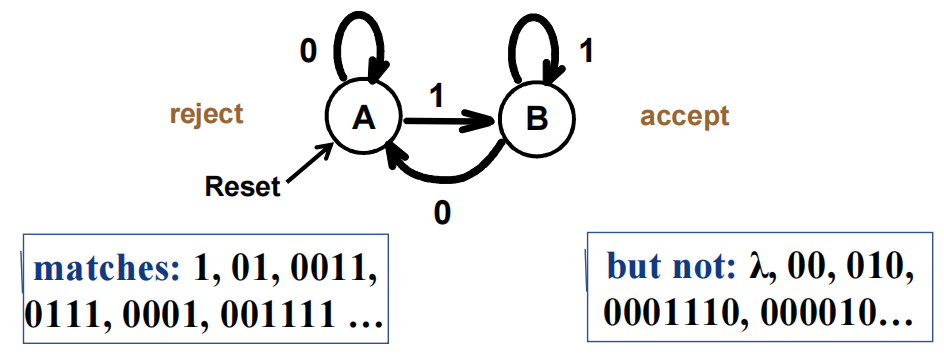
- 有限状态机只能识别有规律的语言,然而现实中有许多例子是无规律的
Other Flip-Flop Types⚓︎
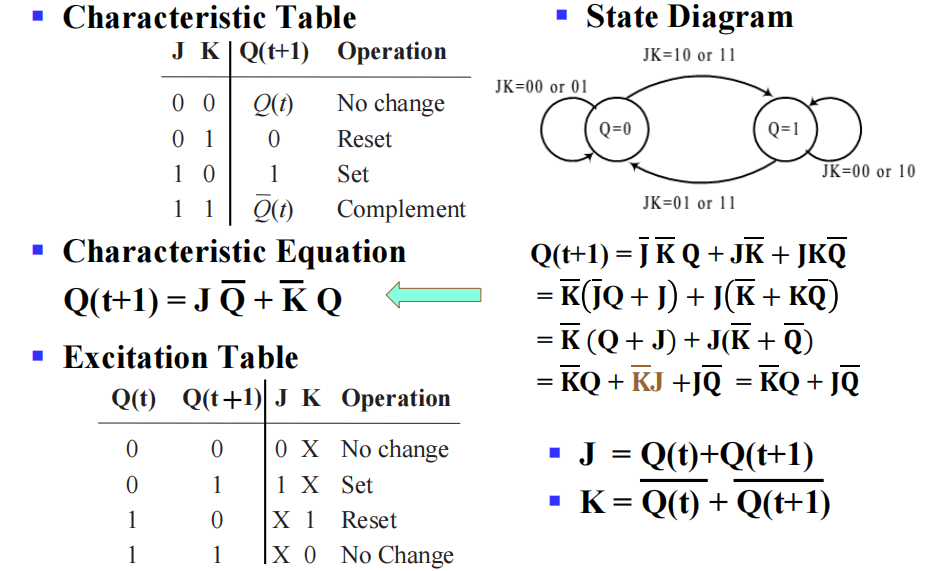
J-K Flip-Flop⚓︎
- 符号:
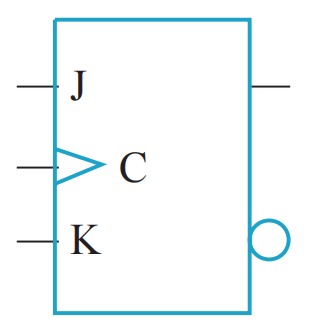
- 类似 S-R 触发器,J 类似 S,K 类似 R,除了该触发器允许 J = K = 1 时的情况
- J = K = 1 时,触发器进入相反状态 (opposite state)
- 作为主从触发器,J-K 触发器也有和 S-R 触发器一样的一次性采样问题,即:如果主锁存器的异常状态会传入从锁存器内
- 为了避免这一问题,可以用边沿 D 触发器作为核心的触发器
电路结构:
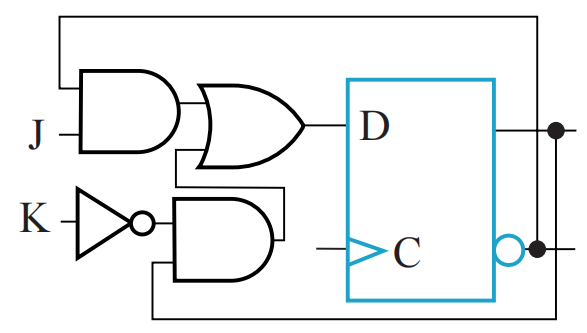
T(Toggle) Flip-Flop⚓︎
- 符号:
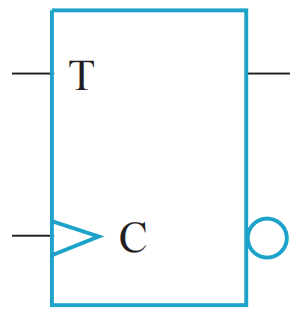
- 只有单个输入 T:当位于上升沿时 ( 如图所示的类型 ),T = 0 时不改变状态;T = 1 时切换至相反状态
- 当 J-K 触发器的输入 J = K = T 时,它与 T 触发器的功能相同
- 不能用输入 T 初始化触发器至确定状态
- 作为主从触发器,也有一次性采样问题,解决方法同上
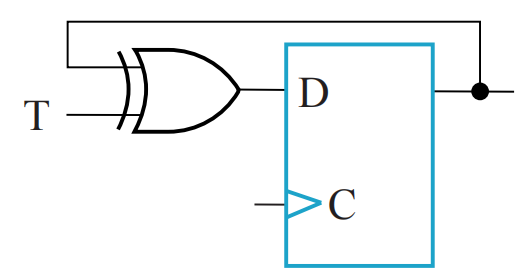
电路结构:
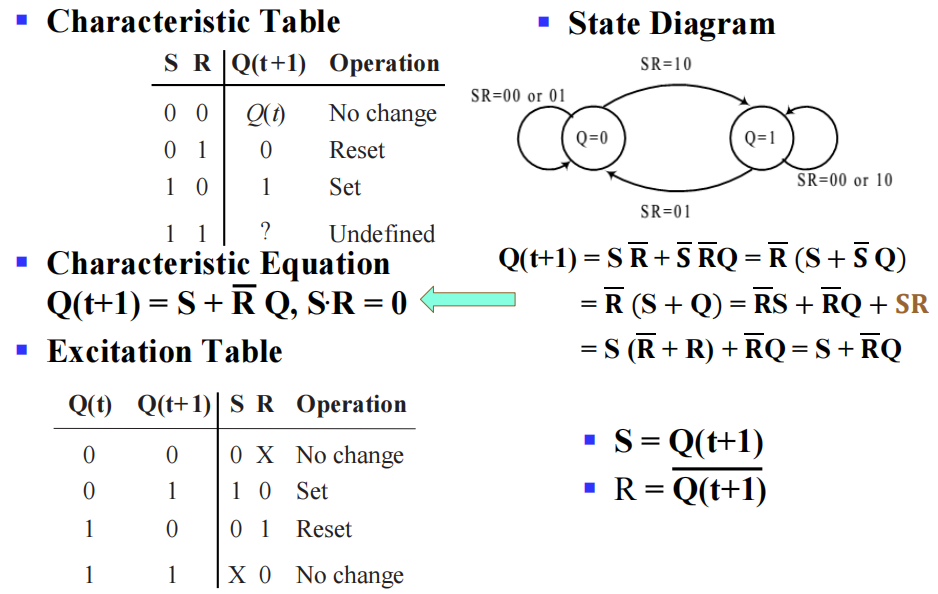
Basic Flip-Flop Descriptors⚓︎
-
用于分析:
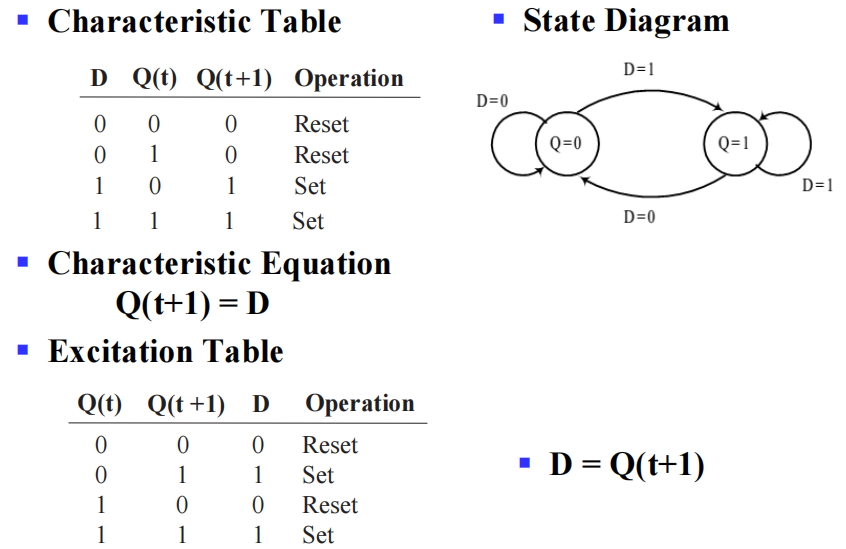
- 特征表:定义关于输入和当前状态的下一状态
- 特征方程( 下一状态方程 ):定义下一状态为输入和当前状态的函数
-
用于设计:
-
激励表:定义关于当前状态和下一状态的输入
- 激励方程:定义输入为当前状态和下一状态的函数
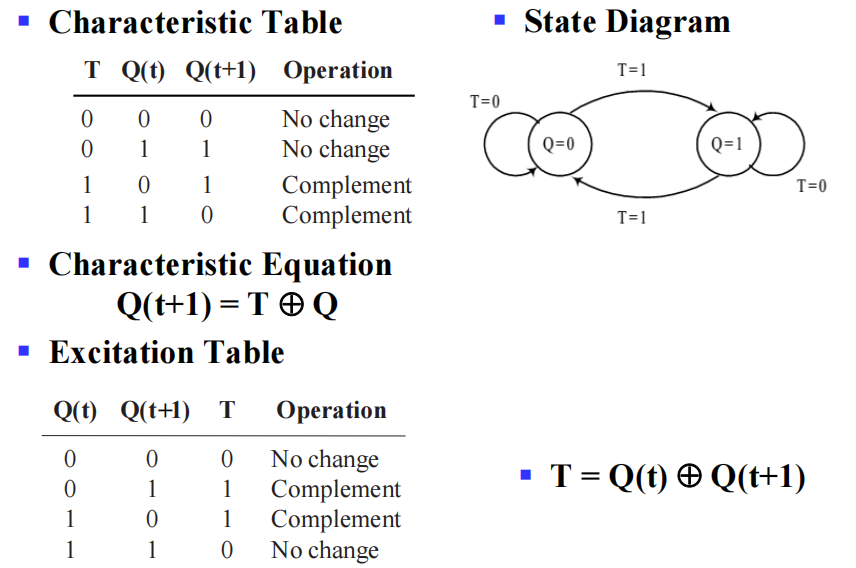
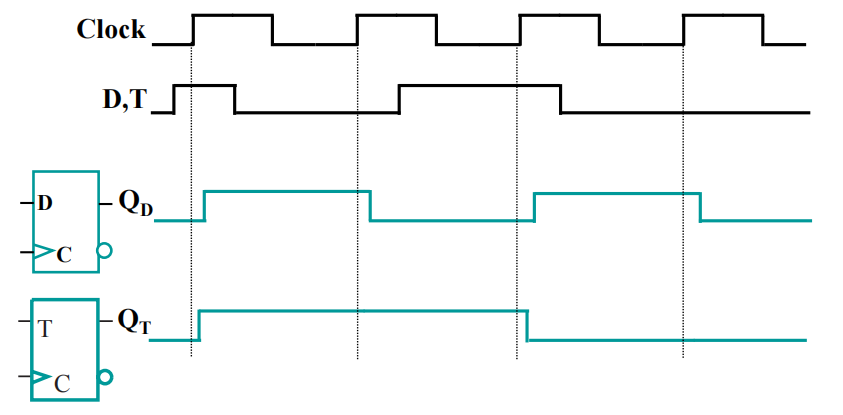
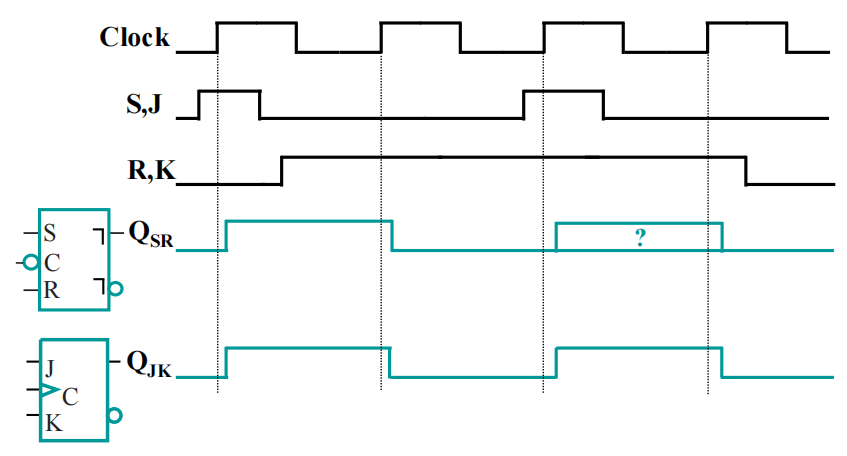
波形图:
Flip-Flop Conversion⚓︎
🌰:D 触发器 \(\rightarrow\) J-K 触发器
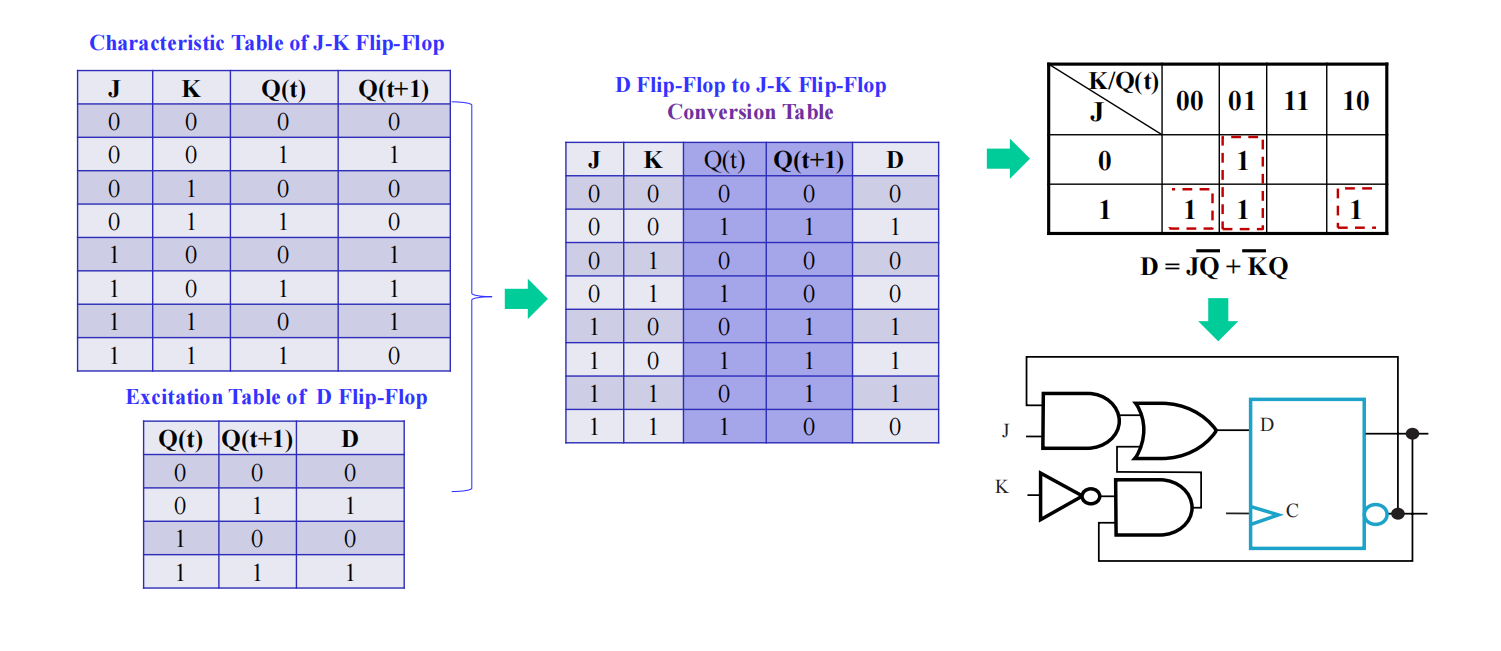
步骤:
- 画出想要得到的触发器的特征表
- 画出给定的触发器的激励表
- 合并两表为转换表
- 找出给定触发器的输入方程
Appendix⚓︎
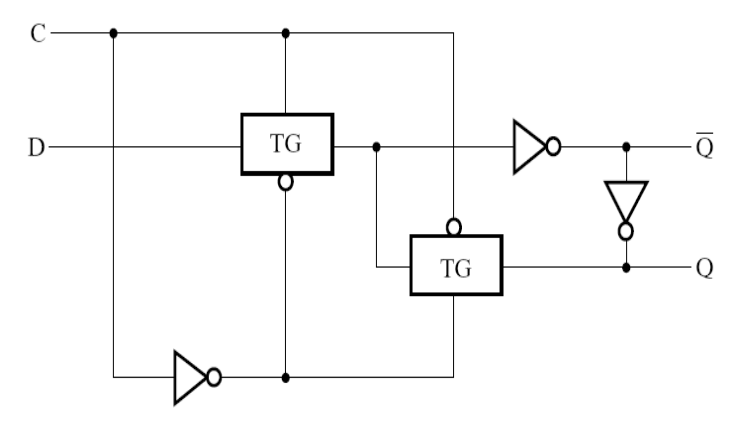
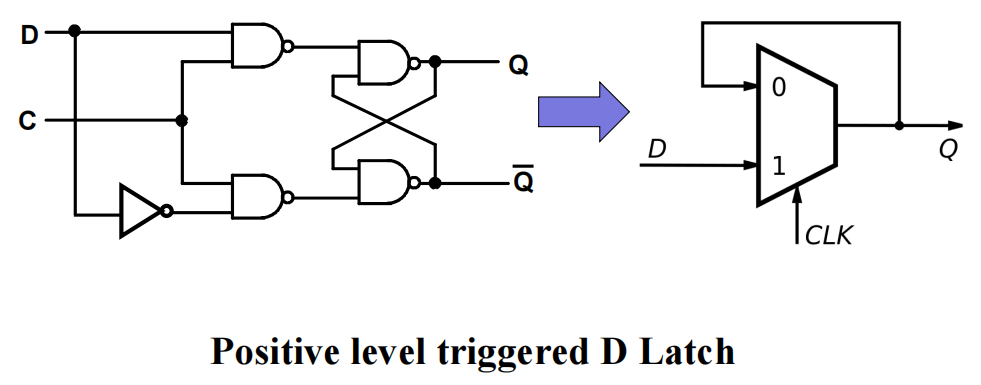
Other Implementation of Latches and Flip-Flops⚓︎
评论区