Chap 3 Combinational Logical Design⚓︎
约 8017 个字 预计阅读时间 40 分钟
核心知识
- 设计流程
- 分层设计
- 工艺参数:重点记忆与延迟相关的知识
- 工艺映射:只能用与非门 / 或非门构建电路
- 基本逻辑函数:值固定、传输、逆转、使能
- 译码器
- 编码器
- 多路复用器
- 加法器:半加器、全加器、行波加法器、超前进位加法器
- 减法的实现
- 补码
- 无符号与有符号
- 加减法器
Design Procedure⚓︎
两类逻辑电路:
-
组合逻辑电路 (combinational logic circuit):逻辑门的输出是只和当前输入有关的函数的电路,它包括:
- \(m\) 个布尔输入
- \(n\) 个布尔输出
- \(n\) 个开关函数,每个函数将 \(2^m\) 种输入组合映射到一个输出,使得当前输出值仅取决于当前输入值
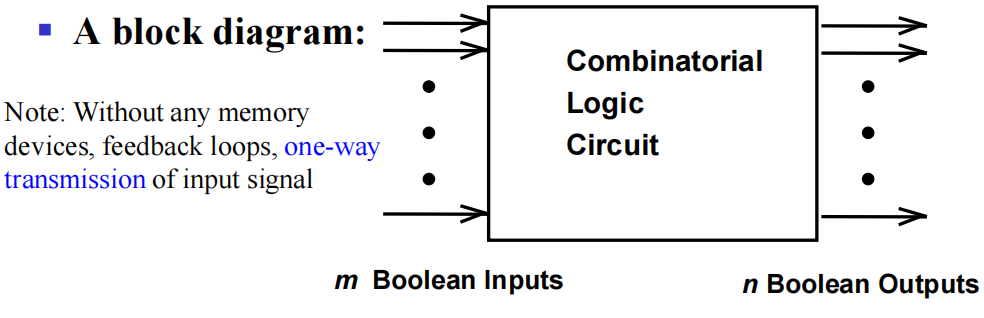
- 时序逻辑电路 (sequential logic circuit):逻辑门的输出是和当前输入,以及之前的输入(被称为状态 (state))都有关的函数的电路
注:Chap 4 会详细介绍时序电路的
Design Concepts and Automation⚓︎
分析逻辑电路的方法:
- 写下电路图对应的布尔函数
- 画出真值表
- 函数分析
- 检验
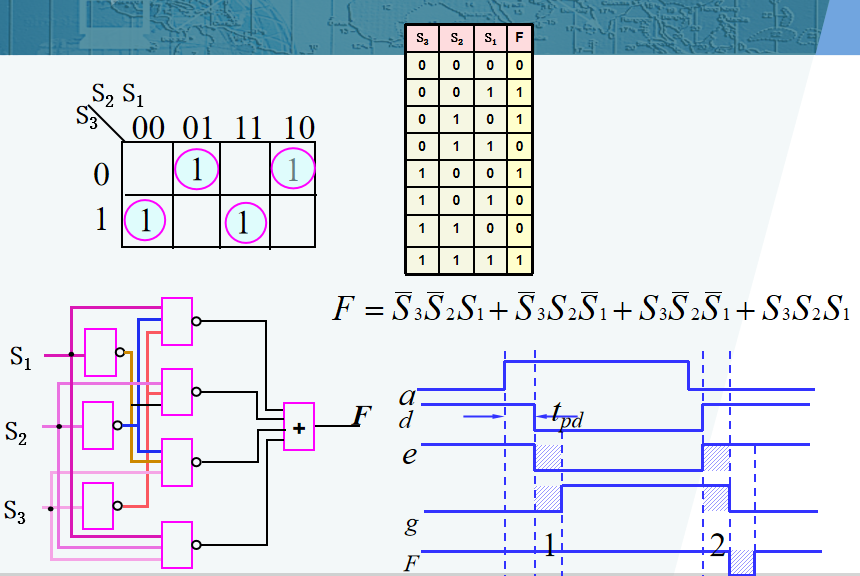
描述逻辑事件的形式:
- 真值表
- 布尔函数
- 卡诺图
- 时间图
- 逻辑电路
Hierarchical Design⚓︎
分层设计 (hierarchical design) 是一种化简组合电路设计的方法:
- 将函数分割成块 (blocks)
- 分割成更小的块,直至足够小
- 不可再分被称为原块 (primitive block)
- 所有的块构成了分层结构
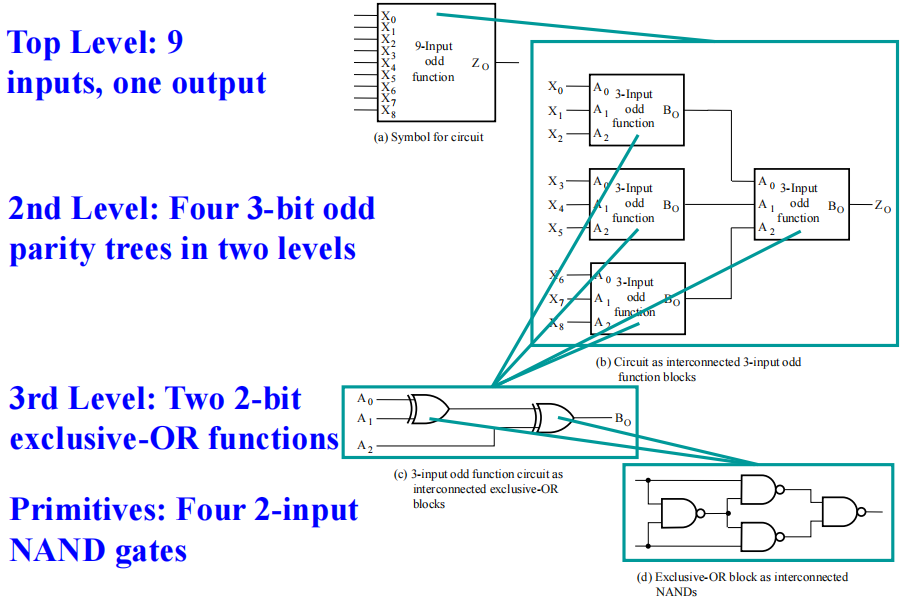
🌰:9 输入”奇偶位树 (parity tree)“
如果直接徒手画,显然是不切实际的,因此按照下面的分层设计,从整体一层层拆分,最后到门级结构
Reusable Function Blocks⚓︎
我们应尽量将复杂的设计分解为常见的、可重用的函数块,这些块应当通过检验,且放入库 (library) 中以供后续使用。 计算机辅助设计(computer-aided design, CAD)常用到函数块,比如:
- 原理图捕获 (schematic capture)
- 逻辑模拟器 (logic simulator)
- 定时验证工具 (tools for timing languages)
- 硬件描述语言 (hardware description languages):Verilog 和 VHDL
- 逻辑合成器 (logic synthesizers)
- 集成电路布局 (integrated circuit layout)
Top-Down versus Bottom-Up⚓︎
- 自顶向下设计 (top-down design) 从抽象的、高级的具体实现出发,通过分解和连续的修改,进行越来越细节的设计,控制整个设计的复杂程度。它回答了:我们需要构建什么样的电路?
- 自底向上 (bottom-up design) 从细节的、原始的块出发,将它们结合起来,形成更大更复杂的函数块,着重于细节。它回答了:我们如何构建电路?
在电子设计中,这两种设计思想往往同时进行。
Design Space⚓︎
Integrated Circuits⚓︎
集成电路 (integrated circuit,又叫芯片 ),是一块具有相互连接的数字门电路和存储元件的半导体
分类:
- SSI(small-scale integrated):少于 10 个门
- MSI(medium-scale integrated):10-100 个门
- LSI(large-scale integrated):100-1000 个门
- VLSI(very large-scale ingegrated):成千上万的门
Technology Parameters⚓︎
工艺参数 (technology parameters)
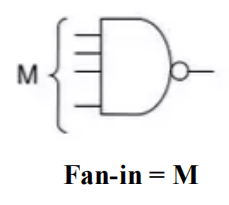
门电路可用的输入数量
在门电路输出的驱动下的标准负载 (standard loads) 数量
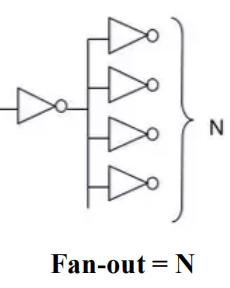
相关知识
1 个标准负载 = 1 个非门 (inverter) 的输入
过渡时间 (transition time):门输出改变 ( 高到低 / 低到高 ) 所需的时间
- 上升时间 (rise time)\(t_{LH}\):低电平 \(\rightarrow\) 高电平
- 下降时间 (fall time)\(t_{HL}\):高电平 \(\rightarrow\) 低电平
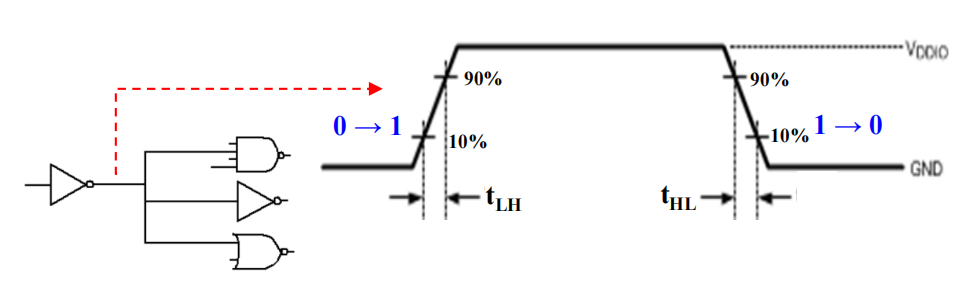
最大扇出 (maximum fan-out):门能够驱动的,不超过规定的最大过渡时间的标准负载的数量

随着标准负载的增加,过渡时间 ( 这里是上升时间 ) 也随之增加
在正常输入上施加的,不会导致电路输出的不良变化的最大外部噪声电压
对于一个门电路对整个集成电路成本的贡献的测量
在集成电路中:
- 门电路成本与门电路占芯片面积的大小成正比
- 门电路的面积大致与晶体管的数量和大小,以及线连接的数量成正比
- 如果无视连线区域,门电路面积大致与门输入数量成正比
- 所以我们用门输入数量大致测量门电路的成本
在上一章中我们已经详细分析过了,如果忘记就回去巩固一下
从输入到输出的传播过程中,信号值发生改变所需的时间
相关知识
高到低(\(t_{PHL}\)) 和低到高(\(t_{PLH}\)) 的输出信号的改变可能有不同的传播延迟。这两者只与输出有关,与输入不相关。
通常,我们通过输入 / 输出的高低电平的中点的延迟差来计算传播延迟,见下图
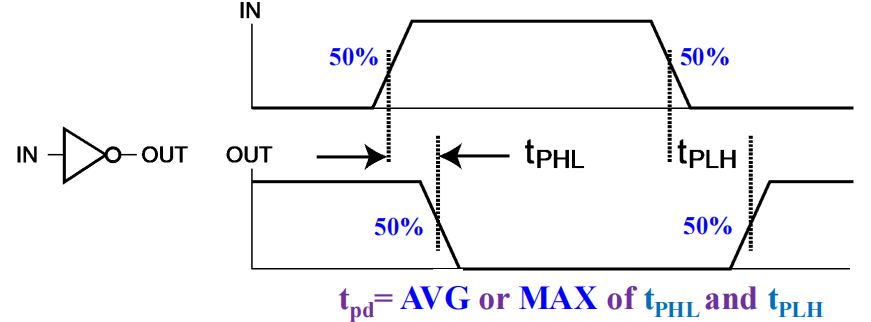
注:注意过渡时间和传播延迟两个概念的区别!
延迟模型 (delay model):用于描述内部固有的门延迟
- 传输延迟 (transport delay):输入发生变化后,输出在固定的一段延迟后才发生相应的变化
- 惯性延迟 (inertial delay):类似传输延迟,但如果出现小于拒绝时间 (rejection time) 的脉冲变化,则输出将不会发生变化。
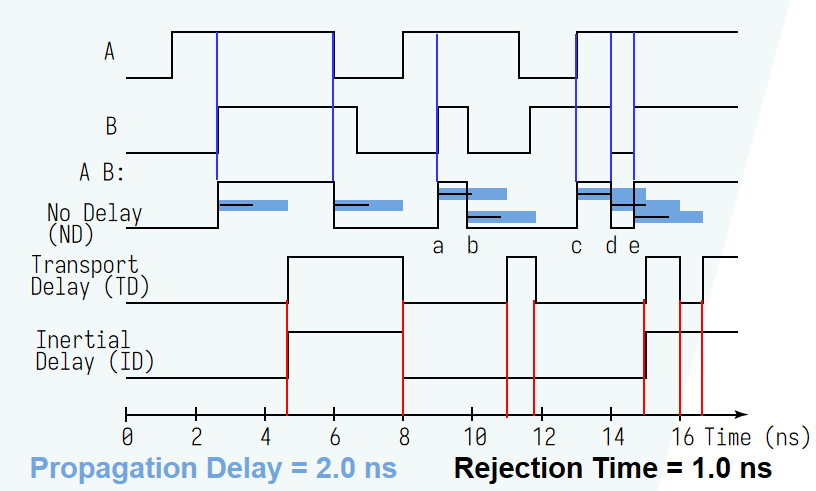
电路延迟 (circuit delay) 包括:
- 电路自身的固定延迟
- 不同负载导致的额外延迟 ( 前面提到的“过渡时间”)
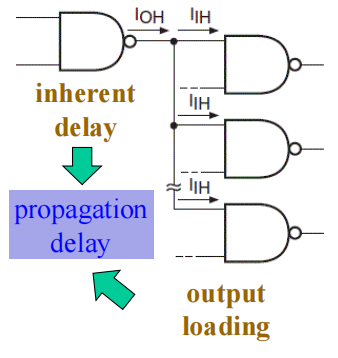
延迟带来的问题:
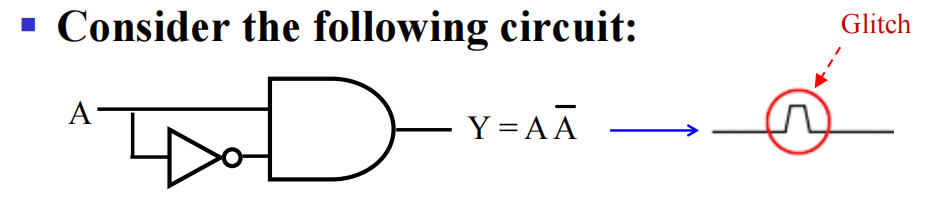
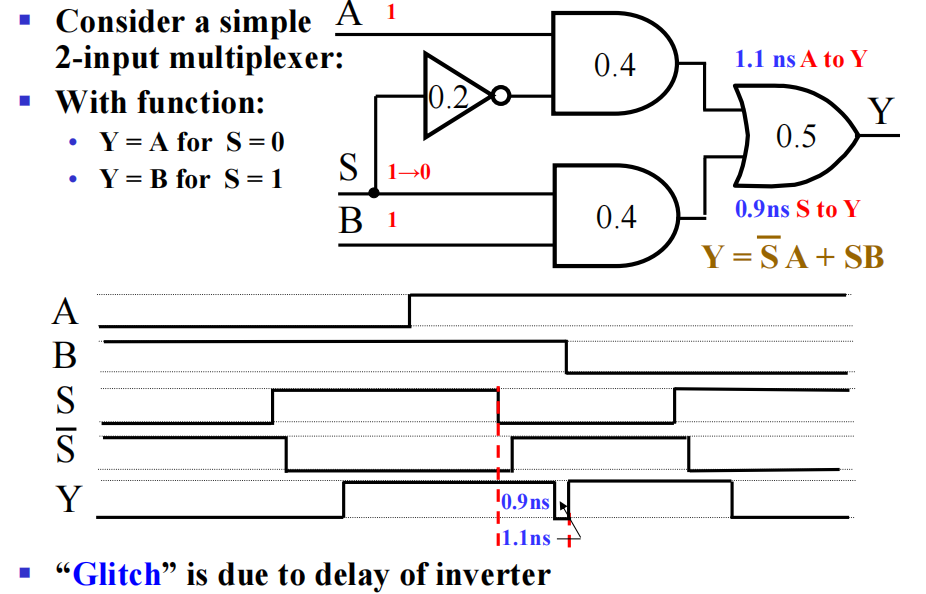
按照布尔代数的知识,我们知道 \(Y = A \overline{A} = 0\),但正因为延迟的存在,就会出现上图的毛刺 (glitch),这自然不是我们期望的结果
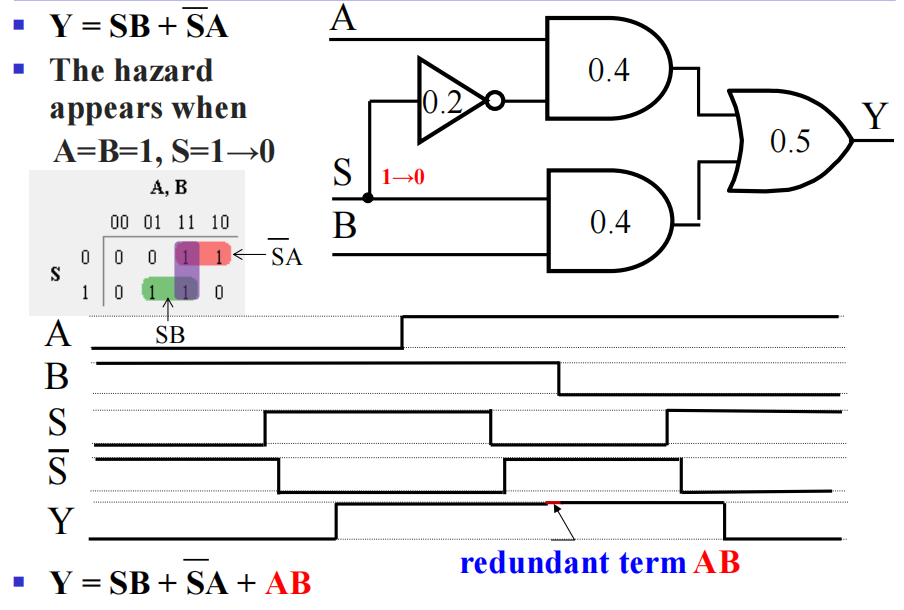
更复杂的🌰:
补救措施:添加一个冗余项 \(AB\)
电源供应和门电路的消耗
Design Trade-Offs⚓︎
在电路设计中,我们常常需要权衡成本 (cost)和性能 (performance)
例题

答案:2
分析:
-
只有一个与非门:
- 延迟:0.45ns
- 成本:2.0
-
与非门 + 缓冲器:
- 延迟:0.33ns
- 成本:2.0 + 1.5 = 3.5
Positive and Negative Logic⚓︎
相同的物理门有不同的逻辑意义,取决于对信号的解释
正逻辑 (Positive Logic):
- 高电位 (HIGH)(more positive) 代表逻辑 1
- 低电位 (LOW)(less positive) 代表逻辑 0
负逻辑 (Negative Logic):
- 低电位 (LOW)(more positive) 代表逻辑 1
- 高电位 (HIGH)(less positive) 代表逻辑 0
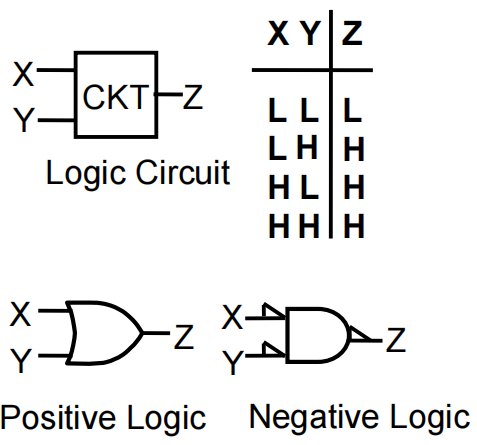
因此,一个执行正逻辑与的函数,也能执行负逻辑或的函数,反之亦然
🌰
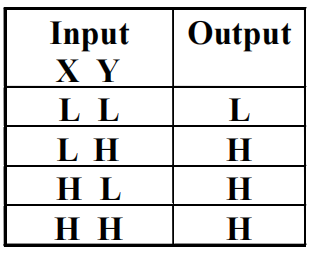
下面两张表分别表示正逻辑和负逻辑的真值表

在门输入和输出上使用极性指示器 (polarity indicator) 代表负逻辑的使用
Design Steps⚓︎
- 规范 (specification):写下电路行为的规范(文本、HDL( 硬件描述语言 ))
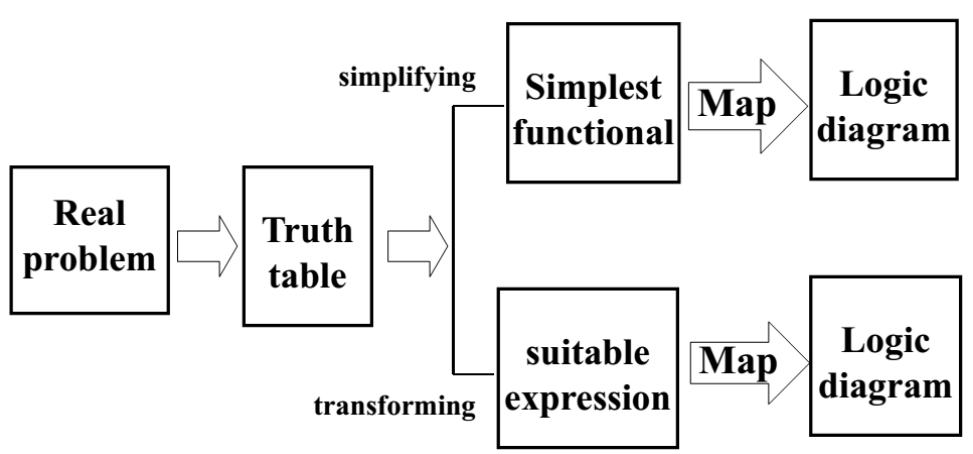
- 构思 (formulation):得到真值表或布尔函数,定义所需的关于输入输出的逻辑关系
- 优化 (optimization):使用两级优化,或者多级优化来最小化所用逻辑门的数量。画出一张用门电路构建的最终电路的逻辑图或网图
- 工艺映射 (technology mapping):使用现有的实现工艺,修改刚才得到的逻辑图或网图
- 检验 (verification):验证最终设计的正确性
Technology Mapping⚓︎
工艺映射 (technology mapping) 是逻辑综合过程中的重要一环,它将不依赖具体工艺的逻辑表述,转化为一个特定的工艺规范(空想 \(\rightarrow\) 现实
Chip design styles⚓︎
-
高度定制 (full customized):关注整个芯片的设计,一直到布局上的细节
- 昂贵
- 适用于密集的、快速的芯片
-
标准单元 (standard cell):在设计前已经构建好模块,或利用之前设计中的模块
- 中等耗费
- 相比 full customized,密度更少,速度更慢
-
门阵列 (gate array):在很多设计中常用的门电路晶体管方案,已经在芯片中建好了。只专注于该芯片中特定的门之间的关系
- 耗费最少
- 相比前两者密度更少、速度更慢
注:门阵列相关知识见 Chap 5
Cells and cell libraries⚓︎
- 单元 (Cell):一个预先设计好的原始模块(前面三种芯片设计风格都会用到它)
- 单元库 (Cell library):对于某个设计的一组可用的单元
- 单元特征 (Cell characterization):由设计者所使用的单元的具体实现,通常基于实际单元设计、制造和测量值
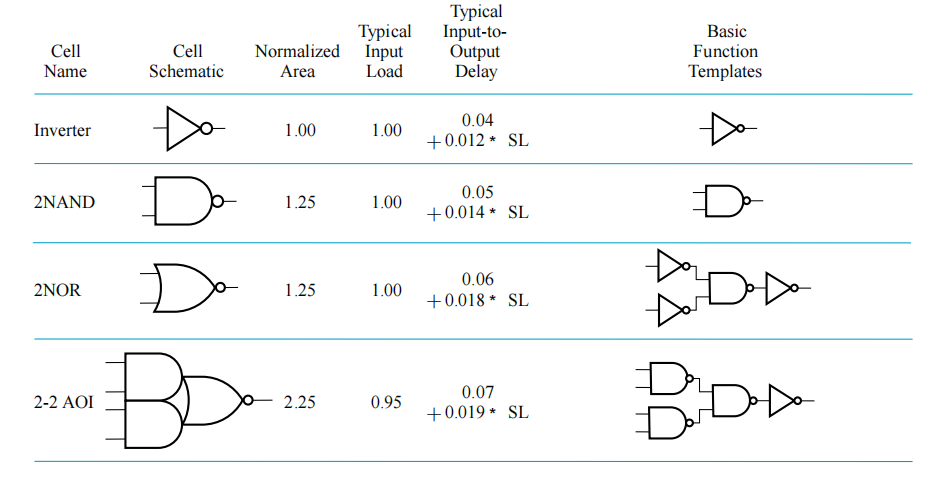
典型单元特征的组成部分:
- 示意图或逻辑图
- 单元区域
- 输入负载(以标准负载)提交给驱动每个输入的输出
- 来自每个输入和输出的延迟
- 一个或多个关于工艺映射的单元模版
- 一个或多个 HDL 模型
-
自动布局:
- 单元电路的物理布局
- 提供单元的输入、输出、电源和接地位置的平面图布局
Mapping to NAND Gates⚓︎
假定:
- 原来的示意图中有与门、或门和非门
- 单元库仅包括一个非门和n 输入与非门(\(n = 2, 3, \dots\))
- 忽略门加载和延迟的时间
实现步骤:
- 移除与门和或门(使用与非门和非门)
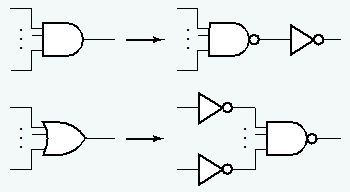
- 尽可能减少非门个数

🌰
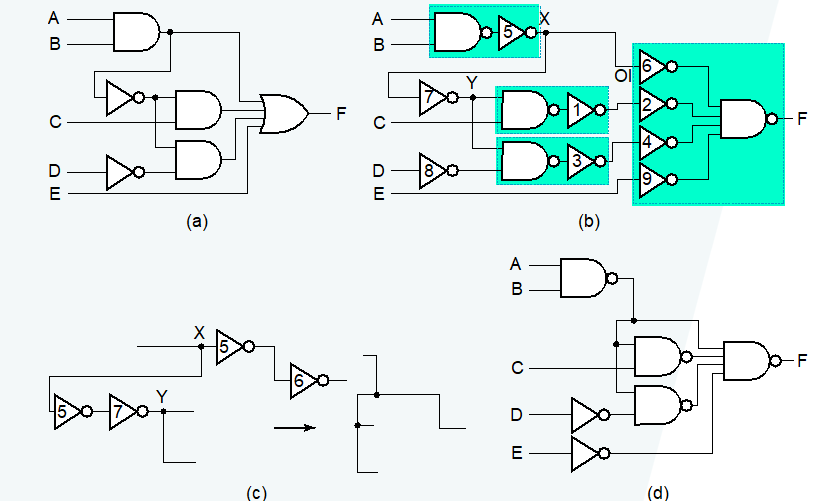
Mapping to NOR Gates⚓︎
假定:
- 原来的示意图中有与门、或门和非门
- 单元库仅包括一个非门和n 输入或非门(\(n = 2, 3, \dots\))
- 忽略门加载和延迟的时间
实现步骤:
- 移除与门和或门(使用与非门和非门)
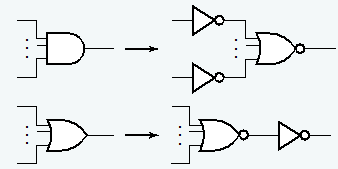
- 尽可能减少非门个数

🌰
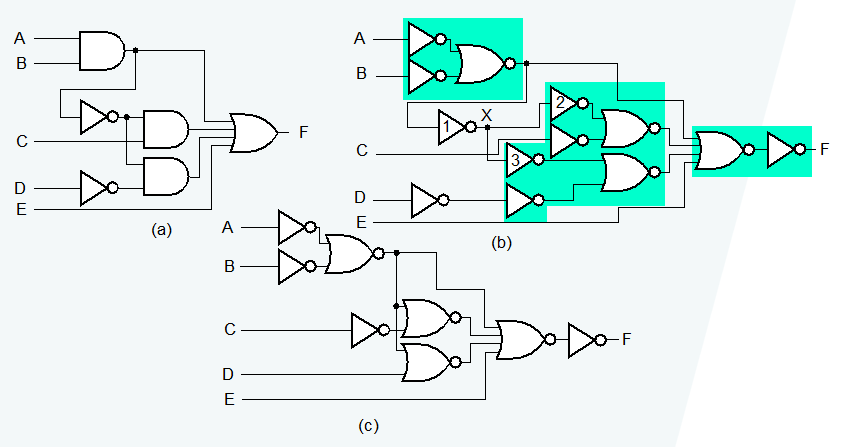
Verification⚓︎
-
人工逻辑分析 (Manual Logic Analysis)
- 根据最终电路,得到真值表,或者布尔方程
- 比较现在得到的和之前得到的真值表,或者证明现在得到的布尔方程和之前得到的布尔方程等价
-
仿真 (Simulation)
- 使用测试输入模拟最终电路、之前得到的真值表、布尔方程或 HDL
- 对于组合电路,我们需要测试所有可能的有意义的输入组合来验证正确性
Combinational Logic⚓︎
Functions and functional blocks⚓︎
函数块 (functional block) 是函数在组合电路上的实现。现在,它们常常由 VLSI( 超大规模集成电路 ) 实现
Big Picture of Four Functioinal Blocks
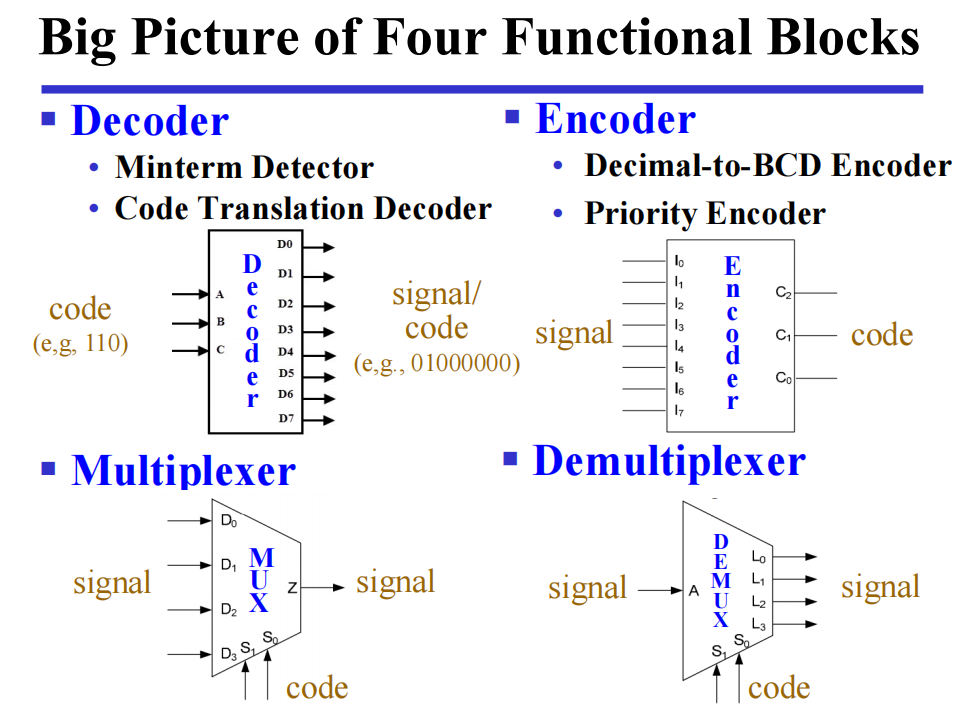
Rudimentary Logic Functions⚓︎
基本组合逻辑函数包括:
- 值固定 (value-fixing):\(F = 0 \text{ or } F = 1\),没有布尔运算符
注:值固定分为暂时固定和永久固定,常用于可编程逻辑设备中 ( 见第 5 章 )
- 传输 (transferring):\(F = X\),没有布尔运算符
- 逆转 (inverting):\(F = \overline{X}\),包含一个逻辑门
- 使能 (enabling):\(F = X \cdot EN \text{ or } F = X + \overline{EN}\),包含一个或两个逻辑门
Note
- 使能 (enabling) 允许输入对影响输出的影响
- 禁用 (disabling) 阻止输入对输出的影响,用一个固定值表示输出。这个值可以是Hi-Z( 高阻抗 ),0 或 1
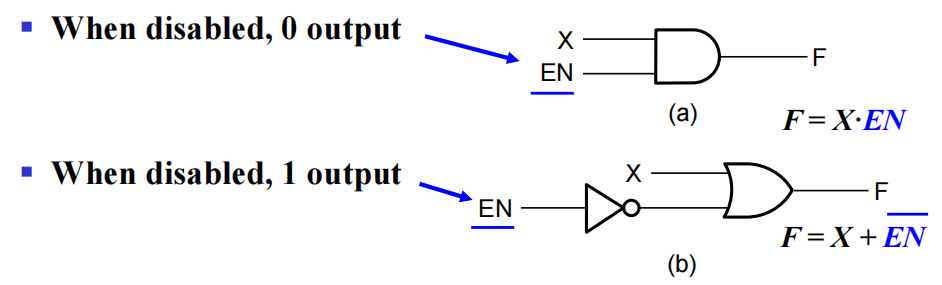
其实,我们在上一章的三态门中已经介绍过使能信号了
其他 3 种基本函数的实现:
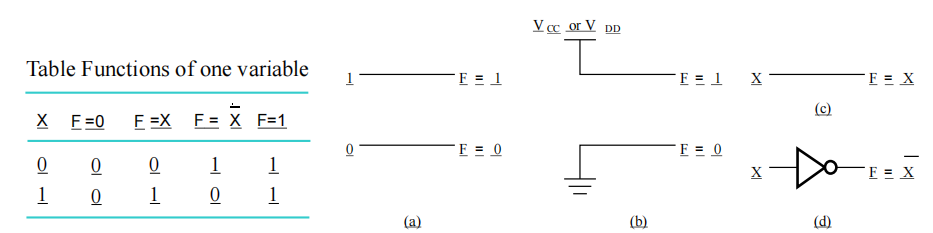
Multiple-bit Rudimentary Functions⚓︎
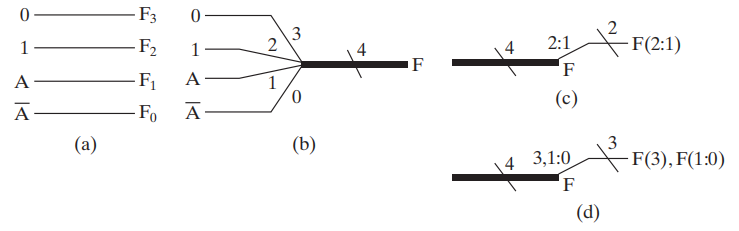
- 粗线用来表示总线 (bus),它是向量 ( 简单理解为“数组”,但不准确 ) 信号
- 对于这样能够传输多位的导线,我们一般会在线上划一笔,并标注它的位数
- 总线可以被分成多个 1 位信号
- 可以从总线中分出一些位出来,且不要求这些位一定要连续 ( 例 (d))
Decoder⚓︎
译码 (decoding):从 \(n\) 位输入码到 \(m\) 位输出码的转换 (\(n \le m \le 2^n\)),使得每个合法的输入码能够产生唯一对应的输出码
译码器 (decoder):执行译码的电路。
译码器的类型:
- 变量译码器 (variable decoder)( 最小项侦测器,minterm detector)
- 显示译码器 (display decoder)
- 编码翻译译码器 (code translation decoder)
常用译码器:
- 74LS139(2-4 译码器 ):2 输入,4 输出
- 74LS138(3-8 译码器 ):3 输入,8 输出
- MC14514(4-16 译码器 ):4 输入,16 输出
🌰:
- 1-2 译码器
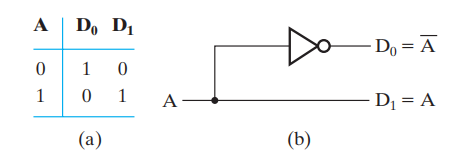
- 2-4 译码器
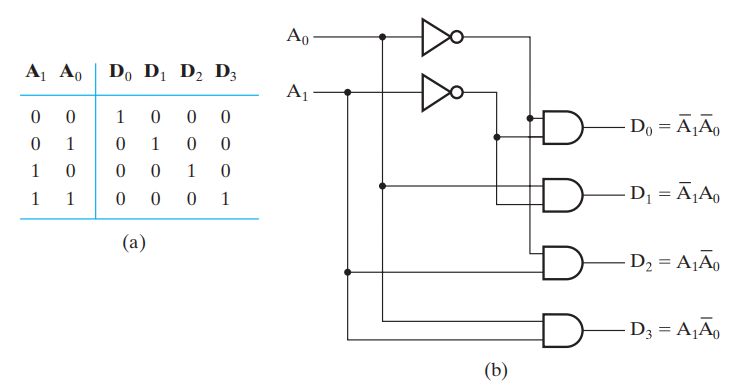
注:2-4 译码器由 2 个1-2 译码器和 4 个与门构成
Decoder Expansion⚓︎
大型的译码器可以通过使用单个的,带有更多输入的与门来实现每个最小项函数来构建
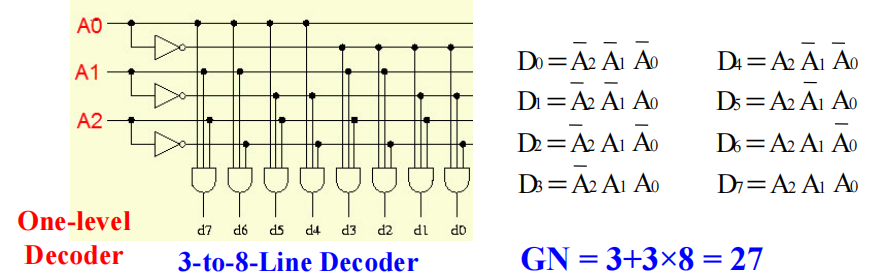
显然,当译码器变得很大时,这种方法是不现实的——它的扇入和门输入成本太大啦!
因此,我们采用前面提到的分层设计 (hierarchical design)( 其实也是一种分治 (divide-and-conquer) 的思想 ) 和一组与门来构建译码器,通过共享项 (shared term) 来减少扇入和门输入成本。
同时,这也体现了自顶向下 (top down) 设计的思想。
Example
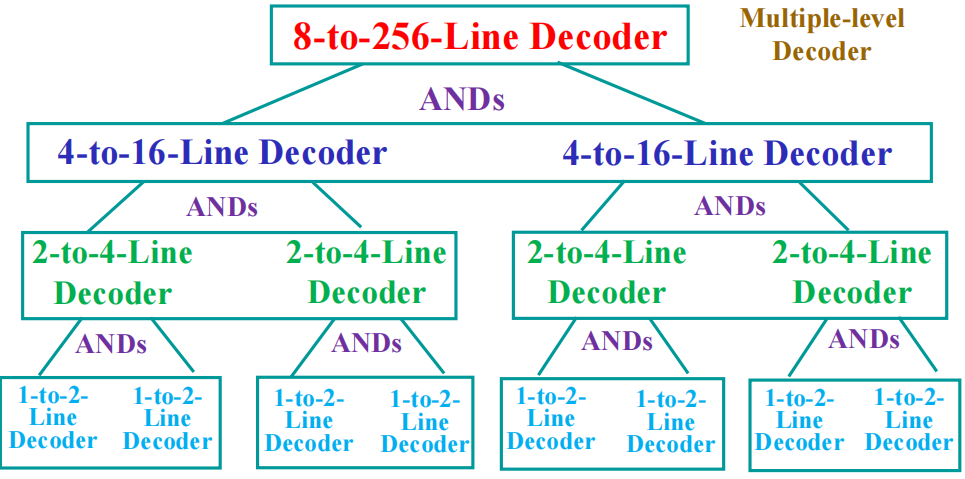
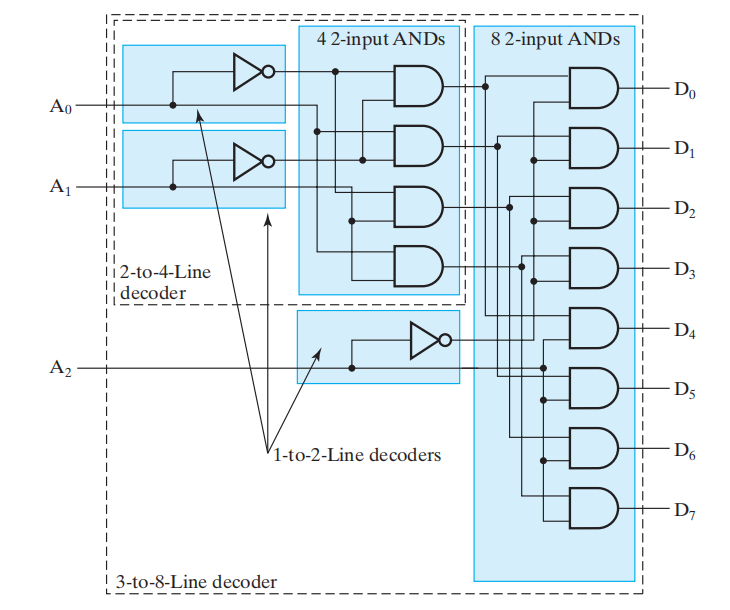
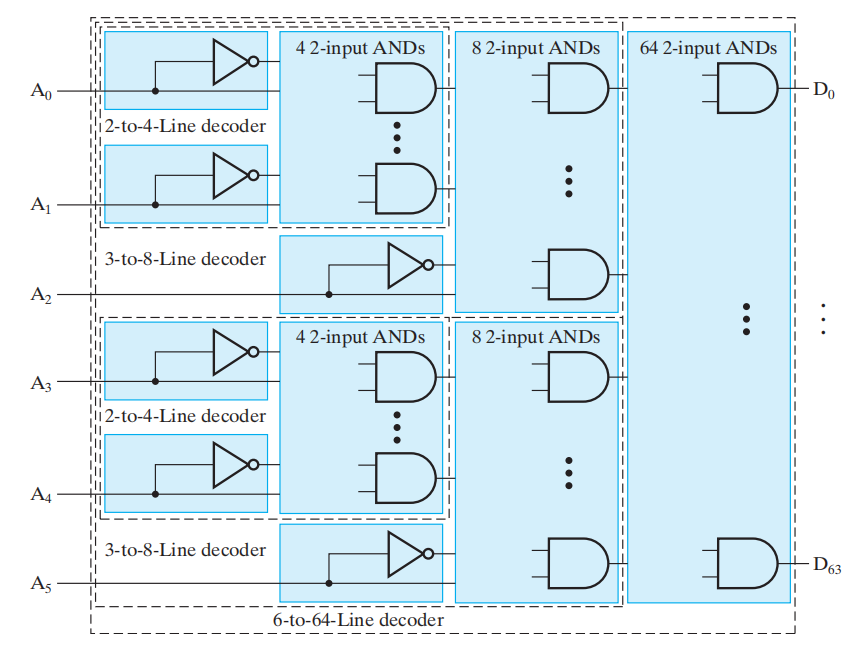
个人理解:译码的实质是将一个二进制数 ( 编码 )转化为独热码的过程
Decoder with Enable⚓︎
- 如何实现:在输出的位置上附上使能电路
- 看下面的真值表:用 \(\times\) 表示 0 或 1,因此两个 \(\times\) 的组合代表 4 种二进制组合
- 这种电路被称为信号分配器 (demultiplexer)
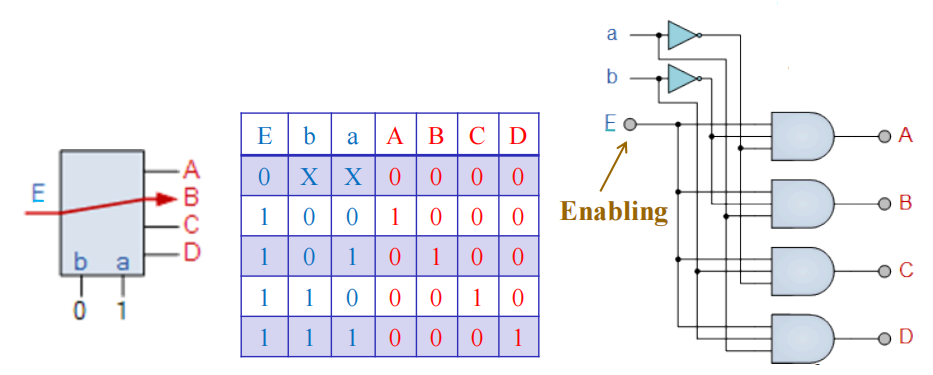
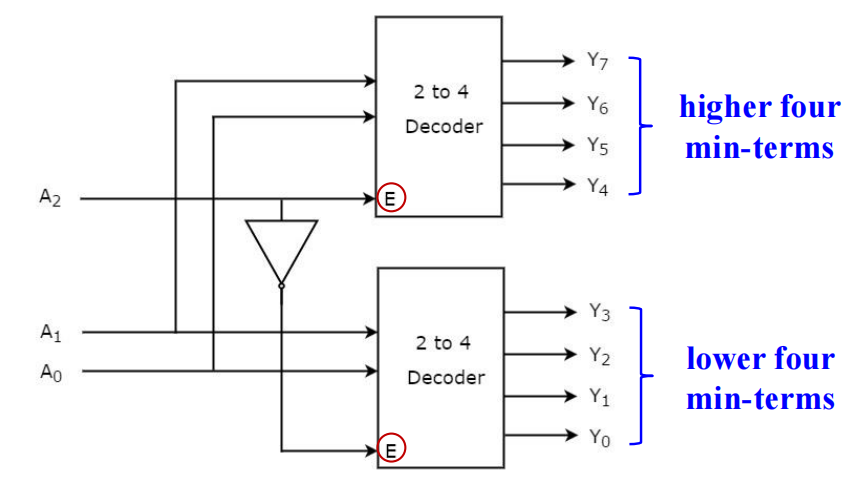
🌰:低阶译码器 + 使能 \(\rightarrow\) 译码器的扩张 ( 以 2-4 译码器扩展至 3-8 译码器为例 )
译码器 + 或门 \(\rightarrow\) 组合逻辑的实现

实现 m 个 n 变量函数需要:
- SOM 表达式
- n-\(2^n\) 译码器
- m 个或门,每个输出对应一个
Example
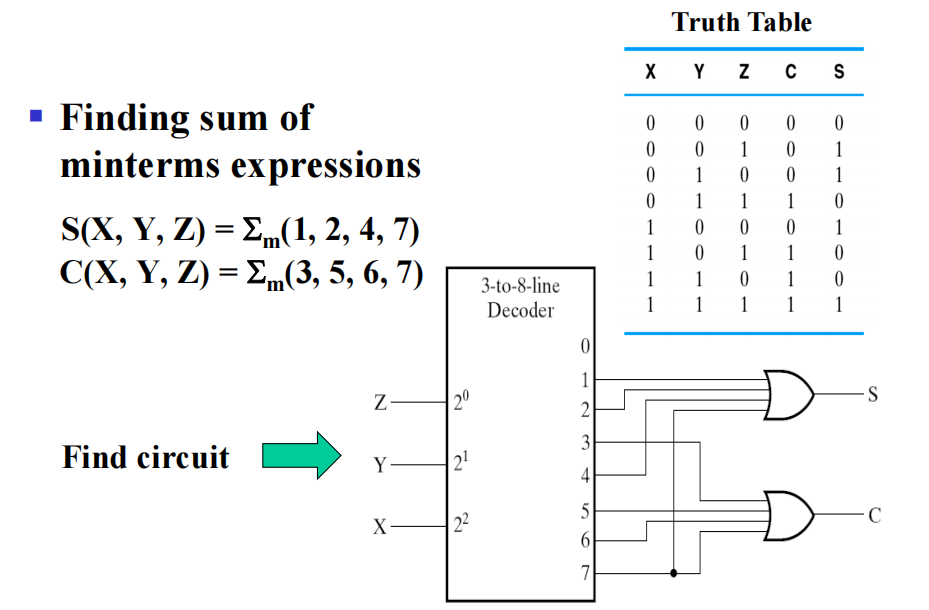
注:后面有系统的讲解

Display Decoder(Seven-Segment Decoder)⚓︎
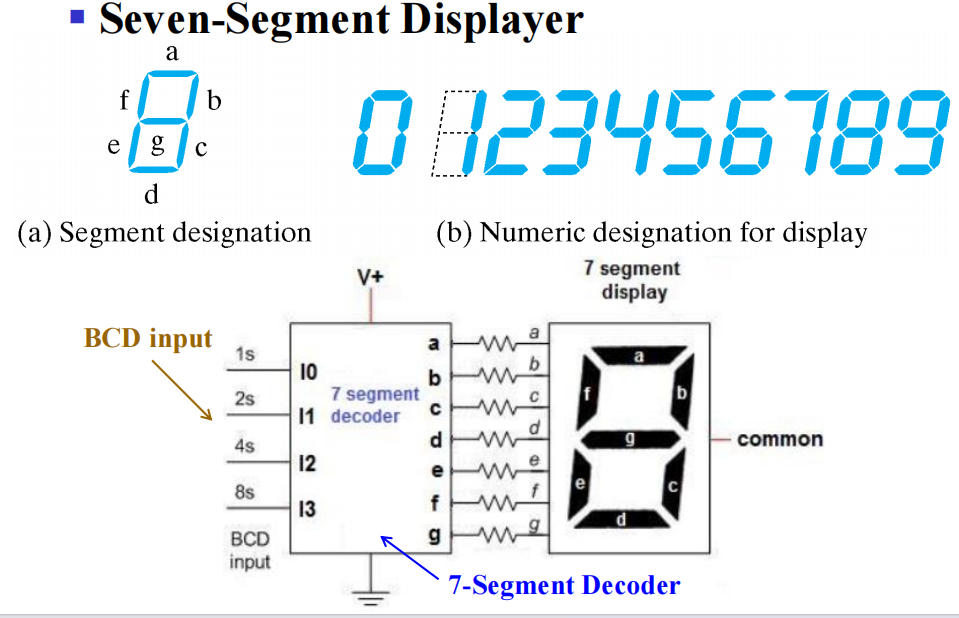
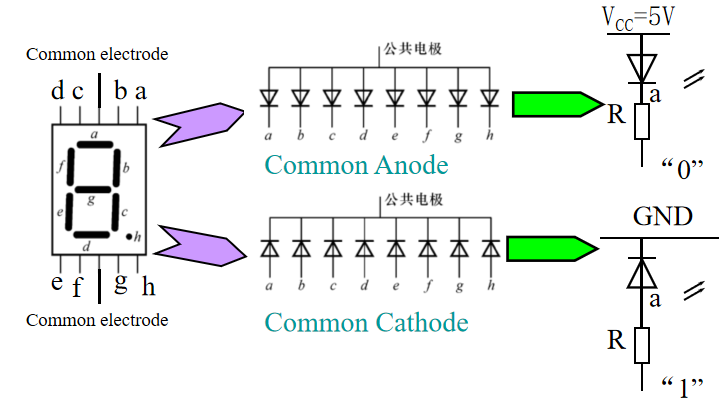
补充
- 共阳极显示 (The Common Anode Display, CAD):如下图所示,如果 a~g = 0,开;a~g = 1,关(低电平活跃)
- 共阴极显示 (The Common Cathode Display, CCD):如下图所示,如果 a~g = 1,开;a~g = 0,关(高电平活跃)
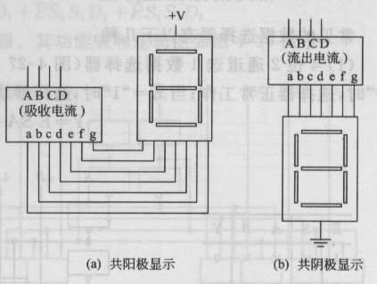

布尔方程:
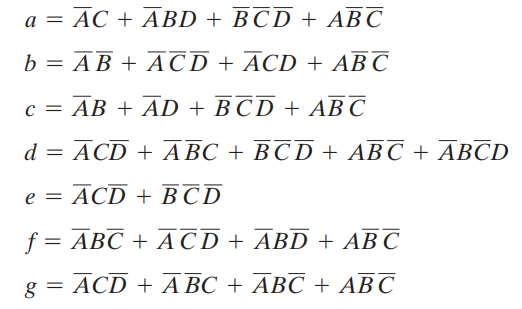
Encoder⚓︎
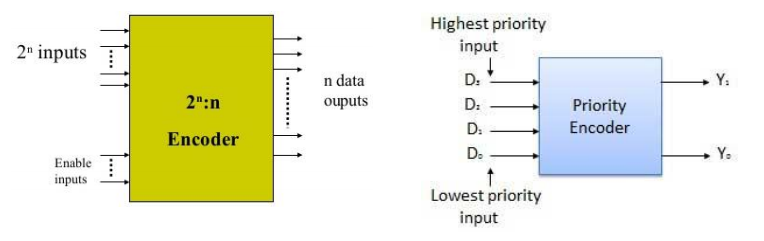
编码 (encoding):与译码相反,将 \(m\) 位输入码转化为 \(n\) 位输出码 (\(n \le m \le 2^n\)),使得每个合法的输入码能够产生唯一的输出码
编码器 (encoder):执行编码的电路
类型:
- 十进制 -BCD 编码器 (decimal-to-BCD encoder)
- 指令编码器 (instruction encoder)
- 优先编码器 (priority encoder)
注:这种编码器被广泛应用于 计算机优先级中断系统 (computer priority interrupt system) 和 键盘编码系统 (keyboard coding system) 中
- 密码编码器 (cypher encoder)
🌰:十进制 -BCD 编码器
- 输入:10 个位,每位对应十进制数 0-9(\(D_0, \dots, D_9\))——独热码 (one-hot encoding)
- 输出:4 位的 BCD 码
- 函数:\(D_i = 1 \rightarrow\) 输出 \((A_3, A_2, A_1, A_0)\) 表示数字 i 的 BCD 码
真值表:
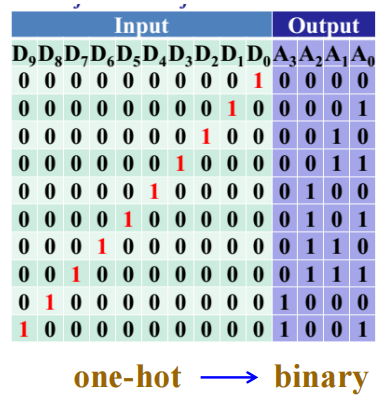
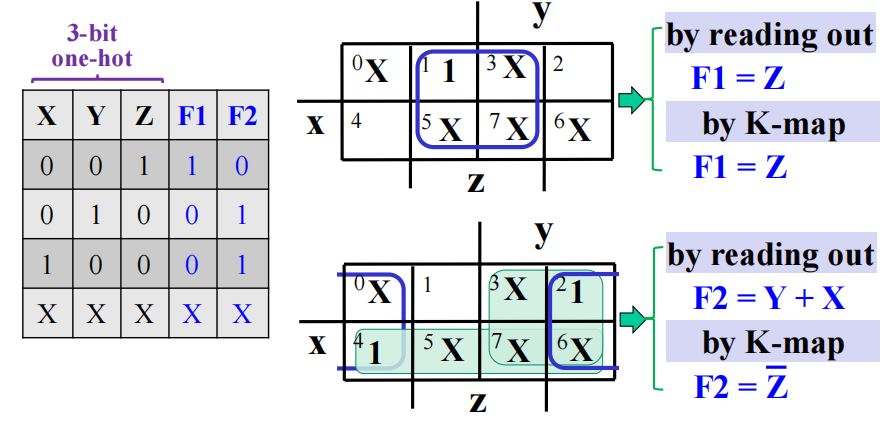
我们得到布尔方程:
我们可以使用 \(F_1 = D_6 + D_7\),得到 \(A_1\) 和 \(A_2\) 的共享项,从而节省成本。
所以,编码的实质即为将独热码转化成二进制数 ( 编码 )
我们可以直接从独热码的结果中进行化简,无需借助 K-map 的帮助。
Priority Encoder⚓︎
普通编码器的问题
如果有多个输入的值为 1,则编码器不能正常工作。
解决方案——优先编码器 (Priority encoder):
能够接受所有输入情况,并且产生有意义的结果的编码器。对于所有值为 1 的输入,它会选择位于最高位(或最低位)的输入,根据该位置输出相应的二进制码
Example
题目:
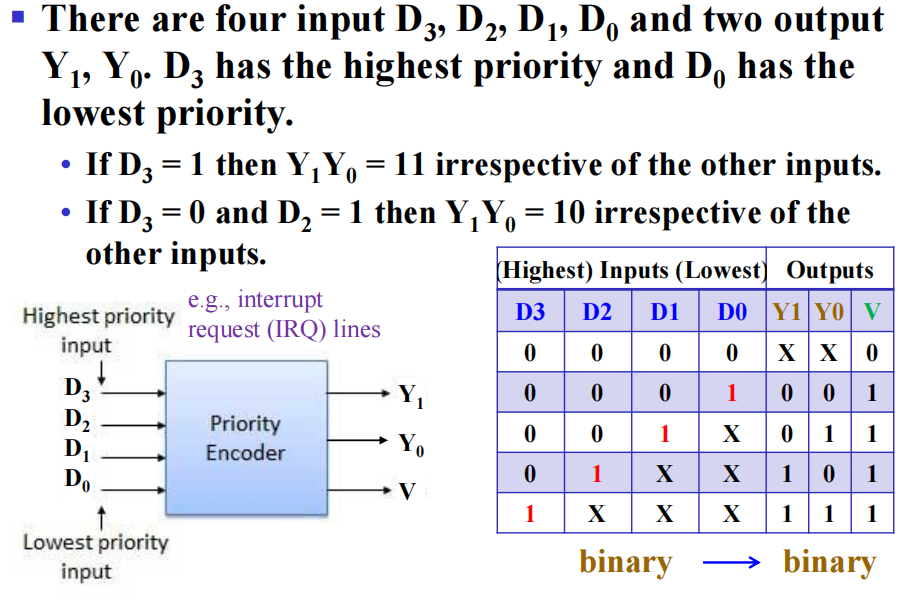
卡诺图:
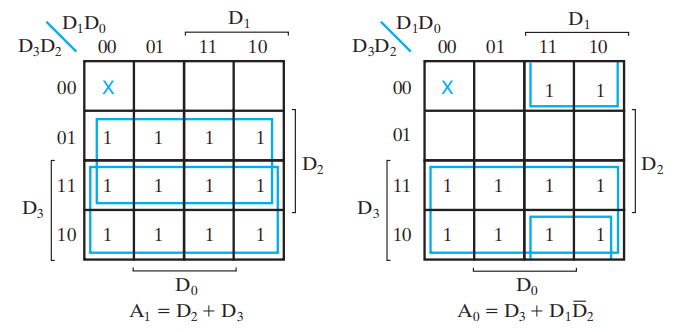
电路实现:
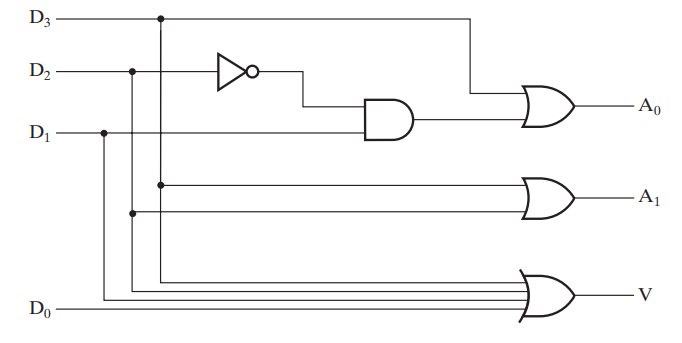
该编码器优先考虑最高位的 1。其中 X 代表 0 或 1,V 代表输入中是否有 1 出现过。不难看出,这张真值表包含了所有 32 种情况。
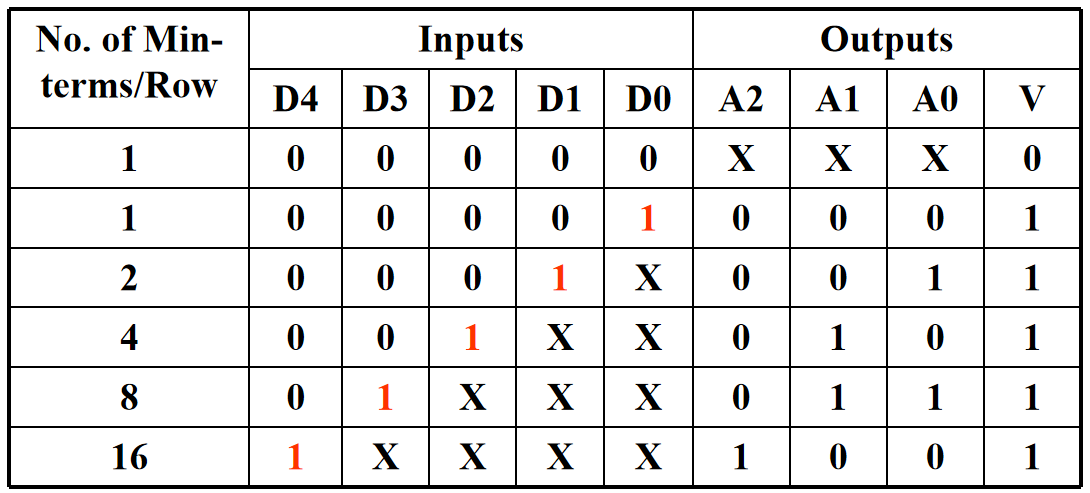
因此我们可以进行化简操作 ( 也可以使用卡诺图 ):
Multiplexer⚓︎
执行选择 (selecting) 功能的电路包含:
- 一组信息输入
- 一组用来做出选择的控制线路
- 单个输出
多路复用器 (Multiplexers, MUX):执行选择的逻辑电路,可由译码器 + 与 - 或门( 其中与门使每个译码器的输出起到使能作用 ),或者由三态门实现
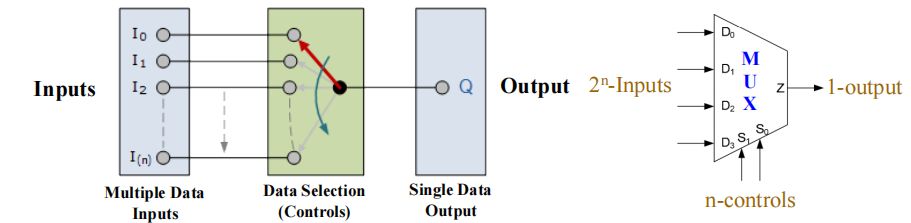
它包含:
- \(n\) 个控制输入 (\(S_{n - 1}, \dots, S_0\)),被称为选择输入 (selection inputs)
- \(2^n\) 个 ( 最大数量 )信息输入 (information inputs)(\(I_{2^n - 1}, \dots, I_0\)),它的实际数量 \(m\) 可以小于 \(2^n\)
- 一个输出\(Y\)
各种多路复用器
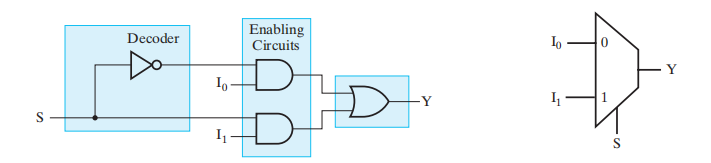
构成:
- 1 个 1-2译码器
- 2 个使能电路
- 1 个 2 输入或门
单个选择变量 \(S\) 有两个值:
- \(S = 0\) 选择输入 \(I_0\)
- \(S = 1\) 选择输入 \(I_1\)
方程:\(Y = \overline{S}I_0 + SI_1\)
根据这个多路复用器的构成,我们可以扩展至 \(2^n\)-1 多路复用器:
- \(n-2^n\) 译码器
- \(2^n \times 2\) 与 - 或门
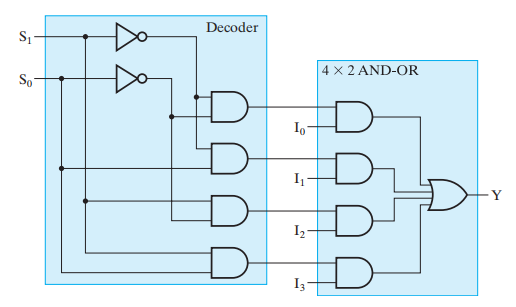
构成: \(2-2^2\) 译码器 + \(2^2 \times 2\) 与 - 或门
门输入成本 = 32
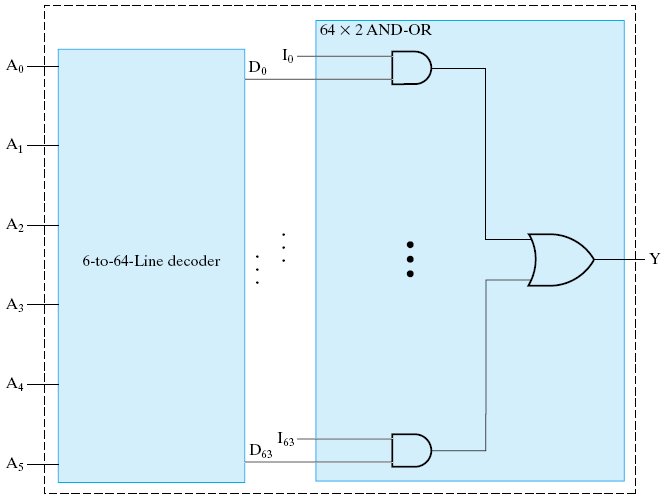
构成:\(6-2^6\) 译码器 + \(2^6 \times 2\) 与 - 或门
注意
对于大规模的电路结构,比如上面的 64-1 多路复用器,以及之后的算术逻辑单元、寄存器等,我们往往只要画出它封装后的模块即可,而不关注它的细节。
Multiplexer Width Expansion⚓︎
方法:
- 使用位向量 (vectors of bits) 而非位 (bit)
- 并行使用多个 \(2^n \times 2\) 与 - 或门
🌰:4-1 四位多路复用器
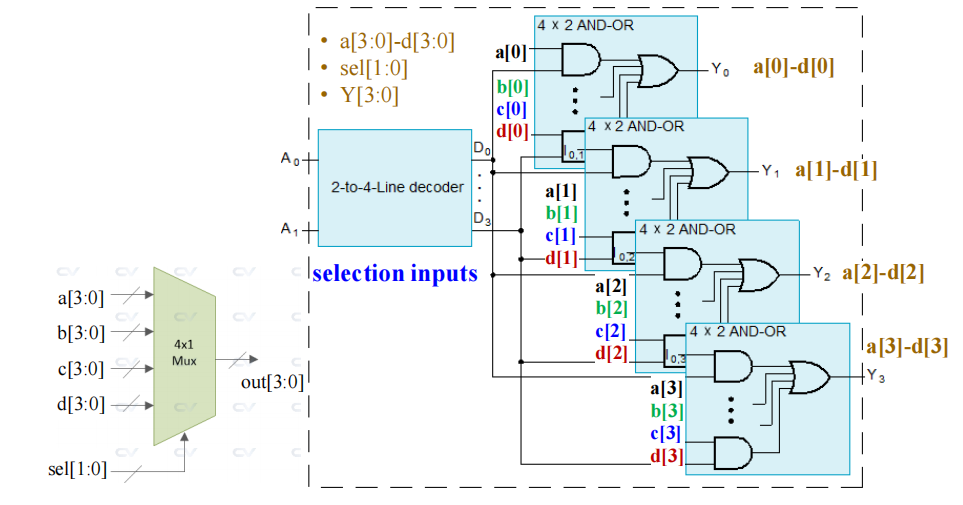
Other Selection Implementations⚓︎
- 用三态门代替与 - 或门
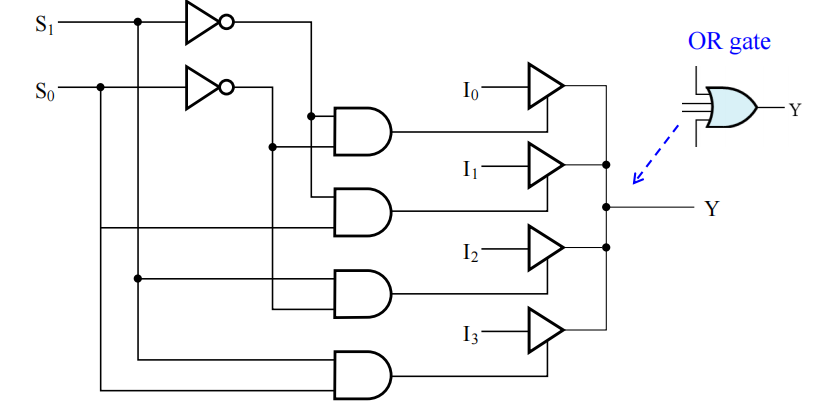
门输入成本:18(2 个非门 + 4 个与门 * 2 + 4 个三态门 * 2)
注:如果使用与 - 或门,成本 = 22
- 用三态门实现译码器
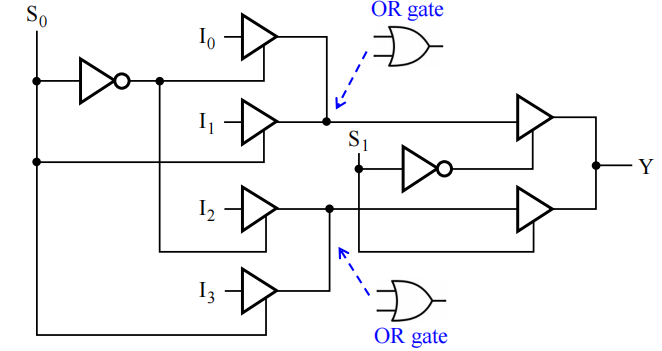
门输入成本:14(2 个非门 + 6 个三态门 * 2)
Combinational Logic Implementation⚓︎
实例分析:格雷码 \(\rightarrow\) 二进制码
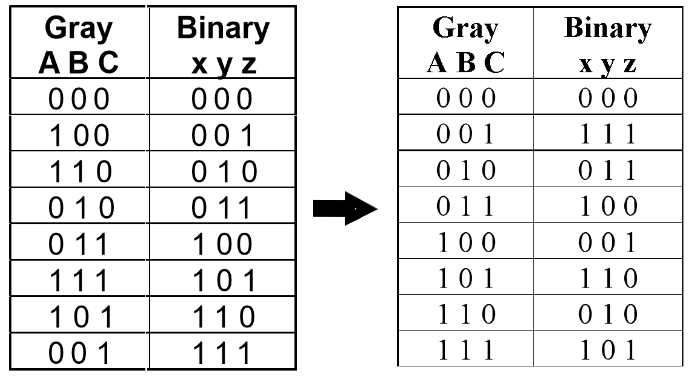
注:将格雷码按照计数顺序重新排列 ( 如右图所示 )
理论知识
实现 m 个 n 变量函数需要:
- SOM 表达式
- 一个 m 位 \(2^n\)-1 多路复用器
设计:
- 找到函数的真值表
- 将函数输入变量与多路复用器的选择输入\(S_{n-1}, \dots, S_0\) 按顺序对应
- 在多路复用器的输出上标注输出变量
- 使用真值表的值对多路复用器的信息输入进行值固定
可以发现,函数 y 和 z 可以用两个 8-1 多路复用器来实现:
- 将 A, B 和 C 连接至多路复用器的选择输入
- 将 y, z 连接至多路复用器的输出
- 分别将它们真值表的值连接至信息输入
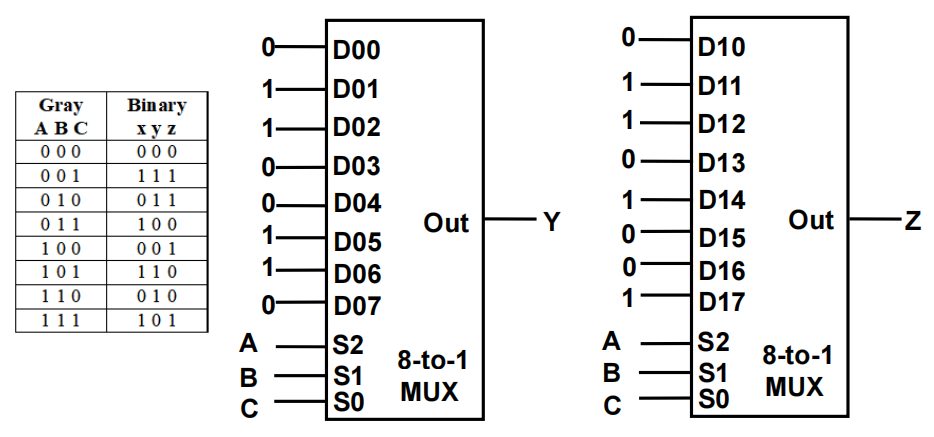
注:在后面的章节中,我们会发现这个值固定的多路复用器,与 3 位地址和 2 位数据的 ROM 是一样的
理论部分
实现 m 个 n 变量的函数需要:
- 一个 m 位的 \(2^{n-1}\)-1 多路复用器
- 一个非门
设计:
- 前 n - 1 个变量连接至选择输入
- 对于每个选择变量的组合,对应的输出是一个关于最后的变量 \((0, 1, X, \overline{X})\) 的函数
- 这些值随后被应用于合适的数据输入中
根据上面的设计原则,得到如下表格:
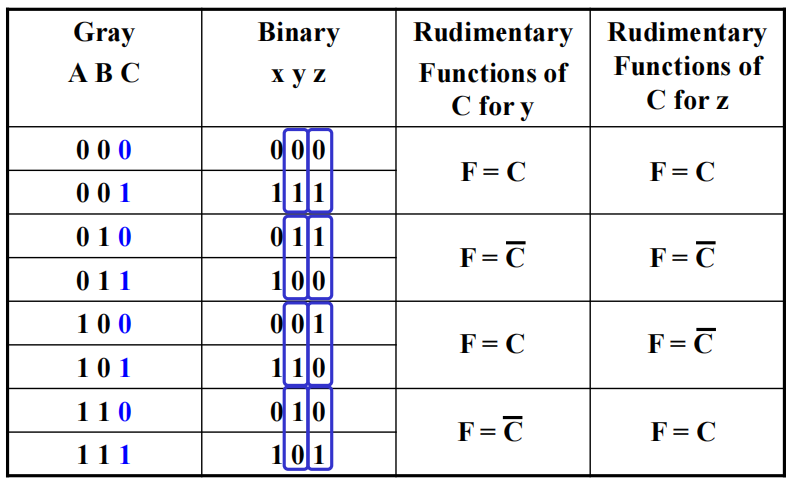
实现:
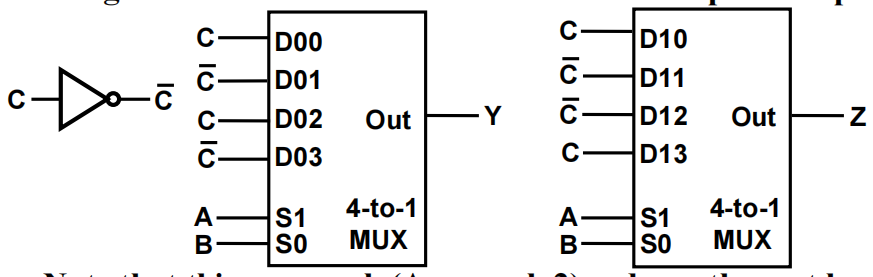
注:
- 这个方法相比前面那个,成本上减少了近乎一半
- 但这个实现就不像 ROM 了
- 扩展:多于 n 变量的函数可以被分解成一些子函数,这些子函数的变量是所有变量的子集。然后用多路复用器在这些子函数中进行选择。
补充:多路复用器 (multiplexer) 与信号分配器 (demultiplexer) 的区别
- 多路复用器是“多对一”的

- 信号分配器是“一对多”的

总体框架:
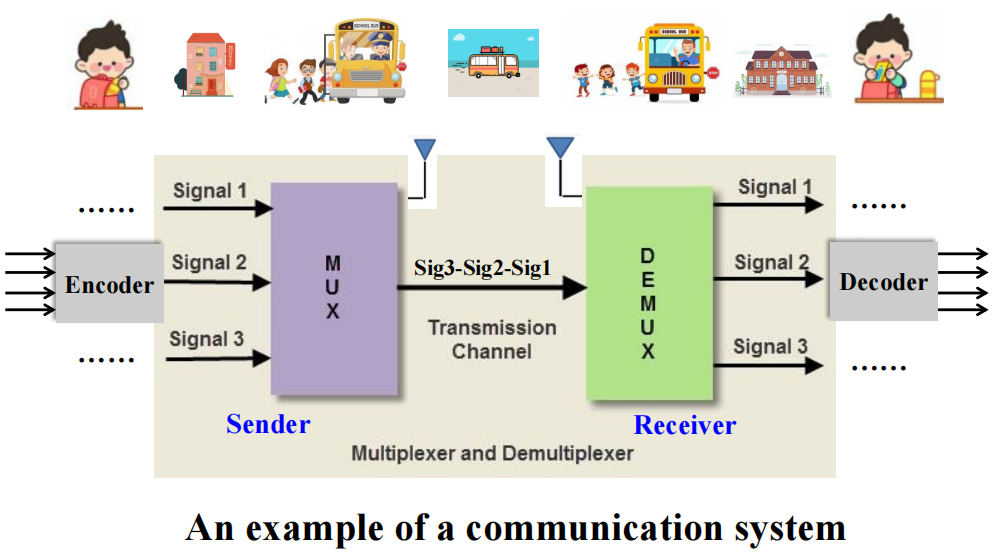
Iterative Combinational Circuits⚓︎
在逻辑电路中,算术计算 (arithmetic calculation) ( 比如加法、减法 ) 其实是一种编码翻译译码器。比如,N 位二进制加法需要 2N-(N+1) 译码器。
然而,当操作数变得很大时,用译码器实现加法就比较困难了。这时,我们可以采用二分法 (bisection method) 来构建大型译码器。但是,这种方法的效率不高。所以,我们需要遵循计算法则 (calculation rules) 为算术函数构建新的函数块。
执行算术的函数块被称为单元 (cell),因此算术运算的总体实现是由一组单元构成的。
迭代组 (iterative array) 是一种通过分解问题进行计算的方法,它利用规律性 (regularity) 的优势,使得大型、多级的算术电路设计变得可行
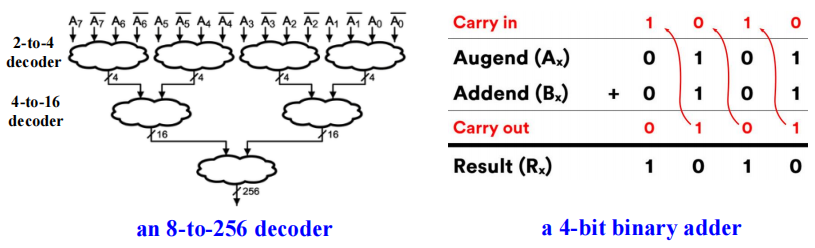
可迭代组合电路 (iterative combinational circuits) 包括:
- 算数函数 (arithmetic functions):对二进制向量进行运算,对其每一位使用相同的子函数。
- 单元 (Cell):子函数块
- 迭代组 (iterative array):具有互相联系的单元的阵列,可以是一维,也可以是多维
Binary Adders⚓︎
分类:
- 半加器 (half-adder):2 输入按位加法函数块
- 全加器 (full-adder):3 输入按位加法函数块
- 行波加法器 (ripple carry adder):执行二进制加法的迭代组
- 超前进位加法器 (carry-look-ahead adder):用来提升加法计算性能的分层结构
Half-Adder(HA)⚓︎
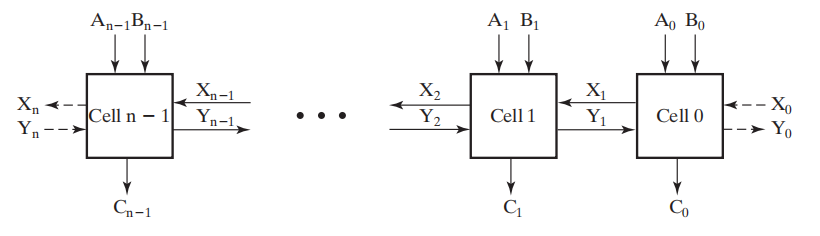
半加器 (half-adder) 是一种 2 输入,位宽为 1 的二进制加法器,将 2 个位相加,得到 1 个 2 位的和。具体如下:
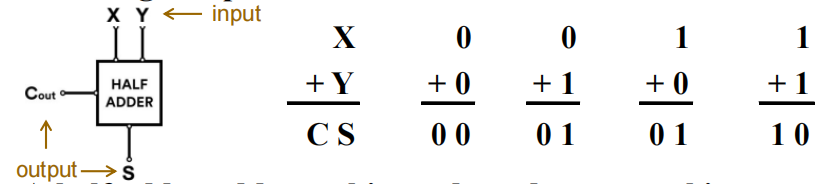
本质上,半加器是一个 2-2 译码器 (2 输入,2 输出 )
真值表:
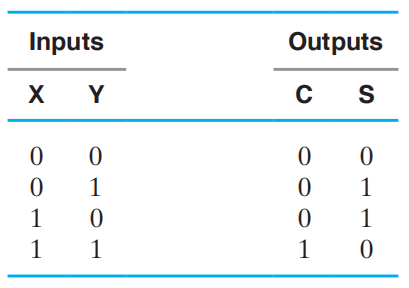
其中 S 被称为和位 (sum bit),C 被称为进位 (carry bit)
卡诺图:
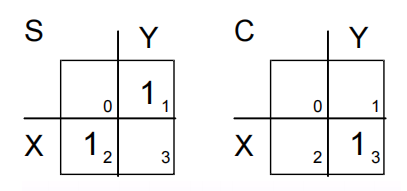
观察得: $$ S = X \oplus Y,\quad C = XY $$
其他等价的布尔方程:
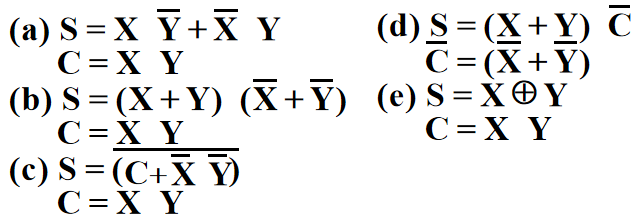
注:
- (a), (b), (e) 中的 S 分别用到了 SOP, POS 和 XOR 表示法
- (c) 中,C 作为 S 的 AND-OR 方程的一项;(d) 中,\(\overline{C}\) 作为 S 的 POS 方程的一项
实现:
- 最常见的实现形式 (\(S = X \oplus Y,\ C = XY\)):
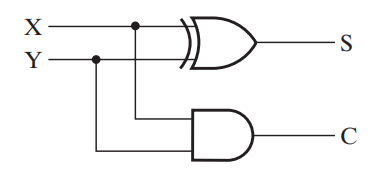
- 与非门的实现 (\(S = (X + Y)\overline{C},\ C = \overline{(\overline{XY})}\)):
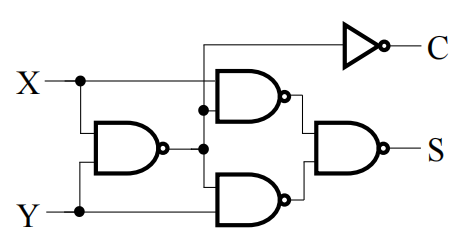
Full-Adder(FA)⚓︎
全加器 (full adder) 的工作原理类似半加器,但它在输入端多了一个(来自上一位的)进位 (carry-in bit) 的输入
框图:
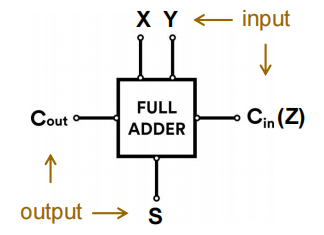
所有的计算情况:

真值表:
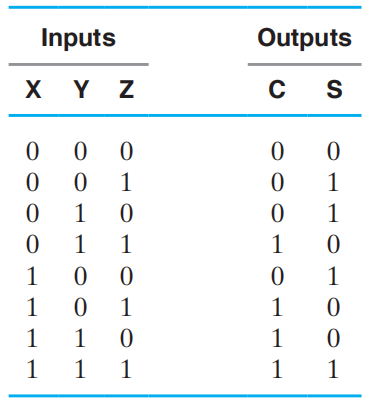
卡诺图:
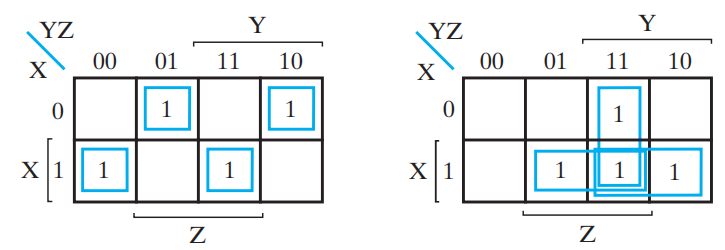
布尔函数:
注:其中,\(X \cdot Y\) 被称为进位生成 (carry generate),\(X \oplus Y\) 被称为进位传播 (carry propagate)
实现:
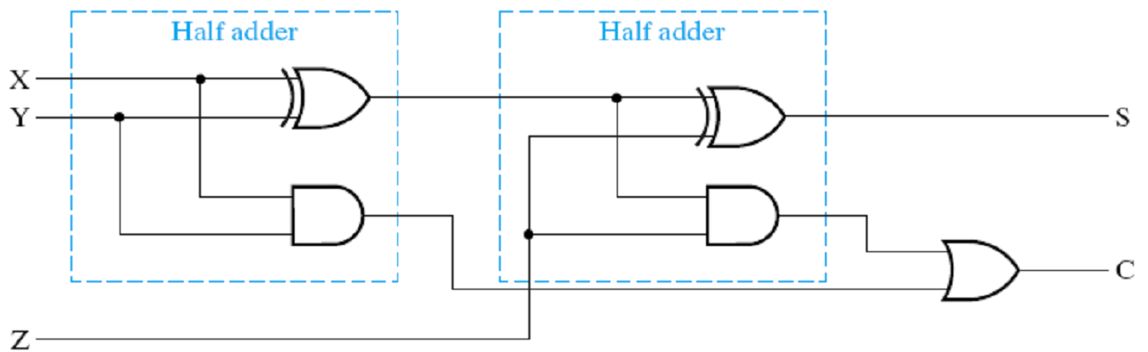
Ripple Carry Adder⚓︎
行波加法器 (ripple-carry binary adder):为了执行多位操作数的加法,我们将所有单个位“捆绑”在一起形成向量,然后使用函数块操作
🌰:四位行波加法器——将输入向量 A(3: 0) 和 B(3: 0) 相加,得到和向量 S(3: 0)

注:单元 i 的输出进位是单元 i+1 的输入进位
框图 (4 位行波加法器 = 4 个全加器 ):
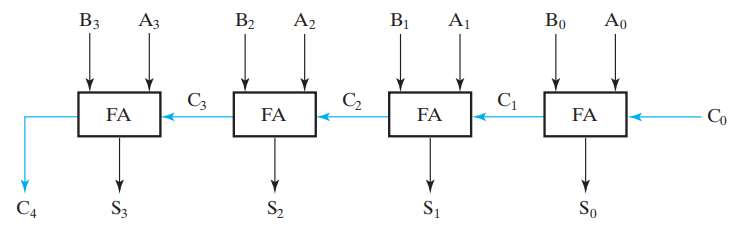
行波加法器的问题——进位的传播 & 延迟
延迟:进位从最低位传播到最高位的时间
上面的四位行波加法器的门级传播路径如下:
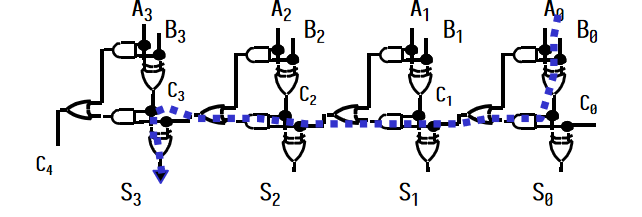
其中最长的路径是从 \(A_0\) 或 \(B_0\) 到 \(S_3\) 的长度
理解延迟的产生
回顾全加器的进位传播和进位生成:对应两个函数:
- 传播函数 (generate function):\(P_i = A_i \oplus B_i\)
- 生成函数 (propagate function):\(G_i = A_iB_i\)
我们得到:\(S_i = P_i \oplus C_i,\ C_{i+1} = G_i + P_iC_i\)
在行波加法器中:
- \(P_i, G_i\) 对于加法器的每个单元是局部的 (local)
- \(S_i, C_{i+1}\) 必须等待 \(C_i\) 的到来
因此就有了传播延迟的问题。
Carry Lookahead Adder(CLA)⚓︎
为了上述弊端,就要用到超前进位加法器 (carry lookahead adder),它基于对输入的替换 (substitution),提前计算进位。
具体做法:单元中的 \(C_{i+1}\) 被一组关于进位的方程替代,因此所有的 \(C_i\) 都可以被 \(C_0\) 和其他变量表示,比如 (4 位加法器 ):
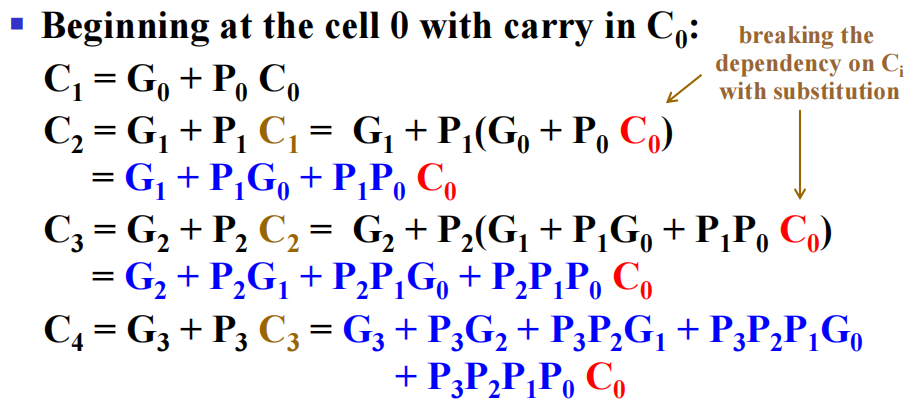
使用这些公式,加法器的时间复杂度从 O(n) 降到 O(1)。
电路实现(了解即可
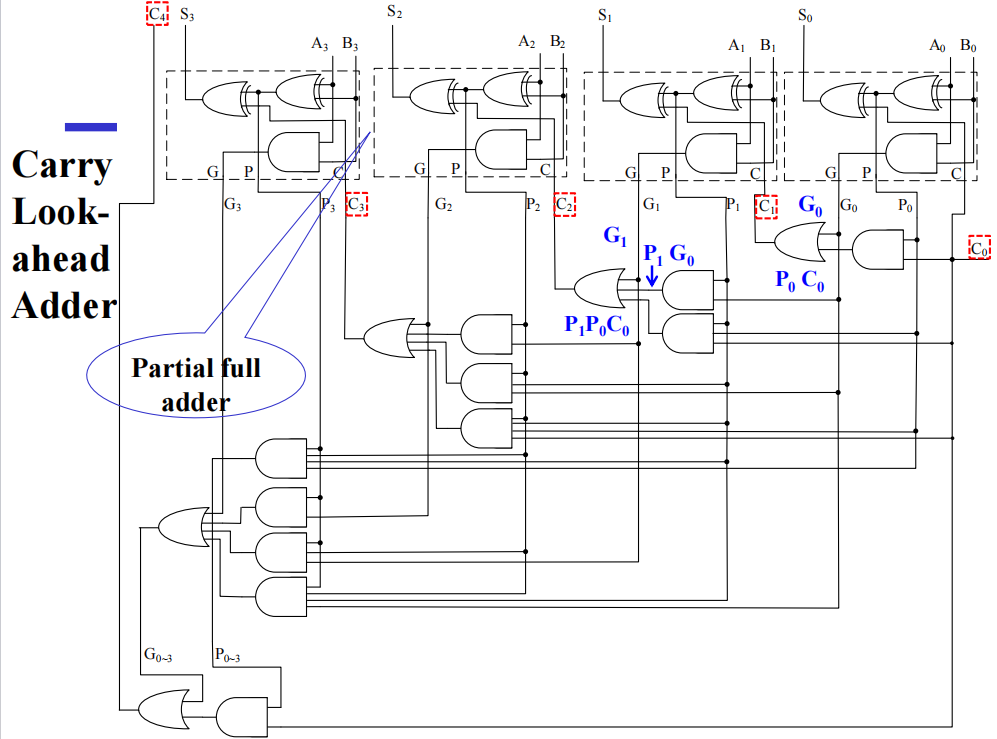
Group Carry Lookahead Logic⚓︎
组合超前进位逻辑 (group carry lookahead logic):实际应用中,由于门扇入的限制,超前进位的方法对于更大的加法器就不太可行。这时我们用到了组合生成 (group generate) (\(G_{0-3}\)) 和组合传播 (group propagate)(\(P_{0-3}\)) 的概念,对于上述四位超前进位加法器:
因此:
🌰:使用 4 个 4 位超前进位加法器进行 16 位的加法运算
布尔方程:
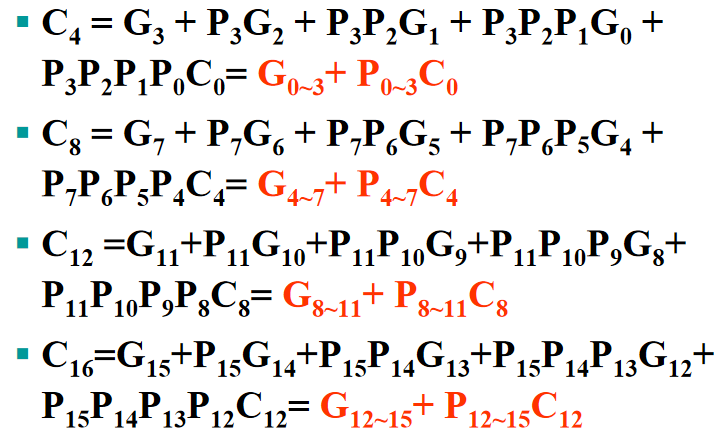
框图实现:
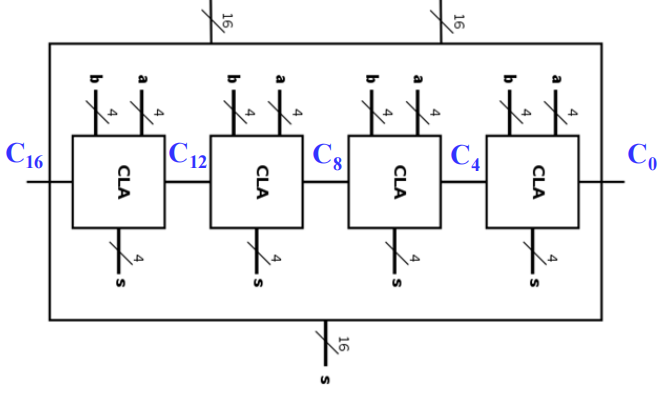
summary
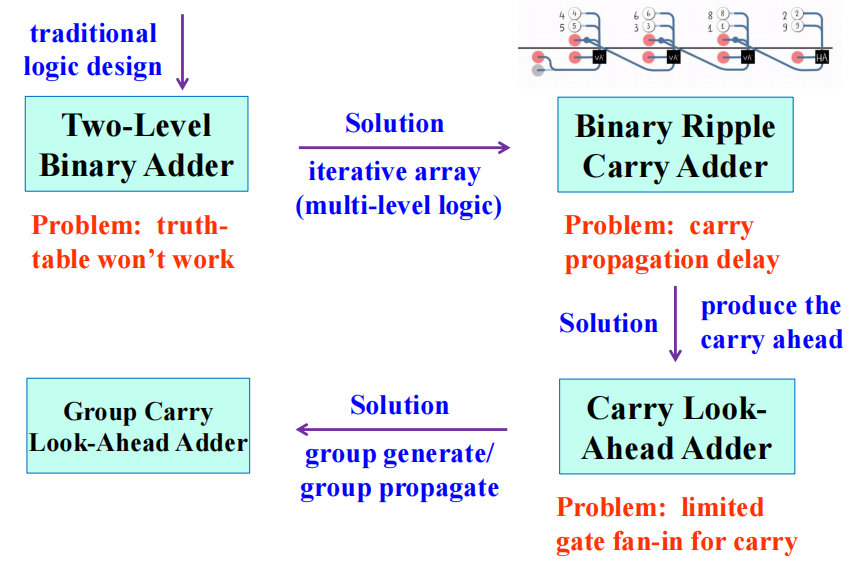
Binary Subtraction⚓︎
Unsigned Subtraction⚓︎
算法:
- 减数 N 减去被减数 M,即 M - N
- 如果没有向末位 ( 指最高位的后一位 ) 借位,则 \(M \ge N\),那么结果是非负且正确的
- 如果向末位借位,则 \(N > M\),那么结果是负的,需要纠正
纠正方法:用差 M - N + \(2^n\) 减去 \(2^n\),得到 M - N 的绝对值 $$ 2^n - (M - N + 2^n) = N - M $$
注:\(2^n\) - X 被称为 X 的补码 (2's complement)(后面会讲到)
🌰:

同时实现无符号加法和无符号减法的电路图:
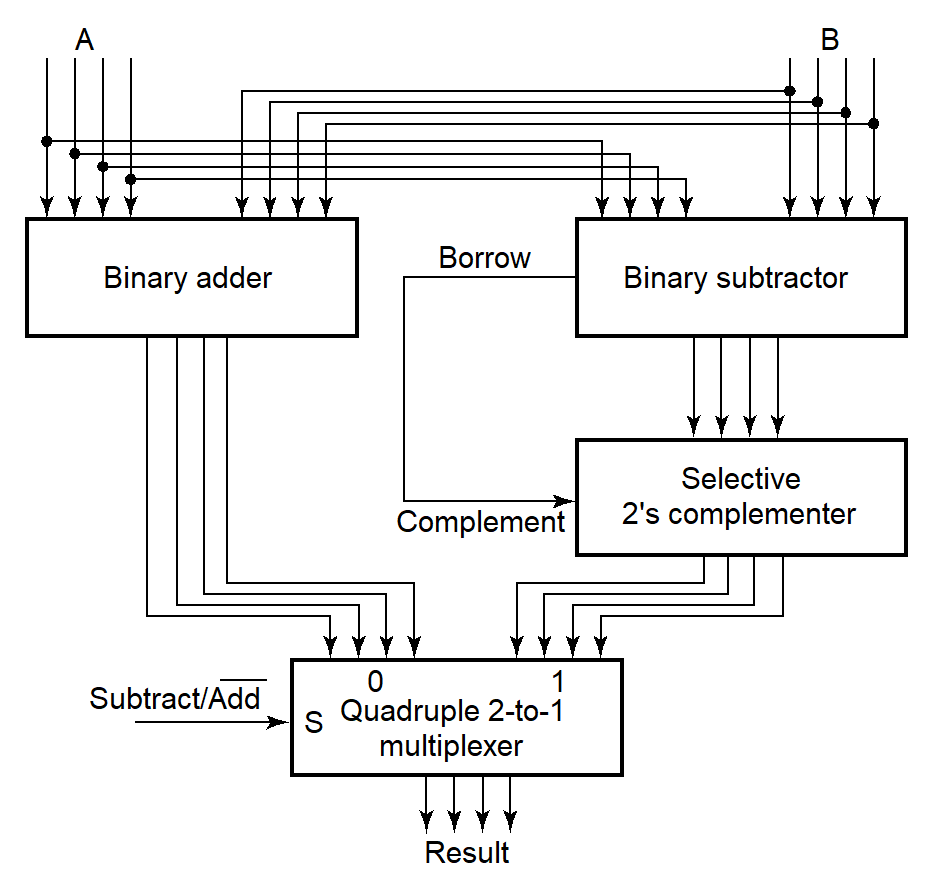
这种实现方法有些复杂,下面我们将介绍更为简单的实现方法
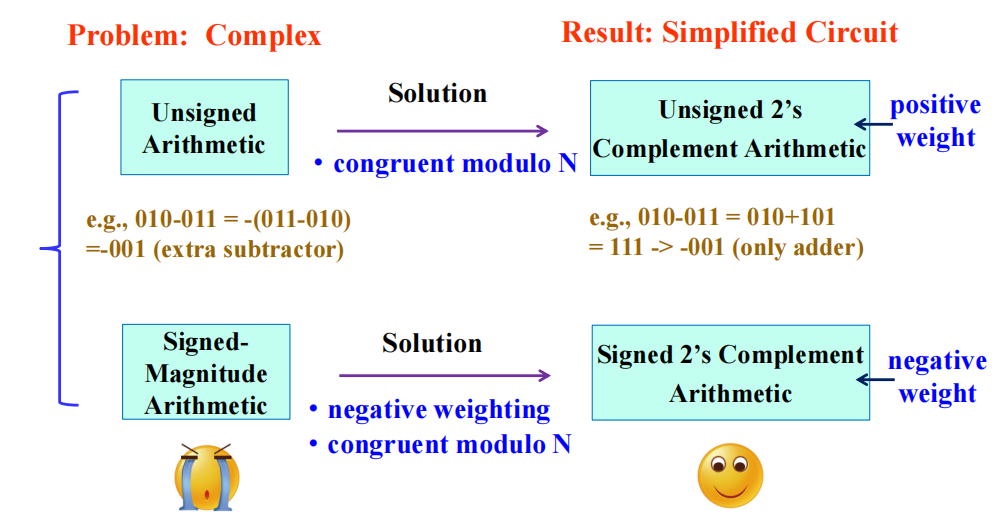
Unsigned 2's Complement Subtraction⚓︎
如果要同时实现无符号的加法和减法,需要用到加法器、减法器和取补器 (complementer),这相当复杂。因此我们需要让加法和减法“共享”一些更简单的逻辑,为此引入“补 (complement)”的概念作为解决方法。
注:这里的概念讲过很多遍了,实在不熟悉的话可以参考一下
补
分类:
-
🌟基数补 (radix complement)——补码
- r 进制:r's complement
- 二进制:2's complement
- N 的补码为 \(r^n - N\)
-
缩小基数补 (diminished radix complement)——反码
- r 进制:(r - 1)'s complement
- 二进制:1's complement
- N 的反码为 \((r^n-1) - N\)
速记 1‘s complement:每 1 位取反,即 \(0 \rightarrow 1, 1 \rightarrow 0\)
2’s complement 的几种取法:
- 根据定义:\(2^n - X\)
- 1‘s complement + 1
- 从最低位开始,从低到高扫描,遇到第 1 个‘1’后,这个‘1’后面所有的位均取反,即 \(0 \rightarrow 1, 1 \rightarrow 0\)
🌰:


已知 n 位无符号整数 \(M, N\),求 \(M - N\)
- \(M - N \Rightarrow M + (2^n - N) = M - N + 2^n\),即将 \(M - N\) 转化为 \(M + \((\)N\) 的补码 )
- 如果 \(M \ge N\),加法产生的末进位 \(2^n\) 直接扔掉,保留 \(M - N\)
- 如果 \(M < N\),加法未产生末进位,此时我们得到的结果是 \(M - N\) 的补码,那么答案为 \(-(N - M)\)
例题


注:比较无符号算术和用补码的无符号算术,可以发现后者可以少用一个减法器,因此设计上更加简单,成本也得到降低
Signed Integers⚓︎
用二进制表示带符号整数 (signed integers):\(sa_{n-1}\dots a_2a_1a_0\),其中对于最高位 s:
- s = 0 \(\rightarrow\) 正数
- s = 1 \(\rightarrow\) 负数
带符号整数的表示法
用最高位表示符号,其余位表示该数的绝对值。对于 2 个数的运算:
-
如果最高位加起来的和的最低位为 0,则:
- 将它们的量相加
- 检查结果是否溢出 ( 有没有来自最高位的进位 )
- 结果的符号同第 1 个操作数
-
如果最高位加起来的和的最低位为 1,则:
- 用第 2 个数的量减去第 1 个数的量
- 如果没有借位,结果的符号同第 1 个操作数
- 如果发生借位,取结果的补码,它的符号为第 1 个操作数的符号
- 不用担心溢出 ( 因为不可能发生 )
Example

流程:
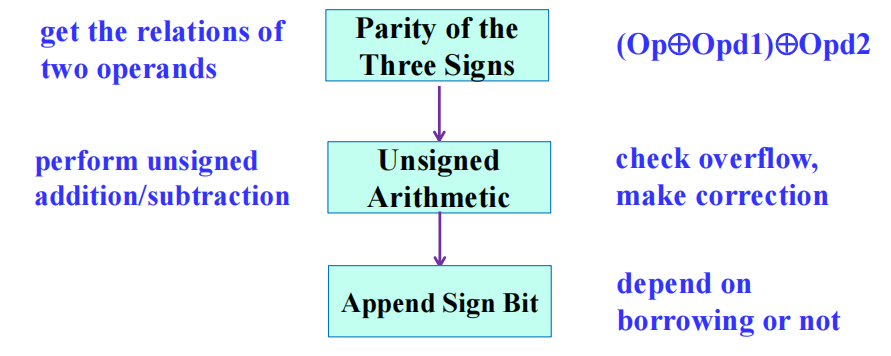
- 带符号 1's complement
- ⭐带符号 2's complement:正数无需变化,负数的话保留符号位,对其余位取补码
🌰:3 位二进制带符号整数
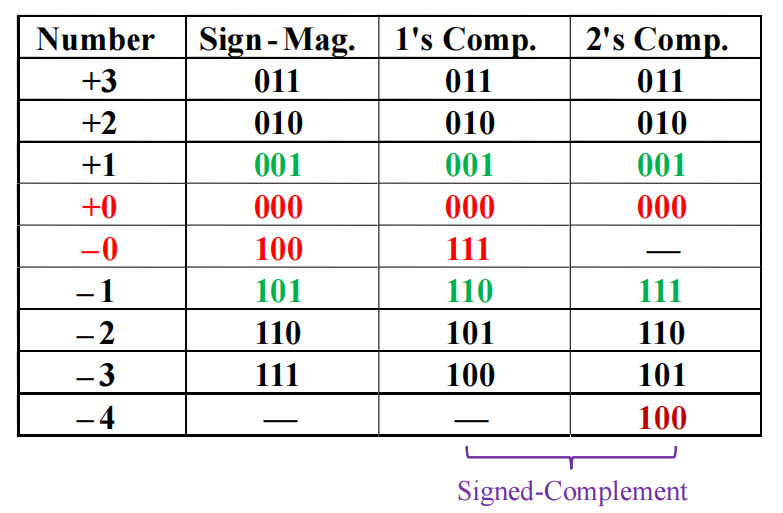
更形象的观察:
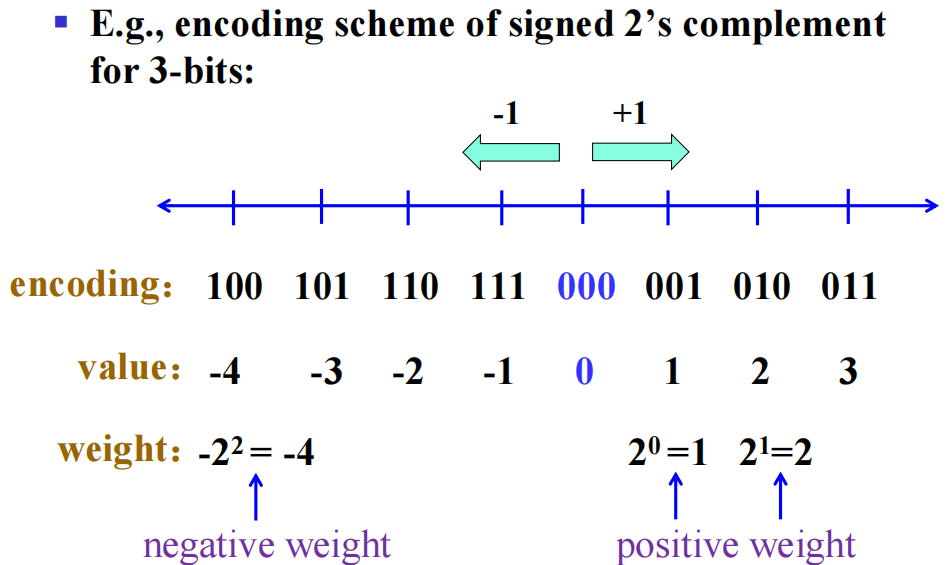
注:n 位带符号的补码
- 上限:\(2^{n - 1} - 1\)
- 下限:\(-2^{n-1}\)
- 且不会出现 +0 和 -0 同时存在的情况
补充
-
符号扩展 (sign extension) 保留补码的值
- 正数:高位添加 0
- 负数:高位添加 1
🌰:0111 \(\rightarrow\) 0000111, 1011 \(\rightarrow\) 1111011
具体原理:

- 在补码的算术运算中,最高位的进位并不一定意味着溢出
🌰:

Signed 2's Complement Arithmetic⚓︎
加法:
- 两数相加 ( 包括符号位 ),扔掉符号位的进位
- 如果两数符号相同,但结果的符号与两数不同,表明发生溢出
- 结果的符号已经从步骤 1 得到
减法:减法 ( 被减数 - 减数 ) \(\rightarrow\) 被减数 + 减数的补,然后用加法的方法做即可
带符号的补码加法器 / 减法器:
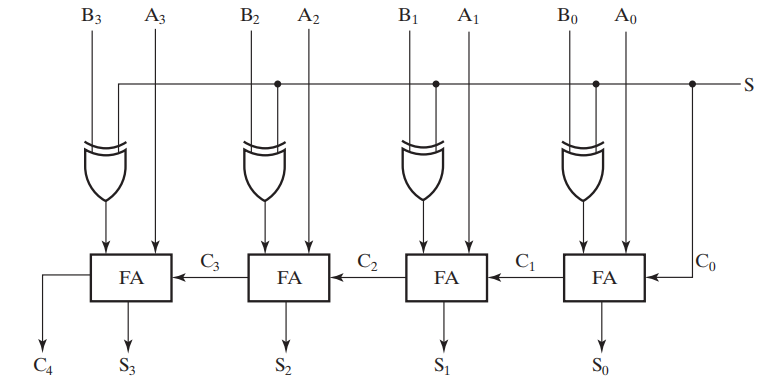
- 当 \(S = 0\) 时,此时 B 没有被改变,执行加法
- 当 \(S = 1\) 时,此时通过异或的取反作用,加上 \(C_0 = 1\),我们得到了 B 的补码,执行减法
Overflow Detection⚓︎
溢出 (overflow) 可能发生于:
- 两个符号相同的操作数的加法
- 两个符号不同的操作数的减法
两个 k 位数的加法:\(X_{k-1}\dots X_0 + Y_{k-1}\dots Y_0 = S_{k-1}\dots S_0\)
侦测错误的公式:\(V = X_{k-1}Y_{k-1}\overline{S_{k-1}} + \overline{X_{k-1}Y_{k-1}}S_{k-1} = C_{k-1} \oplus C_{k-2}\),应对两种情况:
- 下溢 (underflow)
- 上溢 (overflow)

🌰:带溢出侦测的补码加法器 / 减法器
- 简化版:
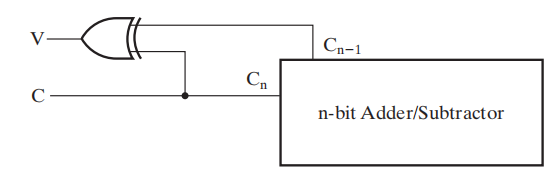
- 用于 4 位行波加法器:
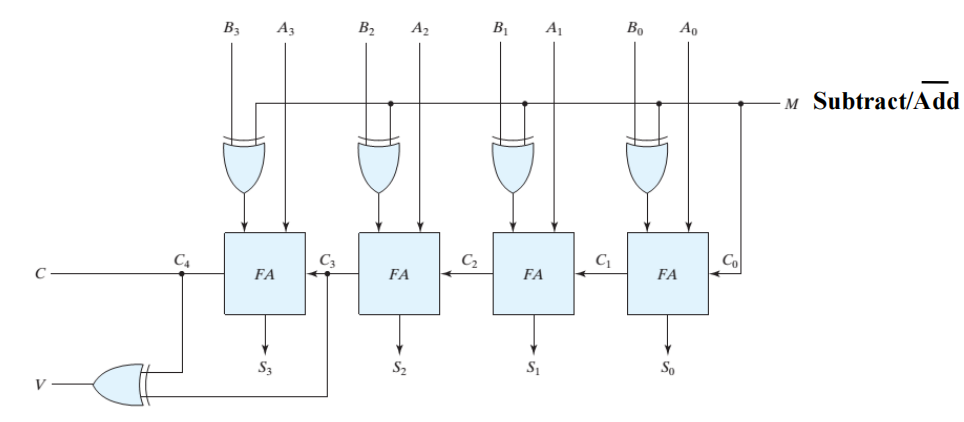
Summary
Other Arithmetic Functions⚓︎
除了加减的算术函数外,还有以下算术函数:
- 自增 (incrementing)
- 自减 (decrementing)
- 乘法 (multiplication)
- 常数除法 (division by a constant)
- ...
Design by Contraction⚓︎
🎯:利用来自之前设计的结果,实现逻辑电路或函数块的设计
我们可以通过使用类似给定电路的工艺,随后“压缩”成更简单的电路(比如利用值固定 (value fixing)、传输 (transfer) 和逆转输入 (inverting on its inputs) 等方法
🌰:将行波加法器压缩成自增器 (incrementer):n = 3, \(A_2A_1A_0 + 1\)
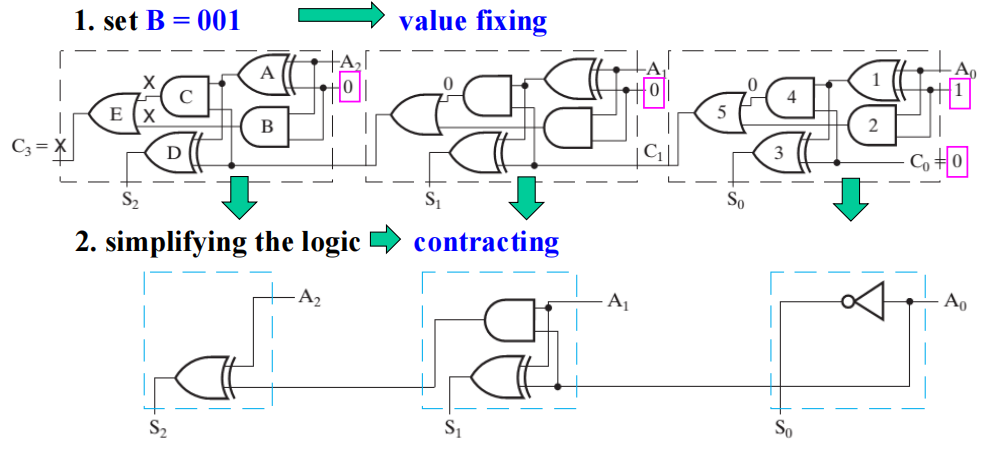
Incrementing and Decrementing⚓︎
自增 (incrementing):
- 函数块:自增器 (incrementer)
- 🌰:A + 1, B + 4
- 作用:算术变量 + 固定值
- 固定值 = 1 时被称为向上计数 (counting up)
自减 (decrementing):
- 函数块:自减器 (decrementer)
- 🌰:A - 1, B - 4
- 作用:算术变量 - 固定值
- 固定值 = 1 时被称为向下计数 (counting down)
注:Chap 6 的计数器一节会涉及该部分知识
Multiplication and Division⚓︎
- 与 \(2^n\) 相乘:向左移 n 位
- 与 \(2^n\) 相除:向右移 n 位
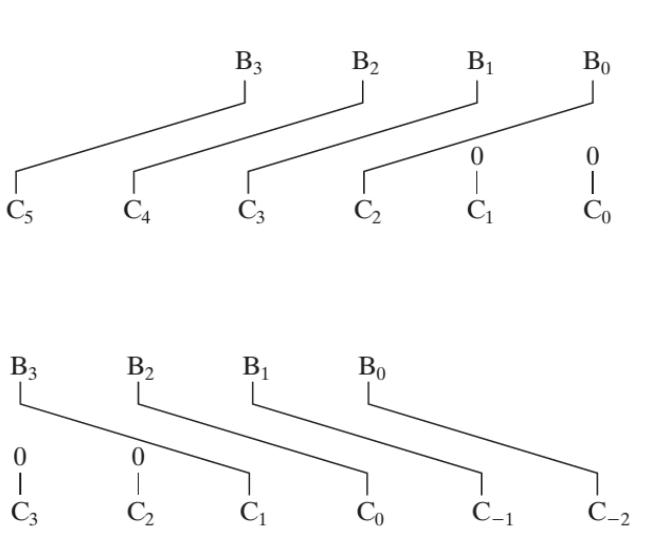
注:上面为乘法,下面为除法
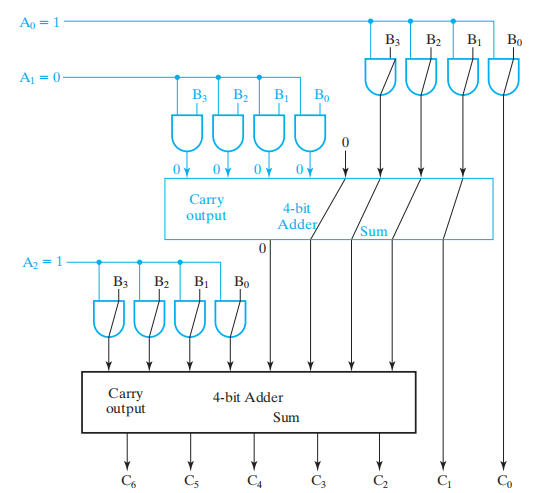
🌰:\(B(3: 0) \times (101)_2\)
Zero Fill⚓︎
添 0(zero fill):通过对 m 位的操作数添 0,该操作数扩展至 n 位 (m < n)。通常在最高位 (MSB) 添 0,也可以在最低位 (LSB) 添 0
🌰:将 11110101 扩成 16 位
- MSB:00000000 11110101
- LSB:11110101 00000000
Sign Extension⚓︎
符号扩展 (sign extension):根据补码表示法的规则,在最高位后添加数字
🌰:
- 正数:01110101 \(\rightarrow\) 00000000 01110101
- 负数:11110101 \(\rightarrow\) 11111111 11110101
Arithmetic Logic Unit(ALU)⚓︎
符号:
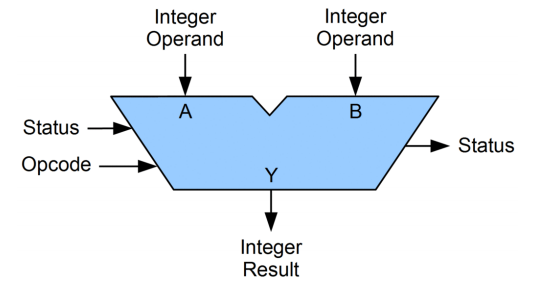
- 2 个 n 位输入:\(A_0 - A_{n-1}, B_0 - B_{n-1}\)
- 符号算术:加 / 减 / 自增 / 自减
- 逻辑运算:与 / 或 / 非 / 异或
- 模式选择:算术 / 逻辑
- 运算选择
- 1 位的进位输入和进位输出
框图:
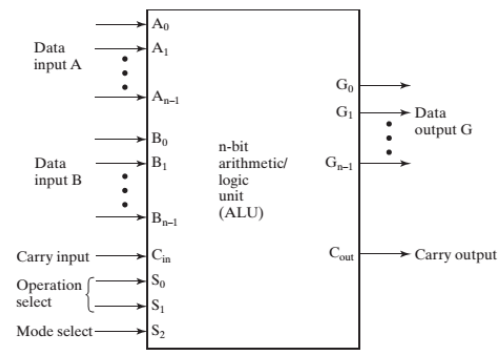
实现:
- 使用逻辑块,对加法器输入 B 的 4 种情况中进行选择
- 改变生成函数 \(G_i\) 和传播函数 \(P_i\)
根据实现方法,分解后的框图:
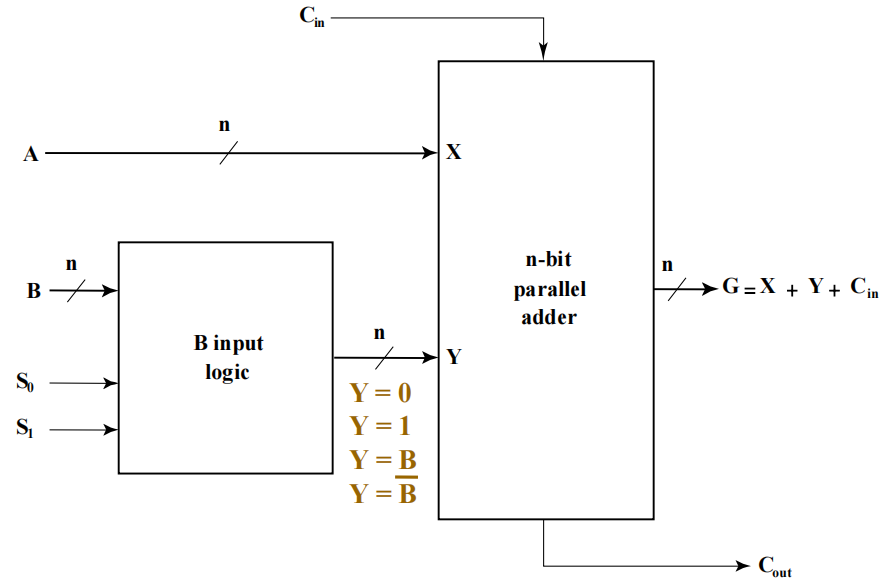
真值表 & K-map:
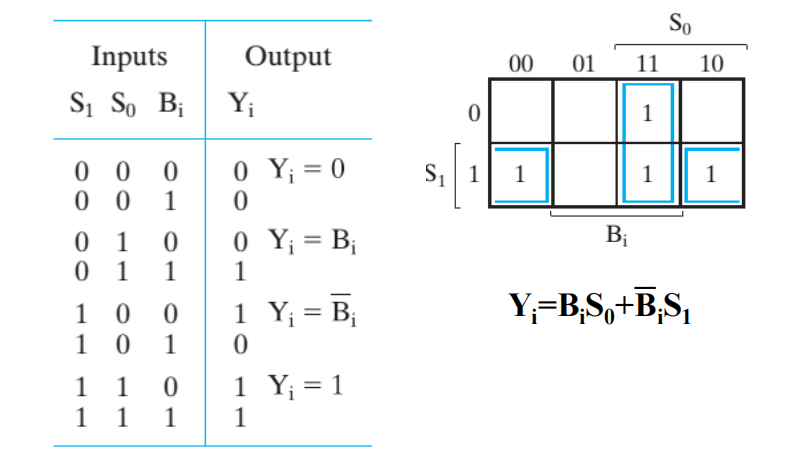
功能表——列出所有有用的函数
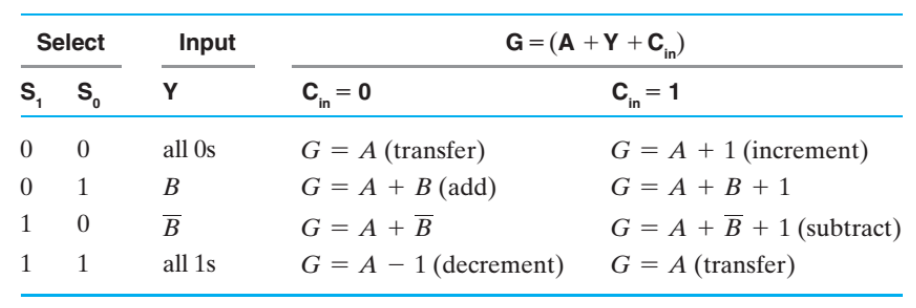
评论区
