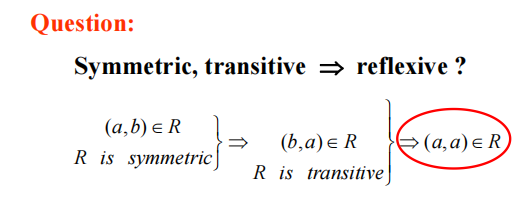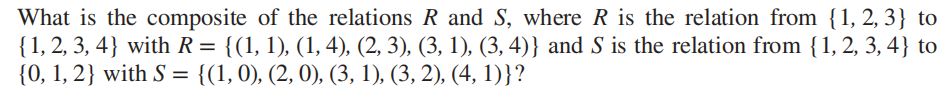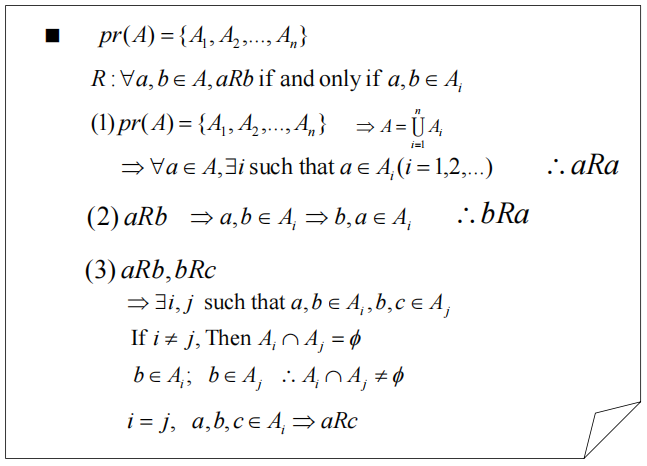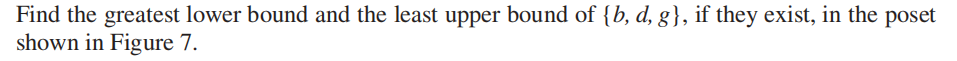Chap 9 Relations⚓︎

Relations and Their Properties⚓︎

令 \(A, B\) 为集合，从 \(A\) 到 \(B\) 的二元关系 (binary relation)是 \(A \times B\)（笛卡尔积）的子集。这个二元关系是一个包含有序对 (ordered pairs)的集合 \(R\).

• \(a\ R\ b\) 表示 \((a, b) \in R\)（被称为 \(a\) 关于 \(R\) 与 \(b\) 有关系）
• \(a \not{R} \ b\) 表示 \((a, b) \notin R\)

注：\(\emptyset\)，\(A \times B\) 也是关系

Functions as Relations⚓︎

从 \(A\) 到 \(B\) 的函数\(f\) 为 \(A\) 中的每个元素赋予 \(B\) 中的唯一一个元素，不难看出 \(f\) 是 \(A \times B\) 的子集，所以它表示从 \(A\) 到 \(B\) 的关系。

关系是函数的一种泛化 (generalization)，它能表示更多关于集合间的联系，比如它能表示函数所不能表示的一对多的联系

Relations on a Set⚓︎

定义：在集合 \(A\) 上的关系 (a relation on a set \(A\))\(R\) 是从 \(A\) 到 \(A\) 的关系，也就是 \(A \times A\) 的子集

如果 \(A\) 有 \(n\) 个元素，则共有 \(2^{n^2}\) 个对于 \(A\) 的关系

Properties of Relations⚓︎

⭐在集合 \(A\) 上的关系的一些性质：

• 自反性 (reflexive)：\(\forall a \in A((a, a) \in R)\)
• 对称性 (symmetric)：\(\forall a, b \in A((a, b) \in R \rightarrow (b, a) \in R)\)

• 反对称性 (antisymmetric)：\(\forall a, b \in A((a, b) \in R \wedge (b, a) \in R) \rightarrow (a = b))\)

  注：

  • 对称性和反对称性不是对立的，一个关系可能同时具有对称性和反对称性
  • 但如果一个关系存在形如 \((a, b), a \ne b\) 的有序对，那么它就不会同时具有这两个性质

• 传递性 (transitive)：\(\forall a, b, c \in A(((a, b) \in R \wedge (b, c) \in R) \rightarrow (a, c) \in R)\)

如果 \(A\) 有 \(n\) 个元素，那么：

• 有 \(2^{n(n - 1)}\) 个自反的关系

  证：\((a, a)\) 必须存在于关系中，其余 \(n(n - 1)\) 可在可不在

• 有 \(2^{\frac{n(n+1)}{2}}\) 个对称的关系

  证：\((a, a)\) 可在可不在，剩下 \(n^2 - n\) 个有序对分成 2 半，\((i, j)\) 和 \((j, i)\) 可同时在，同时不在，因此加起来有 \(2^n + 2^{\frac{n^2 - n}{2}}\) 种

• 有 \(2^n \times 3^{\frac{n^2 - n}{2}}\) 个反对称的关系

  证：类似证对称关系，除了 \((i, j)\) 和 \((j, i)\) 不能同时在，因此对于一对有序对有 3 种选择

• 没有通式来表达传递的关系个数 \(T(n)\)，已知的 \(T(n)\) 为 \(0 \le n \le 18\)

注：这么讲有些抽象，用 9.3 节介绍的零一矩阵来表示就很直观了

思考

问题答案

NO，但我也不清楚怎么解释

若读者清楚如何证明的话，欢迎表达自己的想法！

Combining Relations⚓︎

关系也能像一般的集合那样被结合，回忆一些集合的运算：并集 \(\cup\)、交集 \(\cap\)、差集 \(-\)、对称差集 \(\oplus\)，补集 \(\overline{}\)

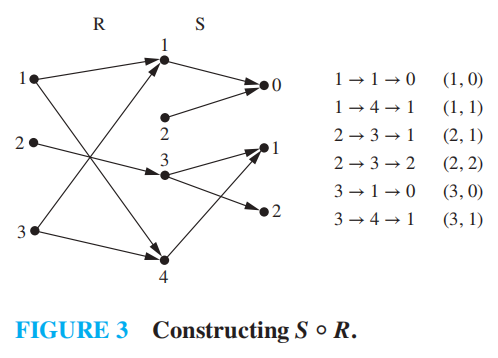
关系也可以像函数一样被复合 (composite)：对于一个从 \(A\) 到 \(B\) 的关系 \(R\)，和一个从 \(B\) 到 \(C\) 的关系 \(S\)，\(R\) 和 \(S\) 的复合关系\(S \circ R\) 由有序对 \((a, c), a \in A, c \in C\) 构成，且存在 \(b \in B\)，使得 \((a, b) \in R, (b, c) \in S\)。

计算两个关系的复合时，我们可以先找到某个元素，它既出现在第一个关系里某个有序对的第二个位置，也出现在第二个关系里某个有序对的第一个位置。

🌰

通过画一张有向图（后面很快会讲到），问题就迎刃而解了：我们要找的就是从最左边到最右边有通路的两个顶点

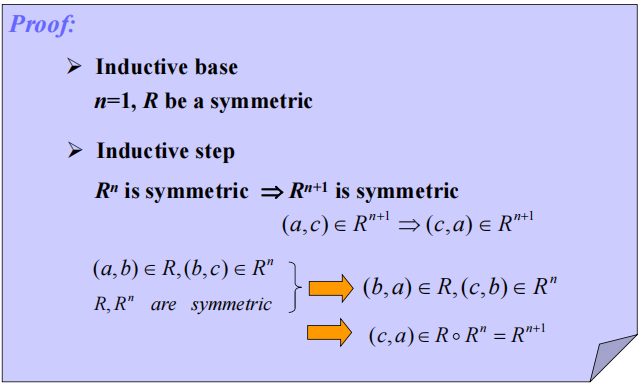
定义：令 \(R\) 是在集合 \(A\) 上的关系，幂 \(R^n, n = 1, 2, 3, \dots\) 被递归定义为： $$ R^1 = R \quad R^{n+1} = R^n \circ R $$ 定理 1：当且仅当 \(R^n \subseteq R, n = 1, 2, 3, \dots\) 时，在集合 \(A\) 上的关系 \(R\) 具有传递性

• 如果 \(R\) 具有自反性，则 \(R^n\) 也具有自反性
• 如果 \(R\) 具有对称性，则 \(R^n\) 也具有对称性

证明

使用数学归纳法

关系运算的性质：

假设 \(R, S\) 是从 \(A\) 到 \(B\) 的关系，\(T\) 是从 \(B\) 到 \(C\) 的关系，\(P\) 是从 \(C\) 到 \(D\) 的关系，那么：

• \((R \cup S)^{-1} = R^{-1} \cup S^{-1}\)
• \((R \cap S)^{-1} = R^{-1} \cap S^{-1}\)
• \((\overline{R})^{-1} = \overline{R^{-1}}\)
• \((R - S)^{-1} = R^{-1} - S^{-1}\)
• \((A \times B)^{-1} = B \times A\)
• \(\overline{R} = A \times B - R\)
• \((S \circ T)^{-1} = T^{-1} \circ S^{-1}\)
• \((R \circ T) \circ P = R \circ (T \circ P)\)
• \((R \cup S) \circ T = R \circ T \cup S \circ T\)

Supplements(from Exercises)⚓︎

• 非自反性 (irreflexive)：\(\forall a \in A((a, a) \notin R)\)

• 不对称性 (asymmetric)：\(\forall a \in A \forall b \in A((a, b) \in R \rightarrow (b, a) \notin R)\)

  注：不要跟前面提到的反对称性 (antisymmetric)弄混淆

• 令 \(R\) 为从 \(A\) 到 \(B\) 的关系，那么从 \(B\) 到 \(A\)逆关系 (inverse relation)\(R^{-1}\)，表示 \(\{(b,a)\ |\ (a, b) \in R\}\)

• 补关系 (complementary relation)\(\overline{R}\) 表示 \(\{(a, b)\ |\ (a, b) \notin R\}\)

n-ary Relations and Their Applications⚓︎

\(n\)-ary Relations⚓︎

定义：令 \(A_1, A_2, \dots, A_n\) 为集合，这些集合的 \(n\) 元关系 (\(n\)-ary relation)是 \(A_1 \times A_2 \times \dots \times A_n\) 的子集。其中 \(A_1, A_2, \dots, A_n\) 被称作域 (domain)，\(n\) 被称为阶 (degree)

Databases and Relations⚓︎

Operations on \(n\)-ary Relations⚓︎

SQL⚓︎

Association Rules from Data Mining⚓︎

Representing Relations⚓︎

表示关系的方法：

• 列出所有有序对
• 通过谓词，用集合构建规则
• 二维表
• 连接矩阵 / 零一矩阵 (connection matrix / zero-one matrix)
• 有向图 (directed graph / digraph)

Representing Relations Using Matrices⚓︎

假设 \(R\) 是从 \(A = \{a_1, a_2, \dots, a_m\}\) 到 \(B = \{b_1, b_2, \dots, b_n\}\) 的关系，那么 \(R\) 可被表示为零一矩阵 \(M_R = [m_{ij}]\)，其中

对于在集合上的关系，它的零一矩阵是一个方阵，我们可以用方阵直观反映前面提到的那些性质：

• 自反性：\(\begin{bmatrix}1&&&&&\\&1&&&&\\&&1&&&\\&&&\ddots&&\\&&&&1&\\&&&&&1\end{bmatrix}\)，这里没有表示主对角线外的元素
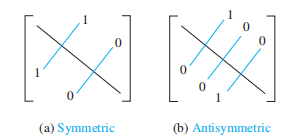
• 对称性和反对称性：

注意到对称性分 2 种情况，反对称性分 3 种情况

• 传递性：\(\overline{(m_{ij} \wedge m_{jk})} \vee m_{ik} = 1\)

  注：利用 \(p \rightarrow q \equiv \overline{p} \vee q\)

利用布尔运算中的并 (join)和交 (meet)，我们可以找到两个关系的并集和交集的零一矩阵。记关系 \(R_1, R_2\) 的零一矩阵分别为 \(M_{R_1}, M_{R_2}\)，则： $$ M_{R_1 \cup R_2} = M_{R_1} \vee M_{R_2} \quad M_{R_1 \cap R_2} = M_{R_1} \wedge M_{R_2} $$ $$ M_{\overline{R}} = [\overline{c_{ij}}] \quad M_{R_1 - R_2} = M_{R_1 \cap \overline{R_2}} = [c_{ij} \wedge \overline{d_{ij}}] $$

利用布尔积，我们可以找到复合关系的零一矩阵： $$ M_{S \circ R} = M_R \odot M_S $$ $$ M_{R^n} = M_R^{[n]} $$

注：这个式子需要自己理解一下，因为并不是很直观

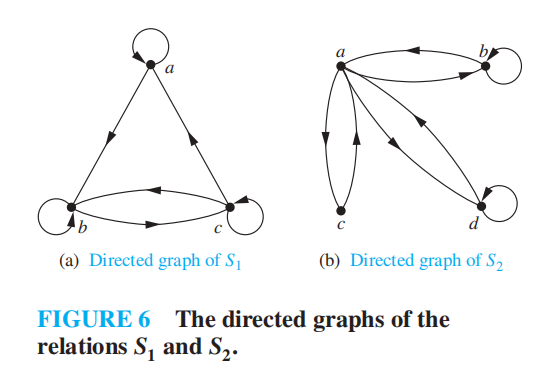
Representing Relations Using Digraphs⚓︎

有向图 (directed graph/digraph)：由包含顶点 (vertice/nodes)的集合 \(V\)，以及包含 \(V\) 中元素的有序对 ( 被称为边 (edge/arc)) 的集合 \(E\) 构成。对于边 \((a, b)\)，顶点 \(a\) 被称为这条边起点 (initial vertex)，顶点 \(b\) 被称为这条边的终点 (terminal vertex)

边 \((a, a)\) 被称为环 (loop)

如果用有向图表示在集合 \(A\) 上的关系 \(R\)，\(A\) 中的元素作为顶点，有序对 \((a, b) \in R\) 作为边。因此，我们建立起在 \(A\) 上的关系与 \(A\) 的有向图之间的双射关系。

注：有向图也可以表示从 \(A\) 到 \(B\) 的关系，但如果 \(A = B\)，它所反映的内涵就不如表示一个集合时那样清楚

通过有向图反映的性质：

• 自反性：有向图的每个顶点都有一个环

• 对称性：两个不同的顶点间要么没有边，要么同时有 2 条双向的边

  注：无向图 (undirected graph)的表示方法也可以体现对称性

• 反对称性：两个不同的顶点间不能同时出现 2 条双向的边

• 传递性：当存在 \(x\) 到 \(y\) 的边，以及 \(y\) 到 \(z\) 的边，那么也存在从 \(x\) 到 \(z\) 的边（形成一个三角形）

Closures of Relations⚓︎

Different Types of Closures⚓︎

引入：如果 \(R\) 是在集合 \(A\) 上的关系，那么它可能有，也可能没有性质 \(P\)，比如自反性、对称性或传递性。如果没有的话，我们希望找到最小的在集合 \(A\) 上的关系 \(S\)，它满足性质 \(P\) 且包括 \(R\)

定义：如果 \(R\) 是在集合 \(A\) 上的关系，那么 \(R\) 关于性质 \(P\) 的闭包 (closure)( 如果存在的话 )，它满足性质 \(P\) 且包括 \(R\)，而且是所有包含 \(R\) 且满足 \(P\) 的 \(A \times A\) 的子集

注：

• 关系 \(R\) 关于性质 \(P\) 的闭包是唯一的，且是最小的满足性质 \(P\) 且包括 \(R\) 的关系
• 对于某些性质 \(P\)，某个关系关于 \(P\) 的闭包可能不存在

类别：

• 自反闭包 (reflexive closure)：记作 \(r(R)\)

• 对称闭包 (symmetric closure)：记作 \(s(R)\)

• 传递闭包 (transitive closure)：记作 \(t(R)\)

  传递闭包的求解有些复杂，过会儿会详细阐述

Paths in Directed Graphs⚓︎

定义：有向图 \(G\) 中，从 \(a\) 到 \(b\) 的路径 (path)，是 \(G\) 上一系列的边 \((x_0, x_1), (x_1, x_2), (x_2, x_3), \dots, (x_{n-1}, x_n)\)，其中 \(n\) 为非负整数，\(x_0 = a, x_n = b\)。这条路径记作 \(x_0, x_1, x_2, \dots, x_{n-1}, x_n\)，长度 (length)为 \(n\)。定义边的空集长度为 0。长度 \(n \ge 1\)，且始末顶点相同 (\(x_0 = x_n\)) 的路径被称为环 (circuit/cycle)。

将有向图关于路径的概念引申至关系：在关系 \(R\) 中，从 \(a\) 到 \(b\) 的路径是指一系列的元素 \(a, x_1, x_2, \dots, x_{n-1}, b\)，满足 \((a, x_1) \in R, (x_1, x_2) \in R, \dots, (x_{n - 1}, b) \in R\)

定理 1：令 \(R\) 为在集合 \(A\) 上的关系，当且仅当 \((a, b) \in R^n\) 时，存在一条长度为 \(n\)，从 \(a\) 到 \(b\) 的路径，其中 \(n\) 为正整数

证明

使用数学归纳法：

Transitive Closures⚓︎

定义：令 \(R\) 为在集合 \(A\) 上的关系。连通关系 (connectivity relation)\(R^*\) 由 \((a, b)\) 组成，这些对满足存在一条从 \(a\) 到 \(b\)，长度至少为 1 的路径

结合上面的定理 1，易得：\(R^*= \bigcup\limits_{n=1}^\infty R^n\)

定理 2：\(R\) 的传递闭包 \(t(R)\) = 连通关系 \(R^*\)

证明

要证该定理，即证 \(R^*\) 满足：

• \(R^*\) 具有传递性
• \(R^*\subseteq S\)，其中 \(S\) 是所有包含 \(R\) 的传递关系

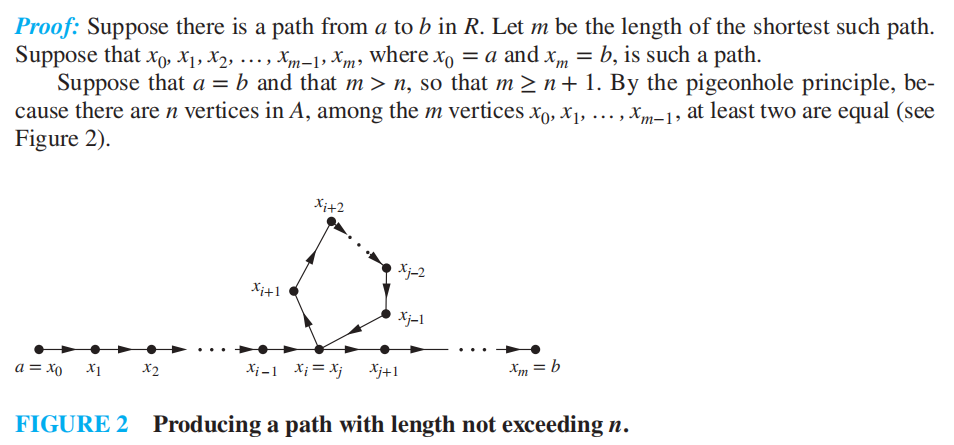
引理 1：令 \(A\) 为有 \(n\) 个元素的集合，\(R\) 为在 \(A\) 上的关系。

• 如果在 \(R\) 中存在一条长度至少为 1 的从 \(a\) 到 \(b\) 的路径，那么路径的长度不超过 \(n\)。
• 如果 \(a \ne b\)，且在 \(R\) 中存在一条长度至少为 1 的从 \(a\) 到 \(b\) 的路径，那么路径的长度不超过 \(n - 1\)

证明

由引理 1，我们可以得到： $$ t(R) = R^*= R \cup R^2 \cup R^3 \cup \dots \cup R^n $$

定理 3：令 \(\mathbf{M}_R\) 为 \(n\) 个元素的集合的关系 \(R\) 的零一矩阵，那么传递闭包 \(R^*\) 的零一矩阵为： $$ \mathbf{M}_{R^*} = \mathbf{M}_R \vee \mathbf{M}_R^{[2]} \vee \mathbf{M}_R^{[3]} \dots \vee \mathbf{M}_R^{[n]} $$

🌰：

算法实现：

分析：

• 所有布尔积的运算次数：\((n-1) \cdot n^2(2n - 1)\)
• 所有取交 (\(\vee\)) 的运算次数：\((n - 1)n^2\)

\(\therefore\) 时间复杂度 = \(O(n^4)\)

Warshall's Algorithm⚓︎

显然，上述算法的实现效率较低，因此这里介绍一种更快的算法——Warshall's algorithm

注：这个算法更知名的名称是弗洛伊德算法 (Floyd algorithm)——没错，就是那个用来求最短路径的那个算法！因此这个算法在图那个章节中可能还会再用到，现在我们利用这个算法来求的是 \(R\) 的传递闭包。在正式介绍算法之前，先引入一些概念：

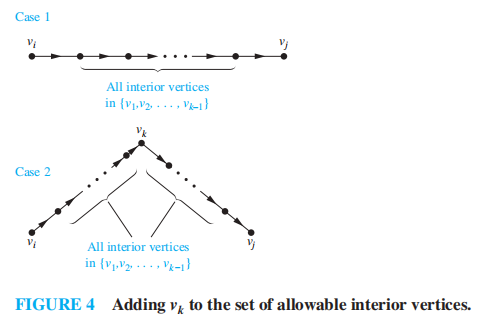
假设 \(R\) 是 \(n\) 个元素的集合的关系，令 \(v_1, v_2, \dots, v_n\) 为 \(n\) 个元素的任意排列。路径 \(a, x_1, x_2, \dots, x_{m-1}, b\) 的内部顶点 (interior vertices)是 \(x_1, x_2, \dots, x_{m-1}\)

❗注：虽然内部顶点不包含路径上始末两个顶点，然而，如果起点或终点在中间还出现过的话，则它们也算内部顶点

Warshall 算法需要一系列的零一矩阵 \(\mathbf{W}_0, \mathbf{W}_1, \dots, \mathbf{W}_n\)，其中：

• \(\mathbf{W}_0 = \mathbf{M}_R\)
• \(\mathbf{W}_n = \mathbf{M}_{R^*}\)
• \(\mathbf{W}_k = [w_{ij}^{(k)}]\)，其中

所以，\(\mathbf{W}_n\) 就是我们要得到的矩阵。

🌰

通过这个例子，不难发现：要计算 \(\mathbf{W}_k\)，我们可以直接在 \(\mathbf{W}_{k-1}\) 的基础上得到，只需再讨论两种情况，如图所示：

引理 2：令 \(\mathbf{W}_k = [w_{ij}^{[k]}]\)（上面已描述过），那么： $$ w_{ij}^{[k]} = w_{ij}^{[k - 1]} \vee (w_{ik}^{[k - 1]} \wedge w_{kj}^{[k - 1]}) $$ 其中\(i, j, k\)为不超过\(n\)的正整数

算法实现：

分析： 从\(\mathbf{W}_{k-1}\)中得到\(\mathbf{W}_k\)需要\(2n^2\)次操作

\(\therefore\) 总的操作数：\(2n^3\) \(\rightarrow\) 时间复杂度：\(O(n^3)\)

思考：如何求满足多个性质的闭包？

先求对称 / 反对称闭包，再求传递闭包，最后求自反闭包

Equivalence Relations⚓︎

Equivalence Relations⚓︎

定义：

• 集合 \(A\) 的某个关系如果同时具备自反性、对称性和传递性，称这种关系为等价关系 (equivalence relation)
• 如果两个元素 \(a, b\) 关于某个等价关系是相关的，则称它们是等价的 (equivalent)，记作 \(a \sim b\)

Equivalence Classes⚓︎

定义：令 \(R\) 为集合 \(A\) 上的等价关系，所有与集合中的元素 \(a\) 相关的元素构成的集合被称为 \(a\) 的等价类 (equivalence class)，记作 \([a]_R\)。如果只考虑一个关系，则可以简写为 \([a]\)。

如果 \(b \in [a]_R\)，则称 \(b\) 为这个等价类的代表 (representative)，因此等价类中的每个元素都可以作为这个等价类的代表。

例题

同余模\(m\)(congruence modulo \(m\))同余类模\(m\)(congruence classes modulo \(m\))位串

同余模 \(m\) 的等价类，记作 \([a]_m\)

Equivalence Classes and Partitions⚓︎

利用等价类，我们可以将一个集合划分为不相交的非空子集

定理 1：令 \(R\) 为集合 \(A\) 的等价关系，以下关于 \(A\) 中元素 \(a, b\) 的几条语句是等价的：

证明

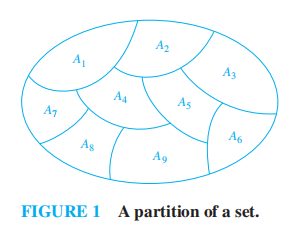
定义：集合 \(S\) 的分区 (partition)是 \(S\) 中一组不相交的非空子集，\(S\) 是它们的并集。满足：

• \(A_i \ne \emptyset \text{ for } i \in I\)
• \(A_i \cap A_j = \emptyset \text{ when } i \ne j\)
• \(\bigcup\limits_{i \in I} A_i = S\)

注：\(I\) 是索引集 (index set)，顾名思义，它存储某个集合的元素的索引

定理 2：

• 令 \(R\) 为集合 \(S\) 的等价关系，那么 \(R\) 的等价类构成了 \(S\) 的分区
• 反过来，给定集合 \(S\) 的分区\(\{A_i\ |\ i \in I\}\)，存在等价关系 \(R\)，它的等价类包括集合 \(A_i, i \in I\)

简单理解：等价类 \(\leftrightarrow\) 分区

证明

例题

同余位串等价关系 & 分区

The Operations of Equivalence Relations⚓︎

如果 \(R_1, R_2\) 是集合 \(A\) 的等价关系，则

• \(R_1 \cap R_2\) 是集合 \(A\) 的等价关系
• \(R_1 \cup R_2\) 是集合 \(A\) 的自反、对称关系
• \((R_1 \cup R_2)^*\) 是集合 \(A\) 的等价关系

Supplements(from Exercises)⚓︎

• 当每个在分区 \(P_1\) 的集合是分区 \(P_2\) 中某个集合的子集，称 \(P_1\) 是 \(P_2\) 的精炼 (refinement)
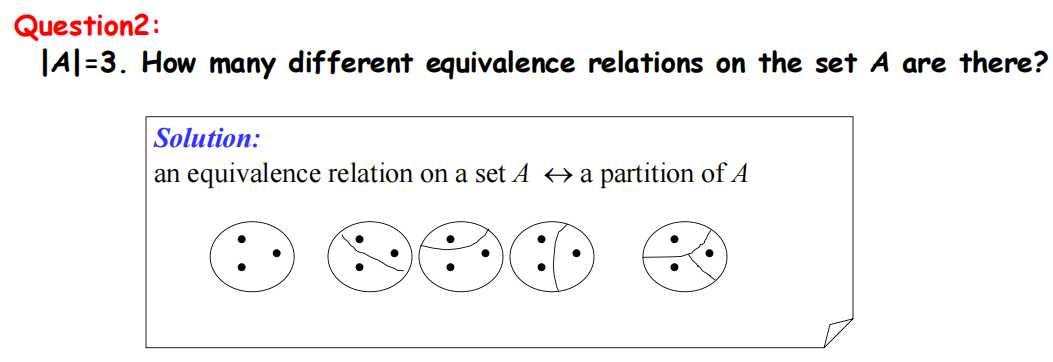
• 令 \(p(n)\) 代表有 \(n\) 个元素的集合的不同等价关系的数量（即分区的数量），则： $$ p(n) = \sum\limits_{j = 0}^{n - 1}C(n - 1, j)p(n - j - 1), \quad p(0) = 1 $$

  注：\(p(n)\) 被称为贝尔数 (Bell numbers)

Partial Orderings⚓︎

定义：集合 \(S\) 上的关系 \(R\)，如果它具有自反性、反对称性和传递性，则它被称为偏序 (partial ordering/partial order)。集合 \(S\) 和它的偏序 \(R\) 统被称为偏序集 (partially ordered set/poset)，记作 \((S, R)\)。\(S\) 中的成员被称为偏序集的元素 (elements)

🌰：

• 大于等于关系(\(\ge\)) 是整数集的偏序
• 整除关系(|) 是正整数集的偏序
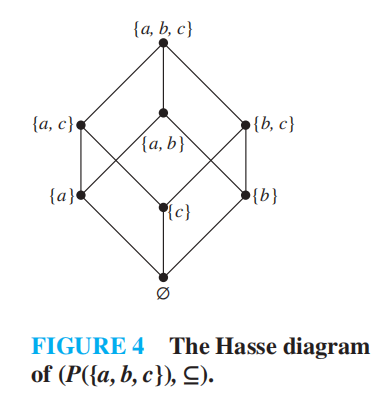
• 包含关系(\(\subseteq\)) 是集合 \(S\) 的幂集的偏序

习惯上，我们用：

• \(a \preceq b\) 来表示在任意偏序集 \((S, R)\) 内的 \((a, b) \in R\)
• \(a \prec b\) 表示 \(a \preceq b \wedge a \ne b\)

当 \(a, b\) 是偏序集 \((S, \preceq)\) 中的元素时，不一定要满足 \(a \preceq b\) 或者 \(b \preceq a\)。下面给出相关定义：

• 偏序集 \((S, \preceq)\) 中的元素 \(a, b\) 如果满足 \(a \preceq b\) 或者 \(b \preceq a\)，称它们是可比的 (comparable)
• 如果既不满足 \(a \preceq b\)，也不满足 \(b \preceq a\)，称它们是不可比的 (incomparable)

定义：如果对于某个偏序集 \((S, \preceq)\)，\(S\) 中的任意两个元素是可比的，称 \(S\) 为全序集 (totally/linearly ordered set)，\(\preceq\) 被称为全序 (total/linear order)。全序集又被称为链 (chain)

🌰：偏序集 \((\mathbf{Z}, \le)\) 是全序的，而偏序集 \((\mathbf{Z}^+, |)\)不是全序的

定义：如果偏序集 \((S, \preceq)\) 满足 :

• \(\preceq\) 是全序
• \(S\) 中的每个非空子集有一个最小元素

称 \((S, \preceq)\) 是良序集 (well-ordered set)

🌰：正整数的有序对的集合 \(\mathbf{Z}^+ \times \mathbf{Z}^+\)，有关系 \((a_1, a_2) \preceq (b_1, b_2)\)，表示：

• \(a_1 < b_1\)
• 或者 \(a_1 = b_1 \wedge a_2 \le b_2\)

（即后面讲到的词典序），这个集合是良序集

定理 1——良序归纳法原则 (THE PRINCIPLE OF WELL-ORDERED INDUCTION)：假设 \(S\) 是一个良序集，如果满足：

归纳步骤 (INDUCTIVE STEP)：对于每个 \(y \in S\)，如果对于所有 \(x \in S\) 且 \(x \prec y\)，\(P(x)\) 为真，则 \(P(y)\) 为真

那么对于所有 \(x \in S\)，\(P(x)\) 为真

注：

• 这个证明和证明良序性的方法非常相似
• 在良序归纳法中，我们不需要基本步骤 (basis step)，因为 \(x_0\) 是良序集内的最小元素，归纳步骤告诉我们 \(P(x_0)\) 为真，这是因为没有元素 \(x \in S\) 使得 \(x \prec x_0\)，所以我们知道 ( 使用空证明 ) 对于所有 \(x \in S\) 且 \(x \prec x_0\)，\(P(x)\) 为真。

Lexicographic Order⚓︎

在两个偏序集 \((A_1, \preceq_1)\) 和 \((A_2, \preceq_2)\) 的笛卡尔积上构造偏序：

在集合 \(A_1 \times A_2\) 上的词典序 (lexicographic ordering)\(\preceq\) 满足：若 \((a_1, a_2) \prec (b_1, b_2)\)，则

• \(a_1 \prec_1 b_1\)
• 或者 \(a_1 = b_1 \wedge a_2 \prec_2 b_2\)

补充：证明词典序是两个偏序集的笛卡尔积的偏序

对于 \(n\) 个偏序集 \((A_1, \prec_1), (A_2, \prec_2), \dots, (A_n, \prec_n)\) 的笛卡尔积 \(A_1 \times A_2 \times \dots \times A_n\)，它的词典序 \(\preceq\) 满足：若\((a_1, a_2, \dots, a_n) \prec (b_1, b_2, \dots, b_n)\)，则

• \(a_1 \prec_1 b_1\)
• 或者存在整数 \(i > 0\)，使得 \(a_1 = b_1, \dots, a_i = b_i\)，且 \(a_{i+1} \prec_{i+1} b_{i+1}\)

我们也可以定义字符串上的词典序：考虑在偏序集 \(S\) 上的两个字符串 \(a_1a_2\dots a_m\) 和 \(b_1b_2 \dots b_n\)，假设它们不相同。令 \(t = \min(m, n)\)，词典序为：若 \(a_1a_2 \dots a_m\) 小于 \(b_1b_2 \dots b_n\)，充要条件为：

• \((a_1, a_2, \dots, a_t) \prec (b_1, b_2, \dots, b_t)\)
• 或者 \((a_1, a_2, \dots, a_t) = (b_1, b_2, \dots, b_t)\) 且 \(m < n\) 其中\(\prec\)表示\(S^t\)的词典序。

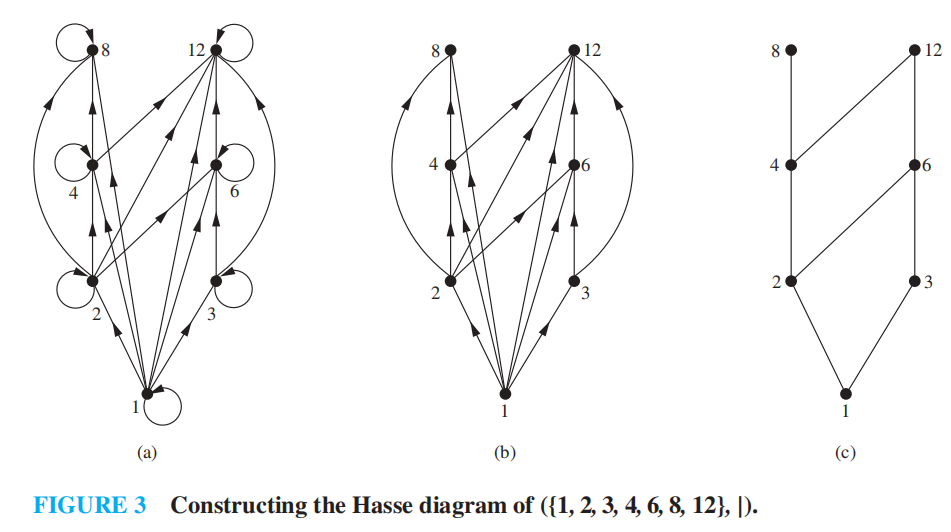
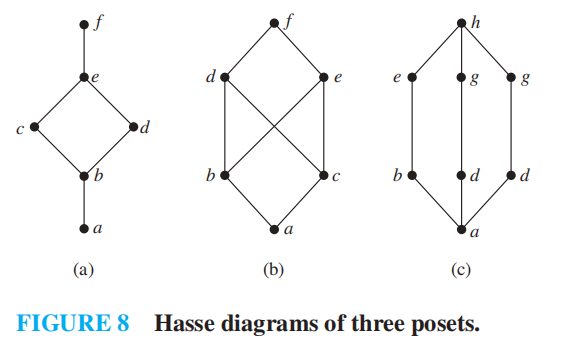
Hasse Diagrams⚓︎

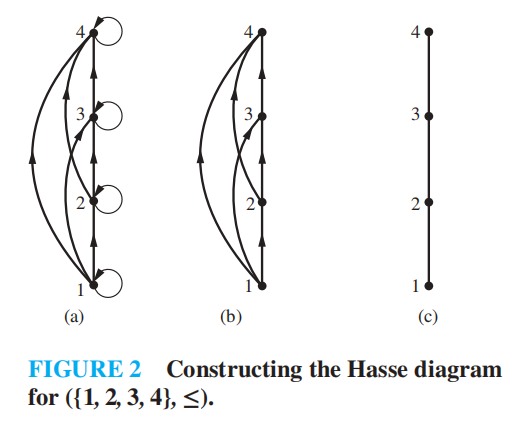
化简表示偏序的有向图——哈斯图 (Hasse diagram)

化简步骤 ( 假设某个有限的偏序集 \((S, \preceq)\))：

• 先画出偏序的有向图
• 因为偏序是自反的，所以每个顶点都会有一个环\((a, a)\)，将这些环全部移除
• 由于其他边的存在和传递性，我们需要移除所有多余的边，即当存在元素 \(z \in S\) 使得 \(x \prec z\) 且 \(z \prec y\) 时，移除边 \((x, y)\)
• 对所有边重新排序，使得起点在终点的下面，并且移除所有箭头 ( 因为现在所有的边都是向上指的，方向已知 )

令 \((S, \preceq)\) 是一个偏序集，对于 \(x, y \in S\)，如果 \(x \prec y\)，且不存在 \(z \in S\) 满足 \(x \prec z \prec y\)，称 \(y\)覆盖 (cover)\(x\)。由对 \((x, y)\) 的集合构成的集合若满足 \(y\) 覆盖 \(x\)，被称为 \((S, \preceq)\) 的覆盖关系 (covering relation)。

观察发现，\((S, \preceq)\) 的哈斯图中向上指的边，与 \((S, \preceq)\) 的覆盖关系相对应。因此，我们可以从覆盖关系中还原它的偏序集，因为偏序集是覆盖关系的自反传递闭包。这告诉我们可以从哈斯图中构造偏序。

例题

例 1 例 2 例 3

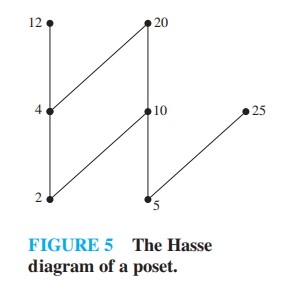
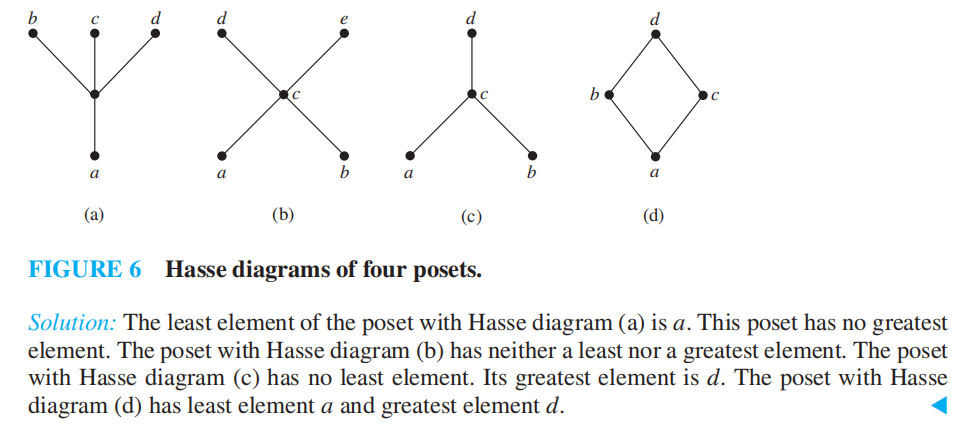
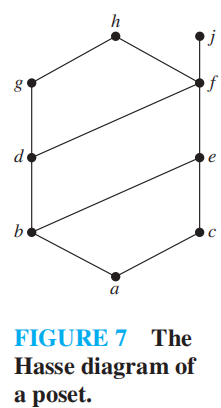
Maximal and Minimal Elements⚓︎

对于偏序集 \((S, \preceq)\) 中的元素 \(a\)：

• 如果不存在 \(b \in S\)，满足 \(a \prec b\)，则称 \(a\) 为极大元素 (maximal)
• 如果不存在 \(b \in S\)，满足 \(b \prec a\)，则称 \(a\) 为极小元素 (minimal)

注：

• 在哈斯图中，它们分别是最顶部( 上面没有顶点 ) 和最底部( 下面没有顶点 ) 的元素
• 极大元素和极小元素可以有多个

• 如果对于所有 \(b \in S\)，满足 \(b \preceq a\)，则称 \(a\) 为最大元素 (greatest element)
• 如果对于所有 \(b \in S\)，满足 \(a \preceq b\)，则称 \(a\) 为最小元素 (least element)

注：若存在最大 / 小元素，则它是唯一的

🌰：

对于偏序集 \((S, \preceq)\) 的子集 \(A\)，如果 \(u, l \in S\)，满足 \(\forall a \in A\)：

• \(a \preceq u\ \Rightarrow\) \(u\) 被称为 \(A\) 的上界 (upper bound)

• \(l \preceq a\ \Rightarrow\) \(l\) 被称为 \(A\) 的下界 (lower bound)

• 如果 \(x\) 是 \(A\) 的上界，且小于任何其他的 \(A\) 的上界，称 \(x\) 为最小上界 (least upper bound)，记作 lub(A)

• 如果 \(y\) 是 \(A\) 的下界，且大于任何其他的 \(A\) 的下界，称 \(y\) 为最大下界 (greatest lower bound)，记作 glb(A)

注：若存在最小上界或最大下界，则它们是唯一的

例题

例 1 例 2 例 3

Lattices⚓︎

格 (lattice)：每对元素都有最小上界和最大下界的偏序集

例题

例 1 例 2 例 3 例 4

Topological Sorting⚓︎

对于某个全序 \(\preceq\) 和偏序 \(R\)，如果当 \(a\ R\ b\) 时，\(a \preceq b\)，则称 \(\preceq\) 与 \(R\) 是兼容的 (compatible)

拓扑排序 (topological sorting)：从偏序中构建一个可兼容的全序

引理 1：每个有限非空偏序集 \((S, \preceq)\) 至少有一个最小元素

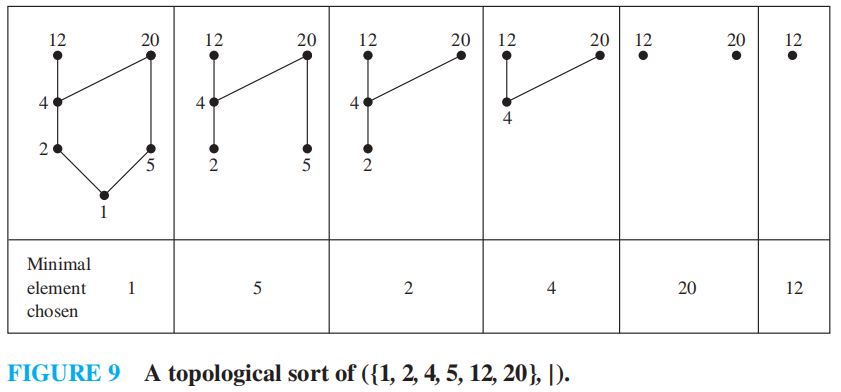
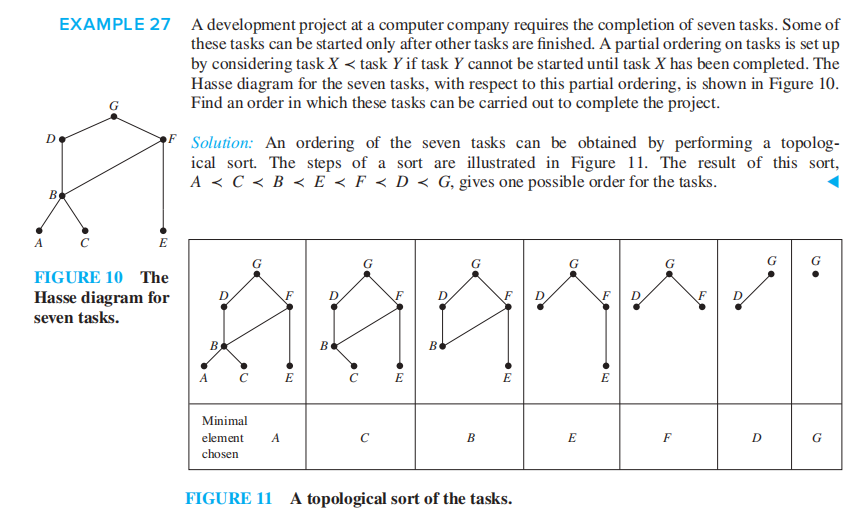
如何进行拓扑排序 ( 在偏序集 \((A, \preceq)\) 中找到全序 )？

• 挑选最小元素 \(a_1\)（由引理 1，一定存在最小元素）
• 此时 \((A - \{a_1\}, \preceq)\) 还是偏序集，如果它是非空的，从中挑选最小的元素 \(a_2\)
• 此时 \((A - \{a_1, a_2\}, \preceq)\) 还是偏序集，如果它是非空的，从中挑选最小的元素 \(a_3\)
• \(\dots\)
• 只要元素还存在，从 \(A - \{a_1, a_2, \dots, a_k\}\) 中挑选最小元素 \(a_{k+1}\)
• 由于 \(A\) 是有限集，所以该过程最终一定会终止。最后我们得到序列 \(a_1, a_2, \dots, a_n\)。全序 \(\preceq _t\) 为：\(a_1 \prec_t a_2 \prec_t \dots \prec_t a_n\)。该全序与原来的偏序兼容。

算法实现：

例题

例 1 例 2

Supplements(from Exercises)⚓︎

• 令 \((S, R)\) 为偏序集，若 \(R^{-1}\) 为 \(R\) 的逆，则 \((S, R^{-1})\) 被称为 \((S, R)\) 的对偶 (dual)，它也是偏序集
• 假设 \((S, \preceq_1)\) 和 \((T, \preceq_2)\) 为偏序集，当 \((s, t) \preceq (u, v)\) 时 \((S \times T, \preceq)\) 为偏序集的充要条件是：\(s \preceq_1 u\) 且 \(t \preceq_2 v\)
• 如果偏序集 \((S, R)\) 是格，则它的对偶偏序集 \((S, R^{-1})\) 也是格
• 集合 \(S\) 中所有分区构成的集合，它的关系 \(P_1 \preceq P_2\) 满足 \(P_1\) 是 \(P_2\) 的精炼 (refinement)，则它们构成了一个格
• 所有全序集是格
• 如果偏序集 \((R, \preceq)\) 中没有无限增长的元素序列 ( 即不存在 \(\dots \prec x_n \prec \dots \prec x_2 \prec x_1\))，称它是良基的 (well-founded)
• 如果 \(\forall x, y \in S\) 且 \(x \prec y\)，存在 \(x \in R\) 使得 \(x \prec z \prec y\)，则称偏序集 \((R, \preceq)\) 是稠密的 (dense)

Supplements(from Exercises)⚓︎

• 假设 \(R_1, R_2\) 是集合 \(A\) 上的自反关系，\(R_1 \oplus R_2\) 是非自反的
• \((a\ R\ b) \wedge (b\ R\ c) \rightarrow c\ R\ a\)，称 \(R\) 是有循环的 (circular)。当且仅当 \(R\) 为等价关系时，\(R\) 即自反又有循环
• 假设 \(R, S\) 为集合 \(A\) 上的关系，且 \(R \subseteq S\)，使得 \(R, S\) 关于性质 \(P\) 的闭包均存在，则 \(R\) 关于 \(P\) 的闭包是 \(S\) 关于 \(P\) 的闭包的子集
• 偏序集上的某个子集
  • 若它的任意两个元素都是可比的，则该子集被称为链 (chain)。即：\((A, \preceq)\) 是偏序集，\(B \subseteq A\)，若 \((B, \preceq)\) 为全序集，则 \(B\) 被称为 \((A, \preceq)\) 的链
  • 链的长度：\(|B|\)（B 为有限集）
  • 若它的任意两个元素都是不可比的，则该子集被称为反链 (antichain)。即：即：\((A, \preceq)\) 是偏序集，\(B \subseteq A\)，若 \(\forall a, b \in B(a \ne b), (a, b) \notin R\) 且 \((b, a) \notin R\)，则 \(B\) 被称为 \((A, \preceq)\) 的反链
  • 在有限偏序集 \((S, \preceq)\) 中的每个最大链( 即不是更大的链的子集的链 ) 包含 \(S\) 中最小的元素
  • 每个有限偏序集能够被分成 \(k\) 条链，其中 \(k\) 这个偏序集中反链的最大个数
• 假设 \((S, \preceq)\) 是良基偏序集，良基归纳法 (the principle of well-founded induction)： $$ P(x) \text{ is true for all } x \in S \text{ if } \forall x (\forall y(y \prec x \rightarrow P(y)) \rightarrow P(x)) $$ 其中，良基归纳法不需要基本情况的说明，即当 \(\forall x (\forall y(y \prec x \rightarrow P(y)) \rightarrow P(x))\) 时，对于所有最小元素 \(u\)，\(P(u)\) 为真
• 如果集合 \(A\) 上的关系 \(R\) 具有自反性和传递性，称 \(R\) 为拟序 (quasi-ordering)
  • 若 \(R\) 为集合 \(A\) 的拟序，则 \(R \cap R^{-1}\) 为等价关系
  • 令 \(R\) 为拟序，\(S\) 为等价类 \(R \cap R^{-1}\) 的集合上的关系，使得 \((C, D) \in S\)，其中 \(C, D\) 是 \(R\) 的等价类，当且仅当 \(c \in C, d \in D\)，使得 \((c, d) \in R\)。此时 \(S\) 为偏序
• 令 \(L\) 为格，定义交(meet, \(\wedge\)) 和并(join, \(\vee\)) 为：\(x \wedge y = \text{glb}(x, y),\ x \vee y = \text{lub}(x, y)\)
  • 交换律：\(x \wedge y = y \wedge x, \quad x \vee y = y \vee x\)
  • 结合律：\((x \wedge y) \wedge z = x \wedge (y \wedge z), \quad (x \vee y) \vee z = x \vee (y \vee z)\)
  • 吸收律：\(x \wedge (x \vee y) x, \quad x \vee (x \wedge y) = x\)
  • 幂等律：\(x \wedge x = x, \quad x \vee x = x\)
  • \(x \vee y = y \leftrightarrow x \wedge y = x\)
  • 格 \(L\) 如果有上界，记作 1，使得 \(\forall x \in L, x \preceq 1\)；且有下界，记作 0，使得 \(\forall x \in L, 0 \preceq x\)，则称 \(L\) 是有界的 (bounded)
  • 分配律不一定成立：\(x \vee (y \wedge z) = (x \vee y) \wedge (x \vee z), \quad x \wedge (y \vee z) = (x \wedge y) \vee (x \wedge z)\)
    • 格 \((P(S), \subseteq)\) 是可分配的，其中 \(P(S)\) 是有限集的幂集
• 有界格 \(L\)( 上界为 1，下界为 0) 上的元素 \(a\) 的补 (complement)为 \(b\)，使得 \(a \vee b = 1\) 且 \(a \wedge b = 0\)。如果格中的每个元素都存在补，则称格是可补的 (complemented)
  • 格 \((P(S), \subseteq)\) 是可补的，其中 \(P(S)\) 是有限集的幂集
  • 若 \(L\) 是有限可分配的格，则 \(L\) 的元素至多有一个补

评论区