第 3 章 多维随机变量及其分布⚓︎

二维离散型随机变量⚓︎

二维离散型随机变量：二维随机变量 \((X, Y)\) 的取值有限或可列。

联合分布⚓︎

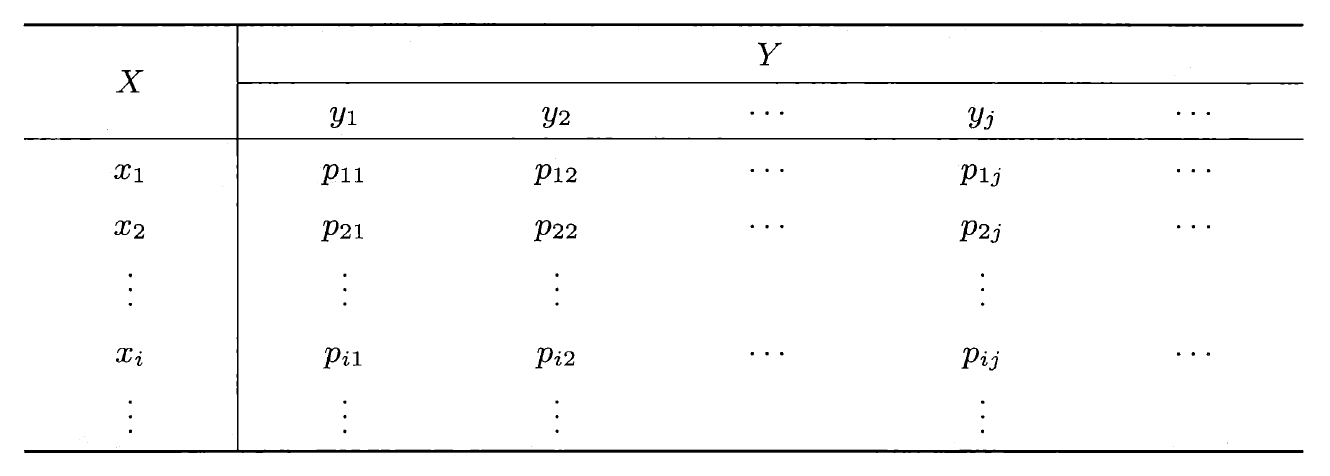
设二维离散型随机变量 \((X, Y)\) 的可能取值为 \((x_i, y_j), i, j = 1, 2, \dots\)，称

为 \((X, Y)\) 的联合概率分布律，简称联合分布律(joint distribution law)。它的列表法形式为：

满足的条件有：

• \(p_{ij} \ge 0, i, j = 1, 2, \dots\)
• \(\sum\limits_i \sum\limits_j p_{ij} = 1\)

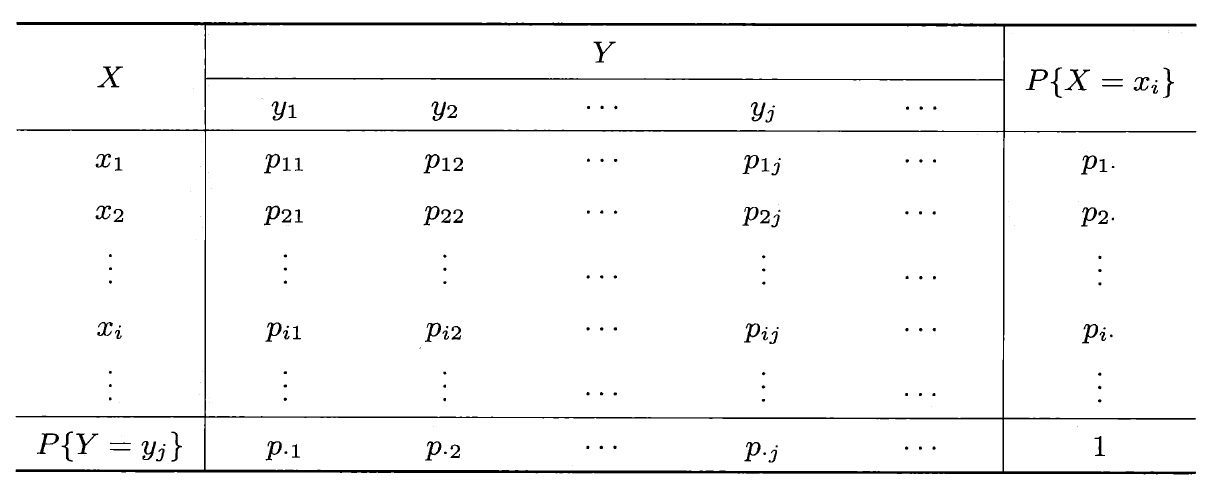
边际分布⚓︎

其中 \(p_{i .} \ge 0, p_{. j} \ge 0, \sum\limits_{i}p_i = 1, \sum\limits_{j}p_{. j} = 1\)

它们分别称为随机变量 \(X\) 与 \(Y\) 的边际分布律(marginal distribution law) 或边缘分布律，可以用以下表格表示：

条件分布⚓︎

当 \(P(Y = y_j) \ne 0\) 时，

当 \(P(X = x_i) \ne 0\) 时，

其中显然有 \(\dfrac{p_{ij}}{p_{. j}} \ge 0, \dfrac{p_{ij}}{p_{i .}} \ge 0\)，且 \(\sum\limits_{i = 1}^{+ \infty}\dfrac{p_{ij}}{p_{. j}} = \sum\limits_{j = 1}^{+ \infty}\dfrac{p_{ij}}{p_{i .}} = 1\)

称为给定条件 \(\{Y = y_i\}\) 条件下 \(X\)/\(\{X = x_i\}\) 条件下 \(Y\) 的条件分布律(conditional distribution law)。

例题

题目答案

二维随机变量的分布函数⚓︎

联合分布函数⚓︎

设二维随机变量 \((X, Y)\)，\(\forall\ x, y\)，称函数

为 \((X, Y)\) 的联合分布函数。

性质：

• 给定 \(x = x_0\)，\(F(x_0, y)\) 关于 \(y\) 单调不减；给定 \(y = y_0\)，\(F(x, y_0)\) 关于 \(x\) 单调不减

  

• \(0 \le F(x, y) \le 1\)，且 \(F(x, -\infty) = F(-\infty, y) = F(-\infty, -\infty) = F(+\infty, +\infty) = 1\)

• \(F(x, y) = F(x + 0, y), F(x, y) = F(x, y + 0)\)，即 \(F(x, y)\) 关于 \(x\) 右连续，关于 \(y\) 右连续

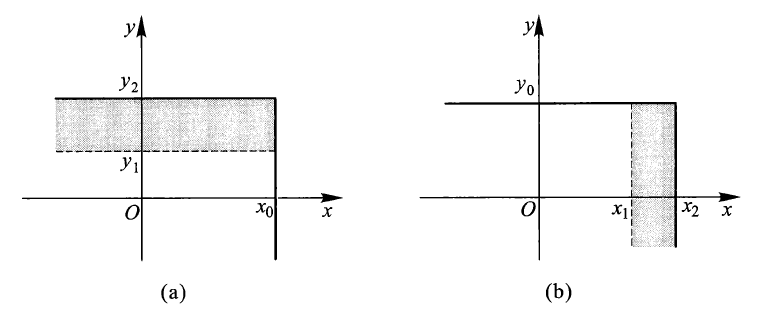
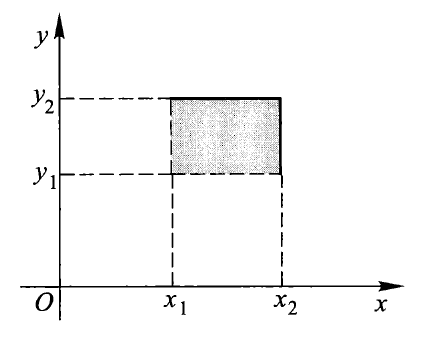
• 令 \(x_2 > x_1, y_2 > y_1\) 时，有

  \[ \begin{align} & F(x_2, y_2) - F(x_1, y_2) - F(x_2, y_1) + F(x_1, y_1) \notag \\ = & P(x_1 < X \le x_2, y_1 < Y \le y_2) \ge 0 \notag \end{align} \]
  

边际分布函数⚓︎

记二维随机变量 \((X, Y)\) 的联合分布函数 \(F(x, y)\)，\(X, Y\) 的边际分布函数分别为 \(F_X(x), F_Y(y)\)，则：

条件分布函数⚓︎

设 \((X, Y)\) 为

• 二维离散型随机变量：当 \(P(X = x_i) \ne 0\) 时，称函数

  \[ F_{Y|X}(y | x_i) = P(Y \le y | X = x_i) \]

  为给定 \(\{X = x_i\}\) 条件下 \(Y\) 的条件分布函数

• 二维连续型随机变量：\(\forall x\)，若 \(P(x < X \le x + \delta) > 0, \delta > 0\)，\(\forall y\)，称函数

  \[ F_{Y|X}(y | x) = \lim\limits_{\delta \rightarrow 0^+}P(Y \le y | x < X \le x + \delta) \]

  为给定 \(\{X = x\}\) 条件下 \(Y\) 的条件分布函数

总结：一般地，对于给定实数 \(x\)，若极限

对任何实数 \(y\) 均存在，则称函数

为给定 \(\{X = x\}\) 条件下 \(Y\) 的条件分布函数，仍记为 \(P(X \le x | Y = y)\)

二维连续型随机变量⚓︎

联合分布⚓︎

设二维随机变量 \((X, Y)\) 的联合分布函数为 \(F(x, y)\)，若存在二元非负函数 \(f(x, y)\)，使对任意的实数 \(x, y\)，有

则称 \((X, Y)\) 为二维连续型随机变量，称 \(f(x, y)\) 为联合密度函数。

性质：

• \(f(x, y) \ge 0\)
• \(\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) \text{d}x\text{d}y = F(+\infty, +\infty) = 1\)

• 在 \(f(x, y)\) 的连续点处有

  \[ \dfrac{\partial^2F(x, y)}{\partial x \partial y} = f(x, y) \]

• \((X, Y)\) 落入 \(xOy\) 平面任一区域 \(D\) 的概率为

  \[ P((X, Y) \in D) = \iint\limits_D f(x, y) \text{d}x\text{d}y \]
  • 当 \(\Delta x \rightarrow 0^+, \Delta y \rightarrow 0^+\) 时，可得
  \[ P(x < X \le x + \Delta x, y < Y \le y + \Delta y) \approx f(x, y)\Delta x \Delta y \]

  即 \((X, Y)\) 落在矩形区域 \(D\) 的概率近似等于 \(f(x, y)\Delta x \Delta y\)，这也表明 \(f(x, y)\) 是描述二维随机变量 \((X, Y)\) 落在点 \((x, y)\) 附近的概率大小的一个量。

边际分布⚓︎

\(X\) 和 \(Y\) 的边际密度函数分别用 \(f_X(x), f_Y(y)\) 表示。

因为：

所以：

条件分布⚓︎

• 给定 \(\{X = x\}(f_X(x) \ne 0)\) 的条件下 \(Y\) 的条件密度函数为：

• 给定 \(\{X = x\}(f_X(x) \ne 0)\) 的条件下 \(X\) 的条件密度函数为：

因为：

所以：

性质（以 \(f_{X|Y}(x|y)\) 为例）：

• \(f_{X|Y}(x|y) \ge 0\)
• \(\int_{-\infty}^{+\infty}f_{X|Y}(x|y) \text{d}x\) = 1
• \(P(a < X < b | Y = y) = \int_a^bf_{X|Y}(x|y) \text{d}x\)
• 在 \(f_{X|Y}(x|y)\) 的连续点 \(x\)，有 \(\dfrac{\text{d}F_{X|Y}(x|y)}{\text{d}x} = f_{X|Y}(x|y)\)
• \(f(x, y) = f_{X|Y}(x|y)f_Y(y) = f_X(x) = f_{Y|X}(y|x)\)

例题

题目答案

二元均值分布和二元正态分布⚓︎

设二维随机变量 \((X, Y)\) 在二维有界区域 \(D\) 上取值，且具有联合密度函数：

则称 \((X, Y)\) 服从 \(D\) 上均匀分布。

若 \(D_1\) 是 \(D\) 的一个子集，则可得到 \(P((X, Y) \in D_1) = \iint\limits_{D_1}f(x, y)\text{d}x\text{d}y\)，即 \(P((X, Y) \in D_1) = \dfrac{\text{Area of}\ D_1}{\text{Area of}\ D}\)

设二维随机变量 \((X, Y)\) 具有联合密度函数

其中 \(-\infty < \mu_1 < +\infty, -\infty < \mu_2 < +\infty, \sigma_1 > 0, \sigma_2 > 0, |\rho| < 1\)，则称 \((X, Y)\) 服从参数为 \((\mu_1, \mu_2; \sigma_1, \sigma_2; \rho)\) 的二元正态分布，记为 \((X, Y) \sim N(\mu_1, \mu_2; \sigma_1, \sigma_2; \rho)\)

下面展示 \(N(0, 0;1, 1;\rho)\) 当 \(\rho = 0, 0.5, -0.5\) 时联合密度函数图集鸟瞰图：

二元正态分布的其他密度函数：

• 边际密度函数（不依赖于参数 \(\rho\)）：

  • \(f_X(x) = \int_{-\infty}^{+\infty}f(x, y)\text{d}y = \dfrac{1}{\sqrt{2\pi}\sigma_1}e^{\frac{(x - \mu_1)^2}{2\sigma_1^2}}\)，即 \(X \sim N(\mu_1, \sigma_1^2)\)
  • \(f_Y(y) = \int_{-\infty}^{+\infty}f(x, y)\text{d}x = \dfrac{1}{\sqrt{2\pi}\sigma_2}e^{\frac{(y - \mu_2)^2}{2\sigma_2^2}}\)，即 \(Y \sim N(\mu_2, \sigma_2^2)\)

• 条件密度函数：

  • 在 \(\{X = x\}\) 的条件下，\(Y\) 的条件分布为 \(N(\mu_2 + \rho \dfrac{\sigma_2}{\sigma_1}(x - \mu_1), (1 - \rho^2)\sigma_2^2)\)，即：
  \[ \begin{align} f_{Y|X}(y|x) & = \dfrac{f(x, y)}{f_X(x)} \notag \\ & = \dfrac{1}{\sqrt{2\pi}\sigma_2\sqrt{1 - \rho^2}}\exp\{\dfrac{-1}{2(1 - \rho^2)\sigma_2^2}[y - (\mu_2 + \rho\dfrac{\sigma_2}{\sigma_1}(x - \mu_1))]^2\} \notag \end{align} \]
  • 在 \(\{Y = y\}\) 的条件下，\(X\) 的条件分布为 \(N(\mu_1 + \rho \dfrac{\sigma_1}{\sigma_2}(y - \mu_2), (1 - \rho^2)\sigma_1^2)\)

随机变量的独立性⚓︎

独立的两种定义：

• 对任意两个实数集合 \(D_1, D_2\)，若：

  \[ P(X \in D_1, Y \in D_2) = P(X \in D_1) \cdot P(Y \in D_2) \]

  则称随机变量 \(X, Y\) 相互独立

  • 当 \(P(X \in D_1) \cdot P(Y \in D_2) \ne 0\) 时，定义亦可写成：
  \[ P(X \in D_1 | Y \in D_2) = P(X \in D_1)\ \text{or}\ P(Y \in D_2 | X \in D_1) = P(Y \in D_2) \]

• 当且仅当对任意实数 \(x, y\)，有

  \[ P(X \le x, Y \le y) = P(X \le x) \cdot P(Y \le y) \]

  成立，即 \(F(x, y) = F_X(x) \cdot F_Y(y)\)，\(X, Y\)（联合分布函数 = 边际分布函数的乘积）相互独立

  • 二维离散型随机变量：设 \(X, Y\) 的可能取值为 \(x_i, y_j, i, j = 1, 2, \dots\)，对任意实数 \(x_i, y_j\)，都有
  \[ p_{ij} = p_{i \cdot} \cdot p_{\cdot j}, i, j = 1, 2, \dots \]

  • 二维连续型随机变量：对任意实数 \(x, y\)，有

    \[ \begin{align} \int_{-\infty}^x [\int_{-\infty}^y f(u, v)\text{d}v]\text{d}u & = \int_{-\infty}^x f_X(u)\text{d}u \int_{-\infty}^y f_Y(v)\text{d}v \notag \\ & = \int_{-\infty}^x [\int_{-\infty}^y f_X(u) \cdot f_Y(v)\text{d}v]\text{d}u \notag \end{align} \]

定理：二维连续型随机变量 \(X, Y\) 相互独立的充要条件是 \(X, Y\) 的联合密度函数 \(f(x, y)\) 几乎处处可写成 \(x\) 的函数 \(m(x)\) 与 \(y\) 的函数 \(n(y)\) 的乘积，即：

证明

n 维随机变量的独立性⚓︎

对于 n 维随机变量 \((X_1, X_2, \dots, X_n)\)，

• 联合分布函数：\(F(x_1, x_2, \dots, x_n) = P(X_1 \le x_1, X_2 \le x_2, \dots, X_n \le x_n)\)

• 边际分布函数：\(F_{X_1}(x_1) = P(X_1 \le x_1) = F(x_1, +\infty, +\infty, \dots, +\infty)\)

  • 当 \(n > 2\) 时，\((X_1, X_2)\) 的联合分布边际函数为
  \[ F_{X_1, X_2}(x_1, x_2) = P(X_1 \le x_1, X_2 \le x_2) = F(x_1, x_2, +\infty, \dots, +\infty) \]

n 维连续型随机变量：随机变量 \((X_1, X_2, \dots, X_n)\)，对于它的分布函数 \(F(x_1, x_2, \dots, x_n)\)，存在非负函数 \(f(x_1, x_2, \dots, x_n)\)，使得

成立。其中 \(f(x_1, x_2, \dots, x_n)\) 为联合密度函数。

• 边际密度函数：

若对于任意实数 \(x_1, x_2, \dots, x_n\)，有

则称 \(X_1, X_2, \dots, X_n\) 相互独立。

设 \((X_1, X_2, \dots, X_m)\) 与 \((Y_1, Y_2, \dots, Y_n)\) 分别为 \(m\) 维和 \(n\) 维的随机变量，分别用 \(F_X(x_1, x_2, \dots, x_m)\) 与 \(F_Y(y_1, y_2, \dots, y_n)\) 表示它们的联合分布函数，再记 \(F(x_1, x_2, \dots, x_m; y_1, y_2, \dots, y_n)\) 为 \((X_1, X_2, \dots, X_m, Y_1, Y_2, \dots, Y_n)\) 的联合分布函数。对任意实数 \(x_i, y_j, i = 1, 2, \dots, m, j = 1, 2, \dots, n\)，若

则称 \((X_1, X_2, \dots, X_m)\) 与 \((Y_1, Y_2, \dots, Y_n)\) 相互独立。

若 \((X_1, X_2, \dots, X_m)\) 与 \((Y_1, Y_2, \dots, Y_n)\) 相互独立，\(g_1, g_2\) 时两个连续函数，则 \(g_1(X_1, X_2, \dots, X_m)\) 与 \(g_2(Y_1, Y_2, \dots, Y_n)\) 相互独立。

多元随机变量函数的分布⚓︎

\(Z = X + Y\) 的分布⚓︎

• \((X, Y)\) 为二维离散型随机变量，设 \(P(X = x_i, Y = y_j) = p_{ij}, i, j = 1, 2, \dots\)，又设 \(Z\) 的可能取值有 \(z_1, z_2, \dots, z_k, \dots\)，则有

  \[ \begin{align} P(Z = z_k) & = P(X + Y = z_k) \notag \\ & = \sum\limits_{i = 1}^{+\infty}P(X = x_i, Y = z_k - x_i), k = 1, 2, \dots \notag \end{align} \]

  或

  \[ \begin{align} P(Z = z_k) & = P(X + Y = z_k) \notag \\ & = \sum\limits_{j = 1}^{+\infty}P(X = z_k - y_j, Y = y_j), k = 1, 2, \dots \notag \end{align} \]
  • 特别地，当 \(X, Y\) 相互独立时，上式可以写成：
  \[ P(Z = z_k) = \sum\limits_{i = 1}^{+\infty}P(X = x_i) \cdot P(Y = z_k - x_i), k = 1, 2, \dots \]

  或

  \[ P(Z = z_k) = \sum\limits_{j = 1}^{+\infty}P(X = z_k - y_j) \cdot P(Y = y_j), k = 1, 2, \dots \]

• \((X, Y)\) 为二维连续型随机变量，设联合密度函数为 \(f(x, y)\)，则 \(Z\) 的分布函数为：

  \[ \begin{align} F_Z(z) & = P(Z \le z) = P(X + Y \le z) \notag \\ & = \iint\limits_{x + y \le z} f(x, y)\text{d}x\text{d}y = \int_{-\infty}^{+\infty} \text{d}x \int_{-\infty}^{+\infty} f(x, y) \text{d}y \notag \end{align} \]
  • 若作积分变量变换 \(\begin{cases}u = x \\ v = x + y\end{cases}\)，可知 \(\text{d}x\text{d}y = \text{d}u\text{d}v\)，
  

  所以 \(F_Z(z) = \int_{z}^{+\infty} \text{d}v \int_{-\infty}^{+\infty} f(u, v - u) \text{d}u\)，从而：

  \[ f_Z(z) = F_Z'(z) = \int_{-\infty}^{+\infty} f(u, z - u) \text{d}u = \int_{-\infty}^{+\infty} f(x, z - x) \text{d}x \]
  • 若作积分变量变换 \(\begin{cases}u = x + y\\ v = y\end{cases}\)，同样可得：
  \[ f_Z(z) = \int_{-\infty}^{+\infty} f(z - y, y) \text{d}y \]
  • 特别地，当 \(X, Y\) 相互独立时，上式可以写成如下形式（称为卷积公式）：
  \[ f_Z(z) = \int_{-\infty}^{+\infty} f_X(x) \cdot f_Y(z - x) \text{d}x = \int_{-\infty}^{+\infty} f_X(z - y) \cdot f_Y(y) \text{d}y \]

\(M = \max\{X, Y\}, N = \min\{X, Y\}\) 的分布⚓︎

记 \(X, Y\) 的联合分布函数为 \(F(x, y)\)，\(X, Y\) 的边际分布函数分别为 \(F_X(t), F_Y(t)\)

• \(M\) 的分布函数：\(F_M(t) = P(\max\{X, Y\} \le t) = P(X \le t, Y \le t) = F(t, t)\)
  • 当 \(X, Y\) 相互独立时，\(F_M(t) = F_X(t) \cdot F_Y(t)\)
• \(N\) 的分布函数：\(F_N(t) = P(\min\{X, Y\} \le t) = P((X \le t) \cup (Y \le t)) = F_X(t) + F_Y(t) - F(t, t)\)，或者 $\(F_N(t) = 1 - P(\min\{X, Y\} > t) = 1 - P(X > t, Y > t)\)
  • 当 \(X, Y\) 相互独立时，\(F_M(t) = F_X(t) + F_Y(t) - F_X(t) \cdot F_Y(t) = 1 - [1 - F_X(t)] \cdot [1 - F_Y(t)]\)

推广到 \(n\) 个变量：设 \(X_1, X_2, \dots, X_n\) 为 \(n\) 个相互独立的随机变量，分布函数分别为 \(F_1(x), F_2(x), \dots, F_n(x)\)，记 \(M = \max\{X_1, X_2, \dots, X_n\}, N = \min\{X_1, X_2, \dots, X_n\}\)，则：

评论区