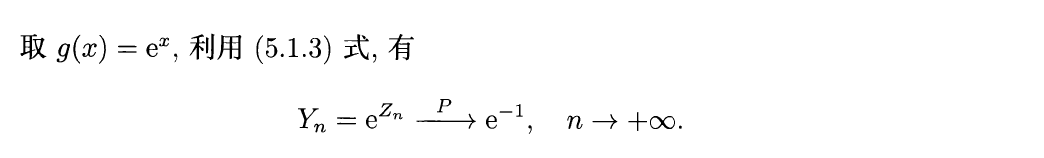第 5 章大数定律及中心极限定理⚓︎

约 1282 个字预计阅读时间 6 分钟

核心知识

依概率收敛的概念
切比雪夫不等式（考的很少，但不意味着不考）
大数定律
- 伯努利大数定律：频率的稳定值 = 概率
- 辛钦大数定律：样本均值 -> 总体均值
中心极限定理
- 林德伯格 - 列维中心极限定理：\(\dfrac{\sum\limits_{i=1}^n X_i - n\mu}{\sigma \sqrt{n}} \stackrel{\text{approximately}}{\sim} N(0, 1)\)
- 棣莫弗 - 拉普拉斯中心极限定理：二项分布 -> 正态分布

大数定律⚓︎

依概率收敛⚓︎

设 \(\{T_n, n \ge 1\}\) 为一随机变量序列，\(c\) 为一常数。若对任意 \(\varepsilon > 0\)，都有

\[ \lim\limits_{n \rightarrow +\infty}P(|Y_n - c| \ge \varepsilon) = 0 \]

成立，则称 \(\{Y_n, n \ge 1\}\)依概率收敛于 \(c\)，记为 \(Y_n \stackrel{P}{\longrightarrow} c, n \rightarrow +\infty\)。它的意义是：当 \(n\) 很大时，\(Y_n\) 十分接近 \(c\)，两者的偏差小于任意给定整数 \(\varepsilon\) 这一事件发生的概率趋于 1，为一大概率事件。上式的等价形式为：

\[ \lim\limits_{n \rightarrow +\infty}P(|Y_n - c| < \varepsilon) = 1 \]

重要性质：设 \(X_n \stackrel{P}{\longrightarrow} a, Y_n \stackrel{P}{\longrightarrow} b, n \rightarrow +\infty\)，其中 \(a, b\) 为常数，若二元函数 \(g(x, y)\) 在点 \((a, b)\) 连续，则有：

\[ g(X_n, Y_n) \stackrel{P}{\longrightarrow} g(a, b), n \rightarrow +\infty \]

两个重要不等式⚓︎

注意

马尔科夫不等式不考！！！

马尔科夫 (Markov) 不等式：若随机变量 \(Y\) 的 \(k\) 阶（原点）矩存在（\(k \ge 1\)），则对任意 \(\varepsilon > 0\)，有：

\[ P(|Y| \ge \varepsilon) \le \dfrac{E(|Y|^k)}{\varepsilon^k} \quad (\text{or } P(|Y| < \varepsilon) \ge 1 - \dfrac{E(|Y|^k)}{\varepsilon^k}) \]

特别地，当 \(Y\) 为取非负值的随机变量且它的 \(k\) 阶矩存在时，则有：\(P(Y \ge \varepsilon) \le \dfrac{E(|Y|^k)}{\varepsilon^k}\)

切比雪夫 (ChebyShev) 不等式：设随机变量 \(X\) 的数学期望和方差存在，分别记为 \(\mu, \sigma^2\)，则对任意的 \(\varepsilon > 0\)，有：

\[ P(|X - \mu| \ge \varepsilon) \le \dfrac{\sigma^2}{\varepsilon^2} \quad (\text{or } P(|X - \mu| < \varepsilon) \ge 1 - \dfrac{\sigma^2}{\varepsilon^2}) \]

切比雪夫不等式是马尔科夫不等式的一个推论。
该不等式的重要性在于：不管随机变量的分布类型是什么，只要已知它的数学期望和方差，就可以对随机变量落入期望附近的区域 \((\mu - \varepsilon, \mu + \varepsilon)\) 内或外的概率给出一个界的估计。\(X\) 的方差越小，对于相同的 \(\varepsilon\)，\(P(|X - \mu| \ge \varepsilon)\) 上界越小，即落入 \((\mu - \varepsilon, \mu + \varepsilon)\) 的概率越大，因此方差能够刻画 \(X\) 的概率分布偏离其中心位置的离散程度。

例题

题目解答

两个大数定律⚓︎

设 \(\{X_i, i \ge 1\}\) 为一随机变量序列，若存在常数序列 \(\{c_n, n \ge 0\}\)，使得对任意 \(\varepsilon > 0\)，有：

\[ \lim\limits_{n \rightarrow +\infty}P(\Bigg|\dfrac{1}{n}\sum\limits_{i = 1}^n X_i - c_n\Bigg| \ge \varepsilon) = 0 \quad (\text{or } \lim\limits_{n \rightarrow +\infty}P(\Bigg|\dfrac{1}{n}\sum\limits_{i = 1}^n X_i - c_n\Bigg| < \varepsilon) = 1) \]

成立，即当 \(n \rightarrow +\infty\) 时，有 \(\dfrac{1}{n}\sum\limits_{i=1}^nX_i - c_n \stackrel{P}{\longrightarrow} 0\)，则称随机变量序列 \(\{X_i, i \ge 1\}\) 服从弱大数定律，简称服从大数定律。特别地，当 \(c_n = c(n = 1, 2, \dots)\) 时，可写为：\(\dfrac{1}{n}\sum\limits_{i=1}^nX_i \stackrel{P}{\longrightarrow} c, n \rightarrow +\infty\)

伯努利 (Bernoulli) 大数定律：设 \(n_A\) 为 \(n\) 重伯努利试验中时间 \(A\) 发生的次数，\(p\) 为事件 \(A\) 在每次试验中发生的概率，即 \(P(A) = p\)，则对任意 \(\varepsilon > 0\)，有：

\[ \lim\limits_{n \rightarrow +\infty}P(\Big|\dfrac{n_A}{n} - p \Big| \ge \varepsilon) = 0 \]

该定律提供了用频率的极限值来定义概率的理论依据，从数学上严格证明了第 1 章提到的“频率的稳定值即为概率”的结论。

辛钦 (Khinchin) 大数定律：设 \(\{X_i, i \ge 1\}\) 为独立同分布的随机变量序列，且数学期望存在，记为 \(\mu\)，则对任意的 \(\varepsilon > 0\)，有：

\[ \lim\limits_{n \rightarrow +\infty} P(\Bigg| \dfrac{1}{n} \sum\limits_{i = 1}^n X_i - \mu \Bigg| \ge \varepsilon) = 0 \]

即 \(\dfrac{1}{n}\sum\limits_{i=1}^n X_i \stackrel{P}{\longrightarrow} \mu (n \rightarrow +\infty)\)，并认为此时随机变量序列 \(\{X_i, i \ge 1\}\) 服从大数定律。

推论：

设 \(\{X_i, i \ge 1\}\) 为独立同分布的随机变量序列，若 \(h(x)\) 为一连续函数，且 \(E(|h(X_1)|) < +\infty\)，则对任意 \(\varepsilon > 0\)，有：

\[ \lim\limits_{n \rightarrow +\infty} P(\Bigg| \dfrac{1}{n} \sum\limits_{i = 1}^n h(X_i) - a \Bigg| \ge \varepsilon) = 0 \]

其中 \(a = E(h(X_1))\)，即 \(\dfrac{1}{n}\sum\limits_{i=1}^n h(X_i) \stackrel{P}{\longrightarrow} a, n \rightarrow +\infty\)
\(f(\overline{X}) \stackrel{P}{\longrightarrow} f(E(X))\)

例题

题目解答

总结

个人认为不需要死记上面的式子，只需记住下面提炼的结论，然后再做几道题差不多就悟了。

伯努利大数定律：在 n 重伯努利试验中，频率稳定于概率
辛钦大数定律：若总体期望存在，则样本期望稳定于总体期望（要用到第 6 章的知识）

中心极限定理⚓︎

独立同分布情形⚓︎

林德伯格 (Lindeberg)- 莱维 (Lévy) 中心极限定理：设 \(\{X_i, i \ge 1\}\) 为独立同分布的随机变量序列，且期望 \(E(X_i) = \mu\) 和方差 \(Var(X_i) = \sigma^2\) 均存在 \((\sigma > 0)\)，则对任意的 \(x \in \bf{R}\)，有：

\[ \begin{align} \lim\limits_{n \rightarrow +\infty} P\Bigg(\dfrac{\sum\limits_{i=1}^n X_i - E(\sum\limits_{i=1}^n X_i)}{\sqrt{Var(\sum\limits_{i=1}^n X_i)}} \le x \Bigg) & = \lim\limits_{n \rightarrow +\infty} P\Bigg(\dfrac{\sum\limits_{i=1}^n X_i - n\mu}{\sigma \sqrt{n}} \le x \Bigg) \notag \\ & = \dfrac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-\frac{t^2}{2}} \text{d}t = \Phi(x) \notag \end{align} \]

该定理表明：期望为 \(\mu\)，方差为 \(\sigma^2\) 的独立同分布的随机变量的部分和 \(\sum\limits_{i=1}^n X_i\) 的标准化变量 \(\dfrac{\sum\limits_{i=1}^n X_i - n\mu}{\sigma \sqrt{n}}\)，当 \(n\) 充分大时，近似地服从标准正态分布\(N(0, 1)\)，即：

\[ \dfrac{\sum\limits_{i=1}^n X_i - n\mu}{\sigma \sqrt{n}} \stackrel{\text{approximately}}{\sim} N(0, 1), \text{when n is sufficiently large} \]

或者记作 \(\dfrac{1}{n} \sum\limits_{i=1}^n X_i \stackrel{\text{approximately}}{\sim} N(\mu, \dfrac{\sigma^2}{n})\)（当 \(n\) 充分大时）

例题

题目解答

将该定理用于 \(n\) 重伯努利试验，可得如下推论：

棣莫弗 (De Moivre)- 拉普拉斯 (Laplace) 中心极限定理：设 \(n_A\) 为 \(n\) 重伯努利试验中事件 \(A\) 发生的次数，\(p\) 为事件 \(A\) 在每次试验中发生的概率，即 \(P(A) = p\)，则对任意 \(x \in \bf{R}\)，有：

\[ \lim\limits_{n \rightarrow +\infty} P(\dfrac{n_A - np}{\sqrt{np(1 - p)}} \le x) = \dfrac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-\frac{t^2}{2}} \text{d}t = \Phi(x) \]