第 8 章 假设检验⚓︎
约 3224 个字 预计阅读时间 16 分钟
核心知识
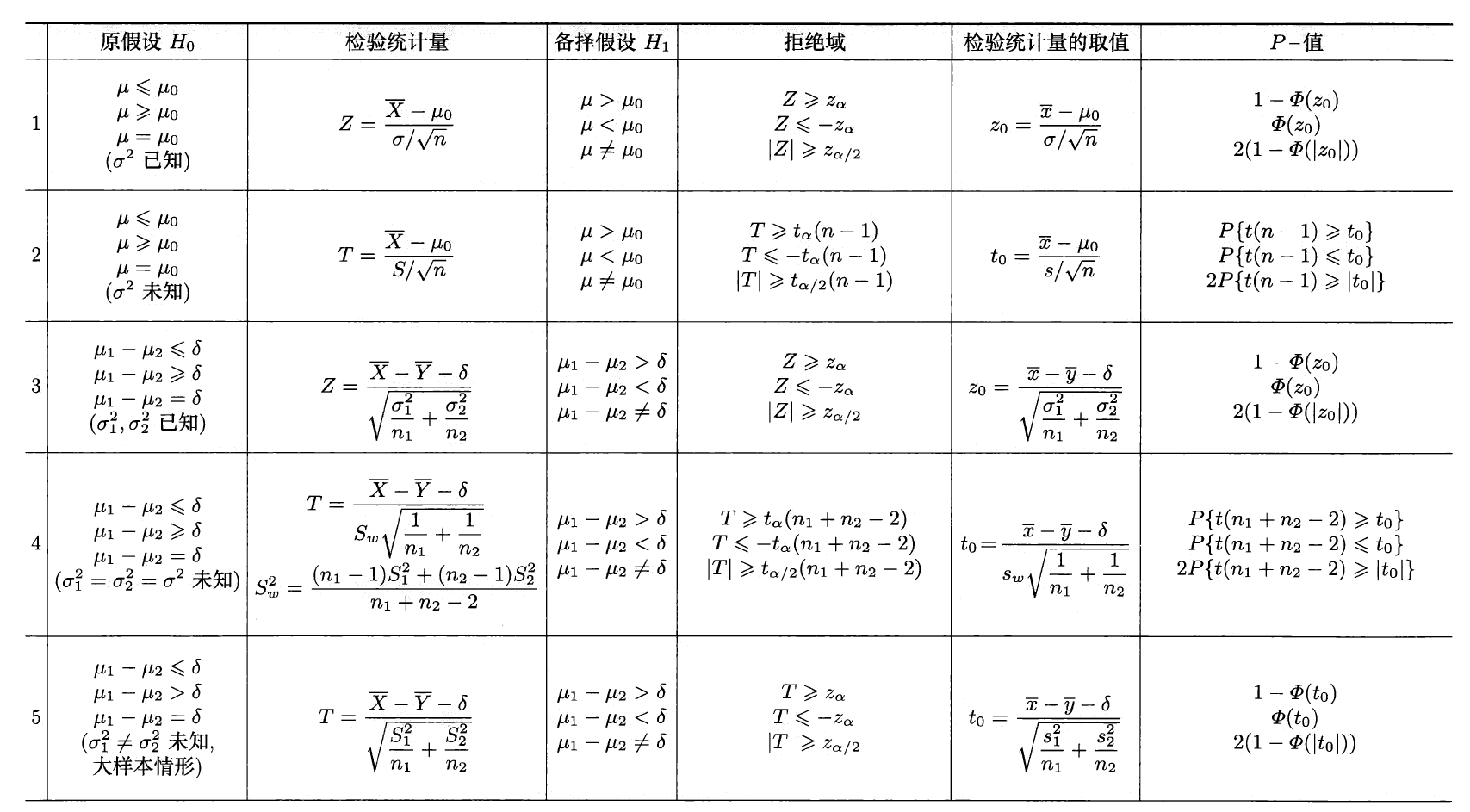
- 一些基本概念:两类假设、三种检验、两类错误、拒绝域、P- 值
- 正态总体参数的假设检验
- 单个 / 两个正态总体、有关均值 / 方差的假设检验
- 与第 7 章“正态总体的区间估计”相关知识结合起来理解
假设检验的基本思想⚓︎
-
问题的提出
- 假设 \(H\),同时提出两个完全相反的假设,分别为原假设 / 零假设\(H_0\) 和备择假设 / 对立假设\(H_1\)(备择假设一般是我们想要支持的假设)
- 关于总体参数 \(\theta\) 的假设,有三种情况(\(\theta_0\) 为已知常数
) :- 左侧检验:\(H_0: \theta \ge \theta_0, H_1: \theta < \theta_0\)
- 右侧检验:\(H_0: \theta \le \theta_0, H_1: \theta > \theta_0\)
- 前两种检验合称为单侧检验,还有两种形式为(需要知道
) :- \(H_0: \theta = \theta_0, H_1: \theta < \theta_0\)(与第 1 种几乎相同)
- \(H_0: \theta = \theta_0, H_1: \theta > \theta_0\)(与第 2 种几乎相同)
- 双侧检验:\(H_0: \theta = \theta_0, H_1: \theta \ne \theta_0\)
-
检验统计量和拒绝域
- 检验统计量:在假设问题中取值大小和原假设 \(H_0\) 是否成立有密切关系的统计量
- 一般情况下,我们用上一章介绍过的枢轴量作为检验统计量
-
拒绝域\(W\):拒绝原假设 \(H_0\) 的样本值范围(样本空间的一个子集)
- 若样本落入 \(W\),就拒绝 \(H_0\)
结论:
- 左侧检验:\(W = \{G_0 < g_{1 - \alpha}\}\)
- 右侧检验:\(W = \{G_0 > g_\alpha\}\)
- 双侧检验:
- \(\mu\) 相关:\(W = \{|G_0| > g_{\alpha / 2}\}\)
- \(\sigma^2\) 相关:\(W = \{G_0 < g_{1 - \alpha / 2} \cup G_0 > g_{\alpha / 2}\}\)
-
接受域\(\overline{W}\):拒绝域的补集
总结
对于正态总体的区间估计和假设检验,可以发现以下对应关系:
- 双侧置信区间 <-> 双侧检验的接受域
- 单侧置信下限 <-> 左侧检验的接受域
- 单侧置信上限 <-> 右侧检验的接受域
- 检验统计量:在假设问题中取值大小和原假设 \(H_0\) 是否成立有密切关系的统计量
-
两类错误
-
在假设检验中可能出现下列四种情形:
- 拒绝了一个错误的原假设
- 接受了一个真实的原假设
- 拒绝了一个真实的原假设
-> 第 I 类错误 / 弃真错误,发生概率记为 \(\alpha\)
- 接受了一个错误的原假设
-> 第 II 类错误 / 存伪错误,发生概率记为 \(\beta\)
- 拒绝了一个错误的原假设
-
计算公式:
\[ \begin{align} \alpha & = P(\text{type I error}) = P(\text{reject } H_0 | H_0 \text{ is true}) = P_{H_0}(\text{reject } H_0) \notag \\ & = P\{(x_1, x_2, \dots, x_n) \in W | H_0 \text{ is true}\} \notag \\ \beta & = P(\text{type II error}) = P(\text{accpet } H_0 | H_0 \text{ is false}) = P_{H_1}(\text{accept } H_0) \notag \\ & = P\{(x_1, x_2, \dots, x_n) \in \overline{W} | H_0 \text{ is false}\} \notag \end{align} \]- 奈曼 - 皮尔逊原则:
- 首先控制第 I 类错误的概率,即选定一个常数 \(\alpha \in (0, 1)\),要求犯第 I 类错误的概率不超过 \(\alpha\)
- 然后在满足这个约束条件的检验下,在寻找检验,使得犯第 II 类错误的概率尽可能小
- \(\alpha\) 称为显著性水平,常取 \(\alpha = 0.01, 0.05, 0.10\) 等
-
-
P- 值与统计显著性
- P- 值:当原假设 \(H_0\) 为真时,检验统计量取比观察到的结果更为极端的数值的概率,用于衡量拒绝 \(H_0\) 的理由是否充分,其值越小拒绝 \(H_0\) 的理由越充分
- 若 P- 值 \(\le \alpha\),则拒绝原假设,此时称检验结果在显著性水平 \(\alpha\) 下是统计显著的
结论:
- 左侧检验:\(P_{-} = P(g < G_0)\)
- 右侧检验:\(P_{-} = P(g > G_0)\)
-
双侧检验:
- \(\mu\) 相关:\(P_{-} = 2P(g > |G_0|)\)
- \(\sigma^2\) 相关:\(P_{-} = 2 \min\{P(g > G_0), P(g < G_0)\}\)
-
具体方法:在试卷第一页抬头寻找 \(g_A = G_0\),则 \(P(g < G_0) = 1 - A, P(g > G_0) = A\)
处理假设检验问题的基本步骤:
- 根据实际问题提出原假设和备择假设
- 提出检验统计量和拒绝域的形式
- 根据奈曼 - 皮尔逊原则和给定的显著性水平 \(\alpha\),求出拒绝域 \(W\) 中的临界值
- 根据实际样本值作出判断
3 和 4 也可如下进行:
- 计算检验统计量的观测值和 P- 值
- 根据给定的显著性水平 \(\alpha\) 作出判断
正态总体参数的假设检验⚓︎
单个正态总体⚓︎
设正态总体 \(X \sim N(\mu, \sigma^2), X_1, X_2, \dots, X_n\) 是来自该总体的样本,记样本均值为 \(\overline{X}\),样本方差为 \(S^2\)。
有关均值的假设检验⚓︎
注
对于之后的 6 张图片,用/表示的阴影部分面积为 \(\alpha\),用\表示的阴影部分面积为 P- 值。
-
\(\sigma^2\) 已知 -> Z 检验
- 检验统计量:\(Z = \dfrac{\overline{X} - \mu_0}{\sigma / \sqrt{n}}\),对应的取值为 \(z_0\)
-
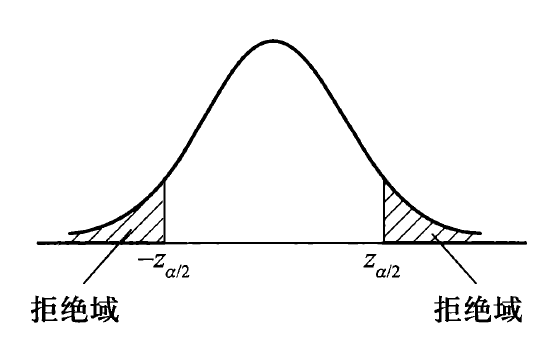
双侧假设:\(H_0: \mu = \mu_0, H_1: \mu \ne \mu_0\)
- 拒绝域:\(W = \{|Z| = \Big|\dfrac{\overline{X} - \mu_0}{\sigma / \sqrt{n}}\Big| \ge z_{\alpha / 2}\}\)
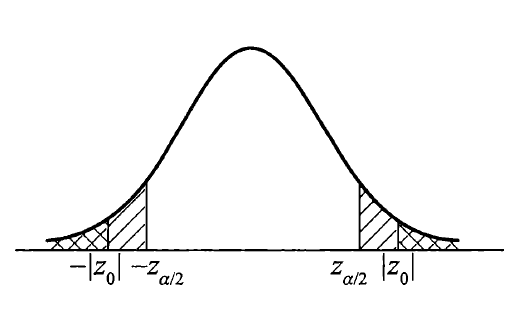
- P- 值 = \(P_{H_0}(|Z| \ge |z_0|) = 2P_{H_0}(Z \ge |z_0|) = 2(1 - \Phi(|z_0|))\)。当 P- 值 \(\le \alpha\) 时,拒绝原假设,否则不能拒绝,如图所示:
-
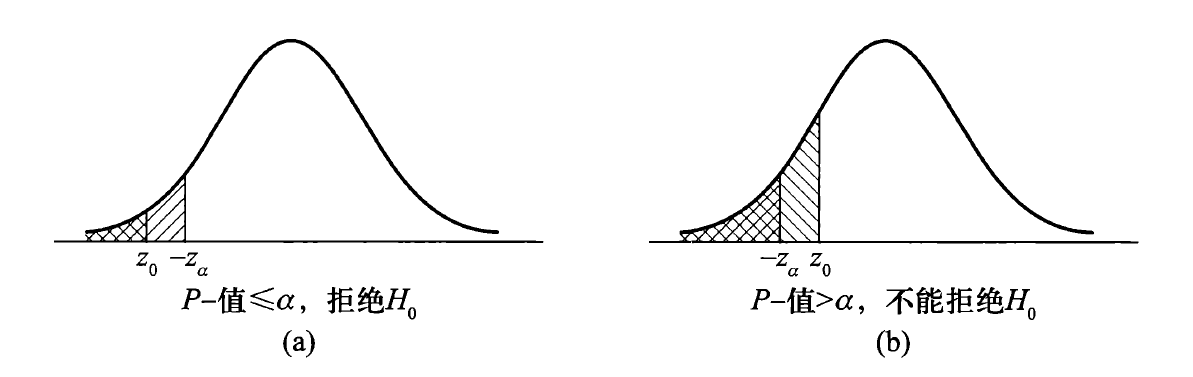
左侧假设:\(H_0: \mu \ge \mu_0, H_1: \mu < \mu_0\)
- 拒绝域:\(W = \{Z = \dfrac{\overline{X} - \mu_0}{\sigma / \sqrt{n}} \le -z_{\alpha}\}\)
- P- 值 = \(\sup\limits_{\mu \ge \mu_0} P(Z \le z_0) = P(Z \le z_0 | \mu = \mu_0) = \Phi(z_0)\),若 P- 值 \(\le \alpha\),则拒绝原假设 \(H_0\),否则不能拒绝
-
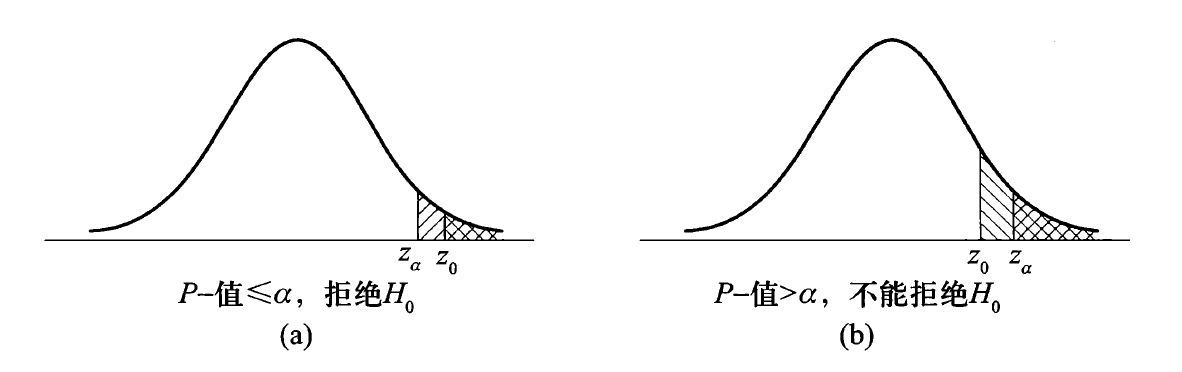
右侧假设:\(H_0: \mu \le \mu_0, H_1: \mu > \mu_0\)
- 拒绝域:\(W = \{Z = \dfrac{\overline{X} - \mu_0}{\sigma / \sqrt{n}} \ge z_\alpha\}\)
- P- 值 = \(\sup\limits_{\mu \ge \mu_0} P(Z \ge z_0) = P(Z \ge z_0 | \mu = \mu_0) = 1 - \Phi(z_0)\)
-
\(\sigma^2\) 未知:用样本方差 \(S^2\) 代替 \(\sigma^2\) -> t 检验
- 检验统计量:\(T = \dfrac{\overline{X} - \mu_0}{S / \sqrt{n}} \sim t(n - 1)\),对应的取值为 \(t_0\)
- 双侧假设:\(H_0: \mu = \mu_0, H_1: \mu \ne \mu_0\)
- 拒绝域:\(W = \{|T| = \Big|\dfrac{\overline{X} - \mu_0}{S / \sqrt{n}}\Big| \ge t_{\alpha / 2}(n - 1)\}\)
- P- 值 = \(2P(t(n-1) \ge |t_0|)\)
- 左侧假设:\(H_0: \mu \ge \mu_0, H_1: \mu < \mu_0\)
- 拒绝域:\(W = \{T = \dfrac{\overline{X} - \mu_0}{S / \sqrt{n}} \le -t_{\alpha}(n - 1)\}\)
- P- 值 = \(\sup\limits_{\mu \ge \mu_0} P(T \le t_0) = P(t(n - 1) \le t_0)\)
- 右侧假设:\(H_0: \mu \le \mu_0, H_1: \mu > \mu_0\)
- 拒绝域:\(W = \{T = \dfrac{\overline{X} - \mu_0}{S / \sqrt{n}} \ge t_{\alpha}(n - 1)\}\)
- P- 值 = \(\sup\limits_{\mu \le \mu_0} P(T \ge t_0) = P(t(n - 1) \ge t_0)\)
有关方差的假设检验⚓︎
此时用到的检验为\(\chi^2\) 检验
不妨假设 \(\mu\) 是未知的,假设问题包括:
- 双侧假设:\(H_0: \sigma^2 = \sigma_0^2, H_1: \sigma^2 \ne \sigma_0^2\)
- 左侧假设:\(H_0: \sigma^2 \ge \sigma_0^2, H_1: \sigma^2 < \sigma_0^2\)
- 右侧假设:\(H_0: \sigma^2 \le \sigma_0^2, H_1: \sigma^2 > \sigma_0^2\)
其中 \(\sigma_0^2\) 为已知常量,此时 \(\sigma^2\) 的无偏估计量 \(S^2 = \dfrac{1}{n - 1}\sum\limits_{i=1}^n(X_i - \overline{X})^2\),取检验统计量 \(\chi^2 = \dfrac{(n - 1)S^2}{\sigma_0^2}\),当 \(\sigma^2 = \sigma_0^2\) 时,\(\chi^2 \sim \chi^2(n - 1)\)。
在给定显著性水平 \(\alpha\) 时,有拒绝域:
- 双侧检验:\(W = \{\chi^2 \ge \chi_{\alpha / 2}^2(n - 1) \text{ or } \chi^2 \le \chi_{1 - \alpha / 2}^2(n - 1)\}\)
- 左侧检验:\(W = \{\chi^2 \le \chi_{1 - \alpha}^2(n - 1)\}\)
- 右侧检验:\(W = \{\chi^2 \ge \chi_{\alpha}^2(n - 1)\}\)
计算 P- 值:\(p_0 = P_{\sigma^2 = \sigma_0^2}(\dfrac{(n - 1)S^2}{\sigma_0^2} \le \dfrac{(n - 1)s^2}{\sigma_0^2}) = P(\chi^2(n - 1) \le \chi_0^2)\)
- 双侧检验:P- 值 = \(2 \min\{p_0, 1 - p_0\}\)
- 左侧检验:P- 值 = \(p_0\)
- 右侧检验:P- 值 = \(1 - p_0\)
两个正态总体⚓︎
设正态总体 \(X \sim N(\mu_1, \sigma_1^2), Y \sim N(\mu_2, \sigma_2^2), X_1, X_2, \dots, X_{n1}, Y_1, Y_2, \dots, Y_{n2}\) 分别是来自这两个总体的样本,记:
- \(\overline{X} = \dfrac{1}{n_1}\sum\limits_{i=1}^{n_1} X_i,\ S_1^2 = \dfrac{1}{n_1-1} \sum\limits_{i=1}^{n_1} (X_i - \overline{X})^2\)
- \(\overline{Y} = \dfrac{1}{n_2}\sum\limits_{j=1}^{n_2} Y_i,\ S_2^2 = \dfrac{1}{n_2-1} \sum\limits_{j=1}^{n_2} (Y_i - \overline{Y})^2\)
有关均值的假设检验⚓︎
考虑双侧假设问题:\(H_0: \mu_1 = \mu_2, H_1: \mu_1 \ne \mu_2\),当原假设 \(H_0\) 成立时,两样本均值取值比较接近,即 \(|\overline{X} - \overline{Y}|\) 取值偏小,因此取检验统计量为 \(\overline{X} - \overline{Y}\)
-
\(\sigma_1^2, \sigma_2^2\) 已知 -> Z 检验
- 拒绝域:\(W = \{\dfrac{|\overline{X} - \overline{Y}|}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \ge z_{\alpha / 2}\}\)
- P- 值 = \(P_{H_0}(|Z| \ge |z_0|) = 2(1 - \Phi(|z_0|))\),其中 \(Z \sim N(0, 1)\),\(z_0\) 为给定样本值时检验统计量的取值
-
\(\sigma_1^2 = \sigma_2^2 = \sigma^2\) 但未知 -> 两样本精确 t 检验
- 检验统计量:\(T = \dfrac{\overline{X} - \overline{Y}}{S_w \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\)
- 拒绝域:\(W = \{|T| \ge t_{\alpha / 2}(n_1 + n_2 - 2)\}\)
- P- 值 = \(P_{H_0}(|T| \ge |t_0|) = 2P(t(n_1 + n_2 - 2) \ge |t_0|)\),其中 \(t_0\) 为给定样本值时检验统计量 \(T\) 的取值
-
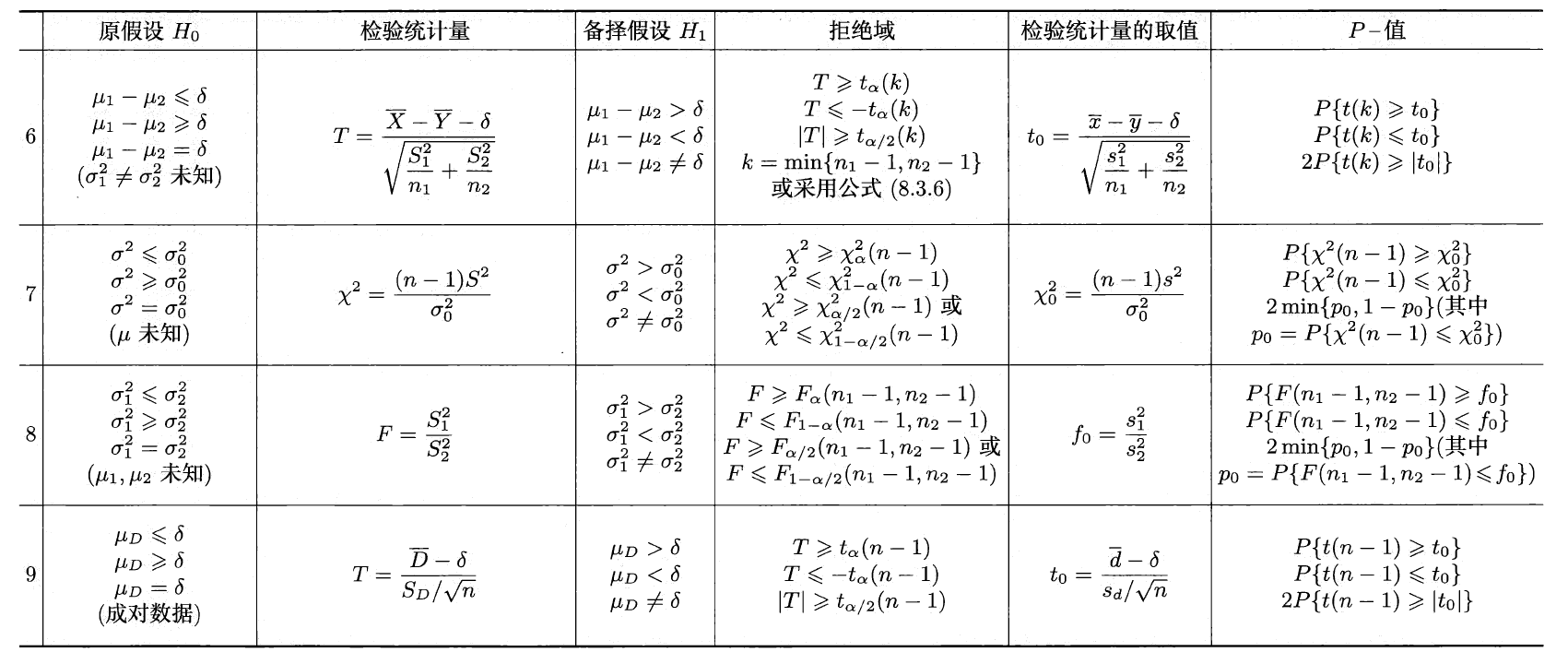
\(\sigma_1^2 \ne \sigma_2^2\) 且未知
注意:该情况不考,仅做了解(感兴趣的话可以点击展开阅读)
- 检验统计量:\(T = \dfrac{\overline{X} - \overline{Y}}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}}\)
- 拒绝域:\(W = \{|T| \ge z_{\alpha / 2}\}\)
- P- 值 = \(P_{H_0}(|T| \ge |t_0|) = 2P(Z \ge |t_0|)\),其中 \(Z \sim N(0, 1)\),\(t_0\) 为给定样本值时检验统计量 \(T\) 的取值
- 对于小样本情形,上述统计量 \(T\) 近似服从 t 分布 -> 两样本近似 t 检验
- 自由度为 \(k = \min\{n_1 - 1, n_2 - 1\}\)
- 更精确的近似自由度 \(k = \dfrac{(S_1^2 / n_1 + S_2^2 / n_2)^2}{\frac{(S_1^2 / n_1)}{n_1 - 1} + \frac{(S_2^2 / n_2)^2}{n_2 - 1}}\)
- 拒绝域:\(W = \{|T| \ge t_{\alpha / 2}(k)\}\)
- P- 值 = \(P_{H_0}(|T| \ge |t_0|) = 2P(t(k) \ge |t_0|)\)
有关方差的假设检验⚓︎
考虑假设问题:\(H_0: \sigma_1^2 = \sigma_2^2, H_1: \sigma_1^2 \ne \sigma_2^2\),取检验统计量 \(F = \dfrac{S_1^2}{S_2^2}\)。当 \(H_0\) 检验时,\(F \sim F(n_1 - 1, n_2 - 1)\),此时 \(F\) 的取值既不能偏大也不能偏小,因此检验的拒绝域为:
将样本值代入后得到的检验统计量的值记为 \(f_0\),即 \(f_0 = \dfrac{s_1^2}{s_2^2}\),设:
P- 值为
- 双侧检验:\(2\min\{p_0, 1 - p_0\}\)
- 左侧检验:\(p_0\)
- 右侧检验:\(1 - p_0\)
假设检验与区间估计⚓︎
设 \(X_1, X_2, \dots, X_n\) 是来自正态总体 \(N(\mu, \sigma^2)\) 的样本,其中方差 \(\sigma^2\) 已知,此时 \(\mu\) 的置信水平为 \(1 - \alpha\) 的置信区间为:\(\Big(\overline{X} - \dfrac{\sigma}{\sqrt{n}}z_{\alpha / 2}, \overline{X} + \dfrac{\sigma}{\sqrt{n}}z_{\alpha / 2}\Big)\)
对于均值 \(\mu\) 的双侧假设问题,在给定显著性水平 \(\alpha\) 下,
- 拒绝域:\(W = \{\Big|\dfrac{\overline{X} - \mu_0}{\sigma / \sqrt{n}}\Big| \ge z-{\alpha / 2}\}\)
- 接受域:\(\overline{W} = \{\Big|\dfrac{\overline{X} - \mu_0}{\sigma / \sqrt{n}}\Big| < z-{\alpha / 2}\} = \{\overline{X} - \dfrac{\sigma}{\sqrt{n}}z_{\alpha / 2} < \mu_0 < \overline{X} + \dfrac{\sigma}{\sqrt{n}}z_{\alpha / 2}\}\),即接受域正好是这个置信区间
对应一般情况,设 \(X_1, X_2, \dots, X_n\) 是来自总体 $ X\sim F(x; \theta)$ 的样本,
- 如果双侧假设问题的显著性水平为 \(\alpha\) 的接受域 \(\overline{W}\) 能等价地写成 \(\widehat{\theta_L} < \theta_0 < \widehat{\theta_U}\) 的形式,那么 \((\widehat{\theta_L}, \widehat{\theta_U})\) 是 \(\theta\) 的置信水平为 \(1 - \alpha\) 的置信区间
- 反之也成立
拟合优度检验⚓︎
注
这块内容不考!!!
设 \(F(x)\) 是总体的未知的分布函数,又设 \(F_0(x)\) 是具有某种已知类型的分布函数,但可能含有若干未知参数,需验证假设 \(H_0: F(x) = F_0(x)\),这类分布的假设验证称为拟合优度检验。下面主要讨论皮尔逊拟合优度 \(\chi^2\) 检验。
基本思想(要求样本容量 \(n \ge 50\),且 \(np_i\)(或 \(n\widehat{p_i}\)
- 对总体 \(X\) 的取值分为互不相容的 \(k\) 类,记为 \(A_1, A_2, \dots, A_k\);设 \(X_1, X_2, \dots, X_n\) 是来自该总体的样本,并记 \(n_i\) 为样本值落在 \(A_i\) 类的个数(实际频数)
- 当 \(H_0\) 中的 \(F_0(x)\) 完全已知时,计算 \(p_i = O_{H_0}(A_i), i = 1, 2, \dots, k\)
- 假设 \(H_0\) 中的 \(F_0(x)\) 含有 \(r\) 个未知参数时,要先在 \(F_0(x)\) 的形式下利用极大似然法估计 \(r\) 个未知的参数,然后求得 \(p_i\) 的估计值 \(\widehat{p_i}\)
- 当 \(H_0\) 为真时,\(n\) 个个体中属于 \(A_i\) 的“期望个数”应为 \(np_i\)(或 \(n\widehat{p_i}\)
) (理论频数) - \(\chi^2 = \sum\limits_{i=1}^k\dfrac{(n_i - np_i)^2}{np_i}\)(或 \(\chi^2 = \sum\limits_{i=1}^k\dfrac{(n_i - n\widehat{p_i})^2}{n\widehat{p_i}}\))作为衡量实际频数与理论频数偏差的综合指标,当 \(H_0\) 为真时,\(\chi^2\) 的值偏小
- 拒绝域:\(W = \{\chi^2 \ge C\}\),其中临界值 \(C\) 为待定常数
- 极限定理:若 \(n\) 充分大,则当 \(H_0\) 为真时,统计量 \(\chi^2\) 近似服从 \(\chi^2(k - r - 1)\) 分布,其中 \(k\) 为分类数,\(r\) 为 \(F_0(x)\) 中含有的未知参数个数,当 \(F_0(x)\) 完全已知时,\(r = 0\)
- 有关上述分布假设的显著性水平 \(\approx \alpha\) 的拒绝域为 \(W = \{\chi^2 \ge \chi_{\alpha}^2(k - r - 1)\}\)
- P- 值 = \(P(\chi^2(k - r - 1) \ge \chi_0^2)\),其中 \(\chi_0^2\) 为 \(\chi^2\) 的观测值,称该 P- 值为拟合优度,其值越大,越无法拒绝原假设。给定 \(\alpha\),当 P- 值 \(\le \alpha\) 时,就拒绝原假设
评论区