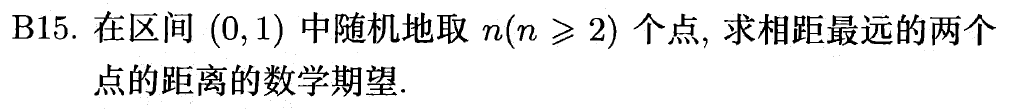题目整理⚓︎
注
以下题目来自教材课后习题和历年卷上的题目,供复习参考。
答案都是基于我自己的思考后再写的,不是完全抄参考答案的,不然就没什么复习效果了。
有些题目我没有给出答案,只是列出我摘录的理由,起到警醒自己的作用。
题目格式:
题目
题目内容
解答
答案略 (bushi)
第 1 章⚓︎
第 2 章⚓︎
第 3 章⚓︎
题目
解答
第 (1) 小题和第 (3) 小题略,解得 \(c = 6\)
下面只分析第 (2) 小题:
- 令 \(Z = X + Y\),题目转化为求 \(P(Z \le 1) = F_Z(1)\)
-
- \(F_Z(z) = \int_{-\infty}^zf_Z(t)\text{d}t\)
- 概率密度函数:\(f_Z(z) & = \int_{-\infty}^{+\infty}f(z - y, y)\text{d}y\)
- 计算(尤其注意 \(y\) 的积分范围
) :
下面就是一通二重积分的计算,要注意的是积分变量的范围,这个很容易搞错(这也是我摘录这道题的原因)
\[ \begin{align} F_Z(1) & = \int_0^1 \int_{\frac{z}{2}}^{z} 6(2y - z) \text{d}y \text{d}z \notag \\ & = \int_0^1 (6y^2 - 6zy) \Big|_{\frac{z}{2}}^z \text{d}z \notag \\ & = \int_0^1 \dfrac{3}{2}z^2 \text{d}z \notag \\ & = \dfrac{1}{2}z^3 \Big|_0^1 \notag \\ & = \dfrac{1}{2} \notag \end{align} \]
题目
解答
很容易得到 \(f_Z(z) = \int_{-\infty}^{+\infty} f(z - y, y)\text{d}y = \int_{-\infty}^{+\infty} \dfrac{3 - z}{3}\text{d}y\),麻烦的点在于确定 \(y\) 的积分范围——除了题目给出的 \(0 < y < 2\) 之外,我们还可以得到另一个范围:\(0 < z - y < 1\),即 \(z - 1 < y < z\),因此需要分类讨论。请务必仔细计算各种情况下的密度函数,答案就不列出来了,计算不难。
第 4 章⚓︎
题目
解答
- 这道题的二维随机变量服从均匀分布,联合密度函数为取值范围(面积)的倒数
- 第 (1) 小题的期望计算类似一维随机变量,但是要用联合密度函数 + 二重积分
- 第 (2) 小题
- 令平均距离 \(Z = \sqrt{X^2 + Y^2}\),原题转化为求 \(E(Z)\)
- \(F_Z(z) = P(Z \le z) = P(X^2 + Y^2 \le z^2) = \dfrac{\pi z^2}{\pi r^2} = \dfrac{z^2}{r^2}\)
- \(f_Z(z) = \dfrac{2z}{r^2}\)
- \(E(Z) = \int_0^r zf_Z(z) \text{d}z= \int_0^r \dfrac{2z^2}{r^2} \text{d}z = \dfrac{2r}{3}\)
题目
解答
- 本题难点在于对随机变量 \(X\) 进行适当的转化
- 令 \(X_i = \begin{cases}1 & \text{ith card is selected at least once} \\ 0 & \text{ith card is never selected}\end{cases}\)
- 那么 \(X = \sum\limits_{i=1}^n X_i\)
- 所以 \(E(X) = E(\sum\limits_{i=1}^n X_i) = \sum\limits_{i=1}^n E(X_i) = nE(X_1) = n \dfrac{1 - (n - 1)^n}{n^n} = \dfrac{n^n - (n - 1)^n}{n^{n - 1}}\)
- \(\lim\limits_{n \rightarrow +\infty} E(\dfrac{X}{n}) =\lim\limits_{n \rightarrow +\infty} \dfrac{n^n - (n - 1)^n}{n^n} = \lim\limits_{n \rightarrow +\infty} 1 - (1 - \dfrac{1}{n})^n = 1 - \dfrac{1}{e}\)
题目
解答
- 本题难点在于如何构造并转化随机变量(和上一题类似)
- 令随机变量 \(X_i\) 为第 \(i\) 个点距原点的距离,由题意易知 \(X_i \sim U(0, 1)\),且 \(X_1, \dots, X_n\) 独立同分布
-
令随机变量 \(Z\) 为相距最远的两个点的距离,可以推出:
\[ Z = \max\{X_1, \dots, X_n\} - \min\{X_1, \dots, X_n\} \] -
令 \(M = \max\{X_1, \dots, X_n\},\ N = \min\{X_1, \dots, X_n\}\),那么:
- \(F_M(m) = P(M \le m) = P(X_1 \le m) \dots P(X_n \le m) = [F(m)]^n = m^n\)
- \(F_N(t) = P(N \le t) = 1 - P(N > t) = 1 - P(X_1 > t)\dots P(X_n > t) = 1 - [1 - F(t)]^n = 1 - (1 - t)^n\)
- \(f_M(m) = nm^{n-1}, f_N(n) = n(1 - t)^{n - 1}\)
-
因此
\[ \begin{align} E(Z) & = E(M) - E(N) \notag \\ & = \int_0^1 nm^n \text{d}m - \int_0^1 n(1 - t)^{n-1}t \text{d}t \notag \\ & = \dfrac{n - 1}{n + 1} \notag \end{align} \]
第 5 章⚓︎
第 6 章⚓︎
第 7 章⚓︎
第 8 章⚓︎
综合题⚓︎
评论区
如果大家有什么问题或想法,欢迎在下方留言~