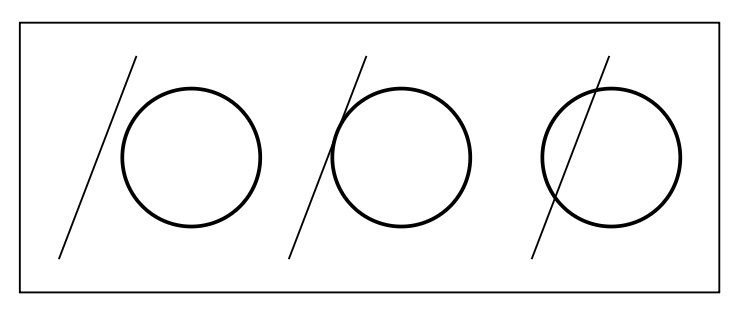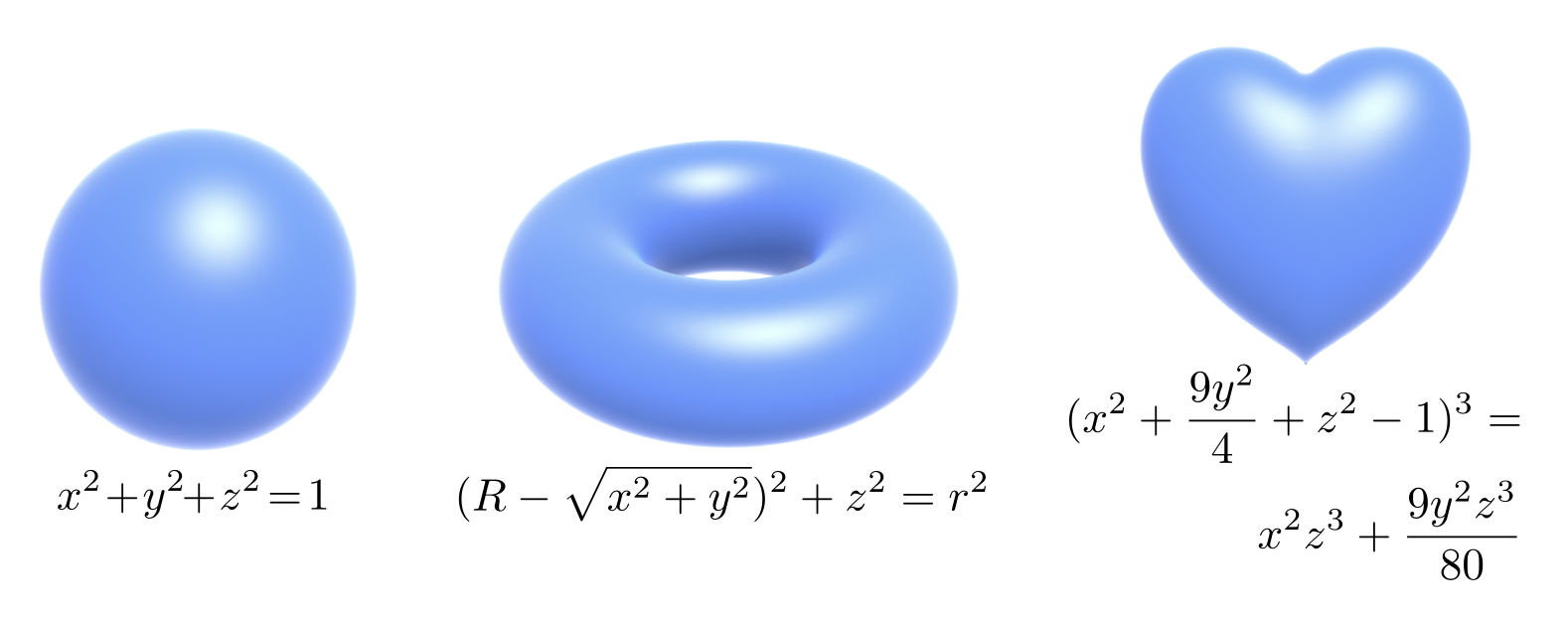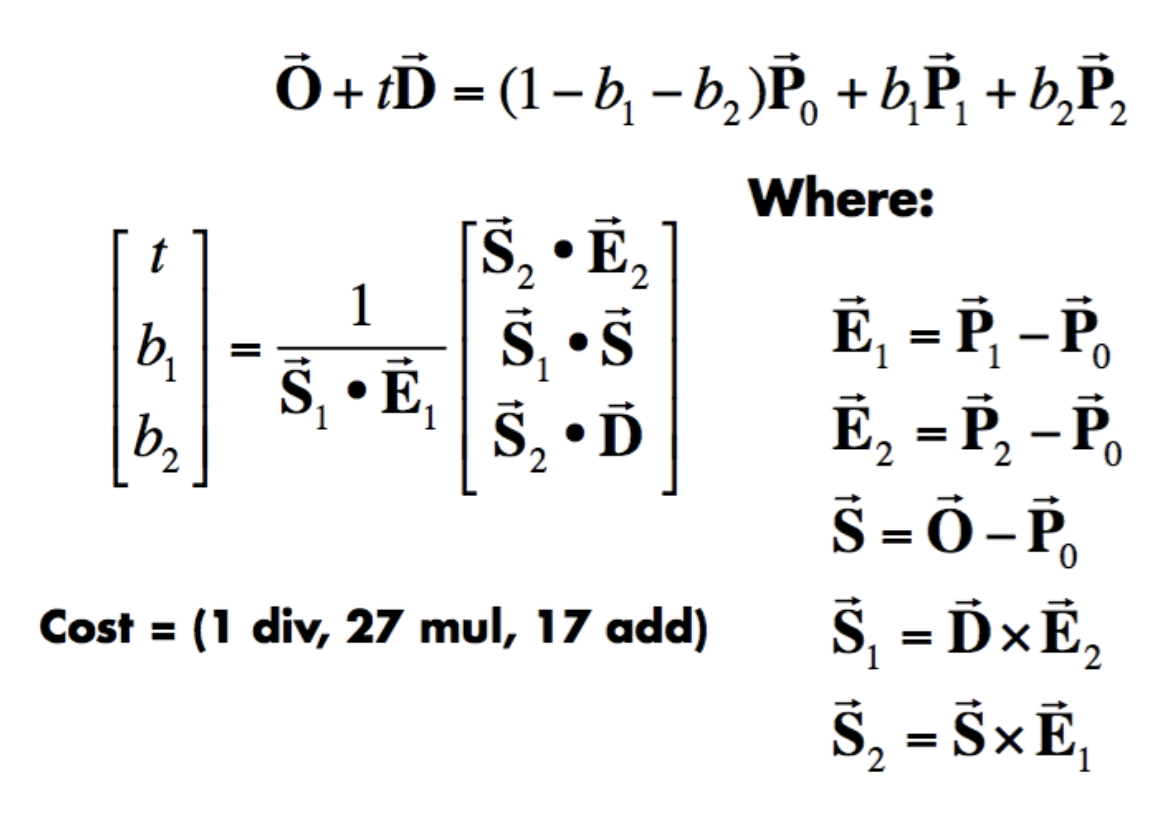Ray Tracing⚓︎
约 8237 个字 79 行代码 预计阅读时间 42 分钟
为什么要学习光线追踪(ray tracing)?因为:
-
光栅化不能处理全局上的效果,包括
- 软阴影
- 尤其是光线反复弹射(>1)的场景
-
光栅化很快,但是质量相对较低
-
光线追踪很准确,但是很慢
- 我们认为光栅化是实时的(real-time),而光线追踪是离线的(offline)
- 生产中过程中,10000 个 CPU 核心小时才能渲染一帧画面
Whitted-Style Ray Tracing⚓︎
Basic Ray-Tracing Algorithm⚓︎
在光线追踪算法中,我们对光线有以下假定:
- 光沿直线传播(尽管这是错的,以为光有波动性)
- 多条光线相交时不会发生“碰撞”(尽管这也是错的)
-
光线从光源到达人眼
- 光线从光源到人眼,那么从人眼出发也能看到光线,这就是光路的可逆性(reciprocity)
“And if you gaze long into an abyss, the abyss also gazes into you.” — Friedrich Wilhelm Nietzsche(尼采)
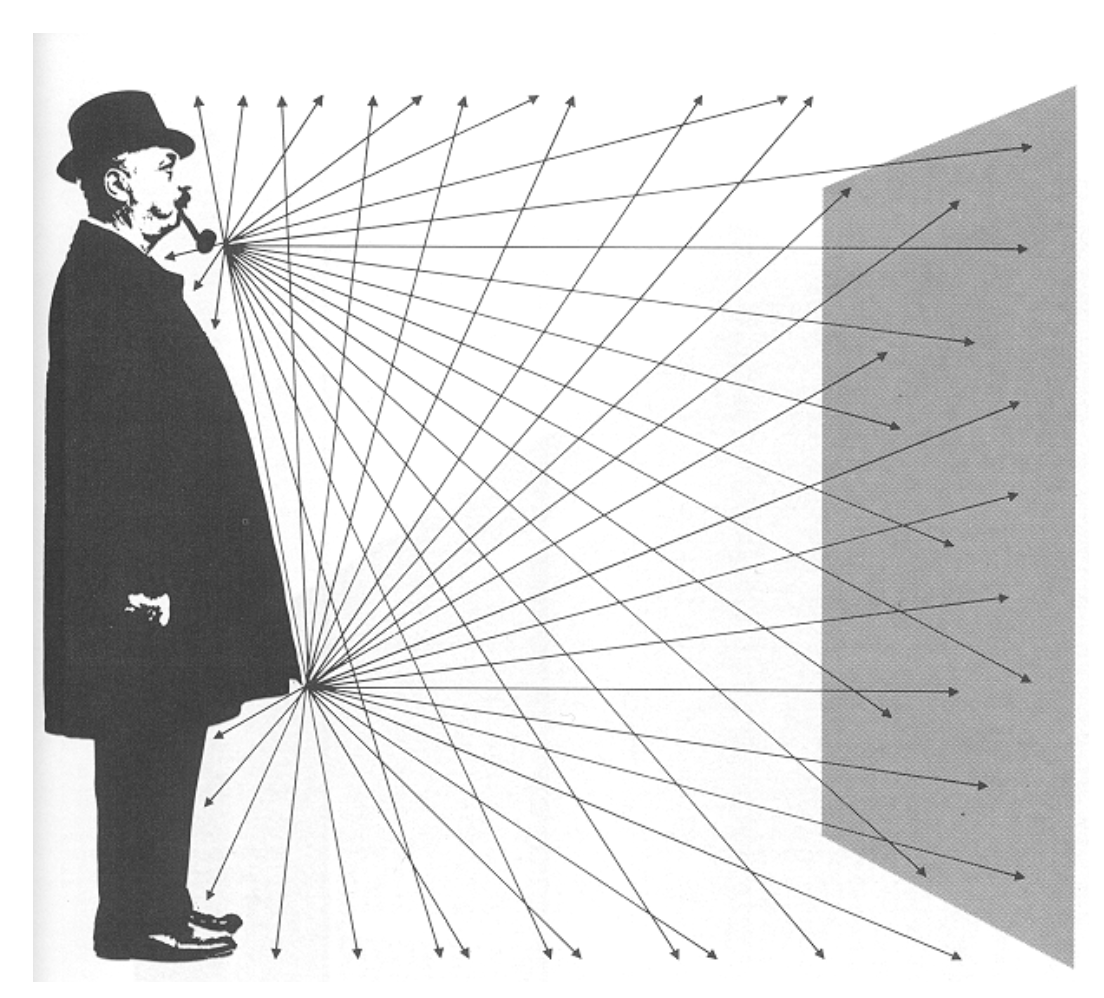
人们对光线追踪的研究可以追溯至几千年前。一开始,不少人认为因为人眼向外界散播一种“感受光线”的东西,我们才能看到身边的世界。现在看来这种理论是十分荒谬的。
而在图形学的光线追踪算法中,首先要了解光线投射(ray casting) 的原理:
- 通过为每个像素点投射一束光线来生成一幅图像
- 通过将光线发射到光源来检查阴影的存在
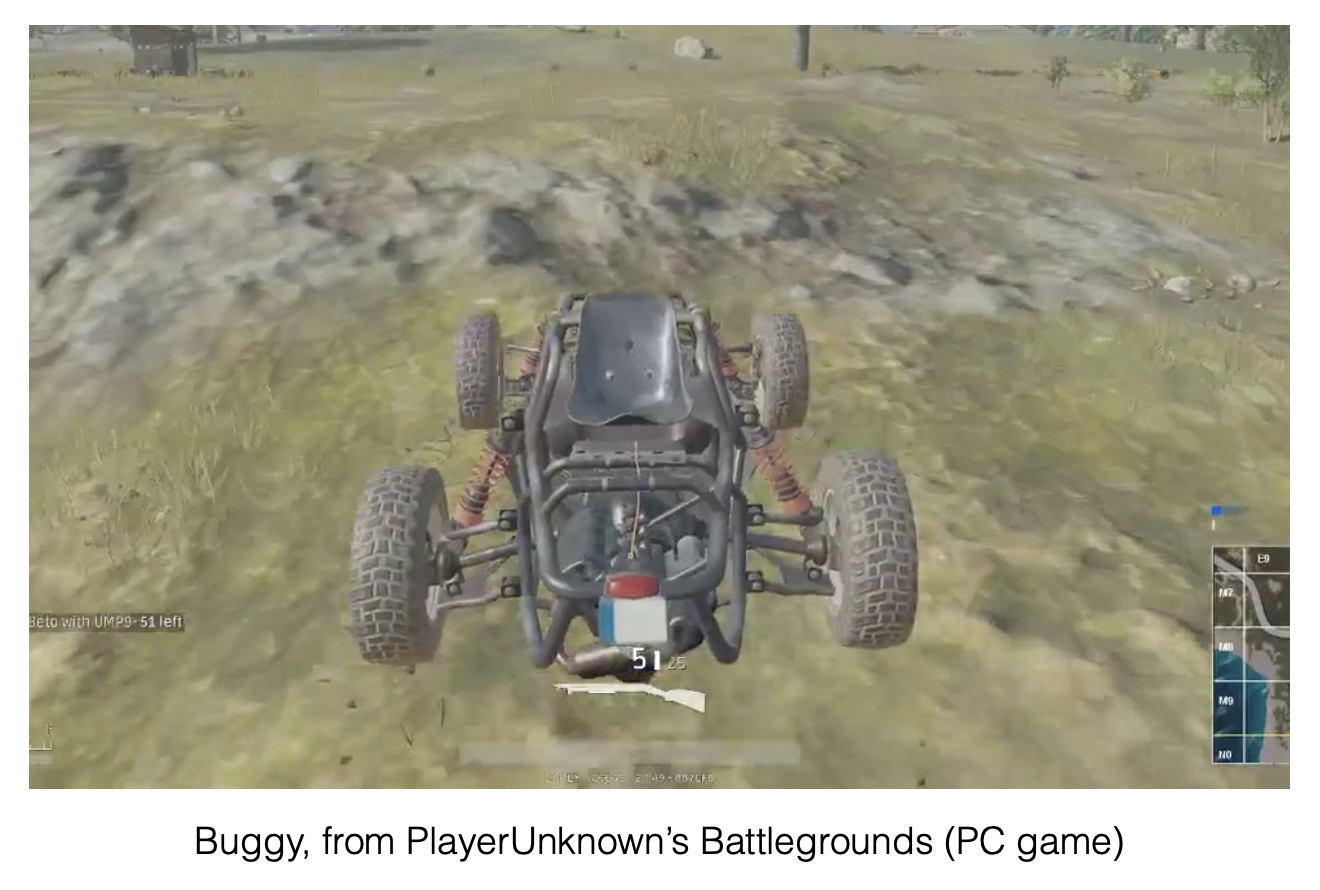
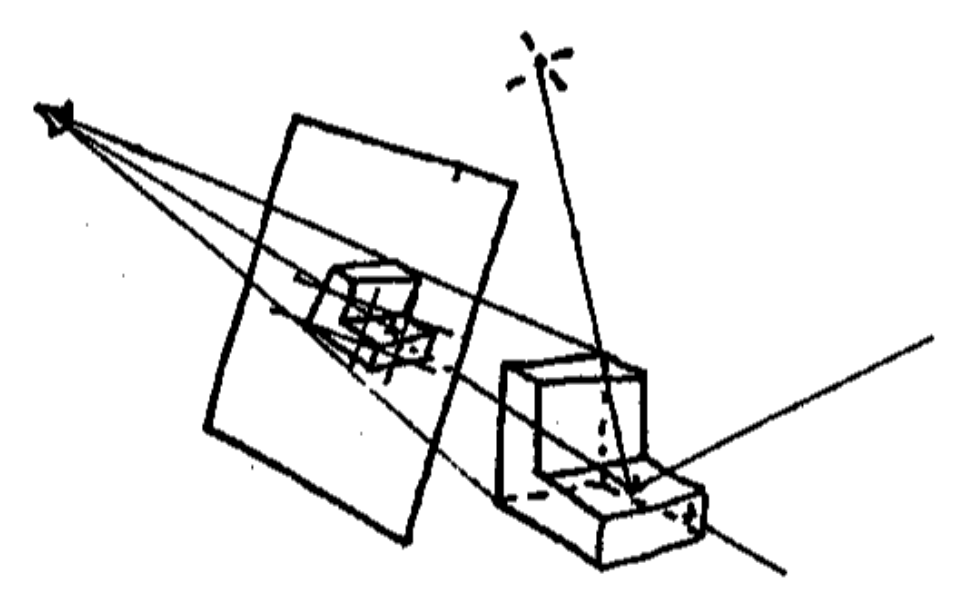
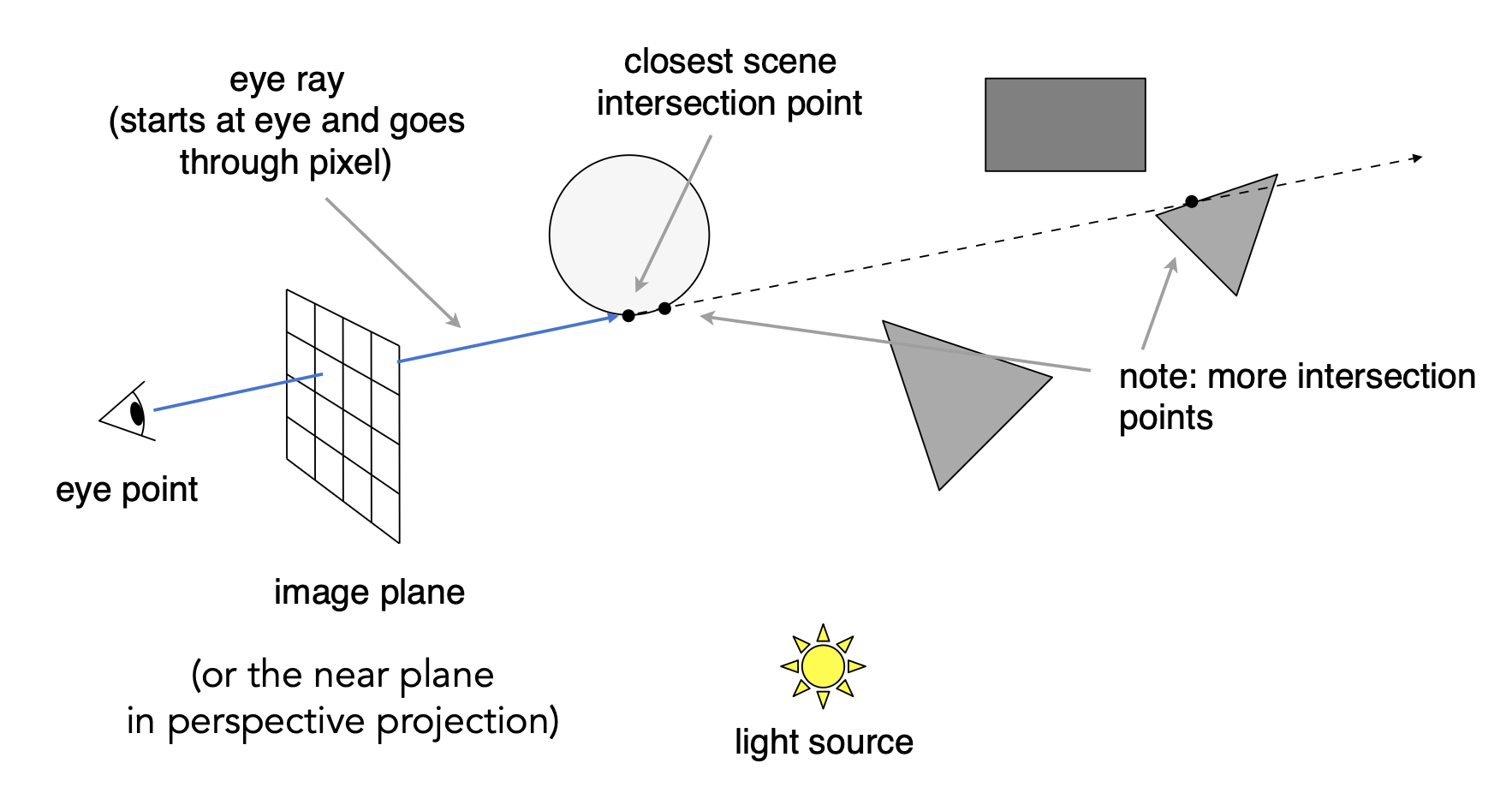
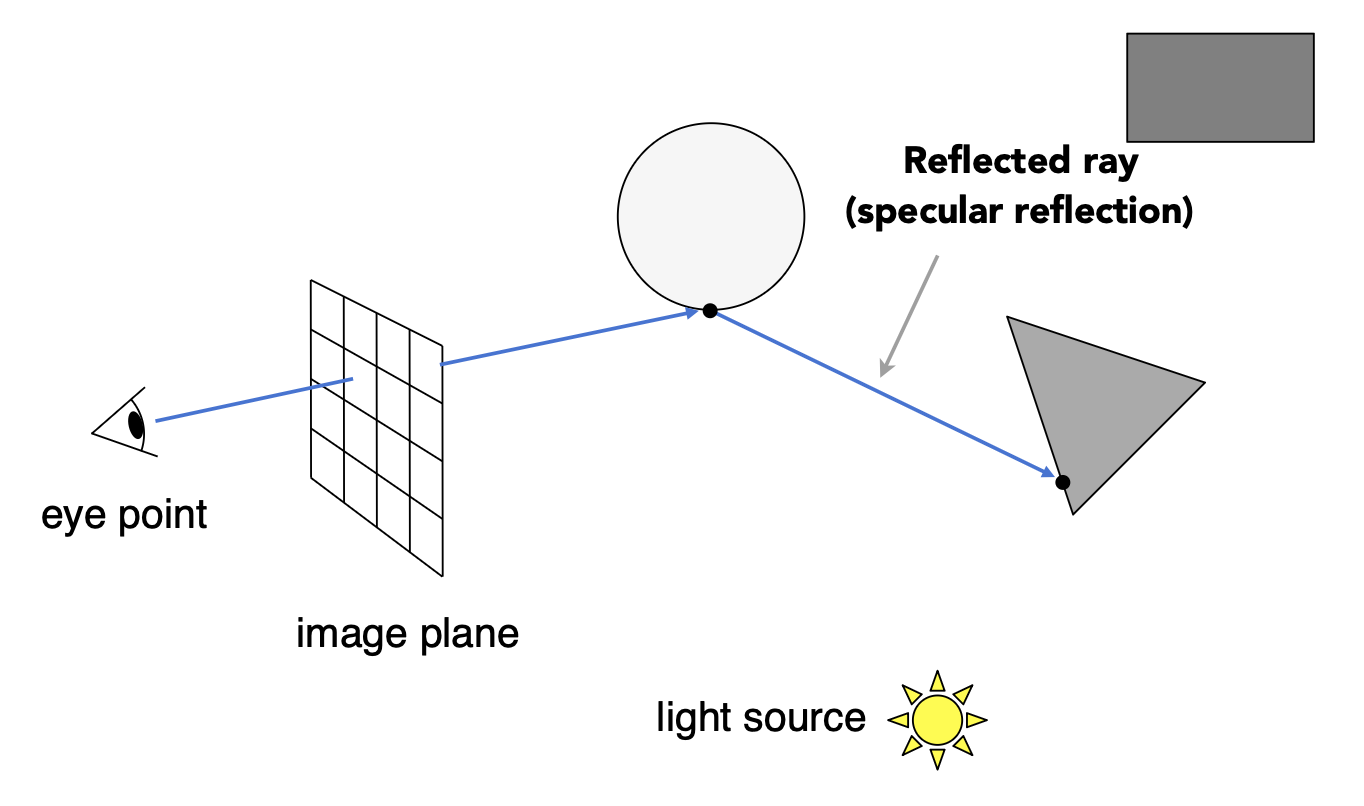
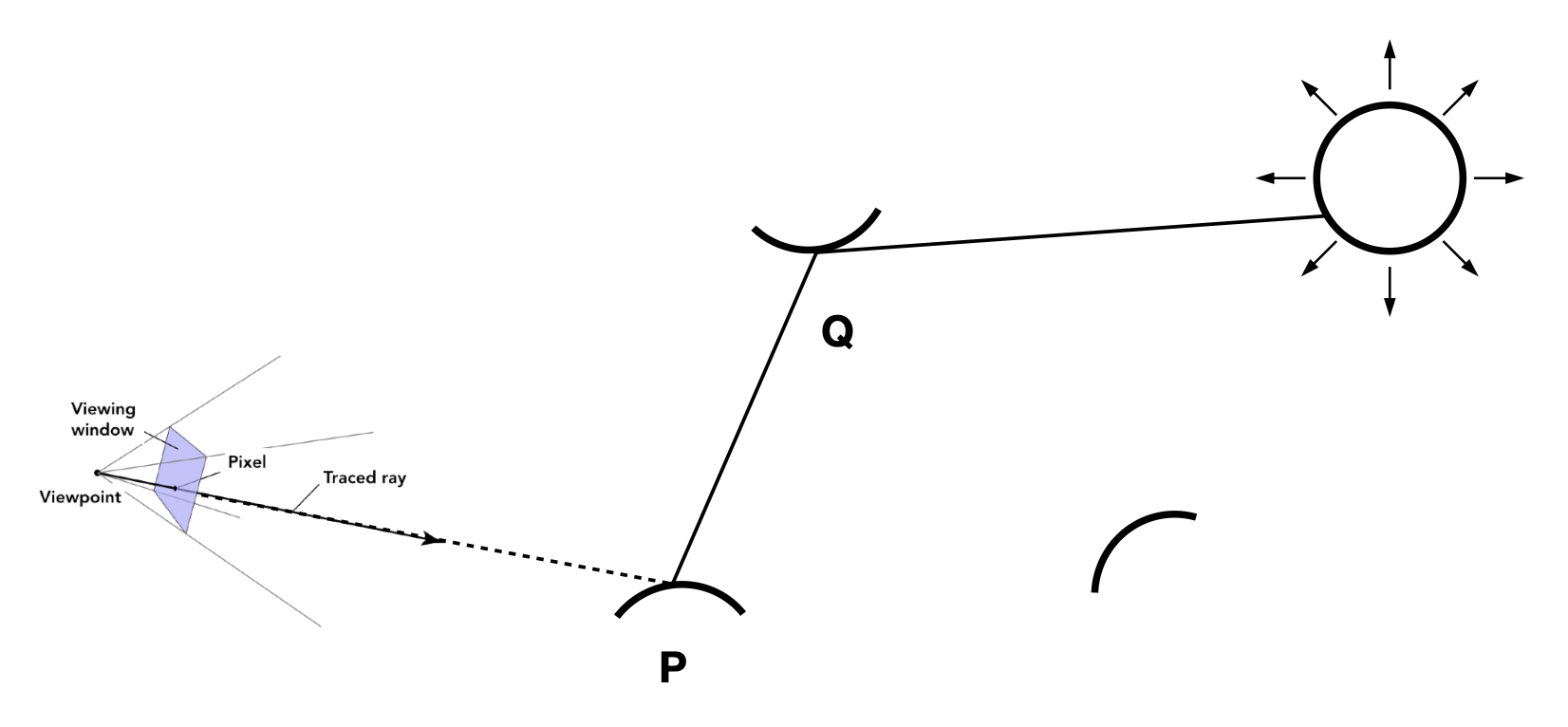
这里的“光线”来自人眼,并且之后我们就把人眼看作是一个针孔相机 (pinhole camera)。下面展示了从人眼出发的光线照到球面,并从球面出发又经过了很多物体的情景。
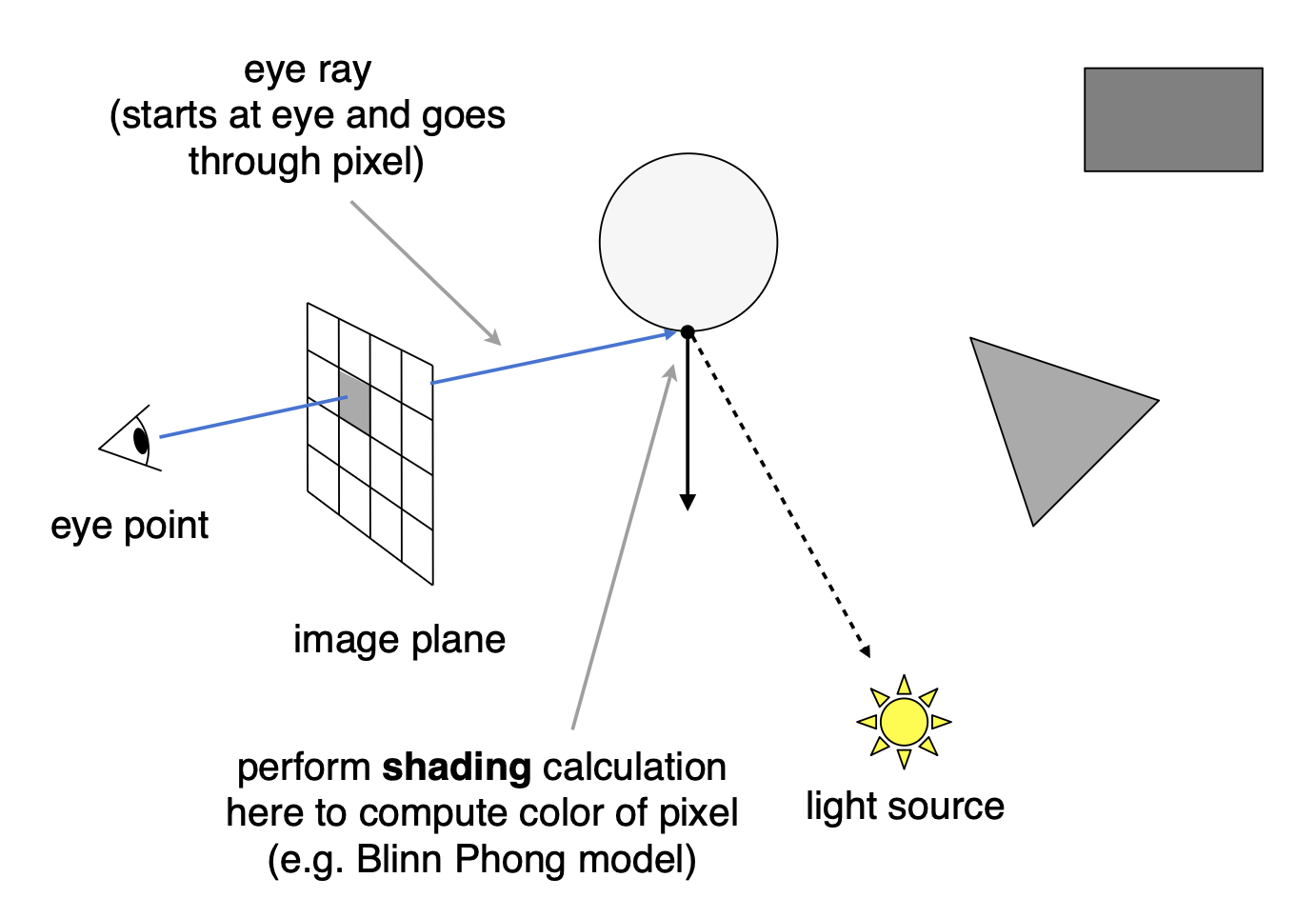
虽然这一束光线和场景中多个物体相交,但我们只考虑离人眼最近的那个交点。对于该交点,执行着色计算,得出该光线对应像素的颜色值。
这种基于光线投射的光线追踪算法叫做递归光线追踪(recursive ray casting),或 Whitted 风格光线追踪,是一种“改进的阴影显示照明模型”。下图就是采用该算法得到的结果:
在不同硬件上的耗时对比:
- VAX 11/780 (1979):74m
- PC (2006):6s
- GPU (2012):1/30s
还是利用前面介绍的例子,现在我们仅考虑照到最近交点的那一段光线。由这条光线,产生其他类型的光线:
-
反射光线(reflected ray)(镜面反射 (specular reflection))
-
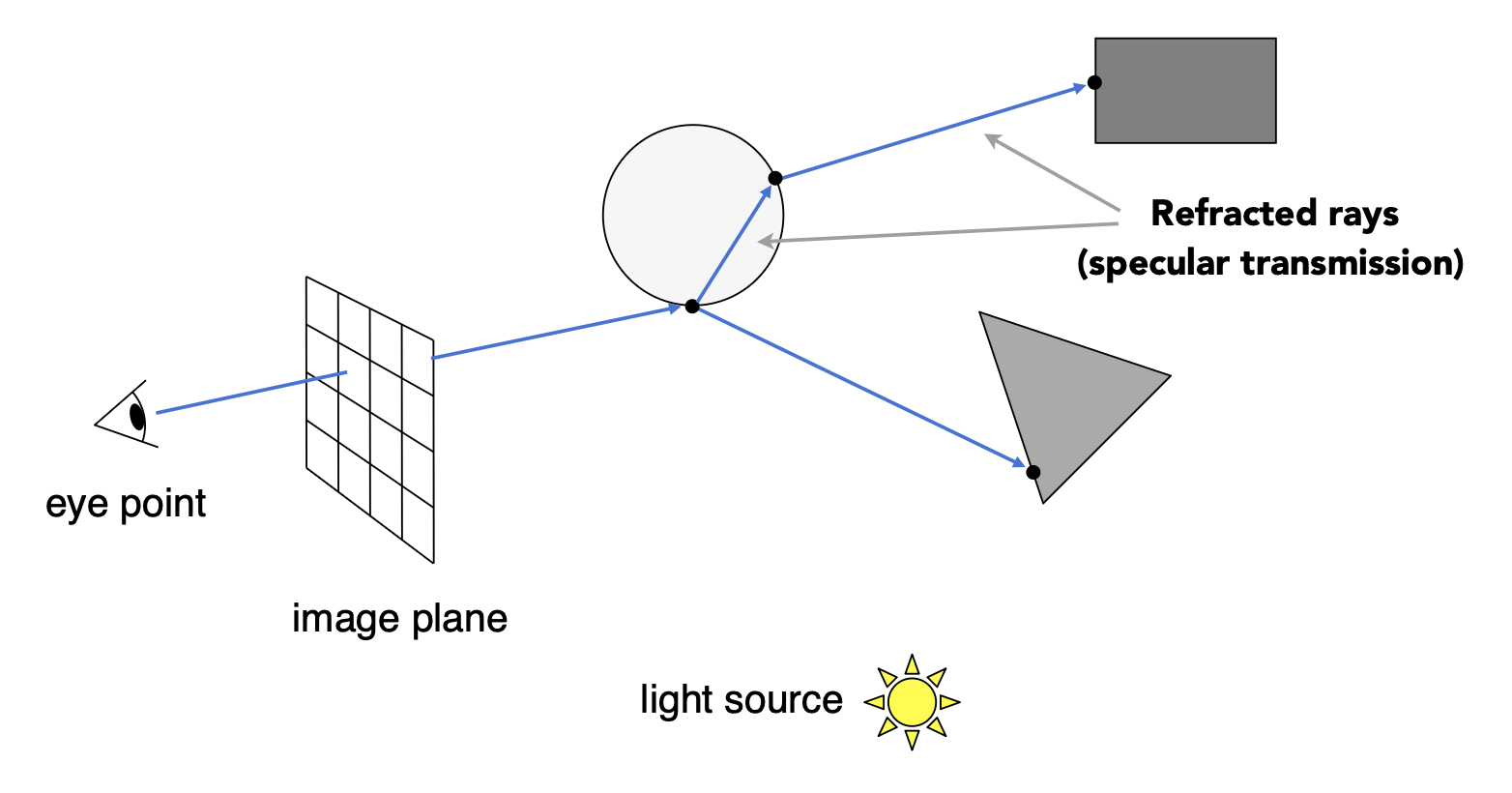
折射光线(refracted ray)(镜面透射 (specular transmission))
-
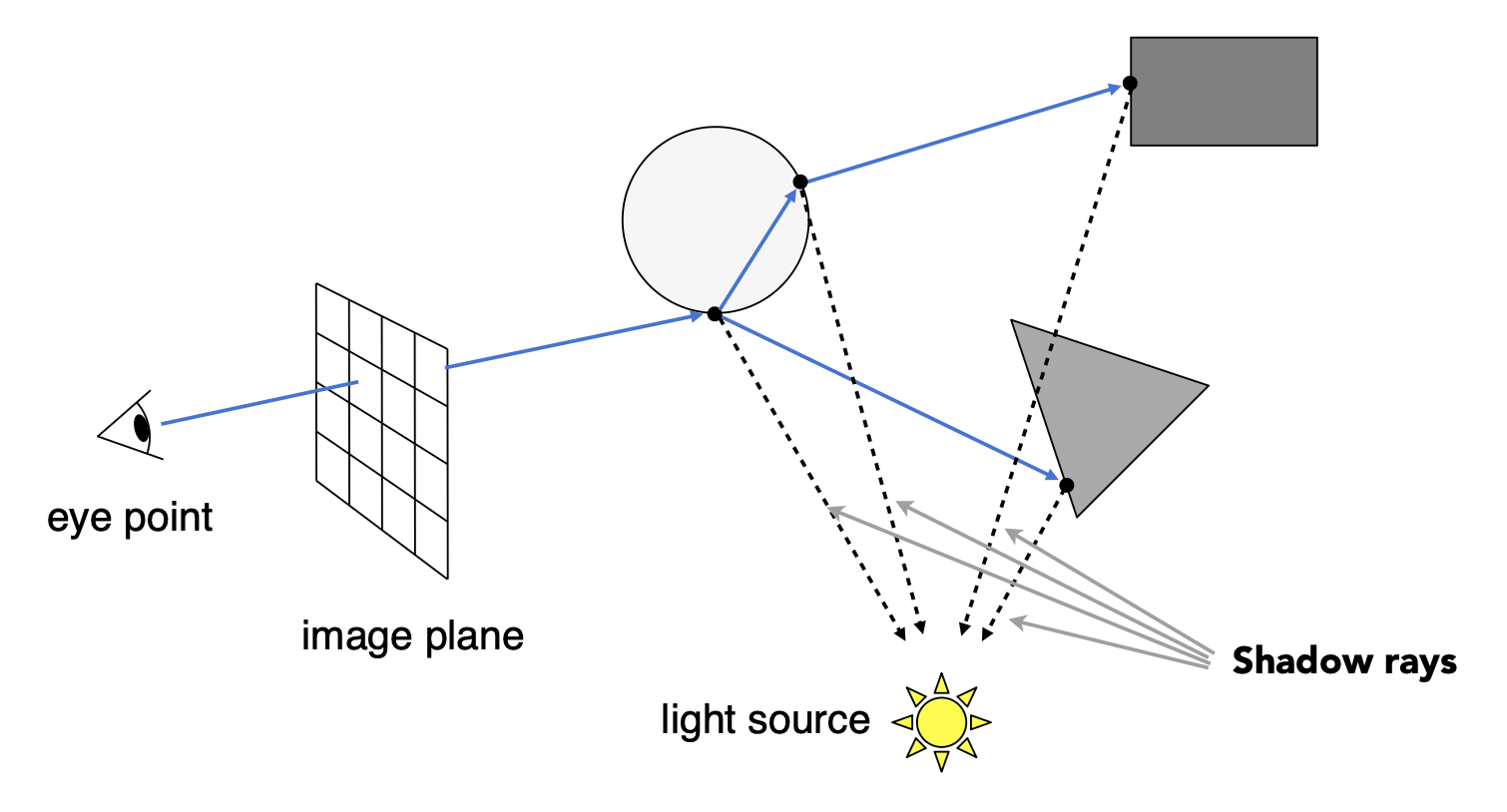
阴影光线(shadow ray)
我们称入射光线为主光线(primary ray),而反射光和折射光线被称为次级光线(secondary ray)。
Ray-Surface Intersection⚓︎
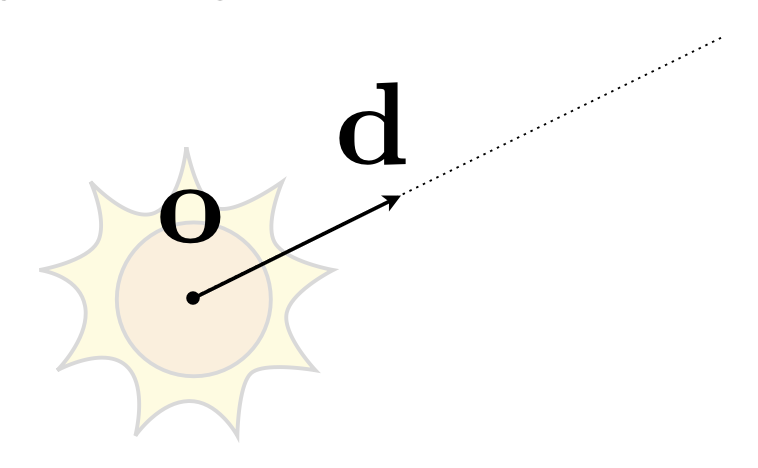
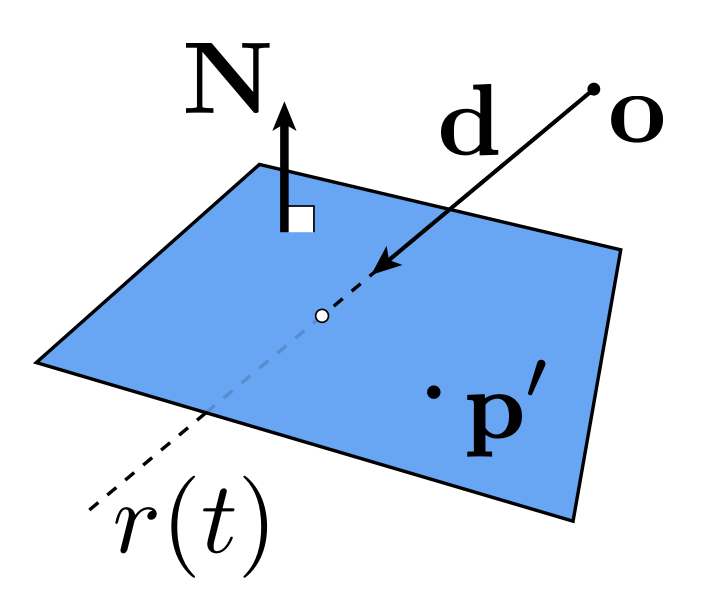
光线可被简单表示为一个原点 + 方向向量(单位向量,长度为 1
- \(\mathbf{r}(t)\):沿着光线上的点
- \(t\):时间
- \(\mathbf{o}\):原点
- \(\mathbf{d}\)
: (归一化后的)方向向量
Spheres⚓︎
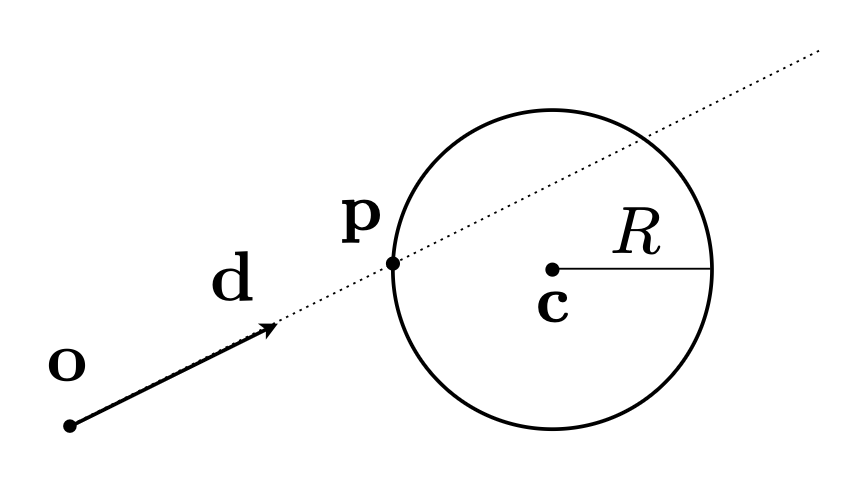
先来看如何求光线在球面上的交点:已知
- 光线:\(\mathbf{r}(t) = \mathbf{o} + t\mathbf{d} \quad 0 \le t < \infty\)
- 球体:\(\mathbf{p}:\ (\mathbf{p} - \mathbf{c})^2 - R^2 = 0\)
那么交点必然同时满足上述两个方程,所以只要将光线方程代入到球体方程即能求解。 $$ (\mathbf{o} + t\mathbf{d} - \mathbf{c})^2 - R^2 = 0 $$
因为这是一个二次方程,所以可以写成 \(at^2 + bt + c = 0\) 的形式,其中
- \(a = \mathbf{b} \cdot \mathbf{b}\)
- \(b = 2(\mathbf{o} - \mathbf{c}) \cdot \mathbf{d}\)
- \(c = (\mathbf{o} - \mathbf{c}) \cdot \mathbf{o} - \mathbf{c} - R^2\)
求根公式 \(t = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}\),将 \(a, b, c\) 代入就能得到最终结果。
Implicit Surfaces⚓︎
更一般地,考虑光线和用隐式法表示的曲面的相交。假设曲面方程为 \(\mathbf{p}:\ f(\mathbf{p}) = 0\),将光线方程代入后求解,其中的正实根就是最终解。
Planes⚓︎
而对于用显式法表示的曲面,三角形是其中最基础,也是最重要的一个。之所以要研究光线和三角形网格的相交关系,是因为
- 从渲染角度看,可见性、阴影和光照等都会涉及到
- 从几何角度看,检测点在几何体的内外
- 检验方法:从该点出发打出一条射线,如果射线经过奇数个点,说明该点在几何体内部,否则在外面
最简单的思路是让光线穿过每一个能够穿过的三角形面。简单起见,我们认为一条光线和一个三角形的相交次数为 0 或 1(忽略多次相交的可能
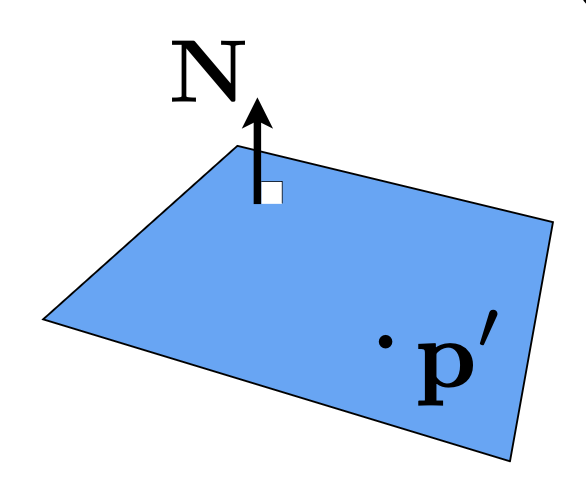
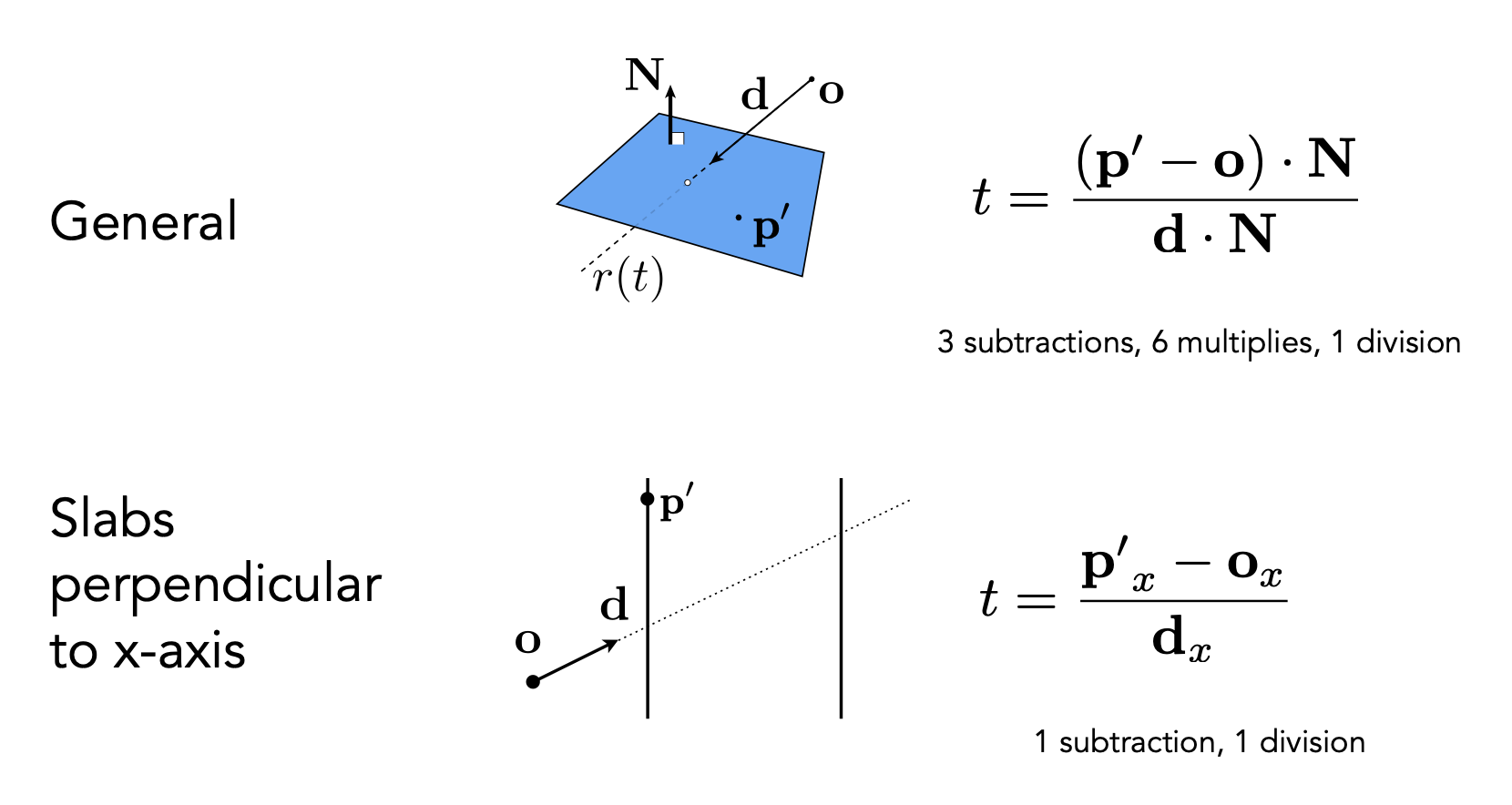
由于三角形是一个平面,因此可以将问题转化为求光线和平面(planes) 的相交,并检验交点是否落在三角形内部。平面由它的法向量以及一个平面上的点来定义,对应的方程为: $$ \mathbf{p}: (\mathbf{p} - \mathbf{p}') \cdot \mathbf{N} = 0 $$
- \(\mathbf{p}\):平面上的所有点
- \(\mathbf{p}'\):平面上一点
- \(\mathbf{N}\):法向量
注:平面方程的一般式:\(ax + by + cz + d = 0\)
同样可以将光线方程代入(令 \(\mathbf{p} = \mathbf{r}(t)\)
这样计算可能还是太麻烦了,一种更快的做法叫做 Möller Trumbore 算法。它利用重心坐标计算,方程和解如下所示:
其中 \((1 - b_1 - b_2), b_1, b_2\) 都是重心坐标。
Accelerating Ray-Surface Intersection⚓︎
光线追踪技术对计算机性能提出了不小的挑战。就以前面介绍的简单的光线 - 场景相交算法为例,我们需要测试每一个三角形和每一条光线的相交情况,并找出其中最近的交点(即 \(t\) 最小时对应的点
注意
为求通用性,我们后续使用“对象”一词替代“三角形”(但未必指整个对象
Bounding Volumes⚓︎
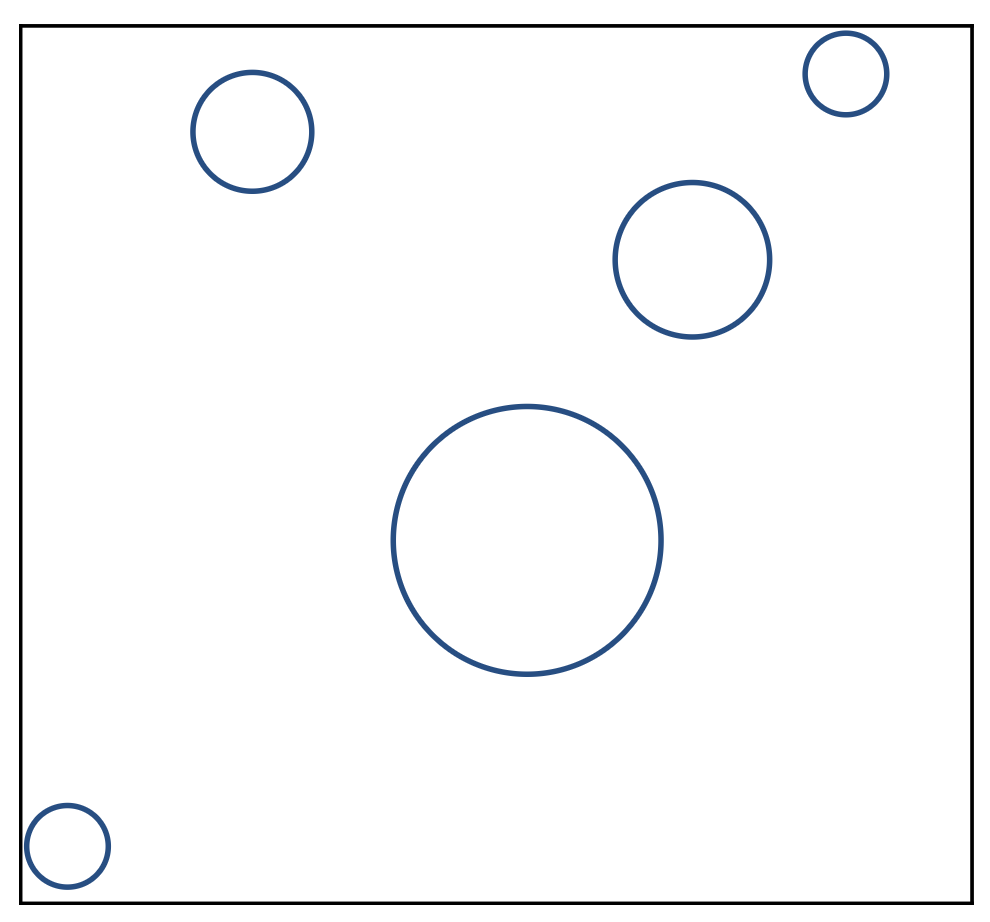
为避免计算光线与复杂物体上的相交关系,我们可以用一个结构简单的包围体(bounding volume) 覆盖复杂物体的周围。注意包围体内的物体一定要尽可能填满整个空间。如果光线没有经过包围体,也就意味着没有经过包围体内的物体,因此检测时可以先看光线是否经过包围体,再看是否经过包围盒内的物体。
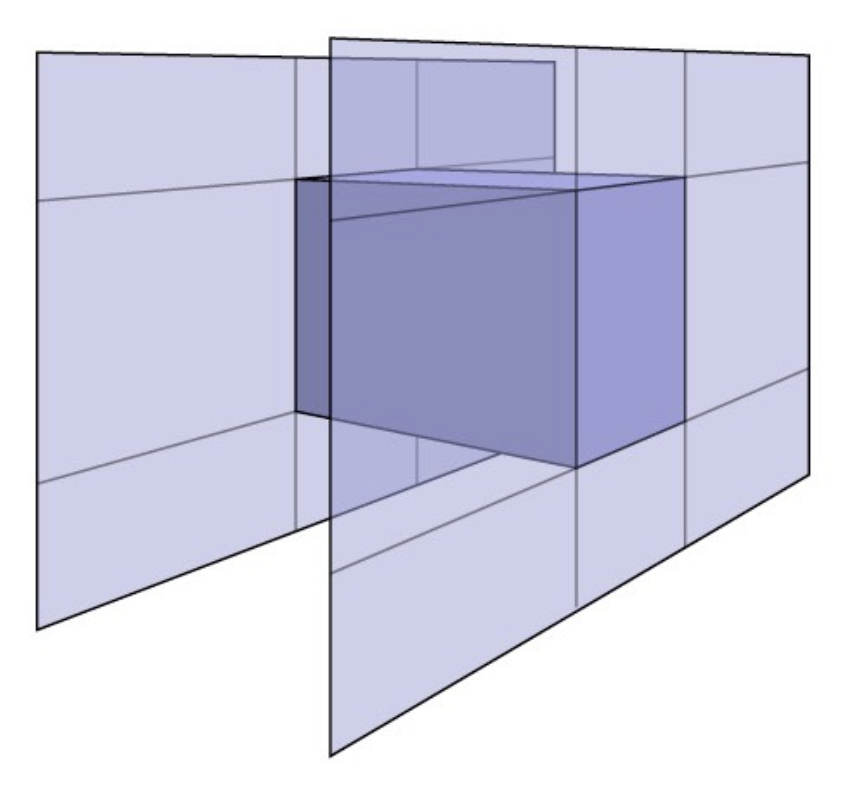
现在我们用一个盒子作为包围体,这个盒子与三对面 (slabs)(也就是长方体的六个面)相交(右图展示了其中一对面
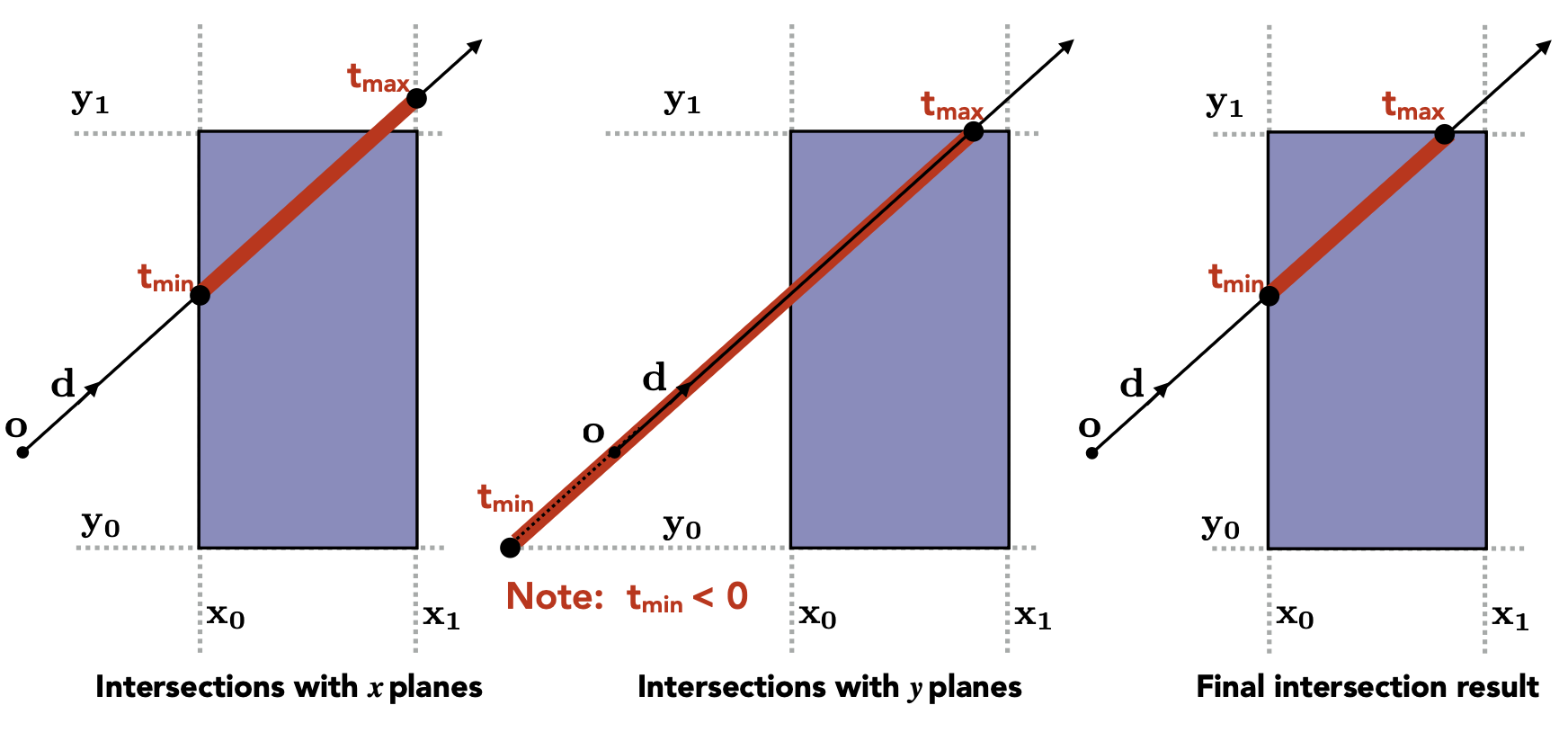
为方便讨论,下面以二维平面上的 AABB 为例讲解具体的计算过程,三维空间同理。核心思想是计算光线到达每个对面的最小时间和最大时间(\(t_{\min}, t_{\max}\),可以是负数
上述计算是合理的原因是:
- 仅当光线进入所有对的面,光线才算进入到包围盒
- 只要光线离开其中一对面,光线就算离开了包围盒
对应的公式为:\(t_{\text{enter}} = \max \{t_{\min}\}, t_{\text{exit}} = \min \{t_{\max}\}\)。当 \(t_{\text{enter}} < t_{\text{exit}}\),我们认为光线在包围盒内经过一会儿,所以它们必定会相交。然而光线不是(无方向的)直线,所以还需检查 \(t\) 是否为正,否则这样的解是无效的。
- \(t_{\text{exit}} < 0\):说明盒子在光线的“后面”,因此无法相交
- \(t_{\text{exit}} \ge 0, t_{\text{enter}} < 0\):光线的原点在盒子内,所以必定相交
所以当且仅当 \(t_{\text{enter}} < t_{\text{exit}} \&\& t_{\text{exit}} \ge 0\) 时,光线和 AABB 相交。
之所以要让包围盒轴对齐,是因为可以简化光线到平面上的计算。
下面就基于 AABB 介绍一些加速光线追踪的具体办法。
Uniform Grids⚓︎
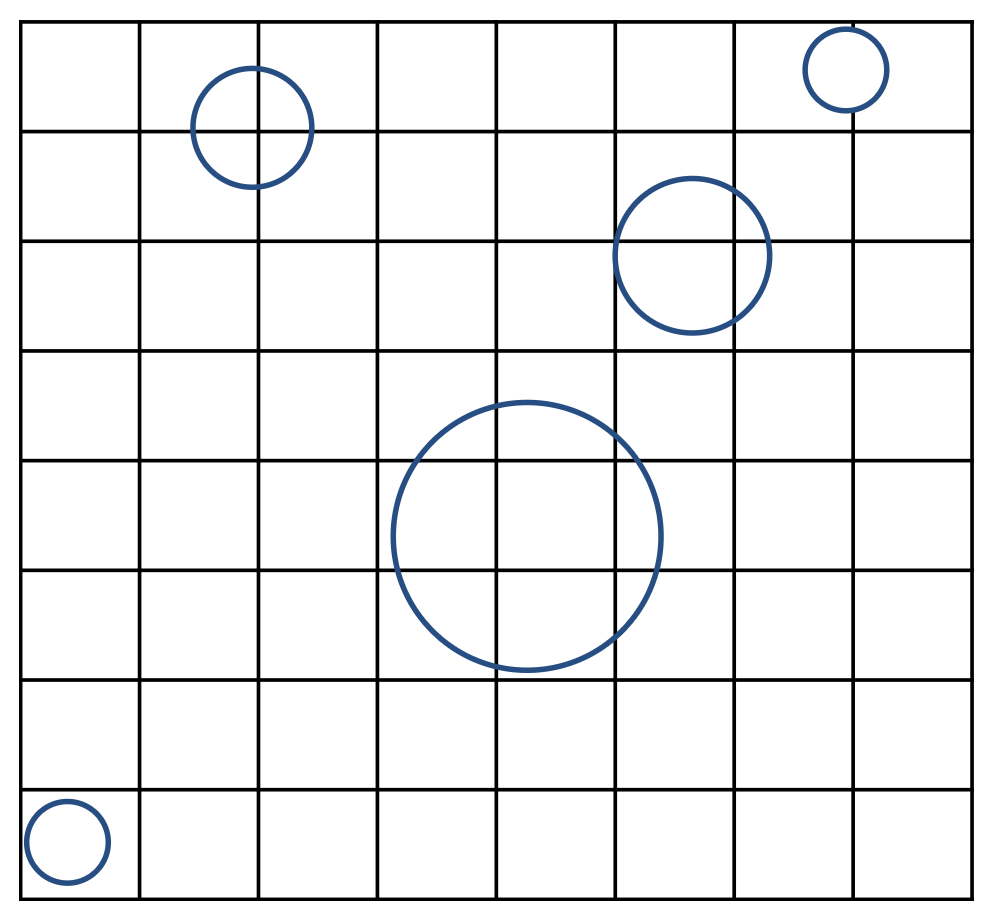
均匀空间划分(uniform spatial partition)(网格 (grid))的步骤如下:
-
预处理:构建加速用的网格
-
得到包围盒
-
创建网格
-
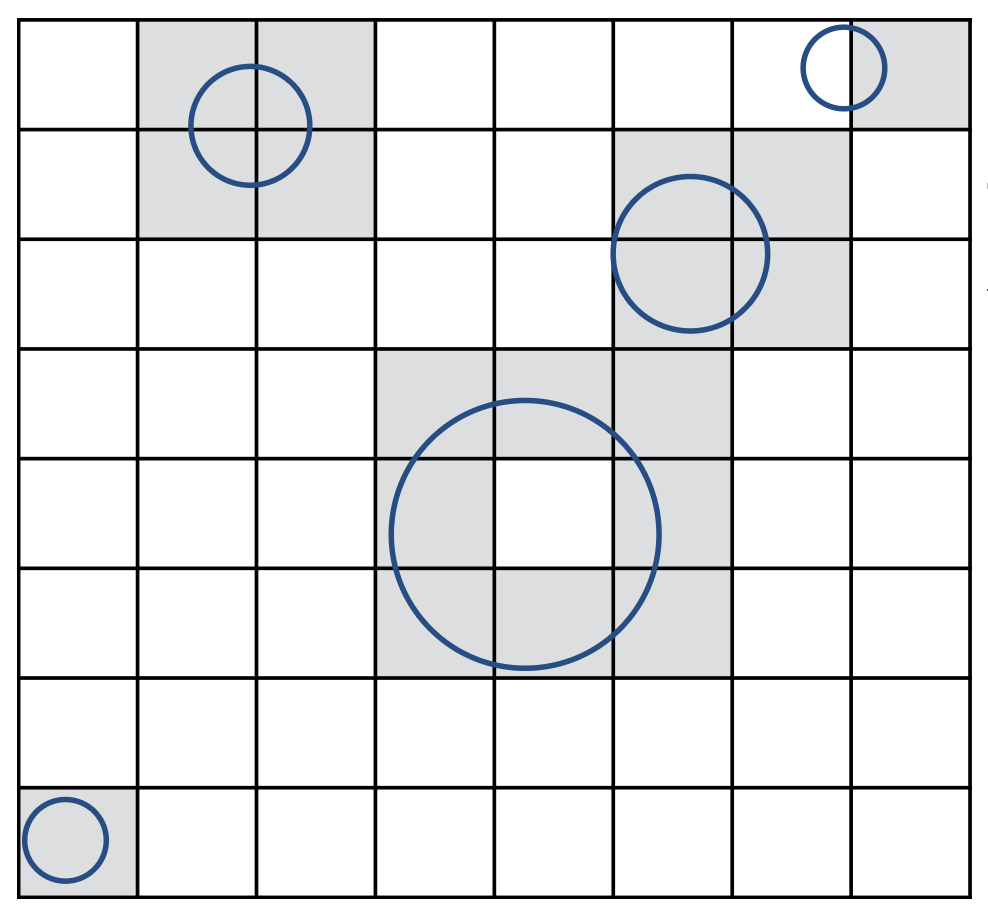
存储和物体(表面)重叠的那些格子
-
-
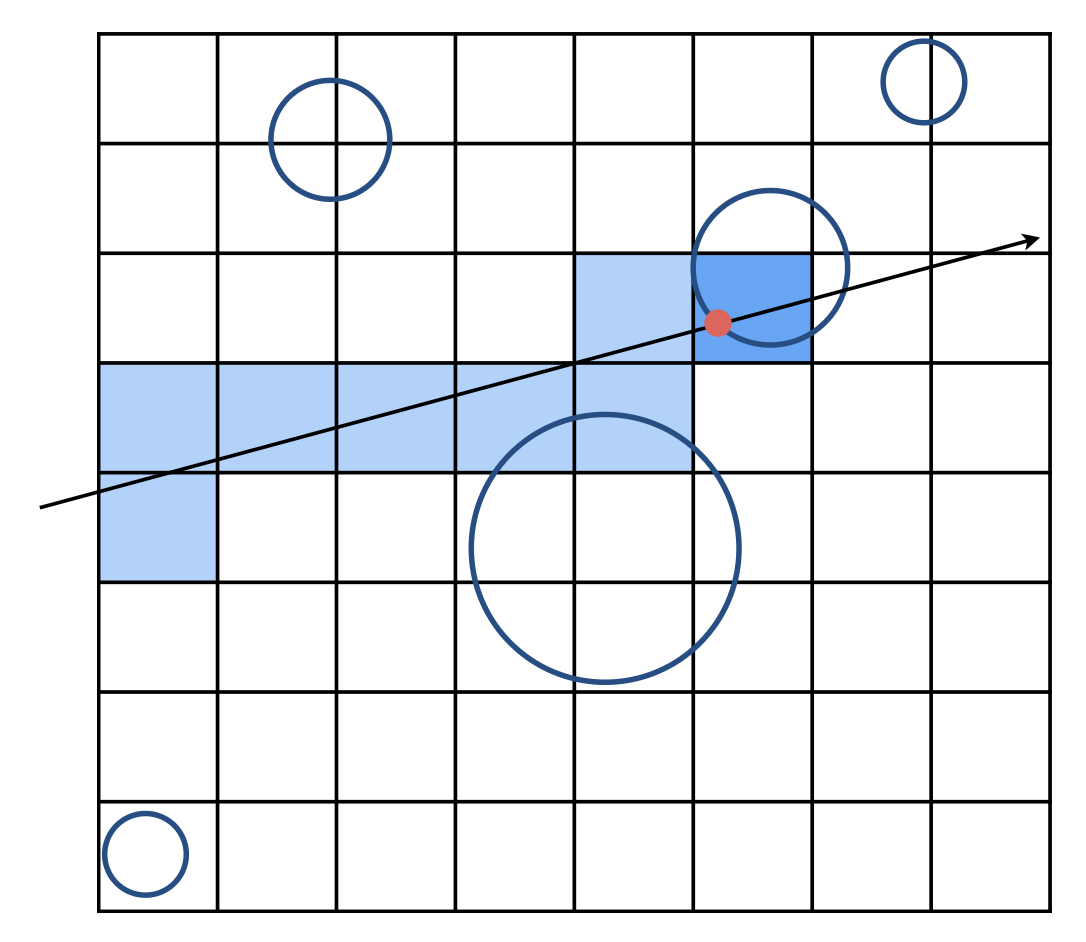
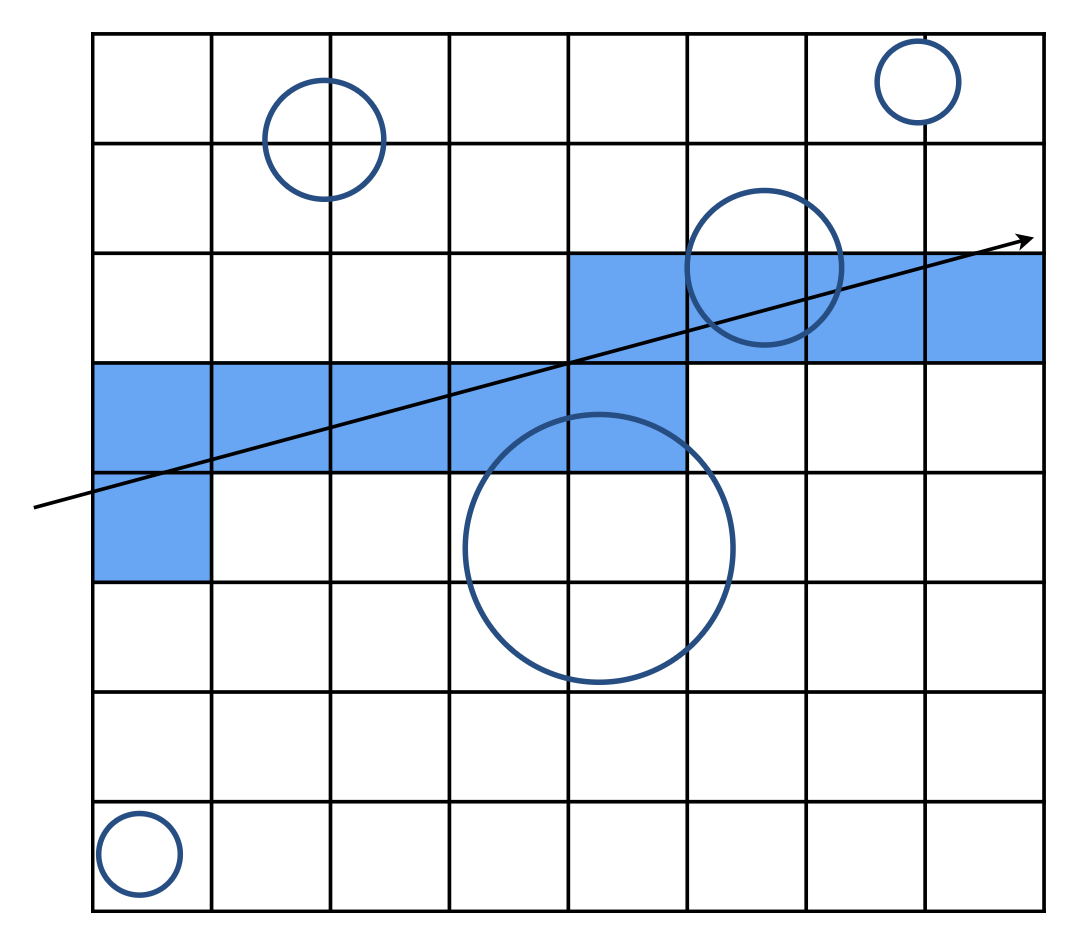
光线和场景的相交
- 标出光线经过的格子
- 对于这些格子,看它们是否在先前的预处理中已经存储过了,若是则说明光线和对应物体相交
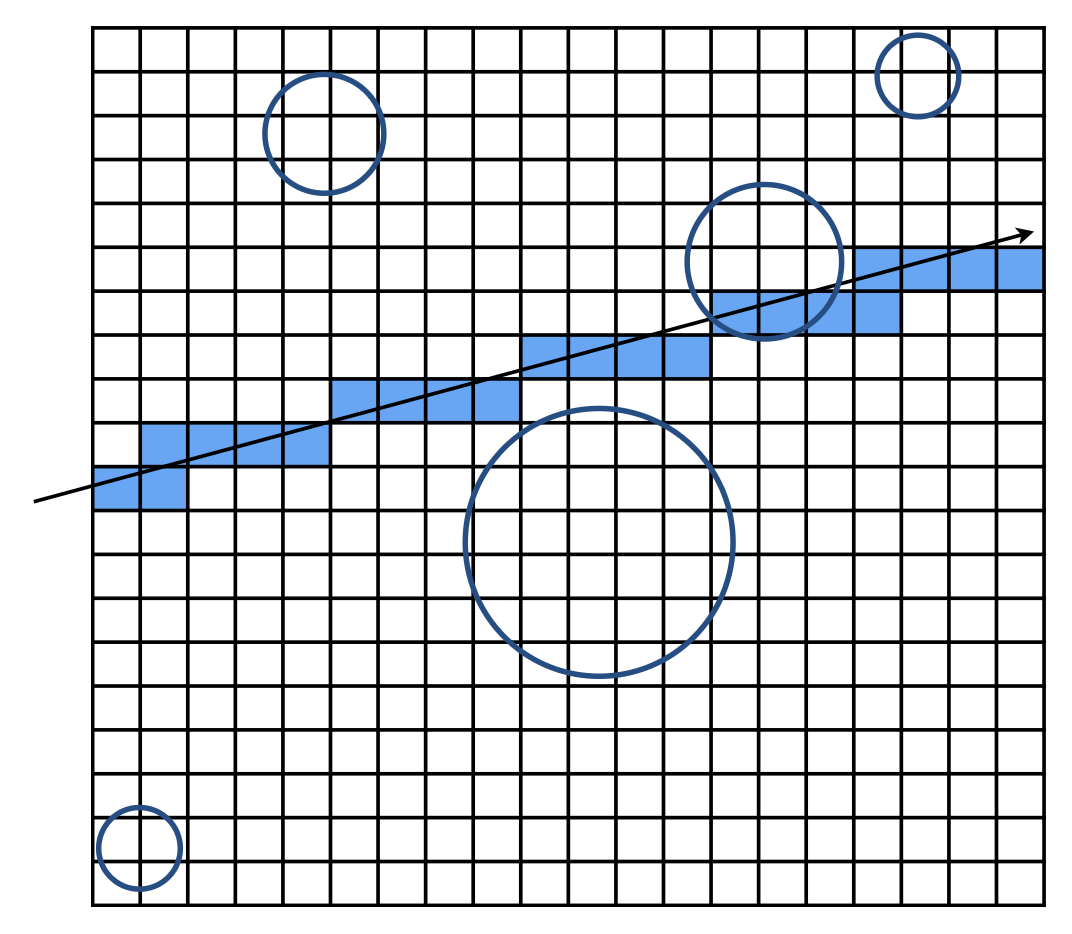
网格的分辨率要适中,不要:
-
划分太少,没有加速效果(极端情况:不划分,将包围盒看成一个格子)
-
划分太多:由于额外的网格遍历导致低效
人们想到用启发式的方法寻找合适的分辨率,结论如下:
- 格子数 = C * 物体数
- C ≈ 27(在 3D 空间中,经验之谈,不用管是怎么来的)
均匀网格的成与败
-
何时适用:有大片的物体,在大小和空间分布上是均匀的
-
何时失效
: “茶壶在体育馆内”的问题,即物体在场景中的分布不均匀,某些地方集中出现很多物体,另一些地方却是大规模的空白(比如下图左上方的拱廊)
Spatial Partitions⚓︎
鉴于均匀网格的局限性,下面引入更多更灵活的空间划分方法:
-
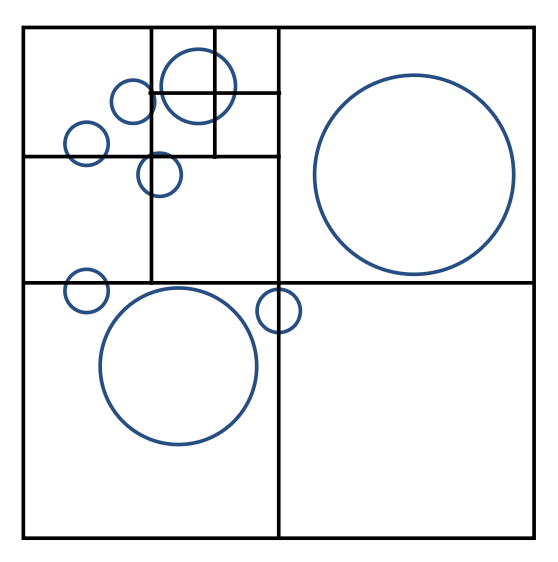
八叉树(oct-tree)
- 将一个立方体横、竖、侧各切一刀,形成八个块,故名“八叉”(图中只展示二维的一个面,因而是“四叉”)
- 对于每个小块,也要切这样的三刀,直到每个小块内没有物体或物体数量足够少时停止
- 缺点:维度越高,切的越多,越复杂
-
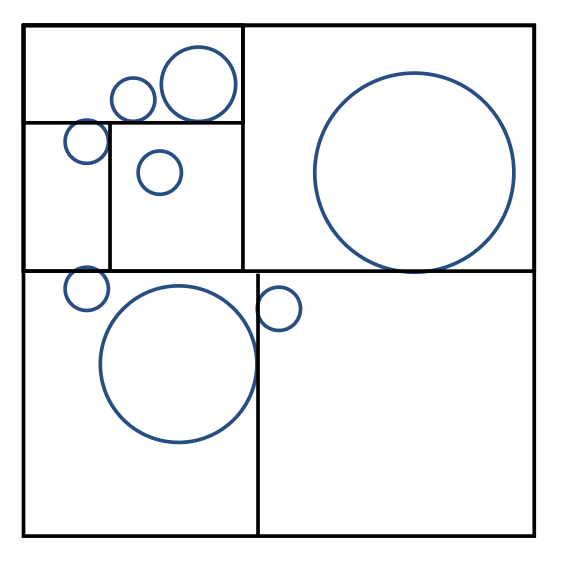
KD 树(KD-tree)
- 相比八叉树的划分更加自由
- 但要遵循“水平 - 竖直 - 水平 ...”的顺序交替方向切割,确保划分均匀
- 因此会得到一棵二叉树
-
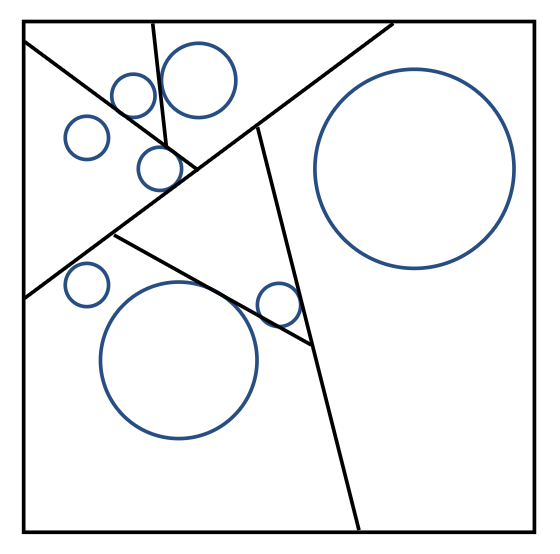
BSP(二元空间划分)树(BSP-tree)
- 更加自由,可以沿任意方向划分
- 但缺点是和前面介绍的 AABB 适配性不高,且维度越高越复杂
综上,接下来就主要介绍 KD 树的处理过程:
-
预处理:
-
数据结构:
- 内部节点
- 分割轴:x/y/z 轴
- 分割位置:沿着轴的分割平面的坐标
- 孩子:指向孩子节点的指针
- 注意:物体不是存储在内部节点的
- 叶节点:一张关于物体的列表
- 内部节点
-
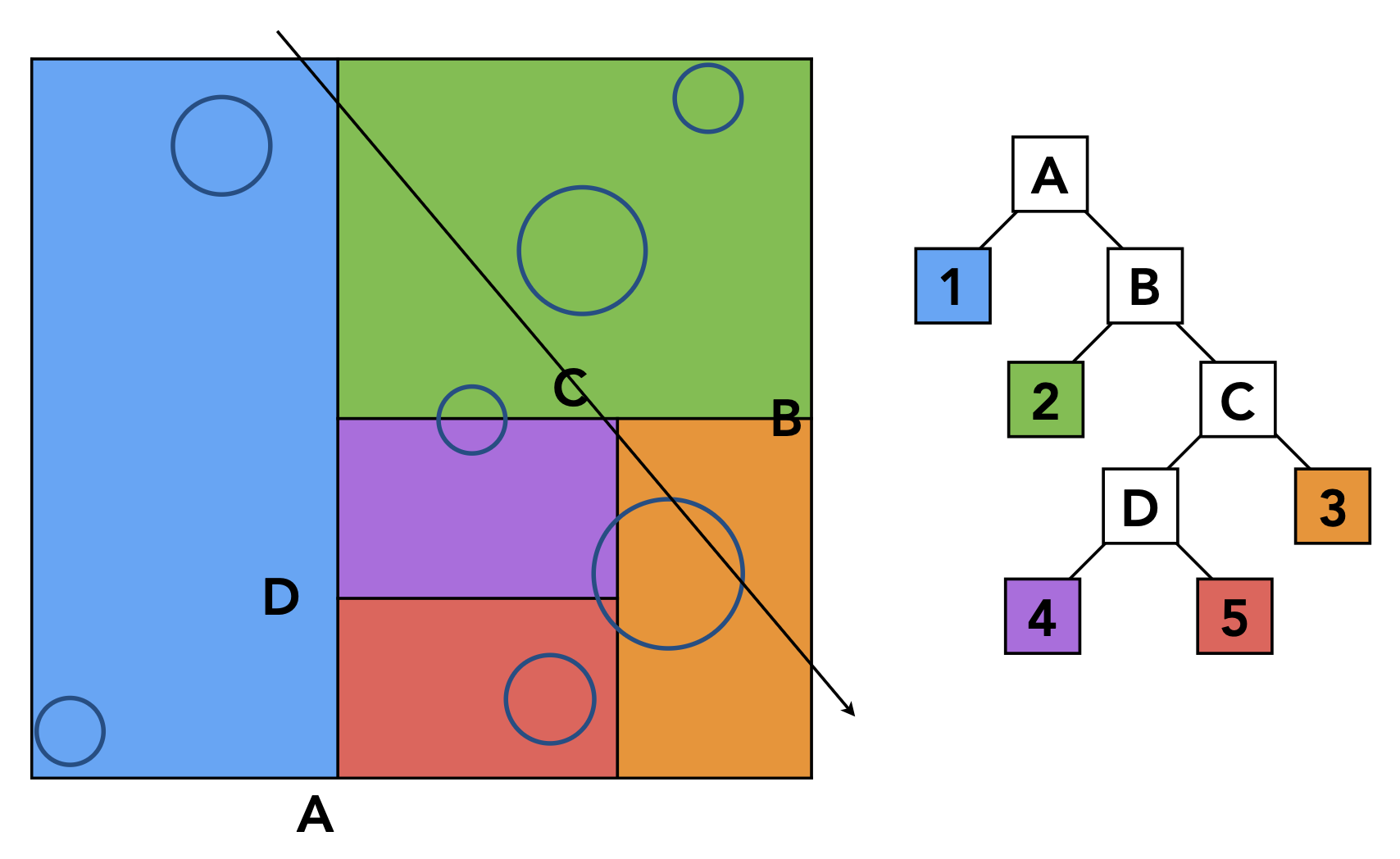
KD 树的遍历
-
假如包围盒内有这样一些物体
-
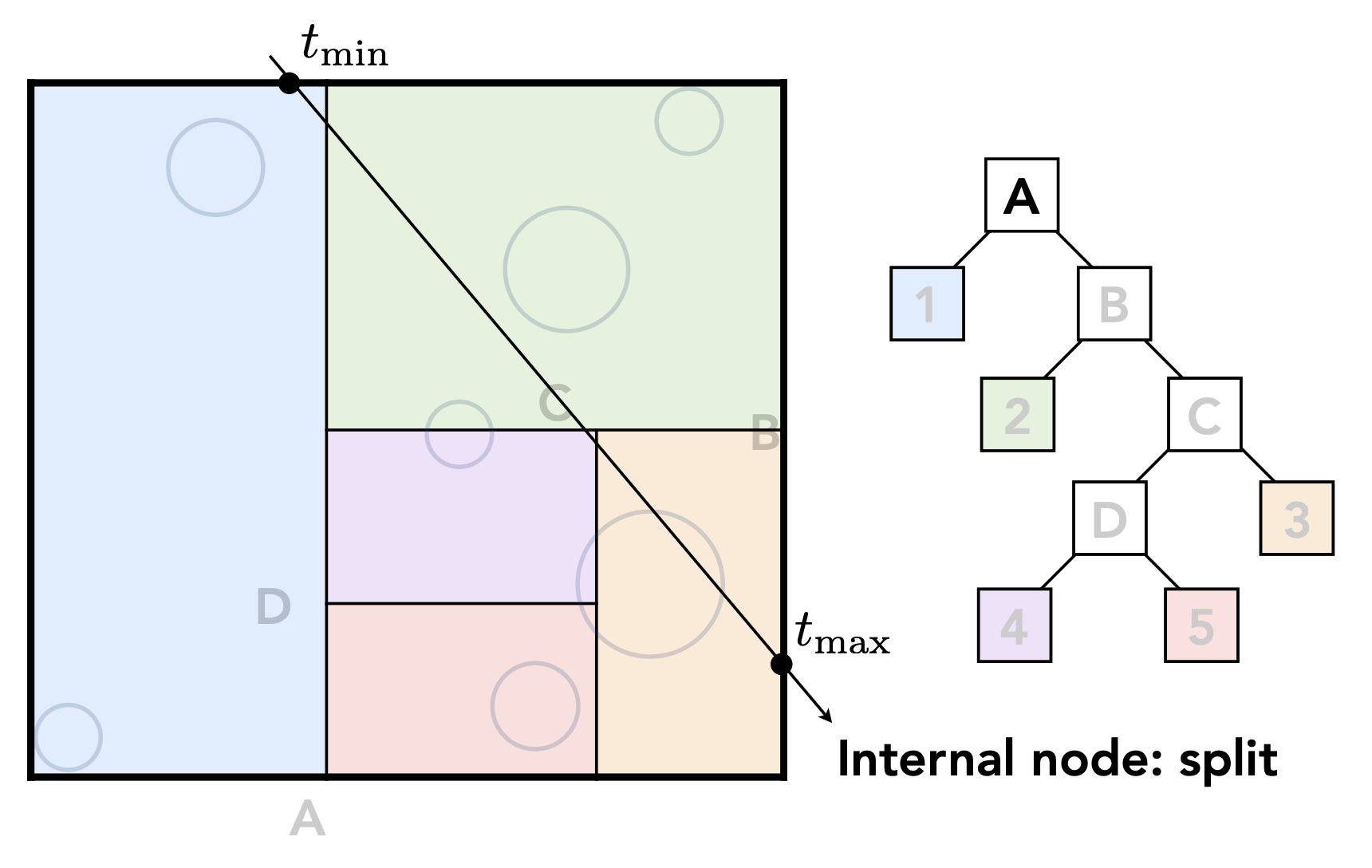
若光线和内部节点对应的区域相交,就要继续分割这块区域,对应内部节点产生两个孩子
-
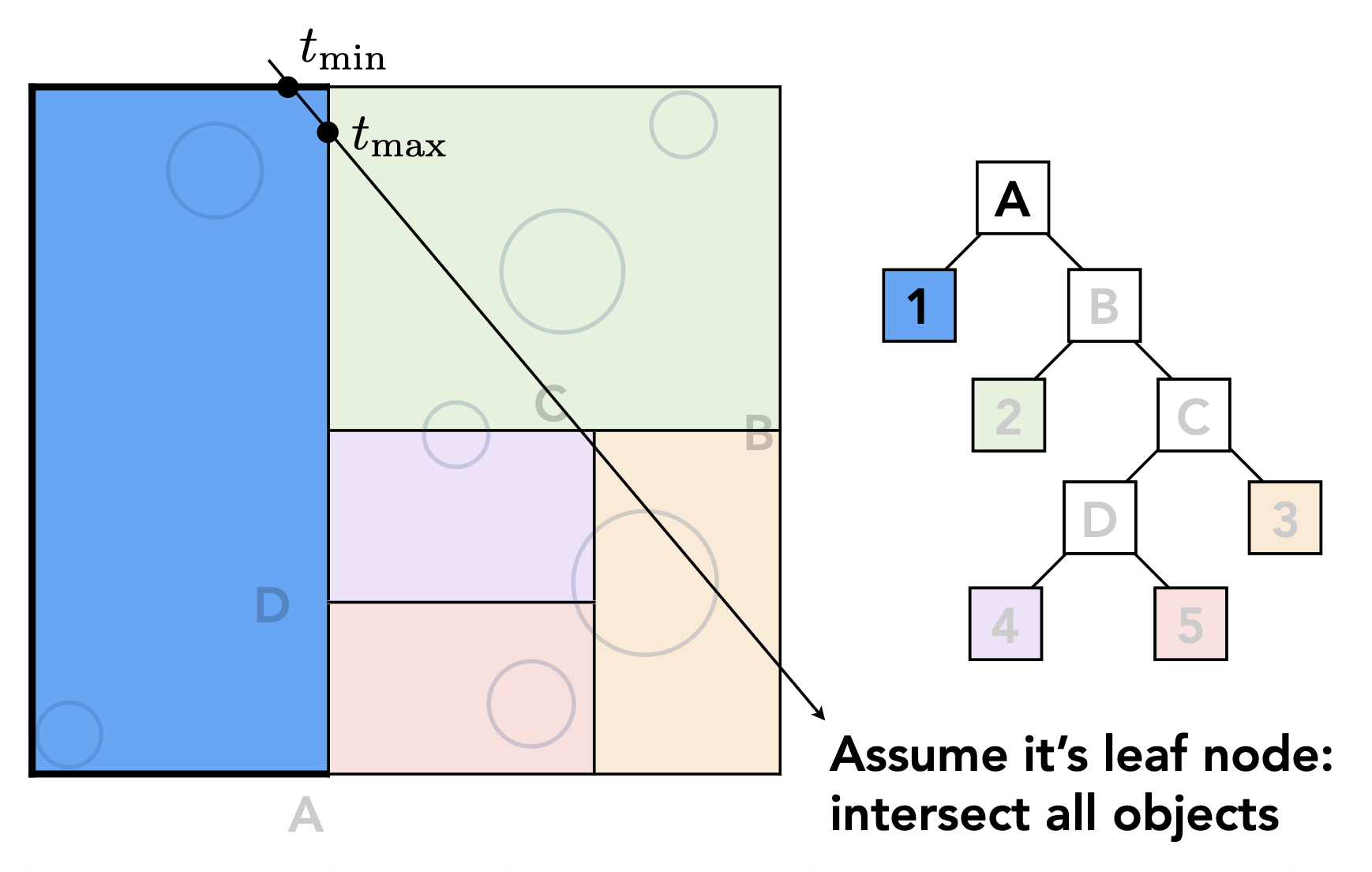
若光线和叶节点对应的区域相交,则认为这条光线和区域内的所有物体相交
-
KD 树的问题
- AABB 和三角形的交点问题,所以 KD 树的建立不简单
- 一个物体可能存在多个盒子(叶节点)中
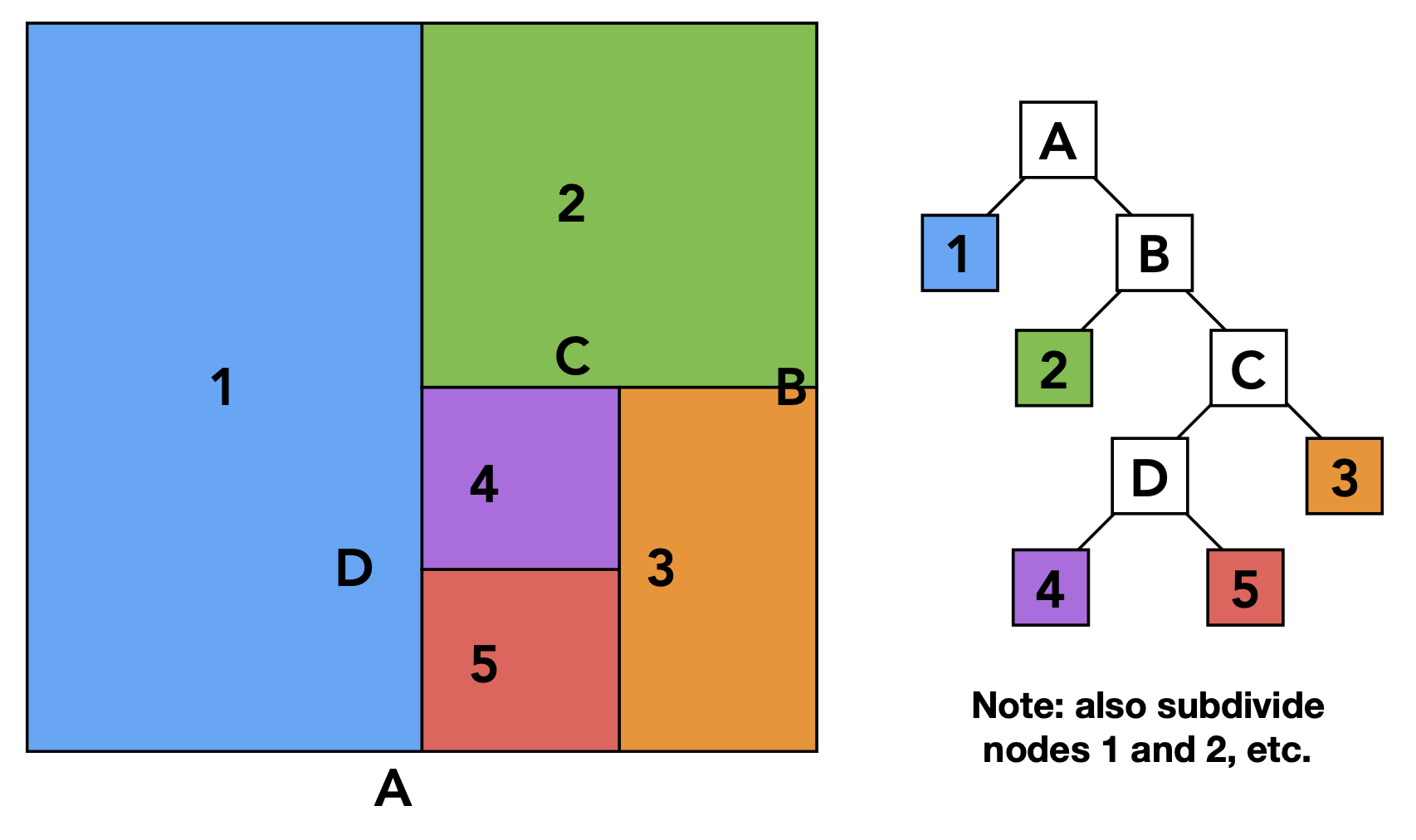
Object Partition and Bounding Volume Hierarchy (BVH)⚓︎
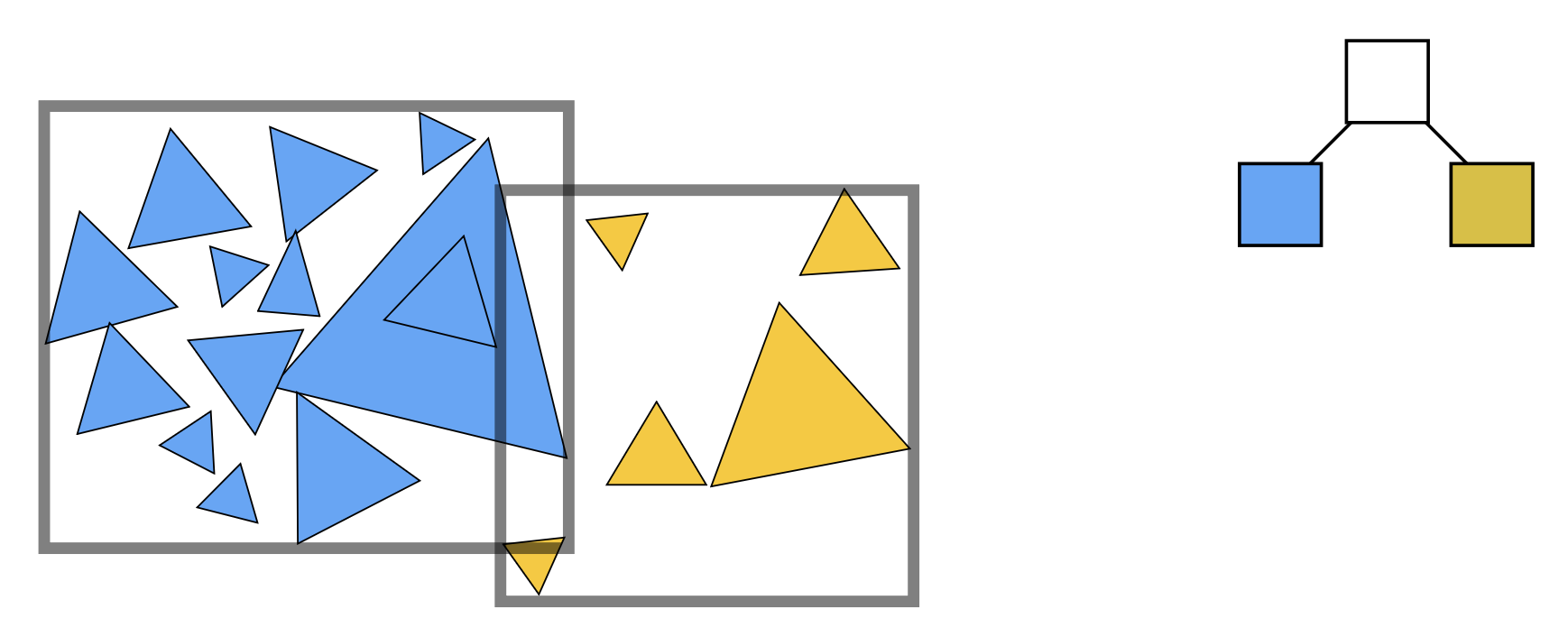
现在我们转变一下思路,不再根据空间划分,而是根据物体划分。
-
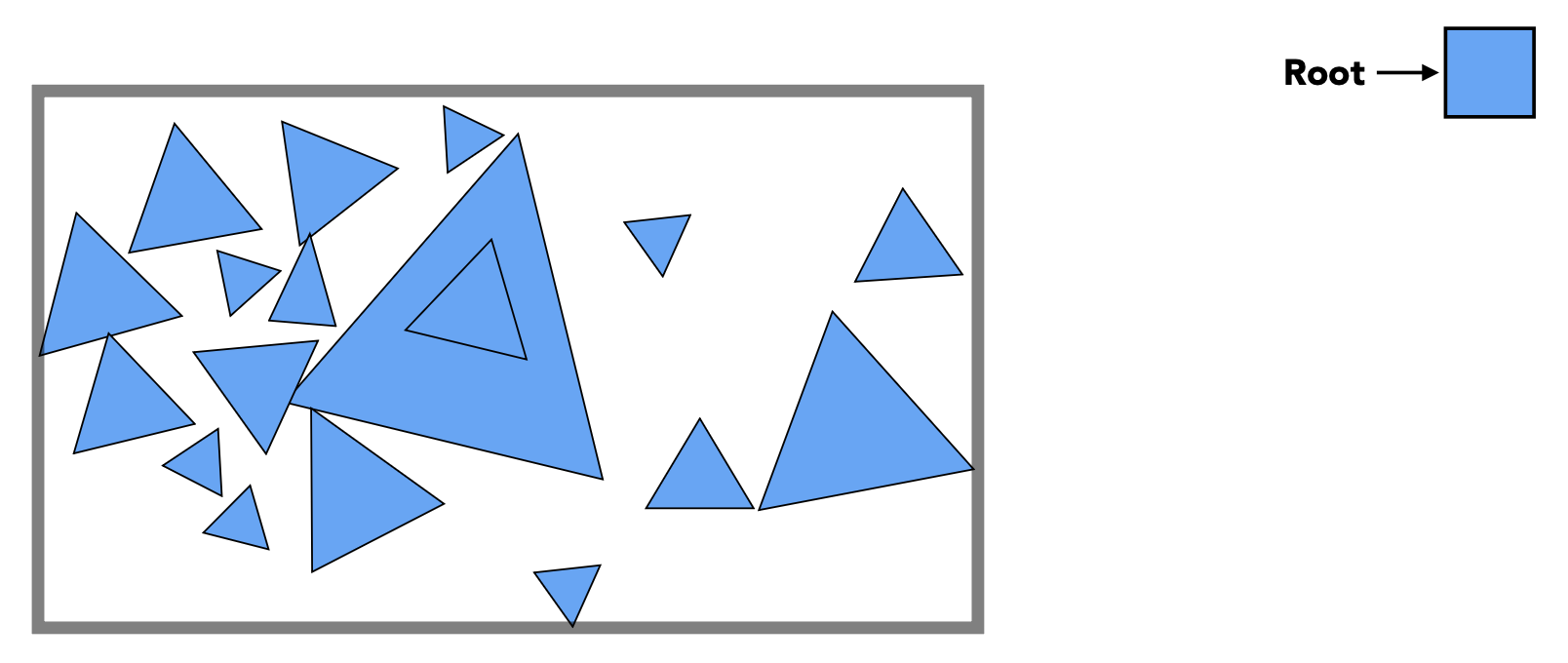
最开始的包围盒是树的根节点
-
将包围盒内的物体分为两部分(对应树上的两个孩子节点
) ,每个部分也是一个包围盒,但每个三角形仅属于一个包围盒 -
继续划分下去,对应的树很好地体现了包围体的层级(bounding volume hierarchy) 结构
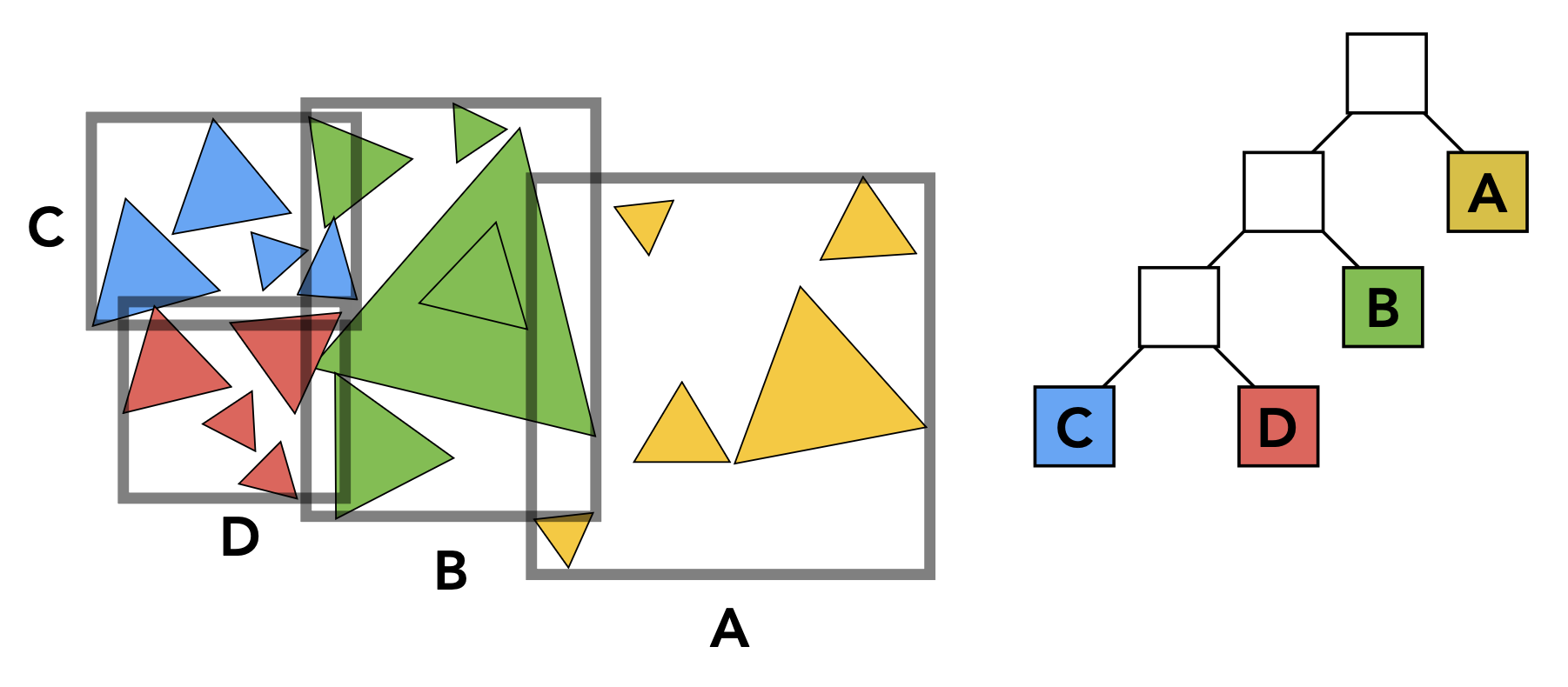
系统总结一下构建 BVH 的过程:
- 找到一个包围盒
- 递归地将包围盒内的物体集合分为两个(不相交的)子集
- 重新计算子集的包围盒
- 重复上述步骤,直到满足条件时(比如包围盒内的物体数量达到一定要求时)停止
- 将物体存储到每个叶节点内
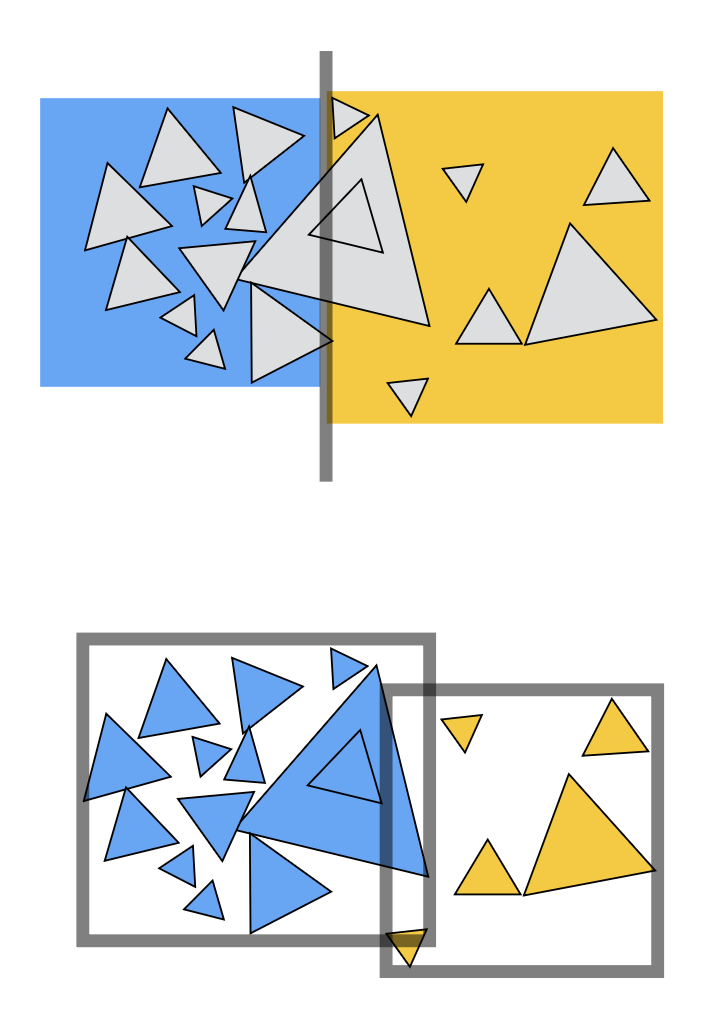
那么如何细分一个节点,即如何“将包围盒内的物体集合分为两个(不相交的)子集”呢?有以下可行的方法:
- 选择一个要分割的维度
- 启发式方法 1:总是沿节点对应区域中最长的轴分割
- 启发式方法 2:按中数(median) 物体所处位置(假如有 n 个物体,沿某个方向数量第 n/2 个物体)分割
- 这样划分后两边的三角形数量就差不多了,让对应的树更加平衡
- 扩展:从 n 个无序的数找出第 i 大的数,可以在 O(n) 时间内完成——快速选择算法(类似快排,但递归时只考虑一边)
结束标准 (termination criteria):
- 启发式:当节点包含足够少的元素时停止(比如 5 个)
BVH 的数据结构:
- 内部节点:
- 包围盒
- 孩子:指向孩子节点的指针
- 叶节点:
- 包围盒
- 一张关于物体的列表
- 节点表示的是场景中基本元素 (primitives)(
? )的子集- 所有的物体都在子树中
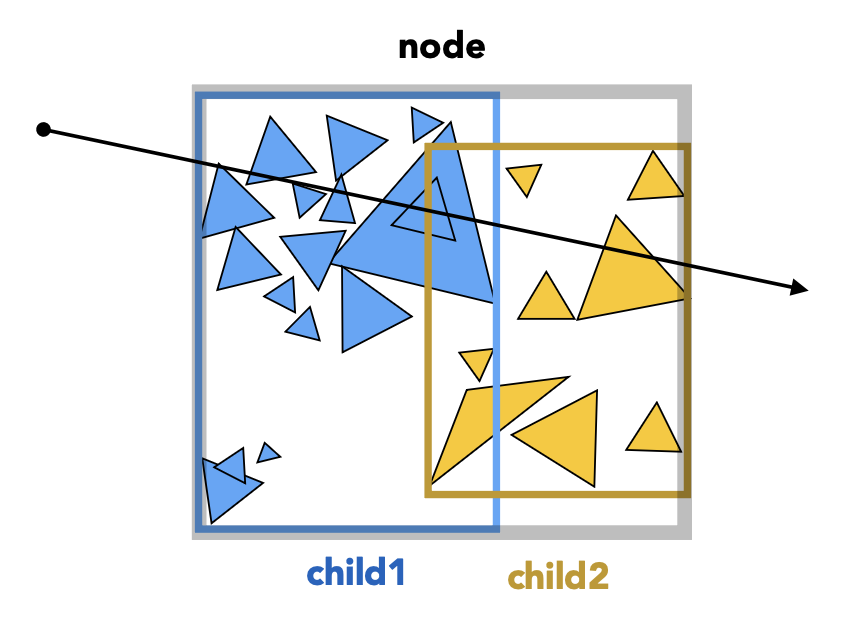
光线遍历 BVH 的算法如下:
Intersect(Ray ray, BVH node) {
if (ray misses node.bbox) return;
if (node is a leaf node)
test intersection with all objs;
return closest intersection;
hit1 = Intersect(ray, node.child1);
hit2 = Intersect(ray, node.child2);
return the closer of hit1, hit2;
}
总结:比较空间划分和物体划分
-
空间划分(代表:KD 树)
- 将空间划分为不重叠的区域
- 一个物体可能被多个区域包含
-
物体划分(代表:BVH)
- 将物体集合划分为不相交的子集
- 每个物体集合对应的包围盒在空间上会有重叠
Basic Radiometry⚓︎
动机
为什么要介绍辐射度量学(radiometry)?因为有以下观察:
- 在作业中,我们实现了 Blinn-Phong 着色模型,其中光照强度设为 10。但这个 "10" 是什么意思,由于没有任何具体的单位,我们无从得知,也很难将它和现实世界对应起来
- 利用 Whitted 风格光线追踪技术得出的渲染结果看起来还不够真实(右图)
上述问题将由辐射度量学来解答。
- 它同时也是“路径追踪 (path tracing)”技术的基础
关于辐射度量学:
- 一种光照的测量系统和单位
- 能够准确测量光的空间性质(不考虑时间维度)
- 相关术语:辐射通量(radiant flux)、辐射强度(radiant intensity)、辐照度(irradiance)、辐射率(radiance)
- 以物理上正确的方式执行光照计算
Radiant Energy and Flux (Power)⚓︎
定义
- 辐射能(radiant energy):电磁辐射的能量,以焦耳 (Joule, J) 为单位进行测量,用符号 \(Q\) 表示
-
辐射通量(功率)(radiant flux(power)):单位时间内发出的、反射的、传输的或接收的能量 $$ \Phi = \dfrac{dQ}{dt} $$
单位为瓦特 (Watt, W) 或流明(lumen, lm)
-
通量 (flux):单位时间内通过传感器的光子 (photons) 数量
-
一些重要的光测量关注点:
- 从光源辐射的光 -> 辐射强度
- 光落在表面上 -> 辐照度
- 光沿着直线传播 -> 辐射率
Radiant Intensity⚓︎
定义
辐射(发光)强度(radiant(luminous) intensity) 是点光源每单位立体角(solid angle) 所发出的功率。计算公式为: $$ I(\omega) = \dfrac{d \Phi}{d \omega} $$
单位为:\(\dfrac{\text{W}}{\text{sr}} \text{ or } \dfrac{\text{lm}}{\text{sr}} = \text{cd}\)(坎德拉 (candela)
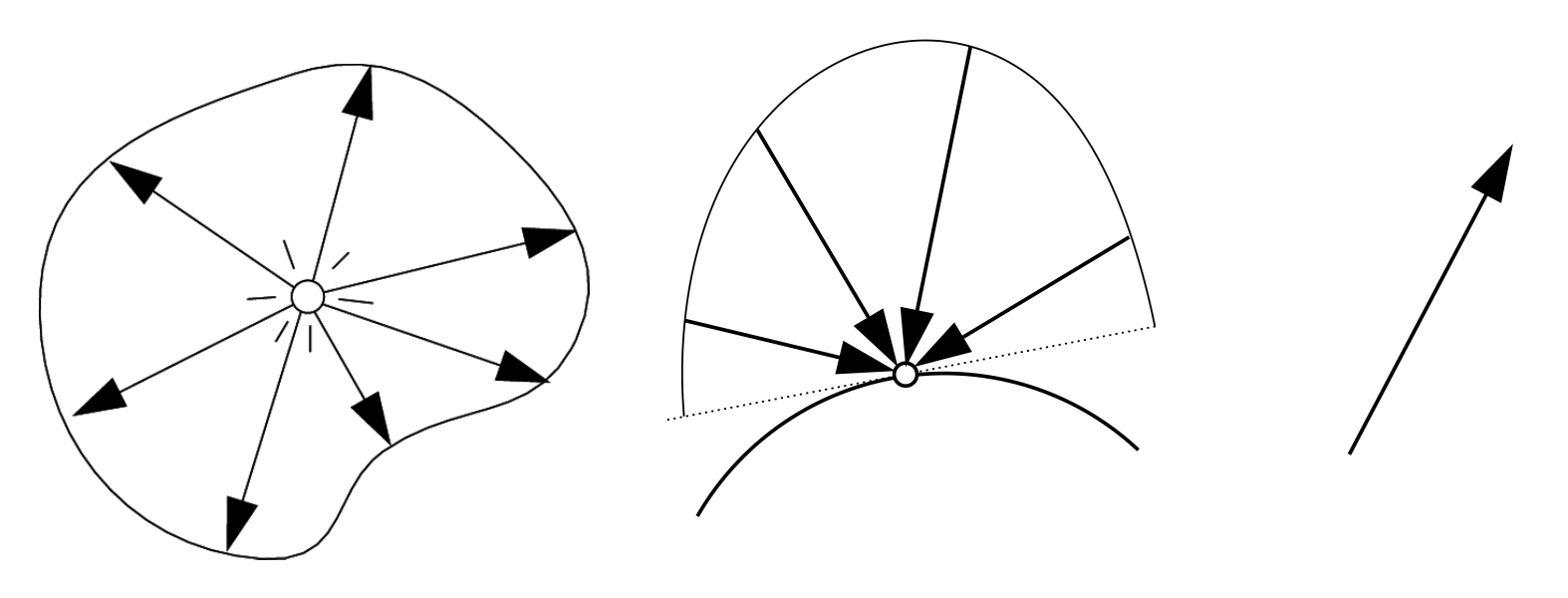
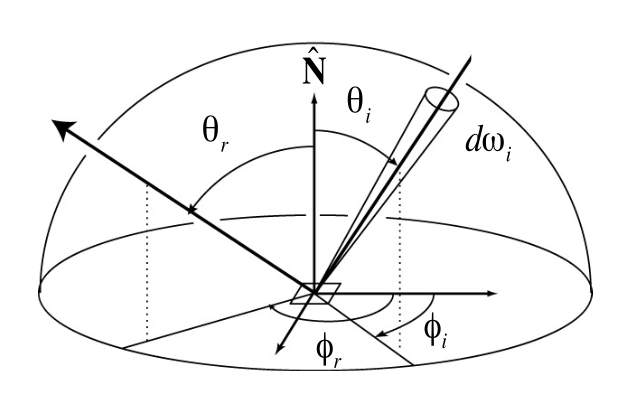
现在来解释一下立体角的概念。比对一般的角和立体角:
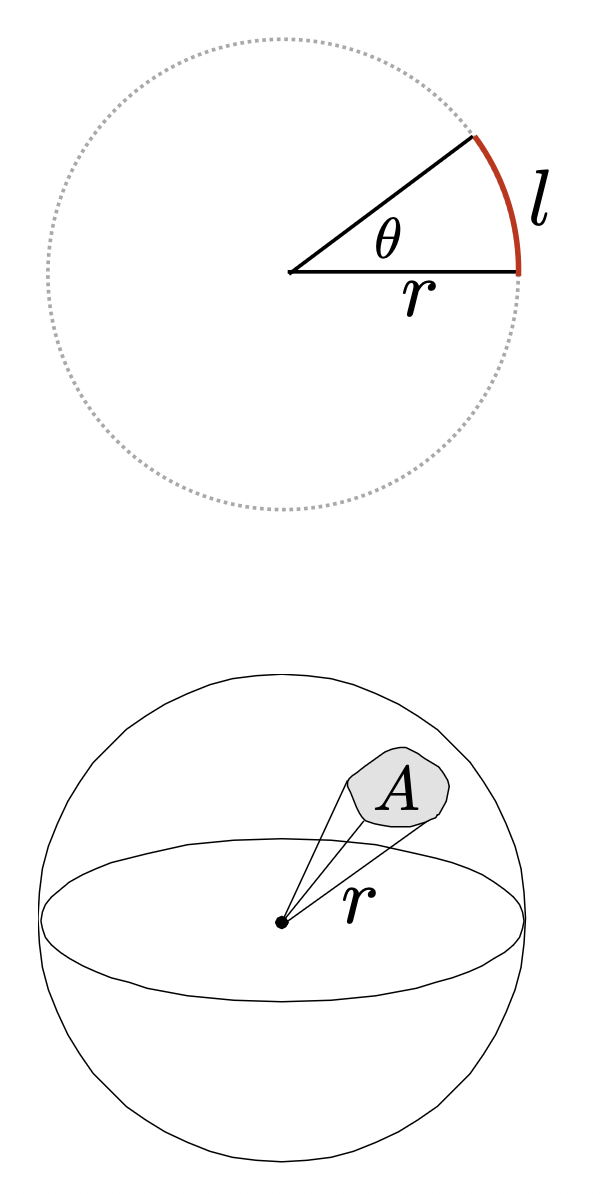
- 角:圆上弧长与半径之比
- \(\theta = \dfrac{l}{r}\)
- 圆的弧度(radian) 为 \(2 \pi\)
- 立体角:球上截面积与半径平方之比
- \(\Omega = \dfrac{A}{r^2}\)
- 球的立体弧度(steradian) 为 \(4 \pi\)
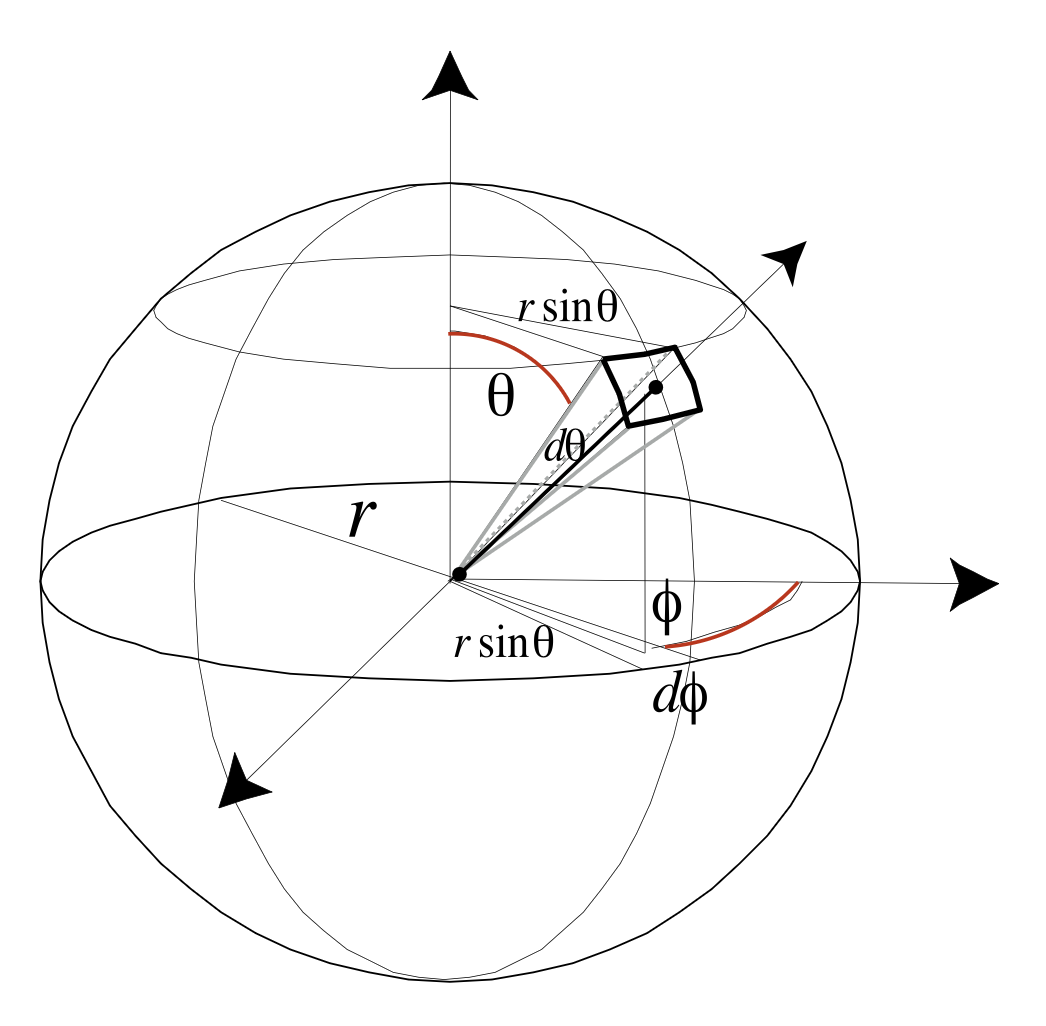
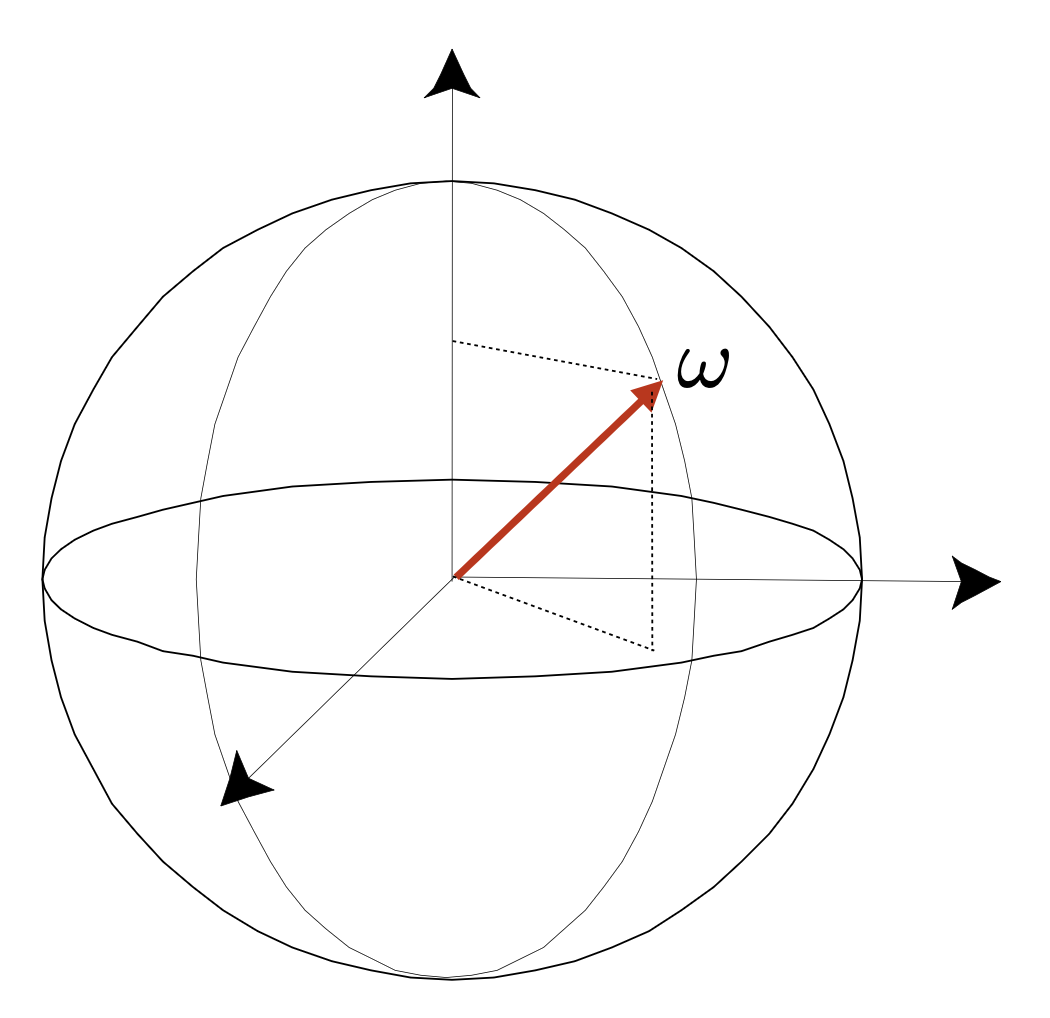
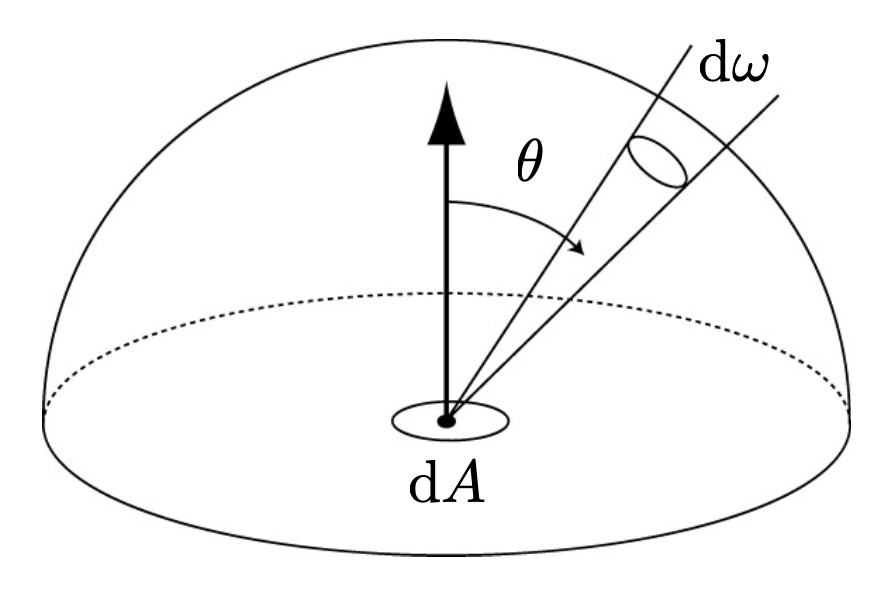
微分立体角(其中 \(\theta\) 是和向上方向的夹角,而 \(\varphi\) 是绕向上方向旋转的角度,微分立体角就是将这两个角施以很小的变化后形成的立体角
可以看到,微分立体角的变化不仅依赖于 \(d \theta, d \varphi\),还受 \(\theta\) 角的影响,所以即便变化的角度数值一样,\(\theta\) 朝赤道变化和朝极点变化带来的影响是不同的。
已知球的表面积为 \(S\),那么整个球的立体角为:
以后就用 \(\omega\) 表示方向向量(direction vector)(单位长度
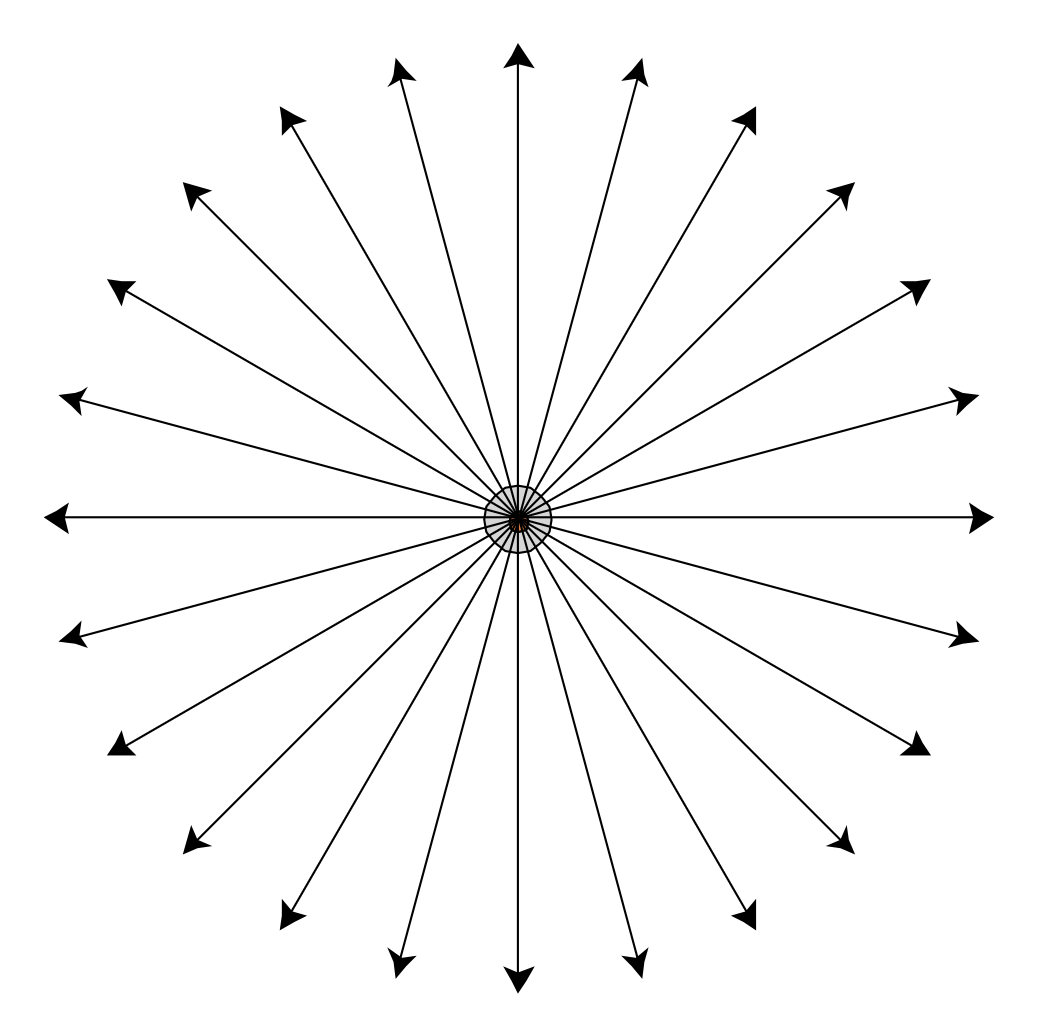
因此对于各同向性光源,辐射通量和辐射强度分别为:
例子:现代 LED 灯
- 如图所示,这个 LED 灯的辐射通量为 815 流明,即 11 W。按包装纸上的说明,它就相当于一盏 60 W 的白炽灯。
- 辐射强度 = 815 流明 / 4π 立体弧度 = 65 坎德拉
Irradiance⚓︎
定义
辐照度(irradiance) 是指单位面积上照射到表面点的功率。计算公式为: $$ E(\mathbf{x}) = \dfrac{d \Phi (\mathbf{x})}{dA} $$
单位:\(\dfrac{\text{W}}{\text{m}^2} \text{ or } \dfrac{\text{lm}}{\text{m}^2} = \text{lux}\)
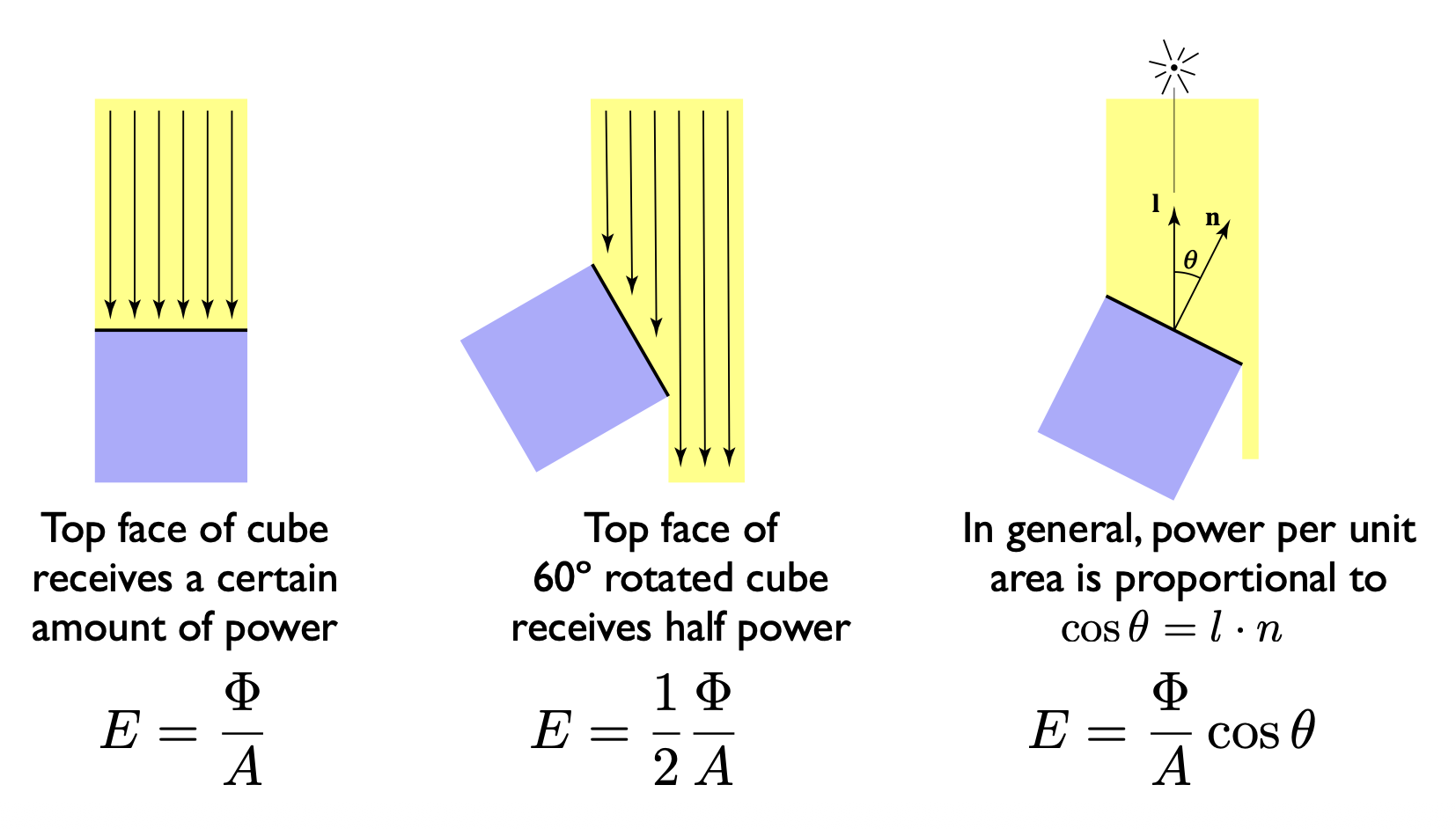
辐照度和在“着色”一讲介绍的朗伯余弦定律有着密切联系:曲面上的辐照度正比于光的方向和曲面发现的夹角的余弦值,即 $$ E = \dfrac{\Phi}{A} \cos \theta $$
注:仅考虑单位面积。
地球一年四季的变化正是因为地球的转轴是倾斜的(23.5° 左右
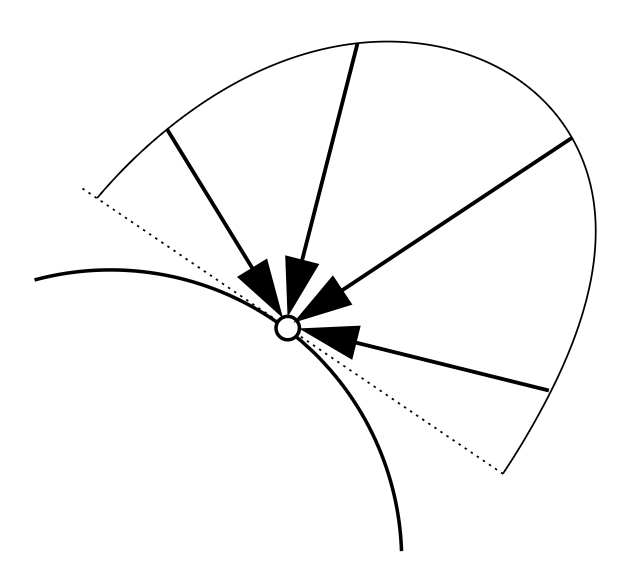
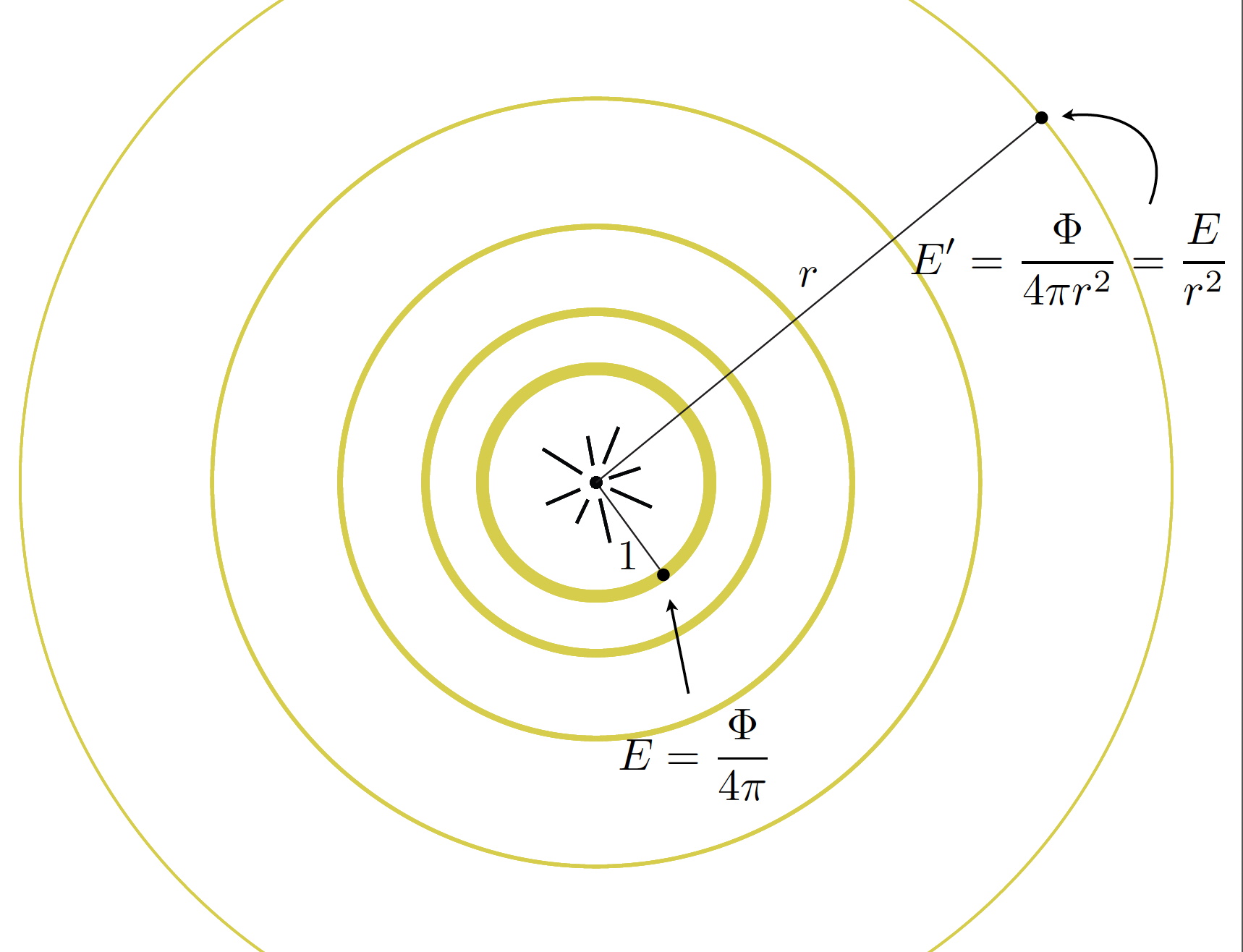
另外,辐照度会随离光源距离的增加而衰减 (falloff)。具体来说,假设光源的以均匀角度分布发射功率为 \(\Phi\) 的光,比较两个以光源为球心的球面上两处辐照度:
- 半径为 1 时,\(E = \dfrac{\Phi}{4\pi}\)
- 半径为 \(r\) 时,\(E' = \dfrac{\Phi}{4\pi r^2} = \dfrac{E}{r^2}\)
Radiance⚓︎
辐射率是描述环境中光分布的基本场量。
- 辐射度是与光线相关的量
- 渲染就是在计算辐射度
定义
辐射率(radiance)(亮度 (luminance))是指单位立体角内,单位投影面积上(很小的方向 + 很小的面)表面发射、反射、传输或接收的功率。计算公式为: $$ L(p, \omega) \equiv \dfrac{d^2 \Phi(p, \omega)}{d \omega d A \cos \theta} $$
单位:\(\dfrac{\text{W}}{\text{sr m}^2} \text{ or } \dfrac{\text{cd}}{\text{m}^2} = \dfrac{\text{lm}}{\text{sr m}^2} = \text{nit}\)
回忆一下:
- 辐照度:每单位投影面积的功率
- 辐射强度:每立体角的功率
所以辐射率既可以看成每立体角的辐照度,又可以当做每单位投影面积的辐射强度。
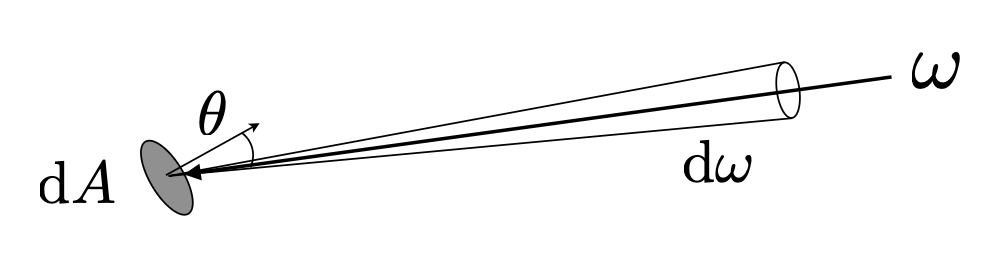
- 入射辐射率(incident radiance):每单位立体角下到达表面的辐照度(即沿着给定光线(表面上的点和入射方向)到达表面的光) $$ L(\text{p}, \omega) = \dfrac{d E(\text{p})}{d \omega \cos \theta} $$
-
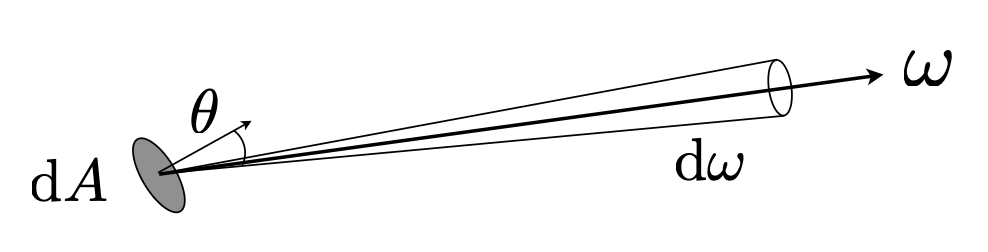
出射辐射率(exiting radiance):每单位投影面积下离开表面的辐射强度 $$ L(\text{p}, \omega) = \dfrac{d I(\text{p}, \omega)}{d A \cos \theta} $$
- 比如对于面光源,它就是沿给定光线发出的光
辐照度 vs. 辐射率
- 辐照度:面积 \(d A\) 接收的辐射功率
- 辐射率:沿 \(d \omega\) 方向面积 \(d A\) 接收的辐射功率
所以:
其中 \(H^2\) 表示单位半球 (hemisphere)
Light Transport⚓︎
The Reflection Equation⚓︎
关于在点上的反射
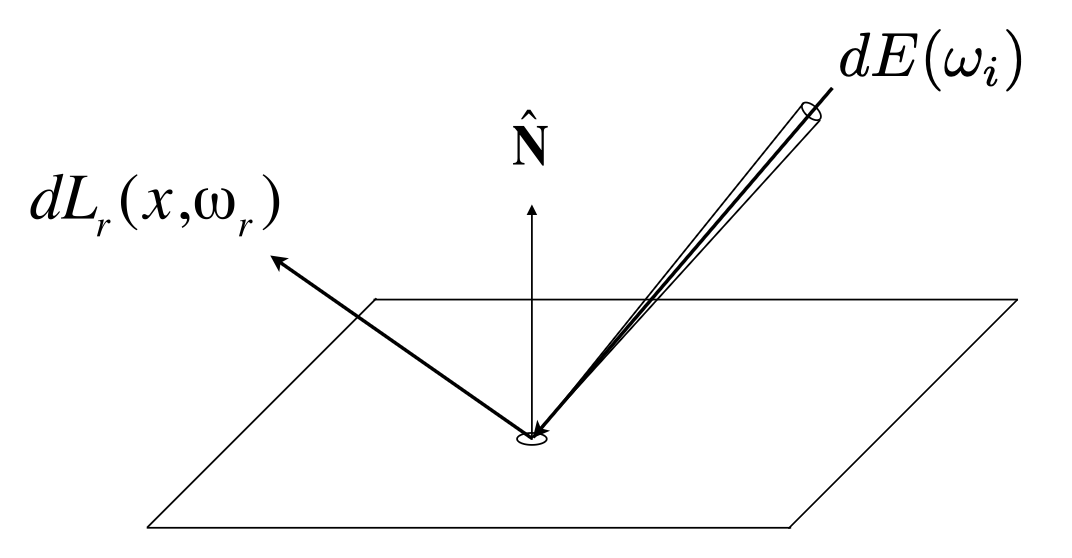
- 来自方向 \(\omega_i\) 的辐射转化为面积 \(dA\) 收到的辐射功率 \(E\)
- 然后功率 \(E\) 将成为任何其他方向 \(\omega_o\) 的辐射
- 微分辐照度入射:\(dE(\omega_i) = L(\omega_i) \cos \theta_i d \omega_i\)
- 微分辐射率出射(来自 \(dE(\omega_i)\)
) :\(L_r(\omega_r)\)
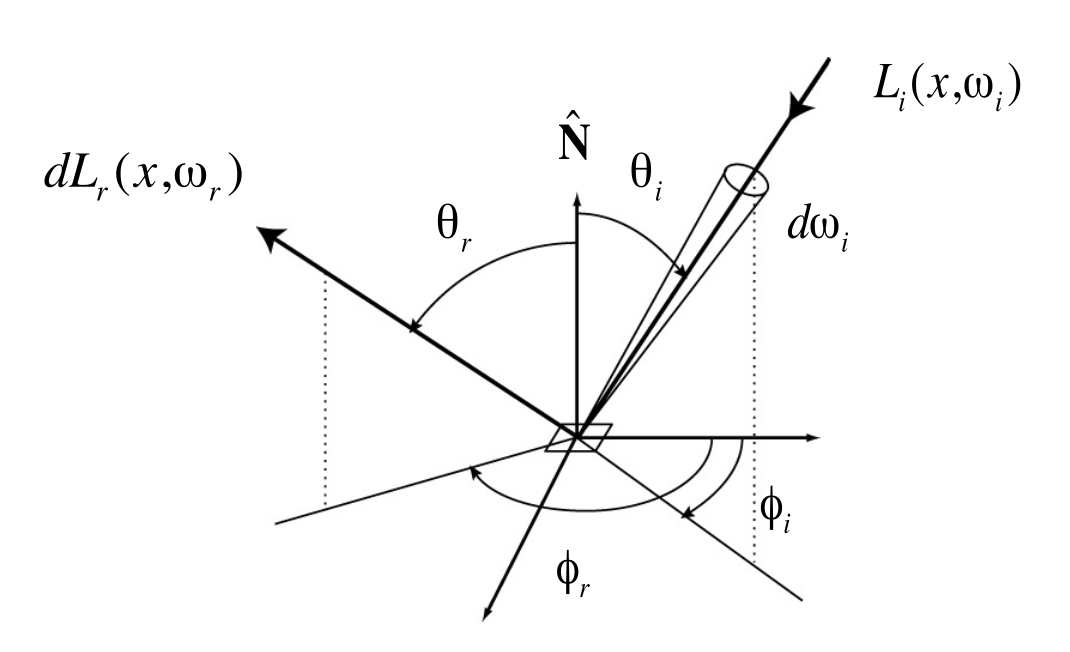
双向反射分布函数(bidirectional reflectance distribution function, BRDF) 表示的是有多少光从各个入射方向被反射到出射方向 \(\omega_r\),式子为: $$ f_r(\omega_i \rightarrow \omega_r) = \dfrac{d L_r(\omega_r)}{d E_i(\omega_i)} = \dfrac{d L_r(\omega_r)}{L(\omega_i) \cos \theta_i d \omega_i} $$
单位:\(\dfrac{1}{\text{sr}}\)
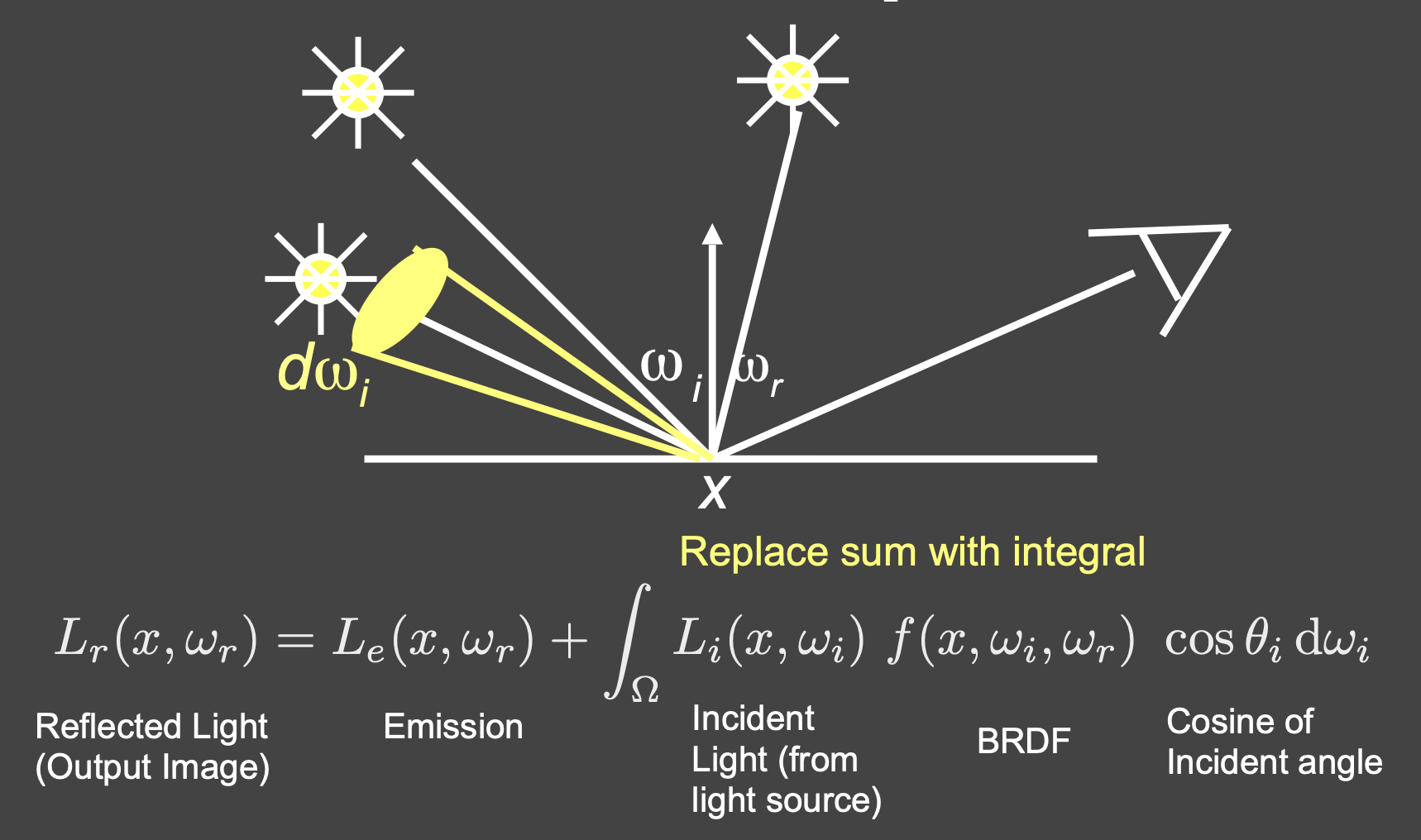
有了 BRDF 后,我们就能得出以下反射方程(reflection equation): $$ L_r(p, \omega_r) = \int_{H^2} f_r(p, \omega_i \rightarrow \omega_r) L_i(\text{p}, \omega_i) \cos \theta_i d \omega_i $$ 这个方程的大致意思是计算半球上所有入射光线对某一方向 \(\omega_r\) 的出射光的总贡献。
反射方程的一个挑战是存在递归现象:入射光也有可能是来自场景中其他点上的出射光,那么也需要用反射公式计算,这样计算量就很大了。
The Rendering Equation⚓︎
冷知识:提出 "Rendering Equation" 的论文标题就是 "Rendering Equation"。
在反射方程的基础上再加一项,代表反射点自己发出的光(考虑更一般的情况
注:假设光线朝向均向外。
至于具体怎么计算就放到后面再介绍,目前的重点放在理解渲染方程是如何推导出来的。
Understanding the Rendering Equation⚓︎
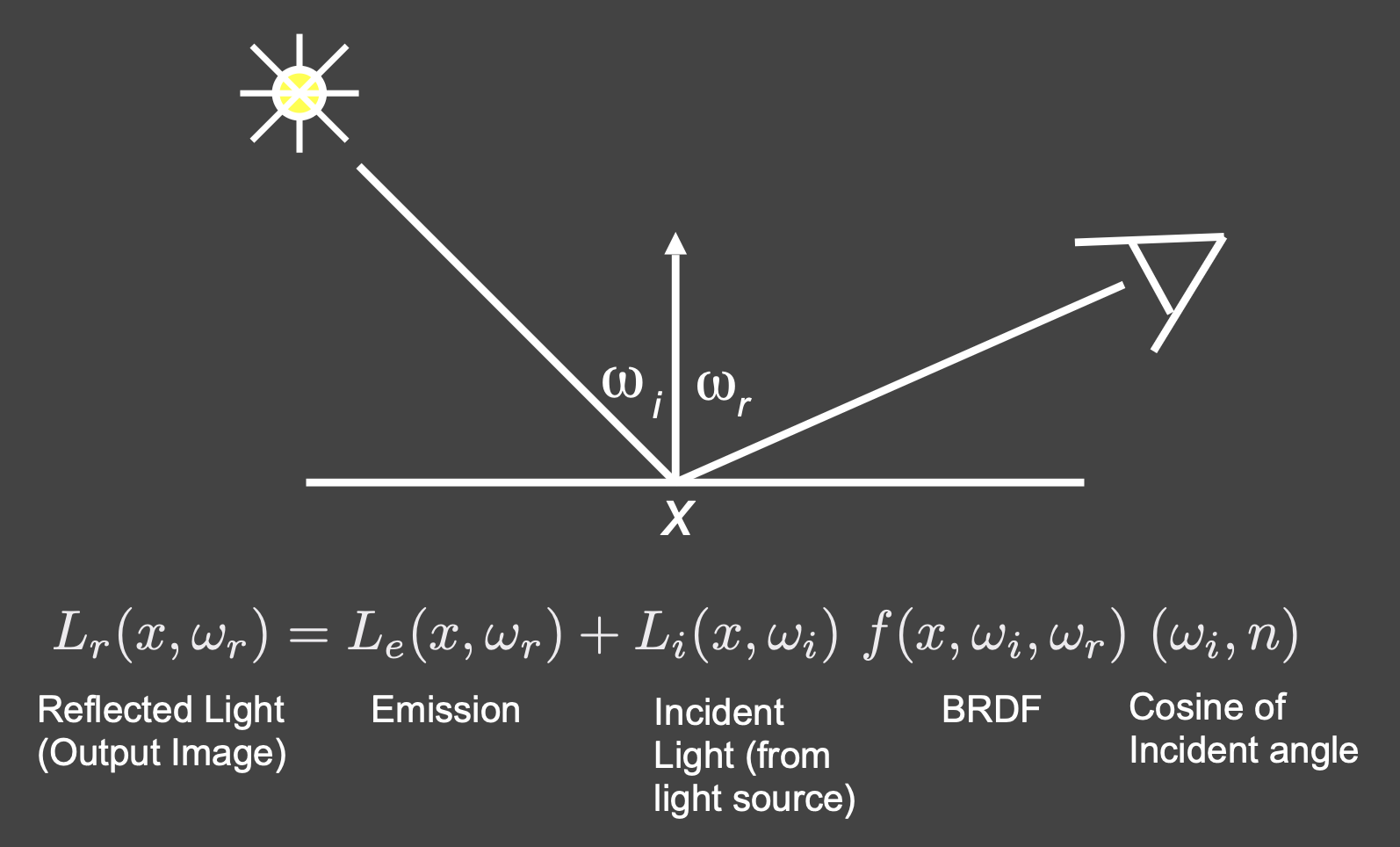
-
只有一个点光源
-
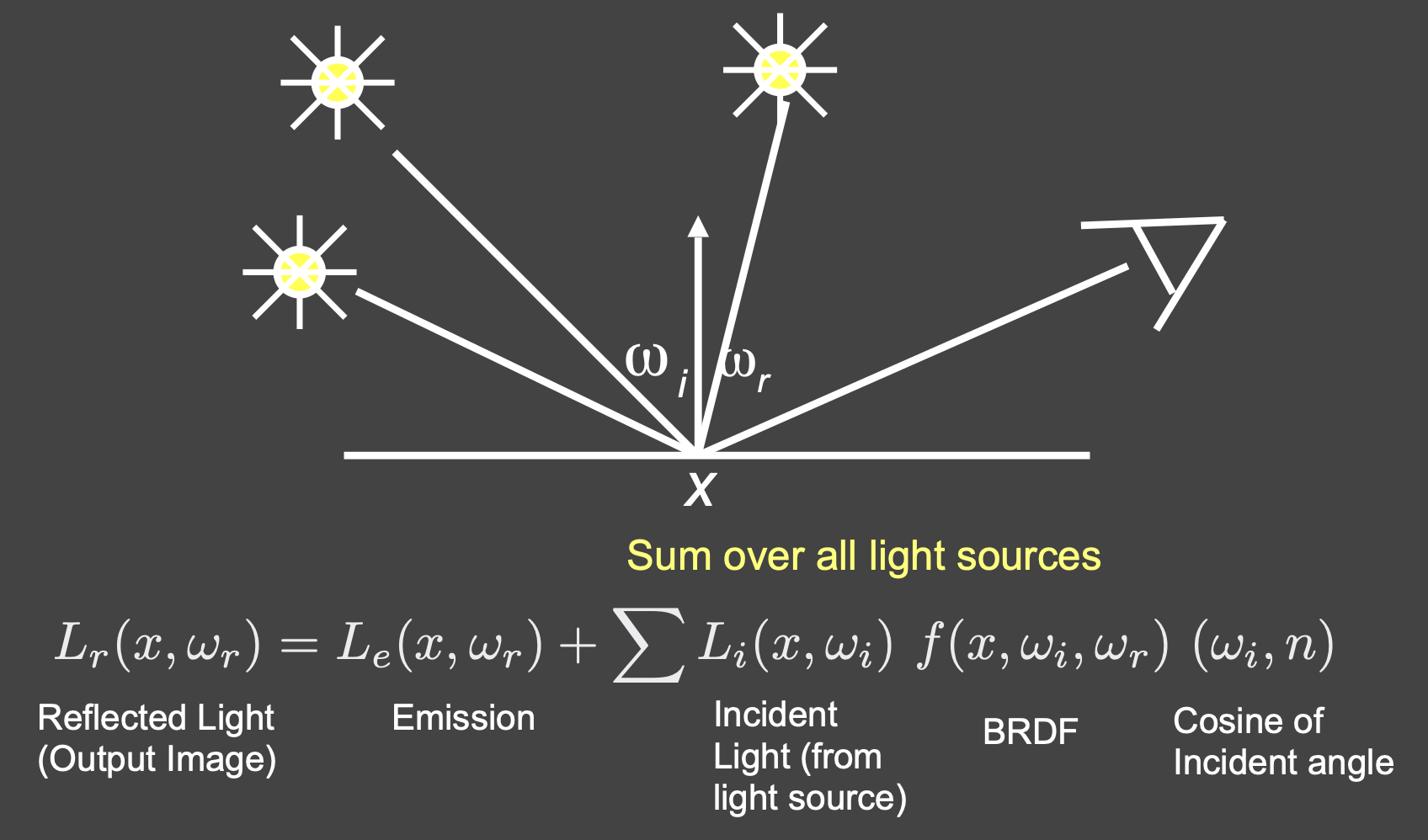
有多个点光源(累加即可)
-
引入面光源(可看成多个连续的点光源,因此求和 -> 积分)
-
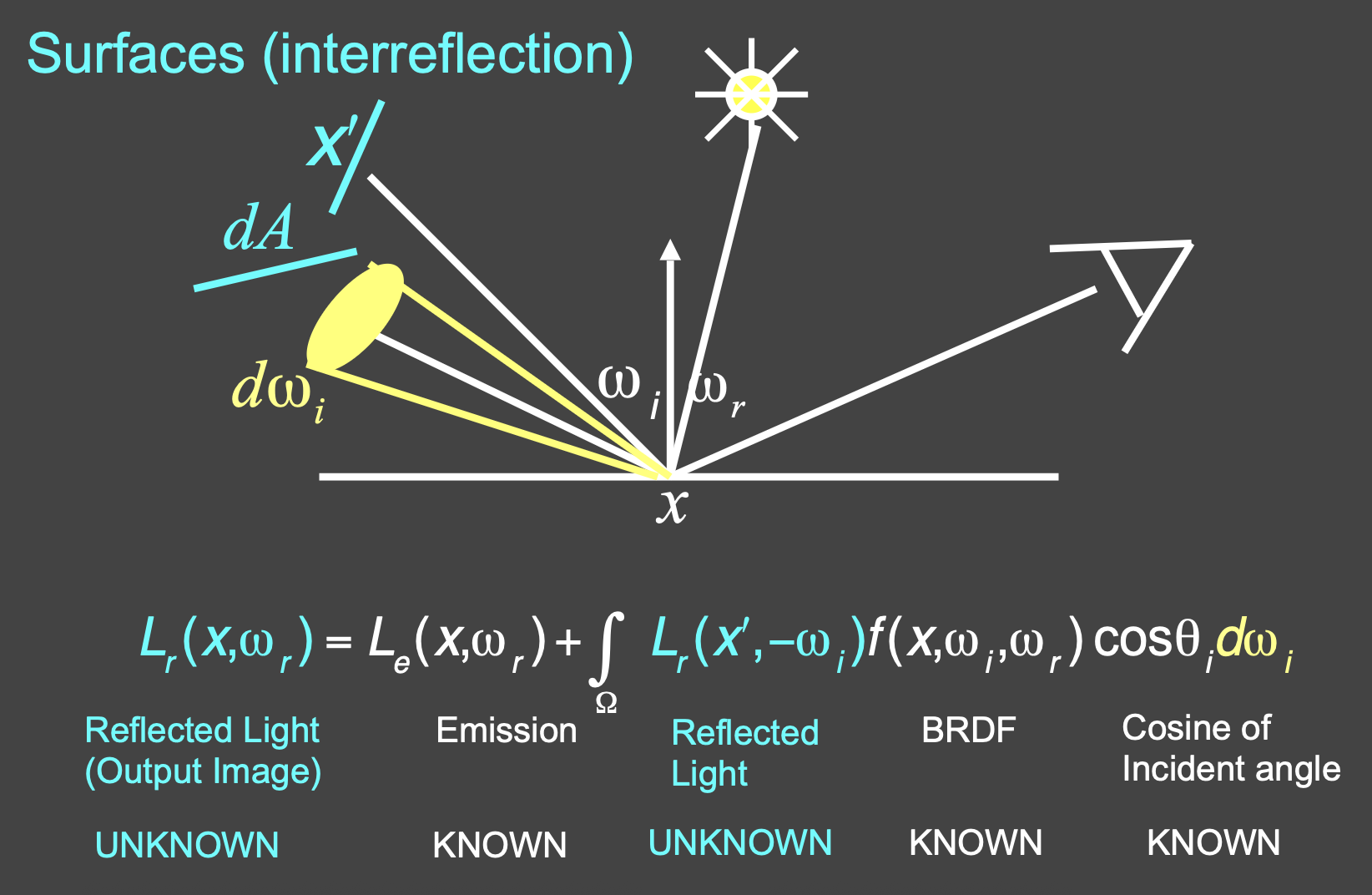
如果入射光来自其他地方的反射光
- 此时入射光的辐射率是未知的,因而无法求出反射光的辐射率
将上述方程简写为: $$ \textcolor{aqua}{l(u)} = e(u) + \int \textcolor{aqua}{I(v)} + \underbrace{K(u, v) \textcolor{yellow}{dv}}_{\text{Kernel of equation}} $$
其中 \(K(u, v) dv\) 是方程的核(kernel),也叫做光传输算子(light transport operator)。
将其离散化为简单的矩阵形式(或者联立线性方程组
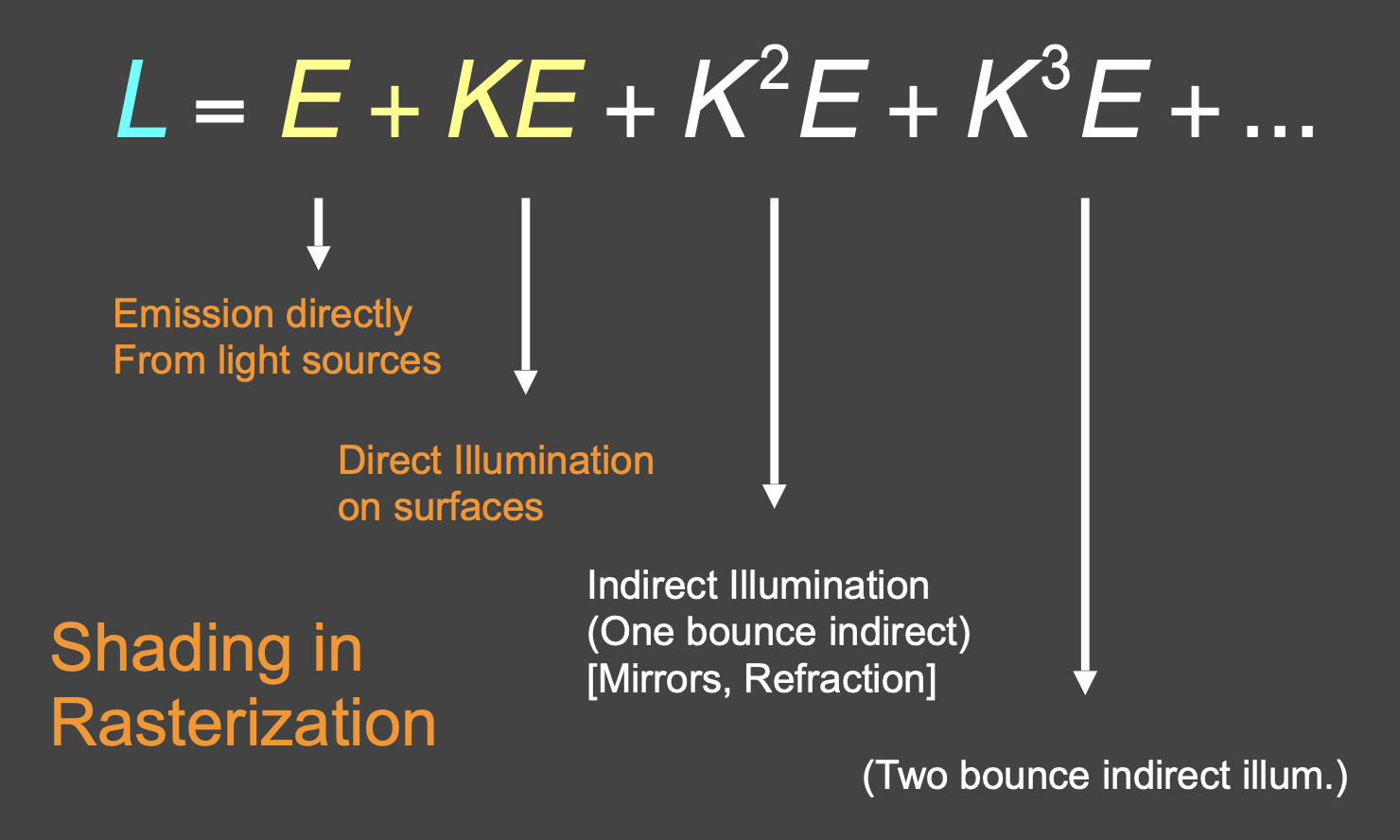
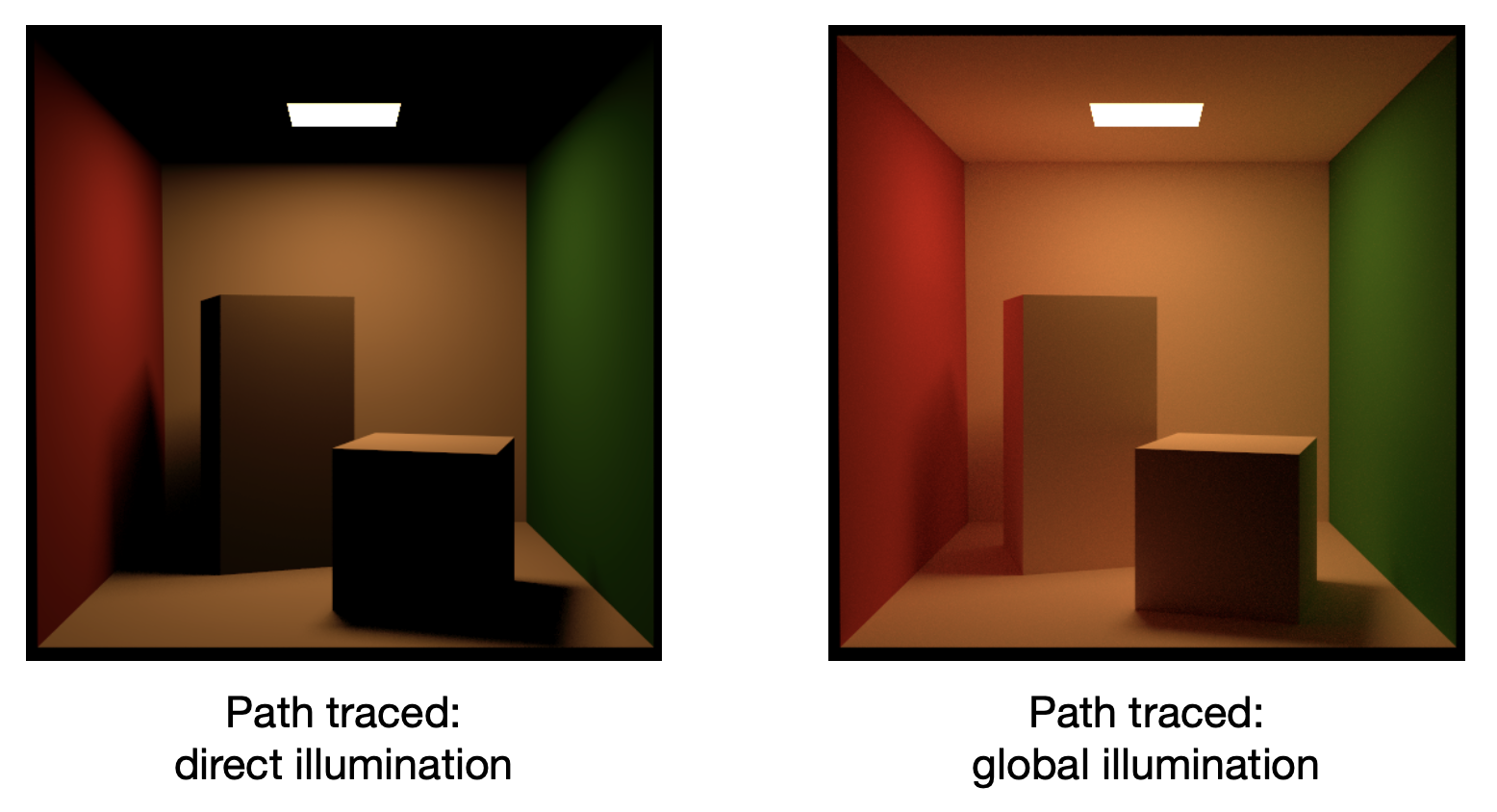
现在这个方程能够近似表示场景中所有光线路径的贡献了。下面列出了等号右边前几项各项的含义:
- 其中前两项是可以在光栅化中实现的
- 除第一项外的项都属于全局光照
例子
Probability Review⚓︎
看起来只需掌握最基本的概率论知识即可,所以懒得记了,就直接把课件内容拷贝下来了。
Morte Carlo Integration⚓︎
引入
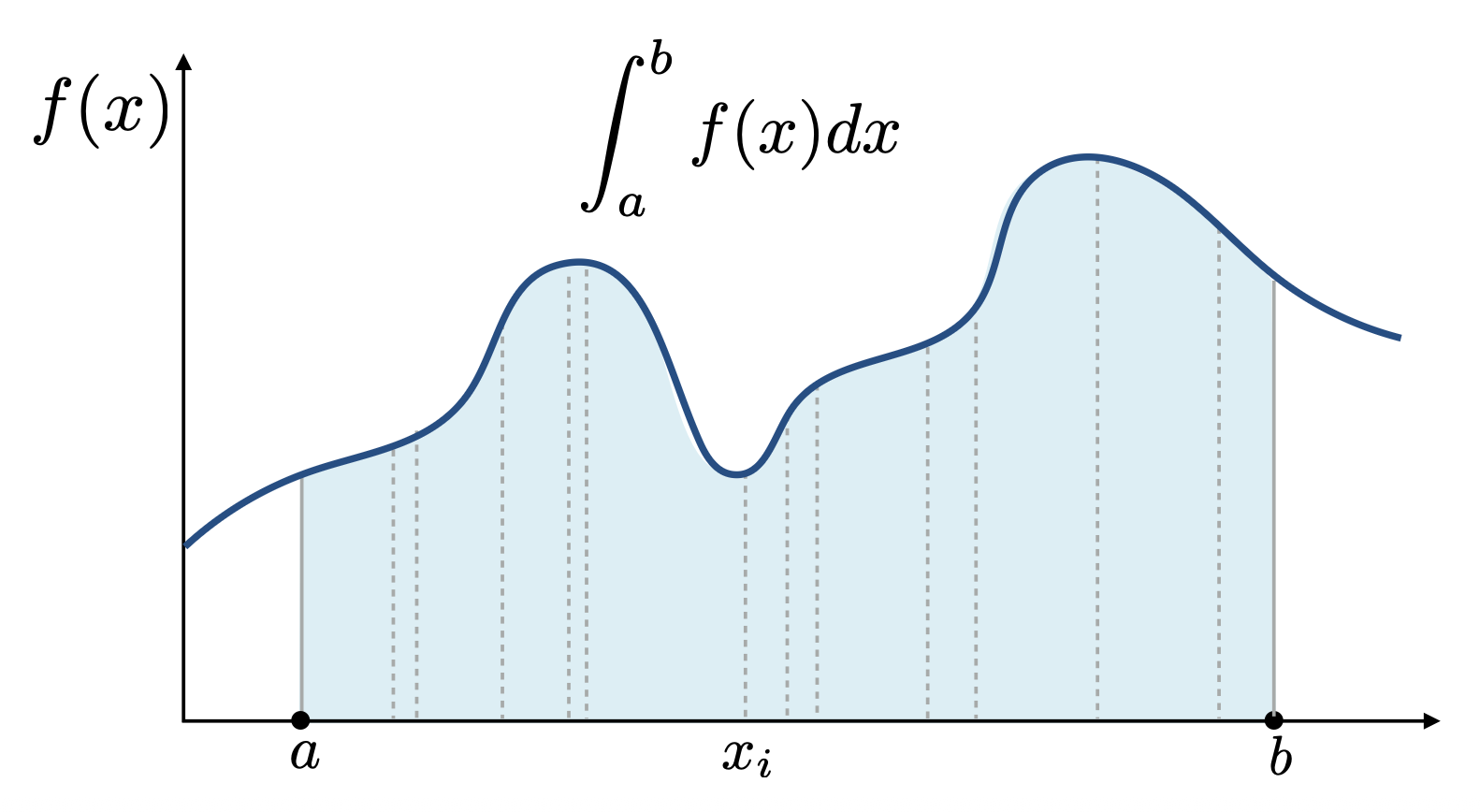
我们求一个定积分时,往往会先计算它的不定积分,再把两个边界值带进去计算后相减,得到的值就是定积分的结果。但有时被积的函数过于复杂,我们可能很难直接求出它对应的不定积分。这就是蒙特卡洛积分法要解决的问题。
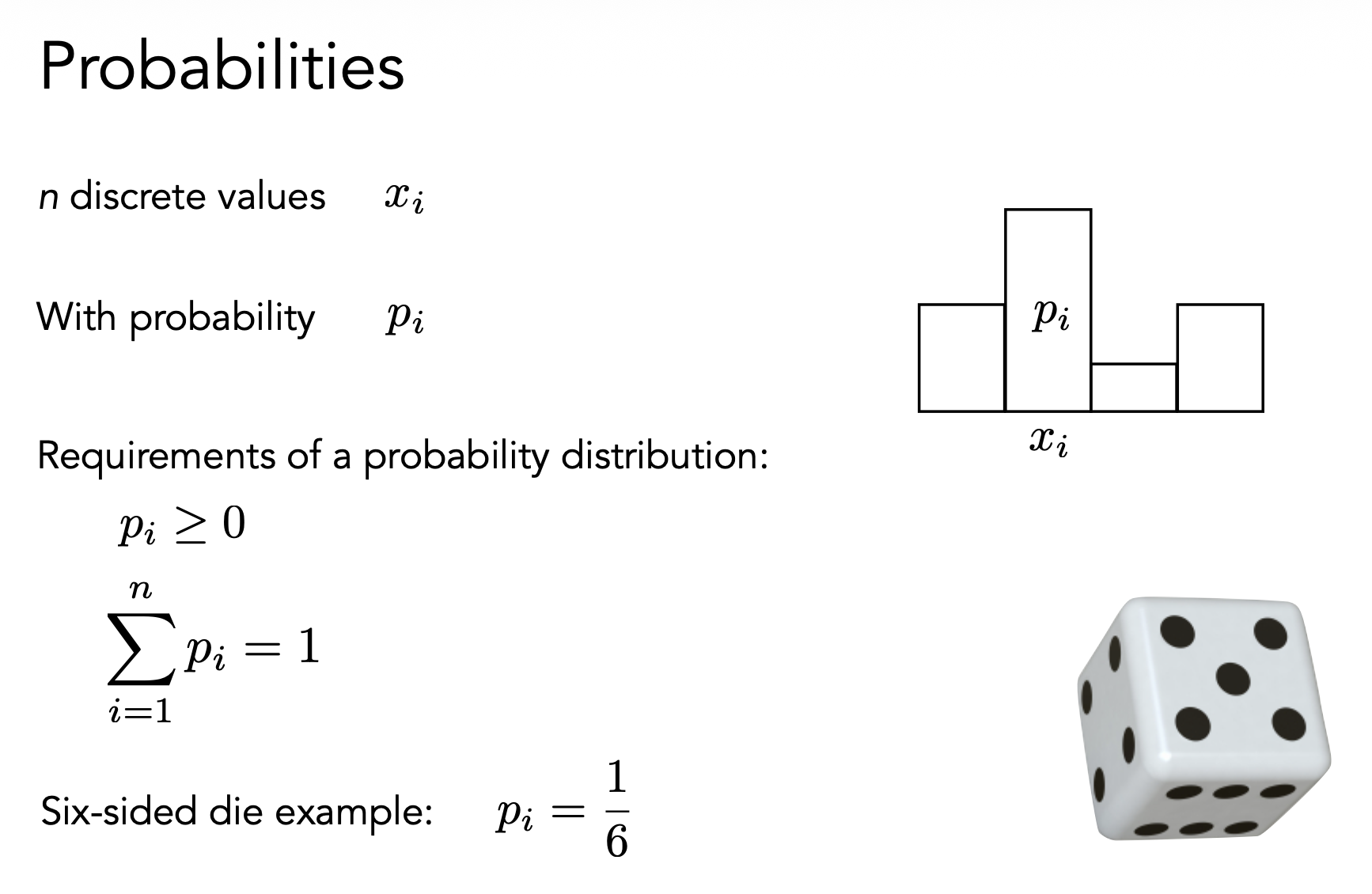
蒙特卡洛积分法(Morte Carlo integration) 将多轮随机采样得到的函数值的平均值作为该函数的积分结果。下面我们为函数 \(f(x)\) 定义一个蒙特卡洛估计器(estimator):
- 定积分:\(\int_a^b f(x) dx\)
- 随机变量:\(X \sim p(x)\)
- 蒙特卡洛估计器:\(F_N = \dfrac{1}{N} \sum_{i=1}^N \dfrac{f(X_i)}{p(X_i)}\)
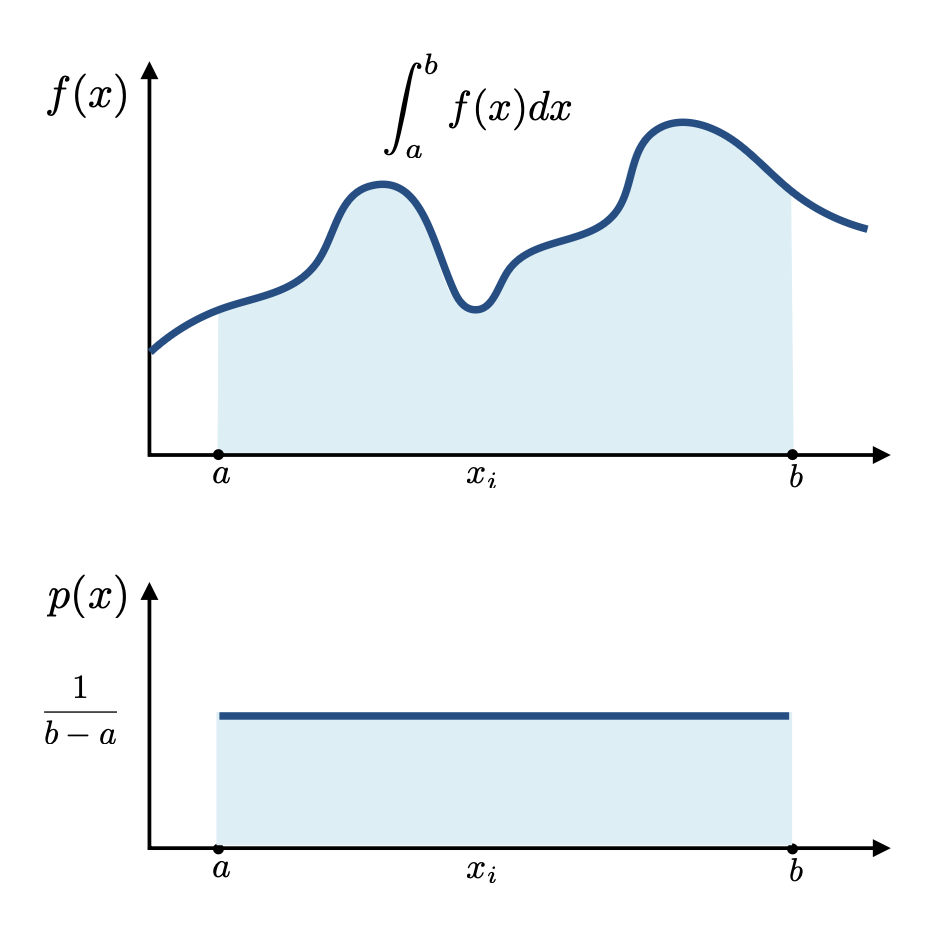
例子:均匀蒙特卡洛估计器
均匀随机变量
- 定积分:\(\int_a^b f(x) dx\)
- 均匀随机变量:\(X \sim p(x) = \dfrac{1}{b - a}\)
- 蒙特卡洛估计器:\(F_N = \dfrac{b - a}{N} \sum_{i=1}^N f(X_i)\)
注
- 采样越多,方差越小
- 对 \(x\) 积分就要在 \(x\) 上采样(看似理所当然的一句话,但后面会派上用场)
Path Tracing⚓︎
Whitted 风格的光线追踪是错误的;但刚才提到的渲染方程符合物理规律(辐射度量学
- 要在一个半球上求积分
- 存在递归部分
A Simple Monte Carlo Solution⚓︎
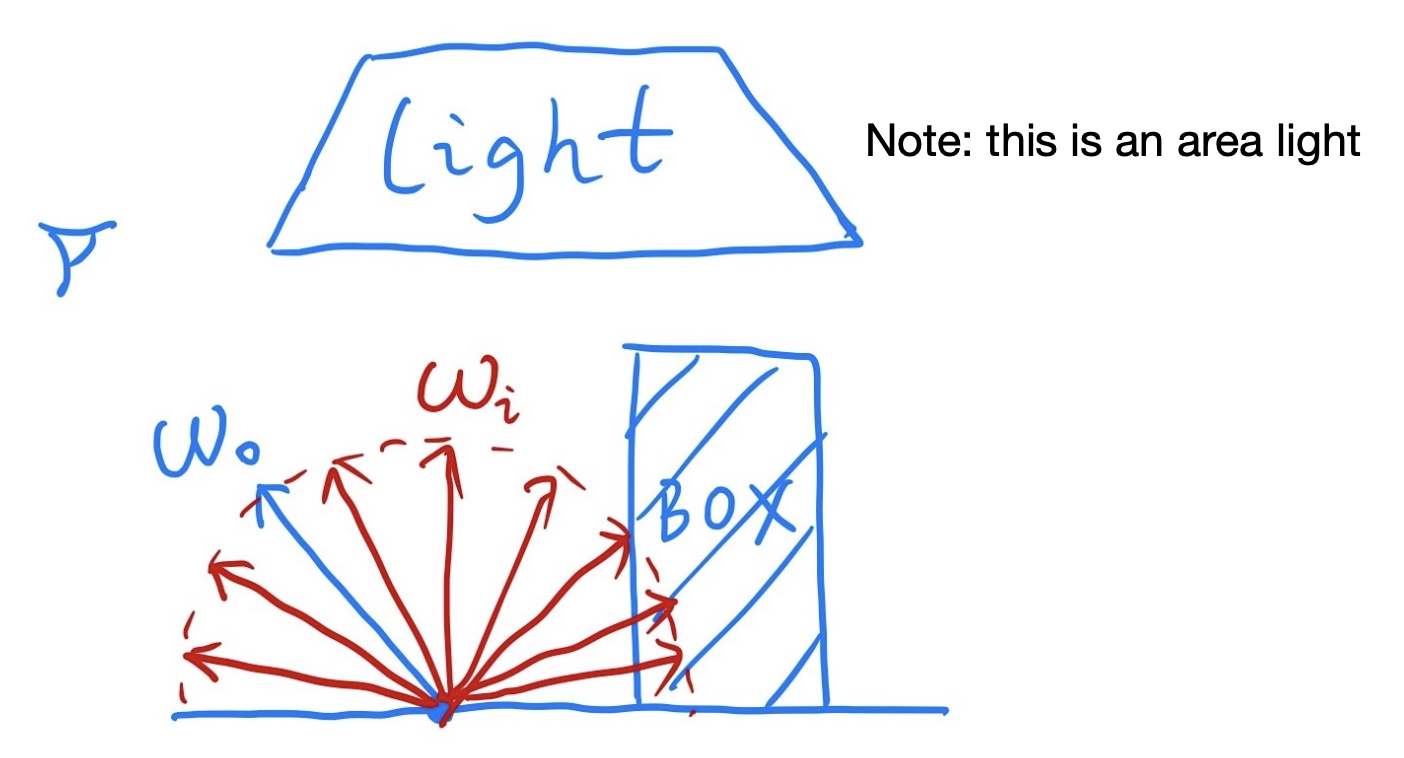
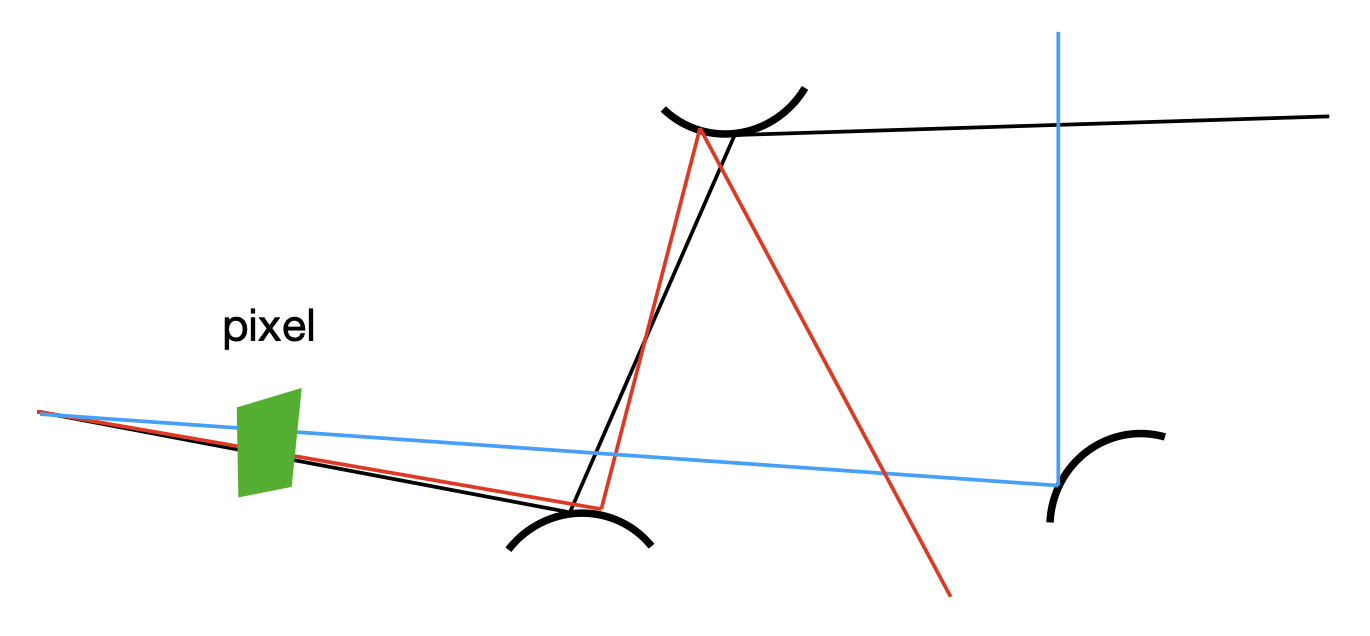
对于第一个问题,这也正是前面先引入蒙特卡洛积分法的原因。现在假设我们想在以下场景中,在仅靠直接光照的情况下渲染一个像素点:
注:这里假设所有方向是朝外的。
回顾一下反射方程(计算 \(p\) 点到相机的辐射率
尽管看上去很复杂,但它本质上就是一个沿各个方向上的积分。所以我们当然可以用蒙特卡洛积分法来做啊!
- 蒙特卡洛积分法 \(\int_a^bf(x)\mathrm{d}x\approx\frac{1}{N}\sum_{k=1}^N\frac{f(X_k)}{p(X_k)}\quad X_k\sim p(x)\),其中:
- \(f(x) = L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)\)
- 概率密度函数 (pdf) \(p(\omega_i) = \dfrac{1}{2 \pi}\)(即(单位)半球面积的倒数,这里假设在半球面上均匀采样)
综上可以得到:
注:这里的 \(i\) 既有表示入射光 (input) 的意思,也有表示采样索引 (index) 的意思,有些混淆,但应该还是好辨认的 hh
上述方程是一种用于直接光照的正确的着色算法。下面以伪代码形式呈现:
shade(p, wo)
Randomly choose N directions wi~pdf
Lo = 0.0
for each wi
Trace a ray r(p, wi)
if ray r hit the light
Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
return Lo
Introducing Global Illumination⚓︎
前面的计算只考虑了直接光照,还没有考虑来自其他物体反射光带来的间接光照。
把间接光照部分加到前面的伪代码上,得到:
shade(p, wo)
Randomly choose N directions wi~pdf
Lo = 0.0
for each wi
Trace a ray r(p, wi)
if ray r hit the light
Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
else if ray r hit an object at q
Lo += (1 / N) * shade(q, -wi) * f_r * cosine // recursive
/ pdf(wi)
return Lo
这就完了吗?No No No,还有不少问题呢!
问题
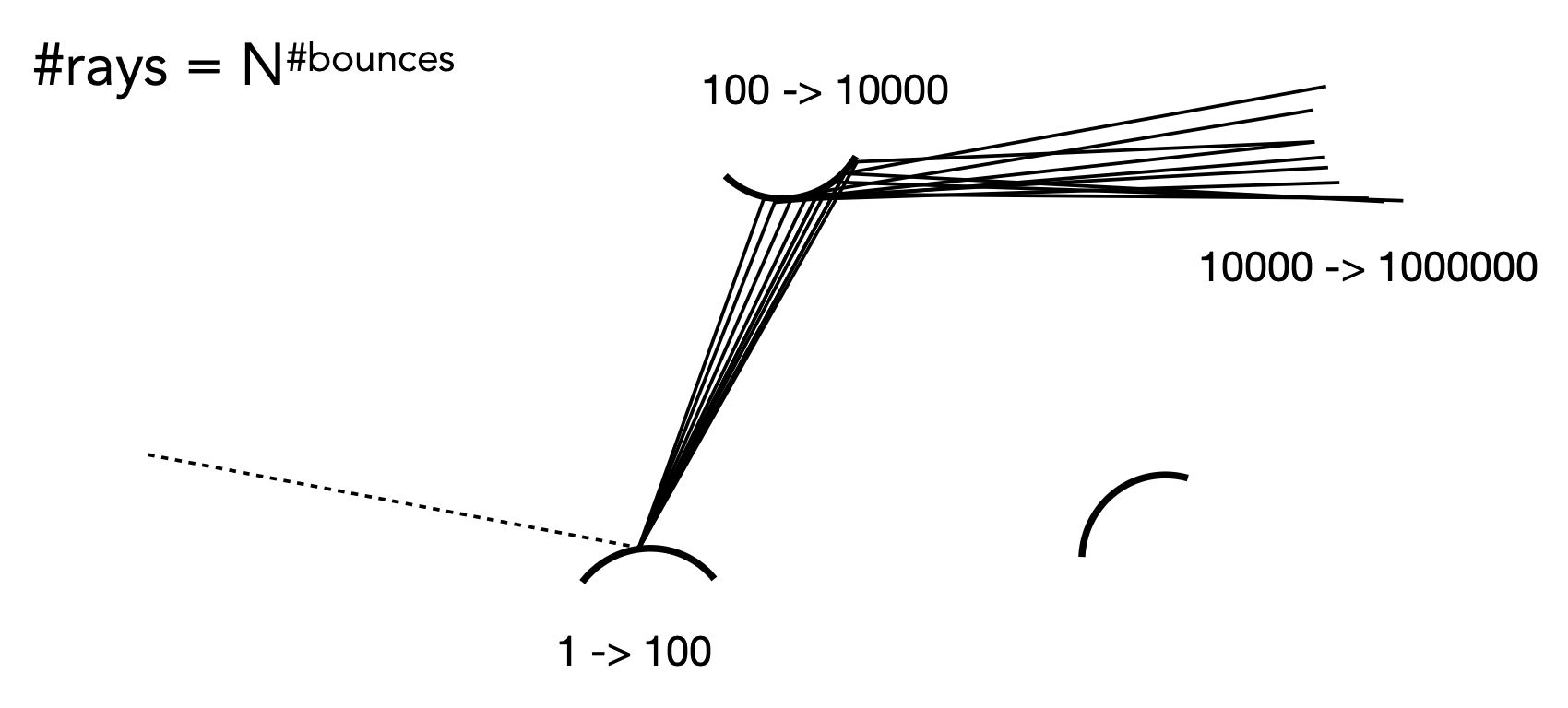
假如一条光线接触到物体表面能反射出 100 条光线,那么只要弹射 3 次,这条光线就有一百万条分支,很快就能耗尽所有的计算资源。
不难发现,只有当 N = 1 时,才不会出现指数爆炸的问题,也就是一条光线只能反射出一条光线。因此从现在开始,我们假设每个着色点上只追踪一条光线:
shade(p, wo)
Randomly choose ONE directions wi~pdf
Lo = 0.0
for each wi
Trace a ray r(p, wi)
if ray r hit the light
Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
else if ray r hit an object at q
Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi) // recursive
return Lo
上述算法就叫做路径追踪(path tracing)。
注:
N != 1时该算法就是分布光线追踪 (distributed ray tracing)。
但这种简化会带来的另外一个问题是带来了噪点 (noise)。不过不用担心,解决方案就是为每个像素点追踪更多的光线,最后将它们的辐射率求个平均值就行了(光线生成 (ray generation)
光线生成算法如下(和介绍光线追踪时提到的光线投射技术很像
是的,上面的伪代码没有考虑到递归的终止条件。但我们会陷入一个困境:现实世界中光线的弹射次数确实是无穷无尽的;也许可以预先设置最大的光线弹射次数,但这会损失掉一部分光线能量。
解决方案:俄罗斯轮盘赌 (Russian Roulette, RR):有 \(0 < p < 1\) 的概率幸存,否则(\(1 - p\))就寄了。
先前,我们总是向一个着色点射出一条光线,并得到着色结果 \(L_o\)。现在我们认为设置一个概率 \(P\ (0 < P < 1)\)
- 有 \(P\) 的概率发出一条光线,并且着色结果要除以 \(P\)(即 \(\textcolor{red}{L_o / P}\))
- 剩下 \(1 - P\) 的概率不发射光线,着色结果自然为 \(\textcolor{red}{0}\)
巧妙的是,\(L_o\) 的期望值仍然是 \(L_o\),因为:\(E = P \cdot (\textcolor{red}{L_o / P}) + (1 - P) \cdot \textcolor{red}{0} = L_o\)
此时伪代码如下:
shade(p, wo)
Manually specify a probability P_RR
Randomly select ksi in a uniform dist. in [0, 1]
if (ksi > P_RR) return 0.0;
Randomly choose ONE direction wi~pdf(w)
Trace a ray r(p, wi)
if ray r hit the light
return L_i * f_r * cosine / pdf(wi) / P_RR
else if ray r hit an object at q
return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
Sampling the Light⚓︎
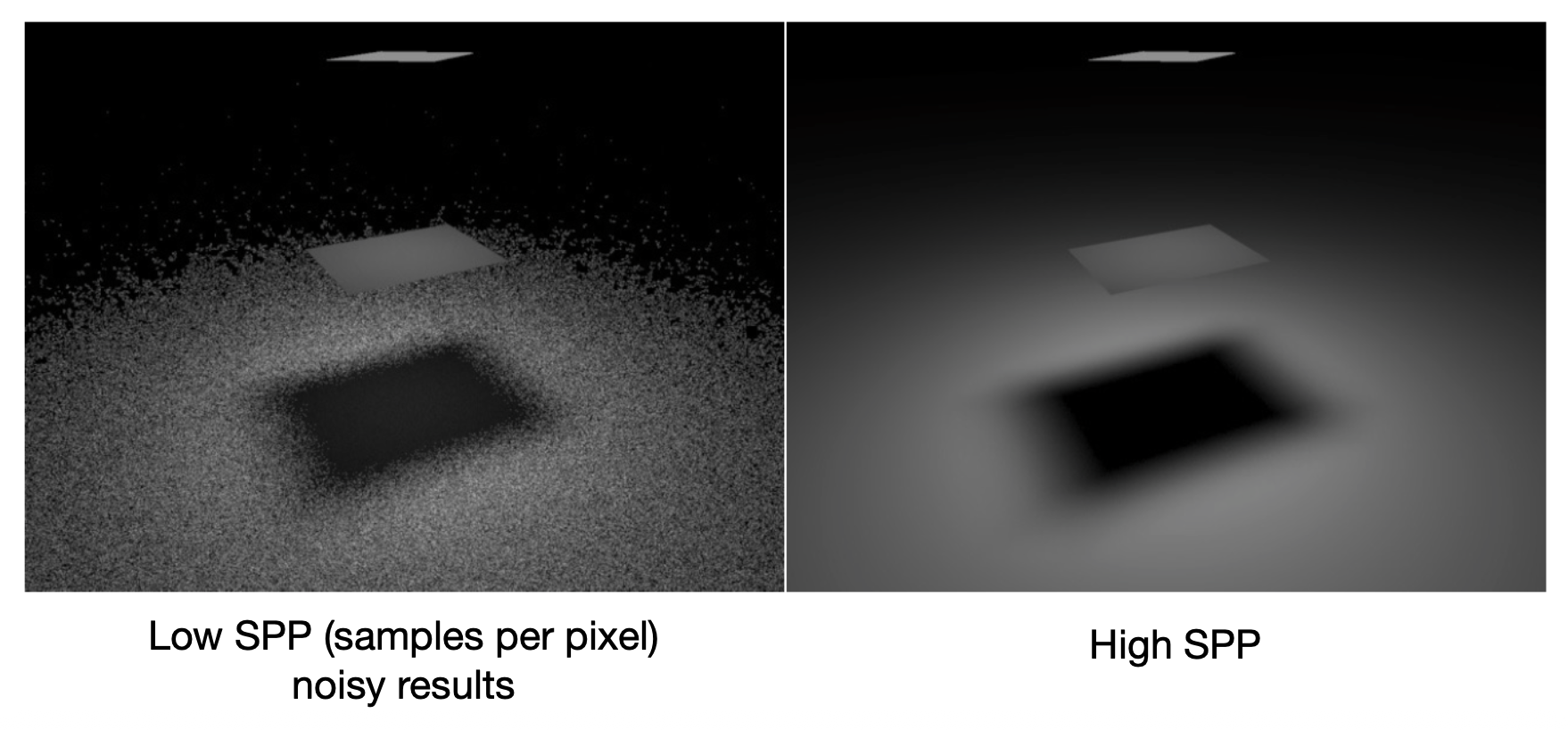
现在我们有了正确的路径追踪算法,但是还不够高效。足够大的 SPP(sample per pixel) 确实能得到不错的结果,但是算起来太慢了(右图
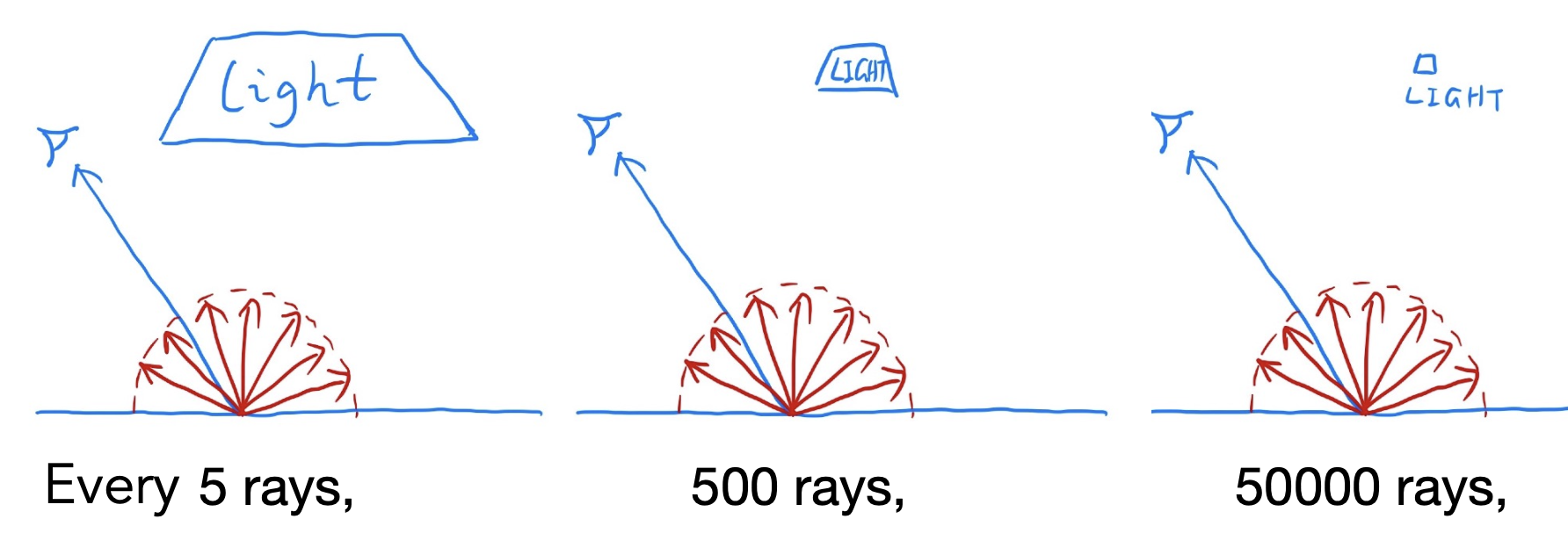
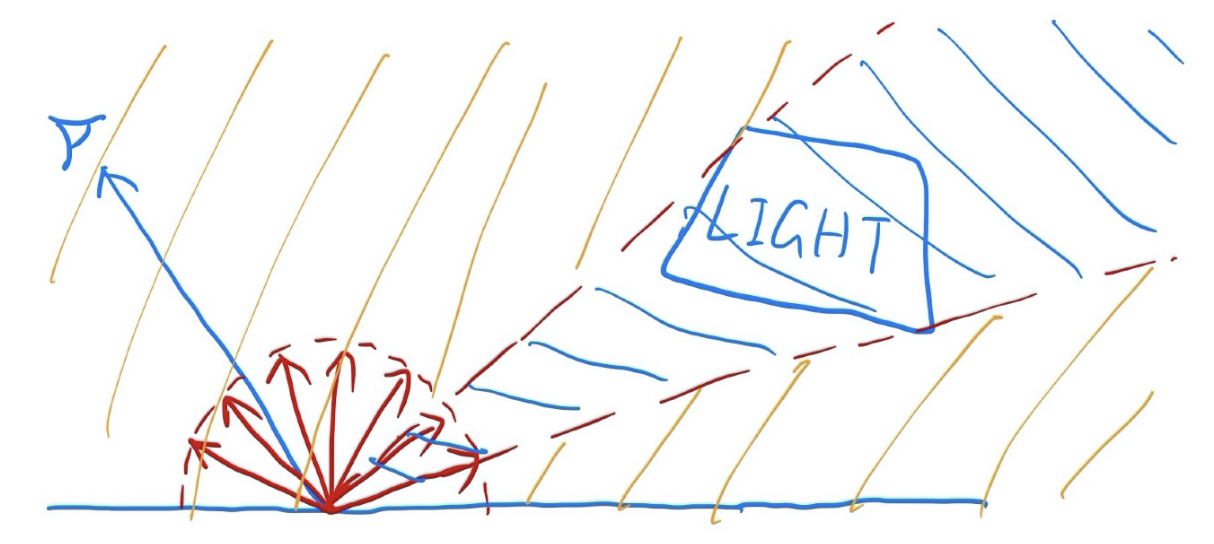
之所以低效,是因为我们只考虑一条光线打在光源上,如果在着色点上以半球形式进行均匀采样,那么其他很多光线就会“作废”。尤其是当光源很小时,要用很多光线才有机会达到光源,浪费的光线就更多了。
这时就又要轮到蒙特卡洛积分法登场了!因为它能作用在任何的采样方法上,所以我们就用它直接对光源采样,这样就不会出现浪费的问题了。
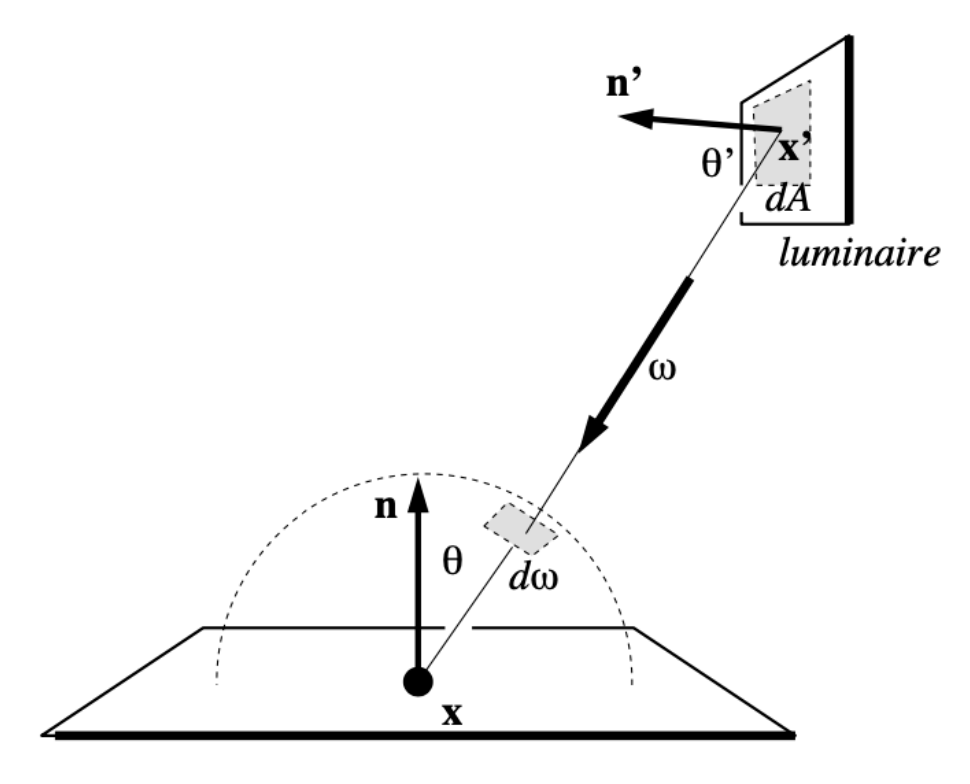
- 假设在光源上均匀采样:\(pdf = \dfrac{1}{A}\)(因为 \(\int pdf \textcolor{red}{dA} = 1\))
- 但渲染方程是在立体角上做积分的:\(L_o = \int L_i f_r \cos \textcolor{red}{d \omega}\)
回忆一下:蒙特卡洛积分法要求采样和积分的对象是同一个,所以既然要在光源上采样,就也要在光源上做积分,因此需要将渲染方程转化为对 \(dA\) 的积分,也就是要找出 \(d \omega\) 和 \(dA\) 之间的关系。
这件事是容易的,因为根据立体角的另一种定义(单位球体的投影面积
现在重写渲染方程为:
重写后的方程就是对光源做积分了。对于蒙特卡洛积分法,\(f(x)\) 是上述积分方程内所有的东西,pdf 就是 \(1 / A\)。
除了光源(直接光照,无需 RR)外,从其他物体发出的反射光(间接光照,需要 RR)也要考虑在内。
综上得到如下伪代码:
shade(p, wo)
// Contribution from the light source.
Uniformly sample the light at x` (pdf_light = 1 / A)
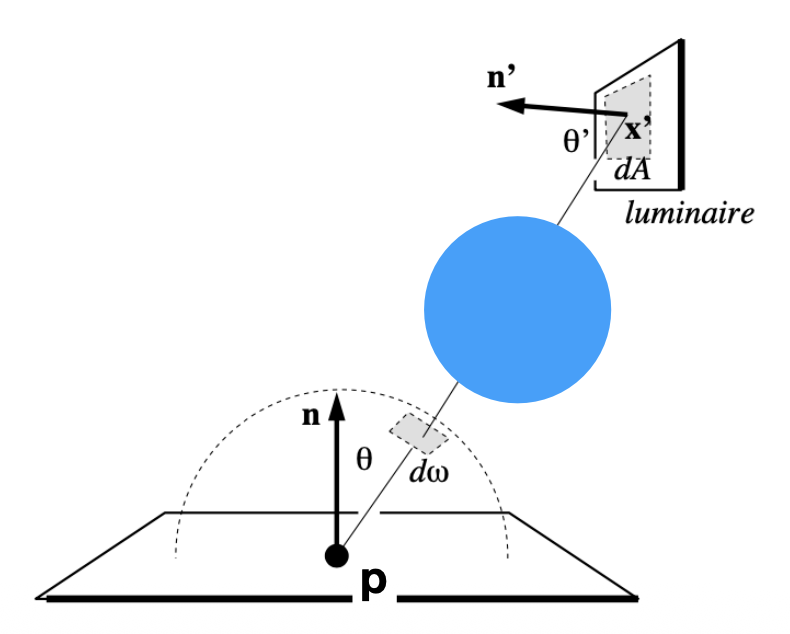
L_dir = L_i * f_r * cos θ * cos θ` / |x` - p|^2 / pdf_light
// Contribution from other reflectors.
L_indir = 0.0
Test Russian Roulette with probability P_RR
Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
Trace a ray r(p, wi)
if ray r hit a non-emitting object at q
L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR
return L_dir + L_indir
最后需要考虑的一件事是在光源上采样的光线有没有被阻挡。只要在伪代码中加上高亮标出的语句检测即可:
// Contribution from the light source.
L_dir = 0.0
Uniformly sample the light at x’ (pdf_light = 1 / A)
Shoot a ray from p to x’
if the ray is not blocked in the middle
L_dir = ...
路径追踪是一个百分百正确的算法,其渲染的效果和照片几乎一模一样。
Asides⚓︎
注
- 路径追踪算法很难!!!
- 它涉及到很多学科的知识:物理学(辐射度量学
) 、概率论、微积分,以及代码能力 - 学习路径追踪的同时也有助于加深对这些知识的理解
- 它涉及到很多学科的知识:物理学(辐射度量学
- 虽然 GAMES 101 中文名为“现代计算机图形学入门”,
但“入门”在哪,实际上这门课更倾向于介绍“现代” CG 知识
“光线追踪”概念的演变
- 过去
, “光线追踪”一词特指 Whitted 风格的光线追踪 - 现在(
其实是闫令琪老师自己的定义,但很有道理) , “光线追踪”一词指代了所有和光传播 (light transport) 的技术,包括:- 单向 / 双向路径追踪
- 光子映射
- Metropolis(
这是算法发明者的姓氏,不是“大都会”的意思)光传播 - VCM(顶点连接与合并)/ UPBP
这些现代(或高级)话题将在第 9 讲介绍!
课程中没有覆盖,也不会覆盖到的内容
- 如何在半球上,或者更一般地,如何在任意函数上做均匀采样?
- 蒙特卡洛积分法允许任意概率密度函数,那么什么样的 pdf 是最好的(重要性采样(importance sampling))
- 随机数是否重要?是滴(低差异序列(low discrepancy sequences),保证随机数分布均匀,且不会出现扎堆或间隔过远的情况)
- 同时在半球和光源上采样效果会更好(多重要性采样(multiple importance sampling))
- 像素的辐射率所有穿过该像素路径(光线)的平均值(也需要做加权平均——像素重构滤波器(pixel reconstruction filter))
- 像素的辐射率是否就是像素的颜色?不是的,要用 Gamma 纠正做一步转换
- 涉及到曲线、色彩空间 (color space) 相关的知识
评论区