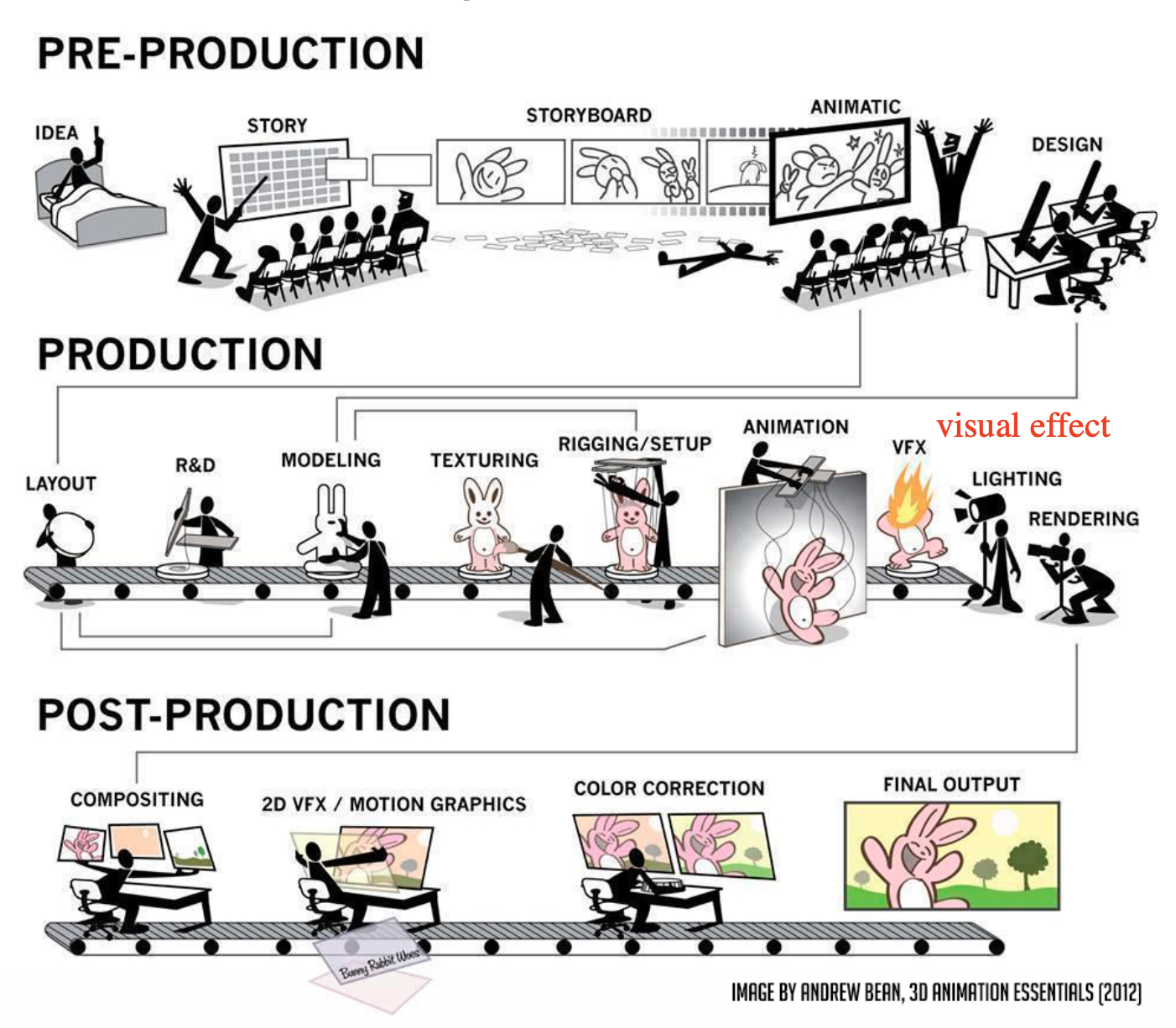
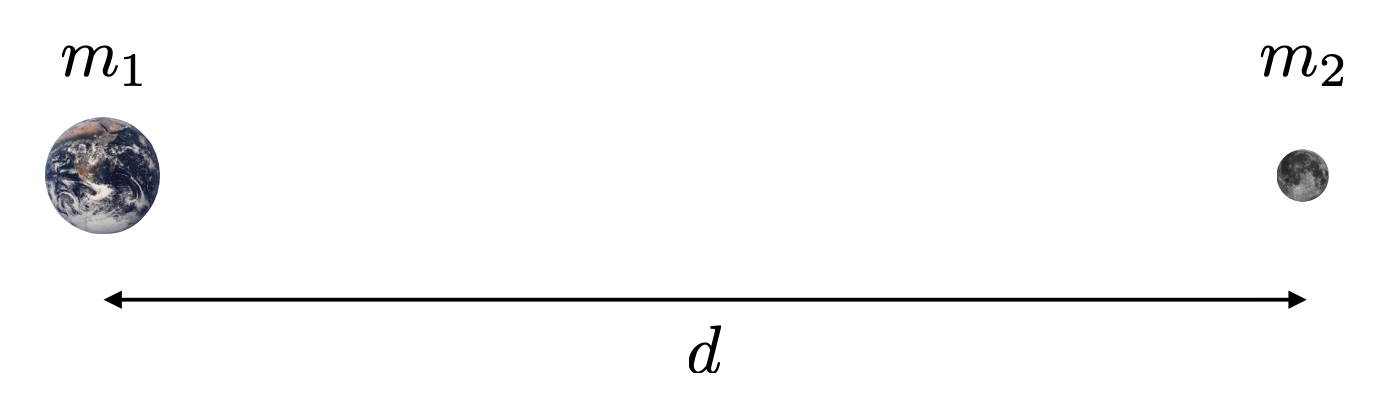Animation⚓︎

约 5149 个字预计阅读时间 26 分钟

正如其字面意思，“动画(animation)”的意思是“让东西活起来 (bring things to life)”。

审美 (aesthetic) 问题往往优先于技术问题
从建模 (modeling) 角度看，动画将场景模型表示为一个关于时间的函数
输出：一系列按顺序观看时能产生动态感 (a sense of motion) 的图像
- 电影：24 fps
- 视频：（一般来说）30 fps
- 虚拟世界（电子游戏）：90 fps

History⚓︎

最早的动画
历史上的动画
第一部电影
- 原本电影是作为科学研究的工具，而非用于娱乐目的
- 电影是加速动画发展的关键技术
首部手绘长篇 (feature-length)（> 40 min）动画
第一个由数码计算机生成的动画
早期的计算机动画
数码恐龙
第一部完全由 CG 技术制作的动画
十几年前的计算机动画
几年前的计算机动画

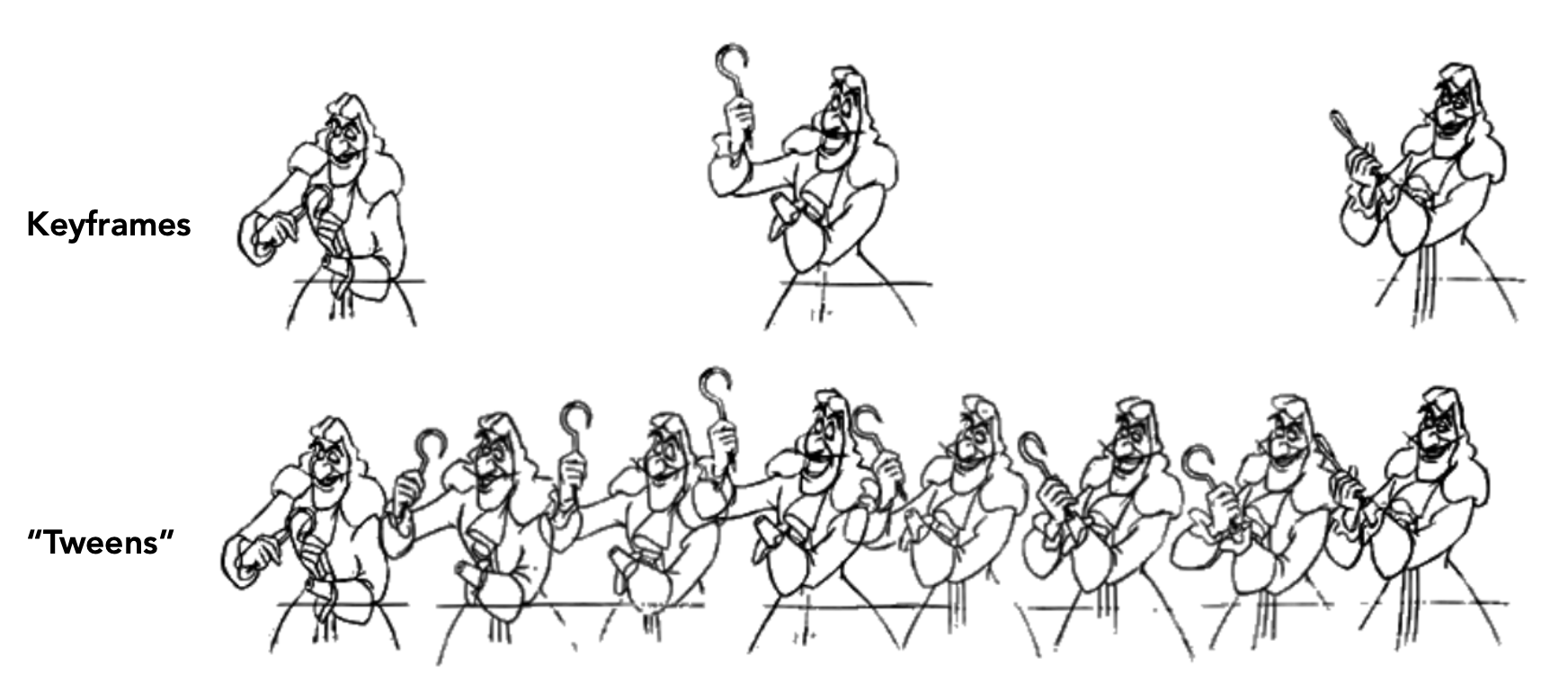
Keyframe Animation⚓︎

动画师绘制关键帧(keyframes)
助手（人 / 电脑）负责补充中间帧(in-between frames)（中间帧生成 (tweening)）

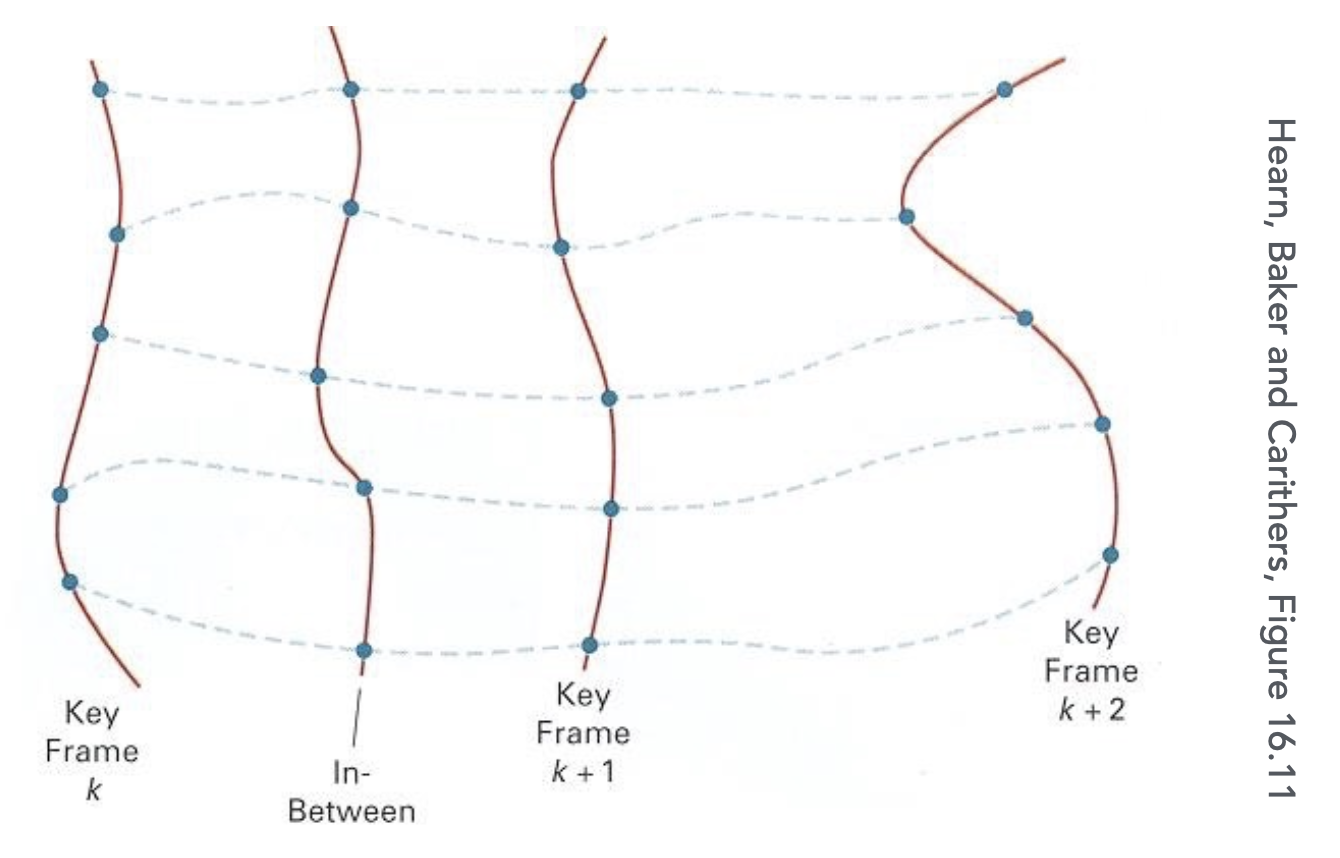
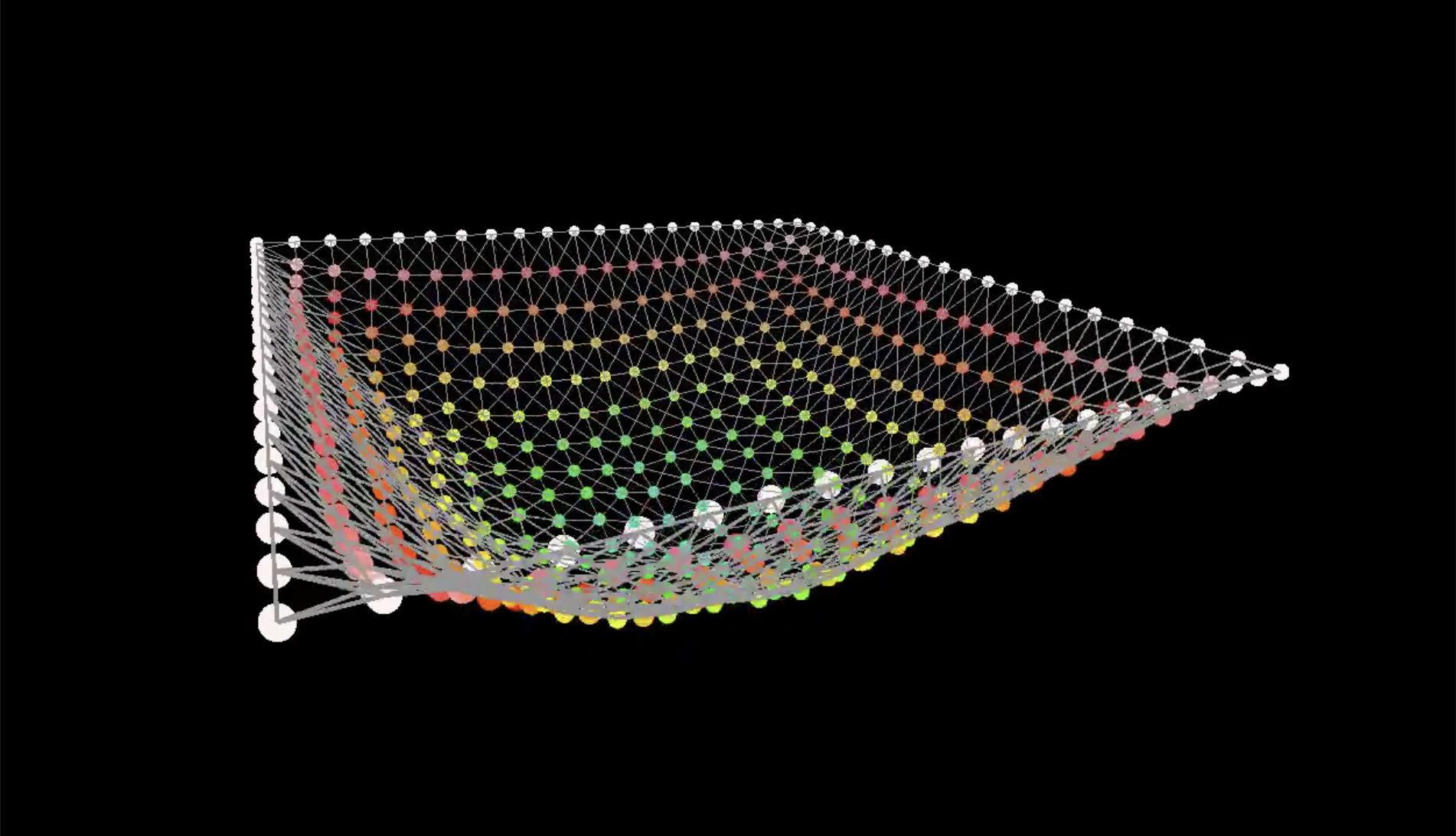
中间帧生成的过程就是对关键帧的插值 (interpolation)。我们可以把每一帧看作一个参数值向量，然后连接连续帧上相同位置的元素，在连线上进行插值。

插值方法有：

线性插值，但通常效果不佳
更常用的是使用样条(spline) 实现平滑 / 可控的插值

Physical Animation⚓︎

先来回忆一下牛顿第二定律：$F = ma$（力 (force) = 质量 (mass) * 加速度 (acceleration)），这是物理动画背后最基本的原理。

物理动画通常采用数值模拟来生成物体的运动。

例子

例 1：布料模拟

=== " 例 2：" 流体

<div style="text-align: center">
    <img src="images/lec12/17.png" width=50%>
</div>

Mass Spring System⚓︎

首先要介绍的物理模拟方法是质点弹簧系统(spring mass system)。

例子

例 1：绳索例 2：头发例 3：网格例 4：布料

视频链接：https://youtu.be/Co8enp8CH34

我们构建以下理想化的弹簧(spring) 模型：

\[ \begin{aligned} \bm{f}_{a \rightarrow b} & = k_s (\bm{b} - \bm{a}) \\ \bm{f}_{b \rightarrow a} & = -\bm{f}_{a \rightarrow b} \end{aligned} \]

拉开弹簧，弹力会让弹簧上两点相互靠近
弹力和位移成正比（胡克定律 (Hooke's law)）
$k_s$ 表示弹簧系数（刚度 (stiffness)）
该模型的问题：只有当弹簧长度为 0 时才没有弹力，这显然不符合物理规律

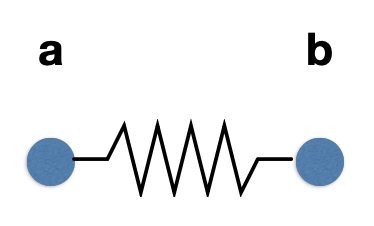
所以我们需要考虑非零静止长度(rest length)（记作 $l$）下的弹簧模型，公式变为： $$ \bm{f}_{a \rightarrow b} = k_s \dfrac{\bm{b} - \bm{a}}{|\bm{b} - \bm{a}|}(|\bm{b} - \bm{a}| - l) $$

但这个模型还有一个问题：一旦拉长弹簧后，弹簧会永远振荡下去，不会停止。这显然是因为没有考虑到其他力的作用。

在继续改进模型前，我们先约定以下记号：

\[ \begin{aligned} & \bm{x} \\ & \bm{\dot{x}} = \bm{v} \\ & \bm{\ddot{x}} = \bm{a} \end{aligned} \]

其中 $\bm{\dot{x}}, \bm{\ddot{x}}$ 分别表示 $\bm{x}$ 的一阶和二阶导数，即速度和加速度。

现在我们引入导致弹簧模型能量损失的来源——一个简单的阻尼(damping)：$\bm{f} = -k_d \bm{\dot{b}}$

这就像一股粘性阻力 (viscous drag)
让沿着速度方向上的运动减速
$k_d$ 为阻尼系数

当然还是由于定义过于简单，新的问题出现了：所有方向上的运动都会减速。原因是模型还没有考虑弹簧内部的损耗。

比如弹簧的两个端点同时向右运动，此时两者的相对位置保持不变，因而不存在什么弹力；但依照目前的模型，这个弹簧仍然会受到阻尼，最终停下来。
又比如将一个弹簧竖直放在空中，让它自由下落；依据当前的模型，它的降落速度会越来越慢，但实际上的空气阻尼不会这么大，几乎可以不用考虑。

所以最后引入在弹簧内部的阻尼，公式改为： $$ \bm{f}_{\bm{b}} = -k_d \dfrac{\bm{b} - \bm{a}}{|\bm{b} - \bm{a}|}(\bm{\dot{b}} - \bm{\dot{a}}) \cdot \dfrac{\bm{b} - \bm{a}}{|\bm{b} - \bm{a}|} $$

$\bm{f}_{\bm{b}}$：作用在 $\bm{b}$ 上的阻尼力
$\bm{\dot{b}} - \bm{\dot{a}}$：假设 $\bm{a}$ 静止时，$\bm{b}$ 的相对速度
$\dfrac{\bm{b} - \bm{a}}{\|\bm{b} - \bm{a}\|}$：$\bm{a}$ 到 $\bm{b}$ 的方向（归一化处理）
$\dfrac{\bm{b} - \bm{a}}{\|\bm{b} - \bm{a}\|}(\bm{\dot{b}} - \bm{\dot{a}})$：相对速度在 $\bm{a}$ 到 $\bm{b}$ 的方向上的投影（结果是标量）

对于该模型：

仅在弹簧长度变化时产生粘性阻力，不会减缓弹簧系统中的整体运动（比如整体的平移或旋转）
注：这只是其中一种特定类型的阻尼

可用弹簧模型构成的结构：

片 (sheet)
块 (block)
其他 ...

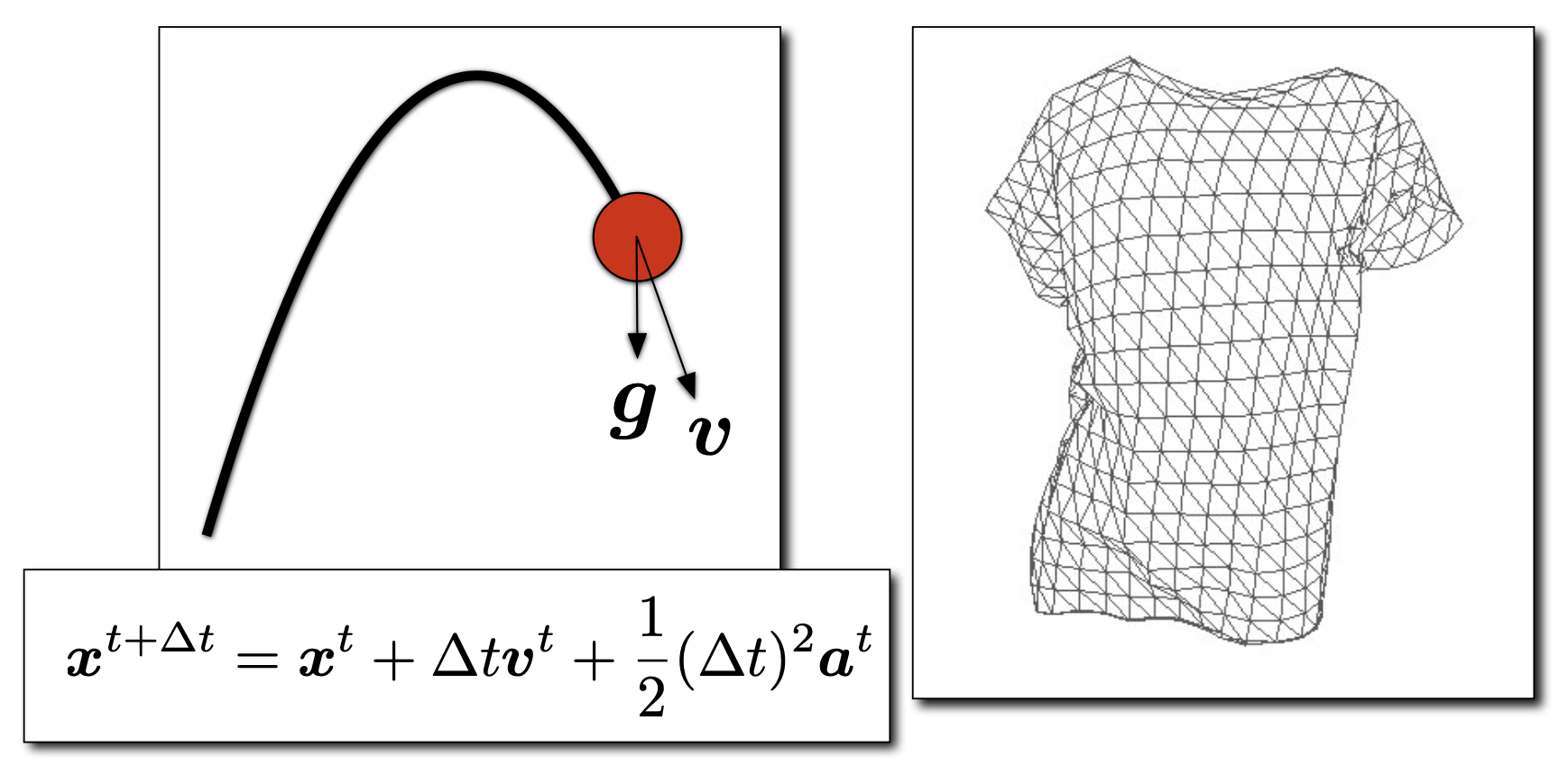
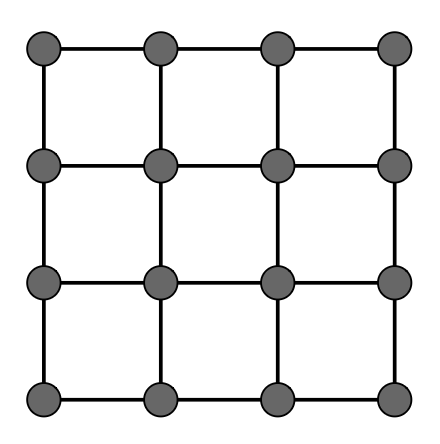
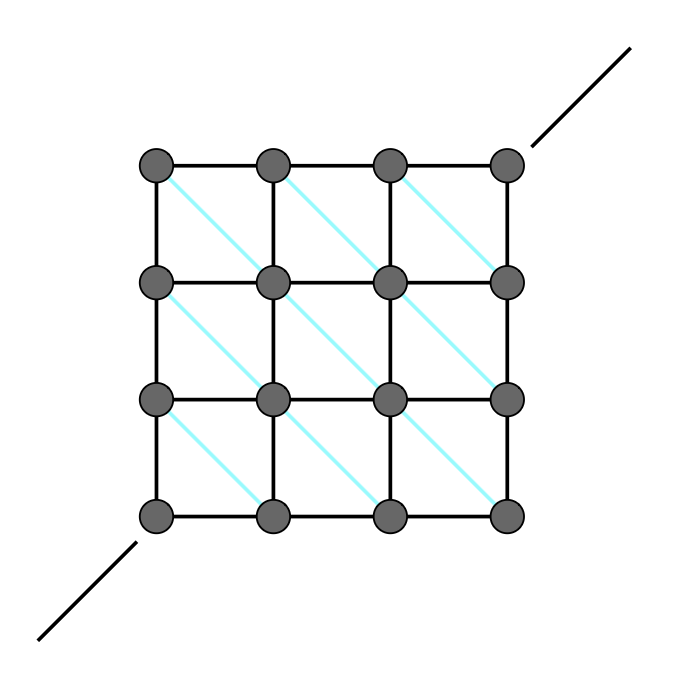
下面主要介绍（用于模拟布料的）片结构。目前的片结构存在两个问题：

无法抵抗切变(shearing) 力（拉住对角线后，被拉住的两端就会被拉长，另一个对角线就会缩短，但（非弹性的）布料不是这样的）
无法抵抗平面外的弯折(out-of-plane bending)（比如对折，但布料是没法做到像纸那样完全对折的）

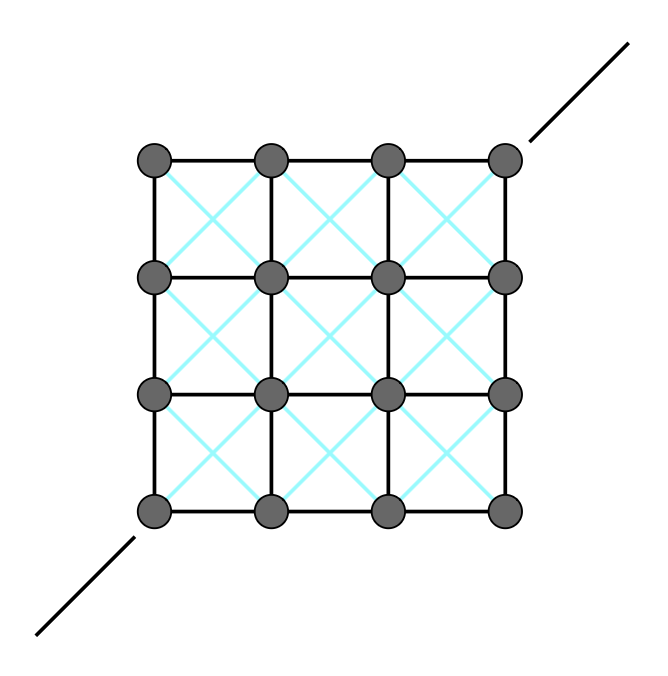
对于第一个问题，可以考虑向网格内加一些垂直对角线来限制：

但这样只考虑了一条对角线，另一条对角线也要有相应的限制，避免各向异性问题：

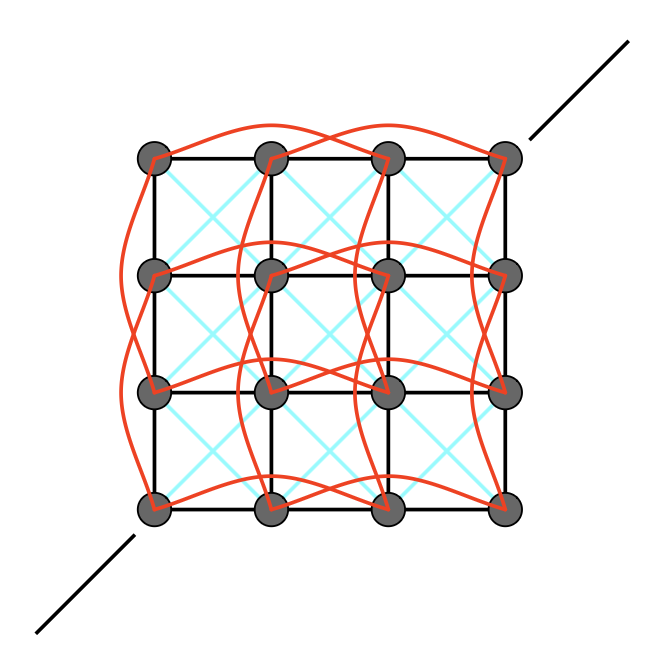
现在第一个问题解决了，那就来看第二个问题吧！这里给出的解决方案是让网格上两点（中间隔开一个点）用一个更弱的弹簧连接（下图用红线表示）。这样在对折时会受到红色弹簧的弹力阻碍而无法成功，从而达到我们的目标。

例子

注

用有限元素法(finite element method, FEM) 也能达到类似质点弹簧系统的效果。

Particle System⚓︎

第二种方法是粒子系统(particle system)，它将一个动态系统建模为大量的粒子，而每个粒子的运动由物理（或非物理）的作用力推动。这是一种在图形学和游戏中比较流行的技术，因为：

易于理解和实现
可扩展的 (scalable)：粒子数量少则速度快，多则可模拟更高的复杂度

构建粒子系统的挑战有：

可能需要大量粒子（比如流体 (fluid)）
可能需要加速结构（比如用于查找最近粒子以进行相互作用）

用粒子系统制作动画的流程为：对于动画的每一帧图像，

（若需要）创建新的粒子
计算每个粒子上的力
更新每个粒子的位置和速度
（若需要）移除不活跃的粒子
渲染粒子

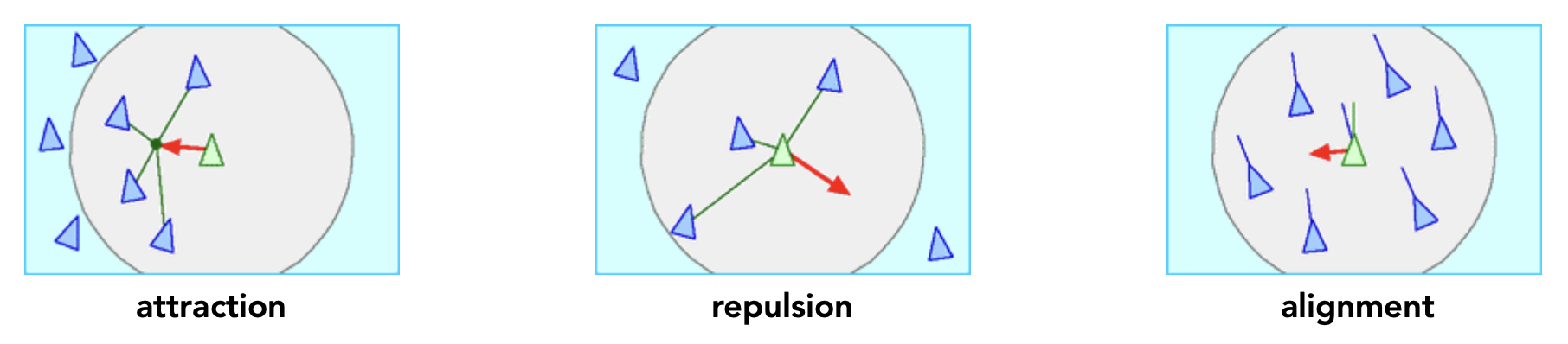
上述流程的关键在于如何计算每个粒子上的力，需要考虑的要素有：

吸引(attraction) 与排斥(repulsion) 力
- 重力、电磁力 ...
  - 根据万有引力定律，两个粒子会互相吸引
    
    \[ \begin{aligned} F_g & = G\dfrac{m_1 m_2}{d^2} \\ G & = 6.67428 \times 10^{-11} \text{N} \cdot \text{m}^2 \cdot \text{kg}^{-2} \end{aligned} \]
- 弹簧、推力 (propulsion)...
- 阻尼力 (damping force)
- 摩擦力、空气阻力、粘滞力
- 碰撞(collision)
- 墙壁、容器、固定物体 ...
- 动态对象，角色身体部位 ...

例子

例 1：星系模拟例 2：基于粒子的流体例 3：模拟动物群集例 4：分子动力学例 5

将鸟群中的每只鸟建模为一个粒子
- 吸引 (attraction) 到邻居们的中心
- 对单个的邻居是排斥 (repulsion) 的
- 向邻居们的平局轨迹 (trajectory) 对齐 (alignment)
这些粒子会受到以下力：
数值模拟大粒子系统的演化
涌现的复杂行为（也见于鱼类、蜜蜂等 ...）

Kinematics⚓︎

Forward Kinematics⚓︎

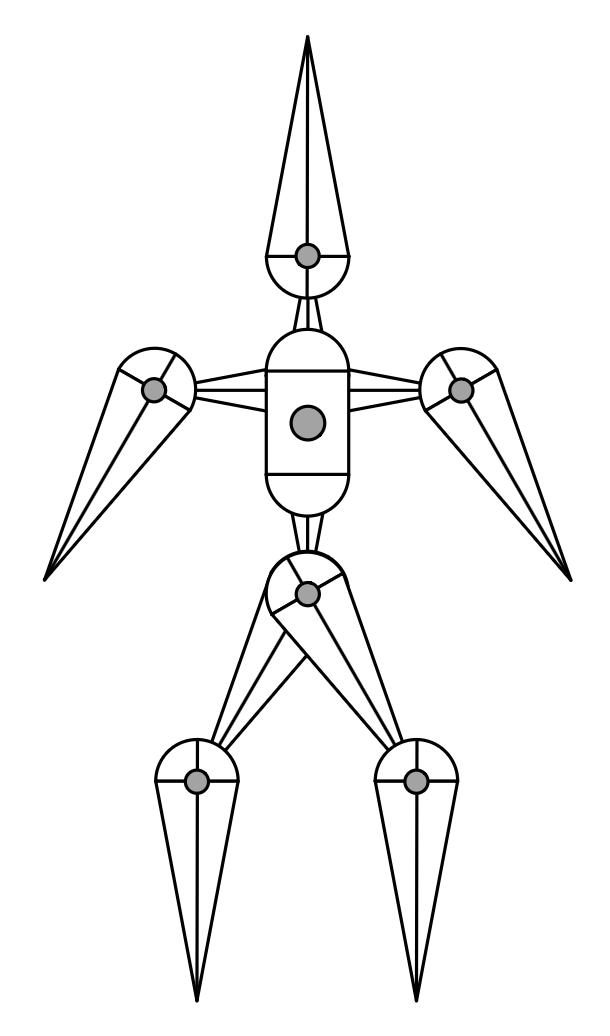
正向运动学(forward kinematics) 涉及以下几部分：

关节骨架 (articulated skeleton)
- 拓扑学 (topology)（什么连接到什么）
- 关节间的几何关系
- 树状结构（没有环状结构）
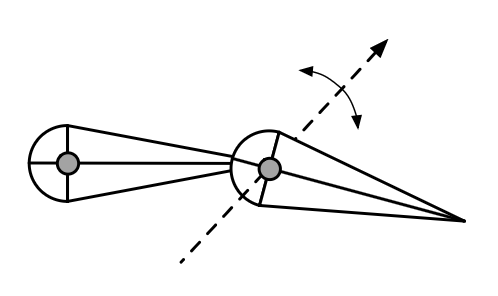
关节类型 (joint types)
- 钉子 (pin)（1D）
- 球 (ball)（2D）
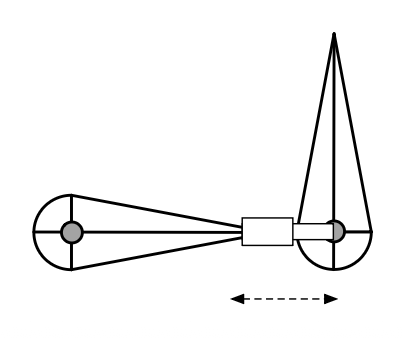
- 棱柱关节 (prismatic joint)（实现平移）

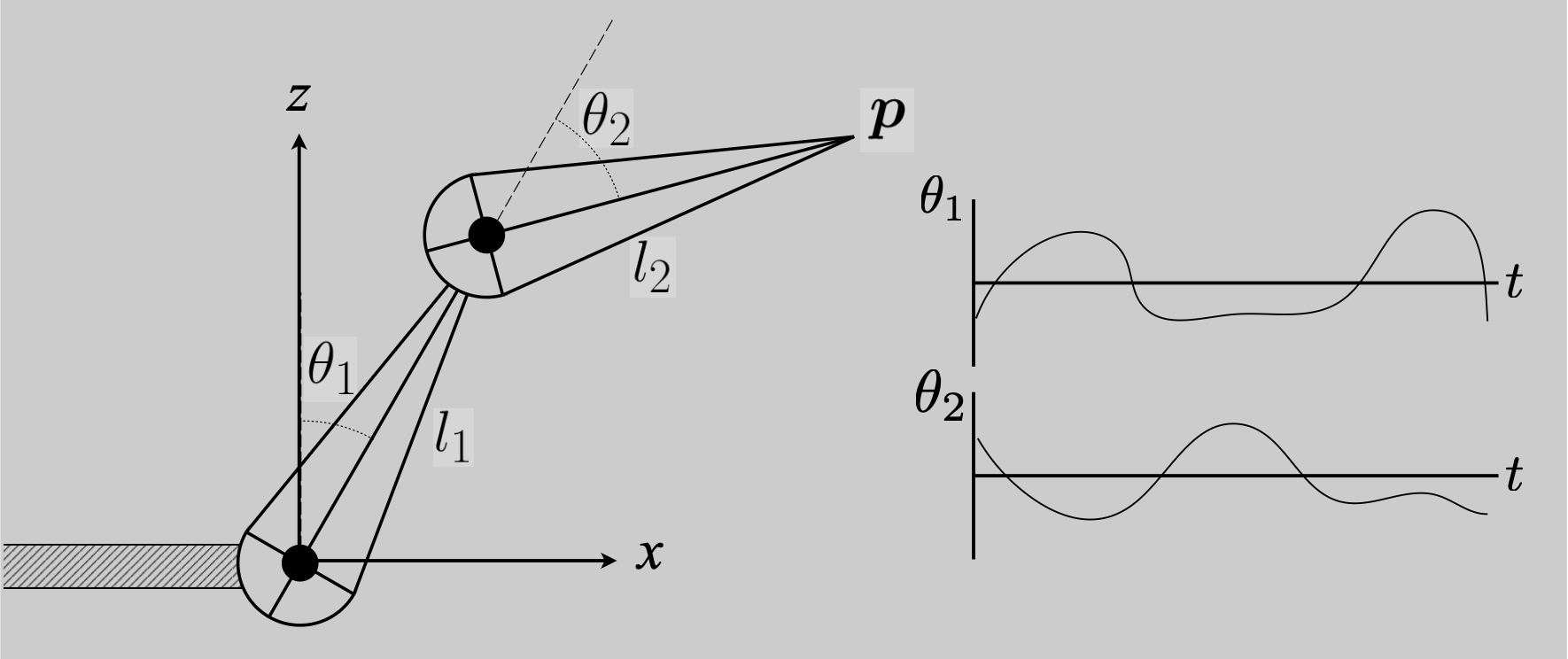
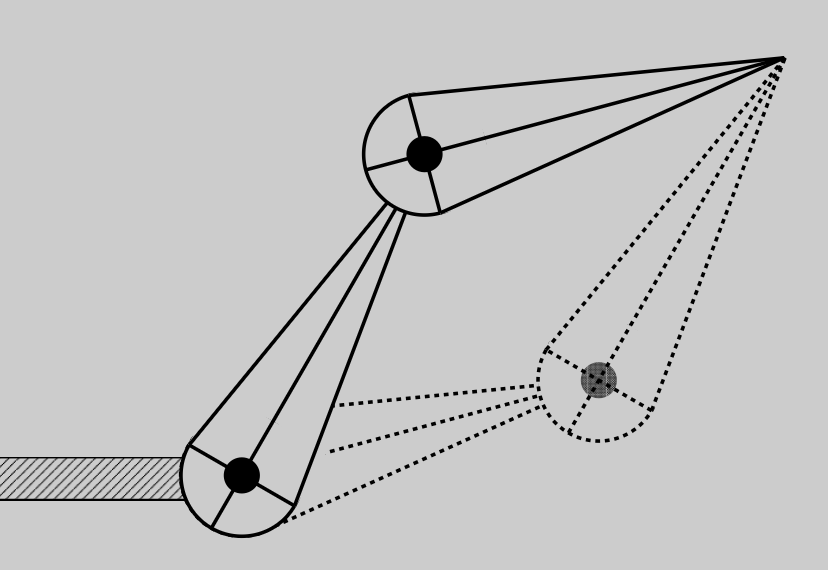
下面是一个简单的 2D 两段手臂：

动画师确定每一段的旋转角度
计算机确定末端执行器 (end effector) $p$ 的位置

\[ \begin{aligned}p_z&=l_1\cos(\theta_1)+l_2\cos(\theta_1+\theta_2)\\p_x&=l_1\sin(\theta_1)+l_2\sin(\theta_1+\theta_2)\end{aligned} \]

这样形成的动画就是一个角度参数值随时间变化的函数。

例子

运动学的优缺点：

优点：
- 方便直接控制
- 实现很直接
缺点：
- 动画表现可能不符物理规律
- 艺术家创作更耗时

Inverse Kinematics⚓︎

例子

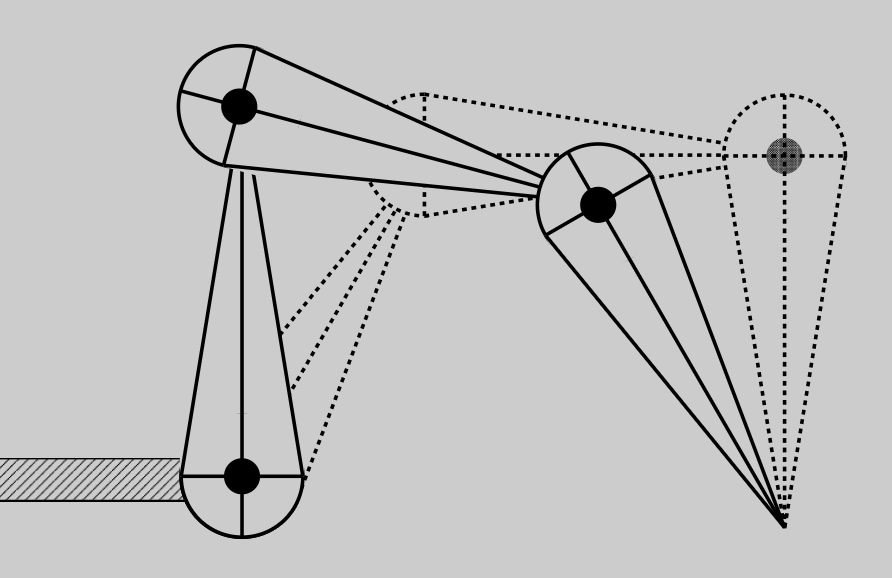
逆向运动学(inverse kinematics) 中，动画师和计算机的工作正好相反：

动画师提供末端执行器的位置
而计算机必须确定关节的旋转角度，同时能满足约束

对于前面那个两段手臂的例子，可直接以分析方式求解参数（即旋转角度）：

\[ \begin{aligned}\theta_2&=\cos^{-1}\left(\frac{p_z^2+p_x^2-l_1^2-l_2^2}{2l_1l_2}\right)\\\theta_1&=\frac{-p_zl_2\sin(\theta_2)+p_x(l_1+l_2\cos(\theta_2))}{p_xl_2\sin(\theta_2)+p_z(l_1+l_2\cos(\theta_2))}\end{aligned} \]

但逆向运动学的诸多问题却很难求解，因为：

对于相同的配置空间，可能存在多个解
有时会出现无解的情况

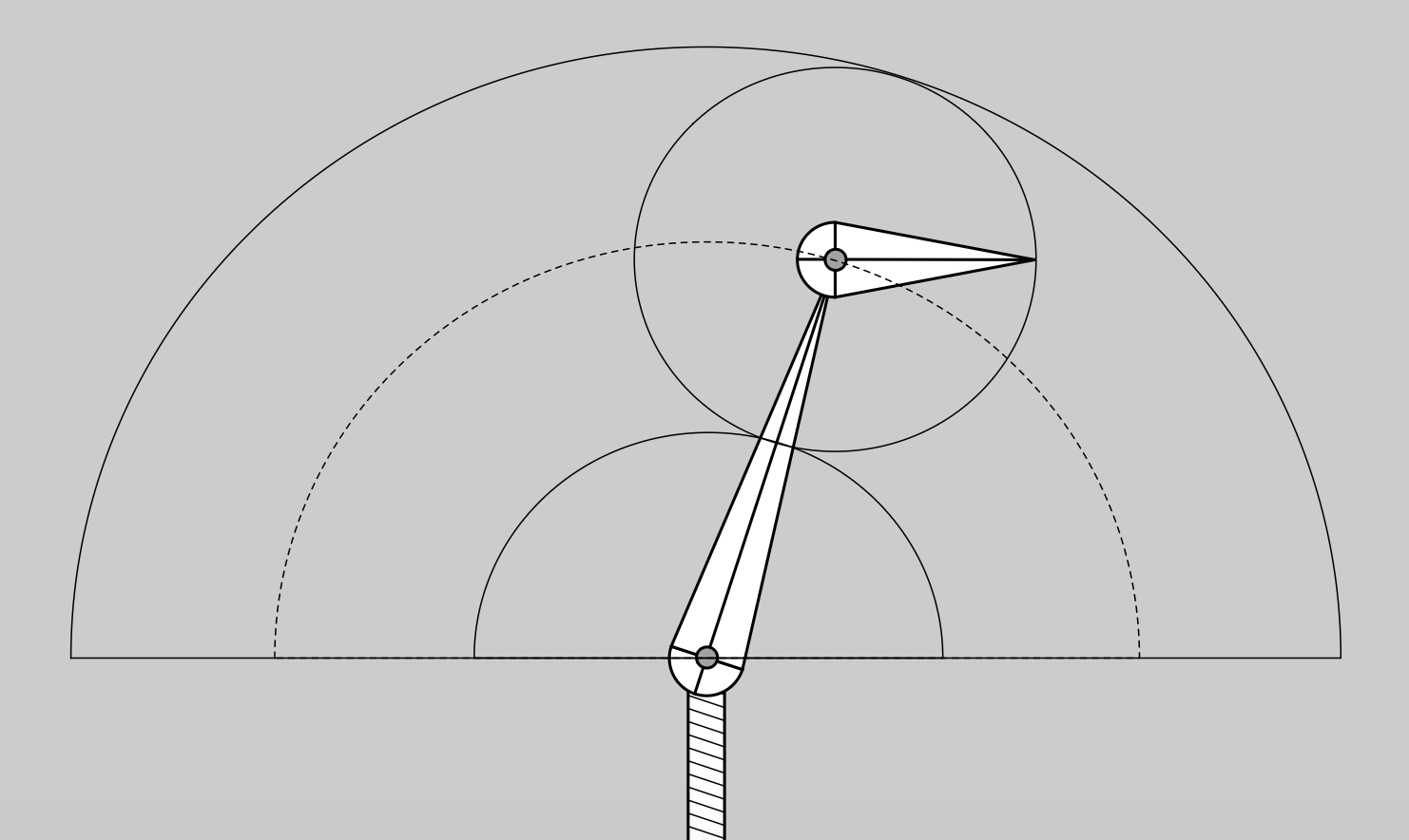
求 N 连接的逆向运动学问题的数值解的一般步骤：

选择初始配置
定义一个误差度量
计算误差关于配置的梯度
应用梯度下降法（或牛顿法等其他优化过程）

例子

Rigging⚓︎

rigging 这玩意儿好像没发现好的中文翻译 ...

rigging 是一套对角色进行更高级别控制的系统，它能够更加迅速且直观地调整姿势、形变、表情等。

类似于控制木偶的提线
捕捉所有有意义的角色变化
因角色而异

但这种技术的问题在于成本高昂：

需要人工的努力
同时对艺术和技术方面的训练提出要求

例子

Blend Shapes⚓︎

混合形状(blend shapes) 的原理是：

不采用骨架，直接在表面之间进行插值
例子：模拟一系列面部表情
最简单的方案：对顶点位置进行线性组合
使用样条曲线来控制随时间变化的权重选择

例子

Motion Capture⚓︎

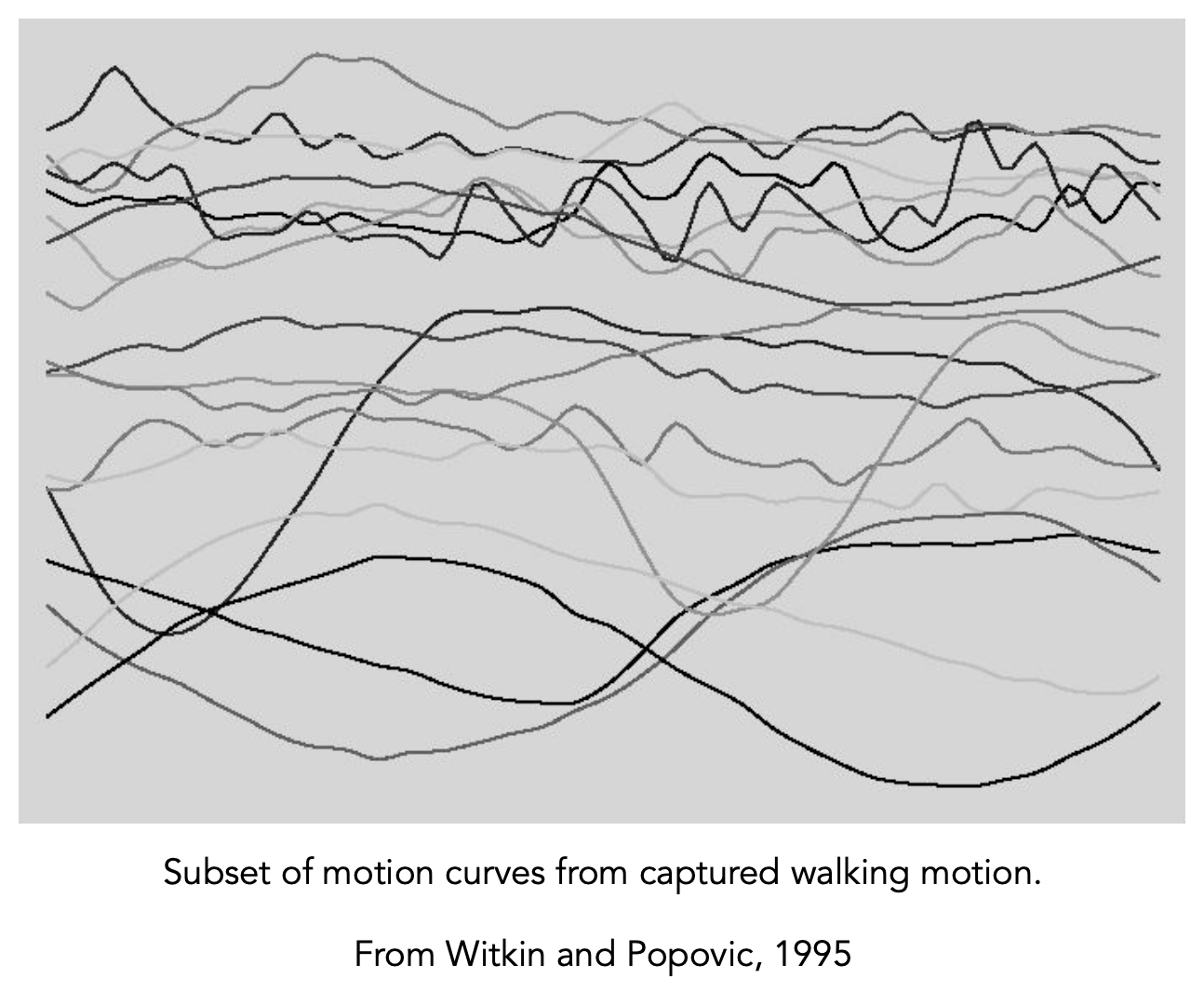
动作捕捉(motion capture) 是一种用于创建动画序列的数据驱动方法。

记录现实世界中的表现（比如某个人在完成某个活动）
从收集的数据中提取姿势，作为一个关于时间的函数

该方法的优缺点为：

优点：
- 能快速捕捉大量现实数据
- 动画的真实性很高
缺点：
- 复杂且设置成本高
- 捕捉到的动画可能无法满足艺术需求，需要额外的调整

动作捕捉的装置有：

光学(optical) 装置
- 在捕捉对象上添加标记物（如下图所示的白色小球）
- 通过多台摄像机进行三角测量定位
- 8 台以上的相机，240 Hz，遮挡困难
例子
磁性(magnetic) 装置：感知磁场以推断位置 / 方向，并且是有线连接的
机械(mechanical) 装置：直接测量关节角度，但运动受限

捕捉到的动作数据：

面部动画遇到的挑战——恐怖谷效应(uncanny valley)：在机器人技术和图形学领域中，当人造角色的外观接近人类的真实感时，我们的情感反应会转为负面，直至其表达达到足够逼真的水平。

例子：面部动作捕捉

总结：动画生产流程

Single Particle Simulation⚓︎

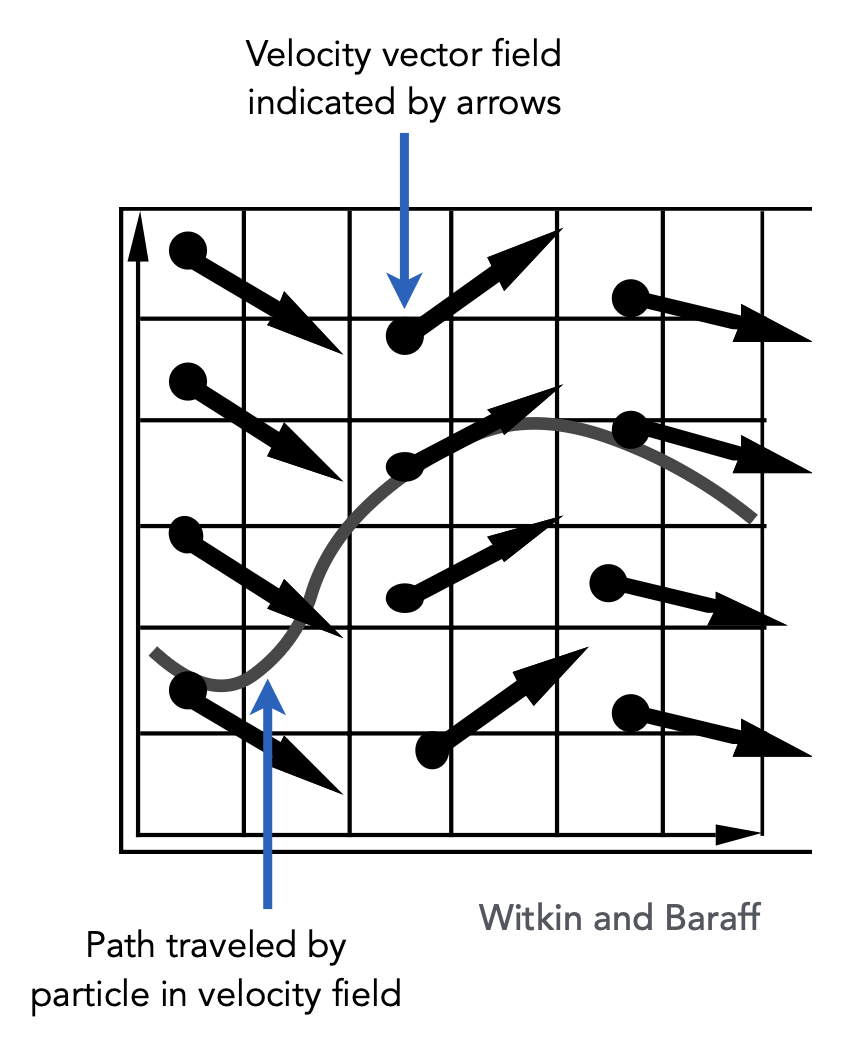
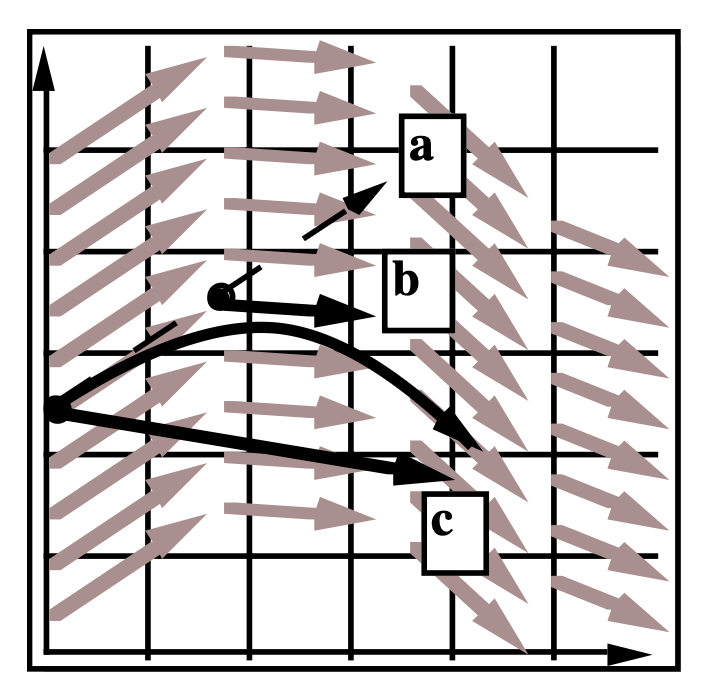
前面介绍过如何用粒子系统模拟物体运动，接下来就从微观角度学习具体如何让单个粒子运动。现在我们假设粒子的运动取决于一个速度向量场(velocity vector field)，这是一个关于位置和时间的函数，记作 $v(x, t)$。在图中，速度向量用箭头表示，而用曲线表示粒子在场中的运动。

要想计算粒子随时间变化过程中所处的位置，就是在求解一个一阶常微分方程(first-order ordinary differential equation, ODE) 问题： $$ \dfrac{dx}{dt} = \dot{x} = v(x, t) $$

“一阶”的意思是计算过程中要用到一阶导数
“常”的意思是没有偏微分计算，即 $x$ 是一个仅关于 $t$ 的函数

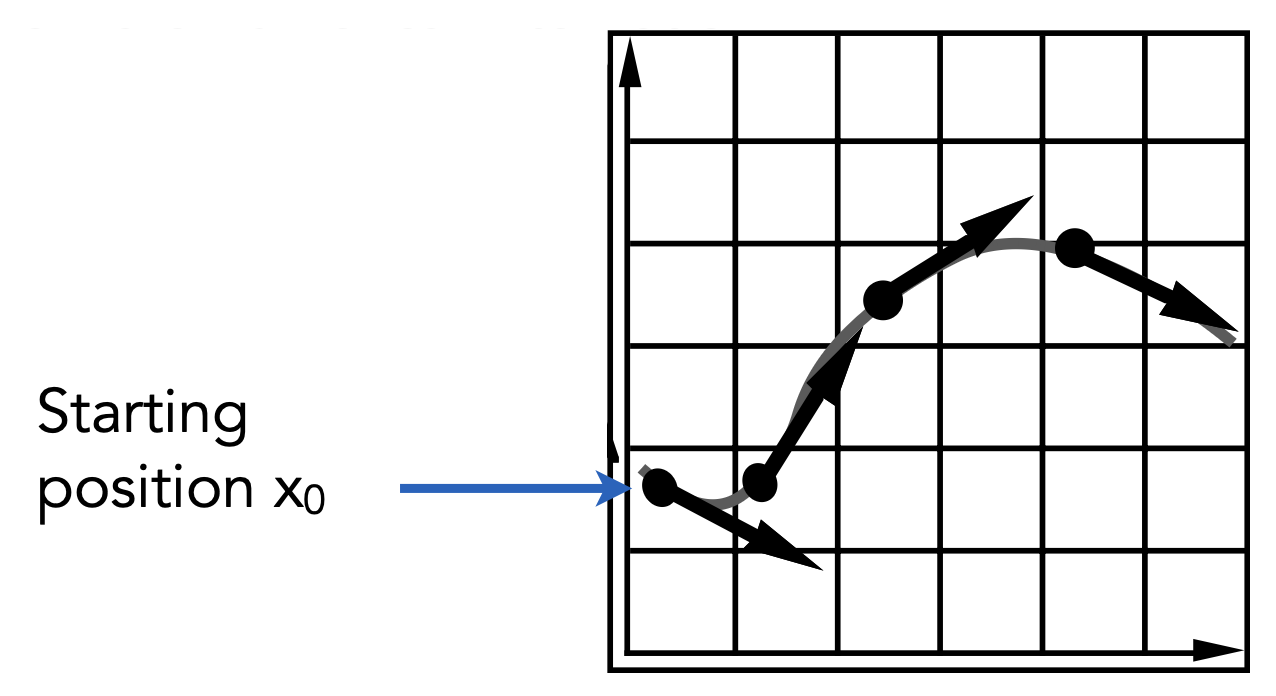
我们可以通过正向数值积分的方法，在给定初始粒子位置 $x_0$ 的条件下求解 ODE

下面就来介绍一些具体解法。

Euler Method⚓︎

第一种方法是欧拉法(Euler method)（又称前向(forward) 欧拉或显式(explicit) 欧拉法）。该方法具有以下特点：

一种简单的迭代法
常用
但非常不准确
且经常出现不稳定(unstable) 的情况

欧拉法的公式如下（在已知当前时刻位置的情况下，求解下一刻（仅相隔微小间隔）的位置）：

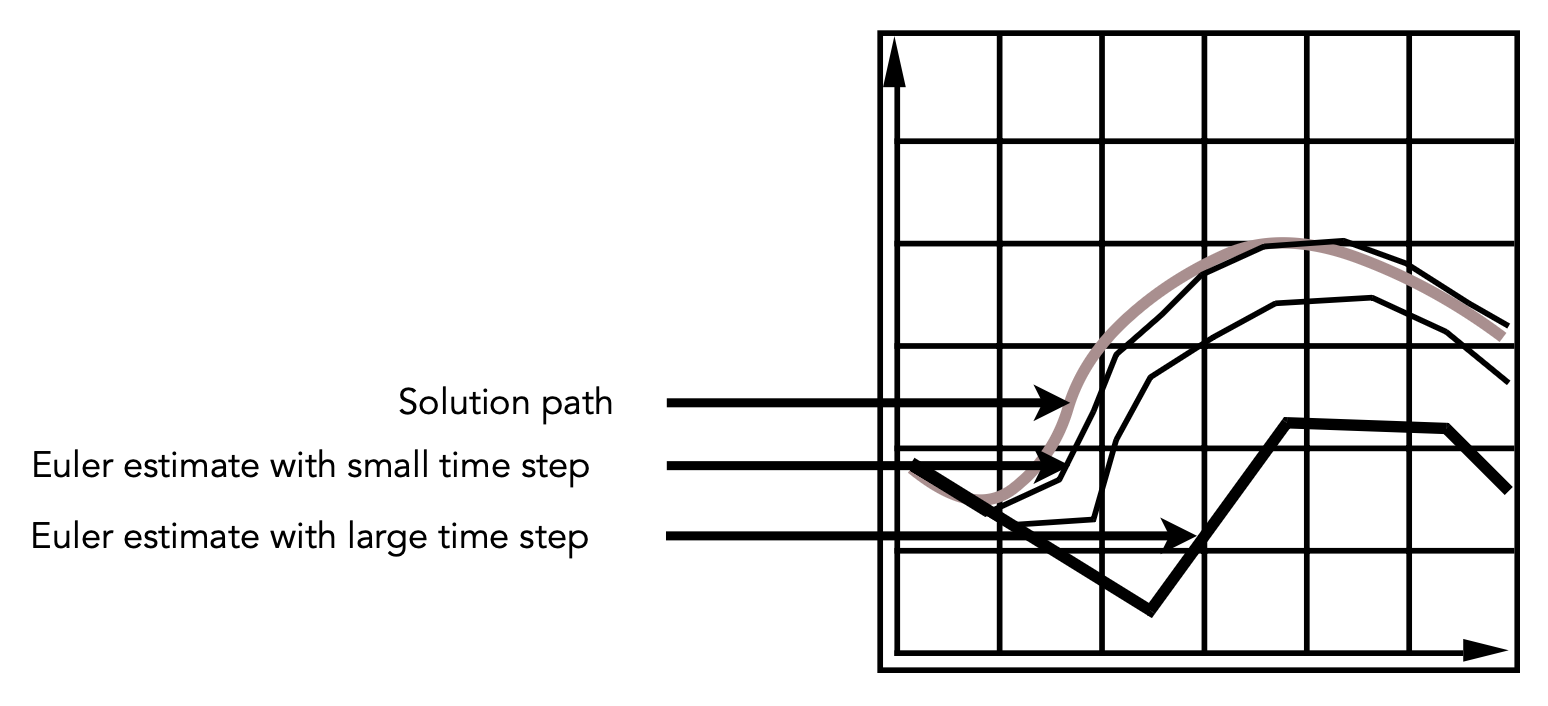
\[ \begin{aligned} \bm{x}^{t + \Delta t} & = \bm{x}^t + \Delta t \bm{\dot{x}}^t \\ \bm{\dot{x}}^{t + \Delta t} & = \bm{\dot{x}}^t + \Delta t \bm{\ddot{x}}^t \end{aligned} \]

由于数值积分的过程会不断积累误差，因此在欧拉法基础上做积分的结果通常很糟。如下图所示，时间间隔取得太大的话，就和真实运动路径相去甚远。

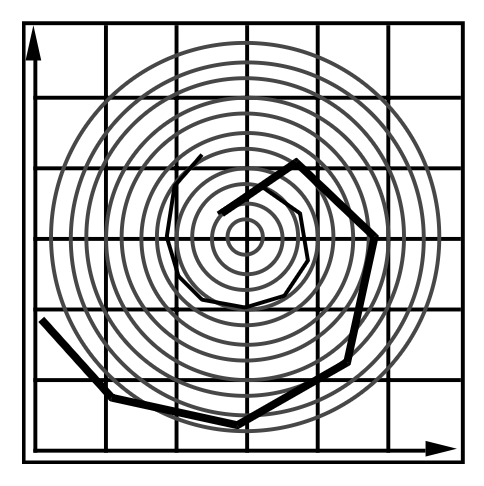
对于稳定性，欧拉法带来的关键问题是模拟运动发散的情况，这是不稳定性导致的常见却严重的问题，比如：

理论上应该严格沿螺旋线移动，但按照欧拉法就会跑到螺旋线外
理论上粒子的运动会收敛到中间这条水平线，但用欧拉法粒子的振荡会越来越大（类似信号处理的正反馈）

Errors and Instability⚓︎

一般来说，通过有限差分进行数值积分求解会引发两个问题：

误差
- 每时间步长下的误差会积累，因此随着模拟的进行，精度会逐渐降低
- 但在图形学应用中，精度不是关键问题
不稳定
- 误差可能会累积，导致模拟结果偏离实际，即便底层系统本身并未发生改变
- 稳定性缺失是模拟中不可被忽视的基本问题

例子

~~来自某吃鸡游戏的例子，视频中的车撞到摩托车后触发「完全なる黄金の回転エネルギー！」~~

视频链接：https://www.youtube.com/watch?v=Bz8n6GBAsys

所以人们想出很多对抗这种不稳定性的方法，下面将会一一介绍。

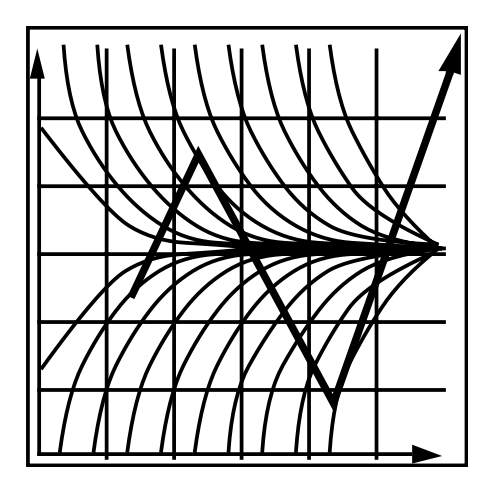
Midpoint Method⚓︎

中点法的思路是：

先用欧拉法计算下一步后的位置（a）
然后计算当前位置和下一步位置中间位置的导数（b）
最后使用这个导数来更新真正的下一步位置（c）

公式如下：

\[ \begin{aligned}x_{\mathrm{mid}}&=x(t)+\Delta t/2\cdot v(x(t),t)\\x(t+\Delta t)&=x(t)+\Delta t\cdot v(x_{\mathrm{mid}},t)\end{aligned} \]

Modified Euler⚓︎

改进欧拉法(modified Euler) 的思路是：

用下一步前后位置的速度的平均值作为下一步的速度
能得到更好的结果

公式如下：

\[ \begin{aligned} \boldsymbol{x}^{t+\Delta t}&=\boldsymbol{x}^t+\frac{\Delta t}{2}(\dot{\boldsymbol{x}}^t+\dot{\boldsymbol{x}}^{t+\Delta t})\\ \dot{\boldsymbol{x}}^{t+\Delta t}&=\dot{\boldsymbol{x}}^t+\Delta t\ddot{\boldsymbol{x}}^t\\ \boldsymbol{x}^{t+\Delta t}&=\boldsymbol{x}^t+\Delta t\dot{\boldsymbol{x}}^t+\frac{(\Delta t)^2}{2}\ddot{\boldsymbol{x}}^t \end{aligned} \]

Adaptive Step Size⚓︎

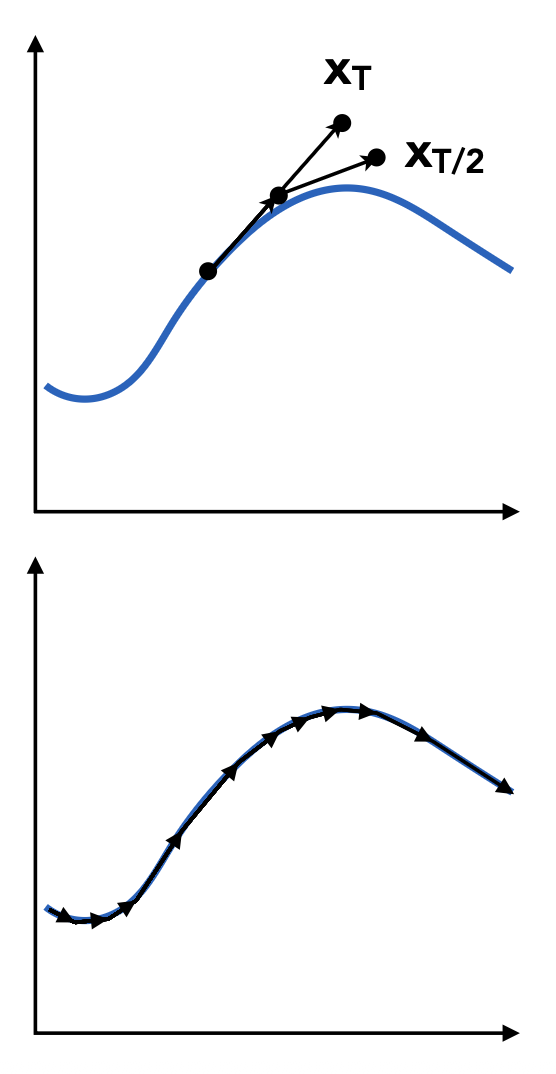
自适应步长(adaptive step size) 是一种基于误差估计选择步长的非常实用的一门技术。一个小问题是有可能需要很小的步长。其基本思路如下——重复以下步骤，直到误差小于阈值：

使用欧拉法得到 $T$ 时刻下的位置 $x_T$
使用欧拉法得到 $T/2$ 时刻下的位置 $x_{T/2}$
计算误差 $\|x_T - x_{T/2}\|$
若误差仍大于阈值，则减小步长并再次尝试

Implicit Euler Method⚓︎

隐式欧拉法(implicit Euler method)（非正式的称呼为反向法(backward method)）不同于一般的欧拉法，它利用的不是当前位置下的速度，而是未来位置上的速度。对于当前步，公式如下：

\[ \begin{aligned} \bm{x}^{t + \Delta t} & = \bm{x}^t + \Delta t \bm{\dot{x}}^{t + \Delta t} \\ \bm{\dot{x}}^{t + \Delta t} & = \bm{\dot{x}}^t + \Delta t \bm{\ddot{x}}^{t + \Delta t} \end{aligned} \]

问题转化为求解关于 $\bm{\dot{x}}^{t + \Delta t}, \bm{\ddot{x}}^{t + \Delta t}$ 的非线性问题。对于这类问题可以使用诸如牛顿法(Newton's method) 等寻根 (root-finding) 算法求解。

隐式欧拉法通常能得到好得多的稳定性。

说了那么多，其实我们还没有定义过，或者量化过“稳定性”这一概念。实际上，稳定性通常用局部截断误差(local truncation error)（对于每一步）和总累积误差(total accumulated error)（总体）来量化。我们不关心误差的绝对值，关心的是误差关于步长的阶数。

隐式欧拉法的误差是一阶的，这意味着（$h$ 表示步长，即 $\Delta t$）
- 局部截断误差：$O(h^2)$
- 总累积误差：$O(h)$
可以这样理解 $O(h)$：如果步长减少一半，那么误差也会减少一半；所以误差阶数是越大越好

Runge-Kutta Families⚓︎

龙格 - 库塔法(Runge-Kutta families) 是一组用于求解 ODE 的高级方法，尤其适用于求解非线性问题。其中它的四阶版本是最常用的，即 RK4。

初始条件：$\dfrac{dy}{dt}=f(t,y),\quad y(t_0)=y_0$
RK4 的解：

\[ \begin{aligned}&y_{n+1}=y_n+\frac{1}{6}h\left(k_1+2k_2+2k_3+k_4\right),\\&t_{n+1}=t_n+h\end{aligned} \]

其中：
- $k_1 = f(t_n, y_n)$
- $k_2=f\left(t_n+\dfrac{h}{2},y_n+h\dfrac{k_1}{2}\right)$
- $k_3=f\left(t_n+\dfrac{h}{2},y_n+h\dfrac{k_2}{2}\right)$
- $k_4=f\left(t_n+h,y_n+hk_3\right)$

Position-based / Verlet Integration⚓︎

最后介绍一种不是基于物理的方法——基于位置的 / Verlet 积分，它的思路是：

使用改进欧拉法计算前向步后，约束粒子位置，以阻止发散的、不稳定的行为
使用约束位置计算速度
这两个思路都会消耗运动粒子的能量，使之趋于稳定

特点：

快速简单
不基于物理实现能量损失，可能会有误差

注

以上内容和《数值分析》课程内容关系紧密，要想更深入地理解这些方法，最好去学一下相关知识。

Rigid Body Simulation⚓︎

对于刚体(rigid body) 模拟，它和模拟粒子运动类似，只是需要考虑更多刚体的性质。除了位置外，计算时还需考虑以下量：

\[ \left.\frac{d}{dt}\left(\begin{array}{c}\mathrm{X}\\\theta\\\mathrm{X}\\\omega\end{array}\right.\right)=\begin{pmatrix}\mathrm{\dot{X}}\\\omega\\\mathrm{F}/M\\\Gamma/I\end{pmatrix} \]