Materials and Appearances⚓︎
约 2357 个字 预计阅读时间 12 分钟
Material⚓︎
自然界中的材质:
CG 中的材质:
从数学角度看,材质(materials) 就是渲染方程中的 BRDF。下面列举一些常见的材质:
-
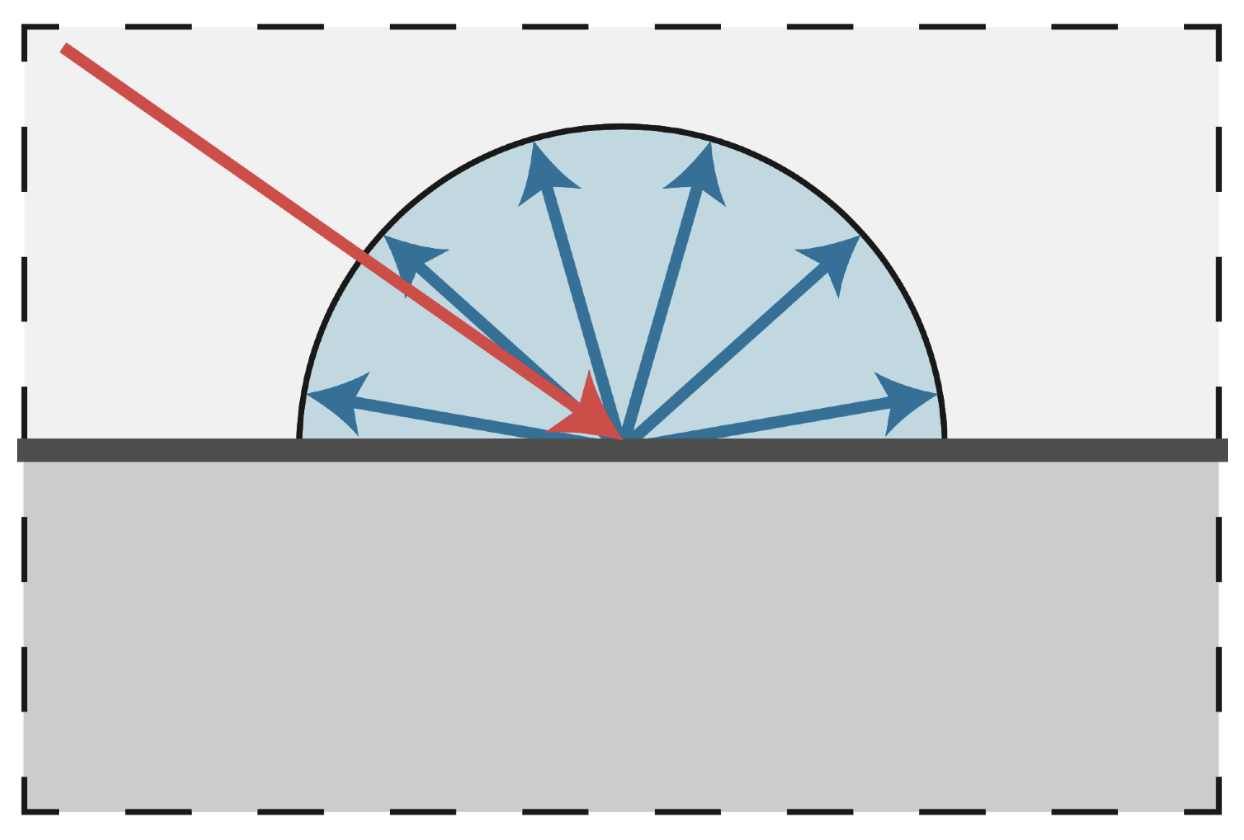
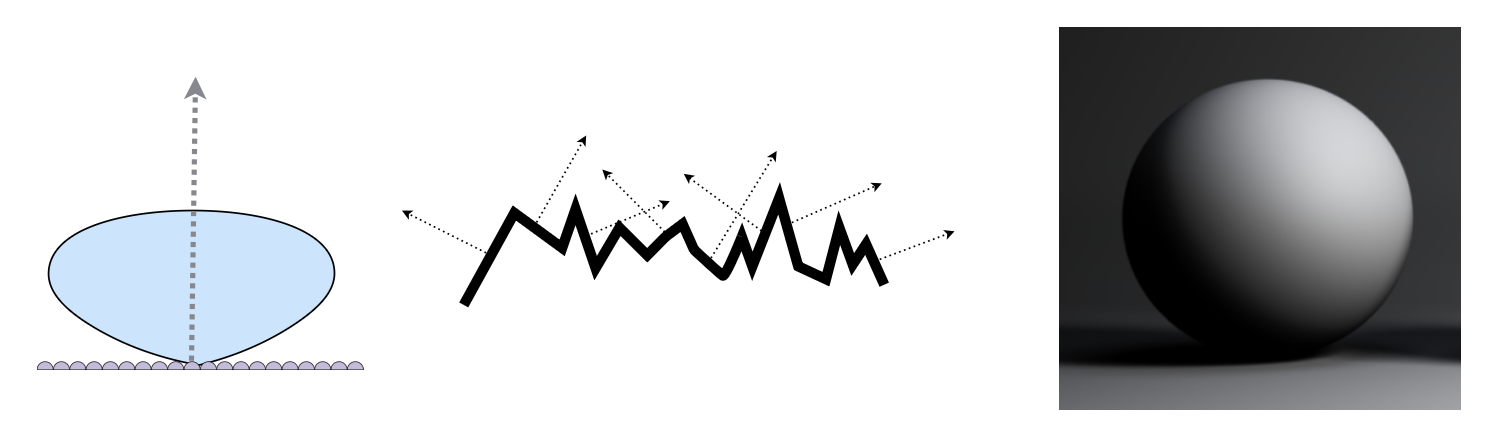
漫反射 / 朗伯(diffuse/Lambertian) 材质
-
原理图:
-
渲染效果:
-
假设入射光线的分布是均匀的,辐射率也是一样的;并且出射光线也是均匀分布,与入射光的辐射率一样(能量守恒
) ,那么\[ \begin{aligned}L_o(\omega_o)&=\int_{H^2}f_rL_i(\omega_i)\cos\theta_i\mathrm{d}\omega_i\\&=f_rL_i\int_{H^2}(\omega_i)\cos\theta_i\mathrm{~d}\omega_i\\&=\pi f_rL_i\end{aligned} \]假设 \(f_r, L_i\) 这两项是常数
-
其中 \(f_r = \dfrac{\rho}{\pi}\),其中 \(\rho\) 叫做反射率(albedo)(取值范围:[0, 1]
) ,和颜色相关
-
-
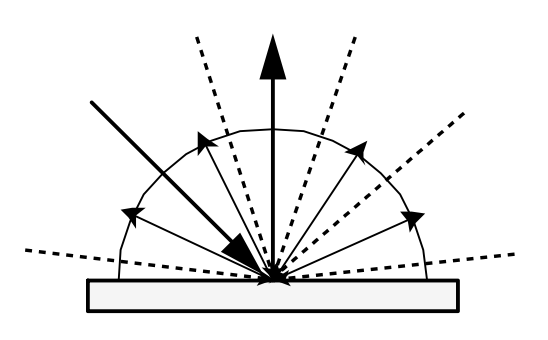
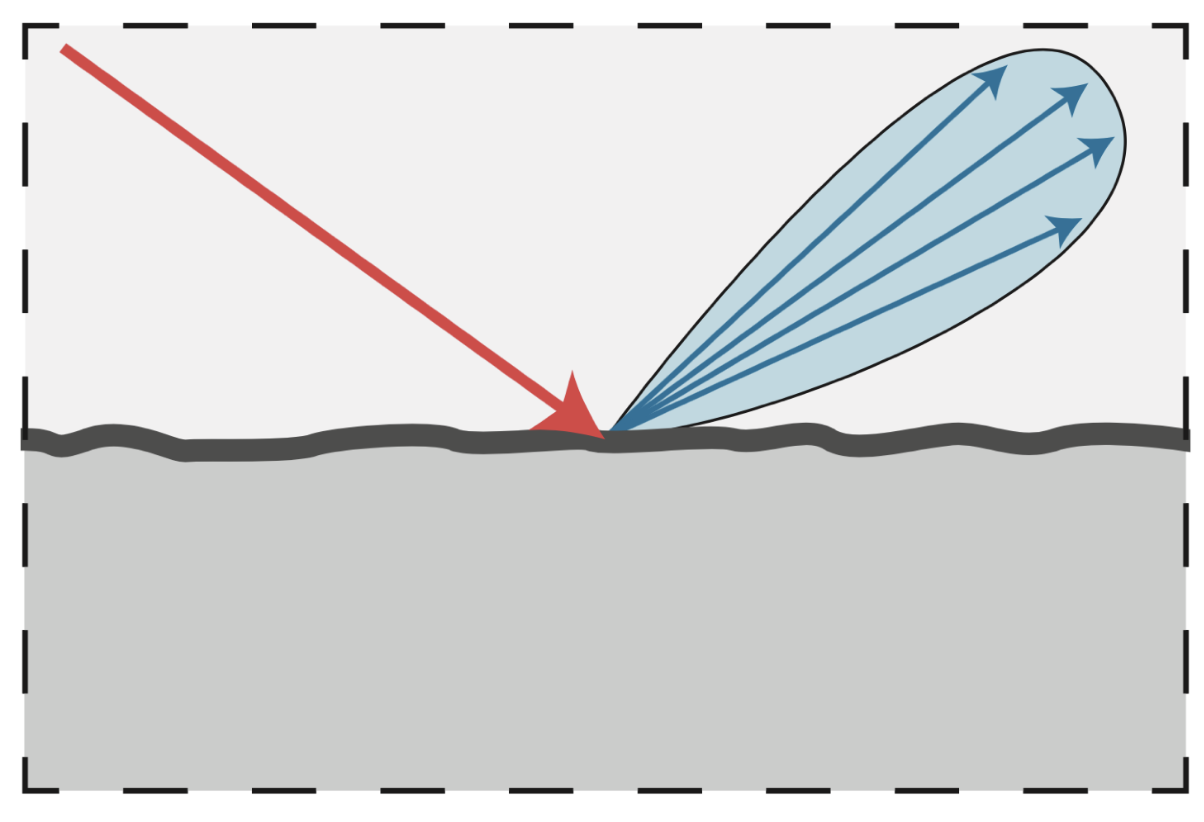
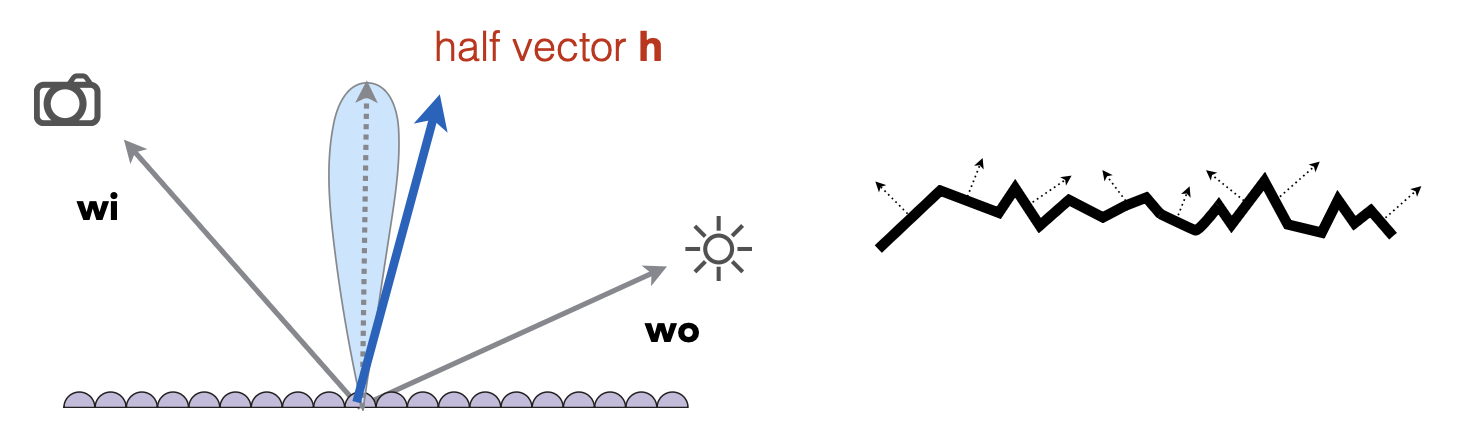
光泽(glossy) 材质
-
原理图:
-
渲染效果:
-
-
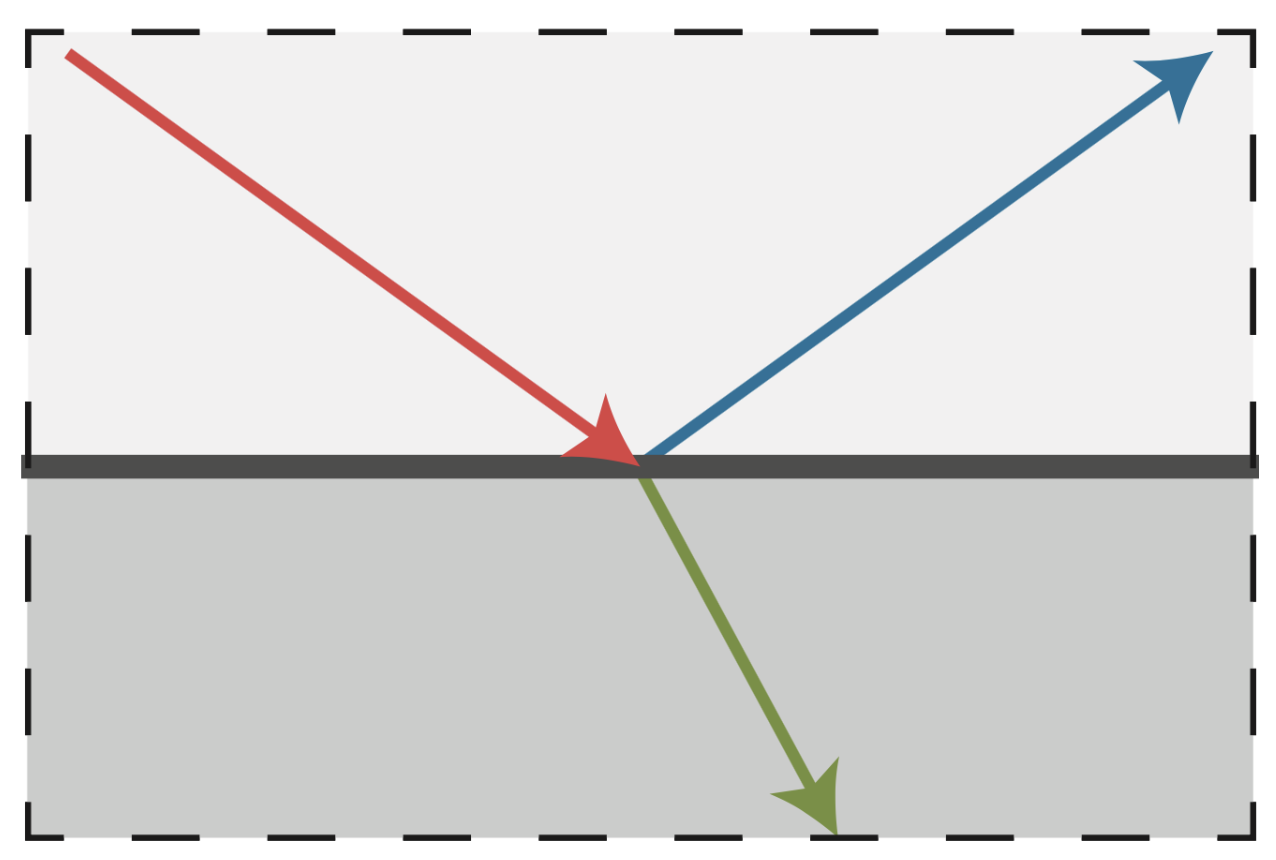
理想反射 / 折射(ideal reflection/refraction) 材质
-
原理图:
-
渲染效果:
- 对于右图,部分折射光被吸收,所以呈现颜色
-
Reflection⚓︎
完美的镜面反射 (perfect specular reflection):
反射的两种理解:
-
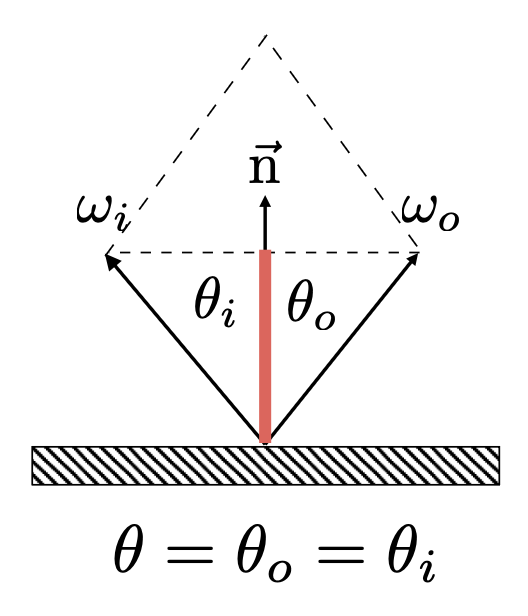
极角(polar angle):
\[ \begin{align*} \omega_o + \omega_i &= 2 \cos \theta \vec{n} = 2 (\omega_i \cdot \vec{n}) \vec{n} \\ \omega_o &= -\omega_i + 2 (\omega_i \cdot \vec{n}) \vec{n} \end{align*} \] -
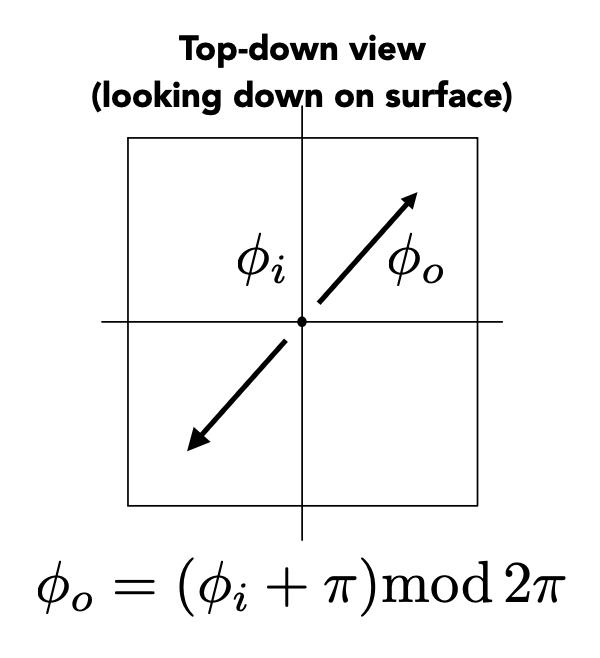
方位角(azimuthal angle):
\[ \varphi_o = (\varphi_i + \pi) \bmod 2\pi \]
渲染效果:
Refraction⚓︎
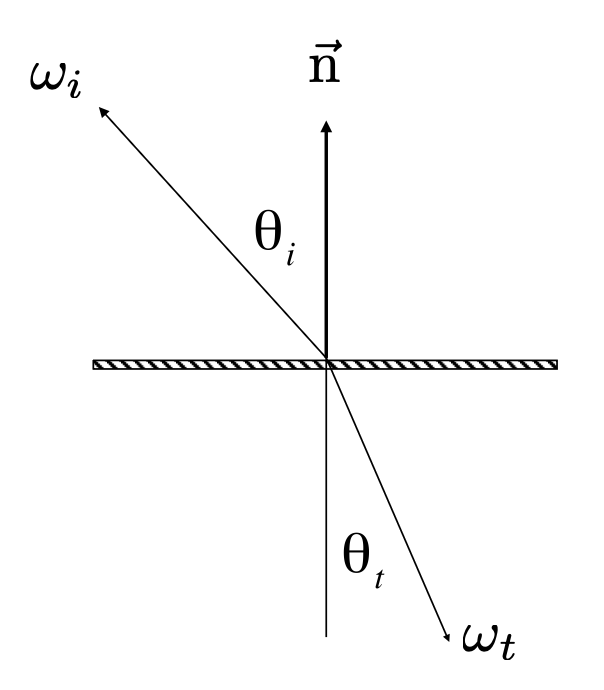
光线除了从物体表面上反射出去,也有可能通过折射穿过表面。当进入新的介质时,光的折射发生。
- 右下角关于海水的那幅图涉及到焦散(caustic) 现象:由光线集中所形成的弯曲、明亮的图案,比如图中海水上的光纹
关于光的折射有一个著名的物理定律,即斯涅尔定律(Snell's Law)(又称折射定律(law of refraction)
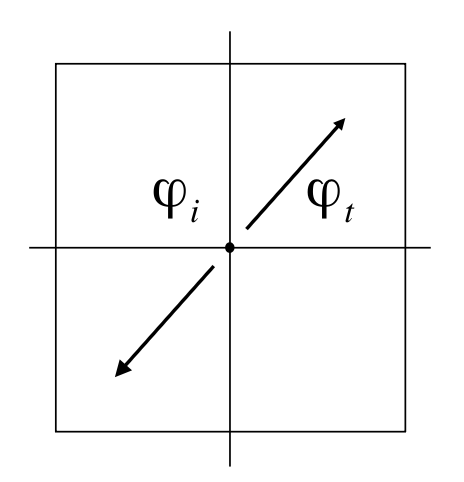
方向角的计算和反射类似: $$ \varphi_t = \varphi_i \pm \pi $$
常见材质的折射率如下:
根据折射定律,在已知入射光和出射光的折射率,以及入射角的情况下,就能计算出射角的大小了:
该式子成立的前提是算术平方根内的式子不小于 0。一旦小于 0,就说明出现了全反射(total internal reflection) 的现象。此时 \(\dfrac{\eta_i}{\eta_t} > 1\),即入射光的反射率大于出射光的反射率。
一种常见的光学现象背后的原理正是全反射,它就是斯涅尔窗 / 圆(Snell's window / circle):从水底往上看时,我们只能看到一块圆形区域内的光照,区域外是一片黑暗。示意图如下:
补充
BSDF("S" 代表散射 (scatter))= BRDF + BTDF("T" 代表透射 (transmit)(折射
Fresnel Term⚓︎
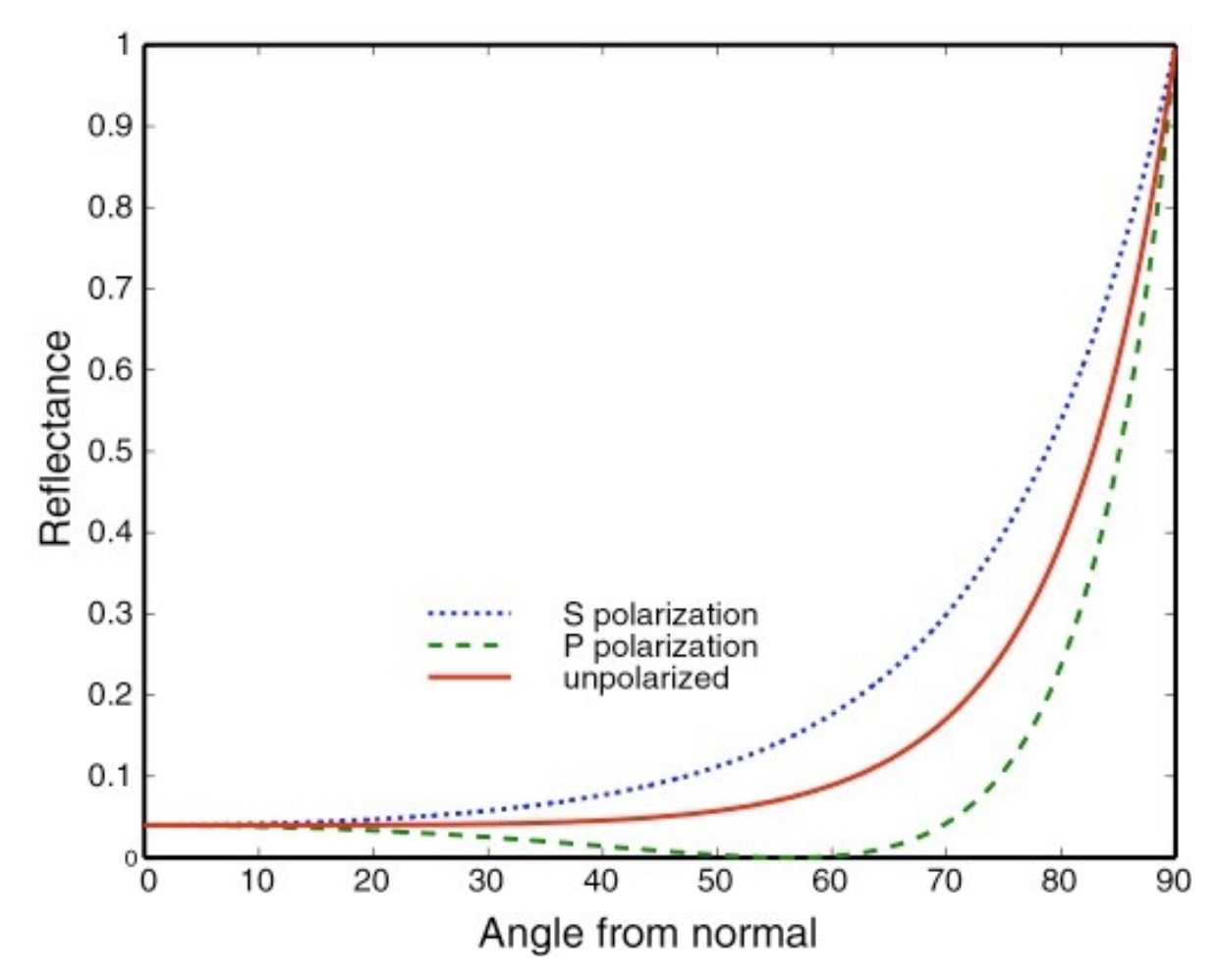
菲涅尔项(Fresnel term):反射率 (reflectance) 取决于入射角度(以及光的偏振 (polarization)
上面的例子反映了反射率随掠射角(grazing angle)(入射光线与法线的夹角)增大(即入射光越靠近表面)而增加(桌子上书本和墙壁的反光越明显
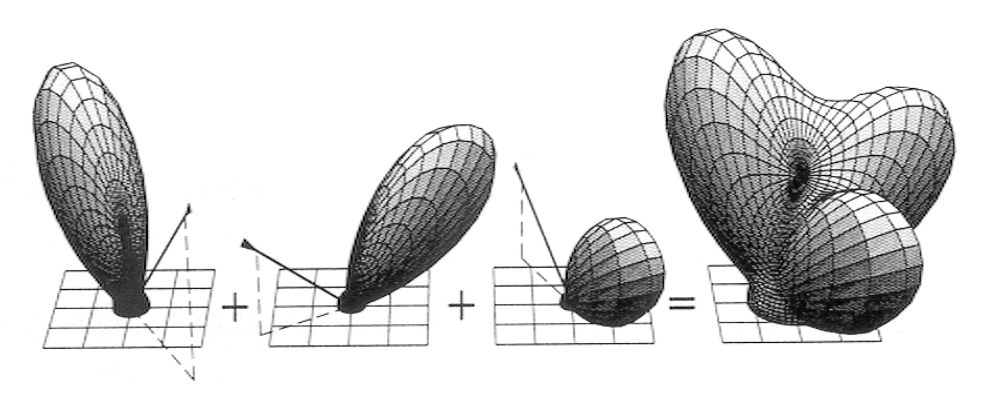
不同物体的菲涅尔项(横轴表示掠射角,纵轴表示反射率;图中的两条虚线表示考虑偏振的情况,不过一般无需考虑)
-
电介质 (dielectric)(\(\eta = 1.5\))
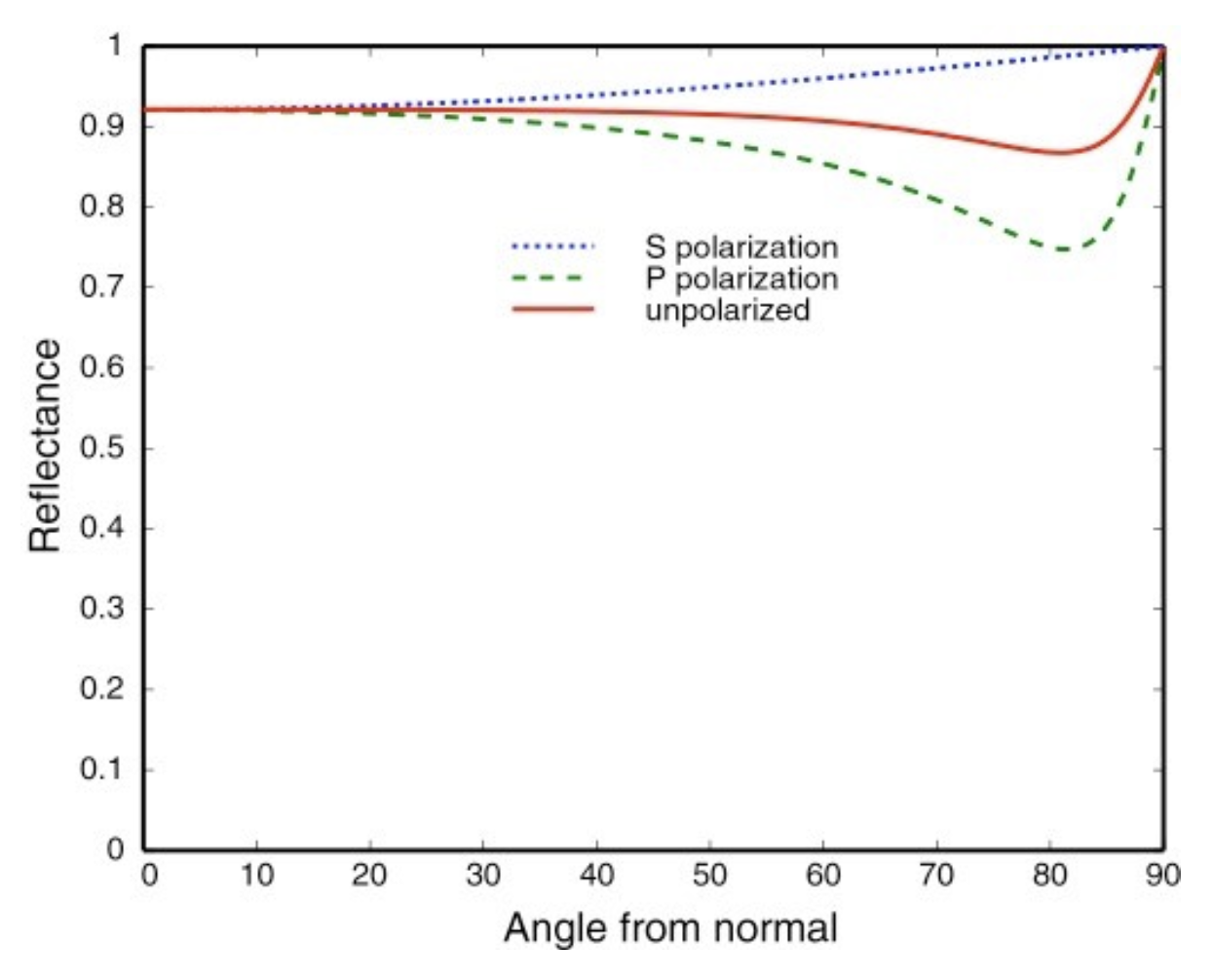
-
导体 (conductor)
补充
导体的折射率是复数(
不是负数)
菲涅尔项的计算公式:
-
精确版:考虑偏振
\[ \begin{align*} R_\mathrm{s}&=\left|\frac{n_1\cos\theta_\mathrm{i}-n_2\cos\theta_\mathrm{t}}{n_1\cos\theta_\mathrm{i}+n_2\cos\theta_\mathrm{t}}\right|^2=\left|\frac{n_1\cos\theta_\mathrm{i}-n_2\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_\mathrm{i}\right)^2}}{n_1\cos\theta_\mathrm{i}+n_2\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_\mathrm{i}\right)^2}}\right|^2 \\ R_\mathrm{p}&=\left|\frac{n_1\cos\theta_\mathrm{t}-n_2\cos\theta_\mathrm{i}}{n_1\cos\theta_\mathrm{t}+n_2\cos\theta_\mathrm{i}}\right|^2=\left|\frac{n_1\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_\mathrm{i}\right)^2}-n_2\cos\theta_\mathrm{i}}{n_1\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_\mathrm{i}\right)^2}+n_2\cos\theta_\mathrm{i}}\right|^2 \\ R_{\text{eff}} & = \dfrac{1}{2} (R_\mathrm{s} + R_\mathrm{p}) \end{align*} \] -
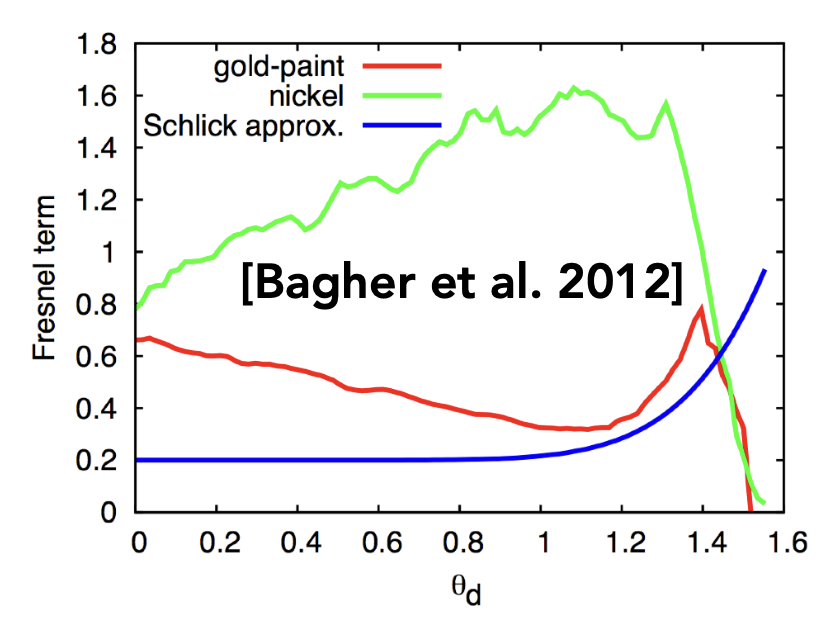
近似版:施利克近似(Schlick’s approximation)
\[ \begin{aligned}R(\theta)&=R_0+(1-R_0)(1-\cos\theta)^5\\R_{0}&=\left(\frac{n_1-n_2}{n_1+n_2}\right)^2\end{aligned} \]
精确版计算过于麻烦,所以在 CG 中如果不做很高的要求,一般就用近似版。
Microfacet Material⚓︎
引入
如图所示,这是从太空拍摄的地球图片。图中一块明亮的部分正是澳大利亚,看起来像一块平滑的表面。但实际上地球表面地形复杂,还有很多建筑,所以不可能是光滑的,但从远处看我们就难以观察这些细节了——这正是微表面材质的思路。
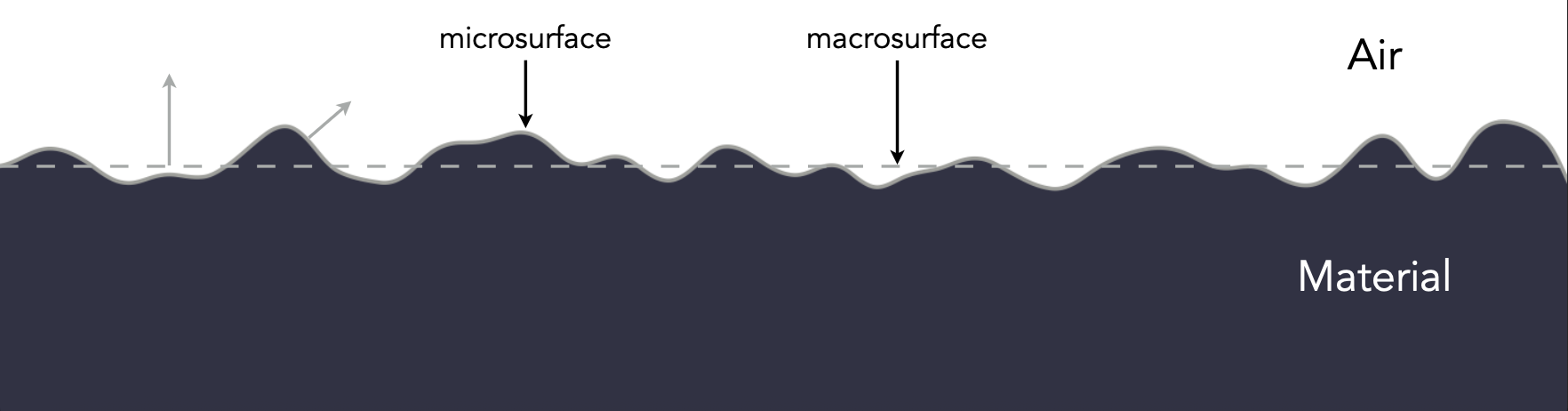
微表面(microfacet) 的理论:
-
对于实际上粗糙的表面
- 宏观角度(材质)看:平坦而粗糙
- 微观角度(几何)看:崎岖而光滑
-
表面上的单个元素就像镜子一样
- 称为微表面
- 每个微表面都有自己的法线
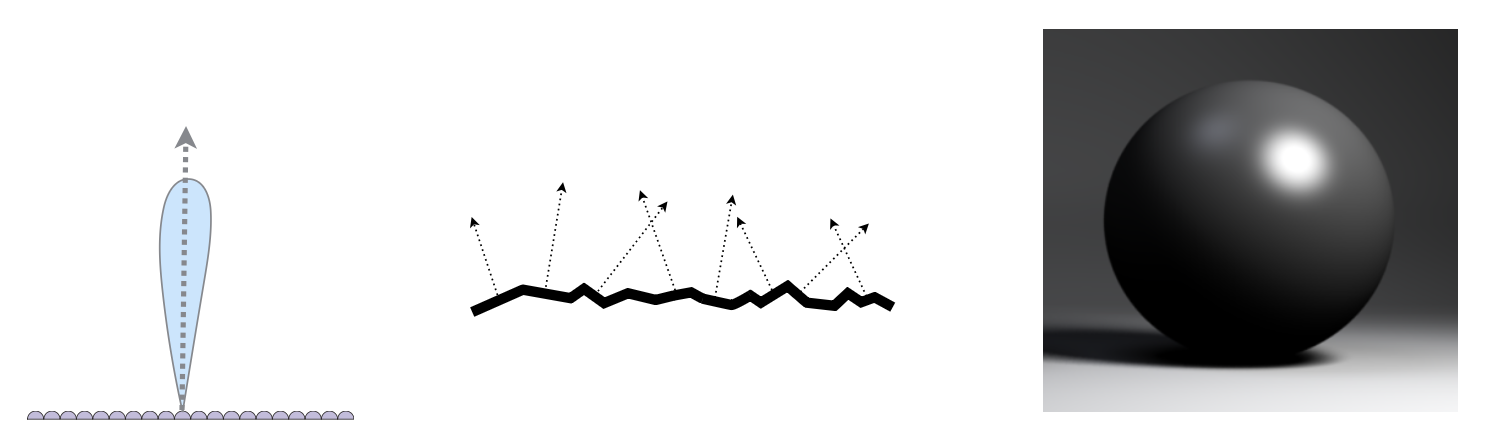
微表面 BRDF 的关键是微表面法线的分布
-
法线分布聚集 <==> 看起来像镜面反射
-
法线分布发散 <==> 看起来像漫反射
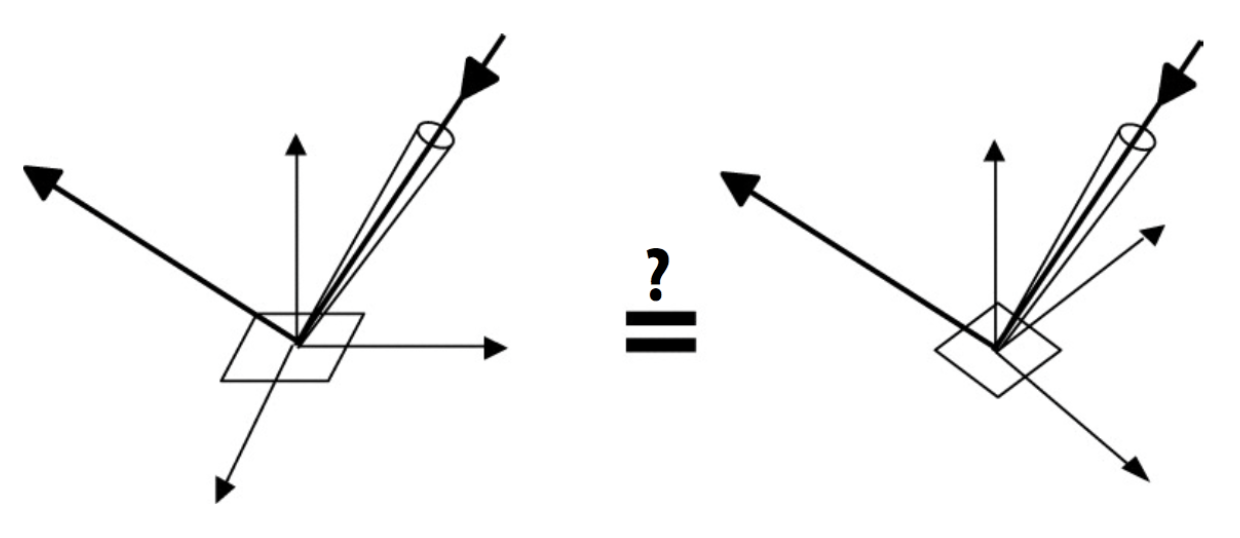
下面来看什么样的微表面会将来自 \(w_i\) 方向的光线沿 \(w_o\) 方向反射: $$ f(\mathbf{i},\mathbf{o})=\frac{\mathbf{F}(\mathbf{i},\mathbf{h})\mathbf{G}(\mathbf{i},\mathbf{o},\mathbf{h})\mathbf{D}(\mathbf{h})}{4(\mathbf{n},\mathbf{i})(\mathbf{n},\mathbf{o})} $$
其中(\(\mathbf{h}\) 表示半向量,即 \(\mathbf{i},\mathbf{o}\) 的角平分线
- \(\mathbf{F}(\mathbf{i},\mathbf{h})\):菲涅尔项
- \(\mathbf{G}(\mathbf{i},\mathbf{o},\mathbf{h})\):阴影遮罩项(几何项)
- 有些微表面的光可能会被挡住(自遮挡
) ,尤其是在光线从偏水平方向入射时更容易发生
- 有些微表面的光可能会被挡住(自遮挡
- \(\mathbf{D}(\mathbf{h})\):法线分布
Isotropic / Anisotropic Materials⚓︎
例子
我们知道,电梯间内部一般都是金属。但顶上的光线打在表面上的结果和之前讲的有些不同——如上图所示,这些光在表面形成了多条亮线。这是因为这些金属是打磨过的,表面和一般的金属并不一样。这样的金属表面具有各向异性(anisotropy)。
各向同性和各向异性的区别来自底层表面的方向性(directionality):
对于各向异性 BRDF,反射依赖于方位角 (azimuthal angle) \(\varphi\)。 $$ f_r(\theta_i,\varphi_i;\theta_r,\varphi_r)\neq f_r(\theta_i,\theta_r,\varphi_r-\varphi_i) $$
这个不等式的意思是这个不等式的意思是 BRDF 值不止和相对的方向角有关,还和绝对的方位角有关。
Properties of BRDFs⚓︎
-
非负性 (non-negativity)
\[ f_r(\omega_i \rightarrow \omega_r) \ge 0 \] -
线性 (linearity)
\[ L_r(\mathrm{p},\omega_r)=\int_{H^2}f_r(\mathrm{p},\omega_i\to\omega_r)L_i(\mathrm{p},\omega_i)\cos\theta_i\mathrm{d}\omega_i \] -
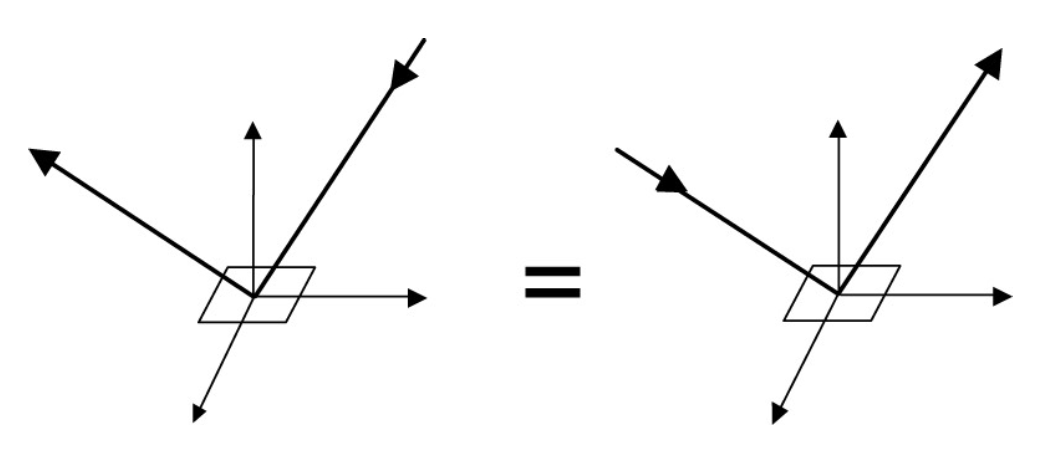
可逆原理 (reciprocity principle)
\[ f_r(\omega_r \rightarrow \omega_i) = f_r(\omega_i \rightarrow \omega_r) \] -
能量保存 (energy conservation)
\[ \forall\omega_r,\ \int_{H^2}f_r(\omega_i\to\omega_r)\cos\theta_i\mathrm{d}\omega_i\leq1 \] -
各向同性 vs. 各向异性
-
如果是各向同性,\(f_r(\theta_i,\varphi_i;\theta_r,\varphi_r)= f_r(\theta_i,\theta_r,\varphi_r-\varphi_i)\)
- 4D -> 3D,简化计算
-
此时根据可逆性
\[ f_r(\theta_i,\theta_r,\varphi_r-\varphi_i)=f_r(\theta_r,\theta_i,\varphi_i-\varphi_r)=f_r(\theta_i,\theta_r,|\varphi_r-\varphi_i|) \]
-
Measuring BRDFs⚓︎
下面列举一些测量 BRDF 的方法:
-
基于图像的测量方法
-
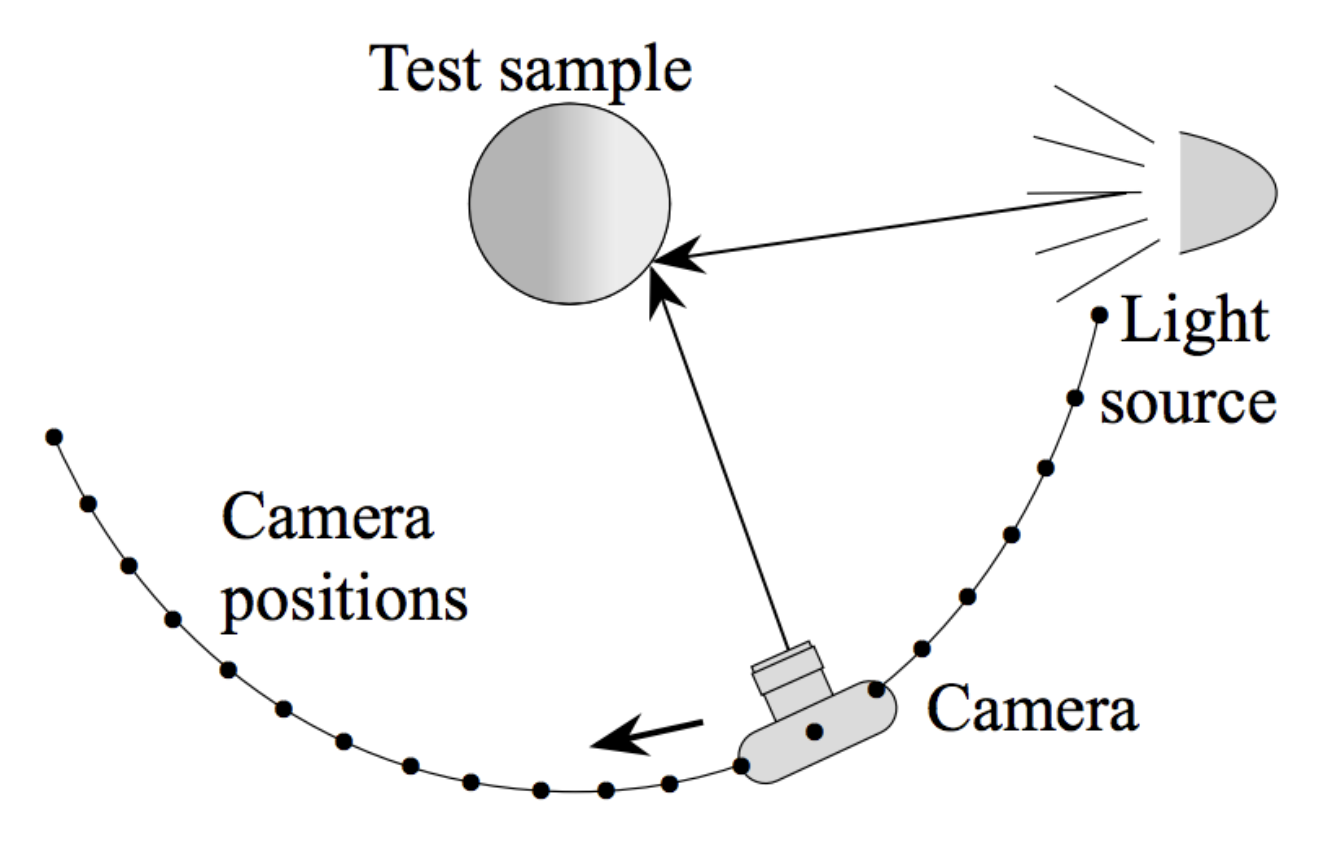
测角反射计 (gonioreflectometer)
- 球形龙门架 (Spherical gantry)(@UCSD)
-
通用方法:
一些改进效率的措施:
- 通过各向同性表面,将方向性从 4D 降至 3D
- 利用可逆性可将需要测量的东西减半
- 设计更精巧的光学系统
- ...
测量 BRDFs 时会遇到的挑战
- 对掠射角的精确测量
- 由于菲涅尔效应,这一点非常重要
- 以足够密集的采样进行测量,以捕捉高频镜面反射
- 逆向反射 (retro-reflection)
- 随空间变化的反射率 (spatially-varying reflectance)
- ...
要表示出测量好的 BRDF,理想的表示应该满足:
- 紧凑的表示
- 对测量数据的精确表示
- 对任意对的方向进行高效求值
- 适用于重要性采样的优良分布
这里介绍其中一种表示法——表格表示 (tabular representation)
- 在 \((\theta_i, \theta_o, |\varphi_i - \varphi_o|)\) 上存储等间距 (regularly-spaced) 的样本
- 更好的做法:重新参数化角度,以更好地匹配高光效果
- 通常需要将测量值重新采样至表格中
- 很高的存储需求
评论区