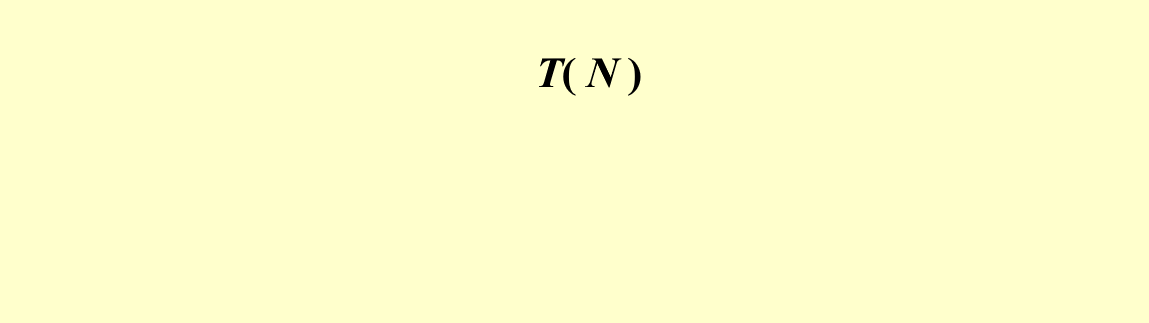Lec 7: Divide and Conquer⚓︎
约 3988 个字 13 行代码 预计阅读时间 20 分钟
分治 (divide and conquer) 算法算是我们的老朋友了——在 FDS 的学习中,我们已经在这些问题中用到了分治算法:
再来简单回顾一下分治的大致思想:
- 将问题分成 (divide) 一系列的子问题
- 递归解决 (conquer) 这些子问题
- 将子问题的解合并起来 (combine),构成原问题的解
时间复杂度的递推公式为:
注
这里给出的只是最简单的一种形式,事实上递推公式等号的右边可能会有更多的递推项。
Examples⚓︎
如果好久没有接触过分治算法,不妨拿下面这道题练练手,温习一下分治算法的做法。
Closest Points Problem⚓︎
问题描述
在平面上给定 \(N\) 个点,请找出距离最近的一对点(如果两个点位于相同的位置,则认为它们之间的距离为 0,但本题保证所有点均分布在不同的位置上
解法
一共有 \(N\) 个点,那么就有 \(\dfrac{N(N - 1)}{2}\) 个距离,逐一遍历和比较这些距离,时间复杂度为 \(T = O(N^2)\)。
回顾一下最大子序列之和的解法:我们先将整个序列拆成两半,然后分别计算左半边子序列,右半边子序列,以及分界线中间区域子序列的最大和,最后取这 3 个结果中的最大者,作为该序列的最大子序列之和。这里我们借鉴这种解法来解决这一问题。
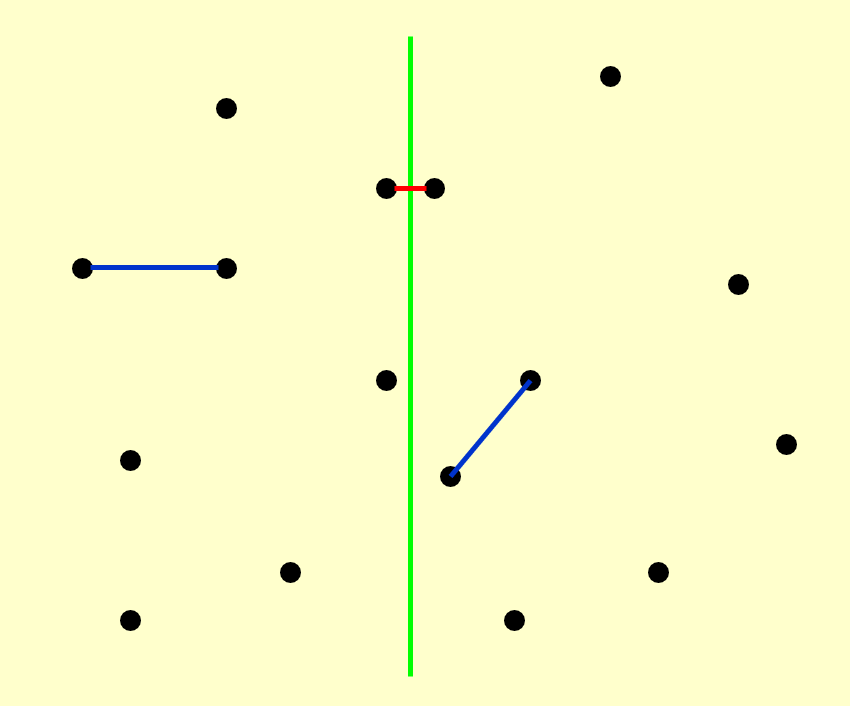
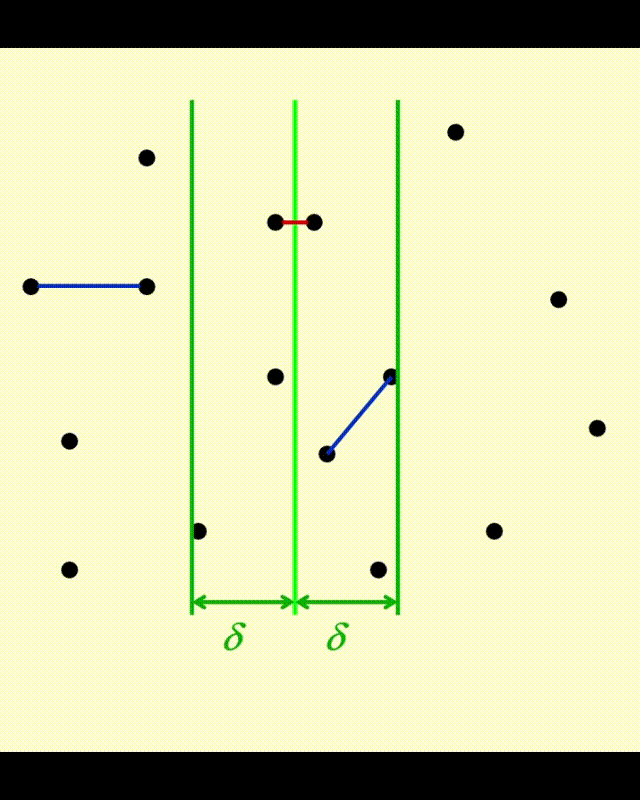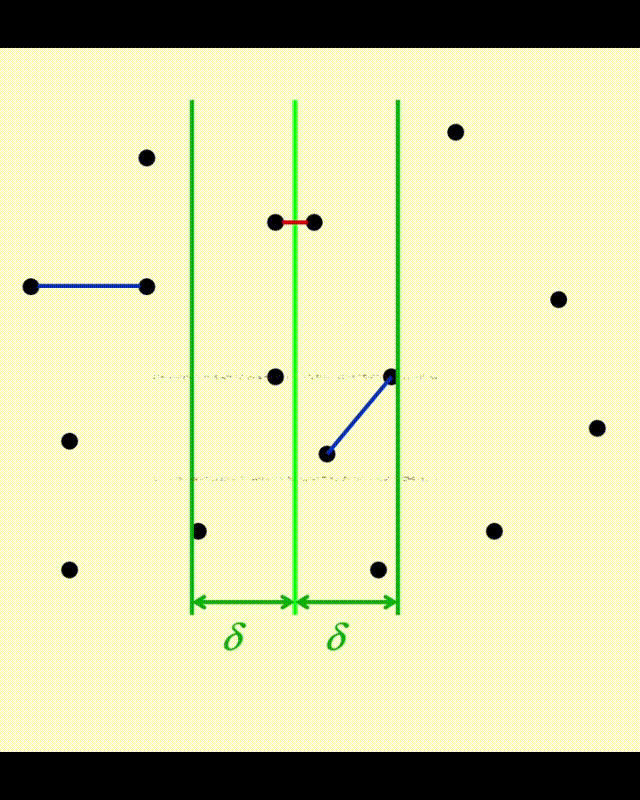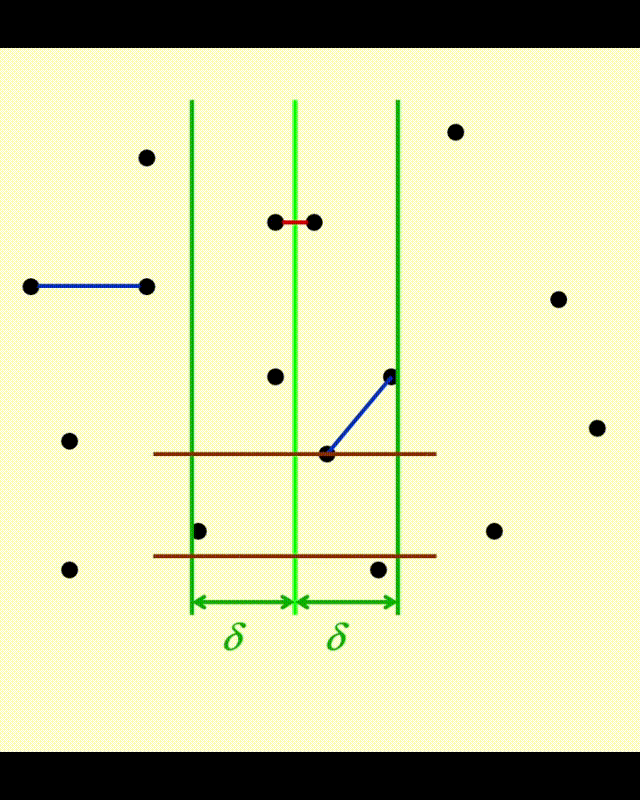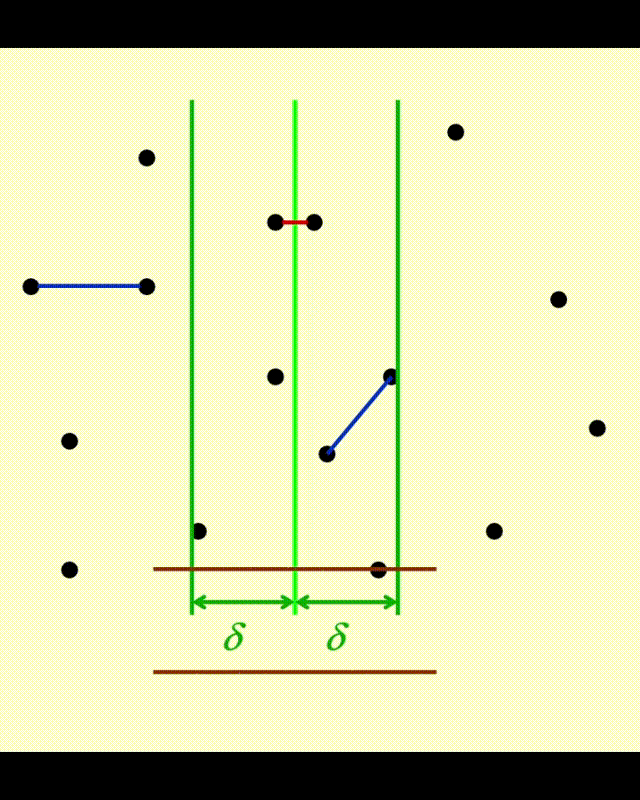
- 首先,我们根据这些点的 x 轴坐标,将整个区域一分为二(用绿色竖线隔开
) ,划分时确保两边的点的数目大致相等 - 这里仅画了三根两点间的连线,分别对应了三种不同的情况:左半边、中间和右半边
-
其中左半边和右半边这两种情况可以递归解决,因此我们最关心的问题是如何处理中间的情况。如果我们能确保计算中间部分的时间复杂度是线性的,那么整个算法的时间复杂度为 \(O(N \log N)\),下面给出解释:
解释
在这个问题中,对于时间复杂度的递推公式 \(T(N) = aT(\dfrac{N}{b}) + f(N)\),\(a = b = 2\),令 \(f(N) = cN\),那么:
\[ \begin{align} T(N) & = 2T(\dfrac{N}{2}) + cN \notag \\ & = 2[2T(\dfrac{N}{2^2}) + c\dfrac{N}{2}] + cN \notag \\ & = 2^2 T(\dfrac{N}{2^2}) + 2cN \notag \\ & = \dots \notag \\ & = 2^k T(\dfrac{N}{2^k}) + kcN \notag \\ & = N + cN \log N = O(N \log N) \notag \end{align} \]所以我们说此时整个算法的时间复杂度为 \(O(N \log N)\)。
如果 \(f(N) = cN^2\),那么:
\[ \begin{align} T(N) & = 2T(\dfrac{N}{2}) + cN^2 \notag \\ & = 2[2T(\dfrac{N}{2^2}) + c\dfrac{N^2}{2^2}] + cN^2 \notag \\ & = 2^2 T(\dfrac{N}{2^2}) + cN^2(1 + \dfrac{1}{2}) \notag \\ & = \dots \notag \\ & = 2^k T(\dfrac{N}{2^k}) + cN^2(1 + \dfrac{1}{2} + \dots + \dfrac{1}{2^{k-1}}) \notag \\ & = O(N^2) \notag \end{align} \]这里用到的分析方法就是下面即将介绍的代换法(substitution)。
-
如果考虑分隔线两边所有的点,那么时间复杂度就会来到了 \(O(N^2)\) 的水平,这显然不是我们所希望的
-
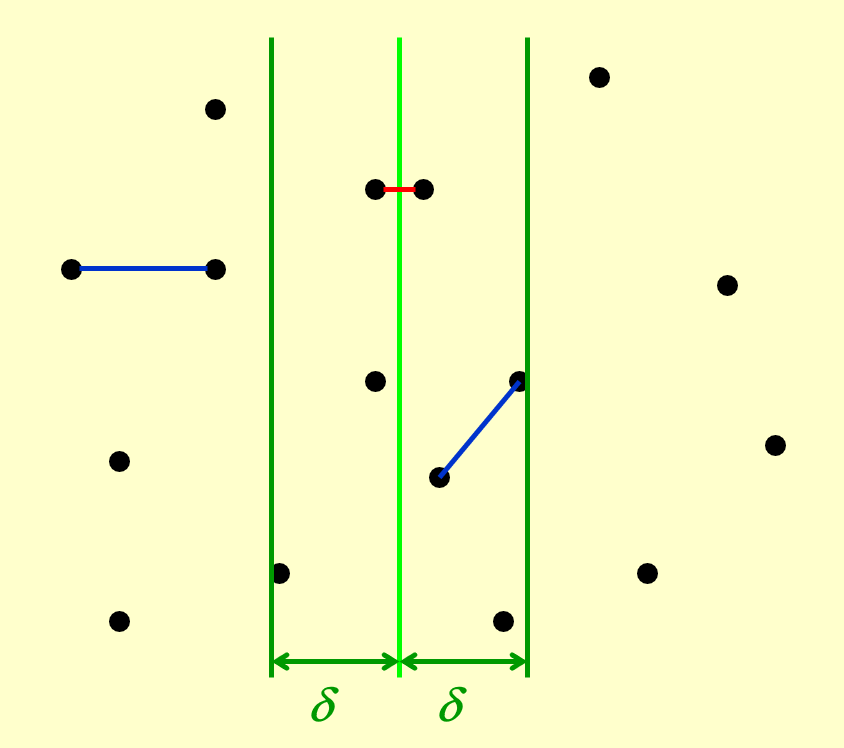
一种可行的改进方法是:仅考虑距分隔线水平距离为 \(\delta\) 内的点,其中 \(\delta\) 是我们提前选定的常数。现在,我们得到了一个位于中间部分,且宽度为 \(2\delta\) 的区域,称为 \(\delta\) 带 (\(\delta\)-strip)。这个区域之外的点显然不会是最近点对的可能点
-
代码实现如下:
-
如果能够确保 \(\delta\) 带内的点数为 \(O(\sqrt{N})\),那么计算中间情况的时间复杂度就是 \(O(\sqrt{N} \times \sqrt{N}) = O(N)\) 了
- 然而,如果 \(\delta\) 没有选好,最坏情况下 \(\delta\) 带内包含了所有点,那这个算法又退回到 \(O(N^2)\) 了。因此需要再次改进这个算法,避免这种最坏情况的发生
-
-
进一步的改进方法是:在确定垂直 \(\delta\) 带区域的基础上,再划分水平 \(\delta\) 带区域。详细步骤为:
- 根据点的 y 坐标,从 y 坐标最大的点开始往下遍历垂直 \(\delta\) 带内的每个点,对于每个点,我们仅计算位于该点下方且距离该点小于等于 \(\delta\) 的点和它之间的距离(划分水平 \(\delta\) 区域)
- 对于 y 坐标相同的点,它们将会被一起处理
-
对于正在被处理的点 \(p\),它一定位于一个 \(2\delta \times \delta\) 的矩形区域内,如图所示:


- 分隔线正好将矩形划分为 2 个方形 L 和 R
- 可以验证,在最坏情况下,每个点只需要考虑与其他 7 个点的距离即可。此时,这些点分布于方形 L 的四个角以及方形 R 的四个角上(其中 L 的右侧与 R 的左侧重合,因此会有一些点重合
) ,在上图分别为红色的四个点和绿色的四个点。 - 因此,即使所有的点都在垂直 \(\delta\) 带内,因为每个点的判断是常数次的,因此中间情况的时间复杂度就是 \(O(N)\) 了
代码实现
综上,本题分治算法的时间复杂度为 \(T(N) = 2T(\dfrac{N}{2}) + O(N) = O(N \log N)\)
Analysis⚓︎
对于时间复杂度的递推公式 \(T(N) = aT(\dfrac{N}{b}) + f(N)\),我们有以下求解方法:
- 代换 (substitution) 法
- 递归树 (recursive-tree) 法
- 主方法 (master method)
在分析的时候,我们会忽略以下细节问题:
- 不关心 \(\dfrac{N}{b}\) 是否是整数
- 对于较小的 \(n\),始终假定 \(T(n) = \Theta(1)\)
Substitution⚓︎
代换法是三种方法中最简单的一种(判断 & 选择常用技巧
- 先猜一个结论(假设)
- 然后代入这个假设,用归纳法证明该结论的正确性
例子
已知 \(T(N) = 2T(\lfloor \dfrac{N}{2} \rfloor) + N\),求 \(T(N)\)。
- 先猜测 \(T(N) = O(N \log N)\)
- 再证明:
证明
- 假设对于 \(m < N\),该结论成立
-
取 \(m = \lfloor \dfrac{N}{2} \rfloor\),那么存在一个常数 \(c > 0\),使得 $$ T(\lfloor \dfrac{N}{2} \rfloor) \le c \lfloor \dfrac{N}{2} \rfloor \log \lfloor \dfrac{N}{2} \rfloor $$
-
将这个式子带入递推公式,得:
- 不必特别在意 \(N = 1\) 的情况:前面的假设 2 已经“忽略”这种 trivial case;或者也可以将 \(N = 2\) 或 \(N = 3\) 作为基本情况 (base case),只要 \(c\) 足够大这个式子一定成立
错误的猜测
如果我们猜测 \(T(N) = O(N)\),那么会有以下证明:
- 假设对于 \(m < N\),该结论成立
-
取 \(m = \lfloor \dfrac{N}{2} \rfloor\),那么存在一个常数 \(c > 0\),使得 $$ T(\lfloor \dfrac{N}{2} \rfloor) \le c \lfloor \dfrac{N}{2} \rfloor $$
-
将这个式子带入递推公式,得:
这样的证明看起来没什么问题,但错误发生在最后一个不等式上:我们得到了 \(cN + N = (c + 1)N\),虽然它的时间复杂度确实是 \(O(N)\),但在形式上它是错误的,因为我们预先假设正确的结论是 \(T(m) \le cm\),所以要根据这个条件证明出形如 \(T(N) \le cN\) 的不等式正确,\((c + 1)N\) 在形式上就不满足要求了。换句话说,我们必须证明出精确的形式(exact form),连系数也必须保持一致。
通过对这个例子的分析,我们发现这个方法最困难的点在于做出一个好的猜测。
小技巧
- 如果时间复杂度的递推关系式中出现类似 \(T(\sqrt{N})\) 等形式,可以考虑换元法:
- 令 \(m = \log n\),那么 \(T(\sqrt{n}) = T(2^{\frac{m}{2}})\),\(T(n) = T(2^m)\)
- 再令 \(S(m) = T(2^m)\),那么 \(S(\dfrac{m}{2}) = T(2^{\frac{m}{2}})\),这样整个递推关系式就被转化为一般的形式了
- 如果出现形如 \(T(f(N) + c)\) 的形式(\(c\) 为常数
) ,由于 \(N\) 足够大,因此可以忽略常数 \(c\)
Recursive Trees⚓︎
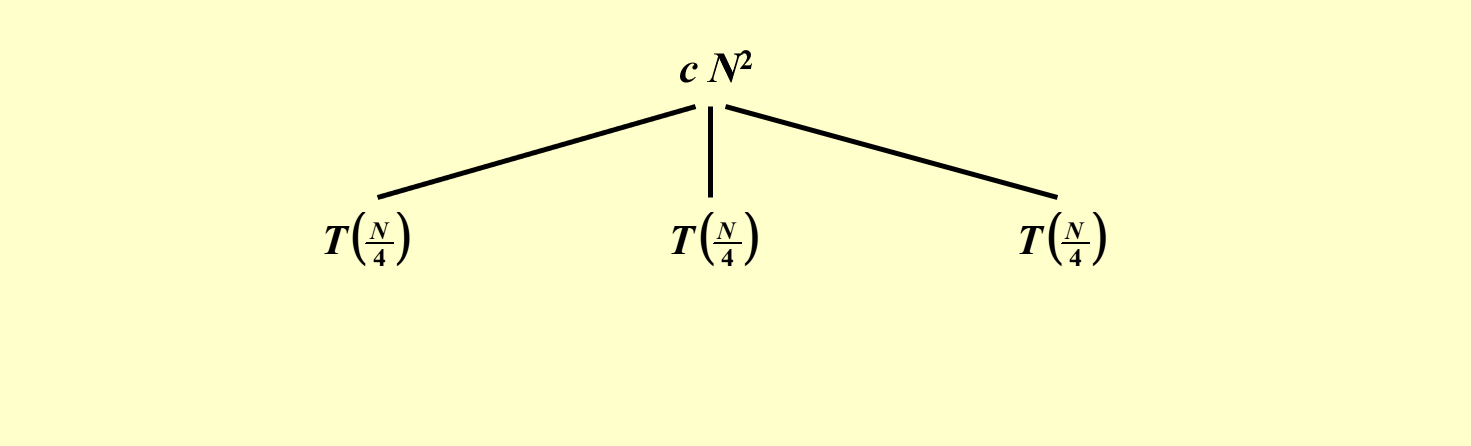
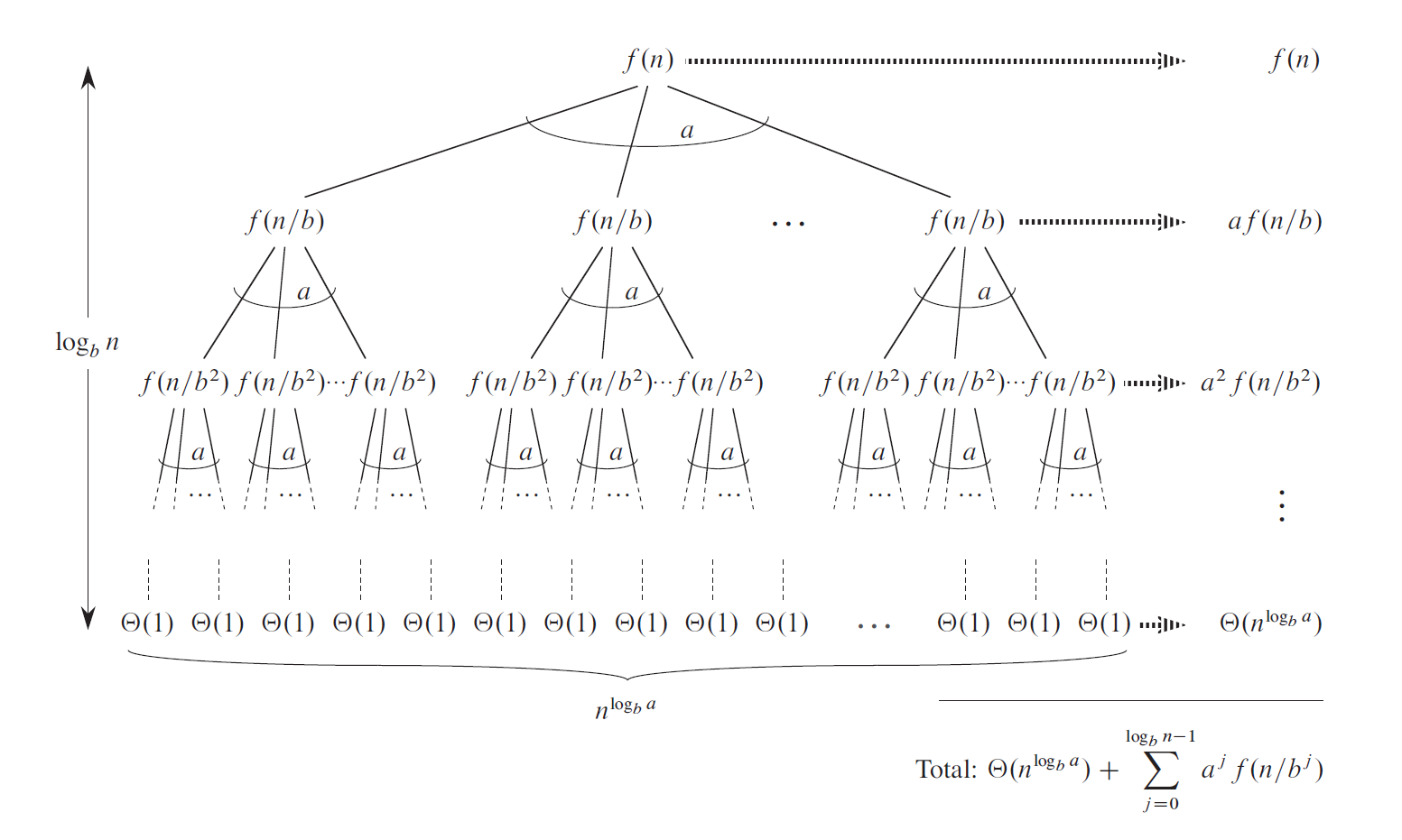
顾名思义,就是根据递推关系递归地来画一棵树。这棵树具有以下特征(假如递推关系形如 \(T(N) = aT(\dfrac{N}{b}) + f(N)\)
- 根节点为 \(f(N)\)
- 一个节点有 \(a\) 个孩子,每个孩子节点为 \(f(\dfrac{N}{b})\),因此这棵树根据递推公式延伸下去,体现了“递归”的特性
- 叶子节点为 \(T(1)\)
- 树的高度为 \(\log_b N\)
- 时间复杂度 = 所有节点之和 = 内部节点(对应合并操作的时间复杂度)之和 + 叶子节点(对于 base case 的时间复杂度)之和
例子
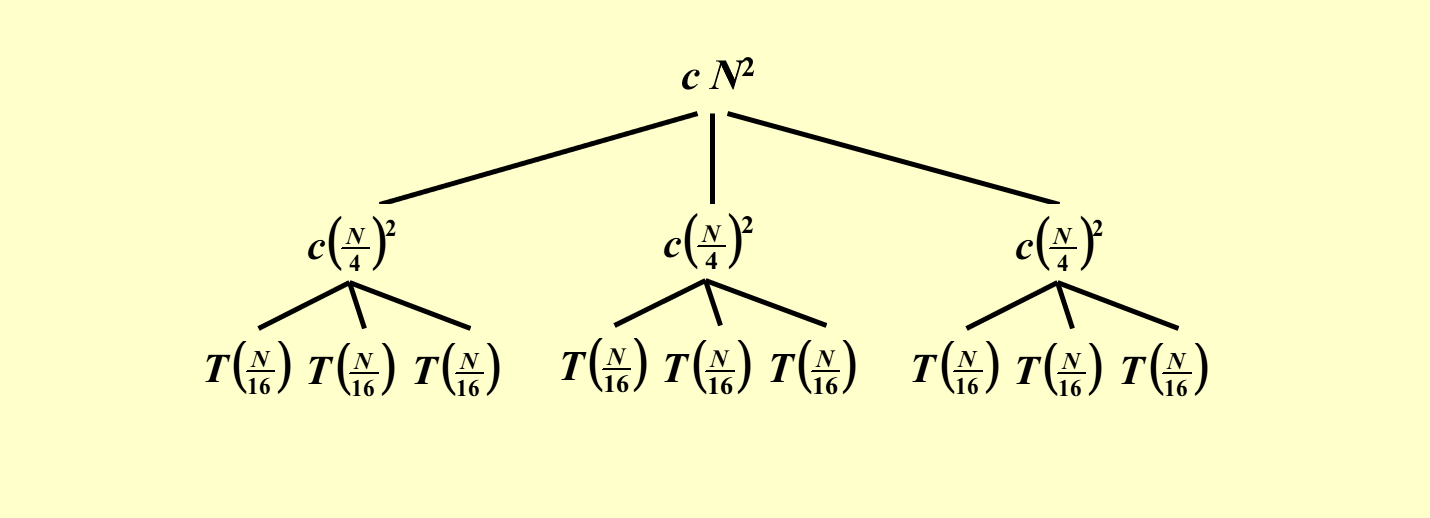
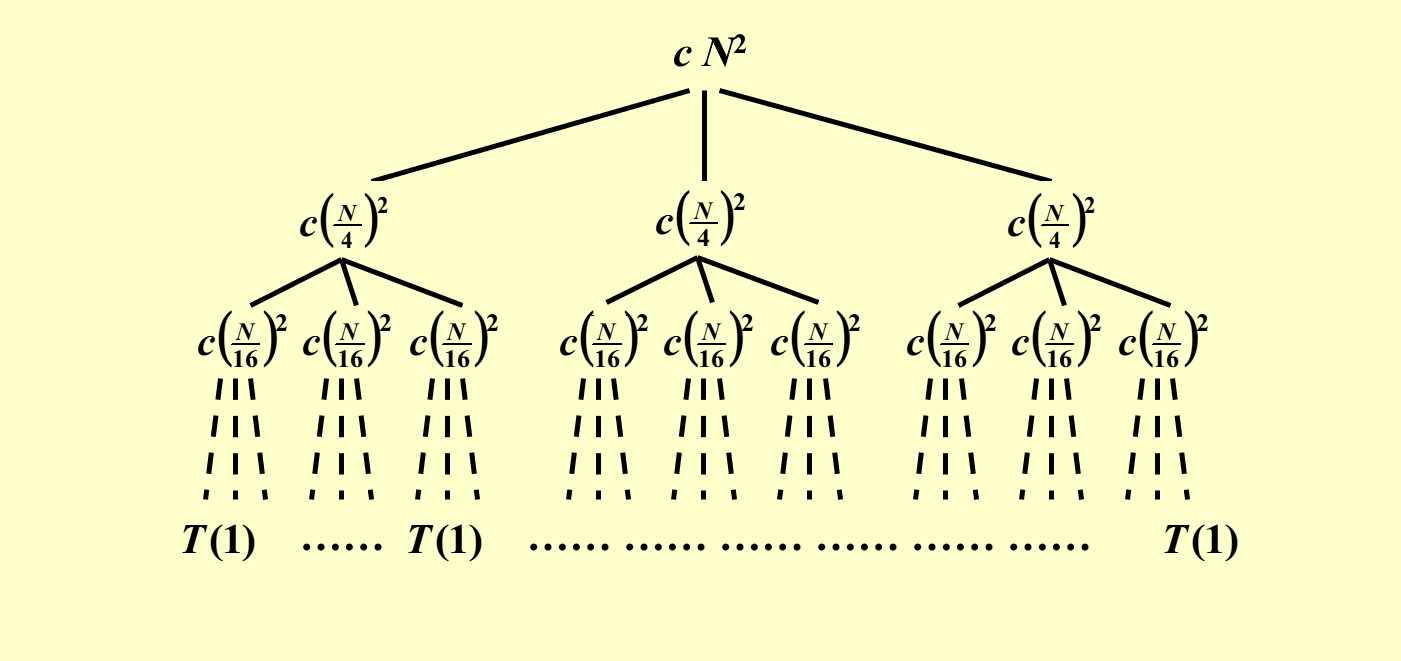
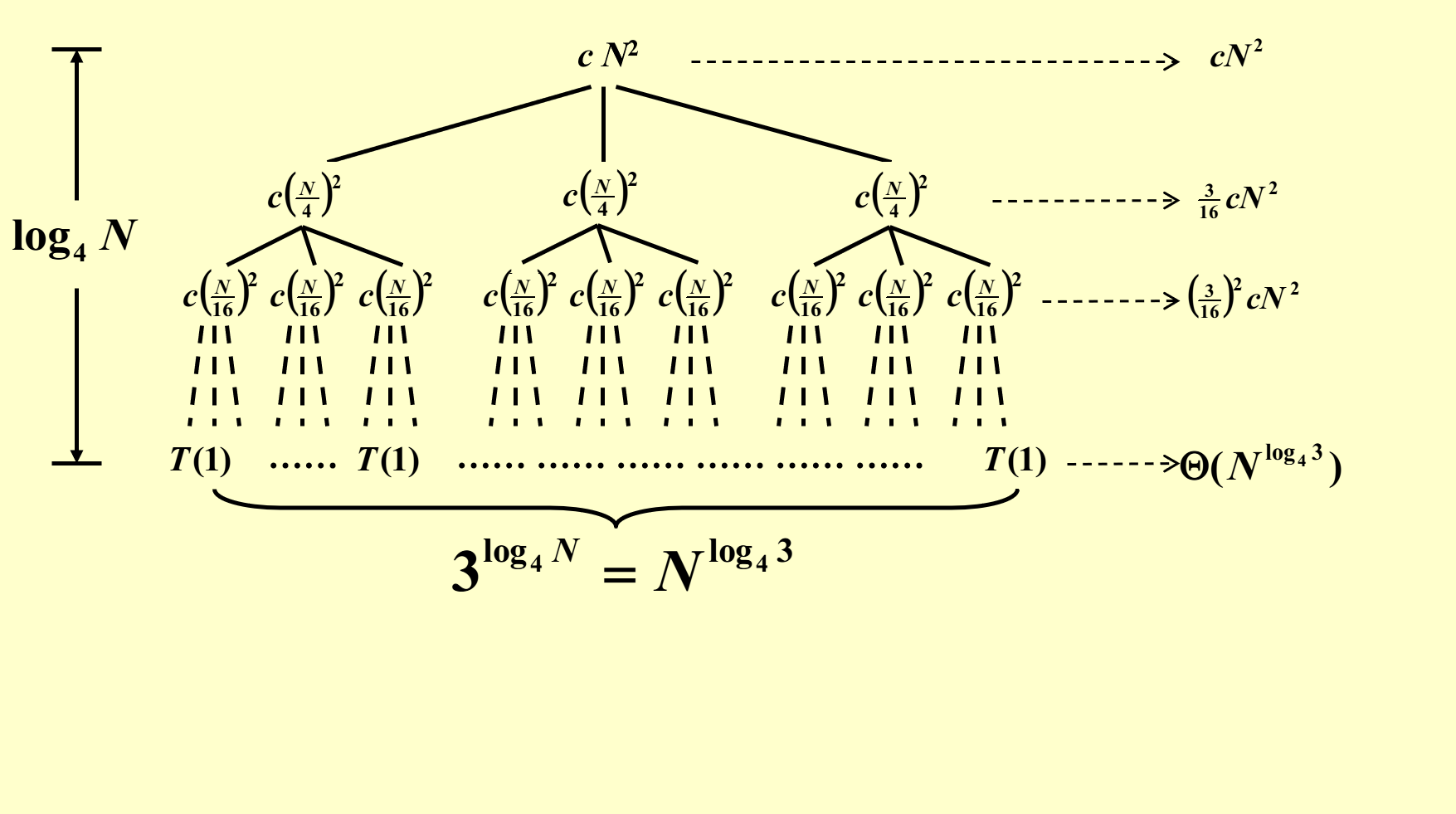
已知 \(T(N) = 3T(\dfrac{N}{4}) + \Theta(N^2)\),求 \(T(N)\)。
根据这个递推关系和递归树的特征,我们可以一层层地画出这棵树:
动画演示
对于这棵递归树,我们可以获得的信息有:
- 树的高度为 \(\log_4 N\)
- 第 \(i\) 层一共有 \(3^i\) 个节点,且节点之和为 \((\dfrac{3}{16})^i cN^2\)
- 由以上两条信息,可以推得最后一层的节点(全是 \(T(1)\))之和为 \(3^{\log_4 N} = N^{\log_4 3} = \Theta(N^{\log_4 3})\)
由以上信息,我们可以计算出 \(T(N)\):
-
第 2 行到第 3 行的不等式中,用到了一个常用的幂级数展开公式: $$ \dfrac{1}{1 - x} = \sum\limits_{n = 0}^{\infty} x^n, |x| < 1 $$
-
这道题可以用代换法来验证答案的正确性
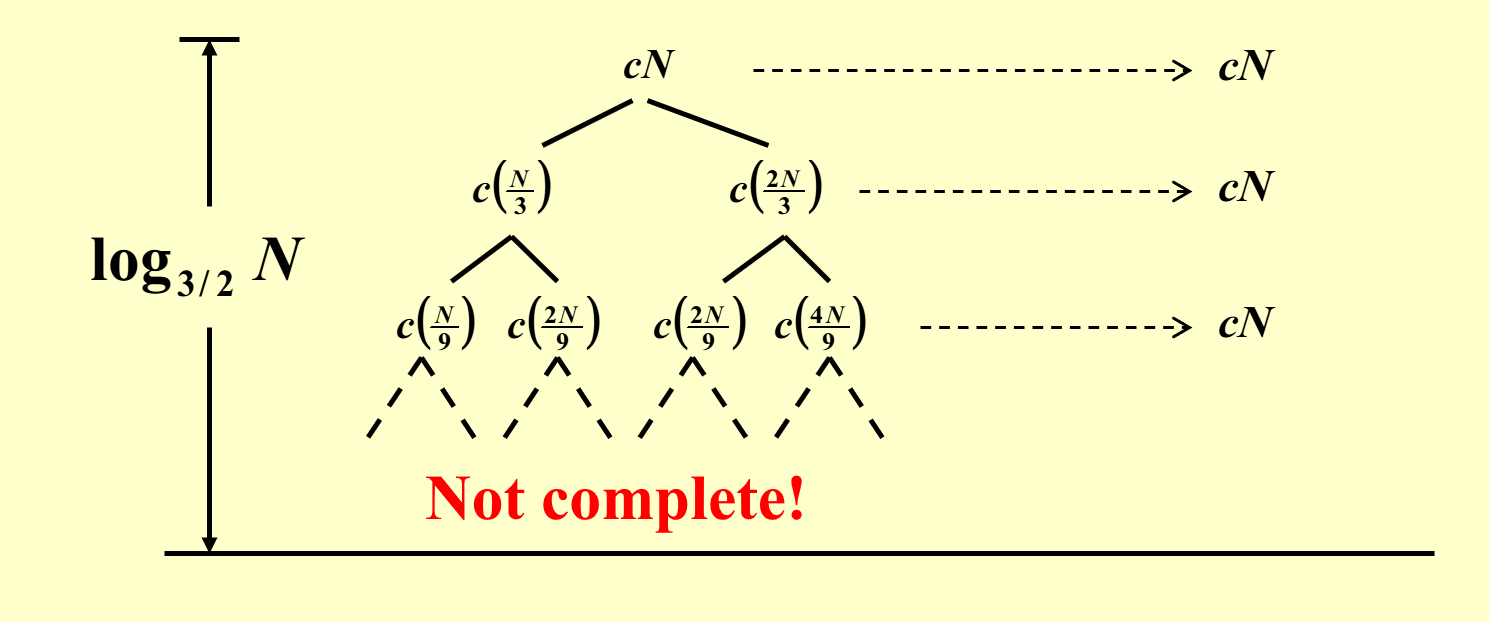
已知 \(T(N) = T(\dfrac{N}{3}) + T(\dfrac{2N}{3}) + cN\),求 \(T(N)\)。
- 先按照上个例子的方法画递归树
- 由于这不是一个标准形式下的递推关系,因此画出来的递归树并不是一棵完全树(即不平衡
) ,而且显然最右侧路径是最深的 -
但好消息是我们可以确定以下信息:
- 树的高度为最右侧路径的高度。可以看到第 \(i\) 层中最右侧的节点为 \(c(N \cdot (\dfrac{2}{3})^i) = c(\dfrac{N}{(\frac{3}{2})^i})\),因此树高为 \(\log_{\frac{3}{2}} N\)
- 每层节点和为 \(cN\)
-
根据这些信息,我们可以做一个稍微有把握的猜测:\(T(N) = O(N \log N)\)——没错,接下来用代换法来证明这个结论的正确性!
证明
Master Method⚓︎
下面罗列了主方法(或者主定理(master theorem)(更常见的叫法
注意
主定理不是万金油,它无法为所有的递推式计算时间复杂度。
Form 1⚓︎
令常数 \(a, b \ge 1\),\(f(N)\) 为关于 \(N\) 的函数,\(T(N) = aT(\dfrac{N}{b}) + f(N)\),那么:
- 若对于常数 \(\varepsilon > 0\),有 \(f(N) = O(N^{\log_b a - \varepsilon})\) 成立,则 \(T(N) = \Theta(N^{\log_b a})\)
- 若 \(f(N) = \Theta(N^{\log_b a})\),则 \(T(N) = \Theta(N^{\log_b a} \log N)\)
- 若对于常数 \(\varepsilon > 0\),有 \(f(N) = \Omega(N^{\log_b a + \varepsilon})\),且对于常数 \(c < 1\) 和充分大的数 \(N\),有 \(af(\dfrac{N}{b}) < cf(N)\) 成立(正则条件 (regularity condition)
) ,那么 \(T(N) = \Theta(f(N))\)
例子
对于归并排序,\(a = b = 2\),且合并操作是线性时间的,那么根据第 2 类情况,我们可以直接得到它的时间复杂度为 \(T = O(N \log N)\)
若 \(a = b = 2, f(N) = N \log N\),我们无法用这种主定理得到合适的时间复杂度,因为:
- 第 1 类:\(N^{\log_b a - \varepsilon} = N^{1 - \varepsilon} < N \log N\),所以不符合第 1 类情况
- 第 2 类:\(N^{\log_b a} = N \ne N \log N\),所以不符合第 2 类情况
- 第 3 类:\(N^{\log_b a + \varepsilon} = N^{1 + \epsilon} > N \log N\)(因为当 \(N\) 足够大时,\(N^{\varepsilon} > \log N(\varepsilon > 0)\)
) ,所以不符合第 3 类情况
可以用递归树来证明主定理的正确性。
证明
先令 \(N = b^k\),其中 \(k\) 为整数
那么这棵树的节点之和为:\(T(N) = \Theta(N^{log_b a}) + \sum\limits_{j = 0}^{\log_b N - 1}a^j f(\dfrac{N}{b^j})\)
可以看到,最麻烦的部分在于这个求和公式。下面我们根据这三种不同的情况分类讨论(后面两种情况我偷个懒,就直接贴上教材截图了
此时 \(f(N) = O(N^{\log_b a - \varepsilon})\),那么:
所以 \(T(N) = T(N) = \Theta(N^{log_b a}) + O(N^{log_b a}) = \Theta(N^{log_b a})\)
Form 2⚓︎
上面介绍的主定理在形式上过于复杂,因此这里给出一个简单形式的主定理(递推关系仍然是 \(T(N) = aT(\dfrac{N}{b}) + f(N)\))
- 若对于常数 \(\kappa < 1\),有 \(af(\dfrac{N}{b}) = \kappa f(N)\) 成立,则 \(T(N) = \Theta(f(N))\)
- 若对于常数 \(K > 1\),有 \(af(\dfrac{N}{b}) = K f(N)\) 成立,则 \(T(N) = \Theta(N^{\log_b a})\)
- 若 \(af(\dfrac{N}{b}) = f(N)\) 成立,则 \(T(N) = \Theta(f(N) \log_b N)\)
这个形式虽然简单,但是能够计算的时间复杂度相当有限,一些能由前一种形式的主定理解决的问题,用这种形式的主定理无法解决;前一种形式的主定理无法解决的问题,这种形式的主定理更无法解决。
例子
已知 \(a = 4, b = 2, f(N) = N\log N\),能否用第二种形式的主定理算出时间复杂度呢?
- 先计算 \(af(\dfrac{N}{b}) = 4(\dfrac{N}{2}) \log (\dfrac{N}{2}) = 2 N \log N - 2N\)
- 显然找不到任何常数 \(c\) 满足 \(cf(N) = 2 N \log N - 2N\),因此无法用这种主定理计算
- 然而,用前一种主定理是可以算出来的:发现 \(O(N^{\log_b a - \varepsilon}) = O(N^{2 - \varepsilon}) = f(N)\),符合第 1 类情况,那么时间复杂度为 \(T = O(N^2)\)
注
想看证明过程的话可以参考修佬的笔记。
Form 3⚓︎
主定理还有一种更为简单的形式(但对形式的限制更大
的解为
例子
对于归并排序,\(a = b = 2, p = 0, k = 1\),满足第 2 种情况(\(a = b^1\)
假设某种分治算法中,对于每次递归,\(a = 3, b = 2\),且合并操作的时间复杂度为 \(O(N)\),即 \(k = 1, p = 0\)。
不难发现,它符合第 1 种情况,因此 \(T(N) = O(N^{\log_2 3}) = O(N^{1.59})\)。
如果合并时间复杂度为 \(O(N^2)\),那么 \(T(N) = O(N^2)\)。
再来解决前两种形式都没法计算的问题:\(a = b = 2, f(N) = N \log N\)(即 \(k = p = 1\)
助记方法
看完主方法的三种形式,各位是否觉得已经被绕晕了(反正我是晕了
拓展:更更强大的主定理(不作要求)
对于递推关系 \(T(N) = aT(\dfrac{N}{b}) + \Theta(N^k \log^p N)\),其中 \(a \ge 1, b > 1, k \ge 0\),\(p\) 为任意实数,那么:
- 若 \(a > b^k\),则 \(T(N) = \Theta(N^{\log_b a})\)
- 若 \(a = b^k\),则
- 若 \(p > -1\),\(T(N) = \Theta(N^k \log^{p+1} N)\)
- 若 \(p = -1\),\(T(N) = \Theta(N^k \log \log N)\)
- 若 \(p < -1\),\(T(N) = \Theta(N^k)\)
- 若 \(a < b^k\),则
- 若 \(p \ge 0\),\(T(N) = \Theta(N^k \log^p N)\)
- 若 \(p < 0\),\(T(N) = \Theta(N^k)\)
评论区