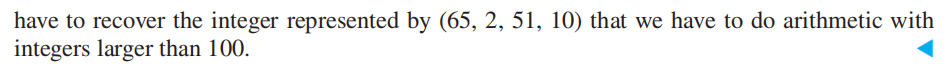Chap 4 Number Theory and Cryptography⚓︎

Divisibility and Modular Arithmetic⚓︎

Division⚓︎

定义：如果 \(a, b\) 是整数且 \(a \ne 0\)，当存在整数 \(c\) 使得 \(b = ac\)，我们说 \(a\)整除\(b\)，记作 \(a | b\)。其中 \(a\) 是 \(b\) 的因数 (divisor/factor)，\(b\) 是 \(a\) 的倍数 (multiple)。\(a \nmid b\) 则表示 \(a\) 不整除 \(b\)

注：对于正整数 \(n, d\)，存在 \(\lfloor \dfrac{n}{d} \rfloor\) 个不超过 \(n\) 的正整数满足被 \(d\) 整除

定理 1：令 \(a, b, c\) 为整数，\(a \ne 0\)，则：

• 如果 \(a | b\) 且 \(a | c\)，则 \(a | (b + c)\)
• 如果 \(a | b\)，那么对于所有整数 \(c\)，均满足 \(a | bc\)
• 如果 \(a | b\) 且 \(b | c\)，则 \(a | c\)

推论 1：如果 \(a, b, c\) 为整数，\(a \ne 0\)，使得 \(a | b\) 且 \(a | c\)，那么对于任意整数 \(m, n\)，都有 \(a | mb + nc\) 成立

The Division Algorithm⚓︎

定理 2——除法算法 (the Division Algorithm)：令 \(a\) 为整数，\(d\) 为正整数，那么存在唯一整数 \(q\) 和 \(r\)，\(0 \le r < d\)，使得 \(a = dq + r\)

其中，\(d\) 被称为除数 (divisor)，\(a\) 被称为被除数 (dividend)，\(q\) 被称为商 (quotient)，\(r\) 被称为余数 (remainder)，且有以下关系：

• \(q = a \ \mathbf{div}\ d \quad r = a \ \mathbf{mod}\ d\)
• \(a \ \mathbf{div}\ d = \lfloor \dfrac{a}{d} \rfloor \quad a \ \mathbf{mod}\ b = a - d\lfloor \dfrac{a}{d} \rfloor\)

当被除数为负数时，记住一条原则：余数不能是负数

Modular Arithmetic⚓︎

定义：如果 \(a, b\) 为整数，且 \(m\) 是正整数，当 \(m\) 能整除 \(a - b\) 时，我们称\(a, b\) 模 \(m\) 同余，记作 \(a \equiv b (\text{mod } m)\)。否则，记作 \(a \not\equiv b (\text{mod } m)\)。其中 \(m\) 被称为模 (modulus)

定理 3：令 \(a, b\) 为整数，且 \(m\) 为正整数。当且仅当 \(a \ \mathbf{mod}\ m = b \ \mathbf{mod}\ m\) 成立时，\(a \equiv b (\text{mod } m)\)

定理 4：令 \(a, b\) 为整数，且 \(m\) 为正整数。当且仅当存在整数 \(k\)，使得 \(a = b + km\) 时，\(a \equiv b (\text{mod } m)\)

所有与 \(a\) 模 \(m\) 同余的整数构成了 \(a\) 模 \(m\) 的同余类 (congruence class)

注：同余类是一种等价类

定理 5：令 \(m\) 为正整数，如果 \(a \equiv b(\text{mod } m)\) 且 \(c \equiv d(\text{mod } m)\)，那么 $$ a + c \equiv b + d(\text{mod } m) \quad ac \equiv bd(\text{mod } m) $$ 推论 2：令 \(a, b\) 为整数，且 \(m\) 为正整数。那么有：

Arithmetic Modulo \(m\)⚓︎

我们将算术运算的域限定到 \(\mathbf{Z}_m\)，它是不超过 \(m\) 的非负数集合，即 \(\{0, 1, \dots, m - 1\}\)，那么有以下定义：

• \(a +_m b = (a + b)\ \mathbf{mod}\ m\)
• \(a \cdot_m b = (a \cdot b)\ \mathbf{mod}\ m\)

其中 \(+_m\) 和 \(\cdot_m\) 运算被称作算术模 \(m\)(arithmetic modulo \(m\))，具有于普通算术运算类似的性质：

• 封闭性 (closure)：如果 \(a, b \in \mathbf{Z}_m\)，则 \(a +_m b, a \cdot_m b \in \mathbf{Z}_m\)
• 可结合性 (associativity)：如果 \(a, b \in \mathbf{Z}_m\)，则 \((a +_m b)+_m c = a +_m (b +_m c)\)，\((a \cdot_m b)\cdot_m c = a \cdot_m (b \cdot_m c)\)
• 可交换性 (commutativity)：如果 \(a, b \in \mathbf{Z}_m\)，则 \(a +_m b = b +_m a\)，\(a \cdot_m b = b \cdot_m a\)
• 单位元素 (identity elements)：0 和 1 分别是加法模 m 和乘法模 m 的单位元素，即 \(a \in \mathbf{Z}_m\)，\(a +_m 0 = 0 +_m a\)，且 \(a \cdot_m 1 = 1 \cdot_m a\)
• 可加逆 (additive inverses)：如果 \(a \ne 0 \in \mathbf{Z}_m\)，则 \(m - a\) 是 \(a\) 模 \(m\) 的可加逆，0 的可加逆是其自身，即 \(a +_m (m - a) = 0, \ 0 +_m 0 = 0\)
• 分配性 (distributivity)：如果 \(a, b, c \in \mathbf{Z}_m\)，则 \(a \cdot_m (b +_m c) = (a \cdot_m b) +_m (a \cdot_m c)\)，\((a +_m b) \cdot_m c = (a \cdot_m c) +_m (b \cdot_m c)\)

• 带有模加法的 \(\mathbf{Z}_m\) 被称为可交换组 (commutative group)
• 带有模加法和模乘法的 \(\mathbf{Z}_m\) 被称为可交换环 (commutative ring)

Supplements(from Exercises)⚓︎

• 如果 \(a|b\) 且 \(b|a\)，那么 \(a = \pm b\)
• \(\lceil \dfrac{n}{k} \rceil = \lfloor \dfrac{n - 1}{k} \rfloor + 1\)
• 如果 \(a \equiv b \text{ (mod } m)\) 且 \(c \equiv d \text{ (mod } m)\)，其中 \(a, b, c, d, m\) 为整数，\(m \ge 2\)，那么 \(a - c \equiv b - d \text{ (mod } m)\)
• 假设 \(n | m\)，其中 \(m, n\) 为大于 1 的整数，如果 \(a \equiv b \text{ (mod } m)\)，其中 \(a, b\) 为整数，那么 \(a \equiv b\text{ (mod } n)\)
• 假设 \(a, b, c, m\) 为整数，\(m \ge 2\)，\(c > 0\)，且 \(a \equiv b \text{ (mod } m)\)，则 \(ac \equiv bc \text{ (mod } mc)\)
• 假设 \(a, b, k, m\) 为整数，\(m \ge 2\)，\(k > 1\)，且 \(a \equiv b \text{ (mod } m)\)，则 \(a^k \equiv b^k \text{ (mod } m)\)

Integer Representation and Algorithms⚓︎

注：隐藏了一些老生常谈的知识点，推荐看一下模指数运算

可忽略

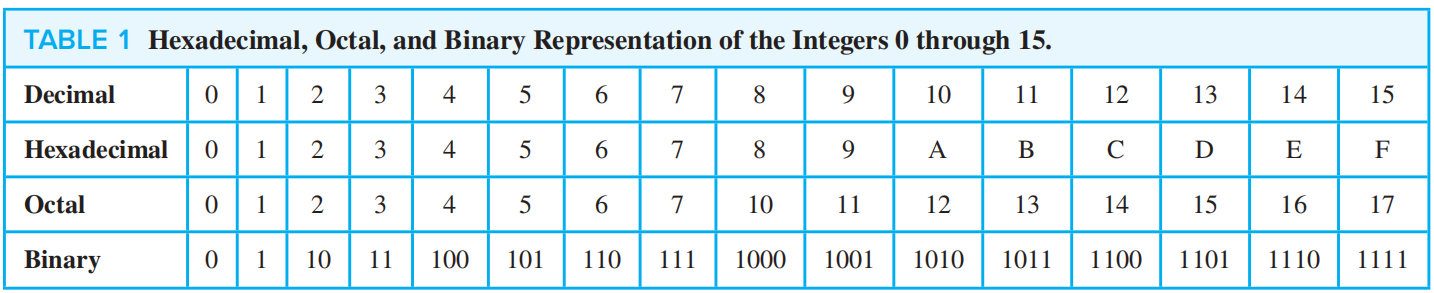
Representations of Integers⚓︎

定理 1(\(n\) 的基底 \(b\) 扩展 , base \(b\) expansion of \(n\))：令 \(b\) 为大于 1 的整数，如果 \(n\) 是正整数，则它能用以下形式唯一表示： $$ n = a_kb^k + a_{k - 1}b^{k - 1} + \dots + a_1b + a_0 $$ 其中\(k\)是非负数，\(a_0, a_1, \dots, a_k\)是小于\(b\)的非负数，且\(a_k \ne 0\)

常见类型：

• 十进制扩展 (decimal expansion)——基底为 10
• 二进制扩展 (binary expansion)——基底为 2
• 八进制扩展 (octal expansion)——基底为 8
• 十六进制扩展 (hexadecimal expansion)——基底为 16

  字节 (Byte)是长度为 8 的位串，它常用 2 位十六进制数表示

---

基底转换的方法 ( 对整数 \(n\) 进行基底 \(b\) 扩展 )：

• 首先，\(b | n\) 得到商和余数，即 \(n = bq_0 + a_0,\ 0 \le a_0 < b\)，其中 \(a_0\) 是 \(n\) 的基底 \(b\) 扩展中最低位的数
• 然后继续 \(b | a_0\)，得到 \(q_0 = bq_1 + a_1,\ 0 \le a_1 < b\)，其中 \(a_1\) 是 \(n\) 的基底 \(b\) 扩展中的第二位数
• 持续这个步骤，直到商为 0 的时候结束，这样我们从右到左得到 \(n\) 的基底 \(b\) 扩展

算法描述：

• 二进制 \(\rightarrow\) 八进制：三位二进制 = 一位八进制
• 二进制 \(\rightarrow\) 十六进制：四位二进制 = 一位十六进制

Algorithms for Integer Operations⚓︎

假设有两个用二进制表示的数 \(a, b\)

\[ a = (a_{n - 1}a_{n - 2}\dots a_1a_0)_2,\ b = (b_{n - 1}b_{n - 2}\dots b_1b_0)_2 \]

二进制加法二进制乘法整除，求余运算

\[ \begin{cases} a_0 + b _0 = c_0 \cdot 2 + s_0&\text{if i = 0,} \\ a_i + b_i + c_{i - 1} = c_i \cdot 2 + s_i & \text{if 0 < i < n,} \\ s_n = c_{n - 1} & \text{if i = n} \end{cases} \quad \therefore a + b = (s_ns_{n - 1}s_{n - 2}\dots s_1s_0)_2 \]

算法：

加法运算次数：\(O(n)\)

\[ \begin{align} ab & = a(b_02^0 + b_12^1 + \dots + b_{n - 1}2^{n - 1}) \notag \\ & = a(b_02^0) + a(b_12^1)+ \dots + a(b_{n - 1}2^{n - 1}) \notag \end{align} \]

为了得到 \(ab_j2^j\)，我们通过在其后面填上 \(j\) 个 0 位的方法，将其向左移动\(ab_jj\) 个位置

算法：

移位次数：\(O(n^2)\)，加法次数：\(O(n^2)\)

算法 ( 这是个暴力算法)：

• 该算法同样适用于 \(a\) 为负数的情况
• 位运算次数：\(O(q \log a),\ a > d\)

Modular Exponentiation⚓︎

适用场合：当进行求余运算的数非常大时 (\(b^n \ \mathbf{mod}\ m\))

方法： 令\(n = (a_{k - 1}\dots a_1a_0)_2\)，则\(b^n = b^{a_{k-1}\cdot 2^{k - 1} + \dots + a_1 \cdot 2 + a_0} = b^{a_{k - 1} \cdot 2^{k - 1}} \dots b^{a_1 \cdot 2} \cdot b^{a_0}\)，要求\(b^n \ \mathbf{mod}\ m\)，计算：

，然后将所有 \(a_j = 1\) 对应的 \(b^{2^j} \ \mathbf{mod}\ m\) 相乘，对积求余，即可得到结果

算法：

乘法次数：\(O(\log_2(n))\)，位运算次数：\(O((\log m)^2 \log n)\)

🌰

Supplements(from Exercises)⚓︎

• 二进制反码 (one's complement)：最左边一位是符号位，0 代表 +，1 代表 -。对于剩下的位：

  • 正数：保持原来的二进制表示
  • 负数：每一位取反—— \(0 \rightarrow 1\)，\(1 \rightarrow 0\)

• 二进制补码 (two's complement)：最左边一位是符号位，0 代表 +，1 代表 -。对于剩下的位：

  • 正数：保持原来的二进制表示
  • 负数：每一位取反—— \(0 \rightarrow 1\)，\(1 \rightarrow 0\) 后，再 +1

注：

• 教材给出的做法：剩下的位 = \(2^{n - 1} - |x|\)
• 具体内容见数逻

• BCD 码：对于一个整数，它的每个位分别用 4 位二进制表示

• 康托扩展 (Cantor expansion)：\(a_n n! + a_{n - 1} (n - 1)! + \dots + a_2 2! + a_1 1!\)，其中 \(0 \le a_i \le i, i = 1, 2, \dots, n\)

Primes and Greatest Common Divisors⚓︎

Primes⚓︎

定义：

• 对于大于 1 的整数 \(p\)，如果它唯一的正因数是 1 和它自身，则 \(p\) 被称为质数 ( 素数 )(primes)
• 不是质数的正整数（大于 1）被称为合数 (composite)

注：

• 1 既不是质数，也不是合数
• 当且仅当存在一个整数 \(a\)，使得 \(a | n\) 且 \(1 < a < n\)，那么整数 \(n\) 为合数

定理 1——算术基本定理 (THE FUNDAMENTAL THEROEM OF ARITHMETIC)：每一个大于 1 的整数能够被唯一表示为一个质数；或者两个及多个质数的乘积，这些质因数按照非递减的顺序排列。

Trial Division⚓︎

定理 2：如果 \(n\) 是合数，则 \(n\) 拥有小于等于 \(\sqrt n\) 的质因数

试除法 (trial division)：要判断整数 \(n\) 是否为质数，可以让 \(n\) 除以小于等于 \(\sqrt n\) 的所有质数。如果这些数都无法整除 \(n\)，则说明 \(n\) 为质数，否则 \(n\) 为合数。这是一种暴力算法 (brute-force algorithm)。

分解质因式 (prime factorization)：要得到 \(n\) 的质因式，通过一连串的质数整除 \(n\)，从最小的质数 2 开始：

• 如果 \(n\) 有质因数，那么将会找到一个不超过 \(\sqrt n\) 的质数 \(p\)。因此如果没有找到不超过 \(\sqrt n\) 的质数，说明 \(n\) 是质数
• 否则的话，即找到质因数 \(p\)，那么按照前面的步骤，继续对 \(\dfrac{n}{p}\) 分解质因式，直到得到一个质数为止。

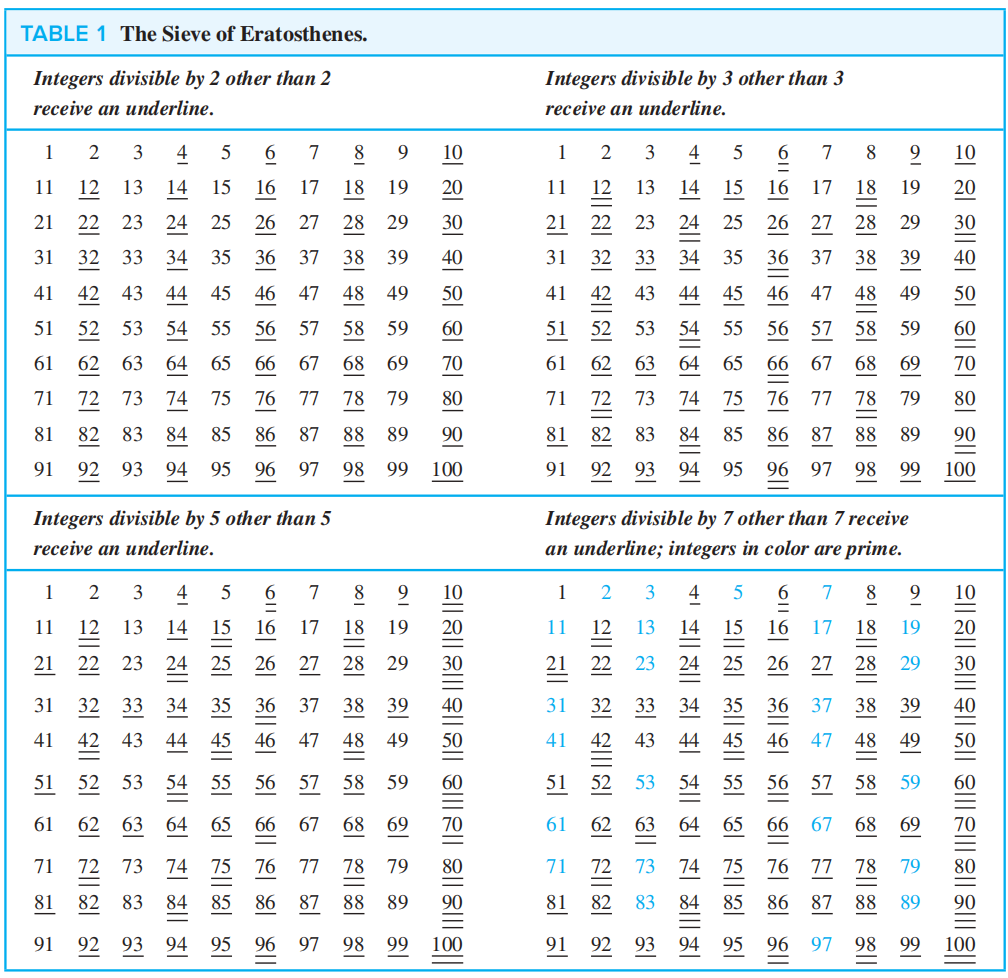
The Sieve of Eratosthenes⚓︎

埃拉托斯提尼筛 (the sieve of Eratosthenes)：用来找到不超过指定正整数的所有质数

方法：找出所有不超过 \(\sqrt n\) 的质数，然后从小到大依次将它们的倍数 ( 不超过 \(n\)) 删去，剩下的数就是不超过 \(n\) 的质数。下面的🌰( 寻找 \(\le\) 100 的质数 ) 会更加直观地体现这一方法👇

定理 3：有无穷多个质数

证明

采用归谬法，由欧几里得证明，被认为是最优雅的数学证明之一：

梅森质数 (Mersenne primes)：形如 \(2^p - 1\) 的质数，其中 \(p\) 为质数。

• 一般认为最大的质数 ( 虽然无法找到 ) 就是一种梅森质数
• 如果 \(p\) 不为质数，则 \(2^p - 1\) 也不是质数
• Lucas-Lehmer test：验证形如 \(2^p - 1\)(\(p\) 为质数 ) 的数是否为质数的一种测试

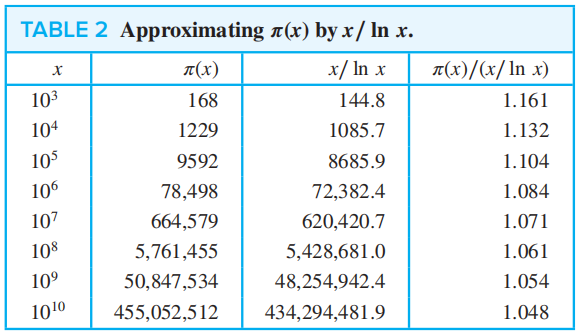
定理 4——质数 ( 素数 ) 定理 (THE PRIME NUMBER THEOREM)：当 \(x\) 无限增长时，\(\pi(x)\)，即不超过 \(x\) 的质数的个数，与 \(\dfrac{x}{\ln x}\) 的比值趋向于 1。（即 \(\lim\limits_{x \rightarrow \infty} \dfrac{\pi (x)}{x/ \ln x} = 1\)）

这张表直观地反映了这个定理👇

应用：

• 从不超过 \(n\) 的正整数中随机选择一个数是质数的概率是：\(\dfrac{\pi (x)}{x} = \dfrac{x/ \ln x}{x} = \dfrac{1}{\ln x}\)

• 正整数 \(n\) 是质数的概率也是 \(\dfrac{1}{\ln n}\)

每一个等差数列 (arithmetic progression)\(ak + b, k = 1,2, \dots\)（其中 \(a, b\) 没有大于 1 的公约数），拥有无穷多个质数

Conjectures and Open Problems About Primes⚓︎

• 对于每一个拥有整数系数的多项式 \(f(n)\)，存在正整数 \(y\)，使得 \(f(y)\) 为合数

• 哥德巴赫猜想 (Goldbach's Conjecture)：对于每一个大于 2 的偶数\(n\)，总能被分解为两个质数的和。

  虽然尚未得到完全的证明，但大多数数学家认为它是正确的。下面是一些弱化的结果：

  • 每个大于 2 的偶数至多是 6 个质数之和
  • 每个足够大的正整数是一种质数的和，或者要么是一个质数，要么是两个质数的乘积

• 存在无穷多个正整数 \(n\)，使得 \(n^2 + 1\) 要么是质数，要么是至多两个质数的乘积

• 孪生素数猜想 (The Twin Prime Conjecture)：
  • 孪生素数 (Twin primes)：相差 2 的质数对
  • 已经证明：有无穷多对 \(p\) 和 \(p+2\)，\(p\) 为质数，\(p+2\) 为质数或者两个质数的乘积
  • 令 \(P(n)\) 表示有无穷多对相差为 \(n\) 的质数。有界间隙猜想 (bounded gap conjecture)——存在整数 \(N\)，使得 \(P(N)\) 为真。

参考资料：张益唐

Greatest Common Divisors and Least Common Multiples⚓︎

定义：令 \(a, b\) 为非 0 整数，使得 \(d|a\) 且 \(d|b\) 的最大整数 \(d\) 被称为 \(a\) 和 \(b\)最大公约数 (greatest common divisor)，记作 \(\text{gcd}(a, b)\)

• 如果两个整数的最大公约数是 1，称这两个数互质 (relatively prime)
• 对于一组整数 \(a_1, a_2, \dots, a_n\)，如果 \(\text{gcd}(a_i, a_j) = 1, 1 \le i < j \le n\)，那么称这组整数两两互质 (pairwise relatively prime)

对两个正整数 \(a, b\) 分解质因数，得到：

那么：\(\text{gcd}(a, b) = p_1^{\min (a_1, b_1)} p_2^{\min (a_2, b_2)} \dots p_n^{\min (a_n, b_n)}\)

定义：令 \(a, b\) 为非 0 整数，能被 \(a\) 和 \(b\) 整除的最小整数被称为 \(a\) 和 \(b\)最小公倍数 (least common multiple)，记作 \(\text{lcm}(a, b)\)

与上面同理：\(\text{lcm}(a, b) = p_1^{\max (a_1, b_1)} p_2^{\max (a_2, b_2)} \dots p_n^{\max (a_n, b_n)}\)

定理 5：令 \(a, b\) 为正整数，那么 \(ab = \text{gcd}(a, b) \cdot \text{lcm}(a, b)\)

The Euclidean Algorithm⚓︎

欧几里得算法 ( 辗转相除法 )(Euclidean algorithm)：一种找到最小公约数的高效算法

引理 1：令 \(a = bq + r\)，其中 \(a, b, q, r\) 为整数，那么 \(\text{gcd}(a, b) = \text{gcd}(b, r)\)

证明

通过这个引理，我们可以得到欧几里得算法的流程：

算法：

时间复杂度：\(O(\log b)\)

gcds as Linear Combinations⚓︎

定理 6——裴蜀定理 (BEZOUT'S THEOREM)：如果 \(a, b\) 是正整数，那么存在正数 \(s, t\)，使得 \(\text{gcd}(a, b) = sa + tb\)

其中 \(s, t\) 被称为裴蜀系数 (Bezout coefficients)，上面的等式被称为裴蜀恒等式 (Bezout's identity)

将两个数的最大公约数表示为两个数的线性组合 (linear combination)的方法：

• 将欧几里得算法的结果往回代 ( 先向前运用欧几里得算法，再向后代入中间值 )
• 拓展欧几里得算法 (extended Euclidean algorithm)： 先令\(s_0 = 1, s_1 = 0, t_0 = 0, t_1 = 1\)，然后令\(s_j = s_{j - 2} - q_{j - 1}s_{j - 1}\)，\(t_j = t_{j - 2} - q_{j - 1}t_{j - 1}\)，其中\(j = 2, 3, \dots, n\)，\(q_j\)是欧几里得算法中得到的一系列商，那么\(\text{gcd}(a, b) = s_na+t_nb\)

例题

方法 1 方法 2

引理 2：如果 \(a, b, c\) 为正整数，使得 \(\text{gcd}(a, b) = 1\) 且 \(a | bc\)，那么 \(a | c\)

引理 3：如果 \(p\) 是质数，且对于每个整数 \(a_i\)，\(p | a_1a_2\dots a_n\)，那么 \(\exists i \in [1, n]\)，\(p\ |\ a_i\)

定理 7：令 \(m\) 为正整数，\(a, b, c\) 为整数，如果 \(ac \equiv bc (\text{mod } m)\) 且 \(\text{gcd}(c, m) = 1\)，那么 \(a \equiv b (\text{mod } m)\)

Supplements(from Exercises)⚓︎

• 如果 \(a, m\) 是大于 1 的整数，且 \(m\) 是奇数，那么 \(a^m + 1\) 是合数
• 对于任意正整数 \(n\)，存在 \(n\) 个连续的合数
• 如果一个数等于除自身外所有因数的和，那么这个数被称为完美 (perfect) 数
• 欧拉函数 (Euler \(\phi\)-function)：\(\phi (n) =\) 不超过 \(n\) 的与 \(n\) 互质的正整数的个数
• 如果 \(a, b\) 是正整数，那么 \((2^a - 1) \ \mathbf{mod}\ (2^b - 1) = 2^{a \ \mathbf{mod}\ b} - 1\)
• 如果 \(a, b\) 是正整数，那么 \(\text{gcd}(2^a - 1, 2^b - 1) = 2^{\text{gcd}(a, b)} - 1\)
• 如果 \(a, b, m\) 是整数，\(m \ge 2\)，且 \(a \equiv b (\text{mod } m)\)，那么 \(\text{gcd}(a, m) = \text{gcd}(b, m)\)
• 对于所有等差数列 \(ak + b, k = 1, 2, \dots\)，其中 \(a, b\) 为正整数，在其中总存在一个合数

Solving Congruences⚓︎

Linear Congruences⚓︎

线性同余 (linear congruences)：形如 \(ax \equiv b (\text{mod } m)\) 的同余，其中 \(m\) 是正整数，\(a, b\) 是整数，\(x\) 是变量

线性同余 \(ax \equiv b(\text{mod } m)\) 的解 (solution)是所有满足同余关系的整数 \(x\)，求解方法后面会讲到。

\(a\) 模 \(m\) 的逆 (inverse)：\(\overline{a}\)，满足 \(\overline{a}a \equiv 1(\text{mod } m)\)

定理 1：如果 \(a, m\) 互质，且 \(m > 1\)，那么 \(a\) 模 \(m\) 的逆存在，且该逆对模 \(m\) 是唯一的

如何找到 \(a\) 模 \(m\) 的逆？

• 当 \(m\) 较小时，采用观察法（暴力算法）
• 高效的做法：由已知得 \(\text{gcd}(a, m) = 1\)，按照与上例相同的方法，逆转欧几里得算法的步骤，得到最大公约数的线性组合表示，即 \(sa + tm = 1\)，则 \(sa + tm \equiv 1 (\text{mod } m)\)。因为 \(tm \ \mathbf{mod}\ m = 0\)，所以 \(sa \equiv 1 (\text{mod } m)\)，因此 \(s\) 即为 \(a\) 模 \(m\) 的逆。

例题

如何求解 \(ax \equiv b (\text{mod } m)\)？

• 找到 \(\overline{a}\)，即 \(a\) 模 \(m\) 的逆
• 对式子两边同时乘上 \(\overline{a}\)

🌰：

The Chinese Remainder Theroem⚓︎

定理 2——中国余数定理 (THE CHINESE REMAINDER THEROEM)：令 \(m_1, m_2, \dots, m_n\) 为两两互质且大于 1 的正整数，且 \(a_1, a_2, \dots, a_n\) 为任意整数，那么下面方程组：

有唯一解的模 \(m = m_1m_2 \dots m_n\)。也就是说，存在一个解 \(x, 0 \le x < m\)，所有其他的解与 \(x\) 模 \(m\) 同余

如何构造联立解 (simultaneous solution)？

法 1 法 2——回代 (back substitution)

• 先令 \(M_k = \dfrac{m}{m_k}, k = 1, 2, \dots, n\)
• 因为 \(m_i, m_k(i \ne k)\) 没有大于 1 的公因数，所以 \(\text{gcd}(m_k, M_k) = 1\)。由定理 1 知，存在整数 \(y_k\) 是 \(M_k\) 模 \(m_k\) 的逆，使得 \(M_ky_k \equiv 1 (\text{mod } m_k)\)
• 得到 \(x = a_1M_1y_1 + a_2M_2y_2 + \dots + a_nM_ny_n\)

下面证明这个式子为联立解：

• 对于上面方程组中的第 \(k\) 行，因为 \(M_j \equiv 0 (\text{mod } m_k), j \ne k\)，所以除了第 \(k\) 项外，这个和式中的其他项与 0 模 \(m_k\) 同余
• 又因为 \(M_ky_k \equiv 1 (\text{mod } m_k)\)
• 所以 \(x \equiv a_kM_ky_k \equiv a_k (\text{mod } m_k), k = 1, 2, \dots, n\)，因而 \(x\) 可以满足所有 \(n\) 个同余关系

🌰

利用 4.1 节定理 4，根据已知条件往回代，最后可以得到形如 \(x = mk + r\) 的形式，则所有解为 \(x \equiv r (\text{mod } m)\)

：

注：倒数第 3 行最右边那个 \(u\) 应该是 \(v\)

Computer Arithmetic with Large Integers⚓︎

令 \(m_1, m_2, \dots, m_n\) 为两两互质的模数，\(m\) 为它们的积。由中国余数定理，可以得到对于一个整数 \(a,\ 0 \le a < m\)，它能够被唯一表示为由它分别除以 \(m_i, i = 1, 2, \dots, n\) 得到的余数构成的 \(n\)元组，即

对于大数的算术运算 :

• 我们可以先将其转化为上述 \(n\) 元组的形式，对其进行分量式运算 (componentwise operations)

• 然后利用前面求解同余方程组的方法将结果还原为正常的表示，即为我们得到的结果

• 这么做的好处是：不仅可以进行范围更大的算术运算，而且还提升运算速度（不同的模运算可以并行处理）

• 一般选择形如 \(2^k - 1(k \in \mathbf{Z^+})\) 的数作为大数运算的模数，因为这样不仅容易进行二进制模运算，而且更容易找到两两互质的模数

这个🌰可以更清楚地展现该方法的威力：

Fermat's Little Theroem⚓︎

定理 3——费马小定理 (MERMAT'S LITTLE THEROEM)：如果 \(p\) 是质数，\(a\) 为整数，且 \(p \nmid a\)，那么 $$ a^{p - 1} \equiv 1 (\text{mod } p) \text{ , i.e. } a^p \equiv a (\text{mod } p) $$ 亦即：如果\(a \in \mathbf{Z}_p\)，那么\(a^{p - 1} = 1 \in \mathbf{Z}_p\)

Pseudoprimes⚓︎

在前面，我们介绍过判断一个整数 \(n\) 是否为质数的方法，但这个方法太低效了——那么有没有更高效的方法？

中国古代的数学家发现，当 \(n\) 为奇数时，它是质数的充要条件是 \(2^{n - 1} \equiv 1 (\text{mod } n)\)。然而，有些合数也满足这个式子，这样的整数被称为对于基底为 2 的伪质数 (pseudoprimes)

定义：令 \(b\) 为正整数，如果 \(n\) 为合数，且 \(b^{n - 1} \equiv 1(\text{mod } n)\)，那么 \(n\) 被称为对于基底为 \(b\) 的伪质数

• 我们可以选择多个基底来确定 \(n\) 是否为质数。如果 \(n\) 通过所有测试，说明 \(n\) 要么为质数，要么是对于所有已测试的基底的伪质数
• 对于不超过 \(x(x \in \mathbf{R}^+)\) 的正整数，对于基底为 \(b\) 的伪质数的个数远小于质数的个数。但即便如此，也无法用这种方法区分质数和伪质数

定义：如果一个合数 \(n\)，对于所有正整数 \(b\)，\(\text{gcd}(b, n) = 1\)，如果满足 \(b^{n - 1} \equiv 1(\text{mod } n)\)，这样的数 \(n\) 被称为卡迈克尔数 (Carmichael number)

注：

• 卡迈克尔数属于伪质数，且有无穷多个卡迈克尔数
• 更具体的介绍

Primitive Roots and Discrete Logarithm⚓︎

定义：以质数 \(p\) 为模的原根 (primitive root)\(r\)，\(r \in \mathbf{Z}_p\)，使得 \(\mathbf{Z}_p\) 中的每一个非零元素都是 \(r\) 的幂

注：对于每一个质数 \(p\)，总存在以质数 \(p\) 为模的原根

定义：假设 \(p\) 为质数，\(r\) 是以 \(p\) 为模的原根，\(a\) 是整数且 \(a \in [1, p - 1]\)。如果 \(r^e \ \mathbf{mod}\ p = a\) 且 \(0 \le e \le p - 1\)，称 \(e\) 为以 \(r\) 为底数，关于 \(a\) 模 \(p\) 的离散对数 (discrete logarithm)，记作 \(\log_ra = e\)

离散对数问题 (discrete logarithm problem)：以上述 \(p, r, a\) 为输入，得到 \(e\)。看似简单的问题，但目前没有多项式时间的算法能够解出结果。

Supplements(from Exercises)⚓︎

• 如果 \(m\) 是大于 1 的整数，且 \(ac \equiv bc(\text{mod } m)\)，那么 \(a \equiv b(\text{mod} \dfrac{m}{\text{gcd}(c, m)})\)
• 如果 \(p\) 为质数，那么对于在 \((1, p - 1)\) 之间的整数，能被划分成 \(\dfrac{p - 3}{2}\) 对整数，满足每对整数互为模 \(p\) 的逆
• 威尔逊定理 (Wilson's theorem)：当 \(p\) 为质数时，满足 \((p-1)! \equiv - 1 (\text{mod } p)\)
• 令 \(m_1, m_2, \dots, m_n\) 为两两互质且大于等于 2 的整数，如果 \(a \equiv b (\text{mod } m_i), i = 1, 2, \dots, n\)，那么 \(a \equiv b (\text{mod } m )\)，其中 \(m = m_1m_2 \dots m_n\)（可用这个结论来证明中国余数定理）
• 如果 \(p\) 为奇质数，那么对于梅森数 \(2^p - 1\)，它的所有因数都将形如 \(2kp + 1\)，其中 \(k\) 为非负数
• 令 \(n\) 为正整数，且令 \(n - 1 = 2^st\)，其中 \(s\) 为非负数，\(t\) 为正奇数。如果 \(b^t \equiv 1(\text{mod } n)\)，或者对于某些 \(j \in [0, s - 1]\)，\(b^{2^jt} \equiv -1 (\text{mod } n)\)，那么称 \(n\) 通过对于基底为 \(b\) 的米勒测试 (Miller's test for the base \(b\))。
• 对于一个合数 \(n\)，如果它能通过对于基底为 \(b\) 的米勒测试，那么称它为对于基底为 \(b\) 的强伪质数 (strong pseudoprime to the base \(b\)) >一个合数通过的米勒测试小于\(\dfrac{n}{4}\)种基底\(b(1 < b < n)\)
• 令 \(m\) 为正整数，如果整数 \(a\) 满足 \(\text{gcd}(a, m) = 1\) 且 \(x^2 \equiv a(\text{mod } m)\) 有解，那么称 \(a\) 关于 \(m\) 的平方剩余 (quadratic residue)。如果 \(a\) 不是关于 \(m\) 的平方剩余，但满足 \(\text{gcd}(a, m) = 1\)，那么称 \(a\) 关于 \(m\) 的平方非剩余 (quadratic nonresidue)
• 如果 \(p\) 为奇质数，且整数 \(a\) 无法被 \(p\) 整除，那么对于勒让德符号 (Legendre symbol)\((\dfrac{a}{p})\)，如果 \(a\) 是关于 \(m\) 的平方剩余，其值为 1，否则为 -1。它具有以下性质 ( 以下 \(p\) 均为奇质数 )：
  • 如果 \(a, b\) 为整数，且 \(a \equiv b (\text{mod } p)\)，那么 \((\dfrac{a}{p}) = (\dfrac{b}{p})\)
  • 欧拉准则 (Euler's criterion)：如果正整数 \(a\) 满足 \(p \nmid a\)，那么 \((\dfrac{a}{p}) \equiv a^{\frac{p - 1}{2}}(\text{mod } p)\)
  • 如果整数 \(a,b\) 无法被 \(p\) 整除，那么 \((\dfrac{ab}{p}) = (\dfrac{a}{p}) (\dfrac{b}{p})\)

Applications of Congruences⚓︎

Hashing Functions⚓︎

具体见数据结构基础

散列函数 (Hashing function)\(h\) 用键 (key)唯一表示记录 (records)。它会给键为 \(k\) 的记录分配内存地址 \(h(k)\)。它具有以下特征：容易求解，是满射函数

一种最常用的散列函数：\(h(k) = k \ \mathbf{mod}\ m\)，\(m\) 为可用内存的个数

因为散列函数不是单射函数，因此可能存在不止一个数据被分配到同一个内存地址的情况，我们称这种情况为冲突 (collision)。一种解决冲突的方法是：为内存位置被占的数据，分配从该位置开始第一个未被占用的内存位置。这种方法可用线性探测函数 (linear probing function)表示：\(h(k, i) = h(k) + i \ \mathbf{mod}\ m\)

Pseudorandom Numbers⚓︎

通过系统方法生成的“随机”数并不真的随机，这样的数被称为伪随机数 (pseudorandom numbers)

生成伪随机数最常用的方法是线性同余法 (linear congruential method)：

• 选择 4 个整数：模数 (modulus)\(m\)，乘数 (multiplier)\(a\)，增量 (increment)\(c\)，种子 (seed)\(x_0\)，且 \(2 \le a < m, 0 \le c < m, 0 \le x_0 < m\) >\(c\)通常设为0
• 通过连续使用以下递归定义的函数，获得一系列的伪随机数 \(\{x_n\}\)，对于所有 \(n\)，满足 \(0 \le x_n < m\) $$ x_{n+1} = (ax_n + c) \mathbf{mod} m $$ 如果要得到0-1之间的伪随机数(经常使用)，只需上面将得到伪随机数除以\(m\)，即\(\dfrac{x_n}{m}\)是在0-1之间的伪随机数

上述伪随机数生成器被称为纯乘法生成器 (pure multiplicative generator)

线性同余法虽然方便，但是它无法像真正的同余数那样显示一些重要的统计学性质。对于这类问题，应采用别的方法

Check Digits⚓︎

校验位 (Check digit)：通常位于位串的末尾，用来侦测位串是否有错误

Supplements(from Exercises)⚓︎

• 另一种解决散列冲突的方法：双重散列 (double hashing)——使用最初的散列函数 \(h(k) = k\ \mathbf{mod}\ p\) 和第二个散列函数 \(g(k) = (k + 1)\ \mathbf{mod}\ (p - 2)\)。当冲突发生时，我们使用检测序列 (probing sequence)\(h(k, i) = (h(k) + i \cdot g(k))\ \mathbf{mod}\ p\)
• 平方取中法 (middle-square method)：从 1 个 n 位整数开始生成伪随机数。将这个数平方，并在结果左边填充 0，使其长度为 2n。取这个结果中间 n 位数字作为伪随机数序列的下一个数字
• 幂生成器 (power generator)（用来生成伪随机数）：指定质数 \(p\) 和正整数 \(d\)，满足 \(p \nmid d\)，和一个种子 \(x_0\)。伪随机数 \(x_1, x_2, \dots\) 通过递归定义 \(x_{n+1} = x_n^d \ \mathbf{mod}\ p\)

Cryptography⚓︎

Classsical Cryptography⚓︎

Public Key Cryptography⚓︎

The RSA Cryptosystem⚓︎

Encryption⚓︎

Decryption⚓︎

RSA as a Public Key System⚓︎

Cryptographic Protocols⚓︎

Homomorphic Encryption⚓︎

评论区