Chap 3 Algorithms⚓︎

Algorithms⚓︎

省流：这里的内容貌似不会直接考察 ( 所以可以选择性忽略这一小节 )

想看就点开来看吧

Algorithms⚓︎

我们可以把很多的问题当作某个通用问题 (general problems) 的一种特殊情况来求解。而要求解这个通用问题，我们需要明确解决问题的流程，也就是算法 (algorithms)——用来执行计算或求解问题的有限步精确指令的序列。

如何描述算法？

• 自然语言（太繁琐❌）
• 编程语言（难以理解❌）
• 伪代码 (pseudocode)（）

  伪代码具体写法见附录（后续会更新🚧）

简单验证算法的正确性：构造一个trace( 我不知道翻译成什么 )，代入自己指定的输入，按照算法一步步往下做，看能不能得到正确的输出

算法的性质：

• 输入 (input)：一个算法应有来自指定集合的输入值
• 输出 (output)：对于每组输入，算法能够产生来自指定集合的输出
• 确定性 (definiteness)：算法的每一步必须被精确定义
• 正确性 (correctness)：对于每组输入，算法应该给出正确的输出值
• 有限性 (finiteness)：对于任何输入，算法应该在经过有限步后给出预期的输出
• 有效性 (effectiveness)：算法的每一步必须在有限的时间里被精确地执行
• 通用性 (generality)：算法应适用于所有预期形式的问题，而不仅仅解决某个特例

🌰

时间复杂度：\(\Theta(n)\)

CS 常见的重要且基本的问题：

• 查找问题 (searching problems)
• 排序问题 (sorting problems)
• 优化问题 (optimization problems)

Searching Algorithms⚓︎

The Linear Search⚓︎

时间复杂度：\(\Theta(n)\)

The Binary Search⚓︎

使用前提：数据必须是有序的（以升序为例）

时间复杂度：\(\Theta(\log n)\)

注

注意这里的二分查找取左半边的部分和通常做法不太一样——这里是j := m而不是j := m - 1，因此判断条件也变了 ( 从i <= j变成i < j )。下表来自我高中信息技术的笔记 ( 用来死记硬背 )

	i	j	m	i 的变化	j 的变化
i <= j	0	n-1	(i + j) / 2	m+1	m -1
i < j	-1	n-1	(i + j + 1) / 2	m	m - 1
	0	n	(i + j) / 2	m + 1	m
i < j+1	-1	n	(i + j) / 2	m	m

口诀 ( 针对中间两行 )：左偏右扩，右偏左扩，哪里扩哪里取 m。

• 所谓“扩”指 i 或 j 的取值相对于第一种情况发生了变化

• 而所谓 " 偏 " 指 m 的取值——这里着重声明一下：

  • (i + j) / 2 指的是 \(\lfloor(i + j) / 2\rfloor\)，这是“左偏”
  • 而 (i + j + 1) / 2 指的是 \(\lceil(i + j) / 2\rceil\)，这是“右偏”

Sorting⚓︎

有许许多多的排序算法，比如下面这些 ( 其中高光部分是等会儿会讲的，其它的后面也都会讲到 )：

• 冒泡排序 (bubble sort)
• 插入排序 (insertion sort)
• 选择排序 (selection sort)
• 二分插入排序 (binary insertion sort)
• 筛动排序 (shaker sort)
• 归并排序 (merge sort)
• 快速排序 (quick sort)
• 联赛排序 (tournament sort)

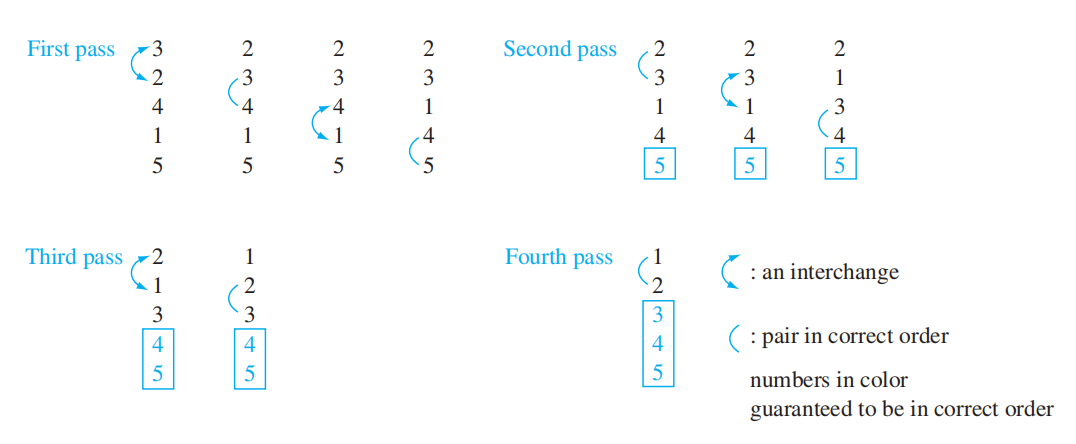
The Bubble Sort⚓︎

思路：以升序为例，比较两个相邻项，如果顺序错误，对调两者，否则不动。这样可以做到小的项往上“冒泡”，大的项往下“沉”，实现排序。

示意图

伪代码

时间复杂度：\(\Theta(n^2)\)

The Insertion Sort⚓︎

思路：对于某个列表第 j 项，前面 j-1 项已经排好序，将第 j 项分别于前 j-1 项进行比较，找到合适的位置，然后“插入”，实现前 j 项的排序

伪代码

时间复杂度：\(\Theta(n^2)\)

String Matching⚓︎

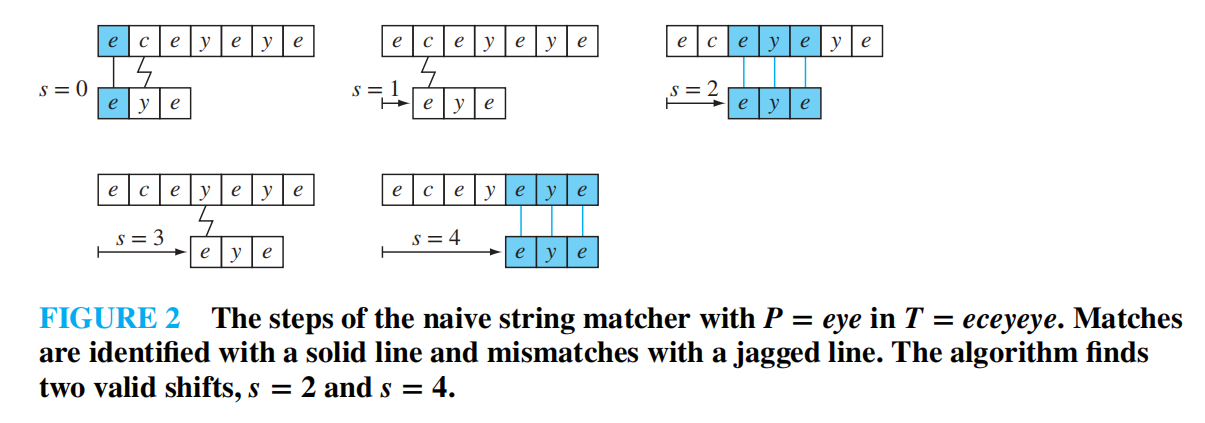
字符串匹配 (string matching) 是搜索和排序问题的其中一种情况：在文本 (text)\(T\) 中找到模式 (pattern)\(P\)。这类问题出现于多个领域中。

简单的算法：简单字符串匹配器 (naive string matcher)

注：这里的下标 \(s\) 被称为移位 (shift)，它是文本中模块出现位置（第一个字符）的前一个位置

配上这个示意图可以更好理解上述算法

Greedy Algorithms⚓︎

优化问题 (optimization problems)：对于给定参数，找到这个问题的最大或最小解

其中一种最简单的算法——贪心算法 (greedy algorithm)

核心思想：局部最优解 \(\rightarrow\) 全局最优解

注意：当我们用贪心算法得到可行解时，不要忘记验证它是否得到的是最优解

典型例子

收银员算法 (Cashier's algorithm)安排讲座

：找最少数目的零钱

然后我们需要证明它是否得到最优解。在证明之前，我们先得到一个引理：

注：America 有四种硬币——quarter(25 cents)，dime(10 cents)，nickel(5 cents)，penny(1 cent)

引理 1：如果 \(n\) 是正整数，通过使用 q、d、n、p 四种硬币找零钱，要找最少数目的零钱，则最多使用 2 个 d、1 个 n、4 个 p，且不能使用 2 个 d 和 1 个 n，而且 d、n、p 的硬币总和不超过 24 cents

可用归谬法证，这个不难理解

证明过程省略，还是采用归谬法（见教材 \(P_{211}\)）

问题：给定一组讲座的开始和结束时间，要求你安排这些讲座的时间，确保在一间大厅里安排尽可能多的讲座。

如何思考：

• 按开始时间先后顺序排❌
• 按持续时间长短升序排序❌
• 按结束时间先后顺序排

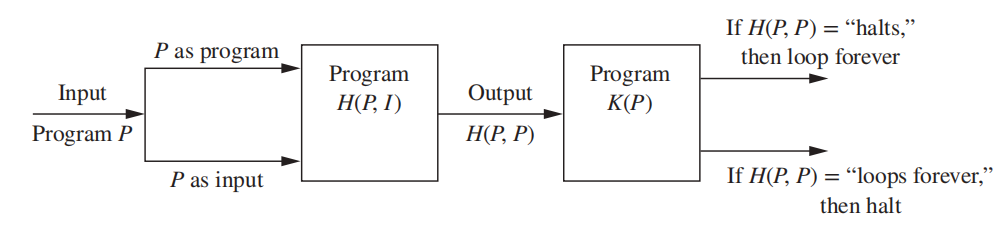
The Halting Problem⚓︎

停机问题 (Halting problem)：这是不可解 (unsolvable)的问题

示意图

仅做了解

Supplements(from Exercises)⚓︎

• 三分查找算法 (Ternary search algorithm)：在升序列表中，通过连续划分三块 ( 尽可能 ) 相等规模的子列表，并限制在其中一块进行搜索要找的元素。

• 选择排序 (Selection algorithm)：首先找到列表中最小的元素，将这个元素移动至最前面。然后在剩下的元素中寻找最小的元素，并放在第二个位置。重复该步骤，直至所有元素均排好序。

• 二分插入排序 (Binary insertion sort)：插入排序的一种变体。通过二分查找而非线性查找的方式，在之前已排好序的元素中找到正确的位置。

The Growth of Functions⚓︎

Big-O Notation⚓︎

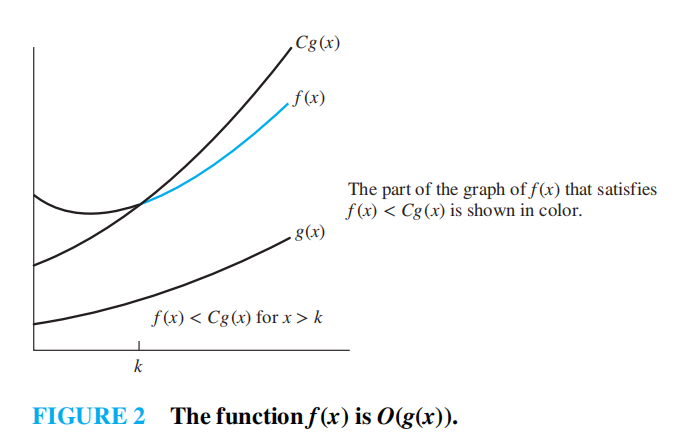
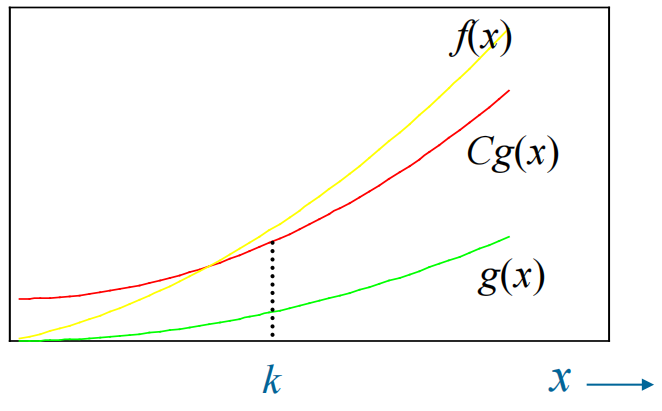
大 \(O\) 表示法的定义：令 \(f\) 和 \(g\) 为从整数集或实数集映射到实数集的函数，如果存在常数 \(C\) 和 \(k\)，当 \(x > k\) 时，使得 \(|f(x)| \le C|g(x)|\)，我们认为 \(f(x)\) 是 \(O(g(x))\)（也就是说，\(f(x)\) 的增长速度慢于 \(g(x)\)）

其中 \(C\) 和 \(k\) 被称为见证者 (witnesses)。如果要证明 \(f(x)\) 是 \(O(g(x))\)，需要找到这么一对见证者。当然，如果能找到一对见证者，也能够找到无数对见证者（很容易证明）

• 如果 \(f(x)\) 是 \(O(g(x))\) 且 \(g(x)\) 是 \(O(f(x))\)，那么称 \(f(x)\) 和 \(g(x)\) 是同阶 (same order)的

• 如果 \(f(x)\) 是 \(O(g(x))\)，且 \(|h(x)| > |g(x)|\)，那么 \(f(x)\) 也是 \(O(h(x))\)

  根据这条性质，虽然可以取很多个增长速率快于 \(f(x)\) 的函数，但为了统一，我们往往选择最小的，且增长速率快于 \(f(x)\)的 \(g(x)\) 作为大 O 阶

注：

• 有时我们会看到 \(f(x) = O(g(x))\)，这是对等号的滥用——因为等号两边的东西并不相等。但我们可以使用 \(f(x) \in O(g(x))\)
• 在之后的篇章中，由于我们研究的都是正数，所以就将绝对值去掉了，以简化计算

Big-O Estimate for Some Important Functions⚓︎

Polynomials⚓︎

定理 1：令 \(f(x) = a_nx^n + a_{n - 1}x^{n - 1} + \dots + a_1x +a_0 (a_0, a_1, \dots, a_{n - 1}, a_n \in \mathbf{R})\)，那么 \(f(x)\) 是 \(O(x^n)\)，即多项式的首项控制整个多项式的增长速率

一些重要结论：

• \(n!\) 是 \(O(n^n)\)
• \(\log n!\) 是 \(O(n \log n)\)
• \(n\) 是 \(O(2^n)\)
• \(\log n\) 是 \(O(n^\alpha), \alpha > 0\)
• 当 \(d > c > 1\) 时，\(n^c\) 是 \(O(n^d)\)，反之不成立
• 当 \(d > c > 1\) 且 \(b > 1\) 时，\((\log_bn)^c\) 是 \(O(n^d)\)，反之不成立
• 当 \(c > b > 1\) 时，\(b^n\) 是 \(O(c^n)\)，反之不成立
• 当 \(c > 1\) 时，\(c^n\) 是 \(O(n!)\)，反之不成立

来自习题的补充：

• \(1^k + 2^k + \dots + n^k\) 是 \(O(n^{k + 1})\)
• 对于所有实数 \(a > 1, b > 1\)，如果 \(f(x)\) 是 \(O(\log_b x)\)，则 \(f(x)\) 是 \(O(\log_a x)\)
• 调和 ( 级 ) 数 (Harmonic number)：\(H_n = 1 + \dfrac{1}{2} + \dots + \dfrac{1}{n}\)，则 \(H_n\) 是 \(O(\log n)\)
• \(n \log n\) 是 \(O(\log n!)\)

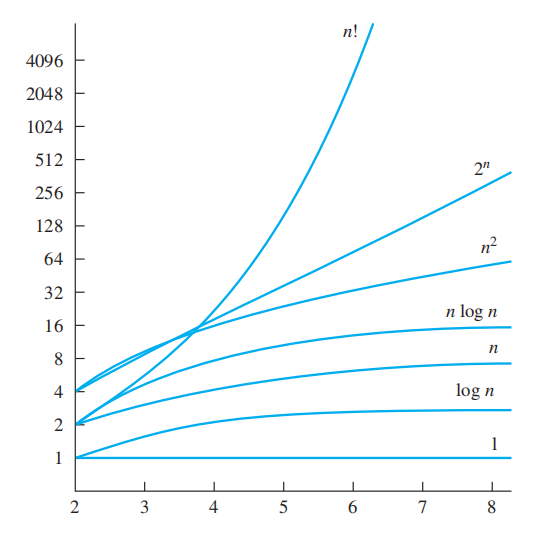
常见函数增长率图象

The Growth of Combinations of Functions⚓︎

定理 2：假设 \(f_1(x)\) 是 \(O(g_1(x))\)，\(f_2(x)\) 是 \(O(g_2(x))\)，那么 \((f_1 + f_2)(x)\) 是 \(O(g(x))\)，其中 \(g(x)=(\max\{|g_1(x)|, |g_2(x)|\}), \forall x\)

推导：由已知，假设当 \(x > k_1\) 时，有 \(|f_1(x)| \le C_1|g_1(x)|\)；当 \(x > k_2\) 时，有 \(|f_2(x)| \le C_2|g_2(x)|\)，则

其中 \(C = C_1 + C_2\)，\(k = \max\{ k_1, k_2\}\)

推论 1：如果 \(f_1(x)\) 和 \(f_2(x)\) 都是 \(O(g(x))\)，那么 \((f_1 + f_2)(x)\) 是 \(O(g(x))\)

定理 3：假设 \(f_1(x)\) 是 \(O(g_1(x))\)，\(f_2(x)\) 是 \(O(g_2(x))\)，那么 \((f_1f_2)(x)\) 是 \(O(g_1(x)g_2(x))\)

推导过程类似前面，具体见教材 \(P_{226}\)

Big-Omega and Big-Theta Notation⚓︎

大 \(O\) 表示法只能检测上限，如果要分析下限，则需要使用大 \(\Omega\) 表示法。

大 \(\Omega\) 表示法的定义：令 \(f\) 和 \(g\) 为从整数集或实数集映射到实数集的函数，如果存在常数 \(C\) 和 \(k\)，当 \(x > k\) 时，使得 \(|f(x)| \ge C|g(x)|\)，我们认为 \(f(x)\) 是 \(\Omega(g(x))\)（也就是说，\(f(x)\) 的增长速度快于 \(g(x)\)）

注：\(f(x)\) 是 \(\Omega(g(x))\)，当且仅当 \(g(x)\) 是 \(O(f(x))\)

除此之外，我们用大 \(\Theta\) 表示法同时表示上下限。

大 \(\Theta\) 表示法的定义：当 \(f(x)\) 是 \(O(g(x))\) 且 \(f(x)\) 是 \(\Omega(g(x))\)，则称 \(f(x)\) 是 \(\Theta(g(x))\)。如果满足这一关系，则 \(f(x)\) 与 \(g(x)\)同阶 (same order)，称 \(f(x)\) 是 \(g(x)\) 的阶 (order)

• 如果 \(f(x)\) 是 \(\Theta(g(x))\)，那么 \(g(x)\) 是 \(\Theta(f(x))\)
• \(f(x)\) 是 \(\Theta(g(x))\) 的充要条件是 \(f(x)\) 是 \(O(g(x))\) 且 \(g(x)\) 是 \(O(f(x))\)
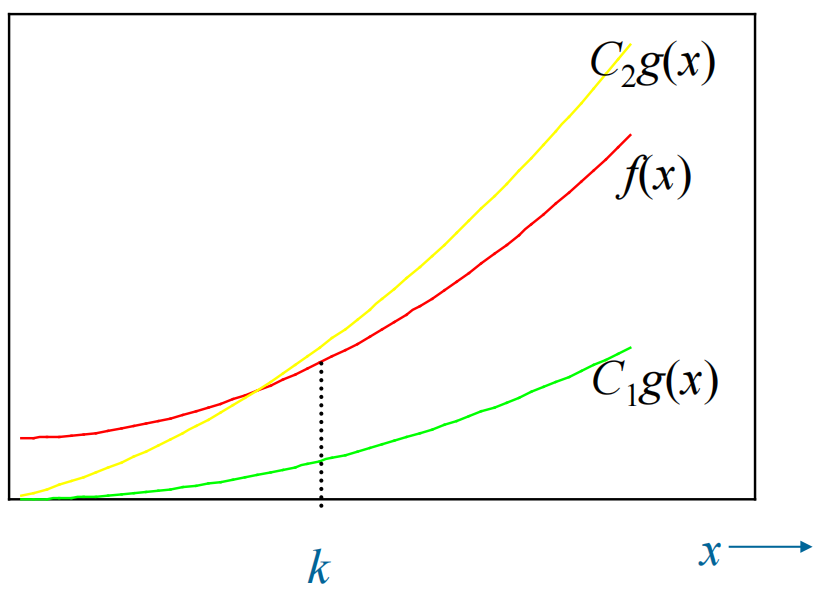
• 另一个充要条件：存在三个正实数 \(C_1, C_2, k\)，当 \(x > k\) 时，满足 \(C_1|g(x)| \le |f(x)| \le C_2|g(x)|\)

定理 4：令 \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\)，其中 \(a_0, a_1, \dots, a_n\) 是实数且 \(a_n \ne 0\)，则 \(f(x)\) 是 \(x^n\) 的阶

注：且 \(f(x)\) 是 \(\Theta(x^n)\)

Supplements(from Exercises)⚓︎

• 如果函数 \(f(x), g(x), h(x)\)，满足 \(f(x)\) 是 \(O(g(x))\) 且 \(g(x)\) 是 \(O(h(x))\)，则 \(f(x)\) 是 \(O(h(x))\)
• 如果函数 \(f(x), g(x), h(x)\)，满足 \(f(x)\) 是 \(\Theta(g(x))\) 且 \(g(x)\) 是 \(\Theta(h(x))\)，则 \(f(x)\) 是 \(\Theta(h(x))\)
• 如果 \(f, g\) 是实数值函数，且 \(f(x)\) 是 \(O(g(x))\)，那么对于任意正整数 \(n\)，\(f^n(x)\) 是 \(O(g^n(x))\)
• 如果 \(f, g\) 是无界递增函数，且 \(f(x)\) 是 \(O(g(x))\)，则 \(\log |f(x)|\) 是 \(O(\log |g(x)|)\)
• 如果 \(f(x)\) 是 \(O(g(x))\)，则 \(2^{f(x)}\) 是 \(O(2^{g(x)})\)
• 令 \(f_1(x), f_2(x)\) 和 \(g(x)\) 是从实数集映射到正实数集的函数，如果 \(f_1(x)\) 和 \(f_2(x)\) 都是 \(\Theta(g(x))\)，那么 \(f_1(x) + f_2(x)\) 是 \(\Theta(g(x))\)
• 令 \(f_1(x), f_2(x)\) 和 \(g(x)\) 是从正整数集映射到实数集的函数，\(f_1(x)\) 是 \(\Theta(g_1(x))\)，\(f_2(x)\) 是 \(\Theta(g_2(x))\)，那么 \((f_1f_2)(x)\) 是 \(\Theta((g_1g_2)(x))\)
• 对于所有正实数 \(x\)，如果 \(f_1(x)\) 是 \(\Theta(g_1(x))\)，\(f_2(x)\) 是 \(\Theta(g_2(x))\)，且 \(f_2(x) \ne 0,\ g_2(x) \ne 0\)，则 \((\dfrac{f_1}{f_2})(x) = \Theta(\dfrac{g_1}{g_2})(x)\)
• 大 \(O\)，大 \(\Omega\) 和大 \(\Theta\) 表示法可以扩展至多元函数。比如，如果存在常数 \(C, k_1, k_2\)，当 \(x > k_1, y > k_2\) 时，有 \(|f(x, y)| \le C|g(x, y)|\) 成立，则 \(f(x, y)\) 是 \(O(g(x, y))\)
• 小 \(o\) 表示法：当 \(\lim\limits_{x \rightarrow \infty} \dfrac{f(x)}{g(x)} = 0\)，则 \(f(x)\) 是 \(o(g(x))\) 与大\(O\)表示法的关系：如果\(f(x)\)是\(o(g(x))\)，则\(f(x)\)是\(O(g(x))\)，反之不一定成立
• 令 \(f_1(x)\) 和 \(g(x)\) 是从实数集映射到实数集的函数，如果 \(\lim\limits_{x \rightarrow \infty} \dfrac{f(x)}{g(x)} = 1\)，称 \(f\) 和 \(g\) 是渐进的 (asympotic)( 或者说是同阶的 )，记作 \(f(x) \sim g(x)\)

Complexity of Algorithms⚓︎

计算复杂度 (computational complexity)：检测一个算法的效率 (efficiency)

• 时间复杂度 (time complexity)：运行时间
• 空间复杂度 (space complexity)：内存空间

  这里我们不讨论空间复杂度，可以参照数据结构相关内容

Time Complexity⚓︎

一个算法的时间复杂度可被有特定规模输入的算法的运算次数( 比如四则运算 ) 来表示，一般不会用计算机运行的真实时间来表示

如何分析：

• 最坏情况复杂度：找到最大的运行次数
• 平均情况复杂度：要找到所有可能输入对应的算法运行次数，比找最坏的更复杂

🌰

注：它之所以能直接除以 \(n\)，是因为每种情况是等可能出现的

Matrix Multiplication⚓︎

矩阵乘法算法的伪代码：

该算法进行了 \(n^3\) 次乘法运算，\(n^2(n-1)\) 次加法运算，因此时间复杂度为 \(O(n^3)\)

布尔积算法的伪代码

\(A \odot B\) 中进行了 \(2n^3\) 次位运算

矩阵链 (matrix-chain)：一系列矩阵的乘法 \(\mathbf{A_1A_2 \dots A_n}\)，规模分别为 \(m_1 \times m_2, m_2 \times m_3, \dots m_n \times m_{n+1}\)

注意：不同的运算顺序会影响到矩阵链的乘法次数

Algorithmic Paradigms⚓︎

算法范式 (algorithmic paradigms)：为了用来构建算法解决某些问题，而采取的通用方法。

种类：

• 暴力算法 (brute-force algorithm)
• 贪心算法 (greedy algorithm)：最短路算法、最小生成树算法等
• 分治算法 (divide-and-conquer algorithm)
• 动态规划 (dynamic programming)
• 回溯法 (backtracking)：DFS
• 概率算法 (probablisitic algorithm)

暴力算法 (brute-force algorithm)：基于问题的描述和项的定义，而采取解决问题的最直接的方法，它没有利用任何特定结构和巧妙的思想

我们已经遇到过许多暴力算法：

• 在序列里找最大数，或者求整个序列的和
• 冒泡、插入、选择排序

虽然暴力算法很低效，但它在下列情况中很有用：

• 当输入规模不大的时候
• 作为设计新的 ( 高效的 ) 算法时的衡量标准

🌰

Understanding the Complexity of Algorithms⚓︎

❗常见时间复杂度

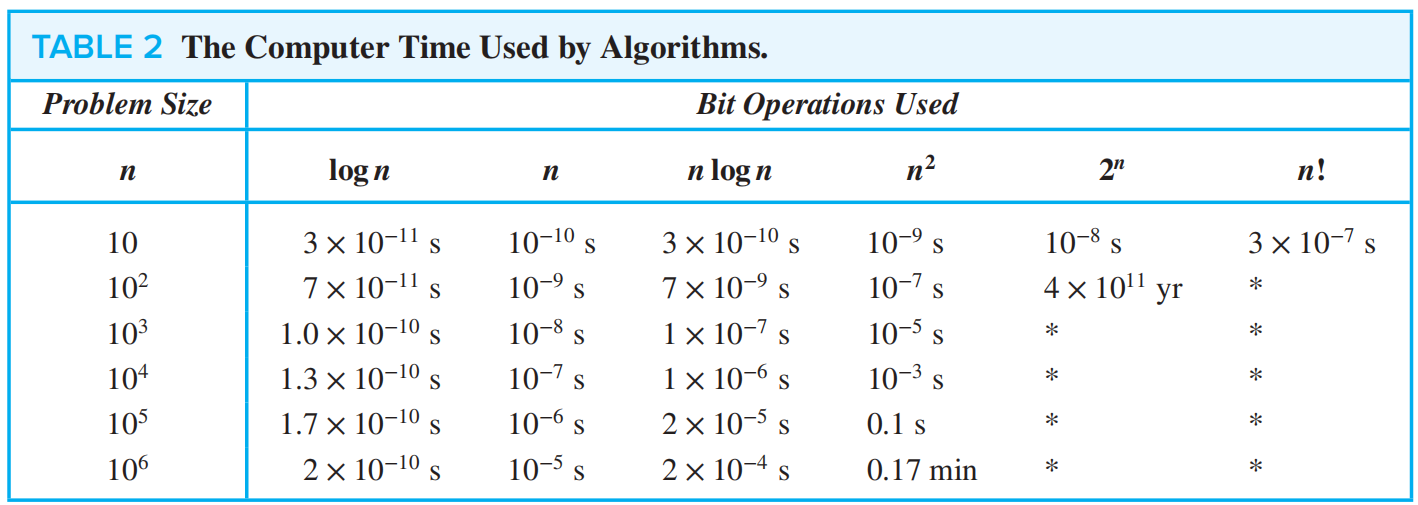
各种复杂度的大致运行时间（采用 2018 年性能最强的计算机）

Tractability⚓︎

注：这边的内容不需多作了解

Supplements(from Exercises)⚓︎

• 对于指定的运算规则，如果没有任何一个算法，解决问题的运算次数小于某个算法，则称这个算法对于该问题是最优的 (optimal)

Suppplements(from Exercises)⚓︎

• The Shaker sort(bidirectional bubble sort)( 双向冒泡排序 )：不同于原版的单向，这个算法先从头到尾比较相邻元素，然后从尾到头比较相邻元素，运用相似的规则排序，直至所有元素有序为止。时间复杂度：\(O(n^2)\)

• The knapsack problem( 背包问题 )：和动态规划有关，这里就不讲了

• approximation algorithm( 近似算法 )：对于一个优化问题，得到一个接近最优解的解。假设这个问题是，找到输入 \(S\)，使得 \(F(X)\) 最小，如果某个算法总能找到输入 \(T\)，使得 \(F(T) \le cF(S)\)，\(c\) 是固定的正整数，那么这个算法被称为c-approximation algorithm

评论区