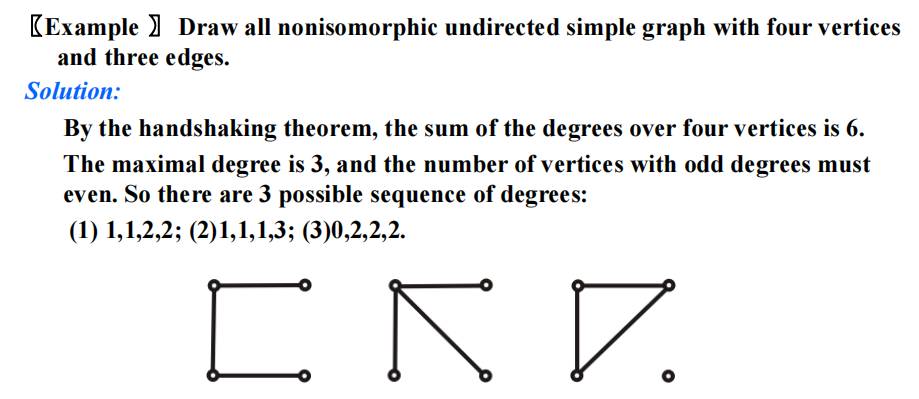
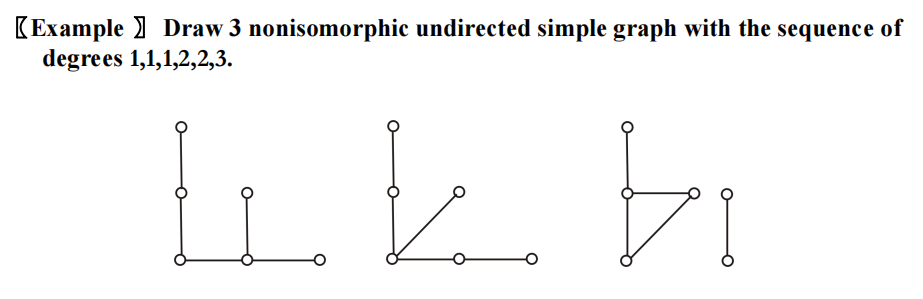
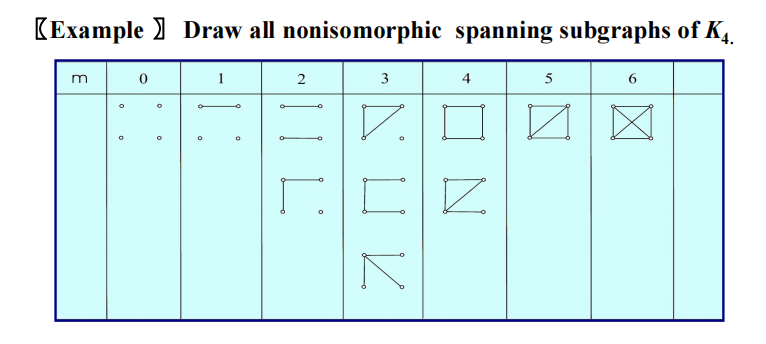
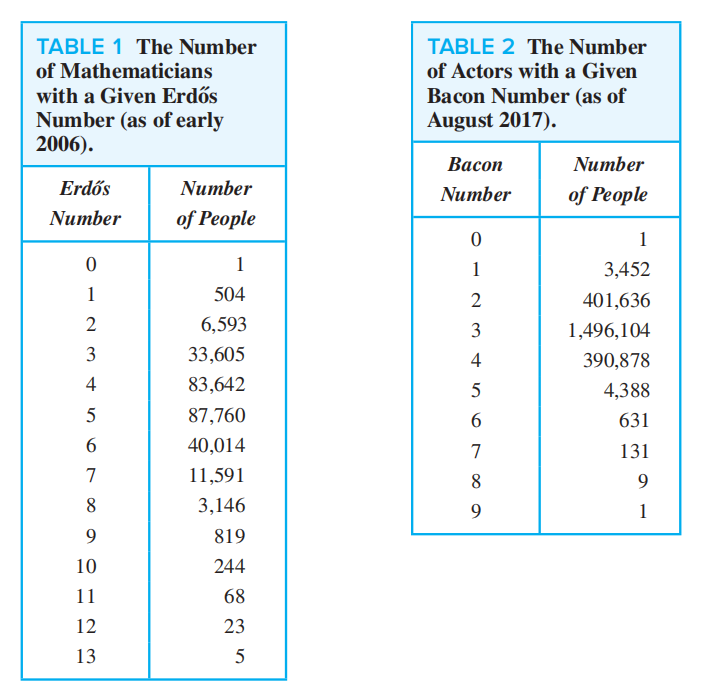
Chap 10 Graph⚓︎
约 13266 个字 预计阅读时间 66 分钟
核心知识
- 基本概念
- 特殊的图
- 二分图、匹配
- 图的表示法:邻接矩阵、关联矩阵
- 图的同构:不变量
- 连通度
- 基本概念:无向图、有向图
- 点连通度、边连通度
- 欧拉环 / 路
- 哈密顿环 / 路
- 最短路:Dijkstra 算法、旅行商问题
- 平面图:欧拉公式、库氏定理
- 图着色问题
感觉列出来的都挺重要的,所以就没有着重标出某一条了
可参照 fds 同名章节
Graphs and Graph Models⚓︎
定义:图 (graph)\(G = (V, E)\),其中 \(V\) 表示顶点 (vertice/nodes)的非空集合,\(E\) 表示边 (edge)的集合。每条边联系 1-2 个顶点,这些顶点被称为端点 (endpoint),称一条边连接它的端点
-
无限图 (infinite graph):包含无限个顶点或无限条边的图
-
有限图 (finite graph):包含有限个顶点和有限条边的图。本章只考虑有限图的问题
-
简单图 (simple graph):每条边连接不同的顶点,且不存在连接同一对顶点的两条边的图。这时,我们可以用顶点对 {u, v} 表示一条边,而不产生歧义
- 多重图 (multigraph):存在连接同一对顶点的重边 (multiple edges)的图。如果顶点 u, v 间有 m 条边,称 {u, v} 是重数为 m 的边
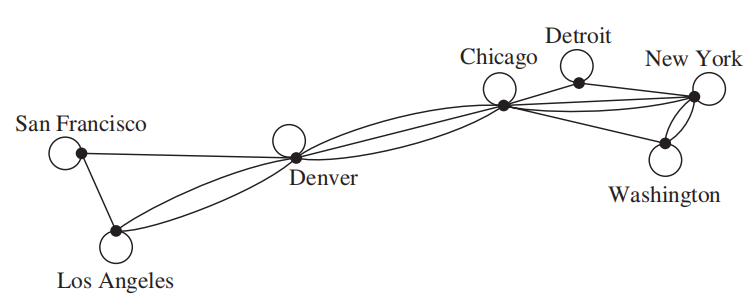
- 伪图 (pseudograph):存在环,且可能有多条边连接同一对顶点或连接顶点自身的图
环 (loop):从某个顶点出发连接自身的边
上述的图均为无向图 (undirected graph)
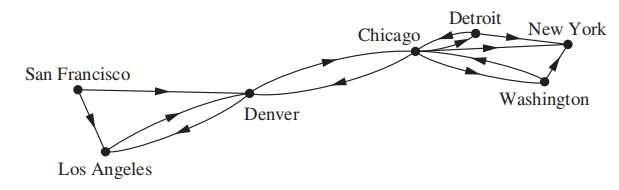
定义:有向图 (directed graph, digraph)\((V, E)\) 包含顶点的非空集合 \(V\) 和有向边 (directed edges/arc)的集合 \(E\)。每条有向边与有序顶点对 (u, v) 有联系,称 v 为起点 (start),v 为终点 (end)
有向图也存在环和多条有向边的情况
- 简单有向图 (simple directed graph):没有环,也没有多条有向边的图
- 有向多重图 (directed multigraph):对于同一有序顶点对 ( 或同一顶点 ) 存在多条有向边 (multiple directed edges)。如果顶点 u, v 间有 m 条有向边,称 (u, v) 是重数 (multiplicity)为 m 的有向边
- 混合图 (mixed graph):既包含有向边,也包含无向边的图
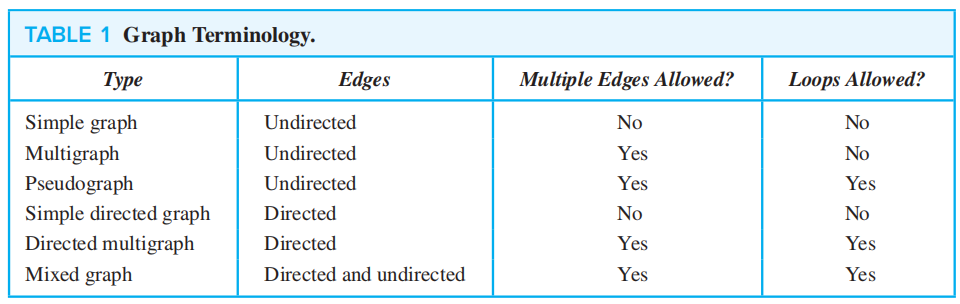
总结:
注:如果题目没有明确说明,默认将图当作无向图
Graph Models⚓︎
注:这部分内容并不重要,因此这里只简单列举一些例子,具体内容见书本
例题
社交网络 (social networks):用顶点表示个体或组织,用边表示个体或组织之间的联系
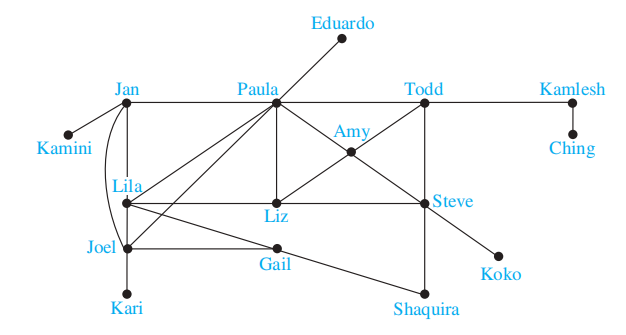
- 熟人 / 朋友关系图 (acquaintanceship and friendship graphs):无向图,无环,没有多重边
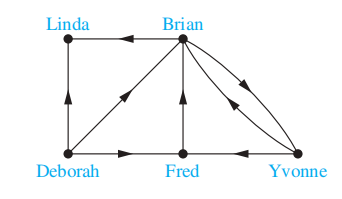
- 影响力图 (influence graphs):有向图,无环,没有多重边
- 合作图 (collaboration graphs):无向图,无环,没有多重边
- 好莱坞图 (Hollywood graph)
- 学术合作图 (academic collaboration graph)
- 网络图 (the web graph):有向图
- 引用图 (citation graphs):有向图,无环,没有多重边
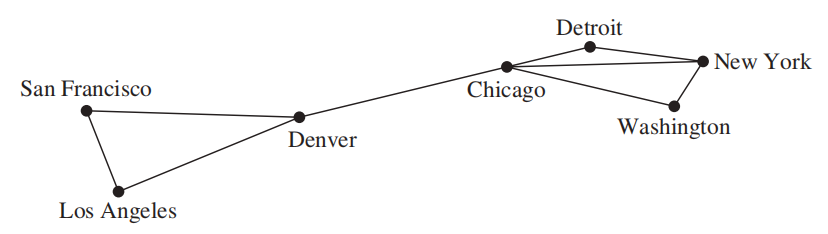
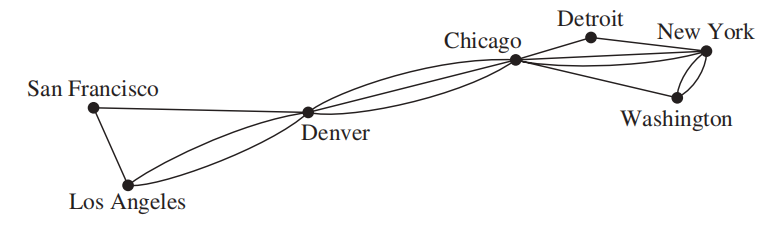
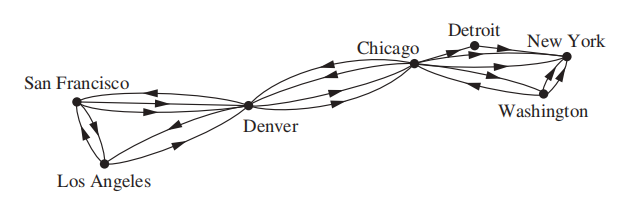
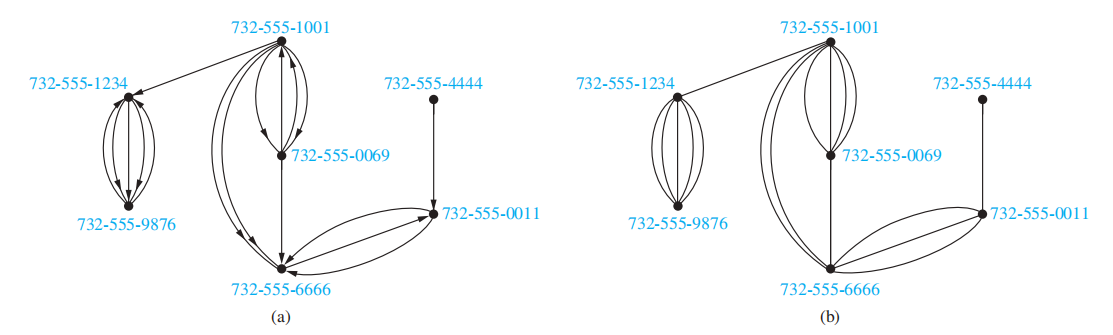
- 航空路程 (airline routes):有向多重图
- 路线网络 (road networks):混合图
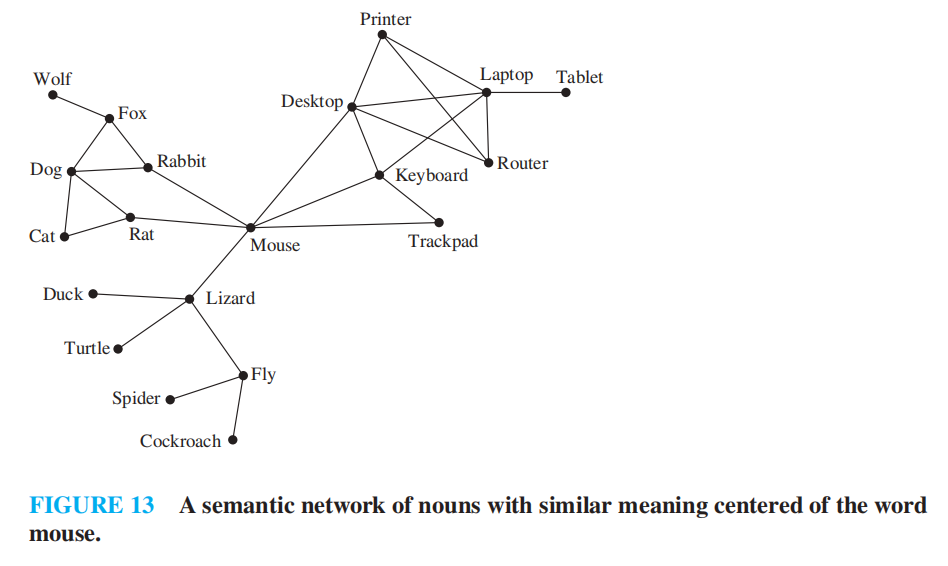
- 自然语言理解 (natural language understanding, NLU):机器分拆并解析人类的话语
注:NLU 是自然语言处理 (NLP) 的子集,也是 NLP 中最困难的部分
- 信息检索 (information retrieval, IR):从基于各种类型的搜索的一组源中获取信息
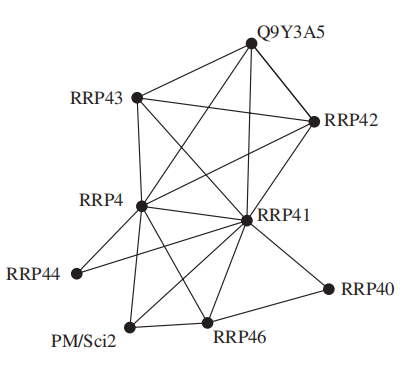
语义关系 (semantic relation):两个或多个单词基于意思的联系
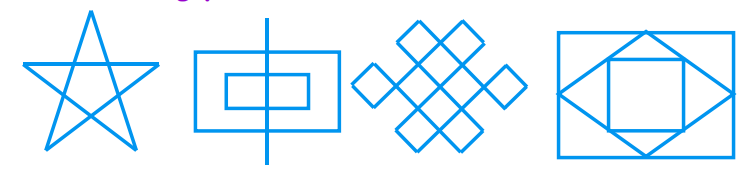
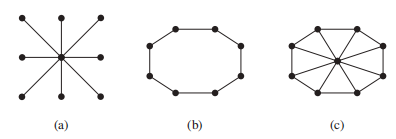
- 一笔画问题 (one-stroke drawing problem):画一幅画,确保连续移动而不提笔,使得画中所有部分仅画一遍
- 拉姆齐问题:每两个人要么是朋友,要么是敌人,那么六个人中有三对朋友和三对敌人
- 排座问题 (seating problem)
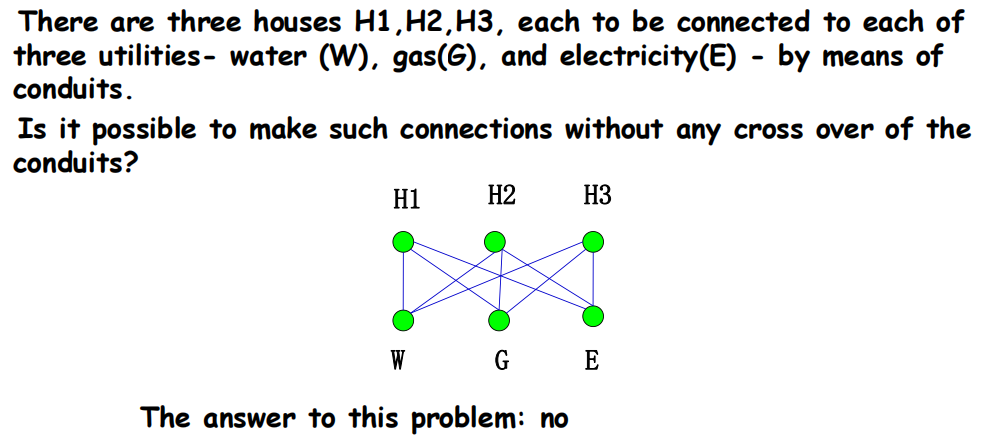
- 公共资源问题 (utilities problem):具体见 wiki,这里仅举个🌰
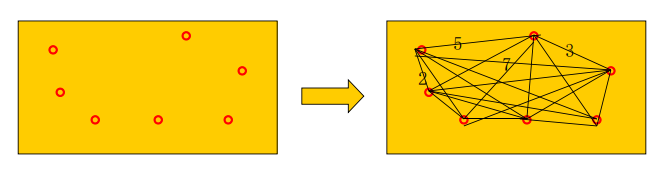
- 钻孔问题 \(\rightarrow\) 最短路问题:找到一种钻孔顺序,使得用时最少
Supplements(from Exercises)⚓︎
关于一组集合 \(A_1, A_2, \dots, A_n\) 的交集图 (intersection graph):它的顶点表示这些元素,它的边表示某两个集合存在非空交集的关系
Graph Terminology and Special Types of Graphs⚓︎
Basic Terminology⚓︎
关于无向图:
定义:
- 如果顶点 u, v 是无向图 G 的边 e 上的两个端点,称这两个顶点是相邻的 (adjacent/neighbors),这样的边 e连接了 u 和 v
- 图 \(G = (V, E)\) 上的顶点 v 的所有相邻顶点构成的集合被称为 v 的邻居 (neighborhood),记作 \(N(v)\)
- 如果 A 是 V 的子集,用 \(N(A)\) 表示所有与 A 中的至少一个顶点相邻的所有顶点构成的集合,所以,\(N(A) = \bigcup\limits_{v \in A}N(v)\)
- 无向图中顶点 v 的度 (degree)= 与该顶点关联的边数,记作 \(deg(v)\)
- 度为 0 的顶点被称为孤立的 (isolated)
- 度为 1 的顶点被称为下垂的 (pendant)
- 顶点的一个环的度为 2
定理 1——握手定理 (THE HANDSHAKING THEOREM):令 \(G = (V, E)\) 是边数为 m 的无向图,则:所有顶点的度之和 = 边数 \(\times\) 2,即:\(2m = \sum\limits_{v \in V}deg(v)\)(该定理同样适用于重边)
🌰:
定理 2:在无向图中,度为奇数的顶点个数为偶数
证明
令 \(V_1, V_2\) 分别表示度为偶数和度为奇数的顶点,由定理 1,有: $$ 2m = \sum\limits_{v \in V}deg(v) = \sum\limits_{v \in V_1}deg(v) + \sum\limits_{v \in V_2}deg(v) $$ 显然:等式左边的数为偶数,且最右边的等式中第1项为偶数。因此第2项,即度为奇数的顶点个数一定是偶数
关于有向图:
定义:
- 当 (u, v) 表示图 G 的有向边时,我们称 u到 v 是相邻的,v来自 u 是相邻的。u 被称为 (u, v) 的起点 (initial vertex),v 被称为 (u, v) 的终点 (terminal/end vertex)。自环的起点、终点是相同的
- v 的入度 (in-degree)= v 作为边的终点时的关联的边数,记作 \(deg^-(v)\)
- v 的出度 (out-degree)= v 作为边的起点时的关联的边数,记作 \(deg^+(v)\)
注:顶点 v 的环使 v 的入度和出度均 +1
定理 3:令 \(G = (V, E)\) 为有向图,则 $$ \sum\limits_{v \in V} deg^-(v) = \sum\limits_{v \in V}deg^+(v) = |E| $$
潜在无向图 (underlying undirected graph):无视有向图中边的方向,得到一张无向图
Some Special Simple Graphs⚓︎
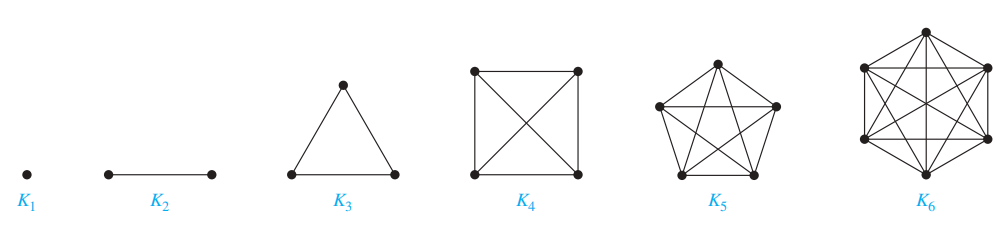
- 完全图 (complete graph)是一张简单图,满足每一对不同的顶点之间有且仅有一条边,记作 \(K_n\)。如果至少有一对不同的顶点没有连接起来,称这样的图是不完全的 (noncomplete)
注:边数 m = C(n, 2)
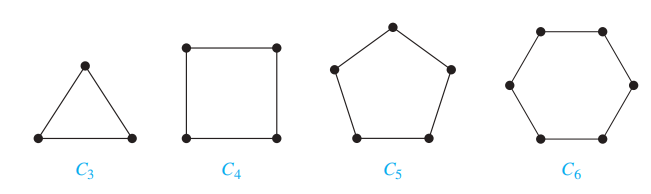
- 环 (cycle):一张包含 n(n \(\ge\) 3) 个顶点,边为 \(\{v_1, v_2\}, \{v_2, v_3\}, \dots, \{v_{n-1}, v_n\}\) 和 \(\{v_n, v_1\}\),记作 \(C_n\)
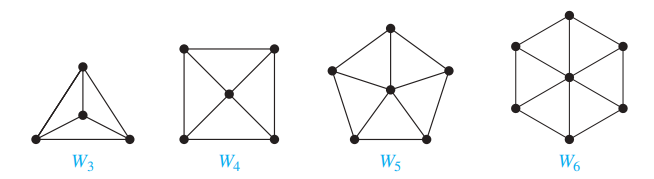
- 轮 (wheel):在环 \(C_n\) 的基础上多一个顶点,且该顶点与原来 n 个顶点间都有一条边,记作 \(W_n\)
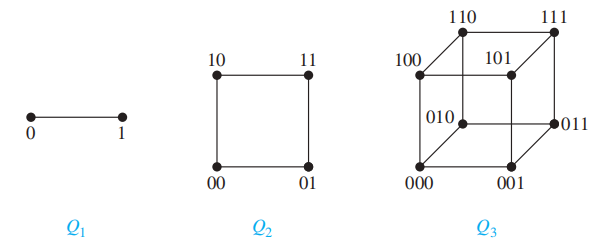
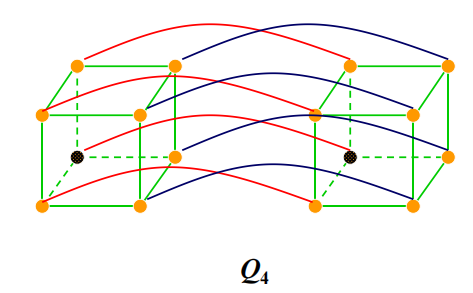
- n 维超立方体 /n 立方 (n-dimensional hypercube/n-cube):记作 \(Q_n\)。图的顶点表示 \(2^n\) 个长度为 n 的位串。当且仅当 2 个顶点的位串只相差 1 位时,两个顶点是相邻的。
我们可以根据 n 立方构造出 (n+1) 立方:
- 得到两个相同的 \(Q_n\)
- 对第 1 个 \(Q_n\) 的所有位串的最左边添 0,对第 2 个 \(Q_n\) 的所有位串的最左边添 1
- 将仅相差 1 位的两个位串 ( 顶点 ) 用边连接起来,如图所示:
因此,我们可以得到 \(Q_n\) 的边数 \(m_n\) 的递推关系: $$ m_n = 2m_{n-1} + 2^{n-1} $$ 解得\(m_n = n \cdot 2^{n-1}\)(利用线性非齐次递推关系的知识求解)
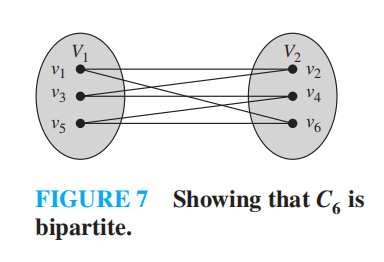
Bipartite Graphs⚓︎
定义:如果一个简单图 G 的顶点集 V 能被分成两个不相交的集合 \(V_1, V_2\),使得图中的每条边连接 \(V_1\) 的 1 个顶点和 \(V_2\) 的 1 个顶点 ( 没有边连接 \(V_1\) 的两个顶点或 \(V_2\) 的两个顶点 ),称 G 是二分的 (bipartite),称 \((V_1, V_2)\) 是 G 的顶点集 V 的二分 (bipartition)。
定理 4:当且仅当用两种不同颜色涂顶点,可以满足相邻的顶点不同色时,该简单图是二分的
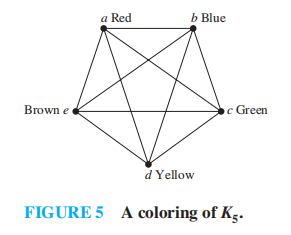
相关知识:图着色问题
判断二分图的另一种方法
二分图的充要条件是——不可能通过遍历奇数条不同的边,从某个顶点出发又回到该顶点。
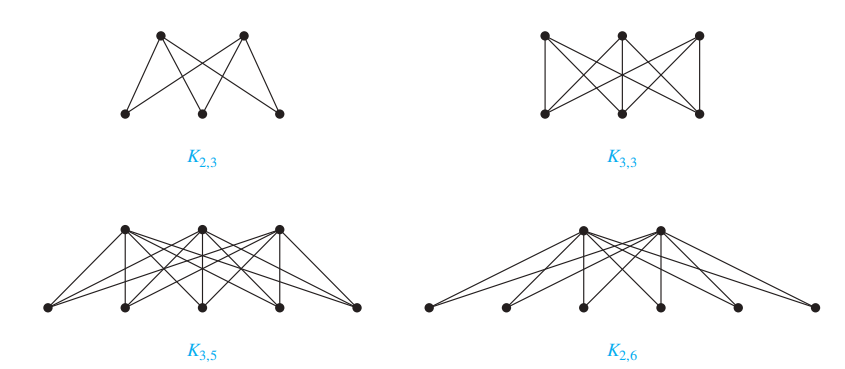
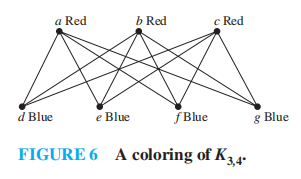
完全二分图 (complete bipartite graph):一张图被分成顶点数分别为 m 和 n 的两个子集,某个子集的顶点连接另一个子集上的所有顶点,但不连接与它属于同一子集的顶点。记作 \(K_{m, n}\)。
Bipartite Graphs and Matchings⚓︎
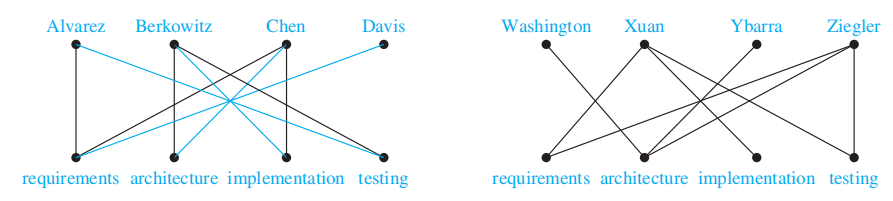
🌰:二分图的应用——工作安排
注:具体内容见书本 \(P_{692-693}\)(
内容有点多,懒得写了)
上述问题可被视为找简单图 G = (V, E) 的匹配 (matching)M,它是边集合 E 的子集,满足没有两条边有共同的顶点,即对于不同的边 {s, t} 和 {u, v},顶点 s, t, u, v 是不同的。
如果有顶点是匹配关系 M 上的某条边的一个端点,称该顶点在 M 中是匹配的 (matched);否则是不匹配的 (unmatched)
最大匹配 (maximum matching)是具有最大边数的匹配
对于二分图 G = (V, E),它的二分为 (\(V_1, V_2\)),如果 \(V_1\) 的每个顶点是匹配 M 某条边的端点,即 \(|M| = |V_1|\),称 M 是 \(V_1\) 到 \(V_2\) 的完全匹配 (complete matching)
🌰:
定理 5——霍尔婚配定理 (HALL'S MARRIAGE THEOREM):对于一个二分图 \(G = (V, E)\),它的二分为 \((V_1, V_2)\),当且仅当对于 \(V_1\) 的所有子集 \(A\),满足 \(|N(A)| \ge |A|\) 时,该二分图有从 \(V_1\) 到 \(V_2\) 的完全匹配
Some Applications of Special Types of Graphs⚓︎
串行 (serial)算法:算法在一个时刻内执行一个步骤 ( 书上给出的算法均是串行的 )。然而,这种算法无法应对高强度计算的问题。
因此就有了并行处理 (parallel processing),使用包含多个自带内存的处理器的计算机,克服只有单个处理器的计算机的局限。
并行算法 (parallel algorithm):将问题分解成能够同时解决的一些子问题,使用多处理器的电脑能够快速解决问题。
在并行处理中,处理器之间需要相互连接。因此要选择合理的连接方法:
- 每对处理器都双向连接,形成完全图 \(K_n\)——最简单,但也是最贵的方法
-
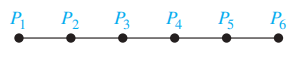
线性数组 (linear array)
- 优点:每个处理器与其他处理器间至多有两条直接连接
- 缺点:有时需要大量的中间连接 ( 被称为跳 (hop)) 来实现处理器间的通信
-
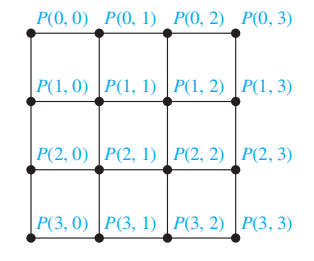
网状网络 (mesh network):n 个处理器被标记为 \(P(i, j)\ (0 \le i \le m - 1, 0 \le j \le m - 1)\)。两个方向的连接使 \(P(i, j)\) 最多有 4 个邻居 ( 在网状网络中的 \(P(i \pm 1, j)\) 和 \(P(i, j \pm 1)\))。此时任意一对处理器间的通信需要 \(O(\sqrt n) = O(m)\) 个中间连接即可。
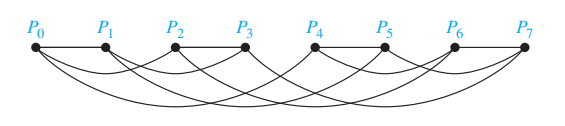
- 超立方体 (hypercube):处理器的数量为 n = \(2^m\),处理器被标记为 \(P_0, \dots, P_{n-1}\)。每个处理器与其他 m 个处理器有双向连接,即 \(P_i\) 跟与 i 仅相差 1 位的处理器之间有双向连接。这种方法权衡了处理器直接连接的数量和中间连接的数量,因此现在很多电脑和并行算法采用超立方体网络。可以用图 \(Q_m\) 表示
New Graphs from Old⚓︎
定义:
- 图 G = (V, E) 的子图 (subgraph)H = (W, F),满足 W \(\subseteq\) V,F \(\subseteq\) E。
- 如果 H 是 G 的子图且 H \(\ne\) G,则 H 是 G 的真子图 (proper subgraph)
- 如果满足 W = V, F \(\subseteq\) E,称 H 是 G 的生成子图 (spanning subgraph)
- 令 G = (V, E) 为简单图,称子集 (W, F) 为顶点集 V 的子集 W 的点诱导子图 (subgraph induced)(边集 F 包含 E 中的边
) ,充要条件为 F 的边上的两个端点都在集合 W 中。
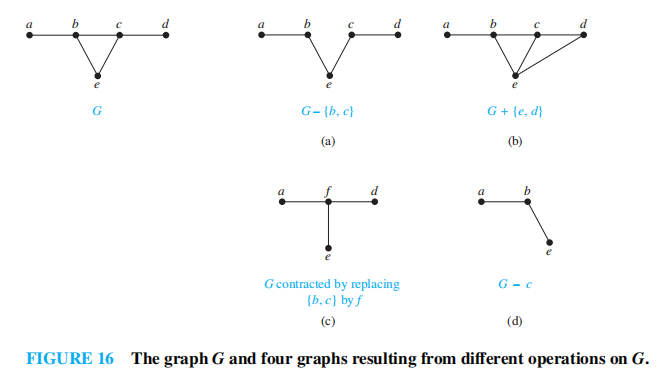
得到新图的几种方式
对于 G = (V, E)
-
移除或添加一条边:
- 移除边 e \(\in\) E:\(G - e = (V, E - \{e\})\)
- 相似地,如果我们要移除边的子集 E',则剩下的 G' = (V, E - E')
- 添加边 e:\(G + e = (V, E \cup \{e\})\)
-
边的压缩 (edge contraction):移除端点为 u, v 的边 e,然后合并 u, v 为新的顶点 w,接着将所有原来与 u 和 v 相连的边改成连接到 w 上。也就是说,对于原来的图 G = (V, E),产生新图 G',它的顶点集 V' = V - {u, v} \(\cup\) {w},它的边集 E' 包含除了以 u 或 v 为端点的所有边,再加上连接 w 的边 ( 这些边原来连接的是 u 或 v)
-
移除顶点:\(G - v = (V - \{v\}, E')\),其中 E' 是除了与 v 相连的所有边
- 移除顶点集 V':(V - V', E‘),其中 E' 是除了与 V' 上所有顶点相连的所有边
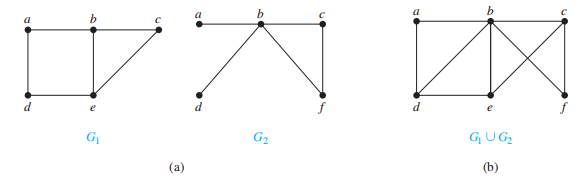
- 图的并集 (union):对于两张简单图 \(G_1 = (V_1, E_1), G_2 = (V_2, E_2)\),它们的并集 \(G_1 \cup G_2 = (V_1 \cup V_2, E_1 \cup E_2)\)
Supplements(from Exercises)⚓︎
- 假设二分图 G = (V, E),它的二分为 \((V_1, V_2)\),且 \(A \subseteq V_1\),则 \(V_1\) 的最大顶点数,为 G 的匹配的端点 = \(|V_1| - \max\limits_{A \subseteq V_1}def(A)\),其中 \(def(A) = |A| - |N(A)|\) 被称为 A 的缺陷 (deficiency)
- 图的度序列 (degree sequence)是指将顶点的度按非递增顺序排列的序列
- 如果序列 \(d_1, d_2, \dots, d_n\) 是简单图的度序列,则称该序列是图化的 (graphic)
- 当且仅当对于非负数且非递增序列 \(d_1, d_2, \dots, d_n\),将序列 \(d_2 - 1, \dots, d_{d_1 + 1} - 1, d_{d_1 + 2}, \dots, d_n\) 重新排列,使得这些项按非递增顺序排列后是个图序列 (graphic sequence),则原来的序列也是图序列
- 每个非负数且非递增序列,若它的和是偶数,则该序列是一个伪图 ( 允许有环的无向图 ) 的度序列
- 如果简单图上的每个顶点都有相同的度,称这个图是正则的 (regular)。如果每个顶点的度均为 n,称该图是n-regular
- \(K_n\) 是 (n-1)-regular
- 简单图 \(G\) 的补图 (complementary graph)\(\overline{G}\) 与 \(G\) 有相同的顶点。当且仅当 \(G\) 上的两个顶点不相邻时,\(\overline{G}\) 上同样的两个顶点是相邻的
- 如果 G 有 n 个顶点,则 \(K_n = G \cup \overline{G}\)
- 如果二分图 G 有 v 个顶点和 e 条边,则 \(e \le \dfrac{v^2}{4}\)
- 有向图 G = (V, E) 的逆 (converse)为有向图 \(G^{conv}\) = (V, F),其中 F 通过逆转 E 的边的方向得到
- \((G^{conv})^{conv} = G\)
- 当且仅当 \(G\) 有对称关系时,\(G\) 存在逆
Representing Graphs and Graph Isomorphism⚓︎
Representing Graphs⚓︎
图的表示法:
- 列出所有的边
- 邻接表
: (前提:图中没有重边)表示出每个顶点的相邻顶点
-
邻接矩阵
-
关联矩阵
Adjacency Matrices⚓︎
当图的边数很多时,用上述的前两种方法就比较麻烦了。为了简化计算,通常用矩阵表示图。
假设有无向图 G = (V, E),|V| = n,它的顶点按任意排序排列:\(v_1, v_2, \dots, v_n\),则它的邻接矩阵 (adjacency matrix)\(\mathbf{A}_G = [a_{ij}]\) 是一个 \(n \times n\) 的零一矩阵,它的元素为:
注:
- 对于同一张 n 顶点的图,共有 n! 种不同的邻接矩阵(因为顶点顺序任意)
- 对于一张简单图,\(a_{ii} = 0, i = 1,2,3, \dots, n\)
- 顶点 \(v_i\) 的环:\(a_{ii} = 1\)
- \(v_i\) 和 \(v_j\) 之间的重边:\(a_{ij}\) = \(\{v_i, v_j\}\) 的重数
- 所有的无向图,包括多重图和伪图,其邻接矩阵都是对称的
- 第 i 行元素之和 + 所有自环的个数 = 第 i 列元素之和 + 所有自环的个数 = \(v_i\) 的度
🌰:
对于有向图的邻接矩阵 \(\mathbf{A} = [a_{ij}]\),它的元素为:
注:
- 有向图的邻接矩阵不一定是对称的
- 有向多重图也可用邻接矩阵表示:\(a_{ij}\) = \((v_i, v_j)\) 的重数
- 第 i 行元素之和 = \(v_i\) 的出度,第 i 列元素之和 = \(v_i\) 的入度
Incidence Matrices⚓︎
假设有无向图 G = (V, E),顶点为 \(v_1, v_2, \dots, v_n\),边为 \(e_1, e_2, \dots, e_m\),那么它的关联矩阵 (incidence matrix)为 \(\mathbf{M} = [m_{ij}]\),是一个 \(n \times m\) 的矩阵,它的元素为:
注:
- 第 i 行元素之和 = \(v_i\) 的度,
- 第 i 列元素之和 = \(\begin{cases}1 & \text{loop} \\ 2 & \text{normal}\end{cases}\)
- 关联矩阵可以表示重边和环,见下面的🌰:
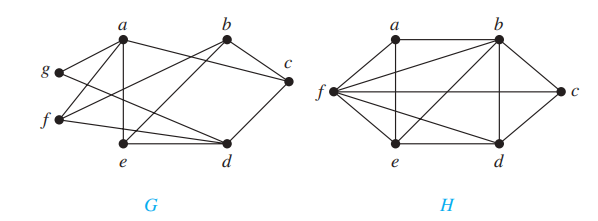
Isomorphism of Graphs⚓︎
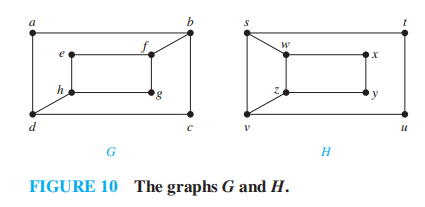
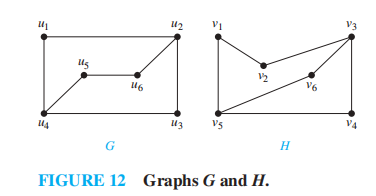
定义:对于两张简单图 \(G_1 = (V_1, E_1), G_2 = (V_2, E_2)\),如果存在一个双射函数 \(f: V_1 \rightarrow V_2\),满足:\(\forall a, b \in V_1\),若 \(a, b\) 相邻,则 \(f(a), f(b) \in V_2\) 且 \(f(a), f(b)\) 相邻,则称这两张图是同构的 (isomorphic),这样的函数 \(f\) 被称为同构 (isomorphism)。如果两张简单图不同构,称它们是非同构的 (nonisomorphic)。
两张简单图的同构是一种等价关系 (equivalent relation)。
Determining whether Two Simple Graphs are Isomorphic⚓︎
对于两张 n 顶点的简单图,有 n! 种可能的双射关系,因此当 n 很大时,直接根据顶点的相邻关系来判断同构是不切实际的;但是,判断两张图不是同构的相对比较容易,我们可以通过比较它们的不变量 (invariant)来求解。
有哪些不变量:
- 顶点数
- 边数
- 每个顶点的度数
然而,我们只能用不变量判断两张图的非同构关系,目前没有已知用来证明两张图是同构的不变量
另一种判断同构的方法:比较两张图的邻接矩阵
求解同构的算法:
- 目前,已知的最佳算法在最坏情况的时间复杂度为指数级
- 2017 年,有人找到一个算法:对于 n 顶点的图,计算它的同构的次数为 \(2^{f(n)}\),\(f(n)\) 为 \(O((\log n)^3)\),因此算法的时间复杂度为准多项式时间 (quasi-polynomial time)
- 同构测试软件:NAUTY
更多的不变量见下面
Supplements(from Exercises)⚓︎
- n 顶点的无向图 \(G_n\) = (V, E) 的密度 (density):\(\dfrac{2|E|}{|V|(|V| - 1)}\)
- 稀疏 (sparse) 图:\(\lim\limits_{n \rightarrow \infty} \dfrac{2|E|}{|V|(|V| - 1)} = 0\)
- 稠密 (dense) 图:\(\lim\limits_{n \rightarrow \infty} \dfrac{2|E|}{|V|(|V| - 1)} = c(c \in \mathbf{R}^+)\)
- 假设 G 和 H 是同构的,则 \(\overline{G}\) 和 \(\overline{H}\) 是同构的
- 有 2 个或多个顶点的二分图,对它的顶点进行一定排序后,能够形成如下形式的邻接矩阵
- 如果简单图 G 和它的补图 \(\overline{G}\) 是同构的,称 G 是自补的 (self-complementary)
- 如果 G 是 v 顶点的自补简单图,则 v \(\equiv\) 0 or 1(mod 4)
- 魔鬼对 (devil's pair):在一个故意的同构测试中,存在一对非同构图,无法检测出这两张图不是同构的
Connectivity⚓︎
Paths⚓︎
定义 ( 无向图 ):
- 令 n 为非负整数,G 为无向图,G 中从 u 到 v,长度为 n 的路径 (path),是 G 上的 n 条边的序列 \(e_1, \dots, e_n\)( 存在顶点序列 \(x_0 = u, x_1, \dots, x_{n-1}, x_n = v\),使得 \(e_i\) 的端点为 \(x_{i-1}\) 和 \(x_i\),\(i = 1, \dots, n\))。
- 在简单图中,路径可以被表示为顶点的序列 \(x_0, x_1, \dots, x_n\)(因为列出的顶点能够表示唯一的路径)
- 如果路径的起点和终点相同,即 u = v,且长度大于 0,则称该路径为环 (circuit)
- 路径或环经过 (pass through)顶点 \(x_1, x_2, \dots, x_{n-1}\),遍历 (traverse)边 \(e_1, e_2, \dots, e_n\)
- 无重复边出现的路径或环认为是简单的 (simple)
注
- 如果不区分重边,则路径可以记作 \(e_1, e_2, \dots, e_n\),其中 \(e_i = \{x_{i-1}, x_i\}, i = 1, 2, \dots, n\)
- 长度为 0 的路径就是单个点
- 在别的书中:
- 路径被称为walk,它是交错的顶点和边的序列:\(v_0, e_1, v_1, e_2, \dots, v_{n-1}, e_n, v_n\),其中 \(v_{i-1}, v_i\) 是 \(e_i\) 的端点 (\(i = 1, 2, \dots, n\))。
- 环被称为closed walk
- 简单路径被称为trail
- 无重复顶点出现的 trail 被称为 path(与上面的定义冲突)
因此,我们需要根据语境判断这些词语的意思
定义 ( 有向图 ):
- 令 n 为非负整数,G 为有向图,G 中从 u 到 v,长度为 n 的路径 (path),是 G 上的 n 条边的序列 \(e_1, \dots, e_n\),使得 \(e_i = (x_{i-1}, x_i)\),\(i = 1, \dots, n\),其中 \(x_0 = u, x_n = v\)。
- 当有向图中没有重边时,路径可以用顶点序列 \(x_0, x_1, x_2, \dots, x_n\) 表示
- 环 (circuit/cycle):长度为 1,起点 = 终点的路径
- 无重复边出现的路径或环认为是简单的 (simple)
注
- 上面的“注”中提到的别称 (walk, closed walk...) 也适用于有向图
- 如果不考虑重边,则可以使用边的序列表示路径
🌰:
- 熟人图 (acquaintanceship graph) 的路径:现在很多社会学家猜想:世界上任意两个人之间的路径很短,仅经过 5 个甚至更少的人——六度分隔理论 (six degree of seperation)
- 合作图 (collaboration graph) 的路径
- Erdos number:m 与数学家 Paul Erdos 之间最短路径的长度
- Bacon number : c 与演员 Kevin Bacon 之间最短路径的长度
Connectedness in Undirected Graphs⚓︎
定义:在一张无向图中,如果每对不同的顶点之间都存在一条路径,称这个无向图是连通的 (connected);不连通的无向图被称为断开的 (disconnected)。如果我们移除图的顶点或边,产生了断开的子图,那么我们断开 (disconnect)了这张图。
定理 1:在连通的无向图中,任意一对不同顶点之间总存在一条简单路径
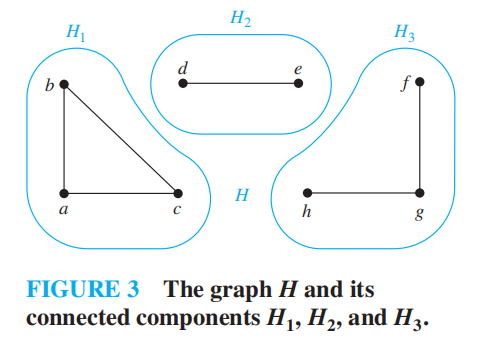
连通分量 (connected component):图 G 的最大连通子图。一张不连通的图包含两个或多个不相交的连通分量,它们的并集构成了整张图
How Connected in a Graph?⚓︎
- 割点 (cut vertices/articulation points)满足:若移除该顶点以及与它关联的边,就会生成 1 个包含更多连通分量的子图 ( 因为移除了 1 个顶点和一些边,相较于原图,剩余的图是它的子图 )
- 割边 (cut edges/bridges)满足:若移除该边,就会生成 1 个包含更多连通分量的子图
Vertex Connectivity⚓︎
并不是所有图都有割点。比如完全图 \(K_n(n \ge 3)\),任意移除 1 个顶点及其关联边,剩下的图为 \(K_{n-1}\),它还是连通图。
- 不可分割图 (nonseparable graph):没有割点的连通图
- 点割集 (vertex cut/seperating set):对于图 G = (V, E) 的顶点集 V 的子集 V',满足 G - V' 是断开的。除了完全图外的所有连通图,都有 1 个点割集
- 点连通度 (vertex connectivity):无向图 G 中,点割集内顶点的最少数量,记作 \(\kappa(G)\)
- 由于完全图没有点割集,因此按上述定义,无法定义 \(\kappa(K_n)\)。因此,我们记 \(\kappa(G) = n - 1\),表示生成仅包含单个顶点的图所需移除顶点的数量
- \(0 \le \kappa(G) \le n - 1\)
- 当且仅当 G 是断开的,或 G = \(K_1\) 时,\(\kappa(G) = 0\)
- 当且仅当 G 是完全图时,\(\kappa(G) = n - 1\)
- 若图有割点时,\(\kappa(G) = 1\)
- 如果 \(\kappa(G) \ge k\),称图为k 点连通 (k-connected/k-vertex-connected)
- 单点连通 (1-connected):图是连通的且顶点数 > 1
- 双点连通 (2-connected/biconnected):图是不可分割的且顶点数 > 2
- 如果 G 是 k 点连通的,则 G 也是 j 点连通的 (\(0 \le j \le k\))
Edge Connectivity⚓︎
- 如果图有割边,我们只需去除割边就能断开该图
-
如果没有,我们需要寻找所需去除的最小的边的集合,使得该图是断开的
-
边割集 (edge cut):边集 E',满足 G - E' 是断开的。除了完全图外的所有连通图,都有 1 个点割集
- 边连通度 (edge connectivity):无向图 G 中,边割集内最小的边数,记作 \(\lambda(G)\)
- \(0 \le \lambda(G) \le n - 1\)
- \(\lambda(G) = 0\):G 不连通或仅包含 1 个顶点
- \(\lambda(G) = n - 1\):当且仅当 \(G = K_n\)
- \(\lambda(G) \le n - 2\):当 G 不是完全图时
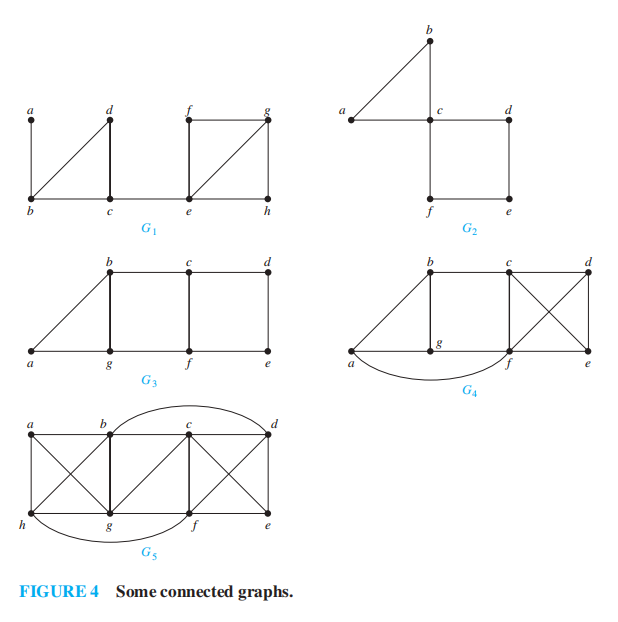
🌰:找出上面 5 张图的边连通度
关于点连通度和边连通度的不等式:对于 G = (V, E),|V| > 2 时, $$ \kappa(G) \le \lambda(G) \le \min\limits_{v \in V} deg(v) $$ 应用:
- 计算机网络的可靠性分析:
- 点连通度:能够断开网络的路由器的最小数量
- 边连通度:能够断开网络的光纤连接的最小数量
- 高速公路网:
- 点连通度:能够阻碍任意两点通行的关闭的交汇点的最小数量
- 边连通度:能够阻碍任意两点通行的关闭的公路的最小数量
Connectedness in Directed Graphs⚓︎
定义:在有向图中
-
如果对于图中任意两点 a, b 都存在一条 \(a \rightarrow b\) 和 \(b \rightarrow a\) 的路径,那么称该图是强连通的 (strongly connected)
注:a, b 可以相等
-
如果对于图中任意两点 a, b,在该图的潜在无向图 (underlying undirected graph)中存在一条路径,那么称该图是弱连通的 (weakly connected)
注:显然强连通的图也满足弱连通
- 强连通分量 (strongly connected component/strong component):最大强连通子图。
- 若 a, b 是无向图中的 2 个顶点,则它们所在的强连通分量要么是相同的,要么是不相交的
应用:网络图的强连通分量
巨强连通分量 (giant strongly connected component, GSCC):原来有向图中与它的潜在无向图中的连通分量对应的子图,有一个非常大的强连通分量以及很多很小的分量,前者被称为 GSCC
具体内容见教材 \(P_{722}\)
Paths and Isomorphism⚓︎
其他的不变量:
- 长度为 k 的简单环(k \(\ge\) 2),用来判断 2 张图是非同构的
- 用路径构建潜在同构 ( 函数 ) 的映射
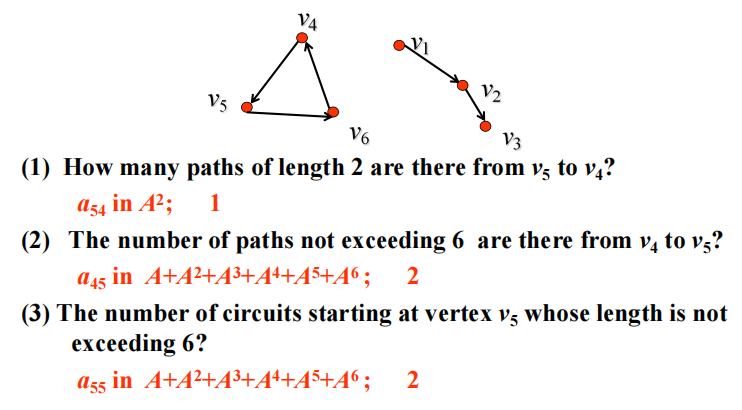
Counting Paths between Vertices⚓︎
定理 2:令图 G 有邻接矩阵 \(\mathbf{A}\),其顶点顺序为 \(v_1, v_2, \dots, v_n\)(有向边、无向边、多重边、环均允许
补充
可达性矩阵 \(\mathbf{P} = [p_{ij}]_{n \times n}\)
\(\therefore\ \mathbf{P} = \mathbf{A} \vee \mathbf{A}^2 \vee \dots \vee \mathbf{A}^n\)
注:这和求传递关系 ( 传递闭包 ) 非常相似
意义:对于有向图,当 \(\mathbf{P}\) 中所有元素均为 1 时,该图是强连通的;也可以用来寻找强连通分量
定理 2 的应用:
- 找到两个顶点间最短路径的长度
- 判断图是否连通
🌰:
Supplements(from Exercises)⚓︎
- 假设 G = (V, E) 是有向图,对于 v, w \(\in\) V,如果存在从 v 到 w 的有向路径,称从 v 出发,w 是可到达的 (reachable)。如果同时存在从 v 到 w 和从 w 到 v 的路径,称 v 和 w 是相互可到达的 (mutually reachable)
- 如果 u 和 v 是相互可到达的,v 和 w 是相互可到达的,则 u 和 w 是相互可到达的
- 每个 n 顶点连通图至少有 n-1 条边
- 对于每个简单图,存在从任意度为奇数的顶点出发,到其他度为奇数的顶点的路径
- 假设 v 是割边的端点,当且仅当该点的度 >1 时,v 是一个割点
- 当且仅当存在顶点 u, v( 不同于顶点 c),使得所有从 u 到 v 的路径都需经过 c 时,c 为简单图 G 的割点
- 至少有 2 个顶点的简单图,至少有 2 个顶点不是割点
- 当且仅当某条边不是简单图中任何简单环的一部分时,该边为割边
- 有向图 G 的点基 (vertex basis)是 G 中顶点的最小集合 B,使得 G 中任意不属于 B 的顶点 v,存在一条从 B 的某些顶点出发,到 v 的路径
- 如果一个简单图有 k 个连通分量,且这些分量分别有 \(n_1, n_2, \dots, n_k\) 个顶点,那么 G 的边数不会超过 \(\sum\limits_{i=1}^kC(n_i, 2)\)
- 有 n 个顶点,且有 k 个连通分量的简单图,至多有 \(\dfrac{(n - k)(n - k + 1)}{2}\) 条边
- 如果 n 顶点的简单图 G 有超过 \(\dfrac{(n - 1)(n - 2)}{2}\) 条边,则该图是连通的
- 令 \(P_1, P_2\) 为简单图 G 中两个顶点 u, v 之间的两条简单路径,且这两条路径不包含相同的边,则 G 中存在一个简单环
Euler and Hamilton Paths⚓︎
注:本节对应 fds 这部分
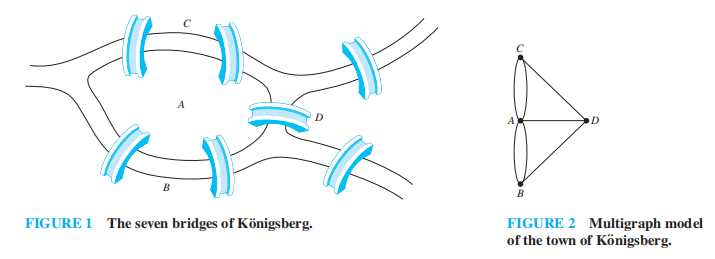
Euler Paths and Circuits⚓︎
定义:
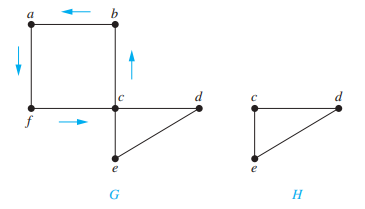
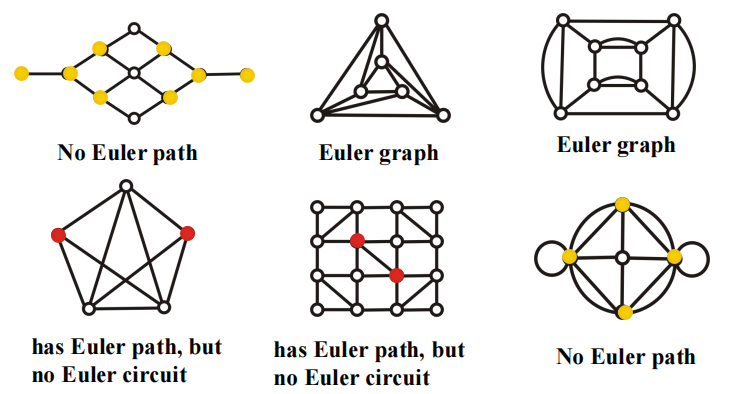
- 欧拉环 (Euler circuit):图 G 中包含所有边的简单环
- 欧拉路 (Euler path):图 G 中包含所有边的简单路径
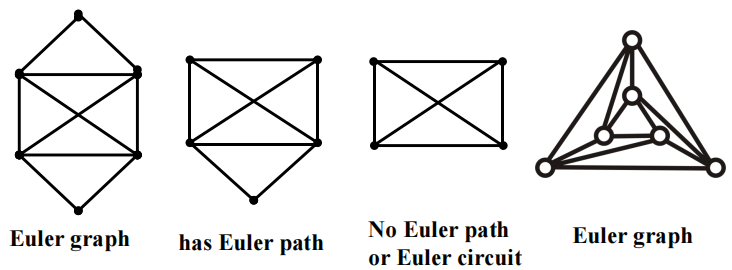
- 欧拉图 (Euler graph):具有欧拉环的图
定理 1:对于一个至少有 2 个顶点的连通多重图,当且仅当其所有顶点的度均为偶数时,该图具有欧拉环
证明
-
( 必要性 ) 欧拉环 \(\rightarrow\) 顶点的度均为偶数
- 我们假定欧拉环以 a 为起点,第一条边为 a 贡献 1 个度
- 欧拉环每过一个顶点,就会为该顶点贡献 2 个度
- 欧拉环终止于起始顶点 ( 即 a),又为 a 贡献 1 个度 ( 加上第一条边的 1 个度,就保证 a 具有偶数个度了 )
- 结合欧拉环的定义,易知所有顶点的度均为偶数
-
( 充分性 ) 顶点的度均为偶数 \(\rightarrow\) 欧拉环。我们将构建一个从 G 中任意顶点 a 出发的一个简单环:
- 简单环经过 \(x_0 = a, x_1, x_2, \dots, x_n = a\)
- 在 G 的子图 H 中构建简单路径:令 w 为刚刚构建的环和 H 的公共顶点,起始于 w,构建 H 的简单路径。由于该路径一定终止于 w,因此我们得到的其实是 H 的一个环
- 通过拼接 H 的环和原来 G 的环,构建一个在 G 中的完整的环
- 重复这个步骤,直至所有边都用过了 ( 根据欧拉环的定义,此时我们得到了一个欧拉环 )
注:充分性的部分还是讲的不太清楚,因为我目前没有完全理解😅
欧拉环算法的伪代码:
定理 2:一个没有欧拉环的连通多重图具有欧拉路的充要条件是——有且仅有 2 个顶点的度为奇数。
🌰:
补充:有向图中的欧拉环和欧拉路
-
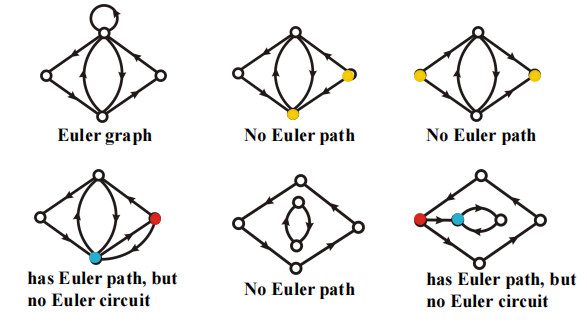
一个没有孤立顶点 ( 度为 0) 的有向多重图,具有欧拉环的充要条件是:
- 图是弱连通的
- 每个顶点的入度 = 出度
-
一个没有孤立顶点的有向多重图,具有欧拉路( 但不是欧拉环 ) 的充要条件是:
- 图是弱连通的
- 每个顶点的入度 = 出度,除了 2 个顶点:一个顶点满足入度 - 出度 = 1,另一个顶点满足出度 - 入度 = 1
🌰:
应用:
- 一类谜题——“一笔画”问题
- 中国邮递员问题
- 其他领域:计算机网络 ( 组播 )、分子生物学……
Hamilton Paths and Circuits⚓︎
定义:
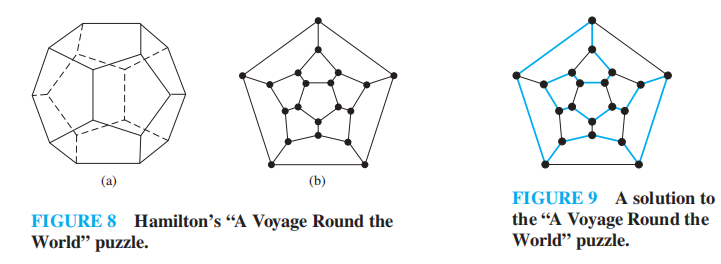
- 哈密顿路 (Hamilton path):图 G 中包含所有顶点的简单路径
- 哈密顿环 (Hamilton circuit):图 G 中包含所有顶点的简单环
注
对于图 G = (V, E),如果 \(V = \{x_0, x_1, \dots, x_{n-1}, x_n\}\),且对于 \(0 \le i < j \le n\),\(x_i \ne x_j\),那么:
- 哈密顿路为简单路 \(x_0, x_1, \dots, x_{n-1}, x_n\)
- 哈密顿环:\(x_0, x_1, \dots, x_{n-1}, x_n, x_0(n > 0)\)
- 哈密顿图 (Hamilton graph):具有哈密顿环的图
一些事实:
- 目前,没有已知的哈密顿环存在性的充要条件,但是有许多关于哈密顿环存在性的充分条件的定理,以及证明哈密顿环不存在的性质
- 如果图的一个顶点的度为 1,那么该图不存在哈密顿环
- 如果一个顶点的度为 2,那么这对应的两条边一定同时存在于任何哈密顿环中
- 如果哈密顿环经过一个顶点,除了构成哈密顿环的 2 条边外,与该顶点关联的其他边均可不作考虑
- 哈密顿环内不包含更小的环
- 当 \(n \ge 3\) 时,\(K_n\) 有一个哈密顿环
- 图的边越多,具有哈密顿环的可能性越大
- 向有哈密顿环的图添加边后,会产生一个具有相同哈密顿环的图
定理 3——狄拉克定理 (DIRAC'S THEOREM):如果 G 是一个具有 n(n \(\ge\) 3) 个顶点的简单图,且每个顶点的度至少为 \(\dfrac{n}{2}\),那么 G 就有一个哈密顿环。
例子:\(K_{n, n}\) 满足定理 3,因此有哈密顿环
定理 4——奥尔定理 (ORE'S THEOREM):如果 G 是一个具有 n(n \(\ge\) 3) 个顶点的简单图,且对于每一对不相邻的顶点对 u, v 满足 deg(u) + deg(v) \(\ge\) n,那么 G 就有一个哈密顿环。
注:上述 2 个定理提供了哈密顿环存在性的充分条件
目前,已知寻找哈密顿环的最佳算法的最坏时间复杂度为指数级 ( 关于顶点数 ),且该问题是一个 NP 完全问题
补充:哈密顿环存在性的必要条件
对于集合 V 的任意非空子集 S,G - S( 去掉部分顶点 ) 的连通分量的个数 <= |S|
注
- 假设 C 是 G 的一个哈密顿环,对于集合 V 的任意非空子集 S,C - S 的连通分量个数 <= |S|。因此我们可以利用该必要条件判断哈密顿环是否存在
- G - S 的连通分量个数 <= C - S 的连通分量个数
Applications of Hamilton Circuits⚓︎
应用:
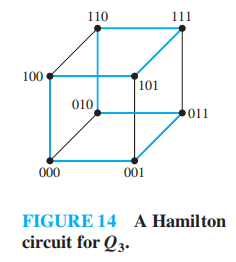
寻找格雷码的问题 \(\rightarrow\) 找到 n 立方 \(Q_n\) 的哈密顿环
Supplements(from Exercises)⚓︎
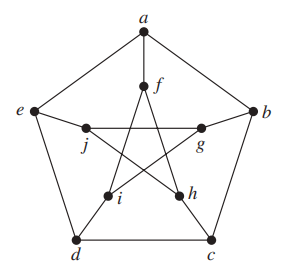
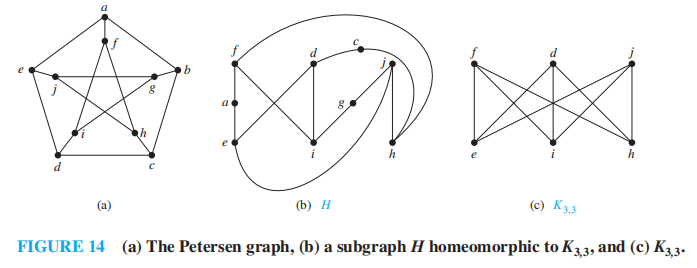
- 彼得森图 (Petersen graph):如图所示。它自身没有哈密顿环,但如果删掉一个顶点及其关联的所有边后,剩余的子图有哈密顿环
- 弗罗莱算法 (Fleury's algorithm):构建欧拉环的一种算法。(wiki)
- 首先在连通多重图中选择任意顶点
- 然后通过连续挑选边来构建环。一旦有一条边被选择,就将其从原来的图中删去。连续挑选边是为了确保每条边开始于上一条边的结束位置,这样保证这条边不是割边,除非没有可替代的边
- 骑士巡逻 (knight's tour)问题
注:由于我不懂国际象棋的规则,这里就略过了 ( wiki )
Shortest-Path Problems⚓︎
注:这一节对应 fds 的相关部分
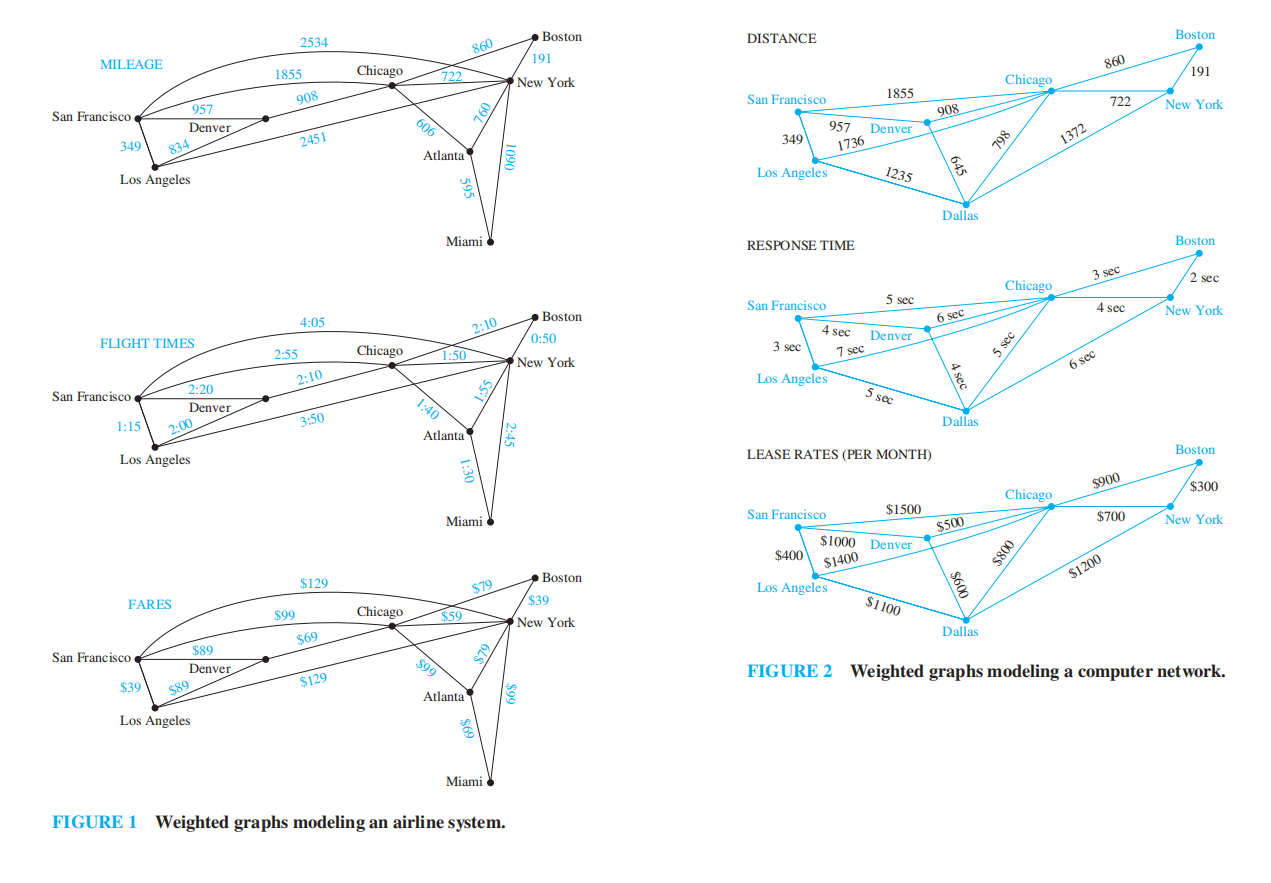
- 带权图 (weighted graph):每条边被赋予一个数字的图
- 带权图的路径长度 (length):路径上所有边的权重和
注:无权图的路径长度为路径上边的条数
带权图的应用 (2 个 ):
A Shortest-Path Algorithm⚓︎
最短路问题:G = (V, E, W) 是一个带权图,w(x, y) 表示 x 和 y 之间边的权重 ( 如果 \(x, y \notin E,\ w(x, y) = \infty\)),\(a, z \in V\),找到 a,z 之间的最短路
变种:
- 找到从顶点 a 到其他所有顶点的最短路
- 找到图上任意 1 对顶点间的最短路
- 权重:全部是 1,正数,或者任意实数
这里,我们介绍的最短路算法是Dijkstra 算法,它是一种贪心算法 (greedy algorithm),能够找到以某个顶点 a 为起始点,到其他所有顶点的最短路径。
注:确保所有的权重为正数
简单介绍一下流程 ( 更详细的介绍见这里 ):
-
初始状态:\(L_0(a) = 0, L_0(v) = \infty, S_0 = \emptyset\),
注:这里的 a 表示起始顶点,L 表示当前计算的从 a 出发的最短路径,其下标表示当前迭代次数,\(S_k\) 表示经过 k 次迭代后,已经标注过的顶点集合
-
构建 \(S_k\):通过添加未标注的 (L 的值 ) 最小顶点 \(u \notin S_{k-1}\),形成 \(S_k\)
- 更新所有不在 \(S_k\) 的顶点的标注,使得 \(L_k(v)\) 表示从 a 到 v 的最短路径 ( 且该路径仅经过 \(S_k\) 上的顶点 ),即:
其中 w(u, v) 表示 u, v 间的边的权重 + 重复上述步骤,直至目标顶点z被添加至\(S_k\)内
算法:
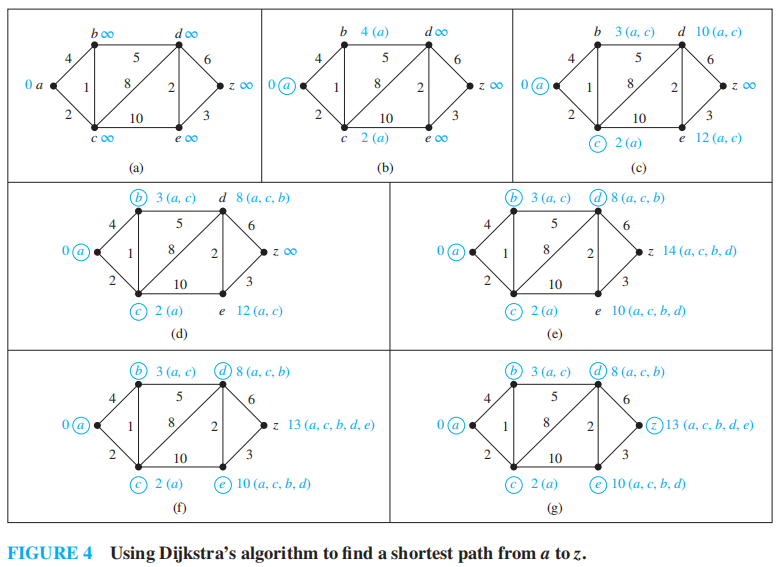
🌰:
定理 1:Dijkstra 算法能够在连通的简单无向带权图中找到两点间的最短路径
定理 2:Dijkstra 算法的运算 ( 加法和比较 ) 次数为 \(O(n^2)\)
The Traveling Saleperson Problem⚓︎
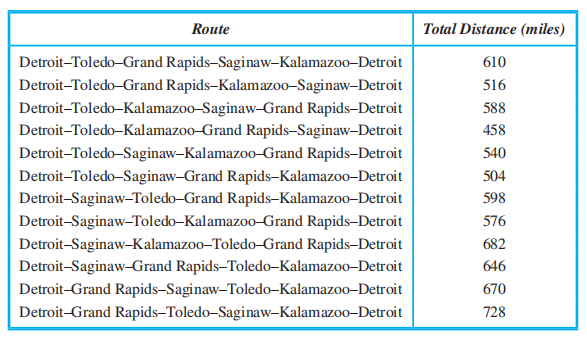
题目:一个旅行商想要访问所有 n 个城市,且对每个城市仅访问 1 遍,最后返回起点。问:何种访问顺序使得访问总距离最短?
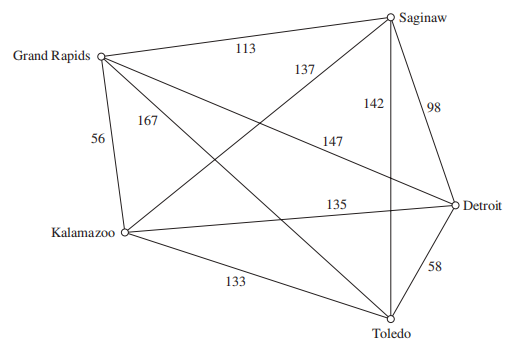
🌰:
枚举出所有路径:
观察得,最短路径 = 458
我们将原问题抽象为:在带权重的、完全的无向图中找到最小总权重的环,使得每个顶点仅被访问 1 次,且返回至起点,即:在完全图中找到最小总权重的哈密顿环
解决方法:
-
检测所有的哈密顿环:一共有 \(\dfrac{(n-1)!}{2}\) 个环——不切实际
注:目前没有多项式级的最坏时间复杂度的算法来求解这个问题——它是个 NP 完全问题
-
近似算法 (approximation algorithm):它并不找出精准解,而是找到尽可能接近精准解的解。比如我们通过近似算法找到某个总权重为 \(W'\) 的哈密顿环,使得 \(W \le W' \le cW\)。目前有多项式级的最坏时间复杂度的近似算法,使得 \(c = \dfrac{3}{2}\)
Supplements(from Exercises)⚓︎
- 弗洛伊德算法 (Floyd's algorithm):在带权连通简单图中寻找所有顶点对的最短长度,但不能用它来构建最短路径。伪代码如下:
- Dijkstra 算法无法在有负权边的图中正常运行
- 最长路问题 (longest path problem):在没有简单环的带权有向图中,要求找到一条路径,使得它的边权和最大
Planar Graphs⚓︎
定义:如果一张图能够在平面上,用不相交的边绘制出来,那么称该图是平面的 (planar)。这样的画法被称为图的平面表示法 (planar representation)
应用:
- 电路设计:用顶点表示元件,用边表示线路。如果电路图不是平面图,那么成本就比较高。因此,我们可以先将电路分成多个平面子图,然后使用多层结构连接起整个电路 ( 具体内容见教材 )
- 道路网
注
- 即使一张图“看起来”有相交的边,但这张图也有可能是平面图 ( 因此需要我们重新画这幅图再观察 )
- 完全二分图 \(K_{2, n}\) 和 \(K_{1, n}\ (n \ge 1)\) 是平面图
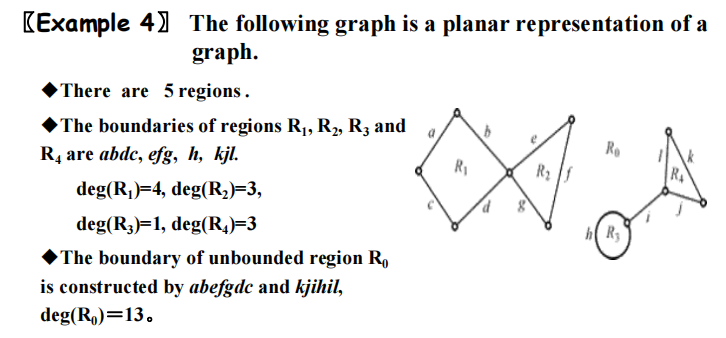
Euler's Formula⚓︎
图的平面表示法将平面划分为多个区域 (regions),包括无边界的区域。而且对于同一张图,它的所有平面表示法划分的区域个数都是一样的
注
- 1 个自环的内部形成一个区域
- 相邻区域:有公共边界的 2 个区域
- 如果边 e 不是割边,则一定是 2 个区域的公共边界
🌰:
定理 1——欧拉公式 (EULER'S FORMULA):令 G 为有 e 条边和 v 个顶点的连通平面简单图,令 r 为 G 的平面表示法形成的区域个数,则 r = e - v + 2
证明
采用归纳法。具体内容见教材 \(P_{756}\),这里只讲大致思路
先去掉所有边,然后连续添加边 ( 每个阶段只添一条边 ),即:
- 先任意选一条边得到 \(G_1\)
- 通过任意选取与 \(G_{n-1}\) 的顶点关联的,且不在 \(G_{n-1}\) 里的边,构建 \(G_n\) 我们用\(r_n, e_n, v_n\)表示图\(G_n\)的3个要素,接下来就用数学归纳法证明啦:
- 基本步骤
-
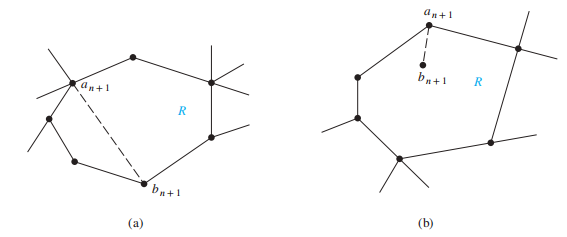
归纳步骤:归纳假设 \(\rightarrow\) 分类讨论
- 新添的边的 2 个端点均包含于 \(G_k\) 里,即它们都在共同的区域 R 的边界上
- 新添的边的其中一个顶点尚未与 \(G_k\) 的其他顶点有相邻关系
补充
对于不连通的简单平面图 G,假设有 k 个连通分量,则:r = e - v + k + 1
推论 1:若 G 为有 e 条边和 v(v \(\ge\) 3) 个顶点的连通平面简单图,那么 \(e \le 3v - 6\)
推论 2:如果 G 是连通平面简单图,那么 G 中存在一个度 \(\le 5\) 的顶点
证明
推论 2 的证明:推论 1 + 握手定理,使用反证法
推论 1 的证明:
先引入概念:区域的度 (degree)——区域边界的边数,记作 deg(R),显然 deg(R) \(\ge\) 3(不然无法形成一个封闭图形了)
易知:\(2e = \sum\limits_{\text{all regions } R}\mathrm{deg}R \ge 3r\) 再结合欧拉公式,联立方程组可得推论1
推论 3:若 G 为有 e 条边和 v(v \(\ge\) 3) 个顶点的连通平面简单图,且没有长度为 3 的环,则 \(e \le 2v - 4\)
Kuratowski's Theorem⚓︎
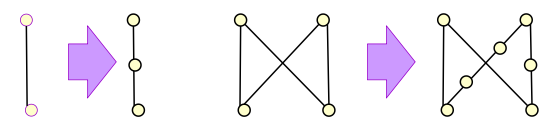
初等细分 (elementary subdivision):对于一张平面图,通过移除边 \(\{u, v\}\),然后添加一个新的顶点 w,并添加边 \(\{u, w\}\) 和 \(\{w, v\}\) 构建新的图
如果两张图 \(G_1 = (V_1, E_1), G_2 = (V_2, E_2)\) 是由同一张图的一系列初等细分操作得到的,称它们是同胚的 (homeomorphic)
🌰:
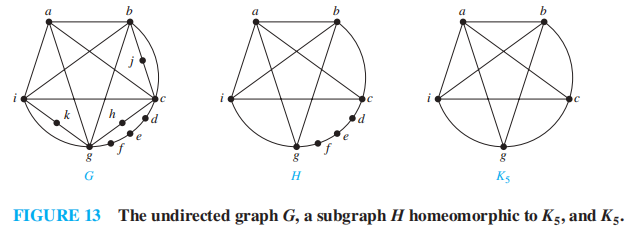
定理 2:对于一张图,当且仅当它包含一个与 \(K_{3, 3}\)( 二分完全图 ) 或者 \(K_5\) 同胚的子图时,该图不是平面的
提出者:Kuratowski
它的逆命题也成立,即:任意非平面图的子图与 \(K_{3, 3}\) 或 \(K_5\) 同胚,但证明起来很困难
Supplements(from Exercises)⚓︎
- 若 G 为有 e 条边和 v(v \(\ge\) 3) 个顶点的连通平面简单图,且没有长度 \(\le 4\) 的环,那么当 \(v \ge 4\) 时,\(e \le \dfrac{5}{3}v - \dfrac{10}{3}\)
- 简单图的交叉数 (crossing number):图上最少数量的交叉数 ( 该图没有 3 条边交于一点的情况 )
- 假设 m. n 是正偶数,\(K_{m, n}\) 的交叉数 \(\le \dfrac{mn(m - 2)(n - 2)}{16}\)
- 简单图 G 的厚度 (thickness)为最小数量的平面子图,它们的并集为 G
- 若 G 为有 e 条边和 v(v \(\ge\) 3) 个顶点的连通平面简单图,那么 G 的厚度至少为 \(\lceil \dfrac{e}{3v - 6} \rceil\)
- \(K_n\) 的厚度至少为 \(\lfloor \dfrac{n+7}{6} \rfloor\)
- 若 G 为有 e 条边和 v(v \(\ge\) 3) 个顶点的连通平面简单图,且没有长度为 3 的环,则 G 的厚度至少为 \(\lceil \dfrac{e}{2v - 4} \rceil\)
- \(K_{m, n}\) 的厚度 (\(m, n\) 不同时为 1) 至少为 \(\lceil \dfrac{mn}{(2m + 2n - 4)} \rceil\)
Graph Coloring⚓︎
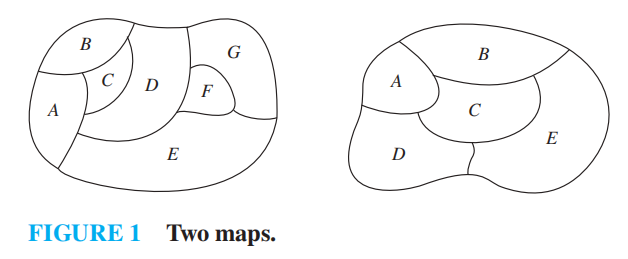
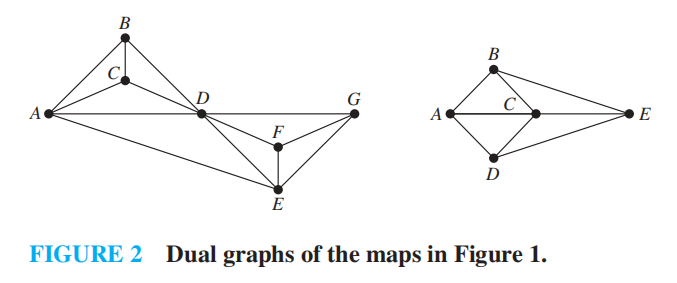
所有的地图 (map) 均可用图 (graph) 表示:
- 用顶点表示区域
- 用边表示这些区域的公共边界( 只交于 1 点的 2 个区域不视为相邻 ) 这样形成的图被称为地图的对偶图 (dual graph)
🌰:
定义:
- 简单图的涂色 (coloring):对图上所有顶点上色,满足任意两个相邻顶点的颜色是不同的
- 图的着色数 (chromatic number):对图上色时所使用的最少的颜色数量,记作 \(\chi(G)\)
定理——四色定理 (THE FOUR COLOR THEOREM):平面图的着色数不超过 4
- 非平面图的着色数可以是任意大的
- 如何证明图的着色数为 k?
- 证明图可以用 k 种颜色来涂色
- 证明图不可以用少于 k 种颜色来涂色
特例
- \(\chi (K_n) = n\)
- \(\chi (K_{m, n}) = 2\)
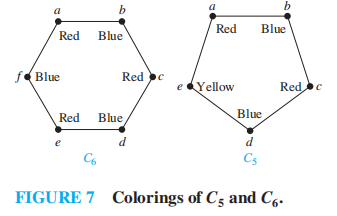
- \(\chi (C_n) = \begin{cases}2 & \text{if }n \text{ is an even positive integer and } n \ge 4 \\ 3 & \text{if }n \text{ is an odd positive integer and } n \ge 3 \end{cases}\)
注:证明见教材 \(P_{765-766}\)
目前,计算着色数的最佳算法的最坏时间复杂度是指数级的,即使是找到计算着色数的近似算法也相当困难。如果能够找到最坏时间复杂度为多项式级的,计算着色数为 2 的幂的近似算法,那么也就存在最坏时间复杂度是多项式级的计算着色数的算法。
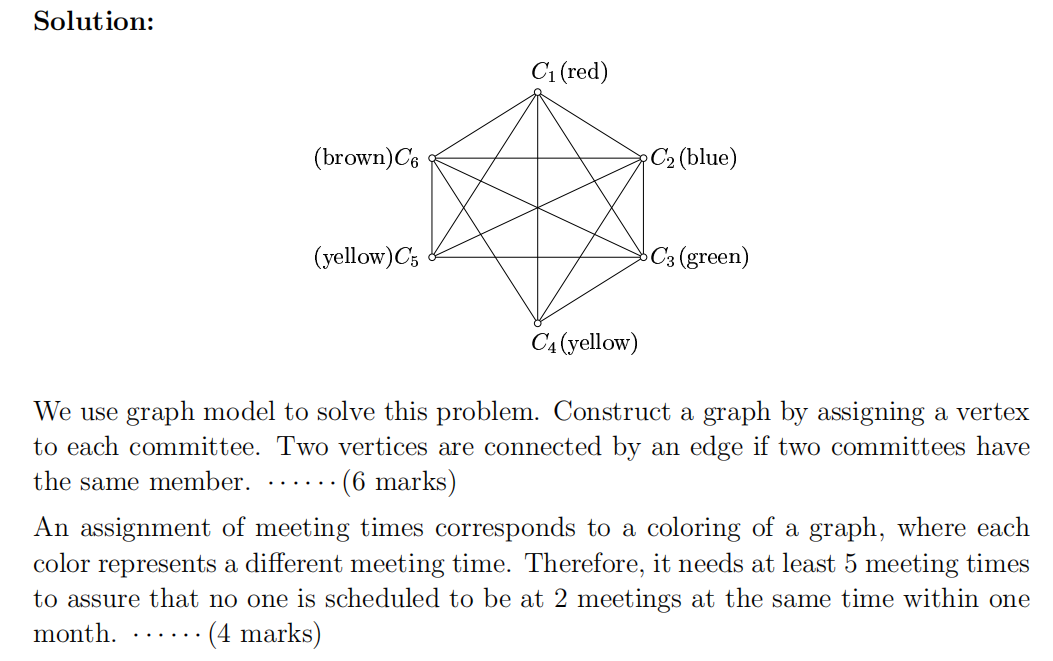
Applications of Graph Colorings⚓︎
应用:
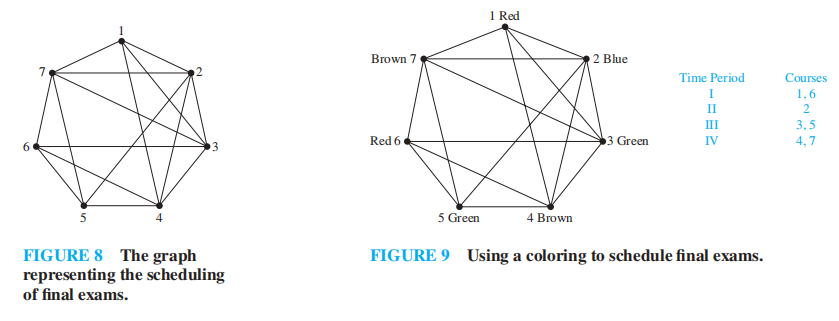
- 安排期末考试:用顶点表示课程,用边表示存在学生同时修这 2 门课,用颜色表示考试时间
图示:
- 频率分配
- ( 关于编译器 ) 索引寄存器
Supplements(from Exercises)⚓︎
- 图的边涂色 (edge coloring):对边上色,满足与同一顶点关联的边的颜色不同。图的边着色数 (edge chormatic number)为在图的边涂色时所使用的最少的颜色数量,记作 \(\chi'(G)\)
- 边着色数 \(\ge\) 图上顶点的最大度数
- 对于有 n 个顶点的图 G,它的边涂色中不超过 \(\dfrac{n}{2}\) 条边具有相同颜色
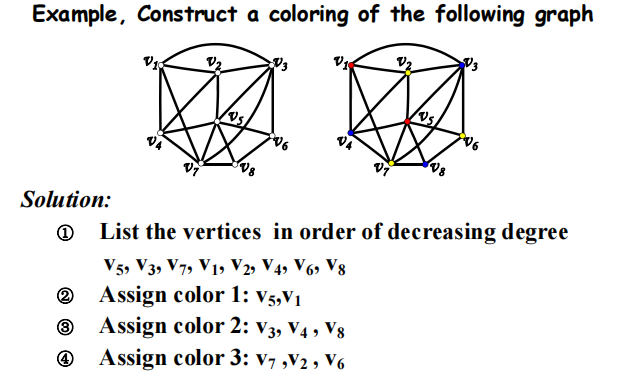
- 对简单图涂色的算法:
- 将所有顶点按度的降序排列,使得 \(\mathrm{deg}(v_1) \ge \mathrm{deg}v_2 \ge \dots \ge \mathrm{deg}(v_n)\)
- 先为 \(v_1\),以及与它不相邻的顶点 ( 若存在的话 ) 赋予颜色 1
- 然后为没有赋予颜色的第 1 个顶点,以及与该顶点不相邻且未赋予颜色的顶点赋予颜色 2
- 重复上述步骤,直至所有顶点都赋上颜色
🌰:
注:这种算法使用的着色数可能不是最少使用颜色的数量
- 如果连通图 G 的着色数为 k,但是对 G 上的每条边,删掉其中一条边后的着色图为 k - 1,则称图 G 是k 色临界的 (chromatically k-critical)
- \(C_n\ (n \ge 3)\) 是 3 色临界的
- \(W_n\ (n \ge 3)\) 是 4 色临界的
- 如果 G 是 k 色临界的,则 G 中每个顶点的度至少为 k - 1
-
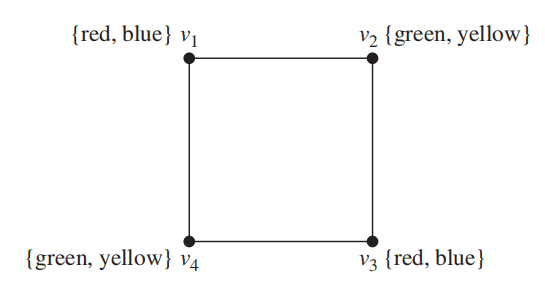
简单图的k 元涂色 (k-tuple coloring)指将一组 k 种不同的颜色分配给 G 中的每个顶点,使得任意 2 个相邻顶点没有共同颜色,我们将最小的颜色数量 n 记作 \(\chi_k(G)\)
- 🌰:\(\chi_2 (C_4) = 4\)
-
美术馆问题 (art gallery problem):wiki
Supplements⚓︎
补充知识 ( 可忽略,考试应该不会考这些 )
- 完全 m 分图 (complete m-partitie graph)\(K_{n_1, n_2, \dots, n_m}\) 将顶点分为 m 个子集,每个子集的顶点数为 \(n_1, n_2, \dots, n_m\),当且仅当顶点位于 2 个不同的子集时,两个顶点是相邻的
- 令无向图 G = (V, E),\(A \subseteq V,\ B \subseteq V\),则:
- \(N(A \cup B) = N(A) \cup N(B)\)
- \(N(A \cap B) \subseteq N(A) \cap N(B)\)
- \(\forall v \in V,\ |N(v)| \le \mathrm{deg}(v)\)
- 当且仅当 G 为简单图时,\(|N(v)| = \mathrm{deg}(v)\)
- 假设 \(S_1, S_2, \dots, S_n\) 是 S 的子集,这些子集的相异代表系 (system of distinct representative, SDR)是指一个有序 n 元组 \((a_1, a_2, \dots, a_n)\),满足 \(a_i \in S_i\ (i = 1,2, \dots, n,\ a_i \ne a_j\ (i \ne j))\)
- 当且仅当对任意 I = {1, 2, …, n} 的子集,满足 \(|\bigcup\limits_{i \in I}| \ge |I|\) 时,存在 SDR
- 简单图 G 的聚类系数 (clustering coefficient)C(G):u, v 为邻居且 v, w 为邻居 \(\rightarrow\) u, w 为邻居的概率 (u, v, w 为 G 上不同的顶点 )
- 简单无向图的团 (clique):极大完全子图
- 简单图的关于顶点的支配集 (dominating set)是一组顶点的集合,满足该组顶点外的所有顶点至少与这个集合上的一个顶点是相邻的。最小顶点数的支配集被称为最小支配集 (minimum dominating set)
- ( 补充 ) 同构图的不变量:
- 连通性
- 哈密顿环的存在
- 欧拉环的存在
- 交叉数 C
- n 个孤立点 ( 度 = 0)
- 二分图
- 如果一个有向图与它的逆 (converse) 是同构的,称该图是自逆的 (self-converse)
- 无向简单图的定向 (orientation):一种对每条边方向的分配,使得生成的有向图是强连通的。如果存在这样的定向,称该图是可定向的 (orientable)
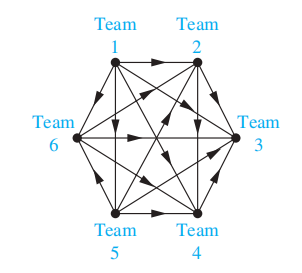
- 竞赛图 (tournament):一种简单有向图,满足:如果 u 和 v 是图上两个不同的点,那么边 (u, v) 和 (v, u) 有且仅有其中一条在该图上
- 每个竞赛图都有哈密顿环
- 假设连通图 G 的顶点为 n,点连通度 \(\kappa (G) = k\),则 G 至少有 \(\lceil \dfrac{kn}{2} \rceil\) 条边
- 对于有 n 个顶点,m 条边的连通图 G = (V, E),如果 \(\kappa (G) = \lambda(G) = \min\limits_{v \in V} \mathrm{deg} v = \dfrac{2m}{n}\),称该图有最优连通度 (optimal connectivity)
- 假设 G 为有 2k 个度为奇数的顶点的连通多重图,那么存在 k 个子图 ( 它们的并集为 G,且任意 2 个子图没有公共边 ),每个子图都有一个欧拉路
- 令 G 为有 n 个顶点的简单图,G 的带宽 (bandwidth)B(G) 是指对于所有顶点的排列 \(a_1, a_2, \dots, a_n\) 的 \(\max\{|i - j|\ |\ a_i \text{ and } a_j \text{ are adjacent}\}\) 的最小数
- 在连通简单图中,两个不同顶点 \(v_1, v_2\) 的距离 (distance)为它们之间最短路的长度。图的半径 (radius)是所有顶点到其他顶点的最大距离的最小值。图的直径 (diameter)是指两个不同顶点的最大距离
- 如果简单图 G 的直径至少为 4,则它的补 \(\overline{G}\) 的直径不多于 2
- 如果简单图 G 的直径至少为 3,则它的补 \(\overline{G}\) 的直径不多于 3
- 假设 G 为有 2m 个度为奇数的顶点的多重图,则任意包含该图所有边的环,至少有 m 条边被包含不止一次
- 如果简单图 G 有至少 11 个顶点,那么 G 或 \(\overline{G}\) 是非平面的
- 对于一张图的某些顶点的集合,如果其中任意一对节点都不是相邻的,称这个顶点的集合是独立的 (independent)。图的独立数 (independence number)是最大的独立顶点集合的顶点数
- 简单图的顶点个数 \(\le\) 独立数 \(\times\) 着色数
- 图的着色数 \(\le\) n - i - 1,其中 n 为图的顶点数,i 是图的独立数
- 当对简单图添加额外的边 ( 不添加额外的点 ) 后仍然保留图的某个性质时,称该性质是单调递增的 (monotone increasing);当对简单图去掉额外的边 ( 不去掉原有的点 ) 后仍然保留图的某个性质时,称该性质是单调递减的 (monotone decreasing)
- 当且仅当图的性质 Q 是单调递减时,图的性质 P 是单调递增的,其中性质 Q:不具备性质 P
- 假设 P 是简单图的单调递增的性质,那么 n 顶点的随机图具备性质 P 的概率为关于某条边被选入该图的概率 p 的一个单调非递减函数
评论区