第十章第二类曲线积分与第二类曲面积分⚓︎

约 4539 个字预计阅读时间 23 分钟

Info

第一类积分：重积分的积分区域是无向的
第二类积分：定积分的积分区域是有向的，所以请关注题目中规定的积分区域方向

第二类曲线积分⚓︎

概念⚓︎

定义：

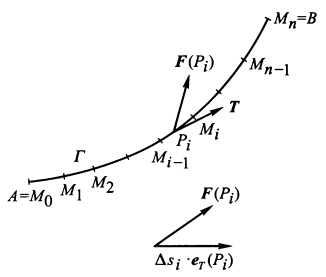
设 $\Gamma$ 是以 A, B 为端点的光滑曲线，并指定从 A 到 B 的方向为曲线方向，在 $\Gamma$ 上每一点 M 处作曲线的单位切矢量：$\bm{e_T} = \cos{\alpha} \bm{i} + \cos{\beta} \bm{j} + \cos{\gamma} \bm{k}$，方向与指定曲线方向一致 ($\alpha, \beta, \gamma$ 分别为 $\bm{e_T}$ 与 Ox 轴、Oy 轴、Oz 轴正向的夹角 )，

又设 $\bm{A}(M) = P(x, y, z)\bm{i} + Q(x, y, z)\bm{j} + R(x, y, z)\bm{k}$，其中 P, Q, R 为定义在 $\Gamma$ 上的有界函数，则 $\bm{A \cdot e_T} = P \cos{\alpha} + Q \cos{\beta} + R \cos{\gamma}$ 在 $\Gamma$ 上的第一类曲线积分 $$ \int\limits_{\Gamma} \bm{A \cdot e_T} \mathrm{d}s = \int\limits_{\Gamma}(P \cos{\alpha} + Q \cos{\beta} + R\cos{\gamma}) \mathrm{d}s $$

被称为 $\bm{A}(P)$ 沿 $\Gamma$ 从 A 到 B 的第二类曲线积分。

注：

$\oint$ 表示封闭曲线上的第二类曲线积分

第二类曲线积分又被称为对坐标曲线积分

性质：

$\int\limits_{\Gamma_{AB}}(\bm{A \cdot e_T}) \mathrm{d}s = - \int\limits_{\Gamma_{BA}}(\bm{A \cdot e_T}) \mathrm{d}s$，若记 $\Gamma^+ = \Gamma_{AB}, \Gamma^- = \Gamma_{BA}$，则：$\int\limits_{\Gamma^+}(\bm{A \cdot e_T}) \mathrm{d}s = - \int\limits_{\Gamma^-}(\bm{A \cdot e_T}) \mathrm{d}s$
若 $\Gamma$ 是由 $\Gamma_1, \Gamma_2$ 首尾相接而成，则：$\int\limits_\Gamma(\bm{A \cdot e_T}) \mathrm{d}s = \int\limits_{\Gamma_1}(\bm{A \cdot e_T}) \mathrm{d}s + \int\limits_{\Gamma_2}(\bm{A \cdot e_T}) \mathrm{d}s$
$\int\limits_{\Gamma}[\alpha \bm{F_1}(x, y, z) + \beta \bm{F_2}(x, y, z)] \mathrm{d}\bm{r} = \alpha \int\limits_{\Gamma}\bm{F_1}(x, y, z) \mathrm{d}\bm{r} + \beta \int\limits_{\Gamma}\bm{F_2}(x, y, z) \mathrm{d}\bm{r}$

记 $d \bm{s} = \bm{e_T} ds$，被称为曲线的有向弧元。

第二类曲线积分的四种形式：

$\int\limits_{\Gamma_{AB}} \bm{A \cdot e_T} \mathrm{d}s$ ( 第二类曲线积分 $\Rightarrow$ 第一类曲线积分 )
$\int\limits_{\Gamma_{AB}} \bm{A} \mathrm{d} \bm{s}$
$\int\limits_{\Gamma_{AB}} (P \cos{\alpha} + Q \cos{\beta} + R \cos{\gamma}) \mathrm{d}s$
$\int\limits_{\Gamma_{AB}} (P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z)$

⭐定理 1：设光滑曲线 $\Gamma_{AB}$ 的方程为 $\begin{cases}x = x(t) \\ y = y(t) \\ z = z(t)\end{cases}$，点 A, B 对应参数分别为 $t_A, t_B$，且 $\bm{A}(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z))$ 的分量 P, Q, R 在 $\Gamma$ 上连续，则

\[ \begin{align} & \int\limits_{\Gamma_{AB}} \bm{A \cdot e_T}\ \mathrm{d}s \notag \\ = & \int_{t_A}^{t_B} [P(x(t), y(t), z(t)) \cdot x'(t) + Q(x(t), y(t), z(t)) \cdot y'(t) + R(x(t), y(t), z(t)) \cdot z'(t)]\ \mathrm{d}t \notag \end{align} \]

本质：第二类曲线积分 $\Rightarrow$ 定积分

格林公式⚓︎

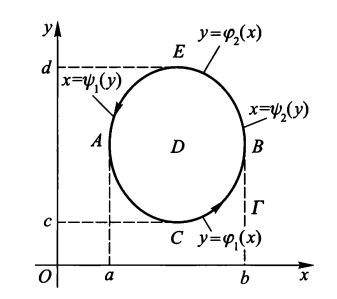
若函数 P, Q 在有界闭区域 $D \subset R^2$ 上连续且有一阶连续偏导数，则：

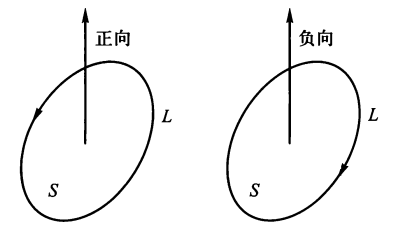
\[ \iint\limits_D (\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y}) \mathrm{d}x\mathrm{d}y = \oint\limits_\Gamma P \mathrm{d}x + Q\mathrm{d}y \]

其中 $\Gamma$ 为区域 D 的边界曲线，并取正向。

格林公式的行列式表示法：

\[ \iint\limits_{D} \begin{vmatrix}\dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} \\ P & Q\end{vmatrix} \mathrm{d}x\mathrm{d}y = \oint\limits_\Gamma P \mathrm{d}x + Q\mathrm{d}y \]

本质：第二类曲线积分 $\Rightarrow$ 二重积分

证明 ( 历年卷考到过类似的证明思想 )

第三种情况用于处理有“洞”的区域，使用格林公式的时候，要算上整个区域所有曲线的积分（注意每条曲线的方向）

计算技巧

若直接求某条曲线的第二类积分太复杂，可以先补一些直线，形成封闭曲线，然后利用格林公式转化为求二重积分的问题，再计算这些直线上的第二类积分，答案即为封闭曲线的积分 - 所有添补的直线的积分。注意方向的问题，不要搞错符号！
令 P = -y，Q = x，可得计算平面区域面积 S的公式：$S = \dfrac{1}{2}\oint\limits_\Gamma -y\mathrm{d}x + x\mathrm{d}y$。

若要求三维的封闭曲线的第二类积分，用斯托克斯公式

平面曲线积分与路径无关性⚓︎

平面单连通区域：没有“洞”的区域——D 内任一封闭曲线所包围的面积均包含于 D 内
平面复连通区域：有“洞”的区域

定理 2：设 $D \subset R^2$ 是平面单连通区域，若函数 P, Q 在区域 D 上连续，且有一阶连续偏导数，则以下 4 个条件等价：

沿 D 中任一按段光滑的闭曲线 L，有 $\oint\limits_L P\mathrm{d}x + Q\mathrm{d}y = 0$
对 D 中任一按段光滑曲线 L，曲线积分 $\int\limits_L P\mathrm{d}x + Q\mathrm{d}y$ 与路径无关，只与 L 的起点和终点有关
$P\mathrm{d}x + Q\mathrm{d}y$ 是 D 内某一函数 u 的全微分，即 $\mathrm{d}u = P\mathrm{d}x + Q\mathrm{d}y, \dfrac{\partial u}{\partial x} = P, \dfrac{\partial u}{\partial y} = Q$
在 D 内的每一点处，有 $\dfrac{\partial P}{\partial y} = \dfrac{\partial Q}{\partial x}$

注

若第二类曲线积分 $\int_{A(x_0, y_0)}^{B(x_1, y_1)} P(x, y) \mathrm{d}x + Q(x, y) \mathrm{d}y$ 与路径无关，则可用一元函数的定积分表示：

\[ \int_{A(x_0, y_0)}^{B(x_1, y_1)} P(x, y) \mathrm{d}x + Q(x, y) \mathrm{d}y = \int_{x_0}^{x_1} P(x, y_0)\mathrm{d}x + \int_{y_0}^{y_1}Q(x_1, y)\mathrm{d}y \]

由定理知 u(x, y) 为 $P \mathrm{d}x + Q \mathrm{d}y$ 的一个原函数，则有：

\[ u(x, y) = \int_{x_0}^{x} P(x, y)\mathrm{d}x + \int_{y_0}^{y}Q(x, y)\mathrm{d}y + C \]

若 $(0, 0) \in D$，则可简写为：$\int_0^x P(x, y)\mathrm{d}x + \int_0^yQ(x, y)\mathrm{d}y + C$

曲线积分的牛顿 - 莱布尼茨公式：若 $\mathrm{d}u = P\mathrm{d}x + Q\mathrm{d}y$，其中 P, Q 有连续偏导数，则： $$ \int_{A(x_0, y_0)}^{B(x_1, y_1)} P \mathrm{d}x + Q \mathrm{d}y = u(x, y) |_{A(x_0, y_0)}^{B(x_1, y_1)} = u(x_1, y_1) - u(x_0, y_0) $$

解题技巧

若题目给出了轨迹曲线的方程 ( 较为复杂 ) 以及它的起点和终点，若用定理 2 发现路径无关性，则我们可以直接将路径改为曲线起点和终点的连线 ( 直线 )，这样就简化了计算过程。

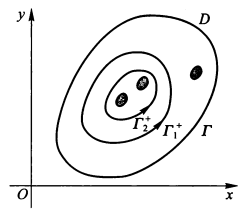
定理 3：设在复连通区域 D 内，P, Q 具有连续的偏导数且 $\dfrac{\partial P}{\partial y} \equiv \dfrac{\partial Q}{\partial x}$，则环绕同一些洞的任意两条闭曲线（同向）上的曲线积分都相等。

注意

在求第二类曲线方程前，一定要先判断积分区域上是否有取不到的“洞”( 关注积分内函数的分母部分，常常是 x 或 y 无法取到 0)。若存在这样的洞，根据定理 3，我们需要另外找一个包含该洞的、且能够简化计算的曲线方程 ( 根据积分内函数的特征构造 )。

第二类曲面积分⚓︎

概念⚓︎

定侧曲面：指定法线方向的双侧曲面

定义：

设 S 是光滑有界的定侧曲面，记 S 上的每点 M(x, y, z) 处沿曲面定侧的单位法矢量为：$\bm{e_n}(M) = \cos{\alpha} \bm{i} + \cos{\beta} \bm{j} + \cos{\gamma} \bm{k}$

又设 $\bm{A}(M) = P(x, y, z)\bm{i} + Q(x, y, z)\bm{j} + R(x, y, z)\bm{k},\ (x, y, z)\in S$，其中 P, Q, R 为定义在 S 上的有界函数，则 $\bm{A \cdot e_n} = P \cos{\alpha} + Q \cos{\beta} + R \cos{\gamma}$ 在 $\Gamma$ 上的第一类曲面积分 $$ \iint\limits_S \bm{A \cdot e_n} \mathrm{d}S = \iint\limits_{\Gamma}(P \cos{\alpha} + Q \cos{\beta} + R\cos{\gamma}) \mathrm{d}S $$ 被称为$\bm{A}(P)$沿定侧曲面S的第二类曲面积分

第二类曲面积分又被称为对坐标曲面积分

方向的规定

$\cos \alpha$：> 0 为前侧，< 0 为后侧
$\cos \beta$：> 0 为右侧，< 0 为前侧
$\cos \gamma$：> 0 为上侧，< 0 为下侧

解题时根据题目规定的方向做，这里的规定仅适用于没有任何规定的情况

性质：

$\iint\limits_{S^+}(\bm{A \cdot e_n}) \mathrm{d}S = - \iint\limits_{S^-}(\bm{A \cdot e_n}) \mathrm{d}S$
若 S 是由两个无公共内点的曲面块 $S_1, S_2$，且 $S_1, S_2$ 的侧与 S 的侧一致，则：$\iint\limits_S(\bm{A \cdot e_n}) \mathrm{d}S = \iint\limits_{S_1}(\bm{A \cdot e_n}) \mathrm{d}S + \iint\limits_{S_2}(\bm{A \cdot e_n}) \mathrm{d}S$

记 $d \bm{s} = \bm{e_n} ds$，被称为曲面的有向面积元素。

第二类曲面积分的四种形式：

$\iint\limits_{S} \bm{A \cdot e_n} \mathrm{d}S$ ( 第二类曲面积分 $\Rightarrow$ 第一类曲面积分 )
$\iint\limits_S \bm{A} \mathrm{d} \bm{S}$
$\iint\limits_{S} (P \cos{\alpha} + Q \cos{\beta} + R \cos{\gamma}) \mathrm{d}S$
$\iint\limits_S P(x, y, z)\mathrm{d}y\mathrm{d}z + Q(x, y, z)\mathrm{d}z\mathrm{d}x + R(x, y, z)\mathrm{d}x\mathrm{d}y$

注：第 4 种形式中，若 $\bm{e_n}$ 改变方向时，它们都要改变符号，与二重积分的面积元素 $\mathrm{d}x\mathrm{d}y$ 总取正值是不同的。

计算⚓︎

计算方法：

\[ \begin{align} & \iint\limits_S P(x, y, z)\mathrm{d}y\mathrm{d}z + Q(x, y, z)\mathrm{d}z\mathrm{d}x + R(x, y, z)\mathrm{d}x\mathrm{d}y \notag \\ = & \iint\limits_S P(x, y, z)\mathrm{d}y\mathrm{d}z + \iint\limits_S Q(x, y, z)\mathrm{d}z\mathrm{d}x + \iint\limits_S R(x, y, z)\mathrm{d}x\mathrm{d}y \notag \end{align} \]

然后分别计算这 3 项：

$\iint\limits_S P(x, y, z)\mathrm{d}y\mathrm{d}z = \mathrm{sgn}(\dfrac{\pi}{2} - \alpha) \iint\limits_{\sigma_{yz}} R(x(y, z), y, z)\mathrm{d}\sigma$
$\iint\limits_S Q(x, y, z)\mathrm{d}z\mathrm{d}x = \mathrm{sgn}(\dfrac{\pi}{2} - \beta) \iint\limits_{\sigma_{zx}} R(x, y(x, z), z)\mathrm{d}\sigma$
$\iint\limits_S R(x, y, z)\mathrm{d}x\mathrm{d}y = \mathrm{sgn}(\dfrac{\pi}{2} - \gamma) \iint\limits_{\sigma_{xy}} R(x, y, z(x, y))\mathrm{d}\sigma$

注：可以利用轮换对称的性质减少计算量。

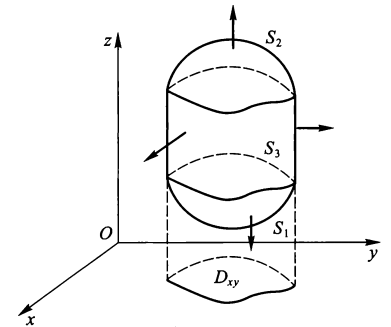
高斯公式⚓︎

设空间区域 V 由分片光滑的双侧封闭曲面 S 构成，若函数 P, Q, R 在 V 上连续，且有一阶连续偏导数，则 $$ \iiint\limits_V(\dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}) \mathrm{d}x\mathrm{d}y\mathrm{d}z = \oiint\limits_S P \mathrm{d}y\mathrm{d}z + Q \mathrm{d}z\mathrm{d}x + R \mathrm{d}x\mathrm{d}y $$ 其中S取外侧。

本质：第二类曲面积分 $\Rightarrow$ 三重积分

注

虽然上面规定 S 取外侧，但是题目可能会取内侧为正侧，需要当心！
若 S 为封闭的简单曲面，$\bm{l}$ 为任何固定方向，则 $\oiint_S \cos{(\bm{n, l})} \mathrm{d}S = 0$，其中 $\bm{n}$ 是曲面的法矢量。

解题技巧

在计算之前，可以先利用给出的曲面方程，对积分的被积函数进行化简
我们可以通过构造的方法，通过增添几个面，使原本不封闭的曲面封闭，然后利用高斯公式求解，最后减去在这多出的几个平面上的积分即可得到要求的结果。

散度场⚓︎

定义：

设 $\bm{A}(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z))$ 为空间区域 V 上的向量函数，对 V 上的每一点 (x, y, z)，称函数 $\dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}$ 为向量函数 $\bm{A}$ 在点 $M(x, y, z)$ 处的散度，记作 $\mathrm{div}\ \bm{A}(x, y, z)$

则高斯公式可以改写为：$\iiint\limits_V \mathrm{div}\ \bm{A} \mathrm{d}V = \oiint\limits_S \bm{A} \cdot \mathrm{d}\bm{S}$

令 V 收缩到点 $M_0$，得到：$\mathrm{div}\ \bm{A}(M_0) = \lim\limits_{V \rightarrow M_0} \dfrac{\oiint_S \bm{A} \cdot \mathrm{d}\bm{S}}{\Delta V}$

散度场：向量场 A 的散度 div A 所构成的数量场

物理意义

假设某一不可压缩流体的流速为向量函数 $\bm{A}$，经过封闭曲面 $S$ 的流量是 $\oiint\limits_S \bf{A}\cdot \mathrm{d}S$，则 $\mathrm{div}\ \bm{A}$ 表示流量对体积的变化率，称它为 $\bm{A}$ 在点 $M_0$ 的流量密度

$\mathrm{div}\ \bm{A}(M_0) > 0$：每一单位时间内有一定数量的流体流出这一点 $\Rightarrow$ 源
$\mathrm{div}\ \bm{A}(M_0) < 0$：每一单位时间内有一定数量的流体被这一点吸收 $\Rightarrow$ 汇
若对每一点皆有 $\mathrm{div}\ \bm{A} = 0$，称 $\bm{A}$ 为无源场

推论：

若在封闭曲面 S 所包围的区域 V 中处处有 $\mathrm{div}\ \bm{A} = 0$，则 $\oiint_S \bm{A} \cdot \mathrm{d}\bm{S} = 0$
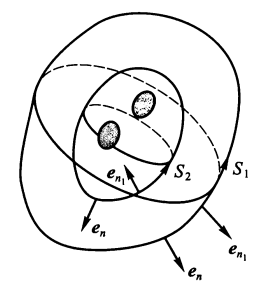
如果仅在区域 V 中某些点（或子区域上）$\mathrm{div}\ \bm{A} \ne 0$ 或 $\mathrm{div}\ \bm{A}$ 不存在（下图阴影部分），其他点都有 $\mathrm{div}\ \bm{A} = 0$，则通过保卫这些点或子区域（被称为“洞”）的 V 内任一封闭曲面积分都是相等的，即是一个常数，有：

\[ \oiint\limits_{S_1} \bm{A} \cdot \mathrm{d}\bm{S} = \oiint\limits_{S_2} \bm{A} \cdot \mathrm{d}\bm{S} \]

其中 $S_1, S_2$ 是包围散度不等于 0，或不存在的点（或区域）的任意两个封闭曲面，其法线单位矢量向外

注：该结论与上一节路径无关性最后那个定理十分类似

斯托克斯公式、空间曲线积分与路径无关性⚓︎

斯托克斯公式⚓︎

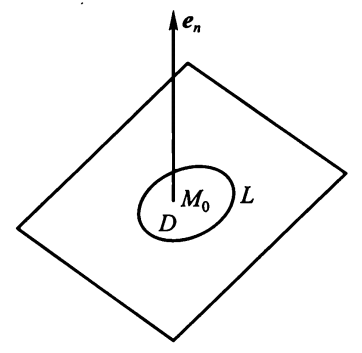
规定双侧曲面 S 的侧与其边界曲线 L 的方向 ( 用右手定则确定 )，如图所示：

定理 4：斯托克斯公式

设光滑曲面 S 的边界 L 是按段光滑的连续曲线，若函数 P, Q, R 在 S( 连同 L) 上连续，且有一阶连续偏导数，则：

\[ \begin{align} & \iint\limits_S(\dfrac{\partial R}{\partial y} - \dfrac{\partial Q}{\partial z})\mathrm{d}y\mathrm{d}z + (\dfrac{\partial P}{\partial z} - \dfrac{\partial R}{\partial x})\mathrm{d}y\mathrm{d}z + (\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y})\mathrm{d}y\mathrm{d}z \notag \\ = & \oint\limits_LP\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z \notag \end{align} \]

其中 S 的侧面与 L 的方向按右手法则确定 ( 见上图 )。

斯托克斯公式的行列式表示法：

\[ \iint\limits_S \begin{vmatrix}\mathrm{d}y\mathrm{d}z & \mathrm{d}z\mathrm{d}x & \mathrm{d}x\mathrm{d}y \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R\end{vmatrix} = \iint\limits_S \begin{vmatrix}\cos \alpha & \cos \beta & \cos \gamma \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R\end{vmatrix}\mathrm{d}S = \oint\limits_LP\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z \]

斯托克斯公式建立起第二类曲线积分和第二类曲面积分之间的联系

总结

求平面曲线的第二类积分 $\Rightarrow$ 格林公式
求空间曲线的第二类积分 $\Rightarrow$ 斯托克斯公式

空间曲线积分与路径无关性⚓︎

定理 5

设 $\Omega \subset \mathbf{R}^3$ 为空间线单连通区域，若函数 P, Q, R 在 $\Omega$ 上连续，且有一阶连续偏导数，则以下四个条件是等价的：

对于 $\Omega$ 内任一按段光滑的封闭曲线 L，有 $\oint\limits_LP\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z = 0$
对于 $\Omega$ 内任一按断光滑的曲线 $\Gamma$，曲线积分 $\oint\limits_LP\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z$ 与路径无关，仅与起点、终点有关
$P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z$ 是 $\Omega$ 内某一函数 u(x, y, z) 的全微分，即存在 $\Omega$ 上的函数 u(x, y, z)，使

\[ \mathrm{d}u = P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z \]

$\dfrac{\partial P}{\partial y} = \dfrac{\partial Q}{\partial x}$, $\dfrac{\partial Q}{\partial z} = \dfrac{\partial R}{\partial y}$, $\dfrac{\partial R}{\partial x} = \dfrac{\partial P}{\partial z}$在$\Omega$内处处成立

注：这个定理与平面积分的路径无关性的定理 2 对应

注

空间线单连通区域：该空间区域 V 中任意封闭曲线 L 不越过 V 的边界曲面，可连续收缩为 V 中的一点。
空间面单连通区域：该空间区域 V 中任意封闭曲面 S 不越过 V 的边界曲面，可连续收缩为 V 中的一点。

一种化简方法

若曲线积分 $I = \oint\limits_{\Gamma_{AB}}P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z$ 与路径无关，则可以将原路径转化为折线路径，便于计算

此时有：

\[ I = \int^{x_1}_{x_0}P(x, y_0, z_0)\mathrm{d}x + \int^{y_1}_{y_0}Q(x_1, y, z_0)\mathrm{d}y + \int^{z_1}_{z_0}P(x_1, y_1, z)\mathrm{d}z \]

若曲线积分仍满足上述条件，则：

\[ u(x, y, z) = \int^{x}_{x_0}P(x, y_0, z_0)\mathrm{d}x + \int^{y}_{y_0}Q(x, y, z_0)\mathrm{d}y + \int^{z}_{z_0}P(x, y, z)\mathrm{d}z + C \]

若 $(0, 0, 0) \in V$，则取 $(x_0, y_0, z_0) = (0, 0, 0)$，使计算方便。

旋度场⚓︎

定义：

设 $\bm{A}(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z))$ 为空间区域 V 上的向量函数，对 V 上一点 $M(x, y, z)$ ，定义向量函数 $(\dfrac{\partial R}{\partial y} - \dfrac{\partial Q}{\partial z}, \dfrac{\partial P}{\partial z} - \dfrac{\partial R}{\partial x}, \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y})$，称它为向量函数 $\bm{A}$ 在点 $M(x, y, z)$ 处的旋度，记作 $\mathbf{rot}\ \bm{A}$。

行列式表示法：

\[ \mathbf{rot}\ \bm{A} = \begin{vmatrix}\bm{i} & \bm{j} & \bm{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix} \]

设 $\bf{e}_T$ 是曲线 L 在点 $M(x, y, z)$ 处于指定的方向一致的单位切向量，向量 $\mathrm{d}\bm{s} = \bf{e}_T \mathrm{d}s$ 被称为弧长元素向量。

$\therefore$ 斯托克斯公式の第 3 种表示法：

\[ \iint\limits_S \mathbf{rot}\ \bm{A} \cdot \mathrm{d}\bm{S} = \oint\limits_L \bm{A} \cdot \mathrm{d}\bm{s} \]

旋度与坐标系选取的无关性

如图所示：

由斯托克斯公式の第 3 种表示法 + 二重积分的中值定理，可得：

\[ (\mathbf{rot}\ \bm{A} \cdot \bm{e}_n)_{M_0} = \lim\limits_{D \rightarrow M_0} \dfrac{\oint\limits_L \bm{A} \cdot \mathrm{d}\bm{s}}{D} \]

其中上式左端为 $\mathbf{rot}\ \bm{A}$ 在法线方向上的投影。该式可作为旋度的另一个定义形式。

旋度场：由向量函数 $\bm{A}$ 的旋度 $\mathbf{rot}\ \bm{A}$ 所定义的向量场
沿闭曲线 L 的环流量：$\oint\limits_L \bm{A} \cdot \mathrm{d}\bm{s}$
无旋场：$\mathbf{rot}\ \bm{A} = 0$

物理意义

流体的速度场的旋度的法线投影在曲面上对面积的曲面积分 = 流体在曲面边界上的环流量

向量微分算子⚓︎

向量微分算子 (Nabla 算子或哈密顿算子 )：$\nabla = \dfrac{\partial}{\partial x}\bm{i} + \dfrac{\partial}{\partial y}\bm{j} + \dfrac{\partial}{\partial z}\bm{k}$

二阶微分算子：$\nabla^2 = \dfrac{\partial^2 u}{\partial x^2} + \dfrac{\partial^2 u}{\partial y^2} + \dfrac{\partial^2 u}{\partial z^2}$

可以用向量微分算子改写上面的式子：

高斯公式：$\iiint\limits_V \nabla \cdot \bm{A} \mathrm{d}V = \oiint\limits_S \bm{A} \cdot \mathrm{d}S$
斯托克斯公式：$\iint\limits_S (\nabla \times \bm{A}) \cdot \mathrm{d}S = \oint\limits_S \bm{A} \cdot \mathrm{d}s$

评论区

如果大家有什么问题或想法，欢迎在下方留言~

第十章 第二类曲线积分与第二类曲面积分⚓︎

第二类曲线积分⚓︎

概念⚓︎

格林公式⚓︎

平面曲线积分与路径无关性⚓︎

第二类曲面积分⚓︎

概念⚓︎

计算⚓︎

高斯公式⚓︎

散度场⚓︎

斯托克斯公式、空间曲线积分与路径无关性⚓︎

斯托克斯公式⚓︎

空间曲线积分与路径无关性⚓︎

旋度场⚓︎

向量微分算子⚓︎

第十章第二类曲线积分与第二类曲面积分⚓︎