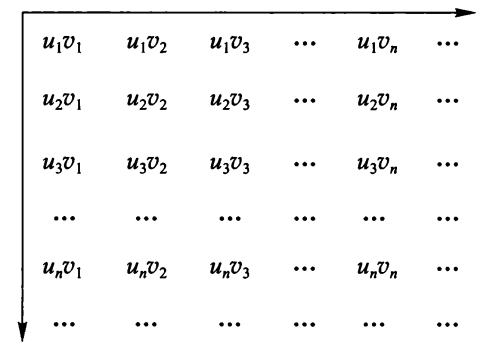第十一章级数⚓︎

约 2376 个字预计阅读时间 12 分钟

数项级数的基本概念⚓︎

概念⚓︎

级数：$\sum\limits_{n = 1}^\infty u_n = u_1 + u_2 + \dots + u_n + \dots$
部分和：$S_n = u_1 + u_2 + \dots + u_n$，且 $\sum\limits_{n = 1}^\infty u_n = \lim\limits_{n \rightarrow \infty}S_n$
- 若 $\lim\limits_{n \rightarrow \infty}S_n = S$，称级数收敛，并称 $S$ 为级数的和
- 若 $\lim\limits_{n \rightarrow \infty}S_n$ 不存在，则称级数发散

一些重要级数

几何级数 ( 等比级数 ) p 级数 $\ln x$ 类级数

\[\sum\limits_{n = 1}^\infty aq^{n-1}(a \ne 0)\]

当 $|q| < 1$ 时收敛，其和为 $\dfrac{a}{1 - q}$
当 $|q| \ge 1$ 时发散

\[\sum\limits_{n = 1}^{\infty}\dfrac{1}{n^p}\]

当 $p > 1$ 时收敛
当 $p \le 1$ 时发散

p = 1 时，该级数又被称为调和级数

\[\sum\limits_{n = 2}^\infty \dfrac{1}{n^p(\ln n)^q}\]

当 $p > 1$，或 $p = 1$ 且 $q > 1$ 时收敛
当 $p < 1$，或 $p = 1$ 且 $q \le 1$ 时发散

性质⚓︎

线性运算法则：若级数 $\sum\limits_{n = 1}^\infty u_n, \sum\limits_{n = 1}^\infty v_n$ 均收敛，且 $\sum\limits_{n = 1}^\infty u_n = A, \sum\limits_{n = 1}^\infty v_n = B$，则对任意常数 $\alpha, \beta$，有

\[ \sum\limits_{n = 1}^{\infty}(\alpha u_n + \beta v_n) = \alpha A + \beta B \]

下列三种情况不会影响级数的敛散性：
- 改变级数的有限项
- 去掉级数前的有限项
- 在级数前增添有限项
收敛级数的结合性：若级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛，则在级数中任意添加括号所得到的新级数也收敛，且其和不变。
级数收敛的必要条件：若级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛，则 $\lim\limits_{n \rightarrow \infty}u_n = 0$。
- 推论 ( 逆否命题 )：若 $\lim\limits_{n \rightarrow \infty}u_n$ 不存在或 $\lim\limits_{n \rightarrow \infty}u_n \ne 0$，则级数 $\sum\limits_{n = 1}^\infty u_n$ 发散。

定理 1( 柯西收敛准则 )：级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛的充要条件是：$\forall \varepsilon > 0, \exists N \in \mathbb{N}_+,$，当 $n > N$ 时，$\forall p \in \mathbb{N}_+, |u_{n+1} + u_{n+2} + \dots + u_{n+p}| < \varepsilon$。

正向级数敛散性的判别法⚓︎

正项级数$\sum\limits_{n = 1}^\infty u_n$ 满足 $u_n \ge 0$

定理 2：正向级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛的充要条件是：正项级数的部分和数列 $\{S_n\}$ 有上界，即存在常数 $M$，$\forall n \in N$，都有 $S_n \le M$。

判别法大全

注：使用下面的方法前可先用级数收敛的必要条件判断

比较判别法比较判别法的极限形式比值判别法根值判别法积分判别法 ( 很少用到 )

设 $\sum\limits_{n = 1}^\infty u_n, \sum\limits_{n = 1}^\infty v_n$ 均为正项级数，且 $u_n \le v_n(n = 1, 2, \dots)$

若 $\sum\limits_{n = 1}^\infty v_n$ 收敛，则 $\sum\limits_{n = 1}^\infty u_n$ 收敛
若 $\sum\limits_{n = 1}^\infty u_n$ 发散，则 $\sum\limits_{n = 1}^\infty v_n$ 发散

注：

此定理可减弱为 $u_n \le v_n(n = k, k+1, \dots)$

$u_n \le v_n$ 可改为 $u_n \le Cv_n$(C > 0 为常数 )

设 $\sum\limits_{n = 1}^\infty u_n, \sum\limits_{n = 1}^\infty v_n$ 均为正项级数，且 $\lim\limits_{n \rightarrow \infty}\dfrac{u_n}{v_n} = l$

当 $0 < l < +\infty$，即 $u_n \sim lv_n(n \rightarrow +\infty)$ 时，两个级数同时收敛或发散
当 $l = 0$ 时，若 $\sum\limits_{n = 1}^\infty v_n$ 收敛，则 $\sum\limits_{n = 1}^\infty u_n$ 收敛
当 $l = +\infty$ 时，若 $\sum\limits_{n = 1}^\infty v_n$ 发散，则 $\sum\limits_{n = 1}^\infty u_n$ 发散

设 $\sum\limits_{n = 1}^\infty u_n$ 是正项级数，并且 $\lim\limits_{n \rightarrow \infty}\dfrac{u_{n+1}}{u_n} = \gamma$( 或 $+\infty$)

当 $\gamma < 1$ 时，级数收敛
当 $\gamma > 1$ 时，级数发散
当 $\gamma = 1$ 时，无法判断

设 $\sum\limits_{n = 1}^\infty u_n$ 是正项级数，并且 $\lim\limits_{n \rightarrow \infty}\sqrt[n]{u_n} = \gamma$( 或 $+\infty$)

当 $\gamma < 1$ 时，级数收敛
当 $\gamma > 1$ 时，级数发散
当 $\gamma = 1$ 时，无法判断

设 $f(x)$ 在 $[1, +\infty)$ 上是非负且递减的连续函数，记 $u_n = f(n), n = 1, 2, 3, \dots$，则级数 $\sum\limits_{n = 1}^\infty u_n$ 与反常积分 $\int_1^{+\infty}f(x)$ 的敛散性相同。

一般级数收敛性的判别法⚓︎

交错级数⚓︎

交错级数：$\sum\limits_{n = 1}^\infty (-1)^{n-1}u_n(u_n > 0)$

定理 3( 莱布尼茨公式 )：若有交错级数 $\sum\limits_{n = 1}^\infty (-1)^{n-1}u_n$ 满足下列条件：

$u_1 \ge u_2 \ge u_3 \ge \dots$
$\lim\limits_{n \rightarrow \infty}u_n = 0$

则 $\sum\limits_{n = 1}^\infty (-1)^{n-1}u_n$ 收敛，且它的和 $S \le u_1$

推论：若交错级数满足莱布尼茨定理的条件，则以 $S_n$ 作为级数和的近似值时，其误差 $R_n$ 不超过 $u_{n+1}$，即 $|R_n| = |S - S_n| \le u_{n+1}$

绝对收敛级数与条件收敛级数⚓︎

定理 4：若 $\sum\limits_{n = 1}^\infty |u_n|$ 收敛，则 $\sum\limits_{n = 1}^\infty u_n$ 也收敛

设 $\sum\limits_{n = 1}^\infty u_n$ 为一般级数

若 $\sum\limits_{n = 1}^\infty |u_n|$ 收敛，称 $\sum\limits_{n = 1}^\infty u_n$绝对收敛
若 $\sum\limits_{n = 1}^\infty |u_n|$ 发散，但 $\sum\limits_{n = 1}^\infty u_n$ 收敛，称 $\sum\limits_{n = 1}^\infty u_n$条件收敛

判别法

绝对值的比值判别法绝对值的根值判别法

设 $\sum\limits_{n = 1}^\infty u_n$ 是一般级数，若 $\lim\limits_{n \rightarrow \infty}\dfrac{|u_{n+1}|}{|u_n|} = \gamma$( 或 $+\infty$)

当 $\gamma < 1$ 时，级数绝对收敛
当 $\gamma > 1$ 时，级数发散
当 $\gamma = 1$ 时，无法判断

设 $\sum\limits_{n = 1}^\infty u_n$ 是正项级数，并且 $\lim\limits_{n \rightarrow \infty}\sqrt[n]{|u_n|} = \gamma$( 或 $+\infty$)

当 $\gamma < 1$ 时，级数绝对收敛
当 $\gamma > 1$ 时，级数发散
当 $\gamma = 1$ 时，无法判断

一类题型：判断绝收、条收还是发散

如果是 2 个复杂的式子相加 / 减，则拆成 2 部分逐个击破
有时级数内会带一个常数 p，那么有可能需要分类讨论（而且很有可能跟p 级数相关）

绝对收敛级数的性质⚓︎

定理 5：设 $\sum\limits_{n = 1}^\infty u_n$ 绝对收敛，则重排的级数 $\sum\limits_{n = 1}^\infty u'_n$ 也绝对收敛，且它的和与原级数的和相等。

定理 6( 柯西定理 )：若级数 $\sum\limits_{n = 1}^\infty u_n, \sum\limits_{n = 1}^\infty v_n$ 绝对收敛，设 $\sum\limits_{n = 1}^\infty u_n = A, \sum\limits_{n = 1}^\infty v_n = B$，则下表中所有乘积 $u_iv_j$ 按任意顺序排列所得的级数 $\sum\limits_{n = 1}^\infty w_n$ 绝对收敛，且其和 = AB。

函数项级数的概念⚓︎

函数项级数：$\sum\limits_{n = 1}^\infty u_n(x) = u_1(x) + u_2(x) + \dots + u_n(x) + \dots$

若 $\exists x_0$，$\sum\limits_{n = 1}^\infty u_n(x_0)$ 收敛，称 $x_0$ 为函数项级数的收敛点。函数项级数全体收敛点的集合被称为函数项级数的收敛域，记为 $D$。

令 $\lim\limits_{n \rightarrow \infty}S_n(x) = S(x), x \in D$，称 $S(x)$ 为函数项级数的和函数。

称 $R_n(x) = S(x) - S_n(x) = u_{n+1}(x) + u_{n+2}(x) + \dots$ 为函数项级数的余项，它满足 $\lim\limits_{n \rightarrow \infty}R_n(x) = 0$

幂级数及其和函数⚓︎

概念⚓︎

幂级数：$\sum\limits_{n = 0}^\infty a_n(x - x_0)^n = a_0 + a_1 (x- x_0) + a_2(x - x_0)^2 + \dots + a_x(x - x_0)^n + \dots$

一般我们只考虑 $x_0 = 0$ 的情况，即 $\sum\limits_{n = 0}^\infty a_n x^n$，因此后面的内容就默认 $x_0 = 0$ 了。

定理 7( 阿贝尔定理 )：

若级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 在 $x = x_0(x_0 \ne 0)$ 处收敛，则满足 $|x| < |x_0|$ 的一切 $x$ 使该幂级数绝对收敛
若级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 在 $x = x_0(x_0 \ne 0)$ 处发散，则满足 $|x| > |x_0|$ 的一切 $x$ 使该幂级数发散

收敛域：以原点为中心的区间 $D$，用 $2R$ 表示区间长度
收敛半径：$R$
收敛区间：$(-R, R)$

注：$(-R, R) \subseteq D \subseteq [-R, R]$，因此最后还要判断一下边界上幂级数是否收敛

求幂级数收敛半径的方法

定理 8( 柯西 - 阿达马公式 )定理 9非标准形式的幂级数

设幂级数 $\sum\limits_{n = 0}^\infty a_n x^n$，若 $\lim\limits_{n \rightarrow \infty}\dfrac{|a_n|}{|a_{n+1}|} = R$

当 $0 < R < +\infty$ 时，级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 在 $(-R, R)$ 内绝对收敛，$|x| > R$ 时发散

注：在 $x = \pm R$ 处，级数可能收敛，也可能发散
当 $R = 0$ 时，级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 仅在 $x = 0$ 处收敛，$x \ne 0$ 时发散
当 $R = + \infty$ 时，级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 在 $(-\infty, +\infty)$ 内绝对收敛

注：若 $a_{n+1}$ 与 $a_n$ 有公因式，且 $\lim\limits_{n \rightarrow \infty}\dfrac{|a_n|}{|a_{n+1}|}$ 存在 ( 或 $= +\infty$) 则采用该定理

设幂级数 $\sum\limits_{n = 0}^\infty a_n x^n$，若 $\lim\limits_{n \rightarrow \infty}\dfrac{1}{\sqrt[n]{|a_n|}} = R$

当 $0 < R < +\infty$ 时，级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 在 $(-R, R)$ 内绝对收敛，$|x| > R$ 时发散
当 $R = 0$ 时，级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 仅在 $x = 0$ 处收敛，$x \ne 0$ 时发散
当 $R = + \infty$ 时，级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 在 $(-\infty, +\infty)$ 内绝对收敛

注：若 $a_n$ 中有 $n$ 次方，且 $\lim\limits_{n \rightarrow \infty}\dfrac{1}{\sqrt[n]{|a_n|}}$ 存在 ( 或 $= +\infty$)，则采用该定理

相邻两项 $x$ 的次数差距大于 1 $\Rightarrow$ 绝对值的比较判别法 / 根值判别法
形如 $(ax + b)^n\ \Rightarrow$ 换元：令 $t = ax + b$，注意换元的时候收敛半径发生了变化

性质⚓︎

若幂级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 的收敛半径为 $R(> 0)$，则：

级数在收敛域上的和函数 $S(x)$ 是连续函数，当然 $S(x)$ 在 $(-R, R)$ 内也连续
级数在 $(-R, R)$ 内逐项可微，微分后所得到的幂级数与原级数有相同的收敛半径，即： $$ (\sum\limits_{n = 0}^\infty a_n x^n)' = \sum\limits_{n = 0}^\infty (a_n x^n)' $$
级数在 $(-R, R)$ 内逐项可积，积分后所得到的幂级数与原级数有相同的收敛半径，即： $$ \int_0^x(\sum\limits_{n = 0}^\infty a_n x^n) \mathrm{d}x = \sum\limits_{n = 0}^\infty (\int_0^x a_n x^n \mathrm{d}x) $$

推论：设 $S(x)$ 为幂级数在收敛区间 $(-R, R)$ 内的和函数，则

在 $(-R, R)$ 内 $S(x)$ 具有任何阶导数且可逐项求导，收敛半径仍为 $R$
唯一性定理：幂级数的系数与 $S(x)$ 在 $x = 0$ 处的各阶导数有如下关系： $$ a_0 = S(0), a_n = \dfrac{S^{(n)}(0)}{n!}, n = 1, 2, \dots $$

运算法则⚓︎

若级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 与 $\sum\limits_{n = 0}^\infty b_n x^n$ 在 $x = 0$ 的某邻域相等，则它们的同次幂项的系数相等，即 $a_n = b_n, n = 0, 1, 2, \dots$
若级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 与 $\sum\limits_{n = 0}^\infty b_n x^n$ 的收敛半径分别为 $R_a, R_b$，则：

\[ \begin{align} \lambda \sum\limits_{n = 0}^\infty a_n x^n & = \sum\limits_{n = 0}^\infty \lambda a_n x^n , |x| < R_a \notag \\ \sum\limits_{n = 0}^\infty a_n x^n \pm \sum\limits_{n = 0}^\infty b_n x^n & = \sum\limits_{n = 0}^\infty (a_n \pm b_n) x^n, |x| < R \notag \\ (\sum\limits_{n = 0}^\infty a_n x^n)(\sum\limits_{n = 0}^\infty b_n x^n) & = \sum\limits_{n = 0}^\infty c_n x^n, |x| < R \notag \end{align} \]

其中 $\lambda$ 为常数，$R = \min\{R_a, R_b\}$，$c_n = \sum\limits_{k = 0}^n a_kb_{n-k}$

和函数⚓︎

两个重要幂级数

幂级数	$\sum\limits_{n = 1}^\infty\dfrac{x^n}{n}$	$\sum\limits_{n = 1}^\infty nx^{n-1}$
收敛半径	$R = 1$	$R = 1$
收敛区间	$(-1, 1)$	$(-1, 1)$
收敛域	$[-1, 1)$	$(-1, 1)$
函数	$-\ln (1-x)$	$\dfrac{1}{(1-x)^2}$

求解的小技巧

$\sum\limits_{n = 1}^\infty \dfrac{x^{n+1}}{n} = x\sum\limits_{n = 1}^\infty \dfrac{x^n}{n}$
$\sum\limits_{n = 1}^\infty \dfrac{x^{n-1}}{n} \xlongequal{\text{当 } x \ne 0} \dfrac{1}{x}\sum\limits_{n = 1}^\infty \dfrac{x^n}{n}$
$\sum\limits_{n = 1}^\infty \dfrac{x^{2n}}{n} \xlongequal{\text{令 } x^2 = y} \dfrac{1}{x}\sum\limits_{n = 1}^\infty \dfrac{y^n}{n}$
$\sum\limits_{n = 1}^\infty \dfrac{x^n}{n(n+1)} = \sum\limits_{n = 1}^\infty (\dfrac{1}{n} - \dfrac{1}{n+1})x^n = \dfrac{1-x}{x}\ln(1-x) + 1, (x \in [-1, 0) \cup (0, 1))$
$\sum\limits_{n = 1}^\infty nx^n = x\sum\limits_{n = 1}^\infty nx^{n-1}$
$\sum\limits_{n = 1}^\infty nx^{2n} \xlongequal{\text{令 } x^2 = y} \sum\limits_{n = 1}^\infty ny^n$
$\sum\limits_{n = 2}^\infty nx^{n-2} = \dfrac{1}{x}(\sum\limits_{n = 2}^\infty nx^{n-1} + 1 - 1)$

求幂级数的和函数常用方法

线性运算法则
变量代换
逐项求导，再利用 $S(x) = S(0) + \int_0^x S'(x) \mathrm{d}x$
逐项积分，再利用 $S(x) = (\int_0^xS(x)\mathrm{d}x)'$
可以利用一些常见幂级数

注意！

无论是求幂级数的和函数，还是函数展成幂级数，千万不要忘记以下两点！

确定收敛域：判断幂级数在边界那两点上是否收敛
关注那些取不到的点

函数展成幂级数⚓︎

泰勒级数⚓︎

回顾：泰勒公式 $$ f(x) = f(x_0) + \dfrac{f'(x_0)}{1!}(x - x_0) + \dfrac{f''(x_0)}{2!}(x - x_0)^2 + \dots + \dfrac{f^{(n)}(x_0)}{n!}(x - x_0)^n + R_n(x) $$

其中拉格朗日余项 $R_n(x) = \dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x - x_0)^{n+1}$，$\xi$ 介于 $x_0, x$ 之间

定理 10：设 $f(x)$ 在区间 $|x - x_0| < R$ 内存在任意阶的导数，幂级数 $\sum\limits_{n = 0}^\infty \dfrac{f^{(n)}(x_0)}{n!}(x - x_0)^n$ 的收敛区间为 $|x - x_0| < R$，则在 $|x - x_0| < R$ 内 $f(x) = \sum\limits_{n = 0}^\infty \dfrac{f^{(n)}(x_0)}{n!}(x - x_0)^n$ 成立的充要条件是：在该区间内，$\lim\limits_{n \rightarrow \infty} R_x(x) = \lim\limits_{n \rightarrow \infty} \dfrac{f^{(n + 1)}(\xi)}{(n+1)!}(x - x_0)^{n+1} = 0$

上述幂级数被称为泰勒级数，当 $x_0 = 0$ 时，被称为麦克劳林级数：

\[ f(0) + \dfrac{f'(0)}{1!}x + \dfrac{f''(0)}{2!}x^2 + \dots + \dfrac{f^{(n)}(0)}{n!}x^n + \dots = \sum\limits_{n = 0}^\infty \dfrac{f^{(n)}(0)}{n!}x^n \]

基本初等函数的幂级数展开⚓︎

常用的麦克劳林展开式

$e^x = 1 + x + \dfrac{x^2}{2!} + \dots + \dfrac{x^n}{n!} + \dots, x \in (-\infty, +\infty)$
$\sin x = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dots + (-1)^n\dfrac{x^{2n+1}}{(2n+1)!} + \dots, x \in (-\infty, +\infty)$
$\cos x = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dots + (-1)^n\dfrac{x^{2n}}{(2n)!} + \dots, x \in (-\infty, +\infty)$
$\ln (1+x) = x - \dfrac{x^2}{2} + \dfrac{x^3}{3} - \dots + (-1)^n\dfrac{x^{n+1}}{n+1} + \dots, x \in (-1, 1]$
$(1 + x)^a = 1 + ax + \dfrac{a(a-1)}{2!}x^2 + \dots + \dfrac{a(a-1)\dots(a - n + 1)}{n!}x^n + \dots. x \in (-1, 1)$
$\dfrac{1}{1 - x} = \sum\limits_{n = 0}^{\infty} x^n, |x| < 1$
$\dfrac{1}{1 + x} = \sum\limits_{n = 0}^{\infty} (-1)^n x^n, |x| < 1$

补充

$\dfrac{1}{2}\ln\dfrac{1+x}{1-x} = \sum\limits_{n = 0}^\infty \dfrac{x^{2n+1}}{2n+1}, x \in (-1, 1)$
$\sqrt{1+x} = 1 + \dfrac{1}{2}x + \sum\limits_{n = 2}^\infty (-1)^{n-1} \dfrac{(2n-3)!!}{(2n)!!}x^n, x \in [-1, 1]$
$\dfrac{1}{\sqrt{1+x}} = 2(\sqrt{1+x})' = 1 + \sum\limits_{n = 1}^\infty (-1)^n \dfrac{(2n-1)!!}{(2n)!!}x^n, x \in (-1, 1]$

其他方法⚓︎

求幂级数的和函数的方法的逆过程

函数的傅里叶展开⚓︎

概念⚓︎

傅里叶级数： $$ \dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos \dfrac{n\pi x}{l} + b_n \sin \dfrac{n \pi x}{l}) $$

其中 $a_n, b_n$ 被称为傅里叶系数，满足：

\[ \begin{cases} a_n = \dfrac{1}{l} \int_{-l}^l f(x)\cos \dfrac{n \pi x}{l} \mathrm{d}x, \quad n = 0, 1, 2, \dots \notag \\ b_n = \dfrac{1}{l} \int_{-l}^l f(x)\sin \dfrac{n \pi x}{l} \mathrm{d}x, \quad n = 1, 2, 3, \dots \notag \end{cases} \]

注意

有时，$a_0$ 项无法通过上面的公式求解 ( 比如 $n$ 作为分母 )，需要单独求解：$a_0 = \dfrac{1}{l} \int_{-l}^l f(x) \mathrm{d}x$

周期函数的傅里叶展开⚓︎

定理 11( 狄利克雷定理 )：如果 $f(x)$ 是以 $T = 2l$ 为周期的周期函数，且 $f(x)$ 在 $[-l, l]$ 上逐段光滑，那么 $f(x)$ 的傅里叶级数在任意点 $x$ 处都收敛，并且收敛于 $f(x)$ 在该点左右极限的平均值，即：

\[ \begin{align} \dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos \dfrac{n\pi x}{l} + b_n \sin \dfrac{n \pi x}{l}) & = S(x) \notag \\ & = \dfrac{f(x - 0) + f(x + 0)}{2}, x \in (-\infty, +\infty) \notag \end{align} \]

更通俗的理解

在 $f(x)$ 的连续点上，$\dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos \dfrac{n\pi x}{l} + b_n \sin \dfrac{n \pi x}{l}) = f(x)$
在 $f(x)$ 的间断点上，$\dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos \dfrac{n\pi x}{l} + b_n \sin \dfrac{n \pi x}{l}) = \dfrac{f(x - 0) + f(x + 0)}{2}$

注

我们通常会研究 $T = 2\pi$ 时的傅里叶级数此时的傅里叶级数为：$\dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos nx + b_n \sin nx)$，傅里叶系数为：

$a_n = \dfrac{1}{\pi} \int_{-\pi}^\pi f(x)\cos nx \mathrm{d}x, \quad n = 0, 1, 2, \dots$
$b_n = \dfrac{1}{\pi} \int_{-\pi}^\pi f(x)\sin nx \mathrm{d}x, \quad n = 1, 2, 3, \dots$

特殊情况的化简

$f(x)$ 为偶函数——傅里叶余弦级数$f(x)$ 为奇函数——傅里叶正弦级数$f(x)$ 为在 $[a, b]$ 上周期为 $T = 2l = b - a$ 的周期函数

此时 $a_n = \dfrac{2}{l} \int_0^l f(x)\cos \dfrac{n \pi x}{l} \mathrm{d}x, b_n = 0$，那么傅里叶级数为：

\[ \dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos \dfrac{n\pi x}{l}) = S(x) = \dfrac{f(x - 0) + f(x + 0)}{2}, x \in (-\infty, +\infty) \]

此时 $a_n = 0, b_n = \dfrac{2}{l} \int_0^l f(x)\sin \dfrac{n \pi x}{l} \mathrm{d}x$，那么傅里叶级数为：

\[ \sum\limits_{n = 1}^\infty (b_n \sin \dfrac{n\pi x}{l}) = S(x) = \dfrac{f(x - 0) + f(x + 0)}{2}, x \in (-\infty, +\infty) \]

傅里叶系数为：

\[ \begin{cases} a_n = \dfrac{2}{b-a}\int_a^b f(x)\cos \dfrac{2n\pi x}{b - a} \mathrm{d}x, n = 0, 1, 2, \dots\\ b_n = \dfrac{2}{b-a}\int_a^b f(x)\sin \dfrac{2n\pi x}{b - a} \mathrm{d}x, n = 1, 2, 3, \dots \end{cases} \]

傅里叶级数为：

\[ \begin{align} \dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos \dfrac{2n\pi x}{b - a} + b_n \sin \dfrac{2n \pi x}{b - a}) & = S(x) \notag \\ & = \dfrac{f(x - 0) + f(x + 0)}{2}, x \in (-\infty, +\infty) \notag \end{align} \]

补充：帕塞瓦尔等式

设 $f(x)$ 可积且平方可积，则 $f(x)$ 的傅里叶系数 $a_n$ 和 $b_n$ 的平方构成的级数 $\dfrac{a_0^2}{2} + \sum\limits_{n = 1}^\infty (a_n^2 + b_n^2)$ 是收敛的，且满足下列等式，即帕塞瓦尔等式

\[ \dfrac{a_0^2}{2} + \sum\limits_{n = 1}^\infty (a_n^2 + b_n^2) = \dfrac{1}{l}\int_{-l}^l f^2(x) \mathrm{d}x \]

有限区间上的傅里叶展开⚓︎

区间 $[-l, l]$ 上的展开式：类似一般周期函数的傅里叶展开式，只是区间发生了变化
在 $[0, l]$ 上的展开式：先在 $[-l, 0]$ 上补充定义，使 $f(x)$ 在 $[-l, l]$ 能够进行傅里叶展开，然后将 $x$ 限制在 $[0, l]$ 上，这样就得到了符合要求的展开式。有 2 种形式：

奇延拓偶延拓

令

\[ F(x) = \begin{cases}f(x), & 0 < x \le l \\ 0, & x = 0 \\ -f(-x), & -l \le x < 0\end{cases} \]

得到 $f(x)$ 在 $[0, l]$ 上的正弦展开： $$ \sum\limits_{n = 1}^\infty (b_n \sin \dfrac{n\pi x}{l}) = S(x) = \dfrac{f(x - 0) + f(x + 0)}{2}, x \in (0, l) $$

其中，$b_n = \dfrac{2}{l} \int_0^l f(x)\sin \dfrac{n \pi x}{l} \mathrm{d}x$，且 $S(0) = S(l) = 0$

$S(x)$ 为周期函数，周期为 $2l$，且为奇函数

令

\[ F(x) = \begin{cases}f(x), & 0 \le x \le l \\ f(-x), & -l \le x < 0\end{cases} \]

得到 $f(x)$ 在 $[0, l]$ 上的余弦展开： $$ \dfrac{a_0}{2} + \sum\limits_{n = 1}^\infty (a_n \cos \dfrac{n\pi x}{l}) = S(x) = \dfrac{f(x - 0) + f(x + 0)}{2}, x \in (0, l) $$

其中，$a_n = \dfrac{2}{l} \int_0^l f(x)\cos \dfrac{n \pi x}{l} \mathrm{d}x$，且 $S(0) = \lim\limits_{x \rightarrow 0^+}f(x), S(l) = \lim\limits_{x \rightarrow l^-}f(x)$

$S(x)$ 为周期函数，周期为 $2l$，且为偶函数

评论区

如果大家有什么问题或想法，欢迎在下方留言~

幂级数	\(\sum\limits_{n = 1}^\infty\dfrac{x^n}{n}\)	\(\sum\limits_{n = 1}^\infty nx^{n-1}\)
收敛半径	\(R = 1\)	\(R = 1\)
收敛区间	\((-1, 1)\)	\((-1, 1)\)
收敛域	\([-1, 1)\)	\((-1, 1)\)
函数	\(-\ln (1-x)\)	\(\dfrac{1}{(1-x)^2}\)

第十一章 级数⚓︎

数项级数的基本概念⚓︎

概念⚓︎

性质⚓︎

正向级数敛散性的判别法⚓︎

一般级数收敛性的判别法⚓︎

交错级数⚓︎

绝对收敛级数与条件收敛级数⚓︎

绝对收敛级数的性质⚓︎

函数项级数的概念⚓︎

幂级数及其和函数⚓︎

概念⚓︎

性质⚓︎

运算法则⚓︎

和函数⚓︎

函数展成幂级数⚓︎

泰勒级数⚓︎

基本初等函数的幂级数展开⚓︎

其他方法⚓︎

函数的傅里叶展开⚓︎

概念⚓︎

周期函数的傅里叶展开⚓︎

有限区间上的傅里叶展开⚓︎

第十一章级数⚓︎