第七章矢量代数与空间解析几何⚓︎

约 2789 个字预计阅读时间 14 分钟

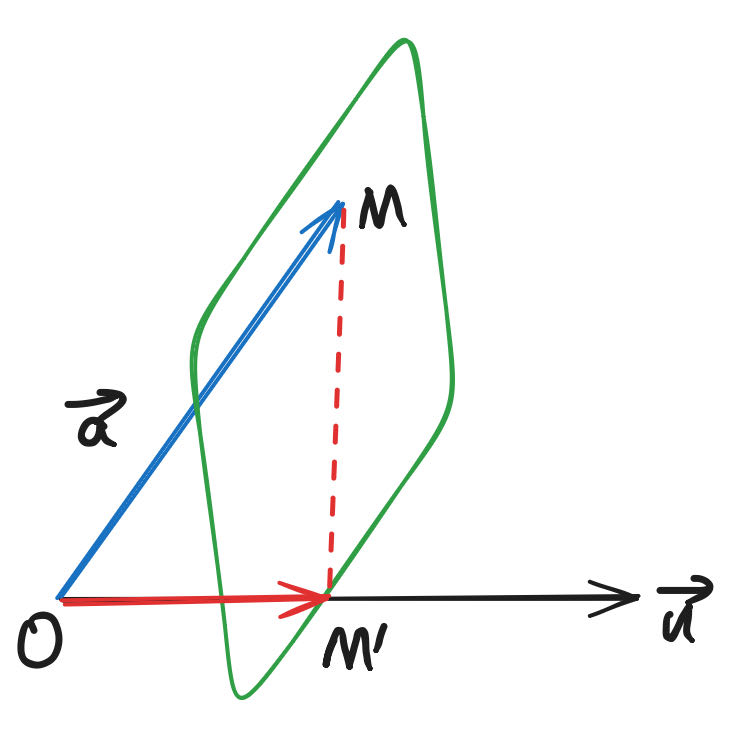
补充：矢量的投影

矢量 $\bm{a}$ 在轴 u 上的投影为：$|\bm{a}| \cos{\varphi} = \dfrac{\bm{a} \cdot \bm{u}}{|\bm{u}|}$

投影矢量：$|\bm{a}| \cos{\varphi} \dfrac{\bm{u}}{|\bm{u}|}$

性质：

$(\bm{a} + \bm{b})_{\bm{u}} = (\bm{a})_{\bm{u}} + (\bm{b})_{\bm{u}}$
$(\lambda \bm{a})_{\bm{u}} = \lambda (\bm{a})_{\bm{u}}$

两矢量的数量积与矢量积⚓︎

数量积⚓︎

数量积 ( 点积 )：$\bm{a} \cdot \bm{b} = |\bm{a}||\bm{b}|\cos \theta$

运算规律：

交换律：$\bm{a} \cdot \bm{b} = \bm{b} \cdot \bm{a}$
结合律：$m(\bm{a} \cdot \bm{b}) = (m\bm{a}) \cdot \bm{b} = \bm{a} \cdot (m\bm{b})$
分配律：$\bm{a} \cdot (\bm{b} + \bm{c}) = \bm{a} \cdot \bm{b} + \bm{a} \cdot \bm{c}$

定理 1：$\bm{a} \perp \bm{b} \Leftrightarrow \bm{a} \cdot \bm{b} = 0$

若 $\bm{a} = (a_1, a_2, a_3), \bm{b} = (b_1, b_2, b_3)$，则：

\[ \cos(\bm{a}, \bm{b}) = \dfrac{\bm{a} \cdot \bm{b}}{|\bm{a}|\ |\bm{b}|} = \dfrac{a_1b_1 + a_2b_2 + a_3b_3}{\sqrt{a_1^2 + a_2^2 + a_3^2} \cdot \sqrt{b_1^2 + b_2^2 + b_3^2}} \]

矢量积⚓︎

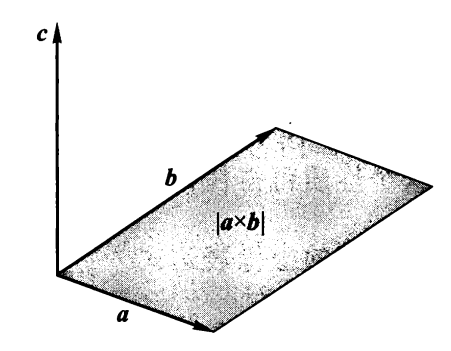
矢量积 ( 叉积 )：$\bm{c} = \bm{a} \times \bm{b}$

大小：$|\bm{c}| = |\bm{a}|\ |\bm{b}|\sin(\bm{a}, \bm{b})$
方向：从 $\bm{a}$ 经角 $(\bm{a}, \bm{b})$ 到 $\bm{b}$ 的右手螺旋定则确定（四指从 $\bm{a}$ 弯向 $\bm{b}$，拇指朝向为 $\bm{a} \times \bm{b}$ 的方向）

几何意义：数值上 = 以 $\bm{a}, \bm{b}$ 为邻边的平行四边形的面积

运算规律：

$\bm{a} \times \bm{b} = - (\bm{b} \times \bm{a})$
结合律：$m(\bm{a} \times \bm{b}) = (m\bm{a}) \times \bm{b} = \bm{a} \times (m\bm{b})$
分配律：$\bm{a} \times (\bm{b} + \bm{c}) = \bm{a} \times \bm{b} + \bm{a} \times \bm{c},\ (\bm{a} + \bm{b}) \times \bm{c} = \bm{a} \times \bm{c} + \bm{b} \times \bm{c}$

定理 2：$\bm{a} \parallel \bm{b} \Leftrightarrow \bm{a} \times \bm{b} = \bm{0}$

坐标表达式：

\[ \bm{a} \times \bm{b} = \begin{vmatrix}\bm{i} & \bm{j} & \bm{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{vmatrix} \]

且：$\bm{a} \parallel \bm{b} \Leftrightarrow \dfrac{a_1}{b_1} = \dfrac{a_2}{b_2} = \dfrac{a_3}{b_3}$

矢量的混合积与二重矢积⚓︎

混合积⚓︎

令 $\bm{a} = (a_1, a_2, a_3), \bm{b} = (b_1, b_2, b_3), \bm{c} = (c_1, c_2, c_3)$

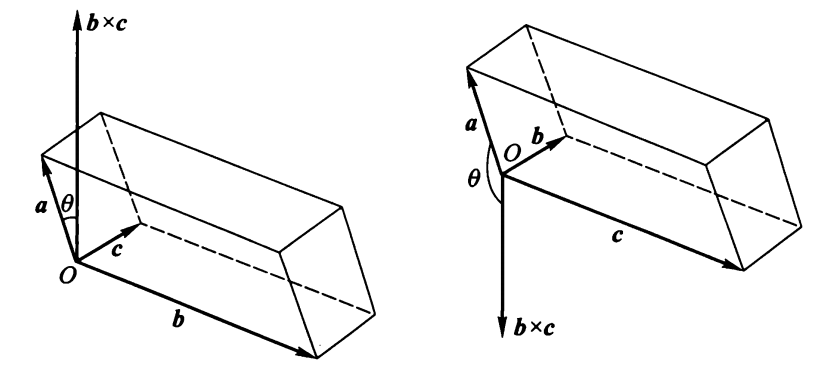
混合积：$\bm{a} \cdot (\bm{b} \times \bm{c}) = \begin{vmatrix}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix}$

定理 3：$\bm{a}, \bm{b}, \bm{c}$ 共面 $\Leftrightarrow\ \bm{a} \cdot (\bm{b} \times \bm{c}) = 0$

几何意义：$|\bm{a} \cdot (\bm{b} \times \bm{c})|$ 的值为以 $\bm{a}, \bm{b}, \bm{c}$ 为棱的平行六面体的体积

性质：

顺次轮换混合积中的三个矢量，所得混合积不变，即 $$ \bm{a} \cdot (\bm{b} \times \bm{c}) = \bm{b} \cdot (\bm{c} \times \bm{a}) = \bm{c} \cdot (\bm{a} \times \bm{b}) $$
任意对调混合积中两矢量的位置所得混合积的绝对值不变，但符号相反，即

\[ \begin{align} \bm{a} \cdot (\bm{b} \times \bm{c}) & = - \bm{a} \cdot (\bm{c} \times \bm{b}) \notag \\ \bm{a} \cdot (\bm{b} \times \bm{c}) & = - \bm{b} \cdot (\bm{a} \times \bm{c}) \notag \\ \bm{a} \cdot (\bm{b} \times \bm{c}) & = - \bm{c} \cdot (\bm{b} \times \bm{a}) \notag \end{align} \]

二重矢积⚓︎

二重矢积：$\bm{a} \times (\bm{b} \times \bm{c})$

定理 4：

\[ \begin{align} \bm{a} \times (\bm{b} \times \bm{c}) & = (\bm{a} \cdot \bm{c}) \bm{b} - (\bm{a} \cdot \bm{b})\bm{c} \notag \\ (\bm{a} \times \bm{b}) \times \bm{c} & = (\bm{c} \cdot \bm{a}) \bm{b} - (\bm{c} \cdot \bm{b})\bm{a} \notag \end{align} \]

平面与直线方程⚓︎

平面及平面方程⚓︎

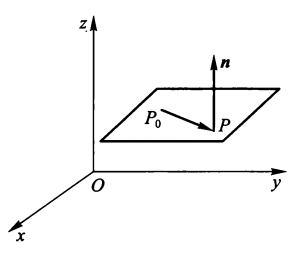
点法式方程：已知一平面过 $P_0(x_0, y_0, z_0)$，且垂直于非零矢量 $\bm{n} = A\bm{i} + B\bm{j} + C\bm{k}$，则平面方程为：

\[ A(x - x_0) + B(y - y_0) + C(z - z_0) = 0 \]

一般式方程：( 其中 $A, B, C$ 不全为 0)

\[ Ax + By + Cz + D = 0 \]

当 $D = 0$，平面过原点
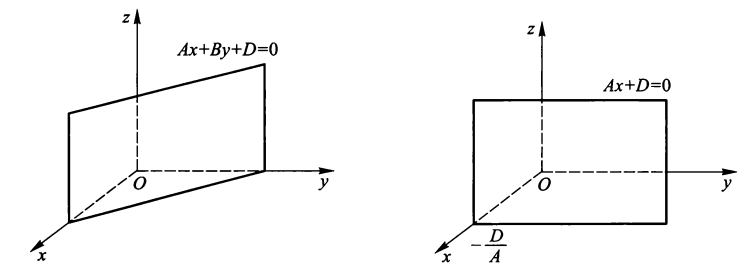
当 $A, B, C$ 三者有一个为 0 时，平面与坐标轴 (Ox/Oy/Oz) 平行
当 $A, B, C$ 三者有两个为 0 时，平面与坐标平面平行

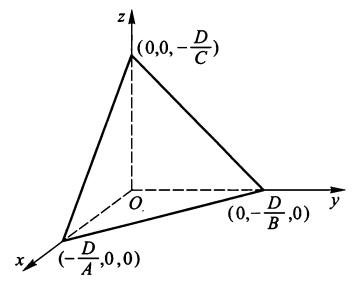
截距式方程：( 其中 $A, B, C, D$ 均不为 0) 令 $a = -\dfrac{D}{A}, b = -\dfrac{D}{B}, c = -\dfrac{D}{C}$，则方程为：

\[ \dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1 \]

三点式方程：若平面过 $M_i(x_i, y_i, z_i)(i = 1, 2, 3)$ 这 3 个定点，则方程为：

\[ \begin{vmatrix} x - x_1 & y - y_1 & z - z_1 \\ x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\ x_3 - x_1 & y_3 - y_1 & z_3 - z_1 \end{vmatrix} = 0 \]

常见题型

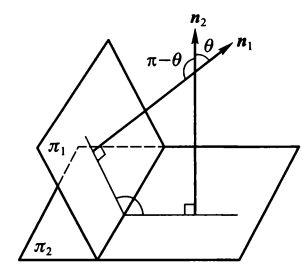
两平面的夹角：设平面 $\pi_1: A_1x + B_1y + C_1z + D_1 = 0,\ \pi_2: A_2x + B_2y + C_2z + D_2 = 0$，则该两平面的夹角的余弦值为：

\[ \cos \theta = \cos(\bm{n}_1, \bm{n}_2) = \dfrac{A_1A_2 + B_1B_2 + C_1C_2}{\sqrt{A_1^2 + B_1^2 + C_1^2}\sqrt{A_2^2 + B_2^2 + C_2^2}} \]

$\pi_1 \perp \pi_2 \Leftrightarrow A_1A_2 + B_1B_2 + C_1C_2 = 0$
$\pi_1 \parallel \pi_2 \Leftrightarrow \dfrac{A_1}{A_2} = \dfrac{B_1}{B_2} = \dfrac{C_1}{C_2}$

点到平面的距离：求空间一点 $P_0(x_0, y_0, z_0)$ 到平面 $Ax + By + Cz + D = 0$ 的距离

\[ d = \dfrac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}} \]

空间直线方程⚓︎

点向式方程 ( 对称式方程 )：设 L 是过点 $P_0(x_0, y_0, z_0)$ 且与一非零矢量 $\bm{v} = l\bm{i} + m\bm{j} + n\bm{k}$ 平行的直线，求其方程：

\[ \dfrac{x - x_0}{l} = \dfrac{y - y_0}{m} = \dfrac{z - z_0}{n} \]

注：若 l, m 或 n 为 0，可以将 0 写在分母的位置上，表示在 Ox/Oy/Oz 轴上的投影为 0，即直线垂直于 Ox/Oy/Oz 轴

参数式方程：(t 为参数 )

\[ \begin{cases}x = x_0 + lt \\ y = y_0 + mt \\ z = z_0 + nt\end{cases},\quad (- \infty < l < + \infty) \]

两点式方程：已知直线上两点 $P_1(x_1, y_1, z_1), P_2(x_2, y_2, z_2)$，则直线方程为：

\[ \dfrac{x - x_1}{x_2 - x_1} = \dfrac{y - y_1}{y_2 - y_1} = \dfrac{z - z_1}{z_2 - z_1} \]

一般式方程：($A_1, B_1, C_1$ 与 $A_2, B_2, C_2$ 不成比例 )

\[ \begin{cases}A_1x + B_1y + C_1z + D_1 = 0 \\ A_2x + B_2y + C_2z + D_2 = 0\end{cases} \]

特别地，$\begin{cases}y = 0 \\ z = 0\end{cases}$，$\begin{cases}x = 0 \\ z = 0\end{cases}$，$\begin{cases}x = 0 \\ y = 0\end{cases}$ 分别表示与 Ox、Oy、Oz 轴重合的直线。

一般式 $\Rightarrow$ 点向式

设一般式方程中：

\[ \begin{align} \pi_1: A_1x + B_1y + C_1z + D_1 = 0 \text{ 的法矢量为 } \bm{n}_1\notag \\ \pi_2: A_2x + B_2y + C_2z + D_2 = 0 \text{ 的法矢量为 } \bm{n}_2\notag \\ \end{align} \]

设直线方向矢量为 $\bm{v}$，取 $\bm{v} = \bm{n}_1 \times \bm{n}_2$，再在直线上取一点即可得到点向式方程。

常见题型

两直线的夹角：两直线方向矢量的夹角 $\theta$ 或它们的补角 $\pi - \theta$，设：

\[ \begin{align} L_1: \dfrac{x - x_1}{l_1} & = \dfrac{y - y_1}{m_1} = \dfrac{z - z_1}{n_1} \notag \\ L_2: \dfrac{x - x_2}{l_2} & = \dfrac{y - y_2}{m_2} = \dfrac{z - z_2}{n_2} \notag \\ \end{align} \]

则 : $cos \theta = \dfrac{l_1l_2 + m_1m_2 + n_1n_2}{\sqrt{l_1^2 + m_1^2 + n_1^2} \sqrt{l_2^2 + m_2^2 + n_2^2}}$

$L_1 \perp L_2 \Leftrightarrow l_1l_2 + m_1m_2 + n_1n_2 = 0$
$L_1 \parallel L_2 \Leftrightarrow \dfrac{l_1}{l_2} = \dfrac{m_1}{m_2} = \dfrac{n_1}{n_2}$

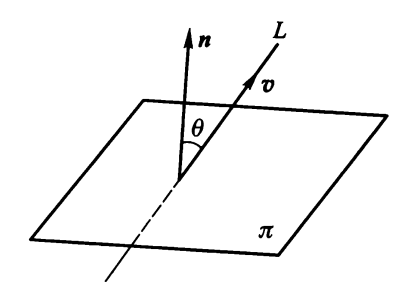
直线与平面的夹角：设平面 $\pi: Ax + By + Cz + D = 0$，其法矢量为 $\bm{n} = A\bm{i} + B\bm{j} + C\bm{k}$；直线 $L: \dfrac{x - x_0}{l} = \dfrac{y - y_0}{m} = \dfrac{z - z_0}{n}$，其方向矢量为 $\bm{v} = l\bm{i} + m\bm{j} + n\bm{k}$。设 $\bm{v}$ 与 $\bm{n}$ 的夹角为 $\theta$，则 $\dfrac{\pi}{2} - \theta$ 或 $\theta - \dfrac{\pi}{2}$ 为 L 与 $\pi$ 的夹角。
- $L \perp \pi \Rightarrow \dfrac{A}{l} = \dfrac{B}{m} = \dfrac{C}{n}$
- $L \parallel \pi \Rightarrow Al + Bm + Cn = 0$

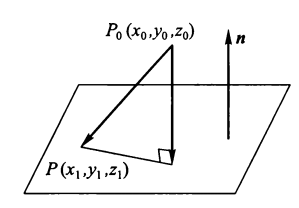
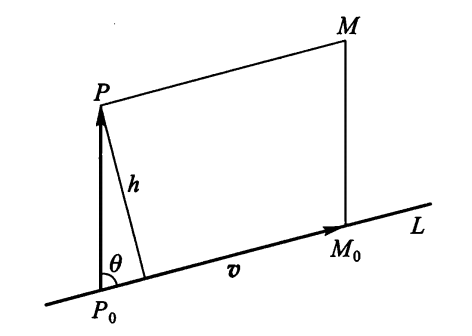
点到直线的距离：已知点 $P(x_1, y_1, z_1)$ 和直线 $L: \dfrac{x - x_0}{l} = \dfrac{y - y_0}{m} = \dfrac{z - z_0}{n}$，求点 P 到直线 L 的距离。

由上图得：

\[ h = |\overrightarrow{P_0P}|\sin(\overrightarrow{P_0P}, \bm{v}) = \dfrac{|\overrightarrow{P_0P} \times \bm{v}|}{|\bm{v}|} \]

直线在平面上的投影直线方程 $\rightarrow$ 分类讨论
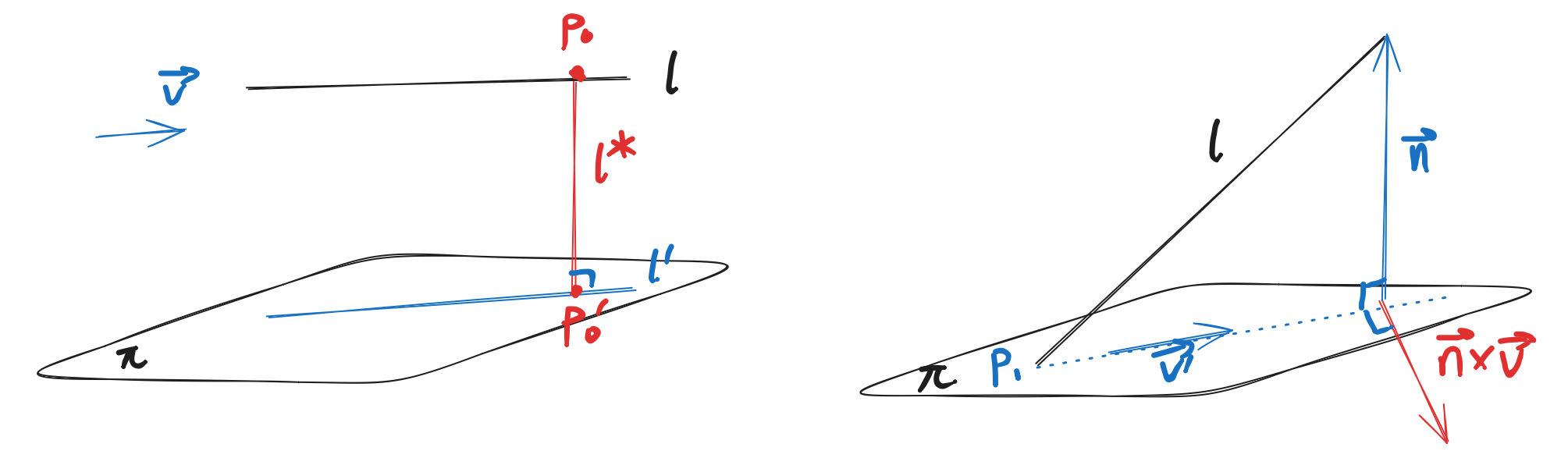
- 直线与平面平行：在直线 l 上取一点 P，过该点作与平面 $\pi$ 垂直的直线 $l^*$，P 在平面上的投影点 $P_0 = l^* \cap \pi$。投影直线的方向向量同原直线，且过 $P_0$，则可求出它的方程。
- 直线与平面相交：设交点为 $P_1$，易知投影直线过该交点。投影直线的方向向量 $\bm{v}' = \bm{n} \times (\bm{n} \times \bm{v}) = (\bm{n} \cdot \bm{v})\bm{n} - |\bm{n}|^2\bm{v}$，其中 $\bm{n}, \bm{v}$ 分别是平面的法向量和直线的方向向量，此时可以求出投影直线的方程了。

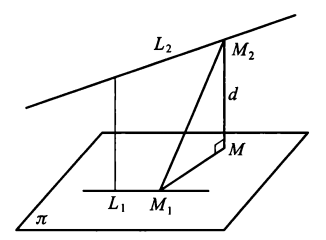
两异面直线的距离：设两异面直线分别为

\[ \begin{align} L_1: \dfrac{x - x_1}{l_1} = \dfrac{y - y_1}{m_1} = \dfrac{z -z_1}{n_1} ,\ \bm{v}_1 = l_1\bm{i} + m_1\bm{j} + n_1\bm{k} \notag \\ L_2: \dfrac{x - x_2}{l_2} = \dfrac{y - y_2}{m_2} = \dfrac{z -z_2}{n_2} ,\ \bm{v}_2 = l_2\bm{i} + m_2\bm{j} + n_2\bm{k} \notag \\ \end{align} \]

过直线 $L_1$ 作平行于 $L_2$ 的平面 $\pi$，那么 $\pi$ 的法向量 $\bm{n} = \bm{v}_1 \times \bm{v}_2$。两异面直线的距离 $d = \dfrac{|\overrightarrow{M_1M_2} \cdot \bm{n}|}{|\bm{n}|}$，即：

\[ d = |(\overrightarrow{M_1M_2})_{\bm{n}}| = \dfrac{|\overrightarrow{M_1M_2} \cdot (\bm{v_1} \times \bm{v_2})|}{|\bm{v_1} \times \bm{v_2}|} \]

平面束方程⚓︎

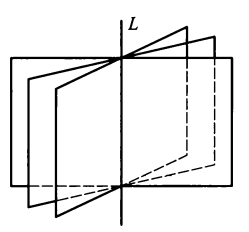
通过一已知直线 L 的平面有无穷多张，这些平面的集合被称为平面束，其中 L 为平面束的轴。

若 $L: \begin{cases}\pi_1: A_1x + B_1y + C_1z + D_1 = 0 \\ \pi_2: A_2x + B_2y + C_2z + D_2 = 0 \end{cases}$，则平面束方程为：

\[ \lambda(A_1x + B_1y + C_1z + D_1) + \mu(A_2x + B_2y + C_2z + D_2) = 0 \]

为了计算的方便，当 $\lambda \ne 0$ 时，令 $\alpha = \dfrac{\mu}{\lambda}$，则平面束方程变成：

\[ A_1x + B_1y + C_1z + D_1 + \alpha(A_2x + B_2y + C_2z + D_2) = 0 \]

注意，该方程无法表示平面 $A_2x + B_2y + C_2z + D = 0$。

小技巧

若题目中要求一个过已知直线的平面时，可以先将直线转化成一般式方程，然后使用平面束方程表示平面。

曲面方程与空间曲线方程⚓︎

曲面方程⚓︎

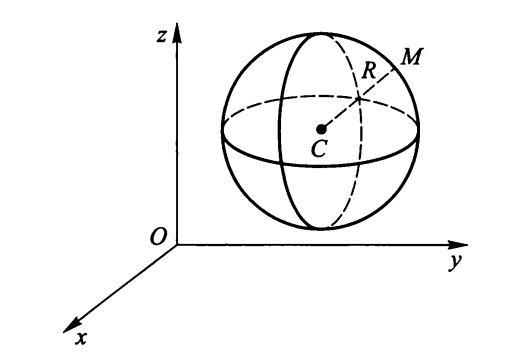
球面方程：$(x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = R^2$

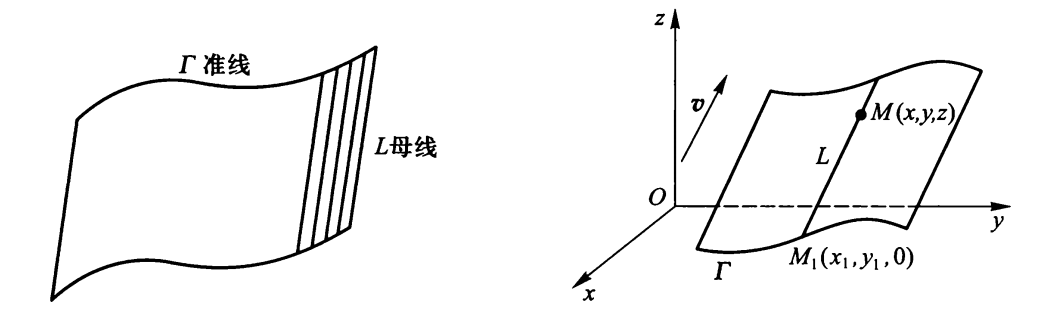
柱面方程 以Oxy平面的曲线$\Gamma: F(x, y) = 0$为准线，母线L的方向矢量为$\bm{v} = a\bm{i} + b\bm{j} + c\bm{k}$的柱面方程为例：先找柱面上任意一点$M(x, y, z)$，再在准线上找一点$M_1(x_1, y_1, 0)$，使得$\overrightarrow{MM_1} \parallel \bm{v}$。然后用$x, y, z$表示$x_1, y_1$，代回准线方程，即可得到柱面方程。

\[ F(x - \dfrac{a}{c}z, y - \dfrac{b}{c}z) = 0 \]

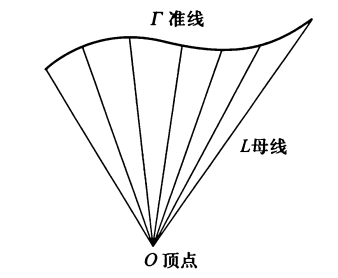
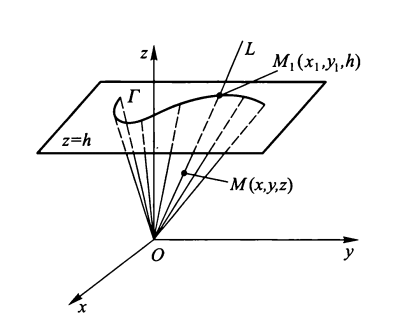
锥面方程 以$z = h(h \ne 0)$平面上的曲线$\Gamma: F(x, y) = 0$为准线，以原点为顶点的锥面方程为例(推导方法同上)

\[ F(\dfrac{h}{z}x, \dfrac{h}{z}y) = 0 \]

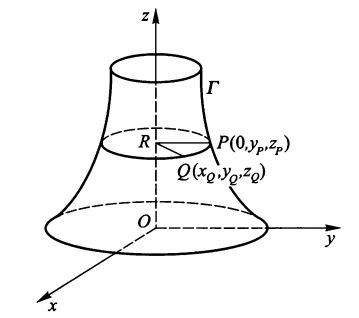
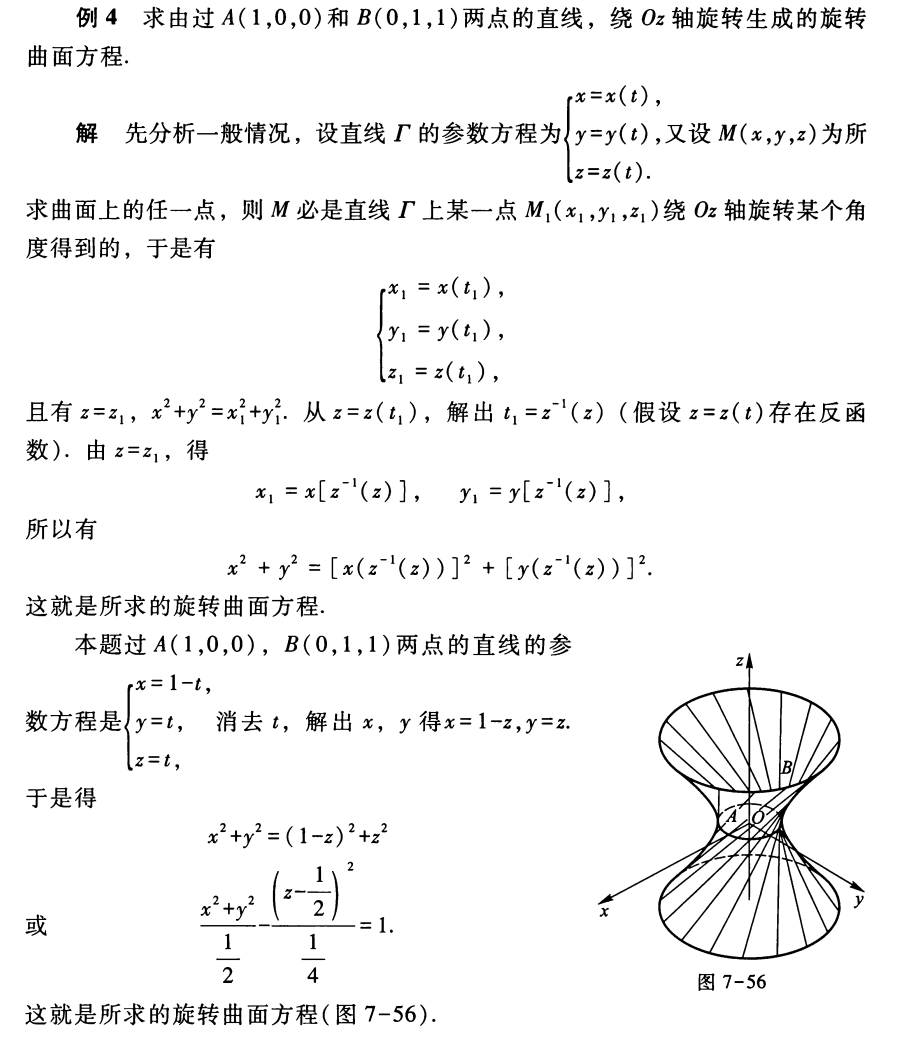
旋转曲面方程：设 $\Gamma$ 是 Oyz 平面上的曲线，方程为 F(y, z) = 0，将该曲线绕 Oz 轴旋转，得到一个以 Oz 轴为轴的旋转曲面，求其方程：

解题思路

取曲线上一点 $P(0, y_P, z_P)$，当曲线绕轴旋转一周后，点 P 的轨迹为一个圆，取圆上任意一点 $Q(x_Q, y_Q, z_Q)$，可得到：

\[ \begin{cases} z_P = z_Q \\ y_P = \pm \sqrt{x_Q^2 + y_Q^2} \end{cases} \]

解得旋转曲面方程为 $F(\pm \sqrt{x^2 + y^2}, z)$

例题

曲线方程⚓︎

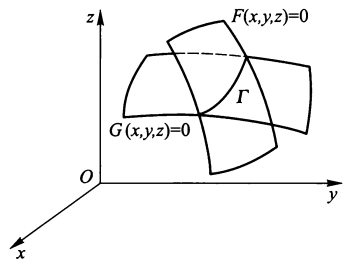
用两曲面交线表示：

\[ \Gamma: \begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases} \]

用参数方程表示：

\[ \Gamma: \begin{cases} x = \varphi(t) \\ y = \psi(t) \\ z = \omega(t) \end{cases} \]

空间曲线在坐标平面上的投影

令空间曲线

\[ \Gamma: \begin{cases} F_1(x, y, z) = 0 \\ F_2(x, y, z) = 0 \end{cases} \]

消去变量 z，得到方程 $\begin{cases}F(x, y) = 0 \\ z = 0 \end{cases}$，这是 $\Gamma$ 在 Oxy 平面上的投影

同理的 $\Gamma$ 在 Oyz 和 Ozx 平面上的投影分别为：

\[ \begin{cases}G(y, z) = 0 \\ x = 0 \end{cases} \quad \begin{cases}H(x, z) = 0 \\ y = 0 \end{cases} \]

更复杂的题型

直线在任意平面上的投影直线空间曲线在任意平面上的投影曲线

设一个过已知直线的平面 $\pi_1$，它与已知平面 $\pi$ 的交线即为要求的投影直线，用一般式 ($\pi, pi_1$ 的平面方程 ) 表示投影直线

可以将投影曲线理解为一个以该曲线为准线的柱体和已知平面的交线，该柱体母线的方向即为已知平面的法向量的方向。然后在空间曲线和投影曲线上各设一个点 $P, P_0$，满足 $\overrightarrow{PP_0} \parallel \bm{n}$，代入已知方程计算求解。

二次曲面⚓︎

注意：这里的图形请务必牢记，因为在后面的积分章节中经常会用到

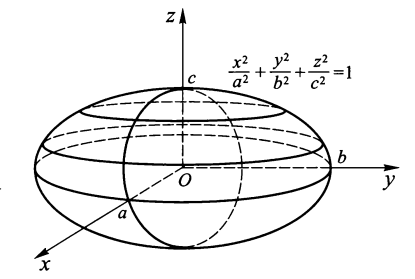
椭球面：$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2} = 1(a > 0, b > 0, c > 0)$

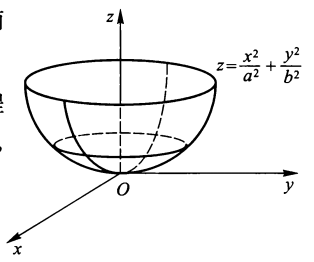
椭圆抛物面：$z = \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}(a > 0, b > 0)$

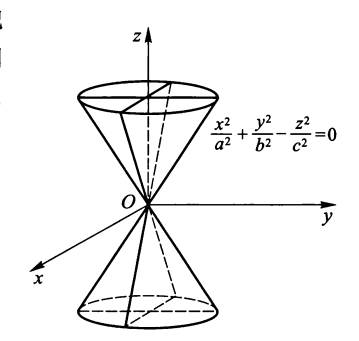
二次锥面：$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2} = 0(a > 0, b > 0, c > 0)$

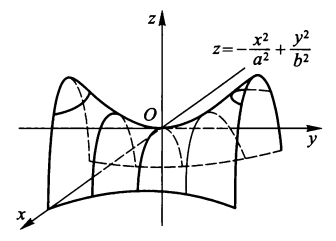
双曲抛物面 ( 马鞍面 )：$z = -\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}$

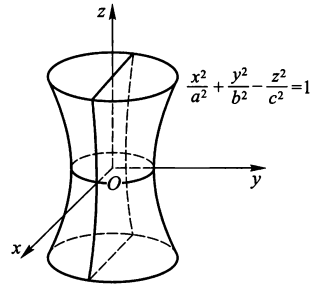
单叶双曲面：$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2} = 1$

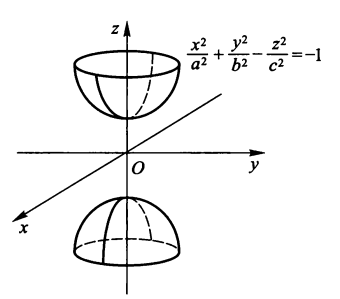
双叶双曲面：$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2} = -1$

评论区

如果大家有什么问题或想法，欢迎在下方留言~

第七章 矢量代数与空间解析几何⚓︎